Energy Cost Optimization for Incorporating Energy Hubs into a Smart Microgrid with RESs, CHP, and EVs
Abstract
1. Introduction
- A description of a new modeling technique for incorporating MECs in an EH that reflects their behavior and interactions with the input and output sources.
- A proposed approach for achieving optimal power flow in an EH by forecasting the energy demand as well as the energy carrier’s cost through an Optimal Load Distribution technique that employs an objective function of load flows in an MEC interconnected network.
- An Energy Management System (EMS) for deploying the method in existing or newly formed SMs and providing an interface with utility operators.
- Validation in an existing Smart Microgrid (SM) of a typical Greek 17-bus low-voltage (LV) distribution network for calculating the Optimal Load Distribution, where results are compared through various operational scenarios and a sensitivity analysis aiming at criteria such as energy cost, total losses, and power generation distribution.
2. Preliminaries
2.1. Smart Microgrids Overview
2.2. Related Work
3. Modeling the Energy Carriers inside an Energy Hub
3.1. Modeling Principles
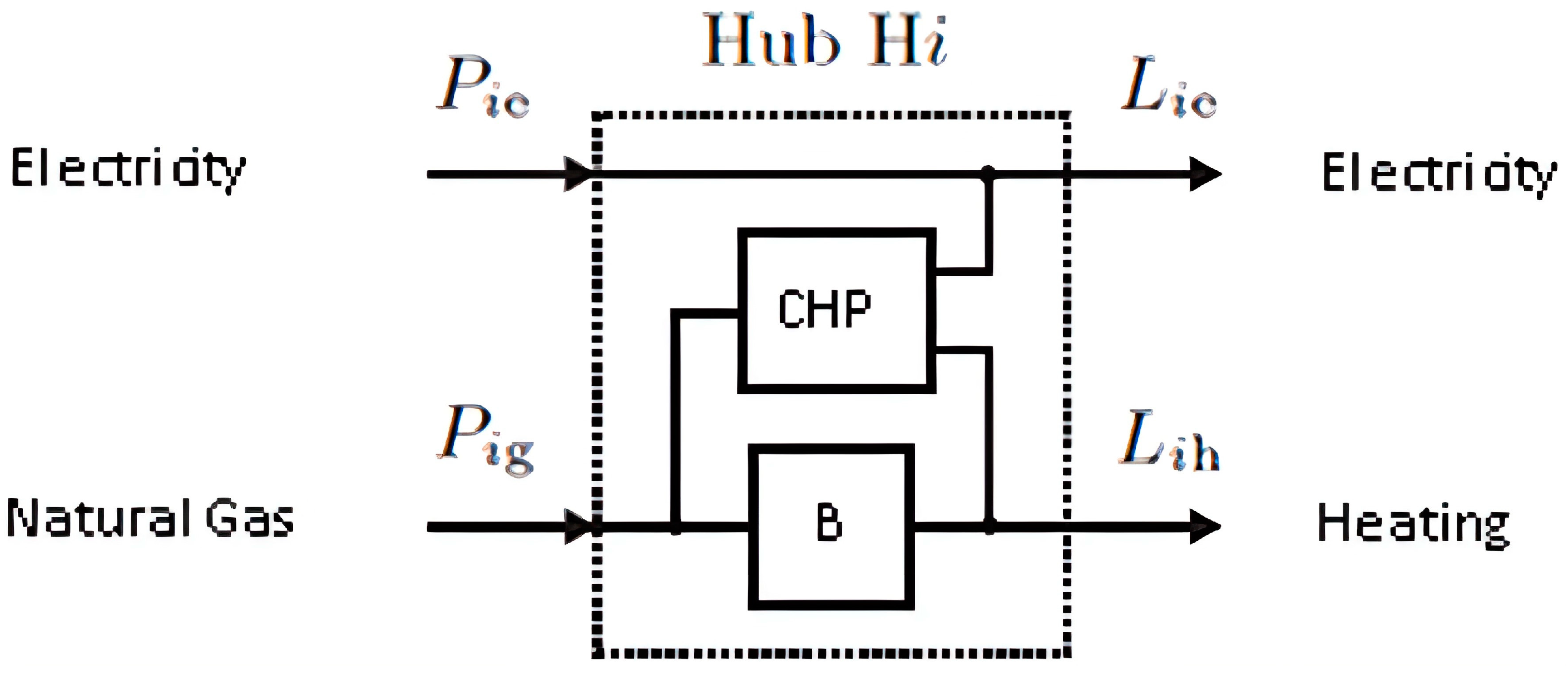
3.2. Energy Hub System Model
4. Proposed Approach for Optimal Load Distribution
4.1. Optimal Power Flow Computation
4.2. Optimal Load Distribution of Energy Carriers with Multiple Energy Sources
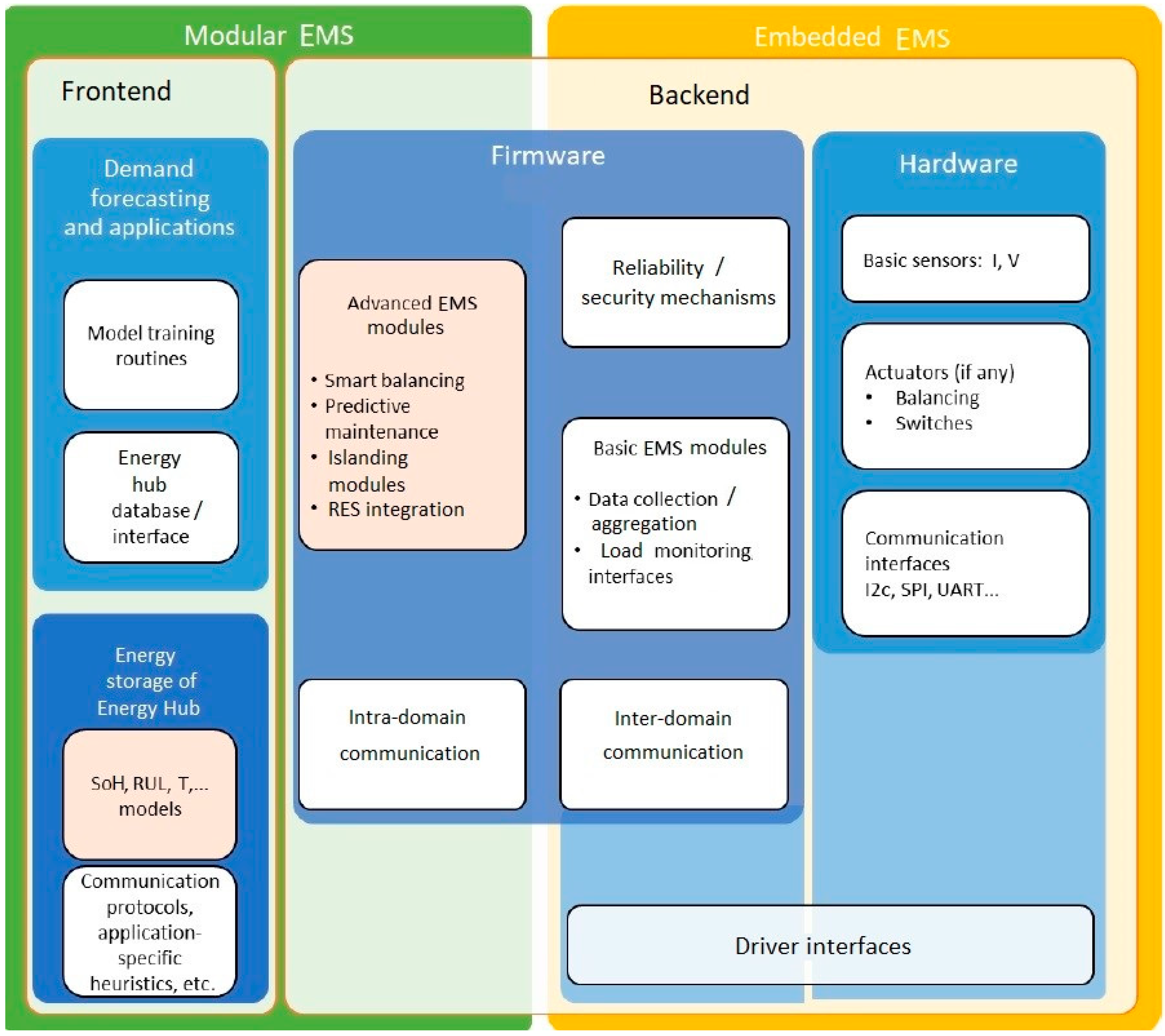
4.3. Energy Management System Integration within the Energy Hub
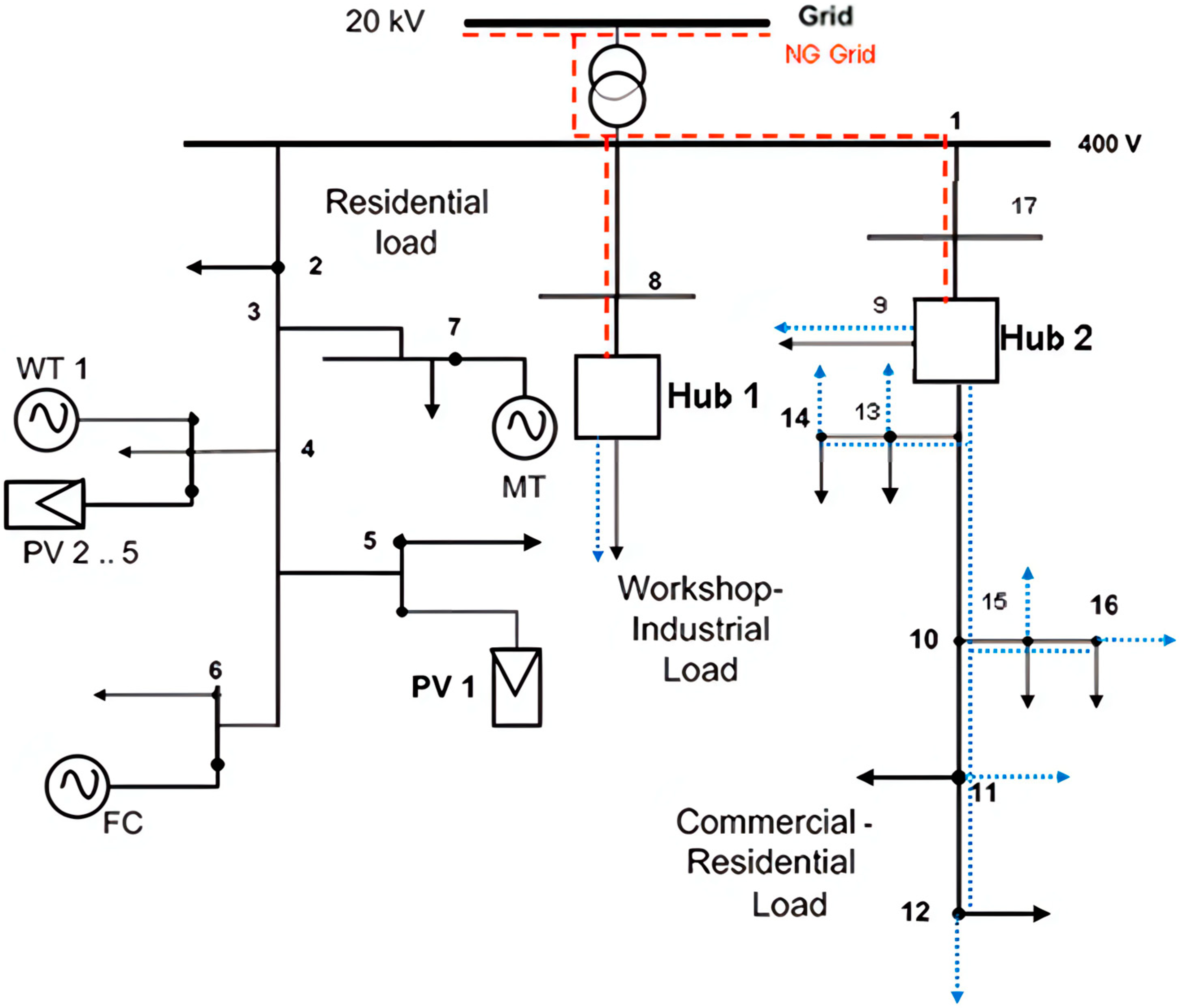
5. Case Study: Energy Hubs in a 17-Bus LV Distribution Network
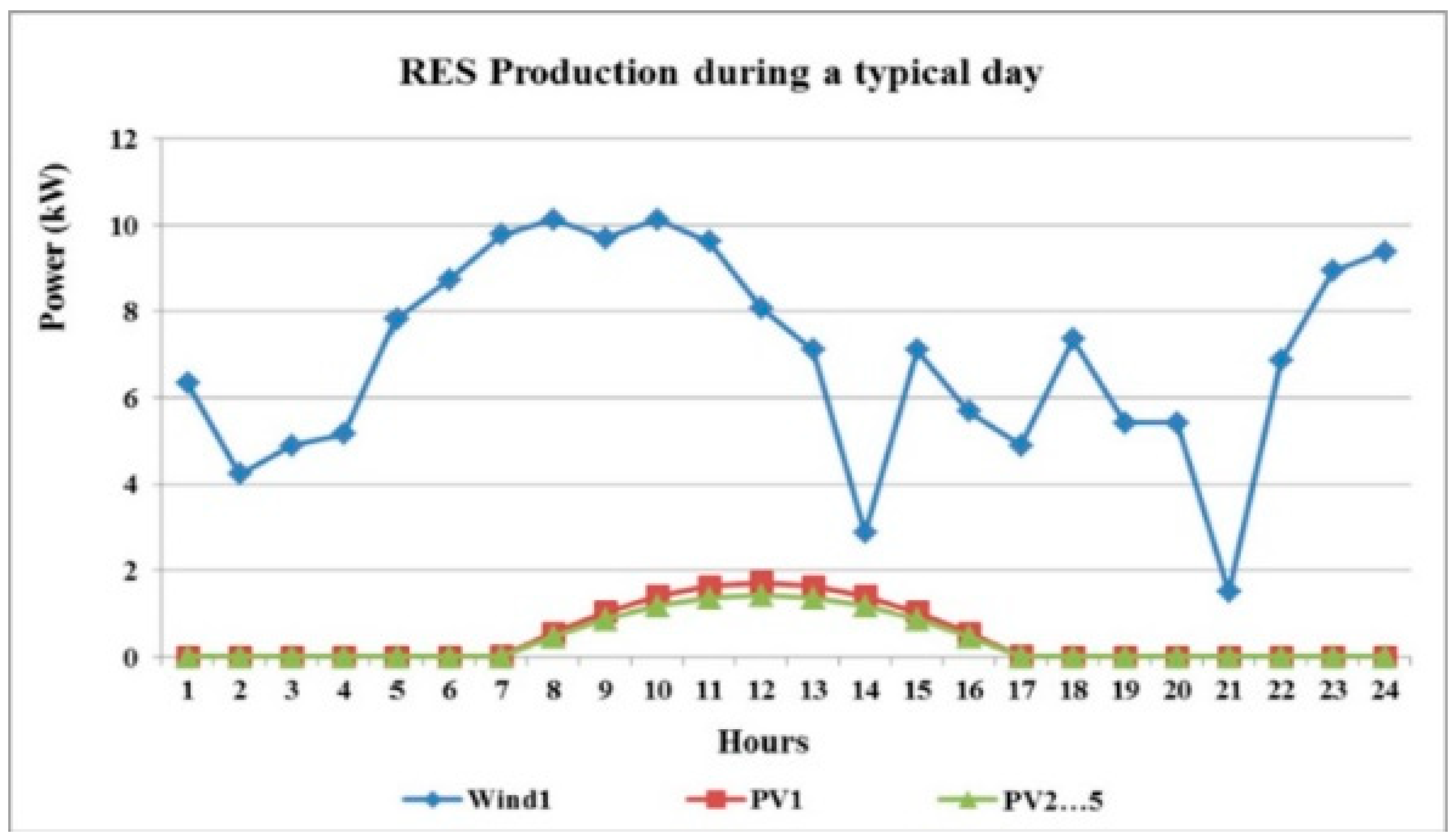
5.1. Data and Assumptions
- ➢
- Each microsource submits a bid for producing electric power, noted as costDG(xi), where xi represents the power output for the i = 1…NDG units as the MT, FC, and boilers. The formula for operation/production costs is expressed as costDG(xi) = ai + bi·xi + ci·x2i. The term ai symbolizes the fixed portion of fuel consumption, including start-up costs if the i-microsource is not utilized during the bidding process, and it is measured in EUR ct/h. The coefficients bi and ci are the variable production costs, expressed in EUR ct/kWh and EUR ct/kWh2, respectively.
- ➢
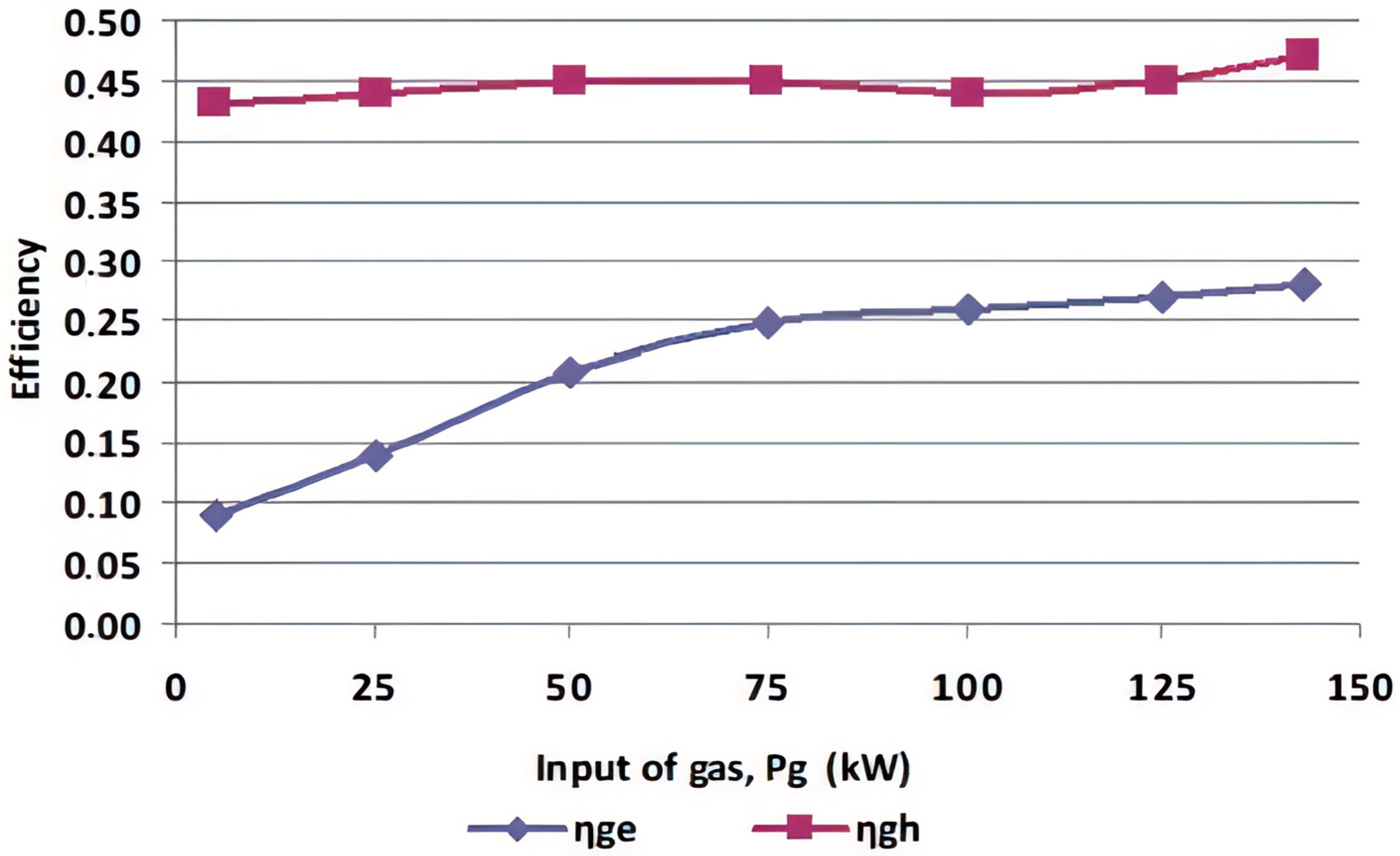
- The output power of the CHP units is dictated by the natural gas input.
- ➢
- The power factor is established at 1 for the PVs and WT, 0.90 for the MT, maintained at 1 for the FC, and set at 0.9 for the CHP units. Additionally, the power factor for the load is assumed to be 0.88.
- ➢
- The calorific value of the input gas, indicated as CV = 0.01115 MWh/Nm3, measures the amount of energy produced from combusting a given volume of gas. In this case, it is calculated based on megawatt-hours (MWh) per normal cubic meter (Nm3) of gas while its cost is assumed to be 0.62 EUR/m3. Hence, the price for each MWh of gas is CostMWh_gas_input = 55.61 EUR/MWh.
- ➢
- The thermal loads are depicted by hourly figures derived from the established district heating network in northern Greece, according to data sourced from [40].
- Scenarios and employed algorithms
- ○
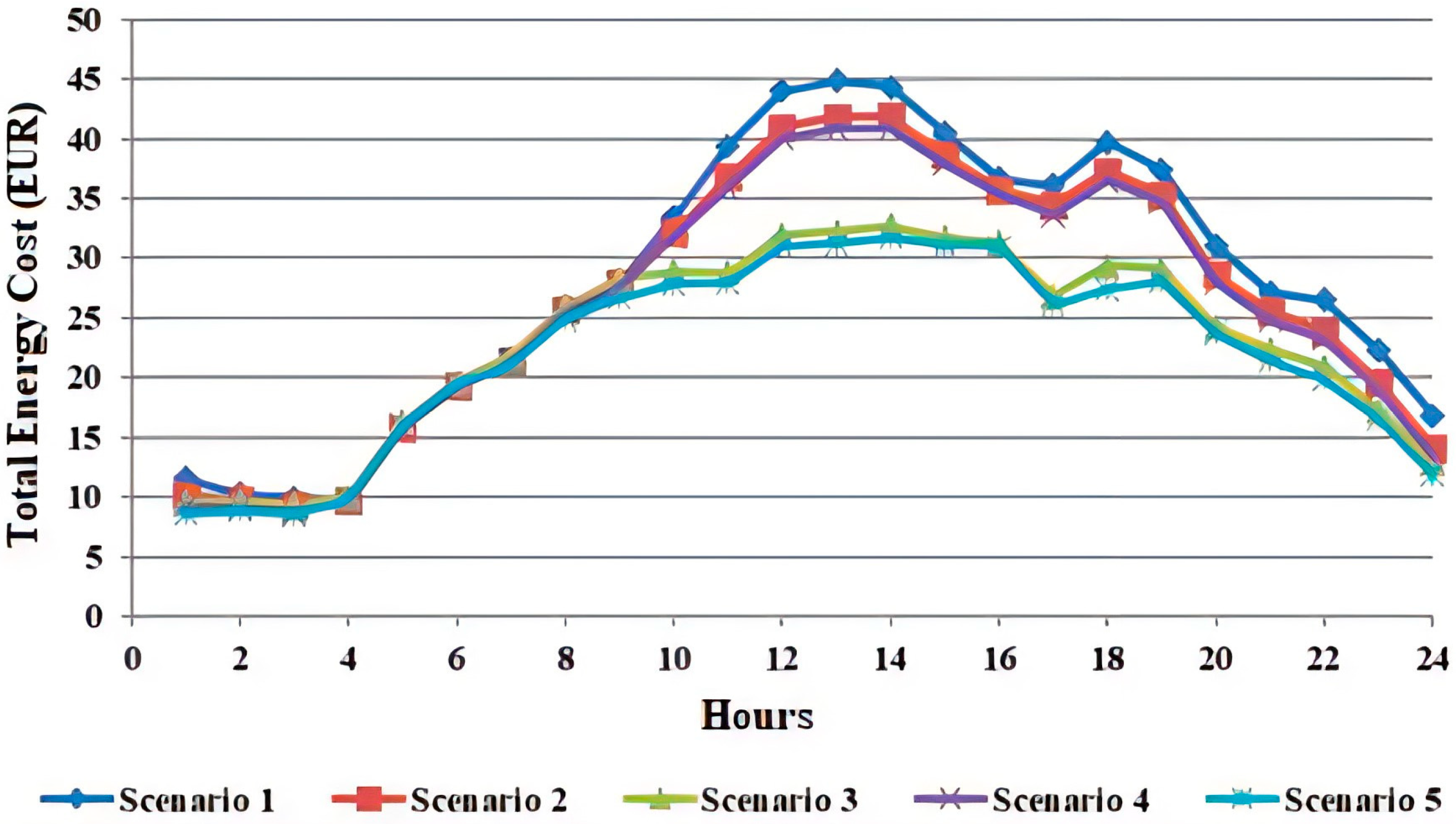
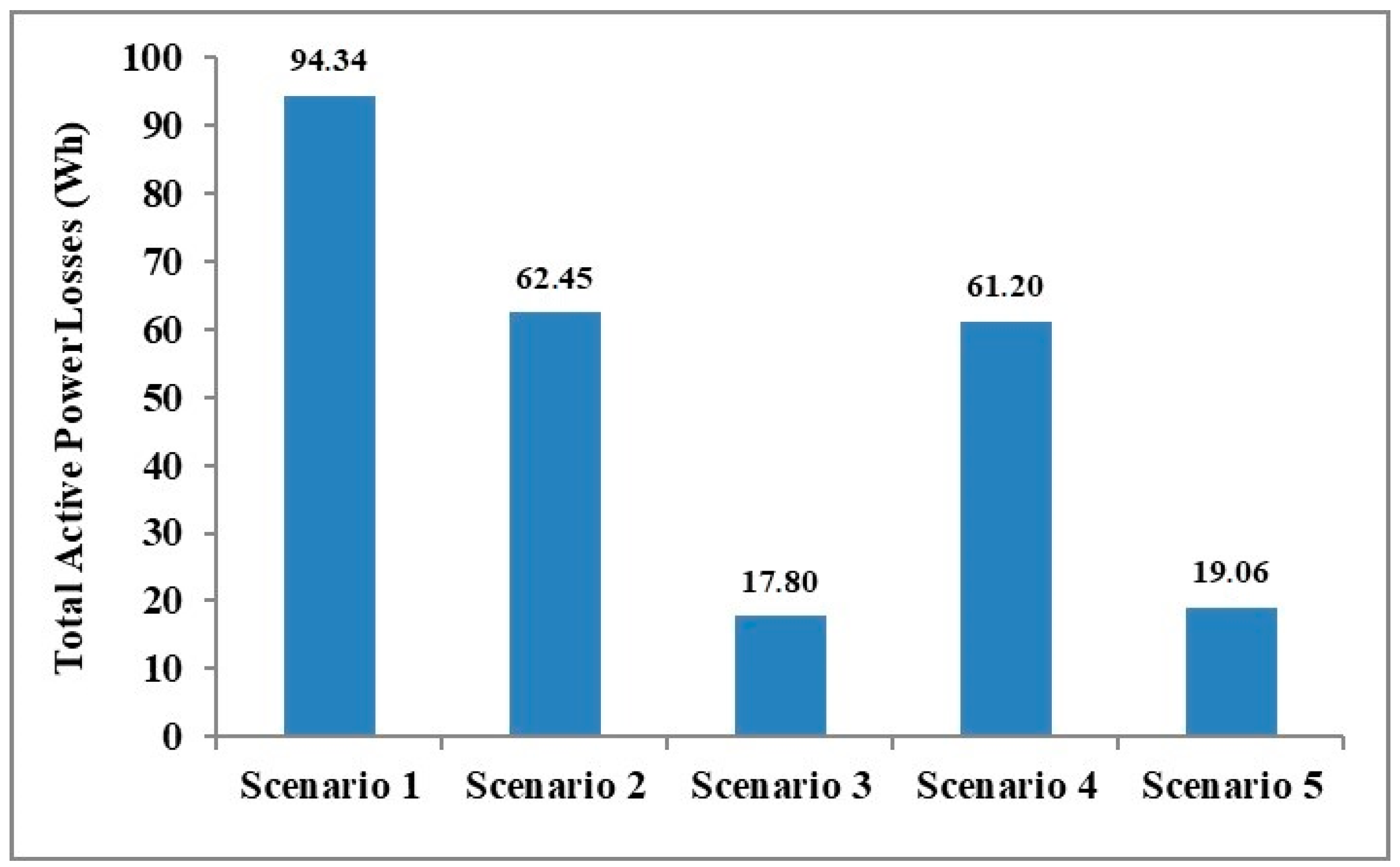
- Scenario 1—No DG units and no CHP systems (No-DG).
- ○
- Scenario 2—DG units operating independently (I-DG) without any CHP systems.
- ○
- Scenario 3—DG units operating independently (I-DG) but with CHP systems.
- ○
- Scenario 4—SM operation without CHP systems.
- ○
- Scenario 5—SM operation including CHP systems (SG-EH) along with Electric Vehicles (EVs) and charging stations.
5.2. Experiments
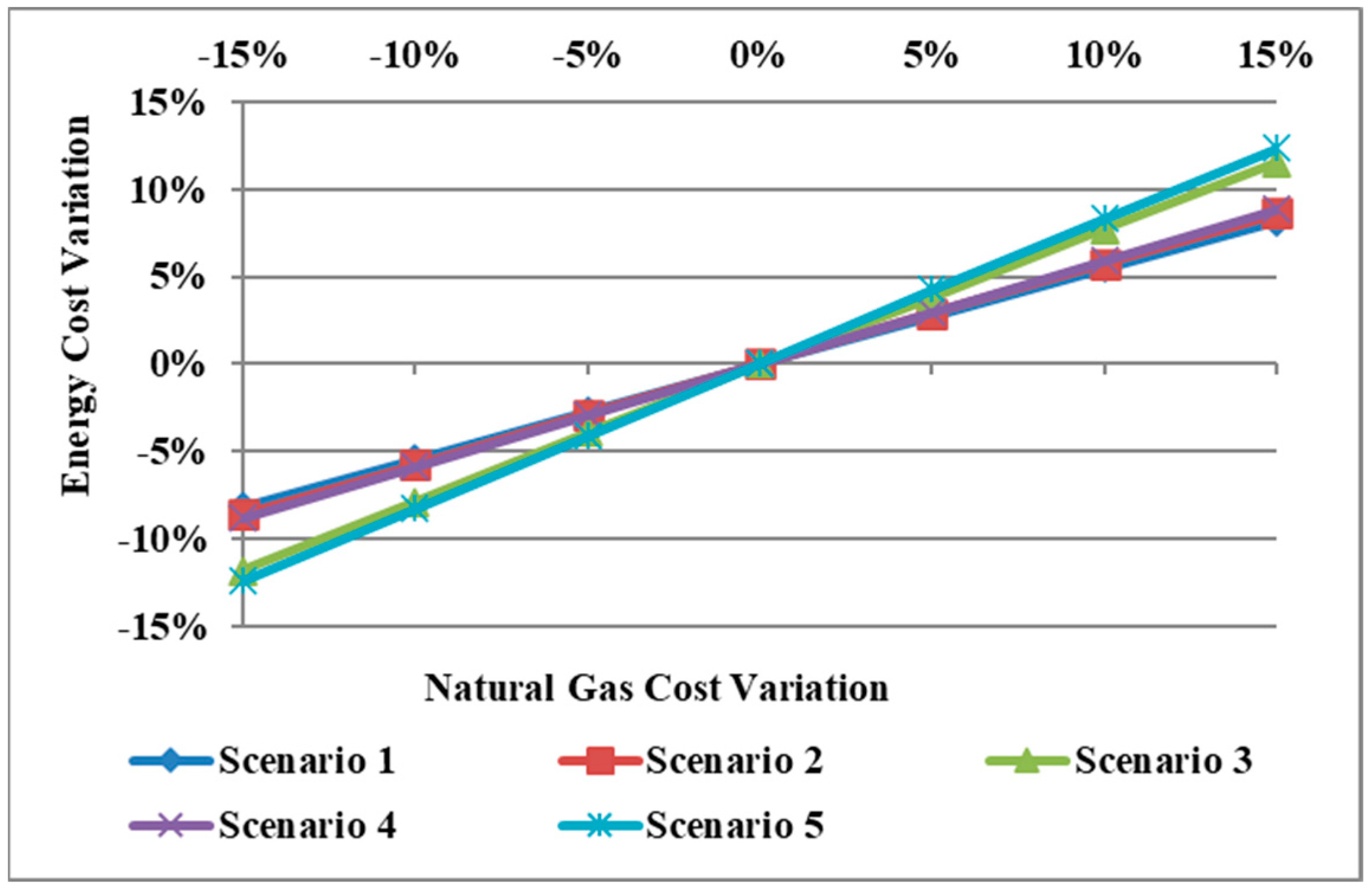
5.3. Sensitivity Analysis
- Electricity Cost Variation
- Natural Gas Cost Variation
- Electrical and Thermal Load Demand Variation
6. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- European Commission. The European Green Deal, Brussels. Available online: https://eur-lex.europa.eu/resource.html?uri=cellar:b828d165-1c22-11ea-8c1f-01aa75ed71a1.0002.02/DOC_1&format=PDF (accessed on 16 May 2024).
- European Commission. Fit for 55: Delivering the EU’s 2030 Climate Target on the Way to Climate Neutrality, Brussels. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:52021DC0550&from=EN (accessed on 16 May 2024).
- Li, C.; Wang, N.; Wang, Z.; Dou, X.; Zhang, Y.; Yang, Z.; Maréchal, F.; Wang, L.; Yang, Y. Energy hub-based optimal planning framework for user-level integrated energy systems: Considering synergistic effects under multiple uncertainties. Appl. Energy 2022, 307, 118099. [Google Scholar] [CrossRef]
- Geidl, M.; Koeppel, G.; Favre-Perrod, P.; Klöckl, B.; Andersson, G.; Fröhlich, K. Energy Hubs for the Future. IEEE Power Energy Mag. 2007, 5, 24–30. [Google Scholar] [CrossRef]
- Geidl, M.; Andersson, G. Optimal Power Flow of Multiple Energy Carriers. IEEE Trans. Power Syst. 2007, 22, 145–155. [Google Scholar] [CrossRef]
- Mohammadi, M.; Noorollahi, Y.; Mohammadi-Ivatloo, B.; Yousefi, H. Energy hub: From a model to a concept—A review. Renew. Sustain. Energy Rev. 2017, 80, 1512–1527. [Google Scholar] [CrossRef]
- Papadimitriou, C.N.; Anastasiadis, G.A.; Psomopoulos, C.S.; Vokas, G. Demand Response schemes in Energy Hubs: A comparison study. Energy Procedia 2019, 157, 939–944. [Google Scholar] [CrossRef]
- Hatziargyriou, N.; Asano, H.; Iravani, R.; Marnay, C. Microgrids. IEEE Power Energy Mag. 2007, 5, 78–94. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Vasquez, J.C.; Savaghebi, M.; Castilla, M. Hierarchical control of droop-controlled AC and DC microgrids—A general approach toward standardization. IEEE Trans. Ind. Electron. 2013, 60, 1254–1262. [Google Scholar] [CrossRef]
- Wang, S.; Wang, X.; Li, X.; Liu, X. Optimal energy management of microgrids with renewable energy and energy storage under uncertainty. Energy 2016, 96, 160–169. [Google Scholar]
- Lasseter, R.H.; Akhil, A.A.; Marnay, C.; Stephens, J.; Dagle, J.E.; Guttromson, R.; Meliopoulous, A.; Yinger, R.; Eto, J.; Piagi, P. Integration of distributed energy resources: The CERTS microgrid concept. Electr. J. 2007, 20, 26–38. [Google Scholar]
- Mohammadi, M.; Noorollahi, Y.; Mohammadi-Ivatloo, B. An Introduction to Smart Energy Systems and Definition of Smart Energy Hubs. In Operation, Planning, and Analysis of Energy Storage Systems in Smart Energy Hubs; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Sari, A.; Lekidis, A.; Butun, I. Industrial Networks and IIoT: Now and Future Trends. Industrial IoT: Challenges, Design Principles, Applications, and Security; Springer Nature: Cham, Switzerland, 2020; pp. 3–55. [Google Scholar]
- Olivares, D.E.; Mehrizi-Sani, A.; Lopes, L.A. Smart microgrids: A review of technologies, applications and operational challenges. Renew. Sustain. Energy Rev. 2014, 51, 975–993. [Google Scholar]
- Anastasiadis, A.G.; Vokas, G.A. Economic benefits of Smart Microgrids with penetration of DER and mCHP units for non-interconnected islands. Renew. Energy 2019, 142, 478–486. [Google Scholar] [CrossRef]
- Hatziargyriou, N.D.; Anastasiadis, G.A.; Vasiljevska, J.; Tsikalakis, A.G. Quantification of Economic, Environmental and Operational Benefits of Microgrids. In Proceedings of the IEEE PowerTech, Bucharest, Romania, 28 June–2 July 2009; p. 512. [Google Scholar] [CrossRef]
- Anastasiadis, A.G.; Konstantinopoulos, S.; Kondylis, G.P.; Vokas, G.A. Electric vehicle charging in stochastic smart microgrid operation with fuel cell and RES units. Int. J. Hydrogen Energy 2017, 42, 8242–8254. [Google Scholar] [CrossRef]
- Mohammadi, M.; Noorollahi, Y.; Mohammadi-ivatloo, B.; Hosseinzadeh, M.; Yousefi, H.; Khorasani, S.T. Optimal management of energy hubs and smart energy hubs—A review. Renew. Sustain. Energy Rev. 2018, 89, 33–50. [Google Scholar] [CrossRef]
- Maroufmashat, A.; Taqvi, S.T.; Miragha, A.; Fowler, M.; Elkamel, A. Modeling and optimization of energy hubs: A comprehensive review. Inventions 2019, 4, 50. [Google Scholar] [CrossRef]
- Javadi, M.S.; Lotfi, M.; Nezhad, A.E.; Anvari-Moghaddam, A.; Guerrero, J.M.; Catalão, J.P. Optimal operation of energy hubs considering uncertainties and different time resolutions. IEEE Trans. Ind. Appl. 2020, 56, 5543–5552. [Google Scholar] [CrossRef]
- Kienzle, F.; Ahčin, P.; Andersson, G. Valuing investments in multi-energy conversion, storage, and demand-side management systems under uncertainty. IEEE Trans. Sustain. Energy 2011, 2, 194–202. [Google Scholar] [CrossRef]
- Unsihuay-Vila, C.; Marangon-Lima, J.W.; de Souza, A.C.Z.; Perez-Arriaga, I.J.; Balestrassi, P.P. A model to long-term, multiarea, multistage, and integrated expansion planning of electricity and natural gas systems. IEEE Trans. Power Syst. 2010, 25, 1154–1168. [Google Scholar] [CrossRef]
- Ji-Yuan, F.; Lan, Z. Real-time economic dispatch with line flow and emission constraints using quadratic programming. IEEE Trans. Power Syst. 1998, 13, 320–325. [Google Scholar] [CrossRef]
- Farag, A.; Al-Baiyat, S.; Cheng, T.C. Economic load dispatch multiobjective optimization procedures using linear programming techniques. IEEE Trans. Power Syst. 1995, 10, 731–738. [Google Scholar] [CrossRef]
- Dhillon, J.S.; Parti, S.C.; Kothari, D.P. Stochastic economic emission load dispatch. Electric Power Syst. Res. 1993, 26, 186–197. [Google Scholar] [CrossRef]
- Yokoyama, R.; Bae, S.H.; Morita, T.; Sasaki, H. Multiobjective generation dispatch based on probability security criteria. IEEE Trans. Power Syst. 1988, 3, 317–324. [Google Scholar] [CrossRef]
- Zia, M.F.; Elbouchikhi, E.; Benbouzid, M. Microgrids energy management systems: A critical review on methods, solutions, and prospects. Appl. Energy 2018, 222, 1033–1055. [Google Scholar] [CrossRef]
- Sadeghi, A.R.; Wachsmann, C.; Waidner, M. Security and privacy challenges in industrial internet of things. In Proceedings of the 52nd Annual Design Automation Conference, San Francisco, CA, USA, 7–11 June 2015; pp. 1–6. [Google Scholar]
- Momoh, J.A.; Koessler, R.J.; Bond, M.S.; Stott, B.; Sun, D.; Papalexopoulos, A.; Ristanovic, P. Challenges to Optimal Power Flow. IEEE Trans. Power Syst. 1997, 12, 444–447. [Google Scholar] [CrossRef]
- Huneault, M.; Galiana, F.D. A Survey of the Optimal Power Flow Literature. IEEE Trans. Power Syst. 1991, 6, 762–770. [Google Scholar] [CrossRef]
- Kuhn, H.W.; Tucker, A.W. Nonlinear programming. In Proceedings of the 2nd Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 31 July–12 August 1951. [Google Scholar]
- Horst, Ρ.; Pardalos, P.M. Handbook of Global Optimization (Nonconvex Optimization and Its Applications, 2), 1995th ed.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2002. [Google Scholar]
- Pardalos, P.M.; Resende, M.G.C. Handbook of Applied Optimization; Oxford University Press: Oxford, UK, 2002; ISBN 0-19-512594-0. [Google Scholar]
- Lekidis, A.; Papageorgiou, E.I. Edge-based short-term energy demand prediction. Energies 2023, 16, 5435. [Google Scholar] [CrossRef]
- Carpentier, J. Optimal power flows. Int. J. Electr. Power Energy Syst. 1979, 1, 3–15. [Google Scholar] [CrossRef]
- Wood Allen, J.; Wollenberg Bruce, F. Power Generation, Operation and Control, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1996; p. 104. [Google Scholar]
- Costa, V.M.; Martins, N.; Pereira, J.L.R. Developments in the Newton Raphson Power Flow Formulation Based on Current Injections. IEEE Trans. Power Syst. 1999, 14, 1320–1326. [Google Scholar] [CrossRef]
- Katiraei, F.; Iravani, M.R.; Lehn, P.W. Micro-grid autonomous operation during and subsequent to islanding process. IEEE Trans. Power Deliv. 2005, 20, 248–257. [Google Scholar] [CrossRef]
- Schaffer, M.; Veit, M.; Marszal-Pomianowska, A.; Frandsen, M.; Pomianowski, M.Z.; Dichmann, E.; Sørensen, C.G.; Kragh, J. Dataset of smart heat and water meter data with accompanying building characteristics. Data Brief 2024, 52, 109964. [Google Scholar] [CrossRef]
- Hellenic Public Power Corporation, S.A. Available online: www.dei.gr (accessed on 16 May 2024).
- Lekidis, A.; Papageorgiou, I.E. Risk Assessment Method for 5G-oriented DLMS/COSEM Communications. In Proceedings of the ΙΕΕΕ Conference on Standards for Communications and Networking (CSCN), Munich, Germany, 6–8 November 2023. [Google Scholar]
- dos Santos Coelho, L.; Mariani, V.C. An improved harmony search algorithm for power economic load dispatch. Energy Convers. Manag. 2009, 50, 2522–2526. [Google Scholar] [CrossRef]








| Units | Min. Capacity [kW] | Max. Capacity [kW] | ai [EUR ct/h] | bi [EUR ct/kWh] | ci [EUR ct/kWh2] |
|---|---|---|---|---|---|
| MT | 6 | 30 | 0.01 | 4.37 | 0.01 |
| FC | 3 | 30 | 0.8415 | 2.41 | 0.033 |
| WT | 0 | 15 | 0 | 0 | 0 |
| PV1 | 0 | 3 | 0 | 0 | 0 |
| PV2…PV5 | 0 | 2.5 | 0 | 0 | 0 |
| CHP | 10 | 286 | 10 | 3.738 | 0 |
| Boiler | 0 | 80 | 0.001 | 5.098 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anastasiadis, A.G.; Lekidis, A.; Pierros, I.; Polyzakis, A.; Vokas, G.A.; Papageorgiou, E.I. Energy Cost Optimization for Incorporating Energy Hubs into a Smart Microgrid with RESs, CHP, and EVs. Energies 2024, 17, 2827. https://doi.org/10.3390/en17122827
Anastasiadis AG, Lekidis A, Pierros I, Polyzakis A, Vokas GA, Papageorgiou EI. Energy Cost Optimization for Incorporating Energy Hubs into a Smart Microgrid with RESs, CHP, and EVs. Energies. 2024; 17(12):2827. https://doi.org/10.3390/en17122827
Chicago/Turabian StyleAnastasiadis, Anestis G., Alexios Lekidis, Ioannis Pierros, Apostolos Polyzakis, Georgios A. Vokas, and Elpiniki I. Papageorgiou. 2024. "Energy Cost Optimization for Incorporating Energy Hubs into a Smart Microgrid with RESs, CHP, and EVs" Energies 17, no. 12: 2827. https://doi.org/10.3390/en17122827
APA StyleAnastasiadis, A. G., Lekidis, A., Pierros, I., Polyzakis, A., Vokas, G. A., & Papageorgiou, E. I. (2024). Energy Cost Optimization for Incorporating Energy Hubs into a Smart Microgrid with RESs, CHP, and EVs. Energies, 17(12), 2827. https://doi.org/10.3390/en17122827







