Evaluation of Film Cooling Adiabatic Effectiveness and Net Heat Flux Reduction on a Flat Plate Using Scale-Adaptive Simulation and Stress-Blended Eddy Simulation Approaches

Abstract

The use of film cooling is crucial to avoid high metal temperatures in gas turbine applications, thus ensuring a high lifetime for vanes and blades. The complex turbulent mixing process between the coolant and the main flow requires an accurate numerical prediction to correctly estimate the impact of ejection conditions on the cooling performance. Recent developments in numerical models aim at using hybrid approaches that combine high precision with low computational cost. This paper is focused on the numerical simulation of a cylindrical film cooling hole that operates at a unitary blowing ratio, with a hot gas Mach number of ${\mathit{Ma}}_m$ = 0.6, while the coolant is characterized by plenum conditions (${\mathit{Ma}}_c$ = 0). The adopted numerical approach is the Stress-Blended Eddy Simulation model (SBES), which is a blend between a Reynolds-Averaged Navier–Stokes approach and a modeled Large Eddy Simulation based on the local flow and mesh characteristics. The purpose of this paper is to investigate the ability of the hybrid model to capture the complex mixing between the coolant and the main flow. The cooling performance of the hole is quantified through the film cooling effectiveness, the Net Heat Flux Reduction (NHFR), and the discharge coefficient $C_D$ calculation. Numerical results are compared both with the experimental data obtained by the University of Karlsruhe during the EU-funded TATEF2 project and with a Scale Adaptive Simulation (SAS) run on the same computational grid. The use of ${\lambda }_2$ profiles extracted from the flow field allows for isolating the main vortical structures such as horseshoe vortices, counter-rotating vortex pairs (e.g., kidney vortices), Kelvin–Helmholtz instabilities, and hairpin vortices. Eventually, the contribution of the unsteady phenomena occurring at the hole exit section is quantified through Proper Orthogonal Decomposition (POD) and Spectral Proper Orthogonal Decomposition methods (SPOD).

1. Introduction

Film cooling is considered a key technology in gas turbine applications. The coolant ejected from the holes generates a thin layer over the blade profile that shields it from the hot flow. This mechanism allows for increasing the turbine inlet temperature, thus improving the thermodynamic efficiency of the turbines. The investigation of the coolant performance of film holes is widely faced by the scientific community, with both experimental tests and numerical simulations. Early studies analyzed the impact of the operating conditions (e.g., blowing ratio, density ratio, cross-flow conditions) on the film cooling performance [1,2,3,4,5]. These studies demonstrated that the jet lift-off increases at higher blowing and density ratios, thus producing a higher penetration of the coolant into the main flow and penalizing the coolant coverage on the blade profile. The hole geometry is another important parameter affecting the film cooling performance, and several publications proved that a diffuser-shaped exit portion of the cooling hole performs better than the cylindrical shape [6,7].

Concerning the numerical approaches, the scientific community often struggles with the limitation of Reynolds-Averaged Navier–Stokes (RANS) methods in predicting the coolant mixing with the main flow, which typically results in an overestimation of the coolant coverage, especially at remarkable distances from the hole exit section. This topic was discussed by Kohli and Bogard [8] and by Jones et al. [9]. However, the latter acknowledged a strong agreement in the velocity field prediction of RANS models if compared with PIV experimental measurements. Despite their weaknesses, RANS approaches are still preferred for optimization purposes, thanks to their affordable computational effort [10,11,12].

Moreover, film cooling performance is mostly governed by both local pressure fluctuations and the unsteady mixing between the main flow and the coolant, both of them caused by component interaction [13]. The effect of unsteadiness on a film cooling application was discussed by Rosafio et al. [14], who used a URANS approach to investigate the effect of pulsations on the generation and propagation of the vortical structure produced during the coolant ejection from a cylindrical film hole. Rosafio et al. [15] used the Scale Adaptive Simulation model to estimate the cooling performance of the same film hole, improving the numerical accuracy in the prediction of the flow field. Recent developments in high-fidelity numerical models led to the implementation of hybrid RANS-LES approaches, such as the SBES model introduced by Menter [16]. The use of SBES in discrete film cooling applications was proposed by Xia et al. [17], who investigated the combination with the Flamelet-Generated Manifold combustion model to obtain an accurate simulation of the turbulent mixing and reaction processes between the free stream and the cooling flow. Ravelli and Barigozzi [18] instead focused on the unsteadiness generated by the jet–mainstream interaction in the pressure side film cooling of a turbine vane.

The current work is focused on the numerical investigation of the cooling performance of a cylindrical film hole under typical gas turbine operating conditions using the SBES model. Moreover, the SAS simulation proposed by Rosafio et al. [15] is post-processed further to calculate the NHFR, and an extensive comparison between the SBES and SAS results is presented. The two numerical closures are chosen to overcome the limits of traditional RANS approaches in predicting the correct mixing in film cooling applications since they offer an intermediate solution toward LES with an affordable computational time. The two approaches are tested on the same computational grid using the same operating conditions to provide a fair comparison between the two numerical models. Results highlight the difference in the accuracy of a hybrid RANS-LES model when compared with a Scale Adaptive model in film cooling applications. Aero-thermal performance was estimated by calculating the adiabatic film cooling effectiveness ${\eta }_{aw}$, the Net Heat Flux Reduction, and the hole discharge coefficient. Numerical results were compared with experiments obtained at the University of Karlsruhe on the same test case. Moreover, the main phenomena that arise at the hole exit section caused by the interaction between the coolant and the main flow, such as the fluid mixing or the traveling mechanism of vortical structures, are studied with the ${\lambda }_2$ iso-surfaces. Finally, the unsteady fluctuation of the flow field was processed using both the Proper Orthogonal Decomposition and the Spectral Proper Orthogonal Decomposition techniques. These instruments were crucial in identifying the main modes of the turbulent phenomena and visualizing them in the spatial and frequency domain.

2. Test Case

In the current work, the commercial solver ANSYS FLUENT^™ (2020R2) is used to run an SBES numerical analysis of a cylindrical film cooling hole that operates at realistic operating conditions. The hole geometry is characterized by $\alpha =30deg$ as the inclination angle, a diameter equal to D = 5 mm, and a length equal to L/D = 6. The numerical domain (Figure 1) reproduces the experimental test rig used by Christian Saumweber [19] in the experimental campaign held at the University of Karlsruhe. The coolant total pressure ${\mathit{P}}_c^0$ and the total temperature ${\mathit{T}}_c^0$ are imposed on the two symmetrical coolant inlets to guarantee ${\mathit{Ma}}_c=0$ inside the plenum. The main flow domain is instead characterized by an overall length of 47D, 16 of which represent the entry length from the inlet of the hot gas to the hole exit section. This entry length ensures the complete development of the wall boundary layer. Periodic conditions are applied on the main flow lateral faces to consider the effect of surrounding holes with a lateral pitch of 4D. Finally, the height of the main flow region was chosen to be equal to 8D to avoid any influence of the top wall on the interaction between the coolant and the hot gas.

The hole is fed by cooling air at plenum conditions (${\mathit{Ma}}_c$ = 0) and discharges the cooling jet into a subsonic main flow (${\mathit{Ma}}_m$ = 0.6) at a unitary blowing ratio (BR).

Table 1. Boundary conditions.

Main flow total pressure	1.26	[bar]
Main flow total temperature	575	[K]
Main flow Reynolds number	3 × ${10}^4$	[-]
Main flow Mach number	0.6	[-]
Coolant total pressure	1.28	[bar]
Coolant total temperature	300	[K]
Coolant Mach number	0	[-]
Nominal blowing ratio	1	[-]
Wall temperature	275	[K]
Numerical sampling frequency	${10}^6$	[Hz]

resumes the operating conditions of the test case analyzed.

Numerical results are compared with experimental measurements in terms of laterally averaged adiabatic effectiveness, laterally averaged NHFR, and hole discharge coefficient. The cooling effectiveness $\eta$ is the primary parameter used to quantify the performance of a cooling hole since it estimates the reduction of the hot gas temperature near the wall. Film cooling effectiveness is computed as reported in Equation (1), where ${\mathit{T}}_{aw}$ is the adiabatic wall temperature, which is typically considered to be the driving temperature for heat transfer into the wall.

$$\eta =\frac{T_{aw}-T_{rec,m}}{T_c^0-T_{rec,m}}$$

(1)

The value of ${\mathit{T}}_{rec,m}$, which is the recovery hot gas temperature, is estimated using Equation (2).

$$T_{rec,m}=T_m^0\frac{1+P{r}^{0.33}\frac{k-1}{2}M{a}_{is}^2}{1+\frac{k-1}{2}M{a}_{is}^2}$$

(2)

${\mathit{T}}_m^0$ and ${\mathit{T}}_c^0$ indicate the main flow and the coolant total temperature, respectively, while ${\mathit{Ma}}_{is}$ is the isentropic Mach number. Apart from the reduction in wall temperature, film cooling is also responsible for an alteration in the local heat transfer coefficient since the main flow boundary layer is disturbed by the interaction with the coolant jet. The actual heat transfer coefficient ${\mathit{h}}_f$ is thus normalized by a reference heat transfer coefficient, which is calculated using an equivalent plate without film cooling. An increase in $h_f$/$h_0$ reduces the cooling performance, vanishing the benefit of a reduced wall temperature. The NHFR was in fact introduced by Sen et al. [20] to estimate the overall film cooling performance combining both the adiabatic film cooling effectiveness $\eta$ and the heat transfer ratio $h_f$/$h_0$ (Equation (3)).

$$\overline{NHFR}=1-\frac{\overline{h_f}}{h_0}(1-\overline{\eta \theta )}+\frac{\overline{h_f^{\prime }{\eta }^{\prime }}}{h_0\theta }$$

(3)

The heat transfer coefficient ${\mathit{h}}_0$ refers to the flat plate conditions without film cooling and is calculated according to the correlation by Kays et al. [21] for the turbulent boundary layer reported in Equation (4).

$$h_0={\rho }_m·U_m·c_{p,m}·0.0287·R{e}_m^{-0.2}·P{r}_m^{-0.4}·{\left(1-{\left(\frac{\xi }{X}\right)}^{0.9}\right)}^{-1/9}·{\left(\frac{T_w}{T_m}\right)}^{-0.39}$$

(4)

In Equation (3), $\theta$ represents the dimensionless temperature ratio, defined as in Equation (5), with ${\mathit{T}}_w$ being the wall temperature.

$$\theta =\frac{T_{rec,m}-T_c^0}{T_{rec,m}-T_w}$$

(5)

Both the cooling effectiveness and the NHFR are computed on the cooled wall, which extends from 0D to 25D in the stream-wise direction and from −2D to 2D in the lateral direction. Laterally averaged quantities are used to quantify the progressive decay of the coolant performance downstream of the hole outlet section, for 2 < X/D < 22 and −2 < Z/D < 2.

Another significant parameter in film cooling applications is represented by the hole discharge coefficient $C_D$. This parameter is calculated as the ratio between the actual ${\dot{m}}_c$ and the ideal mass flow rate, and it is typically affected by the hole geometry and by the inlet and outlet flow conditions. The ideal mass flow rate is computed assuming an isentropic evolution from the total pressure of the coolant ${\mathit{P}}_c^0$ approaching the hole inlet to the static pressure of the main flow ${\mathit{P}}_m$, measured 5D upstream of the hole exit. The discharge coefficient is calculated as indicated in Equation (6), where the coolant mass flow rate and total pressure as well as the main flow static pressure and temperature are time-averaged values.

$$C_D=\frac{\dot{m_c}}{p_c^0{\left(\frac{p_m}{p_c^0}\right)}^{\frac{k+1}{2k}}{\left(\frac{2k}{\left(k-1\right)R{T}_c^0}\left({\left(\frac{p_c^0}{p_m}\right)}^{\frac{k-1}{k}}-1\right)\right)}^{0.5}\pi \frac{D^2}{4}}$$

(6)

3. Numerical Methodology

SBES is a hybrid approach presented by Menter [16] that offers a fast blending between RANS and LES models, shielding the boundary layer to be solved in a RANS mode. This solution overcomes some of the most common issues of Detached Eddy Simulation (DES) such as Grid-Induced Separation (GIS), meaning an artificial separation induced by LES when the boundary layer is modeled.

The RANS-LES transition is performed, acting at the stress level, as indicated in the following Equation (7):

$$\tau ij=\tau i{j}^{RANS}·f_s+\tau i{j}^{LES}·(1-f_s)$$

(7)

where $\tau i{j}^{RANS}$ is the RANS portion and $\tau i{j}^{LES}$ is the LES portion of the stress tensor. Notwithstanding the apparently simple formulation, most of the difficulties are hidden behind the shielding function ${\mathit{f}}_s$, which has to guarantee high flexibility and robustness even for different meshes and different combinations of RANS and LES models. The distinction between the two regions is clearly visible by plotting the shielding function in Figure 2, which blends between 0 in the LES domain and 1 in the RANS modeled domain of the selected case.

The model is tested on the same mesh used by Rosafio et al. [15], with equal discretization schemes and physical settings. The mesh consists of 11 million elements, with 20 prismatic layers positioned to resolve the boundary layer at the walls and to guarantee a ${\mathit{y}}^{+}$ level $<1$. A mesh refinement is applied near the coolant exit region, where the main flow interacts with the coolant. More details about the mesh sensitivity and Grid Convergence Index (GCI) calculation are available in papers by Rosafio et al. [14,15]. The models used are $k-\omega$ SST for the RANS domain and WALE as a Sub-grid Scale Model model for the LES domain. The ideal gas behavior is assumed for air, with the Sutherland law for viscosity and temperature-dependent thermal conductivity. A pressure-based coupled algorithm is used, with a linear scheme for pressure and a second-order upwind scheme for the other flow variables. In order to have an easier convergence, the time formulation is a bounded second-order implicit scheme with a constant time step of ${10}^{-6}$ s. The computational effort of the two methodologies was estimated by considering the simulation time required to run each time step with 30 sub-iterations on 24 cores, resulting in a 10% faster solution for the SBES model.

4. Results

In this section, the numerical results are discussed and validated by comparing them with experimental measures. In Figure 3, the time-averaged adiabatic effectiveness obtained through the SAS and SBES models is compared with the available experimental data for the same conditions. The SBES model features a slightly better prediction than the SAS of the coolant lateral spreading, which roughly covers the full surface of the cooled plate at X/D > 15. Still, both SAS and SBES fail to reproduce the correct interaction between the main flow and the coolant, which results in a very cold region that extends up to X/D = 15 from the hole trailing edge. This behavior is quite evident looking at the laterally averaged values of the adiabatic wall effectiveness shown in Figure 4. Indeed, the adiabatic effectiveness is always over-estimated, with the highest discrepancy occurring over the highly covered region close to the jet. Although the two numerical approaches fail in reproducing the experimental trend of laterally averaged effectiveness, the hybrid RANS-LES model confirms the result of the SAS model, which allows for concluding that the misprediction is likely attributable to a difference either in the operating conditions or in the geometrical definition (i.e., a filleted hole) of the test case rather than to a lack of numerical accuracy. This problem was already underlined by Rosafio et al. [15] and was attributed to a mismatch of a momentum ratio and a density ratio with experiments, since this information is not specified in the experimental reports. Despite the cooling performance overestimation, the fast decay of laterally averaged effectiveness occurring at X/D > 10 and the increasing lateral coverage indicate a strong mixing interaction between the coolant and the hot gas, which is not captured by RANS or URANS approaches. The effectiveness maps reported by Rosafio et al. [14] are indeed characterized by a narrow strip at the centerline, without any lateral spreading of the cooling jet.

In Figure 5, time-averaged maps of the NHFR are plotted. The contour plots reveal a positive distribution of the NHFR above the cooled region, where the coolant film adheres to the wall. Small negative stripes are visible only at the lateral interface between the coolant and the hot gas, up to X/D = 3 for SAS (Figure 5a) and up to X/D = 2 for SBES (Figure 5b). In this region, the free stream is supposed to be altered by the impact with the cooling jet, thus producing a local increase in the surface heat transfer coefficient. Laterally averaged values are instead compared in Figure 6. In the experimental case, negative values of the NHFR are found for X/D > 14, which is conformal with an increase in heat transfer coefficient induced by the coolant interaction with the main flow.

On the other hand, both numerical approaches overestimate the NHFR distribution in the cooled region. The NHFR, indeed, coherently increases according to the greater values of $\eta$ found with both SAS and SBES, as the adiabatic effectiveness appears in the NHFR formulation (Equation (3)). Moreover, as discussed for the cooling effectiveness, in the numerical case, it is evident that the coolant penetration into the main flow is much lower than what was reported in the experimental study. The coolant flow, thus, adheres to the wall, reducing the local stream-wise velocity. This phenomenon consequently leads to a $\frac{h_f}{h_o}$ ratio < 1, which increases the overall NHFR distribution.

Finally, the discharge coefficient obtained numerically with the SBES model ($C_{D,SBES}=0.71$) shows a good agreement with experiments held on a cylindrical hole with $\alpha =30$, ${\mathit{Ma}}_c$ = 0, and ${\mathit{Ma}}_m$ = 0.6 by Gritsch et al. [22] ($C_D$, [22] = 0.68).

5. Flow Field

The different behavior described by the two numerical models can be appreciated through instantaneous iso−surfaces of the ${\lambda }_2$ modulus, shown for both SAS and SBES simulations in Figure 7 and Figure 8.

The higher is the modulus of ${\lambda }_2$ used to generate the iso-surfaces, the smaller are the minimum length scales of the vortical structures that are visible after post-processing data from the simulations. The iso−surfaces shown in Figure 7 are generated by using a modulus of ${\lambda }_2$ one order of magnitude lower than the one used in Figure 8. Results demonstrate that SAS and SBES models are able to predict the local interaction between the coolant and the hot gas that occurs at lower length scales. In fact, Figure 8 shows that the continuous coherent structures originating at the coolant hole exit are broken up into smaller eddies under the influence of the hot gas. Apart from the size of turbulent structures, both Figure 7 and Figure 8 demonstrate the ability to predict the unsteady coolant–main flow interaction further downstream of the coolant hole. That outcome can be speculated from the transport of the coherent structures along the hot gas path.

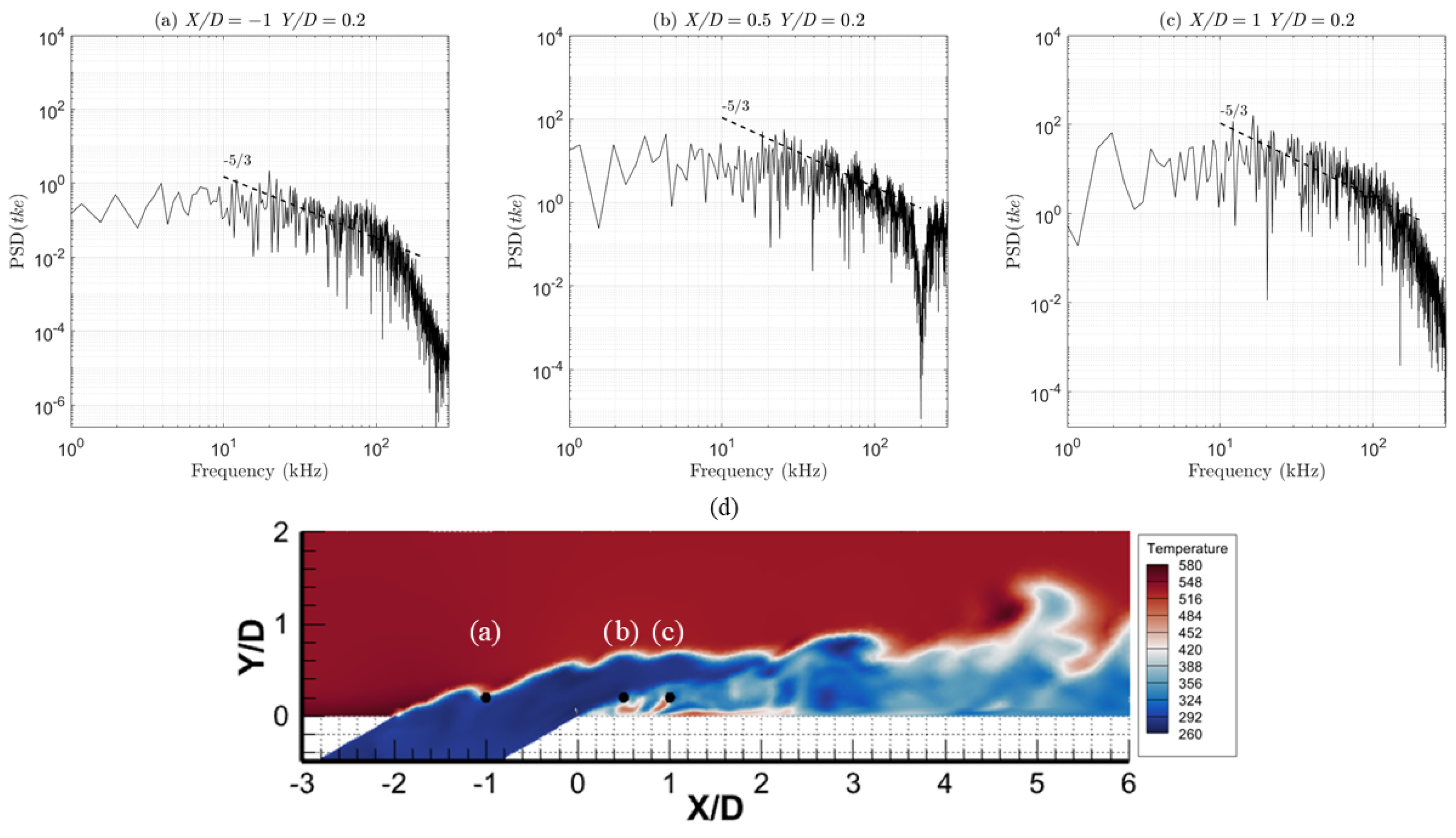
Further considerations about the turbulent energy captured by the SBES model can be deduced from the power spectral density (PSD) analysis. Figure 9a–c show the PSD of turbulent kinetic energy ($\mathit{tke}$) at $\mathit{Y}/\mathit{D}$ = 0.2, $\mathit{X}/\mathit{D}$ = −1, $\mathit{X}/\mathit{D}$ = 0.5, and $\mathit{X}/\mathit{D}$ = 1, respectively. In all cases, the energy decay aligns with the −5/3 slope of the energy cascade in the inertial sub-range, up to frequencies with a magnitude of ${10}^2$ [KHz]. The points selected for the analysis belong to the hole centerline ($\mathit{Z}/\mathit{D}$ = 0). Point (a) captures the shear layer between the coolant and the main flow, while points (b) and (c) investigate the coolant detachment from the wall (Figure 9d).

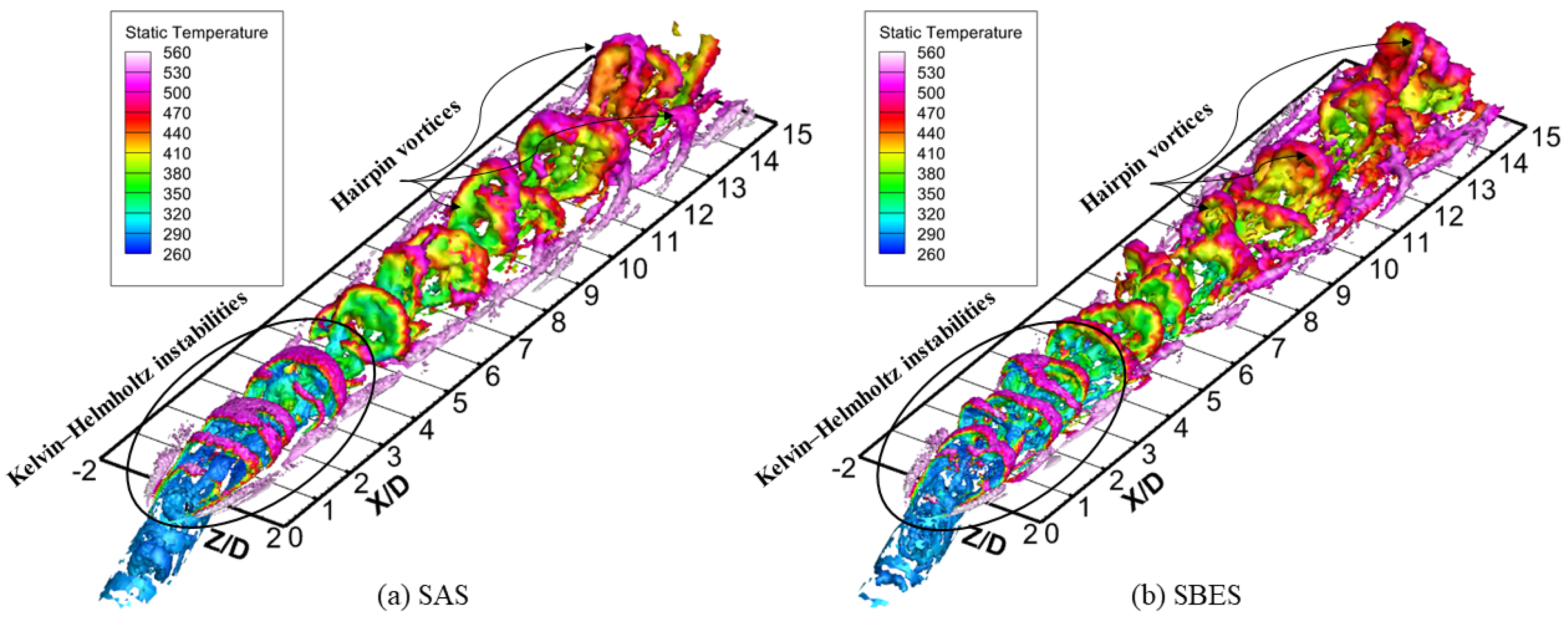
Several structures emerge from the coolant–hot gas interaction, in particular horseshoe vortices, counter-rotating pairs (kidney vortices), Kelvin–Helmholtz instabilities, and hairpin vortices. Kidney vortices are visible in Figure 10 in a plane orthogonal to the main flow direction located at $\mathit{X}/\mathit{D}=6$ and are responsible for the typical jet lift-off, which locally decrease the effectiveness by removing cold flow from the surface. Additionally, their rotational motion moves hot gas toward the wall surface. This behavior is usually counteracted by using shaped holes with expanding sections, which promote the generation of anti-kidney vortices and mitigate the cooling jet lift-off [23].

Kelvin–Helmholtz instabilities are predominant in the jet region (up to $\mathit{X}/\mathit{D}=5$), and they are produced by the relative motion between the coolant and the main flow. At increasing longitudinal distances, they are rapidly destroyed into smaller structures, mainly dominated by the hairpin vortices (Figure 7 and Figure 8) that are instead characterized by a stretched arched shape with inclined and quasi-stream-wise legs. The vortex legs start from the wall and rotate with an outward $\mathit{X}$ vorticity (therefore, with opposite rotation with respect to the horseshoe vortex), while the portion of the vortex farthest from the wall is defined as ‘head’ and rotates with a $\mathit{Z}$ vorticity [24]. Consecutive hairpin heads incorporate hot gas bubbles within them, and this mechanism is the main cause of the coolant mixing with the main flow.

Notwithstanding the major similarities between the two numerical models, some differences can be noticed. It is clear how the SBES approach can capture the flow features with even more precision than SAS. This difference is clearly evident when observing the Kelvin–Helmholtz instabilities that rapidly develop in smaller structures in the mixing region in Figure 10b. The longitudinal distance between consecutive ridges is strongly reduced in the SBES case, and this emerges from the Z vorticity representation in Figure 11a obtained using SAS when compared with the SBES case in Figure 11b.

At the coolant hole exit, the interaction between the coolant and the main flow generates shedding vortices with an alternating positive and negative vorticity. Negative vorticity marks the roll-up of the coolant flow, whereas positive vorticity originates from the break-up of the coolant jet due to the hot gas penetration. Notwithstanding the evident discrepancy in the flow structures’ discretization described by the two models, the overall jet penetration is coherent between SAS and SBES, as the vertical lift of the flow ridges is almost equal. As regards the flow field inside the cylindrical hole, the unsteadiness of the separation bubble predicted at the hole inlet section generates fluctuations in the coolant mass flow rate (Figure 11). These fluctuations propagate through the hole length and affect the coolant penetration into the main flow. The time evolution of the coolant mass flow rate was thus processed with Fast Fourier Transform (FFT) to convert the signal in the frequency domain and to identify the periodicity of turbulent phenomena. Results are plotted in Figure 12. SAS and SBES reveal some behavioral similarities, especially referring to the peak $f_1$, which occurs at the lowest notable frequency of ≈2.4 KHz. This frequency corresponds to the slowest period $T_1$ extracted from the unsteady signal, and all time-averaged quantities reported in this paper are computed on 4$T_1$. The other significant peaks are identified as $f_2$, $f_3$, and $f_4$, and they correspond to frequencies of 5.99 KHz, 11.59 KHz, and 15.99 KHz for SAS, while 7.06 KHz, 11.77 KHz, and 16.44 KHz for SBES. The latter is coherent with the dominant frequency found by Rosafio et al. [14] using RANS and a filleted hole at the exit section.

6. POD

The proper orthogonal decomposition is a technique used to process an ensemble of signals through a modal decomposition. The application of this methodology in the turbulence context was extensively discussed by Bakewell and Lumley [25] and Berkooz et al. [26]. This approach is used to extract coherent spatial features in the flow field and to isolate physical phenomena that are not evident from raw data [27]. The method uses a series of consecutive snapshots containing the average-free fluctuations of a certain field variable (e.g., velocity components or temperature ${\mathit{T}}^{\prime }$), which are decomposed in a set of spatial functions ${\mathrm{\Phi }}_k\left(x\right)$ modulated by time coefficients $a_k\left(t\right)$ as defined in Equation (8).

$$T_{x,t}^{\prime }=\sum _{k=1}^N{a}_k\left(t\right){\mathrm{\Phi }}_k\left(x\right)$$

(8)

In the current work, the POD analysis is limited to the ejection zone, up to $\mathit{X}/\mathit{D}=5$ downstream of the coolant hole exit. A total of 2556 two-dimensional consecutive snapshots are decomposed, highlighting the cooling jet lifting and traveling phenomenon on the central plane and the separation and reattachment effect on the cooled region. The static temperature was selected as an unsteady quantity to be analyzed, since temperature fluctuations easily underline the interactions between the coolant and the hot gas flow.

The POD spectrum for the central plane is reported in Figure 13a,b. POD modes are sorted from the most to the least energetic ones. Only the first two modes will be discussed in this section, as they include most of the overall energy content. This is particularly evident for the SAS simulation in Figure 13a, as a clear gap emerges between the first two modes and the following ones. Meanwhile, in the SBES case (Figure 13b), the energy decay is moderate and the first two modes account only for ≈12% of the total energy amount.

Looking at Figure 14, modes #1 and #2 capture the traveling phenomenon of the Kelvin–Helmholtz instabilities, which develop from the interaction between the coolant and the main flow. This can be deduced by comparing the POD results with $iso-{\lambda }_2$ structures that emerged in Figure 10, since the position and the size of POD modes coincide with the temperature pulsation induced by the propagation of consecutive ridges in the flow structure.

For the SAS simulation in Figure 14a,c, the energy content appears evenly distributed along the X direction, and the size of the wave packets progressively increases as the dimension of the structures increases. Meanwhile, in the SBES simulation (Figure 14b,d), most of the activity is concentrated at $1<\mathit{X}/\mathit{D}<3$, where vortex structures are fully developed and incorporate hot gas bubbles within them. Looking only at the first two modes, the other areas appear completely devoid of energy, so in this case, it would be appropriate to also check the subsequent modes to obtain a faithful representation of the flow field. This is coherent with the POD spectrum, where the SBES energy fraction is evenly distributed among the modes, while for SAS, it shows a steep gap between the first two modes and the following ones.

It is also interesting to notice that, for both SAS and SBES models, modes #1 and #2 appear almost equal in space but shifted in phase, and this is due to the traveling and alternating character of the vortical structures [27]. This behavior is confirmed by the time coefficient shown in Figure 13c,d, where it is evident that $a_2\left(t\right)$ is only time-shifted with respect to $a_1\left(t\right)$ and they present equivalent periodicity and amplitude.

The POD spectrum for the cooled region is reported in Figure 15a,b. Once again, the mode energy fraction gradually decays for SBES, while it suddenly drops for SAS. This huge difference can be motivated by looking at the mode shapes in Figure 16.

SAS modes $\#1$ (Figure 16a) and $\#2$ (Figure 16c) reveal small equally spaced marked zones, which contain a decreasing amount of energy moving from the hole trailing edge to the end of the analysis region. A remarkable energy contribution is also notable around the hole exit section, where the temperature fluctuations are induced by the presence of horseshoe vortices. It is evident that modes $\#1$ and $\#2$ capture almost the entire physical phenomenon of cooling reattachment in the cooled region.

Meanwhile, in the SBES map (Figure 16b,d), the distribution of high energetic zones is asymmetrical to the centerline. The energy content for mode $\#1$ (Figure 16b) is concentrated on a single pair of spatial structures, with stronger intensity at negative values of $Z/D$. Meanwhile, mode $\#2$ (Figure 16d) highlights smaller structures placed at $0<\mathit{X}/\mathit{D}<4$. From this comparison, it is possible to conclude that the first two modes of the SBES simulation emphasize the coolant reattachment downstream from the hole exit section, almost neglecting the effect of the horseshoe vortex around the hole edge, which is likely associated with lower modes. Moreover, SBES modes appear more spaced in the Z direction, which is coherent with the greater coolant lateral spreading described by the effectiveness maps. In this case, time coefficients are not coherent between the two approaches: the second mode for SAS is a time shifting of the first mode (Figure 15c), thus confirming the traveling behavior of the wave packets highlighted from the first mode. In the SBES case (Figure 15d), however, the second mode cannot be associated with the first one, and this is also notable by observing the mode shape in Figure 16b,d, which are not coherent between each other.

7. SPOD

The Spectral Proper Orthogonal Decomposition differs from the Proper Orthogonal Decomposition for its capability of extracting modes that are simultaneously coherent in space and time [28]. The methodology requires a series of consecutive snapshots ${\mathit{q}}_k$ in which the desired unsteady flow variable is collected on the N grid points of the analysis region. Considering M time instances ${\mathit{t}}_{k+1}={\mathit{t}}_k+\Delta \mathit{t}$, the overall dataset $\mathit{Q}$ contains $\mathit{M}$ snapshots ${\mathit{q}}_k$ with a corresponding dimension $\mathit{N}$.

$$Q=[q_1,q_2,...,q_M]\in R^{N\times M}$$

(9)

At this point, the method proposed by Welch [29] is used to extract the SPOD modes: the overall dataset is first divided into a set of smaller and partially overlapping blocks ${\mathit{N}}_b$, each of them containing ${\mathit{N}}_f$ snapshots, ${\mathit{N}}_o$ of which are overlapping. Each block can hence be represented as in Equation (10).

$$Q^{\left(n\right)}=[q_1^n,q_2^n,...,q_{N_f}^n]\in R^{N\times N_f}$$

(10)

Once the blocks are created, the Discrete Fourier Transform (DFT) is computed for each block (Equation (11)).

$${\widehat{Q}}^{\left(n\right)}=DFT\left(Q^{\left(n\right)}\right)$$

(11)

At this point, the data matrix can be sorted according to the frequency ${\mathit{f}}_k$, and the cross-spectral density tensor S at frequency ${\mathit{f}}_k$ is computed as in the following Equation (12):

$$S_{f_k}=\frac{1}{N_b}{W}^{\frac{1}{2}}{\widehat{Q}}_{f_k}{\widehat{Q}}_{f_k}^{\ast }{W}^{\ast \frac{1}{2}}$$

(12)

where $\mathit{W}$ is the weight matrix. The resulting eigenvalue decomposition can be written as reported in Equation (13).

$$S_{f_k}W{\mathrm{\Psi }}_{f_k}={\mathrm{\Psi }}_{f_k}{\mathrm{\Lambda }}_{f_k}$$

(13)

In Equation (13), the columns of ${\mathrm{\Psi }}_{f_k}$ contain the SPOD modes, which are sorted according to the corresponding eigenvalue contained in the diagonal matrix ${\mathrm{\Lambda }}_{f_k}$.

The SPOD analysis is performed on the same number of snapshots used for the POD, using the Matlab toolbox provided by Schmidt [30]. The SPOD spectra are plotted with the Strouhal number $St=\frac{fD}{U}$, where $\mathit{U}$ = 288.4 m/s is the velocity of the main flow. The number of snapshots for each block is ${\mathit{N}}_f=256$ with an overlapping factor of $50\%$ that corresponds to ${\mathit{N}}_o=128$ and ${\mathit{N}}_b=18$. This choice guarantees a small frequency resolution in order to capture high-frequency phenomena and a sufficient number of blocks to avoid uncertainty errors. The SPOD mode shapes are represented in terms of magnitude to get a clear distinction between relevant and non-relevant energetic zones. The mode phase instead reveals the shape and the distance between coherent wave packets in the flow field.

The SPOD spectrum indicates the energy spreading in the frequency domain. Most of the energy is carried by low-frequency phenomena, while for increasing frequencies, the energy decays as the dimension of the corresponding structures diminishes.

The SPOD spectrum of the cooled region in Figure 17a shows two leading spikes at St = 0.4 and St = 0.74 for SAS. Similarly, for the SBES spectrum in Figure 17b, a peak appears at St = 0.33, which is, however, preceded by a first one at St = 0.2. The main difference between the two energy spectra lies in the distance between the first mode and the other ones, since a huge separation can be noticed in the SAS model. This indicates that the phenomenon described by the first mode is predominant compared with the other modes, and in this case, the flow field shows low-rank behavior [31].

Figure 18 highlights the regions of the cooled wall that are more influenced by temperature oscillations. SAS and SBES show good agreement at St = 0.2 and St = 0.4, respectively (Figure 18a,b): the phenomenon that occurs at the corresponding frequencies is asymmetrical to the centerline and hits the cooled region at negative values of $\mathit{Z}/\mathit{D}$. A similar behavior can be noticed also for the second peak captured by SBES at St = 0.33 (Figure 18d), while SAS at St = 0.74 (Figure 18c) shows an energy content that is almost symmetrical to the centerline. In all cases, it is evident that marked regions are confined within an overall longitudinal length of $\mathit{X}/\mathit{D}=5$. This aspect motivates that the majority of the reattachment phenomena occur in this region, and the coolant jet lift from the wall disappears at larger distances. For similar reasons, the low energy content along the centerline is caused by the fact that coolant here stays almost attached to the wall. These observations find consistency in the effectiveness distribution close to the hole trailing edge represented in Figure 3, where a narrow strip of high $\eta$ follows the centerline downstream the hole exit until full reattachment occurs at larger distances.

The phase contour is instead used to visualize coherent wave packets in the flow field, since zones with equal phases propagate in a synchronized manner at the corresponding frequency. Figure 19 reveals remarkable differences in the description of the reattachment mechanism between the two numerical methods. In the SAS simulation, the most energetic phenomenon (St = 0.4) presents in-phase fronts, which are spaced 2D apart from each other in the X direction. A secondary contribution is instead given by closer structures at $St=0.74$.

The SBES analysis at St = 0.33 confirms the flow behavior described by SAS at St = 0.4, with a coherent description of the mode shape and phase. For the peak at St = 0.2, a full phase cycle is contained within X = 3D.

The energy spectrum for the central plane is plotted in Figure 20. The SBES analysis in this region shows good agreement with SAS, since the first relevant peak occurs at St = 0.4 (SAS) and St = 0.33 (SBES) and the second peak is found at St = 0.74 with both approaches. The mode shape at the corresponding frequencies, reported in Figure 21, shows that the main energy contribution spreads along the shear layer between the coolant and the hot gas, where the temperature field is affected by intense fluctuations. The mode magnitude plot of the SPOD analysis is coherent with the results shown in the POD section: the high-energy region is wider but less intense for the SAS model, while most of the energy content for the SBES case is concentrated in a narrow region at $0<\mathit{X}/\mathit{D}<3$. This can be due to the greater distance between consecutive structures modeled by SAS, which allows a greater penetration of the main flow within the coolant jet (see Figure 11). The flow structures that emerge from the phase visualization in Figure 22a–d are equally placed in the two cases, with in-phase zones spaced by $\mathit{X}/\mathit{D}\approx 2$ for $St$ = 0.4 (SAS) and $St$ = 0.33 (SBES) and by $\mathit{X}/\mathit{D}\approx 1$ for $\mathit{St}=0.74$ In general, the spatial distance between coherent structures decrease with increasing $St$ numbers. The phase contour in the central plane is coupled with an instantaneous representation of the temperature field in Figure 22e,f. From this plot, it is possible to visualize that this region is dominated by Kelvin–Helmholtz instabilities, whose spacing coincides with the phase fronts at $St$ = 0.4 and $St$ = 0.33 in SAS and SBES, respectively.

8. Conclusions

In this work, the SBES model was used to simulate the ejection condition through a cylindrical film cooling hole. The hybrid model was compared with the results obtained by Rosafio et al. [15] with a Scale Adaptive Simulation (SAS) model and with the experimental campaign held at the University of Karlsruhe by Christian Saumweber [19].

SBES results are coherent with the SAS model, confirming a similar prediction of film cooling effectiveness and net heat flux reduction. However, in both cases, the penetration of the coolant into the main flow is significantly underestimated, and this results in a stronger cooling action up to X/D = 15 if compared with the experimental estimation. The hole discharge coefficient predicted numerically is instead in good agreement with the experimental measures of Gritsch et al. [22].

As regards the flow field, iso-${\lambda }_2$ profiles are used to isolate the main turbulent structures: Kelvin–Helmholtz instabilities dominate the ejection zone (X/D < 5). At higher distances, these vortices rapidly evolve into smaller structures, mainly characterized by hairpin vortices. Counter-rotating pairs emerge from the lateral plane visualization, and they are responsible for the jet lift from the cooled wall. The main difference between the two numerical approaches emerges from the flow field visualization, as SBES predicts smaller vortical structures with higher precision than SAS.

The POD analysis performed on the central plane demonstrates that the main energetic contribution is carried by the Kelvin–Helmholtz instabilities. However, while, for the SAS model, the POD modes $\#1$ and $\#2$ are sufficient to capture the entire flow evolution on the central plane visualization, in the SBES case, the energy contribution is evenly distributed among modes and the first two ones only show the traveling behavior of the Kelvin–Helmholtz instabilities occurring at 1 < X/D < 3. In the cooling region visualization, the flow wave packets highlighted by the POD modes for SAS and SBES have different patterns: the former shows smaller marked zones that extend from the hole exit section up to X/D = 5, with mode $\#2$ being only a temporal translation of mode $\#1$. In the latter, the energy content is concentrated in a smaller number of spatial structures, which differs from mode $\#1$ to mode $\#2$.

As regards the SPOD analysis, the first two significant frequencies were selected from mode $\#1$. In the cooled region, the two main frequencies correspond to St = 0.4 and to St = 0.74 for SAS, and to St = 0.2 and St = 0.33 for SBES. In all cases, the activity is concentrated in a pair of high energetic regions where the coolant attachment with the wall occurs. This activity is caused by the oscillating cooling mass flow rate, which produces a pulsating penetration into the main flow and a consecutive alteration in the reattachment position. In the central plane visualization, the peaks correspond to St = 0.4 and St = 0.74 for SAS, and to St = 0.33 and St = 0.74 for SBES. The mode magnitude plots show a narrow energetic concentration at 0 < X/D < 3 for SBES, which is coherent with POD results, while a wider spreading of energy for SAS. In both cases, the mode shapes coincide with the shear layer between the coolant and the free stream.

The results presented in this paper demonstrate the ability of high-fidelity approaches to describe the coolant–main flow interaction in film cooling applications. For the selected operating conditions (${\mathit{Ma}}_c$ = 0, ${\mathit{Ma}}_m$ = 0.6, BR = 1), the SAS simulation provides reliable accuracy in the flow field description as well as in the cooling performance prediction if compared with the SBES case, demonstrating good capabilities in adjusting the turbulent scale according to the characteristics of the flow field. Despite the similarities, some non-negligible aspects emerge from this comparison: the SBES solution indeed shows smaller structures that SAS does not capture, improving the overall resolution of the turbulent flow. It is important to remember that SBES allows an accurate solution of the inertial scales where the grid is sufficiently fine. However, SAS may also be used on coarser meshes, thus leading to a reduced computational time. The present activity is performed on the same mesh with the same numerical setup except for the turbulence closure, so SBES results in a higher accuracy with no drawbacks on computational time. As a result of the improved solution, the POD energy fraction in the SBES case slowly decays between consecutive modes, while the SAS modes $\#1$ and $\#2$ carry almost the entire energy content. Eventually, the better resolution of the turbulent flow improves the description of the mixing phenomenon, which produces a wider lateral spreading of the cooling jet and a faster decay of local film cooling effectiveness at large distances from the hole exit section than traditional RANS approaches. This information can be crucial in determining the real protection that the film executes on the metal profile. Consequently, the number of film holes or their position can be adapted during the design step of a cooling system to avoid areas critically exposed to high temperatures.