Auxiliary Heat System Design and Off-Design Performance Optimization of OTEC Radial Inflow Turbine
Abstract
1. Introduction
2. Materials and Methods
2.1. Radial Inflow Turbine Auxiliary Heat System Design and Variable Operating Conditions Realization Methods
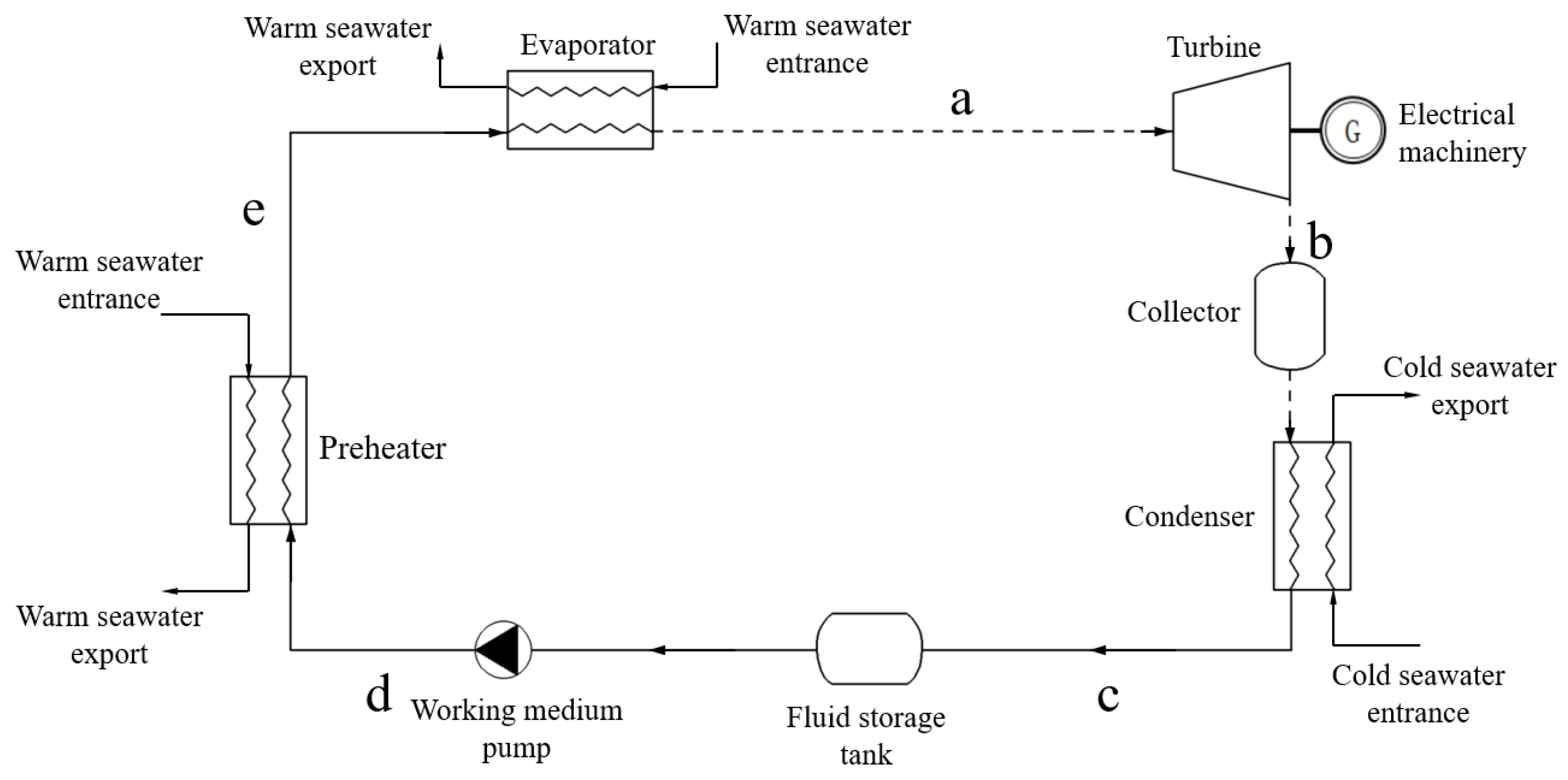
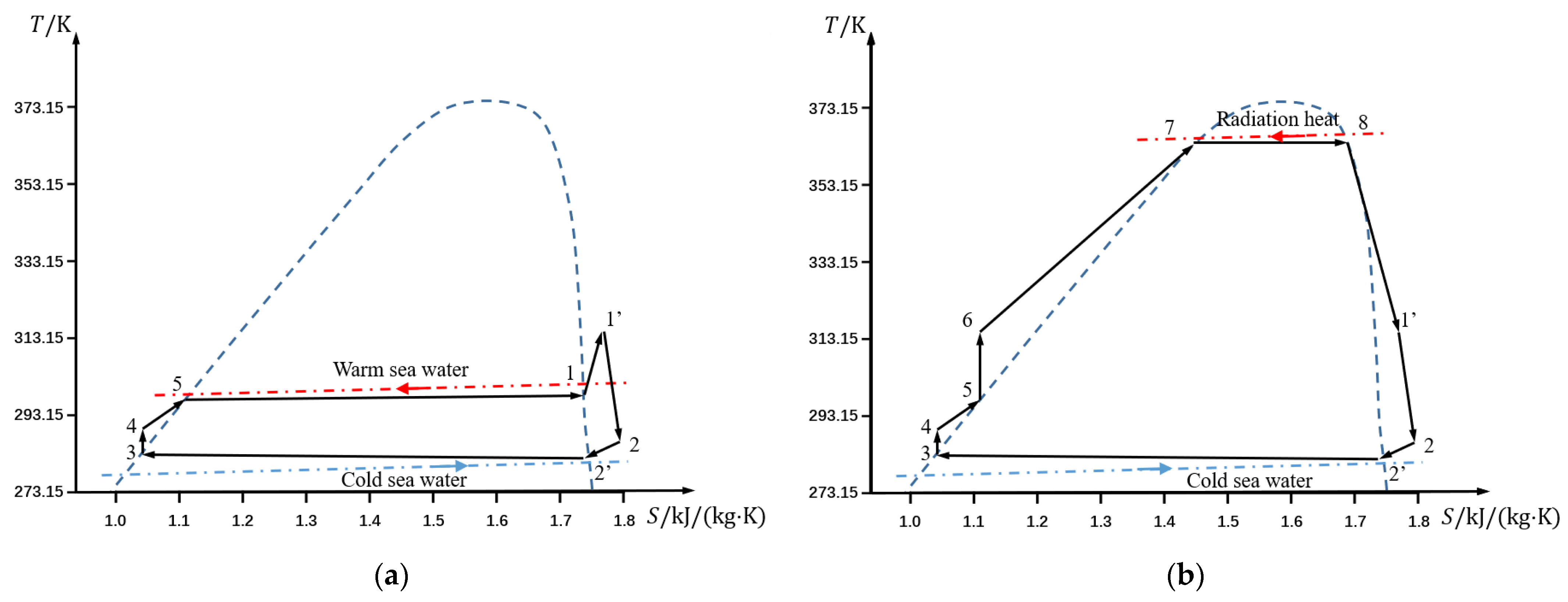
2.1.1. Mathematical Model of OTEC System without Auxiliary Heat
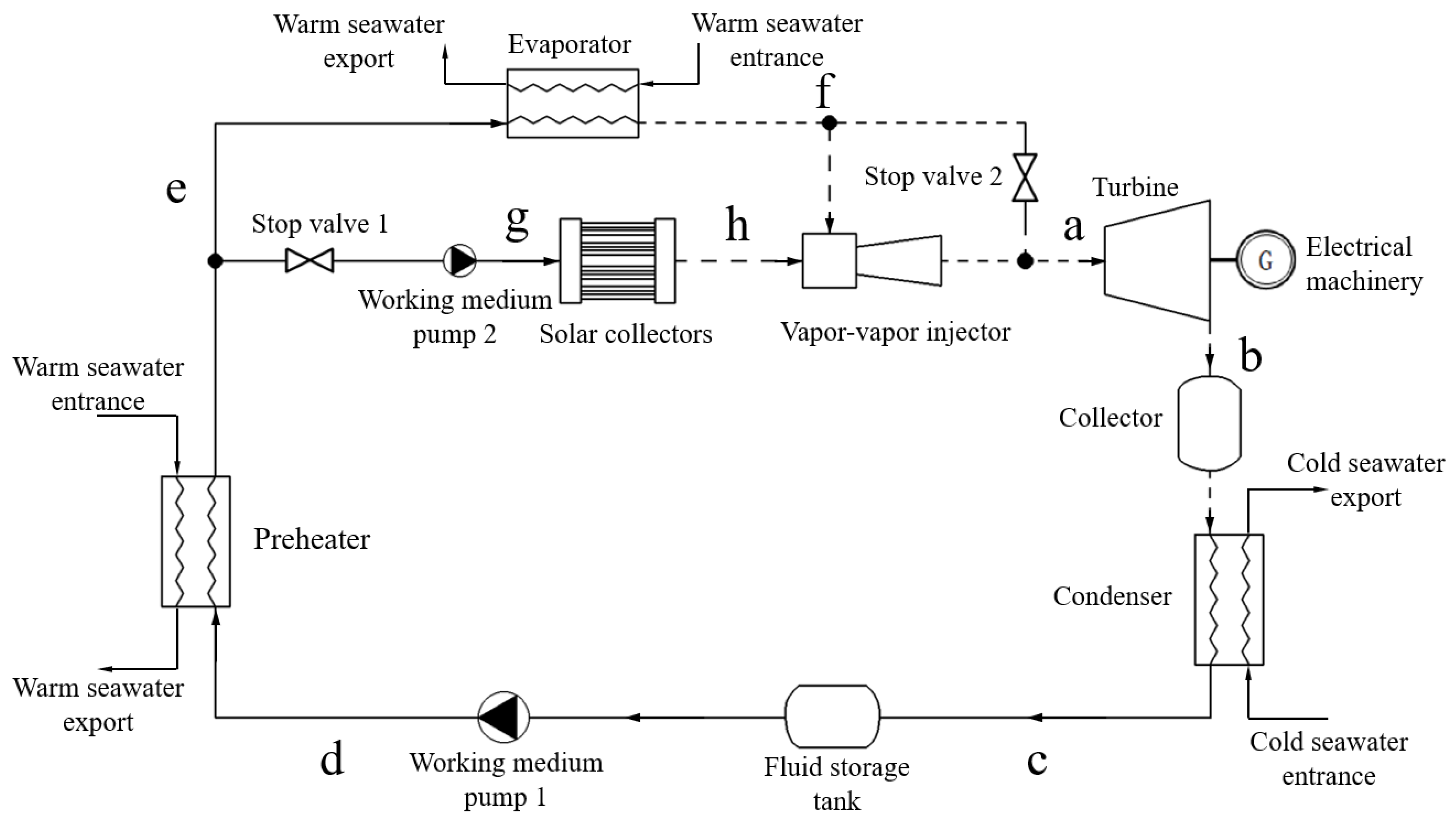
2.1.2. Design of Auxiliary Heat System
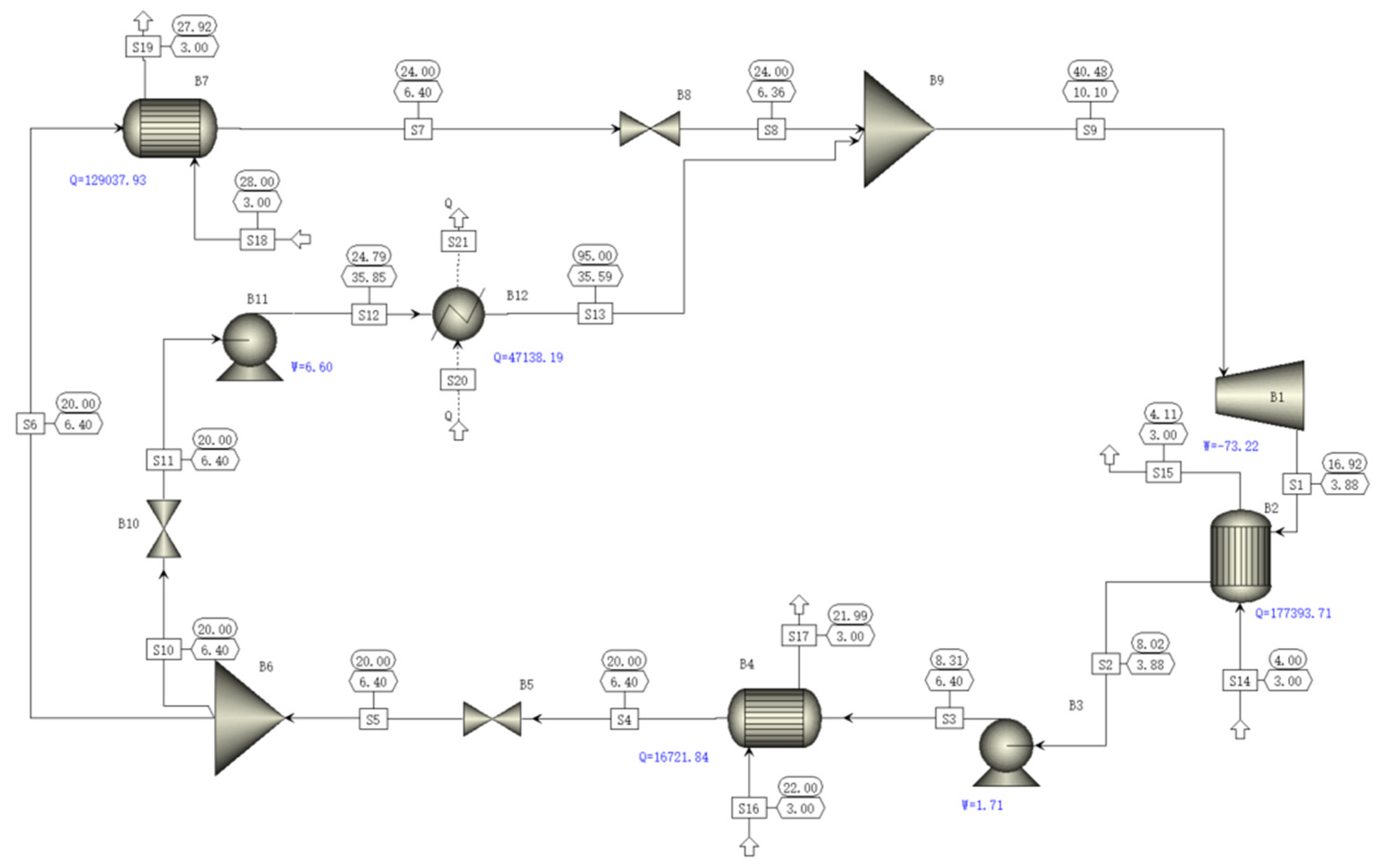
2.2. Process Simulation of Auxiliary Heat System
2.2.1. System Parameters Setting
2.2.2. Circular Process Simulation by Aspen Plus
2.3. Optimization Method for the Performance under Off-Design Conditions of Radial Inflow Turbine
2.3.1. Modeling and Numerical Simulation of Radial Inflow Turbines
2.3.2. Multi-Objective Optimization Method of Radial Inflow Turbine Based on Support Vector Regression and NSGA-III
3. Results
3.1. Auxiliary Heat System Process Simulation Results
3.2. Numerical Simulation Results of 40 Groups of Radial Turbines
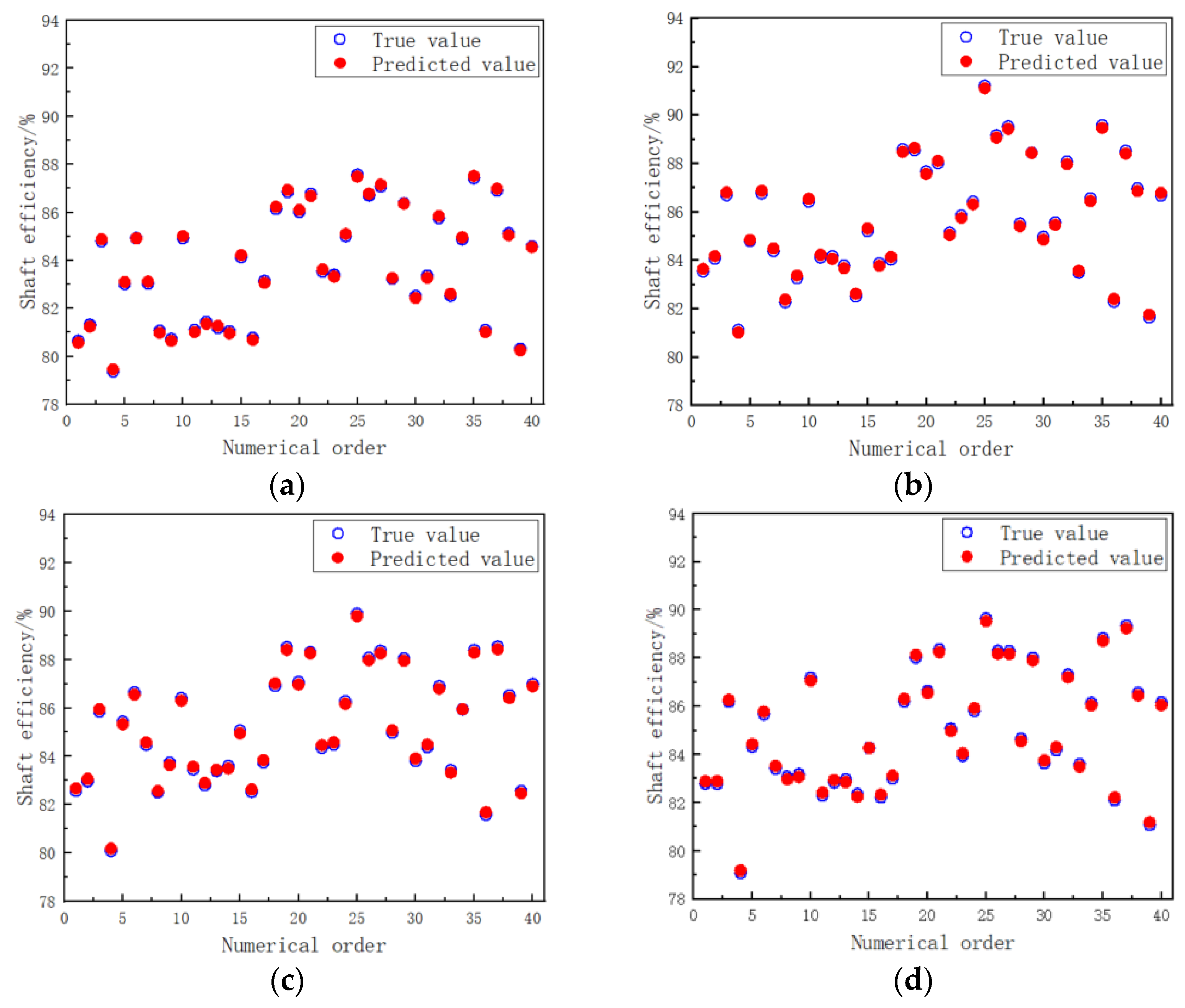
3.3. Comparison of Training and Prediction Results
3.4. Multi-Objective Optimization of Radial Inflow Turbine Rotor Parameters Based on NSGA-III
4. Discussion
4.1. Comparative Analysis of Auxiliary Thermal Systems
4.2. Performance Analysis of Variable Working Conditions
5. Conclusions
- (1)
- Based on the ORC system, a solar collector and ejector were added, and the OTEC system with solar auxiliary heat was designed for the R134a working mass, and the mathematical model of the new OTEC system was established and process simulation calculations of the auxiliary heat working condition parameters were carried out. Finally, using Aspen Plus, the system cycle efficiency was calculated to be 2.269% higher than the cycle efficiency of the OTEC system without auxiliary heat.
- (2)
- Under three different off-design conditions with auxiliary heat sources, 40 groups of radial turbines with different rotor modeling parameters were numerically simulated using CFX. Based on CFX-post 2020 R2 software, the simulation results of axial power and axial efficiency of these radial turbines were obtained through parameterization and batch processing. The simulation results of axial efficiency and axial power were used as training samples, and performance prediction models under different off-design conditions were established using the support vector regression method.
- (3)
- The nonlinear mapping relationship between rotor modeling parameters and radial turbine shaft efficiency was obtained using the support vector regression prediction method. Further, the NSGA-III algorithm was used to optimize the radial inflow turbine’s rotor parameters. The optimization objectives include design performance, off-design performance and tip clearance. The optimal scheme obtained by the multi-objective optimization algorithm also has the best performance under off-design condition. Under different off-design conditions, the optimal performance scheme, the initial scheme and the maximum tip clearance scheme were simulated by CFD, and the shaft power and shaft efficiency curves were obtained. The results show that with the increase in inlet pressure, the axial power tends to increase linearly, while the axial efficiency decline with fluctuation. The reason for the decrease in efficiency is that there is no auxiliary heat source in the initial design condition of all schemes, and the adaptability of impeller structure and working condition is the highest at low inlet pressure. The optimized scheme’s performance is better than that of the original scheme over the entire off-design working range. The shaft efficiency under the design condition is 92.219%, which is 0.89% higher than the original scheme. Under the saturation condition of 313.15 K, the shaft efficiency is 89.93%, which is 0.628% higher than the initial scheme. In other off-design conditions, the shaft efficiency of the optimized scheme is also increased by 0.403–1.903%.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, F.Y.; Liu, W.M.; Peng, J.P. Development and prospect of ocean thermal energy generation technology. Green Sci. Technol. 2012, 11, 246–248. [Google Scholar]
- Park, S.; Chun, W.; Kim, N. Simulated production of electric power and desalination using solar-OTEC hybrid system. Int. J. Energy Res. 2017, 41, 637–649. [Google Scholar] [CrossRef]
- Talluri, L.; Manfrida, G.; Ciappi, L. Exergo-economic assessment of OTEC power generation. E3S Web Conf. 2021, 238, 01015. [Google Scholar] [CrossRef]
- Qixuan, C. Research on solar-assisted ocean thermal energy conversion system. IOP Conf. Ser. Earth Environ. Sci. 2021, 687, 012135–012137. [Google Scholar]
- Yamada, N.; Hoshi, A.; Ikegami, Y. Performance simulation of solar-boosted ocean thermal energy conversion plant. Renew. Energy 2009, 34, 1752–1758. [Google Scholar] [CrossRef]
- Aydin, H.; Lee, H.S.; Kim, H.J.; Shin, S.K.; Park, K. Off-design performance analysis of a closed-cycle ocean thermal energy conversion system with solar thermal preheating and superheating. Renew. Energy 2014, 72, 154–163. [Google Scholar] [CrossRef]
- Dezhdar, A.; Assareh, E.; Keykhah, S.; Bedakhanian, A.; Lee, M. A transient model for clean electricity generation using solar energy and ocean thermal energy conversion (OTEC)-case study: Karkheh dam-southwest Iran. Energy Nexus 2023, 9, 100176. [Google Scholar] [CrossRef]
- Tian, Z.; Zou, X.; Zhang, Y.; Gao, W.; Chen, W.; Peng, H. 4E analyses and multi-objective optimization for an innovative solar-ocean thermal energy conversion/air conditioning system. J. Clean. Prod. 2023, 414, 137532. [Google Scholar] [CrossRef]
- Bian, Y.N.; Pan, J.X.; Liu, Y.; Zhang, F.; Yang, Y.; Arima, H. Performance analysis of a combined power and refrigeration cycle. Energy Convers. Manag. 2019, 185, 259–270. [Google Scholar] [CrossRef]
- Schuster, S.; Markides, C.N.; White, A.J. Design and off-design optimisation of an Organic Rankine Cycle (ORC) system with an integrated radial turbine model. Appl. Therm. Eng. 2020, 174, 115192. [Google Scholar] [CrossRef]
- Wu, T.; Shao, L.; Wei, X.; Ma, X.; Zhang, G. Design and structure optimization of small-scale radial inflow turbine for Organic Rankine Cycle system. Energy Convers. Manag. 2019, 199, 111940. [Google Scholar] [CrossRef]
- Sauret, E.; Gu, Y.T. 3D CFD simulations of a candidate r143a radial-inflow turbine for geothermal power applications. In Proceedings of the ASME Power Conference 2014, Baltimore, MD, USA, 28–31 July 2014. [Google Scholar]
- Sauret, E.; Gu, Y.T. Three-dimensional off-design numerical analysis of an Organic Rankine Cycle radial-inflow turbine. Appl. Energy 2014, 135, 202–211. [Google Scholar] [CrossRef]
- Binder, N.; Carbonneau, X.; Chassaing, P. Off-design considerations through the properties of some pressure-ratio line of radial inflow turbines. Int. J. Rotating Mach. 2008, 2008, 273296. [Google Scholar] [CrossRef]
- Kumar, M.; Panda, D.; Behera, S.K.; Sahoo, R.K. Experimental investigation and performance prediction of a cryogenic turboexpander using artificial intelligence techniques. Appl. Therm. Eng. 2019, 162, 114273. [Google Scholar] [CrossRef]
- Rahbar, K.; Mahmoud, S.; Al-Dadah, R.K.; Moazami, N. Modelling and optimization of Organic Rankine Cycle based on a small-scale radial inflow turbine. Energy Convers. Manag. 2015, 91, 186–198. [Google Scholar] [CrossRef]
- Chen, F.Y. Research on Thermal Performance and Comprehensive Utilization of Marine Thermal Energy Generation Device. Ph.D. Thesis, Harbin Engineering University, Harbin, China, 2016. [Google Scholar]
- Wang, H.Y. Performance Simulation and Experimental Study of Ejector’s Influence on Ocean Thermal Cycle. Master’s Thesis, Shandong University, Jinan, China, 2020. [Google Scholar]
- Wu, Z.J. Study on the Performance of Fork Row Tube Bundle Seawater Heat Exchanger under Sea Wave Conditions. Ph.D. Thesis, Tianjin University, Tianjin, China, 2020. [Google Scholar]
- Yu, Z.T.; Wang, C.J.; Rong, F.H.; Liang, W. Optimal coupling design for Organic Rankine Cycle and radial turbine rotor using CFD modeling, machine learning and genetic algorithm. Energy Convers. Manag. 2023, 275, 116493. [Google Scholar]
- Wang, Y.; Chen, Y.; Xue, G.; Zhang, T.; Liu, Y. Parameter optimization and performance research: Radial inflow turbine in ocean thermal energy conversion. J. Mar. Sci. Eng. 2023, 11, 2293. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part i: Solving problems with box constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Jain, H.; Deb, K. An evolutionary many-objective optimization algorithm using reference-point based nondominated sorting approach, part ii: Handling constraints and extending to an adaptive approach. IEEE Trans. Evol. Comput. 2014, 18, 602–622. [Google Scholar] [CrossRef]
- Zhang, C.; Li, Y.; Tong, Z. Impact analysis and optimization of the preliminary design parameters for an Organic Rankine Cycle radial inflow turbine. J. Braz. Soc. Mech. Sci. Eng. 2023, 45, 10. [Google Scholar] [CrossRef]
- Caballero, G.C.; Escorcia, Y.C.; Venturini, O.J.; Silva Lora, E.E.; Alviz Meza, A.; Mendoza Castellanos, L.S. Unidimensional and 3D analyses of a radial inflow turbine for an Organic Rankine Cycle under design and off-design conditions. Energies 2023, 16, 3383. [Google Scholar] [CrossRef]



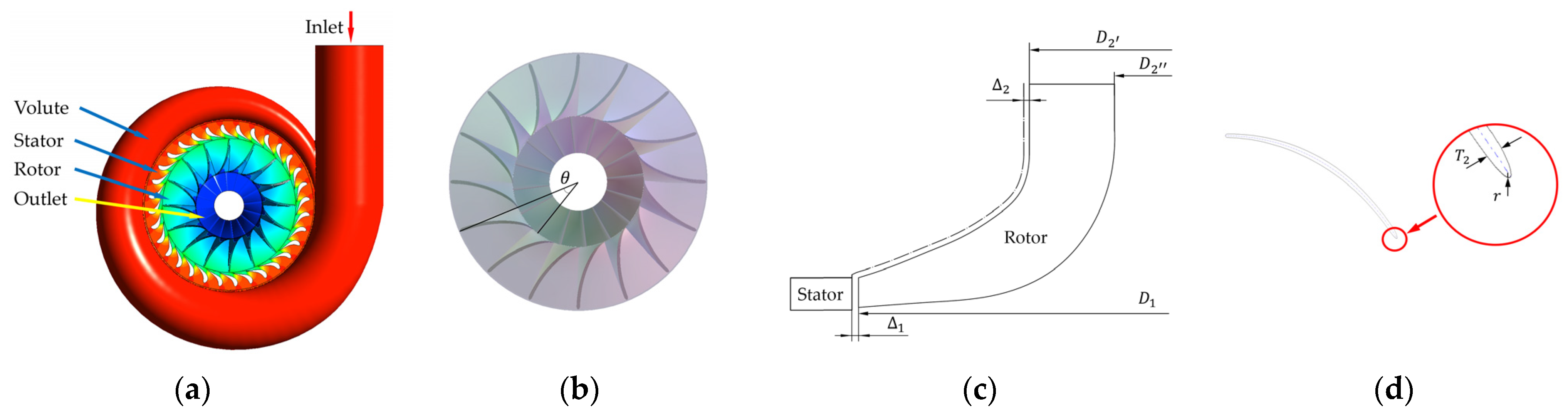






| OTEC System Parameters (without Auxiliary Heat) | Values | OTEC System Parameters (with Auxiliary Heat) | Values |
|---|---|---|---|
| Total inlet pressure /MPa | 0.645 | Total inlet pressure /MPa | 1.016 |
| Total inlet temperature /K | 297.15 | Total inlet temperature /K | 313.15 |
| Outlet static pressure /MPa | 0.387 | Outlet static pressure /MPa | 0.387 |
| Mass flow rate /(kg/s) | 3.684 | Mass flow rate /(kg/s) | 3.684 |
| Isentropic efficiency /% | ≥85 | Isentropic efficiency /% | ≥85 |
| Rotating speed /(r/min) | ≤15,000 | Rotating speed /(r/min) | ≤15,000 |
| generated output /kW | 30 | generated output /kW | 60 |
| Parameters | Numerical Value | Parameters | Numerical Value |
|---|---|---|---|
| Reactivity Ω | 0.479 | Leaf gate inlet height /mm | 8.601 |
| Aspect ratio | 0.421 | Impeller inlet diameter /mm | 217 |
| Gear ratio | 0.65 | Outside diameter of rotor outlet /mm | 110.83 |
| Velocity coefficient of leaf grating | 0.96 | Inside diameter of rotor outlet /mm | 52.78 |
| Impeller speed coefficient | 0.85 | Radial clearance /mm | 2.553 |
| Absolute airflow angle at rotor inlet /° | 16.0 | Leaf top clearance /mm | 0.273 |
| Impeller outlet relative airflow angle /° | 37.2 | Blade thickness /mm | 1.582 |
| Impeller inlet relative airflow angle /° | 85.19 | Blade outlet fillet radius /mm | 3.152 |
| Impeller inlet circumferential speed /(m/s) | 93.17 | Impeller blade twist angle /° | 43.378 |
| Impeller inlet absolute velocity /(m/s) | 99.32 | Isentropic efficiency (physics) /% | 88.169 |
| Impeller inlet relative speed /(m/s) | 27.47 | Shaft efficiency /% | 86.228 |
| Absolute airflow angle at rotor outlet /° | 86.58 | Number of revolutions per minute /(r/min) | 8200 |
| Impeller outlet circumferential speed /(m/s) | 37.27 | Number of leaf blades | 32 |
| Absolute velocity of rotor outlet /(m/s) | 29.46 | Number of rotor blades | 16 |
| Impeller outlet relative velocity /(m/s) | 48.86 | Impeller axial length | 65.1 |
| Parameters | Value |
|---|---|
| 0.38~0.468 | |
| 12~20 | |
| 35°~55° | |
| 2~3 mm | |
| 0.15~1.5 mm | |
| 1~3 mm | |
| 0.1~5 mm |
| Month | 0~400 W/m2 | 400~600 W/m2 | 600~800 W/m2 | 800~1000 W/m2 | 1000~1200 W/m2 |
|---|---|---|---|---|---|
| 1 | 65.19 | 6.05 | 8.47 | 17.07 | 3.23 |
| 2 | 64.51 | 8.05 | 7.05 | 9.77 | 10.63 |
| 3 | 65.73 | 8.47 | 6.45 | 8.6 | 10.75 |
| 4 | 65.69 | 8.05 | 4.72 | 8.48 | 13.05 |
| 5 | 63.84 | 7.8 | 7.66 | 8.87 | 11.83 |
| 6 | 65.27 | 8.75 | 13.06 | 8.33 | 4.59 |
| 7 | 65.05 | 9.94 | 9.95 | 10.75 | 4.3 |
| 8 | 66.4 | 7.93 | 10.48 | 9.14 | 6.05 |
| 9 | 67.5 | 9.17 | 8.89 | 7.64 | 6.8 |
| 10 | 72.44 | 9.94 | 9.81 | 5.77 | 2.02 |
| 11 | 71.26 | 7.92 | 8.61 | 10.56 | 1.67 |
| 12 | 72.59 | 8.47 | 8.88 | 10.08 | 0 |
| System Parameters (without Auxiliary Heat) | Results | System Parameters (with Auxiliary Heat) | Results |
|---|---|---|---|
| Power consumption of process pump 1/kW | 1.508 | Power consumption of process pump 1/kW | 1.715 |
| Power consumption of process pump 2/kW | 0 | Power consumption of process pump 2/kW | 6.595 |
| Turbine power/kW | 33.16 | Turbine power/kW | 65.898 |
| Evaporator heat absorption/kW | 943.95 | Evaporator heat absorption/kW | 827.06 |
| Collector Heat Absorption/kW | 0 | Collector Heat Absorption/kW | 197.36 |
| Net power generation/kW | 31.652 | Net power generation/kW | 57.588 |
| Cyclic efficiency/% | 3.353 | Cyclic efficiency/% | 5.622 |
| Working Condition | Extremely Poor | Average Value | Variance |
|---|---|---|---|
| Design condition | 8.059 | 83.75 | 5.619 |
| 303.15 K saturated working condition | 10.088 | 85.722 | 5.803 |
| 308.15 K saturated working condition | 9.805 | 85.241 | 5.22 |
| 313.15 K saturated working condition | 10.54 | 84.989 | 6.173 |
| Num. | Design Condition | 303.15 K Condition | 308.15 K Condition | 313.15 K Condition | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.468 | 12 | 37.56 | 2.44 | 1.08 | 2.23 | 2.74 | 80.648 | 83.533 | 82.575 | 82.807 |
| 2 | 0.423 | 13 | 38.59 | 2.95 | 1.14 | 1.51 | 0.73 | 81.315 | 84.065 | 82.971 | 82.791 |
| 3 | 0.382 | 16 | 45.77 | 2.77 | 0.85 | 1.00 | 3.12 | 84.799 | 86.688 | 85.854 | 86.197 |
| 4 | 0.448 | 15 | 51.92 | 2.41 | 1.36 | 2.74 | 1.61 | 79.374 | 81.108 | 80.090 | 79.094 |
| 5 | 0.418 | 13 | 44.23 | 2.36 | 0.92 | 2.85 | 5.00 | 83.018 | 84.788 | 85.429 | 84.330 |
| 6 | 0.439 | 18 | 36.54 | 2.46 | 0.79 | 1.41 | 4.87 | 84.926 | 86.753 | 86.642 | 85.678 |
| 7 | 0.441 | 20 | 53.97 | 2.64 | 1.01 | 1.36 | 3.74 | 83.037 | 84.371 | 84.476 | 83.421 |
| 8 | 0.396 | 16 | 52.44 | 2.23 | 1.40 | 1.97 | 3.87 | 81.063 | 82.259 | 82.513 | 83.067 |
| 9 | 0.457 | 19 | 45.26 | 2.67 | 1.04 | 2.80 | 4.25 | 80.723 | 83.254 | 83.734 | 83.176 |
| 10 | 0.445 | 15 | 37.05 | 2.15 | 0.66 | 1.31 | 0.60 | 84.934 | 86.412 | 86.401 | 87.173 |
| 11 | 0.448 | 16 | 39.62 | 2.77 | 0.82 | 2.90 | 0.48 | 81.097 | 84.113 | 83.468 | 82.311 |
| 12 | 0.414 | 13 | 40.64 | 2.18 | 1.27 | 1.15 | 3.24 | 81.436 | 84.151 | 82.808 | 82.845 |
| 13 | 0.400 | 17 | 36.03 | 2.74 | 1.33 | 2.33 | 3.37 | 81.183 | 83.770 | 83.400 | 82.961 |
| 14 | 0.407 | 19 | 48.33 | 2.90 | 1.20 | 2.03 | 0.85 | 81.041 | 82.506 | 83.597 | 82.354 |
| 15 | 0.385 | 18 | 42.69 | 2.38 | 0.69 | 3.00 | 1.11 | 84.140 | 85.202 | 85.059 | 84.270 |
| 16 | 0.443 | 14 | 47.31 | 2.92 | 1.24 | 1.67 | 4.50 | 80.763 | 83.856 | 82.535 | 82.226 |
| 17 | 0.452 | 19 | 49.36 | 2.21 | 0.72 | 2.13 | 0.35 | 83.139 | 84.027 | 83.749 | 83.016 |
| 18 | 0.427 | 19 | 51.41 | 2.85 | 0.28 | 2.49 | 2.24 | 86.148 | 88.565 | 86.921 | 86.204 |
| 19 | 0.434 | 12 | 42.18 | 2.56 | 0.31 | 1.26 | 3.49 | 86.853 | 88.533 | 88.504 | 88.031 |
| 20 | 0.380 | 17 | 54.49 | 2.33 | 0.56 | 1.77 | 1.23 | 86.020 | 87.654 | 87.071 | 86.625 |
| 21 | 0.389 | 16 | 41.67 | 2.05 | 0.40 | 1.87 | 3.87 | 86.767 | 87.998 | 88.308 | 88.355 |
| 22 | 0.464 | 15 | 49.87 | 2.08 | 0.88 | 1.72 | 4.12 | 83.536 | 85.130 | 84.362 | 85.068 |
| 23 | 0.421 | 18 | 53.46 | 2.10 | 0.63 | 2.95 | 3.62 | 83.400 | 85.833 | 84.489 | 83.945 |
| 24 | 0.387 | 20 | 46.28 | 2.62 | 0.76 | 2.18 | 4.62 | 85.017 | 86.401 | 86.269 | 85.817 |
| 25 | 0.432 | 18 | 47.82 | 2.31 | 0.18 | 1.05 | 2.49 | 87.573 | 91.196 | 89.895 | 89.633 |
| 26 | 0.416 | 15 | 40.13 | 3.00 | 0.34 | 2.39 | 4.37 | 86.704 | 89.151 | 88.074 | 88.291 |
| 27 | 0.412 | 14 | 46.79 | 2.82 | 0.24 | 1.92 | 0.23 | 87.078 | 89.511 | 88.362 | 88.281 |
| 28 | 0.403 | 20 | 43.21 | 2.13 | 1.11 | 1.21 | 1.98 | 83.234 | 85.489 | 84.984 | 84.646 |
| 29 | 0.405 | 19 | 35.51 | 2.69 | 0.47 | 1.62 | 1.48 | 86.372 | 88.424 | 88.046 | 88.005 |
| 30 | 0.391 | 14 | 50.38 | 2.87 | 0.98 | 2.64 | 2.36 | 82.509 | 84.942 | 83.814 | 83.649 |
| 31 | 0.436 | 14 | 52.95 | 2.51 | 0.95 | 1.10 | 0.98 | 83.354 | 85.541 | 84.388 | 84.191 |
| 32 | 0.466 | 17 | 43.72 | 2.97 | 0.53 | 1.46 | 2.11 | 85.762 | 88.055 | 86.897 | 87.310 |
| 33 | 0.430 | 17 | 38.08 | 2.00 | 1.14 | 2.54 | 2.61 | 82.524 | 83.486 | 83.420 | 83.593 |
| 34 | 0.398 | 12 | 35.00 | 2.49 | 0.60 | 2.44 | 1.86 | 84.881 | 86.533 | 85.945 | 86.134 |
| 35 | 0.455 | 17 | 39.10 | 2.28 | 0.21 | 2.54 | 2.99 | 87.435 | 89.552 | 88.394 | 88.818 |
| 36 | 0.394 | 14 | 44.74 | 2.26 | 1.30 | 2.08 | 0.10 | 81.093 | 82.281 | 81.586 | 82.110 |
| 37 | 0.409 | 15 | 55.00 | 2.59 | 0.37 | 1.82 | 4.75 | 86.910 | 88.495 | 88.535 | 89.344 |
| 38 | 0.425 | 13 | 48.85 | 2.03 | 0.50 | 2.28 | 1.36 | 85.122 | 86.950 | 86.514 | 86.554 |
| 39 | 0.461 | 18 | 41.15 | 2.54 | 1.43 | 1.56 | 1.73 | 80.303 | 81.637 | 82.566 | 81.082 |
| 40 | 0.459 | 13 | 50.38 | 2.72 | 0.44 | 2.69 | 2.86 | 84.580 | 86.670 | 86.988 | 86.153 |
| Regression Evaluation Indicators | Training Set Value | Test Set Value |
|---|---|---|
| MAE | 0.0750 | 0.1116 |
| RMSE | 0.0773 | 0.1187 |
| 0.9989 | 0.9926 |
| Parameters | Initial Scheme | Scheme 1 ( and ) | Scheme 2 () |
|---|---|---|---|
| 0.421 | 0.439 | 0.406 | |
| 16 | 17 | 16 | |
| /° | 43.378 | 45.061 | 48.538 |
| /mm | 2.553 | 2.532 | 2.507 |
| /mm | 0.273 | 0.281 | 0.512 |
| /mm | 1.582 | 1.666 | 1.987 |
| /mm | 3.152 | 2.302 | 2.435 |
| /% | 88.467 | 87.993 | 85.705 |
| /% | 89.482 | 90.002 | 87.043 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Liu, Y.; Zhang, Q. Auxiliary Heat System Design and Off-Design Performance Optimization of OTEC Radial Inflow Turbine. Energies 2024, 17, 2767. https://doi.org/10.3390/en17112767
Wang Y, Liu Y, Zhang Q. Auxiliary Heat System Design and Off-Design Performance Optimization of OTEC Radial Inflow Turbine. Energies. 2024; 17(11):2767. https://doi.org/10.3390/en17112767
Chicago/Turabian StyleWang, Yiming, Yanjun Liu, and Qiang Zhang. 2024. "Auxiliary Heat System Design and Off-Design Performance Optimization of OTEC Radial Inflow Turbine" Energies 17, no. 11: 2767. https://doi.org/10.3390/en17112767
APA StyleWang, Y., Liu, Y., & Zhang, Q. (2024). Auxiliary Heat System Design and Off-Design Performance Optimization of OTEC Radial Inflow Turbine. Energies, 17(11), 2767. https://doi.org/10.3390/en17112767







