Stability Assessment of the High-Speed Flywheel with AMBs on a Rotating Platform

Abstract

With the continuous improvement of the performance and capabilities of spacecrafts, the application of active magnetic bearings (AMBs) has become a major focus in current research. The AMBs-flywheel system is not only responsible for attitude control but also provides the required energy during shadow periods. In magnetically suspended single gimbal control moment gyroscope (SGCMG), self-excited vibration caused by high-speed rotor rotation significantly affects the stability of the AMB system. The research focus lies in magnetically supporting the flywheel at high speeds with low power consumption to explore gyroscopic mechanics at ultra-high speeds and assess the corresponding stability. This study presents an assessment of the stability performance of a high-speed flywheel equipped on a single gimbal with an angular momentum of 75 Nm. To achieve ultra-high-speed operation under low driving power, a high-precise dynamic balance was performed followed by a novel unbalance control strategy of a radial and axial automatic balancing algorithm to suppress effectively synchronous vibrations due to nutation and precession. Corresponding experiments including static stable suspension experiments as well as low-speed, high-speed, and series-based stability assessments were conducted. Stable suspension at any speed ranging from 0 to 30,000 r/min was successfully implemented. The stability performance of the high-speed flywheel on a rotating platform at different gimbal speeds was verified, with a maximum speed reaching 31,200 r/min. The entire output torque process within the range of 30,000 r/min was revealed.

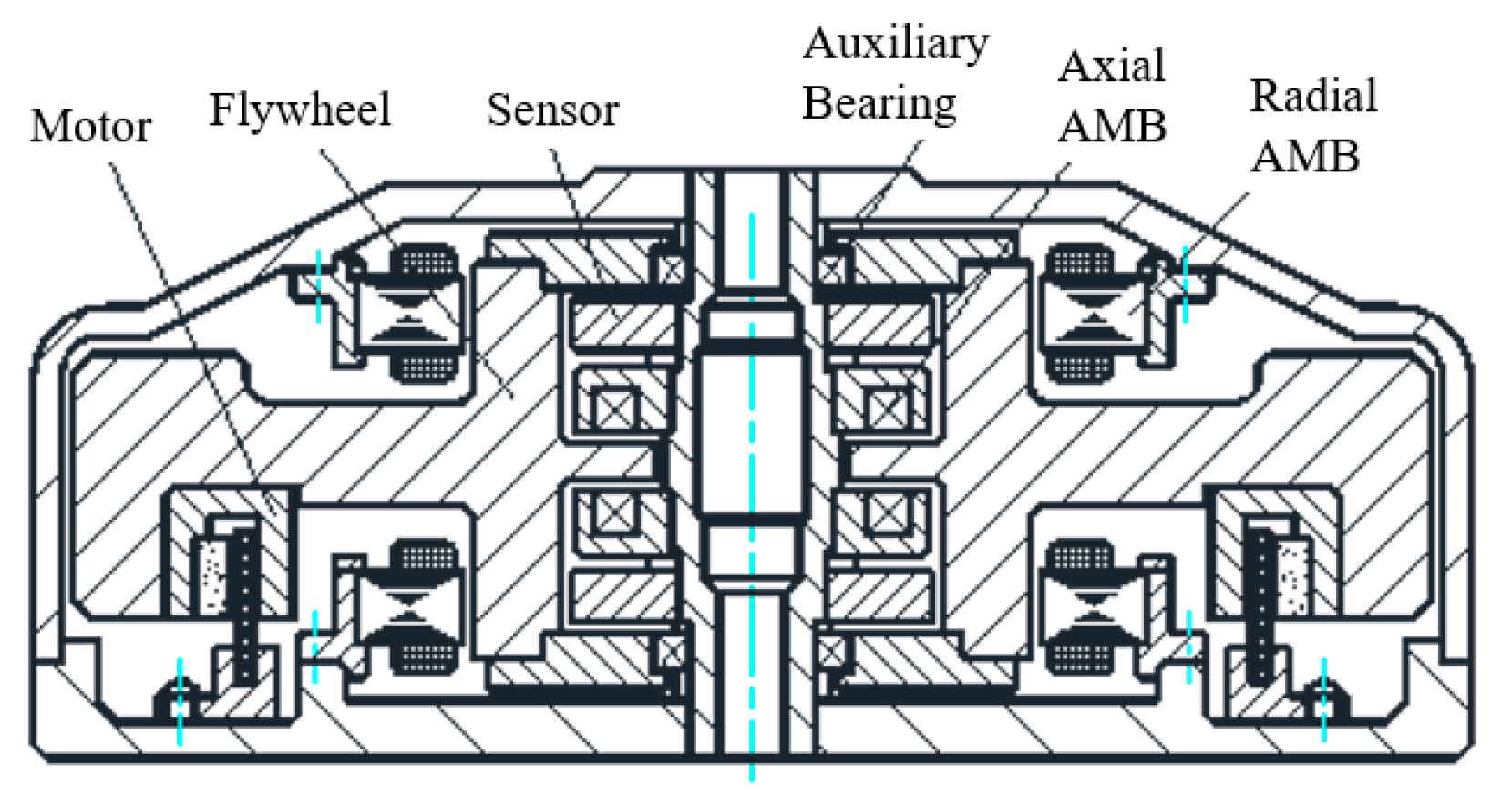
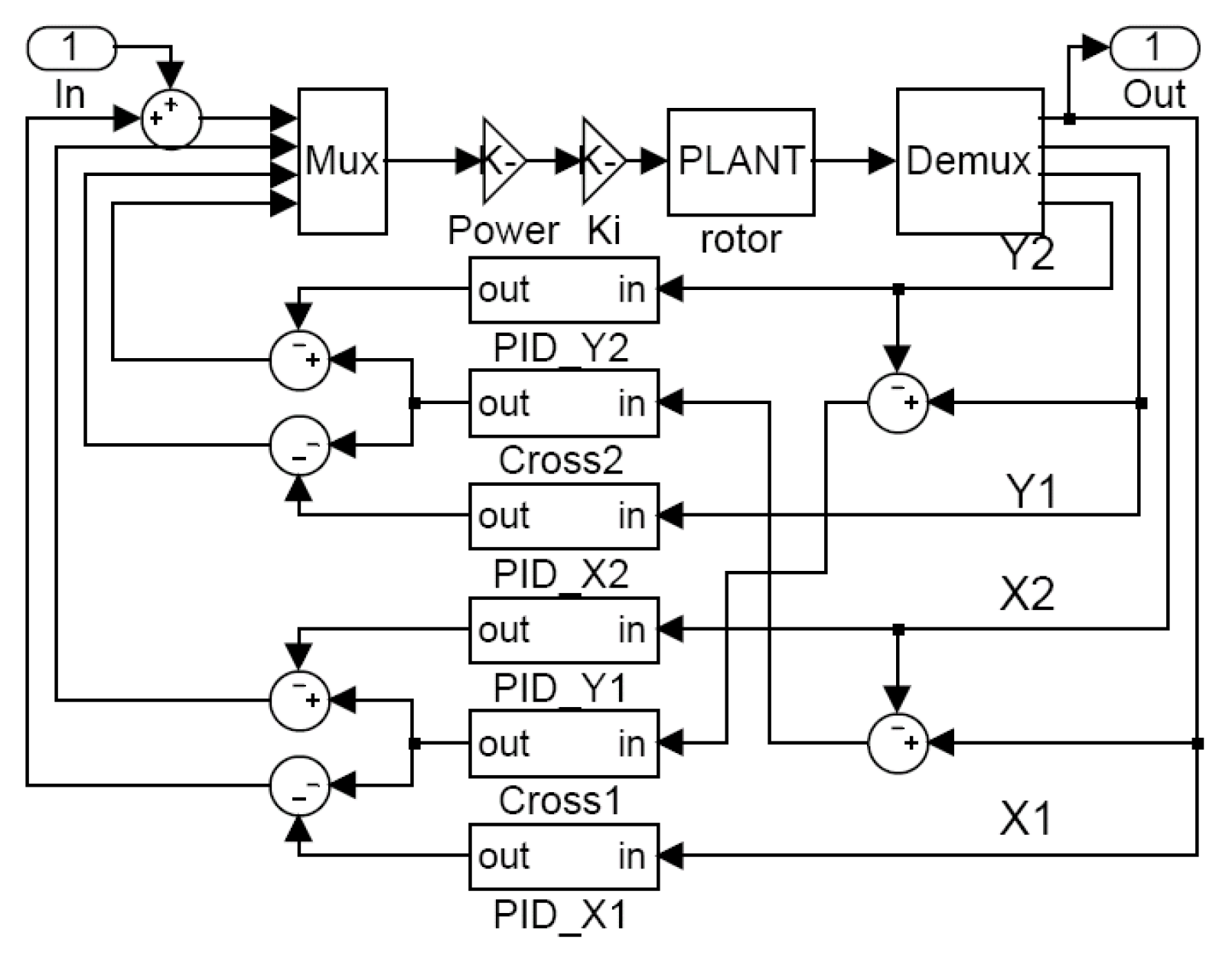
1. Introduction

The utilization of a high-speed flywheel enables the simultaneous control of spacecraft attitude and storage of energy, resulting in an augmented payload capacity. By incorporating magnetic bearings into the SGCMG, it becomes possible to operate at high speeds without encountering typical issues associated with passive bearings, such as wear, lubrication, and heating problems. Moreover, by providing adjustable stiffness and damping properties, synchronous vibrations and disturbances in angular momentum can be actively suppressed while compensating for machining errors without necessitating hardware adjustments, which significantly enhances operational stability and accuracy.

From the 1990s, the United States Air Force and NASA started research on the application of the maglev flywheel system for spacecraft energy storage and attitude control, and successively carried out a series of research programs such as FESS, IPACS, HEFF, AMPSS, and COMET [1]. The G2 AMB-flywheel is being used to replace chemical batteries on the International Space Station, while making attitude adjustments to the station and integrating energy storage and attitude control capabilities, and is designed to have a service life of up to 20 years [2]. Han B C, Hu G, and Fang J C et al. proposed a magnetically suspended reaction flywheel (MSRW) with a maximum speed of 10,000 rpm [3]. Xie J J et al. put forward a composite compensation method for the load torque to improve the suspension accuracy of the magnetically suspended rotor in a double-gimbal magnetically suspended control moment gyro (DGMSCMG) [4]. Zhang L et al. established a dynamic model of a small MSCMG gimbal and studied the adjustable range of AMB stiffness under stable conditions, the relationship between support stiffness and attitude control torque accuracy, as well as the adjustable range of AMB control parameters [5]. Liang T et al. developed a system model to describe the translational and rotational motion of an AMB-suspended rigid rotor in an SGCMG onboard a rigid satellite, which strictly reflected the motion characteristics of the rotor by considering the dynamic and static imbalance as well as the coupling between the gimbal’s and the rotor’s motion on a satellite platform [6].

The AMBs-flywheel system is a complex variable multi-coupled nonlinear system, whose complexity is further compounded by unbalance, gyroscopic effects, and external loads, particularly when rotating at high speeds, necessitating a highly sophisticated controller design to actively control and compensate for the adverse impact of the gyroscopic effect on stability, effectively addressing precession and nutation instabilities. Moreover, considering dynamics, rotation accuracy, and stability requirements, controller parameters play a crucial role in determining stiffnesses, damping characteristics, and dynamic responses. By incorporating displacement and velocity cross-feedback mechanisms into control strategies, nutation and precession can be effectively suppressed while ensuring sufficient modal damping [7]. Additionally, combination with a notch filter allows for effective suppression of the flexible mode.

The dynamic characteristics of AMBs are not only related to structural parameters, but also to adopted control strategies and parameters. The controllable performance of AMBs can effectively address the issues of dynamic mismatch commonly observed in traditional bearings. By employing appropriate control strategies, the controller enables real-time vibration control. The selection of a suitable controller is closely associated with both static and dynamic AMB characteristics, as well as rotational accuracy and braced forces.

Currently, the most commonly utilized control strategy in engineering applications is the PID control algorithm, particularly for rigid rotors. However, as to flexible rotors, given the uncertainty of parameters, the PID control capacity to resist significant unknown disturbances weakens [8]. Therefore, the improved PID controllers, such as H∞ controllers [9], μ controllers [10], sliding mode controllers [11], fuzzy control algorithms [12], genetic algorithms [13], neural network controllers [14], LQG controllers [15,16], etc., have gained widespread attentions.

In practical applications, control strategies not only require consideration of system stability but also take into account the rotor unbalance. Due to the material non-uniformity and machining errors, an unbalanced mass exists in the rotor, resulting in synchronous unbalanced vibrations and corresponding control currents. There are two major strategies for AMB unbalance control, unbalance compensation, and automatic balancing algorithms.

The unbalance compensation algorithm, also known as the zero-displacement control algorithm, has wide applicability to occasions of high rotation accuracy. Based on coefficient identification, it is relatively straightforward and effective, including adaptive identification [17], variable step size iterative search algorithm [18], beetle antennae search algorithm [19], and others, which exhibit good convergence and anti-interference properties. However, these algorithms typically require significant computational resources during signal processing phases. Therefore, Zheng et al. [20] proposed a novel iterative learning control algorithm which enhances control instantaneity by concurrently operating control strategy and signal extraction algorithm in parallel. Xu et al. [21] introduced a compensation control algorithm established on the combination of a first-order all-pass filter (APF) and the synchronous rotating frame (SRF) algorithm, demonstrating its efficiency in significantly reducing unbalance vibration while ensuring excellent stability. Disturbance observers [22] are frequently employed in the unbalance compensation control, while dependent on the system model. Under high-speed conditions, generating high-frequency compensation currents for unbalance compensation tends to induce power amplifier and actuator saturation. Consequently, high-speed unbalance control primarily relies on automatic balancing.

The automatic balancing control, also known as the zero-vibration power control, is suitable for applications with smooth operation and minimal external force transmission. Given its simplicity and practical advantages, the adaptive notch filter (ANF) has been widely adopted, making it the most mature and effective method currently available. To address instability at low speeds caused by the notch filter in the closed-loop system, Gong et al. [23] proposed a 4-factor polarity switching control algorithm. To ensure stable operation over a wide speed range, Liu et al. [24] designed a phase compensator which can be adjusted according to the speed. Li et al. [25] developed a dual-input notch filter based on the orthogonal characteristics of displacements in both x and y directions to effectively track and suppress multi-frequency interferences associated with harmonic vibrations. Peng et al. [26] introduced a feedforward compensation considering the phase lag of power amplifier, which eliminated residual synchronous components to maximize synchronous vibration suppression. Considering uncertainties in operation parameters, Hu et al. [27] proposed an online closed-loop parameter identification method for zero-vibration dynamic control to enhance control accuracy. Xu et al. [28] designed an adaptive regulator to mitigate adverse impacts on feedforward compensation induced by variations in working conditions such as temperature.

As for the flat rotor with severe gyroscopic effect, the utilization of a PID controller in combination with a cross-feedback notch filter [29] or the state feedback combined with a disturbance observer [30] can be adopted to achieve unbalance vibration suppression in the full speed range with the consideration of coupling. Additionally, research studies have also been conducted on algorithms such as robust control [31], unbalance identification [32], and second-order repetitive control [33]. However, most of these approaches suffer from poor practicality and are challenging to implement in industrial applications. Furthermore, many of the algorithms necessitate precise rotational speeds. Actually, limitations imposed by size, structure, cost constraints, and other factors often restrict the installation of speed sensors, thus requiring the unbalance control with the capability to estimate rotational speeds.

2. Dynamic Analysis

The SGCMG acquires angular momentum through the high-speed rotating rotor and regulates the external output torque by manipulating the direction of angular momentum. Figure 1 illustrates the configuration of SGCMG which comprises an AMBs-flywheel, a gimbal, and motors for both the rotor and the gimbal, respectively. The structure of the flywheel is depicted in Figure 2, in which the radial translation and rotation are controlled by the radial AMBs and the axial translation by the axial AMB. The flywheel rotation is propelled by the motor. Detailed parameters are revealed in

Table 1. Parameters.

Mass, m	5.4 kg
Polar moment of inertia, Jp	0.027 kg·m2
Equatorial moment of inertia, Jd	0.014 kg·m2
Distance between radial AMBs, l	40 mm
Rated speed, Ω	30,000 r/min, 500 Hz
Maximum vibration quantity at rated speed	10.0 μm
Steady-state power consumption	<20 W
Maximum angular momentum	75 N·ms

.

The gimbal is propelled by a servo motor and rotates at a preset angular speed. Consequently, the direction of angular momentum changes in accordance with gimbal angular velocity. A gyroscopic reaction moment, also known as the gyroscopic torque, is induced by the flywheel precession and imposed on the base subsequently, equivalent to the vector product of the gimbal speed and the flywheel angular momentum. A 3-DOF attitude control for satellites can be achieved through three or more SGCMGs.

The real-time monitoring system is developed based on LabVIEW 2017 SP1 platform. There are five signal channels of displacement measurement in the data acquisition system, and each displacement signal channel corresponds to positive and negative control currents. Eddy current displacement sensors of differential structure are equipped. The phase and speed of the motor are measured by a Hall sensor, which is embedded in the motor stator. The photoelectric sensor is adopted to measure contactlessly the rotor speed.

2.1. Gyro-Rotor Dynamic Analysis

As shown in Figure 3, the base is assumed to be fixed, with coordinates x_s, y_s, and z_s. The fixed coordinates of the flywheel are x_g, y_g, and z_g.

The distances between the AMBs and the rotor center are denoted as a and b, respectively. O denotes the center of mass, m the mass of the flywheel, J_p the polar moment of inertia, J_d the transverse moment of inertia, and Ω the rotational speed around the z axis. The stiffness matrix is K = diag[k₁, k₂, k₃, k₄], and the damping matrix D = diag[d₁, d₂, d₃, d₄]. The dynamic equations of the flywheel are as follows:

$$\left\{\begin{array}{l}m\ddot{x}=F_{x_1}+F_{x_2}\\ m\ddot{y}=F_{y_1}+F_{y_2}\\ J_d\ddot{\alpha }=a{F}_{y_1}-b{F}_{y_2}-J_p\Omega \dot{\beta }\\ J_d\ddot{\beta }=-a{F}_{x_1}+b{F}_{x_2}+J_p\Omega \dot{\alpha }\end{array}\right.$$

(1)

in which x and y denote the translational displacements of the mass center in the x_s and y_s axes, respectively, α and β the rotational angles, and F_x1, F_x2, F_y1 and F_y2 the magnetic forces at the cross sections of AMBs. The coordinates of the mass center are q = [β, x, −α, y]^T, and the bearing coordinate q_b = [x₁, x₂, y₁, y₂]^T:

$$q_b=Tq$$

(2)

in which,

$$T=\left[\begin{array}{cccc}-a& 1& 0& 0\\ b& 1& 0& 0\\ 0& 0& -a& 1\\ 0& 0& b& 1\end{array}\right]$$

(3)

The gimbal rotates around the x_s axis at a constant speed of ${\omega }_n$. The rotational angle relative to the rotor is determined as follows:

$$\theta ={\omega }_{n}t+{\theta }_0$$

(4)

in which, θ₀ denotes the initial angle, and t the interval of time. The magnetic forces applied on the rotor are calculated assuming a linearization of minor deviations.

$$\left\{\begin{array}{l}{F}_{x_1}=-(k_1{x}_1+d_1{\dot{x}}_1)\\ F_{x_2}=-(k_2{x}_2+d_2{\dot{x}}_2)\\ F_{y_1}=-[k_3(y_1-a({\omega }_{n}t+{\theta }_0))+d_3({\dot{y}}_1-a{\omega }_n)]\\ F_{y_2}=-[k_4(y_2+b({\omega }_{n}t+{\theta }_0))+d_4({\dot{y}}_2+b{\omega }_n)]\end{array}\right.$$

(5)

The dynamic equations with q_b = [x₁, x₂, y₁, y₂]^T can be derived accordingly. It is assumed that the rotor displacement relative to the gimbal remains negligible within a short time scale. The steady-state solution can be formulated as follows:

$$\left\{\begin{array}{l}{x}_1=x_{1r}t+x_{10}\\ x_2=x_{2r}t+x_{20}\\ y_1=y_{1r}t+y_{10}\\ y_2=y_{2r}t+y_{20}\end{array}\right.$$

(6)

in which the subscripts r and 0 denote the relative and the initial displacements, respectively. Accordingly, Equation (6) is substituted into Equation (1) for solution. It is derived as follows:

$$\left\{\begin{array}{l}{x}_1=x_{10}=-\frac{J_p\Omega {\omega }_n}{(a+b)k_1}\\ x_2=x_{20}=\frac{J_p\Omega {\omega }_n}{(a+b)k_2}\\ y_1=y_{1r}t+y_{10}=a({\omega }_{n}t+{\theta }_0)\\ y_2=y_{2r}t+y_{20}=-b({\omega }_{n}t+{\theta }_0)\end{array}\right.$$

(7)

$$\left\{\begin{array}{l}{F}_{x_1}=\frac{J_p\Omega {\omega }_n}{a+b}\\ F_{x_2}=-\frac{J_p\Omega {\omega }_n}{a+b}\\ F_{y_1}=0\\ F_{y_2}=0\end{array}\right.$$

(8)

The steady state reveals the absence of any relative movements in the y-axis direction. The AMBs generate electromagnetic forces in the x-axis direction, resulting in an external output torque:

$$M_{out}=-(-a{F}_{x_1}+b{F}_{x_2})=J_p\Omega {\omega }_n$$

(9)

in which M_out denotes the output torque of the flywheel, transmitted to the base.

2.2. State-Space Model

The state-space model is capable of accurately describing the coupling between multiple variables. According to Equation (1), the transfer function of the rotor, G_r(s), can be expressed as follows:

$$Z_B(s)=G_r(s)f(s)$$

(10)

in which s is the operator in Laplace transforms,

$$Z_B={\left[\begin{array}{cccc}{x}_1& x_2& y_1& y_2\end{array}\right]}^T$$

(11)

$$f={\left[\begin{array}{cccc}{F}_{x1}& F_{x2}& F_{y1}& F_{y2}\end{array}\right]}^T$$

(12)

$$G_r(s)=\left[\begin{array}{cccc}\frac{1}{m{s}^2}+\frac{a^2{J}_{d}s}{den}& \frac{1}{m{s}^2}-\frac{ab{J}_{d}s}{den}& -\frac{a^2{J}_p\Omega }{den}& \frac{ab{J}_p\Omega }{den}\\ \frac{1}{m{s}^2}-\frac{ab{J}_{d}s}{den}& \frac{1}{m{s}^2}+\frac{b^2{J}_{d}s}{den}& \frac{ab{J}_p\Omega }{den}& -\frac{b^2{J}_p\Omega }{den}\\ \frac{a^2{J}_p\Omega }{den}& -\frac{ab{J}_p\Omega }{den}& \frac{1}{m{s}^2}+\frac{a^2{J}_{d}s}{den}& \frac{1}{m{s}^2}-\frac{ab{J}_{d}s}{den}\\ -\frac{ab{J}_p\Omega }{den}& \frac{b^2{J}_p\Omega }{den}& \frac{1}{m{s}^2}-\frac{ab{J}_{d}s}{den}& \frac{1}{m{s}^2}+\frac{b^2{J}_{d}s}{den}\end{array}\right]$$

(13)

$$den={J_d}^2{s}^3+{J_p}^2{\Omega }^{2}s$$

(14)

The electromagnetic force is linearized at the equilibrium position. The radial ith force, F_xi, is expressed as follows:

$$F_{xi}=k_{ii}{I}_i+k_{xi}{x}_i (i=1,2,3,4)$$

(15)

in which k_ii denotes the ith current stiffness, k_xi the ith displacement stiffness, I_i and x_i the ith current and displacement, respectively. The relationship between force-displacement coefficient matrix, force-current coefficient matrix, and transfer function is deduced as follows, taking into account the gyroscopic effect:

$$f(s)=K_{i}I(s)+K_s{Z}_B(s)$$

(16)

$$Z_B(s)=G_r(s)[K_{i}I(s)+K_s{Z}_B(s)]$$

(17)

$$G_r(s)K_{i}I(s)=-[G_r(s)K_s-I_{4\times 4}]Z_B(s)$$

(18)

in which, $K_i=diag\left(\begin{array}{cccc}{k}_{i1}& k_{i2}& k_{i3}& k_{i4}\end{array}\right)$, $K_s=diag\left(\begin{array}{cccc}{k}_{x1}& k_{x2}& k_{y1}& k_{y2}\end{array}\right)$, $I={\left[\begin{array}{cccc}{I}_{c1}& I_{c2}& I_{c3}& I_{c4}\end{array}\right]}^T$. The following is obtained:

$$M_1{\ddot{Z}}_c+G_1{\dot{Z}}_c+T_{b}f=0$$

(19)

in which $Z_c={\left[\begin{array}{cccc}x& \alpha & y& \beta \end{array}\right]}^T$, and I_c1 to I_c4 denote the ith control current, respectively. M₁, G₁, and T_b are all real coefficient matrixes. The relationship between Z_c and Z_B is deduced as follows:

$$Z_c=T_B{Z}_B$$

(20)

in which, T_B denotes the transfer matrix. Accordingly, it is obtained as follows:

$$M{\ddot{Z}}_B+G{\dot{Z}}_B+K_s{Z}_B+K_{i}U=0$$

(21)

in which $M=\left[\begin{array}{cccc}{m}_a& m_0& 0& 0\\ m_0& m_b& 0& 0\\ 0& 0& m_a& m_0\\ 0& 0& m_0& m_b\end{array}\right]$, $G=\frac{J_p\Omega }{l^2}\left[\begin{array}{cccc}0& 0& 1& -1\\ 0& 0& -1& 1\\ -1& 1& 0& 0\\ 1& -1& 0& 0\end{array}\right]$, $m_a=\frac{m{b}^2+J_d}{l^2}$, $m_a=\frac{m{a}^2+J_d}{l^2}$, $m_0=\frac{mab-J_d}{l^2}$. m_a and m_b denote the equivalent mass at the radial AMBs, respectively. m₀ denotes the coupling mass, which quantifies the degree of movement coupling at both rotor ends.

The state-space model has now been established. The state vector, control vector, and output vector are presented below:

$$X(t)={[{\begin{array}{cccccccc}{x}_1& x_2& x_3& x_4& {\dot{x}}_1& {\dot{x}}_2& {\dot{x}}_3& \dot{x}\end{array}}_4]}^T$$

(22)

$$U(t)=I={[\begin{array}{cccc}{I}_{c1}& I_{c2}& I_{c3}& I_{c4}\end{array}]}^T$$

(23)

$$Y(t)={[\begin{array}{cccc}{y}_1& y_2& y_3& y_4\end{array}]}^T$$

(24)

in which $y_i(i=1,2,3,4)$ denotes the displacement output vector. The equation of the state space is obtained as follows:

$$\left\{\begin{array}{l}\dot{X}=AX+BU\\ Y=CX\end{array}\right.$$

(25)

in which $A=\left[\begin{array}{cc}{0}_{4\times 4}& I_4\\ M^{-1}{K}_s& -M^{-1}G\end{array}\right]$, $B=\left[\begin{array}{c}{0}_{4\times 4}\\ M^{-1}{K}_I\end{array}\right]$, $C=\left[\begin{array}{cc}{I}_4& 0_{4\times 4}\end{array}\right]$, $X={\left[\begin{array}{cc}{\dot{Z}}_B& Z_B\end{array}\right]}^T$.

The displacement at the radial electromagnet needs to be converted by sensor probes. c and d denote the distances between the left sensor and the right one from the center of mass, O. Z_S denotes the displacement of the probe and Z_B the displacement of the electromagnet:

$$Z_S=T_{SB}{Z}_B$$

(26)

in which T_SB denotes the coupling matrix of sensors, shown as follows:

$$T_{SB}=\left[\begin{array}{cccc}\frac{b+c}{b+a}& \frac{a-c}{b+a}& 0& 0\\ \frac{b-d}{b+a}& \frac{d+a}{b+a}& 0& 0\\ 0& 0& \frac{b+c}{b+a}& \frac{a-c}{b+a}\\ 0& 0& \frac{b+c}{b+a}& \frac{d+a}{b+a}\end{array}\right]$$

(27)

The magnetic force is designated as input, while the installation position of displacement sensor probes as output. The corresponding transfer function can be expressed as follows:

$$G_0(s)=G_s(s)T_{SB}{G}_r(s)$$

(28)

3. Control Strategy

3.1. LQR Controller

The linear quadratic regulator (LQR), as a centralized control method, fully considers the interdependence of each DOF. Based on Equation (25), it is assumed that $\dot{Z}(t)=Y(t)$. The augmented form of state equation can be derived as follows:

$${\dot{X}}_1=A_1{X}_1+B_{1}U$$

(29)

in which

$$X_1=\left[\begin{array}{c}X\\ Z\end{array}\right],A_1=\left[\begin{array}{cc}A& 0\\ C& 0\end{array}\right],B_1=\left[\begin{array}{c}B\\ 0\end{array}\right]$$

The optimization of the performance index function is truly the core of the algorithm. The linear quadratic performance index function is as follows:

$$J={\displaystyle {\int }_0^{+\infty }\left({X_1}^{T}Q{X}_1+U^{T}RU\right)dt}$$

(30)

The Q matrix is a non-negative definite symmetric matrix, and the R matrix a positive definite matrix. The first term in the integral expression reflects the requirement for minimizing the controlled quantity or maximizing its decay rate, and the second term reflects the constraint on control energy. Consequently, the optimal feedback control which satisfies the minimum value of the performance index function can be obtained as follows:

$$u^{*}(t)=-F{X}_1(t)=-R^{-1}{B_1}^{T}P{X}_1(t)$$

(31)

in which, F denotes the optimal feedback matrix, and P the solution of the Riccati matrix equation, which is the following:

$$P{A}_1+{A_1}^{T}P-P{B}_1{R}^{-1}{B_1}^{T}P+Q=0$$

(32)

As to only the rigid mode, it can be reasonably optimized by ensuring that the number of output signals is greater than or equal to the variable one. Consequently, a comprehensive observation of the flywheel status can be achieved.

LQR requires solving the problem of selecting two weighted matrices for the objective function: one denotes bounded constraints on the control quantity U, while the other ensures the coordination among internal weights of performance indicators. The former reflects physical limitations imposed on the input U, and adjustments in damping ratio can be made through the allocation of the internal weight in the performance indexes.

3.2. Static-Suspension Controller

In the initial stage of controller design, it is challenging to design directly a high-performance controller due to the lack of precise parameters. Typically, the first step involves designing a controller that achieves static and stable suspension. Based on the frequency identification through sweeping, specific information is obtained to meet the actual requirements of a high-performance controller. Therefore, the static suspension controller is designed by combining theoretical and experimental analysis in an iterative optimization process.

The design of a low stiffness system controller is based on the principle of minimum control energy. The R matrix is set to the identity matrix, and the Q matrix is selected as follows:

$$Q=\left[\begin{array}{ccc}{Q}_p{I}_{4\times 4}& & \\ & Q_D{I}_{4\times 4}& \\ & & Q_I{I}_{4\times 4}\end{array}\right]$$

(33)

By selecting the appropriate Q matrix, the optimal feedback matrix is obtained as below:

$$F=\left[\begin{array}{cccccccccccc}8021& -11& 0& 0& 26& -2& 0& 0& 202228& 0& 0& 0\\ -11& 8021& 0& 0& -2& 26& 0& 0& 0& 202228& 0& 0\\ 0& 0& 8021& -11& 0& 0& 26& -2& 0& 0& 202228& 0\\ 0& 0& -11& 8021& 0& 0& -2& 26& 0& 0& 0& 202228\end{array}\right]$$

(34)

The optimal feedback matrix reveals that radial orthogonal DOFs are decoupled in the absence of gyroscopic effect when the rotor speed is 0. The displacement, velocity, and integral terms significantly outweigh the cross term. To achieve stable suspension, a decentralized PID controller is employed. An exemplary PID controller is as follows:

$$G(s)=8021+26s+\frac{202228}{s}$$

(35)

The ideal PID controller is converted into a practical and implementable one with a transfer function as follows:

$$G_1(s)=\frac{25000(s+280.8)(s+27.7)}{(s+942.5)(s+2.094)}$$

(36)

The actual suspended states can be observed in Figure 4.

The static suspension cannot be satisfactorily achieved solely through a distributed PID controller designed for an ideal model. It is evident that the vibration primarily originates from the structural mode near 370 Hz, necessitating effective suppression.

3.3. Notch Filter

Given the aforementioned results of the system identification, the structural modes with intermediate frequency are observed, which are motivated by the lower cover shell and the connecting parts with support bolts. However, in the LQR controller design, no consideration was given to these structural modes which can be excited during high-speed operation. Additionally, the high-frequency noise signals can also stimulate this mode leading to increased vibrations. The amplitude of vibration at the structural modal frequency is determined by its corresponding gain. Therefore, effective suppression of structural modal vibration can be achieved through reduction of the gain via controller design strategies.

To address this issue specifically for a frequency of 370 Hz, a notch filter was designed utilizing a Chebyshev II band-block filter.

3.4. Zero-Pole Phase Compensator

The principle behind the zero-pole phase algorithm lies in shaping the phase to enhance the damping ratio at the mode frequency. For each ith structural mode, a phase compensator is employed:

$$G_{phi}=\frac{\left(s+{\omega }_1\right)\left(s+{{\omega }_1}^{*}\right)}{\left(s+{\omega }_2\right)\left(s+{{\omega }_2}^{*}\right)}$$

(37)

in which, $\omega$ and $\omega$* are conjugate values, and ${\omega }_1$ and ${\omega }_2$ the zero poles of the phase compensator, respectively. The specific compensators are illustrated in Equations (38) and (39):

$$G_1(s)=\frac{s^2+370s+4.436\times {10}^6}{s^2+370s+6.773\times {10}^6}$$

(38)

$$G_2(s)=\frac{s^2+370s+4.973\times {10}^6}{s^2+370s+6.142\times {10}^6}$$

(39)

Given the structure mode operating at a frequency of 370 Hz, the center frequency for phase compensation is determined to be 370 Hz. The bandwidth in Equations (38) and (39) are specified as 40 Hz and 80 Hz, respectively.

With the increase of the bandwidth, the damping increases, while the gain of the low frequency band of the amplitude–frequency characteristic curve gradually increases before the peak of the phase frequency wave. Therefore, the selection of bandwidth needs comprehensive consideration.

3.5. Cross-Feedback Controller

The centralized controller was designed using the LQR algorithm, resulting in obtaining optimal feedback matrix elements for displacement and speed cross-feedback terms. Compensation for the gyroscopic effect was achieved by introducing a cross-feedback channel in addition to the distributed PID controller. The parameters remain unchanged from those of the static-suspension controller. The optimal feedback matrix calculated by LQR at 400 Hz remains as follows:

$$F=\left[\begin{array}{cccccccccccc}4411& 3592& 4985& -4985& 18& 4& 0& 0& 120042& 82186& 98623& -98623\\ 3592& 4411& -4985& 4985& 4& 18& 0& 0& 82186& 120042& -98623& 98623\\ -4985& 4985& 4411& 3592& 0& 0& 18& 4& -98623& 98623& 120042& 82186\\ 4985& -4985& 3592& 4411& 0& 0& 4& 18& 98623& -98623& 82186& 120042\end{array}\right]$$

(40)

The specific speed of the rotor induces non-zero displacement coupling terms (F(1,3), F(1,4), F(2,3), F(2,4), F(3,1), F(3,2), F(4,1), F(4,2)) and velocity terms (F(1,7), F(1,8), F(2,7), F(2,8), F(3,5), F(3,6), F(4,5), F(4,6)) in the feedback matrix due to the gyroscopic effect at high speed. These values are comparable to the displacement and speed feedback terms, respectively.

Figure 5 illustrates a practical decentralized PID controller with a cross-feedback channel. The LQR algorithm can serve as a basis for parameter selection in the decentralized PID controller coupled with cross feedback. The step response at a speed of 400 Hz is shown in Figure 6, revealing an observed instability caused by nutation. Through effective cross feedback, it is possible to suppress nutation vibration and achieve an improved stability margin.

3.6. Unbalance Controller

3.6.1. Automatic Unbalance Controller

Rotor unbalance arises from variations in quality, material, machining, and assembly errors. Even a minor residual unbalance can significantly impact the system at high speeds. Unbalance control reduces synchronous excitation to enhance stability and effective capacity of AMBs while minimizing power consumption. The automatic unbalance control strategy capitalizes on controllable stiffness and damping to prevent controller response to synchronous displacements. It enables the rotor to rotate around its inertial principal axis and ultimately achieve force-free operation while eliminating external transmission.

To eliminate synchronous disturbances effectively, corresponding signal resonances should be suppressed at input points. The automatic unbalance controller and the original PID controller operate on different time scales, effectively functioning independently of each other. The control strategy eliminates rotor-induced synchronous interference with the base and enables rotation around the inertial principal axis.

Accurately determining the gain and phase of rotor unbalanced vibration is crucial for designing a high-performance unbalanced controller. By constructing a synchronous filter that ensures stability of the closed-loop system, it is possible to minimize synchronous current while striking a balance between stability and trap depth.

3.6.2. Base Vibration Suppression Controller upon Axial Force-Free Control

During acceleration experiments, the automatic balancing control was applied to the radial end. However, when accelerated to a certain speed, severe axial vibrations occurred between the axial end and the base, inducing system instability. Real-time detection reveals that while synchronous current at the radial end has been filtered out completely, significant synchronous periodic vibrations are observed at the axial end along with a sharp increase in both axial displacement and control current. Consequently, the automatic balancing control for radial ends fails to meet the requirements of the AMBs-flywheel.

To address the issue of axial vibration, a control method was proposed to eliminate axial forces at the base, effectively enhancing system stability and ultra-stationary operation. The simultaneous periodic vibrations primarily stem from mass unbalance and geometric errors in the displacement sensor reference surface. During dynamic balancing, limitations in accuracy result in unavoidable residual unbalances. Additionally, factors such as sensor noise, natural modes of vibration, assembly errors, nonlinearity of electromagnetic field, and other disturbances can impact position adjustment stability and power consumption.

In the case of external-rotor flywheels, when there exists a certain range for both vertical accuracy of the axial datum plane and rotational axis alignment, geometric errors induce additional base vibrations whose amplitude is determined by residual unbalances and geometric inaccuracies. The displacement sensor is highly sensitive to the quality of the rotor surface. In the case of small probes, additional control algorithms are required to compensate for geometric errors such as surface roughness, roundness, unbalanced displacement, and straightness error. Direct measurement of axial displacement signals in external rotors is not possible, while only being obtained through differential sensors installed at each end. Due to geometric errors, it is challenging to fully guarantee perpendicularity between the axial measurement surface and the rotating axis. The geometric relationship between the ideal and actual conditions is illustrated in Figure 7 and Figure 8.

The schematic diagram of the actual structure is elaborated in Figure 9 and Figure 10. r denotes the radial displacement, and h the axial displacement. Axial displacement sensors A and B are arranged in a differential configuration. The angles between the axial measurement surface and the horizontal direction are denoted as α₁ and α₂, respectively. Given the geometric error of the axial measurement surface:

(1)

${\alpha }_1>0,{\alpha }_2<0$

$$\left\{\begin{array}{c}{z}_A=h\cos {\alpha }_1-r\sin {\alpha }_1\\ z_B=-h\cos {\alpha }_2-r\sin {\alpha }_2\\ z=\frac{h\cos {\alpha }_1-r\sin {\alpha }_1-(-h\cos {\alpha }_2-r\sin {\alpha }_2)}{2}\end{array}\right.$$

(41)

When $\left|{\alpha }_1\right|=\left|{\alpha }_2\right|$, the radial coupled disturbance is eliminated correspondingly, there remaining only axial components in the measured signals. However, when $\left|{\alpha }_1\right|\ne \left|{\alpha }_2\right|$, the radial coupled disturbance is involved, which will have an impact on the axial control.

(2)

${\alpha }_1>0,{\alpha }_2>0$

$$\left\{\begin{array}{c}{z}_A=h\cos {\alpha }_1-r\sin {\alpha }_1\\ z_B=-h\cos {\alpha }_2+r\sin {\alpha }_2\\ z=\frac{h\cos {\alpha }_1-r\sin {\alpha }_1-(-h\cos {\alpha }_2+r\sin {\alpha }_2)}{2}\end{array}\right.$$

(42)

In this scenario, the occurrence of radial coupled disturbance is inevitable. The axial control is undeniably influenced by radial unbalanced responses. Due to high precision of machining, α₁ and α₂ are typically quite small, usually less than $1^{\circ }$, accompanied by additional axial vibration. The rotor rotates around the principal axis of inertia through the radial automatic balancing control, resulting in synchronous components in the radial signals due to unbalance. Given differential structures of axial sensors, complete decoupling between axial and radial signals cannot be achieved due to limitations in structural accuracy. Consequently, the final axial signals consist of both axial displacement signals and coupling radial ones.

An axial unbalanced control was implemented. A 5-DOF automatic unbalancing control was realized, in which the rotor rotates around the inertial principal axis without eliciting synchronous responses from the axial controller or transmitting corresponding synchronous axial forces to its base.

4. High-Speed Rotation Experiments

The designed controller was utilized to conduct system operation experiments, aiming to verify its effectiveness based on the previous theoretical analysis and system identification.

4.1. Stable Static Suspension and Vibration Suppression of Structural Modes

The rotor orbits and the radial displacement spectrum are depicted in Figure 11. In the static suspension experiments, the zero-pole phase compensation controller was employed to effectively mitigate vibration of the structure mode. The vibration amplitude in each DOF was maintained below 1 μm, ensuring stable static suspension.

After effectively suppressing the structural mode, the displacement spectrum of the radial AMB during acceleration is depicted in Figure 12, revealing a relatively small amplitude compared to the same frequency.

4.2. Suppression of Gyroscopic Effect

When the AMBs-flywheel operates at high speeds, the frequencies of nutation and precession bifurcate. The precession frequency gradually decreases to zero, while the nutation frequency continues to increase. Experiments were conducted to investigate the suppressive effect of cross-feedback control on gyroscopic effects.

Without the cross-feedback compensation control, as depicted in Figure 13, the precession instability occurs at a low frequency of 40 Hz. Given that the precession frequency typically falls within a lower range, effectively damping induced vibrations becomes challenging. The unstable precession frequency is measured at 8 Hz. The decentralized PID controller fails to provide sufficient modal damping. Therefore, incorporating a positive displacement cross-feedback controller is recommended.

The instability of 110 Hz, characterized by a nutation frequency of 210 Hz, is depicted in Figure 14. The ratio between the nutation frequency and rotor speed stands at 1.91, slightly surpassing the moment of inertia ratio of 1.9. To mitigate effectively nutation vibration, it is recommended to incorporate negative displacement and speed cross-feedback into the decentralized PID controller.

The cross-feedback control was combined with dedicated high-pass and low-pass filters, respectively. By optimizing control parameters, continuous acceleration experiments were conducted. Figure 15 illustrates the orbits and spectrum at 150 Hz with the adoption of cross-feedback control. Both nutation and precession modes were effectively suppressed while ensuring system stability.

4.3. Unbalance Control

The acceleration experiments were conducted continuously with automatic balancing control as follows:

(1)

Turn off the unbalance control and propel the rotor in a stable suspended state with an acceleration up to 150 Hz. The corresponding orbits, spectrum, and control currents are depicted in Figure 15 and Figure 16.

(2)

Activate the unbalance control on the radial end only and initiate rotor propulsion in a stable suspended state, gradually accelerating to 150 Hz. The corresponding orbits, spectrum, and control currents are depicted in Figure 17 and Figure 18.

(3)

The radial end and axial end force-free control should be simultaneously activated to propel the rotor into a stable suspended state with an acceleration of up to 150 Hz. Figure 19 and Figure 20 depict the corresponding orbits, spectrum, and control currents.

Radial unbalance control proves advantageous in reducing synchronous components present in the radial control currents. The rotor exhibits a tendency to rotate around its inertial principal axis, resulting in smaller orbits. With axial automatic balancing control involved, the synchronous components within control currents are effectively eliminated. This not only reduces the energy consumption but also prevents premature saturation of the power amplifier and lowers requirements. The diminished orbits primarily stem from the elimination of rigid sympathetic vibration through automatic balancing control, thereby creating a system that appears devoid of external synchronous support stiffness.

Certain limitations must be acknowledged when employing automatic balancing control. In instances where initial balance quality is low, collisions between the rotor and auxiliary bearings may occur due to displacement pulsation exceeding the gap between them, leading to system instability. Generally, vibrations should not exceed half of the amplitude of the gap during acceleration. It is imperative to conduct high-precision dynamic balancing prior to engaging in high-speed experiments.

The vibration intensity of the base was detected using a vibration analyzer, VA-12. Figure 21 compares the radial vibration spectrums of the base with and without the radial unbalance control at a rotation speed of 30 Hz. Without radial automatic balancing control, the base experiences severe radial vibrations that tend to increase correspondingly with acceleration, which seriously affects operation accuracy. However, almost all synchronous radial vibrations were eliminated by implementing radial automatic balancing control.

With automatic balancing control on the radial end, continuous rotor acceleration leads to serious axial synchronous vibrations at 50 Hz, hence, axial unbalance control is necessary. Figure 22 shows that axial automatic balancing control reduces vibration amplitude by approximately 50%. Experimental results confirmed suppression of synchronous vibrations and demonstrated that gravity can also be controlled. Radial and axial automatic balancing controls improve stability and enable ultra-static operation.

4.4. Dynamic Balance Experiment

Upon implementing automatic balancing control, the flywheel was accelerated to a frequency of 400 Hz. The orbits and spectrum of 400 Hz before and after dynamic balance are depicted in Figure 23 and Figure 24, respectively, while the corresponding currents can be observed in Figure 25 and Figure 26.

After achieving dynamic balance, the orbits exhibit a significant reduction in conjunction with a decrease in synchronous displacement amplitude. The control currents demonstrate an almost complete absence of components at the same frequency as the rotor. Consequently, the operational stability has been enhanced.

4.5. High-Speed Experiment

The flywheel can be smoothly accelerated to the rated speed of 500 Hz, due to the utilization of high-precision dynamic balance and meticulously designed relevant controllers. The resulting Figure 27 and Figure 28 depict the orbits, spectrums, and currents.

It can be observed that the amplitude of the synchronous vibration is less than 2 μm. In addition, with effective suppression of high-speed precession and nutation, there is no noticeable vibration. The bias current is relatively small, effectively controlling overall energy consumption. The control current exhibits no obvious glitch. Dynamic balancing improves the balance quality of flywheel, enhancing stability at high speeds.

Figure 29 illustrates the vibration spectrum of the base at 500 Hz. Both flywheel and base vibrations were maintained within a narrow range to ensure system stability across a wide range. The actual maximum speed reaches 31,200 rpm with excellent stability, approaching the material ultimate strength limit. Considering operation safety, further acceleration was not pursued. The synchronous vibration intensity of the base was measured at 0.016 mm/s. The maximum vibration intensity, derived from a power frequency of 50 Hz, remains below the general industrial standard by less than 0.1 mm/s. In Figure 30, the moment of resistance measures less than 0.011 Nm.

Considering ultra-high-speed operation experiments, both the rated working speed and synchronous vibration levels between the rotor and base meet the expected design requirements and demonstrate effective control effect. Key performance metrics are presented in

Table 2. Key performance metrics.

Performance Metrics	Values
Rated speed, r/min	30,000
Maximum speed, r/min	31,200
Radial synchronous vibration, μm	<2
Base vibration intensity, mm/s	0.016
Total energy consumption, W	17.82

.

5. High-Speed Stability Experiments

Stability experiments were conducted to validate the entire system. The operating conditions are divided into four types:

(1)

The outer frame remains stationary while the flywheel accelerates from a standstill to its rated speed

(2)

The outer frame is locked while the flywheel rotates at its rated speed

(3)

The flywheel maintains its rated speed while the frame rotates at a set angular speed

(4)

The outer frame is locked while the flywheel decelerates from the rated speed to a standstill.

The maximum angular momentum of the AMBs-single frame moment gyroscope is 85 Nm·s. Stable operation of the flywheel is achieved at 500 Hz with a potential for further improvement.

Output torque experiments were conducted to evaluate high-speed stability and analyze the influence of the frame speed on the rotor orbits and control currents. Additionally, actual maximum output torque under different frame speeds was also determined.

5.1. Maximum Output Torque with Limitation of Gravity and Magnetic Saturation Restriction

The magnetic forces exerted on the rotor in the x direction can be described as F_x1+, F_x1−, F_x2+, and F_x2−. The maximum capacity of a single electromagnet can be calculated as follows:

$$f_{\max }=\frac{{B_{\max }}^2{A}_a}{{\mu }_0}$$

(43)

in which A_a denotes the area of the poles, B_max the maximum magnetic flux density, and ${\mu }_0$ the permeability of vacuum. When a silicon alloy transformer sheet is selected, the recommended maximum magnetic flux density is B_max = 1.5 T, and the maximum capacity f_max = 198.23 N. The forces are analyzed as follows when the flywheel is in a stable suspended state:

$$\left\{\begin{array}{l}mg=F_{x1+}-F_{x1-}+F_{x2+}-F_{x2-}\\ M_{out}=a(F_{x1+}-F_{x1-})-b(F_{x2+}-F_{x2-})\end{array}\right.$$

(44)

The theoretical maximum capacity for each individual magnet is f_max, and the corresponding maximum output torque is as follows:

$$M_{\max }=f_{\max }\cdot (a+b)-mg\cdot b$$

(45)

In the actual experiments, magnetic bearings were required to counteract the influence of gravity. The stable operating points differ from those in the actual space environment. Gravity diminishes the effective value of the output torque, as depicted in Figure 31. The output torque increases correspondingly in a weightless environment. The experiments on output torque were conducted on the ground, resulting in partial consumption of electromagnetic force by rotor gravity and further limitation imposed by magnetic saturation.

5.2. High-Speed Stability Experiment

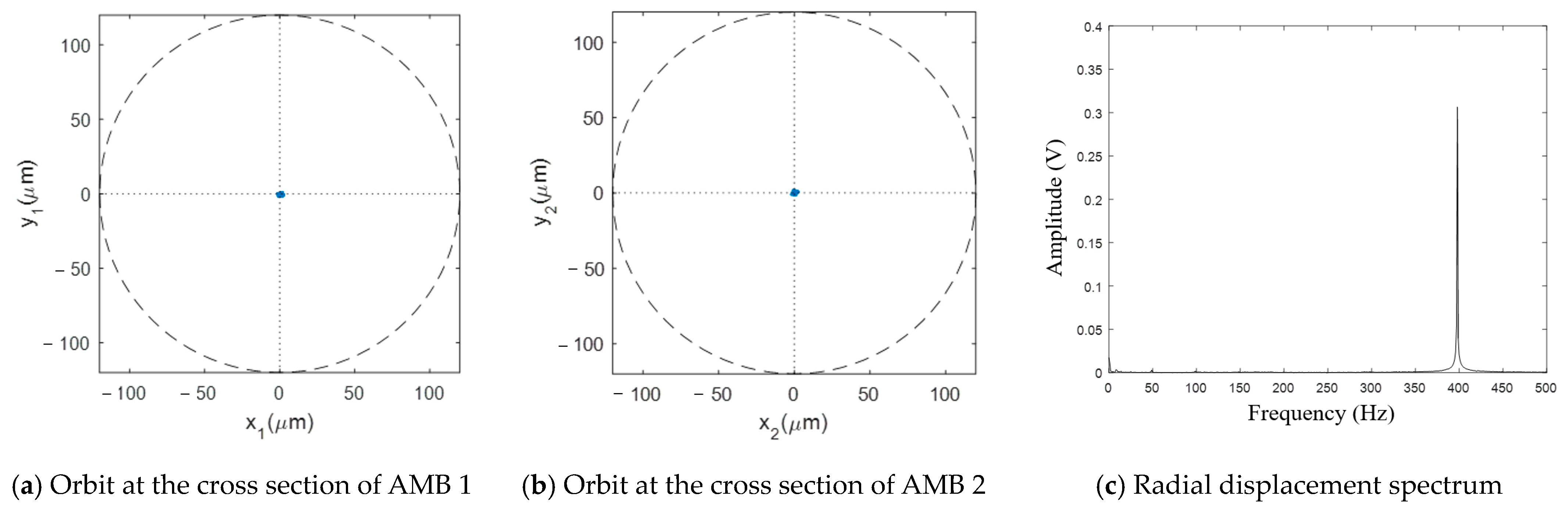
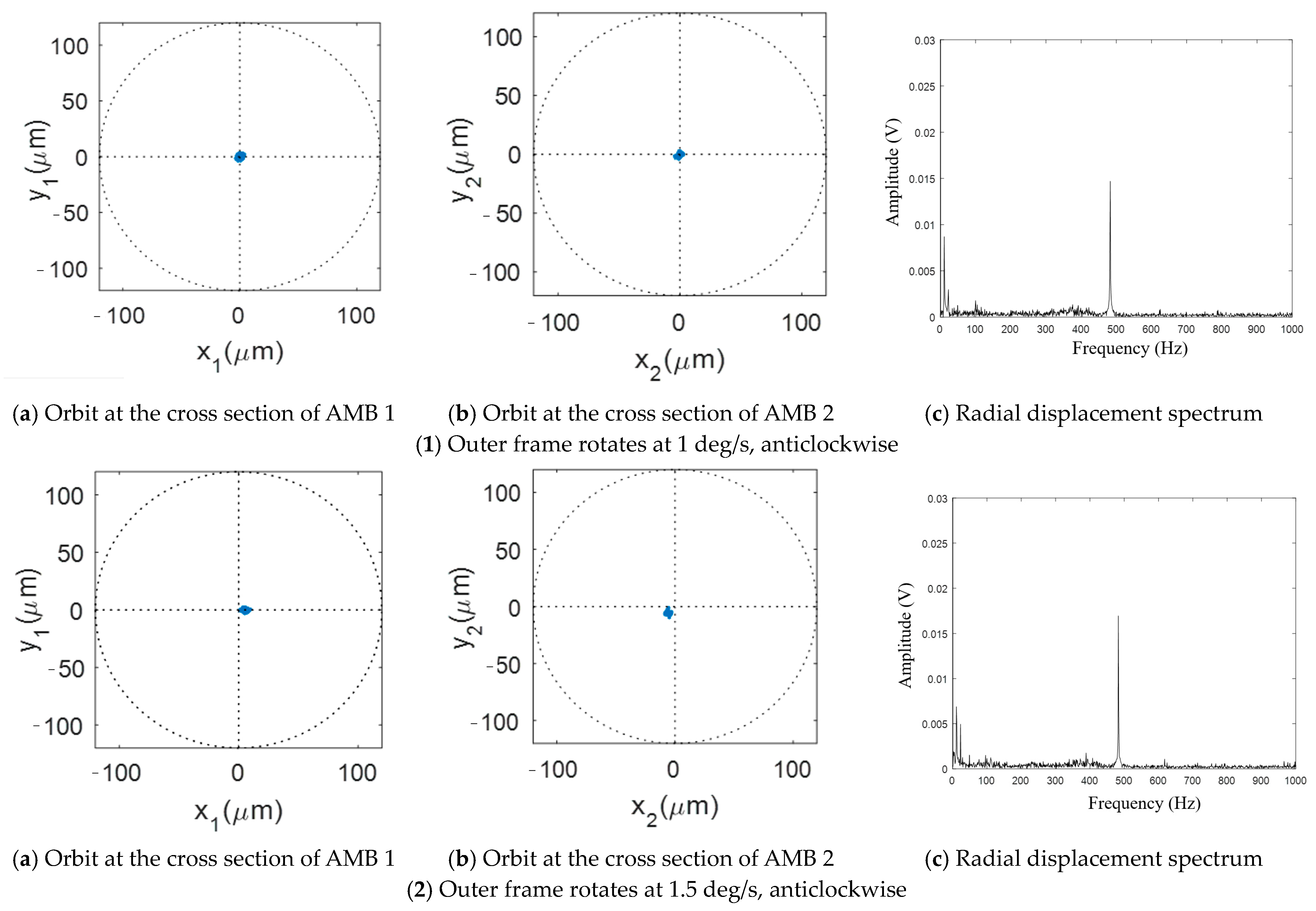
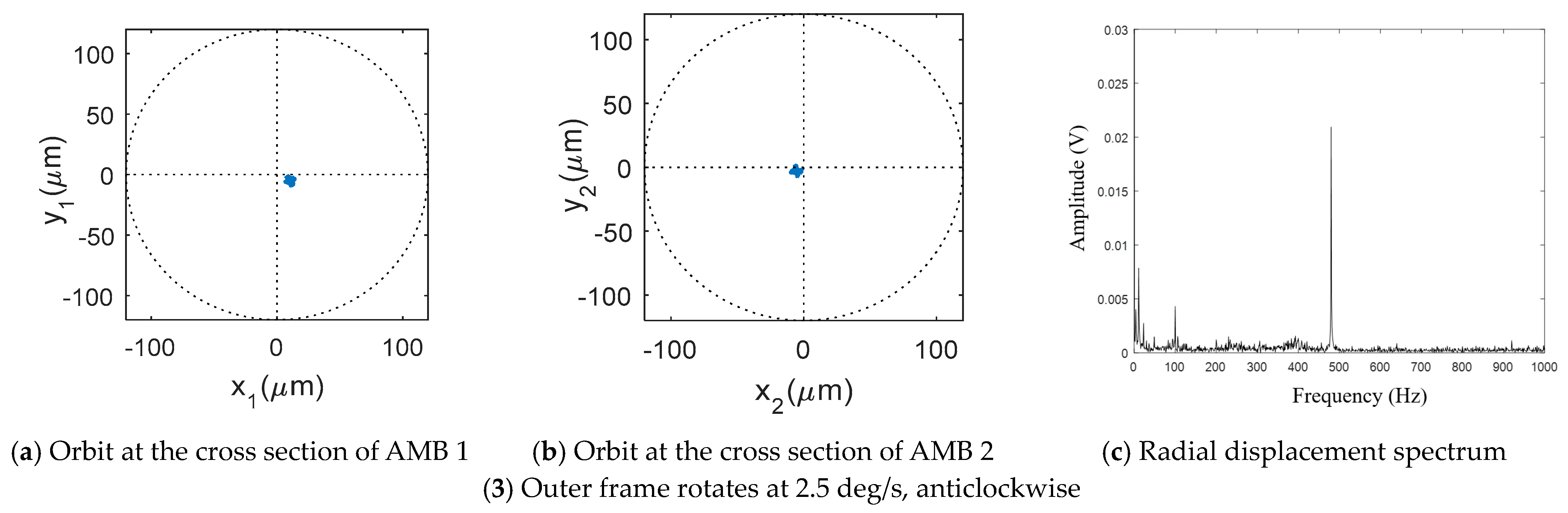
The flywheel accelerates to the rated speed of 500 Hz and maintains stable operation, while the outer frame rotates at varying angular speeds. The orbits of the rotor and the radial displacement spectrum are depicted in Figure 32.

The experimental results demonstrated that increasing the frame speed does not significantly impact the rotor orbits, thereby confirming the superior robustness and anti-jamming capability of the AMB control system. The dynamic stability of the high-speed flywheel with AMBs was validated, enabling precise spacecraft posture adjustment through high-precision output torque.

5.3. Dynamic Experiments of Output Torque

The flywheel was accelerated to a specific speed and maintained stability. The frame was propelled to rotate at varying angular speeds, while recording the radial AMB currents at each DOF. As mentioned above, when only the steady-state response is considered, there is no relative motion between the rotor and the frame in the y direction. The external output torque was generated by electromagnetic force in the x direction.

In actual output torque tests, due to minimal changes in y-direction current, only the x-direction current was discussed. By gradually increasing the frame speed until magnetic saturation occurs, the characteristics of output torque during acceleration up to the rated speed were studied correspondingly. Figure 33 and Figure 34 depict variations in the x-direction current corresponding to frame speed as the flywheel accelerates to 100 Hz and 200 Hz, respectively.

The control currents vary with the speeds of both the flywheel and the outer frame. It was demonstrated that the flywheel can be stably suspended even when rotating at high speeds. It is assumed that rotor displacements remain constant. The magnetic force was calculated as f_x = k_ii − k_xx, F_x1 = f_x1+ − f_x1−, F_x2 = f_x2+ − f_x2−. The current of each DOF in the bearing can be characterized by the corresponding magnetic force.

When the flywheel rotates at a stable fixed speed, the speed of the frame is gradually accelerated until reaching magnetic saturation. The dynamic characteristics of the output torque are as follows:

(1)

The output torque is relatively small at low rotational speeds of the frame. The magnitudes of magnetic forces f_x1+ and f_x2+ are greater than those of f_x1− and f_x2−. Consequently, the resultant magnetic forces at both ends of the rotor are in the positive direction along the x-axis, as depicted in Figure 35a. Most of the magnetic force provided by the AMBs is utilized to counteract gravity, with only a minor portion contributing to external output torque

(2)

As the rotation speed of the outer frame continues to increase, F_x1 keeps rising while F_x2 decreases until reaching zero, as shown in Figure 35b. At this point, F_x2 = 0, the rotor is only propelled by F_x1, the magnetic force provided by the AMB 1, which remains in a cantilever state

(3)

The external output torque further increases with an acceleration in frame speed. F_x1 increases positively along the x-axis direction while F_x2 decreases negatively, as illustrated in Figure 35c. The resultant magnetic forces at both ends stimulate forcibly rotor rotation. The majority of the magnetic forces contribute in providing output torque while a smaller portion counteracts gravity.

The dynamic characteristics of the output torque align with the aforementioned theoretical analysis. The output torque exhibits a numerical proportionality to both the speeds of the flywheel and the outer frame. Furthermore, an increase in polar moment of inertia results in a corresponding increase in output torque. The magnetic forces are primarily responsible for generating the output torque. The maximum capacity directly determines the magnitude of the output torque.

5.4. Ultimate Performance Experiments

The flywheel was accelerated to various speeds and maintained stability. Simultaneously, the gimbal speed was increased to its maximum until the rotor exhibited violent oscillations. The actual utilization rate of output torque $\eta$ can be evaluated by the following:

$$\eta =\frac{M_{out}}{M_{\max }}\times 100\%=\frac{J_p\Omega {\omega }_n}{M_{\max }}\times 100\%$$

(46)

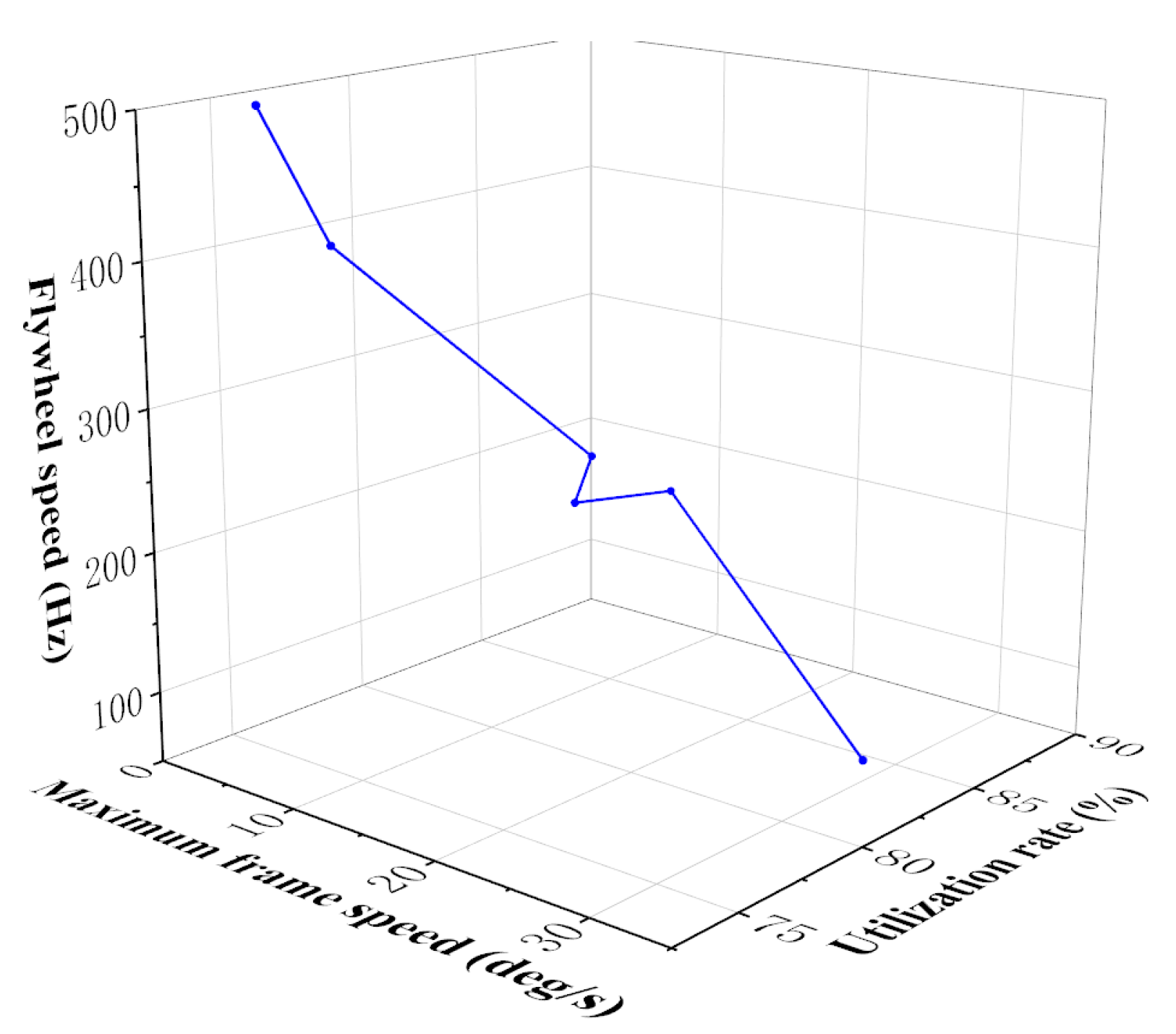
The actual utilization rate and the maximum gimbal speed are depicted in Figure 36, respectively. It was realized that the flywheel rotates at the rated speed of 500 Hz, achieving a utilization rate of 74.95% and a maximum gimbal speed of 3.5 deg/s.

The stable working points observed in ground experiments and their corresponding results differ from those obtained in the real space environment. The presence of gravity reduces the effective value of the output torque, while under conditions of weightlessness the output torque will increase accordingly.

6. Conclusions

A study was presented to enable an assessment of the stability of a high-speed flywheel suspended magnetically on a movable platform. Initially, static stable suspension experiments were conducted. Upon the suppression of structural modal vibration, low-speed experiments were carried out in conjunction with a distributed PID controller and a zero-pole phase compensation controller. During continuous acceleration, a cross-feedback controller was introduced to suppress effectively nutation and precession. Combined with high-precision dynamic balancing, a radial and axial automatic balancing controller was utilized to achieve ultra-high-speed operation with low driving power consumption. Successful implementation of stable suspension at any speed from 0 to 30,000 r/min ensures system stability on a large scale. Moreover, stability experiments at an ultra-high speed of up to 31,200 r/min were conducted to evaluate ultimate performance indicators. The influence of gimbal speed on orbits and control currents was examined, while characteristics of the entire output torque process within the range of 0 to 30,000 r/min were obtained. Performance indicators such as actual output torque utilization rate, and maximum gimbal speed were accordingly revealed. Stable operation of the flywheel at different gimbal speeds was achieved at the rated speed of 500 Hz, confirming the high accuracy of the output torque.