Influence of Coherent Vortex Rolls on Particle Dynamics in Unstably Stratified Turbulent Channel Flows
Abstract
1. Introduction
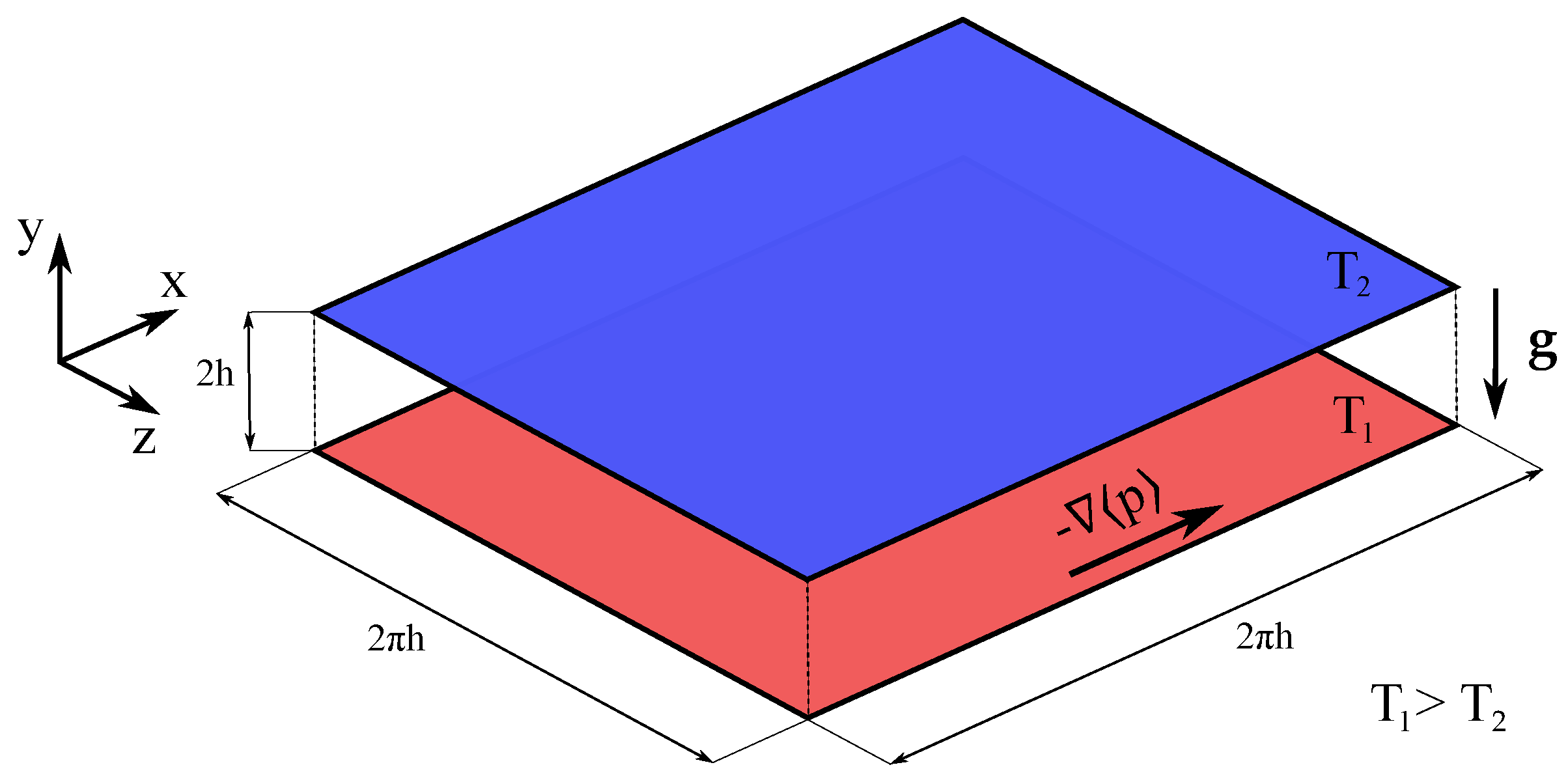
2. Physical Model and Methodological Instruments
2.1. Governing Equations
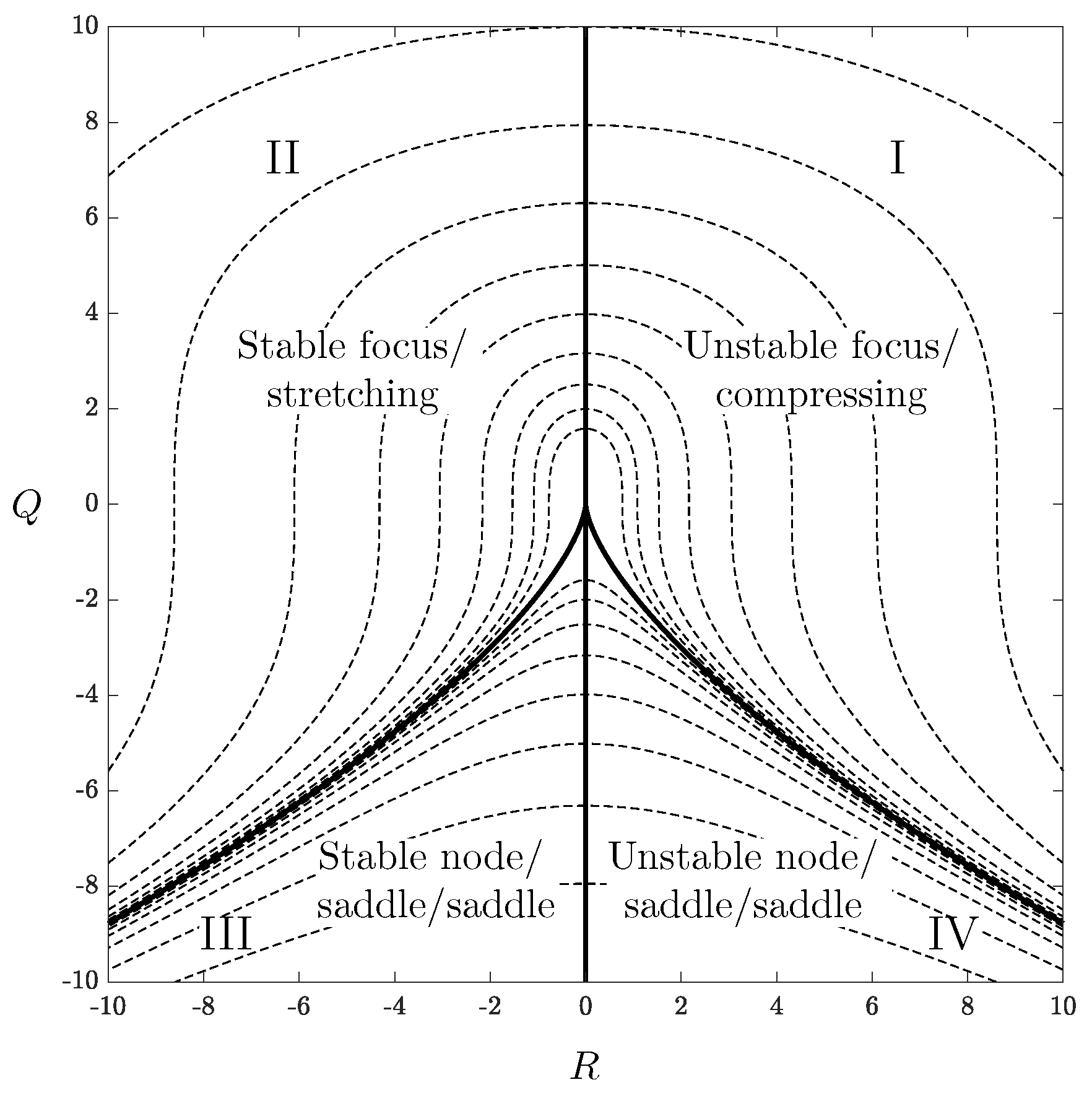
2.2. Invariants of the Velocity Gradient Tensor
3. Results and Discussion
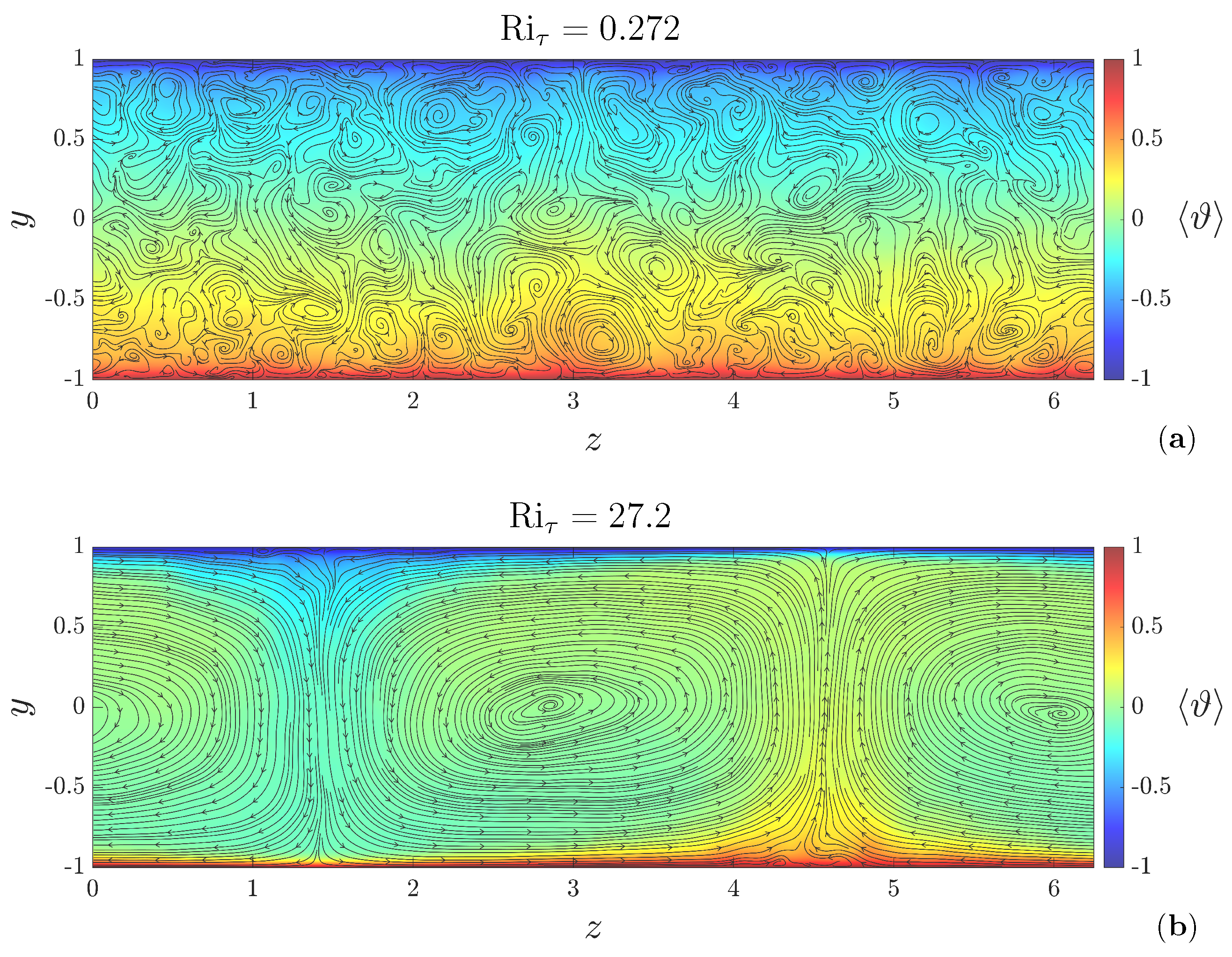
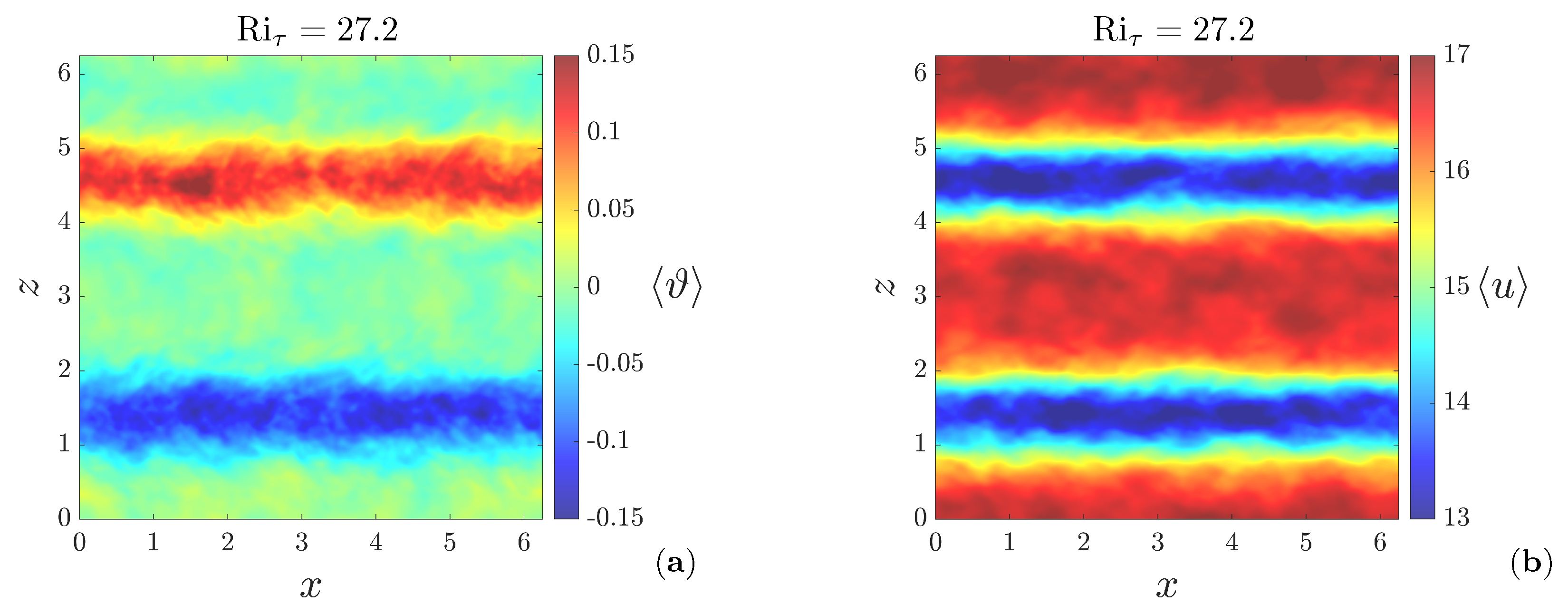
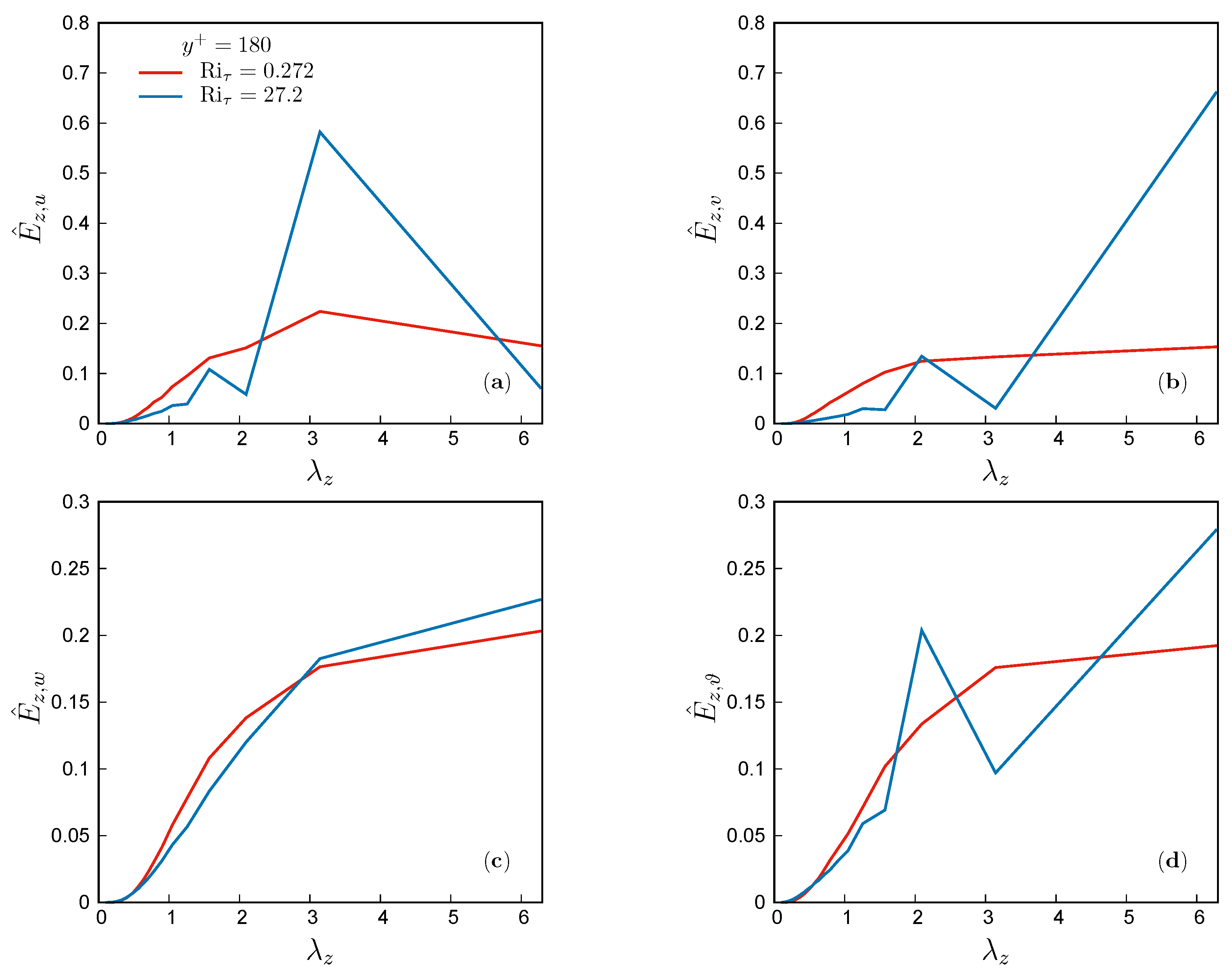
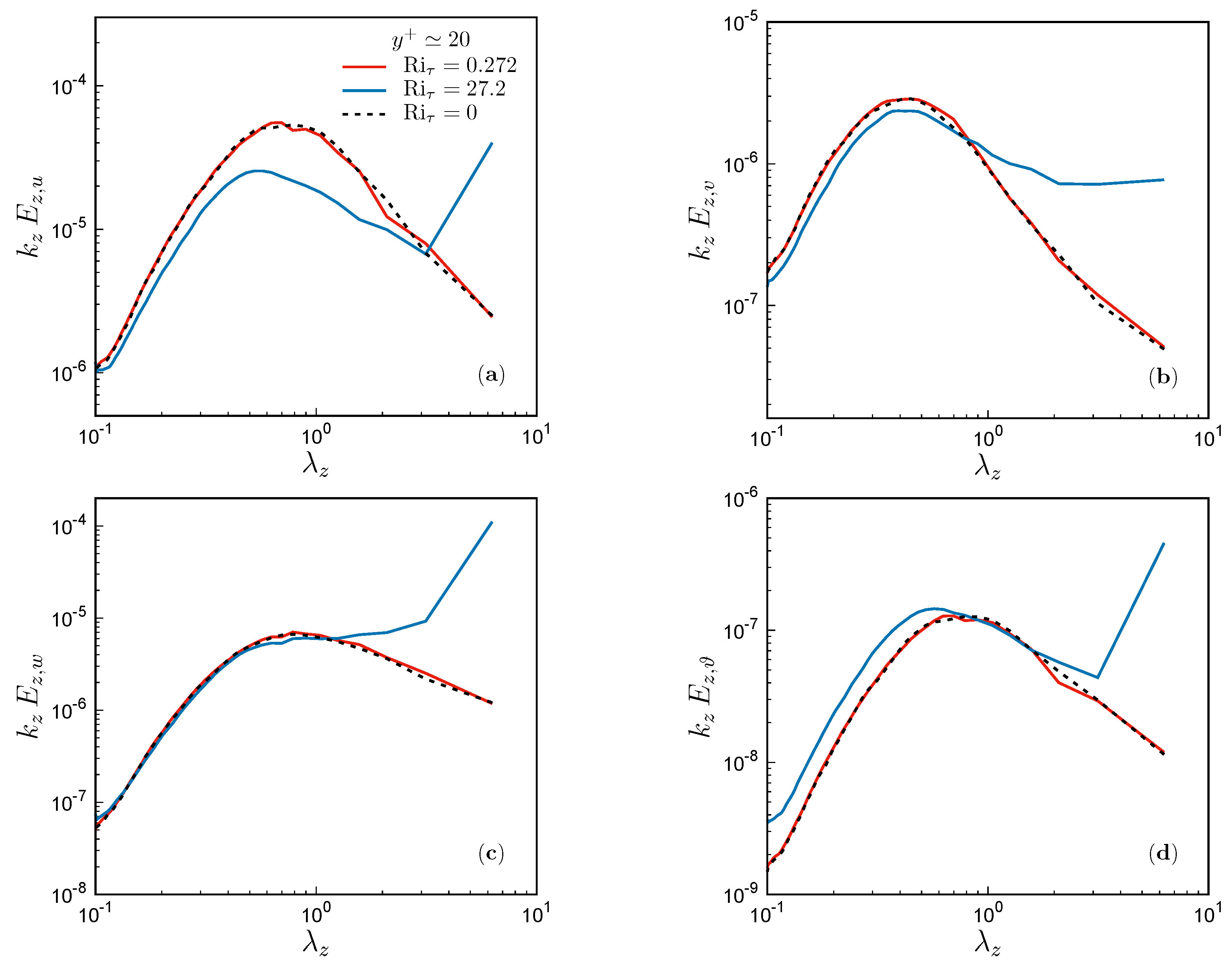
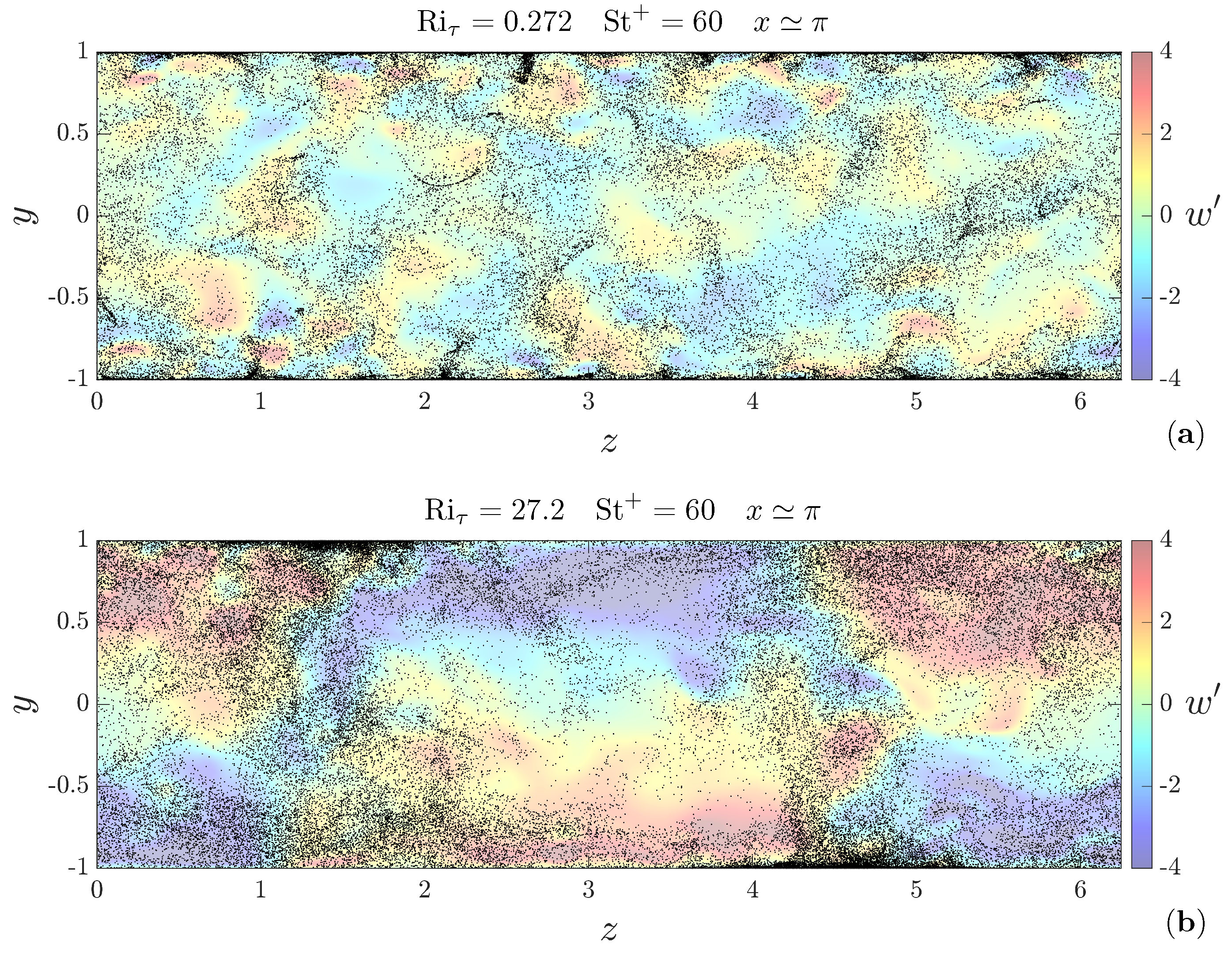
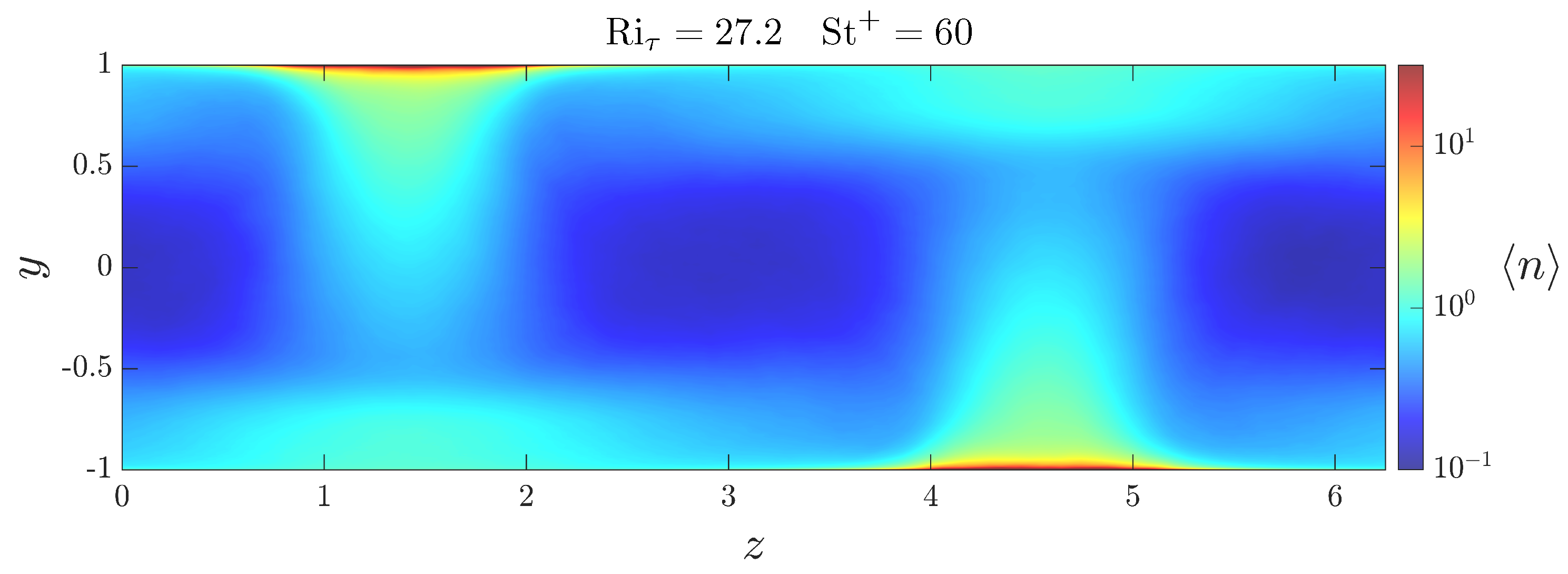
3.1. Flow Organization
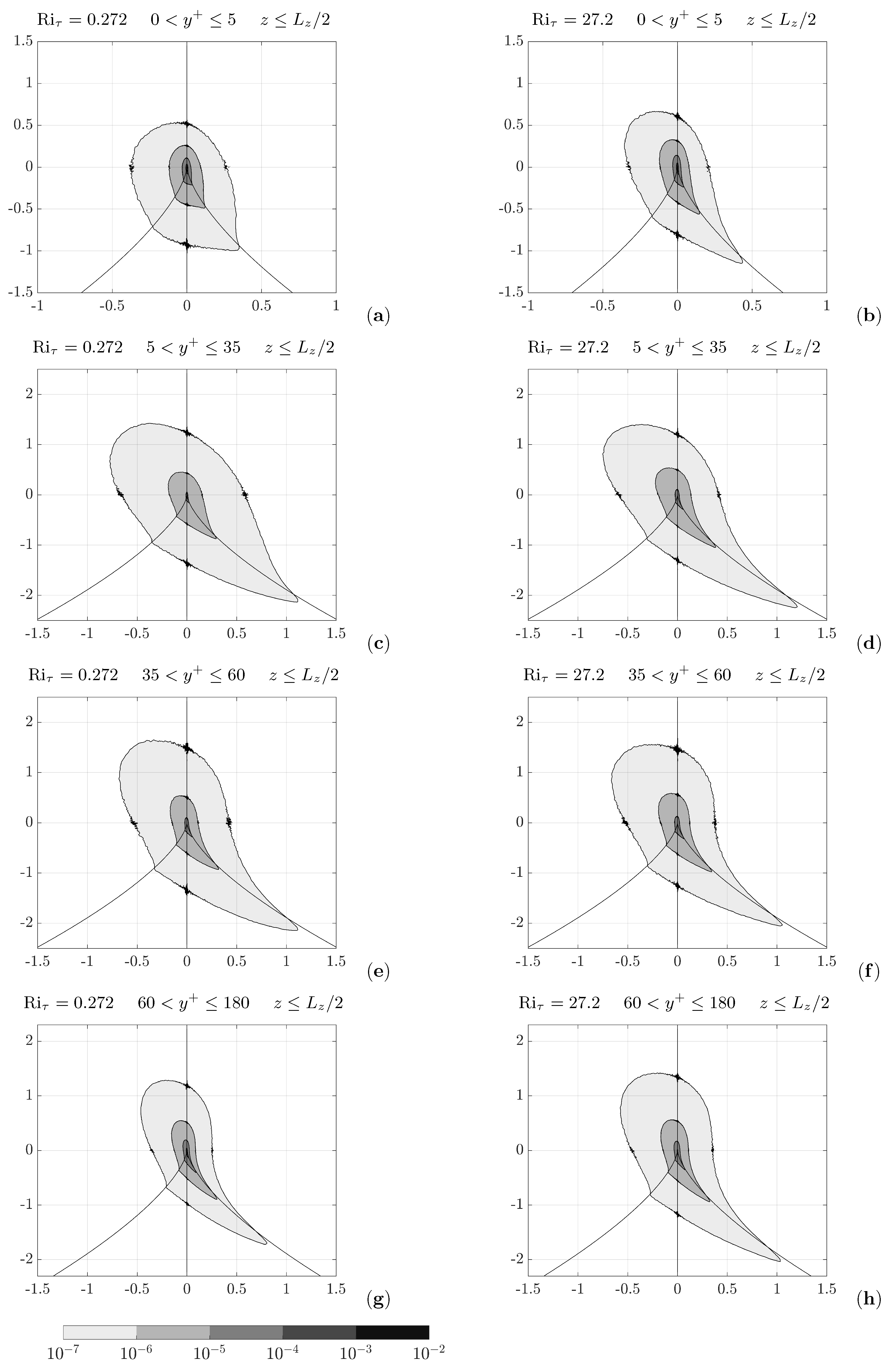
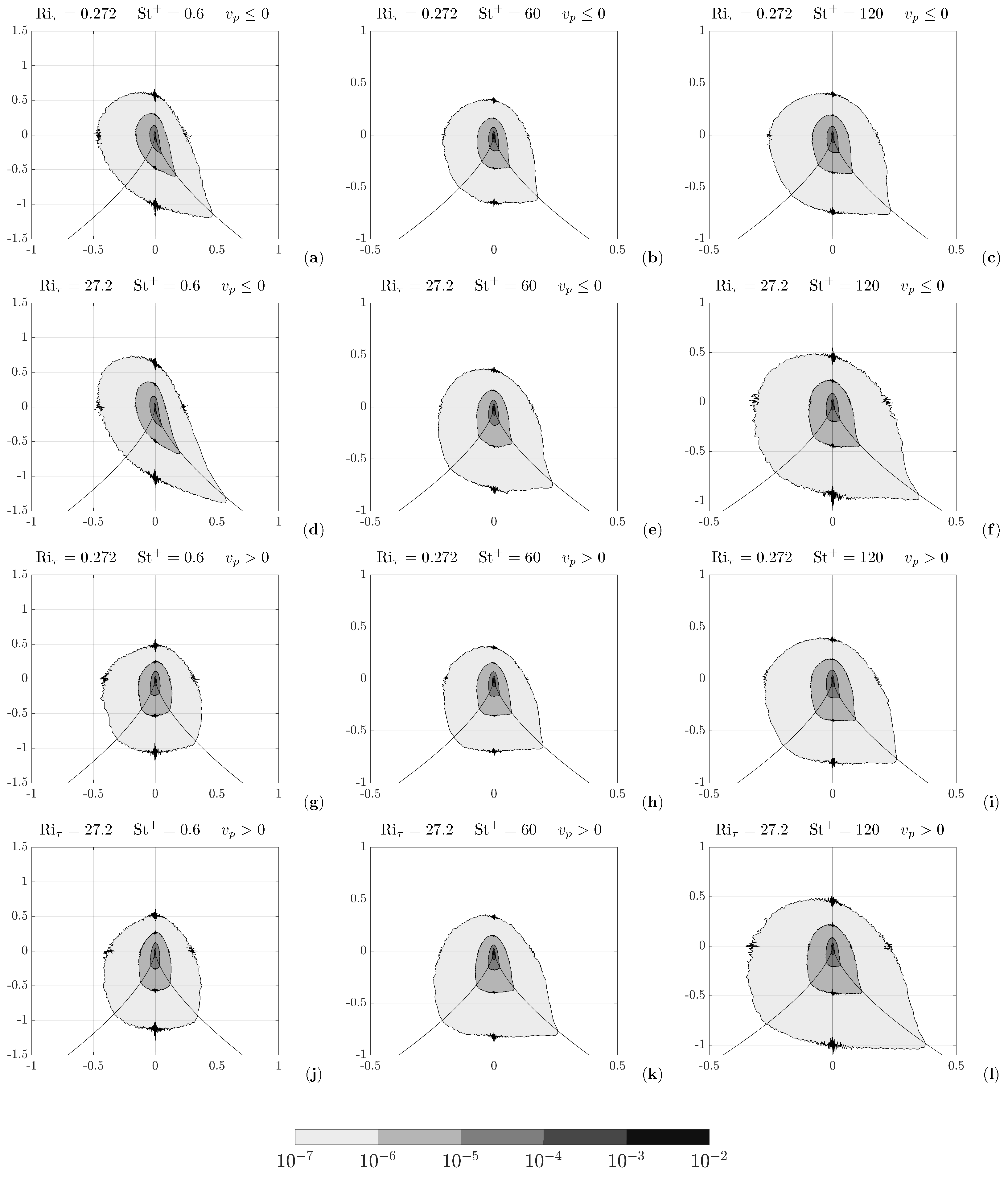
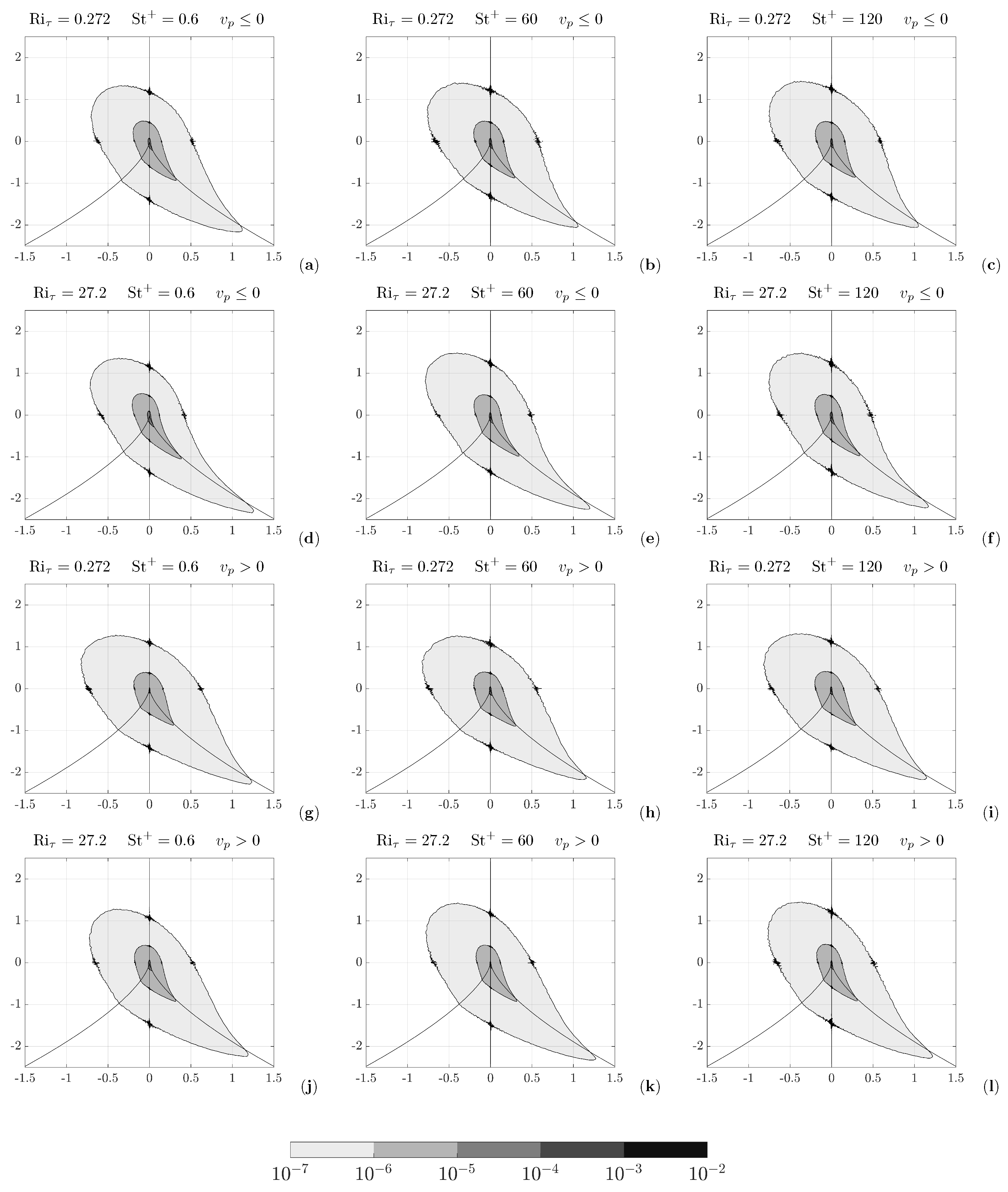
3.2. Local Flow Topology
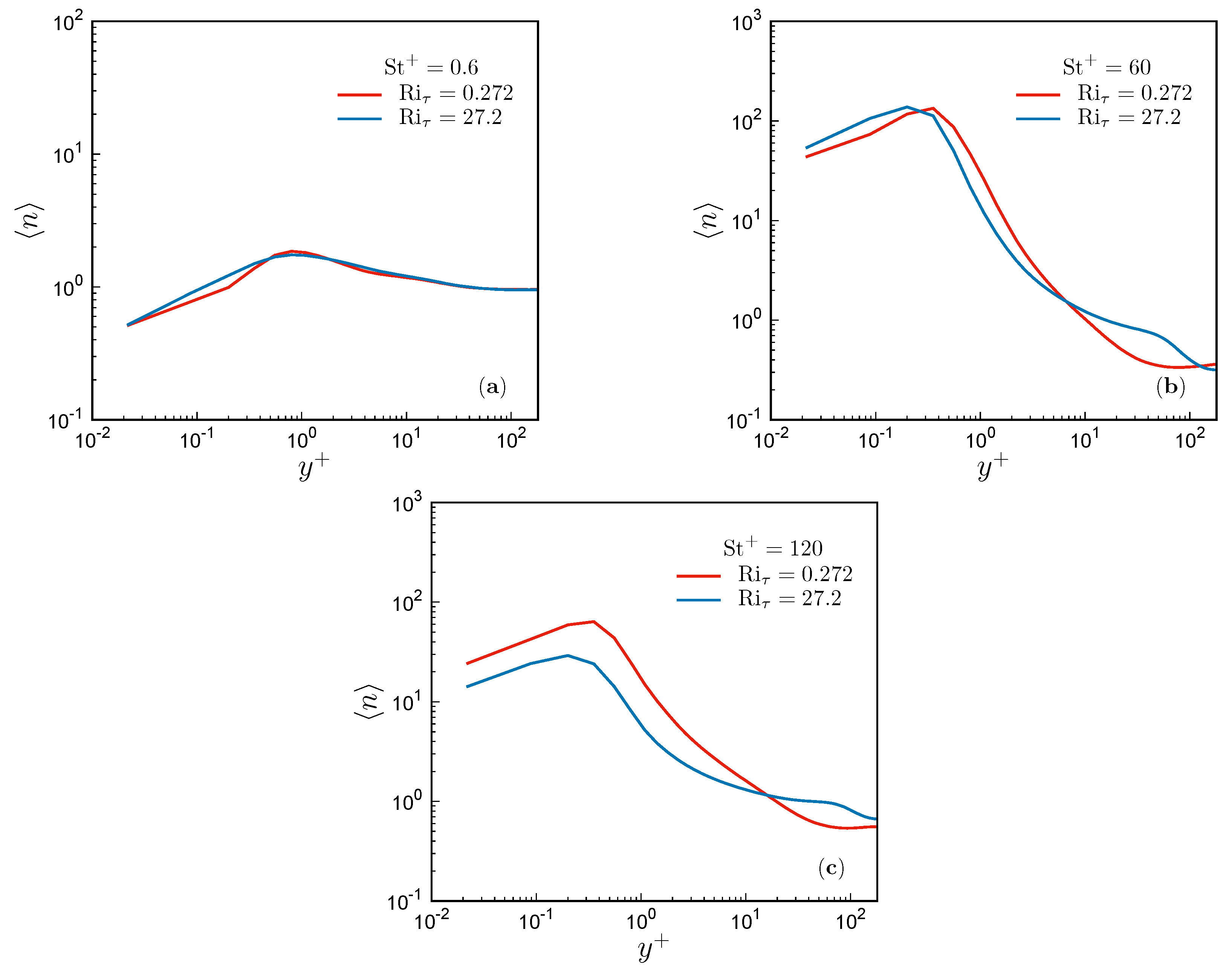
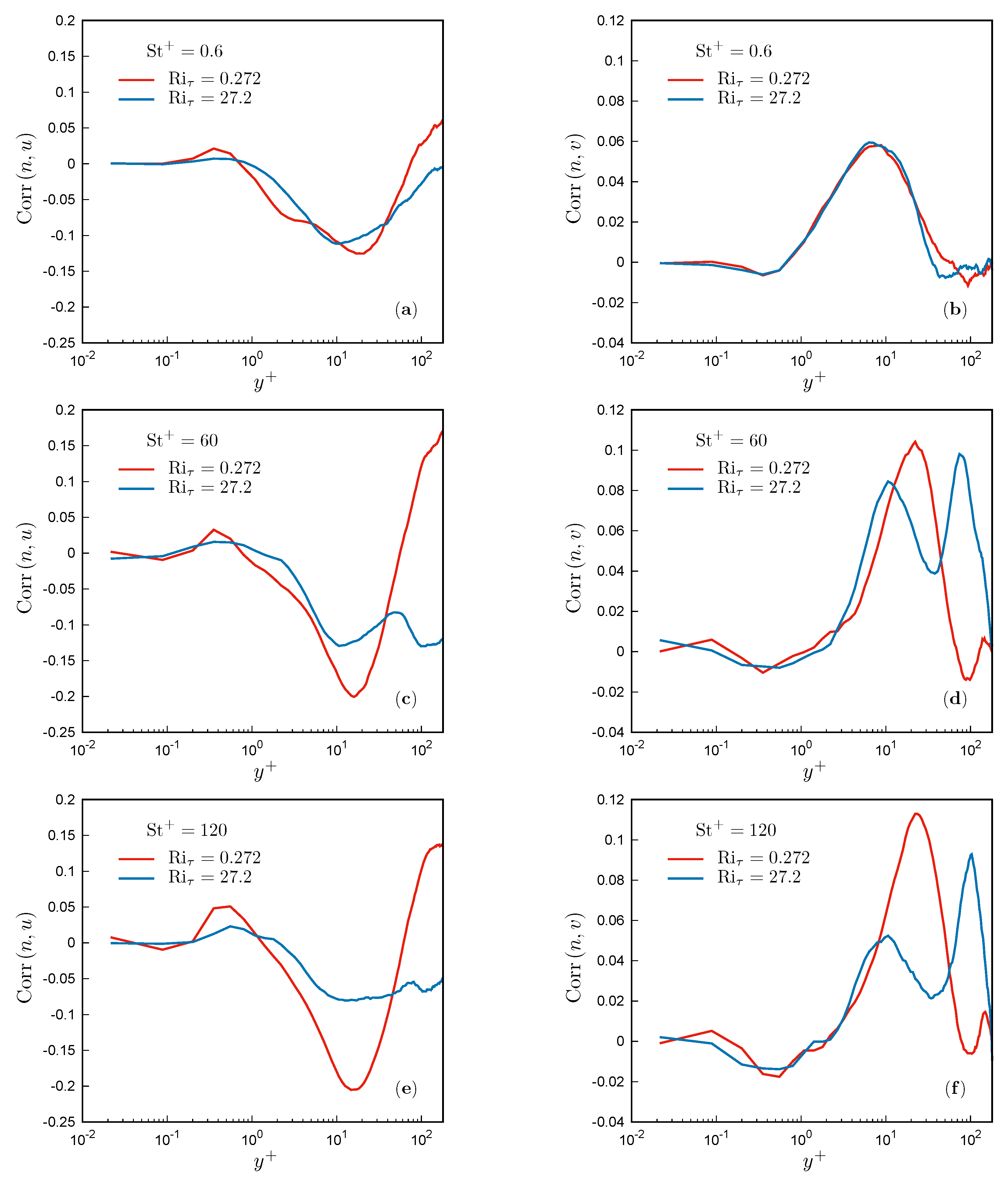
3.3. Particle Distribution
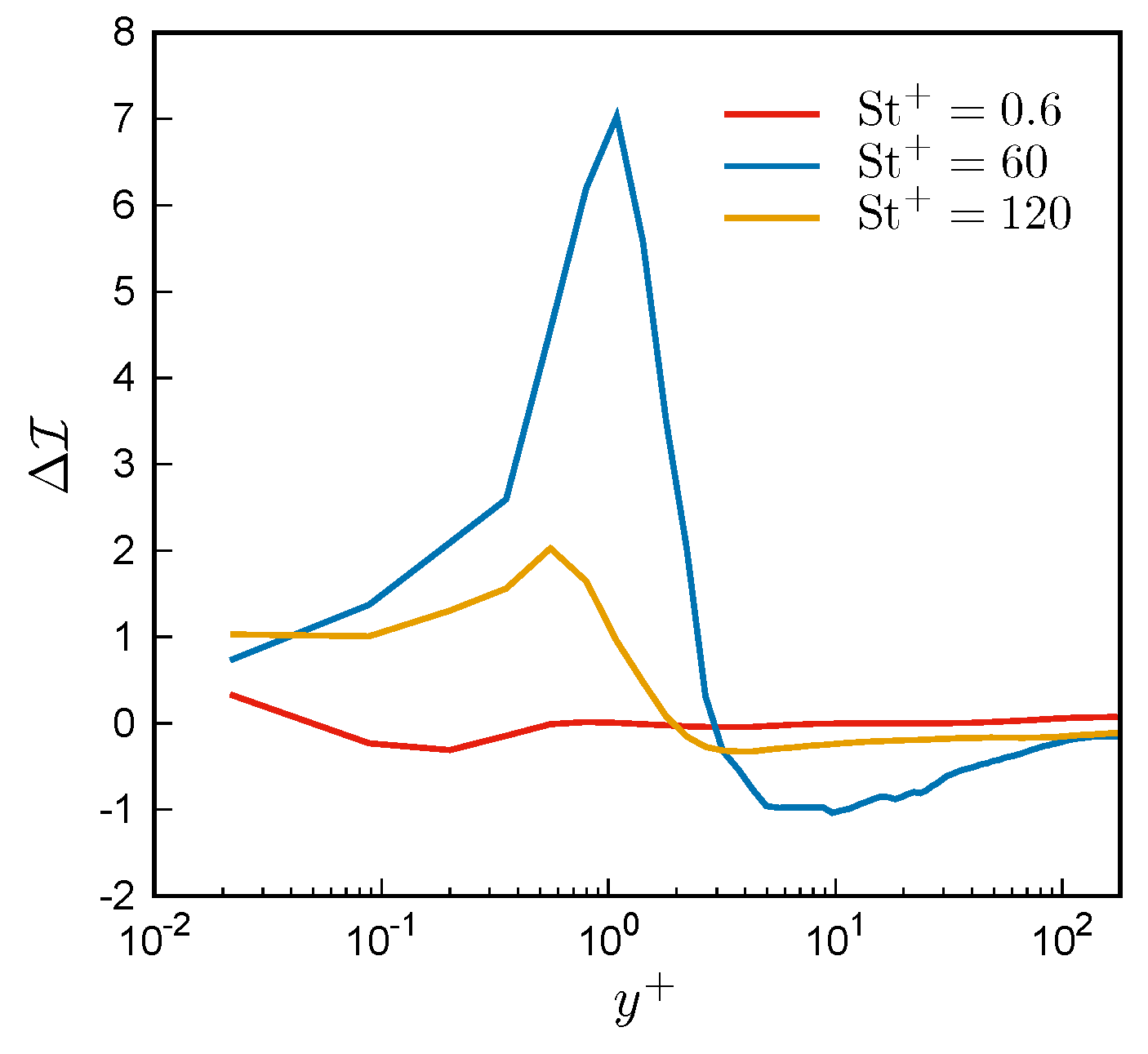
3.4. Particle Concentration and Local Flow Topology
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Arya, S.P.S. Buoyancy effects in a horizontal flat-plate boundary layer. J. Fluid Mech. 1975, 68, 321–343. [Google Scholar] [CrossRef]
- Komori, S.; Ueda, H.; Ogino, F.; Mizushina, T. Turbulence structure in stably stratified open-channel flow. J. Fluid Mech. 1983, 130, 13–26. [Google Scholar] [CrossRef]
- Garg, R.P.; Ferziger, J.H.; Monismith, S.G.; Koseff, J.R. Stably stratified turbulent channel flows. I. Stratification regimes and turbulence suppression mechanism. Phys. Fluids 2000, 12, 2569–2594. [Google Scholar] [CrossRef]
- Iida, O.; Kasagi, N.; Nagano, Y. Direct numerical simulation of turbulent channel flow under stable density stratification. Int. J. Heat Mass Transf. 2002, 45, 1693–1703. [Google Scholar] [CrossRef]
- Armenio, V.; Sarkar, S. An investigation of stably stratified turbulent channel flow using large-eddy simulation. J. Fluid Mech. 2002, 459, 1–42. [Google Scholar] [CrossRef]
- Moestam, R.; Davidson, L. Numerical simulations of a thermocline in a pressure-driven flow between two infinite horizontal plates. Phys. Fluids 2005, 17, 075109. [Google Scholar] [CrossRef]
- García-Villalba, M.; del Álamo, J.C. Turbulence modification by stable stratification in channel flow. Phys. Fluids 2011, 23, 045104. [Google Scholar] [CrossRef]
- Zonta, F.; Onorato, M.; Soldati, A. Turbulence and internal waves in stably-stratified channel flow with temperature-dependent fluid properties. J. Fluid Mech. 2012, 697, 175–203. [Google Scholar] [CrossRef]
- Mizushina, T.; Ogino, F.; Katada, N. Ordered motion of turbulence in a thermally stratified flow under unstable conditions. Int. J. Heat Mass Transf. 1982, 25, 1419–1425. [Google Scholar] [CrossRef]
- Fukui, K.; Nakajima, M. Unstable stratification effects on turbulent shear flow in the wall region. Int. J. Heat Mass Transf. 1985, 28, 2343–2352. [Google Scholar] [CrossRef]
- Domaradzki, J.A.; Metcalfe, R.W. Direct numerical simulations of the effects of shear on turbulent Rayleigh-Bénard convection. J. Fluid Mech. 1988, 193, 499–531. [Google Scholar] [CrossRef]
- Fukui, K.; Nakajima, M.; Ueda, H. Coherent structure of turbulent longitudinal vortices in unstably-stratified turbulent flow. Int. J. Heat Mass Transf. 1991, 34, 2373–2385. [Google Scholar] [CrossRef]
- Iida, O.; Kasagi, N. Direct Numerical Simulation of Unstably Stratified Turbulent Channel Flow. J. Heat Transf. 1997, 119, 53–61. [Google Scholar] [CrossRef]
- Zonta, F.; Soldati, A. Effect of Temperature Dependent Fluid Properties on Heat Transfer in Turbulent Mixed Convection. J. Heat Transf. 2013, 136, 022501. [Google Scholar] [CrossRef]
- Sid, S.; Dubief, Y.; Terrapon, V.E. Direct Numerical Simulation of Mixed Convection in Turbulent Channel Flow: On the Reynolds number dependency of momentum and heat transfer under unstable stratification. In Proceedings of the 8th International Conference on Computational Heat and Mass Transfer, Istanbul, Turkey, 25–28 May 2015; p. 190. [Google Scholar]
- Pirozzoli, S.; Bernardini, M.; Verzicco, R.; Orlandi, P. Mixed convection in turbulent channels with unstable stratification. J. Fluid Mech. 2017, 821, 482–516. [Google Scholar] [CrossRef]
- Zaza, D.; Iovieno, M. Mixed convection in turbulent particle-laden channel flow at Reτ = 180. J. Phys. Conf. Ser. 2024, 2685, 012003. [Google Scholar] [CrossRef]
- Mori, Y.; Uchida, Y. Forced convective heat transfer between horizontal flat plates. Int. J. Heat Mass Transf. 1966, 9, 803–817. [Google Scholar] [CrossRef]
- Fukui, K.; Nakajima, M.; Ueda, H. The longitudinal vortex and its effects on the transport processes in combined free and forced laminar convection between horizontal and inclined parallel plates. Int. J. Heat Mass Transf. 1983, 26, 109–120. [Google Scholar] [CrossRef]
- Cossu, C. Onset of large-scale convection in wall-bounded turbulent shear flows. J. Fluid Mech. 2022, 945, A33. [Google Scholar] [CrossRef]
- Brooke, J.W.; Kontomaris, K.; Hanratty, T.J.; McLaughlin, J.B. Turbulent deposition and trapping of aerosols at a wall. Phys. Fluids A Fluid Dyn. 1992, 4, 825–834. [Google Scholar] [CrossRef]
- Pedinotti, S.; Mariotti, G.; Banerjee, S. Direct numerical simulation of particle behaviour in the wall region of turbulent flows in horizontal channels. Int. J. Multiph. Flow 1992, 18, 927–941. [Google Scholar] [CrossRef]
- Marchioli, C.; Soldati, A. Mechanisms for particle transfer and segregation in a turbulent boundary layer. J. Fluid Mech. 2002, 468, 283–315. [Google Scholar] [CrossRef]
- Squires, K.D.; Eaton, J.K. Particle response and turbulence modification in isotropic turbulence. Phys. Fluids A Fluid Dyn. 1990, 2, 1191–1203. [Google Scholar] [CrossRef]
- Wang, L.P.; Maxey, M.R. The Motion of Microbubbles in a Forced Isotropic and Homogeneous Turbulence. Appl. Sci. Res. 1993, 51, 291–296. [Google Scholar] [CrossRef]
- Fessler, J.R.; Kulick, J.D.; Eaton, J.K. Preferential concentration of heavy particles in a turbulent channel flow. Phys. Fluids 1994, 6, 3742–3749. [Google Scholar] [CrossRef]
- Rouson, D.W.I.; Eaton, J.K. On the preferential concentration of solid particles in turbulent channel flow. J. Fluid Mech. 2001, 428, 149–169. [Google Scholar] [CrossRef]
- Aliseda, A.; Cartellier, A.; Hainaux, F.; Lasheras, J. Effect of preferential concentration on the settling velocity of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 2002, 468, 77–105. [Google Scholar] [CrossRef]
- Sardina, G.; Schlatter, P.; Brandt, L.; Picano, F.; Casciola, C. Wall accumulation and spatial localization in particle-laden wall flows. J. Fluid Mech. 2012, 699, 50–78. [Google Scholar] [CrossRef]
- Petersen, A.J.; Baker, L.; Coletti, F. Experimental study of inertial particles clustering and settling in homogeneous turbulence. J. Fluid Mech. 2019, 864, 925–970. [Google Scholar] [CrossRef]
- Zaza, D.; Iovieno, M. Mixed convection in a particle-laden channel flow: One and two-way coupling regimes. In Progress in Turbulence X; Springer Proceedings in Physics; Örlü, R., Talamelli, A., Peinke, J., Eds.; Springer International Publishing: Cham, Switzerland, 2024; Volume 1066. [Google Scholar] [CrossRef]
- Blackburn, H.M.; Mansour, N.N.; Cantwell, B.J. Topology of fine-scale motions in turbulent channel flow. J. Fluid Mech. 1996, 310, 269–292. [Google Scholar] [CrossRef]
- Chong, M.S.; Perry, A.E.; Cantwell, B.J. A general classification of three-dimensional flow fields. Phys. Fluids A Fluid Dyn. 1990, 2, 765–777. [Google Scholar] [CrossRef]
- Picciotto, M.; Marchioli, C.; Soldati, A. Characterization of near-wall accumulation regions for inertial particles in turbulent boundary layers. Phys. Fluids 2005, 17, 098101. [Google Scholar] [CrossRef]
- Bijlard, M.; Oliemans, R.; Portela, L.; Ooms, G. Direct numerical simulation analysis of local flow topology in a particle-laden turbulent channel flow. J. Fluid Mech. 2010, 653, 35–56. [Google Scholar] [CrossRef]
- Kuerten, J.G.M. Point-Particle DNS and LES of Particle-Laden Turbulent flow-a state-of-the-art review. Flow Turbul. Combust. 2016, 97, 689–713. [Google Scholar] [CrossRef]
- Maxey, M.R.; Riley, J.J. Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids 1983, 26, 883–889. [Google Scholar] [CrossRef]
- Armenio, V.; Fiorotto, V. The importance of the forces acting on particles in turbulent flows. Phys. Fluids 2001, 13, 2437–2440. [Google Scholar] [CrossRef]
- Arcen, B.; Tanière, A.; Khalij, M. Heat transfer in a turbulent particle-laden channel flow. Int. J. Heat Mass Transf. 2012, 55, 6519–6529. [Google Scholar] [CrossRef]
- Kuerten, J.G.M.; van der Geld, C.W.M.; Geurts, B.J. Turbulence modification and heat transfer enhancement by inertial particles in turbulent channel flow. Phys. Fluids 2011, 23, 123301. [Google Scholar] [CrossRef]
- Zonta, F.; Marchioli, C.; Soldati, A. Direct numerical simulation of turbulent heat transfer modulation in micro-dispersed channel flow. Acta Mech. 2008, 195, 305–326. [Google Scholar] [CrossRef]
- Morsi, S.A.; Alexander, A.J. An investigation of particle trajectories in two-phase flow systems. J. Fluid Mech. 1972, 55, 193–208. [Google Scholar] [CrossRef]
- Pan, Y.; Banerjee, S. Numerical simulation of particle interactions with wall turbulence. Phys. Fluids 1996, 8, 2733–2755. [Google Scholar] [CrossRef]
- Elghobashi, S.E. On predicting particle-laden turbulent flows. Flow Turbul. Combust. 1994, 52, 309–329. [Google Scholar] [CrossRef]
- Zaza, D.; Iovieno, M. On the Preferential Concentration of Particles in Turbulent Channel Flow: The Effect of the Added-Mass Factor. Energies 2024, 17, 783. [Google Scholar] [CrossRef]
- Lozano-Durán, A.; Holzner, M.; Jiménez, J. Multiscale analysis of the topological invariants in the logarithmic region of turbulent channels at a friction Reynolds number of 932. J. Fluid Mech. 2016, 803, 356–394. [Google Scholar] [CrossRef]
- Carbone, M.; Bragg, A.D. Is vortex stretching the main cause of the turbulent energy cascade? J. Fluid Mech. 2020, 883, R2. [Google Scholar] [CrossRef]
- Smith, C.R.; Metzler, S.P. The characteristics of low-speed streaks in the near-wall region of a turbulent boundary layer. J. Fluid Mech. 1983, 129, 27–54. [Google Scholar] [CrossRef]
- Chernyshenko, S.; Baig, M. The mechanism of streak formation in near-wall turbulence. J. Fluid Mech. 2005, 544, 99–131. [Google Scholar] [CrossRef]
- Reeks, M.W. The transport of discrete particles in inhomogeneous turbulence. J. Aerosol Sci. 1983, 14, 729–739. [Google Scholar] [CrossRef]
- Young, J.B.; Hanratty, T.J. Trapping of solid particles at a wall in a turbulent flow. AIChE J. 1991, 37, 1529–1536. [Google Scholar] [CrossRef]
- Eaton, J.; Fessler, J. Preferential concentration of particles by turbulence. Int. J. Multiph. Flow 1994, 20, 169–209. [Google Scholar] [CrossRef]
- Brandt, L.; Coletti, F. Particle-Laden Turbulence: Progress and Perspectives. Annu. Rev. Fluid Mech. 2022, 54, 159–189. [Google Scholar] [CrossRef]
- Richter, F.M. Convection and the large-scale circulation of the mantle. J. Geophys. Res. 1973, 78, 8735–8745. [Google Scholar] [CrossRef]
- Richter, F.M.; Parsons, B. On the interaction of two scales of convection in the mantle. J. Geophys. Res. 1975, 80, 2529–2541. [Google Scholar] [CrossRef]
- Panet, I.; Pajot-Métivier, G.; Greff-Lefftz, M.; Métivier, L.; Diament, M.; Mandea, M. Mapping the mass distribution of Earth’s mantle using satellite-derived gravity gradients. Nat. Geosci. 2014, 7, 131–135. [Google Scholar] [CrossRef]

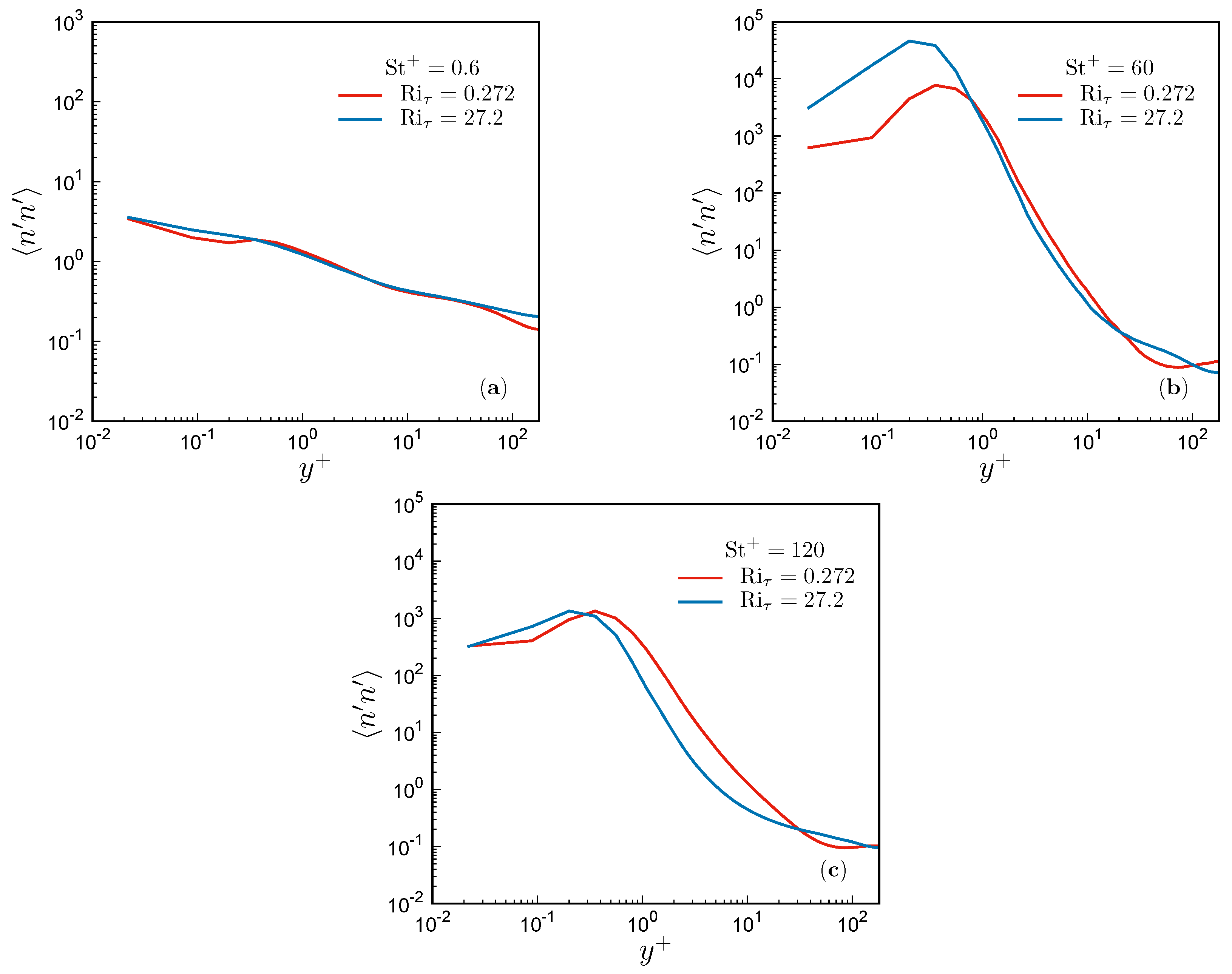
| Run 1 | 180 | 0.272 | 5606 | 0.6 | ||
| Run 2 | 180 | 0.272 | 5606 | 60 | ||
| Run 3 | 180 | 0.272 | 5606 | 120 | ||
| Run 4 | 180 | 27.2 | 4984 | 0.6 | ||
| Run 5 | 180 | 27.2 | 4984 | 60 | ||
| Run 6 | 180 | 27.2 | 4984 | 120 |
| 60 | ||||
| 120 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaza, D.; Iovieno, M. Influence of Coherent Vortex Rolls on Particle Dynamics in Unstably Stratified Turbulent Channel Flows. Energies 2024, 17, 2725. https://doi.org/10.3390/en17112725
Zaza D, Iovieno M. Influence of Coherent Vortex Rolls on Particle Dynamics in Unstably Stratified Turbulent Channel Flows. Energies. 2024; 17(11):2725. https://doi.org/10.3390/en17112725
Chicago/Turabian StyleZaza, Domenico, and Michele Iovieno. 2024. "Influence of Coherent Vortex Rolls on Particle Dynamics in Unstably Stratified Turbulent Channel Flows" Energies 17, no. 11: 2725. https://doi.org/10.3390/en17112725
APA StyleZaza, D., & Iovieno, M. (2024). Influence of Coherent Vortex Rolls on Particle Dynamics in Unstably Stratified Turbulent Channel Flows. Energies, 17(11), 2725. https://doi.org/10.3390/en17112725






