Abstract
The ongoing electrification of the transport sector is expected to cause an increase in electricity demand and, therefore, trigger significant network investments to accommodate it. This paper focuses on investment decision-making for electricity distribution grids and specifically on the strategic and incremental investment network planning approaches. In particular, the former involves network planning with the consideration of a long-term multi-stage study horizon, as opposed to a shorter–term view of the future that applies to the latter case. An investment analysis that is carried out underlines the economic savings generated from adopting a strategic investment perspective over an incremental one. These economic savings are achieved from the fact that the associated fixed investment costs are incurred only once in the horizon under strategic planning. On the other hand, incremental planning involves a series of network reinforcement decisions, thereby incurring the fixed cost multiple times. In addition, sensitivity analyses that are carried out capture the effect of key parameters, such as investment cost, discount rate and investment delay, on the generated economic savings.
1. Introduction
The ongoing electrification of the transport sector constitutes an integral part of the global decarbonisation effort to address the challenges of climate change. In this context, one such considerable challenge involves the expected increase in the electricity demand peak, which needs to be addressed through associated capital-intensive infrastructure reinforcements to safely accommodate the resulting increased power flows needed for the charging of the anticipated Electric Vehicle (EV) fleet [1,2,3,4].
The current paper focuses on two fundamental network planning approaches that characterise investment decision-making in the electricity sector. These include the approaches of strategic planning and incremental planning.
Specifically, the strategic planning approach involves the adoption of a long-term study horizon, which in turn involves predicting the electricity demand over many stages/epochs into the future and then proceeding with network planning on the basis of this prediction. On the other hand, the incremental planning approach is characterised by a shorter study horizon and involves making investment decisions focused on this shorter-term perspective. As will be explained further in the text, the strategic planning approach tends to involve a single large investment with a magnitude sufficiently large enough to cover the future system needs, whereas incremental planning involves a number of investments of a smaller magnitude [5]. The next table, Table 1, summarises key points related to the two investment approaches.

Table 1.
Summary of the key points related to the incremental and strategic planning approaches for investments in the infrastructure of electricity grids.
These anticipated capital-intensive investments in electricity distribution infrastructure are primarily conventional and mainly include investments in electricity distribution lines and primary substations. Investments in primary substations play a crucial role in electricity distribution networks by performing the necessary voltage transformations such as stepping the voltage magnitude down to levels suitable for local distribution. Furthermore, primary substations also act as hubs, branching out feeder lines that carry the medium voltage electricity to secondary distribution substations closer to residential and commercial areas. In this context, investments in primary substations become imperative in light of the increased power flows as a result of the electrification of the transport sector, to ensure the security of electricity supply and to accommodate the increased demand peaks. In the same vein, investments in electricity distribution lines are essential to make sure that their thermal ratings suffice for enabling the new power flows to reach the electricity consumers at all times.
These are the types of investments that the paper is focused on. Such conventional investments are characterised by long build times as well as higher investment costs compared to smart grid investments [6,7,8].
In this context, the contributions of this paper are as follows.
- Presentation, for the first time in the literature, of the economic evaluation of the incremental and strategic investment approaches for conventional reinforcement in distribution grids.
- Comparison of the differences in the adopted planning approach between electricity distribution lines and primary substations.
- Presentation of an in-depth sensitivity analysis to identify the factors driving the differences between the two investment approaches.
The remainder of the paper is structured as follows: Section 2 presents the literature review. Section 3 focuses on the methodology followed in the paper. Then, Section 4 describes the case study. Then, Section 5 discusses the results, while Section 6 provides the concluding remarks and identifies possible pathways for future work.
2. Literature Review
Investments in primary substations have historically been considered strategic and crucial for building a future-proofed, resilient and sustainable electricity distribution grid [9]. The authors in [10] highlight the complexity of strategic planning in the face of increased demand and model the corresponding investment decision-making problem through mixed integer programming. Also, in [11] the authors present an economic study on power substation investments through the use of strategic planning with a focus on urban distribution substations, underlying the economic benefits of superconducting cables as this technology can offer higher transmission capability, lower energy losses and reduced environmental impact, despite the higher up-front costs involved compared to conventional cables. Furthermore, ref. [12] explores the impact of various network configurations on long-term (strategic) substation investments through the use of a mixed-integer linear programming framework, showing that the type of network topology adopted significantly affects the associated investment decisions, demonstrating the importance of such considerations in optimising costs and efficiency. In addition, ref. [13] presents a hybrid heuristic and evolutionary algorithm for the optimisation of distribution substation planning within large electrical networks. The algorithm combines a heuristic approach to determine preliminary substation service areas and an evolutionary algorithm to refine the solution towards global optimality. The effectiveness of the proposed method is validated through its application to illustrative systems and a real-world large-scale distribution network. Also, ref. [14] introduces a substation planning method that makes use of weighted Voronoi diagrams, underlining its practical applicability. In [15], the strategic and incremental approaches are compared for an investment portfolio consisting of storage and soft open point technologies, while in [16], they are compared for a portfolio of dynamic line rating technology and storage, and in [17], they are compared for a portfolio of EV-related technologies such as Vehicle to Grid and Vehicle to Building.
In addition, ref. [10] presents an approach to planning investments in substations using a large-scale mixed-integer programme that can optimise the size and location of new substation investments, as well as the expansion of existing ones based on forecasted demands. Also, ref. [18] discusses investment strategies for electricity distribution companies and evaluates different investment strategies, considering investment costs, and suggesting long-term strategic network development. In [19], the authors explore incremental approaches for distribution grids using a ‘system dynamics’ approach to model and analyse the interaction among various market participants; the paper highlights the importance of understanding dynamic relationships among network participants to enhance decision-making. In [20], the paper focuses on incremental investments in distribution networks and outlines how these investments facilitate the integration of new technologies and investments, focusing on maximising economic returns and improving system reliability. Also, ref. [21] proposes a bilevel planning model for incremental investments in distribution networks considering energy storage systems and the uncertainty of distributed generation (DG) and load. Case study results show that although incorporating storage systems may increase the total investment cost, due to their high prices, it can generate profits through their operation, which should be considered in the planning stage of incremental investments. In addition, ref. [22] proposes a bilevel model to identify the optimal wind power investment decisions of a strategic investor who participates in both the day-ahead and balancing electricity markets. Case studies based on the IEEE 24-node and 118-node systems demonstrate that by adopting a strategic position, the wind investor can significantly increase profits compared to a non-strategic approach, especially under transmission congestion conditions. Furthermore, ref. [23] proposes a substation planning method for a distribution network that accounts for the widespread integration of distributed generators in a low-carbon economy.
Moreover, ref. [24] proposes a methodology to assist a strategic producer in making generation investment decisions within a market environment. The resulting bilevel model is formulated as a large-scale mixed-integer linear programming (MILP) problem that can be solved using branch-and-cut techniques. The results show that by behaving strategically, the producer can significantly increase its profits compared to a price-taker approach. In terms of [25], it presents a methodology for evaluating strategic investments under uncertainty considering flexibility in decision-making using Real Options Analysis. The results emphasise the importance of considering the value of flexibility in investment projects, as it can significantly increase the project’s value compared to the traditional NPV approach. What is more, ref. [26] proposes a Nash–Cournot equilibrium model to study strategic investment in power and heat markets using a novel optimisation approach, while ref. [27] used Bayesian optimisation.
The above literature review provides a comprehensive overview of prior research on strategic and incremental approaches to investing in electricity distribution grids. Specifically, the cited papers discuss various aspects of these investment approaches, such as:
- The importance of strategic planning for building future-proof and resilient distribution grids [9,10,11].
- The impact of network configurations and topologies on strategic substation investments [12,13,14].
- Comparisons of strategic and incremental approaches for different investment portfolios, such as storage technologies, dynamic line rating and EV-related technologies [15,16,17].
- Methods for optimising substation investments based on forecasted demands [10,18].
- Incremental approaches for distribution grids and their benefits [19,20,21].
- Strategic investment models for wind power and transmission infrastructure [22,23].
- Methodologies for assisting strategic decision-making in generation investments and under uncertainty [24,25].
- Novel optimisation approaches for studying strategic investments in power and heat markets [26,27].
While these papers provide valuable insights into various aspects of strategic and incremental planning in electricity distribution grids, the paper contributes to the existing literature in several unique ways.
First, the paper focuses specifically on comparing the economic benefits of strategic and incremental approaches for conventional reinforcement in distribution grids, which has not been explicitly addressed in the reviewed literature. It also highlights the differences in the adopted planning approach between electricity distribution lines and primary substations, providing a more granular analysis of the investment decision-making process.
Secondly, the paper presents an in-depth sensitivity analysis to identify the key factors driving the differences between the two investment approaches, such as investment cost, discount rate and investment delay. This analysis provides valuable insights into the conditions under which each approach may be more favourable.
Third, the case study in the paper demonstrates the potential economic savings generated by adopting a strategic planning approach over an incremental one in the context of accommodating increased electricity demand due to the growth of electric vehicles. This specific context has not been explored in the reviewed literature.
In summary, while the literature review provides a solid foundation for understanding the various aspects of strategic and incremental planning in electricity distribution grids, the paper contributes novel insights; these contributions help to bridge the gap between the existing literature and the practical application of these investment approaches in the face of evolving grid requirements.
3. Methodology
The methodology is applied to an electricity distribution grid, which consists of several buses and a primary substation. In this system, the load is expected to increase over time, potentially due to the charging of electric vehicles, whose number is expected to increase. That is, the system load is characterised by two components: the baseload demand as well as the electric vehicle charging demand, each of which has a corresponding peak.
The EV peak demand is found according to the following formula [28,29,30] where k is the number of electric vehicles in the system, f is the charger capacity (kW) per electric vehicle and z is the coincidence factor.
Note that the coincidence factor represents the fact that not all electric vehicles charge at the same time [5], meaning that the peak electricity demand that these vehicles cause is in reality less than the product of . For this reason, the coincidence factor z attains values between 0 and 1. Specifically, it is calculated using the following formula, where, as mentioned, k is the number of electric vehicles in the system.
In addition, the study horizon is discretised into a number of epochs/stages of equal length (years). The study is conducted on the system shown in Figure 1. Then, in Figure 2, below, the horizon is broken down into 4 stages/epochs covering 3 years each.
A fundamental concept in this analysis is the build time or investment delay. Specifically, as mentioned, investments in distribution lines and substations are types of conventional investments. Such investments are characterised by a time difference between the time when the investment decision is made and the time when the actual investment becomes materialised. This time difference is known as investment delay or build time and is there because conventional reinforcements, such as investments in substation upgrades, require significant public works and licensing procedures. As such, if the decision to invest in the substation is taken in period t, then the substation upgrade will be realised in period t + 1; the total investment cost will be incurred in period t (i.e., before the realisation of the investment). The consideration of the investment delay is crucial. Longer investment delays may lead to higher investment costs, given that the decision maker needs to make investments earlier than the time they are needed.
The next step is the discretisation of the horizon according to the strategic approach and the incremental approach, as shown in Figure 3. In this figure, the 12-year horizon is broken down into four three-year epochs, and for the strategic approach, all blocks/nodes are connected with each other (which indicates that the planner considers all 4 stages for investment decision-making), while for the incremental approach, the nodes/blocks are connected in pairs (e.g., of two).
Then, the calculations are based on the concept of the time value of money. Particularly, the time value of money principle implies that, provided money can earn interest, any amount of money is worth more the sooner it is received. This leads to the concept of discounting, which is the process of determining the present value of a future amount of money. By discounting, we calculate how much a future sum of money is worth in today’s terms. This involves applying a discount rate, which reflects the interest rate or the rate of return that could be earned on an investment over a specified period. In this context, any investment made at the current time has a discounted value equal to the current value.
Consequently, the premise of the strategic approach is that a large single investment is made at the current time (i.e., with no discounting). On the other hand, the incremental approach involves multiple investments; the first one at the current time, and future ones in subsequent stages, which requires discounting.
In this analysis, the factors that play a role and affect the eventual valuation include the discount rate, the fixed cost of the conventional investment under the strategic and the incremental approaches, the length of the epoch/stage (i.e., how many years are included in one epoch/stage), etc. Then, sensitivity analysis can be conducted around these parameters and observe the effect of each of them on the resulting costs and comparison of the two approaches.
4. Case Study
4.1. Description
Figure 1 below shows the illustrative electricity distribution system used in the analysis. In particular, the depicted 11 kV grid consists of 6 buses in total, where buses 2–5 have electricity load connected. Also, there is a 33/11 kV primary substation located at bus 1. In total, the system’s total peak demand is 5 MW. This demand includes typical household demand, known as baseload demand. That is, there are no electric vehicles connected to the system at the beginning of the study horizon. This baseload demand is assumed to stay equal to 5 MW across the entire time horizon. Any growth in the total demand is attributed to the connection of electric vehicles in the system.
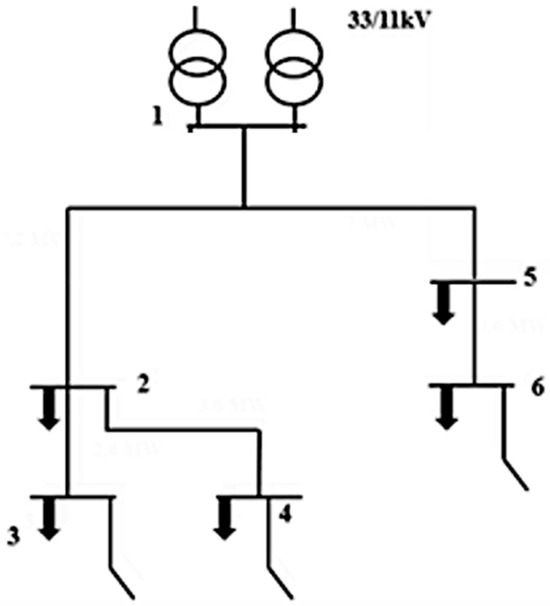
Figure 1.
Illustrative electricity distribution network used in the analysis. Bus 1 includes the primary 33/11 kV substation that consists of two transformers (N − 1 criterion). Buses 2–6 have electricity demand connected.
The system also has normally open switches, as can be seen in buses 3, 4 and 6. This indicates that there are no power flows underneath. In addition, the primary substation includes two transformers according to the N − 1 criterion. The N − 1 criterion in electricity distribution is a reliability standard ensuring that the system can withstand the failure of any single component (like a transformer or a transmission line) without causing a widespread power outage. This criterion helps maintain system stability and continuous power supply, even during unforeseen failures.
Figure 2 below shows the horizon broken down into four periods and the corresponding electricity demand. Each period (also known as stage) covers a 3-year duration. Thus, this is a 12-year time horizon. In addition, the notation x (y) indicates that the total system annual peak demand is equal to x MW and the system includes of a total of y electric vehicles. As mentioned, the baseload annual peak demand is equal to 5 MW, which stays the same across the 12-year horizon. That is, the baseload annual peak across periods 1–4 is equal to 5 MW. Hence, the growth in the total peak demand from 5 MW (in period 1) to 11.5 MW (in period 4) is caused purely by the connection of electric vehicles in the network. For example, in period 2, there are 379 electric vehicles in the system causing 0.5 MW peak demand. Thus, the total peak demand, which is equal to the sum of the baseload peak demand plus the EV peak demand, is equal to 5 MW + 0.5 MW, yielding 5.5 MW. Regarding period 3, the total number of electric vehicles in the system is 1893. The peak baseload demand is 5 MW. Hence, these 1893 electric vehicles cause a 1.9 MW peak demand.
In terms of the EV peak demand, this is found according to Formulas (1) and (2) as explained in the previous section, according to the number k of electric vehicles shown in Figure 2 (e.g., in period 2 there are 379) and assuming the charger capacity per electric vehicle f is at 10 kW. For example, in period 2, the baseload peak demand (annual) is equal to 5 MW. Then, the annual peak demand caused by the electric vehicles that are in the system is equal to the product of 379 (number of vehicles in the system), 10 kW (the charger per electric vehicle) and 0.14, which is the coincidence factor that is equal to . This product yields approximately 0.5 MW.

Figure 2.
Illustration of the time horizon consisting of 4 periods (also known as stages). The current time is period 1. The notation x (y) means that the total peak demand is x MW, including a total number of y electric vehicles in the system. Each node shows annual values. For instance, in period 2, the 5.5 (379) means that in each of the 3 years of period 2, the total peak load is 5.5 MW, with 379 electric vehicles (i.e., annual values).
4.2. Investment Costs
In the context of this analysis, it is assumed that the cost of investing in a 12 MW substation transformer is equal to GBP 400,000. This is a lifetime cost and not an annualised value. It is discounted to the present time, i.e., period 1. Similarly, a 7 MW substation transformer incurs an investment cost of GBP 380,000. Notice that the two investment costs are close to each other because the main factor driving these costs is the amount of public works required. In addition, an annual discount rate of 3.5% is used for discounting the costs in the analysis.
Also, as mentioned in the previous section, a fundamental concept in this analysis is the concept of build time or investment delay. In this context, it is assumed that the investment delay is equal to the duration of one period, i.e., 3 years. This assumption is reasonable given that investments in substations, such as the upgrade or the replacement of the transformer capacity, may take a significant amount of time to materialise.
4.3. Implementation
Figure 3, shown below, displays two investment approaches across a 12-year horizon broken down into four periods. The investment approach at the top constitutes the strategic investment planning, while that at the bottom is the incremental one. Notice there are four periods linked to each other, sequentially. In this 12-year horizon, the electricity demand at the present time stands at 5 MW and then rises to 11.5 MW in period 4. As mentioned, this load growth takes place due to the connection of electric vehicles, while the baseload peak demand stays the same at 5 MW (equal to the value at the very beginning).
As mentioned, the current peak electricity demand is equal to 5 MW, as shown at the state corresponding to period 1. This peak demand is accommodated through the presence of two 5 MW transformers at the primary substation. Note that although one transformer would suffice, the presence of two transformers is required due to the N − 1 criterion. These transformers are placed in the primary substation at bus 1.
The accommodation of the 11.5 MW peak demand of period 4 involves the first-period investment decision for the removal of the two existing power transformers and the placement of two 12 MW transformers at the primary substation located in bus 1. The investment decisions for the deployment of these two transformers will be made in period 1 under the assumption that it requires approximately three years (equal to the duration of one period) for the works to be fully completed; this is the duration of the build time, as mentioned previously. That is, the two 12 MW transformers will become operational starting from the beginning of period 2. As a result, for a total cost of GBP 400,000 for each of the 12 MW transformers, the resulting total investment cost to be incurred at period 1 (i.e., current time) is calculated as .
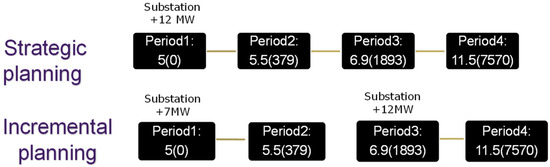
Figure 3.
Strategic versus incremental planning. The top scenario corresponds to a longer-term perspective, as required by strategic planning. Whereas, the bottom one corresponds to incremental planning, where the horizon is split into 4 blocks. Each block is known as a ‘state’ or ‘node’.
Under incremental planning, the network planner adopts a shorter-term view of the future. According to Figure 3, incremental planning includes four periods split into two pairs. In this case, the network planner who is at the beginning of period 1 (present time) can only look until the end of period 2, and the planner who is at the beginning of period 3 can only look until the end of period 4. That is, incremental planning involves a two-stage view of the horizon. Hence, at the beginning of period 1, the two existing 5 MW transformers are removed and two new 7 MW (each) transformers are placed to cover the 5.5 MW total peak demand of period 2. At a cost of GBP 380,000 per 7 MW transformer, this investment corresponds to a total investment cost of . Subsequently, at the beginning of period 3, another investment is made. Specifically, the two 7 MW substation transformers are removed so that two 12 MW transformers are placed to cover the 11.5 MW peak demand occurring at period 4, according to the N − 1 criterion. Hence, at a cost of GBP 400,000 per transformer, this investment amounts to a total discounted (at a 3.5% rate) investment cost of GBP 650,800, as shown in the equation below. Notice that this is discounted given the 6-year difference to period 1.
Thus, the total investment cost corresponding to the incremental planning is equal to GBP 760,000 + GBP 650,800 = GBP 1,410,800.
Hence, strategic planning results in a cost of GBP 800,000, whereas incremental planning corresponds to a cost of GBP 1,410,800. As a result, the economic savings that are accrued by adopting a strategic planning approach to upgrading the distribution grid against the incremental planning approach, amount to 43% as calculated below.
4.4. Sensitivity Analysis
In this section, sensitivity analysis is conducted on three factors of the above analysis: namely the transformer investment cost, the discount rate and the investment delay. The goal of this analysis is to identify the parameters that can affect the accrued economic benefit from adopting a strategic instead of an incremental approach.
Starting with investment costs, as mentioned in the analysis, the 12 MW transformer costs GBP 800,000 to deploy, while the 7 MW transformer costs GBP 380 k; these values represent lifetime investment costs discounted to period 1 (present time). With regards to the sensitivity analysis, the investment cost of the 12 MW transformer stays at GBP 800,000, while that of the 7 MW transformer varies and takes a range of values as shown in the horizontal axis of Figure 4 below.
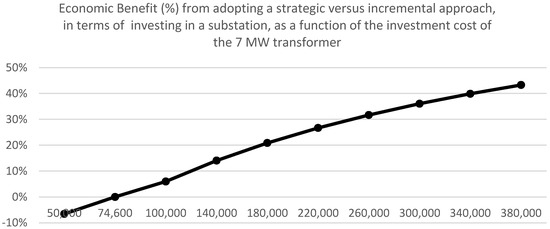
Figure 4.
Economic benefit (shown on the vertical axis, in percentage terms) from investing in the primary substation according to the strategic planning approach, versus the incremental one. The benefit is shown as a function of the investment cost of the 7 MW transformer of the primary substation.
In particular, the vertical axis of this figure shows the economic benefit accrued from investing in the primary substation according to the strategic approach against the incremental approach. The horizontal axis shows the investment cost of the 7 MW transformer of the primary substation. It can be seen that as the investment cost of the 7 MW transformer reduces, the cost of the incremental approach reduces as well, while that of the strategic approach stays the same at GBP 800,000. Hence, the cost difference between the two strategies drops. This means that it becomes less attractive to invest according to the strategic investment approach. That is, the economic benefit accrued from investing strategically reduces as can be seen in the numerator of Equation (3) above. Moreover, in Figure 4 it can be seen that there is a value for the investment cost on the horizontal axis where the economic benefit becomes equal to 0%; this value is at GBP 74,600. For values of the investment cost that are less than GBP 74,600, the economic benefit (%) becomes negative, meaning that investing incrementally is the economically beneficial approach.
Regarding the discount rate, Figure 5 shows the relationship between the discount rate, shown on the horizontal axis, and the economic benefit accrued from investing in the primary substation, according to the strategic approach against the incremental one. In particular, Figure 5 shows that as the discount rate increases, the economic benefit, shown on the vertical axis, reduces because the cost of the incremental strategy decreases, making the strategic approach less attractive to adopt. However, unlike the previous case (Figure 4) there is no point where the economic benefit becomes negative. Also, notice the values on the vertical axis (the economic benefit) vary much less than those in Figure 4. This means that the discount rate is of less significance as a factor in affecting the economic benefit of investing strategically.
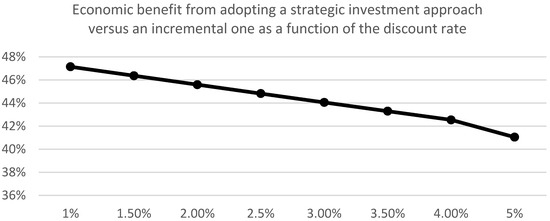
Figure 5.
Economic benefit (shown on the vertical axis, in percentage terms) from investing in the primary substation according to the strategic planning approach, versus the incremental one. The benefit is shown as a function of the annual discount rate.
Regarding the investment delay, the analysis was conducted assuming a 1-period duration, i.e., that for the transformer to be operational in period 2, the corresponding investment decision needed to have been made in period 1. Specifically, with a delay equal to 1 period (i.e., 3 years), the strategic planning approach required the decision to be made in period 1, while the incremental approach required investment decisions to be made in periods 1 and 3 (see Figure 3 above).
On the other hand, when the investment delay is equal to 0 periods, this means that there is no time difference between the time when the investment decision is made and the time when the investment becomes realised. In this case, the strategic planning approach requires the investment decision to be made in period 2, while the incremental approach requires the investment decision to be made in periods 2 and 4. The resulting economic benefit in both cases ends up being the same and equal to 43%. This is because the change in investment delay affects both of the approaches in the same way.
5. Discussion
The analysis has focused on the strategic and incremental planning approaches for network investments to accommodate increased electricity demand from electric vehicle (EV) adoption. It compares long-term strategic investments against incremental ones for upgrading distribution networks to handle EV-driven load growth. This analysis is conducted in light of the electrification of the transport sector, which is integral to global decarbonisation efforts.
Strategic planning involves a long-term horizon and large one-time upfront investments, while incremental planning has a shorter-term perspective with multiple smaller investments, i.e., involving phased investments. The analysis uses an illustrative 11 kV distribution network with a 33/11 kV primary substation. Baseload demand is 5 MW, with EV adoption driving total peak demand growth to 11.5 MW over 12 years.
Under strategic planning, two 12 MW transformers are installed in period 1 at a total cost of GBP 800 k. With incremental planning, two 7 MW transformers are installed in period 1 (GBP 760 k) and replaced with 12 MW units in period 3 (GBP 650.8 k), totalling GBP 1.41 M. Strategic planning results in 43% cost savings compared to incremental in the base case. The sensitivity analysis shows that lower transformer costs and higher discount rates reduce the cost advantage of strategic planning.
These analyses emphasise the fact that there is no absolute determination as to which of the two approaches is the most economical one. Although the case study found that significant economic savings are generated as a result of the strategic approach, the sensitivity analysis demonstrates that there are cases where the incremental approach may be the cost-optimal one of the two.
The sensitivity analysis showed the significant impact on the eventual economic savings that the fixed cost of the transformer has. Specifically, as the investment cost of the 7 MW transformer reduces, the cost of the incremental approach reduces as well, hence, the cost difference between the two strategies drops. This means that it becomes less attractive to invest according to the strategic investment approach.
However, from Figure 4, it can be seen that in the majority of the cases, the strategic approach is the optimal one. Particularly, by looking at the horizontal axis, the incremental approach becomes more economically attractive for values for the fixed cost that are smaller than GBP 74,600. At the same time, the values on the vertical axis indicate that the amount by which the incremental approach can become more attractive than the strategic one is smaller than the amount by which the strategic one can be more attractive.
In terms of other factors, the discount rate analysis has shown that higher rates decrease the benefits of the strategic planning approach but never make it negative, as is observed in the case with the analysis of the transformer fixed cost. Furthermore, the investment delay (i.e., the build time) is shown to affect both approaches equally when the delay is zero, thereby maintaining the 43% economic benefit for strategic planning.
6. Conclusions
The anticipated electrification of the transport sector may lead to a significant increase in peak electricity demand. As a result, a considerable amount of network reinforcement may be required to ensure that the expected increased power flows are safely accommodated. This amount of conventional reinforcement may happen either by following a strategic network planning approach or an incremental one.
If a strategic network planning approach is adopted across a long-term multi-stage planning horizon, then a larger investment in substation capacity is made at the beginning of the horizon. On the other hand, if an incremental planning approach is adopted, then network reinforcement takes place at the beginning as well as at a future period. Hence, under the strategic planning approach, the planner avoids carrying out network reinforcement multiple times, whereas, under the incremental planning approach, the planner incurs the fixed costs multiple times.
Analysis as to which of the two approaches is more economical depends on the specific data of the problem at hand. As the sensitivity analysis demonstrated, there can be cases where adopting an incremental approach may be economically optimal against adopting a strategic approach. Hence, careful analysis needs to be conducted for the appropriate assessment of the most economic approach.
In this context, the key points of this work can be summarised as follows.
- Investments in the infrastructure of electricity grids can be conducted by following either a strategic or an incremental approach.
- The key difference between the strategic and the incremental approaches is that the former involves the adoption of a long-term view of the horizon, while the incremental approach involves a shorter-term perspective. As such, the strategic approach incurs the fixed investment cost once, whereas the incremental approach incurs the fixed cost multiple times.
- The case study shows that the savings generated from adopting a strategic approach over the incremental approach amount to 43%. However, generally, there is not an absolute answer. Rather, which one is the more economical depends on the data of the problem under study and can be determined after careful analysis.
- A sensitivity analysis has been carried out and underlines the importance of the investment cost of the substation transformer as the driver of the economic benefit of the strategic approach over the incremental approach. That is, the economic evaluation of the incremental and strategic investment approaches is mainly determined by the fixed cost of the technology invested (e.g., the transformer at the primary substation), while other factors, such as the discount rate, have a lower impact.
Future work includes the extension of the planning approach to accommodate the presence of endogenous or decision-dependent uncertainties. Such uncertainties are realised only as a response to some action taken by the planner/decision maker. For example in [31], uncertainty related to demand-side response flexibility is resolved as a response to investment and operational decisions taken by the planner, while in [32], the uncertainty around the cost of storage is resolved after investments in storage are made.
Another area of interest for the authors is the development of decomposition approaches for large-scale optimisation models, so that these models can be used for the study of strategic and incremental approaches in power systems. Examples of such methods include multicut Benders decomposition [33] and nested decomposition [34]. Such approaches can make the study of the strategic and incremental approaches more tractable in large power systems.
Moreover, it is of interest to the authors to compare the economic benefits resulting from the presented analysis to benefits arising from the application of other frameworks such as Backwards Induction methodology [35], machine-learning approaches [36] and stochastic optimisation [37]. Finally, the authors are interested in expanding the sensitivity analysis to include more parameters, such as changes in consumer behaviour, external economic factors and different geographical regions with varying energy demands and backgrounds.
Author Contributions
Conceptualization, S.G., D.P. and G.S.; Methodology, I.K. and G.S.; Validation, S.G.; Formal analysis, S.G., T.Z. and I.K.; Investigation, S.G., T.Z. and D.P.; Data curation, T.Z.; Visualization, T.Z. and D.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Climate Change 2022: Impacts, Adaptation and Vulnerability. Available online: https://www.ipcc.ch/report/ar6/wg2/ (accessed on 1 September 2022).
- COP26 Summary Report. Available online: https://www.un.org/en/climatechange/cop26 (accessed on 1 September 2022).
- The Paris Agreement. Available online: https://unfccc.int/sites/default/files/english_paris_agreement.pdf (accessed on 1 September 2022).
- Global Status Report for Buildings and Construction. Available online: https://globalabc.org/resources/publications/2021-global-status-report-buildings-and-construction (accessed on 1 September 2022).
- Baringo, L.; Conejo, A.J. Transmission and Wind Power Investment. IEEE Trans. Power Syst. 2012, 27, 885–893. [Google Scholar] [CrossRef]
- Strbac, G.; Konstantelos, I.; Aunedi, M.; Pollitt, M.; Green, R. Delivering Future-Proof Energy Infrastructure: Report for National Infrastructure Commission; University of Cambridge & Imperial College London: London, UK, 2016. [Google Scholar]
- Konstantelos, I.; Giannelos, S.; Strbac, G. Strategic Valuation of Smart Grid Technology Options in Distribution Networks. IEEE Trans. Power Syst. 2017, 32, 1293–1303. [Google Scholar] [CrossRef]
- Conejo, A.J.; Carrion, M.; Morales, J.M. Decision Making under Uncertainty in Electricity Markets; Springer: New York, NY, USA, 2010. [Google Scholar]
- Hossain, S.Z.; Khan, L.; Mahmud, H. Planning and design of future-proofed substations for smart grids. IET Eng. 2022, 4, 192–203. [Google Scholar]
- Cebeci, M.E.; Eren, S.; Tor, O.B.; Güven, N. Transmission and substation expansion planning using Mixed Integer Programming. In Proceedings of the 2011 North American Power Symposium, Boston, MA, USA, 4–6 August 2011; pp. 1–5. [Google Scholar] [CrossRef]
- Gu, C.; Zhang, Y.; Li, F.; Yuan, W. Economic analysis of interconnecting distribution substations via superconducting cables. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–5. [Google Scholar] [CrossRef]
- Yurtseven, K.; Karatepe, E. Distribution Substation Expansion Planning Considering Different Geographical Configurations. In Proceedings of the 2021 12th International Symposium on Advanced Topics in Electrical Engineering (ATEE), Bucharest, Romania, 25–27 March 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Mazhari, S.M.; Monsef, H.; Romero, R. A Hybrid Heuristic and Evolutionary Algorithm for Distribution Substation Planning. IEEE Syst. J. 2015, 9, 1396–1408. [Google Scholar] [CrossRef]
- Ge, S.; Wang, S.; Lu, Z.; Liu, H. Substation planning method in an active distribution network under low-carbon economy. J. Mod. Power Syst. Clean Energy 2015, 3, 468–474. [Google Scholar] [CrossRef]
- Giannelos, S.; Konstantelos, I.; Strbac, G. Investment Model for Cost-effective Integration of Solar PV Capacity under Uncertainty using a Portfolio of Energy Storage and Soft Open Points. In Proceedings of the 2019 IEEE Milan PowerTech, Milan, Italy, 23–27 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Giannelos, S.; Konstantelos, I.; Strbac, G. Option value of dynamic line rating and storage. In Proceedings of the 2018 IEEE International Energy Conference (ENERGYCON), Limassol, Cyprus, 3–7 June 2018; pp. 1–6. [Google Scholar]
- Borozan, S.; Giannelos, S.; Strbac, G. Strategic network expansion planning with electric vehicle smart charging concepts as investment options. Adv. Appl. Energy 2021, 5, 100077. [Google Scholar] [CrossRef]
- Lassila, J.; Kaipia, T.; Partanen, J.; Lohjala, J. New Investment Strategies in the Modern Electricity Distribution Business—Reliability in the Long-Term Planning. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–8. [Google Scholar] [CrossRef]
- Zhai, X.; Wang, J.; Zhu, D.; Cang, M.; Wang, Q.; Wu, S. Evaluation of Investment Benefits for the Incremental Distribution Network based on System Dynamics. In Proceedings of the 2023 IEEE 6th International Electrical and Energy Conference (CIEEC), Hefei, China, 12–14 May 2023; pp. 3837–3842. [Google Scholar] [CrossRef]
- Gao, Q.; Wang, Q.; Luo, Y.; Lian, C.; Zhang, Z.; Liu, S.; Han, C.; Zhang, T. Investment Benefit Evaluation of Incremental Distribution Network Considering Regional Power Supply Growth. In Proceedings of the 2019 IEEE Sustainable Power and Energy Conference (iSPEC), Beijing, China, 21–23 November 2019; pp. 1285–1290. [Google Scholar] [CrossRef]
- Wu, G.; Zhang, L.; Chen, X.; Huang, D.; Wang, J. Incremental Distribution Network Planning with Energy Storage. In Proceedings of the 2019 IEEE International Conference on Energy Internet (ICEI), Nanjing, China, 27–31 May 2019; pp. 127–131. [Google Scholar] [CrossRef]
- Baringo, L.; Conejo, A.J. Strategic Wind Power Investment. IEEE Trans. Power Syst. 2014, 29, 1250–1260. [Google Scholar] [CrossRef]
- Tian, K.; Sun, W.; Han, D. Strategic Investment in Transmission and Energy Storage in Electricity Markets. J. Mod. Power Syst. Clean Energy 2022, 10, 179–191. [Google Scholar] [CrossRef]
- Kazempour, S.J.; Conejo, A.J.; Ruiz, C. Strategic Generation Investment Using a Complementarity Approach. IEEE Trans. Power Syst. 2011, 26, 940–948. [Google Scholar] [CrossRef]
- Pringles, R.; Olsina, F.; Garcés, F. Power transmission investment under uncertainty: A Real Option framework. In Proceedings of the 2015 18th International Conference on Intelligent System Application to Power Systems (ISAP), Porto, Portugal, 11–16 September 2015; pp. 1–7. [Google Scholar] [CrossRef]
- Chen, S.; Wei, Z.; Sun, G.; Zhou, Y. Strategic Investment in Power and Heat Markets: A Nash–Cournot Equilibrium Model. IEEE Trans. Ind. Inform. 2022, 18, 6057–6067. [Google Scholar] [CrossRef]
- Jalali, M.; Taheri, S.; Kekatos, V. Strategic Investment in Energy Markets using Bayesian optimization. In Proceedings of the 2023 IEEE Power & Energy Society General Meeting (PESGM), Orlando, FL, USA, 16–20 July 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Pindyck, R.S. Irreversible Investment, Capacity Choice, and the Value of the Firm. Am. Econ. Rev. 1988, 78, 969–985. [Google Scholar]
- Triantis, A.J. Real Options. In Handbook of Modern Finance; American Institutes for Research: New York, NY, USA, 2003. [Google Scholar]
- Dixit, A. Entry and Exit Decisions under Uncertainty. J. Polit. Econ. 1989, 97, 620–638. [Google Scholar] [CrossRef]
- Giannelos, S.; Konstantelos, I.; Strbac, G. Option Value of Demand-Side Response Schemes under Decision-Dependent Uncertainty. IEEE Trans. Power Syst. 2018, 33, 5103–5113. [Google Scholar] [CrossRef]
- Giannelos, S.; Konstantelos, I.; Strbac, G. A new class of planning models for option valuation of storage technologies under decision-dependent innovation uncertainty. In Proceedings of the 2017 IEEE Manchester PowerTech, Manchester, UK, 18–22 June 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Giannelos, S.; Borozan, S.; Aunedi, M.; Zhang, X.; Ameli, H.; Pudjianto, D.; Konstantelos, I.; Strbac, G. Modelling Smart Grid Technologies in Optimisation Problems for Electricity Grids. Energies 2023, 16, 5088. [Google Scholar] [CrossRef]
- Falugi, P.; Konstantelos, I.; Strbac, G. Application of novel nested decomposition techniques to long-term planning problems. In Proceedings of the PSSC ’16, Genoa, Italy, 20–24 June 2016. [Google Scholar]
- Giannelos, S.; Borozan, S.; Strbac, G. A Backwards Induction Framework for Quantifying the Option Value of Smart Charging of Electric Vehicles and the Risk of Stranded Assets under Uncertainty. Energies 2022, 15, 3334. [Google Scholar] [CrossRef]
- Giannelos, S.; Moreira, A.; Papadaskalopoulos, D.; Borozan, S.; Pudjianto, D.; Konstantelos, I.; Sun, M.; Strbac, G. A Machine Learning Approach for Generating and Evaluating Forecasts on the Environmental Impact of the Buildings Sector. Energies 2023, 16, 2915. [Google Scholar] [CrossRef]
- Giannelos, S.; Jain, A.; Borozan, S.; Falugi, P.; Moreira, A.; Bhakar, R.; Mathur, J.; Strbac, G. Long-Term Expansion Planning of the Transmission Network in India under Multi-Dimensional Uncertainty. Energies 2021, 14, 7813. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).