Optimal Capacity and Charging Scheduling of Battery Storage through Forecasting of Photovoltaic Power Production and Electric Vehicle Charging Demand with Deep Learning Models

Abstract

The transition from internal combustion engine vehicles to electric vehicles (EVs) is gaining momentum due to their significant environmental and economic benefits. This study addresses the challenges of integrating renewable energy sources, particularly solar power, into EV charging infrastructures by using deep learning models to predict photovoltaic (PV) power generation and EV charging demand. The study determines the optimal battery energy storage capacity and charging schedule based on the prediction result and actual data. A dataset of a 15 kWp rooftop PV system and simulated EV charging data are used. The results show that simple RNNs are most effective at predicting PV power due to their adept handling of simple patterns, while bidirectional LSTMs excel at predicting EV charging demand by capturing complex dynamics. The study also identifies an optimal battery storage capacity that will balance the use of the grid and surplus solar power through strategic charging scheduling, thereby improving the sustainability and efficiency of solar energy in EV charging infrastructures. This research highlights the potential for integrating renewable energy sources with advanced energy storage solutions to support the growing electric vehicle infrastructure.

1. Introduction

In recent years, there has been a significant shift from traditional internal combustion engine (ICE) vehicles to electrical vehicles (EVs). This trend is driven primarily by environmental and economic concerns. Electric vehicles (EVs) offer many financial benefits. For example, the cost of electricity needed to power an EV is significantly less than the cost of fueling an equivalent ICE vehicle to travel the same distance [1], and the maintenance expenses are also reduced, since EVs have fewer moving parts and require less upkeep. Additionally, EV Owners can also benefit from reduced utility rates for off-peak charging and exemptions from congestion charges in some cities. With the introduction of the latest EV models, battery technology in the automotive sector has undergone a rapid evolution [2]. To promote truly sustainable road transport, electric vehicles also play a key role in harnessing renewable energy sources (RES) [1], which are abundant and do not produce greenhouse gases [3]. Solar power, which has been widely adopted in many sectors, is a prominent form of RES. However, the integration of solar power into the electricity grid to fulfill the EV charging demand poses challenges due to its variable and intermittent nature, which creates uncertainties in the electricity sector. To overcome these challenges and effectively integrate solar energy into EV charging stations, using an energy storage system (ESS) is essential. This combination of solar energy and energy storage offers significant benefits and supports EV charging infrastructure in homes, workplaces, and public facilities.

The increasing adoption of electric vehicles has led to a surge in demand for EV charging stations. This demand poses a challenge to energy providers who need to meet the growing demand. A viable solution involves integrating solar energy with appropriate energy storage to support the power required by these facilities. As the demand for EV charging is dynamic and can change rapidly, it is essential that research is conducted to determine the optimal capacity of battery energy storage required to balance the charging demand with energy from solar power and the grid. In addition, the operation and maintenance of charging stations consume significant amounts of energy, resulting in high operating costs. Accurate forecasting of energy consumption is essential to optimize the use of charging stations and minimize operating costs. Load forecasting is also critical to the sustainable and profitable management of these assets. In addition, solar power output from PV installations is highly dependent on weather conditions, making it difficult to predict the availability of power to support EV charging demand on a consistent basis. Therefore, when solar power alone is not sufficient, solar power forecasting is required to balance the use of energy from the grid.

This study is organized into two stages. In the first stage, we conducted a comparative analysis followed by the determination of optimal capacity. Below, we have provided a detailed description and objectives of this study:

• Comparative analysis: we conducted a comparative analysis of deep learning models for forecasting PV power generation and EV charging demand.
• Optimal capacity determination and charging scheduling: we used the forecasting result to determine the optimal battery energy storage capacity, considered different initial battery installed capacities in kWh, and devised a charging schedule based on different initial states of charge of battery energy storage.

The remainder of the paper is structured as follows: Section 2 provides a literature review which is related to our study. Section 3 provides an overview of the architectural design employed in the construction of the deep learning models. Section 4 provides a detailed overview of the datasets utilized for both PV power forecasting and EV charging demand forecasting. Section 5 presents the proposed approach. Section 6 presents the simulation results and analysis. Finally, Section 7 provides a conclusion to the paper.

2. Literature Review

In the field of photovoltaic power forecasting, several methodologies have been proposed with the objective of enhancing prediction accuracy and applicability across different environmental conditions. In a study by Limouni et al. [4], a new hybrid model combining long short-term memory (LSTM) with Temporal Convolutional Networks (TCNs) was proposed. This model, designated as the LSTM-TCN model, represents a significant advancement in the field of PV power forecasting. The model demonstrates robustness and efficacy in diverse climatic and meteorological conditions, substantiating its suitability for a range of environmental settings. In a further contribution to the field of PV power forecasting, Li et al. [5] present a recurrent neural network (RNN)-based model. The method utilizes data from both adjacent days and the same day in an effort to mitigate nonlinearity effects, thereby enhancing accuracy. This novel approach ensures more precise prediction of photovoltaic power output.

Wang et al. [6] propose a gate recurrent unit (GRU)-based model. This methodology effectively incorporates the influence of specific features and past photovoltaic energy generation on future energy output, offering enhanced precision compared to conventional techniques. This represents a significant advancement in the field of photovoltaic power forecasting. Chen et al. [7] propose an LSTM model with Pearson feature selection for PV power forecasting. This approach results in a reduction in noise and an improvement in the model’s predictive performance. This is evidenced by the lower error rates in mean absolute error (MAE) and root mean square error (RMSE) compared to traditional methods, which demonstrate the efficacy and precision of their forecasting technique.

In the field of electric vehicle (EV) charging demand forecasting, a number of innovative models have been proposed with the aim of enhancing prediction accuracy and efficiency. The methodology employed by Shanmuganathan et al. [3] involves a combination of techniques, including empirical mode decomposition (EMD) for signal splitting; an arithmetic optimization algorithm (AOA) for processing; and long short-term memory (LSTM) for retaining past data. This approach is coupled with deep learning, which enhances the accuracy of the forecast results. The integrated methodology employed ensures precise and reliable forecasting, with each method contributing to the overall strength of the approach. Yin et al. [8] integrate Partial Least Squares Regression (PLSR) and Light Gradient Boosting Machine (LightGBM) into their model, thereby enhancing its predictive capabilities. These algorithms are capable of accurately predicting the demand for electric vehicle (EV) charging by effectively considering the nonlinear and time series nature of the data. This combination enhances the model’s capacity to handle complex patterns in EV charging demand. Deng et al. [9] propose a model for EV charging load forecasting based on the technique of gene expression programming (CFMM-GEP). The objective of this model is to achieve more accurate and efficient predictions of EV charging load by utilizing gene expression programming (GEP), thereby enhancing interpretability and effectiveness in the forecasting process.

Battery charging scheduling is a critical element of modern sustainable transportation systems, as it can extend battery life, reduce operating costs, and minimize grid impact. This literature review examines various methods proposed by researchers to improve battery charging scheduling. In one study [10], the authors present a reinforcement learning-based approach using a Deep Q Network (DQN) with Prioritized Experience Replay (PER). This method optimizes battery charging and discharging schedules and outperforms a benchmark Mixed-Integer Linear Programming (MILP) approach. Key contributions include the integration of BESS controllers with automatic transfer switches, which significantly reduces electricity costs by 51% compared to uncontrolled methods and 33% compared to MILP and improves the reliability of the power supply. The algorithm effectively handles dynamic and uncertain conditions in the energy market.

Mohammed et al. [1] propose the integration of solar energy and EV charging through an artificial neural network (ANN)-based forecasting and scheduling system. This approach has the potential to enhance economic and environmental sustainability. By leveraging the predictive power of ANN models, their system optimizes charging schedules based on predicted energy availability from solar sources, thereby ensuring efficient energy use and reducing reliance on non-renewable energy sources. Qian et al. [11] developed an uninterruptible charging schedule optimized for solar power availability using a two-stage hierarchical optimization approach. This method ensures that charging times are aligned with periods of high solar power availability, thus maximizing the use of renewable energy and minimizing interruptions. The hierarchical structure enables the complex optimization problems to be broken down into more manageable sub-problems, thus allowing for the handling of such problems.

Lu et al. [12] made significant contributions to the field of dual-objective optimization, developing a framework that simultaneously minimizes company expenses and EV user costs. The framework employs a comprehensive linear programming model, detailed probability models, and Monte Carlo simulations, enabling the prediction of accurate travel and charging patterns for electric vehicles. The framework has been validated with real-world data, demonstrating its practical applicability and effectiveness. Additionally, their study employs scenario analysis to identify optimal strategies across a range of circumstances, thereby offering a robust, efficient solution for EV-charging infrastructure optimization. The study by Pozzi [13] focused on the development of a neural network-based predictive control algorithm for optimizing EV charging. This approach employs Model Predictive Control (MPC), combined with recurrent neural networks (RNNs) and long short-term memory (LSTM) layers, to address the challenges of EV charging in dynamic environments where conditions and parameters are unknown. The method is robust and computationally efficient, demonstrating superior performance in comparison to traditional model-based approaches in a range of practical applications.

This study is based on a review of the relevant literature and aims to address the forecasting of PV power and EV charging demand using deep learning models. The study will concentrate on a comparative analysis of the most popular models for these forecasting tasks. Furthermore, the findings of the literature review will inform the selection of methodologies for modeling charging scheduling and battery optimization in PV installations. The objective of this study is to utilize the forecasting results in order to determine the optimal battery capacity and charging scheduling for PV infrastructure battery systems to support EV charging station unit. A summary of the literature review is provided in

Table 1. Summary of main contribution.

Topic	Reference	Proposed Methodology	Description of Main Contribution
PV power forecasting	Limouni et al. [4]	Proposes a hybrid model combining long short-term memory (LSTM) and Temporal Convolutional Network (TCN)	Model excels in diverse weather, proving adaptability.
	Li et al. [5]	Recurrent neural network (RNN)-based model	The method enhances accuracy by considering nearby days and intra-day data, minimizing nonlinear effects.
	Wang et al. [6]	Gate recurrent unit (GRU)-based model	Method integrates past PV energy and features for more accurate future output prediction, surpassing conventional methods.
	Chen et al. [7]	LSTM model with Pearson feature selection	The proposed approach reduces noise and enhances predictive performance with lower MAE and RMSE compared to traditional methods.
EV charging demand forecasting	Shanmuganathan et al. [3]	Empirical mode decomposition (EMD)—optimization algorithm (AOA)-LSTM	The model employs a combination of techniques, including empirical mode decomposition for signal splitting, arithmetic optimization for processing, LSTM for retaining past data, and deep learning for enhanced accuracy.
	Yin et al. [8]	The model integrates the Partial Least Squares Regression (PLSR) and Light Gradient Boosting Machine (LightGBM)	The model accurately predicting the demands for electric vehicle (EV) charging, taking into account the nonlinear and time series nature of the data.
	Deng et al. [9]	EV charging load forecasting model mining based on gene expression programming (CFMM-GEP)	The model employs the technique of gene expression programming in order to achieve more accurate and efficient EV charging load predictions, thereby enhancing the interpretability of the process.
Battery optimization/battery charging scheduling/EV charging scheduling	Selim et al. [10]	Reinforcement learning-based approach using a Deep Q Network (DQN)	The algorithm effectively handles dynamic and uncertain conditions in the energy market
	Mohammed et al. [1]	Artificial neural network (ANN) model	The integration of forecasting and optimal charging scheduling represents a promising approach to enhancing economic and environmental sustainability.
	Qian et al. [11]	Two-stage hierarchical optimization	Development of an uninterruptible charging schedule that optimizes charging times based on solar power availability.
	Lu et al. [12]	Monte Carlo simulation, linear programing model, probability models.	The study develops effective approach to minimize company expenses and EV user costs.
	Pozzi [13]	Model Predictive Control (MPC), recurrent neural networks (RNNs) with long short-term memory (LSTM) layers	The model is effective in uncertain conditions, offering a robust and efficient solution

.

3. Deep Leaning Models’ Architecture

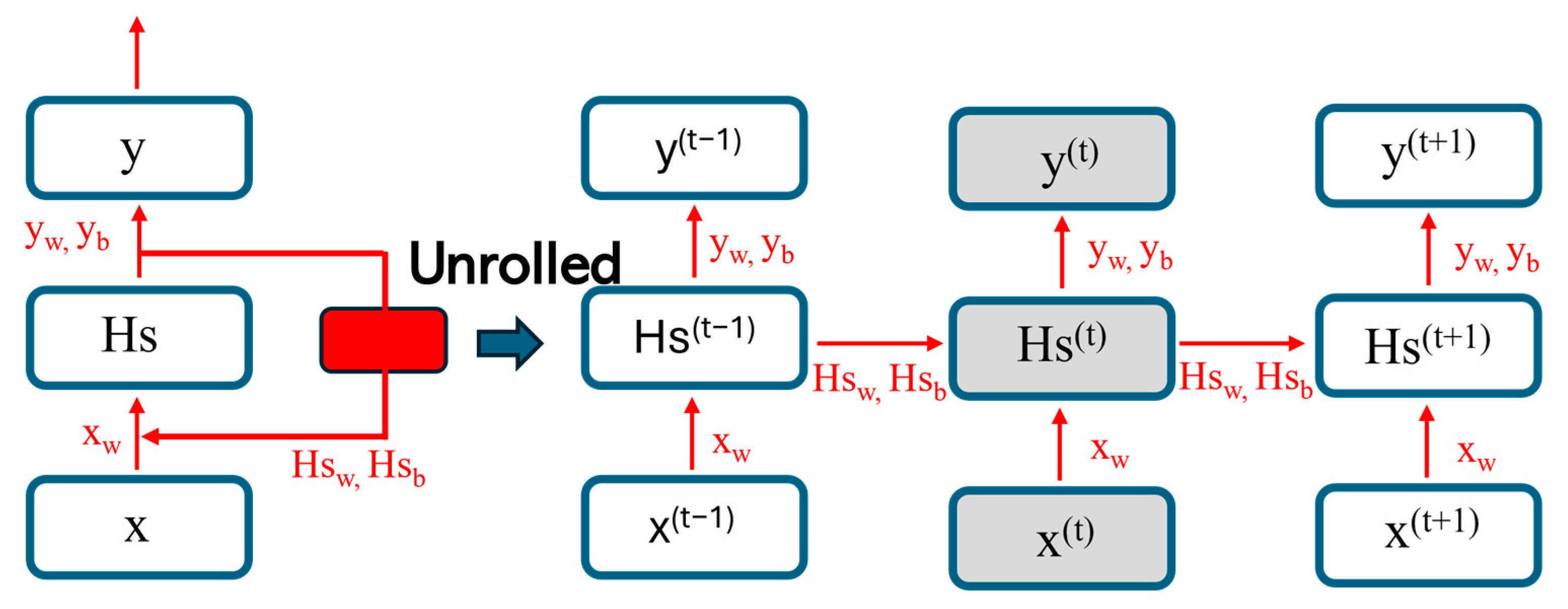
A time series is a chronological sequence of data points used to track the evolution of various phenomena over time. Time series forecasting projects future values in this sequence, supporting informed decision-making strategies. Deep learning, a key component of machine learning, excels at handling complex, high-dimensional time series data beyond the scope of traditional methods [14]. This research explores several deep learning models, including simple recurrent neural networks (RNNs), long short-term memory (LSTM) networks, and gated recurrent units (GRUs), that can be used to forecast PV power generation and EV load demand. RNNs, which are essential in deep learning for processing sequential data, leverage memory mechanisms to integrate past inputs for dynamic output modulation. The architecture of the RNN model, depicted in Figure 1, is distinguished by a hidden state that transfers information across time steps, illustrating its computational efficiency.

In the unrolled recurrent neural network (RNN) unit (see Figure 1), the current hidden state (Hs^(t)) at a given time step is determined by both the previous hidden state (Hs^(t−1)) and the present input (x^(t)). This mechanism provides a memory function that allows information from the previous time step to be retained while the information from the current time step is undergoing processing. Consequently, previous elements within the sequence continually influence the output at the current time step of the RNN, which is represented by the variable y^(t). Across all time steps, the connections between the input, the hidden state, and the output of the evolved RNN unit are characterized by weights w and biases b. Essentially, the RNN architecture represents a simple, yet powerful, model used in various forecasting scenarios. Nevertheless, the utilization of backpropagation through time presents certain challenges, namely, those pertaining to the so-called exploding and vanishing gradient problem. This issue arises from the potential for multiplicative gradients to either diminish or escalate exponentially with the number of layers, thereby impeding the effectiveness of conventional RNNs in the capture of long-term dependencies. To overcome these difficulties, alternative categories of RNNs, such as long short-term memory (LSTM) and Gated Recurrent Units (GRU), are employed. These models represent an extension of the conventional RNNs and facilitate the management of long-term dependencies. This allows information to be retained over extended periods, thus avoiding the issues associated with exploding or vanishing gradients [15].

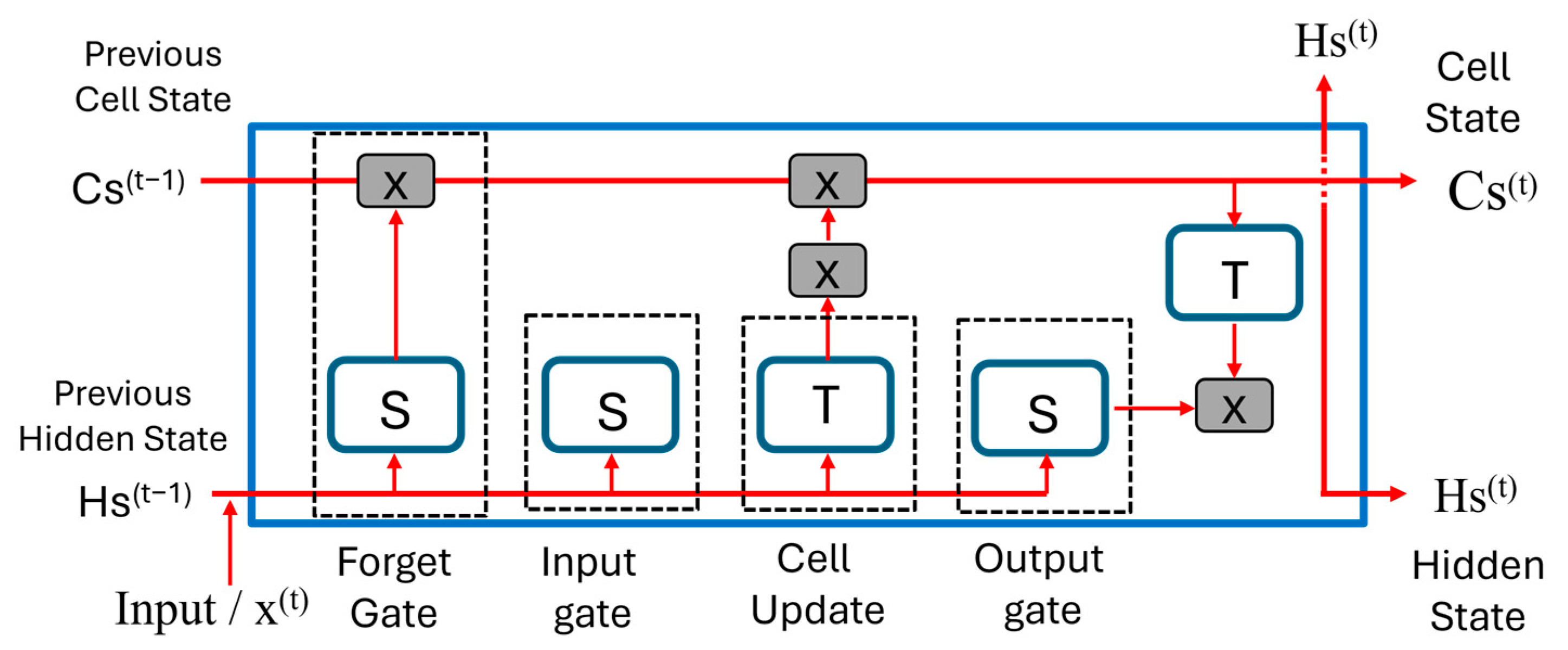
In reference [15], the LSTM model was introduced to address the vanishing gradient problem. It incorporates memory cells and gates to regulate network information. A typical LSTM architecture includes memory blocks called cells that maintain two distinct states: the cell state and the hidden state. These cells facilitate decision-making by selectively storing and ignoring information through three main gates, as shown in Figure 2.

An LSTM cell operates through a series of gates that control how information flows in each sequence. The forget gate assigns values between 0 and 1 to each component of the state and uses a sigmoid function to decide which parts of the cell state should be retained or discarded. At the same time, using another sigmoid function to update parts of the state and a Tanh layer to generate new candidate values, the input gate decides what new information to add. These decisions lead to the update of the cell state, modifying the old state to forget certain aspects and add new information, in effect managing the memory of the cell. Finally, the output gate, using the sigmoid function, selects the parts of the updated cell state to be output. This structured process allows the LSTM to carry relevant information through the sequence and to capture the dependencies of both the most recent and more distant inputs, which is essential for tasks in which context is critical.

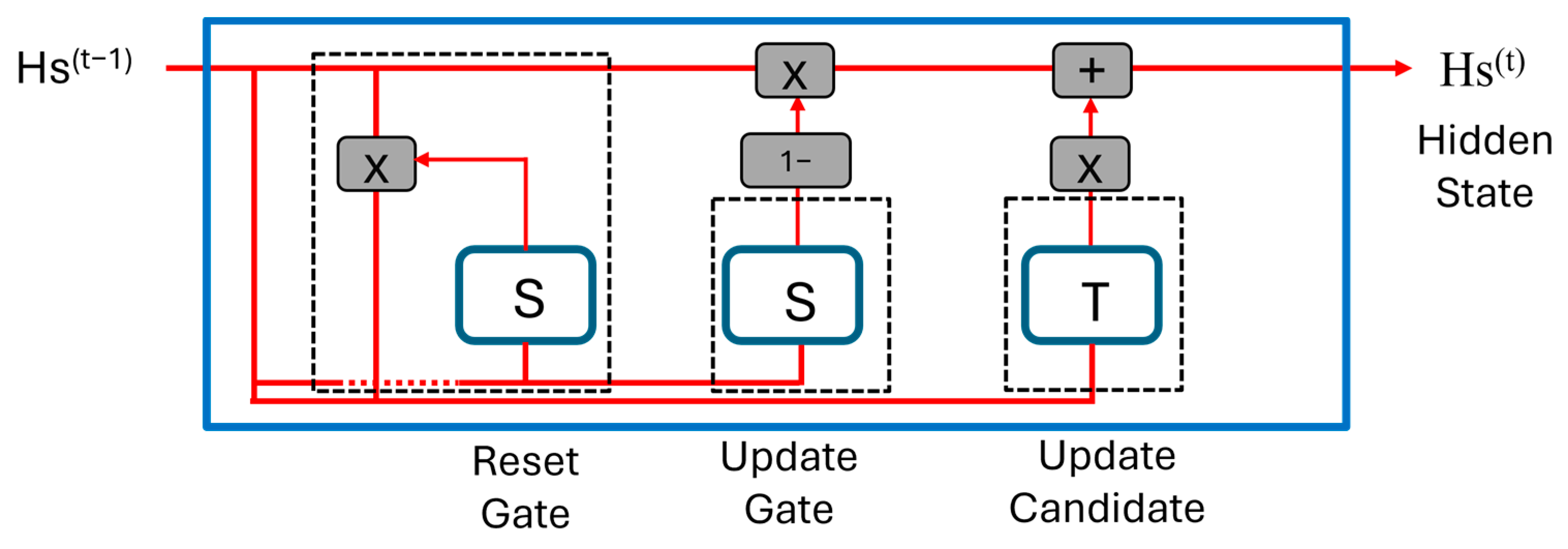
The GRU model is a variant of the LSTM that operates without a separate cell state. It relies solely on the hidden state to convey information and comprises two gates: the update gate (U_g), which is depicted in Figure 3, and the reset gate (R_g). The update gate combines the functionalities of the input and forget gates from LSTM, determining the relevance of incoming information, and the reset gate governs the extent of past information to discard. The values assigned to these gates subsequently dictate the new hidden state, thereby serving to represent the output of the network. These models are widely used for prediction tasks in various domains. In comparison, RNN, LSTM, and GRU each have distinct advantages, disadvantages, and variants. A summary of these characteristics is provided in

Table 2. Model description.

Description	RNN	LSTM	GRU
Fundamental	Sequence models process sequences iteratively. The output of the previous step is used as input for the current step [16].	Improves on standard RNNs used to capture the sequence of long-term dependencies [17]	A variation of the LSTM with a simplified gate mechanism [6].
Variant	Vanilla RNN, stacked RNN, bidirectional RNN [18]	Vanilla LSTM, stacked LSTM, bidirectional LSTM, autoencoder LSTM	GRU
Main component	Allow memory block retention	Having an input gate, forget gate, cell update, and output gate. Moving information along the sequence using cell state and hidden state	Obtain reset gate, update gate and update candidate. Merging cell state and hidden state
Advantages	Problems with vanishing and exploding gradients [19].	Greater computational power than RNNs and greater complexity	In some cases, it may not be possible to capture long-term dependencies such as LSTM.

.

4. Dataset Description

The objective of this study is to develop a forecasting model for PV power generation and another for EV charging demand. The purpose of this work is to utilize these forecasts to determine the optimal installed capacity of battery storage required to support the EV charging infrastructure at university facilities. To meet the forecasting requirements, it is necessary to obtain historical time series data of both PV power generation and EV charging demand.

In this study, a prediction simulation was performed using a real dataset of Photovoltaic (PV) power generation from the university’s infrastructure. The dataset, collected from a 15 kWp rooftop PV system, consists of power measurements in watts recorded at hourly intervals over the period 1 January 2020 to 30 December 2020. To align with the EV dataset, which records EV charging demand at 15 min intervals, the original PV power dataset was resampled to 15 min intervals and the power measurements were converted to kW units. In addition, the EV charging demand data were obtained from the emobpy package due to the lack of real EV charging demand data. Emobpy is a tool that is specifically designed to generate time series data for electric vehicles based on empirical data [20]. This dataset demonstrates the utility of emobpy by incorporating German mobility statistics and includes four time series: vehicle mobility, driving electricity consumption, grid availability, and grid electricity demand at full capacity [20,21]. This study utilized the original 15 min time series generated by emobpy, with a focus on analyzing vehicle mobility, driving electricity consumption and full-capacity grid demand [20]. These EV charging-demand data were used in the simulation for EV charging load demand forecasting, with the assumption that EVs were charging in university car parks.

The original EV dataset includes several parameters such as the date, time, EV ID, charging station, required power, grid demand at full capacity (load), and grid state of charge (SoC) at full capacity. The dataset focuses exclusively on electric vehicles that need to be charged in the workplace, as the objective is to develop optimal battery storage solutions to support the workplace EV charging infrastructure (specifically in the university car park). The dataset shows that there are seven electric vehicles that frequently require charging at this workplace, each with different power ratings. For analysis purposes, we aggregate all EV charging load demands from these vehicles at each recorded time point to assess the overall workplace (university car parks) charging demand.

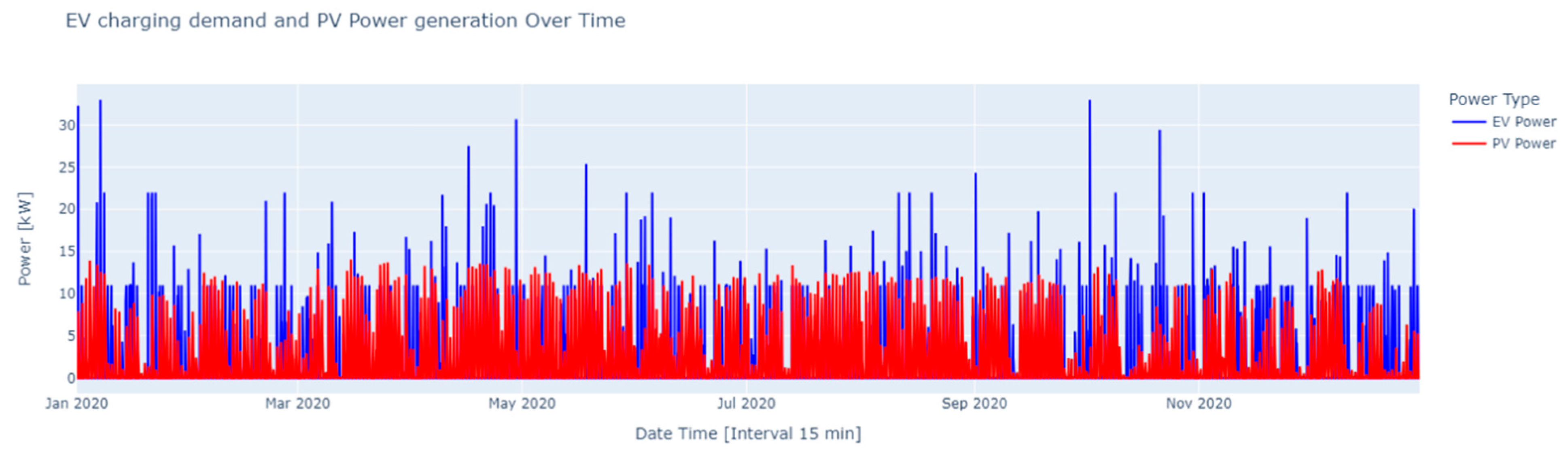
The PV power dataset only shows PV power in kW (see Figure 4). The example of both datasets is shown in

Table 3. Example of dataset.

Date Time	EV Dataset					PV Dataset
	EV ID	Charging Station	Power Rating Required [kW]	Grid Demand Full Capacity (Load) [kW]	Grid Demand Full Capacity (SoC)	PV Power Generation [kW]
3 January 2020 07:00	2	Workplace	11	11	0.957	0.14413
3 January 2020 07:15	2	Workplace	11	8.698	1	0.67393
3 January 2020 07:30	2	Workplace	11	0	1	1.20373

. According to our dataset analysis, the maximum PV power generation in 2022 is 14.06 kW, the minimum is 0 kW, and the average power generation for one year is 1.95 kW. On the other hand, the EV charging demand as electric load shows that maximum load for some charged EVs is 33 kW, the minimum load is 0, and the average load of one-year measurements is 0.42 kW.

5. Proposed Approach

5.1. Data Preprocessing for Forecasting Approaches

In order to conduct simulations of deep learning models for electrical load forecasting and solar power forecasting, it is of paramount importance to manage and prepare the appropriate datasets for these models. The initial stage involves gathering the necessary data pertaining to photovoltaic power generation and electric vehicle load charging demand. In this study, data are collected from various sources to ensure the quality of the data are not compromised. Following the data collection phase, it is of great importance to undertake data preprocessing. This involves applying techniques with the objective of enhancing the quality and suitability of the raw data for use with deep learning (DL) models, which can be sourced from various origins. The process is invaluable in enabling the identification and extraction of valuable insights from the data. In the present study, a series of data preprocessing techniques will be employed, commencing with data normalization and dataset partitioning, followed by the restructuring of the data structure using the sliding window method.

Datasets frequently originate from a variety of sources, and their characteristics may differ in units and scales. This discrepancy can influence the performance of DL models during the learning process, potentially leading to increased generalization errors. Consequently, it is essential to standardize all variables within the dataset. DL models demonstrate improved performance when input variables are scaled to a standardized range. The technique of min–max normalization has emerged as a popular approach, whereby the original values of the dataset are reassigned to a new range. The mathematical formula utilized for min–max normalization in this investigation is depicted in Equation (1) below.

$$y_{norm}=\frac{y-\mathit{min}\left(y\right)}{\mathit{max}\left(y\right)-\mathit{min}\left(y\right)}$$

(1)

Following the normalization of the data, this study employs a sliding window method to adjust the dimensions of the dataset to align with the deep learning model’s requirements. Time series prediction is a supervised learning task, necessitating the transformation of the dataset structure from a sequential format to a supervised learning format with input patterns (X) and output patterns (y). The sliding window method is a technique that is commonly employed for this purpose; it involves the utilization of values from the preceding time step as the input variable, while those from the succeeding time step serve as the output variable. The sliding window technique employed in this study has an input window of eight for the input variables (see red hyphen box) and one for the forecast horizon (see blue hyphen box). This implies that the input comprises the last eight steps (equivalent to two hours before, assuming a data resolution of 15 min) to predict the value one step ahead (equivalent to 15 min ahead, with a 15 min time resolution). This method was applied to all subsets of the training, validation, and test time series datasets. The illustration of a sliding window is shown in Figure 5.

To develop and evaluate a predictive model, it is often necessary to preprocess the input data appropriately and divide them into training, validation, and test datasets. The training data are used to train the model, which is then fine-tuned using the validation data to prevent overfitting. Finally, the testing data are employed to evaluate the model’s performance. By following this process, we can guarantee that the model is robust, generalizable to new data, and performs well in a real-world setting. It is important to note that there is no universal approach to determining the optimal splitting ratio. Commonly employed methodologies include a 90% training and 10% testing split or an 80% training and 20% testing split [22,23]. However, in the context of this study, an 80% training set, 10% validation set, and 10% testing set were deemed an appropriate approach to data splitting based on the studies presented in the references [24,25]. In this study, both the PV power dataset and the EV charging demand dataset cover the period of 2020 only. This one-year measurement dataset was then split for various scenarios. For the training dataset, data from 1 January 2020, 00:00:00 to 18 October 2020, 21:45:00 were used. The validation dataset covered the period from 18 October 2020 22:00:00 to 24 September 2020, 09:30:00. Finally, the testing dataset spanned from 24 September 2020, 09:45:00 to 30 December 2020, 23:15:00.

5.2. Building Forecasting Models and Training Stage

The objective of this study was to develop and evaluate two distinct forecasting models specifically tailored to the domains of photovoltaic (PV) power generation and electric vehicle (EV) charging load demand. The goal was to identify the most suitable deep learning model for short-term forecasting tasks in both domains. In the training stage, all deep learning models were fed with input training dataset with a size of (28,024-8-1) The dataset has 28,024 samples, each with 8 features or time steps, and each feature/time step has a single value. This format is suitable for time series data where there are eight time steps per sequence, or for tabular data where there are eight features per instance. It can be used in various deep learning models, including RNN, LSTM, and GRU for sequential data.

The model development and training section involved building and configuring the PV power generation and EV charging load demand models in the same form for each variant. Details of the structure and configuration of the deep learning model are shown in

Table 4. Deep learning model layers.

Deep Learning Models	Structure	Configuration
Simple RNN	1 Simple RNN layer (15 neurons + activation = ‘relu’) + 1 Simple RNN layer (15 neurons + activation = ‘relu’) + 1 Dense layer (1 neuron)	Optimizer: Adam, loss: mse, epochs: 30, verbose: 0, batch size: 32, include validation data
Vanilla LSTM	1 LSTM layer (15 neurons + activation = ‘relu’) + 1 Dense layer (1 neuron)	Optimizer: Adam, loss: mse, epochs: 30, verbose: 0, batch size: 32, include validation data
Stacked LSTM	1 LSTM layer (15 neurons + activation = ‘relu’) + 1 LSTM layer (15 neurons + activation = ‘relu’) + 1 Dense layer (1 neuron)	Optimizer: Adam, loss: mse, epochs: 30, verbose: 0, batch size: 32, include validation data
Bidirectional LSTM	1 bidirectional LSTM layer (15 neurons + activation = ‘relu’) + 1 bidirectional LSTM layer (15 neurons + activation = ‘relu’) + 1 Dense layer (1 neuron)	Optimizer: Adam, loss: mse, epochs: 30, verbose: 0, batch size: 32, include validation data
GRU	1 GRU layers (15 neurons) + 1 GRU layers (15 neurons, activation = ‘relu’) + 1 Dense layer (1 neuron)	Optimizer: Adam, loss: mse, epochs: 30, verbose: 0, batch size: 32, include validation data

. In the following phase, the model preparation involved running the simulations sequentially. First, a model was developed to predict PV generation at a selected site, which was calibrated using both training and validation data. Each model was carefully trained and evaluated individually. All relevant training information was documented, including the history of model performance metrics such as loss and validation loss, and the computational time required for training. The predictive accuracy of the model was then assessed by applying the trained variants to a test dataset and calculating the corresponding error metrics. A similar approach was followed for the EV charging load demand forecasting model in the second phase of the study. This stage was crucial because the forecasting results for PV power generation and EV load demand were utilized to determine the appropriate battery storage capacity required to support the EV charging infrastructure and charging scheduling of battery energy storage.

5.3. Deep Learning Model Evaluation

Evaluating the performance and accuracy of the deep learning model using metric scores is of critical importance in the context of model assessment. The selection of evaluation metrics for this study was informed by recommendations from relevant literature and studies in the field of predictive analytics. These metrics, defined by specific formulas presented in the following equations, include the mean square error (MSE), the root mean square error (RMSE), and the mean absolute error (MAE) [26]. The mean square error (MSE) is a statistical measure that calculates the average of the squares of the errors between estimated and actual values. It emphasizes larger errors. The root mean square error (RMSE) is the square root of MSE, providing errors in the same units as the data and highlighting larger discrepancies. The mean absolute error (MAE) is a metric that measures the average absolute difference between predictions and actual outcomes. Unlike MSE and RMSE, it does not heavily penalize large errors, making it a more straightforward metric. The value of these metrics can be used to assess the performance of a deep learning model in learning the data. A higher value indicates a poor performance, while a lower value indicates a better performance. In this study, the scikit learn library was used to calculate the mentioned metric score [27]. The formula of these metrics is described in Equations (2)–(4). The actual value and the predicted value at time t are, respectively, denoted as $\mathrm{y}\mathrm{t}-\widehat{\mathrm{y}}\mathrm{t}$, and N is the sample size of the test dataset.

$$\mathrm{M}\mathrm{S}\mathrm{E}=\frac{\sum _{t=1}^N{\left(yt-\widehat{y}t\right)}^2}{N}$$

(2)

$$\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{\frac{\sum _{t=1}^N{\left(yt-\widehat{y}t\right)}^2}{N}}$$

(3)

$$\mathrm{M}\mathrm{A}\mathrm{E}=\frac{\sum _{t=1}^N\left|yt-\widehat{y}t\right|}{N}$$

(4)

5.4. Optimal Battery Capacity and Battery Charging Scheduling

This study only considers rooftop photovoltaic (PV) installations at the infrastructure site. However, the main objective is to determine the optimal battery capacity and charging schedule to support the planning of the EV charging infrastructure for future needs, assuming the installation of battery storage and EV charging stations. There are different methodologies that can be used to determine the capacity of battery energy storage, including technical calculations that assess the energy demand, evaluate the energy generation and determine the back-up requirements, as presented in references [28,29]. However, this study takes an alternative approach by using the forecast results of the PV power generation and the EV charging demand to determine both the optimal capacity and the optimal charging schedule of the battery energy storage system, thereby improving the utilization of the EV charging stations. As shown in Figure 6, the unit of the EV charging station is powered by several sources of energy, including the electricity grid, the photovoltaic system, and the battery energy storage system. Therefore, only the movement of energy into and out of the system is considered in the power flow. Meanwhile, the information flow is used for PV power generation and EV load demand forecasting to determine the optimal battery storage capacity for the infrastructure installation and to develop charge scheduling services for the BESS.

To determine the optimal battery storage capacity, the algorithm starts by converting the minimum and maximum capacity values of the battery into integers for iteration. It then initializes a list to store the results for each of the tested capacity values. For each capacity, the algorithm iterates in defined steps from minimum to maximum capacity. It initializes the daily state of charge (SoC) to zero and resets the daily grid energy used and the overflow energy trackers to zero. For each hour within the PV power and demand data provided, the algorithm calculates the net energy for that time interval by subtracting the demand from the PV power. The SoC is then updated based on this net energy. If the SoC exceeds the current capacity, the excess energy is recorded and the SoC is set to the current capacity. Conversely, if the SoC falls below zero, the grid energy consumed is increased to cover the deficit and the SoC is reset to zero. This hourly processing loop continues until all hours for the day have been processed. Once the daily loop is complete, the algorithm moves to the next capacity value and repeats the process. This iterative process allows the algorithm to evaluate and store results for each capacity tested and is repeated for all capacity values within the specified range. The estimated grid energy consumed and the overflow or excess energy that cannot be stored in the battery energy storage system (BESS) are output at the end of the process. Based on the range of battery storage capacities, the aim of this study is to find the minimum amount of grid energy used and the minimum amount of overflow. A comprehensive explanation of the algorithm used to determine the optimal battery capacity is provided in

Table 5. Algorithm for optimal battery capacity.

Step	Procedure to Determine Optimal Battery Capacity
Step 1: Input data	PV Power: predicted or actual photovoltaic power generation EV charging demand: predicted or actual EV charging demand Minimum Capacity: minimum potential BESS capacity (predetermined) Maximum Capacity: maximum potential BESS capacity (predetermined) Step: Incremental step to evaluate capacities between the minimum and maximum
Step 2: Capacity algorithm	Convert minimum and maximum capacities to integers for iteration  Initialize list to store results for each capacity    for each capacity from minimum to maximum in steps do          Initialize daily SoC to zero          Reset daily grid energy used and overflow trackers to zero          for each hour in PV Power and Demand do                     Calculate net energy for the hour (PV Power—Demand)                       Update SoC based on net energy                       if SoC exceeds current capacity:                               Record overflow energy                                 Set SoC to current capacity                           if SoC falls below zero:                                   Increase grid energy used to cover deficit                                       Reset SoC to zero                   End hourly loop         End capacity loop
Step 3: Output/ Result	Record results for the current capacity: Capacity level Total grid energy used for the day Total overflow energy for the day Create table result: capacity, grid energy used, and overflow

.

To perform charging scheduling, the algorithm processes data for each specific time interval. For each interval, it calculates the net energy. This is calculated by subtracting the power demand from the PV power production. The state of charge (SoC) of the battery is then updated. This is achieved by adding the net energy to the current SoC. The algorithm checks whether the updated SoC exceeds the maximum capacity of the battery and, if so, sets it to the maximum capacity to ensure that the SoC remains within the capacity limits. Likewise, if the current SoC is below zero, it is set to zero to prevent negative charging states. Next, the algorithm determines whether it is optimal to charge the battery. If there is excess PV power (i.e., if the net energy is positive) and the SoC is below the maximum capacity, it sets a flag indicating the best time to charge as true. Otherwise, it sets this flag to false. The algorithm also manages energy shortfalls. It calculates the amount of energy required from the grid if the new SoC is less than the original SoC, indicating a deficit. If the required grid energy exceeds the maximum charge or discharge rate of the battery, it is limited to the maximum rate. This grid energy requirement is then added to the new SoC to account for the deficit and the amount of grid energy used during the interval is recorded. Finally, relevant data for each time interval, such as the updated SoC, charging status and grid energy used, are logged for future analysis and monitoring. This approach ensures efficient use of PV energy, optimizes battery-charging schedules, and maintains system reliability by addressing energy shortfalls with grid support. A detailed description of the algorithm used for BESS charging scheduling based on forecasting approaches can be found in

Table 6. Algorithm for battery charging scheduling.

Step	Procedure for Battery Charging Scheduling
Step 1: Input data	Time: time intervals for operation (15 min interval) PV Power: predicted or actual photovoltaic power generation per 15 min interval EV charging demand: predicted or actual EV charging demand per 15 min interval
Step 2: Initialize variables	Initial SoC (state of charge) of BESS: 10 kWh (predetermined) Maximum capacity of BESS: 15 kWh (based on the result of battery storage capacity) Maximum charge/discharge rate per hour: 5 kWh
Step 3: Scheduling algorithm	for each interval in Time:          Calculate net energy: PV Power - Demand          Update SoC: SoC + net energy          If new SoC > maximum capacity:            Set SoC to maximum capacity          If new SoC < 0:           Set SoC to 0         Determine if it is optimal to charge:           If net energy > 0 and SoC < maximum capacity:             Set best time to charge as True           Else:             Set best time to charge as False         Manage deficits:           If new SoC < initial SoC (indicating a deficit):             Calculate grid energy needed: absolute value of (new SoC - initial SoC)           If grid energy needed > max charge/discharge rate:               Set grid energy needed to max charge/discharge rate               Add grid energy needed to new SoC                Update grid energy used for the interval         Log data for the current interval       End for loop
Step 4: Output/ Result	Create table with columns for hour, PV power, eV charging demand, SoC start, net energy, grid energy used, SoC end, and best time to charge Present final SoC and total grid energy used

.

6. Simulation Result and Analysis

6.1. Training Process Result

This section discusses the training stage results for EV charging demand and PV power generation within the university infrastructure. The models used belong to the RNN family, which includes simple RNN models, vanilla LSTM models, stacked LSTM models, bidirectional LSTM models, and GRU models. This discussion covers both the training and evaluation phases. During the training phase, each model was subjected to sequential training and evaluation using normalized power output datasets. Throughout the training process, key parameters such as training time and model loss, including validation loss, were meticulously recorded. This provided a comprehensive assessment of the computational efficiency, aiding optimization, model comparison, and resource estimation for deployment. Furthermore, tracking model loss and validation loss during training facilitated monitoring of the model’s learning trajectory, enabling detection of overfitting or underfitting phenomena and improving predictive accuracy.

Table 7. Training duration of deep learning models.

Forecasting Case	Training Duration [Second]
	Simple RNN	Vanilla LSTM	Stacked LSTM	Bidirectional LSTM	GRU
PV power generation models	341.736	279.4	850.607	1022.831	747.357
EV charging demand models	268.394	281.81	832.711	1019.43	741.855

shows the training times for the PV power and EV charging demand forecasting models. The data show that the bidirectional LSTM model requires the longest training time among the PV power models, while the vanilla LSTM model has the shortest duration in this forecasting scenario. Conversely, in the case of EV charging demand forecasting, the bidirectional LSTM model again takes the longest to train. In contrast, the simple RNN model takes the least time. A comparative overview of the training times for each model for both forecasting scenarios is shown in Table 7.

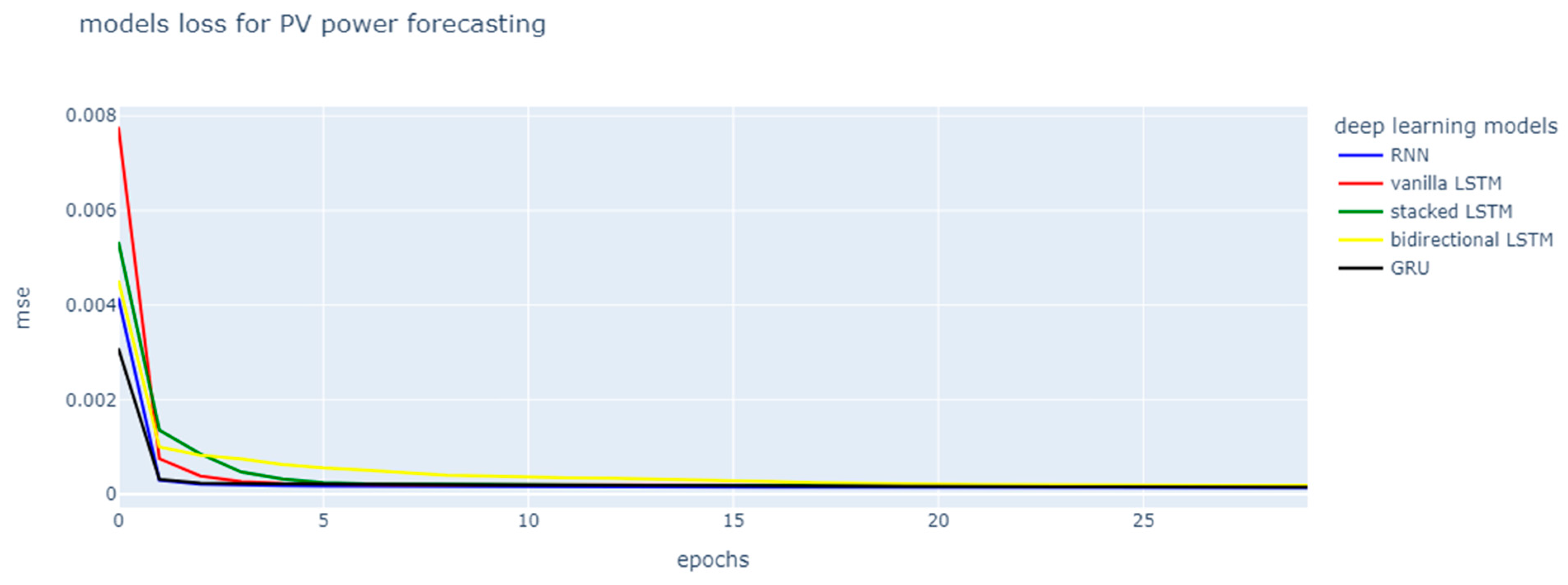
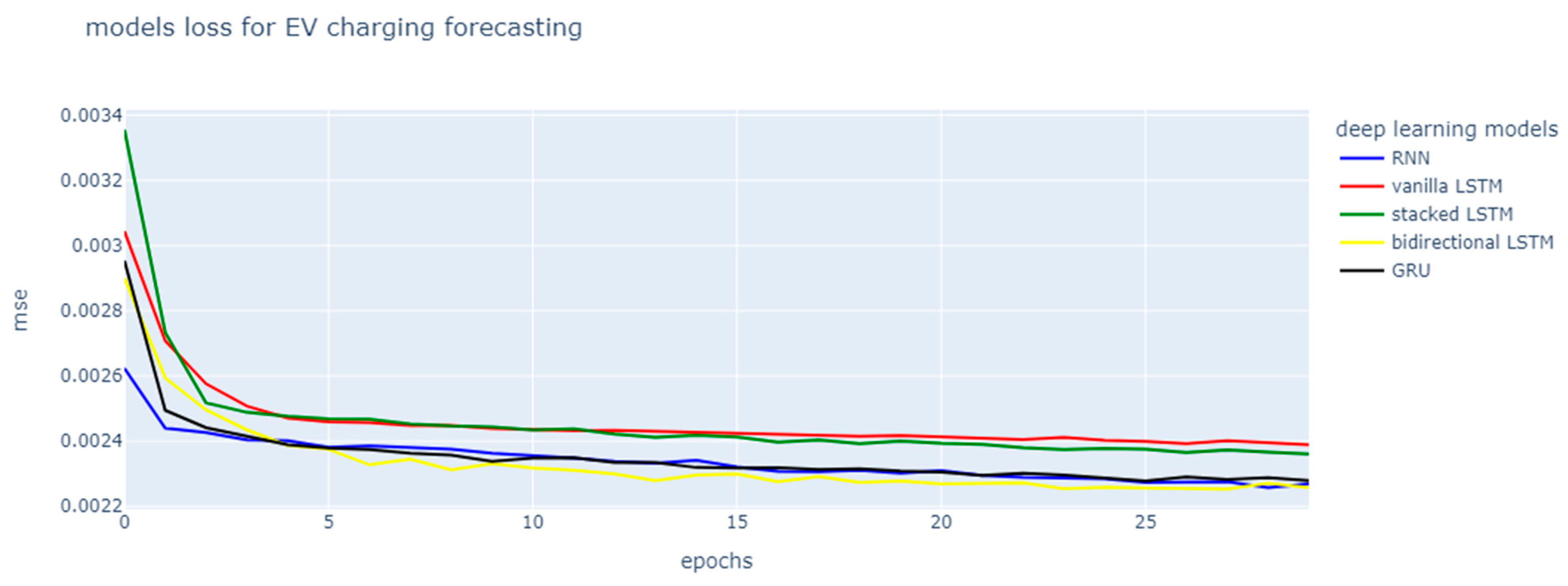
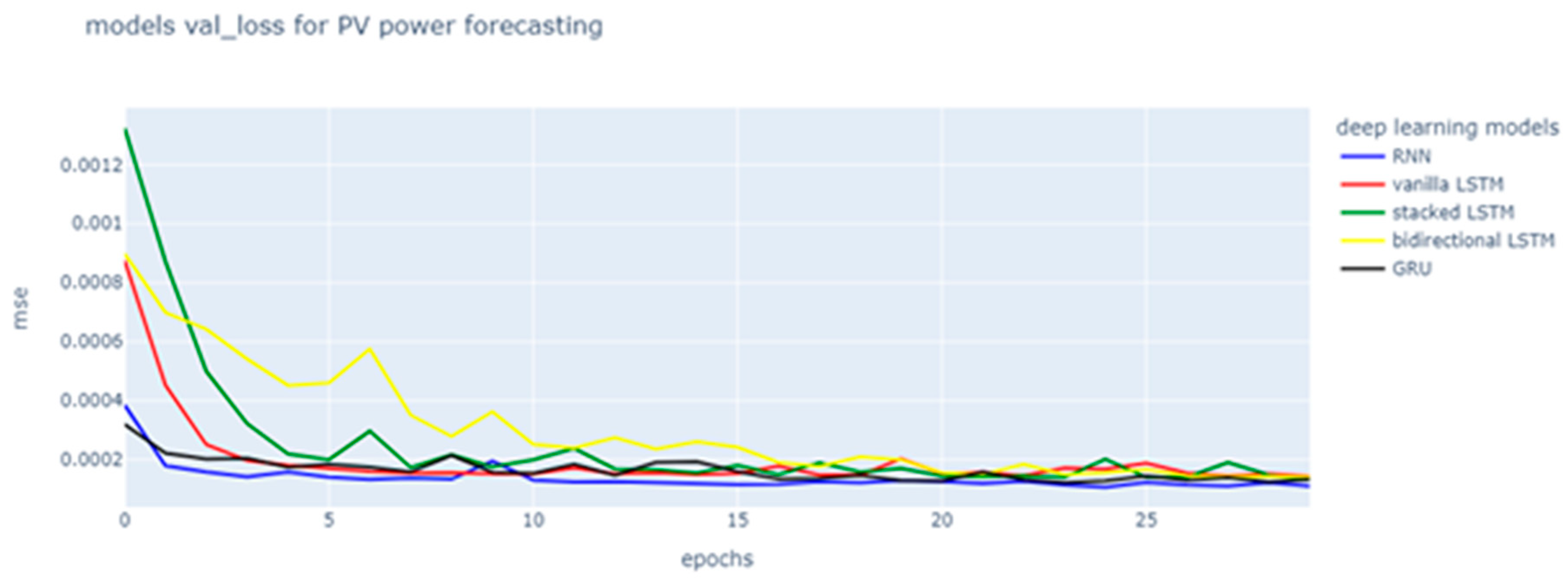
In this section, we would like to present the line graph that shows the training loss and validation loss (see Figure 7, Figure 8, Figure 9 and Figure 10) of different deep learning models used to predict PV (photovoltaic) power and EV charging demand over a series of epochs. The loss metric used is mean squared error (MSE), which is a measure of the average squared difference between predicted and actual values. The number of epochs (X-axis) represents the number of complete passes through the training dataset. As the number of epochs increases, the models gain more opportunities to learn from the data. While MSE (Y-axis): The mean squared error values are plotted on the y-axis. Lower MSE values indicate that the model is getting closer to predicting the actual values, implying that its performance is improving.

The model loss line chart for PV forecasting, as shown in Figure 7, indicates that all models improve their performance as the number of epochs increases, which is shown by the decrease in MSE that occurs by the end of the training period. The models converge to a similar MSE value after a certain number of epochs, indicating they have learned as much as they can from the dataset provided. Meanwhile, for model validation loss (see Figure 9) PV forecasting is achieved as a measure of error from the model when it predicts new, unseen data. A lower validation loss indicates that a model achieves better generalization of the training data to new data. In the initial epochs, a rapid decline in validation loss across all models was observed, indicating effective learning and enhanced predictive accuracy on unfamiliar data. Notably, after around five epochs, the simple RNN and GRU models distinguished themselves with the lowest loss values, signifying their superior ability to generalize from the training dataset. As the epochs progressed, the validation loss across the models plateaued, suggesting that each model had reached its learning potential with respect to the validation dataset. Moreover, the validation loss demonstrated minimal volatility in contrast to the training loss, indicating that it possessed robustness against overfitting. Ultimately, after 25 epochs, the simple RNN model emerged with the smallest validation loss, with the GRU close behind, underscoring their exceptional generalization capabilities within the evaluated models.

For EV charging demand forecasting scenarios, it is shown that as the number of epochs increases, three models have lower MSE scores. They are bidirectional LSTM, GRU and simple RNN. From visual observation (see Figure 8), bidirectional LSTM is the model that achieves the lowest MSE score at the end of the learning period. Meanwhile, with regard to the validation loss of each model (see Figure 10), the bidirectional LSTM, GRU, and simple RNN can also achieve lower MSE scores, but the values fluctuate as the number of epochs increases.

After about 10 epochs, the performance varies, with some models showing fluctuations in validation loss. This could indicate that the models are starting to overfit or that they are sensitive to the particular nuances of the validated set. With consistently lower loss values throughout the training period, the GRU and bidirectional LSTM models appear to offer the most stable performance. These variations, especially when the validation set is challenging or the models are complex, are normal when training deep learning models. The key takeaway is that, despite the fluctuations, if the validation loss does not increase significantly, it is likely that the models are still generalizing well.

6.2. Forecasting Result

This section presents the short-term forecasting results for a 15 min horizon. To find optimal battery storage scheduling and determine the ideal battery capacity required to support charging infrastructure planning, the forecasts of PV generation and EV charging demand are critical. Upon completion of the training sessions, it is imperative to validate the effectiveness of each model variant within the respective forecast scenarios using a test dataset. In this context, the trained models are tasked with making predictions on unseen data, estimating the power output of the PV installations and the demand for charging of electric vehicles. These predictions are then compared to the actual data from the test set and evaluated based on a number of metrics that have been described in the previous chapter. The evaluation metrics used include the MSE, the RMSE, and the MAE. The general comparison of model evaluation for PV power generation forecasting and EV charging demand forecasting can be seen in

Table 8. Model evaluation score result.

Forecasting Scenario	Metric Score	Simple RNN	Vanila LSTM	Stacked LSTM	Bidirectional LSTM	GRU
PV power generation [kW]	MSE	0.015	0.019	0.018	0.019	0.019
	RMSE	0.124	0.137	0.134	0.137	0.137
	MAE	0.037	0.054	0.058	0.067	0.076
EV charging demand [kW]	MSE	2.49081	2.61397	2.58038	2.41685	2.45462
	RMSE	1.578	1.617	1.606	1.555	1.567
	MAE	0.595	0.643	0.478	0.403	0.425

.

Based on the performance results presented in Table 4, the simple RNN model emerges as the superior choice for predicting PV power generation. This model is capable of accurately forecasting PV power output 15 minutes ahead. It can achieve a lower value of the MSE with 0.015 kW, 0.124 kW of the RMSE, and 0.037 of the MAE. The stacked LSTM model then follows. From our observation, it is surprising to see that the simple RNN model can achieve a better performance compared to other models that are well known for the forecasting task. There are some reasons why a simple RNN can sometimes outperform LSTM and GRU models in PV power generation forecasting, mainly due to its suitability for problems with simple temporal patterns and short-term dependencies. The lower complexity of a simple RNN can prevent overfitting and provide a better generalization capability when dealing with smaller datasets. In addition, the reduced number of parameters in simple RNNs not only reduces the computational load, allowing for faster training cycles, but also simplifies the process of tuning the hyper-parameters.

Conversely, the evaluation results for the prediction of EV charging demand, as detailed in Table 8, show that the bidirectional LSTM model outperformed its counterparts, closely followed by the GRU model, exhibiting marginal differences in MSE, RMSE, and MAE. The bidirectional LSTM model achieves metric values of 2.41 kW for the MSE, 1.55 for the RMSE, and 0.403 for the MAE, while the GRU model achieves values of 2.45 for the MSE, 1.567 for the RMSE, and 0.425 for the MAE. Unsurprisingly, both the bidirectional LSTM and GRU models show strong potential for accurately predicting EV charging demand 15 min into the future, given their reputations in forecasting tasks. 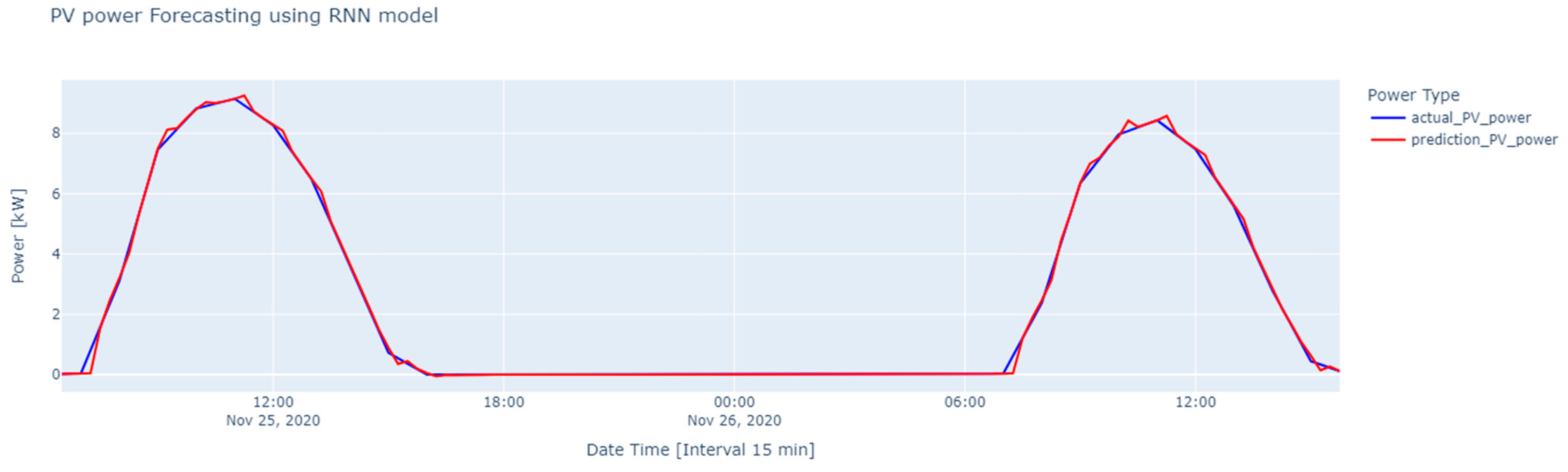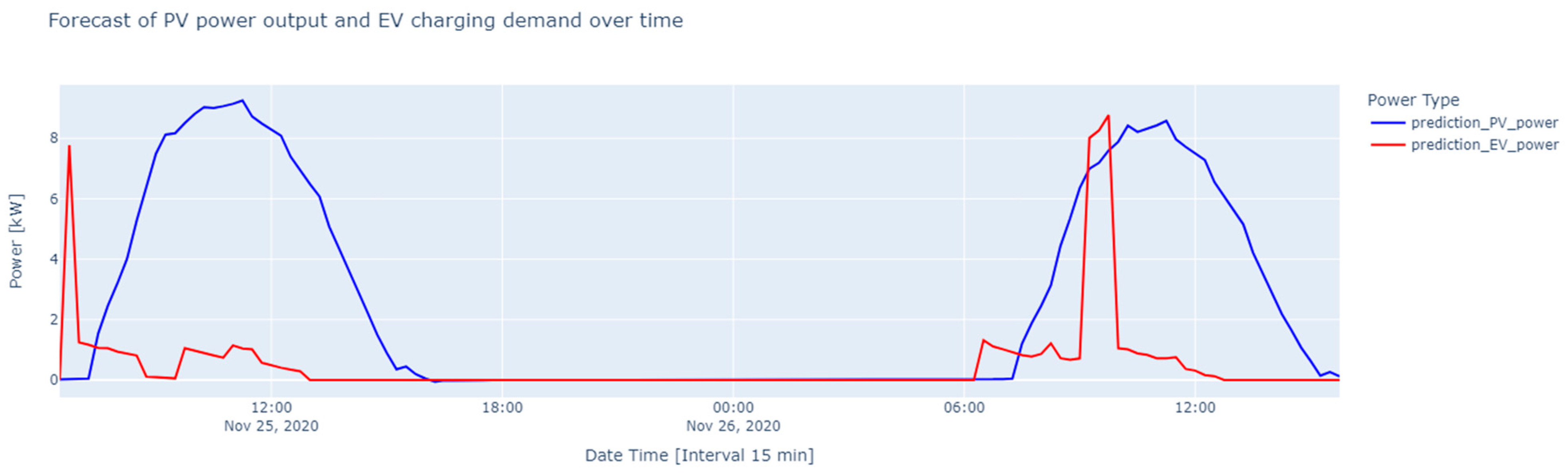Figure 11 shows the predicted versus actual results for PV generation 15 min ahead, from 25 November 2020 at 06:30 to 26 November 2020 at 16:00. Similarly, Figure 12 shows a comparative analysis of forecast and actual EV charging demand. The result indicates that the differences between actual and predicted EV charging requirements could be attributed to several factors. Due to its architecture and chosen hyperparameters, the bidirectional LSTM model may have limitations in capturing complex demand patterns with small datasets. Data quality issues, such as inaccuracies or gaps in historical data and missing long-term data, can significantly affect the predicted results. The forecasts of both PV generation and EV charging demand used for battery storage scheduling are also shown in Figure 13.

6.3. Optimal Battery Capacity and Charging Scheduling

In this section, we present our simulation to determine the optimal battery storage capacity for EV charging infrastructure planning, using both actual and forecast data on PV generation and EV charging demand based on our developed PV power forecast model and EV charging demand forecast model. This simulation, which is based on annually monitored data, produces simulation results with three key parameters: battery storage capacity, which is the proposed capacity needed to support the infrastructure; grid energy used, which refers to the energy consumed from the grid during the monitoring period to charge the battery; and overflow, which refers to the excess solar energy generated that cannot be stored in the battery storage system because it is already at full capacity. For this scenario, a minimum of 1 kWh to a maximum of 15 kWh is the predetermined range for the proposed battery storage capacity. Based on the results of the simulation, the recommended battery capacity to be installed is 15 kWh, with an estimated 4548 kWh of grid energy consumed during the monitoring period, and approximately 5549 kWh to be expected based on the forecast data. The detailed results can be seen in

Table 9. Optimal battery storage capacity simulation.

Battery Storage Capacity	Actual PV Power and Load Data		Forecast PV Power and Load Data
	Grid Energy Used [kWh]	Overflow [kWh]	Grid Energy Used [kWh]	Overflow [kWh]
1	8159	61,946	10,467	56,826
2	7664	61,451	9968	56,328
3	7242	61,028	9513	55,872
4	6885	60,669	9088	55,447
5	6571	60,354	8681	55,040
6	6289	60,071	8293	54,652
7	6036	59,818	7920	54,279
8	5801	59,581	7558	53,917
9	5587	59,367	7208	53,567
10	5391	59,169	6867	53,226
11	5204	58,981	6542	52,900
12	5026	58,802	6257	52,613
13	4856	58,632	6000	52,356
14	4697	58,471	5766	52,120
15	4548	58,322	5549	51,903

.

For the charging schedule, the proposed algorithm determines the optimal charging times for each interval of time. It also provides the final state of charge (SoC) and the total grid energy consumed during the monitoring period. An example of these results is shown in

Table 10. Example of charging scheduling status.

Datetime	PV Power	EV Load Demand	SoC Start	Net Energy	Grid Energy Used	SoC End	Best Time to Charge
1 January 2020 02:00	0	0	10	0	0	10	FALSE
………	………	………	………	………	………	………	………
1 January 2020 09:30	6.38	0.0000	5	6.38	0	11.38	TRUE

. In this simulation, actual data on PV generation and EV charging demand were used to examine various cases with different initial SoCs to determine the final SoC and total grid energy consumption. These results have been compared with the predicted data that were derived from our forecasting models. The simulation results show that for different initial SoC levels in kWh, the total grid energy consumption varies when charging the battery storage. However, after the initial SoC reaches 5 kWh, we observed that the total grid energy consumption becomes relatively constant. The detailed results can be found in

Table 11. Initial SoC and final SoC of battery scheduling simulation.

Initial Soc [kWh]	Actual PV Power and Load Data		Forecast PV Power and Load Data
	Final Soc [kWh]	Total Grid Energy Used [kWh]	Final Soc [kWh]	Total Grid Energy Used [kWh]
1	15	529	15	9475
2	15	5302	15	9485
3	15	5312	15	9495
4	15	5322	15	9505
5	15	5332	15	9515

.

7. Conclusions

This study has effectively demonstrated the usefulness of deep learning models in predicting PV power generation and EV charging demand. These predictions are essential for determining optimal battery energy-storage capacity and developing services for charging scheduling. Our research compared some popular deep learning models such as simple RNN, vanilla LSTM, stacked LSTM, bidirectional LSTM, and GRU. The analysis showed that simple RNN models excelled in predicting PV power due to their fast adaptation to patterns with a lower value of MSE of 0.015 kW, RMSE of 0.124 kW, and MAE of 0.037 kW, while bidirectional LSTM models performed best in capturing the complex dynamics of EV charging demand compared other models, achieving metric values of 2.41 kW for MSE, 1.55 kW for RMSE, and 0.403 for MAE. These findings have enabled the development of a dynamic charging schedule. This maximizes the use of solar energy and reduces grid dependency. Based on a given range from a minimum of 1 to a maximum of 15 kWh, the recommended battery storage capacity to be installed is 15 kWh. This result is simulated based on real and predicted data. This study has provided alternative solutions to determine the optimal capacity of battery storage where it can optimize the use of the PV system and can ensure a reliable energy supply for EV charging.

These research findings highlight the critical importance of selecting appropriate models based on data characteristics and forecasting needs. This approach provides valuable insights for stakeholders involved in renewable energy projects. It ensures that they can make informed decisions to optimize their operations. In conclusion, this study not only validates the effectiveness of specific deep learning models in energy forecasting, but also highlights their practical applications in the improvement of energy system efficiency and sustainability. The results show how deep learning models can provide good accuracy of energy forecasting, leading to better resource management and cost savings. Moreover, the practical applications of these models extend to various areas, including grid management, load balancing, and renewable energy integration. These applications can lead to more reliable energy systems, a reduction in the carbon footprint, and an increase in the use of renewable energy sources.