Numerical and Thermodynamic Analysis of the Effect of Operating Temperature in Methane-Fueled SOFC
Abstract
1. Introduction
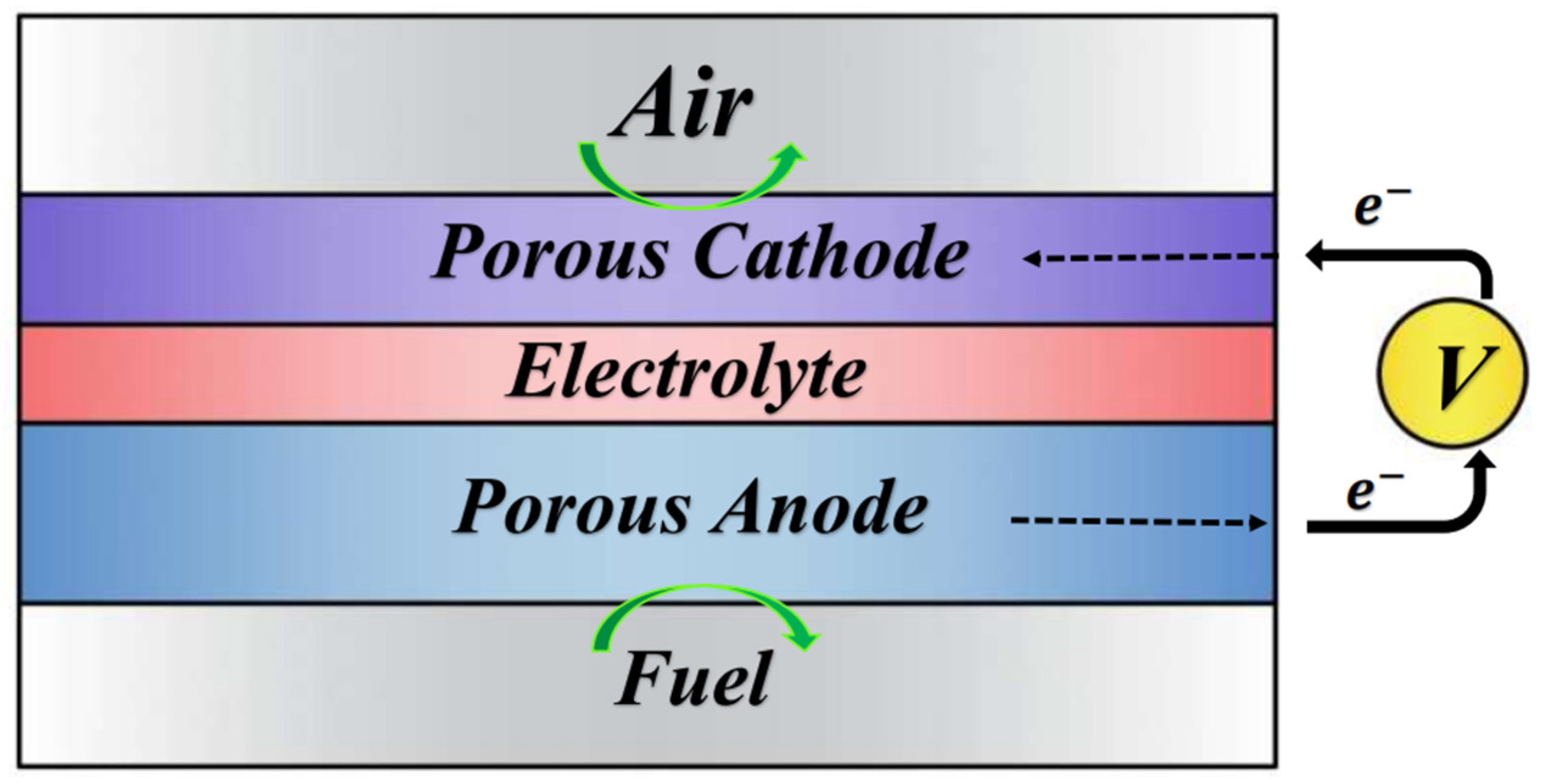
2. Materials and Methods
2.1. Numerical Analysis
2.2. Thermodynamic Analysis
3. Results and Discussion
3.1. Numerical Results
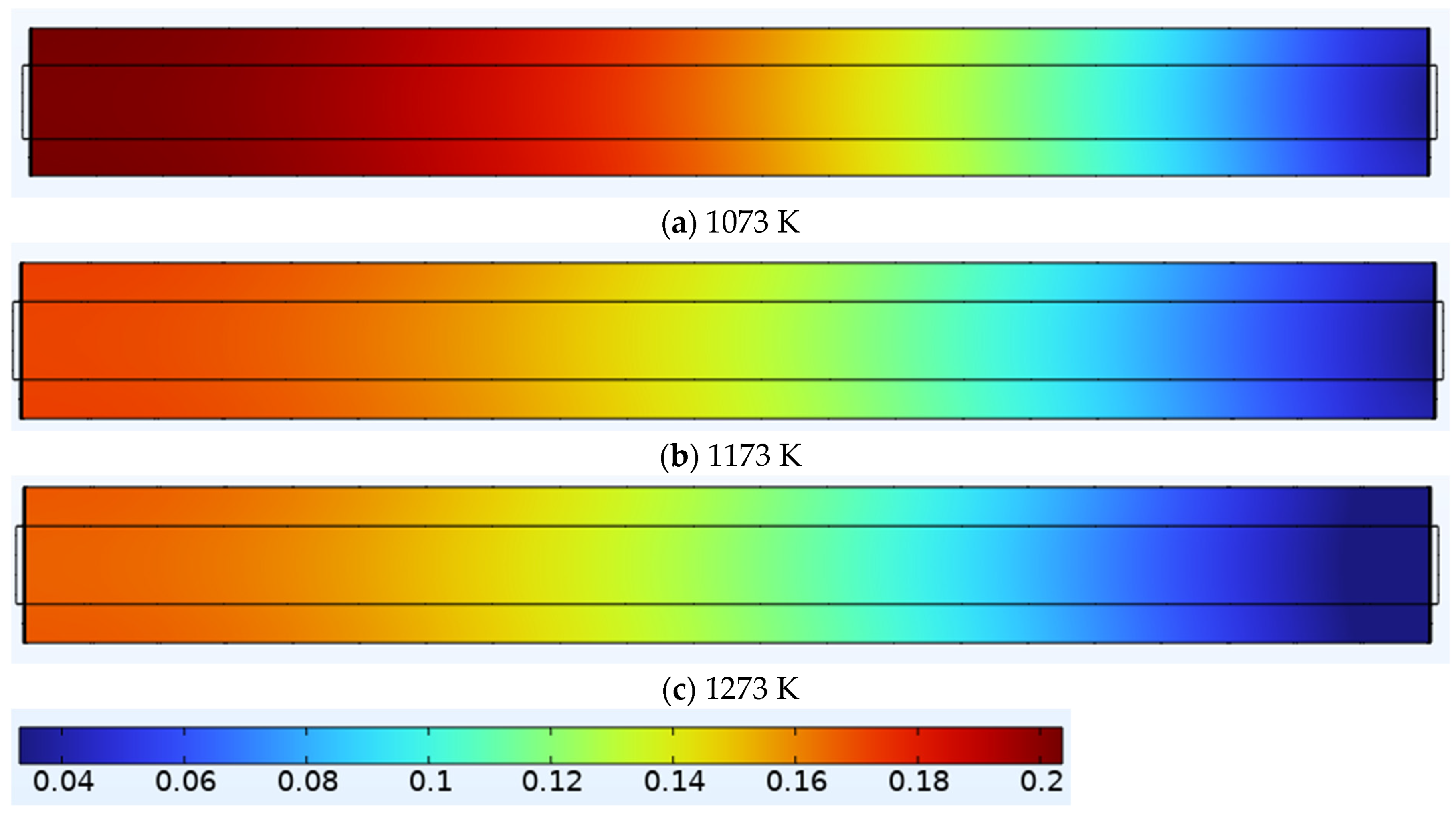
3.1.1. The Methane (CH4) Mole Distribution at Different Temperatures
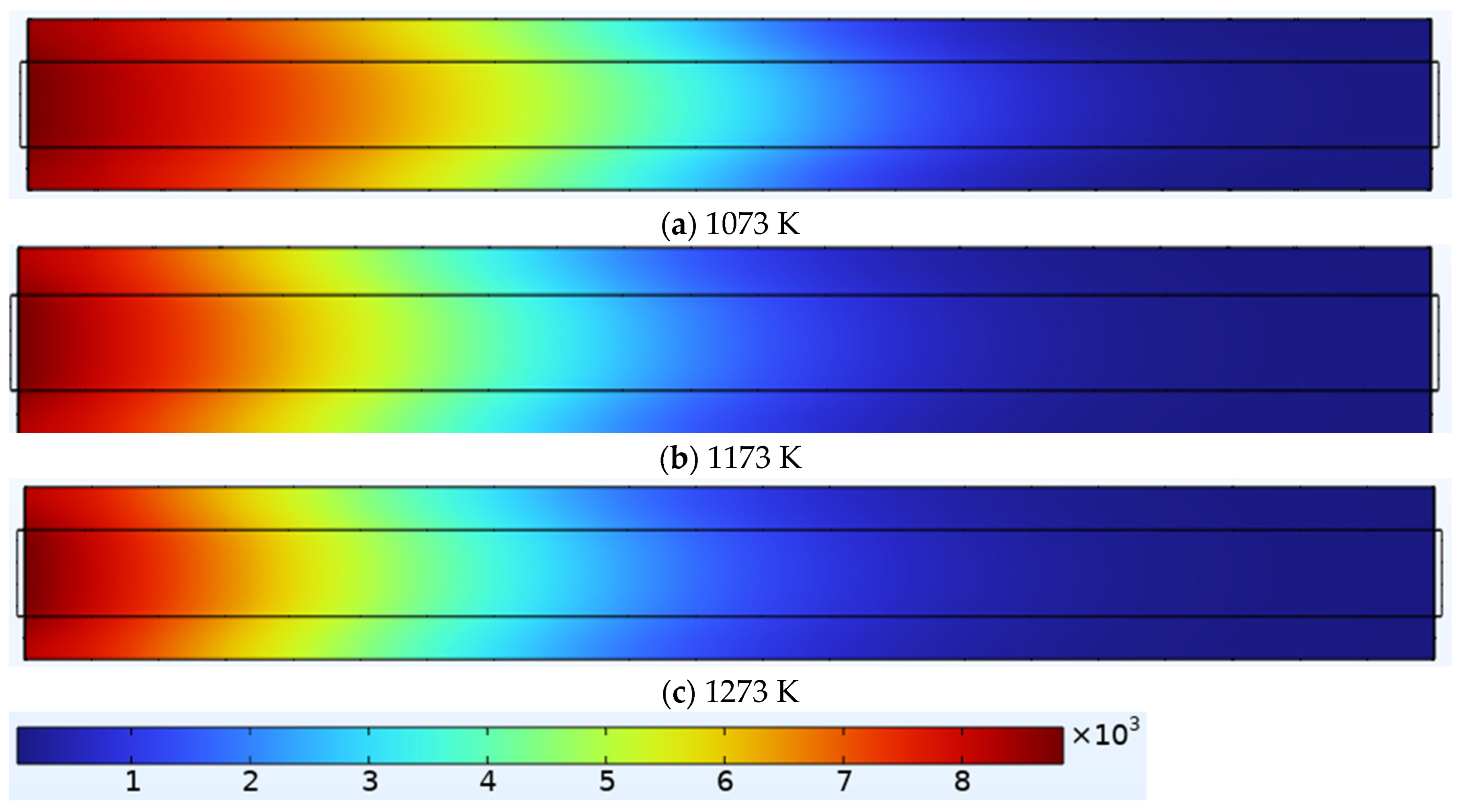
3.1.2. Electrolyte Current Density at Different Temperatures
3.1.3. Validation of Numerical Results
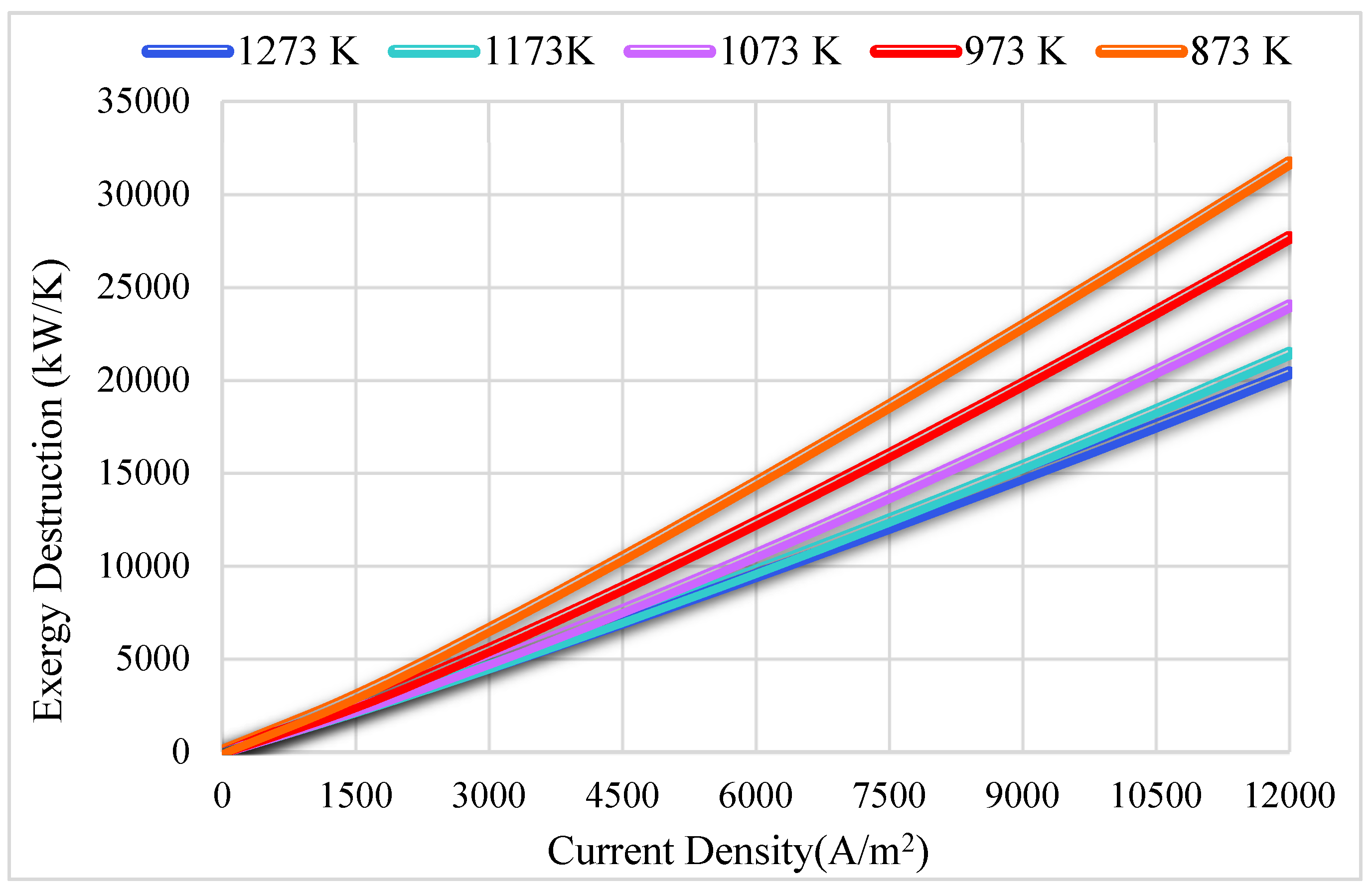
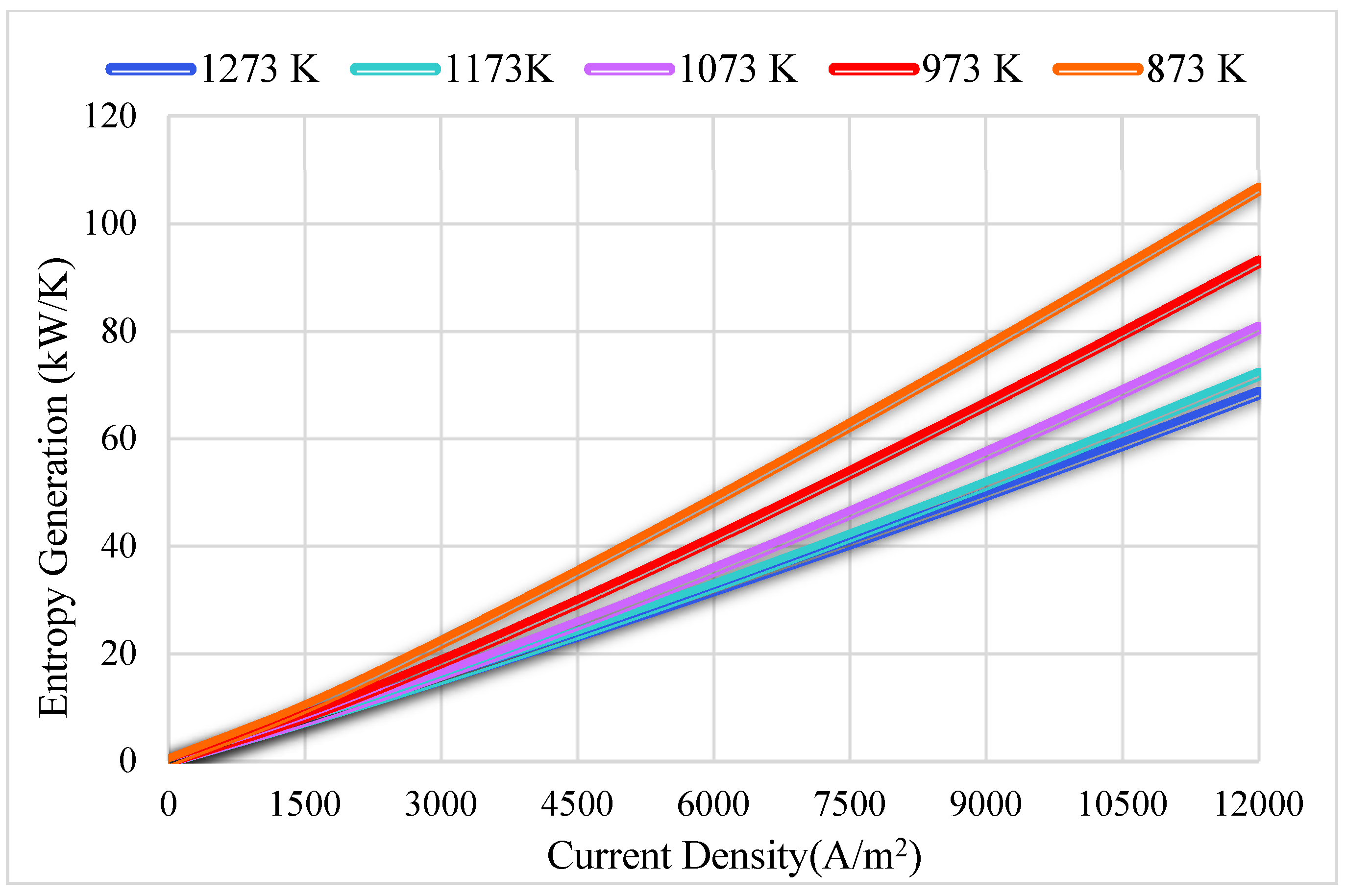
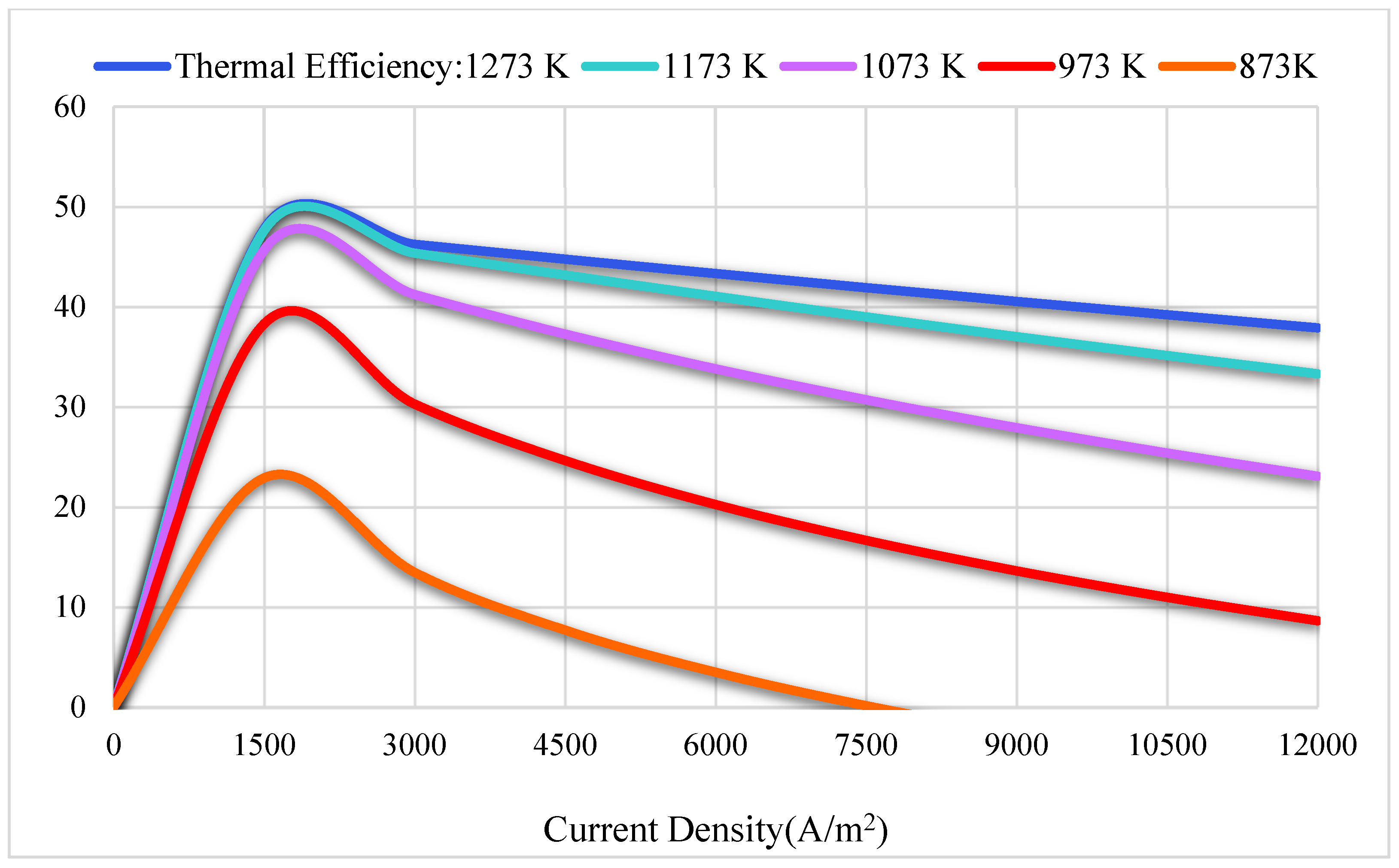
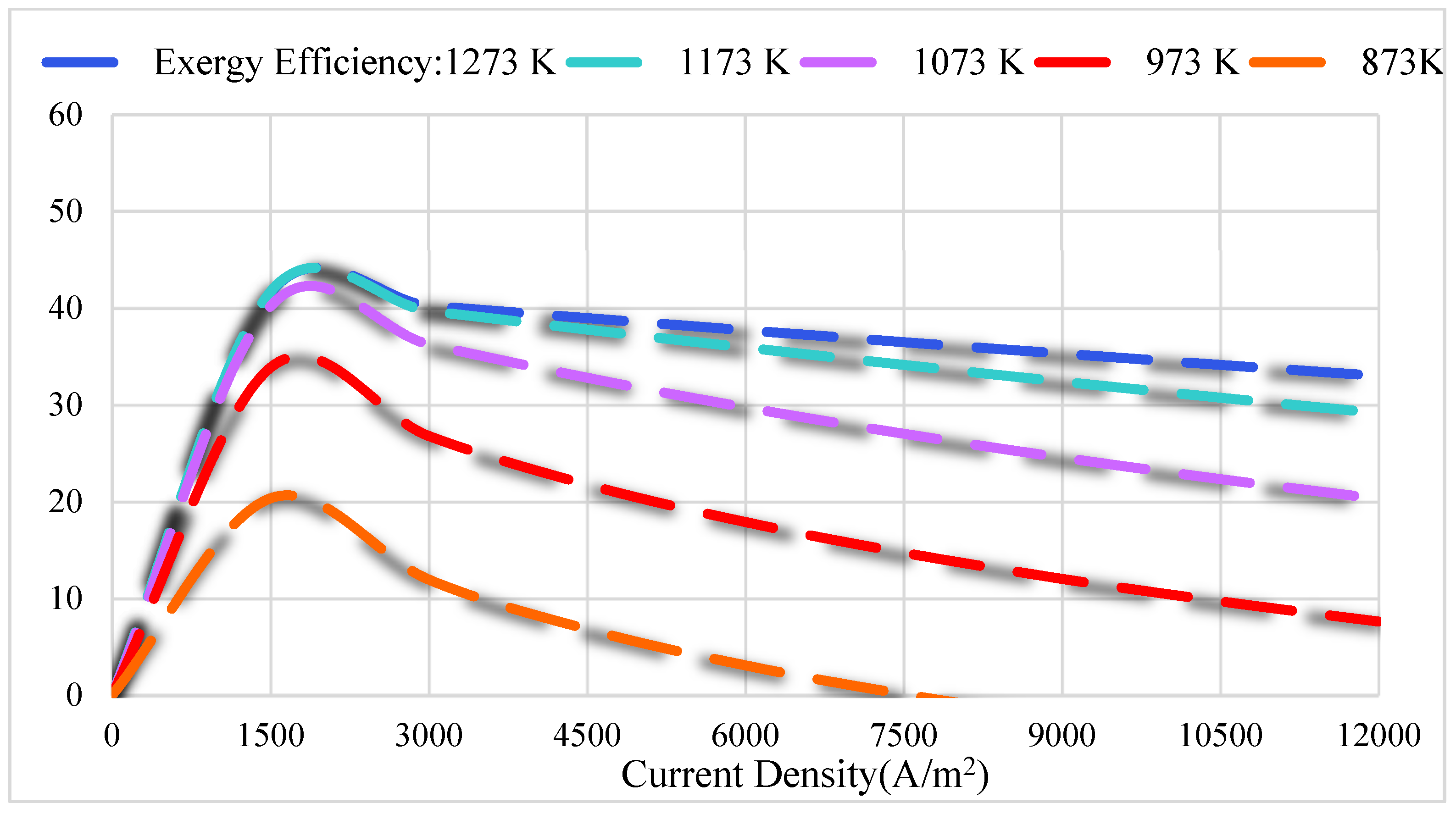
3.2. Thermodynamics Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Vielstich, W.; Lamm, A.H.G. Handbook of Fuel Cells: Fundamentals, Technology, Applications; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2003. [Google Scholar]
- Halis, S.; Atak, N.N.; Doğan, B. Investigation of the performance of cathode supported solid oxide fuel cell with energy and exergy analysis at different operating temperatures. Int. J. Energy Stud. 2024, 9, 21–42. [Google Scholar] [CrossRef]
- Altindal, S.; Erol, E.G.; Gurel, B. Numerical analysis of the effects of interconnector design and operating parameters on solid oxide fuel cell performance. Int. J. Hydrogen Energy 2024, 52, 1475–1490. [Google Scholar] [CrossRef]
- Jiang, X.; Xu, Q.; Shi, Y.; Li, X.; Zhou, W.; Xu, H.; Zhang, Q. Synthesis and properties of Sm3+-deficient Sm1−xBaCo2O5+δ perovskite oxides as cathode materials. Int. J. Hydrogen Energy 2014, 39, 10817–10823. [Google Scholar] [CrossRef]
- Yatoo, M.A.; Kawale, S.S.; Skinner, S.J. Perovskite and layered oxide materials for intermediate temperature solid oxide fuel cells. In Intermediate Temperature Solid Oxide Fuel Cells; Elsevier: Amsterdam, The Netherlands, 2020; pp. 315–346. [Google Scholar]
- Xie, Y.; Ding, H.; Xue, X. Direct methane fueled solid oxide fuel cell model with detailed reforming reactions. Chem. Eng. J. 2013, 228, 917–924. [Google Scholar] [CrossRef]
- Konwar, D.; Yoon, H.H. A methane-fueled SOFC based on a thin BaZr0.1Ce0.7Y0.1Yb0.1O3−δ electrolyte film and a LaNi0.6Co0.4O3 anode functional layer. J. Mater. Chem. A 2016, 4, 5102–5106. [Google Scholar] [CrossRef]
- Mehrabian, M.; Mahmoudimehr, J. A numerical study to determine proper steam-to-fuel ratio in a biogas-fueled solid oxide fuel cell for different levels of biogas methane content. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2023, 238, 2439–2455. [Google Scholar] [CrossRef]
- Hu, F.; Chen, K.; Ling, Y.; Huang, Y.; Zhao, S.; Wang, S.; Gui, L.; He, B.; Zhao, L. Smart Dual-Exsolved Self-Assembled Anode Enables Efficient and Robust Methane-Fueled Solid Oxide Fuel Cells. Adv. Sci. 2024, 11, 2306845. [Google Scholar] [CrossRef]
- Fragiacomo, P.; Piraino, F.; Genovese, M.; Corigliano, O.; De Lorenzo, G. Experimental Activities on a Hydrogen-Powered Solid Oxide Fuel Cell System and Guidelines for Its Implementation in Aviation and Maritime Sectors. Energies 2023, 16, 5671. [Google Scholar] [CrossRef]
- Höber, M.; Königshofer, B.; Schröttner, H.; Fitzek, H.; Menzler, N.H.; Hochenauer, C.; Subotić, V. Experimental identification of the impact of direct internal and external methane reforming on SOFC by detailed online monitoring and supporting measurements. J. Power Sources 2023, 581, 233449. [Google Scholar] [CrossRef]
- Zhang, P.; Yang, Z.; Jin, Y.; Liu, C.; Lei, Z.; Chen, F.; Peng, S. Progress report on the catalyst layers for hydrocarbon-fueled SOFCs. Int. J. Hydrogen Energy 2021, 46, 39369–39386. [Google Scholar] [CrossRef]
- Gong, C.; Xu, Y.; Cai, S.; Chi, B.; Tu, Z. Comparative study on thermodynamic analysis of solid oxide fuel cells supplied with methanol or ammonia. Int. J. Hydrogen Energy 2024, 50, 1293–1301. [Google Scholar] [CrossRef]
- Rath, M.K.; Kossenko, A.; Kalashnikov, A.; Zinigrad, M. Novel anode current collector for hydrocarbon fuel solid oxide fuel cells. Electrochim Acta 2020, 331, 135271. [Google Scholar] [CrossRef]
- Randolph, K.L.; Dean, A.M. Hydrocarbon fuel effects in solid-oxide fuel cell operation: An experimental and modeling study of n-hexane pyrolysis. Phys. Chem. Chem. Phys. 2007, 9, 4245–4258. [Google Scholar] [CrossRef]
- Lin, Y.; Zhan, Z.; Liu, J.; Barnett, S.A. Direct operation of solid oxide fuel cells with methane fuel. Solid State Ion. 2005, 176, 1827–1835. [Google Scholar] [CrossRef]
- Dokamaingam, P.; Assabumrungrat, S.; Soottitantawat, A.; Sramala, I.; Laosiripojana, N. Modeling of SOFC with indirect internal reforming operation: Comparison of conventional packed-bed and catalytic coated-wall internal reformer. Int. J. Hydrogen Energy 2009, 34, 410–421. [Google Scholar] [CrossRef]
- Fu, Q.; Li, Z.; Liu, Z.; Wei, W. Performance study of solid oxide fuel cell with Ni-foam indirect internal reformer: Intrinsic reforming kinetics and temperature uniformity. Chem. Eng. J. 2023, 457, 141170. [Google Scholar] [CrossRef]
- Wójcik, M.; Szabłowski, Ł.; Dybiński, O. Comparison of mathematical models of steam methane reforming process for the needs of fuel cells. Int. J. Hydrogen Energy 2024, 52, 965–982. [Google Scholar] [CrossRef]
- Aguiar, P.; Chadwick, D.; Kershenbaum, L. Modelling of an indirect internal reforming solid oxide fuel cell. Chem. Eng. Sci. 2002, 57, 1665–1677. [Google Scholar] [CrossRef]
- Dokmaingam, P.; Assabumrungrat, S.; Soottitantawat, A.; Laosiripojana, N. Modelling of tubular-designed solid oxide fuel cell with indirect internal reforming operation fed by different primary fuels. J. Power Sources 2010, 195, 69–78. [Google Scholar] [CrossRef]
- Klein, J.M.; Hénault, M.; Roux, C.; Bultel, Y.; Georges, S. Direct methane solid oxide fuel cell working by gradual internal steam reforming: Analysis of operation. J. Power Sources 2009, 193, 331–337. [Google Scholar] [CrossRef]
- Murray, E.; Tsai, T.; Barnett, S.A. A direct-methane fuel cell with a ceria-based anode. Nature 1999, 400, 649–651. [Google Scholar] [CrossRef]
- Saebea, D.; Authayanun, S.; Patcharavorachot, Y. Performance analysis of direct steam reforming of methane in SOFC with SDC-based electrolyte. Energy Rep. 2020, 6, 391–396. [Google Scholar] [CrossRef]
- Tu, B.; Yin, Y.; Zhang, F.; Su, X.; Lyu, X.; Cheng, M. High performance of direct methane-fuelled solid oxide fuel cell with samarium modified nickel-based anode. Int. J. Hydrogen Energy 2020, 45, 27587–27596. [Google Scholar] [CrossRef]
- Hu, Y.; Han, C.; Li, W.; Hu, Q.; Wu, H. Experimental evaluation of SOFC fuel adaptability and power generation performance based on MSR. Fuel Process. Technol. 2023, 250, 107919. [Google Scholar] [CrossRef]
- Saadabadi, S.A.; Illathukandy, B.; Aravind, P.V. Direct internal methane reforming in biogas fuelled solid oxide fuel cell; the influence of operating parameters. Energy Sci. Eng. 2021, 9, 1232–1248. [Google Scholar] [CrossRef]
- Sugihara, S.; Iwai, H. Experimental investigation of temperature distribution of planar solid oxide fuel cell: Effects of gas flow, power generation, and direct internal reforming. Int. J. Hydrogen Energy 2020, 45, 25227–25239. [Google Scholar] [CrossRef]
- Lei, L.; Keels, J.M.; Tao, Z.; Zhang, J.; Chen, F. Thermodynamic and experimental assessment of proton conducting solid oxide fuel cells with internal methane steam reforming. Appl. Energy 2018, 224, 280–288. [Google Scholar] [CrossRef]
- Wang, Z.; Fan, W.; Zhang, G. Comparison of the exergy efficiency of four power generation systems from methane using fuel cells. RSC Adv. 2017, 7, 39391–39402. [Google Scholar] [CrossRef]
- Wang, Z.; Mao, J.; He, Z.; Liang, F. Energy-exergy analysis of an integrated small-scale LT-PEMFC based on steam methane reforming process. Energy Convers. Manag. 2021, 246, 114685. [Google Scholar] [CrossRef]
- Heidarshenas, B.; Abdullah, M.M.; Sajadi, S.M.; Yuan, Y.; Malekshah, E.H.; Aybar, H. Exergy and environmental analysis of SOFC-based system including reformers and heat recovery approaches to establish hydrogen-rich streams with least exergy loss. Int. J. Hydrogen Energy 2024, 52, 845–853. [Google Scholar] [CrossRef]
- Singh, U.R.; Bhogilla, S. Exergy analysis of reversible sofc coupled with organic Rankine cycle and hydrogen storage for renewable energy storage. Int. J. Hydrogen Energy 2023, 48, 39169–39181. [Google Scholar] [CrossRef]
- Hussain, J.; Ali, R.; Akhtar, M.N.; Jaffery, M.H.; Shakir, I.; Raza, R. Modeling and simulation of planar SOFC to study the electrochemical properties. Curr. Appl. Phys. 2020, 20, 660–672. [Google Scholar] [CrossRef]
- Xie, Y.; Ding, H.; Xue, X. Multi-physicochemical modeling of direct methane fueled solid oxide fuel cells. J. Power Sources 2013, 241, 718–727. [Google Scholar] [CrossRef]
- Chaudhary, T.N.; Mehmood, M.; Saleem, U.; Abbasi, M.S.; Chen, B. Modeling of thermal impacts in a single direct methane steam reforming solid oxide fuel cell. J. Power Sources 2020, 472, 228605. [Google Scholar] [CrossRef]
- Iliev, I.K.; Gizzatullin, A.R.; Filimonova, A.A.; Chichirova, N.D.; Beloev, I.H. Numerical Simulation of Processes in an Electrochemical Cell Using COMSOL Multiphysics. Energies 2023, 16, 7265. [Google Scholar] [CrossRef]
- Zhao, F.; Virkar, A.V. Dependence of polarization in anode-supported solid oxide fuel cells on various cell parameters. J. Power Sources 2005, 141, 79–95. [Google Scholar] [CrossRef]
- Wang, Z.; Lan, Q.; Zhang, D.; Li, M.; Cui, D.; Han, F. Optimizing ammonia-fueled planar SOFCs for low-temperature operation: Multiphysics simulation and performance sensitivity analysis. Appl. Therm. Eng. 2024, 242, 122442. [Google Scholar] [CrossRef]
- Ni, M.; Leung, M.K.H.; Leung, D.Y.C. Parametric study of solid oxide fuel cell performance. Energy Convers. Manag. 2007, 48, 1525–1535. [Google Scholar] [CrossRef]
- Chan, S.H.; Ho, H.K.; Tian, Y. Multi-level modeling of SOFC-gas turbine hybrid system. Int. J. Hydrogen Energy 2003, 28, 889–900. [Google Scholar] [CrossRef]
- Chan, S.H.; Xia, Z.T. Polarization effects in electrolyte/electrode-supported solid oxide fuel cells. J. Appl. Electrochem. 2002, 32, 339–347. [Google Scholar] [CrossRef]
- Ferguson, J.R.; Fiard, J.M.; Herbin, R. Three-dimensional numerical simulation for various geometries of solid oxide fuel cells. J. Power Sources 1996, 58, 109–122. [Google Scholar] [CrossRef]
- Liu, Z.; Tao, T.; Deng, C.; Yang, S. Proposal and analysis of a novel CCHP system based on SOFC for coalbed methane recovery. Energy 2023, 283, 128996. [Google Scholar] [CrossRef]
- Chan, S.H.; Khor, K.A.; Xia, Z.T. Complete polarization model of a solid oxide fuel cell and its sensitivity to the change of cell component thickness. J. Power Sources 2001, 93, 130–140. [Google Scholar] [CrossRef]
- Akikur, R.K.; Saidur, R.; Ping, H.W.; Ullah, K.R. Performance analysis of a co-generation system using solar energy and SOFC technology. Energy Convers. Manag. 2014, 79, 415–430. [Google Scholar] [CrossRef]
- Akkaya, A.V. Performance Analysis of Solid Oxide Fuel Cell Based Energy Generation Systems with Alternative Criteria. Ph.D. Thesis, Yıldız Teknik Üniversitesi, Esenler, Turkiye, 2007. [Google Scholar]
- Sadeghi, M.; Jafari, M.; Hajimolana, Y.S.; Woudstra, T.; Aravind, P.V. Size and exergy assessment of solid oxide fuel cell-based H2-fed power generation system with alternative electrolytes: A comparative study. Energy Convers. Manag. 2021, 228, 113681. [Google Scholar] [CrossRef]
- Sadeghi, M.; Nemati, A.; Ghavimi, A.; Yari, M. Thermodynamic analysis and multi-objective optimization of various ORC (organic Rankine cycle) configurations using zeotropic mixtures. Energy 2016, 109, 791–802. [Google Scholar] [CrossRef]
- Ranjbar, F.; Chitsaz, A.; Mahmoudi, S.M.S.; Khalilarya, S.; Rosen, M.A. Energy and exergy assessments of a novel trigeneration system based on a solid oxide fuel cell. Energy Convers. Manag. 2014, 87, 318–327. [Google Scholar] [CrossRef]
- Hanapi, S.; Tijani, A.S.; Rahim, A.H.A.; Mohamed, W.A.N.W. Exergy Efficiency Profile of A 1kW Open Cathode Fuel Cell with Pressure and Temperature Variations; Elsevier B.V.: Amsterdam, The Netherlands, 2015; Volume 79. [Google Scholar] [CrossRef]
- Liu, J.; Barnett, S.A. Operation of anode-supported solid oxide fuel cells on methane and natural gas. Solid State Ion. 2003, 158, 11–16. [Google Scholar] [CrossRef]
- Tu, B.; Wen, H.; Yin, Y.; Zhang, F.; Su, X.; Cui, D.; Cheng, M. Thermodynamic analysis and experimental study of electrode reactions and open circuit voltages for methane-fuelled SOFC. Int. J. Hydrogen Energy 2020, 45, 34069–34079. [Google Scholar] [CrossRef]



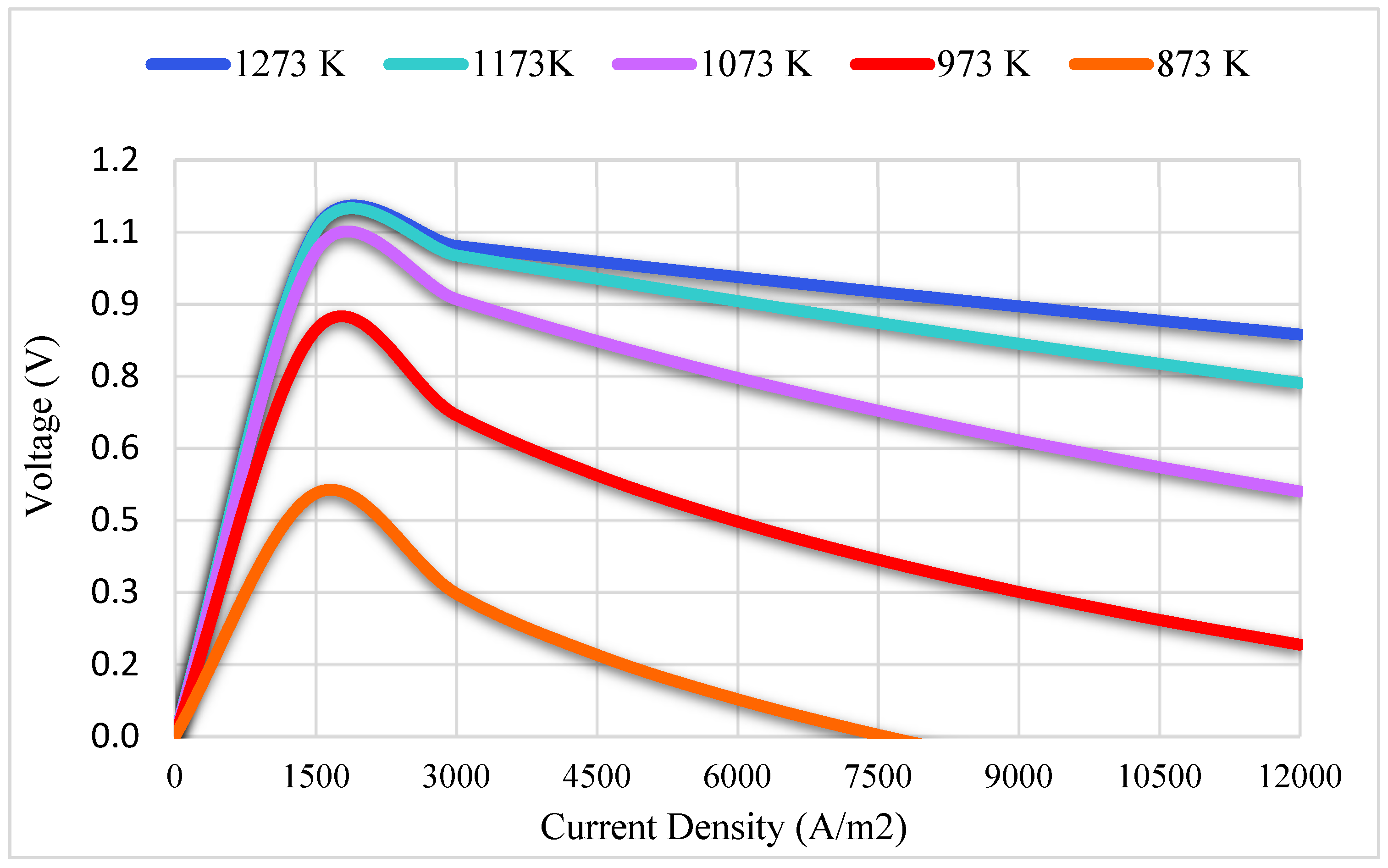
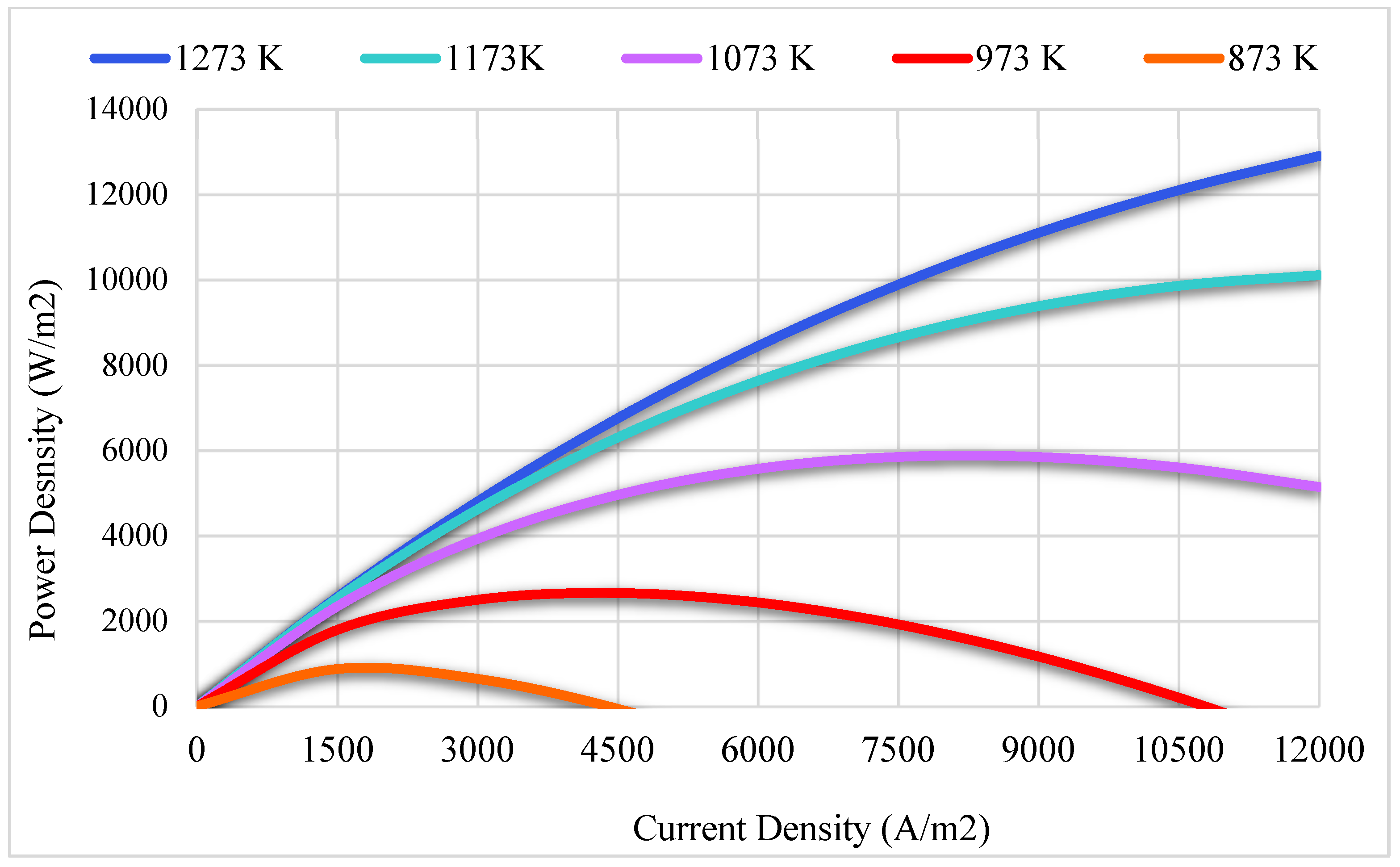
| Reference | Active Cell Area [m2] | Operating Temperature [K] | Current Density [A/m2] | Cell Potential [V] | Power Density (W/m2) |
|---|---|---|---|---|---|
| The present study | 0.01 m2 | 873–1273 K | 0–12,000 A/m2 | 0–1.22 V | 0–13,000 W/m2 |
| Zhao and Virkar [38] | 0.02 m2 | 873–1073 K | 0–30,000 A/m2 | 0.1–1.12 V | 0–12,000 W/m2 |
| Altindal et al. [3] | - | 873–1273 K | 0–0.7 A/m2 | 0.35–1.13 V | 0.02–0.24 W/m2 |
| Wang et al. [39] | - | 973–1073 K | 0–5000 A/m2 | 0.68–1.25 V | 0–0.45 W/cm2 |
| Items | Unit | Value |
|---|---|---|
| Active cell area, A | [m2] | 0.01 |
| Gas flow channel width | [m] | 0.5 × 10−3 |
| Rib width | [m] | 0.5 × 10−3 |
| Anode electrode thickness, | [m] | 1.5 × 10−4 |
| Cathode electrode thickness, | [m] | 10−4 |
| Electrolyte thickness, | [m] | 10−4 |
| Gas flow channel height | [m] | 0.5 × 10−3 |
| Flow channel length | [m] | 0.01 m |
| Average pore radius, | [m] | 2 × 10−6 |
| Average grain size, | [m] | 1.5 × 10−6 |
| Porosity, | - | 0.4 |
| Permeability | [m2] | 10−10 m2 |
| Anode’s tortuosity, | - | 5.4 |
| Average grain contact length, X | - | 0.7 |
| Symmetrical factor, | - | 0.5 |
| Nernst Equation | |
|---|---|
| Activation overpotential equation | ; i = a, c |
| Concentration overpotential equation | |
| Ohmic overpotential equation | |
| Items | Unit | Value |
|---|---|---|
| Faraday constant, F | [C/mol] | 96,485 |
| Universal gas constant, R | [J/mol K] | 8.3145 |
| Temperature of operation, T | [K] | 1073–1273 |
| The pressure of operation, P | [bar] | 1 |
| Anode activation energy, | [J/mol] | 1.344 × 1010 |
| Cathode activation energy, | [J/mol] | 2.051 × 109 |
| Parameters | Value |
|---|---|
| 1.005 kJ/kg K | |
| 14.3 kJ/kg K | |
| 0.918 kJ/kg K | |
| 3 kJ/kg K | |
| kJ/kmol K | |
| kJ/kmol K | |
| kJ/kg K | |
| 1.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumuk, B.; Atak, N.N.; Dogan, B.; Ozer, S.; Demircioglu, P.; Bogrekci, I. Numerical and Thermodynamic Analysis of the Effect of Operating Temperature in Methane-Fueled SOFC. Energies 2024, 17, 2603. https://doi.org/10.3390/en17112603
Kumuk B, Atak NN, Dogan B, Ozer S, Demircioglu P, Bogrekci I. Numerical and Thermodynamic Analysis of the Effect of Operating Temperature in Methane-Fueled SOFC. Energies. 2024; 17(11):2603. https://doi.org/10.3390/en17112603
Chicago/Turabian StyleKumuk, Berre, Nisa Nur Atak, Battal Dogan, Salih Ozer, Pinar Demircioglu, and Ismail Bogrekci. 2024. "Numerical and Thermodynamic Analysis of the Effect of Operating Temperature in Methane-Fueled SOFC" Energies 17, no. 11: 2603. https://doi.org/10.3390/en17112603
APA StyleKumuk, B., Atak, N. N., Dogan, B., Ozer, S., Demircioglu, P., & Bogrekci, I. (2024). Numerical and Thermodynamic Analysis of the Effect of Operating Temperature in Methane-Fueled SOFC. Energies, 17(11), 2603. https://doi.org/10.3390/en17112603






