Abstract
Kaplan turbines are widely utilized in low-head and large flow power stations. This paper employs Computational Fluid Dynamics (CFD) to complete numerical calculations of the full flow channel under different blade angles and various guide vane openings, based on 25 off-cam experimental working conditions. The internal flow characteristics of the runner blade and draft tube are analyzed, and a discriminant number for quantitatively assessing the flow uniformity of the draft tube is proposed. The results indicate that low-frequency and high-amplitude pressure pulsations occur on the high- and low-pressure edge of the blade when the opening is small, with pulsations decreasing as the opening increases. The inner flow line of the draft tube is disturbed when both the blade angle and opening are small. Additionally, the secondary frequency of the draft tube inlet is double that of the vane passing frequency. The discriminant number of the flow inhomogeneity approaches 0 under optimal flow conditions. The number increases continuously with the decrease in efficiency, and the flow in the three piers of draft tube becomes more nonuniform. The research results provide a reference for enhancing performance and ensuring the operational stability of Kaplan turbines.
1. Introduction
The axial flow turbine is generally suitable for hydropower stations with a low head and large flow rate [1]. It offers the advantages of high speed and efficiency under the condition of large flow rate variation [2]. At present, the axial flow turbine is one of the main types used for the development and utilization of hydropower resources in low-head sections. In comparison to the Francis turbine, the axial flow turbine has a smaller runner diameter and better flow performance; hence, it is widely applied in small and medium-sized hydropower stations. Furthermore, it has fewer blades and a large overflow space, making it more suitable for overflow compared with the Francis turbine [3], while also possessing environmental protection characteristics.
According to the direction of flow in the runner, the reaction turbine is divided into three types: mixed flow, oblique flow and axial flow. The axial flow turbine can be divided into fixed impeller type and rotary impeller type according to whether the blade can rotate. The Kaplan turbine (propeller turbine with adjustable blades) can realize the double regulation of the guide vane and runner blade. When the unit speed and unit flow rate are constant, the guide vane opening and runner blade angle with the highest efficiency are constant, and this working condition becomes the on-cam working condition. In the on-cam working condition, the relationship between the guide vane opening α and blade angle β is called the on-cam relationship. When the turbine is operated in the on-cam condition, the unit can achieve the maximum benefit and the most stable operation. Due to the influence of mechanical and hydraulic factors, the cam relationship between the guide vane and blade fluctuates randomly when the axial flow turbine is running under a fluctuating load. In order to study the influence of random fluctuations on the cam relationship, Wei et al. [4] use the Chebyshev polynomial approximation method to analyze the stochastic dynamic characteristics of turbines in the transient process. It is found that the transient performance can be improved by controlling the random intensity and PID parameters.
During the operation of the Kaplan turbine, pressure pulsation will occur inside and outside the turbine due to the interaction between the blade and fluid flow. These pressure pulsations may lead to vibration, noise and even fatigue damage to the turbine structure, so it is vital for the stable operation and life of the Kaplan turbine. With the Kaplan turbine as the research object, scholars at home and abroad have carried out a series of studies on pressure pulsation prediction and simulation, pressure pulsation source and characteristics, pressure pulsation experiments and so on.
In terms of prediction and simulation, high-precision numerical simulation methods such as Computational Fluid Dynamics (CFD) are widely utilized to predict pressure pulsations, including Direct Numerical Simulation (DNS), Large Eddy Simulation (LES) and models based on Reynolds Averaged Navier–Stokes (RANS). Among them, RANS-based models have limitations in predicting pressure fluctuations [5], while LES and DNS are especially suitable for the study of pressure fluctuations due to their high accuracy in simulating turbulence and complex flow structures. However, these two methods usually require higher computational resources. Yen et al. [6] studied the geometric structure and performance optimization of micro-axial flow turbines based on the CFD method of transient turbulent LES. Ma et al. [7] conducted numerical simulation of three-dimensional turbulent flow in a Kaplan turbine based on the RANS equation and SST k-ω turbulence model, and the results reveal the influence of tip clearance on flow characteristics. The results demonstrated that the negative pressure area in the middle of the suction side (SS), near the tip of the blade, and at the tip becomes more and more obvious with the increase in tip clearance. Liu et al. [8] used the standard k-ε turbulence model to analyze the steady turbulence of the full channel of the axial flow turbine, and compared the numerical results with the performance results of the model test. Jost et al. [9] used the Shear Stress Transport (SST) turbulence model, Scale Adaptive Simulation (SAS), SST model and Zonal Large Eddy Simulation (ZLES) to simulate the unsteady state of a six-blade axial flow turbine. Since the steady-state simulation results of various turbulence models differ greatly from the measured data at full discharge rate, the effects of an advection scheme and mesh refinement were tested, and the results of the ZLES model were found to be accurate at all operating points. Wu et al. [10] used the RANS equation combined with the RNG k-ε turbulence model to calculate the transient flow of the full passage of a prototype Kaplan turbine, and compared the frequency and amplitude of the pressure fluctuation between the prototype and the model. The results demonstrated that the pressure pulsation of the prototype and model were similar except for the low frequency. Liu et al. [11] simulated the pressure fluctuation of a Kaplan turbine based on the improved RNG k-ε turbulence model, and the numerical results were in good agreement with the experimental data, but the pressure fluctuation amplitude of the prototype turbine was significantly different from that of the model turbine. Liu et al. [12] numerically simulated the transient runaway characteristics of a Kaplan turbine, and solved the unsteady RANS equation of the runner’s rotational motion equation, continuity equation and RNG k-ε turbulence model in an iterative manner. The results showed that the swirling flow in the draft tube became stronger in the later stage of the transient process. A vortex rope was generated in the draft tube and pressure fluctuation was caused. Minakov et al. [13] used several methods to simulate the unsteady state of a Kaplan turbine operating under non-designed loads, and found that the Reynolds Stress Model (RSM), Detached Eddy Simulation (DES) model and LES model could reproduce well the average velocity component and the intensity of its fluctuations and pressure pulsations.
In terms of exploring the sources and characteristics of pressure pulsation, the research mainly focuses on identifying the sources of pressure pulsation, including unsteady flow from the impeller, water shock effect, tailwater eddy current, etc. High-speed pressure sensors are usually used to monitor pressure changes at different locations, and the theoretical analysis of fluid mechanics is combined to explain the pressure change mode. Liu et al. [14] studied the phenomenon of water reverse hammer caused by the rapid closure of the guide vane in the transient state of load rejection of a Kaplan turbine through experiments and theoretical analysis, and found that the site where the water reverse hammer occurred was behind the guide vane, and the pressure at the exit of the guide vane was lowest in the transient state of load rejection.
In terms of experimental research, experimental research is still a crucial part of pressure pulsation research. This includes model testing and the monitoring of prototypes, as well as the use of advanced measurement techniques such as Laser Doppler Velocimetry (LDV) and high-frequency pressure sensors [15]. Liu et al. [16] predicted the pressure pulsation of a Kaplan turbine, and the calculated pressure pulsation was basically consistent with that obtained by experiments, which verified the correctness of the calculated results. The results indicated that under similar working conditions, the model turbine and the prototype turbine had the same pressure pulsation frequency and rotation frequency, but the amplitude of pressure pulsation between them was not similar. Dehkharqani et al. [17] conducted start-up cycle experiments on a prototype Kaplan turbine. The unsteady pressure and strain of the runner blade and shaft and the bending and torsional strain on the shaft were measured simultaneously. The results implied that the pressure on the runner blade had a low-frequency fluctuation after opening the guide vane from the fully closed position. Dehkhargani et al. [18] also predicted the flow conditions and load fluctuations of a Kaplan turbine runner during several steady-state operations by measuring the shaft in the rotating and static reference systems, and found that the guide vane opening corresponding to the minimum pressure and strain fluctuations on the runner blade could be obtained through axial, torsional and bending measurements. Amiri et al. [19] measured the unsteady pressure of the blades and fixed components during load change under off-cam working conditions, and the results revealed that the transition between high load and optimal efficiency point was smooth when the load changed, and there was no rotating vortex rope in the draft tube at the optimal efficiency point. Liu et al. [20] predicted the hydraulic instability of the model turbine by using the full-channel three-dimensional unsteady turbulence method with dynamic–static interaction, and found that the predicted frequency and amplitude were in good agreement with the test data. The low-frequency pressure fluctuation generated by the draft tube was the largest, and the second harmonic of the rotating frequency was more important than the blade passing frequency. Rivetti et al. [21] compared CFD results with prototype measurement temporary signals at the same position, mainly studying the blade clearance flow and pressure distribution at the discharge ring in large Kaplan turbines. From the perspective of the rotating reference frame, the average pressure fluctuated with the change in guide vane passage. Mulu et al. [22] compared the experimental velocity and pressure measurements of steady and unsteady turbulence in a Kaplan turbine draft tube with simulation results, and studied the simulation results of various turbulence models. The results verified that unsteady flow field simulation was able to significantly improve the accuracy of flow simulation in the cone region, but no turbulence model could accurately predict the complex phenomena in the experiment. Ohiemi et al. [23] measured dynamic pressure pulsation under different base gap and different flow conditions through pressure sensors installed in axial flow turbines, and the experimental results confirmed that the reduction in the base gap would increase the pressure pulsation.
To sum up, there is a lack of in-depth research on the internal flow characteristics of large axial flow turbines under off-cam working conditions. In this paper, a large Kaplan turbine unit is taken as the research object, three-dimensional modeling is carried out and numerical simulation is carried out using the CFD method to analyze the pressure pulsation, pressure distribution and flow characteristics of the high- and low-pressure sides of the runner blades. Based on the comprehensive analysis of the inlet pressure fluctuation of the draft tube, the internal flow pattern of the three piers and the turbine efficiency, the discriminant number for quantitatively judging the flow uniformity of the draft tube support pier is proposed. The research results provide a reference for the structural design of axial flow turbines and the prediction of internal pressure fluctuations. Furthermore, it also has a certain theoretical and engineering value for the stable operation of large axial flow turbines.
2. Researched Kaplan Turbine Unit
2.1. Basic Parameters
The researched machine is a vertical Kaplan turbine unit with a rated output of 200 MW. The rated head of the turbine is 25 m. The other parameters of the researched unit are listed in Table 1.

Table 1.
Basic parameters.
2.2. Model and Mesh
A certain type of Kaplan turbine is composed of five flow components, namely, a spiral casing, stay vane, guide vane, runner and draft tube. The calculation domain model of the turbine is shown in Figure 1, and each calculation subdomain is connected through the interface. The spiral casing calculation subdomain is shown in Figure 2a, and the draft tube is shown in Figure 2b, which has three piers. The runner, as shown in Figure 2c, consists of a hub body, blades and a drain cone. The stay vane and guide vane are shown in Figure 2d.
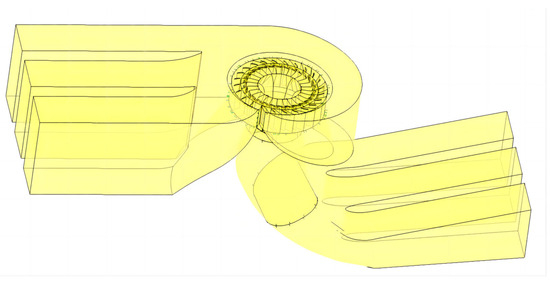
Figure 1.
Model of the researched Kaplan turbine.
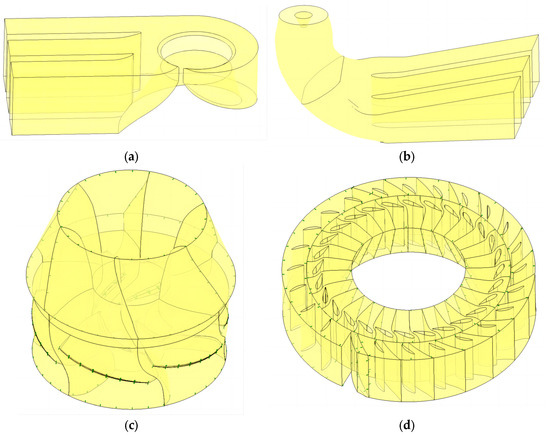
Figure 2.
Computational subdomain models: (a) Spiral casing; (b) Draft tube; (c) Runner; (d) Stay vane and guide vane.
The grid division of each calculation domain of the turbine is conductive to improving the accuracy of the numerical calculations. Tetrahedral unstructured mesh is used for the spiral casing, as shown in Figure 3a, and structured hexahedral mesh is used for the draft tube, runner, stay vane and guide vane, as shown in Figure 3b–d.

Figure 3.
Grid division of computing domain: (a) Spiral casing; (b) Draft tube; (c) Runner; (d) Stay vane and guide vane.
The fine mesh division can improve the calculation accuracy. However, too many grids will lead to too high a calculation cost, so it is necessary to choose an appropriate grid division method and grid number in engineering practice. As shown in Figure 4, four sets of grids are divided into rated working conditions, and the efficiency of the turbine under the different division schemes is compared. After the number of grids exceeds 5 million, the efficiency gradually levels off. The difference between the number of the third set of grids and the fourth set of grids is about 7.8 × 105, but the difference in efficiency is only 0.05%. Considering computer performance and time cost, the third grid is selected for subsequent calculations, and the wall y+ value is less than 300.
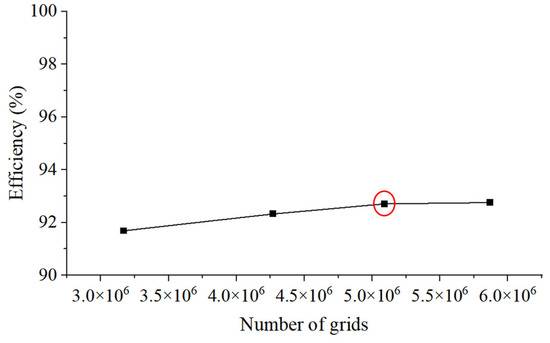
Figure 4.
Grid independence verification: the red circle represents the grid scheme chosen for the calculation.
2.3. Boundary Conditions, Selection of Operating Points
In this paper, the fluid dynamics analysis software ANSYS CFX is used to calculate the full channel flow of the axial flow impeller turbine. The turbulence model is selected as an SST k-ω model, the impeller is taken to turn 1° in one time step and the convergence standard is 1.0 × 10−5. For boundary conditions, static pressure is selected at the exit of the calculation domain and total pressure is selected at the entrance. The transient calculation takes the steady result as the initial flow field, and the discrete format of the convection term and the time term is set to the High-Resolution format and the Second-Order Backward Euler format, respectively. The turbulence numerical format is High Resolution.
According to the off-cam working conditions selected in the field experiment, the guide vane opening is changed under 5 blade angles (β = −0.55°, 2°, −3.6°, −9°, −15.8°), and a total of 25 working conditions are calculated. In the safe operation zone of the Kaplan turbine, different combinations of guide blade opening and blade angle are selected. When the blade angle is constant, 4–8 different openings are selected for the experiment. And a total of 7 blade angles were selected during the experiment. The relationship between the blade and movable guide vane is shown in Figure 5. When β = −9°, the efficiency of 4 calculation conditions and test conditions are compared, as shown in Table 2. The error is less than 1%, which proves the accuracy of the calculation model.
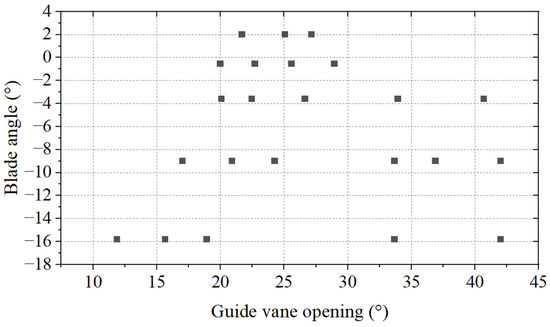
Figure 5.
Selection of calculation working conditions: the black points represent β = −0.55°.

Table 2.
Comparison of calculation and experimental results.
3. Comparative Analysis of Different Working Conditions
3.1. Flowline and Pressure Pulsation Comparison of Runner Blade
As shown in Figure 6a and Figure 7a, when β = 2°, the amplitude of the pressure pulsation on the high-pressure edge and low-pressure edge of the blade decreases with the increase in the opening; when α = 21.69°, the low-frequency and high-amplitude pressure pulsation on the high-pressure edge and low-pressure edge changes sharply. After the opening is increased to 25.07°, the amplitude change in pressure pulsation is most obvious only at the main frequency and the secondary frequency. As shown in Figure 6b and Figure 7b, the streamlines of the high-pressure and low-pressure sides of the blades also tend to be smooth with the increase in the opening, mainly because the streamlines near the hub change from disordered to smooth. As shown in Figure 6c and Figure 7c, the pressure from the high-pressure edge hub to the rim gradually increases, and the high-pressure area near the rim increases with the increase in the opening. The pressure at the low-pressure edge of the blade changes little, and the low-pressure area near the rim increases with the increase in the opening.
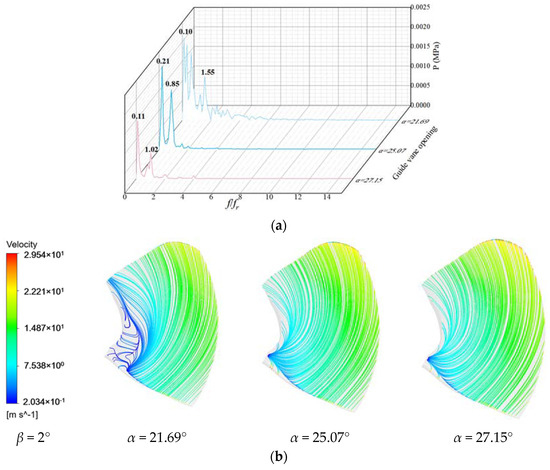
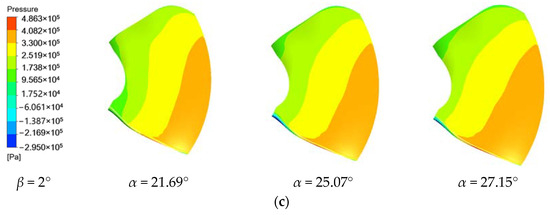
Figure 6.
Pressure pulsation and flow state of high-pressure edge of blade with blade angle β = 2°: (a) Pressure pulsation frequency domain; (b) Streamline; (c) Pressure distribution.
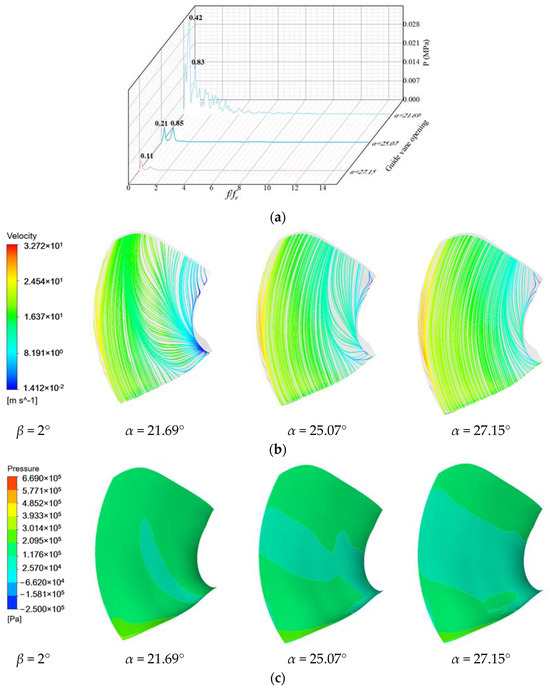
Figure 7.
Pressure pulsation and flow state of low-pressure edge of blade with blade angle β = 2°: (a) Pressure pulsation frequency domain; (b) Streamline; (c) Pressure distribution.
As shown in Figure 8 and Figure 9, when β = −0.55°, the pressure pulsations of the high- and low-pressure sides change dramatically at 0–4 times the frequency of rotation under the working conditions α = 20.09° and α = 22.72°. Under α = 25.58° and α = 28.96° conditions, the pressure pulsation of the high-pressure side and the low-pressure side changes obviously only at the main frequency and the secondary frequency, and the flow line is smooth, while the pressure near the high-pressure side is higher.
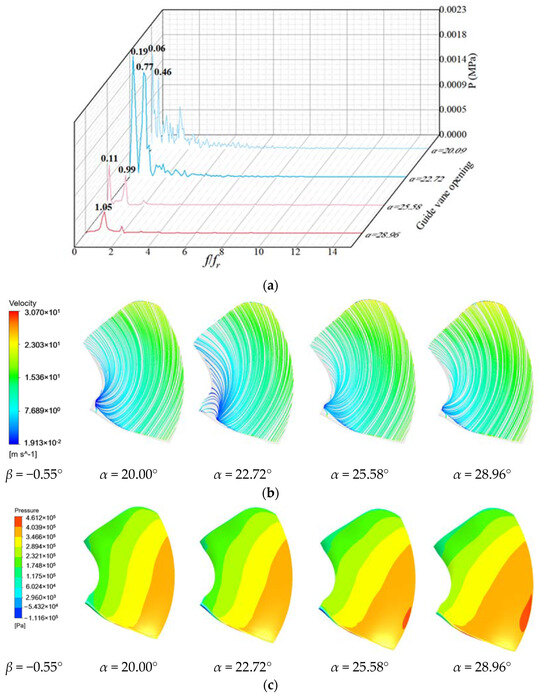
Figure 8.
Pressure pulsation and flow state of high-pressure edge of blade with blade angle β = 0.55°: (a) Pressure pulsation frequency domain; (b) Streamline; (c) Pressure distribution.
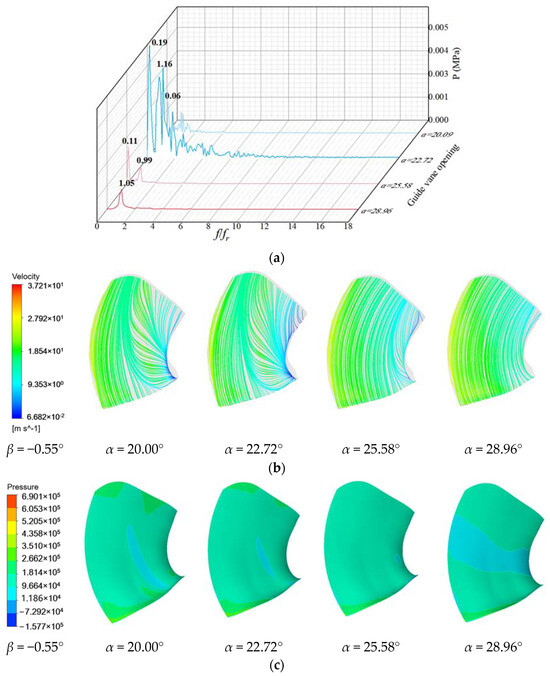
Figure 9.
Pressure pulsation and flow state of low-pressure edge of blade with blade angle β = 0.55°: (a) Pressure pulsation frequency domain; (b) Streamline; (c) Pressure distribution.
As shown in Figure 10 and Figure 11, when β = −3.6°, α = 20.09° and α = 22.48°, the pressure pulsation of the high-pressure edge and low-pressure edge of the blade at the low frequency changes greatly. And the flow line is disordered under this condition. Under the working conditions α = 26.64°, α = 33.94° and α = 40.68°, the main frequency of the high-pressure edge and the low-pressure edge is about 1 time the rotation frequency, the pulsation is more regular and the flow line is smoother. The high-pressure area near the rim of the high-pressure edge increases with the increase in the opening degree, and the low-pressure area near the rim increases with the increase in the opening degree.
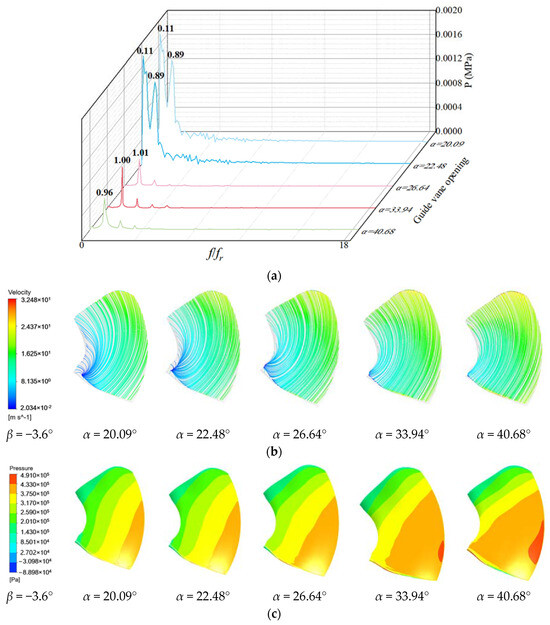
Figure 10.
Pressure pulsation and flow state of high-pressure edge of blade with blade angle with blade angle β = 3.6°: (a) Pressure pulsation frequency domain; (b) Streamline; (c) Pressure distribution.
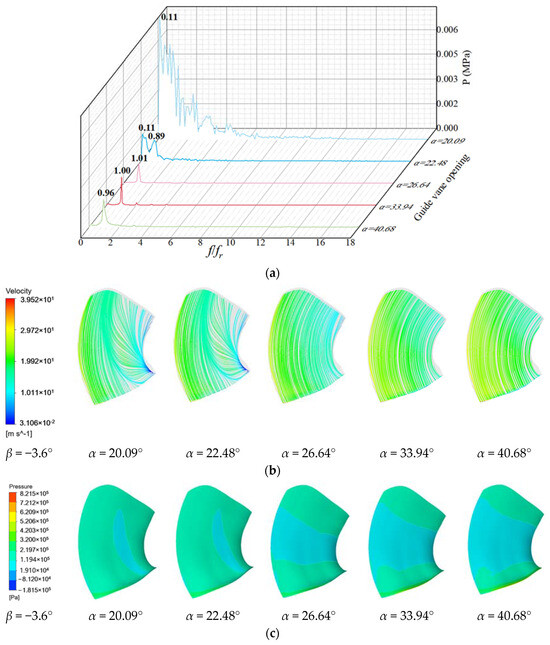
Figure 11.
Pressure pulsation and flow state of low-pressure edge of blade with blade angle β = 3.6°: (a) Pressure pulsation frequency domain; (b) Streamline; (c) Pressure distribution.
As shown in Figure 12 and Figure 13, when β = −9°, the pressure pulsation of the high-pressure side and the low-pressure side at the low frequency varies greatly and the flow line is disordered under the working condition α = 17.04°. Under other opening conditions, the pressure pulsation is more regular, and the flow line is smoother. The high-pressure area near the rim of the high-pressure edge increases with the increase in the opening degree, and the low-pressure area near the rim increases with the increase in the opening degree.
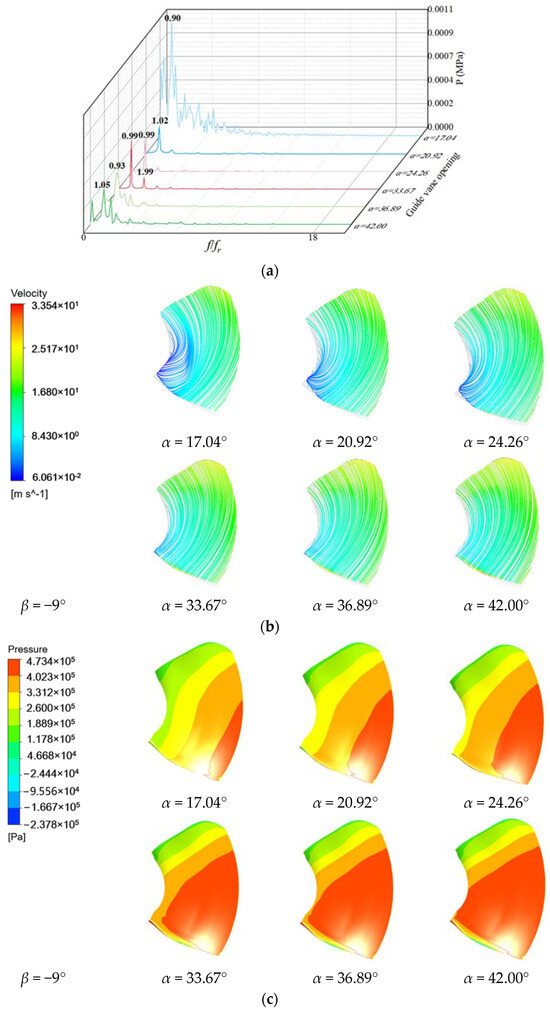
Figure 12.
Pressure pulsation and flow state of high-pressure edge of blade with blade angle β = −9°: (a) Pressure pulsation frequency domain; (b) Streamline; (c) Pressure distribution.
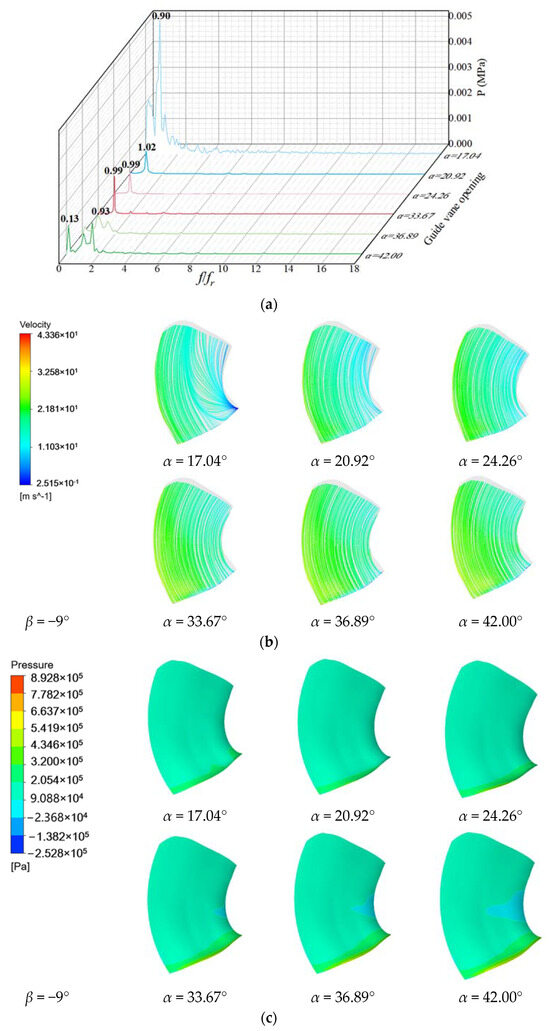
Figure 13.
Pressure pulsation and flow state of low-pressure edge of blade with blade angle β = −9°: (a) Pressure pulsation frequency domain; (b) Streamline; (c) Pressure distribution.
As shown in Figure 14 and Figure 15, when β = −15.8°, the pressure pulsation of the high-pressure side and the low-pressure side at the low frequency varies greatly under the working condition α = 11.88°. Under other opening conditions, the pressure pulsation is more regular, and the flow line is smoother. The high-pressure area near the rim of the high-pressure edge increases with the increase in the opening degree, and the low-pressure area near the rim increases with the increase in the opening degree.
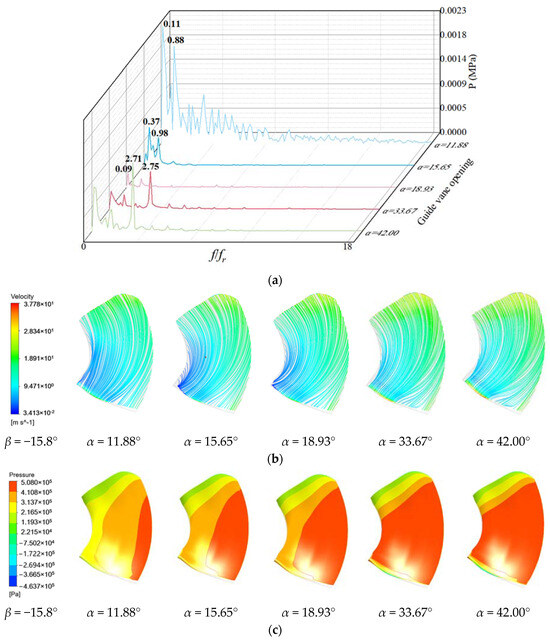
Figure 14.
Pressure pulsation and flow state of high-pressure edge of blade with blade angle β = −15.8°: (a) Pressure pulsation frequency domain; (b) Streamline; (c) Pressure distribution.
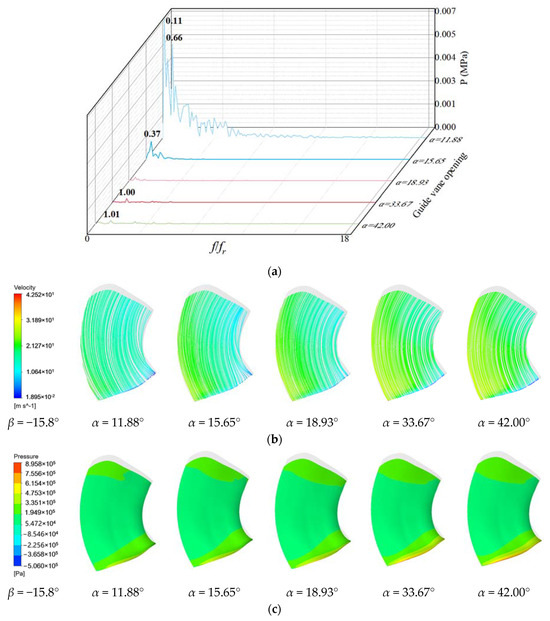
Figure 15.
Pressure pulsation and flow state of low-pressure edge of blade with blade angle β = −15.8°: (a) Pressure pulsation frequency domain; (b) Streamline; (c) Pressure distribution.
3.2. Flowline and Pressure Pulsation Comparison of Draft Tube
The axial flow propeller turbine has a wide operating range, and the pressure pulsation characteristics are different under different operating conditions. In off-cam working conditions, a vortex is generated at the bent elbow of the draft tube, or a forced vortex is generated in the tube, because the rotating water flow at the outlet of the runner forms a backflow, resulting in pressure pulsation in the draft tube and then vibration of the wall of the tube, the water guide mechanism and other components. For large axial flow turbine units, when the vibration is severe, the output swing will cause damage to the stability of the power system and can even lead to the system decoupling.
As shown in Figure 16, the pressure pulsation under the condition β = 2° is characterized by low frequency and high amplitude, and approximate low-frequency components are also found in the calculation results of the pressure pulsation at the high- and low-pressure sides of the runner blade. This indicates that the low-frequency pressure pulsation caused by the formation of the low-pressure vortex zone in the draft tube causes the low-frequency pulsation when it propagates to the upstream flow channel, and this low-frequency pulsation is one of the main pulsation sources of pressure pulsation in the turbine. The sub-frequency of the pressure pulsation under the three opening degrees is 6 times and 12 times the rotation frequency, that is, 1 time the blade overflow frequency and 2 times the blade frequency (second harmonic), which is generated by the wake flow of the blade periodically passing through the space fixed point. At α = 25.07° and α = 27.15°, water flows into the inlet of the draft tube after rotating by the runner. The velocity of the water flow at the circumference of the inlet of the draft tube is larger at α = 21.69°, and the flow line in the diffusion section of the draft tube is the most disordered. As shown in Figure 17, when β = −0.55° and α = 22.72°, the amplitude is highest, at 0.13 times the frequency of rotation, and the velocity of the draft tube elbow section is larger.
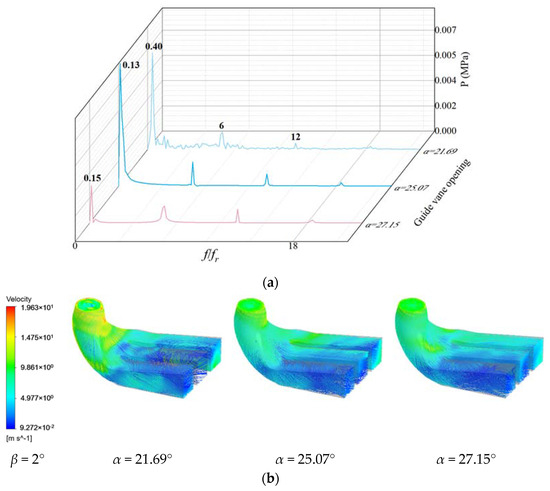
Figure 16.
Pressure pulsation and streamline of low-pressure edge of draft tube with blade angle β = 2°: (a) Pressure pulsation frequency domain; (b) Streamline.
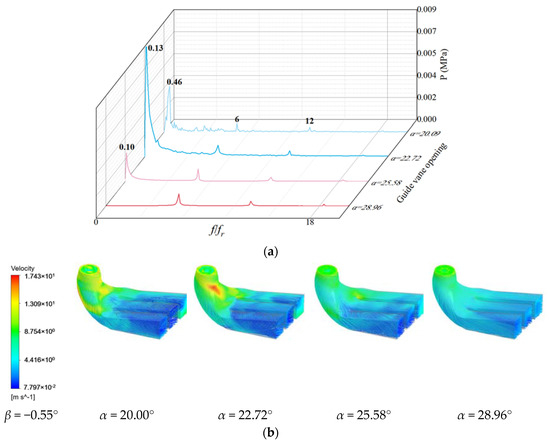
Figure 17.
Pressure pulsation and streamline of low-pressure edge of draft tube with blade angle β = −0.55°: (a) Pressure pulsation frequency domain; (b) Streamline.
As shown in Figure 18, when β = −3.6°, the flow line is relatively smooth, and there are low-frequency and high-amplitude pressure pulsations at α = 20.09° and α = 22.48°, and the sub-frequency pressure pulsations are 6 times and 12 times. When α = 26.64°, α = 33.94° and α = 40.68°, the main frequency is 6 times the frequency of revolution, and the secondary frequency is 12 times the frequency of revolution. When α = 40.68°, the velocity at the junction between the draft tube inlet and the runner drain cone is very large, and there is a high-speed zone of the draft water inlet. As shown in Figure 19, when β = −9° and α = 20.09°, the main frequency is 0.11 times the rotation frequency, and the main frequency is 6 times the rotation frequency under other opening degrees. When α = 36.89° and α = 42.00°, the pressure amplitude is also obvious at the low-frequency doubling, and the speed at the connection between the draft tube inlet and the runner is larger. As shown in Figure 20, when β = −15.8°, α = 11.88°, the pressure amplitude of the monitoring point changes irregularly, the flow in the middle diffusion section of the draft tube is insufficient, and the flow is mainly through the left and right diffusion sections. When α = 15.65° and α = 18.93°, the main frequency is 6 times the rotation frequency. When α = 33.67° and α = 42.00°, the amplitudes are larger at 0.77 times and 0.70 times the revolutions, respectively, the sub-frequency is 6 times the revolutions, and the middle diffusion section of the draft tube has almost no flow. When β = −9°, β = −15.8°, the amplitude is almost 0 at 12 times the frequency.
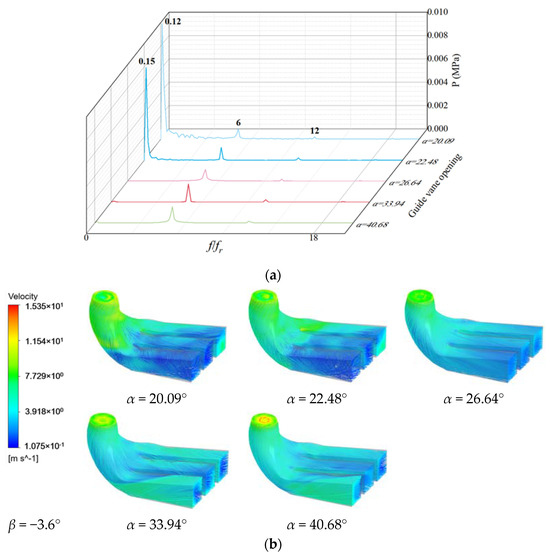
Figure 18.
Pressure pulsation and streamline of low-pressure edge of draft tube with blade angle β = −3.6°: (a) Pressure pulsation frequency domain; (b) Streamline.
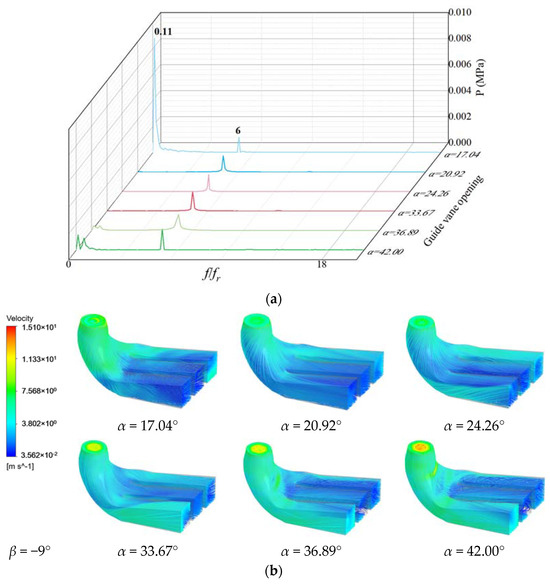
Figure 19.
Pressure pulsation and streamline of low-pressure edge of draft tube with blade angle β = −9°: (a) Pressure pulsation frequency domain; (b) Streamline.
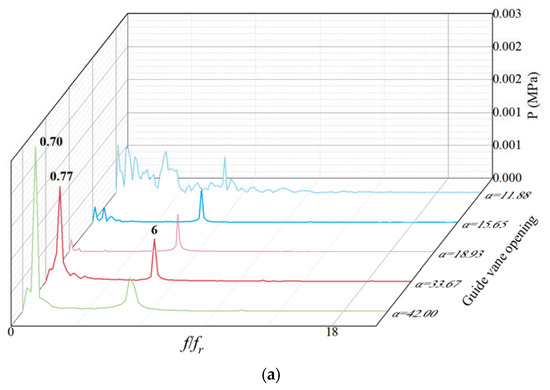
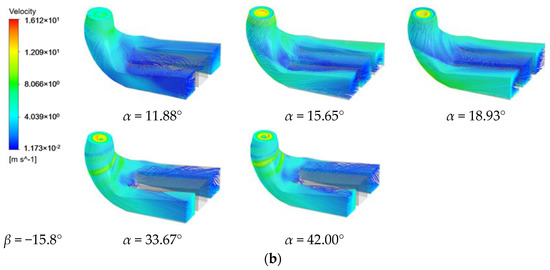
Figure 20.
Pressure pulsation and streamline of low-pressure edge of draft tube with blade angle β = −15.8°: (a) Pressure pulsation frequency domain; (b) Streamline.
In general, the pressure pulsation changes at the monitoring point of the draft tube inlet under the five blade angles have certain rules. Under the condition of a small blade angle, the main frequency is a low frequency due to the influence of the draft tube vortex band, the pressure pulsation presents a high amplitude and the flow line is chaotic. Due to the proximity of the runner outlet, affected by the flow at the runner outlet, the next frequency of the blade under small opening conditions with a small blade angle is 1 or 2 times the blade passing frequency, and the main frequency under large blade angle or opening conditions is 6 times the rotation frequency. In addition, the amplitude of the obtained vortex band frequency is smaller than that of the Francis turbine, which is one of the advantages of the Kaplan turbine. The reason is that the Kaplan turbine can adapt to changes in the water head and flow rate by changing the blade angle to maintain the state of high power, and can approximately maintain the normal outlet when changing, so that the development degree of the liner vortex band is low.
3.3. Efficiency Comparison
As shown in Figure 21, at a blade angle of 2°, the efficiency is only 82% when the opening is 21.69°, and the flow state of the draft tube is poor. When the opening is increased to 25.07°, the efficiency is increased to 92.3%, and the draft tube streamline is smooth. At a blade angle of −0.55°, the efficiency increases with the increase in the opening. At a blade angle of −3.6°, the efficiency of each calculated opening is greater than 90.2%. At a blade angle of −9°, the efficiency exceeds 91.4% in the opening range of 17.04° to 24.26°, and the efficiency is as low as 86.7% when the opening is increased to 33.67°. At a blade angle of −15.8°, the efficiency of the five openings is lower than 85.3%.
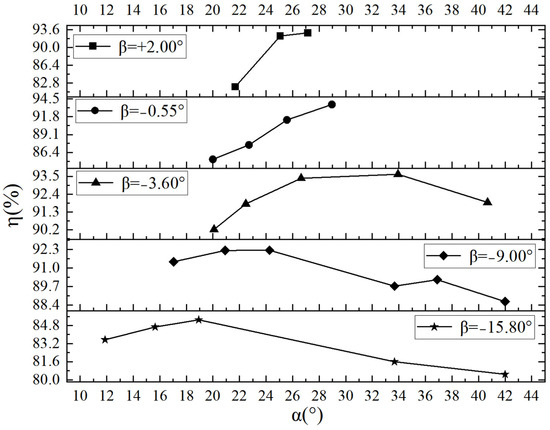
Figure 21.
The relationship between blade angle and efficiency.
3.4. Differential Number of Flow Heterogeneity
In order to quantitatively represent the flow uniformity of the three support piers of the draft tube, based on the analysis of the relationship between the flow pattern of the draft tube and the unit efficiency in the above two sections, this paper puts forward a clear discrimination number to determine flow uniformity. The discriminant number ξ is shown in Equation (1). When the ξ value approaches 0, the flow state of the three piers is the most uniform, and the flow velocity of each pier is almost the same.
where, x, y and z represent the overflow of the three piers, respectively, and k is a constant (k = 1.0).
As shown in Figure 22, the curve represents the corresponding discriminant number under different efficiencies. It is found that the discriminant number increases with the decrease in efficiency, and the flow in the three piers becomes more nonuniform. When the efficiency is between 80.487% and 87.527%, the discriminant number decreases slowly with the increase in efficiency. In this efficiency interval, the discriminant number ξ is above 0.92, and the flow pattern in the three piers of the draft tube is poor and the flow is uneven. When the efficiency increases from 87.527% to 90.18%, the value of ξ decreases from 0.92 to 0.80. After the efficiency of 90.18%, the discriminant number ξ is extremely sensitive to the change in efficiency. With the increase in efficiency, the value of the discriminant number ξ decreases rapidly. When the efficiency increases to 93.626%, the value of ξ decreases to 0.187, and the overflow rate in the three piers is almost equal.
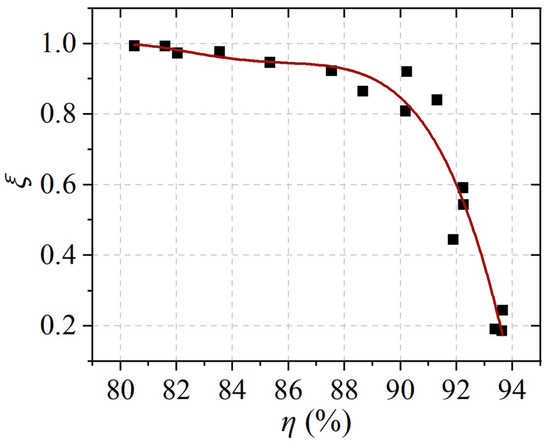
Figure 22.
The relationship between efficiency and the discriminant number ξ of flow heterogeneity.
4. Conclusions
(1) Under conditions with a small guide vane opening, the pressure pulsation of the runner blade is severe and the streamline near the hub is disorganized. With the increase in the guide vane opening, the degree of pressure pulsation on both the high- and low-pressure edges of the blade decreases, resulting in a smoother streamline. Compared with the low-pressure side, the pressure distribution of the high-pressure side is more sensitive to changes in the opening.
(2) Under different blade angles, the pressure fluctuation of the draft tube with each guide vane opening has certain rules. When the blade angle is the same, the inner flow of the three support piers of the draft tube has a vortex zone or backflow under the condition of a small guide vane opening, and the draft tube inlet has low-frequency and high-amplitude pressure fluctuations under the influence of the vortex zone under the condition of a small opening. The sub-frequency affected by the runner outlet flow is the frequency doubling of the blade passing frequency.
(3) In order to quantitatively represent flow uniformity in the three support piers of the draft tube, the paper proposes the discrimination number ξ for judging the flow uniformity. When the value of ξ tends to 0, the flow velocity in the three piers is almost the same. With the decrease in efficiency, the discriminant number increases and the flow uniformity decreases. When the efficiency increases to 90.18%, the discriminant number is extremely sensitive to the change in efficiency, and the value of the number decreases rapidly with the increase in efficiency.
Author Contributions
Conceptualization, D.Y. and H.L.; methodology, W.Z.; software, D.Y. and H.L.; validation, Y.W. and X.F.; formal analysis, X.F.; investigation, Y.W. and L.Z.; data curation, L.Z.; writing—original draft preparation, D.Y. and H.L.; writing—review and editing, D.Y. and W.Z.; visualization, W.Z.; supervision, Z.W., Y.W. and X.F.; project administration, Z.W. and H.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China No. 52079141.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Acknowledgments
The author would like to express sincere gratitude for the project support received from Guangxi Dateng Gorge Water Conservancy Development Co., Ltd. for the “Research on the Safe and Stable Operation of the Dateng Gorge Large Kaplan Turbine Project”.
Conflicts of Interest
Authors Haiqiang Luo, Yibin Wu and Xiaofu Fan were employed by the company Guangxi Dateng Gorge Water Conservancy Project Development Co., Ltd. Author Weiqiang Zhao was employed by the company Institute of Renewable Energy and Energy Storage Technologies, PowerChina Renewable Energy Co., Ltd., Beijing 100101, China. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Ridha, W.K.M.; Kashyzadeh, K.R.; Ghorbani, S. Common Failures in Hydraulic Kaplan Turbine Blades and Practical Solutions. Materials 2023, 16, 3303. [Google Scholar] [CrossRef] [PubMed]
- Polák, M. A Brief History of the Kaplan Turbine Invention. Energies 2021, 14, 6211. [Google Scholar] [CrossRef]
- Pracheil, B.M.; DeRolph, C.R.; Schramm, M.P.; Bevelhimer, M.S. A fish-eye view of riverine hydropower systems: The current understanding of the biological response to turbine passage. Rev. Fish Biol. Fish. 2016, 26, 153–167. [Google Scholar] [CrossRef]
- Wei, P.; Li, S. Stochastic dynamic analysis of a Kaplan turbine system considering synergistic regulation. Mod. Phys. Lett. B 2021, 35, 2150260. [Google Scholar] [CrossRef]
- Iovănel, R.G.; Dunca, G.; Cervantes, M.J. Study on the Accuracy of RANS Modelling of the Turbulent Flow Developed in a Kaplan Turbine Operated at BEP. Part 2—Pressure Fluctuations. J. Appl. Fluid Mech. 2019, 12, 1463–1473. [Google Scholar] [CrossRef]
- Yen, Y.-H.; ElGammal, T.; Amano, R.S.; Millevolte, J.; Lequesne, B.; Mueller, R.J. Numerical Optimization of Micro Kaplan Hydro Turbine System. In Proceedings of the ASME 2016 Fluids Engineering Division Summer Meeting Collocated with the ASME 2016 Heat Transfer Summer Conference and the ASME 2016 14th International Conference on Nanochannels, Microchannels, and Minichannels, Washington, DC, USA, 10–14 July 2016. [Google Scholar]
- Ma, Y.; Qian, B.; Feng, Z.; Wang, X.; Shi, G.; Liu, Z.; Liu, X. Flow behaviors in a Kaplan turbine runner with different tip clearances. Adv. Mech. Eng. 2021, 13, 16878140211015879. [Google Scholar] [CrossRef]
- Liu, S.; Wu, Y.; Chen, T.; Nishi, M. Development of Numerical Performance Test Stand for a Kaplan Turbine. Int. J. Turbo Jet-Engines 2009, 26, 253–262. [Google Scholar] [CrossRef]
- Jošt, D.; Škerlavaj, A.; Lipej, A. Improvement of Efficiency Prediction for a Kaplan Turbine with Advanced Turbulence Models. Stroj. Vestn.-J. Mech. Eng. 2014, 60, 124–134. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, S.; Dou, H.-S.; Wu, S.; Chen, T. Numerical prediction and similarity study of pressure fluctuation in a prototype Kaplan turbine and the model turbine. Comput. Fluids 2012, 56, 128–142. [Google Scholar] [CrossRef]
- Liu, S.; Shao, J.; Wu, S.; Wu, Y. Numerical simulation of pressure fluctuation in Kaplan turbine. Sci. China Technol. Sci. 2008, 51, 1137–1148. [Google Scholar] [CrossRef]
- Liu, S.; Zhou, D.; Liu, D.; Wu, Y.; Nishi, M. Runaway transient simulation of a model Kaplan turbine. In Proceedings of the 25th IAHR Symposium on Hydraulic Machinery and Systems, Timisoara, Romania, 20–24 September 2010. [Google Scholar] [CrossRef]
- Minakov, A.V.; Platonov, D.V.; Litvinov, I.V.; Shtork, S.I.; Hanjalić, K. Vortex ropes in draft tube of a laboratory Kaplan hydroturbine at low load: An experimental and LES scrutiny of RANS and DES computational models. J. Hydraul. Res. 2017, 55, 668–685. [Google Scholar] [CrossRef]
- Zhang, C.; Tang, H.; Liu, Y.; Chang, J. Study on reverse water hammer of the kaplan turbine. In Proceedings of the 16th Asia and Pacific Division Congress of the International Association of Hydraulic Engineering and Research/3rd IAHR International Symposium on Hydraulic Structures, Nanjing, China, 23 October 2008; pp. 2208–2213. [Google Scholar]
- Mulu, B.; Jonsson, P.; Cervantes, M. Experimental investigation of a Kaplan draft tube—Part I: Best efficiency point. Appl. Energy 2012, 93, 695–706. [Google Scholar] [CrossRef]
- Liu, S.; Mai, J.; Shao, J.; Wu, Y. Pressure pulsation prediction by 3D turbulent unsteady flow simulation through whole flow passage of Kaplan turbine. Eng. Comput. 2009, 26, 1006–1025. [Google Scholar] [CrossRef]
- Dehkharqani, A.S.; Engström, F.; Aidanpää, J.-O.; Cervantes, M.J. Experimental Investigation of a 10 MW Prototype Kaplan Turbine during Start-Up Operation. Energies 2019, 12, 4582. [Google Scholar] [CrossRef]
- Dehkharqani, A.S.; Engström, F.; Aidanpää, J.-O.; Cervantes, M.J. An Indirect Measurement Methodology to Identify Load Fluctuations on Axial Turbine Runner Blades. Sensors 2020, 20, 7220. [Google Scholar] [CrossRef] [PubMed]
- Amiri, K.; Mulu, B.; Raisee, M.; Cervantes, M.J. Unsteady pressure measurements on the runner of a Kaplan turbine during load acceptance and load rejection. J. Hydraul. Res. 2016, 54, 56–73. [Google Scholar] [CrossRef]
- Liu, S.; Li, S.; Wu, Y. Pressure Fluctuation Prediction of a Model Kaplan Turbine by Unsteady Turbulent Flow Simulation. J. Fluids Eng. 2009, 131, 101102. [Google Scholar] [CrossRef]
- Rivetti, A.; Lucino, C.; Liscia, S.; Muguerza, D.; Avellan, F. Pressure pulsation in Kaplan turbines: Prototype-CFD comparison. In Proceedings of the 26th IAHR Symposium on Hydraulic Machinery and Systems, Beijing, China, 19–23 August 2012. [Google Scholar] [CrossRef]
- Mulu, B.G.; Cervantes, M.J.; Devals, C.; Vu, T.C.; Guibault, F. Simulation-based investigation of unsteady flow in near-hub region of a Kaplan Turbine with experimental comparison. Eng. Appl. Comput. Fluid Mech. 2015, 9, 139–156. [Google Scholar] [CrossRef][Green Version]
- Ohiemi, I.E.; Sheng, Y.S.; Singh, P.; Li, Y. Experimental investigation on the effect of axial gap on performance and unsteady pressure pulsations of low head axial flow hydraulic turbine. Flow Meas. Instrum. 2022, 88, 102255. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).