Evaluating Outdoor Performance of PV Modules Using an Innovative Explicit One-Diode Model
Abstract
1. Introduction
2. Database
3. Development of the Explicit One-Diode Model
3.1. Explicit One-Diode Model Equation at STC
3.2. One-Diode Model under Real Weather Conditions
- 1.
- The effective solar irradiance Geff is determined taking into account the degree of cleanliness of the PV module:
- 2.
- The operating temperature of the solar cell is calculated as:
- 3.
- The photocurrent is linearly linked with the incident solar irradiance and can be obtained by considering the thermal coefficient of the short-circuit current αI
- 4.
- The saturation current is determined as:
- 5.
- The diode ideality factor and the series resistance and shunt resistance remain the same as at STC:
3.3. Explicit One-Diode Model at MPP
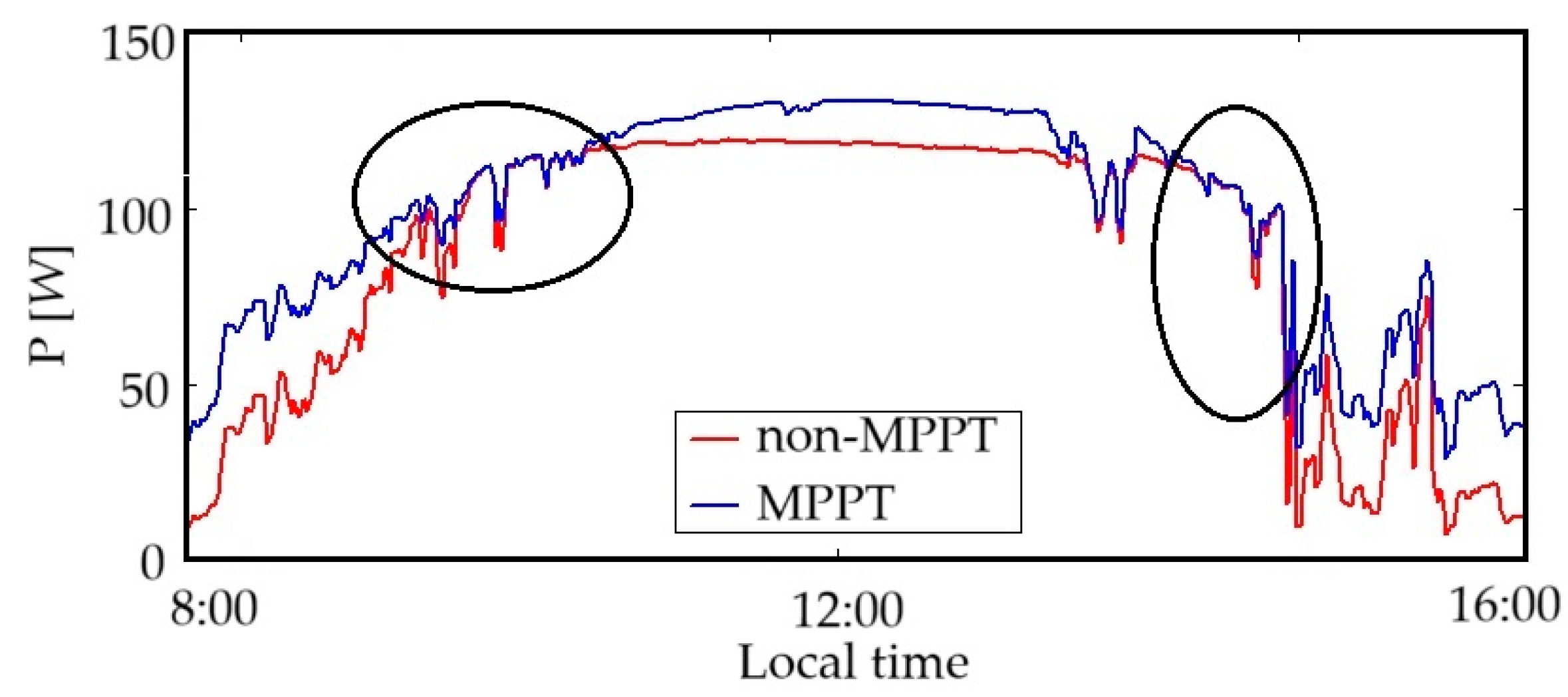
4. MPPT Performance: A Case Study
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- IEA. World Energy Outlook 2023; IEA: Paris, France, 2023; Available online: https://www.iea.org/reports/world-energy-outlook-2023 (accessed on 1 April 2024).
- Paulescu, M.; Paulescu, E.; Gravila, P.; Badescu, V. Weather Modeling and Forecasting of PV Systems Operation; Springer: London, UK, 2013. [Google Scholar]
- Reference Air Mass 1.5 Spectra. 2024. Available online: https://www.nrel.gov/grid/solar-resource/spectra-am1.5.html (accessed on 1 April 2024).
- Nelson, J. The Physics of Solar Cells; Imperial College Press: London, UK, 2013. [Google Scholar]
- Yang, B.; Wang, J.; Zhang, X.; Yu, T.; Yao, W.; Shu, H.; Zeng, F.; Sun, L. Comprehensive overview of metaheuristic algorithm applications on PV cell parameter identification. Energy Convers. Manag. 2020, 208, 112595. [Google Scholar] [CrossRef]
- Wang, M.; Peng, J.; Luo, Y.; Shen, Z.; Yang, H. Comparison of different simplistic prediction models for forecasting PV power output: Assessment with experimental measurements. Energy 2022, 224, 120162. [Google Scholar] [CrossRef]
- Li, J.; Qin, C.; Yang, C.; Ai, B.; Zhou, Y. Extraction of single diode model parameters of solar cells and PV modules by combining an intelligent optimization algorithm with simplified equation based on Lambert W function. Energies 2023, 16, 5425. [Google Scholar] [CrossRef]
- Saloux, E.; Teyssedou, A.; Sorin, M. Explicit model of photovoltaic panels to determine voltages and current at the maximum power point. Sol. Energy 2011, 85, 713–722. [Google Scholar] [CrossRef]
- Lun, S.; Du, C.; Yang, G.; Wang, S.; Guo, T.; Sang, J.; Li, J. An explicit approximate I-V characteristic model of a solar cell based on pade approximants. Sol. Energy 2013, 92, 147–159. [Google Scholar] [CrossRef]
- Corless, R.M.; Gonnet, G.H.; Hare, D.E.G.; Jeffrey, D.J.; Knuth, D.E. On the Lambert W function. Adv. Comput. Math. 1996, 5, 329–359. [Google Scholar] [CrossRef]
- Roibas-Millan, E.; Cubero-Estalrrich, J.L.; Gonzalez-Estrada, A.; Jado-Puente, R.; Sanabria-Pinzon, M.; Alfonso-Corcuera, D.; Alvarez, J.M.; Cubas, J.; Pindado, S. Lambert W-function simplified expressions for photovoltaic current-voltage modelling. In Proceedings of the 2020 IEEE International Conference on Environment and Electrical Engineering and 2020 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Madrid, Spain, 9–12 June 2020; pp. 1–6. [Google Scholar]
- Alombah, N.H.; Harrison, A.; Kamel, S.; Fotsin, H.B.; Aurangzeb, M. Development of an efficient and rapid computational solar photovoltaic emulator utilizing an explicit PV model. Sol. Energy 2024, 271, 112426. [Google Scholar] [CrossRef]
- Mathew, L.E.; Panchal, A.K. An exact and explicit PV panel curve computation assisted by two 2-port networks. Sol. Energy 2022, 240, 280–289. [Google Scholar] [CrossRef]
- Boutana, N.; Mellit, A.; Lughi, V.; Pavan, M. Assessment of implicit and explicit models for different photovoltaic modules technologies. Energy 2017, 122, 128–143. [Google Scholar] [CrossRef]
- Toledo, F.J.; Galiano, V.; Herranz, V.; Blanes, J.M.; Batzelis, E. A comparison of methods for the calculation of all the key points of the PV single-diode model including a new algorithm for the maximum power point. Optim. Eng. 2023, 1–35. [Google Scholar] [CrossRef]
- Katche, M.L.; Makokha, A.B.; Zachary, S.O.; Adaramola, M.S. A Comprehensive Review of Maximum Power Point Tracking (MPPT) Techniques Used in Solar PV Systems. Energies 2023, 16, 2206. [Google Scholar] [CrossRef]
- Humada, A.M.; Darweesh, S.Y.; Mohammed, K.G.; Kamil, M.; Mohammed, S.F.; Kasim, N.K.; Tahseen, T.A.; Awad, O.I.; Mekhilef, S. Modeling of PV system and parameter extraction based on experimental data: Review and investigation. Sol. Energy 2020, 199, 742–760. [Google Scholar] [CrossRef]
- Kumar, M.; Malik, P.; Chandel, R.; Chandel, S.S. Development of a novel solar PV module model for reliable power prediction under real outdoor conditions. Renew. Energy 2023, 217, 119224. [Google Scholar] [CrossRef]
- Sabadus, A.; Paulescu, M. A New Explicit Five-Parameter Solar Cell Model. In Proceedings of the 8th World Conference on Photovoltaic Energy Conversion (WCPEC-8 2022), Milan, Italy, 26–30 September 2023; pp. 454–456. [Google Scholar] [CrossRef]
- Solar Platform of the West University of Timisoara, Romania. Available online: http://solar.physics.uvt.ro/srms/ (accessed on 1 May 2024).
- Cotfas, D.T.; Deaconu, A.M.; Cotfas, P.A. Application of successive discretization algorithm for determining photovoltaic cells parameters. Energy Convers. Manag. 2019, 196, 545–556. [Google Scholar] [CrossRef]
- Paulescu, M.; Badescu, V.; Dughir, C. New performance and field-test to assess photovoltaic module performance. Energy 2014, 70, 49–57. [Google Scholar] [CrossRef]







| Equation | Parameters | |||||
|---|---|---|---|---|---|---|
| Implicit Equation (1) | 7.67 | 10−7 | 1.070 | 0.0022 | 23.2 | 0.990 |
| Explicit Equation (5) | 7.67 | 10−7 | 1.061 | 0.001 | 13 | 0.997 |
| Cleanliness Degree | Perfect | Proper | Medium | Low |
|---|---|---|---|---|
| 1.00 | 0.98 | 0.96 | 0.92 |
| Relative Sunshine | Relative Error [%] |
|---|---|
| 76.9 | |
| 45.1 | |
| 23.9 | |
| 13.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sabadus, A.; Stefu, N.; Paulescu, M. Evaluating Outdoor Performance of PV Modules Using an Innovative Explicit One-Diode Model. Energies 2024, 17, 2547. https://doi.org/10.3390/en17112547
Sabadus A, Stefu N, Paulescu M. Evaluating Outdoor Performance of PV Modules Using an Innovative Explicit One-Diode Model. Energies. 2024; 17(11):2547. https://doi.org/10.3390/en17112547
Chicago/Turabian StyleSabadus, Andreea, Nicoleta Stefu, and Marius Paulescu. 2024. "Evaluating Outdoor Performance of PV Modules Using an Innovative Explicit One-Diode Model" Energies 17, no. 11: 2547. https://doi.org/10.3390/en17112547
APA StyleSabadus, A., Stefu, N., & Paulescu, M. (2024). Evaluating Outdoor Performance of PV Modules Using an Innovative Explicit One-Diode Model. Energies, 17(11), 2547. https://doi.org/10.3390/en17112547






