Next Article in Journal
Impact of Economic Awareness on Sustainable Energy Consumption: Results of Research in a Segment of Polish Households
Previous Article in Journal
Smart City and Energy: A Bibliometric Review of the Smart City and Smart Energy Concept from the Perspective of the Bioclimatic Approach
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Energies
Volume 17
Issue 11
10.3390/en17112487
energies-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

State of Health Estimation for Lithium-Ion Batteries with Deep Learning Approach and Direct Current Internal Resistance

by
Zhongxian Sun
1,
Weilin He
1,
Junlei Wang
1 and
Xin He
1,2,*
1
College of Electrical Engineering, Sichuan University, Chengdu 610065, China
2
School of Chemical Engineering, Sichuan University, Chengdu 610065, China
*
Author to whom correspondence should be addressed.
Energies 2024, 17(11), 2487; https://doi.org/10.3390/en17112487
Submission received: 24 April 2024 / Revised: 15 May 2024 / Accepted: 19 May 2024 / Published: 22 May 2024
(This article belongs to the Section D2: Electrochem: Batteries, Fuel Cells, Capacitors)
Browse Figures
Versions Notes

Abstract

:
Battery state of health (SOH), which is a crucial parameter of the battery management system, reflects the rate of performance degradation and the aging level of lithium-ion batteries (LIBs) during operation. However, traditional machine learning models face challenges in accurately diagnosing battery SOH in complex application scenarios. Hence, we developed a deep learning framework for battery SOH estimation without prior knowledge of the degradation in battery capacity. Our framework incorporates a series of deep neural networks (DNNs) that utilize the direct current internal resistance (DCIR) feature to estimate the SOH. The correlation of the DCIR feature with the fade in capacity is quantified as strong under various conditions using Pearson correlation coefficients. We utilize the K-fold cross-validation method to select the hyperparameters in the DNN models and the optimal hyperparameter conditions compared with machine learning models with significant advantages and reliable prediction accuracies. The proposed algorithm is subjected to robustness validation, and the experimental results demonstrate that the model achieves reliable precision, with a mean absolute error (MAE) less than 0.768% and a root mean square error (RMSE) less than 1.185%, even when LIBs are subjected to varying application scenarios. Our study highlights the superiority and reliability of combining DNNs with DCIR features for battery SOH estimation.

1. Introduction

Rechargeable lithium-ion batteries (LIBs) have emerged as pivotal components in various applications, such as electric vehicles (EVs) [1], portable electronics [2], and energy storage systems [3]. Their widespread adoption is attributed to their remarkable attributes, including high energy density and long cycle life. However, cyclic charging and discharging processes trigger a cascade of irreversible degradation reactions within LIBs, including the increase in impedance [4], the loss of electrode materials [5], and the loss of lithium inventory [6]. These reactions have significant implications for the performance and lifespan of the battery. Given the safety issues that may arise from the degradation in performance of LIBs, batteries in EVs should be replaced when their state of health (SOH) fades to 80% [7]. This preventive measure aims to reduce the risk of unexpected failures due to battery aging. Therefore, accurately estimating the SOH of LIBs is critical to improving the safety and stability of batteries.
At present, this primarily involves model-based and data-driven methods. The former encompass equivalent circuit models (ECMs) [8], Kalman filter (KF) models [9], and pseudo-two-dimensional (P2D) models [10]. However, the output accuracy of these models relies on precise parameter design, intricate computational processes, and a deep understanding of electrochemistry. To address the challenges associated with modeling and the limited accuracy of model-based approaches, researchers have increasingly turned to data-driven techniques for battery SOH estimation, which improve the accuracy of SOH estimation by analyzing high-throughput data from the battery charging and discharging process and using machine learning and data mining techniques to identify and model the features of the battery’s SOH [11,12]. Such methods mainly include Gaussian process regression (GPR) [13,14,15], support vector machine (SVM) [16,17,18], long short-term memory (LSTM) networks [19,20,21], and convolutional neural networks (CNNs) [22,23,24]. However, the reliable acquisition of battery aging features remains a significant research challenge.
Extracting correlation features such as peak, slope, and area from incremental capacity curves (ICA) to estimate battery SOH is now widely recognized [25,26,27]. Weihan Li et al. [28] extracted correlation features from incremental capacity curves and established a transferable deep learning framework to accomplish battery capacity estimation. However, establishing the basis for ICA requires high-frequency data acquisition and differential voltage calculations, a process that increases the burden on the battery management system. The correlation features extracted from voltage and current profiles have been widely used for battery SOH estimation [29,30,31] with voltage and current features. Darius Roman et al. [32] used the threshold voltage method to extract the segment voltage data and computed their statistical features to realize battery SOH estimation. Michael Knapp et al. [33] calculated the voltage profile from the relaxation state of the battery as a statistical feature to estimate the battery capacity. However, the use of such methods requires complex experimental design and efficient data processing techniques, which increases the experimental cost. Electrochemical impedance spectroscopy (EIS), as a non-destructive testing technique, can effectively resolve the material properties and degradation mechanisms inside the battery. It has been demonstrated that the correlation features extracted from EIS can be applied to battery SOH estimation [34,35,36]. Alpha A. Lee et al. [37] used electrochemical impedance for battery capacity estimation based on a data-driven model. However, the high experimental cost and complicated usage conditions make its wide application to battery SOH estimation difficult. Compared with alternating current internal resistance, direct current internal resistance (DCIR) reflects the real state of battery cycle aging more effectively. The DCIR of LIBs is mainly presented in the form of polarization, which can be divided into ohmic internal resistance, diffusion internal resistance, and electrochemical reaction internal resistance according to the dynamics [38,39,40]. Therefore, establishing the relationship between DCIR and cycle capacity can reflect the SOH of the battery.
The main contributions of this study can be summarized as shown in Figure 1:
Battery aging test: this collects historical cycle data from LIBs, including the open-circuit voltage, pulse current, and polarization voltage.
Feature engineering: this enables the calculation of DCIR based on Ohm’s law and the quantification of the correlation between DCIR and battery capacity through Pearson’s correlation.
Constructing a deep learning framework: based on the capacity-fading characteristics of LIBs, the use of the DNN model is proposed to estimate the battery SOH, and K-fold cross-validation and robustness validation methods are used to test the effectiveness of the proposed method.
The rest of this paper is organized as follows: Section 2 describes the experimental dataset. Section 3 describes the health feature extraction and analysis. Section 4 describes the health state assessment model based on DNN. Section 5 verifies the validity of the methodology proposed in this paper. Section 6 summarizes this research.

2. Dataset

In this study, a total of 12 pouch LIBs supplied by two battery manufacturers were tested. The entire experimental process involved modifying the ambient temperature and charge–discharge modes to imitate diverse usage scenarios. This study meticulously documented data from all 12 cells alongside setup parameters, which are summarized in Table 1. Set cycle test conditions: (I) relaxation for 10 min; (II) constant current charging to a cut-off voltage of 3.65 V; (III) relaxation for 10 min; and (IV) constant current discharging to a cut-off voltage of 2.30 V. The cycle test was run from (I) to (IV) until the end of battery life. According to the cycling conditions and battery types, the data of 12 LIBs were divided into three groups: B#1, B#2, and B#3. B#1 contains seven LFP cells with a nominal capacity of 1000 mAh, and the cycling test was carried out using a fixed current of 1 C or 2 C. B#2 contains three LFP cells with a nominal capacity of 1000 mAh. B#2-1 and B#2-3 were tested for cyclic aging using fixed currents of 0.5 C and 4 C. B#2-2 was tested for cyclic aging using variable current, and it was necessary to set (II) in the cyclic test conditions to a constant current charging of 0.5 C up to a cut-off voltage of 3.30 V, and then use a constant current charging of 1 C up to a cut-off voltage of 3.65 V. B#3 contains two LFP cells with a nominal capacity of 6000 mAh, and the cycling test was carried out using a fixed current of 0.5 C or 1 C.

3. Health Feature Extraction Based on Ohm’s Law

3.1. SOH Definition

The current maximum usable capacity indirectly reflects the aging of the battery. Typically, the SOH is defined as the ratio of the battery’s current maximum usable capacity to its nominal capacity, as shown in Equation (1):
S O H = C i C n o m × 100 %
where Ci denotes the current maximum capacity of the battery and Cnom denotes the nominal capacity of the battery. Therefore, an accurate estimation of Ci is beneficial for obtaining information about the SOH of the battery.

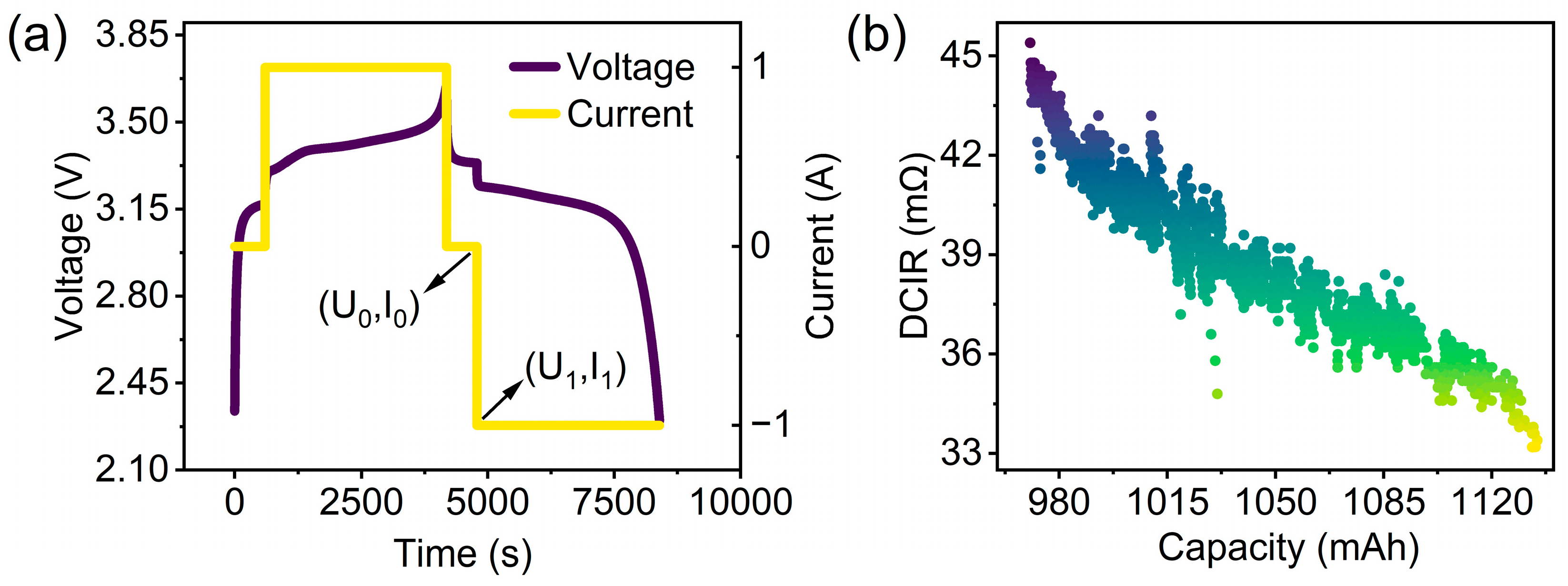
3.2. DCIR Feature

DCIR cannot be directly measured by test equipment. Instead, it is the result of calculating the relationship between voltage and current according to Ohm’s law. As shown in Figure 2a, the voltage and current curves of B#2-1 are taken as the object of analysis in this study, and the DCIR can be calculated as shown in Equation (2):
R = U 1 − U 0 I 1 − I 0
where U0 and I0 denote the voltage and current from the last moment of cycle setting condition (III), and U1 and I1 denote the voltage and current at the moment of entering cycle setting condition (IV). Figure 2b depicts the discharge capacity and DCIR of the B#2-1 cell over cycling. As the capacity fades, the DCIR behavior gradually increases, showing that there is a significant correlation between the fade in capacity and the increase in DCIR of the battery.

3.3. Feature Correlation Analysis

To further understand the correlation between the fade in battery capacity and the increase in DCIR, we can calculate Pearson’s correlation coefficient between capacity and DCIR, as shown in Equation (3):
ρ = ∑ i = 1 N ( C i - C ¯ ) ( R i - R ¯ ) ∑ i = 1 N ( C i - C ¯ ) 2 ∑ i = 1 N ( R i - R ¯ ) 2
where ρ denotes the Pearson correlation coefficient, which ranges from −1 to 1, while |ρ| is closer to 1, indicating a stronger correlation. N denotes the number of cycles, Ci denotes the discharge capacity of the ith cycle, C ¯ denotes the average capacity of the N cycle, Ri denotes the DCIR of the ith cycle, and R ¯ denotes the average DCIR of the N cycle. In this study, Pearson’s correlation analysis was conducted on 12 cells, as depicted in Table 2. The results reveal that all correlations between DCIR as a feature and capacity are above 0.818, indicating a negative correlation.

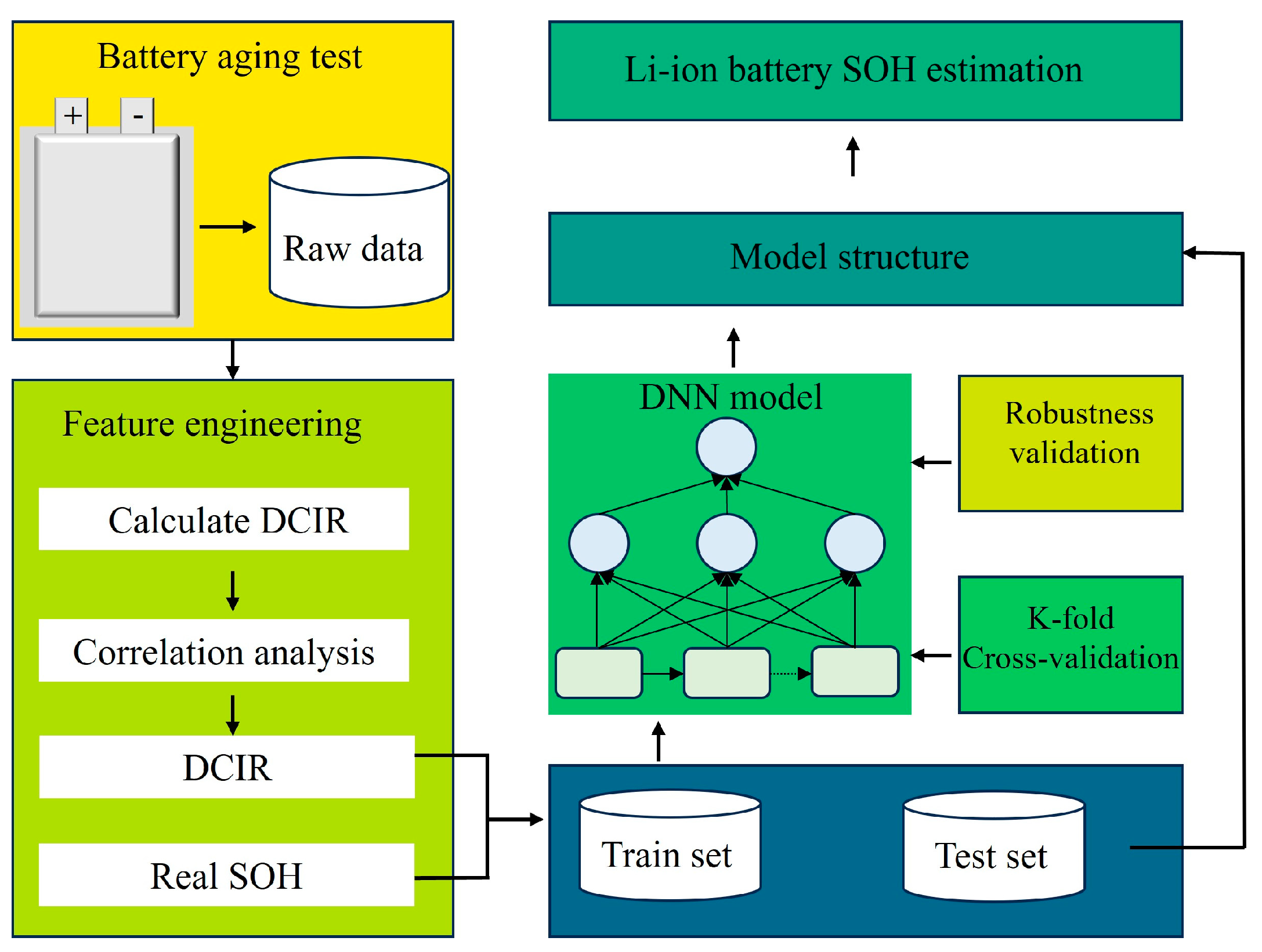
4. DNN-Based Model for Battery SOH Estimation

4.1. DNN Model Structure

The LSTM model’s gating mechanism is composed of an input gate, forget gate, and output gate, and the computation process is shown in Equation (4):
f t = σ ( W f h t − 1 , x t + b f ) i t = σ ( W i h t − 1 , x t + b i ) C i ¯ = tanh ( W c h t − 1 , x t + b c ) C t = f t ⊙ C t − 1 + i ⊙ C t ¯ o t = σ ( W o h t − 1 , x t + b o ) h t = O t ⊙ tanh ( C t )
where xt denotes the input vector; it, ft, and ot denote the input gate, forget gate, and output gate, respectively; Ct denotes the cell state; ht denotes the hidden layer; Wi, Wf, and Wo denote the weights of each gating unit, respectively; and bi, bf, and bo denote the deviations in each gating unit, respectively. σ denotes the Sigmoid activation function. In this study, based on the LSTM model, we design the DNN model structure, as shown in Figure 3. The LSTM layer is used to obtain hidden vectors, the ReLU activation function is used to introduce nonlinear factors to enhance the model’s ability to model in complex patterns, and the Linear layer is used to map the last layer of the model output to the target variable for SOH estimation.

4.2. Training of DNN

The model is initialized with the following hyperparameters selected for the trained DNN: the number of network layers of the LSTM model is set to 1, the number of hidden layers is set to 128, the minimum batch size is set to 1024, the initial learning rate is set to 0.0001, and the maximum epoch is set to 2000. By selecting the MSE loss function by back-propagation to calculate the error and weights of the training model and updating the network parameters, the error loss is calculated as shown in Equation (5):
loss = 1 N ∑ i = 1 N ( y i − y ' i ) 2
where yi denotes the real capacity value, y′i denotes the estimated capacity value, and N denotes the total number of training samples. In the experiment, based on the PyTorch framework used to build the model, NVIDIA GeForce RTX4060 GPUs are used to accelerate the model training, and Python 3.11.5 is used for processing and analyzing the data, which contains Pandas, Numpy, and Scikit-Learn.

5. Results and Discussion

5.1. Model Evaluation Metrics

To evaluate the performance of the model, the mean absolute error (MAE) and root mean square error (RMSE) are utilized as evaluation metrics in this study, as shown in Equation (6):
MAE = 1 N ∑ i = 1 N y i − y ' i × 100 % RMSE = 1 N ∑ i = 1 N ( y i − y ' i ) 2 × 100 %

5.2. K-Fold Cross-Validation

To comprehensively evaluate the accuracy of the DNN model proposed in this study for estimating battery capacity using the DCIR feature, we focus on seven cells from the B#1 dataset in this section. Employing K-fold cross-validation with K set to 7, we conducted experiments for model training and testing. During each cross-validation iteration, data from one of the seven cells were sequentially designated as the test set, while those from the remaining cells were utilized for model training. The training MSE loss curves are shown in Appendix A. This iterative process ensured that the DCIR features of all cells were evaluated for the models. Such results also made the DCIR feature more reliable in estimating battery capacity. Additionally, the results from each cross-validation experiment offered an independent assessment of the model’s performance, thereby contributing to a holistic understanding of its efficacy across diverse datasets.

5.2.1. Effects of Hyperparameter Settings on Estimation Performance

We investigated the effects of some crucial hyperparameters on the performance of battery SOH estimation, including the activation function and the size of hidden layers of the LSTM model. For the activation function, setting the size of hidden layers to 128, we compared the performance of the ReLU, Sigmoid, and LogSigmoid activation functions. For the hidden layers, we selected ReLU as the activation function and set the size of these layers to 32, 64, and 128 for performance comparison, respectively. The average MAE and RMSE of the experimental results are summarized in Table 3 and the estimated error metrics for each cell are shown in Appendix B (Table A1). In the comparison of activation functions, ReLU exhibits the lowest error metrics, so we prioritize this function when designing the DNN. In the comparison of the size of hidden layers, increasing this size reduces the estimation error of the model. This is because doing so improves the complexity of the model and enhances the model’s ability to understand the knowledge of the nonlinear degradation of the battery, which improves the estimation of the model.

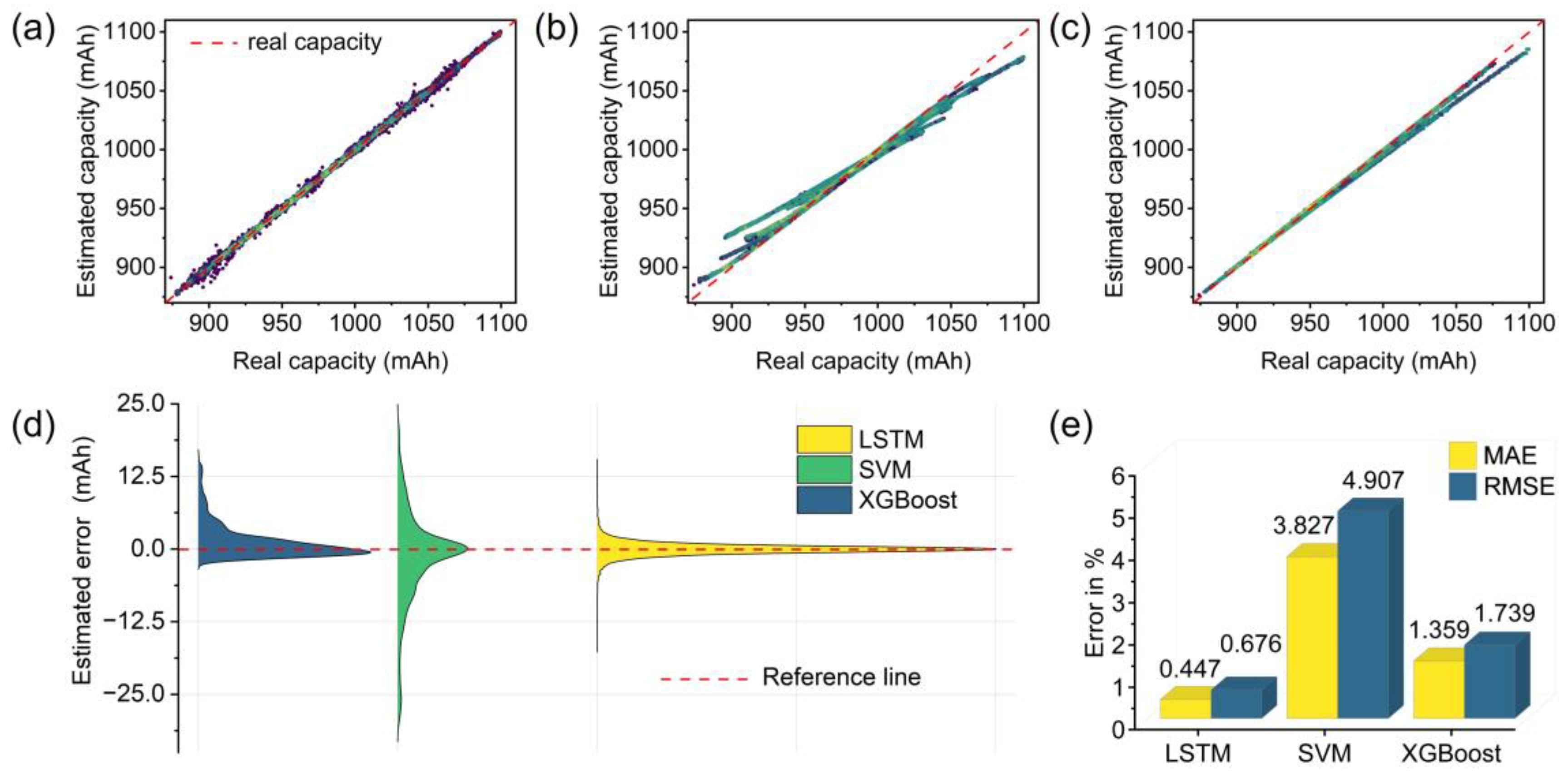
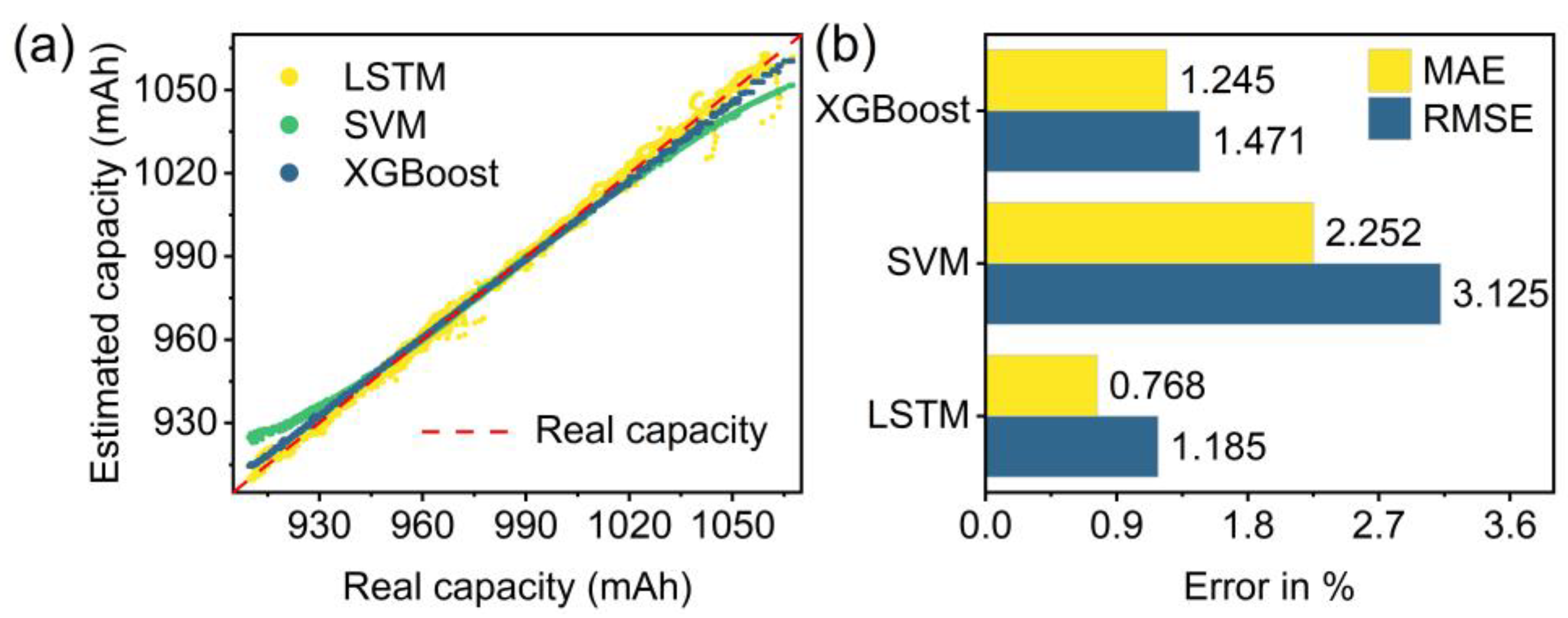
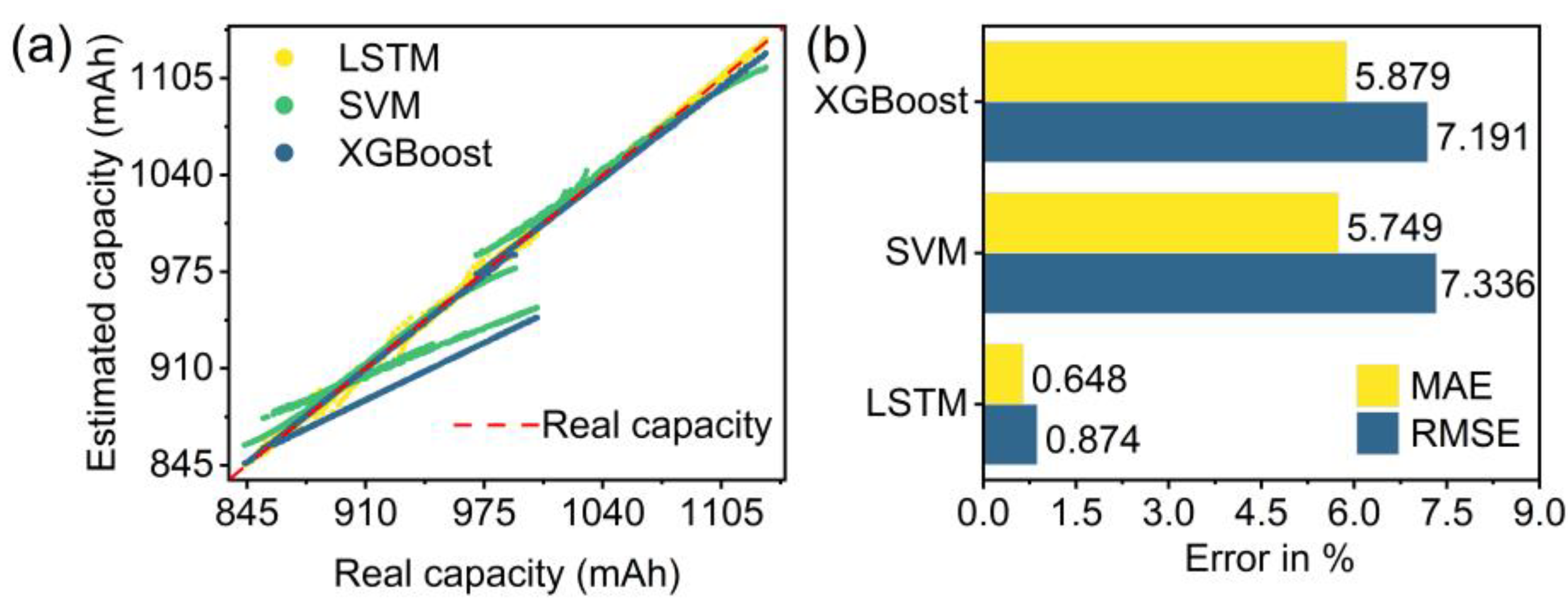
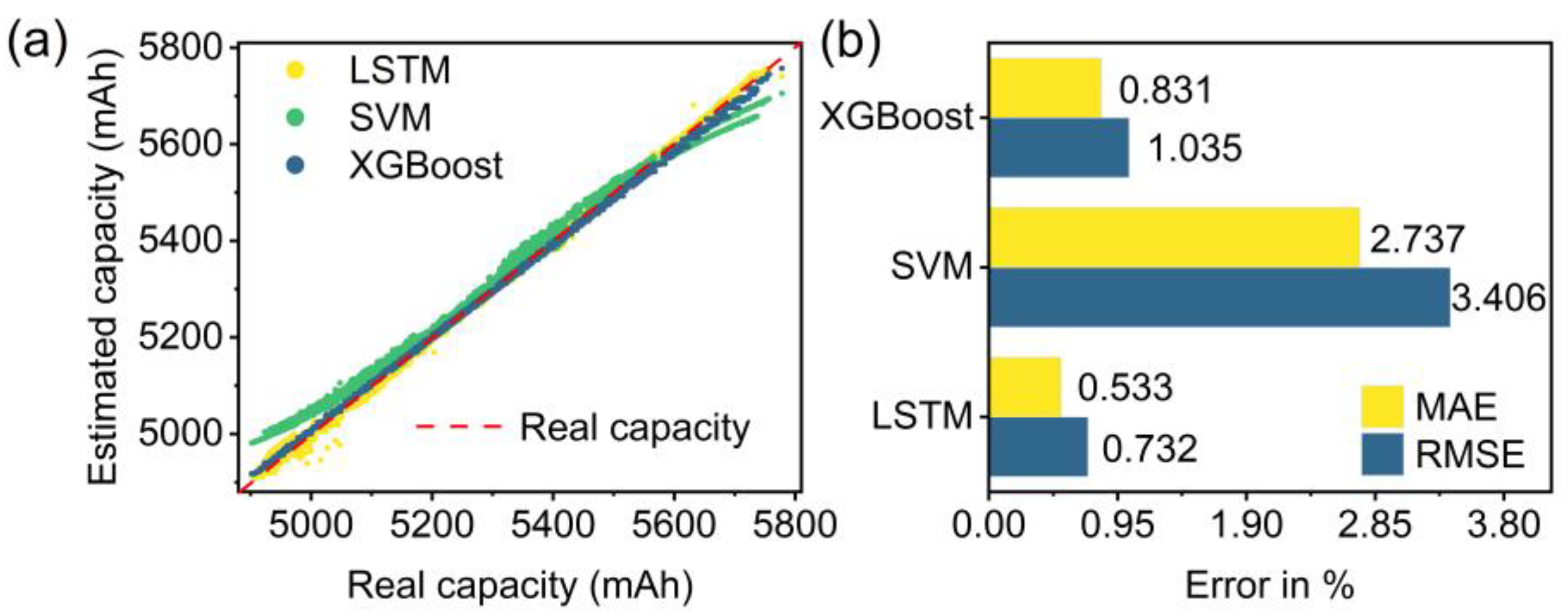
5.2.2. Comparison of DNN and Machine Learning Models

To validate the efficacy of the designed DNN model for estimating battery capacity, this study incorporated SVM and XGBoost models in machine learning for comparative analysis. The cross-validation results in Figure 4a demonstrate that the estimated capacity fits well with the real capacity. Contrasting the predictions of the SVM and XGBoost models (Figure 4b,c) reveals the LSTM model’s notable advantage in tracking capacity-fading trajectories. Despite variations in test schemes for each cell, the estimated capacity errors for each cycle predominantly cluster around the reference line (estimated capacity error equal to 0 mAh) (Figure 4d), with peaks closely aligned with the reference line compared to errors from the SVM and XGBoost models.
The average MAE and RMSE of the LSTM, SVM, and XGBoost estimation results are displayed in Figure 4e, and the estimated error metrics for each cell are shown in Appendix B (Table A2). The errors are only 0.447 and 0.676% using the LSTM model, while the errors are all higher than 1% and reach 4.907% using the machine learning model. These results indicate that the deep learning algorithm has a significant advantage compared to the traditional machine learning model in battery SOH estimation. The deep learning algorithm better adapts to the dynamic characteristics of the battery system through its flexible nonlinear modeling capability, which improves the accuracy and reliability of the battery SOH estimation.

5.3. Robustness Validation

The use of practical processes, operating temperature conditions, or charging and discharging mode changes will affect the rate of fade in LIB capacity. In addition, differences in battery manufacturing processes among manufacturers introduce variability in battery performance. These factors pose challenges to accurately estimating battery capacity using models. Hence, models intended for practical deployment require robust validation to ensure their reliability. This operation aims to evaluate the model’s generalization ability and stability when encountering different operating conditions, reflecting the model’s ability to process and adapt to different data distributions. In this study, we conducted experiments to validate the model’s robustness from three perspectives: the cross-temperature change condition, the cross-charge and -discharge mode, and the cross-manufacturing process.

5.3.1. Validation of Cross-Temperature Change Condition

It is imperative to assess the generalization ability and stability of the model under unknown operating temperature conditions in practical deployment. This evaluation reflects the model’s capacity to adapt to fluctuations in the rate of fade in capacity due to temperature variations. To this end, the model is trained in this study using the B#1 dataset of B#1-1, B#1-2, and B#1-3 cells tested at a constant temperature of 30 °C. In addition, the model is tested using the B#1 dataset of B#1-4 and B#1-6 cells tested at variable temperatures, where the model’s sensitivity to changes in operating temperatures is evaluated. The training MSE loss curves are shown in Appendix A (Figure A2a).
The results of the validation of the cross-temperature change condition, depicted in Figure 5a, demonstrate a strong fit between the estimated and actual capacities. In Figure 5b, the average MAE and RMSE of the LSTM, SVM, and XGBoost estimation results are presented, and the estimated error metrics for each cell are shown in Appendix B (Table A2). Compared with the machine learning models, the LSTM model can maintain high prediction precisions, even under varying operating temperature conditions, with lower error metrics, averaging 0.768% for the MAE and 1.185% for the RMSE. These results explained the robustness of the DNN model in adapting to data changes brought about by different operating temperatures.

5.3.2. Validation of Cross-Charge and -Discharge Modes

The generalization ability and stability of the model when subjected to charging and discharging mode changes need to be evaluated in practical deployment. This will reflect the ability of the model to continuously track changes in the rate of fade in capacity caused by changes in charging and discharging modes. To this end, this study trained the models using B#1-4, B#1-5, B#1-6, and B#1-7 cell data from the B#1 dataset and tested the models using B#2-1, B#2-2, and B#2-3 cell data from the B#2 dataset, where the model’s ability to cope with changes in charging and discharging modes was evaluated. The training MSE loss curves are shown in Appendix A (Figure A2b).
Figure 6a presents the results of the validation of cross-charge and -discharge modes. The experiment demonstrates that LSTM effectively tracks the capacity-fading trajectory when changed by the charging and discharging mode, and the estimated capacity fits well with the real capacity. However, machine learning models exhibit significant shortcomings in adapting to the battery capacity degradation trajectory. The average MAE and RMSE of the LSTM, SVM, and XGBoost estimation results are displayed in Figure 6b, and the estimated error metrics for each cell are shown in Appendix B (Table A2). Compared with the machine learning models, the LSTM model demonstrates superior performance with lower error metrics, averaging 0.648% for the MAE and 0.874% for the RMSE. These results demonstrate the robustness of the DNN model in adapting to different charging and discharging modes that cause changes in the capacity-fading trajectory.

5.3.3. Validation of Cross-Manufacturing Process

The generalization ability and stability of the model when subjected to changes in the manufacturing process of the battery need to be evaluated in practical deployment, which reflects the ability of the model to adapt to the changes in the capacity-fading trajectory. To this end, this study uses B#1-1, B#1-2, and B#2-1 cell data to train the models, and B#3-1 and B#3-2 cell data as test sets to evaluate the ability of the models to cope with changes in the battery manufacturing process. The training MSE loss curves are shown in Appendix A (Figure A2c).
The validation results of the cross-manufacturing process in Figure 7a demonstrate that the estimated capacity of the LSTM and XGBoost models fit well with the real capacity. The average MAE and RMSE of the LSTM, SVM, and XGBoost estimation results are displayed in Figure 7b, and the estimated error metrics for each cell are shown in Appendix B (Table A2). The LSTM and XGBoost models have high prediction precisions even when the battery manufacturing process is changed, with the LSTM model exhibiting the lowest error metrics. These results explain the robustness of DNN models in adapting to data variations caused by different manufacturing processes.

5.4. Comparison with Current Research Methods

The experimental results of this study were compared with those of other studies, as shown in Table 4. The deep learning-based algorithm proposed in this paper to estimate the battery SOH using the DCIR feature has lower error metrics. Compared with previous studies, our DNN model was robust enough to adapt to different application scenarios and to make accurate predictions of the battery SOH. In addition, compared with previous feature extraction, this study used the open-circuit voltage, polarization voltage, and pulse current based on Ohm’s law to obtain the DCIR feature during the battery cycling process, which is efficient and reliable.

5.5. Discussion and Outlook

The rapid advancement in artificial intelligence has significantly enhanced the diagnosis of the battery health state. Yet, traditional machine learning models often exhibit limited robustness in real-world applications. While the XGBoost model demonstrates high prediction accuracy during robust validation across manufacturing processes, its efficacy in estimating battery SOH diminishes under varied application scenarios. In this study, the proposed deep learning algorithm utilizes the DCIR feature to cultivate a resilient model. This model demonstrates consistent precision, even when applied to diverse scenarios.
Future work can enrich the developed framework through two avenues: First, by broadening the dataset and refining the structure of the DNN model to enhance its adaptability and practicality. Additionally, incorporating unsupervised learning and transfer learning methodologies can augment the deployability of the models. Secondly, given the existence of multiple aging mechanisms within batteries, inferring internal aging mechanisms based on measurable signals and integrating feature fusion can enhance the precision of battery health state diagnosis. This strategy facilitates the extension of models tailored for specific application scenarios to a broader spectrum of applications.

6. Conclusions

In this study, a DNN model approach is proposed and combined with the DCIR feature to evaluate the battery health state. Pearson correlation coefficients quantify the strong correlation between the increase in DCIR and the fade in battery capacity, providing a reliable basis for the DNN model to estimate the battery SOH. K-fold cross-validation methods are used for hyperparameter design and reliability validation to comprehensively evaluate the ability of DNN models to estimate the battery SOH. DNN models under optimal hyperparameters are used for comparison with traditional machine learning models to evaluate the advantages of DNN models in estimating the battery SOH. The experimental results show that the DNN model designed in this study has a significant advantage in tracking the trajectory of the fade in battery capacity, and even if the battery is under imbalanced usage conditions, the DNN model shows strong robustness in estimating the battery SOH. The main conclusions of this study are as follows:
We introduced a reliable DCIR feature for battery capacity estimation, which reaches a correlation metric of higher than 0.818 in any scenario.
We validated the DNN model for battery capacity estimation in specific scenarios, and its prediction accuracy can achieve an average MAE of 0.447% and RMSE of 0.676%.
We deployed the DNN model in unknown application scenarios, and its error metrics can maintain an average MAE of 0.768% and RMSE of 1.185%.
In summary, this study highlights the potential of DNN models combined with the DCIR feature in the evaluation of the battery health state. The proposed method provides a reliable solution for establishing a stable battery health management system.

Author Contributions

Conceptualization and Methodology, Z.S.; Validation, W.H.; Resources, X.H.; Writing—Original Draft Preparation, Z.S.; Writing—Review and Editing, J.W. and X.H.; Supervision, X.H. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Conflicts of Interest

The authors declare no conflicts of interest.

Appendix A

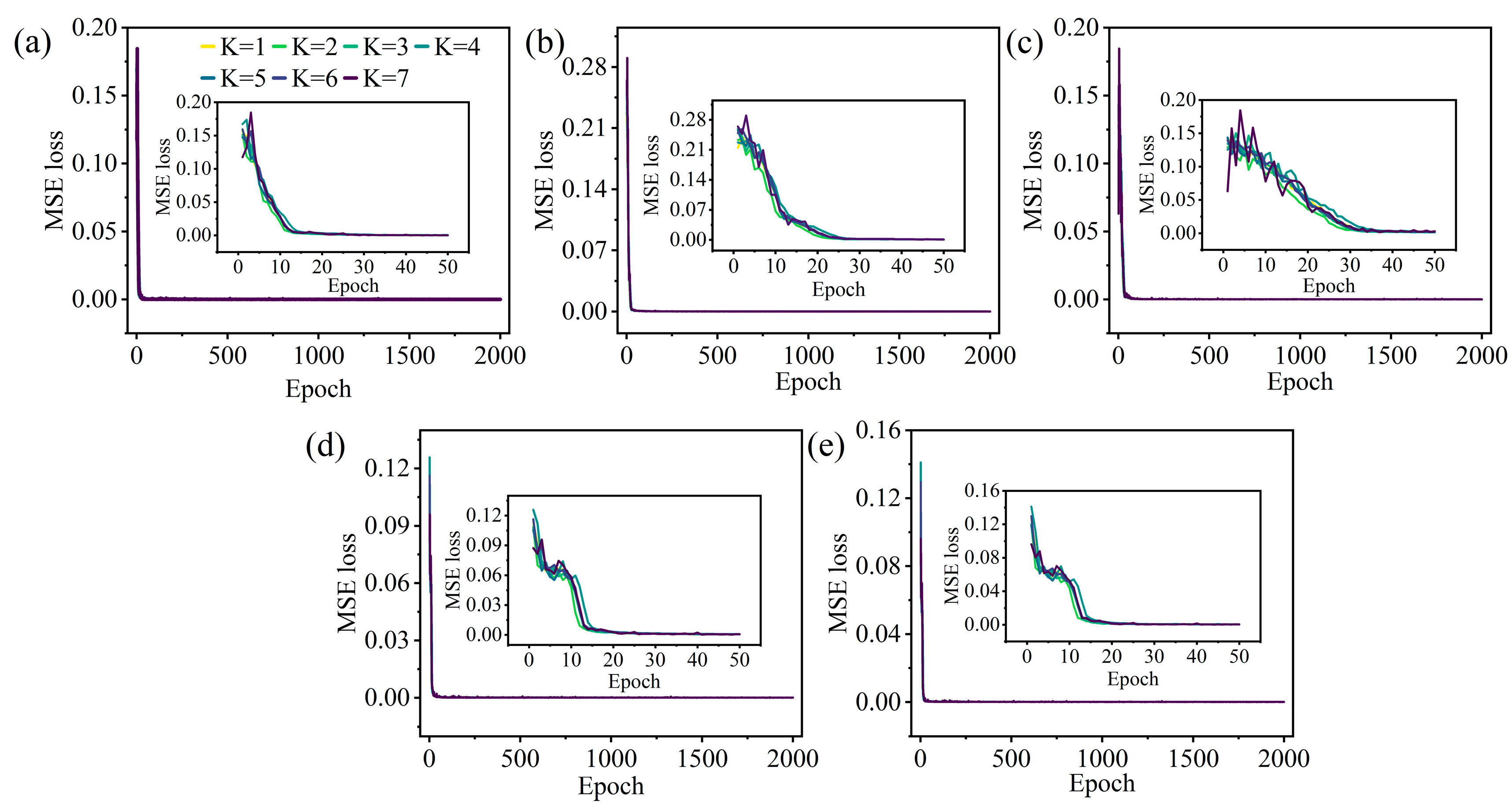
Energies 17 02487 g0a1
Figure A1. MSE loss in different hyperparametric designs. (a) ReLU activation function; hidden size is set to 128. (b) ReLU activation function; hidden size is set to 64. (c) ReLU activation function; hidden size is set to 32. (d) Sigmoid activation function. (e) LogSigmoid activation function.
Figure A1. MSE loss in different hyperparametric designs. (a) ReLU activation function; hidden size is set to 128. (b) ReLU activation function; hidden size is set to 64. (c) ReLU activation function; hidden size is set to 32. (d) Sigmoid activation function. (e) LogSigmoid activation function.
Energies 17 02487 g0a1
Energies 17 02487 g0a2
Figure A2. MSE loss for robustness validation. Validation of (a) cross-temperature change condition, (b) cross-charge and -discharge modes, and (c) cross-manufacturing process.
Figure A2. MSE loss for robustness validation. Validation of (a) cross-temperature change condition, (b) cross-charge and -discharge modes, and (c) cross-manufacturing process.
Energies 17 02487 g0a2

Appendix B

Table A1. MAE and RMSE for each cell of the experiment in Section 5.2.1.
Table A1. MAE and RMSE for each cell of the experiment in Section 5.2.1.
Test SetSigmoidLogSigmoid3264
MAEMAEMAERMSEMAERMSEMAERMSE
B#1-10.497%0.646%0.527%0.676%0.395%0.520%0.347%0.458%
B#1-20.524%0.674%0.404%0.502%0.382%0.489%0.309%0.448%
B#1-30.733%1.061%0.264%0.415%1.258%1.939%0.520%0.769%
B#1-40.486%0.710%0.474%0.687%0.429%0.636%0.380%0.577%
B#1-50.941%1.469%0.889%1.364%0.800%1.263%0.757%1.217%
B#1-60.836%1.202%0.695%1.007%0.521%0.799%0.582%0.865%
B#1-70.907%1.400%0.813%1.241%0.698%1.080%0.713%1.095%
Table A2. MAE and RMSE for each cell of the experiments in Section 5.2.2 and Section 5.3.
Table A2. MAE and RMSE for each cell of the experiments in Section 5.2.2 and Section 5.3.
Experimental SectionTest SetDNNSVMXGBoost
MAERMSEMAERMSEMAERMSE
5.2.2B#1-10.294%0.383%4.869%5.982%3.767%4.738%
B#1-20.264%0.386%2.797%3.837%0.831%1.085%
B#1-30.275%0.395%10.028%11.532%2.025%2.704%
B#1-40.416%0.617%2.149%3.169%0.612%0.747%
B#1-50.661%1.100%2.560%3.707%0.678%0.814%
B#1-60.521%0.789%1.995%2.818%0.598%0.700%
B#1-70.696%1.061%2.388%3.299%1.000%1.382%
5.3.1B#1-40.703%1.073%2.297%3.253%1.249%1.506%
B#1-60.833%1.295%2.207%2.996%1.241%1.437%
5.3.2B#2-10.385%0.506%3.674%4.475%1.602%2.062%
B#2-20.725%1.050%3.023%3.649%0.708%0.877%
B#2-30.835%1.066%10.549%13.883%15.327%18.633%
5.3.3B#3-10.484%0.623%3.098%3.640%0.642%0.777%
B#3-20.581%0.842%2.376%3.172%1.020%1.294%

References

  1. Bresser, D.; Hosoi, K.; Howell, D.; Li, H.; Zeisel, H.; Amine, K.; Passerini, S. Perspectives of Automotive Battery R&D in China, Germany, Japan, and the USA. J. Power Sources 2018, 382, 176–178. [Google Scholar]
  2. Stallard, J.C.; Wheatcroft, L.; Booth, S.G.; Boston, R.; Corr, S.A.; De Volder, M.F.L.; Inkson, B.J.; Fleck, N.A. Mechanical Properties of Cathode Materials for Lithium-Ion Batteries. Joule 2022, 6, 984–1007. [Google Scholar] [CrossRef]
  3. Bila, M.; Opathella, C.; Venkatesh, B. Grid Connected Performance of a Household Lithium-Ion Battery Energy Storage System. J. Energy Storage 2016, 6, 178–185. [Google Scholar] [CrossRef]
  4. Bharathraj, S.; Adiga, S.P.; Patil, R.S.; Mayya, K.S.; Song, T.; Sung, Y. An Efficient and Chemistry Independent Analysis to Quantify Resistive and Capacitive Loss Contributions to Battery Degradation. Sci. Rep. 2019, 9, 6576. [Google Scholar] [CrossRef] [PubMed]
  5. Zhang, Q.; White, R.E. Capacity Fade Analysis of a Lithium Ion Cell. J. Power Sources 2008, 179, 793–798. [Google Scholar] [CrossRef]
  6. Birkl, C.R.; Roberts, M.R.; McTurk, E.; Bruce, P.G.; Howey, D.A. Degradation Diagnostics for Lithium Ion Cells. J. Power Sources 2017, 341, 373–386. [Google Scholar] [CrossRef]
  7. Vatanparvar, K.; Al Faruque, M.A. Electric Vehicle Optimized Charge and Drive Management. ACM Trans. Des. Autom. Electron. Syst. 2017, 23, 25. [Google Scholar] [CrossRef]
  8. Amir, S.; Gulzar, M.; Tarar, M.O.; Naqvi, I.H.; Zaffar, N.A.; Pecht, M.G. Dynamic Equivalent Circuit Model to Estimate State-of-Health of Lithium-Ion Batteries. IEEE Access 2022, 10, 18279–18288. [Google Scholar] [CrossRef]
  9. Topan, P.A.; Ramadan, M.N.; Fathoni, G.; Cahyadi, A.I.; Wahyunggoro, O. State of Charge (SOC) and State of Health (SOH) Estimation on Lithium Polymer Battery via Kalman Filter. In Proceedings of the 2016 2nd International Conference on Science and Technology-Computer (ICST), Yogyakarta, Indonesia, 27–28 October 2016; pp. 93–96. [Google Scholar]
  10. Liu, B.; Tang, X.; Gao, F. Joint Estimation of Battery State-of-Charge and State-of-Health Based on a Simplified Pseudo-Two-Dimensional Model. Electrochim. Acta 2020, 344, 136098. [Google Scholar] [CrossRef]
  11. Ng, M.F.; Zhao, J.; Yan, Q.; Conduit, G.J.; Seh, Z.W. Predicting the State of Charge and Health of Batteries Using Data-Driven Machine Learning. Nat. Mach. Intell. 2020, 2, 161–170. [Google Scholar] [CrossRef]
  12. Li, Y.; Liu, K.; Foley, A.M.; Zülke, A.; Berecibar, M.; Nanini-Maury, E.; Van Mierlo, J.; Hoster, H.E. Data-Driven Health Estimation and Lifetime Prediction of Lithium-Ion Batteries: A Review. Renew. Sustain. Energy Rev. 2019, 113, 109254. [Google Scholar] [CrossRef]
  13. Yang, D.; Zhang, X.; Pan, R.; Wang, Y.; Chen, Z. A Novel Gaussian Process Regression Model for State-of-Health Estimation of Lithium-Ion Battery Using Charging Curve. J. Power Sources 2018, 384, 387–395. [Google Scholar] [CrossRef]
  14. Li, X.; Yuan, C.; Li, X.; Wang, Z. State of Health Estimation for Li-Ion Battery Using Incremental Capacity Analysis and Gaussian Process Regression. Energy 2020, 190, 116467. [Google Scholar] [CrossRef]
  15. Yu, J. State of Health Prediction of Lithium-Ion Batteries: Multiscale Logic Regression and Gaussian Process Regression Ensemble. Reliab. Eng. Syst. Saf. 2018, 174, 82–95. [Google Scholar] [CrossRef]
  16. Feng, X.; Weng, C.; He, X.; Han, X.; Lu, L.; Ren, D.; Ouyang, M. Online State-of-Health Estimation for Li-Ion Battery Using Partial Charging Segment Based on Support Vector Machine. IEEE Trans. Veh. Technol. 2019, 68, 8583–8592. [Google Scholar] [CrossRef]
  17. Patil, M.A.; Tagade, P.; Hariharan, K.S.; Kolake, S.M.; Song, T.; Yeo, T.; Doo, S. A Novel Multistage Support Vector Machine Based Approach for Li Ion Battery Remaining Useful Life Estimation. Appl. Energy 2015, 159, 285–297. [Google Scholar] [CrossRef]
  18. Yang, D.; Wang, Y.; Pan, R.; Chen, R.; Chen, Z. State-of-Health Estimation for the Lithium-Ion Battery Based on Support Vector Regression. Appl. Energy 2018, 227, 273–283. [Google Scholar] [CrossRef]
  19. Gao, M.; Bao, Z.; Zhu, C.; Jiang, J.; He, Z.; Dong, Z.; Song, Y. HFCM-LSTM: A Novel Hybrid Framework for State-of-Health Estimation of Lithium-Ion Battery. Energy Rep. 2023, 9, 2577–2590. [Google Scholar] [CrossRef]
  20. Van, C.N.; Quang, D.T. Estimation of SoH and Internal Resistances of Lithium Ion Battery Based on LSTM Network. Int. J. Electrochem. Sci. 2023, 18, 100166. [Google Scholar]
  21. Goh, H.H.; Lan, Z.; Zhang, D.; Dai, W.; Kurniawan, T.A.; Goh, K.C. Estimation of the State of Health (SOH) of Batteries Using Discrete Curvature Feature Extraction. J. Energy Storage 2022, 50, 104646. [Google Scholar] [CrossRef]
  22. Li, Y.; Tao, J. CNN and Transfer Learning Based Online SOH Estimation for Lithium-Ion Battery. In Proceedings of the 2020 Chinese Control and Decision Conference (CCDC), Hefei, China, 22–24 August 2020; pp. 5489–5494. [Google Scholar]
  23. Yang, N.; Song, Z.; Hofmann, H.; Sun, J. Robust State of Health Estimation of Lithium-Ion Batteries Using Convolutional Neural Network and Random Forest. J. Energy Storage 2022, 48, 103857. [Google Scholar] [CrossRef]
  24. Lee, G.; Kwon, D.; Lee, C. A Convolutional Neural Network Model for SOH Estimation of Li-Ion Batteries with Physical Interpretability. Mech. Syst. Signal Process. 2023, 188, 110004. [Google Scholar] [CrossRef]
  25. Zhang, Z.; Min, H.; Guo, H.; Yu, Y.; Sun, W.; Jiang, J.; Zhao, H. State of Health Estimation Method for Lithium-Ion Batteries Using Incremental Capacity and Long Short-Term Memory Network. J. Energy Storage 2023, 64, 107063. [Google Scholar] [CrossRef]
  26. He, J.; Bian, X.; Liu, L.; Wei, Z.; Yan, F. Comparative Study of Curve Determination Methods for Incremental Capacity Analysis and State of Health Estimation of Lithium-Ion Battery. J. Energy Storage 2020, 29, 101400. [Google Scholar] [CrossRef]
  27. Li, L.; Cui, W.; Hu, X.; Chen, Z. A State-of-Health Estimation Method of Lithium-Ion Batteries Using ICA and SVM. In Proceedings of the 2021 Global Reliability and Prognostics and Health Management (PHM-Nanjing), Nanjing, China, 15–17 October 2021; pp. 5–9. [Google Scholar]
  28. Wang, Q.; Ye, M.; Cai, X.; Sauer, D.U.; Li, W. Transferable Data-Driven Capacity Estimation for Lithium-Ion Batteries with Deep Learning: A Case Study from Laboratory to Field Applications. Appl. Energy 2023, 350, 121747. [Google Scholar] [CrossRef]
  29. Naha, A.; Han, S.; Agarwal, S.; Guha, A.; Khandelwal, A.; Tagade, P.; Hariharan, K.S.; Kolake, S.M.; Yoon, J.; Oh, B. An Incremental Voltage Difference Based Technique for Online State of Health Estimation of Li-Ion Batteries. Sci. Rep. 2020, 10, 9526. [Google Scholar] [CrossRef]
  30. Lu, J.; Xiong, R.; Tian, J.; Wang, C.; Sun, F. Deep Learning to Estimate Lithium-Ion Battery State of Health without Additional Degradation Experiments. Nat. Commun. 2023, 14, 2760. [Google Scholar] [CrossRef]
  31. Yang, J.; Xia, B.; Huang, W.; Fu, Y.; Mi, C. Online State-of-Health Estimation for Lithium-Ion Batteries Using Constant-Voltage Charging Current Analysis. Appl. Energy 2018, 212, 1589–1600. [Google Scholar] [CrossRef]
  32. Roman, D.; Saxena, S.; Robu, V.; Pecht, M.; Flynn, D. Machine Learning Pipeline for Battery State-of-Health Estimation. Nat. Mach. Intell. 2021, 3, 447–456. [Google Scholar] [CrossRef]
  33. Zhu, J.; Wang, Y.; Huang, Y.; Bhushan Gopaluni, R.; Cao, Y.; Heere, M.; Mühlbauer, M.J.; Mereacre, L.; Dai, H.; Liu, X.; et al. Data-Driven Capacity Estimation of Commercial Lithium-Ion Batteries from Voltage Relaxation. Nat. Commun. 2022, 13, 2261. [Google Scholar] [CrossRef]
  34. Jones, P.K.; Stimming, U.; Lee, A.A. Impedance-Based Forecasting of Lithium-Ion Battery Performance amid Uneven Usage. Nat. Commun. 2022, 13, 4806. [Google Scholar] [CrossRef]
  35. Liu, Y.; Wang, L.; Li, D.; Wang, K. State-of-Health Estimation of Lithium-Ion Batteries Based on Electrochemical Impedance Spectroscopy: A Review. Prot. Control Mod. Power Syst. 2023, 8, 1–17. [Google Scholar] [CrossRef]
  36. Jiang, B.; Zhu, J.; Wang, X.; Wei, X.; Shang, W.; Dai, H. A Comparative Study of Different Features Extracted from Electrochemical Impedance Spectroscopy in State of Health Estimation for Lithium-Ion Batteries. Appl. Energy 2022, 322, 119502. [Google Scholar] [CrossRef]
  37. Zhang, Y.; Tang, Q.; Zhang, Y.; Wang, J.; Stimming, U.; Lee, A.A. Identifying Degradation Patterns of Lithium Ion Batteries from Impedance Spectroscopy Using Machine Learning. Nat. Commun. 2020, 11, 1706. [Google Scholar] [CrossRef]
  38. Qin, Q.; Li, X.; Wang, Z.; Wang, J.; Yan, G.; Peng, W.; Guo, H. Experimental and Simulation Study of Direct Current Resistance Decomposition in Large Size Cylindrical Lithium-Ion Battery. Electrochim. Acta 2023, 465, 142947. [Google Scholar] [CrossRef]
  39. Ruan, H.; Sun, B.; Jiang, J.; Zhang, W.; He, X.; Su, X.; Bian, J.; Gao, W. A Modified-Electrochemical Impedance Spectroscopy-Based Multi-Time-Scale Fractional-Order Model for Lithium-Ion Batteries. Electrochim. Acta 2021, 394, 139066. [Google Scholar] [CrossRef]
  40. Nyman, A.; Zavalis, T.G.; Elger, R.; Behm, M.; Lindbergh, G. Analysis of the Polarization in a Li-Ion Battery Cell by Numerical Simulations. J. Electrochem. Soc. 2010, 157, A1236. [Google Scholar] [CrossRef]
  41. Zhao, H.; Chen, Z.; Shu, X.; Shen, J.; Lei, Z.; Zhang, Y. State of Health Estimation for Lithium-Ion Batteries Based on Hybrid Attention and Deep Learning. Reliab. Eng. Syst. Saf. 2023, 232, 109066. [Google Scholar] [CrossRef]
Energies 17 02487 g001
Figure 1. Schematic summary of this work.
Figure 1. Schematic summary of this work.
Energies 17 02487 g001
Energies 17 02487 g002
Figure 2. Feature analysis on cell B#2-1. (a) Voltage and current curves. (b) Discharge capacity and DCIR correlation.
Figure 2. Feature analysis on cell B#2-1. (a) Voltage and current curves. (b) Discharge capacity and DCIR correlation.
Energies 17 02487 g002
Energies 17 02487 g003
Figure 3. Schematic diagram of DNN model structure.
Figure 3. Schematic diagram of DNN model structure.
Energies 17 02487 g003
Energies 17 02487 g004
Figure 4. Results of K-fold cross-validation experiments. (a) LSTM-, (b) SVM-, (c) and XGBoost-estimated capacity and real capacity. (d) Estimated capacity and real capacity error (y-y′). (e) Average MAE and RMSE of 7 cells.
Figure 4. Results of K-fold cross-validation experiments. (a) LSTM-, (b) SVM-, (c) and XGBoost-estimated capacity and real capacity. (d) Estimated capacity and real capacity error (y-y′). (e) Average MAE and RMSE of 7 cells.
Energies 17 02487 g004
Energies 17 02487 g005
Figure 5. Results of robustness validation experiments under cross-temperature change conditions. (a) Estimated capacity and real capacity. (b) Average MAE and RMSE.
Figure 5. Results of robustness validation experiments under cross-temperature change conditions. (a) Estimated capacity and real capacity. (b) Average MAE and RMSE.
Energies 17 02487 g005
Energies 17 02487 g006
Figure 6. Results of robustness validation experiments under cross-charge and -discharge modes. (a) Estimated capacity and real capacity. (b) Average MAE and RMSE.
Figure 6. Results of robustness validation experiments under cross-charge and -discharge modes. (a) Estimated capacity and real capacity. (b) Average MAE and RMSE.
Energies 17 02487 g006
Energies 17 02487 g007
Figure 7. Results of robustness validation experiments under cross-manufacturing process conditions. (a) Estimated capacity and real capacity. (b) Average MAE and RMSE.
Figure 7. Results of robustness validation experiments under cross-manufacturing process conditions. (a) Estimated capacity and real capacity. (b) Average MAE and RMSE.
Energies 17 02487 g007
Table 1. Parameters and operating conditions for sample cells.
Table 1. Parameters and operating conditions for sample cells.
Cell
Name		Nominal Capacity (mAh)Current
Rate (C)		Cut-off
Voltage (V)		Cycling Temperature
B#1-110001/13.65/2.3030 °C
B#1-210001/13.65/2.3030 °C
B#1-310002/23.65/2.3030 °C
B#1-410001/13.65/2.30Room
B#1-510001/13.65/2.30Room
B#1-610002/23.65/2.30Room
B#1-710002/23.65/2.30Room
B#2-110000.5/0.53.65/2.30Room
B#2-210000.5 + 1/23.30 + 3.65/2.30Room
B#2-310004/43.65/2.30Room
B#3-160001/13.65/2.3030 °C
B#3-260000.5/0.53.65/2.30Room
Varying room temperature (21~39 °C), 1 C = 1000 mA for batteries with a nominal capacity of 1000 mAh, and 1 C = 6000 mA for batteries with a nominal capacity of 6000 mAh.
Table 2. DCIR and capacity correlation analysis.
Table 2. DCIR and capacity correlation analysis.
Cell NameρCell Nameρ
B#1-1−0.948B#1-2−0.992
B#1-3−0.818B#1-4−0.971
B#1-5−0.938B#1-6−0.933
B#1-7−0.865B#2-1−0.950
B#2-2−0.986B#2-3−0.832
B#3-1−0.969B#3-2−0.981
Table 3. Average MAE and RMSE for different hyperparameters.
Table 3. Average MAE and RMSE for different hyperparameters.
Activation FunctionHidden Size MAE RMSE
ReLU1280.447%0.676%
Sigmoid1280.703%1.023%
LogSigmoid1280.581%0.842%
ReLU640.515%0.776%
ReLU320.640%0.961%
Table 4. Comparison of errors for existing studies.
Table 4. Comparison of errors for existing studies.
MethodRefs.FeaturesData SourcesEstimation Error
HFCM-LSTM[19]HFCM extracts features from raw dataNASA
Oxford		RMSE < 2.3%
LSTM[25]ICANASAMAPE < 2%
ElasticNet
XGBoost
SVR		[33]Statistical featuresLaboratory experimentRMSE < 1.7%
GPR[36]EISLaboratory experimentMAE < 2.2%
CNN-LSTM-Attention[41]TemperatureOxford(MAE, RMSE) < 1.3%
DNN in this study DCIRLaboratory experimentMAE < 0.768%
RMSE < 1.185%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Sun, Z.; He, W.; Wang, J.; He, X. State of Health Estimation for Lithium-Ion Batteries with Deep Learning Approach and Direct Current Internal Resistance. Energies 2024, 17, 2487. https://doi.org/10.3390/en17112487

AMA Style

Sun Z, He W, Wang J, He X. State of Health Estimation for Lithium-Ion Batteries with Deep Learning Approach and Direct Current Internal Resistance. Energies. 2024; 17(11):2487. https://doi.org/10.3390/en17112487

Chicago/Turabian Style

Sun, Zhongxian, Weilin He, Junlei Wang, and Xin He. 2024. "State of Health Estimation for Lithium-Ion Batteries with Deep Learning Approach and Direct Current Internal Resistance" Energies 17, no. 11: 2487. https://doi.org/10.3390/en17112487

APA Style

Sun, Z., He, W., Wang, J., & He, X. (2024). State of Health Estimation for Lithium-Ion Batteries with Deep Learning Approach and Direct Current Internal Resistance. Energies, 17(11), 2487. https://doi.org/10.3390/en17112487

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop