Thermodynamic Comparison of the Steam Ejectors Integrated at Different Locations in Cogeneration Systems
Abstract
1. Introduction
2. System Description
2.1. Traditional Coal-Fired Cogeneration System (Basic System)
2.2. Cogeneration System Integrated with the Steam Ejector
3. Calculation Model and Evaluation Method
3.1. Calculation Model
3.2. Evaluation Method
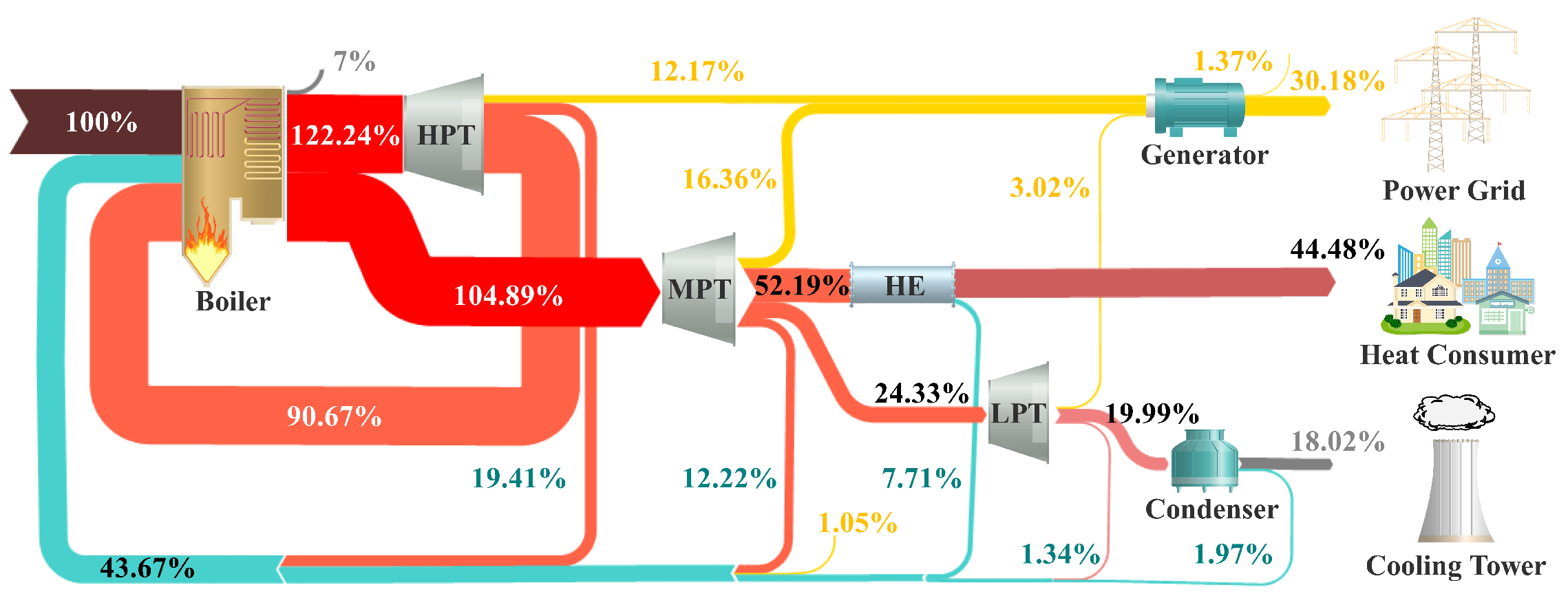
4. Result and Discussion
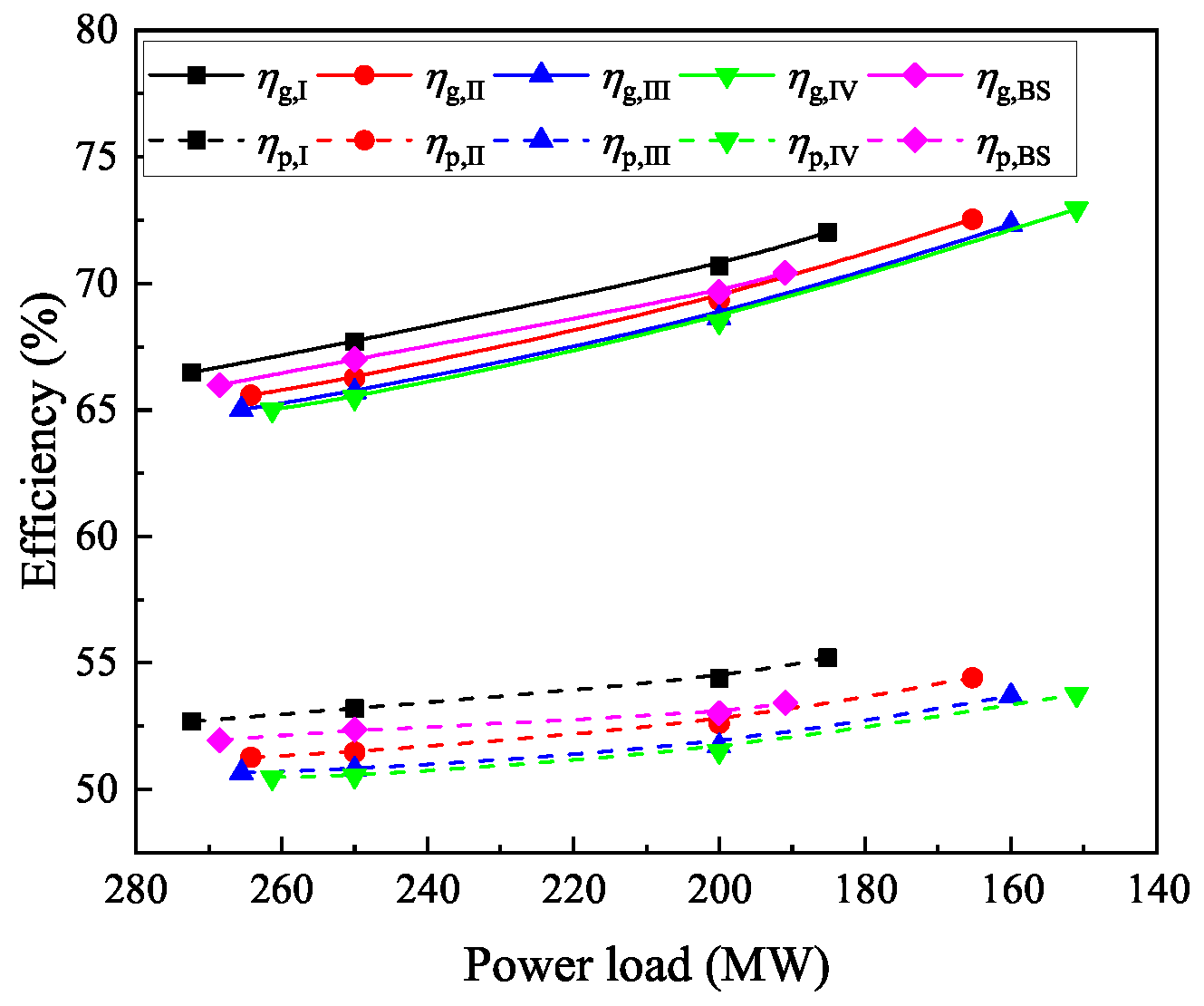
4.1. Thermodynamic Performance under the Design Condition
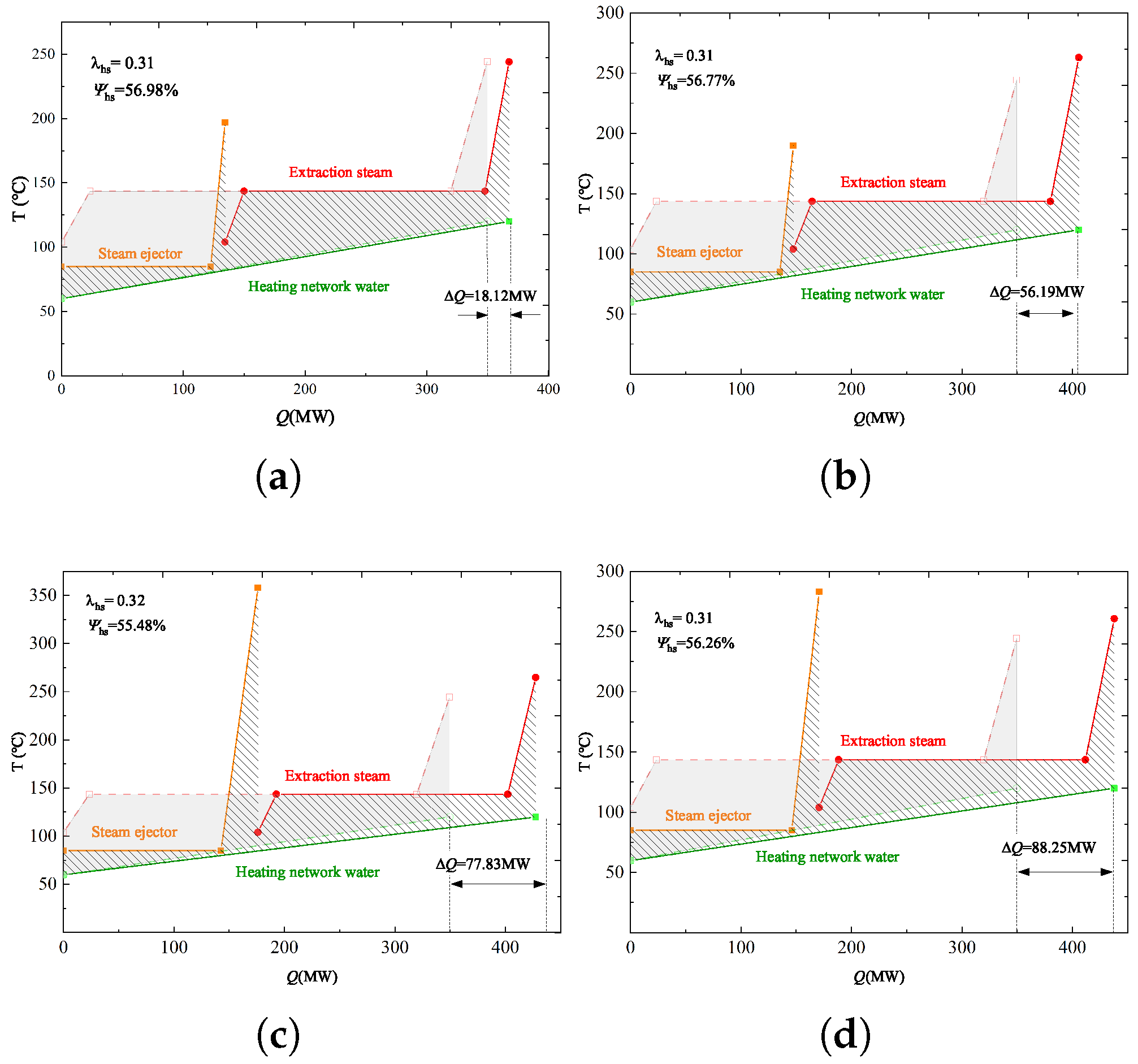
4.2. Heating Process Analysis under the Design Conditions
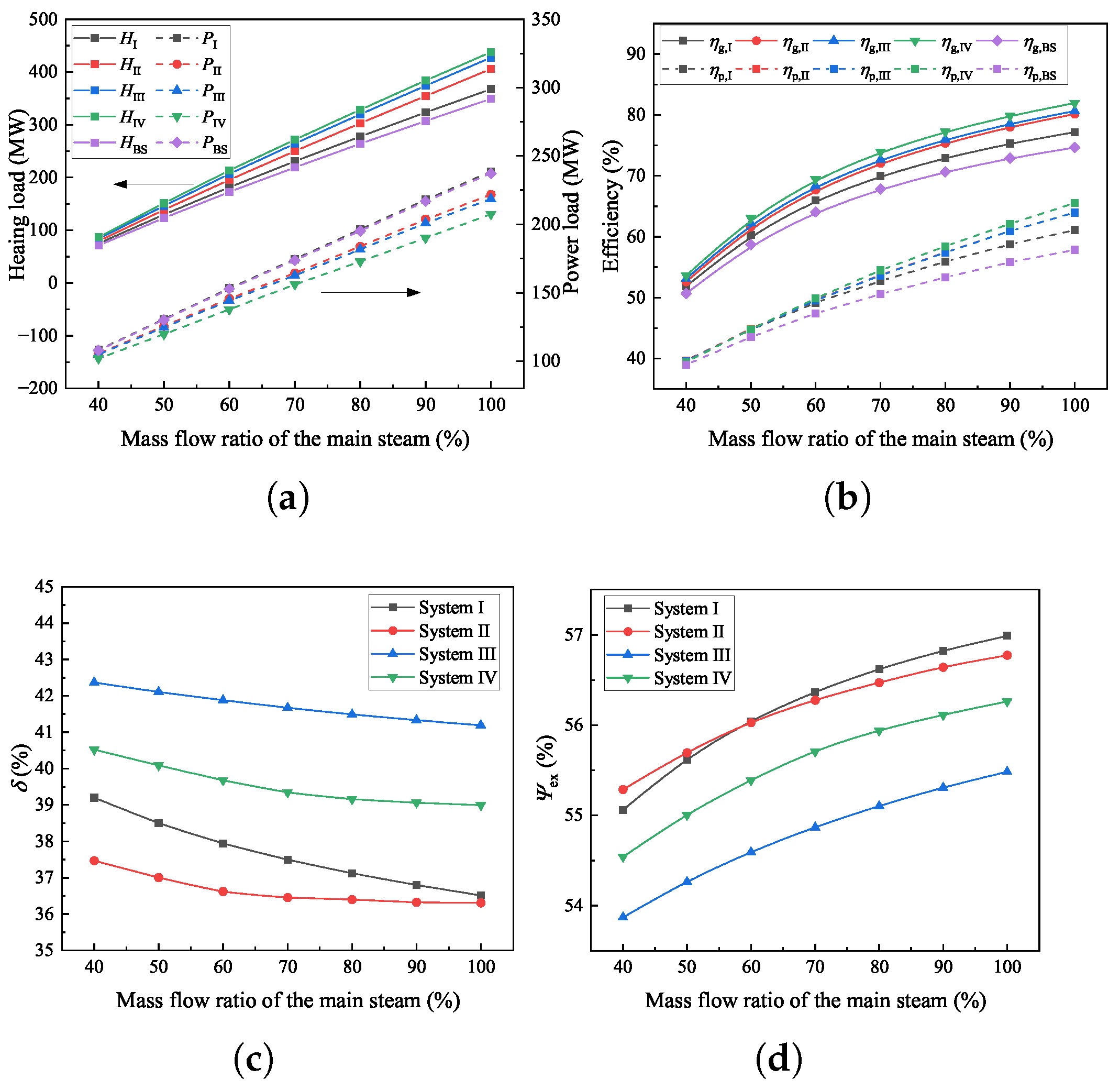
4.3. Thermodynamic and Operational Performance under the Off-Design Conditions
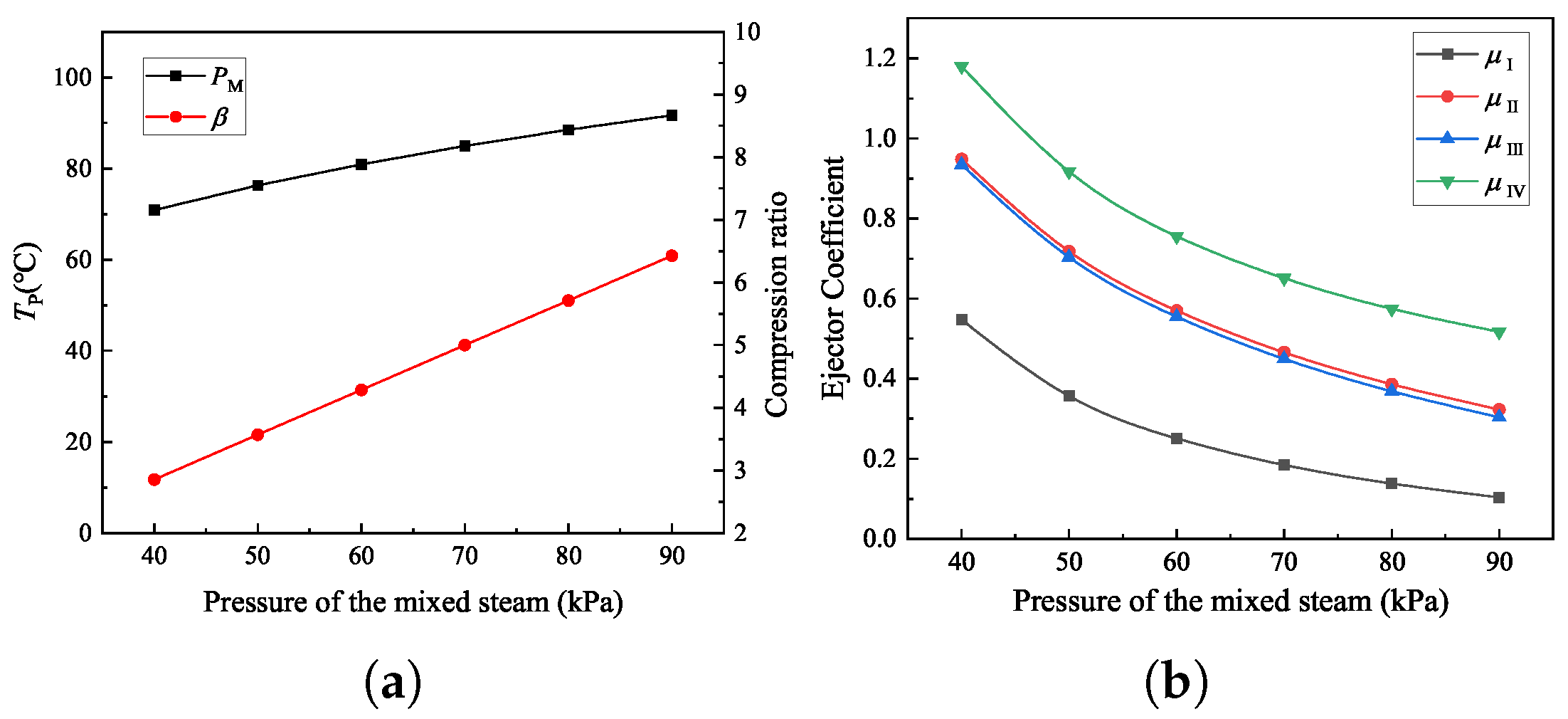
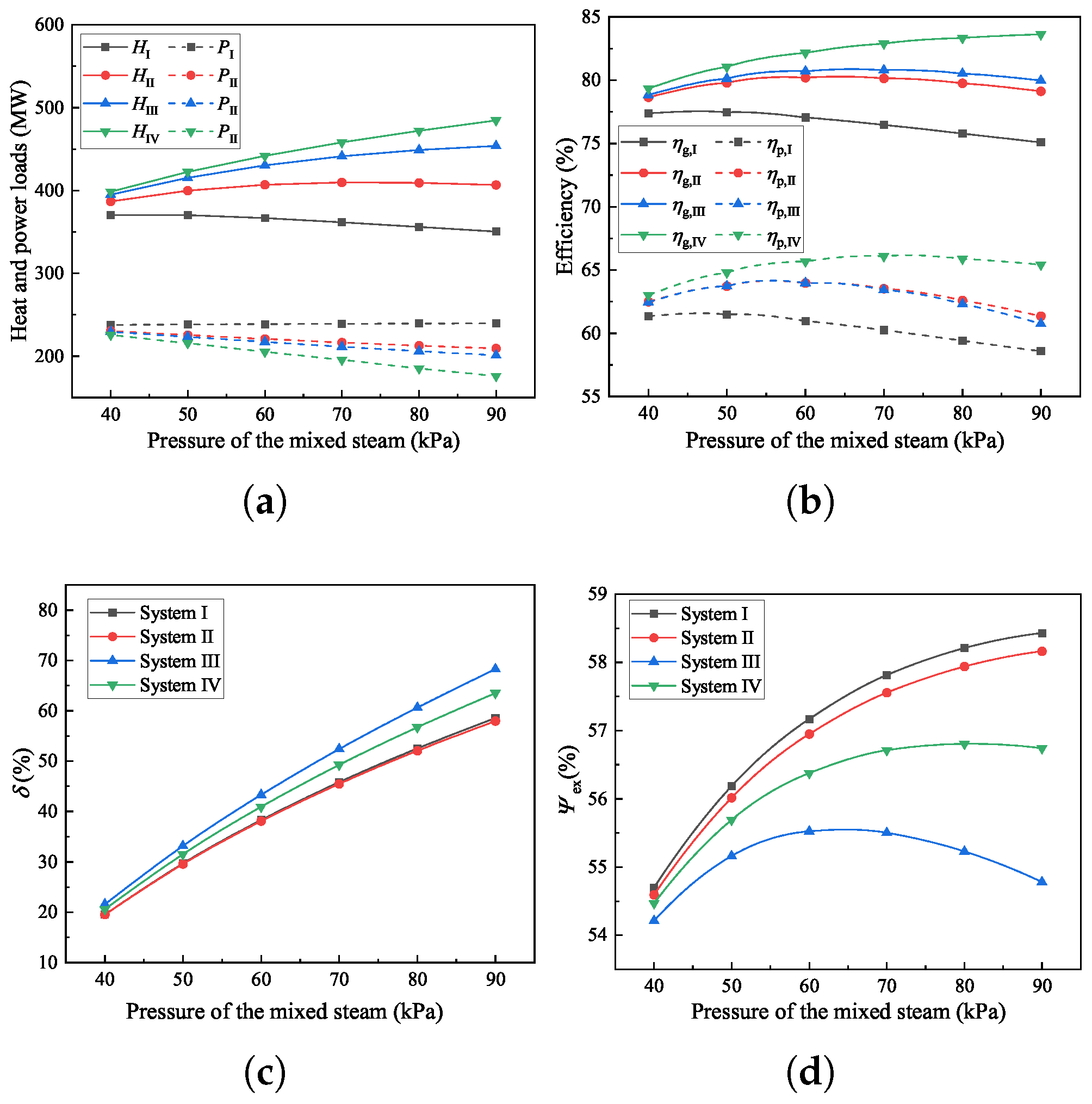
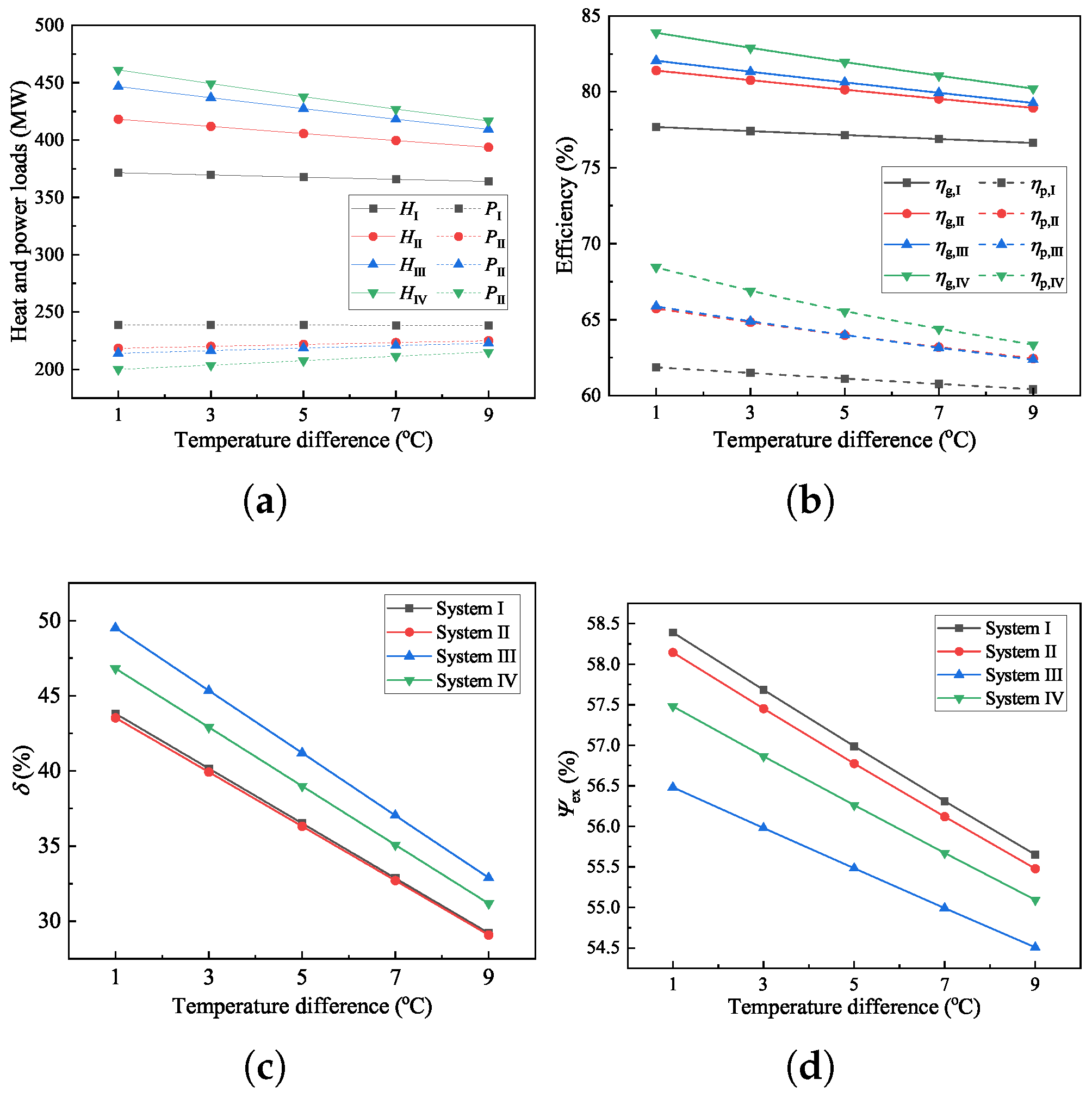
4.4. Sensitivity Analysis of the Heating Process
4.5. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AHP | Absorption heat pump |
| BS | Basic system |
| DH | District heating |
| EHP | Electric heat pump |
| HE | Heat exchanger |
| HPT | High-pressure turbine |
| LPT | Low-pressure turbine |
| MPT | Medium-pressure turbine |
| ORC | Organic Rankine cycle |
| RE | Relative error |
| RH | Regenerative heater |
| THA | Turbine heat acceptance |
| TMCR | Turbine maximum continuous rating |
References
- Lu, D.; Peng, Y.; Sun, J. Dual-Stage Optimization Scheduling Model for a Grid-Connected Renewable Energy System with Hybrid Energy Storage. Energies 2024, 17, 737. [Google Scholar] [CrossRef]
- Coal 2022: Analysis and Forecast to 2025; Technical Report; International Energy Agency: Paris, France, 2022.
- Adamo, A.; De La Hoz, J.; Martín, H.; Rubio, J.; Coronas, S. An Analysis of the Development of the Cogeneration Sector in Spain: A Comprehensive Review of the Period 1980–2020 from a Regulatory Perspective. Energies 2024, 17, 625. [Google Scholar] [CrossRef]
- Armoo, E.A.; Mohammed, M.; Narra, S.; Beguedou, E.; Agyenim, F.B.; Kemausuor, F. Achieving Techno-Economic Feasibility for Hybrid Renewable Energy Systems through the Production of Energy and Alternative Fuels. Energies 2024, 17, 735. [Google Scholar] [CrossRef]
- Wang, X.; Cui, C.; Pan, C.; Zhang, C.; Ren, H.; Ghias, A.M. A Deep Reinforcement Learning Control Strategy to Improve the Operating Flexibility of CHP Units under Variable Load Conditions. Therm. Sci. Eng. Prog. 2024, 49, 102482. [Google Scholar] [CrossRef]
- Neacșa, A.; Panait, M.; Mureșan, J.D.; Voica, M.C.; Manta, O. The Energy Transition between Desideratum and Challenge: Are Cogeneration and Trigeneration the Best Solution? Int. J. Environ. Res. Public Health 2022, 19, 3039. [Google Scholar] [CrossRef] [PubMed]
- Gu, Z.; He, S.; Li, X.; Sun, P.; Wu, J.; Hu, H.; Zhang, Q.; Jiang, J. Hundred-Watt Implantable TEG Module for Large-Scale Exhaust Gas Waste Heat Recovery. Energies 2024, 17, 665. [Google Scholar] [CrossRef]
- Park, H. Locational Role Analysis of Energy Storage Systems Based on Optimal Capacity Needs and Operations under High Penetration of Renewable Energy. Energies 2024, 17, 743. [Google Scholar] [CrossRef]
- Wang, J.; You, S.; Zong, Y.; Træholt, C.; Dong, Z.Y.; Zhou, Y. Flexibility of Combined Heat and Power Plants: A Review of Technologies and Operation Strategies. Appl. Energy 2019, 252, 113445. [Google Scholar] [CrossRef]
- Figaj, R. Energy and Economic Sustainability of a Small-Scale Hybrid Renewable Energy System Powered by Biogas, Solar Energy, and Wind. Energies 2024, 17, 706. [Google Scholar] [CrossRef]
- Yu, Y.X. Sodium/Potassium Intercalation on the Cu4S4 Nanosheet Accompanied by a Surface Phase Transition and Their Competition with Protons. ACS Appl. Energy Mater. 2023, 6, 10048–10060. [Google Scholar] [CrossRef]
- Sun, F.; Zhao, X.; Chen, X.; Fu, L.; Liu, L. New Configurations of District Heating System Based on Natural Gas and Deep Geothermal Energy for Higher Energy Efficiency in Northern China. Appl. Therm. Eng. 2019, 151, 439–450. [Google Scholar] [CrossRef]
- Amaris, C.; Miranda, B.; Balbis-Morejón, M. Experimental Thermal Performance and Modelling of a Waste Heat Recovery Unit in an Energy Cogeneration System. Therm. Sci. Eng. Prog. 2020, 20, 100684. [Google Scholar] [CrossRef]
- Giordano, L.; Benedetti, M. A Methodology for the Identification and Characterization of Low-Temperature Waste Heat Sources and Sinks in Industrial Processes: Application in the Italian Dairy Sector. Energies 2022, 15, 155. [Google Scholar] [CrossRef]
- Farshi, L.G.; Khalili, S. Thermoeconomic Analysis of a New Ejector Boosted Hybrid Heat Pump (EBHP) and Comparison with Three Conventional Types of Heat Pumps. Energy 2019, 170, 619–635. [Google Scholar] [CrossRef]
- Abdelkareem, M.A.; Maghrabie, H.M.; Sayed, E.T.; Kais, E.C.A.; Abo-Khalil, A.G.; Radi, M.A.; Baroutaji, A.; Olabi, A. Heat Pipe-Based Waste Heat Recovery Systems: Background and Applications. Therm. Sci. Eng. Prog. 2022, 29, 101221. [Google Scholar] [CrossRef]
- Nandhini, R.; Sivaprakash, B.; Rajamohan, N. Waste Heat Recovery at Low Temperature from Heat Pumps, Power Cycles and Integrated Systems—Review on System Performance and Environmental Perspectives. Sustain. Energy Technol. Assess. 2022, 52, 102214. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, Y.; Liu, X.; Duan, C. Energy and Exergy Analysis of a New Cogeneration System Based on an Organic Rankine Cycle and Absorption Heat Pump in the Coal-Fired Power Plant. Energy Conv. Manag. 2020, 223, 113293. [Google Scholar] [CrossRef]
- Zhao, S.; Wang, W.; Ge, Z. Thermodynamic, Operational, and Techno-Economic Analysis of the Cascade Heating System with a Double-Unit. Energy Conv. Manag. 2020, 226, 113558. [Google Scholar] [CrossRef]
- Chen, H.; Xiao, Y.; Xu, G.; Xu, J.; Yao, X.; Yang, Y. Energy-Saving Mechanism and Parametric Analysis of the High Back-Pressure Heating Process in a 300 MW Coal-Fired Combined Heat and Power Unit. Appl. Therm. Eng. 2019, 149, 829–840. [Google Scholar] [CrossRef]
- Chen, C.; Ge, Z.; Zhang, Y. Study of Combined Heat and Power Plant Integration with Thermal Energy Storage for Operational Flexibility. Appl. Therm. Eng. 2023, 219, 119537. [Google Scholar] [CrossRef]
- Wang, X.; Wu, Y.; Fu, L. Evaluation of Combined Heat and Power Plants with Electricity Regulation. Appl. Therm. Eng. 2023, 227, 120364. [Google Scholar] [CrossRef]
- Zhang, Y.; Ge, Z.; Yang, Y.; Hao, J.; Xu, L.; Du, X.; Træholt, C. Carbon Reduction and Flexibility Enhancement of the CHP-based Cascade Heating System with Integrated Electric Heat Pump. Energy Conv. Manag. 2023, 280, 116801. [Google Scholar] [CrossRef]
- Ahmed, F.; Chen, W. Investigation of Steam Ejector Parameters under Three Optimization Algorithm Using ANN. Appl. Therm. Eng. 2023, 225, 120205. [Google Scholar] [CrossRef]
- Paul, S.; Kumar, P.; Rao, S.M. Thermodynamic Analysis on the Effect of Supercritical CO2 Ejector in Cogeneration Cycle for Dairy Application. Therm. Sci. Eng. Prog. 2023, 39, 101729. [Google Scholar] [CrossRef]
- Siddiqui, M.A.; Khaliq, A.; Kumar, R. Proposal and Analysis of a Novel Cooling-Power Cogeneration System Driven by the Exhaust Gas Heat of HCCI Engine Fuelled by Wet-Ethanol. Energy 2021, 232, 120954. [Google Scholar] [CrossRef]
- Ifaei, P.; Safder, U.; Tayerani Charmchi, A.S.; Yoo, C. An Integrated Steam Jet Ejector Power Plant for Drought Adaptation Considering Water-Exergy Nexus in an Optimal Platform. Energy Conv. Manag. 2021, 227, 113622. [Google Scholar] [CrossRef]
- Pang, J.; Ge, Z.; Zhang, Y.; Du, X. Comparative Designs and Optimizations of the Steam Ejector for a CHP System. Appl. Therm. Eng. 2023, 226, 120345. [Google Scholar] [CrossRef]
- Liu, M.; Liu, M.; Wang, Y.; Chen, W.; Yan, J. Thermodynamic Optimization of Coal-Fired Combined Heat and Power (CHP) Systems Integrated with Steam Ejectors to Achieve Heat—Power Decoupling. Energy 2021, 229, 120707. [Google Scholar] [CrossRef]
- Chen, H.; Wang, Y.; Li, J.; Xu, G.; Lei, J.; Liu, T. Thermodynamic Analysis and Economic Assessment of an Improved Geothermal Power System Integrated with a Biomass-Fired Cogeneration Plant. Energy 2022, 240, 122477. [Google Scholar] [CrossRef]
- Cao, Y.; Dhahad, H.A.; Togun, H.; Haghghi, M.A.; Anqi, A.E.; Farouk, N.; Rosen, M.A. Seasonal Design and Multi-Objective Optimization of a Novel Biogas-Fueled Cogeneration Application. Int. J. Hydrogen Energy 2021, 46, 21822–21843. [Google Scholar] [CrossRef]
- Fazeli, A.; Zandi, S.; Golbaten Mofrad, K.; Salehi, G.; Khoshgoftar Manesh, M.H.; Shirmohammadi, R. Comparative Thermoeconomic Optimization and Exergoenvironmental Analysis of an Ejector Refrigeration Cycle Integrated with a Cogeneration System Utilizing Waste Exhaust Heat Recovery. Environ. Prog. Sustain. Energy 2022, 41, e13875. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiong, N.; Ge, Z.; Zhang, Y.; Hao, J.; Yang, Z. A Novel Cascade Heating System for Waste Heat Recovery in the Combined Heat and Power Plant Integrating with the Steam Jet Pump. Appl. Energy 2020, 278, 115690. [Google Scholar] [CrossRef]
- Liu, M.; Liu, M.; Chen, W.; Yan, J. Operational Flexibility and Operation Optimization of CHP Units Supplying Electricity and Two-Pressure Steam. Energy 2023, 263, 125988. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, S.; Ahmed, F.; Fan, J.; Chong, D.; Yan, J. Simulation Investigation on Performance of a Power—Water Cogeneration System Coupled with a Two-Stage Thermal Vapor Compressor. Case Stud. Therm. Eng. 2021, 28, 101435. [Google Scholar] [CrossRef]
- Tan, Z.; Feng, X.; Wang, Y. Performance Comparison of Different Heat Pumps in Low-Temperature Waste Heat Recovery. Renew. Sustain. Energy Rev. 2021, 152, 111634. [Google Scholar] [CrossRef]
- Zhao, S.; Ge, Z.; Sun, J.; Ding, Y.; Yang, Y. Comparative Study of Flexibility Enhancement Technologies for the Coal-Fired Combined Heat and Power Plant. Energy Conv. Manag. 2019, 184, 15–23. [Google Scholar] [CrossRef]
- Li, Y.; An, H.; Li, W.; Zhang, S.; Jia, X.; Fu, L. Thermodynamic, Energy Consumption and Economic Analyses of the Novel Cogeneration Heating System Based on Condensed Waste Heat Recovery. Energy Conv. Manag. 2018, 177, 671–681. [Google Scholar] [CrossRef]
- Ma, J.; Wu, Y.; Chen, X. A New Integration Scheme for CO2 Capture in Low-Rank Coal Fired Power Plants with Energy Savings. Appl. Therm. Eng. 2023, 228, 120476. [Google Scholar] [CrossRef]
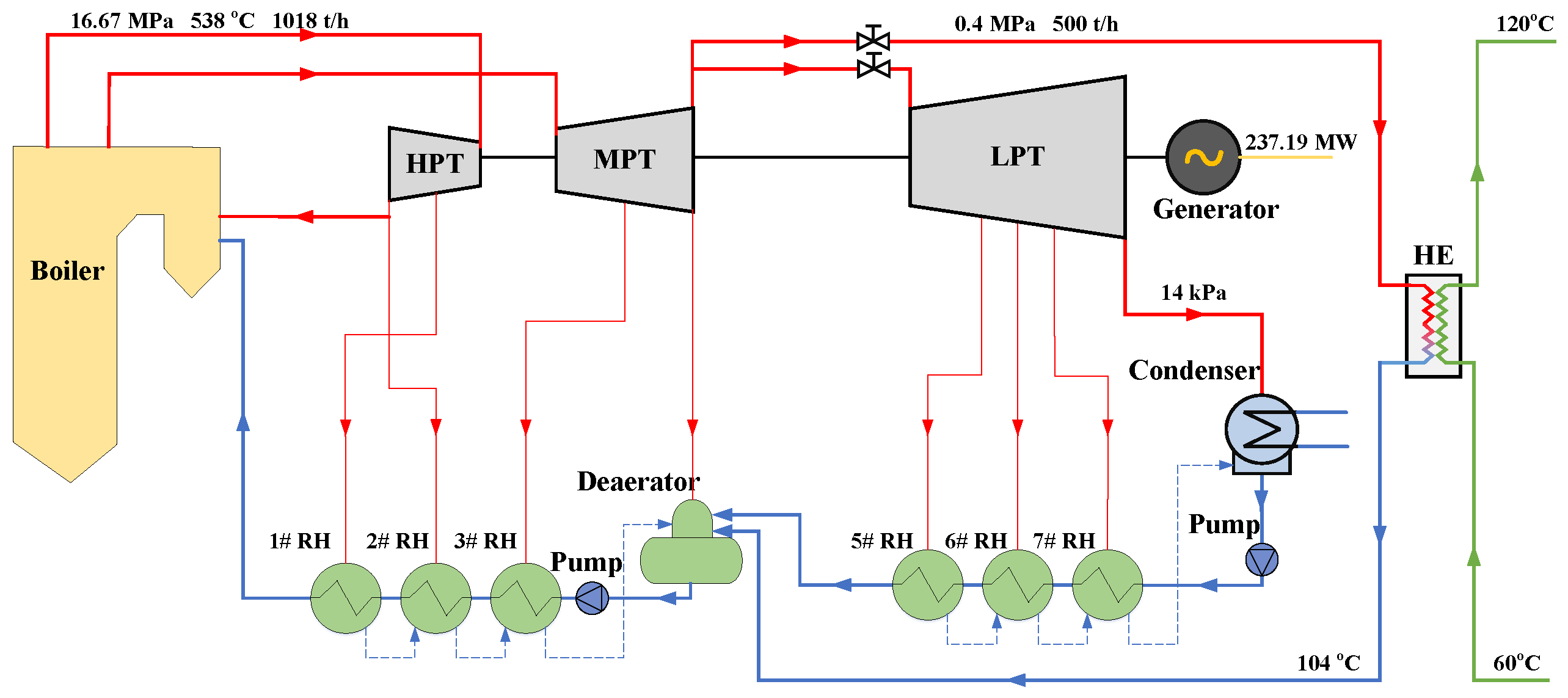
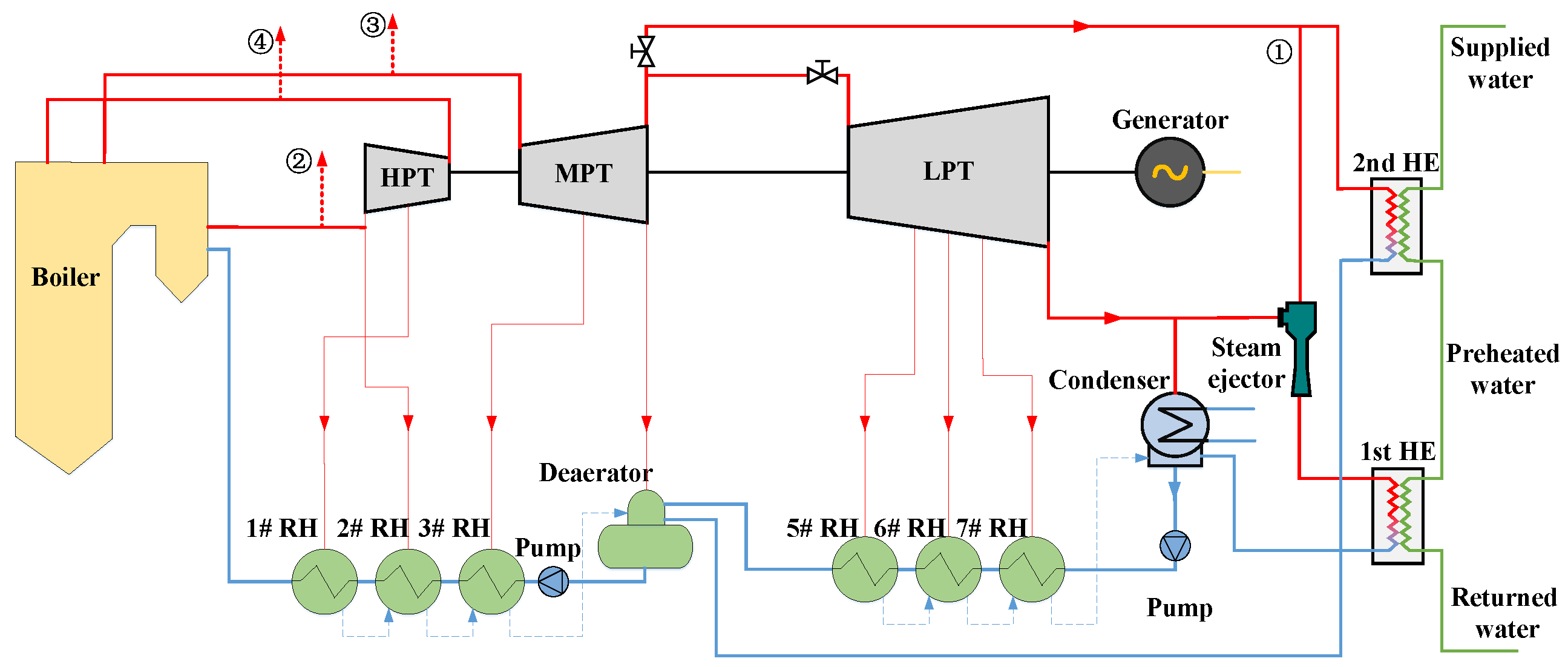


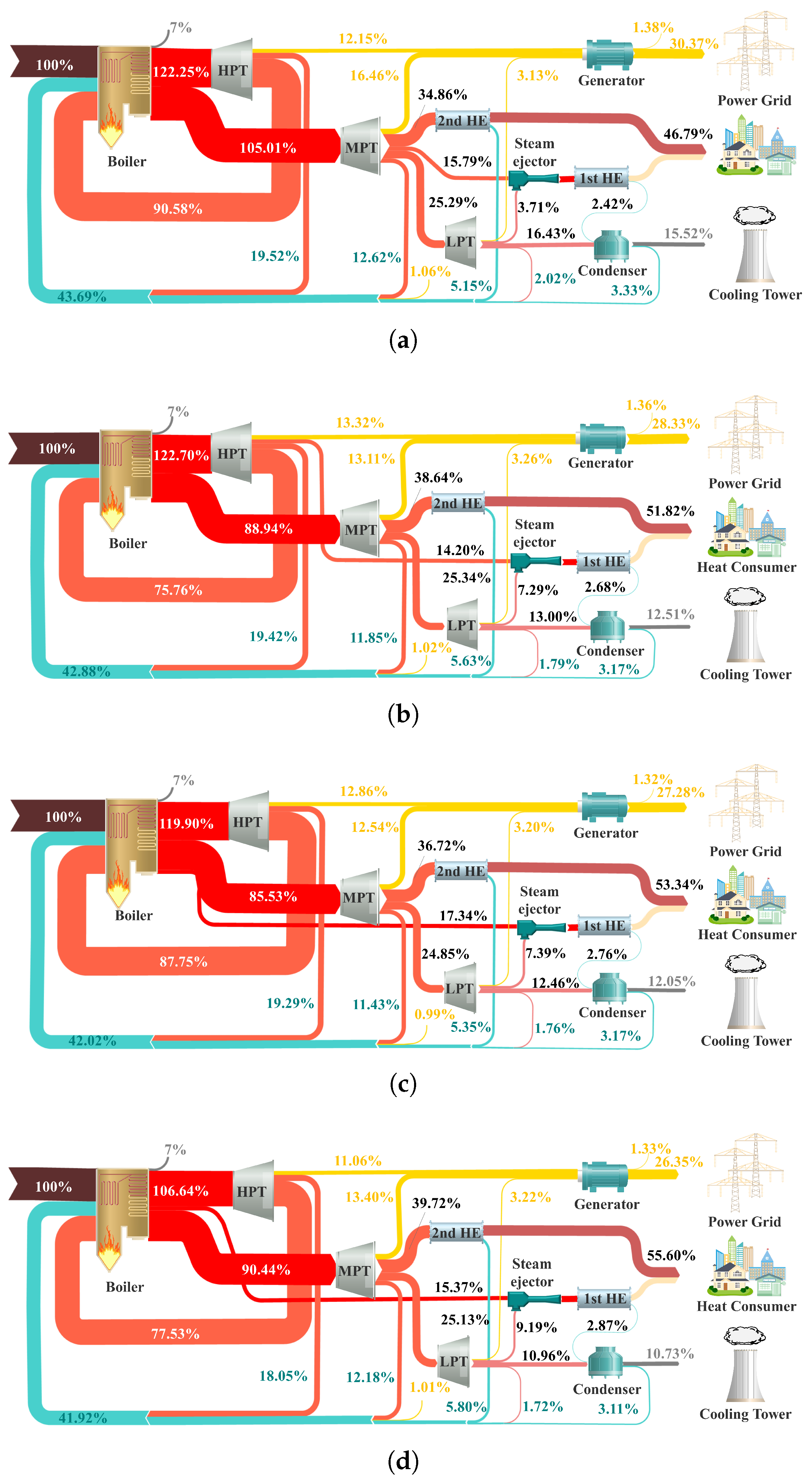
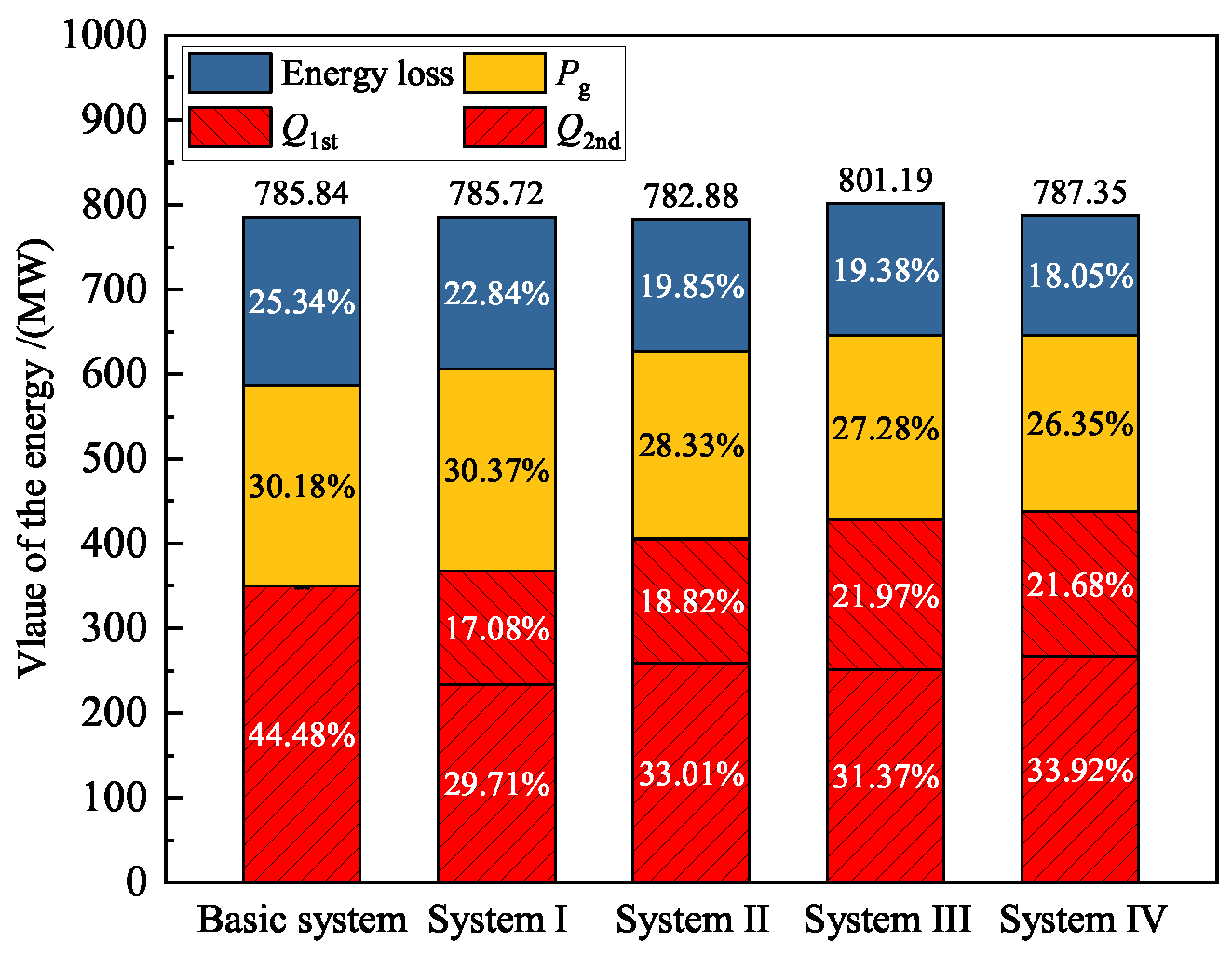
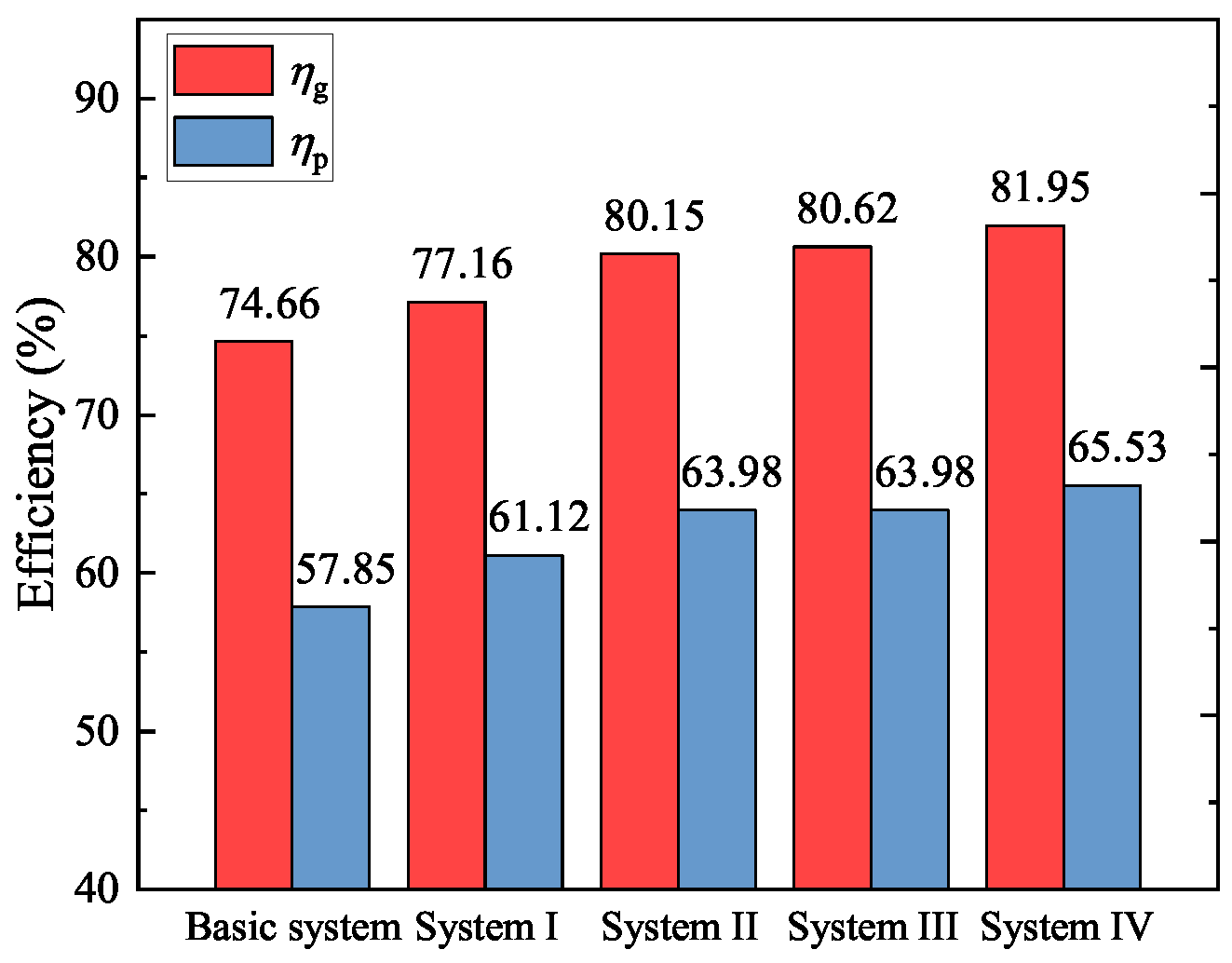

| Items | Unit | TMCR | Maximum Heating (Design) |
|---|---|---|---|
| Main steam | |||
| Mass flow rate | t/h | 1017.92 | 1017.92 |
| Pressure | MPa | 16.67 | 16.67 |
| Temperature | °C | 538 | 538 |
| Reheated steam | |||
| Mass flow rate | t/h | 847.02 | 839.05 |
| Pressure | MPa | 3.58 | 3.48 |
| Temperature | °C | 538 | 538 |
| Extraction steam for heating | |||
| Mass flow rate | t/h | – | 500 |
| Pressure | MPa | – | 0.4 |
| Steam temperature | °C | – | 244.28 |
| Drain water temperature | °C | – | 104 |
| Heat load | MW | – | 428.97 |
| Power load | MW | 322 | 245.47 |
| Net power load | MW | 313.42 | 237.19 |
| Energy input | MW | 797.42 | 797.42 |
| Back pressure | kPa | 14 | 14 |
| Items | Unit | RH1 | RH2 | RH3 | Deaerator | RH5 | RH6 | RH7 |
|---|---|---|---|---|---|---|---|---|
| Pressure | MPa | 6.20 | 3.98 | 1.90 | 1.03 | 0.63 | 0.26 | 0.089 |
| Temperature | °C | 390.4 | 332.6 | 442.7 | 355.9 | 294.5 | – | – |
| Enthalpy | kJ/kg | 3151.5 | 3051.3 | 3343.3 | 3170.5 | 3049.9 | 2868.2 | 2677.8 |
| Mass flow | t/h | 69.41 | 60.00 | 33.66 | 29.60 | 43.69 | 41.50 | 47.60 |
| Items | Basic System | System 1 | System 2 | System 3 | System 4 |
|---|---|---|---|---|---|
| 0.246 | 0.245 | 0.275 | 0.260 | ||
| 0.348 | 0.348 | 0.350 | 0.350 | 0.350 | |
| 0.348 | 0.311 | 0.312 | 0.319 | 0.315 | |
| 0.177 | 0.177 | 0.177 | 0.177 | 0.177 | |
| 50.88% | 56.98% | 56.77% | 55.48% | 56.26% |
| Items | Unit | System 1 | System 2 | System 3 | System 4 |
|---|---|---|---|---|---|
| Extraction steam | MW | 124.09 | 111.20 | 138.92 | 120.98 |
| Exhaust steam | MW | 29.16 | 57.07 | 59.20 | 72.34 |
| Return water | MW | 18.99 | 20.96 | 22.06 | 22.62 |
| Compression ratio () | % | 4.13 | 4.13 | 4.13 | 4.13 |
| Expansion ratio () | % | 28.57 | 234.40 | 207.95 | 1190.71 |
| Ejector coefficient () | % | 0.27 | 0.60 | 0.58 | 0.78 |
| % | 36.51% | 36.31% | 41.19% | 38.99% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, S.; Wang, C.; Duan, F.; Tian, Z. Thermodynamic Comparison of the Steam Ejectors Integrated at Different Locations in Cogeneration Systems. Energies 2024, 17, 2463. https://doi.org/10.3390/en17112463
Zhao S, Wang C, Duan F, Tian Z. Thermodynamic Comparison of the Steam Ejectors Integrated at Different Locations in Cogeneration Systems. Energies. 2024; 17(11):2463. https://doi.org/10.3390/en17112463
Chicago/Turabian StyleZhao, Shifei, Chunlan Wang, Fan Duan, and Ze Tian. 2024. "Thermodynamic Comparison of the Steam Ejectors Integrated at Different Locations in Cogeneration Systems" Energies 17, no. 11: 2463. https://doi.org/10.3390/en17112463
APA StyleZhao, S., Wang, C., Duan, F., & Tian, Z. (2024). Thermodynamic Comparison of the Steam Ejectors Integrated at Different Locations in Cogeneration Systems. Energies, 17(11), 2463. https://doi.org/10.3390/en17112463






