Abstract
Partial discharge (PD) is a crucial and intricate electrical occurrence observed in various types of electrical equipment. Identifying and characterizing PDs is essential for upholding the integrity and reliability of electrical assets. This paper proposes an ensemble methodology aiming to strike a balance between the model complexity and the predictive performance in PD pattern recognition. A simple convolutional neural network (SCNN) was constructed to efficiently decrease the model parameters (quantities). A quadratic support vector machine (QSVM) was established and ensembled with the SCNN model to effectively improve the PD recognition accuracy. The input for QSVM consisted of the circular local binary pattern (CLBP) extracted from the enhanced image. A testing prototype with three types of PD was constructed and 3D phase-resolved pulse sequence (PRPS) spectrograms were measured and recorded by ultra-high frequency (UHF) sensors. The proposed methodology was compared with three existing lightweight CNNs. The experiment results from the collected dataset emphasize the benefits of the proposed method, showcasing its advantages in high recognition accuracy and relatively few mode parameters, thereby rendering it more suitable for PD pattern recognition on resource-constrained devices.
1. Introduction
Partial discharge (PD), characterized by localized and transient discharges that typically occur at defects within insulation systems, is a critical and intricate electrical phenomenon in various types of electrical equipment. PD does not completely bridge the insulation between conductors [1]; instead, it represents a localized flashover within an insulation system due to a large localized electric field being greater than the dielectric withstand capability while the overall insulation system remains capable of withstanding the applied electrical field. PD is diverse in both form and location. It can transpire in various electrical equipment, including transformers, generators, insulators, cables, and switchgear. The occurrence of PD in these systems can be ascribed to uneven electric field distributions, material imperfections, or operational stresses, leading to the generation of various signals, including lights, heats, smells, sounds, electromagnetic waves, and high-frequency electric currents.
Detecting and characterizing PD is paramount in maintaining the integrity and reliability of electrical assets. PD measurements are used to evaluate the safety condition of insulation systems, enabling the identification of potential defects and facilitating proactive maintenance. There are several techniques for detecting PD in electrical systems. Ultrasonic detection involves capturing the ultrasonic noise emitted by PD using sensitive sensors, providing insights into the discharge localization and severity. Electromagnetic interference (EMI) detection monitors electromagnetic signals to locate areas of partial discharge activity. Acoustic emission detection focuses on capturing and analyzing the acoustic signals produced by PD, offering valuable information about discharge characteristics. High-frequency current transient measurements are effective in assessing insulation conditions and identifying potential failure points. Dissolved gas analysis (DGA) involves monitoring and analyzing the composition of gasses dissolved in insulating oil, providing indications of PD and potential insulation degradations. Electric field measurements detect anomalies and areas of increased field intensity, serving as an indicator of partial discharge activity. In engineering applications, the original measured data are processed to extract the statistical feature parameters and generate the phase-resolved partial discharge (PRPD) patterns [2]. Subsequently, PD pattern recognition is carried out based on these processed data. PD pattern recognition involves the identification and analysis of the characteristic electromagnetic, acoustic, and ultrasonic signals to distinguish the type of PD activity based on its unique pattern feature. By utilizing advanced signal processing techniques and machine learning algorithms, PD pattern recognition enables the classification of partial discharge sources within high-voltage equipment. Consequently, PD pattern recognition plays a crucial role in condition monitoring, allowing for the early detection of insulation defects in an electrical system.
Traditional PD pattern features typically include the waveform characteristics, the spectral features, the pulse counts, the phase characteristics, and the amplitude features. Traditional machine learning methods, such as artificial neural networks (ANNs) and support vector machines (SVMs), are conventionally utilized to learn from these features for pattern recognition. Tang et al. proposed a minimum-redundancy maximum-relevance (mRMR) algorithm-based feature optimization selection method to select the statistical features under a PRPD model [3]. The results indicated that the PD severity assessment accuracy with the optimal feature set had a higher stability of precisions than that with the traditional feature set. Zhou et al. utilized both time domain and frequency domain features and introduced an optimized SVM algorithm for the pattern recognition of PD using ultrasonic signals [4]. The results showed that the proposed SVM algorithm had a higher recognition accuracy and a faster convergence speed. Carvalho et al. compared three clustering algorithms (K-means, Gaussian mixture model, and mean-shift) and the SVM method for PD classifications; the supervised SVM demonstrated a notably high average accuracy [5]. Furthermore, global optimization algorithms have been used to optimize the hyperparameters of SVM models in some studies. Sun et al. proposed an improved whale optimization algorithm (IWOA) to optimize the hyperparameters of SVMs to identify different types of PD [6]. The resultant accuracy verified that IWOA had a good effect on the parameter optimization of SVMs. Sun et al. also proposed an improved northern goshawk optimization (SCNGO) to optimize the parameter penalty factor and the kernel parameter of the SVM [7]. Fujioka et al. utilized the maximum intensity observed in the PRPD pattern as the input data of an ANN [8]. The classification accuracy was improved by shifting the phase of the maximum sensor output to 0°, as proposed. Haiba et al. utilized ANNs for classifying defects in ceramic insulators [9]. The results from the ANN indicated that the overall recognition rate was dependent on the number of the collected signals, a greater number of captured signals led to a higher recognition rate. The findings of the ANN technique were also verified by SVM and KNN models in [9]. Nevertheless, the major drawback of using traditional machine learning methods for PD pattern recognition is the necessity to extract features in advance.
In recent years, studies on the recognition of PRPDs, phase-resolved pulse sequences (PRPSs) [10], and other spectrograms in the direction of PD pattern recognition have demonstrated outstanding performance attributable to advancements in image recognition technology. Aldosari et al. combined long short-term memory (LSTM) networks and convolutional neural networks (CNNs) to identify the form of PD patterns, demonstrating that the integrated CNN–LSTM network outperformed an individual CNN or an LSTM network [11]. Additionally, they found that image data augmentation had a better effect in both grayscale and RGB images. Fu et al. employed the DenseNet model in conjunction with transfer learning to extract features from the time domain signal map of a gas-insulated switchgear PD [12]. The proposed method enabled direct pattern recognition research on the unstructured data time–domain waveform spectrogram of PD. Yin et al. constructed a model for identifying the statistical parameters of PRPD patterns based on the Hausdorff-like distance and an improved CNN for PRPD pattern recognition [13]. They utilized Dempster–Shafer (D-S) evidence theory to combine the results of the two pattern recognition methods, thus enhancing the accuracy of PD pattern recognition. Song et al. utilized the histogram of oriented gradient (HOG) features of the 3D PRPSs and designed the attribute selective Naïve Bayes (ASNB) classifier to recognize the 3D PRPS graphs [10]. The contrasting results compared to those using statistical feature parameters indicated that the use of HOG features resulted in a higher recognition accuracy and a stronger robustness in PD recognition under different voltages. Wang et al. enhanced the PRPS graph using the contrast-limited adaptive histogram equalization (CLAHE) algorithm and employed uniform local binary patterns (LBPs) as the feature vector of the PRPS graph [14]. They then used the Adaboost cascade classifier for the integrated learning of different classification models. The experimental results indicated that using ULBP as the feature vector could enhance the generalization ability of traditional algorithms, and the use of CLAHE enhancements improved the upper limit of the recognition rate. Nevertheless, due to their limited number of layers, these models may not comprehensively extract the PD features.
Lightweight CNNs are increasingly being employed in the recognition of PD due to their hardware-friendly nature [15,16,17,18]. A lightweight CNN, in the context of deep learning, refers to a neural network architecture designed with a relatively small number of parameters and computations, enabling an efficient inference on resource-constrained devices such as mobile phones or edge devices. These networks are tailored to strike a balance between model complexity and predictive performance, making them ideal for deployments in PD pattern recognition. Currently, the most widely used mobile networks include ShuffleNet [19], MobileNet [20,21,22], and EfficientNet [23]. It should be pointed out that even though significant progress has been made in lightweight CNN-based methods for recognizing PD patterns, the large model size still poses challenges in using lightweight CNN-based methods for recognizing PD patterns to satisfy the real-time recognition requirements, especially when deployed to embedded devices. Acknowledging the limitations of existing lightweight CNN-based methods, this paper proposes an ensemble learning method that combines SVM and CNN, with improved recognition accuracy, high solution efficiency, and reduced parameter quantity. A simplification of MobileNet V2 (SCNN) was undertaken to address the demand for more efficient models while preserving the problem-solving accuracy. Furthermore, the integration of a quadratic SVM (QSVM) with the SCNN model effectively enhances the accuracy of PD recognition. These innovations collectively demonstrate the efforts in streamlining complex network architectures while maintaining accuracy, and in integrating traditional machine learning methods with modern CNN models to improve the recognition accuracy. This approach not only advances the field by achieving enhanced recognition results, but also showcases practical relevance by being more suitable for deployment on terminal devices, aligning with the demands of real-world applications. The research makes a significant scientific contribution by addressing the challenges of real-time recognition requirements and deployment on embedded devices in the context of identifying PD patterns in electrical systems.
2. The Proposed PD Pattern Recognition Methodology
To be self-contained, 3D Graph of PRPS and MobileNet V2 will firstly be briefed, and the proposed PD pattern recognition methodology will then be detailed.
2.1. Three-Dimensional Graph of PRPS
According to the generating mechanism, PD can be classified into suspended electrode discharge, surface discharge, and metal tip discharge. Suspended electrode discharge comes from the presence of free or floating conductive particles within an insulation material. When subjected to an electric field, these particles can lead to localized discharges due to the concentration of electric fields in their neighbors. Surface discharge transpires when the electric field at the surface of the insulator exceeds the dielectric strength limit of the material. This can occur due to surface irregularities, impurities, or imperfections, leading to the formation of localized discharge along the insulation surface. Metal tip discharge comes from high electric field concentrations at the tips of protruding conductive elements within the insulation system. This concentration of the electric field at the tips leads to the initiation of localized discharge.
The 3D-PRPS graphs in PD analysis are visualization tools that represent the distribution of partial discharge events in three-dimensional space, and provide a comprehensive view of the period, phase, and discharge amplitude of PD [10]. Typical 3D-PRPS graphs of suspended electrode discharge, surface discharge, and metal tip discharge are shown in Figure 1. For suspended electrode discharge, there are obvious discharge pulses in both the positive and negative half of the phase. Comparatively, the phase width of a surface discharge is broader, while the pulse pattern of a metal tip discharge appears sporadic and dispersed. In conclusion, PRPS graphs manifest diverse visual patterns across various discharges, thus forming the fundamental basis for PD pattern recognition.
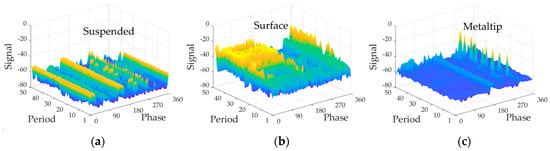
Figure 1.
Typical 3D−PRPS graphs of (a) suspended electrode discharge, (b) surface discharge, and (c) metal tip discharge.
2.2. MobileNet V2
MobileNet V2 is a neural network architecture designed to facilitate efficient and high-performance deep learning on resource-constrained devices such as mobile phones and embedded systems [21]. The MobileNet V2 network uses inverted residual blocks with linear bottlenecks and shortcut connections based on the depthwise separable convolution of MobileNet V1, as shown in Figure 2, where W, H, and C are the width, the height, and the channel of the input image, respectively; N is the size of the kernel of the depthwise convolution; M is the number of kernels in the pointwise convolution. In Figure 2a, the depthwise separable convolution splits standard convolutions into depthwise convolutions and pointwise convolutions. Inverted residual blocks, as shown in Figure 2b, are types of building blocks which are designed to capture nonlinearities more effectively compared to traditional residual blocks. The input is first expanded to a higher-dimensional space using a 1 × 1 pointwise convolution, then processed with depthwise convolutions, and finally projected back to a lower-dimensional space. Within linear bottlenecks, a linear activation function is utilized to alleviate the information collapse that arises when information undergoes nonlinear mapping from a high-dimensional space to a low-dimensional space. Additionally, shortcut connections are employed to facilitate information flow and aid in gradient propagation in training. It is reported that MobileNet V2 will achieve an accuracy of 72% on ImageNet classifications [24].
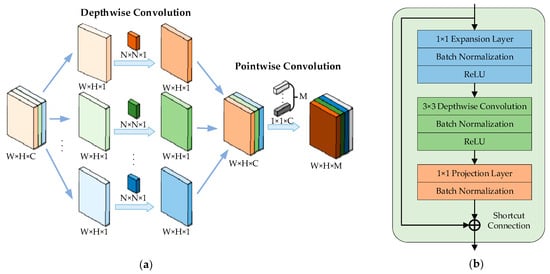
Figure 2.
Central features of MobileNet V2: (a) depthwise separable convolution consisting of depthwise convolutions and pointwise convolutions; (b) bottleneck residual block.
2.3. CLAHE and Circular LBP Features
Contrast-limited adaptive histogram equalization (CLAHE) is an image processing technique used to improve the local contrast of an image by adjusting the intensity distribution in small regions [25]. Unlike traditional histogram equalization, CLAHE limits the contrast enhancement to prevent the over-amplification of noises. By adaptively modifying the contrast in different areas of the image, CLAHE effectively enhances the visual appearance of images, particularly in regions with varying contrast levels.
Circular local binary pattern (CLBP) is a texture descriptor used in computer vision and image analysis [26]. It works by comparing each pixel with its neighboring pixels on a circle to encode the local texture information into a binary pattern. The LBP feature vector is created by calculating the frequency of the occurrences of these patterns within a local neighborhood. This method is robust to monotonic grayscale changes and provides a compact representation of the texture information.
2.4. The Proposed PD Pattern Recognition Methodology
2.4.1. Three-Dimensional PRPSs Acquisition
This study firstly developed a PD defect test prototype by using an ultra-high-frequency (UHF) sensor to obtain PD signals. The voltage came from a non-partial discharge booster transformer. The PD spectrogram and amplitude of partial discharge UHF signals under simulated defects were measured by the UHF sensor. The prototype device is shown in Figure 3. In Figure 3, the resistance–capacitance voltage-dividing device is composed of the coupled capacitance and the measuring impedance. The UHF sensor was 3 m away from the PD generator. The schematic diagram of the prototype is shown in Figure 3. Three types of discharges—suspended electrode discharge, surface discharge, and metal tip discharge—could be generated in the PD generator. The discharging data for a total of 50 power frequency cycles at every 5° angle were recorded by the UHF sensor. The finally collected data sizes for suspended electrode discharge, surface discharge, and metal tip discharge were 262, 64, and 319, respectively.
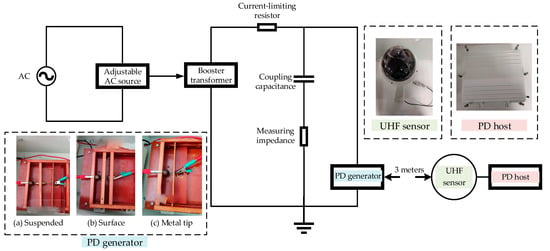
Figure 3.
The prototype testing device for PD.
2.4.2. SCNN Structure Design
This paper presents a simple CNN (SCNN) structure based on the fundamental bottleneck residual block of MobileNetV2, aiming to strike a high balance between the size of the CNN model and the training accuracy. In order to examine the influence of the quantity of bottleneck residual blocks, this study initially investigated the recognition accuracy of a CNN with varying numbers of bottleneck residual blocks using all the collected data. The recognition process was repeated 10 times; the averaged accuracy is shown in Table 1. From Table 1, it is apparent that with an increase in the number of blocks from one to six, there is a corresponding rise in the recognition accuracy. However, the difference in the recognition efficiency between using five blocks and six blocks was marginal, within an error of 1%. Subsequent increases in the number of blocks did not yield significant improvements in the recognition efficiency. Consequently, the number of blocks in this study was selected to be six, considering the computational resources and the recognition accuracy.

Table 1.
Accuracy under different numbers of bottleneck residual blocks.
It has been proven that a swish activation function outperforms the ReLU function [27]. The H-swish activation function approximates the sigmoid function in swish through an approximation function, exhibiting similar performance to swish while reducing the computational costs and improving the execution speed [22]. Therefore, an H-swish activation function is more suitable for applications in mobile devices requiring real-time image processing. Hence, in this study, the H-swish function was used as the activation function in the first and second layers of the model, as well as in the final layer.
The final structure of the proposed SCNN is shown in Table 2, where t represents the expansion factor compared to the input channels in the inverted residual structure using 1 × 1 convolutions, c denotes the depth of the output feature map (channel), n signifies the repetition of the bottleneck, and s indicates the stride of the depthwise convolution in the first bottleneck of each row.

Table 2.
The proposed SCNN body architecture.
Furthermore, to determine the most suitable batch size when using batch training for SCNN, various values for minibatch were investigated. After five repeated runs of each setting, the averaged training time and accuracy are shown in Table 3. Compromising the computational time and the recognition accuracy, the minibatch size was set as eight in this study when training the SCNN.

Table 3.
Accuracy and runtime under different training minibatch sizes.
2.4.3. CLBP and QSVM
For the obtained 3D PRPS graph, more than half of the image space lacked feature information. Consequently, 2D processing was performed from the top view. Subsequently, the processed 2D color image underwent grayscale processing using the floating-point method, followed by image enhancement through CLAHE. CLBP feature extraction was performed to generate the feature space of CLBP. The method described in [14] was adopted to select features within the CLBP feature space. Ultimately, 59 CLBP features were obtained and used as input data of the SVM. The whole processing procedure and results are shown in Figure 4.

Figure 4.
Image preprocessing for SVM training.
To determine the most suitable SVM model, experiments were conducted for six types of SVMs: linear SVM, quadratic SVM, cubic SVM, coarse SVM, medium SVM, and fine SVM. The training data comprised all the data for three types of PD. The training of different SVMs was conducted using the classification learner in MATLAB R2022b. The receiver operating characteristic (ROC) curve and the area under the curve (AUC) [28] were used to criticize the performance of different SVMs. The ROC curve is a graphical tool that plots the true positive rate against the false positive rate. The ROC curve provides a visual representation of a classifier ability to discriminate between classes across different threshold values. A steeper ROC curve indicates better performance, and the area under the ROC curve (AUC) quantifies the overall performance of the classifier. AUC values range from 0 to 1, where a value closer to 1 indicates a better discrimination performance, while a value near 0.5 suggests a performance similar to random guessing. The results of the ROC curves and AUC values for different types of PD are shown in Figure 5. The ROC curves and AUC values are shown in Figure 4. Observing Figure 5, it is apparent that among the six types of SVM models, the quadratic SVM demonstrated higher AUC values across the three fault types. Therefore, the quadratic SVM model (QSVM) was selected to construct the PD pattern recognition model for the CLPB features.
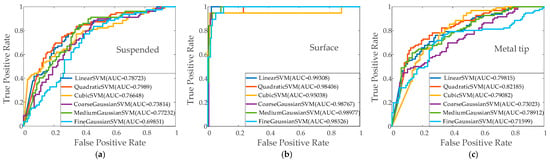
Figure 5.
The ROC curves and AUC values for (a) suspended electrode discharge, (b) surface discharge, and (c) metal tip discharge.
2.4.4. Procedures of the Proposed ENS–SCNN–QSVM
Based on the aforementioned studies, our PD pattern recognition methodology was proposed; its overall procedure is explained in Figure 6 to facilitate its implementation by fellow researchers. After collecting data from UHF sensors, the obtained images were initially preprocessed, involving image resizing, image rotation, image graying, and image enhancement. For the SCNN model, the image needed to be processed to be identical in size to the input size of the network: 224 × 224. For the QSVM model, the CLBP features were extracted, as shown in Figure 4. After image preprocessing, SCNN and QSVM models were separately established. The output scores of the SCNN and QSVM, with as many categories as the types of PD, were concatenated into one input vector, serving as the input for the ensemble learning model, and the ensemble learning model was trained using the bagging and discriminant method.
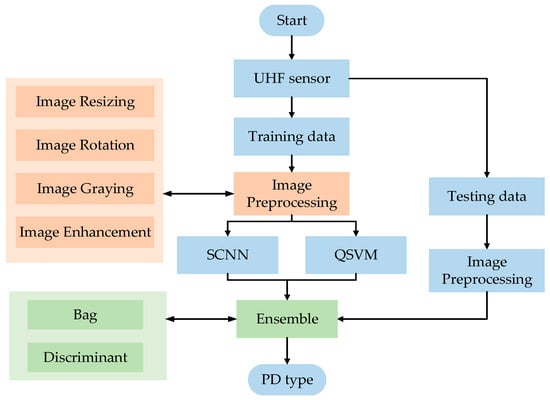
Figure 6.
The procedure of the proposed PD pattern recognition methodology.
3. Experimental Study
To demonstrate the performance of the proposed PD pattern recognition methodology, comprehensive experiments were conducted. In the experimental study, all recorded data were split into two parts, 70% for training and 30% for testing; the training dataset sizes for suspended electrode discharge, surface discharge, and metal tip discharge were 183, 45, and 223, respectively. Comparison was performed among SCNN, QSVM, random forest (RF) [29], extreme gradient boosting (XGBoost) [30], ensemble learning of SCNN and QSVM (ENS–SCNN–QSVM), and some existing lightweight networks, MobileNet V2 [21], EfficientNetB0 [23], and ShuffleNet [19]. The comparison focused on the recognition accuracy, the parameter quantity, and the training time. For the identification of the three types of PD, each classifier was run independently 10 times to obtain an averaged recognition efficiency and an averaged training time. For SCNN, ENS–SCNN–QSVM, MobileNet V2, EfficientNetB0, and ShuffleNet, batch training was used, while the minibatch size was set at 8, the max number of training epochs was 20, and the learn rate was 0.001. For RF, the number of trees was 100, the minimum number of samples for each leaf node was 5, each tree was trained using a random selection of 10 features, and the maximum depth of each tree was 100. For XGBoost, the number of weak classifiers was 100, the maximum depth was 10, and the learning rate was 0.1. CLBP features were used in both the RF model and the XGBoost model. The experiments were conducted in MATLAB R2022b, using a single GPU on an AMD Ryzen 7 4800H with Radeon Graphics 2.90 GHz, NVIDIA GeForce GTX 1650 Ti. Notably, MobileNet V2, EfficientNetB0, and ShuffleNet were trained using transfer learning, where the pre-trained networks from ImageNet [24] were loaded. The initial weights of the main backbone were frozen; then, retraining was conducted using the training data presented in this paper. The PD recognition results are shown in Table 4. The confusion matrices for the eight methods run once on the testing data are shown in Figure 7. The precision, recall, and accuracy for each method with the testing data are presented in Table 5.

Table 4.
PD recognition results using 8 different methods.
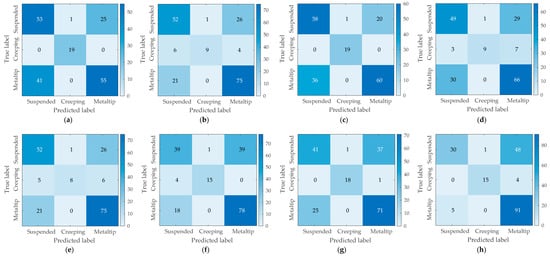
Figure 7.
Confusion matrices of the testing data with (a) SCNN, (b) QSVM, (c) ENS–SCNN–QSVM, (d) RF, (e) XGBoost, (f) MobileNet V2, (g) EfficientNetB0, and (h) ShuffleNet.

Table 5.
The precision, recall, and accuracy for 8 methods on the testing data.
From the results presented in Table 4, it is obvious that the recognition accuracy of a separate SCNN is not as good as the three comparative lightweight networks. At the same time, the XGBoost and SVM models established using CLBP features exhibit superior performance with the training data; however, their abilities with the testing data are deemed unsatisfactory. However, the proposed ENS–SCNN–QSVM ensemble with SCNN and QSVM has the highest recognition accuracy on the testing data, 71.70%, slightly higher than ShuffleNet’s 71.24%. In terms of runtime, EfficientNetB0 takes the longest time, 724.65 s, while the training time for QSVM is the shortest, only 0.244 s. Compared to the three comparative lightweight networks, ENS–SCNN–QSVM benefits from its simple structure, having the shortest training time of only 109.34 s. In terms of model parameter quantity, the parameter quantity of the three comparative lightweight networks is at the level of millions, while the proposed ENS–SCNN–QSVM has only 92.1 k parameters. Considering the recognition accuracy of the testing data, runtime, and model parameter quantity, the proposed method in this paper demonstrates significant advantages. Additionally, it can be observed that the traditional machine learning methods, namely, QSVM, RF, and XGBoost, generally outperform deep learning methods on the training data. However, the accuracy of these methods on the test data is inferior to those of deep learning networks and the method proposed in this paper. More specifically, from Figure 7 and Table 5, it can be seen that on the testing data, the performance of QSVM is the worst, especially in the recognition of surface discharge, with a recall of 47.4%. Only 9 out of 19 instances of surface discharge could be correctly identified, while SCNN and ENS–SCNN–QSVM both achieved a recall of 100%. Among the eight methods for PD pattern recognition, suspended electrode discharge and metal tip discharge were easily misidentified. For the overall recognition rate on the testing dataset, the proposed ENS–SCNN–QSVM is the highest, at 70.6%.
4. Conclusions
The precise identification of PD is pivotal for ensuring the reliability of power supply within a power system. As CNNs are progressively employed in PD pattern recognition, the challenge of large model sizes persists, especially when striving to meet real-time demands, particularly on embedded devices. This paper introduces an ensemble learning method that combines SCNN and QSVM for identifying PD patterns. An SCNN was constructed based on the inverted residual blocks utilized in MobileNet V2. The QSVM model was established using the CLBP vectors, which was extracted from the enhanced 2D gray image. The SCNN and QSVM scores were ensembled using bagging and discriminant methods. Comparative results with existing lightweight CNNs demonstrate the proposed method’s advantages in recognition accuracy, response efficiency, and parameter quantity, making it more suitable for deployment on terminal devices for PD pattern recognition.
In conclusion, the presented method shows advances in the field of PD pattern recognition, offering potential applications in the real-time identification of online PD in electrical equipment such as switchgear. By situating the UHF PD sensor outside the pertinent electrical equipment designated for testing, and subsequently connecting it to the oscilloscope or computer host through the PD host, one can display the PRPS spectrum, facilitating the application of the proposed method. Further research and development in this direction can contribute to explore multi-source mixed PD pattern recognition, focusing on separating PD mixed signals and extracting the respective characteristics, and investigate different methodologies to combine SCNN and QSVM.
Author Contributions
Conceptualization, Z.F. and S.Y.; methodology, Z.F. and S.Y.; software, Z.F. and Y.L.; validation, Y.L.; formal analysis, Y.L.; investigation, Z.F. and S.Y.; resources, Z.F.; data curation, Z.F.; writing—original draft preparation, Z.F. and Y.L.; writing—review and editing, Z.F., Y.L. and S.Y.; visualization, Z.F. and Y.L.; supervision, S.Y.; project administration, Z.F. and S.Y.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Acknowledgments
We would like to express our heartfelt gratitude to all those who have contributed to this research project.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- High-Voltage Test Techniques—Partial Discharge Measurements: = Techniques Des Essais à Haute Tension—Mesures Des Décharges Partielles, Internationale Elektrotechnische Commission, Ed.; International Standard/International Electrotechnical Commission; Edition 3.1, 2015–11, consolidated version/version consolidée; IEC Central Office: Geneva, Switzerland, 2015; ISBN 978-2-8322-3053-4.
- Drechsel, J.; Barth, H.; Rebenklau, L. Handling and Analysis of Large Datasets Using the Example of Partial Discharge Measurement. In Proceedings of the 2022 45th International Spring Seminar on Electronics Technology (ISSE), Vienna, Austria, 11–15 May 2022; pp. 1–6. [Google Scholar]
- Tang, J.; Jin, M.; Zeng, F.; Zhou, S.; Zhang, X.; Yang, Y.; Ma, Y. Feature Selection for Partial Discharge Severity Assessment in Gas-Insulated Switchgear Based on Minimum Redundancy and Maximum Relevance. Energies 2017, 10, 1516. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, Y.; Wang, N.; Han, X.; Li, J. Partial Discharge Ultrasonic Signals Pattern Recognition in Transformer Using BSO-SVM Based on Microfiber Coupler Sensor. Measurement 2022, 201, 111737. [Google Scholar] [CrossRef]
- Carvalho, I.F.; da Costa, E.G.; Nobrega, L.A.M.M.; da Costa Silva, A.D. Identification of Partial Discharge Sources by Feature Extraction from a Signal Conditioning System. Sensors 2024, 24, 2226. [Google Scholar] [CrossRef]
- Sun, W.; Ma, H.; Wang, S. A Novel Fault Diagnosis of GIS Partial Discharge Based on Improved Whale Optimization Algorithm. IEEE Access 2024, 12, 3315–3327. [Google Scholar] [CrossRef]
- Sun, W.; Ma, H.; Wang, S. Application of SCNGO-VMD-SVM in Identification of Gas Insulated Switchgear Partial Discharge. IEEE Access 2024, 12, 43838–43848. [Google Scholar] [CrossRef]
- Fujioka, S.; Kawano, H.; Kozako, M.; Hikita, M.; Eda, O.; Yaguchi, S.; Shiina, Y. Examination of Insulation Diagnosis in Substation by Neural Network with Phase-Resolved Partial Discharge Pattern Reconstruction. Electron. Commun. Jpn. 2022, 105, e12360. [Google Scholar] [CrossRef]
- Haiba, A.S.; Eliwa Gad, A. Artificial Neural Network Analysis for Classification of Defected High Voltage Ceramic Insulators. Sci. Rep. 2024, 14, 1513. [Google Scholar] [CrossRef]
- Song, S.; Qian, Y.; Wang, H.; Zang, Y.; Sheng, G.; Jiang, X. Partial Discharge Pattern Recognition Based on 3D Graphs of Phase Resolved Pulse Sequence. Energies 2020, 13, 4103. [Google Scholar] [CrossRef]
- Aldosari, O.; Aldowsari, M.A.; Batiyah, S.M.; Kanagaraj, N. Image-Based Partial Discharge Identification in High Voltage Cables Using Hybrid Deep Network. IEEE Access 2023, 11, 50325–50333. [Google Scholar] [CrossRef]
- Fu, Y.; Liang, L.; Huang, W.; Huang, G.; Huang, P.; Zhang, Z.; Chen, C.; Wang, C. Partial Discharge Pattern Recognition Method Based on Transfer Learning and DenseNet Model. IEEE Trans. Dielectr. Electr. Insul. 2023, 30, 1240–1246. [Google Scholar] [CrossRef]
- Yin, K.; Wang, Y.; Liu, S.; Li, P.; Xue, Y.; Li, B.; Dai, K. GIS Partial Discharge Pattern Recognition Based on Multi-Feature Information Fusion of PRPD Image. Symmetry 2022, 14, 2464. [Google Scholar] [CrossRef]
- Wang, H.; Song, S.; Qian, Y.; Zang, Y.; Sheng, G.; Jiang, X. Recognition Algorithm of GIS Partial Discharge Phase Resolved Pulse Sequence Based on CLAHE Enhancement. High Volt. Eng. 2021, 47, 3836–3844. [Google Scholar] [CrossRef]
- Wang, Y.; Yan, J.; Sun, Q.; Li, J.; Yang, Z. A MobileNets Convolutional Neural Network for GIS Partial Discharge Pattern Recognition in the Ubiquitous Power Internet of Things Context: Optimization, Comparison, and Application. IEEE Access 2019, 7, 150226–150236. [Google Scholar] [CrossRef]
- Wang, Y.; Yan, J.; Yang, Z.; Zhao, Y.; Liu, T. GIS Partial Discharge Pattern Recognition via Lightweight Convolutional Neural Network in the Ubiquitous Power Internet of Things Context. IET Sci. Meas. Technol. 2020, 14, 864–871. [Google Scholar] [CrossRef]
- Sun, Y.; Ma, S.; Sun, S.; Liu, P.; Zhang, L.; Ouyang, J.; Ni, X. Partial Discharge Pattern Recognition of Transformers Based on MobileNets Convolutional Neural Network. Appl. Sci. 2021, 11, 6984. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Y.; Hu, M.; Li, S.; Fang, J.; Rao, Z. Online Recognition Method of Transformer Partial Discharge Based on Audio Detection. AIP Adv. 2022, 12, 015023. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, X.; Lin, M.; Sun, J. ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices. arXiv 2017, arXiv:1707.01083. [Google Scholar]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.-C. MobileNetV2: Inverted Residuals and Linear Bottlenecks. arXiv 2019, arXiv:1801.04381. [Google Scholar]
- Howard, A.; Sandler, M.; Chu, G.; Chen, L.-C.; Chen, B.; Tan, M.; Wang, W.; Zhu, Y.; Pang, R.; Vasudevan, V.; et al. Searching for MobileNetV3. arXiv 2019, arXiv:1905.02244. [Google Scholar]
- Tan, M.; Le, Q.V. EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks. arXiv 2020, arXiv:1905.11946. [Google Scholar]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. ImageNet Large Scale Visual Recognition Challenge. arXiv 2015, arXiv:1409.0575. [Google Scholar] [CrossRef]
- Zuiderveld, K. VIII.5.—Contrast Limited Adaptive Histogram Equalization. In Graphics Gems; Heckbert, P.S., Ed.; Academic Press: Cambridge, MA, USA, 1994; pp. 474–485. ISBN 978-0-12-336156-1. [Google Scholar]
- Ojala, T.; Pietikainen, M.; Maenpaa, T. Multiresolution Gray-Scale and Rotation Invariant Texture Classification with Local Binary Patterns. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 971–987. [Google Scholar] [CrossRef]
- Ramachandran, P.; Zoph, B.; Le, Q.V. Searching for Activation Functions. arXiv 2017, arXiv:1710.05941. [Google Scholar]
- Hanley, J.A.; McNeil, B.J. The Meaning and Use of the Area under a Receiver Operating Characteristic (ROC) Curve. Radiology 1982, 143, 29–36. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13 August 2016; ACM: New York, NY, USA, 2016; pp. 785–794. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).