Effects of CO₂ Geosequestration on Opalinus Clay

Abstract

CO₂ geosequestration is an important contributor to United Nations Sustainable Development Goal 13, i.e., Climate Action, which states a global Net-Zero CO₂ emissions by 2050. A potential impact of CO₂ geosequestration in depleted oil and gas reservoirs is the variations in induced pressure across the caprocks, which can lead to significant local variations in CO₂ saturation. A detailed understanding of the relationship between the pressure gradient across the caprock and local CO₂ concentration is of utmost importance for assessing the potential of CO₂ geosequestration. Achieving this through experimental techniques is extremely difficult, and thus, we employ a coupled Computational Fluid Dynamics (CFD) and Finite Element Method (FEM) based solver to mimic sub-critical CO₂ injection in Opalinus Clay under various pressure gradients across the sample. The geomechanical and multiphase flow modelling utilising Darcy Law helps evaluate local variations in CO₂ concentration in Opalinus Clay. Well-validated numerical results indicate favourable sub-critical CO₂ geosequestration under a positive pressure gradient across Opalinus Clay. In the absence of a positive pressure gradient, a peak CO₂ concentration of 5% has been recorded, which increases substantially (above 90%) as the pressure gradient across the sample increases.

1. Introduction

Carbon capture and storage (CCS) has become a viable technology in the search for sustainable energy solutions and the reduction of anthropogenic greenhouse gas emissions. The main component of CCS is the injection of CO₂ into deep geological formations, where it may be safely stored for geologically long periods. These formations often consist of salty aquifers or depleted oil and gas reservoirs. The behaviour of subsurface formations, particularly the caprock, which serves as a primary seal to inhibit the upward migration of injected CO₂, is crucial to the effectiveness and safety of CCS. Shale formations are among the most popular options for caprock materials due to their low permeability and widespread occurrence. However, little is known about the hydromechanical response of shale caprocks to CO₂ injection [1]. Shale formations are often chosen as caprocks for CO₂ storage reservoirs due to their fine-grained structure and low permeability [2]. To ensure the long-term containment of injected CO₂, these caprocks must remain intact. Therefore, it is essential to understand how shale caprocks react to CO₂ injection to assess the security and feasibility of CCS operations [3,4]. The hydromechanical response of shale caprocks to CO₂ injection involves a complex interplay of fluid flow and geomechanical deformation [5,6]. The injection of CO₂ alters the shale’s pore pressure and fluid content, thereby affecting its mechanical characteristics [7]. These interconnected processes have the potential to impact caprock structural integrity and CO₂ confinement [8,9].

The hydromechanical reaction of shale caprocks to CO₂ injection can effectively be modelled and analysed using numerical methods [10]. Finite Element Method (FEM) is often employed to evaluate the mechanical integrity of reservoir rocks and caprocks under the stresses induced by CO₂ injection [11]. It aids in predicting probable deformation, fractures, and important elements in guaranteeing the long-term containment of CO₂. The assessment of CO₂ saturation and hydromechanical response has been studied extensively using Computational Fluid Dynamics (CFD) to model fluid flow within reservoirs and surrounding formations, accounting for factors such as porosity, permeability, and fluid properties [12,13]. Moreover, CFD is used for evaluating risks involved with the dispersion of CO₂ in the atmosphere as a result of leakage, leading to its high-velocity release [14]. Such studies provide accurate predictions of gas phase transportation and help evaluate the risks involved in CCS projects. In order to describe the complex behaviour of shale caprocks when CO₂ is injected into them, the numerical models can accurately predict the multiphase flow mechanisms and complex constitutive linkages [15,16]. While significant progress has been made in the accuracy of numerical predictions, numerous unknowns and challenges persist in predicting the hydromechanical response of shale caprocks to CO₂ injection [17,18]. These include validating the numerically predicted results against laboratory and field tests, accurately representing shale variability, understanding fluid-rock interactions, and addressing coupled processes at various spatial and temporal scales.

Apart from validating the numerical models, another important factor is the assessment of CO₂ geosequestration in shale caprocks like Opalinus Clay. This requires local measurements of CO₂ concentration within the caprock, which is not easily achievable using experimental techniques. Numerical modelling, however, can be used to evaluate local CO₂ concentration in caprocks. Resolving this critical issue is crucial for enhancing our understanding of shale caprock behaviour for CO₂ storage and improving the predictive capability of numerical models [19]. The design, management, and risk assessment of CCS projects are significantly impacted by these findings, which also influence methods to maintain the integrity and efficacy of CO₂ storage in shale formations over the long term [20,21].

Regional pressure variations play a significant role in dictating CO₂ geosequestration in geological formations [22,23]. The extent of CO₂ geosequestration significantly impacts how much CO₂ can be stored in shale caprocks. However, published literature is severely lacking in analysing this important aspect of CO₂ geosequestration. Thus, we aim to bridge this gap in scientific knowledge through numerical modelling. A coupled CFD-FEM model utilizing Darcy’s Law is employed to better understand the complex dynamics of local variations in CO₂ concentration in shale caprock Opalinus Clay, which is the primary aim of this investigation. It is envisaged that through the results obtained through this investigation, well-informed decisions can be made in future while planning CCS projects and evaluating their technical feasibility and economic viability.

2. CFD-FEM Model

A coupled CFD-FEM model has been utilized to model the complex geomechanical and multiphase flow behaviour of sub-critical CO₂ injection in a water-saturated sample of Opalinus Clay. As there are two phases involved in the numerical model, i.e., water and CO₂, where CO₂ injection leads to water displacement in the sample, their mass balance is modelled as follows:

$$\frac{\partial }{\partial \mathrm{t}}\left(\mathsf{\phi }{\mathrm{S}}_{\mathsf{\beta }}{\mathsf{\rho }}_{\mathsf{\beta }}\right)-\nabla ·\left({\mathsf{\rho }}_{\mathsf{\beta }}{\mathrm{u}}_{\mathsf{\beta }}\right)-{\mathsf{\Psi }}_{\mathsf{\beta }}=0$$

(1)

where β represents a phase, φ is porosity, S is saturation, $\mathsf{\rho }$ is density, u is Darcy velocity, and Ψ is the source term. The Darcy velocity (u) can be expressed as:

$${\mathrm{u}}_{\mathsf{\beta }}=-\frac{{\mathrm{k}}_{\mathrm{a}}{\mathrm{K}\mathrm{r}}_{\mathsf{\beta }}}{{\mathsf{\mu }}_{\mathsf{\beta }}}{\nabla \mathrm{P}}_{\mathsf{\beta }}$$

(2)

where k_a is absolute permeability, ${\mathrm{K}}_{\mathrm{r}}$ is relative permeability, and P is pore pressure. The source term (Ψ) in Equation (1) can be defined as:

$${\mathsf{\Psi }}_{\mathsf{\beta }}={\mathsf{\rho }}_{\mathsf{\beta }}{\mathsf{\alpha }}_{\mathrm{B}}\left(\frac{\partial {\mathsf{\epsilon }}_{\mathrm{v}\mathrm{o}\mathrm{l}}}{\partial \mathrm{t}}\right)$$

(3)

here, $\mathsf{\alpha }$ is the Biot coefficient and ${\mathsf{\epsilon }}_{\mathrm{v}\mathrm{o}\mathrm{l}}$ is volumetric strain, which is modelled as:

$${\mathsf{\epsilon }}_{\mathrm{v}\mathrm{o}\mathrm{l}}=\frac{1}{2}\left[{\left(\nabla \mathrm{d}\right)}^2+\nabla \mathrm{d}\right]{\mathsf{\epsilon }}_{\mathrm{i}\mathrm{j}}=\frac{1}{2}\left(\frac{{\partial \mathrm{d}}_{\mathrm{i}}}{{\partial \mathrm{x}}_{\mathrm{j}}}+\frac{{\partial \mathrm{d}}_{\mathrm{j}}}{{\partial \mathrm{x}}_{\mathrm{i}}}\right)$$

(4)

where d is the displacement of the sample. The effects of gravity are ignored, and thus, the pressure gradient acts as the only driving force for the transport of CO₂ within the sample. The relationship between the Biot coefficient ($\mathsf{\alpha }$) in Equation (3) and Biot Modulus (M) is:

$$\frac{1}{\mathrm{M}}=\frac{\mathsf{\phi }}{{\mathrm{K}}_{\mathrm{d}}}+\frac{{\mathsf{\alpha }}_{\mathrm{B}}-\mathsf{\phi }}{{\mathrm{K}}_{\mathrm{s}}}$$

(5)

where ${\mathrm{K}}_{\mathrm{d}}$ is the drained bulk modulus and ${\mathrm{K}}_{\mathrm{s}}$ is the solid bulk modulus. Moreover:

$$\frac{\partial }{\partial \mathrm{t}}\left(\mathsf{\phi }{\mathrm{S}}_{\mathsf{\beta }}{\mathsf{\rho }}_{\mathsf{\beta }}\right)=\frac{1}{\mathrm{M}}\frac{\partial \left({\mathrm{S}}_{\mathsf{\beta }}{\mathsf{\rho }}_{\mathsf{\beta }}{\mathrm{p}}_{\mathsf{\beta }}\right)}{\partial \mathrm{t}}$$

(6)

Now, the governing mass conservation equation can be obtained for the fully coupled numerical model as:

$$\left(\frac{\mathsf{\phi }}{{\mathrm{K}}_{\mathrm{d}}}+\frac{{\mathsf{\alpha }}_{\mathrm{B}}-\mathsf{\phi }}{{\mathrm{K}}_{\mathrm{s}}}\right)\frac{\partial \left({\mathrm{S}}_{\mathsf{\beta }}{\mathsf{\rho }}_{\mathsf{\beta }}{\mathrm{p}}_{\mathsf{\beta }}\right)}{\partial \mathrm{t}}-\nabla ·\left(\frac{{\mathrm{k}}_{\mathrm{a}}{\mathrm{K}\mathrm{r}}_{\mathsf{\beta }}{\mathsf{\rho }}_{\mathsf{\beta }}}{{\mathsf{\mu }}_{\mathsf{\beta }}}{\nabla \mathrm{P}}_{\mathsf{\beta }}\right)={\mathsf{\rho }}_{\mathsf{\beta }}{\mathsf{\alpha }}_{\mathrm{B}}\left(\frac{\partial {\mathsf{\epsilon }}_{\mathrm{v}\mathrm{o}\mathrm{l}}}{\partial \mathrm{t}}\right)$$

(7)

The force equilibrium (or solid deformation) can be represented as:

$$\nabla ·\mathsf{\sigma }+\left({\mathsf{\rho }}_{\mathsf{\beta }}\mathsf{\phi }+{\mathsf{\rho }}_{\mathsf{\beta }}\right)\mathrm{g}=0$$

(8)

$$\mathsf{\sigma }={\mathsf{\sigma }}^{\prime }-{\mathsf{\alpha }}_{\mathrm{B}}{\mathrm{P}}_{\mathsf{\beta }}\mathrm{I}$$

(9)

where $\mathsf{\sigma }$ and ${\mathsf{\sigma }}^{\prime }$ are total and effective stress, respectively, and I is the second-order identity tensor. The porosity (φ) is dependent on the elastic modulus (E) as [24]:

$$\mathrm{l}\mathrm{n}\left(\frac{\mathrm{E}}{{\mathrm{E}}_{\mathrm{i}}}\right)=-\mathrm{d}\left({\mathsf{\phi }}_{\mathrm{i}}-\mathsf{\phi }\right)$$

(10)

As the caprock sample undergoes compression, the ability of multiphase flow through it changes. Thus, the permeability (k) can be modelled as [25]:

$$\mathrm{k}={\mathrm{k}}_{\mathrm{i}}{\left\{1\pm \frac{1}{2}{\left[\frac{9\left(1-{\mathsf{\nu }}^2\right)}{2}{\left(\frac{\pi \Delta \mathsf{\sigma }}{\mathrm{E}}\right)}^2\right]}^{1/3}\right\}}^2$$

(11)

where ${\mathrm{k}}_{\mathrm{i}}$ is the initial matrix permeability. The positive sign refers to dilatational loading, while the negative sign corresponds to compression loading.

The effective viscosity (${\mathsf{\mu }}_{\mathrm{e}\mathrm{f}\mathrm{f}})$ is modelled as:

$${\mathsf{\mu }}_{\mathrm{e}\mathrm{f}\mathrm{f}}=\frac{{\mathsf{\rho }}_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}}{\frac{{\mathrm{K}}_{\mathrm{r}\mathrm{w}}{\mathsf{\rho }}_{\mathrm{w}}}{{\mathsf{\mu }}_{\mathrm{w}}}-\frac{{\mathrm{K}}_{\mathrm{r}\mathrm{g}}{\mathsf{\rho }}_{\mathrm{g}}}{{\mathsf{\mu }}_{\mathrm{g}}}}$$

(12)

while the total density is represented as:

$${\mathsf{\rho }}_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}={\mathrm{S}}_{\mathrm{w}}{\mathsf{\rho }}_{\mathrm{w}}+{\mathrm{S}}_{\mathrm{g}}{\mathsf{\rho }}_{\mathrm{g}}$$

(13)

The Brooks and Corey model [26] has been utilized to find out the saturation of each phase in the caprock as:

$${\mathrm{S}}_{\mathrm{g}}=\frac{({\mathrm{S}}_{\mathrm{i}\mathrm{g}}-{\mathrm{S}}_{\mathrm{r}\mathrm{g}})}{(1-{\mathrm{S}}_{\mathrm{r}\mathrm{g}}-{\mathrm{S}}_{\mathrm{r}\mathrm{w}})}$$

(14)

$${\mathrm{S}}_{\mathrm{w}}=\frac{({\mathrm{S}}_{\mathrm{i}\mathrm{w}}-{\mathrm{S}}_{\mathrm{r}\mathrm{w}})}{(1-{\mathrm{S}}_{\mathrm{r}\mathrm{g}}-{\mathrm{S}}_{\mathrm{r}\mathrm{w}})}$$

(15)

where the subscripts i, r, w, g represent initial, residual, water, and gas (CO₂), respectively.

3. Methods and Materials

3.1. Opalinus Clay Model and Properties

The Opalinus Clay caprock has been modelled as a 35 mm × 12 mm two-dimensional (2D) rectangular flow domain having a bulk density of 2.75 g/cm³, as considered by Minardi et al. [27]. 2D geometric modelling of Opalinus Clay is appropriate given the expected laminar flow in the domain and the absence of Reynolds stresses. Moreover, 2D modelling significantly reduces the computational cost provided that the model is well-validated against experimental data. The different properties of the Opalinus Clay model are summarized in

Table 1. Properties of Opalinus Clay model [27].

Property	Value
Initial Porosity	0.1 [-]
Initial Permeability	2.4 × 10−20 [m2]
Young Modulus	6 [GPa]
Poisson ratio	0.25 [-]
Initial Pore Pressure	1 [atm]
Entry capillary pressure	5 [Pa]
Pore size distribution index	0.67 [-]
Biot-Willis coefficient	0.76 [-]

.

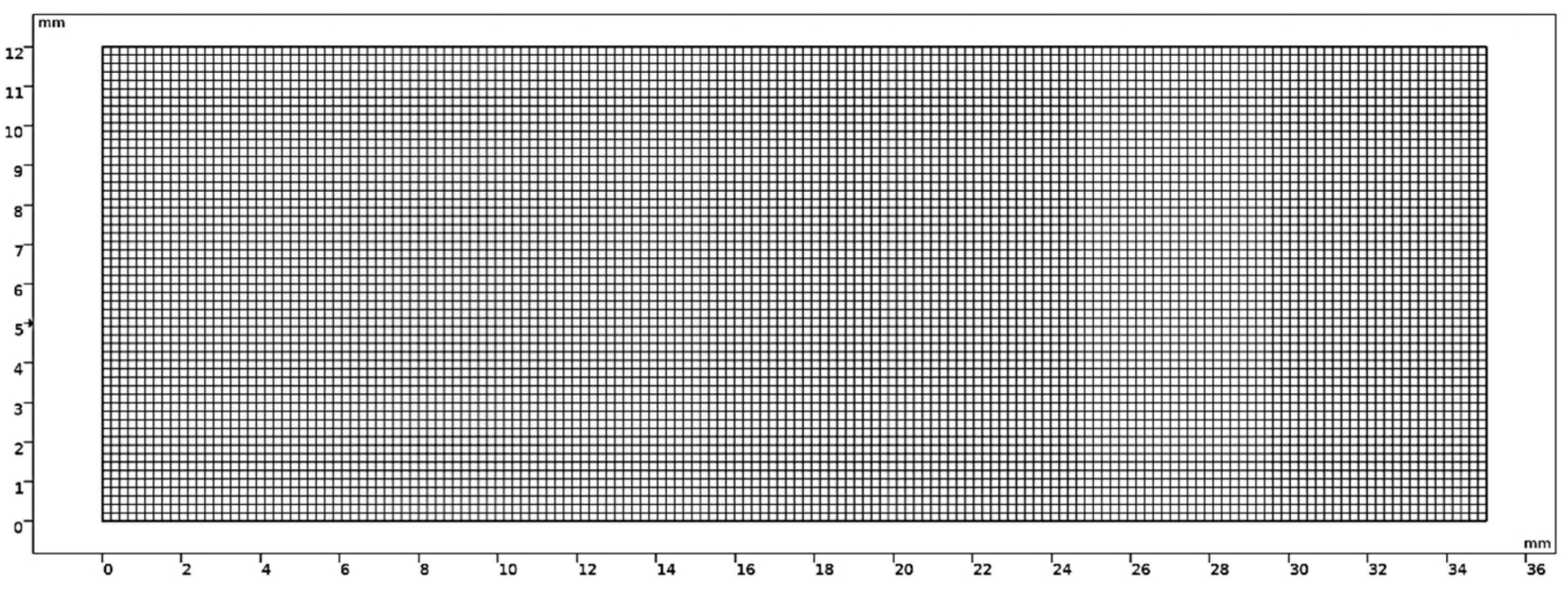
3.2. Meshing of the Flow Domain

The numerical work builds upon the experimental findings of Minardi et al. [27] and posits that CO₂ is injected into the model under different pressure gradients across the Opalinus Clay model. This injection pressure is countered by water pressure acting in the opposite direction to offset the impact of CO₂ injection. Thus, CO₂ displaces water in the model. To assess CO₂ saturation response, the flow domain has been spatially discretised, as illustrated in Figure 1. The mesh shown here comprises 0.9 × 10⁴ structured elements.

To ensure the numerical predictions are robust and independent of mesh sizing used [10], four additional meshes are generated, comprising 0.5 × 10⁴, 0.6 × 10⁴, 0.75 × 10⁴ and 2 × 10⁴ elements. All the meshes generated are analysed for sample displacement (d), a key parameter later used to validate our numerical model against the experimental data [27]. The results of the mesh independence tests are depicted in Figure 2. Notably, as the number of elements increased from 0.5 × 10⁴ to 0.9 × 10⁴, the displacement also increased. However, the difference in displacement between 0.9 × 10⁴ and 2 × 10⁴ elements was negligible. Consequently, the mesh with 0.9 × 10⁴ elements, shown in Figure 1, has been selected for further analysis.

3.3. Scope of Work

As this investigation evaluates the potential of sub-critical CO₂ geosequestration in Opalinus Clay, the maximum injection pressure of CO₂ is limited to 8 MPa [27]. Extensive numerical investigations have been carried out under two specific conditions, i.e., no pressure gradient across the Opalinus Clay sample and a positive pressure gradient.

$${\mathrm{P}}_{\mathrm{i}\mathrm{n}}-{\mathrm{P}}_{\mathrm{o}\mathrm{u}\mathrm{t}}=\left\{\begin{array}{c}=0\mathrm{no}\mathrm{pressure}\mathrm{gradient}\\ >0\mathrm{positive}\mathrm{presure}\mathrm{gradient}\end{array}\right.$$

where P_in is CO₂ injection pressure (limited to 8 MPa), and P_out is the pressure at the outlet of the model. For no pressure gradient condition, P_in and P_out remain the same, while for positive pressure gradient, P_in > P_out. The complete scope of the work is presented in

Table 2. Scope of the numerical modelling.

Pin	Pout	Pressure Gradient
(MPa)	(MPa)
1	1	No
	0	Yes
2	2	No
	1	Yes
	0	Yes
4	4	No
	2	Yes
	0	Yes
8	8	No
	6	Yes
	4	Yes
	2	Yes
	0	Yes

.

3.4. Numerical Model Setup

COMSOL Multiphysics 6.1 has been used to analyse two-phase fluid flow in Opalinus Clay, which has been modelled as porous media, incorporating geomechanics. Both the poroelastic module (which couples Darcy’s law with solid mechanics) and multiphase modules (which couples Darcy’s law with phase transportation) are utilized. The numerical model’s execution involves updating porosity values based on generated strain in the caprock following convergence at each time step. An adaptive time-stepping method has been used, which automatically adjusts the actual time step size in order to achieve solver convergence. CO₂ injection total time is 48 h and is based on the experimental work of Minardi et al. [27].

The updated porosity values are used to determine spatially varying elastic modulus. The Opalinus Clay model’s permeability is defined as a function of volumetric strain. Updated values are iteratively returned to the property definition after each time step (t + Δt). The PARADISO (Parallel Direct Solver) with a pivoting perturbation of 10⁻⁸ is utilized to solve the nonlinear system of equations in conjunction with the Newton nonlinear method.

4. Results and Discussion

This section presents the results obtained from the numerical investigations, highlighting the role of pressure gradient across Opalinus Clay in CO₂ geosequestration. The primary multiphase flow parameter that has been analysed is the concentration of CO₂ in Opalinus Clay, as it clearly demonstrates the potential of CO₂ sequestration in geological formations, which cannot be easily measured through experimental procedures.

4.1. Validation of the Numerical Model

In order to gain confidence in the numerical results obtained, the numerical model has been validated against the experimental data. Minardi et al. [27] experimentally studied the injection of sub-critical CO₂ in the Opalinus Clay core sample at different injection and outlet pressures, summarised in

Table 3. Comparison of numerical and experimental vertical displacement of Opalinus Clay sample.

Pin	Pout	dexperimental	dnumerical	Difference
(MPa)	(MPa)	(mm)	(mm)	(%)
2	2	0.004	0.0042	+5.0
4	2	0.007	0.0068	+2.8

, and measured the core sample’s vertical displacement (d). The scope of work includes the conditions considered by Minardi et al. [27]. It can be clearly seen that the numerically predicted vertical displacement of the Opalinus Clay model matches accurately with experimentally measured vertical displacement of the core sample (maximum difference of 5%), clearly demonstrating the efficacy of the developed numerical model to be used for other pressure gradient conditions summarized in Table 2.

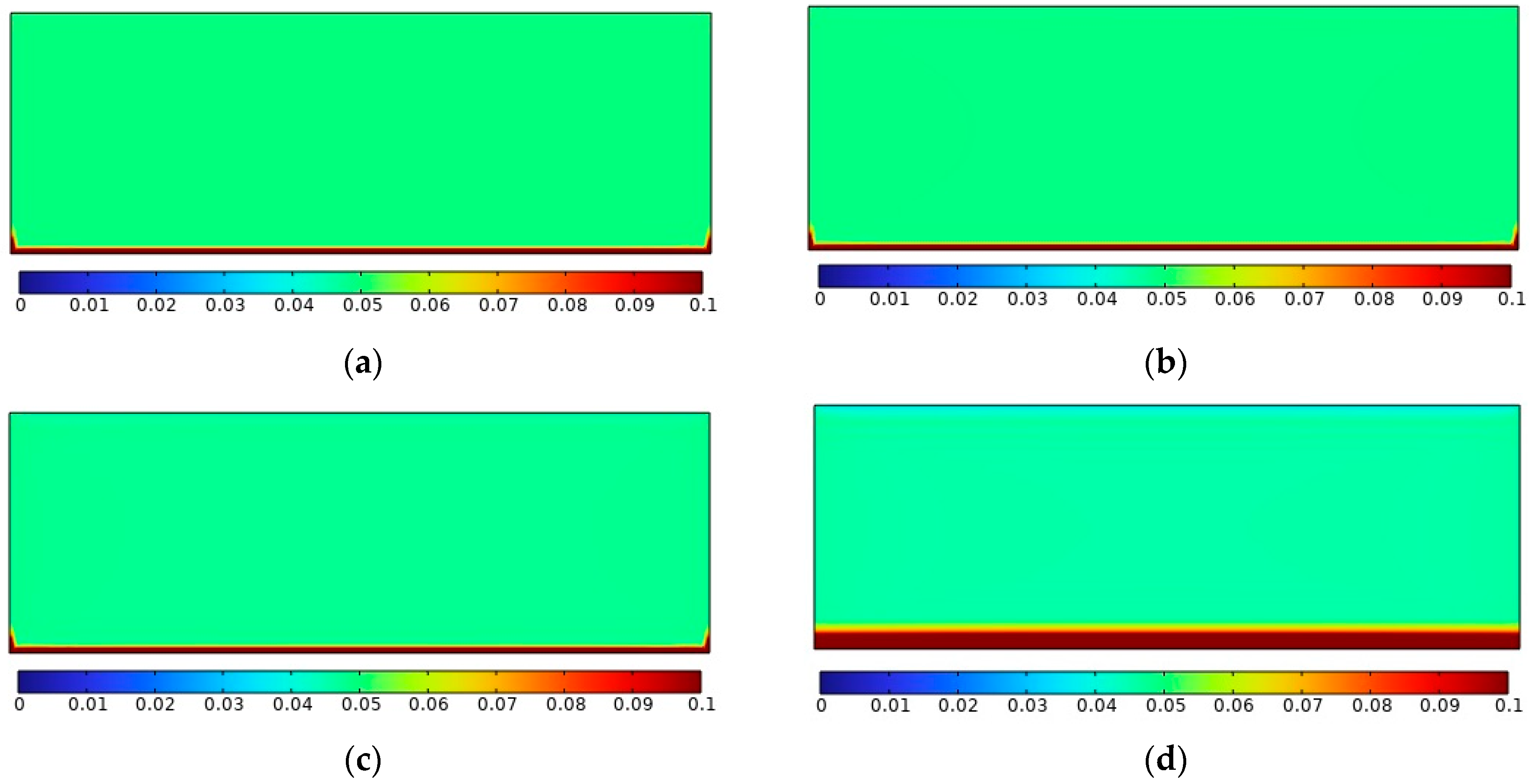
4.2. CO₂ Saturation under No Pressure Gradient

This section provides detailed qualitative and quantitative analyses of the numerical results obtained for no pressure gradient across the Opalinus Clay sample, corresponding to the Pressure Gradient [No] in Table 2. Thus, this section’s CO₂ injection and outlet pressures remain the same. Figure 3 depicts CO₂ saturation in the Opalinus Clay sample for the different injection pressures considered, i.e., 1 MPa, 2 MPa, 4 MPA, and 8 MPa. It can be clearly seen that as CO₂ is injected into the sample, despite no pressure difference between the inlet and outlet boundaries of the sample, CO₂ concentration increases in the vicinity of the inlet boundary of Opalinus Clay. Increasing CO₂ injection pressure further saturates the clay sample from the inlet boundary side, i.e., CO₂ penetrates the inlet boundary further downstream and gets stored in the sample. The scale in Figure 3 has been kept constant (0% to 10% concentration) for the different injection pressure values for effective comparison purposes. Interestingly, even when CO₂ injection pressure increases eightfold (between Figure 3a,d), the peak CO₂ concentration value doesn’t change noticeably, a phenomenon that needs further investigation.

Figure 4 depicts CO₂ concentration profiles in the axial direction of the Opalinus Clay model under no pressure gradient and for different injection pressures considered. The Y-axis shows the length of the sample while the X-axis shows CO₂ concentration, the scale of which has been zoomed in to show concentration variations from 4% to 6% only. It can be seen that at a CO₂ injection pressure of 1 MPa, its concentration is very high (100%) until y/Y < 0.05. This is potentially due to the boundary condition in the numerical solver. At y/Y = 0.05, a CO₂ concentration of 5% has been recorded, which then remains the same throughout the clay sample. Increasing CO₂ injection pressure to 2 MPa and 4 MPa decreases CO₂ concentration to 4.9% and 4.8%, respectively, throughout the sample; however, no significant change occurs near the inlet boundary, i.e., these concentration values are obtained at y/Y = 0.05. As the injection pressure increases to 8 MPa, which is very close to CO₂’s critical pressure, we observe three significant changes. Firstly, at y/Y = 0.05, a CO₂ concentration of 12% is recorded, which eventually drops to 5% at y/Y = 0.1. Thus, CO₂ is injected deeper into the clay sample at this injection pressure. Secondly, between 0.1 < y/Y < 0.95, a constant CO₂ concentration of 4.5% is recorded. When the injection pressure increased from 1 MPa to 2 MPa, this concentration decreased by 2%. When the injection pressure increased from 2 MPa to 4 MPa, this concentration further decreased by 2%. When the injection pressure increased from 4 MPa to 8 MPa (still two folds increase), this concentration decreased by 6.25%. Thus, although near-inlet CO₂ concentration has more than doubled, inner sample concentration has decreased.

Lastly, it can be observed that CO₂ concentration drastically decreases (to 3.9%) near the outlet boundary of the numerical model. As this has not been observed in the case of injection pressure of 1 MPa, and some minor decrease is observed at 2 MPa and 4 MPa, it is anticipated that this phenomenon is not due to the boundary condition at the outlet boundary of the model, rather seems influenced by the operating pressure of the sample. In conclusion, the potential of sub-critical CO₂ geosequestration in Opalinus Clay is severely limited and is not the preferred method.

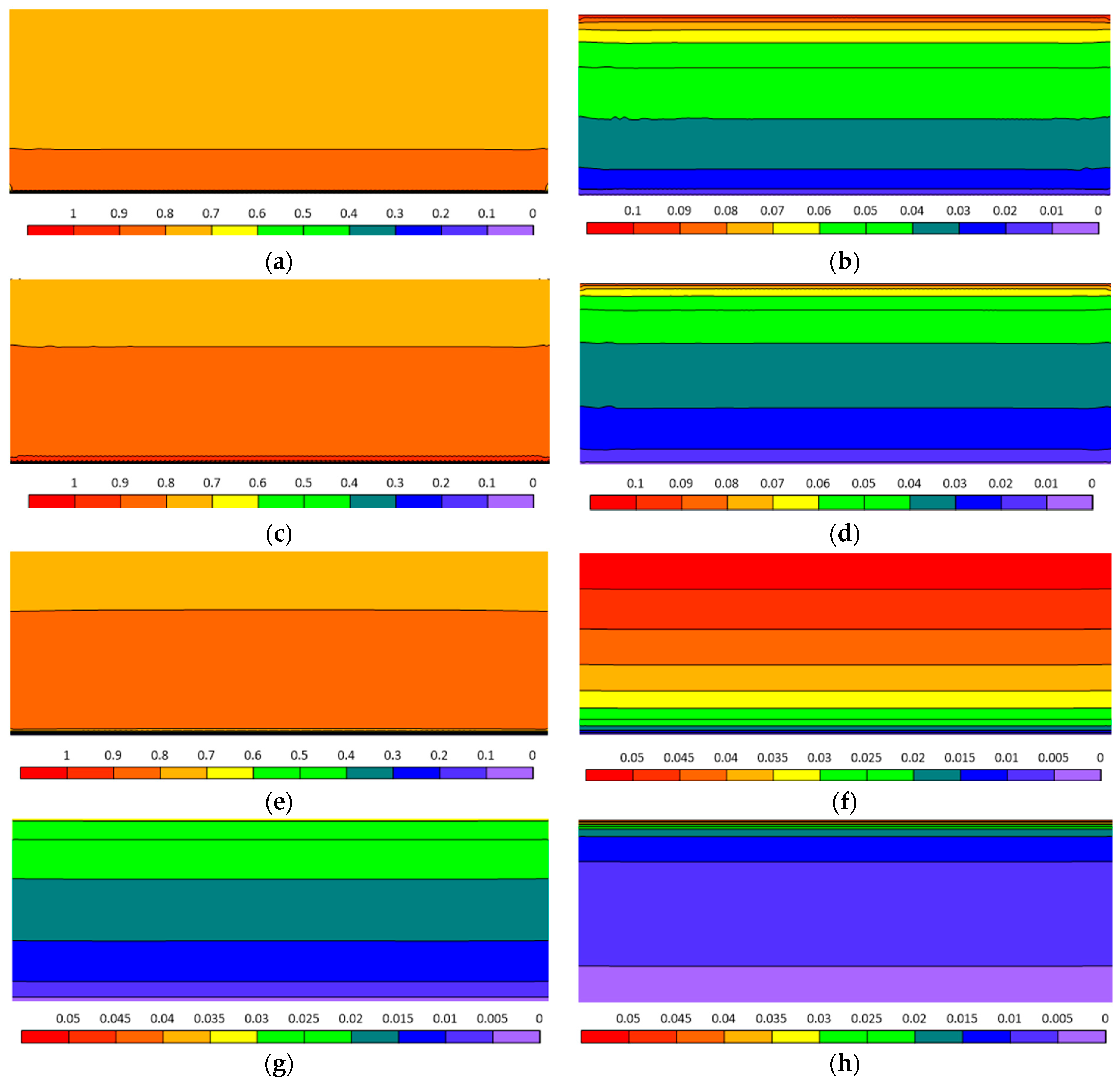
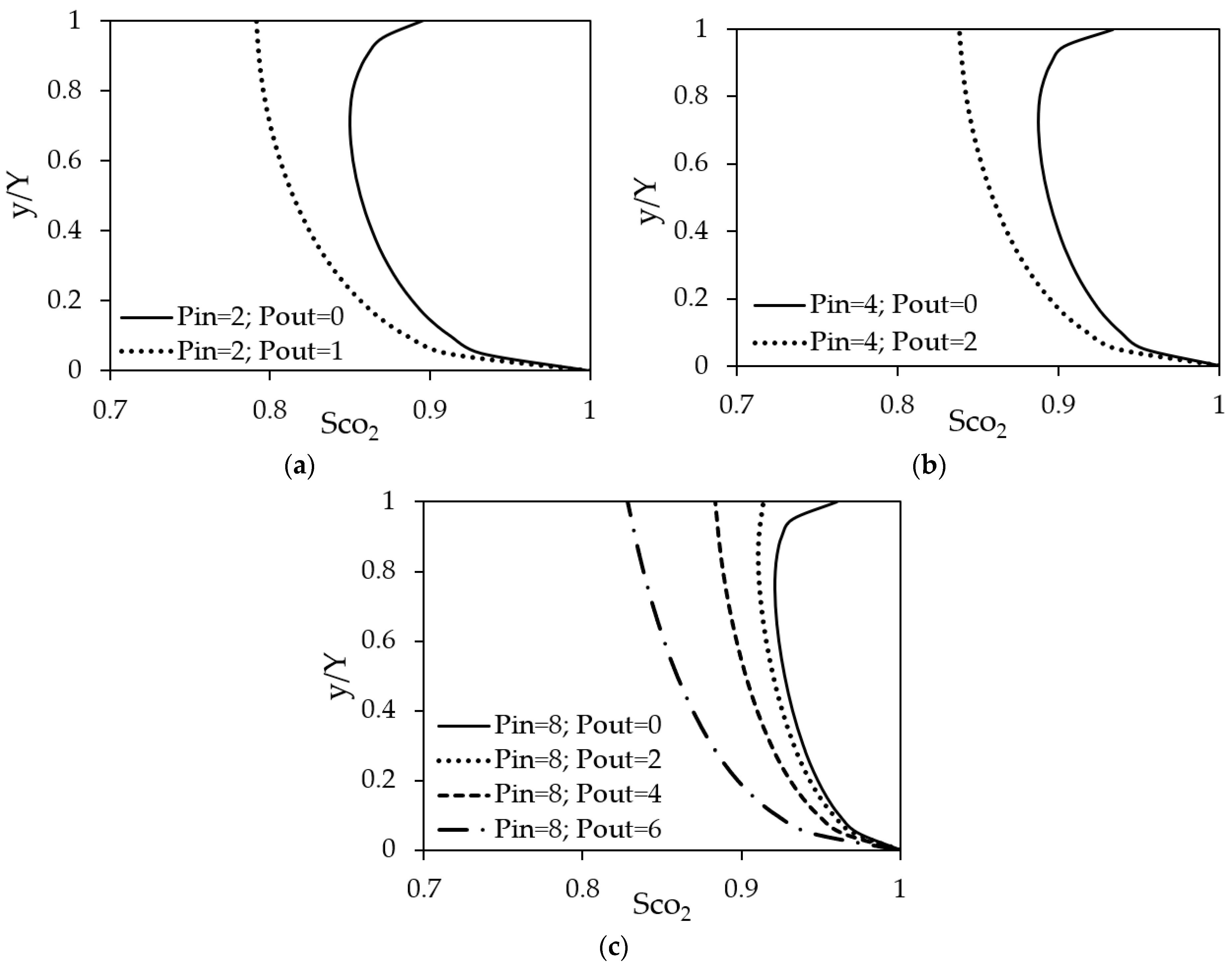
4.3. CO₂ Saturation under Positive Pressure Gradient

This section presents the numerical results obtained under positive pressure gradient conditions when the outlet pressure is kept constant at 0 MPa (gauge). Figure 5 depicts spatial variations in CO₂ concentration at different injection pressures considered. The scale of these variations has been fixed to 84% to 100% based on the results obtained. As observed in the case of no pressure gradient cases, CO₂ concentration increases from the inlet boundary side; the same is observed in the case of the positive pressure gradient. However, contrary to no pressure gradient, significantly higher CO₂ concentration and considerable axial variations are observed. It can be seen in the figure that as the injection pressure increases, and consequently the pressure gradient, CO₂ concentration increases significantly in the Opalinus Clay model, clearly demonstrating favourable CO₂ sequestration in Opalinus Clay when subjected to the positive pressure gradient. A sudden positive jump in CO₂ concentration at the outlet boundary is visible and is attributed to the operating pressure, which needs further analysis.

Figure 6 depicts the axial CO₂ concentration profiles in the Opalinus Clay model at different injection pressures while the outlet pressure is kept constant at 0 MPa. At y/Y = 0 (inlet boundary), the concentration of CO₂ is 100%, irrespective of the pressure gradient. Moving axially downstream, CO₂ concentration drops, but this drop is dependent on the pressure gradient. As the pressure gradient increases, this drop in CO₂ concentration also decreases; thus, a higher pressure gradient leads to higher CO₂ storage in Opalinus Clay. Contrary to no pressure gradient cases, the axial CO₂ concentration profiles do not remain constant till the outlet boundary. Rather, the curves are (somewhat) C-shaped, i.e., CO₂ concentration, moving downstream from the inlet boundary, keeps decreasing till y/Y = 0.7 before increasing again till the outlet boundary (i.e., y/Y = 1.0). CO₂ concentration recovery of almost 5% is recorded for all the cases under consideration. In conclusion, a higher pressure gradient leads to higher CO₂ concentration in Opalinus Clay, facilitating CO₂ geosequestration.

4.4. Effects of Outlet Pressure on CO₂ Saturation

In the previous section, a positive pressure gradient was considered based on increasing injection pressure (P_in), while the outlet pressure (P_out) was kept constant at 0 MPa. In order to understand the impact of outlet pressure on CO₂ geosequestration, this section presents detailed analyses of the effects of increasing the outlet pressure on CO₂ concentration in the Opalinus Clay model. Figure 7 depicts the difference in CO₂ concentration in the Opalinus Clay model with respect to lower pressure gradient/s; thus, Figure 7a is basically the CO₂ concentration contour at (P_in = 2; P_out = 1) minus CO₂ concentration contour obtained for (P_in = 2; P_out = 2), while Figure 7b corresponds to (P_in = 2; P_out = 0) minus (P_in = 2; P_out = 1). Hence, Figure 7a depicts the difference in CO₂ concentration between a low positive pressure gradient and no pressure gradient, while Figure 7b depicts the difference between a high positive pressure gradient and a low positive pressure gradient. Expectedly (from earlier results), as a pressure gradient (of 1 MPa) is introduced across the Opalinus Clay model, CO₂ concentration shoots up, and thus we see very large difference values (mostly brown). In comparison, when the pressure gradient rises further by 1 MPa, CO₂ concentration increases further; however, the difference is not as high as observed in Figure 7a. This further highlights the impact of pressure gradient on CO₂ storage in Opalinus Clay. The same is observed for P_in of 4 MPa however, as the injection pressure doubles, the penetration of CO₂ is observed further downstream the inlet boundary (as seen in Figure 7c). Meanwhile, very interestingly, increasing the pressure gradient leads to lesser changes near the inlet boundary. This is because CO₂ has already reached a very high concentration level in the near-inlet zone (as depicted in Figure 6), and thus, there is less margin for further enhancing CO₂ concentration in the near-inlet region. Following this explanation, it can be seen that in Figure 7e–h, the increase in CO₂ concentration slows down till we observe in Figure 7h that the increase in CO₂ concentration is only marginal. Thus, we conclude that knowing the injection pressure of CO₂ alone is not enough to predict CO₂ concentration in Opalinus Clay and that outlet pressure plays a significant role in dictating the extent of CO₂ geosequestration.

Realising that the aforementioned explanation needs further (quantitative) analyses, CO₂ concentration profiles in the axial direction have been drawn in Figure 8 for all the remaining cases from Table 2. It is noteworthy that these profiles do not show differences in CO₂ concentration, as was the case in Figure 7. Each graph in the figure is drawn in order to highlight the effect of outlet pressure on CO₂ concentration in the Opalinus Clay model. The solid line curves are the same as shown in Figure 6, for injection pressures of 2 MPa, 4 MPa, and 8 MPa. It can be seen in Figure 8a that increasing the outlet pressure to 1 MPa, which consequently results in a lower pressure gradient, leads to significantly lower CO₂ concentration in Opalinus Clay. While in the case of a 2 MPa pressure gradient, the lowest CO₂ concentration recorded was 85% at y = Y = 0.7, in the case of a 1 MPa pressure gradient, the lowest CO₂ concentration of 79% is observed at the outlet boundary. It is also noteworthy that with a reduced pressure gradient, the curve does not resemble the C-shape anymore; rather, a gradual decrease in CO₂ concentration is observed from y = Y = 0.05 to 1. The same trends are observed at injection pressures of 4 MPa and 8 MPa.

5. Conclusions

The pressure gradient across caprocks plays an important role in CO₂ geosequestration. Numerical investigations have been carried out to evaluate the role of CO₂ injection pressure and the core (downstream) pressure towards local CO₂ concentration in the Opalinus Clay model. A coupled geomechanical and multiphase flow model based on CFD-FEM coupling, has been employed to gauge the complex nature of this phenomena. Detailed investigations and extensive quantitative analyses have revealed a number of interesting facts. Based on the results obtained, we conclude the following:

• Sub-critical CO₂ injection in Opalinus Clay for geosequestration is possible under the right conditions.
• Sub-critical CO₂ injection in Opalinus Clay under no pressure gradient leads to very low CO₂ concentration (maximum 5%).
• An increase in pressure gradient leads to higher CO₂ concentration in Opalinus Clay.
• An increase in outlet pressure results in lower CO₂ concentration in the model.
• For optimal sub-critical CO₂ geosequestration in Opalinus Clay, the injection pressure should be 8 MPa, and the outlet pressure should be minimum, ideally close to 0 MPa.

It is envisaged that the results of this study will aid in deciding the appropriateness of the geological formation for CCS projects, leading towards their technical feasibility and economic viability.