Abstract
The licensing of new reactors implies the use of verified and validated neutronic codes. Numerical validation can rely on sensitivity and uncertainty studies, but they require repeated execution of time-consuming neutron flux and depletion calculations. The computational costs can be reduced by using perturbation theories. However, the uncoupled Depletion Perturbation Theory is restricted to single integral values such as nuclide density. Relying on reduced-basis approaches, which reconstruct all nuclide densities at once, is one way to get around this restriction. Furthermore, the adjoint-based reduced-order model uses the direct and adjoint equations for projection. For diffusion or transport calculations, the Exact-to-Precision Generalized Perturbation Theory was developed. Still, no models for depletion calculations are readily available. Therefore, this paper describes a novel adjoint-based reduced-order model for the Bateman Equation. It uses a range-finding algorithm to create the basis and the uncoupled Depletion Perturbation Theory for the reconstruction of the first order replaced by with a first order formulation. Our paper shows that for several perturbed cases, the depletion reduced-order model successfully reconstructs the nuclide densities. As a result, this serves as a proof of concept for our adjoint-based reduced-order model, which can perform sensitivity and uncertainty burn-up analysis in a shorter time.
1. Introduction
Nuclear power plants are a response to the production of low-carbon electricity and heat in the context of global warming. New reactor designs heavily rely on neutronic codes, which must be verified and validated. For example, one must ensure that these codes correctly evaluate the reactivity and power map of the cores throughout their entire cycle. Sensitivity and uncertainty studies can be used for the numerical validation step, but they require repeated execution of time-consuming neutron flux and depletion calculations. Hence, reducing the time required for these calculations can result in a significant reduction in the cost of numerical validation studies.
Perturbation theories help diminish the coupled diffusion and depletion calculation time. Indeed, perturbation theories are approximated computational schemes that avoid a direct calculation to obtain the responses of a perturbed problem. They often rely on a first-order approximation and the properties of the adjoint problem as in the Standard Perturbation Theory [], which allows for the calculation of the multiplication factor perturbation. In addition, the Depletion Perturbation Theory [] and the Generalized Perturbation Theory [,] use the method of Lagrange multipliers to define a generalization of the adjoint problem with the importance function [,]. This generalization enables the calculation of a reaction rate or a nuclide density perturbation. High-order methods are also available [,], but they come with an inflated computational burden. Although widely used since the seventies in reactor physics, perturbation theories are restricted to single-integral-value perturbations, such as the reaction rate, reactivity, or nuclide density. Thus, they are not of interest when the number of required responses is high, as is the case with the entire power map of a nuclear reactor core.
Reduced-basis methods are a response to this limitation. The main property of these methods is the projection of the whole solution of the perturbed problem on a reduced basis. This allows for the calculation of the full-power map or nuclide densities in a shorter period than solving the direct problem. They are usually divided into two phases, namely an offline phase carried out once and an online phase for each new calculation. The offline phase’s main goal is the computation of the reduced basis, while the online phase computes the perturbed problem solution. In reactor physics, proper orthogonal decomposition [,] or principal component analysis in statistics [] are commonly used for the creation of the basis. The basis can be constructed using a range-finding algorithm [], which captures the active subspace of our problem and provides an a posteriori estimator for the precision []. This algorithm uses randomly created snapshots and singular-value decomposition to create the basis; more details are provided in Section 2.1. Modal expansion, which uses the eigenvectors as a basis, could also be used, but it has been proven faulty for interesting perturbed neutron flux reconstruction cases []. Concerning the online phase, most reduced-order models are based on projections. For example, Galerkin projection allows for the solution of a reduced-order system instead of the full system [,,]. Separately, an adjoint-based reduced-order model uses the adjoint equation to calculate the expansion coefficients []. Hence, one does not solve a reduced-order system but simply calculates the projection of the solution on the reduced basis. Because of their computational performance, particularly for first-order formulation, where the proximity between all the calculations is taken into account, adjoint-based reduced-order models are highly appealing for sensitivity and uncertainty studies. Furthermore, only one adjoint calculation per vector of the basis is needed rather than one adjoint calculation per isotope, as in the uncoupled Depletion Perturbation Theory.
In reactor physics, the Exact-to-Precision Generalized Perturbation Theory was developed for diffusion or transport calculations []. This adjoint-based reduced-order model relies on a range-finding algorithm for the creation of the basis and the Generalized Perturbation Theory for the calculation of the expansion coefficients. For the depletion calculations, work has been done on reduced-order modeling [], but no adjoint-based reduced-order model is currently available.
Therefore, this paper describes a novel adjoint-based reduced-order model for the Bateman Equations. The novelty lies in the conjoint use of the uncoupled Depletion Perturbation Theory [] for the reconstruction of the nuclide densities in the online phase and a range-finding algorithm to create the basis in the offline phase []. Using the uncoupled Depletion Perturbation Theory would require one adjoint importance function calculation per nuclide density, which could result in up to hundreds of thousands of evaluations. Indeed, in a pressurized water reactor calculation, it is common to have a few hundred thousand depleting media, with up to fifty nuclides per medium. In comparison, our reduced-order model requires only one adjoint importance function calculation per vector of the reduced basis; thus, the number of required adjoint importance functions is independent of the number of responses. Since our reduced-order model takes advantage of the correlation between nuclide densities due to the transition matrices and the flux’s smooth spatial variation for the reduced-basis creation process, its size is often limited to a few hundred vectors. Finally, for the calculation of all nuclide densities, the number of adjoint importance calculations is divided by a factor of at least a few thousand with our adjoint-based reduced-order model compared to the uncoupled Depletion Perturbation Theory.
In this paper, the theory behind our novel adjoint-based reduced-order model is detailed in Section 2. Then, as a proof of concept, this method is tested on an elementary example proposed in Section 3. This example is a depletion calculation of the simplified chain of uranium, xenon, and samarium with nuclear data using two energy groups and a constant neutron flux.
2. Theory
We can define the nuclide densities as relevant to I isotopes (i) over time (t). This field is then governed by the Bateman Equation.
with the following burn-up and decay matrix:
The coefficients often have the following terms:
- —the decay constant of isotope i;
- —the absorption reaction rate of isotope i;
- —the fission reaction rate of isotope i;
- —the fraction of fission product j divided bythe fission of isotope i (fission yield of fissile isotope i relative to fission product j).
Given the fact that the initial density is and is time-independent, we have
We can also define a perturbed configuration as follows:
where and .
In this paper, we develop a reduced-order model of the nuclide densities at the final time () as follows:
A reduced basis () of size R is obtained with a range-finding algorithm. It is called the offline phase. Then, the expansion coefficients are calculated in the online phase, which is based on the uncoupled Depletion Perturbation Theory. This reduced-order model can then be called adjoint-based. It can replace the depletion solver for sensitivity and uncertainty burn-up analysis.
2.1. The Offline Phase
The basis () is created during the offline phase by using a range-finding algorithm. This algorithm constructs an active subspace of the nuclide densities for a precision given by the user.
If we consider that the input parameter vector () defines the coefficients of the burn-up and decay matrix () for the unperturbed case, we can also define for a set of randomized input parameters. Randomization of the input parameters is carried out on the nuclear data and the neutron flux. These data are sampled according to a normal distribution, with their nominal values as mean and a standard deviation given by the user.
First, one has to calculate R snapshots () as follows:
R is chosen by the user and can be increased if the real precision is lower than the wanted precision (), as tested in Equation (8).
Then, after the calculation of R snapshots, we can factorize using a compact singular value decomposition as follows:
Since , is an semi-unitary matrix, is an square diagonal matrix, and is an semi-unitary matrix, is the reduced basis for our reduced-order model.
The precision of the basis () can be estimated using the a posteriori estimator derived in Ref. []:
with and s is the number of trials for the estimator. With s trials, the following relation holds:
with a probability of at least for every i. One can, for example, take a value of 10 for s to have a probability of at least .
If the a posteriori estimation of the precision () is lower than the user precision, one can add new snapshots by increasing R and carry out another compact singular-value decomposition to obtain a new reduced basis. Thus, this process can be considered iterative.
The offline phase is summarized in Figure 1.
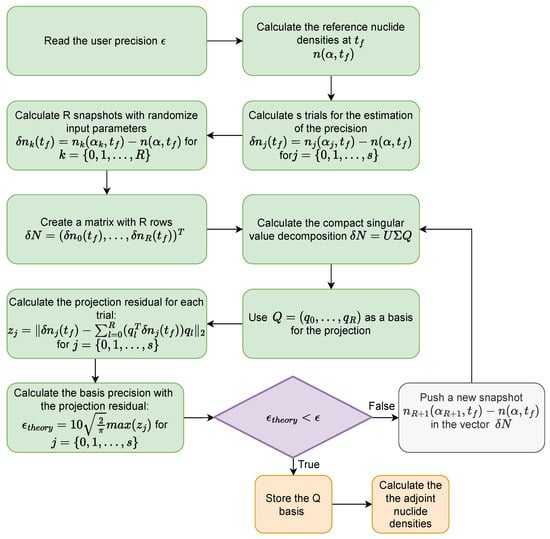
Figure 1.
Flow chart of the offline phase for the adjoint-based reduced-order model’s offline phase.
2.2. The Online Phase
Once the basis (Q) is created, the coefficients have to be calculated. If the nuclide density map is known at , we have
because of the compact singular-value decomposition process. Hence, can be calculated with the uncoupled Depletion Perturbation Theory.
Considering , if we want to calculate , we can use the method of Lagrange multipliers []. This method allows for the calculation of the changes in under the constraint of the Bateman Equation (1). First, we can define the following:
where represents the adjoint nuclide densities.
By expanding for the first order, we have
If we try to make stationary relative to all the variables except , we can derive two equations. The first one is the Bateman Equation (1).
The second one is the adjoint Bateman Equation:
By setting , the terms and vanish, and we have
Enforcing the adjoint nuclide densities to fulfill the adjoint Bateman Equation (16):
is the only term remaining in Equation (15).
Thus, for the first order, we have the following:
Each expansion coefficient () can be evaluated independently. This allows for a trivial parallelization of the online phase.
To evaluate the integral term in Equation (17), one can use a numerical integration algorithm like the trapezoidal rule. This algorithm requires the calculation of several values of and from 0 to . These calculations are performed once during the offline phase. It is worth noting that in the context of decay heat calculation, a robust time discretization is needed because of the short-lived nuclides []. For this example, one can benefit from a more advanced algorithm like the composite Simpson’s rule, allowing for a decrease in the number of samples compared to the trapezoidal integration. An example illustrating the calculation of is available in Figure 2. One can see that is equal to 0 except for the 239Pu. This allows for the calculation of at using the uncoupled Depletion Perturbation Theory. Without perturbations in , is equal to the integral , as represented in blue in Figure 2.
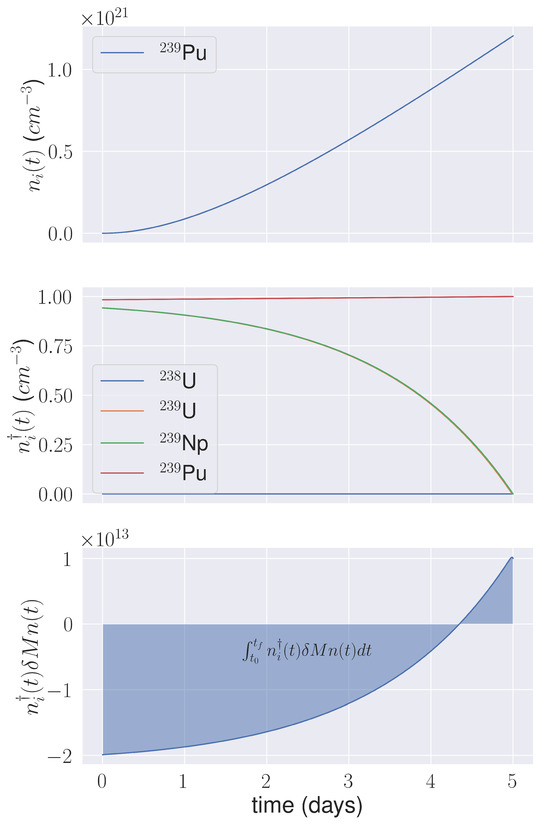
Figure 2.
Illustration for the calculation of for a vector () equal to 0 except for the 239Pu, which is equal to 1. is chosen among the 100 perturbations tested in the Results section.
In contrast to the Exact-to-Precision Generalized Perturbation Theory, we derive only a first-order formulation. Indeed, for the exact variation, the coefficient values are as follow:
and the term requires knowledge of the perturbed densities for every t, which cannot be linked to the first-order formulation without approximation like in the Exact-to-Precision Generalized Perturbation Theory.
As the basis and the adjoint densities are computed solely for a given final time, the reduced model only works for this final time. When the depletion solver is replaced by our adjoint-based reduced-order model, this imposes the use of a constant time step of length during the depletion.
3. Results and Discussion
In this section, we apply our adjoint-based reduced-order model described in Section 2 to the simplified depletion chain of uranium, xenon, and samarium with nuclear data using two energy groups. This numerical example is a proof of concept for our novel method. The description of the chains and the nuclear data values are available in Appendix A. The results of the reduced-order model are compared to the uncoupled Depletion Perturbation Theory for each nuclide. The purpose of the reduced-order model is the reconstruction of n for a depletion of 5 days. For this numerical example, vector n has the following definition:
The uncoupled Depletion Perturbation Theory results use one adjoint nuclide density calculation for each isotope, with the final values equal to 0 except for the density of the isotope of interest, which is equal to 1. The adjoint-based reduced-order model relies on the range-finding algorithm described in Section 2.1. Since the dimension of is small for this simple problem, 13 snapshots are calculated, and 10 trials are evaluated to estimate the precision. With a singular-value decomposition using 13 snapshots, the resulting basis is complete and has no approximation for this example. Hence, for this proof of concept, a complete basis with 13 vectors and an approximation with 8 vectors are tested. In the case of the complete basis with the adjoint-based reduced-order model, the errors are linked to the first-order approximation only. For each snapshot () or trial (), the nuclear data and the flux are sampled according to a normal distribution, with their nominal values as the mean and 1% as their standard deviation. The standard deviation value is set to 1% because it is the order of magnitude of the uncertainties for the nuclear data and the flux. It is noteworthy that in our example, the reduced basis is established and evaluated for a single state point, namely after a depletion of five days. Although the precision is not checked for these, it might be applicable to additional state points.
The a posteriori estimation of the precision of the basis (7) is plotted in Figure 3 as a function of the size of the basis. Results show that when the size of the basis tends towards the range of the depletion problem, the theoretical error () tends toward the machine precision.
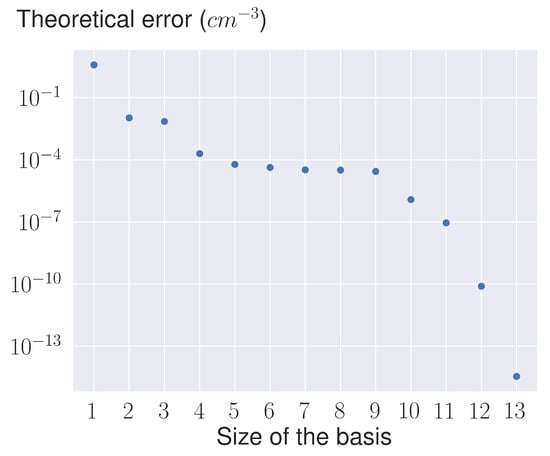
Figure 3.
Reduced-basis theoretical errors () (7) versus the size of the basis.
One can see that even for this elementary case, the adjoint-based reduced-order model can diminish the number of adjoint density calculations compared to the uncoupled Depletion Perturbation Theory. Furthermore, the range-finding algorithm will likely be more efficient for real cases where it is common to have a few hundred thousand depleting media with up to fifty nuclides. Indeed, the compact singular-value decomposition takes advantage of the correlation between nuclide densities due to the transition matrices and the flux’s smooth spatial variation for the reduced-basis creation process. It is common for this kind of real case to have the size of the reduced basis limited to a few hundred vectors [].
Figure 4 presents the distribution of the reduced-order model and uncoupled Depletion Perturbation Theory errors () as a box plot [] for 100 nuclear data and neutron flux random perturbations. The perturbed values are sampled according to a normal distribution, with their nominal values as their mean and 1% as their standard deviation. The uncoupled Depletion Perturbation Theory errors are solely related to the first-order approximation, whereas the reduced-order model’s errors depend on the precision of the reduced basis too.
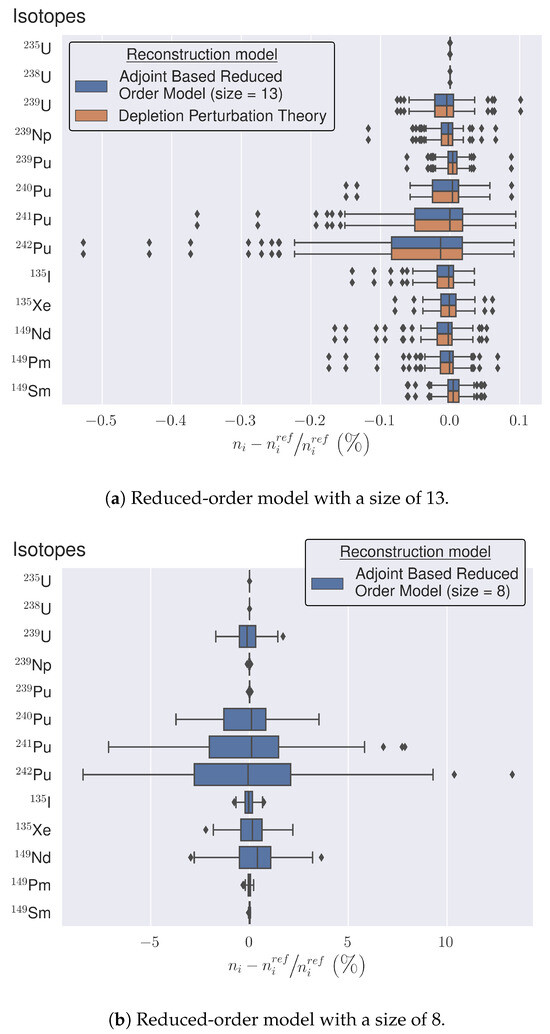
Figure 4.
Adjoint-based reduced-order model errors at compared to the uncoupled Depletion Perturbation Theory for 100 input parameter perturbations. The perturbed values are sampled according to a normal distribution, with their nominal values as mean and 1% as their standard deviation. The box plots correspond to the results with a complete basis using 13 vectors at the top (a) and one with only 8 vectors at the bottom (b).
Results show that the errors are identical for the uncoupled Depletion Perturbation Theory and the adjoint-based reduced-order model with a basis of size 13. The magnitudes of the errors are lower for 235U and 238U, which have the highest concentration values compared to the other isotopes. When the size of the basis is eight, the errors increase for the isotopes with the lowest densities, like 242Pu.
The identical errors for the uncoupled Depletion Perturbation Theory and the adjoint based reduced order model suggest that with the basis reaching machine precision, both methods have the same precision. This validates the theory and the implementation of our novel adjoint-based reduced-order model for this depletion calculation. The higher errors for the isotopes compared to 235U and 238U are linked to the first-order approximation. Indeed, the other isotopes are more sensitive to the initial perturbation, and their maximal concentration perturbations could be up to 10% when 235U and 238U are approximately 2%.
The fact that errors increase when the size of the basis diminishes is consistent with the theoretical precision and is linked to the wide range of nuclide densities, namely for 242Pu to for 238U. This could be an issue for isotopes with low densities and large cross sections like 135Xe and is inherent to the compact singular-value decomposition process. One way to take into account the importance of the isotope and not only its concentration is to weigh each nuclide density according to its absorption cross section. This was successfully applied in Ref. [] with weights equal to the absorption cross section of the isotope divided by the absorption cross section of 238U.
Finally, the computational time of our adjoint-based reduced-order model is not linked to the number of responses of interest but to the number of vectors in the basis. This time also depends on the integration algorithm and the number of samples used. For our simple case, when we use a basis of size 8 with 12 samples and the trapezoidal rule, the reduced-order model is 20% faster than the exact resolution-based model using the matrix exponential method. When we increase the number of samples, the computational time is increased. It is, for example, 300% slower than the exact resolution with 120 samples. However, these results could be improved for a real case with a better use of the singular-value decomposition.
Overall, this serves as a proof of concept for our adjoint-based reduced-order model, which can replace the depletion solver for sensitivity and uncertainty burn-up analysis.
4. Conclusions
Our results serve as a proof of concept for the novel adjoint-based reduced-order model presented in this paper. This reduced-order model makes use of both the uncoupled Depletion Perturbation Theory and a range-finding algorithm. This allows for the reconstruction of the whole nuclide densities with a number of adjoint importance functions independent of the number of responses. Our results show that this reduced-order model achieves promising results for the reconstruction of the perturbed nuclide densities. Therefore, it can readily replace the depletion solver to perform sensitivity and uncertainty studies in a shorter time.
Future work will focus on employing this methodology to real case applications like full pressurized water reactor or sodium-cooled fast reactor calculations. This will support the results and demonstrate the performance of the model in a real test case.
Concerning the perspectives, this theory could be extended in several ways. First, the weighted-basis case has to be taken into account. A quasi-exact formulation could be derived with a linear approximation for the variation of the perturbed densities. Finally, an alternative adjoint-based reduced-order model using the coupled Depletion Perturbation Theory could be of great interest.
Author Contributions
Conceptualization, T.S.; methodology, T.S.; software, T.S.; writing—original draft preparation, T.S.; writing—review and editing, P.A. and F.N.; supervision, P.A. and F.N.; project administration, P.A. and F.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data and software used in this study are openly available at https://github.com/ThibaultSauzedde/depletion_adjoint_rom (accessed on 13 May 2024).
Acknowledgments
The authors wish to thank Laurent Buiron and Jean Tommasi for helpful discussions of the manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Description of the Depletion Chains
The depletion chains used in the proof of concept are given in Figure A1, Figure A2, Figure A3. They have been simplified to fit a Pressurized Water Reactor’s needs. The nuclear data using two energy groups are given in Table A1. They are inspired by the one in example two of Ref. [] and are not chosen to be particularly realistic. The definitions of the parameters are:
- —the absorption cross section of the group g;
- —the fission cross section of the group g;
- —the capture cross section of the group g;
- g—the energy group, with the values 0 (fast neutrons) and 1 (thermal neutrons);
- —the initial concentration;
- Y—the fraction of fission products by the fission of all the isotopes (fission yield of all the isotopes);
- —the decay constant.
The neutron flux values are for the fast group and for the thermal one.

Table A1.
Nuclear data values for the numerical example, blank cells correspond to null values.
Table A1.
Nuclear data values for the numerical example, blank cells correspond to null values.
| Isotope | (barn) | (barn) | (barn) | (barn) | (cm− 3) | Y | (s− 1) |
|---|---|---|---|---|---|---|---|
| 235U | 1.80 | 100.0 | 1.5 | 55.0 | |||
| 238U | 0.35 | 2.000 | |||||
| 239U | |||||||
| 239Np | |||||||
| 239Pu | 2.00 | 190.0 | 1.8 | 120.0 | |||
| 240Pu | 0.20 | 110.0 | |||||
| 241Pu | 2.50 | 180.0 | 0.5 | 140.0 | |||
| 242Pu | 0.70 | 70.00 | |||||
| 135I | 0.0640 | ||||||
| 135Xe | 0.0010 | ||||||
| 149Nd | 0.0109 | ||||||
| 149Pm | |||||||
| 149Sm |
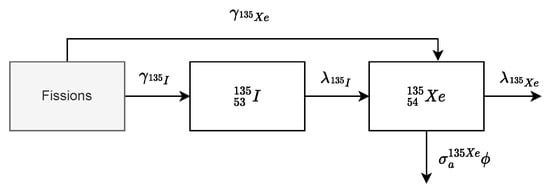
Figure A1.
Simplified depletion chain of the Xe.
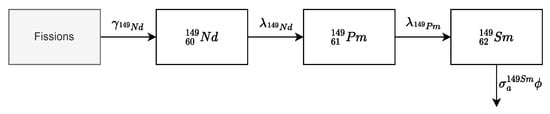
Figure A2.
Depletion chain of the Sm.
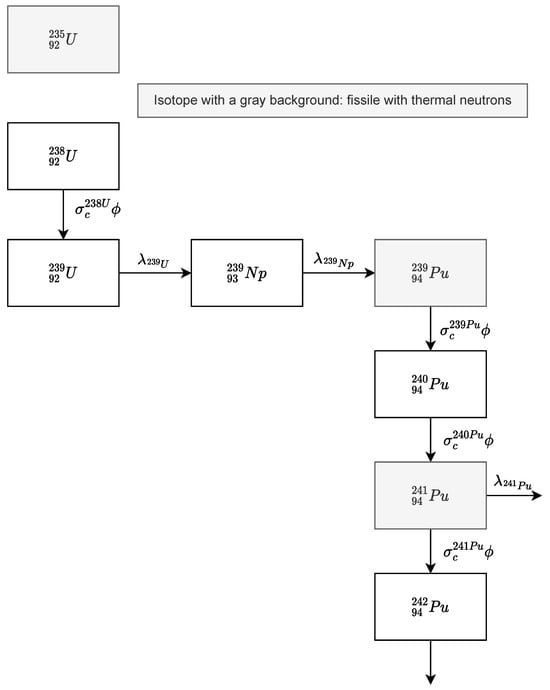
Figure A3.
Simplified depletion chain of uranium.
References
- Usachev, L.N. Perturbation theory for the breeding factor, and other ratios of a number of different processes in a reactor. Sov. At. Energy 1963, 15, 1255–1265. [Google Scholar] [CrossRef]
- Williams, M.L. Perturbation and Sensitivity Theory for Reactor Burnup Analysis; Technical Report; Office of Scientific and Technical Information (OSTI): Oak Ridge, TN, USA, 1979. [Google Scholar] [CrossRef][Green Version]
- Gandini, A. A generalized perturbation method for bi-linear functionals of the real and adjoint neutron fluxes. J. Nucl. Energy 1967, 21, 755–765. [Google Scholar] [CrossRef]
- Kiedrowski, B.C. Review of Early 21st-Century Monte Carlo Perturbation and Sensitivity Techniques for k-Eigenvalue Radiation Transport Calculations. Nucl. Sci. Eng. 2017, 185, 426–444. [Google Scholar] [CrossRef]
- Lewins, J. Importance: The Adjoint Function: The Physical Basis of Variational and Perturbation Theory in Transport and Diffusion Problems; North-Holland Publishing Company: Amsterdam, The Netherlands, 1965. [Google Scholar]
- Pomraning, G. A Variational Principle for Linear Systems. J. Soc. Ind. Appl. Math. 1964, 13, 511–519. [Google Scholar] [CrossRef]
- Mitani, H. Higher Order Perturbation Method in Reactor Calculations. Nucl. Sci. Eng. 1973, 51, 180–188. [Google Scholar] [CrossRef]
- Sauzedde, T.; Archier, P.; Nguyen, F. Strengths and weaknesses of the modal expansion method for perturbations calculations in nuclear reactor physics. Ann. Nucl. Energy 2023, 193, 110024. [Google Scholar] [CrossRef]
- Buchan, A.G.; Pain, C.C.; Fang, F.; Navon, I.M. A POD reduced-order model for eigenvalue problems with application to reactor physics. Int. J. Numer. Methods Eng. 2013, 95, 1011–1032. [Google Scholar] [CrossRef]
- Bang, Y.; Wang, C.; Abdel-Khalik, H.S. State-Based Adjoint Method for Reduced Order Modeling. Transp. Theory Stat. Phys. 2012, 41, 101–132. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150202. [Google Scholar] [CrossRef]
- Abdel-Khalik, H.S. Adaptive Core Simulation. Ph.D. Thesis, North Carolina State University, Raleigh, NC, USA, 2004. [Google Scholar]
- Halko, N.; Martinsson, P.G.; Tropp, J.A. Finding Structure with Randomness: Probabilistic Algorithms for Constructing Approximate Matrix Decompositions. SIAM Rev. 2011, 53, 217–288. [Google Scholar] [CrossRef]
- Cherezov, A.; Sanchez, R.; Joo, H.G. A reduced-basis element method for pin-by-pin reactor core calculations in diffusion and SP3 approximations. Ann. Nucl. Energy 2018, 116, 195–209. [Google Scholar] [CrossRef]
- Quarteroni, A.; Rozza, G. Reduced Order Methods for Modeling and Computational Reduction; Springer International Publishing: Berlin/Heidelberg, Germany, 2014. [Google Scholar] [CrossRef]
- German, P.; Ragusa, J.C. Reduced-order modeling of parameterized multi-group diffusion k-eigenvalue problems. Ann. Nucl. Energy 2019, 134, 144–157. [Google Scholar] [CrossRef]
- Wang, C.; Abdel-Khalik, H.S. Exact-to-Precision Generalized Perturbation Theory for Eigenvalue Problems. Nucl. Eng. Des. 2013, 256, 130–140. [Google Scholar] [CrossRef]
- Castagna, C.; Aufiero, M.; Lorenzi, S.; Lomonaco, G.; Cammi, A. Development of a Reduced Order Model for Fuel Burnup Analysis. Energies 2020, 13, 890. [Google Scholar] [CrossRef]
- Kalman, D. Leveling with Lagrange: An Alternate View of Constrained Optimization. Math. Mag. 2009, 82, 186–196. [Google Scholar] [CrossRef]
- Linden, N.; Tsilanizara, A.; Tommasi, J. Depletion Perturbation Theory in decay heat calculation context. Ann. Nucl. Energy 2023, 185, 109743. [Google Scholar] [CrossRef]
- Sauzedde, T.; Archier, P.; Nguyen, F. A Comparison of the Modal Expansion Method and Exact-to-Precision Generalized Perturbation Theory Capabilities in Reactor Physics. In Proceedings of the International Conference on Physics of Reactors, San Francisco, CA, USA, 21–24 April 2024. [Google Scholar]
- Krzywinski, M.; Altman, N. Visualizing samples with box plots. Nat. Methods 2014, 11, 119–120. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).