Optimization of Renewable Energy Hydrogen Production Systems Using Volatility Improved Multi-Objective Particle Swarm Algorithm
Abstract
1. Introduction
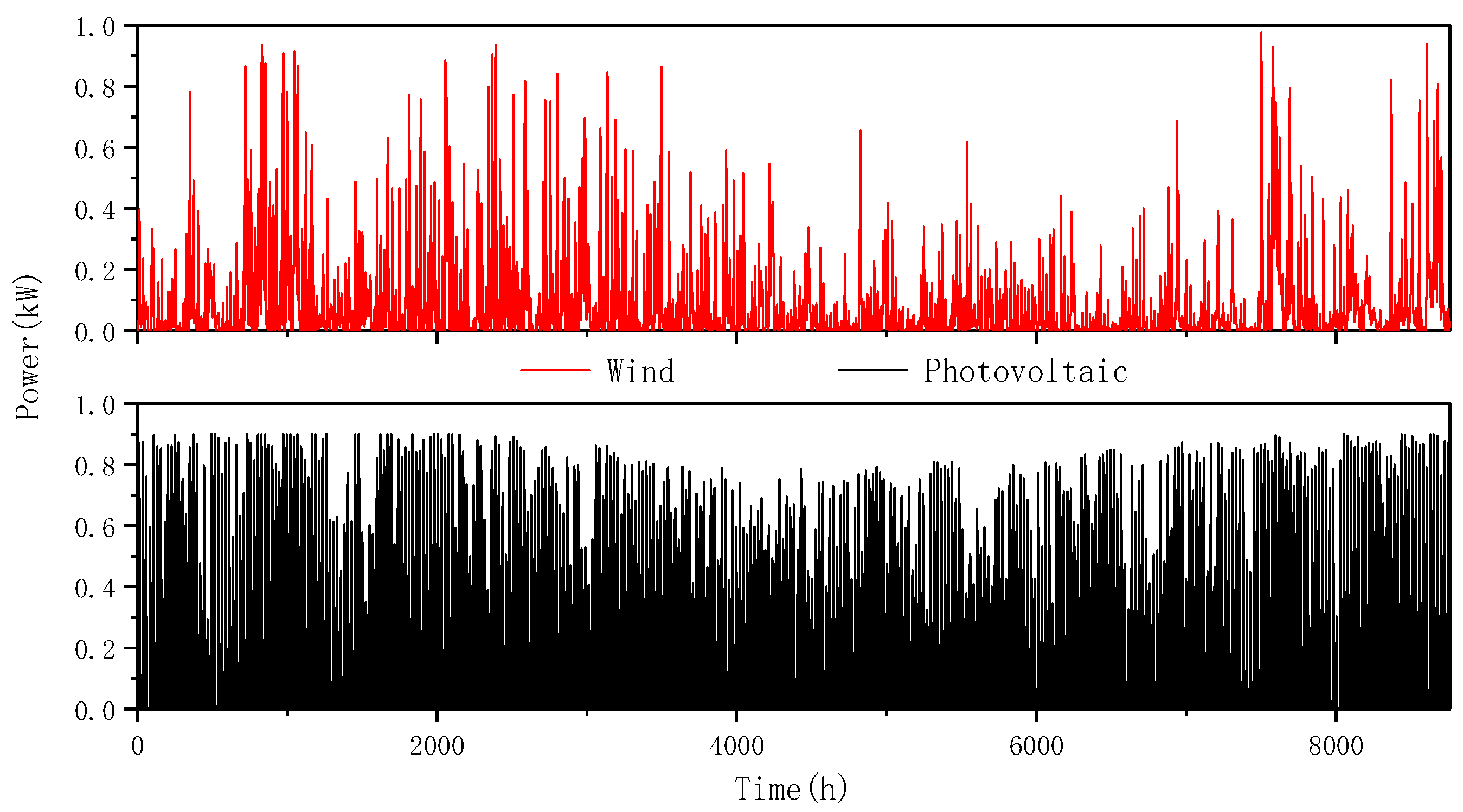
2. Analysis of Natural Resources and Hydrogen Energy Loads
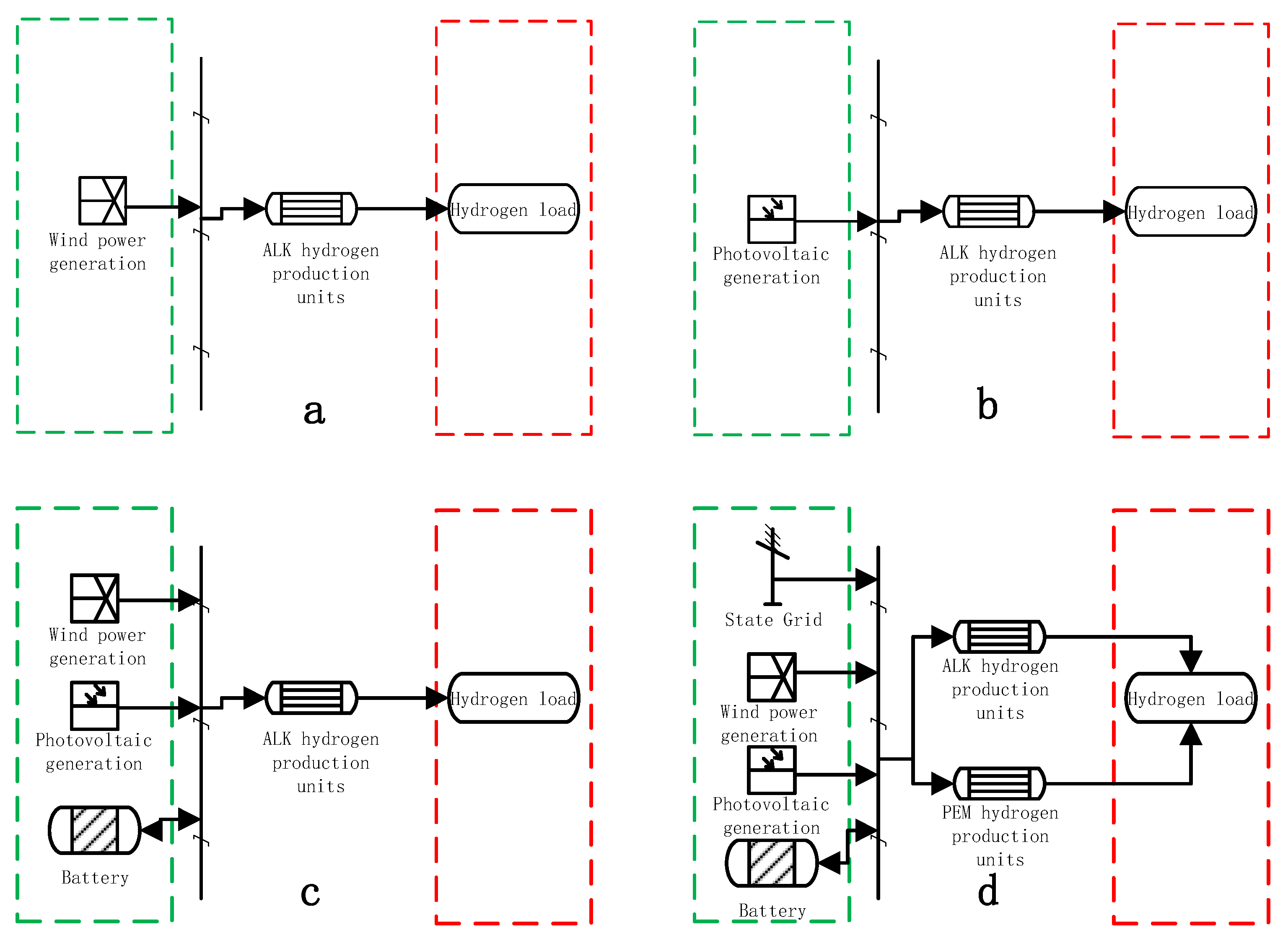
3. Different Power Source Scenarios for Hydrogen Production System Architecture and Mathematical Models
3.1. Mathematical Model of Wind Power Generation
3.2. Photovoltaic Power Generation Mathematical Model
3.3. Energy Storage Battery and Hydrogen Production System Model
3.4. System Architecture Design
3.5. Mathematical Optimization Modeling of System Capacity
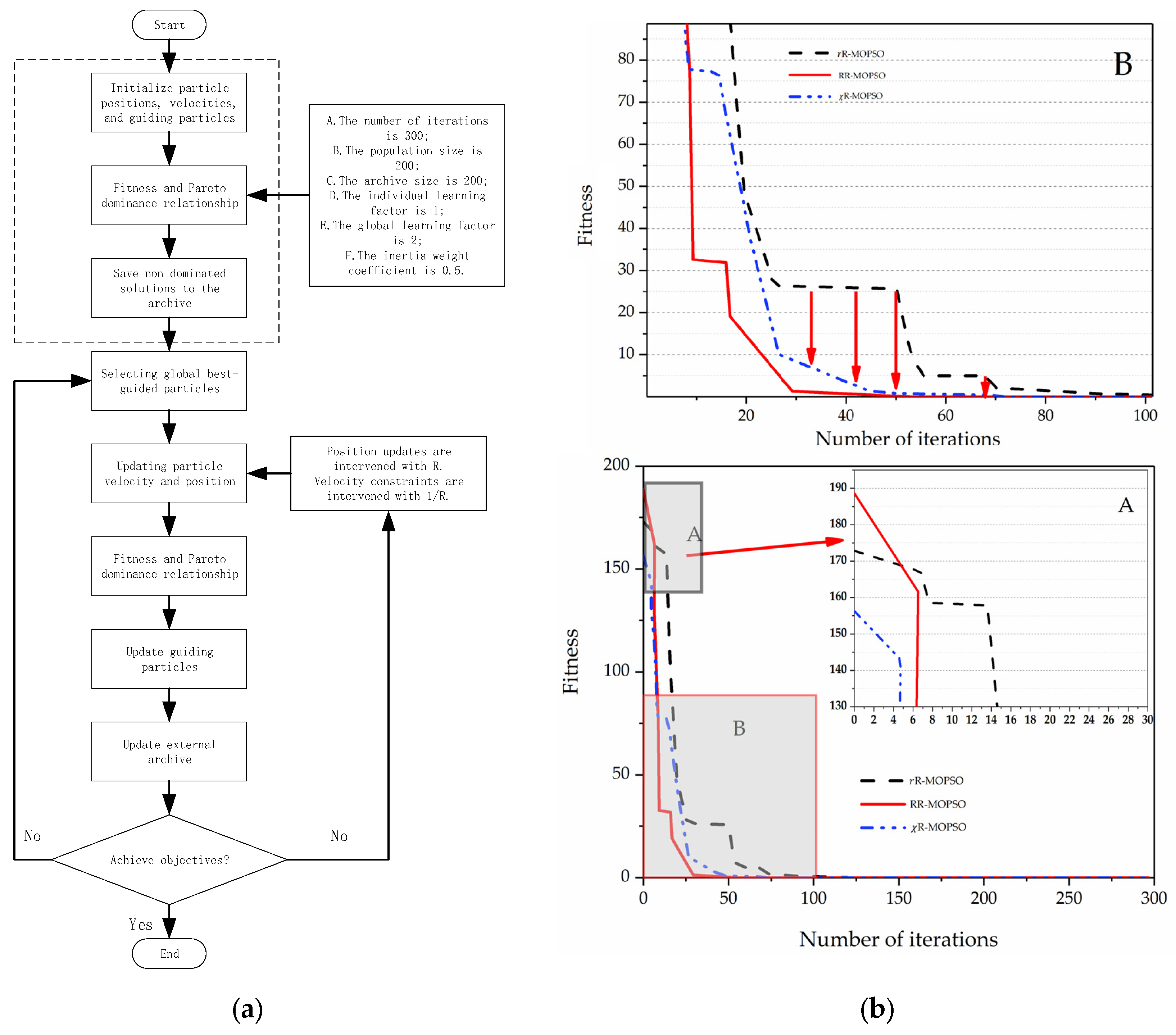
3.6. Optimization Process
4. Results and Discussion
4.1. Optimization Results of Wind Power Generation–ALK Electrolytic Hydrogen Production
4.2. Optimization Results of Photovoltaic Generation-ALK Electrolytic Hydrogen Production
4.3. Optimization Results of Photovoltaic Generation–ALK Electrolytic Hydrogen Production
4.4. Optimization Results of Wind Power Generation–Photovoltaic Generation–Battery Energy Storage–Grid-Connected without Grid Dependence–ALK–PEM Electrolytic Hydrogen Production
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Zhang, D.; Ji, Q.; Shi, X. Regional renewable energy development in China: A multidimensional assessment. Pergamon 2020, 124, 109797. [Google Scholar] [CrossRef]
- Yang, Y.; Sun, J.; Li, Q. Status and Prospect of Research on China’s Energy Structure Optimization. Coal Eng. 2019, 51, 149–153. [Google Scholar]
- Liu, L.; Zhai, R.; Hu, Y. Performance evaluation of wind-solar-hydrogen system for renewable energy generation and green hydrogen generation and storage: Energy, exergy, economic, and enviroeconomic. Energy 2023, 2276, 127386. [Google Scholar] [CrossRef]
- Wang, X.; Virguez, E.; Xiao, W.; Mei, Y.; Patiño-Echeverri, D.; Wang, H. Clustering and dispatching hydro, wind, and photovoltaic power resources with multiobjective optimization of power generation fluctuations: A case study in southwestern China. Energy 2019, 189, 116250. [Google Scholar] [CrossRef]
- Noureldeen, O.; Ibrahim, A.M.A. Modeling, Implementation and Performance Analysis of a Grid-Connected Photovoltaic/Wind Hybrid Power System. In Proceedings of the 2018 International Conference on Innovative Trends in Computer Engineering (ITCE), Aswan, Egypt, 19–21 February 2018. [Google Scholar]
- Parra, D.; Patel, M.K. Techno-economic implications of the electrolyser technology and size for power-to-gas systems. Int. J. Hydrogen Energy 2016, 41, 3748. [Google Scholar] [CrossRef]
- Zhang, B.; Yang, Y. Status and trend of wind/photovoltaic power development. Electr. Power 2006, 39, 65–69. [Google Scholar]
- Li, Y.; Deng, X.; Zhang, T.; Liu, S.; Song, L.; Yang, F.; Ouyang, M.; Shen, X. Exploration of the configuration and operation rule of the multi-electrolyzers hybrid system of large-scale alkaline water hydrogen production system. Appl. Energy 2023, 331, 120413. [Google Scholar] [CrossRef]
- Yu, D.; Zhang, J.; Wang, X. Optimal Capacity Configuration of Grid-connected Wind-PV-storage Hybrid Power Generation System. Proc. CSU-EPSA 2019, 31, 7. [Google Scholar]
- Li, J.; Cheng, R.; Liu, J. Stochastic Optimal of Integrated Energy System in Low-carbon Parks Considering Carbon Capture Storage and Power to Hydrogen. Electr. Power 2024, 1–8. [Google Scholar]
- Carmo, M.; Fritz, D.L.; Mergel, J.; Stolten, D. A comprehensive review on PEM water electrolysis. Int. J. Hydrogen Energy 2013, 38, 4901–4934. [Google Scholar] [CrossRef]
- Li, H.; Sun, B.; Li, J. Progress of green hydrogen production technology under dual carbon goal. Battery Bimon. 2024, 54, 271–275. [Google Scholar]
- Shami, T.M.; El-Saleh, A.A.; Alswaitti, M.; Al-Tashi, Q.; Summakieh, M.A.; Mirjalili, S. Particle swarm optimization: A comprehensive survey. IEEE Access 2022, 10, 10031–10061. [Google Scholar] [CrossRef]
- Fukuyama, Y.; Nishida, H.; Todaka, Y. Particle swarm optimization for optimal operational planning of energy plants. Stud. Comput. Intell. 2009, 248, 159–173. [Google Scholar]
- Zhang, T.; Li, W.; Wang, R. Surrogated-assisted multimodal multi-objective optimization for hybrid renewable energy system. Complex Intell. Syst. 2022, 9, 4075–4087. [Google Scholar] [CrossRef]
- Aghajani, G.R.; Shayanfar, H.A. Shayeghi, H. Presenting a multi-objective generation scheduling model for pricing demand response rate in micro-grid energy management. Energy Convers. Manag. 2015, 106, 308–321. [Google Scholar] [CrossRef]
- Hasankhani, A.; Hakimi, S.M. Stochastic energy management of smart microgrid with intermittent renewable energy resources in electricity market. Energy 2021, 219, 119668. [Google Scholar] [CrossRef]
- Zheng, H.; Xie, L.; Ye, L. Hybrid Energy Storage Smoothing Output Fluctuation Strategy Considering Photovoltaic Dual Evaluation Indicators. Trans. China Electrotech. Soc. 2021, 36, 1805–1817. [Google Scholar]
- Lu, J.; Huang, D.; Ren, H. Data-driven source-load robust optimal scheduling of integrated energy production unit including hydrogen energy coupling. Glob. Energy Interconnect. 2023, 6, 375–388. [Google Scholar] [CrossRef]
- Zhu, J.; Jin, Y.; Zhu, W.; Lee, D.-K.; Bohlooli, N. Multi-objective planning of micro-grid system considering renewable energy and hydrogen storage systems with demand response. Int. J. Hydrogen Energy 2023, 48, 15626. [Google Scholar] [CrossRef]
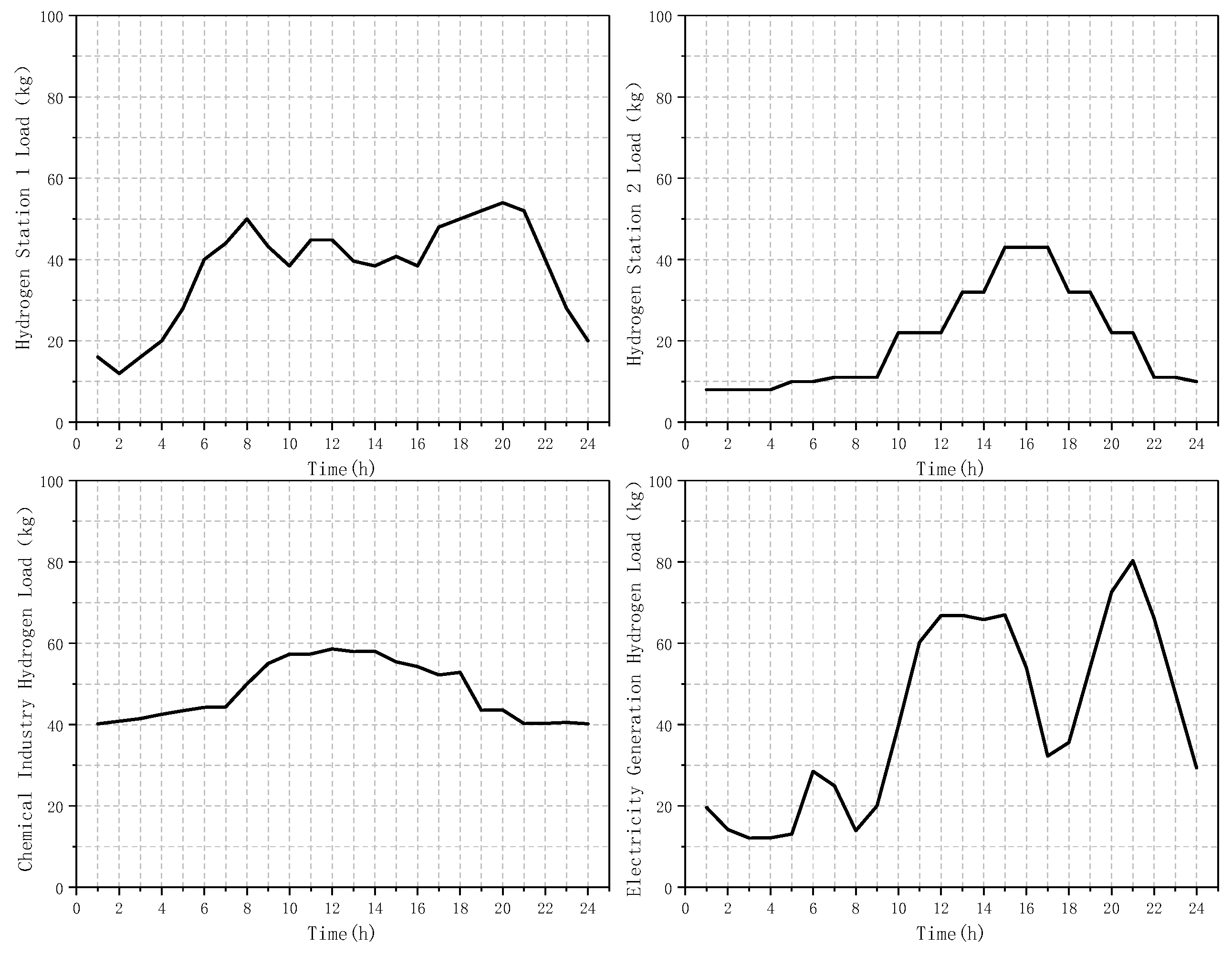
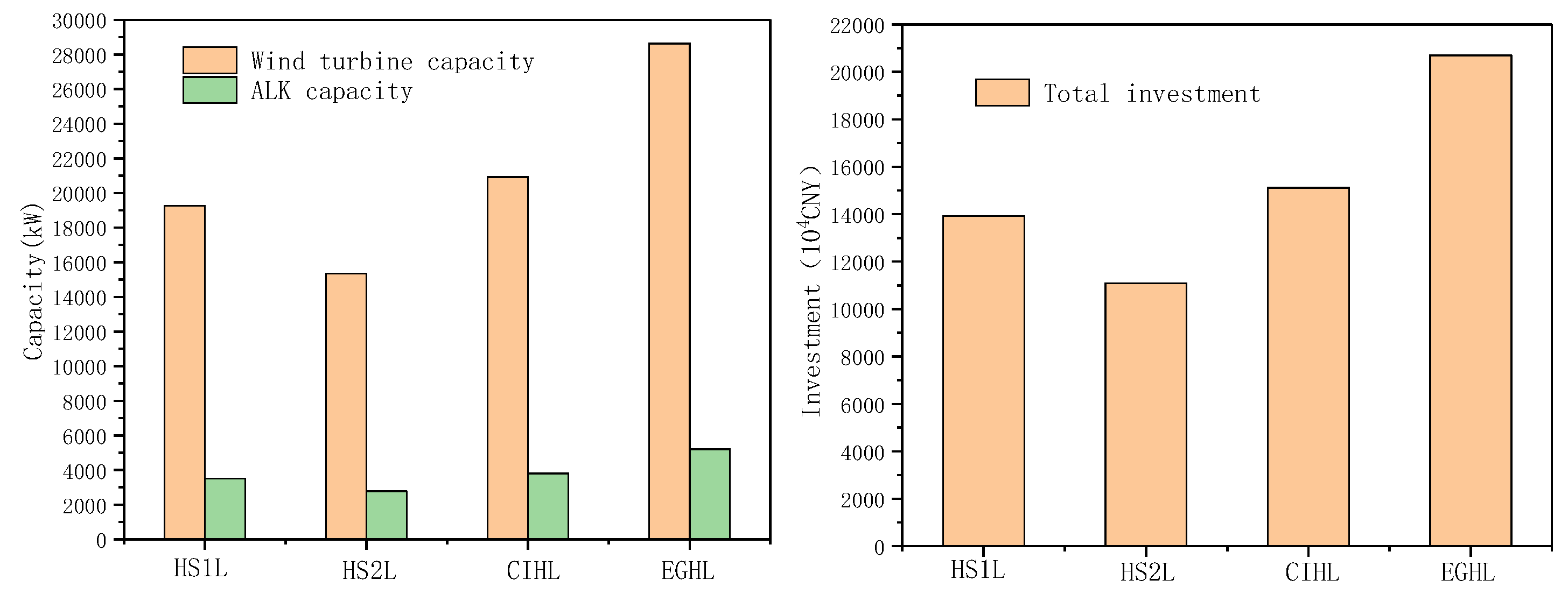
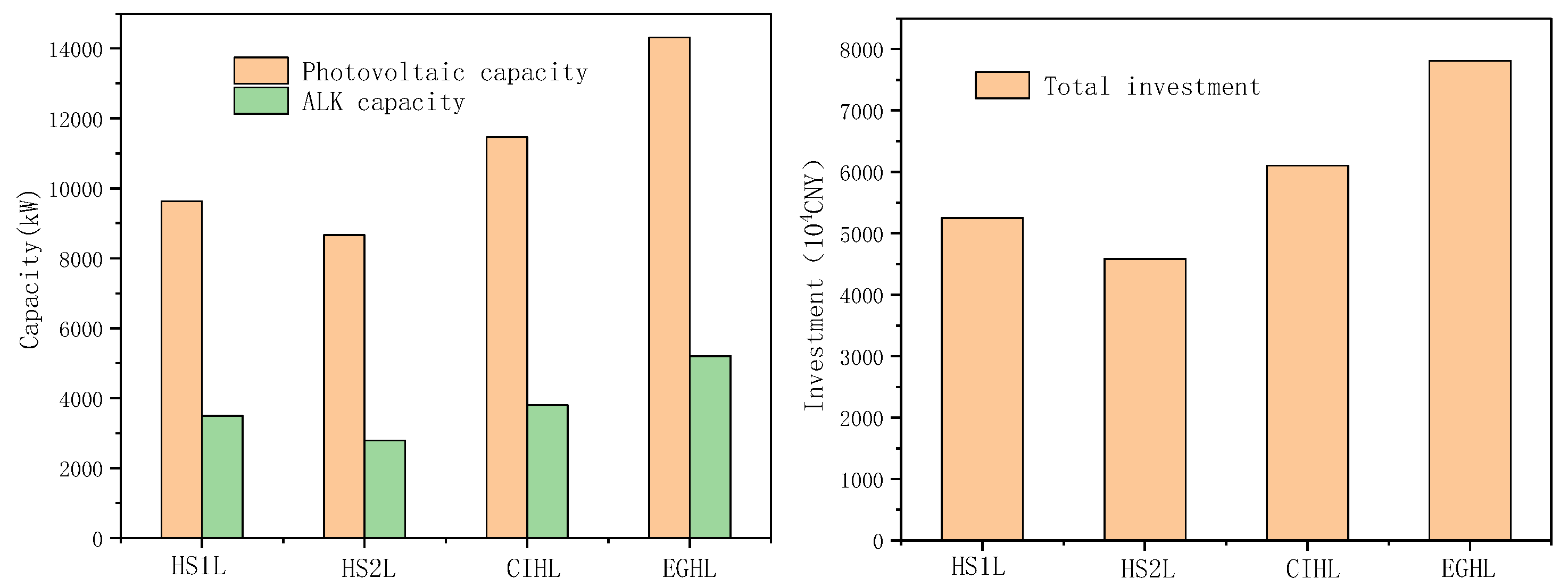
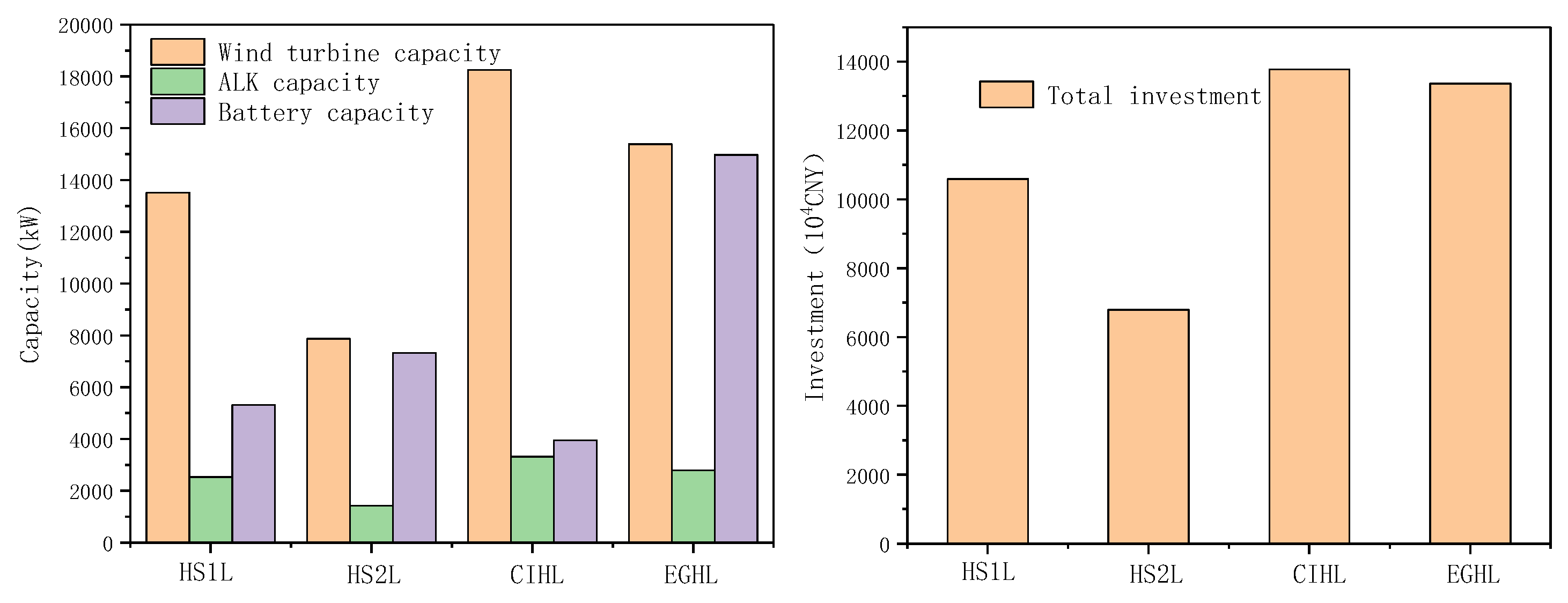
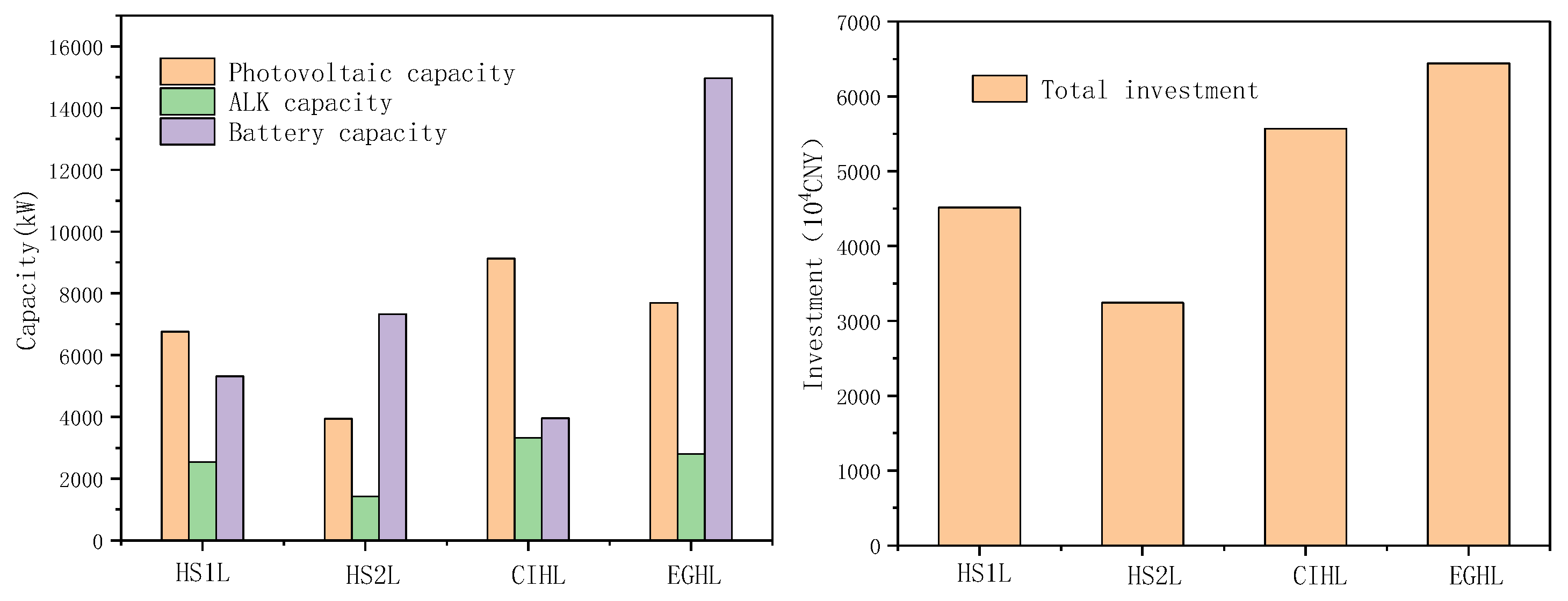
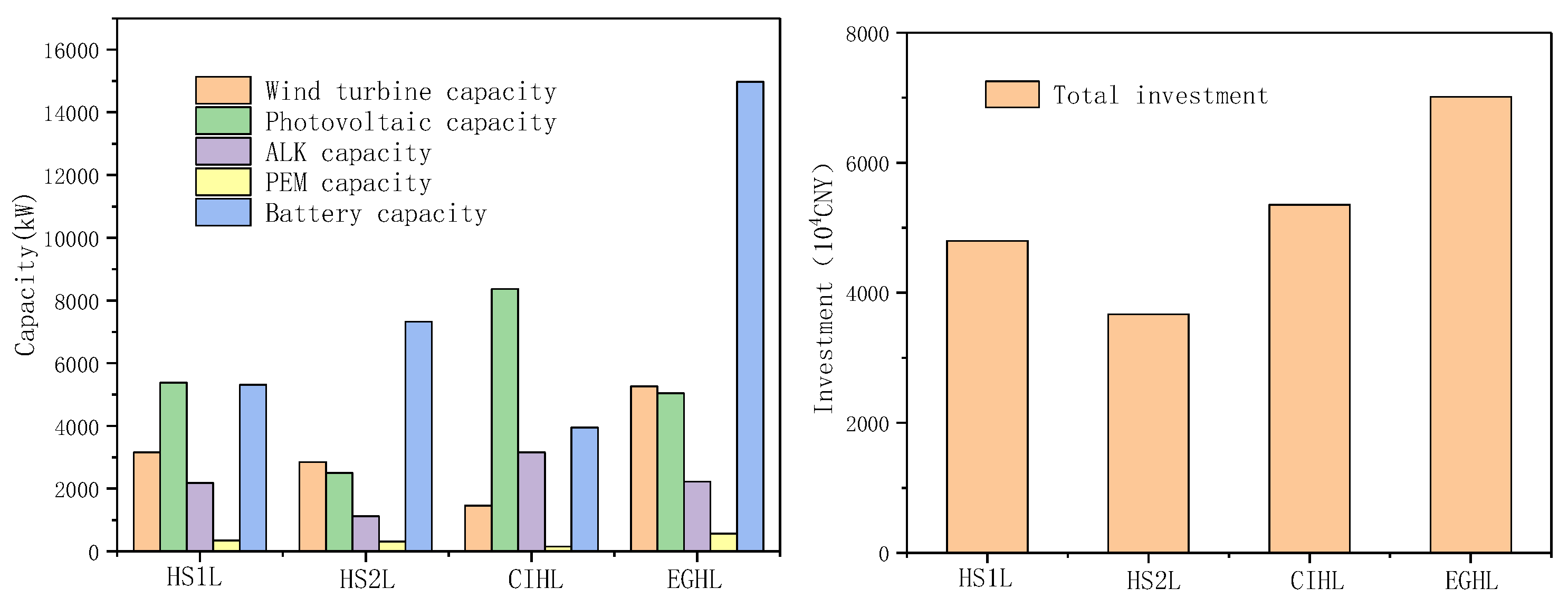
| Hydrogen Station 1 Load | Hydrogen Station 2 Load | Chemical Industry Hydrogen Load | Electricity Generation Hydrogen Load | |
|---|---|---|---|---|
| Daily Load (kg/d) | 898 | 484 | 1154 | 997 |
| Peak Load (kg/h) | 54 | 43 | 59 | 80 |
| Volatility | 0.0467 | 0.0723 | 0.016 | 0.0684 |
| Item Name | Unit Price (CNY) |
|---|---|
| Wind power generation | 6500/kW |
| Photovoltaic generation | 4000/kW |
| Battery | 1500/kW |
| ALK hydrogen production units | 4000/kW |
| PEM hydrogen production units | 12,000/kW |
| System Scheme | Hydrogen Station 1 Load | Hydrogen Station 2 Load | Chemical Industry Hydrogen Load | Electricity Generation Hydrogen Load |
|---|---|---|---|---|
| Hybrid system and wind–ALK hydrogen production system (Generator capacity) | 55.69% | 65.14% | 53.02% | 64.03% |
| Hybrid system and photovoltaic–ALK hydrogen production system (Generator capacity) | 11.39% | 30.28% | 6.04% | 28.05% |
| Hybrid hydrogen production mode and the ALK hydrogen production mode (Hydrogen production unit capacity) | 27.57% | 48.69% | 12.77% | 46.27% |
| Hybrid system and wind–ALK hydrogen production system (Investment cost) | 65.53% | 66.89% | 64.59% | 66.11% |
| Hybrid system and photovoltaic–ALK hydrogen production system (Investment cost) | 8.63% | 12.25% | 6.16% | 10.18% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Chen, X.; Yang, Q.; Li, B.; Yue, Z.; Ampah, J.D.; Liu, H.; Yao, M. Optimization of Renewable Energy Hydrogen Production Systems Using Volatility Improved Multi-Objective Particle Swarm Algorithm. Energies 2024, 17, 2384. https://doi.org/10.3390/en17102384
Wang H, Chen X, Yang Q, Li B, Yue Z, Ampah JD, Liu H, Yao M. Optimization of Renewable Energy Hydrogen Production Systems Using Volatility Improved Multi-Objective Particle Swarm Algorithm. Energies. 2024; 17(10):2384. https://doi.org/10.3390/en17102384
Chicago/Turabian StyleWang, Hui, Xiaowen Chen, Qianpeng Yang, Bowen Li, Zongyu Yue, Jeffrey Dankwa Ampah, Haifeng Liu, and Mingfa Yao. 2024. "Optimization of Renewable Energy Hydrogen Production Systems Using Volatility Improved Multi-Objective Particle Swarm Algorithm" Energies 17, no. 10: 2384. https://doi.org/10.3390/en17102384
APA StyleWang, H., Chen, X., Yang, Q., Li, B., Yue, Z., Ampah, J. D., Liu, H., & Yao, M. (2024). Optimization of Renewable Energy Hydrogen Production Systems Using Volatility Improved Multi-Objective Particle Swarm Algorithm. Energies, 17(10), 2384. https://doi.org/10.3390/en17102384








