Energy Management of Hydrogen Hybrid Electric Vehicles—Online-Capable Control
Abstract
1. Introduction
1.1. Context and Motivation
1.2. Literature Review
- (a)
- The potential for NO reduction is much larger for H-HEVs than for conventional diesel-powered HEVs, as well as standard H vehicles.
- (b)
- Although ultra-lean combustion of hydrogen–air mixtures allows HICEs to emit near-zero NO emissions, this is a highly delicate process. Small deviations from the chosen operating point of the HICE can increase the instantaneous NO emissions by over two orders of magnitude.
- (c)
- The mixed hybrid drivetrain architecture is required to achieve consistent NO reductions across a wide range of challenging driving missions. However, it is more complex than the standard parallel or series hybrid architectures.
1.3. Research Statement
- To the authors’ best knowledge, this publication presents the first online-capable EMS controller for a H-HEV, explicitly accounting for the H-NO trade-off.
- A case study, using the same mixed H-HEV as discussed in [18], allows for a comparison between the proposed online-capable EMS controller and the full theoretically reachable Pareto front obtained by the DP algorithm. The results show that the proposed online-capable controller reaches close-to-optimal performance on all investigated driving missions, covering a broad range of driving scenarios.
1.4. Paper Structure
2. Modeling
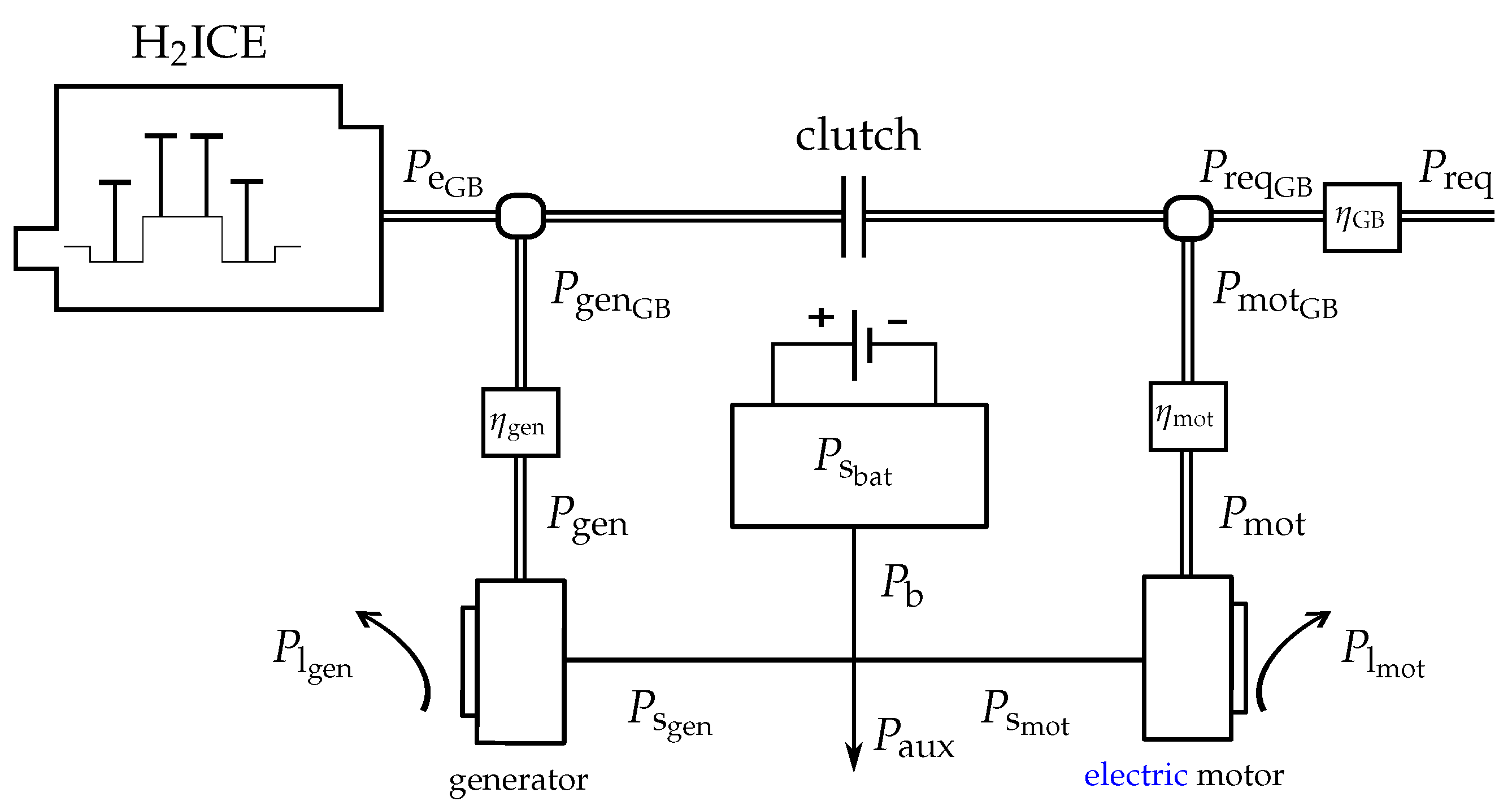
2.1. Map-Based Powertrain Model
2.1.1. Driving Modes
2.1.2. Rotational Speeds
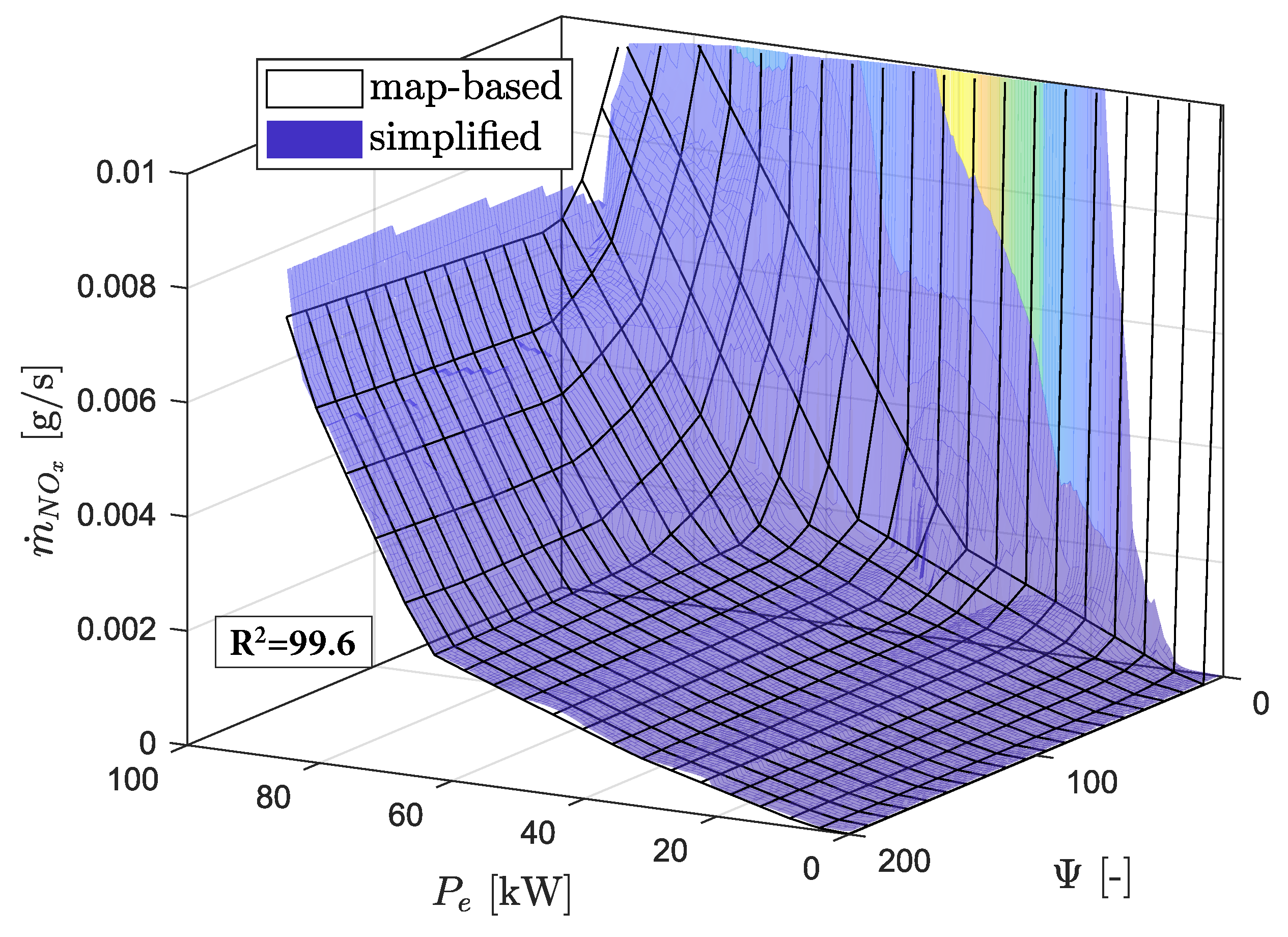
2.1.3. EMS Including NO
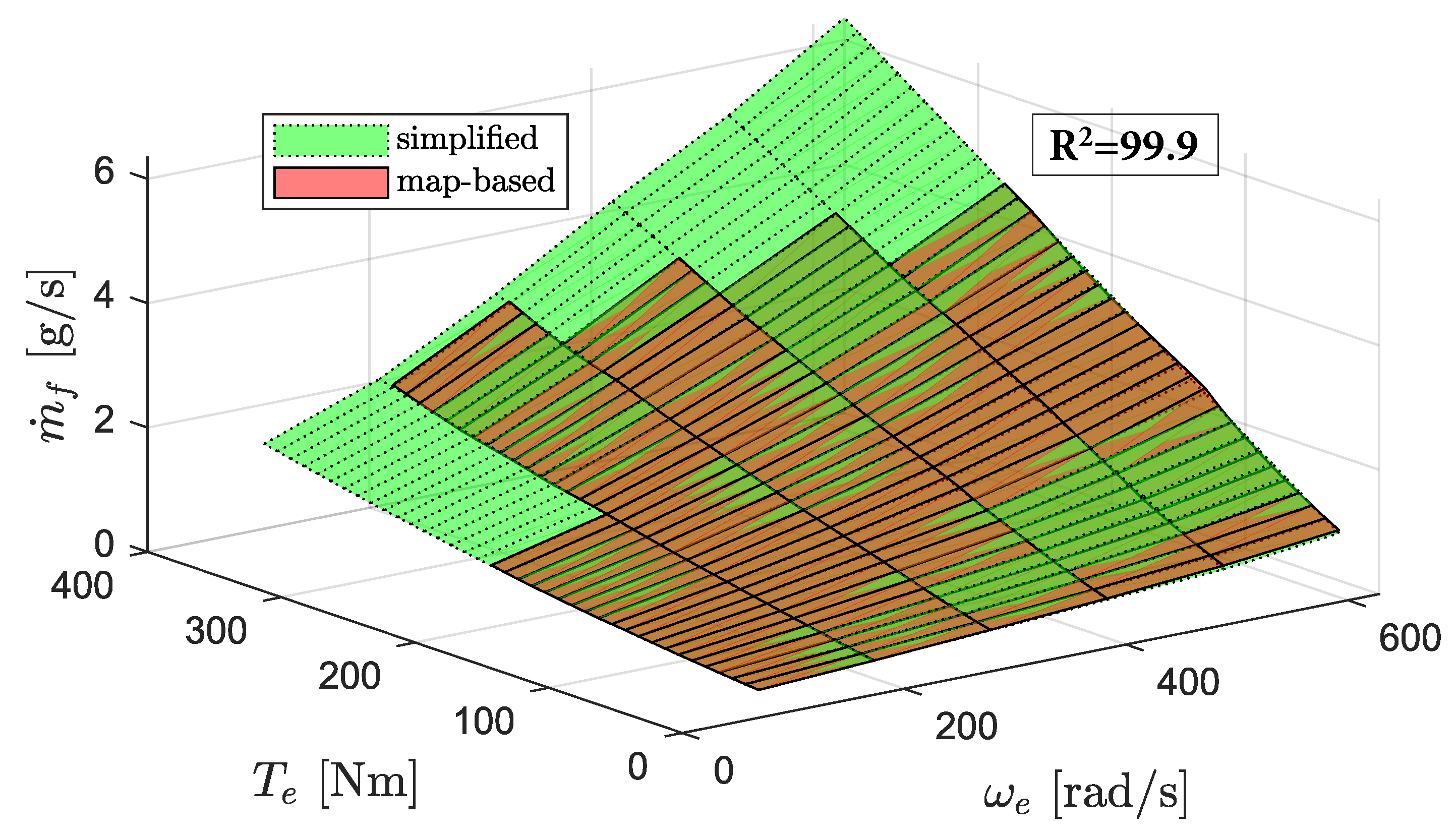
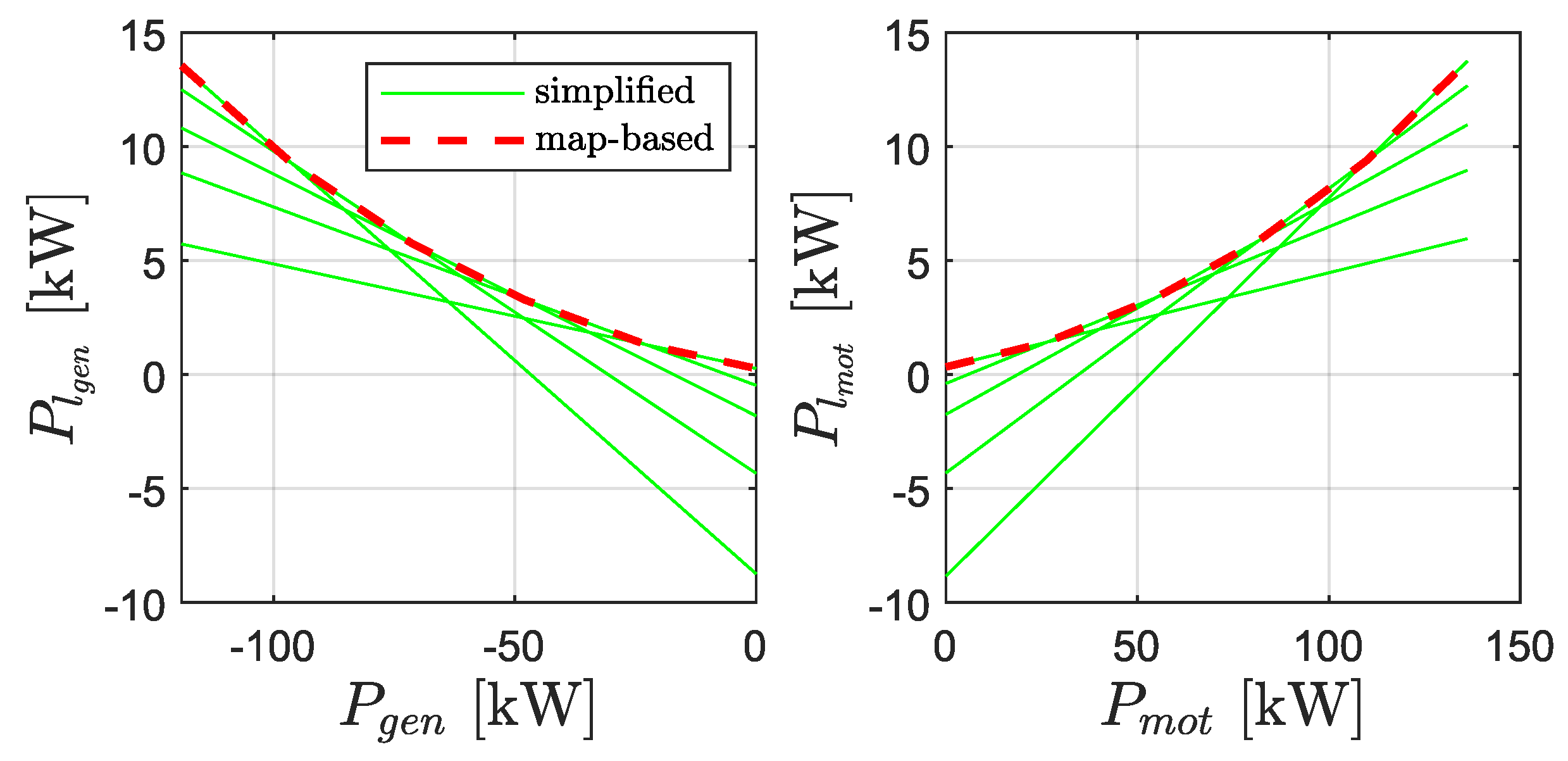
2.2. Simplified Powertrain Model
2.2.1. Parallel Mode
2.2.2. Series Mode
- Step 1: The generator power and the trade-off factor () are discretized.
- For each realizable , all possible combinations (, ) that result in are identified. By using the map-based model, the corresponding hydrogen consumption and the NO emissions are calculated (steps 3–5).
- By looping over all , Equation (19) is used to formulate the extended cost for all identified pairs of (, ) and the corresponding trade-off weight (step 7).
- Minimizing the extended cost function over all previously identified operating points (, ) yields the optimal engine operating point (, ) for the corresponding (step 8).
- Finally, for the generator power () and the trade-off parameter (), the following optimal values are stored for later use: optimal engine power (), optimal hydrogen consumption (), and optimal NO emissions () (steps 9–11).
| Algorithm 1 Pre-optimization for series mode. |
|
2.3. Optimization Parameters
3. Control-Oriented Optimization Problem
3.1. Driving Mode Estimation
3.2. Convex Optimization Problem
3.2.1. Cost Function and Dynamics
3.2.2. Power Split
3.2.3. Constraint Relaxations
3.2.4. Battery
3.2.5. Input and State Domains
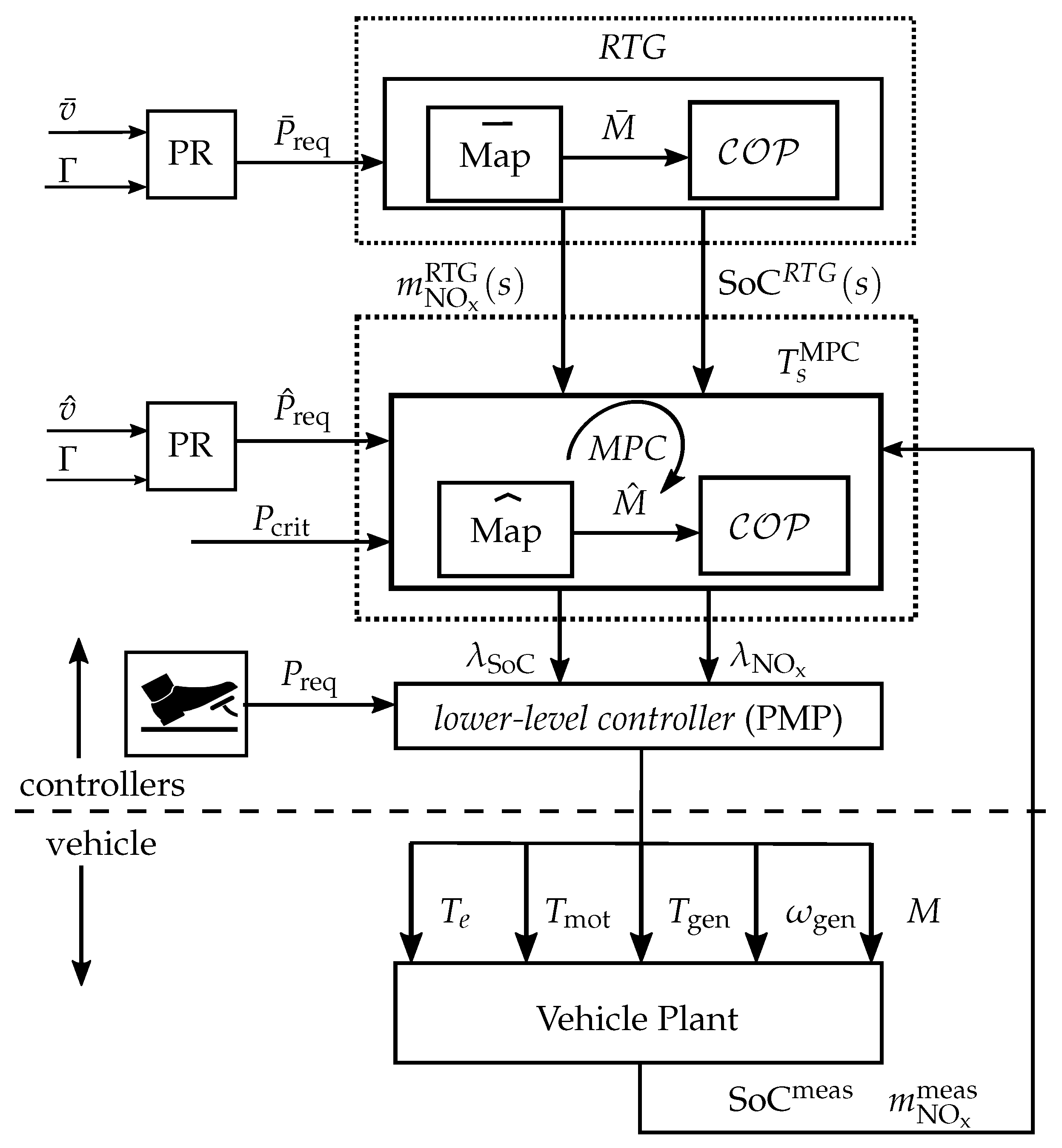
4. Controller Structure
4.1. Lower-Level Controller
4.2. MPC
4.3. Reference Trajectory Generator
| Algorithm 2 RTG iterations. |
|
5. Case Study
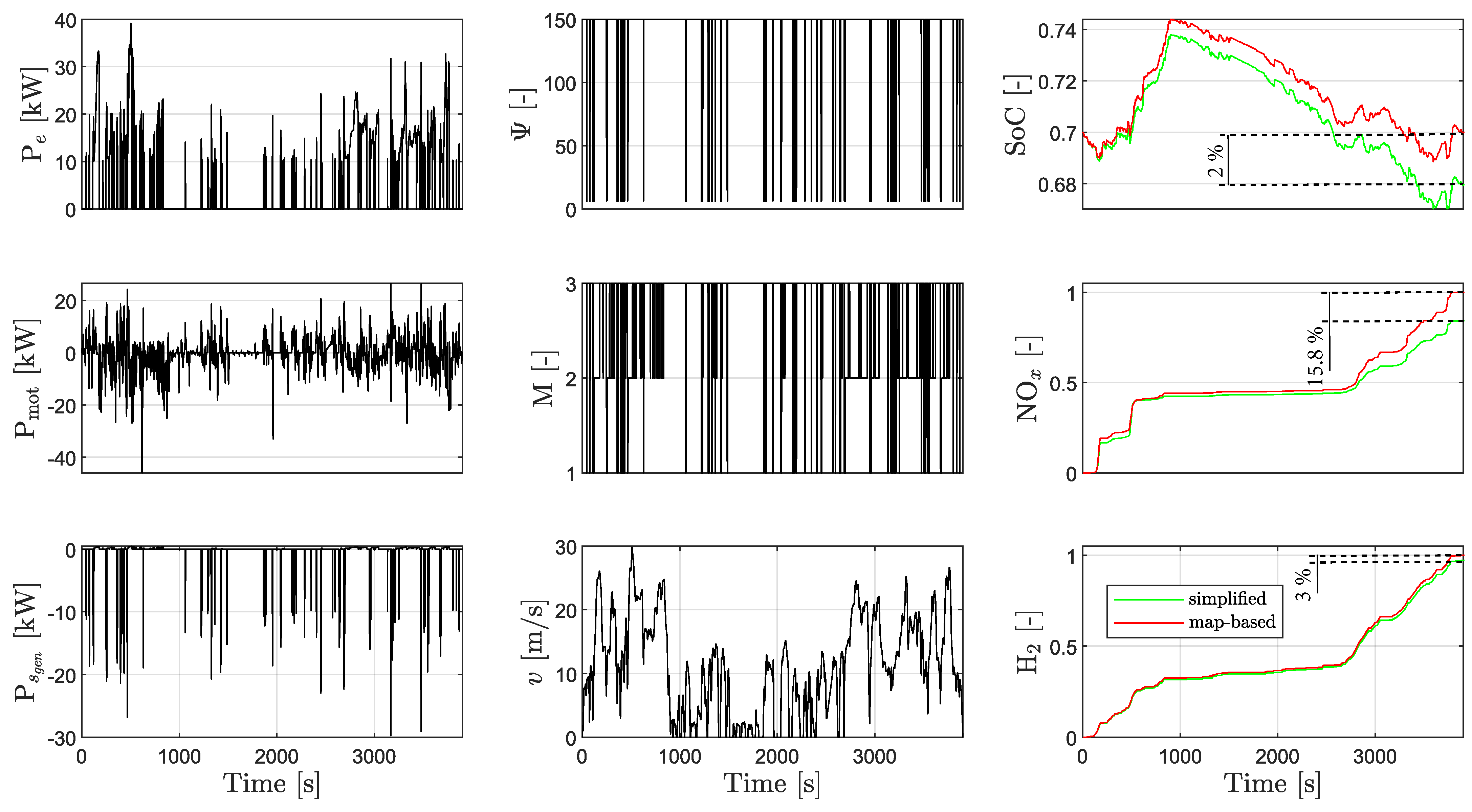
5.1. Driving Missions
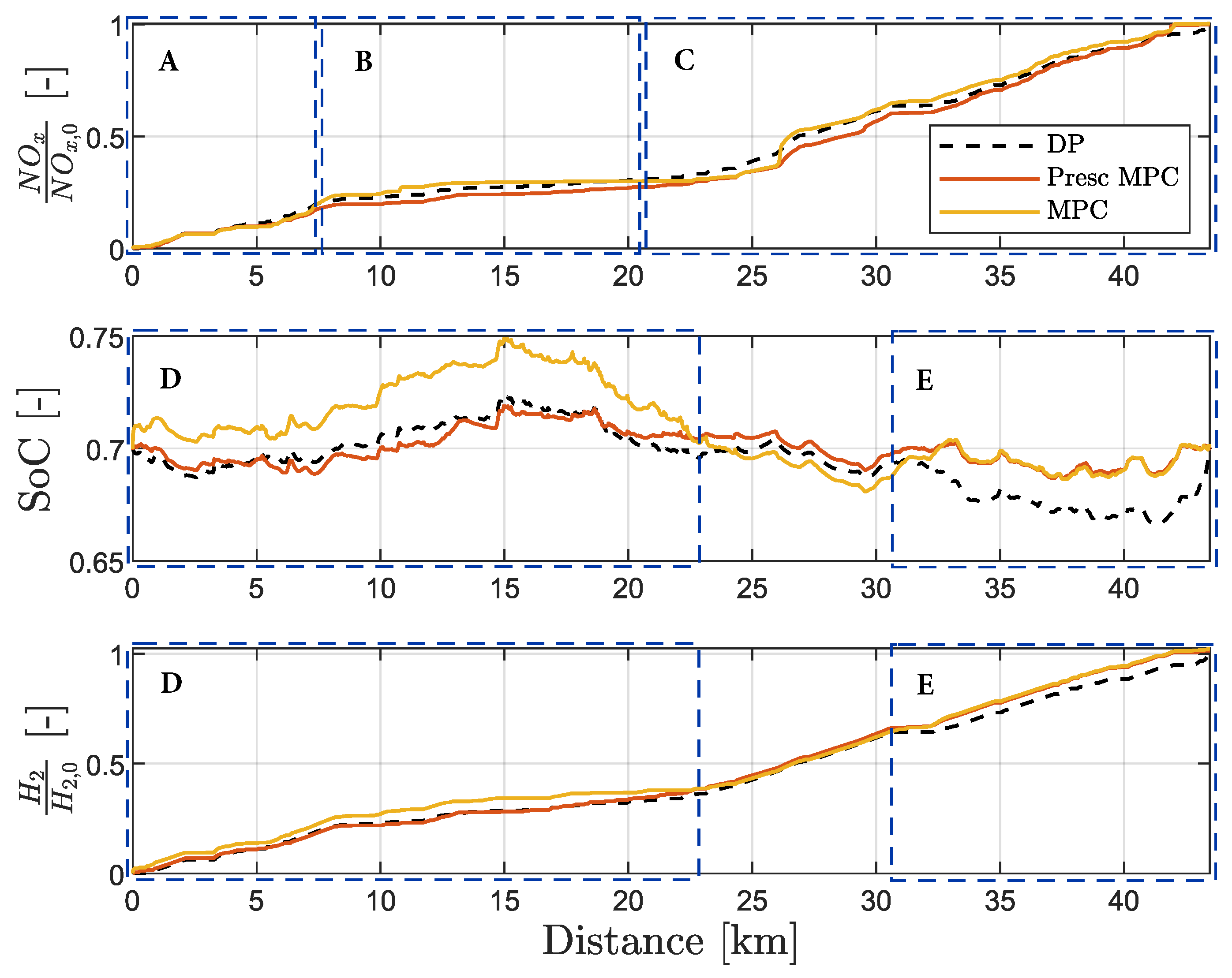
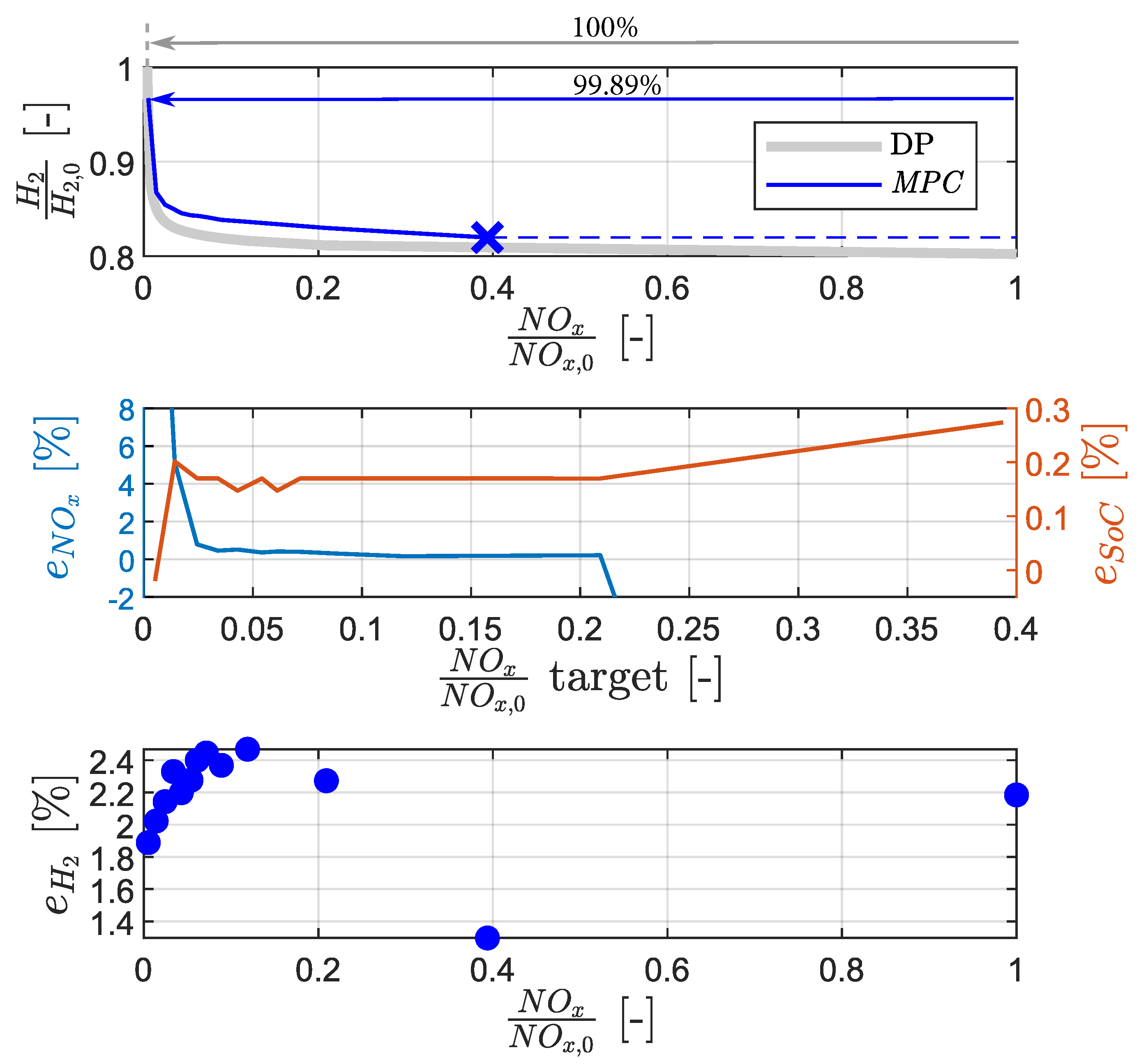
5.2. Single-NO-Target Adherence
5.3. NO-Target Expansion
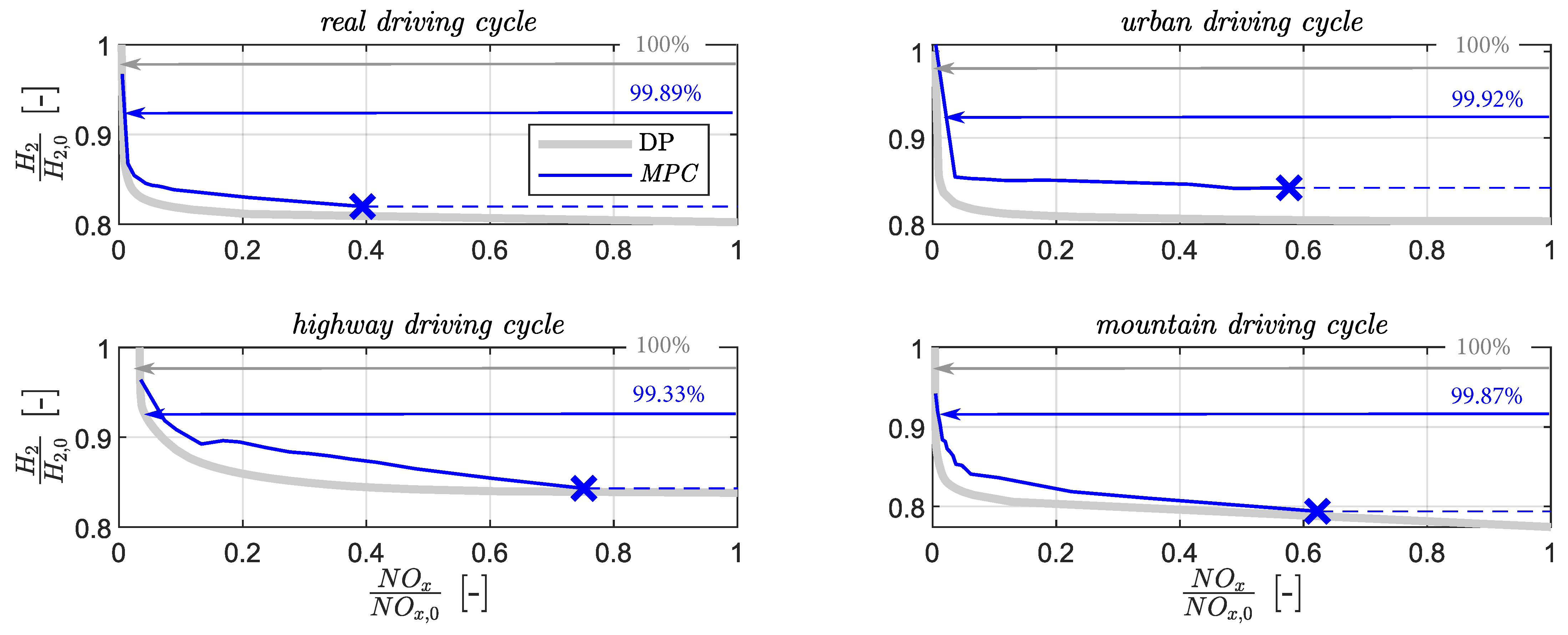
5.4. Driving Mission Generalization
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CO | carbon dioxide |
| convex optimization problem | |
| DP | dynamic programming |
| EMS | energy management system |
| EU | European Union |
| EV | electric vehicle |
| GB | gearbox |
| H | hydrogen |
| HICE | hydrogen combustion engine |
| HEV | hybrid electric vehicle |
| MPC | model predictive control |
| NO | nitrogen oxides |
| NO | engine-out nitrogen oxides |
| OCP | optimal control problem |
| PMP | Pontryagin’s minimum principle |
| PR | power request (block diagram schematic) |
| RTG | reference trajectory generator |
| SoC | state of charge |
References
- IEA. CO2 Emissions in 2022; International Energy Agency: Paris, France, 2022. [Google Scholar]
- EPA. epa.gov. 2021. Available online: https://www.epa.gov/regulations-emissions-vehicles-and-engines/final-rule-revise-existing-national-ghg-emissions (accessed on 8 June 2023).
- EU Regulation. Regulation (EU) 2019/631 of the European Parliament and of the Council of 17 April 2019 Setting CO2 Emission Performance Standards for New Passenger Cars and for New Light Commercial Vehicles, and Repealing Regulations (EC) No 443/2009 and (EU) No 510/2011. 2019. Available online: https://eur-lex.europa.eu/legalcontent/EN/TXT (accessed on 10 January 2024).
- IEA. Global EV Outlook 2023; International Energy Agency: Paris, France, 2024. [Google Scholar]
- Hänggi, S.; Elbert, P.; Bütler, T.; Cabalzar, U.; Teske, S.; Bach, C.; Onder, C. A review of synthetic fuels for passenger vehicles. Energy Rep. 2019, 5, 555–569. [Google Scholar] [CrossRef]
- Hassan, Q.; Azzawi, I.D.; Sameen, A.Z.; Salman, H.M. Hydrogen Fuel Cell Vehicles: Opportunities and Challenges. Sustainability 2023, 15, 11501. [Google Scholar] [CrossRef]
- Lider, A.; Kudiiarov, V.; Kurdyumov, N.; Lyu, J.; Koptsev, M.; Travitzky, N.; Hotza, D. Materials and techniques for hydrogen separation from methane-containing gas mixtures. Int. J. Hydrogen Energy 2023, 48, 28390–28411. [Google Scholar] [CrossRef]
- Sementa, P.; de Vargas Antolini, J.B.; Tornatore, C.; Catapano, F.; Vaglieco, B.M.; Sánchez, J.J.L. Exploring the potentials of lean-burn hydrogen SI engine compared to methane operation. Int. J. Hydrogen Energy 2022, 47, 25044–25056. [Google Scholar] [CrossRef]
- Zhao, F.C.; Sun, B.G.; Yuan, S.; Bao, L.Z.; Wei, H.; Luo, Q.H. Experimental and modeling investigations to improve the performance of the near-zero NOx emissions direct-injection hydrogen engine by injection optimization. Int. J. Hydrogen Energy 2023, 49, 713–724. [Google Scholar] [CrossRef]
- Güler, İ.; Kılıçaslan, A.; Küçük, T.; Corsini, D. Transient and altitude performance analysis of hydrogen fuelled internal combustion engines with different charging concepts. Int. J. Hydrogen Energy 2023, 49, 1112–1122. [Google Scholar] [CrossRef]
- Bao, L.Z.; Sun, B.G.; Luo, Q.H. Experimental investigation of the achieving methods and the working characteristics of a near-zero NOx emission turbocharged direct-injection hydrogen engine. Fuel 2022, 319, 123746. [Google Scholar] [CrossRef]
- Sciarretta, A.; Back, M.; Guzzella, L. Optimal control of parallel hybrid electric vehicles. IEEE Trans. Control. Syst. Technol. 2004, 12, 352–363. [Google Scholar] [CrossRef]
- Ambühl, D. Energy Management Strategies for Hybrid Electric Vehicles. Ph.D. Thesis, ETH Zurich, Zürich, Switzerland, 2009. [Google Scholar]
- Machacek, D.T.; Barhoumi, K.; Ritzmann, J.M.; Huber, T.; Onder, C.H. Multi-level model predictive control for the energy management of hybrid electric vehicles including thermal derating. IEEE Trans. Veh. Technol. 2022, 71, 10400–10414. [Google Scholar] [CrossRef]
- Hu, Q.; Amini, M.R.; Kolmanovsky, I.; Sun, J.; Wiese, A.; Seeds, J.B. Multihorizon model predictive control: An application to integrated power and thermal management of connected hybrid electric vehicles. IEEE Trans. Control. Syst. Technol. 2021, 30, 1052–1064. [Google Scholar] [CrossRef]
- Ritzmann, J.; Peterhans, C.; Chinellato, O.; Gehlen, M.; Onder, C. Model Predictive Supervisory Control for Integrated Emission Management of Diesel Engines. Energies 2022, 15, 2755. [Google Scholar] [CrossRef]
- Kyjovskỳ, Š.; Vávra, J.; Bortel, I.; Toman, R. Drive cycle simulation of light duty mild hybrid vehicles powered by hydrogen engine. Int. J. Hydrogen Energy 2023, 48, 16885–16896. [Google Scholar] [CrossRef]
- Machacek, D.T.; Ozan, N.; Huber, T.; Onder, C.H. Energy Management of Hydrogen Hybrid Electric Vehicles—A Potential Study. arXiv 2023, arXiv:2309.09804. [Google Scholar]
- Hannah, L.A.; Dunson, D.B. Multivariate convex regression with adaptive partitioning. J. Mach. Learn. Res. 2013, 14, 3261–3294. [Google Scholar]
- Machacek, D.T.; van Dooren, S.; Huber, T.; Onder, C.H. Learning-Based Model Predictive Control for the Energy Management of Hybrid Electric Vehicles Including Driving Mode Decisions. IEEE Trans. Veh. Technol. 2023, 73, 5113–5127. [Google Scholar] [CrossRef]
- Kerrigan, E.C.; Maciejowski, J.M. Soft Constraints and Exact Penalty Functions in Model Predictive Control. In Proceedings of the United Kingdom Automatic Control Council (UKACC) International Conference on Control, Cambridge, UK, 6–8 July 2000. [Google Scholar]
- Murgovski, N.; Johannesson, L.; Hu, X.; Egardt, B.; Sjöberg, J. Convex relaxations in the optimal control of electrified vehicles. In Proceedings of the 2015 American control conference (ACC), Chicago, IL, USA, 1–3 July 2015; pp. 2292–2298. [Google Scholar]
- Lofberg, J. YALMIP: A toolbox for modeling and optimization in MATLAB. In Proceedings of the 2004 IEEE International Conference on Robotics and Automation (IEEE Cat. No. 04CH37508), Taipei, Taiwan, 2–4 September 2004; pp. 284–289. [Google Scholar]
- MOSEK ApS. The MOSEK Optimization Toolbox for MATLAB Manual; Version 9.0.; MOSEK ApS: Copenhagen, Denmark, 2019. [Google Scholar]
- Guzzella, L.; Sciarretta, A. Vehicle Propulsion Systems; Springer: Berlin/Heidelberg, Germany, 2013; Volume 3. [Google Scholar]
- Boltyanskiy, V.; Gamkrelidze, R.; Mishchenko, Y.; Pontryagin, L. Mathematical Theory of Optimal Processes; John Wiley & Sons: Hoboken, NJ, USA, 1962. [Google Scholar]
- Kim, N.; Cha, S.; Peng, H. Optimal control of hybrid electric vehicles based on Pontryagin’s minimum principle. IEEE Trans. Control. Syst. Technol. 2010, 19, 1279–1287. [Google Scholar]
- Ambuhl, D.; Guzzella, L. Predictive reference signal generator for hybrid electric vehicles. IEEE Trans. Veh. Technol. 2009, 58, 4730–4740. [Google Scholar] [CrossRef]
- Behrisch, M.; Bieker, L.; Erdmann, J.; Krajzewicz, D. SUMO–simulation of urban mobility: An overview. In Proceedings of the SIMUL 2011, The Third International Conference on Advances in System Simulation. ThinkMind, Barcelona, Spain, 23–29 October 2011. [Google Scholar]
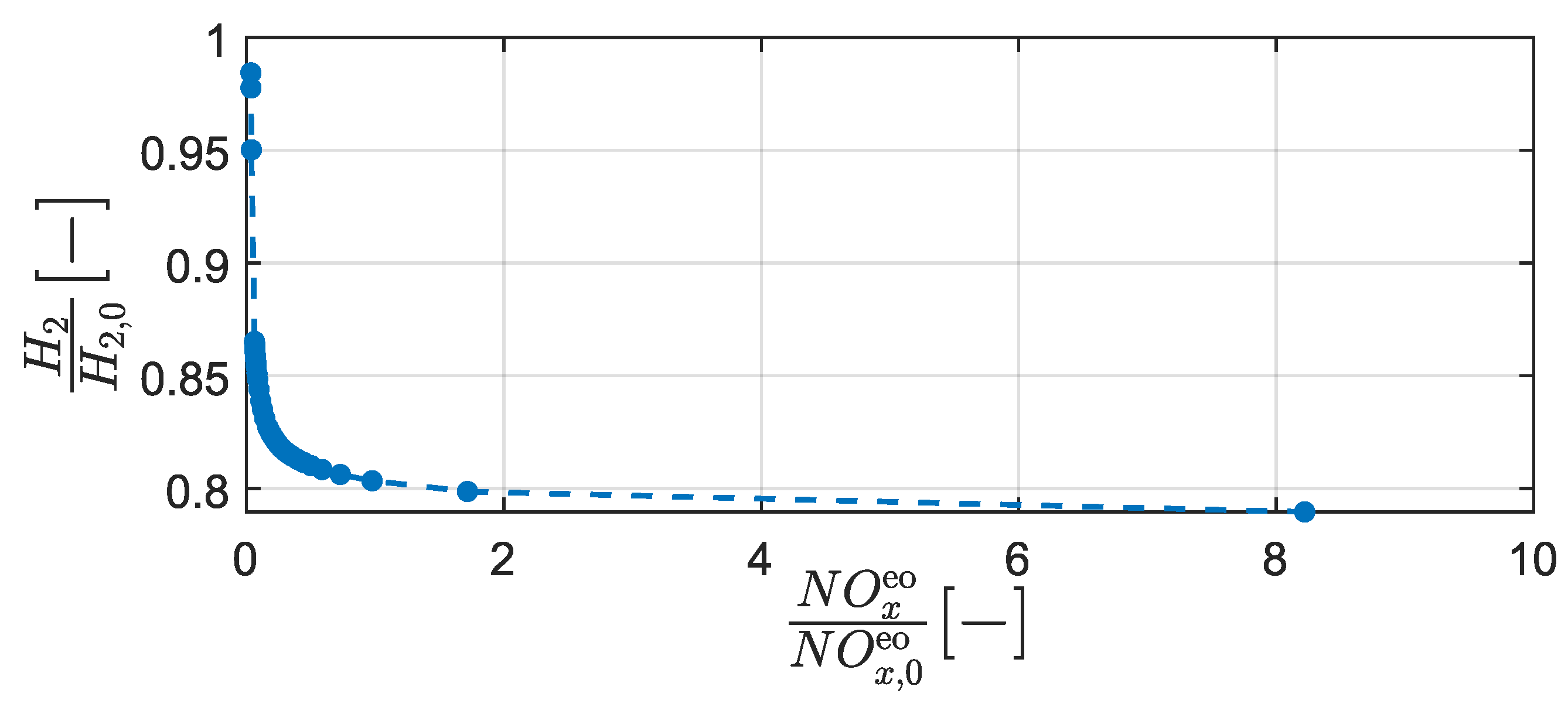
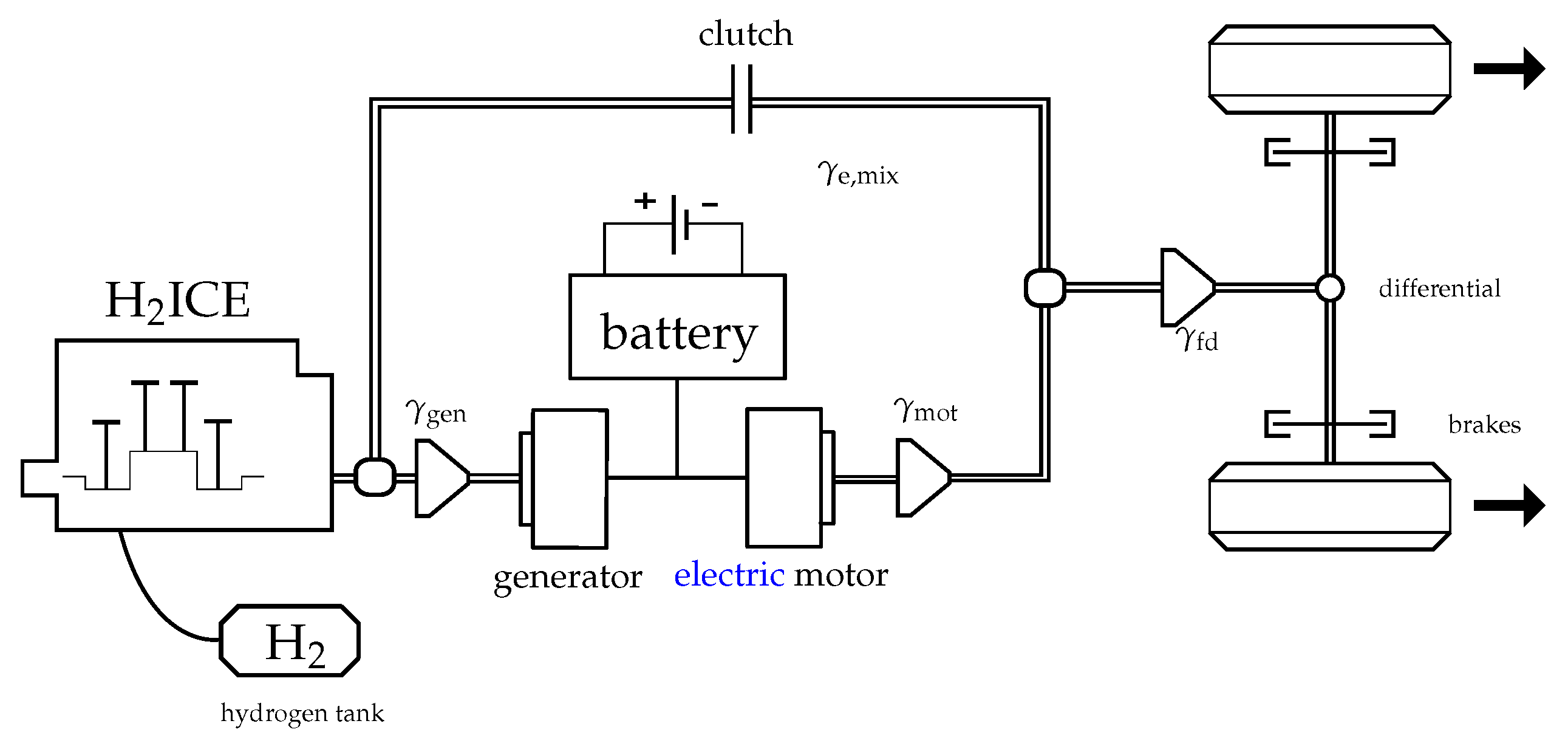


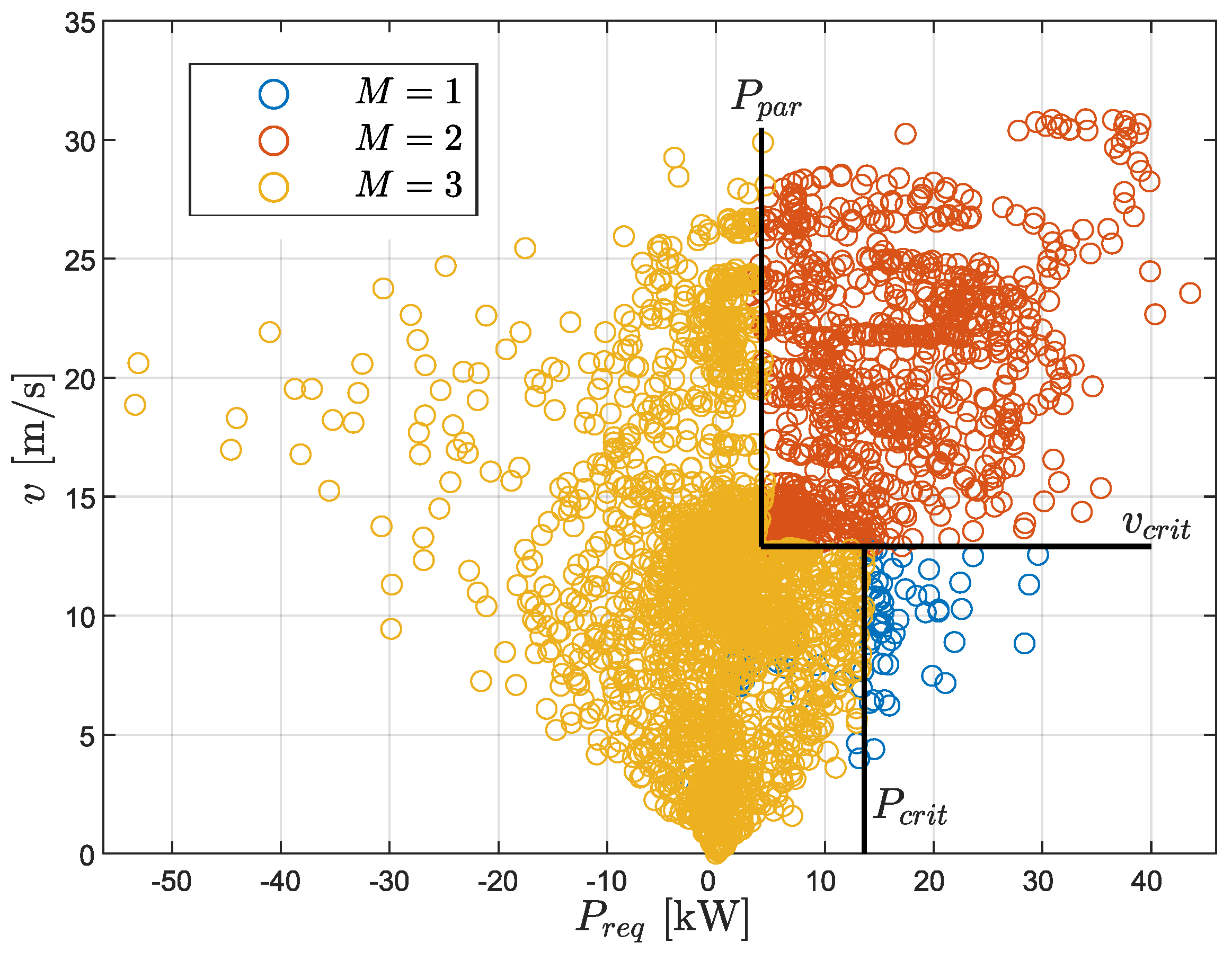

| Series mode | HICE = ON | clutch = OPEN | |
| Parallel mode | HICE = ON | clutch = CLOSED | |
| EV mode | HICE = OFF | clutch = OPEN |
| Real driving mission | 2.18% | 2.47% |
| Urban driving mission | 4.66% | 5.13% |
| Mountain driving mission | 3.79% | 6.62% |
| Highway driving mission | 4.15% | 6.91% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Machacek, D.; Yasar, N.; Widmer, F.; Huber, T.; Onder, C. Energy Management of Hydrogen Hybrid Electric Vehicles—Online-Capable Control. Energies 2024, 17, 2369. https://doi.org/10.3390/en17102369
Machacek D, Yasar N, Widmer F, Huber T, Onder C. Energy Management of Hydrogen Hybrid Electric Vehicles—Online-Capable Control. Energies. 2024; 17(10):2369. https://doi.org/10.3390/en17102369
Chicago/Turabian StyleMachacek, David, Nazim Yasar, Fabio Widmer, Thomas Huber, and Christopher Onder. 2024. "Energy Management of Hydrogen Hybrid Electric Vehicles—Online-Capable Control" Energies 17, no. 10: 2369. https://doi.org/10.3390/en17102369
APA StyleMachacek, D., Yasar, N., Widmer, F., Huber, T., & Onder, C. (2024). Energy Management of Hydrogen Hybrid Electric Vehicles—Online-Capable Control. Energies, 17(10), 2369. https://doi.org/10.3390/en17102369






