Design and Optimization of Cross-Corrugated Triangular Ducts with Trapezoidal Baffles Based on Response Surface Methodology and CFD
Abstract
1. Introduction
2. Response Surface Design
3. Model
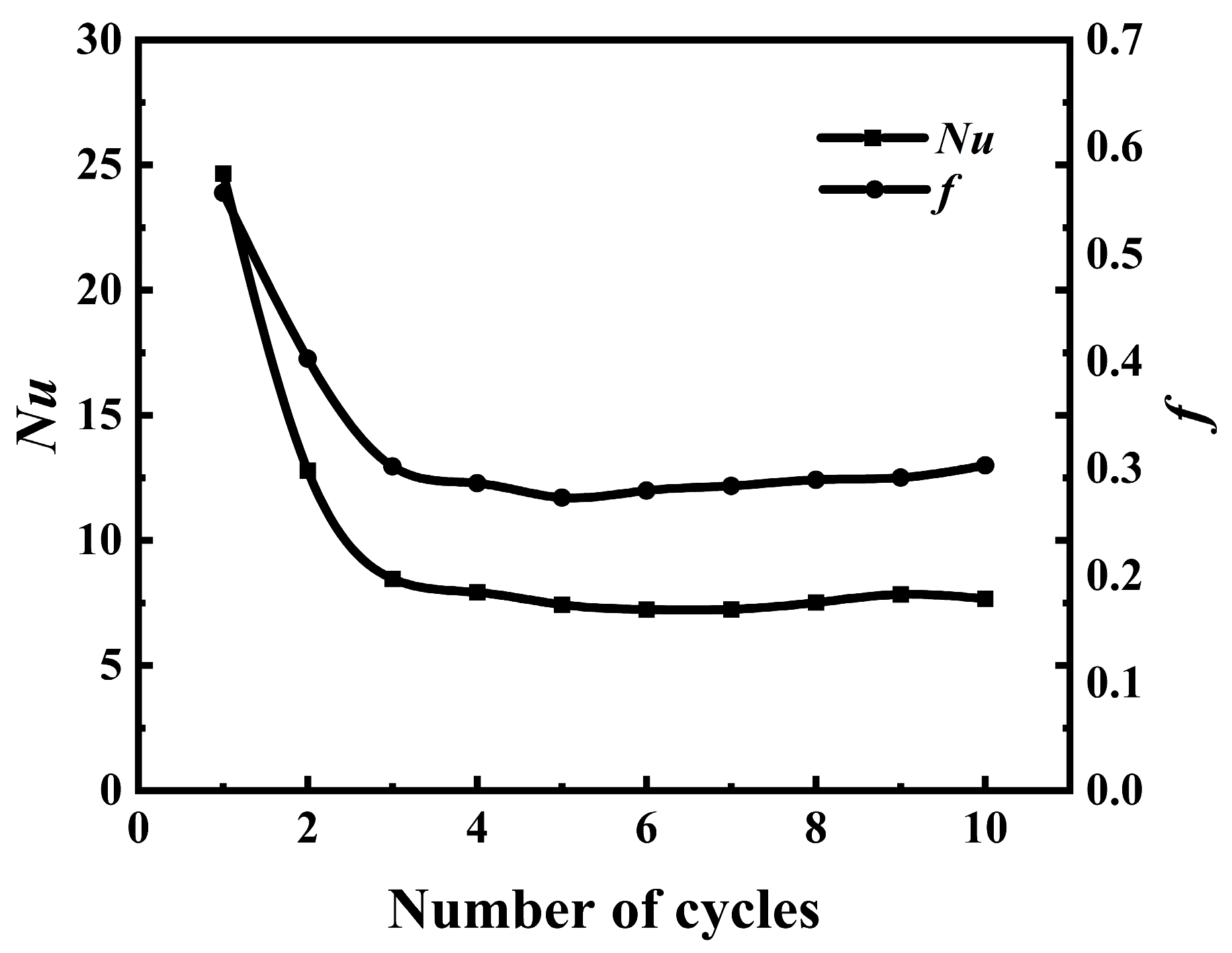
3.1. Solution Procedure
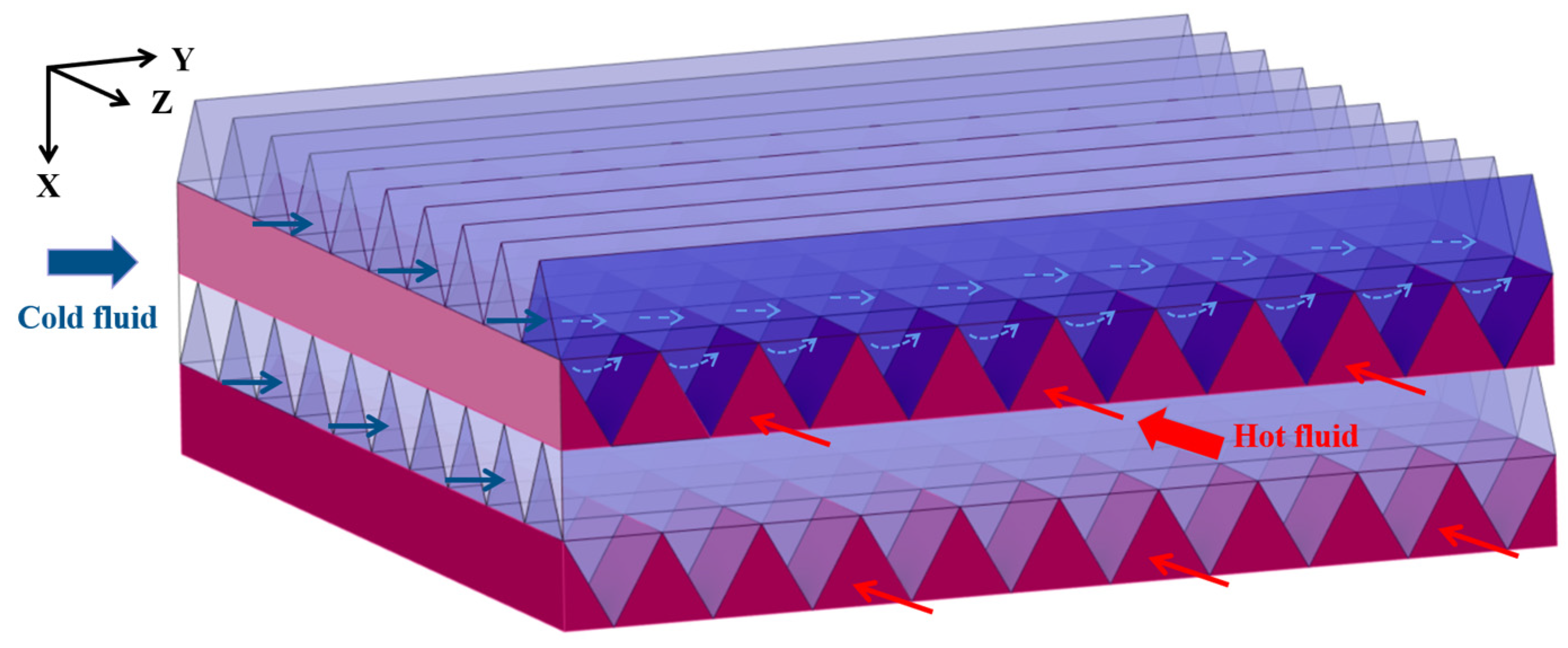
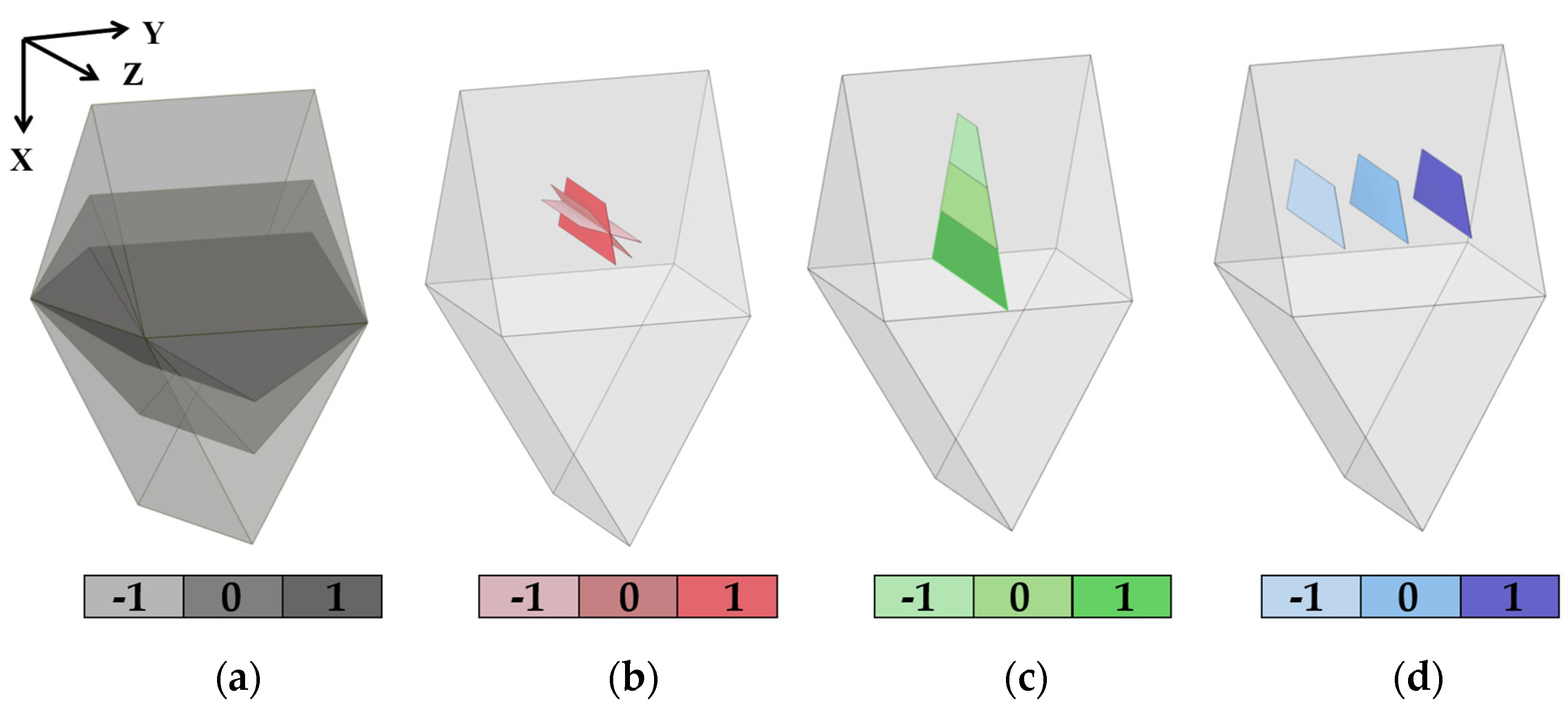
3.2. Computational Domain
3.3. Boundary Conditions
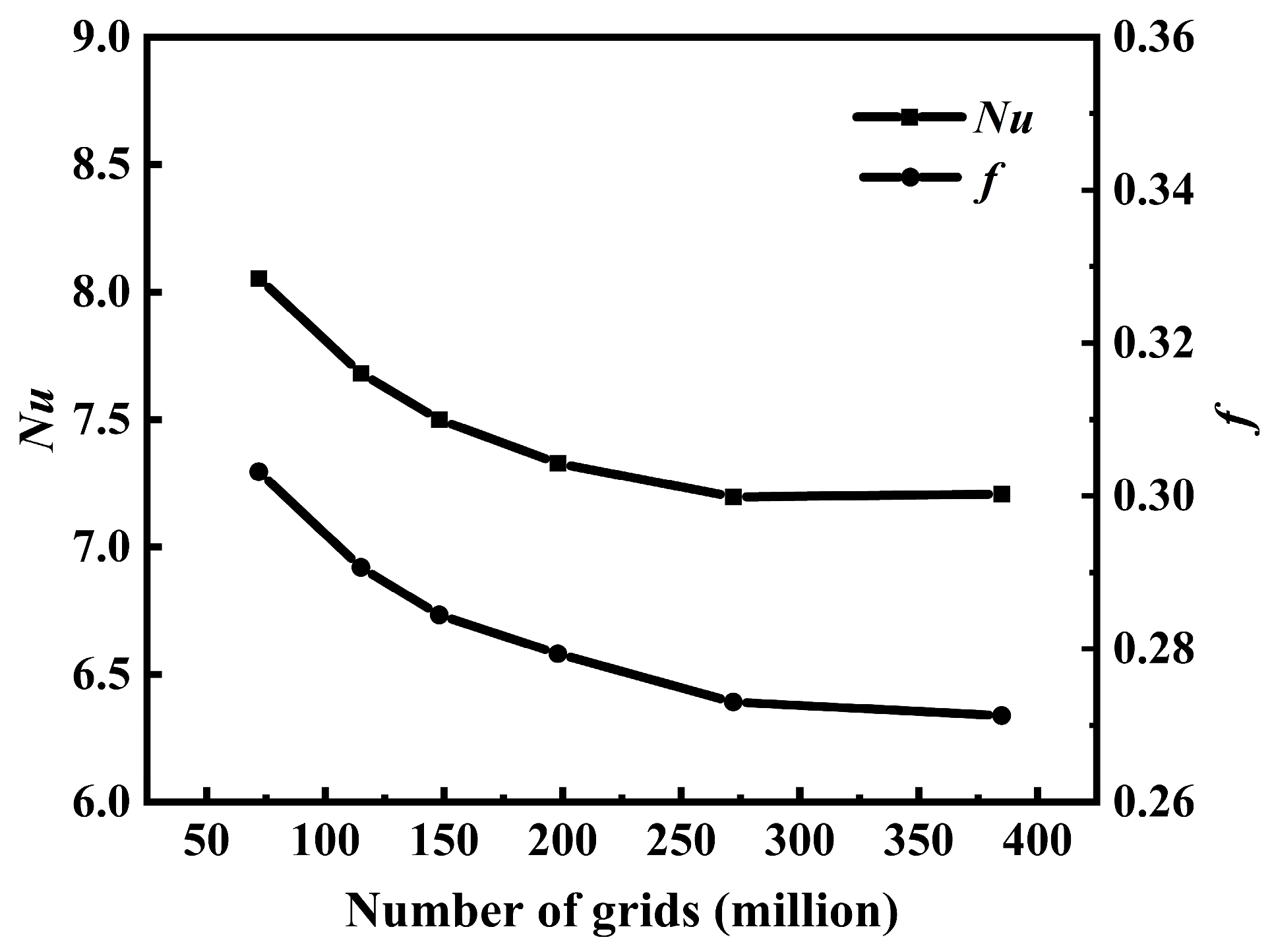
3.4. Grid Independence Test
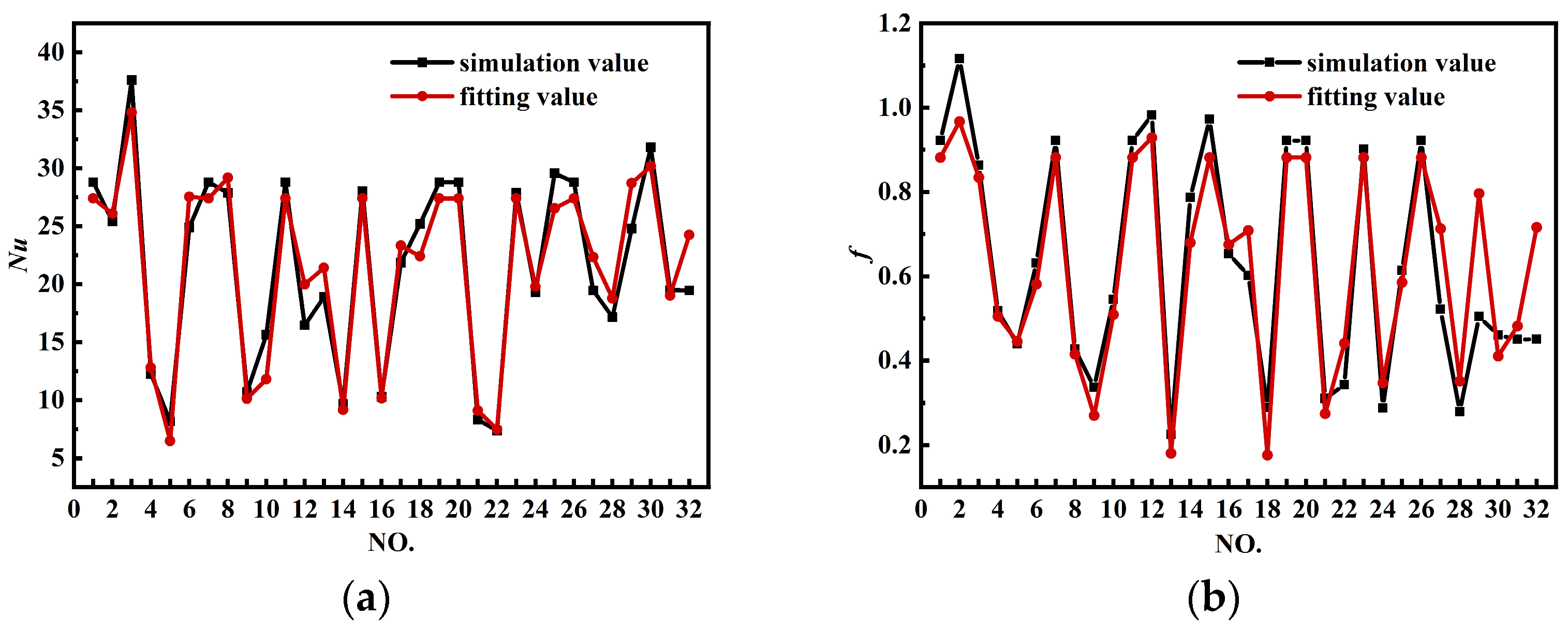
3.5. Model Validation
4. Results and Discussion
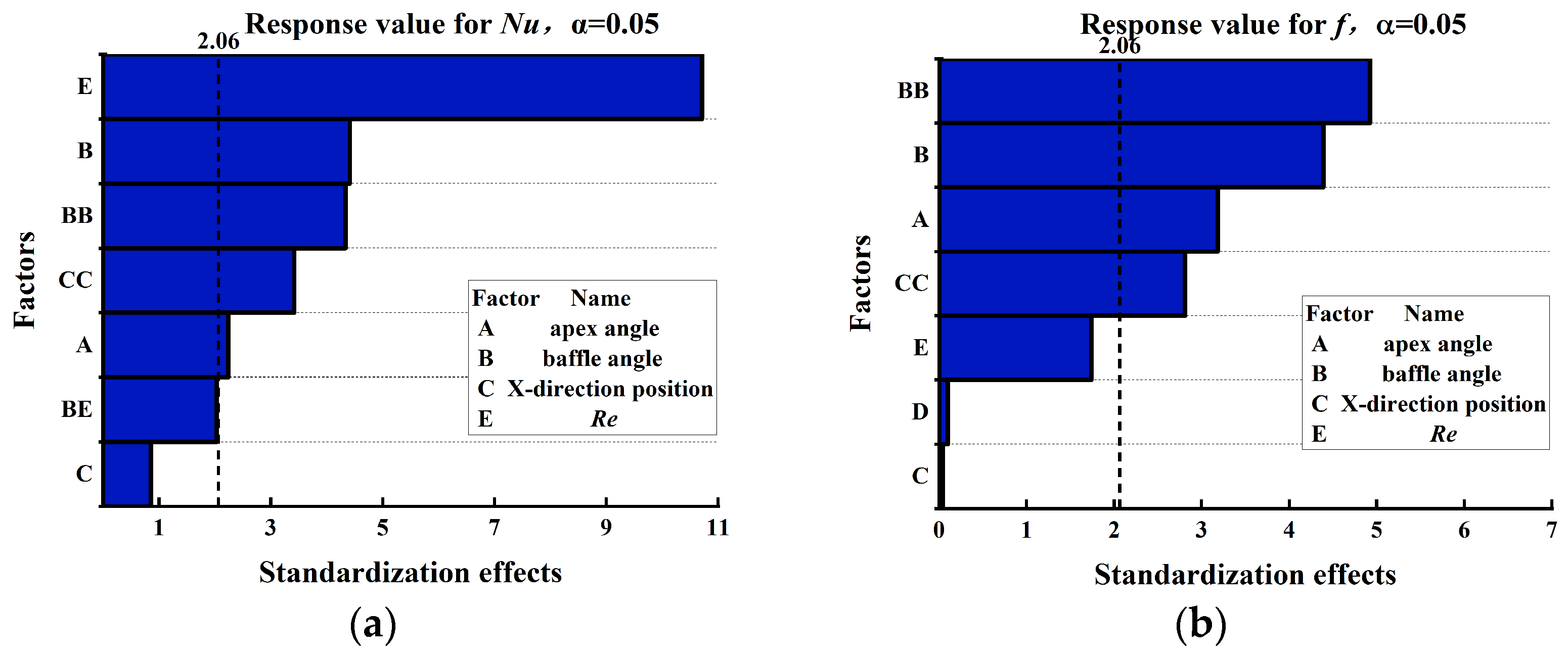
4.1. ANOVA Parameter Modeling
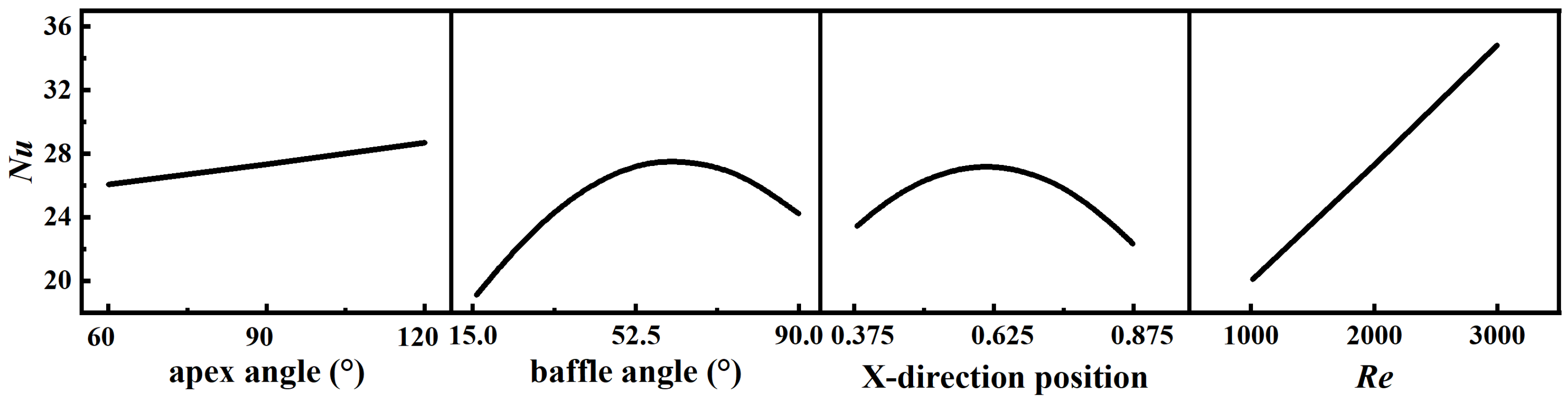
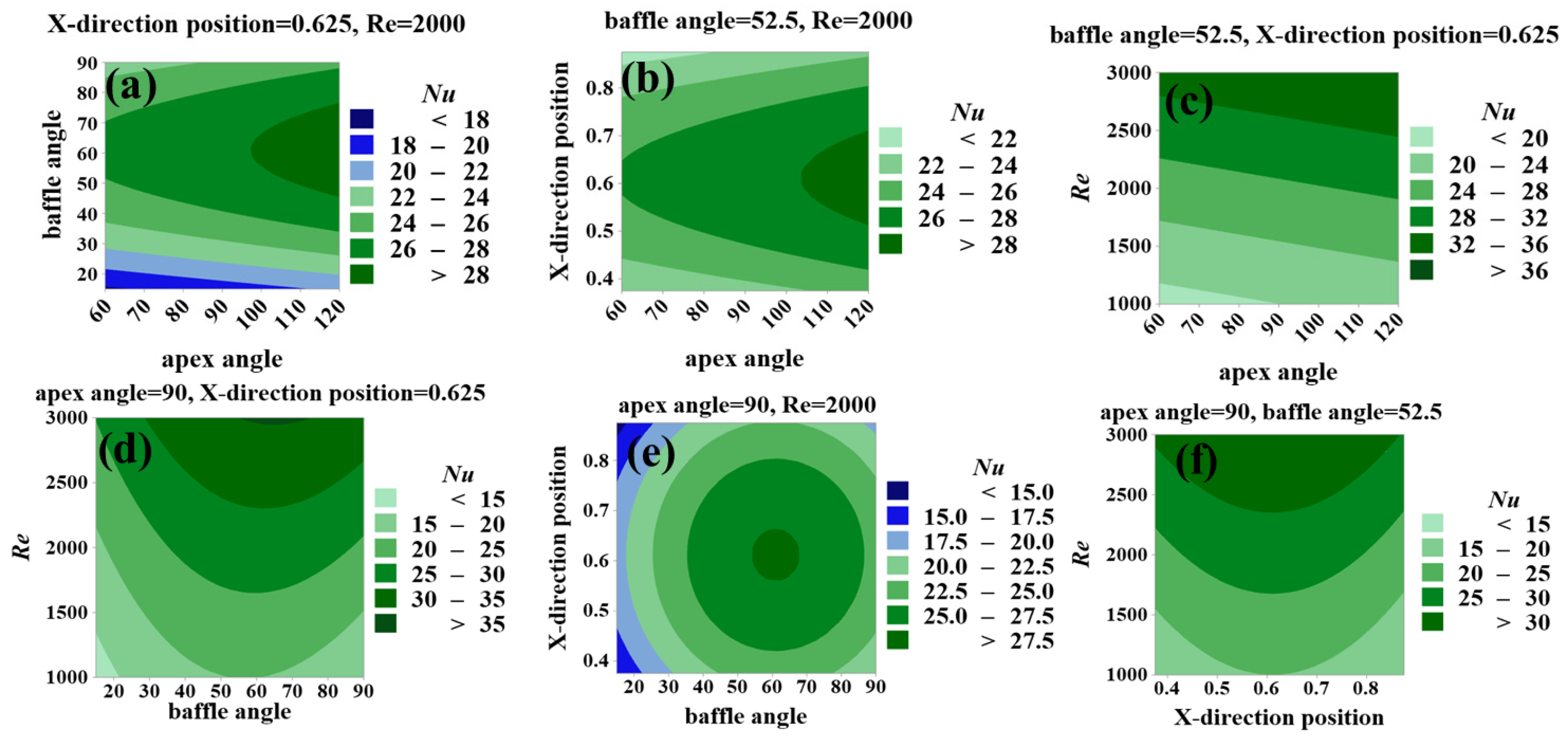
4.2. Analysis of Factors
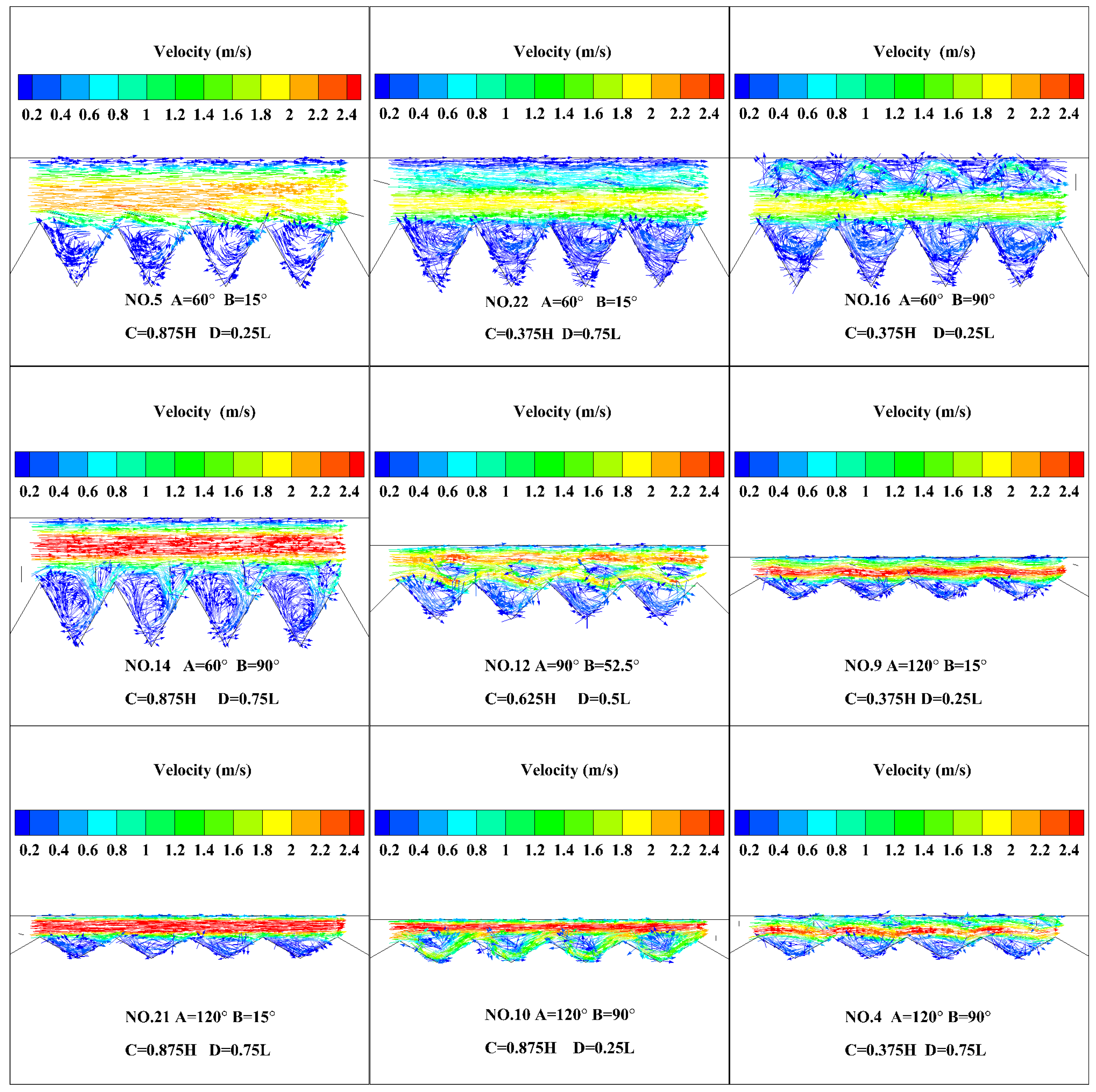
4.3. Velocity Field Distribution
4.4. Temperature Distribution
5. Conclusions
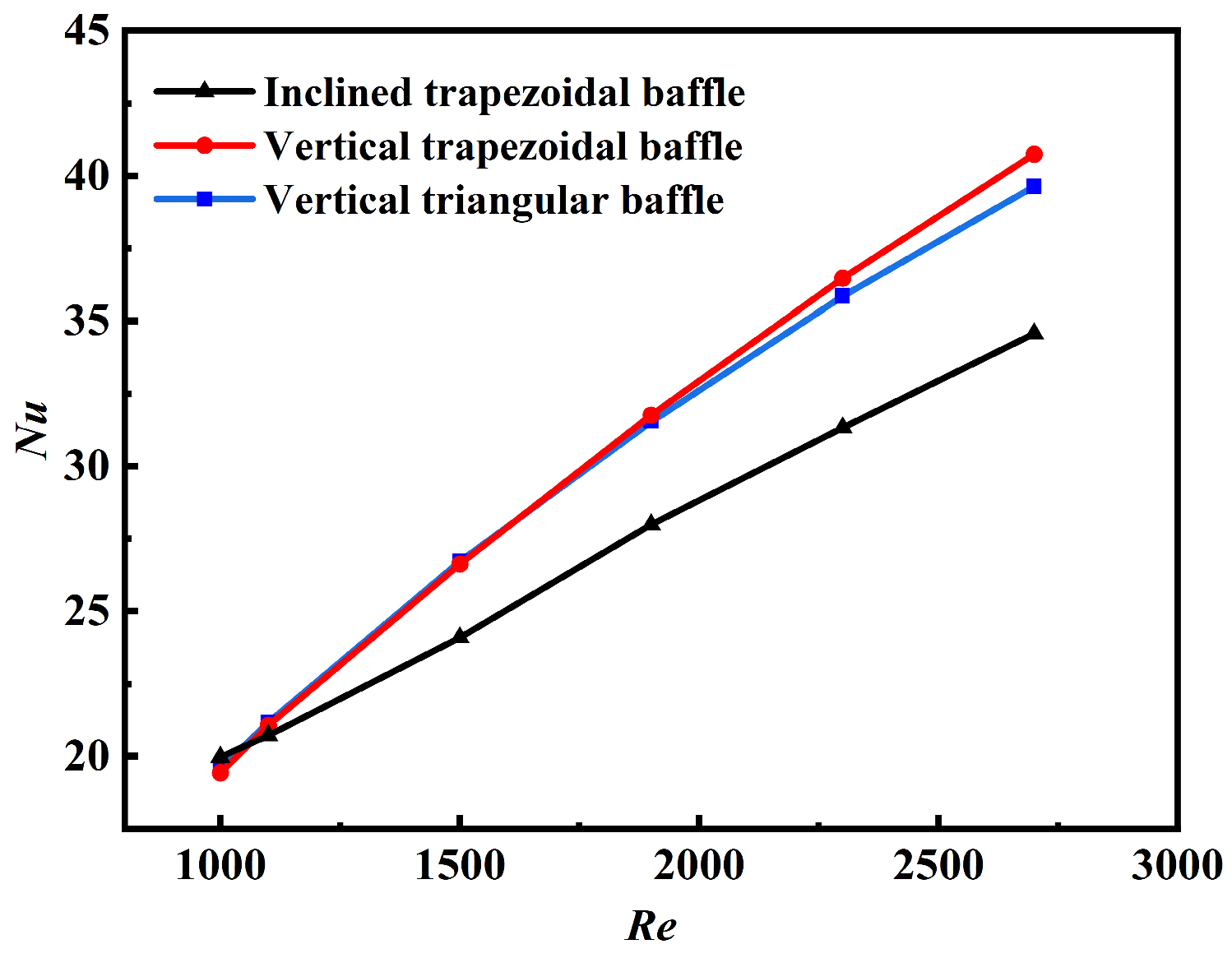
- When the response value is Nu, the four factors that have a significant influence are the apex angle, baffle angle, X-direction position, and Re. The factor with the greatest influence factor is Re, which exceeds the other factors by more than two times. Nu rises linearly with the increase in Re. The factors baffle angle and X-direction position have a parabolic relationship with Nu. As these factors increase, Nu first increases and then decreases. Compared to these three factors, the effect of the apex angle factor is smaller and slightly increases with increasing Re. The best heat transfer performance of the model is achieved when optimized for maximum Nu, with a factor apex angle of 120°, baffle angle of 65°, X-direction position of 0.612H, and Re of 3000. Under the same apex angle and Re conditions, Nu values are 1.54 times that of a non-baffled channel;
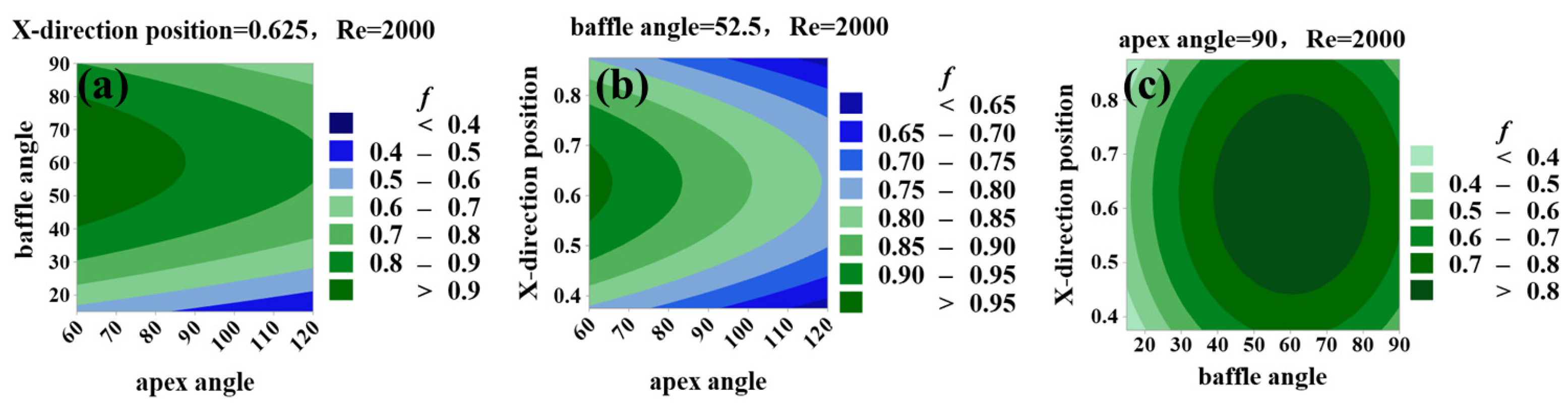
- If the response value is f, the four factors that have a significant effect are the apex angle, baffle angle, X-direction position, and Re. The baffle angle has the largest effect, while the others gradually decrease. The baffle angle and X-direction position exhibit a parabolic trend, increasing and then decreasing, while the apex angle and Re show a negative linear relationship with f. The value of f decreases slowly as the apex angle and Re increase. When optimized for minimum f, the factor apex angle is 120°, baffle angle is 15°, X-direction position is 0.875H, and Re is 3000. Under these conditions, the pressure drop of the model is minimized. This value is close to the non-baffled channel and even lower than it by 0.007 with the same apex angle and Re;
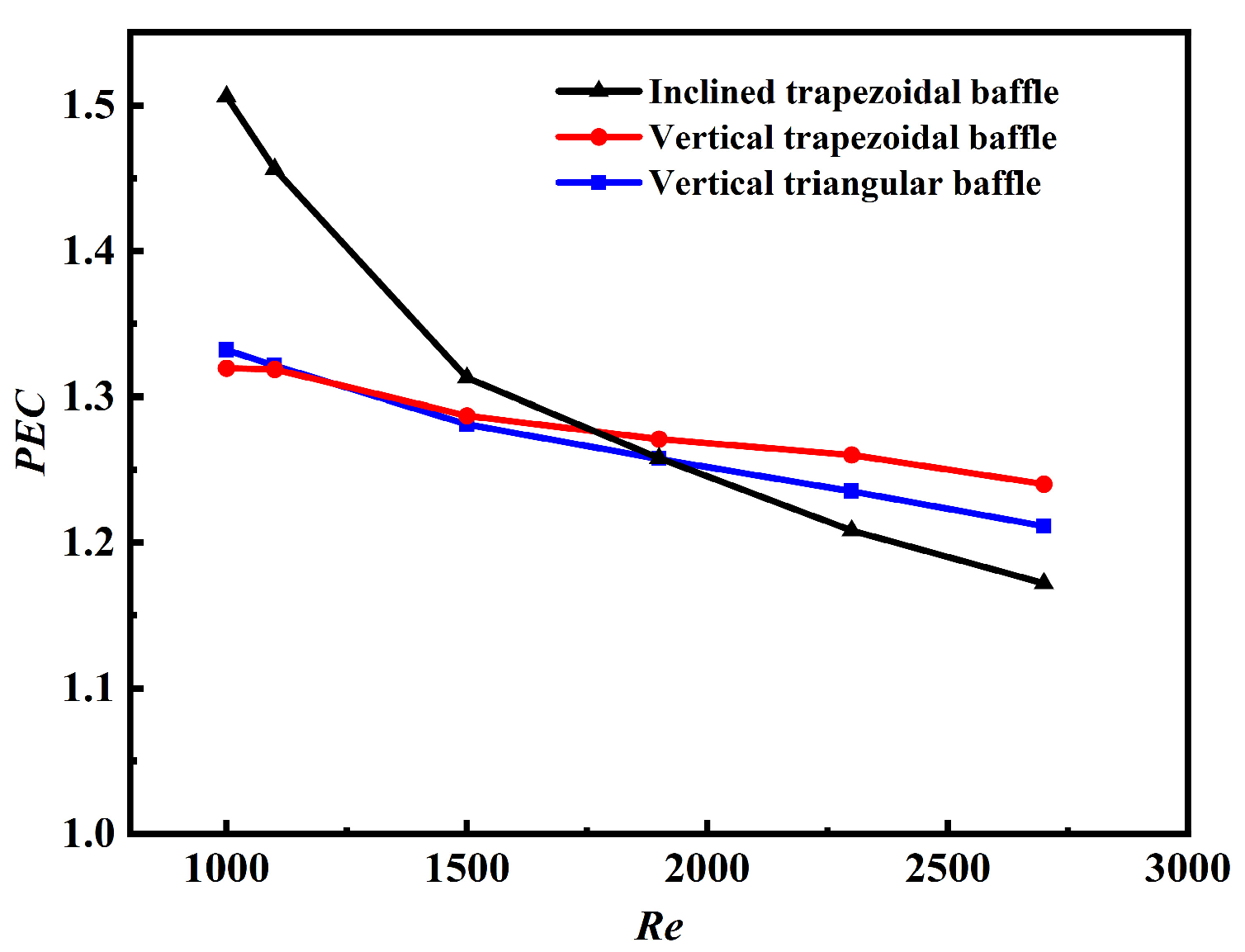
- The optimal PEC was found to be 90° for the factor apex angle, 52.5° for the baffle angle, 0.625H for the X-direction position, and 1000 for Re. The inclined baffle significantly outperforms the vertical baffle at low Re and this is no longer obvious as the Re increases.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | |
| Aci | Cross-sectional area at inlet or outlet, m2 |
| Acyc | Surface area of a cycle, m2 |
| cp | Specific heat of the fluid, kJ/(kg·K) |
| Dh | Hydraulic diameter of the channel, m |
| f | Friction factor |
| H | Corrugation height of a cycle, m |
| h | Convective heat transfer coefficient, W/(m2·K) |
| L | Corrugation length of a cycle, m |
| N | Number of trials |
| Nu | Nusselt number |
| P | Pressure, Pa |
| PEC | Performance Evaluation Criteria |
| Pr | Prandtl number |
| Re | Reynold number |
| R-sq | Degree of fitting |
| S | Standard deviation |
| T | Temperature, °C |
| ∆Tm | Logarithmic mean temperature, °C |
| u | Velocity, m/s |
| Vcyc | volume of a cycle, m3 |
| W | corrugation width of a cycle, m |
| x, y, z | coordinates, m |
| Greek letters | |
| σ | error term |
| ρ | density, kg/m3 |
| Superscripts | |
| * | dimensionless |
| Subscripts | |
| i, o | inlet and outlet |
| w | wall |
| m | mean value |
| 0 | unbaffled channel |
| ∞ | bulk flow |
| Codes | |
| A | apex angle (°) |
| B | baffle angle (°) |
| C | X-direction position |
| D | Y-direction position |
| E | Re |
Appendix A. ANOVA for Nu before Elimination
| Source | Degree of Freedom | Adj SS | Adj MS | F-Value | p-Value |
| Model | 20 | 1972.11 | 98.606 | 12.98 | 0.000 |
| Linear | 5 | 1153.60 | 230.719 | 30.38 | 0.000 |
| A | 1 | 31.11 | 31.111 | 4.10 | 0.068 |
| B | 1 | 121.57 | 121.566 | 16.01 | 0.002 |
| C | 1 | 4.47 | 4.467 | 0.59 | 0.459 |
| D | 1 | 7.34 | 7.336 | 0.97 | 0.347 |
| E | 1 | 989.12 | 989.116 | 130.24 | 0.000 |
| Square | 5 | 750.60 | 150.119 | 19.77 | 0.000 |
| A * A | 1 | 2.24 | 2.239 | 0.29 | 0.598 |
| B * B | 1 | 106.80 | 106.798 | 14.06 | 0.003 |
| C * C | 1 | 71.70 | 71.704 | 9.44 | 0.011 |
| D * D | 1 | 8.97 | 8.968 | 1.18 | 0.300 |
| E * E | 1 | 2.32 | 2.321 | 0.31 | 0.591 |
| Two-factor interaction | 10 | 67.92 | 6.792 | 0.89 | 0.566 |
| A * B | 1 | 0.25 | 0.245 | 0.03 | 0.861 |
| A * C | 1 | 8.92 | 8.922 | 1.17 | 0.302 |
| A * D | 1 | 1.51 | 1.506 | 0.20 | 0.665 |
| A * E | 1 | 0.14 | 0.135 | 0.02 | 0.896 |
| B * C | 1 | 11.48 | 11.476 | 1.51 | 0.245 |
| B * D | 1 | 11.48 | 11.478 | 1.51 | 0.245 |
| B * E | 1 | 25.85 | 25.847 | 3.40 | 0.092 |
| C * D | 1 | 2.90 | 2.897 | 0.38 | 0.549 |
| C * E | 1 | 4.95 | 4.952 | 0.65 | 0.436 |
| D * E | 1 | 0.46 | 0.460 | 0.06 | 0.810 |
| Residual | 11 | 83.54 | 7.594 | - | - |
| Lack of Fit | 6 | 74.96 | 12.494 | 7.29 | 0.023 |
| Pure Error | 5 | 8.57 | 1.715 | - | - |
| Total | 31 | 2055.65 | - | - | - |
Appendix B. ANOVA for f before Elimination
| Source | Degree of Freedom | Adj SS | Adj MS | F-Value | p-Value |
| Model | 20 | 1.96770 | 0.098385 | 5.30 | 0.003 |
| Linear | 5 | 0.42174 | 0.084348 | 4.55 | 0.017 |
| A | 1 | 0.13097 | 0.130969 | 7.06 | 0.022 |
| B | 1 | 0.25130 | 0.251302 | 13.54 | 0.004 |
| C | 1 | 0.00004 | 0.000036 | 0.00 | 0.966 |
| D | 1 | 0.00050 | 0.000496 | 0.03 | 0.873 |
| E | 1 | 0.03894 | 0.038937 | 2.10 | 0.175 |
| Square | 5 | 1.50997 | 0.301995 | 16.28 | 0.000 |
| A * A | 1 | 0.00029 | 0.000292 | 0.02 | 0.902 |
| B * B | 1 | 0.33834 | 0.338336 | 18.24 | 0.001 |
| C* C | 1 | 0.16582 | 0.165819 | 8.94 | 0.012 |
| D * D | 1 | 0.03323 | 0.033231 | 1.79 | 0.208 |
| E * E | 1 | 0.02553 | 0.025532 | 1.38 | 0.266 |
| Two-factor interaction | 10 | 0.03598 | 0.003598 | 0.19 | 0.992 |
| A * B | 1 | 0.01869 | 0.018691 | 1.01 | 0.337 |
| A * C | 1 | 0.00562 | 0.005615 | 0.30 | 0.593 |
| A * D | 1 | 0.00028 | 0.000283 | 0.02 | 0.904 |
| A * E | 1 | 0.00065 | 0.000646 | 0.03 | 0.855 |
| B * C | 1 | 0.00078 | 0.000781 | 0.04 | 0.841 |
| B * D | 1 | 0.00156 | 0.001561 | 0.08 | 0.777 |
| B * E | 1 | 0.00003 | 0.000032 | 0.00 | 0.968 |
| C * D | 1 | 0.00023 | 0.000234 | 0.01 | 0.913 |
| C * E | 1 | 0.00793 | 0.007930 | 0.43 | 0.527 |
| D * E | 1 | 0.00021 | 0.000211 | 0.01 | 0.917 |
| Residual | 11 | 0.20409 | 0.018553 | - | - |
| Lack of Fit | 6 | 0.18616 | 0.031026 | 8.65 | 0.016 |
| Pure Error | 5 | 0.01793 | 0.003586 | - | - |
| Total | 31 | 2.17179 | - | - | - |
References
- Agency, I.E. World Energy Outlook 2023. Available online: https://origin.iea.org/reports/world-energy-outlook-2023 (accessed on 21 November 2023).
- Zukowski, M.; Topolanska, J. Comparison of Thermal Performance between Tube and Plate Ground-Air Heat Exchangers. Renew. Energy 2018, 115, 697–710. [Google Scholar] [CrossRef]
- García-Castillo, J.L.; Picón-Núñez, M.; Abu-Khader, M.M. Improving the Prediction of the Thermohydraulic Performance of Secondary Surfaces and Its Application in Heat Recovery Processes. Energy 2022, 261, 125196. [Google Scholar] [CrossRef]
- Chennu, R. Numerical Analysis of Compact Plate-Fin Heat Exchangers for Aerospace Applications. HFF 2018, 28, 395–412. [Google Scholar] [CrossRef]
- Aneesh, A.M.; Sharma, A.; Srivastava, A.; Chaudhury, P. Effects of Wavy Channel Configurations on Thermal-Hydraulic Characteristics of Printed Circuit Heat Exchanger (PCHE). Int. J. Heat Mass Transf. 2018, 118, 304–315. [Google Scholar] [CrossRef]
- Zhang, L.; Che, D. Influence of Corrugation Profile on the Thermalhydraulic Performance of Cross-Corrugated Plates. Numer. Heat Transf. Part A Appl. 2011, 59, 267–296. [Google Scholar] [CrossRef]
- Liao, J.; Xue, P.; Jin, L.; Zhao, M.; Zhang, N.; Liu, J. Optimization of Corrugated Sheet Packing Structure Based on Analysis of Falling Film Flow Characteristics. Sustainability 2022, 14, 5861. [Google Scholar] [CrossRef]
- Younis, O.; Abderrahmane, A.; Hatami, M.; Mourad, A.; Kamel, G. Thermal Energy Storage Using Nano Phase Change Materials in Corrugated Plates Heat Exchangers with Different Geometries. J. Energy Storage 2022, 55, 105785. [Google Scholar] [CrossRef]
- Verdério Júnior, S.A.; Coelho, P.J.; Scalon, V.L.; Del Rio Oliveira, S. Numerical and Experimental Study of Natural Convection Heat Transfer on Flat and Corrugated Plates. HFF 2023, 33, 3286–3307. [Google Scholar] [CrossRef]
- Krishnan, E.N.; Ramin, H.; Guruabalan, A.; Simonson, C.J. Experimental Investigation on Thermo-Hydraulic Performance of Triangular Cross-Corrugated Flow Passages. Int. Commun. Heat Mass Transf. 2021, 122, 105160. [Google Scholar] [CrossRef]
- Sarraf, K.; Launay, S.; Tadrist, L. Complex 3D-Flow Analysis and Corrugation Angle Effect in Plate Heat Exchangers. Int. J. Therm. Sci. 2015, 94, 126–138. [Google Scholar] [CrossRef]
- Cao, X.; Chen, D.; Du, T.; Liu, Z.; Ji, S. Numerical Investigation and Experimental Validation of Thermo-Hydraulic and Thermodynamic Performances of Helical Baffle Heat Exchangers with Different Baffle Configurations. Int. J. Heat Mass Transf. 2020, 160, 120181. [Google Scholar] [CrossRef]
- Handoyo, E.A.; Ichsani, D.; Prabowo; Sutardi. Numerical Studies on the Effect of Delta-Shaped Obstacles’ Spacing on the Heat Transfer and Pressure Drop in v-Corrugated Channel of Solar Air Heater. Sol. Energy 2016, 131, 47–60. [Google Scholar] [CrossRef]
- Karabulut, K. Heat Transfer and Pressure Drop Evaluation of Different Triangular Baffle Placement Angles in Cross-Corrugated Triangular Channels. Therm. Sci. 2020, 24 Pt A, 355–365. [Google Scholar] [CrossRef]
- Alnak, D.E. Thermohydraulic Performance Study of Different Square Baffle Angles in Cross-Corrugated Channel. J. Energy Storage 2020, 28, 101295. [Google Scholar] [CrossRef]
- Akcay, S. Numerical Analysis of Heat Transfer Improvement for Pulsating Flow in a Periodic Corrugated Channel with Discrete V-Type Winglets. Int. Commun. Heat Mass Transf. 2022, 134, 105991. [Google Scholar] [CrossRef]
- Akcay, S.; Akdag, U. Heat Transfer Enhancement in a Channel with Inclined Baffles under Pulsating Flow: A Cfd Study. J. Enhanc. Heat Transf. 2023, 30, 61–79. [Google Scholar] [CrossRef]
- Liang, C.; Tong, X.; Lei, T.; Li, Z.; Wu, G. Optimal Design of an Air-to-Air Heat Exchanger with Cross-Corrugated Triangular Ducts by Using a Particle Swarm Optimization Algorithm. Appl. Sci. 2017, 7, 554. [Google Scholar] [CrossRef]
- Feng, C.-N.; Liang, C.-H.; Li, Z.-X. Friction Factor and Heat Transfer Evaluation of Cross-Corrugated Triangular Flow Channels with Trapezoidal Baffles. Energy Build. 2022, 257, 111816. [Google Scholar] [CrossRef]
- Li, Z.-X.; Sun, S.-Q.; Wang, C.; Liang, C.-H.; Zeng, S.; Zhong, T.; Hu, W.-P.; Feng, C.-N. The Effect of Trapezoidal Baffles on Heat and Flow Characteristics of a Cross-Corrugated Triangular Duct. Case Stud. Therm. Eng. 2022, 33, 101903. [Google Scholar] [CrossRef]
- Atkinson, A.C. Optimum and Other Response Surface Designs. Comments on “Response Surface Design Evaluation and Comparison” by Anderson-Cook, Borror and Montgomery. J. Stat. Plan. Inference 2009, 139, 662–668. [Google Scholar] [CrossRef]
- Sharma, R.; Mishra, D.P.; Wasilewski, M.; Brar, L.S. Application of Response Surface Methodology and Artificial Neural Network to Optimize the Curved Trapezoidal Winglet Geometry for Enhancing the Performance of a Fin-and-Tube Heat Exchanger. Energies 2023, 16, 4209. [Google Scholar] [CrossRef]
- Yu, C.; Chen, J.; Zeng, M.; Gao, B. Numerical Study on Turbulent Heat Transfer Performance of a New Parallel-Flow Shell and Tube Heat Exchanger with Sinusoidal Wavy Tapes Using RSM Analysis. Appl. Therm. Eng. 2019, 150, 875–887. [Google Scholar] [CrossRef]
- Kola, P.V.K.V.; Pisipaty, S.K.; Mendu, S.S.; Ghosh, R. Optimization of Performance Parameters of a Double Pipe Heat Exchanger with Cut Twisted Tapes Using CFD and RSM. Chem. Eng. Process. Process Intensif. 2021, 163, 108362. [Google Scholar] [CrossRef]
- Rezaei, P.; Moheghi, H.R.; Amiri Delouei, A. Design and Optimization of a Spiral-Tube Instantaneous Water Heater Using Response Surface Methodology. Water 2023, 15, 1458. [Google Scholar] [CrossRef]
- Support|Minitab. Available online: https://www.minitab.com/ (accessed on 3 June 2023).
- Zhang, L. Convective Mass Transport in Cross-Corrugated Membrane Exchangers. J. Membr. Sci. 2005, 260, 75–83. [Google Scholar] [CrossRef]
- Bahiraei, M.; Mazaheri, N.; Hanooni, M. Employing a Novel Crimped-Spiral Rib inside a Triple-Tube Heat Exchanger Working with a Nanofluid for Solar Thermal Applications: Irreversibility Characteristics. Sustain. Energy Technol. Assess. 2022, 52, 102080. [Google Scholar] [CrossRef]
- Močnik, U.; Muhič, S. Experimental and Numerical Analysis of Heat Transfer in a Dimple Pattern Heat Exchanger Channel. Appl. Therm. Eng. 2023, 230, 120865. [Google Scholar] [CrossRef]
- Liu, X.P.; Niu, J.L. Effects of Geometrical Parameters on the Thermohydraulic Characteristics of Periodic Cross-Corrugated Channels. Int. J. Heat Mass Transf. 2015, 84, 542–549. [Google Scholar] [CrossRef]
- Sharif, A.; Ameel, B.; T’Jollyn, I.; Lecompte, S.; De Paepe, M. Comparative Performance Assessment of Plate Heat Exchangers with Triangular Corrugation. Appl. Therm. Eng. 2018, 141, 186–199. [Google Scholar] [CrossRef]
- Ansys|Engineering Simulation Software. Available online: https://www.ansys.com/ (accessed on 13 August 2023).
- Li, Z.; Gao, Y. Numerical Study of Turbulent Flow and Heat Transfer in Cross-Corrugated Triangular Ducts with Delta-Shaped Baffles. Int. J. Heat Mass Transf. 2017, 108, 658–670. [Google Scholar] [CrossRef]
- Tian, L.; Song, Y.; Zhao, N.; Shen, W.; Wang, T. AD/RANS Simulations of Wind Turbine Wake Flow Employing the RSM Turbulence Model: Impact of Isotropic and Anisotropic Inflow Conditions. Energies 2019, 12, 4026. [Google Scholar] [CrossRef]
- Peng, H.; Ling, X.; Li, J. Performance Investigation of an Innovative Offset Strip Fin Arrays in Compact Heat Exchangers. Energy Convers. Manag. 2014, 80, 287–297. [Google Scholar] [CrossRef]
- Liu, Y.; Luo, P.; Tang, Y. Improved Prediction of Turbomachinery Flows Using Reynolds Stress Model with γ Transition Model. Aerosp. Sci. Technol. 2024, 144, 108812. [Google Scholar] [CrossRef]
- Parekh, J.; Rzehak, R. Euler–Euler Multiphase CFD-Simulation with Full Reynolds Stress Model and Anisotropic Bubble-Induced Turbulence. Int. J. Multiph. Flow 2018, 99, 231–245. [Google Scholar] [CrossRef]







| Factors | Codes | Levels | ||
|---|---|---|---|---|
| −1 | 0 | 1 | ||
| apex angle (°) | A | 60 | 90 | 120 |
| baffle angle (°) | B | 15 | 52.5 | 90 |
| X-direction position | C | 0.375H | 0.625H | 0.875H |
| Y-direction position | D | 0.25L | 0.5L | 0.75L |
| Re | E | 1000 | 2000 | 3000 |
| Run | Levels | Factors | Response Values | |||||
|---|---|---|---|---|---|---|---|---|
| Apex Angle (°) | Baffle Angle (°) | X-Direction Position | Y-Direction Position | Re | Nu | f | ||
| 1 | 0 | 90 | 52.5 | 0.625H | 0.50L | 2000 | 28.805 | 0.922 |
| 2 | −1 | 60 | 52.5 | 0.625H | 0.50L | 2000 | 25.414 | 1.116 |
| 3 | −1 | 90 | 52.5 | 0.625H | 0.50L | 3000 | 37.602 | 0.864 |
| 4 | 1 | 120 | 90.0 | 0.375H | 0.75L | 1000 | 12.250 | 0.518 |
| 5 | 1 | 60 | 15.0 | 0.875H | 0.25L | 1000 | 8.177 | 0.439 |
| 6 | 1 | 60 | 90.0 | 0.375H | 0.75L | 3000 | 24.888 | 0.632 |
| 7 | 0 | 90 | 52.5 | 0.625H | 0.50L | 2000 | 28.805 | 0.922 |
| 8 | 1 | 120 | 90.0 | 0.875H | 0.75L | 3000 | 27.880 | 0.427 |
| 9 | 1 | 120 | 15.0 | 0.375H | 0.25 | 1000 | 10.717 | 0.337 |
| 10 | 1 | 120 | 90.0 | 0.875H | 0.25L | 1000 | 15.615 | 0.545 |
| 11 | 0 | 90 | 52.5 | 0.625H | 0.50L | 2000 | 28.805 | 0.922 |
| 12 | −1 | 90 | 52.5 | 0.625H | 0.50L | 1000 | 16.452 | 0.983 |
| 13 | 1 | 120 | 15.0 | 0.875H | 0.25L | 3000 | 18.899 | 0.225 |
| 14 | 1 | 60 | 90.0 | 0.875H | 0.75L | 1000 | 9.673 | 0.787 |
| 15 | −1 | 90 | 52.5 | 0.625H | 0.75L | 2000 | 28.028 | 0.973 |
| 16 | 1 | 60 | 90.0 | 0.375H | 0.25L | 1000 | 10.291 | 0.654 |
| 17 | −1 | 90 | 52.5 | 0.375H | 0.50L | 2000 | 21.864 | 0.602 |
| 18 | 1 | 120 | 15.0 | 0.375H | 0.75L | 3000 | 25.213 | 0.289 |
| 19 | 0 | 90 | 52.5 | 0.625H | 0.50L | 2000 | 28.805 | 0.922 |
| 20 | 0 | 90 | 52.5 | 0.625H | 0.50L | 2000 | 28.805 | 0.922 |
| 21 | 1 | 120 | 15.0 | 0.875H | 0.75L | 1000 | 8.339 | 0.310 |
| 22 | 1 | 60 | 15.0 | 0.375H | 0.75L | 1000 | 7.372 | 0.342 |
| 23 | −1 | 90 | 52.5 | 0.625H | 0.25L | 2000 | 27.901 | 0.902 |
| 24 | 1 | 60 | 15.0 | 0.375H | 0.25L | 3000 | 19.315 | 0.288 |
| 25 | 1 | 60 | 90.0 | 0.875H | 0.25L | 3000 | 29.564 | 0.614 |
| 26 | 0 | 90 | 52.5 | 0.625H | 0.50L | 2000 | 28.805 | 0.922 |
| 27 | −1 | 90 | 52.5 | 0.875H | 0.50L | 2000 | 19.451 | 0.521 |
| 28 | 1 | 60 | 15.0 | 0.875H | 0.75L | 3000 | 17.150 | 0.279 |
| 29 | −1 | 120 | 52.5 | 0.625H | 0.50L | 2000 | 24.790 | 0.504 |
| 30 | 1 | 120 | 90.0 | 0.375H | 0.25L | 3000 | 31.805 | 0.460 |
| 31 | −1 | 90 | 15.0 | 0.625H | 0.50L | 2000 | 19.471 | 0.450 |
| 32 | −1 | 90 | 90.0 | 0.625H | 0.50L | 2000 | 19.465 | 0.451 |
| Source | Degree of Freedom | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 7 | 1908.54 | 272.648 | 44.48 | 0.000 |
| Linear | 4 | 1146.26 | 286.565 | 46.75 | 0.000 |
| A | 1 | 31.11 | 31.111 | 5.08 | 0.034 |
| B | 1 | 121.57 | 121.566 | 19.83 | 0.000 |
| C | 1 | 4.47 | 4.467 | 0.73 | 0.402 |
| E | 1 | 989.12 | 989.116 | 161.37 | 0.000 |
| Square | 2 | 736.43 | 368.216 | 60.07 | 0.000 |
| B * B | 1 | 116.05 | 116.052 | 18.93 | 0.000 |
| C * C | 1 | 73.09 | 73.091 | 11.92 | 0.002 |
| Two-factor interaction | 1 | 25.85 | 25.847 | 4.22 | 0.051 |
| B * E | 1 | 25.85 | 25.847 | 4.22 | 0.051 |
| Residual | 24 | 147.11 | 6.130 | - | - |
| Lack of Fit | 19 | 138.54 | 7.291 | 4.25 | 0.058 |
| Pure Error | 5 | 8.57 | 1.715 | - | - |
| Total | 21 | 2055.65 | - | - | - |
| Source | Degree of Freedom | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 6 | 1.84654 | 0.307757 | 23.66 | 0.000 |
| Linear | 4 | 0.42124 | 0.105311 | 8.09 | 0.000 |
| A | 1 | 0.13097 | 0.130969 | 10.07 | 0.004 |
| B | 1 | 0.25130 | 0.251302 | 19.32 | 0.000 |
| C | 1 | 0.00004 | 0.000036 | 0.00 | 0.958 |
| E | 1 | 0.03894 | 0.038937 | 2.99 | 0.096 |
| Square | 2 | 1.42530 | 0.712649 | 54.78 | 0.000 |
| B * B | 1 | 0.27825 | 0.278247 | 21.39 | 0.000 |
| C * C | 1 | 0.10219 | 0.102188 | 7.85 | 0.010 |
| Residual | 25 | 0.32524 | 0.013010 | - | - |
| Lack of Fit | 20 | 0.30731 | 0.015366 | 4.28 | 0.057 |
| Pure Error | 5 | 0.01793 | 0.003586 | - | - |
| Total | 31 | 2.17179 | - | - | - |
| S | R-sq | R-sq (Adjustment) | R-sq (Projections) | |
|---|---|---|---|---|
| Nu | 2.47581 | 92.84% | 90.76% | 86.38% |
| f | 0.114060 | 85.02% | 81.43% | 73.51% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, C.; Zhang, R.; Mao, C.; Dong, Y.; Yao, X.; Hu, W.; Li, Z. Design and Optimization of Cross-Corrugated Triangular Ducts with Trapezoidal Baffles Based on Response Surface Methodology and CFD. Energies 2024, 17, 2335. https://doi.org/10.3390/en17102335
Liang C, Zhang R, Mao C, Dong Y, Yao X, Hu W, Li Z. Design and Optimization of Cross-Corrugated Triangular Ducts with Trapezoidal Baffles Based on Response Surface Methodology and CFD. Energies. 2024; 17(10):2335. https://doi.org/10.3390/en17102335
Chicago/Turabian StyleLiang, Caihang, Rui Zhang, Chaojian Mao, Yanfang Dong, Xiong Yao, Weipeng Hu, and Zhenxing Li. 2024. "Design and Optimization of Cross-Corrugated Triangular Ducts with Trapezoidal Baffles Based on Response Surface Methodology and CFD" Energies 17, no. 10: 2335. https://doi.org/10.3390/en17102335
APA StyleLiang, C., Zhang, R., Mao, C., Dong, Y., Yao, X., Hu, W., & Li, Z. (2024). Design and Optimization of Cross-Corrugated Triangular Ducts with Trapezoidal Baffles Based on Response Surface Methodology and CFD. Energies, 17(10), 2335. https://doi.org/10.3390/en17102335






