Extracting Accurate Parameters from a Proton Exchange Membrane Fuel Cell Model Using the Differential Evolution Ameliorated Meta-Heuristics Algorithm

Abstract

The electrochemical proton exchange membrane fuel cell (PEMFC) is an electrical generator that utilizes a chemical reaction mechanism to produce electricity, serving as a sustainable and environmentally friendly energy source. To thoroughly analyze and develop the features and performance of a PEMFC, it is essential to use a precise model that incorporates exact parameters to effectively suit the polarization curve. In addition, parameter extraction plays a crucial role in the simulation analysis, evaluation, optimum control, and fault detection of the proton exchange membrane fuel cell (PEMFC) system. Despite the development of many algorithms for parameter extraction in PEMFC, obtaining accurate and trustworthy results rapidly remains a challenge. This study presents a hybridized algorithm, namely differential evolution ameliorated (DEA) for reliably estimating PEMFC model parameters. To evaluate the proposed DEA-based parameter identification, a comparison analysis with previously published methods is conducted using MATLAB/Simulink^TM (R2016b, MathWorks, Natick, MA, USA) in terms of system correctness and convergence process. The proposed DEA algorithm is tested to extract the parameters of two PEMFC models: SR-12 500 W and 250 W. The sum of the squared errors (SSE) between the experimental and the obtained voltage data is defined as an objective function. The simulation results prove that the suggested DEA algorithm is capable of identifying the optimal PEMFC parameters rapidly and accurately in comparison with other optimization algorithms.

1. Introduction

Both small-scale power consumption and large-scale industrial operations require renewable energy sources due to the quick depletion of fossil fuels and the rising power demand [1]. The utilization of alternative sources of energy, such as solar and wind, is commonly employed. However, the generation of electric power using these sources is unstable and intermittent because environmental factors influence it. Solar irradiation and temperature significantly impact photovoltaic arrays, while wind speed affects the generated power from wind energy plants. To overcome this issue, employing large-scale energy storage and conversion systems may greatly increase the utilization rate of renewable energy [2]. Fuel cells are one of these energy storage and conversion systems, and they are affected by temperature, hydrogen, oxygen pressures, and membrane water content.

Consequently, fuel cells (FCs) have been developed to complement and enhance the existing green energy sources [3]. In addition, FCs have been a growing focus on this technology as a means of generating electricity that is both efficient and environmentally friendly [4]. Typically, the voltage produced by each individual fuel cell falls in the range of 0.5–0.9 volts. Multiple FCs are linked in a series configuration to achieve a substantial voltage and power output, as well as to be compatible with high-power generation systems [5]. The proton exchange membrane fuel cell (PEMFC) is a type of fuel cell that has demonstrated significant promise and strong competitiveness in automotive, portable, and distributed applications [6]. This is due to its lower operating temperature, excellent transient responses, solid-state electrolyte, high power density, high energy efficiency, compactness, scalability, low noise, and zero emissions to the environment [7]. Despite substantial advancements in PEMFC technology in recent years, ongoing research is focused on optimizing the design and control of the PEMFC stack.

Electrochemical modeling is essential for optimizing the performance of PEMFC and is crucial for designing controllers and detecting faults in the PEMFC stack [8,9]. Throughout recent decades, numerous electrochemical models have been constructed to elucidate the characteristics of PEMFC. These models exhibit varying degrees of complexity and can be broadly categorized into two distinct groups: mechanical modeling and semi-empirical modeling [10]. The mechanical modeling utilizes sophisticated electrochemical, thermodynamic, and fluidic transport equations [11,12]. The second category is semi-empirical modeling, which integrates mechanistic validity with empirical simplicity to anticipate the performance accurately and optimize control parameters of PEMFC in real time based on non-linear polarization curves [13]. Amphlett has proposed a viable mathematical model for representing PEMFC among different semi-empirical models in [14]. This approach has garnered widespread acceptance among numerous scientific experts. The PEMFC model is considered a multi-variable, non-linear, and intricate model. Thus, conventional methodologies are inadequate for accurately representing the actual output features of PEMFC models [7,15].

The process of estimating model parameter values is typically intricate, crucial, and requires careful attention. Therefore, the simplification methods for obtaining PEMFC model parameters have been addressed as optimization problems in meta-heuristic approaches because the conventional optimization approaches are not practical [16]. Generally, meta-heuristics (Mh) are used to optimize the precise parameters of a PEMFC model. Many optimization approaches in engineering have utilized the no-free-lunch theorem based on these concepts to solve a wide range of optimization issues [17,18]. Furthermore, Mh can be classified into four primary categories: swarm-based, nature-based, physics-based, and evolutionary-based. These categories have been thoroughly examined by researchers in the literature to identify the most effective values for the unidentified parameters of PEMFC models [19]. From the categories mentioned above, the genetic algorithm (GA) was utilized to address the optimization challenge of modeling PEMFCs [20]. The constraints of GA are limited efficiency, reliance on the initial states of variables, and providing poor solutions. To enhance the performance provided by GA, particle swarm optimization (PSO) has been employed in addition to other optimization algorithms, such as vortex search algorithm (VSA) [21,22], differential evolution (DE) [23], grey wolf optimizer (GWO) [24], flower pollination algorithm (FPA) [25], and equilibrium optimizer (EO) [26]. Recently, the algorithms mentioned above have been considered conventional Mh algorithms. These algorithms still have certain shortcomings that require enhancement in terms of precision, stability, and resilience. To achieve advancements in enhancing the capabilities and efficiency of Mhs algorithms, modern optimization techniques have been developed [27]. The Improved Fluid Search Optimization Algorithm proposed by Qin et al. can achieve superior performance while minimizing computing complexity and is an enhanced search optimizer for assessing the parameters of PEMFCs [27]. In order to evaluate the precision of metaheuristic algorithms, many forms of errors may be used, including mean squared error (MSE), coefficient of determination (R2), cross-validation factor (Q2), residual sum of squares (RSS), and sum squared error (SSE) [28]. The sum of squared errors (SSE) between the experimental and estimated data was used as the objective to be achieved. A Bayesian-regularized neural network was utilized to determine the optimal parameters for PEMFC [29]. In [30], Yuan et al. propose a sunflower optimizer to estimate the unknown parameters for PEMFCs. All of the above optimization techniques have been implemented to enhance the precision of PEMFC parameters. However, the majority of them failed to meet the necessary criteria for precise precision. Hence, it is necessary to explore more contemporary techniques in order to accurately determine the parameters of the PEMFC model with rapid convergence. For this reason, the development of hybridized algorithms that combine many methods is an inevitability for addressing the limitations of a single methodology and improving the effectiveness of exploration and exploitation characteristics to precisely identify the parameters. Isa et al. have combined the antlion and dragonfly optimizers to estimate the unknown parameters for PEMFCs [31]. This work presents an upgraded version of the differential evolution (DE) by combining it with the Firefly algorithm to enhance the optimization performance of parameter extraction for PEMFC. The main contributions of this study are as follows:

• The parameters of the PEMFC model are tuned to their optimal values using the suggested DE ameliorate (DEA) technique;
• The estimated outcomes of two PEMFC models, SR-12 500 W and 250 W, are compared comprehensively, using various algorithms;
• The performance characteristics of the PEMFC polarization curve are extracted and the SSE of the evaluated methods is verified.

The subsequent sections of this work are delineated as follows: Section 2 provides an exposition of the mathematical model used to explain the functioning of PEMFC stacks. The formulation of the goal function is outlined in Section 3. Section 4 details the proposed DEA algorithm. Section 5 presents the simulation findings of the two types of PEMFC models: SR-12 500 W and 250 W. Section 6 highlights the main conclusions.

2. Mathematical Model of PEM Fuel Cell

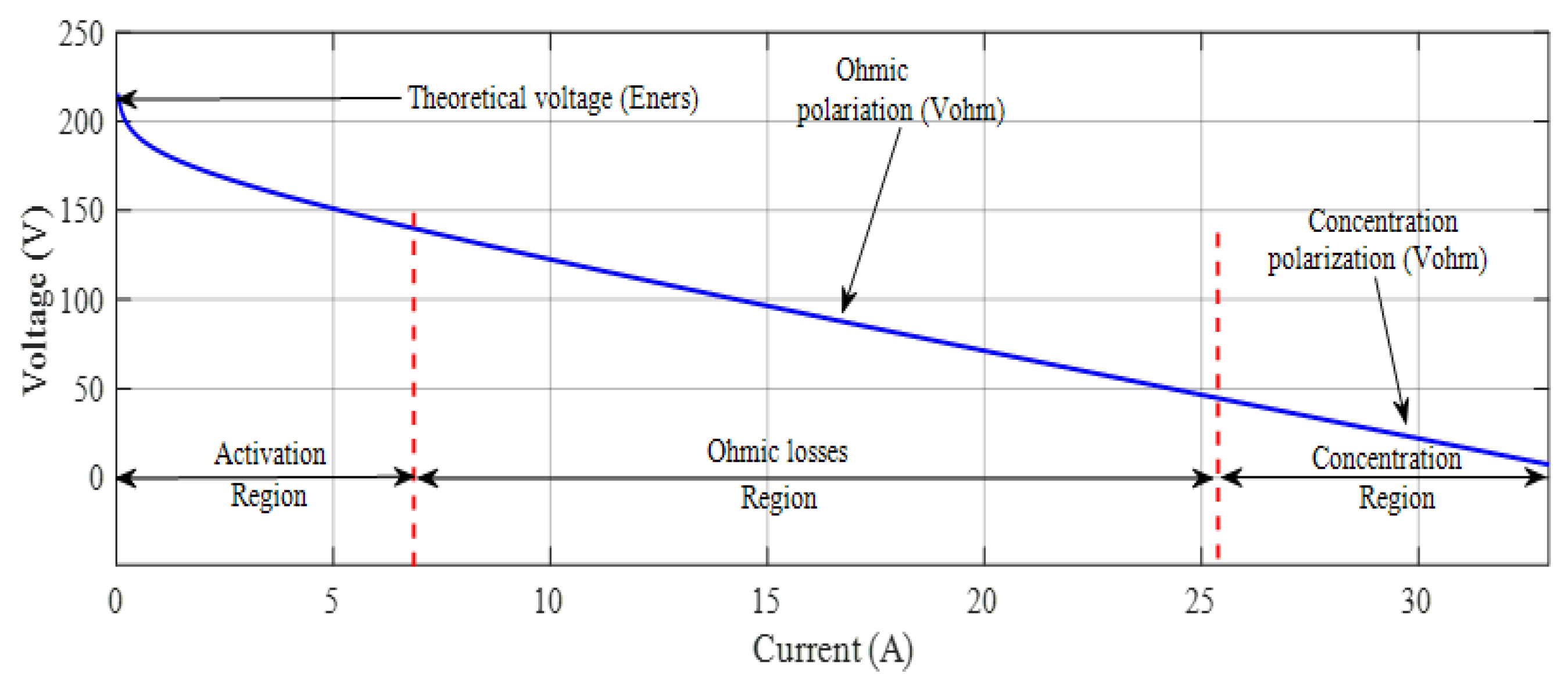
Figure 1 displays the polarization curve of a proton exchange membrane fuel cell (PEMFC). The graphic illustrates three distinct parts of the characteristic curve that correspond to various types of losses observed in the fuel cell: activation region, ohmic losses region, and concentration region.

For practical purposes, multiple individual PEMFCs are combined into a stack to generate the necessary power output. The output voltage V of a PEMFC stack linked in series with N_cell can be expressed using Equation (1). The terminal voltage V_cell of a single PEMFC can be computed using the semi-empirical Equation (2) proposed by the Amphlett model [14]:

$$V=N_{cell}{V}_{cell}$$

(1)

$$V_{cell}=E_{Nernst}-V_{act}-V_{ohm}-V_{con}$$

(2)

The E_Nernst value corresponds to the reversible voltage obtained in thermodynamic equilibrium when there is no current flowing. It can be calculated using a modified version of the Nernst Equation (3). To consider the variations in pressure and temperature compared to the typical conditions of 298.15 K and 1 bar [19], we use the following:

$$E_{Nernst}=1.229-(0.85\times {10}^{-3})\times T_{FC}-298.15)+(4.31\times {10}^{-5}\times T_{FC}\times \ln (p_{O_2})\times 0.5\times \ln (p_{O_2}))$$

(3)

Thus, 1.229 represents the reference potential for electricity at the standard state. TFC represents the cell temperature, while P_H2 and P_O2 represent the effective partial pressure of hydrogen and oxygen, respectively. The reactants are P_H2 and P_O2 and the partial pressures can be determined using Equations (4) and (5), respectively.

$$P_{H_2}=0.5\times R_{HA}\times P_{H_{2}O}\left[{\left(\frac{R_{HA}\times P_{H_{2}O}}{P_A}\times e^{\left(\frac{1.635I_{FC}/A}{T_{FC}{ }^{1.1334}}\right)}\right)}^{-1}-1\right]$$

(4)

$$P_{O_2}=R_{HC}\times P_{H_{2}O}\left[{\left(\frac{R_{HC}\times P_{H_{2}O}}{P_C}\times e^{\left(\frac{4.912I_{FC}/A}{T_{FC}{ }^{1.1334}}\right)}\right)}^{-1}-1\right]$$

(5)

The variables P_A and P_C represent the inlet pressure of the anode and cathode, while R_HA and R_HC indicate the relative humidity of vapor in the anode and cathode. I_FC represents the cell operating current, and A represents the active area of the membrane. P_H2O represents the saturation pressure of the water vapor, which can be expressed as a function of the cell temperature T_FC in Kelvin using Equation (6):

$${\log }_{10}(P_{{ }_{H_{2}O}})=2.95\times {10}^{-2}(T_{FC}-273.15)-9.18\times {10}^{-5}{(T_{FC}-273.15)}^2+1.4\times {10}^{-7}{(T_{FC}-273.15)}^3-2.18$$

(6)

V_act refers to the voltage drop that occurs due to the slowdown of the reactions occurring on the active surfaces of the anode and cathode. This drop can be calculated using a semi-empirical Equation (7):

$$V_{act}=-\left[{\xi }_1+{\xi }_2{T}_{FC}+{\xi }_3{T}_{{ }_{FC}}\ln (C_{{ }_{O_2}})+{\xi }_4{T}_{FC}\ln (I_{{ }_{FC}})\right]$$

(7)

The activation voltage Equation includes semi-empirical constants ξ_1,2,3,4, which have well-defined physical significance in terms of kinetics, thermodynamics, and electrochemistry. The concentration of dissolved oxygen on the catalytic interface of the cathode C_O2 can be determined using Henry’s Law, represented by Equation (8):

$$C_{O_{{ }_2}}=\frac{P_{O_2}}{5.08\times {10}^{{ }^6}}{e}^{\left(-498/T_{{ }_{FC}}\right)}$$

(8)

The voltage drop due to resistance V_ohm is determined by three factors: the equivalent membrane resistance R_M, the contact resistance R_C of proton conduction, and the stack current I_FC. The computation process is outlined in Equations (9)–(11). The value of R_M is determined by the resistivity of the exchange membrane (pρ_m), the thickness of the membrane (l), and the membrane area (A). In Equation (11), λ represents the water content of the membrane, which is one of the unidentified variables that need to be determined. λ influenced by the membrane on the polarization curve. Since the proton conductivity of the membrane increases with increasing water content, the ohmic losses in the membrane decrease with increasing water content. Thus, better performance can be achieved with higher water content [19]:

$$V_{ohm}=I_{FC}(R_M+R_C)$$

(9)

$$R_M=({\rho }_m\times 0.0128)/A$$

(10)

$${\rho }_m=\frac{\mathrm{1.81.6}\left[0.062{\left(\frac{T_{FC}}{303}\right)}^2{\left(\frac{I_{FC}}{A}\right)}^{2.5}+0.03\left(\frac{I_{FC}}{A}\right)+1\right]}{\left[\lambda -0.634-3\left(\frac{I_{FC}}{A}\right)\right]\times e^{4.18\times (T_{FC}-303)/T_{FC}}}$$

(11)

The concentration voltage drop is determined using the following formula:

$$V_{con}=-\beta \ln \left(1-\frac{j}{j_{\max }}\right)$$

(12)

The parameter β represents the parametric coefficient, which is dependent on the cell and its operational state [32]. j denotes the current density (A/cm²), whereas j_max represents the maximum current density (A/cm²).

3. Formulation of PEMFC Parameters Extraction Problem

The operation parameters T_FC, P_a, P_c, R_HA, R_HC, P_H2, and P_O2 in Equations (1)–(12) can be measured and are possibly influenced by the operating conditions. On the other hand, the physical parameters ξ₁, ξ₂, ξ₃, ξ₄, λ, R_C, and β are not known, the ranges of which are provided in the preceding literature [33], as illustrated in

Table 1. Range of unknown seven parameters.

Ranges
Parameters	Min	Max
ζ1	−1.1997	−0.08532
ζ2 × 10−3	0.8	6.00
ζ3 × 10−5	3.60	9.80
ζ4 × 10−4	−2.60	−0.954
A	10.00	24.00
β	0.0136	0.5
RC × 10−4	1.00	8.00

.

Given that the unknown parameter X = [ξ₁, ξ₂, ξ₃, ξ₄, λ, R_C, β] has a substantial impact on the model findings, it is crucial to extract them with precision in order to closely replicate the actual voltage–current (V-I) characteristic of PEMFC.

The proposed approach is employed to extract the seven unidentified parameters and compare them with the existing literature. The objective of this article is to identify a set of ideal parameter values that will minimize the sum of squared errors (SSE) [34] between the experimental voltage (V_exp) and the model-estimated voltage (V_mod) calculated using Equation (1) [35]:

$$OBF=\min SSE(X)=\min \left({{\displaystyle \sum _{i=1}^N\left[V_{exp}-V_{mod}\right]}}^2\right)$$

(13)

The variable N represents the number of data points that have been measured.

4. Differential Evolution Ameliorated Algorithm

4.1. Differential Evolution Algorithm

The DE algorithm, introduced by Storn and Price in [36], is a variant of the evolutionary algorithm employed for solving continuous optimization issues. It possesses notable advantages over other evolutionary approaches and swarm-based techniques in terms of robustness, ease of implementation, and convergence speed. The DE algorithm consists of three main steps: mutation, crossover, and selection. During these steps, each potential solution is assessed by comparing it to a target set. The mutation is employed to achieve the desired outcome, while a crossover is guaranteed between the possible solution and the collected target. Equation (14) represents the mutation, whereas S_a represents a potential solution, and S_aT denotes the goal vector for S_a derived from S_b, S_c, and S_d [36,37].

$$S_{aT}=S_b+f(S_{{ }_c}-S_d),f\in \left[0,2\right]$$

(14)

In this context, the variable f represents the scaling vector that controls the amplification of changes. The crossover is implemented using the operator illustrated in Equation (15), which utilizes S_aT and S_a.

$$S_{{ }_{aT.I}}+\left\{\begin{array}{l}{S}_{{ }_{aT.I}}\hspace{1em}\hspace{1em}if rand <C_r\\ S_{{ }_{aT.I}}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}else\end{array}\right.\hspace{1em}\hspace{1em}{C}_r\in \left[0,1\right]$$

(15)

The rate of crossing is represented by the symbol C_r. The selection process is performed with the operator specified in Equation (16).

$$S_{{ }_{a.next}}=\left\{\begin{array}{l}{S}_{aU}\hspace{1em}\hspace{1em}if f(S_{aU})\le f(S_a)\\ S_a\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}else\end{array}\right.$$

(16)

4.2. Proposed Ameliorated DE

The DE can still be used to solve many complex problems in the real world. However, it needs to be simplified and become more robust to track the optimal solutions for engineering problems. Since the standard Firefly is a powerful algorithm and has a major advantage, the characteristic distance is added to an optimization problem. For this reason, common methods can be modified by adding the Firefly to straightforwardly define the attractiveness coefficient.

This study introduces a novel hybrid algorithm called DEA, which is based on the Firefly algorithm (FA) and differential evolution (DE).

FA is founded upon three key concepts [38]:

• First, all the fireflies are viewed as having no gender distinction and we attempt to approach the fireflies that emit more light until the entire population is evaluated.
• The allure of fireflies is linked to the intensity of their luminous messages. In the scenario where there is a choice between two fireflies, the one that emits a stronger light is favored. It is important to observe that the brightness diminishes as the distance rises.
• The luminosity of a firefly is determined by the fitness function’s optimization problem value.

The FA can be formally expressed using the following equations:

$$w(r)=w_0\exp \left(-k_r^m\right),m\ge 1$$

(17)

$$r_{ij}=\sqrt{{\displaystyle \sum _{k=1}^d{\left(x_{i,k}-x_{j,k}\right)}^2}}$$

(18)

$$x_i=x_i+w_0\exp (-k_r{ }_{ij}^2)(x_j-x_i)+\alpha (randn-1/2)$$

(19)

The part mentioned above was added to DE to enhance the convergence speed, performance, and robustness.

Equation (18) defines the length between any two populations. Also, the movement of the ith firefly attracted to a brighter firefly is represented in Equation (19). The best solution for sorting fireflies is employed to evaluate the new mutated vector in Equation (14). Next, we apply the crossover using the operator illustrated in Equation (15). If the cost obtained is better than the one chosen by the firefly population, it will be kept. In the opposite case, the proposed algorithm kept the best solution given by Firefly for the next generation. The flowchart of the proposed DEA is presented in Figure 2.

5. Test Types and Simulations Result

In this part, the effectiveness of the proposed differential evolution ameliorated (DEA) algorithm is demonstrated by two test cases: 250 W PEMFC and SR-12 modular. The characteristics of PEMFC types are presented in

Table 2. Specifications of the commercial PEMFC stacks.

Datasheet Parameters
Types of PEMFC	SR-12 Modular	250 W Stack
Ncell	48	24
A (cm2)	62.5	27
L (µm)	25	127
jmax (A/cm2)	0.672	0.680
PH2 (atm)	1.47628	1
PO2 (atm)	0.2095	1
T (K)	323	343.15

.

Table 3. Initialization parameter.

Algorithms	Values
Proposed DEA	Pcr = 0.6
	gamma = 1.2
	beta0 = 2
	alpha = 0.095
DE	Pcr = 0.6
FFA	K = 2
	n = 30
BBO	Keep Rate = 0.2

represents the initialization parameters of the studied algorithms.

The proposed algorithm aims to determine the ideal parameters of PEMFC stacks by minimizing the difference between measured and estimated data.

The proposed DEA algorithm outcomes are contrasted with several techniques presented in previously published works. The parameters of DEA consist of a population of 30, a maximum number of iterations is set to 300, and the implementation is repeated 30 times for all algorithms.

To validate the proposed DEA validation, the computed stack voltages are compared with the stack voltages measured via experimentation. The discrepancy between the estimated and measured stack voltages is evaluated using the integral of absolute error (IAE), as shown in Equation (20).

$$IAE=\left|V_{\exp }-V_{mod}\right|$$

(20)

The stability, accuracy, and effectiveness of the proposed DEA in determining the precise values of unknown parameters in PEMFC are tested. Furthermore, a comprehensive examination of sensitivity and statistical data is conducted for all the PEMFC stacks under investigation. The statistical results of the DEA algorithm are compared with conventional algorithms, including BBO, FFA, DE, GOA, RSA, and PDO. The comparison is performed based on many metrics, mostly focusing on the best and worst values of the objective function, the mean value of the objective function, RMSE, and MAE. These metrics can be mathematically represented as given in Equations (21) and (22):

$$RMSE=\sqrt{\frac{{\displaystyle \sum _{i=1}^{30}{(SE{E}_i-SS{E}_{\min })}^2}}{30}}$$

(21)

$$MAE=\frac{{\displaystyle \sum _{i=1}^{30}{(SE{E}_i-SS{E}_{\min })}^2}}{30}$$

(22)

Where Pcr, gamma, beta, alpha, K, n, and Kr represent mutation coefficient light, absorption coefficient, attraction coefficient base value, crossover probability, number of sections, number of solutions in each section, and Kr the keep rate, respectively. The common parameter between the DEA and DE is Pcr, which has the same value.

5.1. Type 1: Modular SR-12

This research study aims to optimize the model parameters of the SR-12PEM 500 W. The findings and data of this model can be found in

Table 4. Statistical results of the first case study for SR 12 PEMFC.

	Algorithms
	Proposed DEA	BBO	FFA	DE	GOA [39]	RSA [39]	PDO [39]
SSE min	1.0537	1.0593	1.0538	1.0539	1.0566	1.0566	1.0566
SSE mean	1.0537	1.0749	1.0661	1.0559	1.0566	1.0566	1.0586
SSE max	1.0537	1.0955	1.0936	1.0620	1.0566	1.0566	1.0719
STD	2.6113 × 10−12	0.0091	0.0111	0.0019	1.8709 × 10−13	1.7200 × 10−06	1.733 × 10−6
RMSE	3.9545 × 10−11	1.4659 × 10−02	1.7029 × 10−02	5.4665 × 10−03	4.7296 × 10−15	4.7296 × 10−15	5.5914 × 10−3
MEA	1.5638 × 10−21	2.1491 × 10−04	2.8999 × 10−04	2.9883 × 10−05	4.3594 × 10−15	4.3594 × 10−15	2.0417 × 10−3

,

Table 5. Comparative analysis of several algorithms for SR-12 PEMFC.

Algorithms	ζ1	ζ2 × 10−3	ζ3 × 10−5	ζ4 × 10−5	λ	RC × 10−4	β	SSE
Proposed DEA	−1.1021	3.7687	8.2004	−9.5400	24	8.000	0.1769	1.05374
BBO	−1.0949	3.4000	5.7105	−1.0022	15.5184	4.0834	0.1825	1.0593
FFA	−0.9623	3.5655	9.6835	−9.5453	17.4364	8.0000	0.1769	1.0538
DE	−1.0341	3.1365	5.4776	−9.5400	14.5475	8.0000	0.1767	1.0539
GOA [39]	−0.9298	3.5932	9.7999	−9.5400	23.0000	6.7231	0.1753	1.0566
RSA [39]	−0.9289	3.5932	9.7999	−9.5400	23.0000	6.7231	0.1753	1.0566
PDO [39]	−0.8532	2.7571	6.2497	−9.5400	23.0000	6.7237	0.1753	1.0566

and

Table 6. The absolute errors for the SR-12 PEMFC stack, as well as the experimental and simulated stack voltages.

N0	Experimental Data		Simulated Data
	Iexp	Vexp	Vmod	IAE
1	1.0040	43.1700	43.3333	0.1638
2	3.1660	41.1400	41.0844	0.0555
3	5.0190	40.0900	39.9101	0.1798
4	7.0270	39.0400	38.8541	0.1858
5	8.9580	37.9900	37.9317	0.0582
6	10.9700	37.0800	37.0142	0.6577
7	13.0500	36.0300	36.0893	0.0509
8	15.0600	35.1900	35.1737	0.0162
9	17.0700	34.0700	34.2456	0.1756
10	19.0700	33.0200	33.2876	0.2676
11	21.0800	32.0400	32.2760	0.2360
12	23.0100	31.2000	31.2435	0.0435
13	24.9400	29.8000	30.1332	0.3332
14	26.8700	28.9600	28.9224	0.0375
15	28.9600	28.1200	27.4614	0.6585
16	30.8100	26.3000	25.9928	0.3071
17	32.9700	24.0600	32.9805	0.0794
18	34.9000	21.4000	21.7733	0.3733

.

The first objective of this study is to enhance the model parameters of the SR-12 PEM. The relevant information and results are detailed in Table 4 and Table 5.

The results demonstrate that the suggested DEA achieves the lowest SSE (1.05374), outperforming other algorithms. The statistical comparison between numerous conventional algorithms and the proposed DEA is shown in Table 4. It is clear that the DEA algorithm outperforms BBO, FFA, DE, GOA, RSA, and PDO regarding standard deviation (STD), root mean squared error (RMSE), and mean absolute error (MAE).

Table 5 presents the identified seven parameters of PEMFC from the DEA, BBO, FFA, DE, GOA, RSA, and PDO results. When the minimal value of the goal function is selected using the studied algorithms, we found that the best result delivered by DEA is 1.05374; on the other hand, the best results obtained using the BBO, FFA, and DE algorithms are 1.0593, 1.0538, 1.0539, and 1.0566 for GOA, RSA, and PDO, respectively.

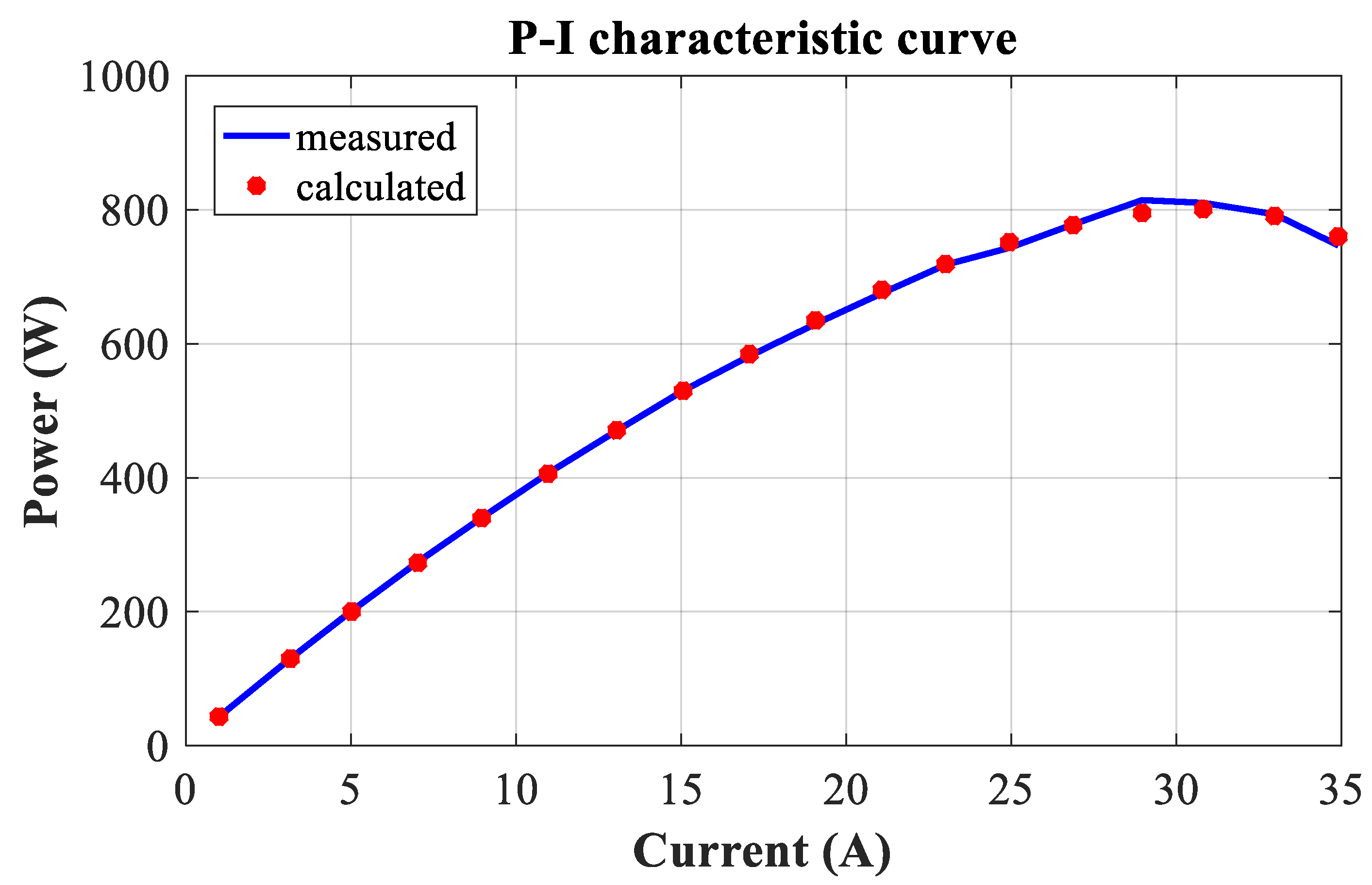
Figure 3 and Figure 4 show the V-I and P-I curves of SR-12 PEM, which were drawn using experimental measurements and estimated data generated by the DEA method. Therefore, Figure 3 and Figure 4 demonstrate the highest degree of similarity between the DEA V-I and P-I curves and the relevant experimental curves.

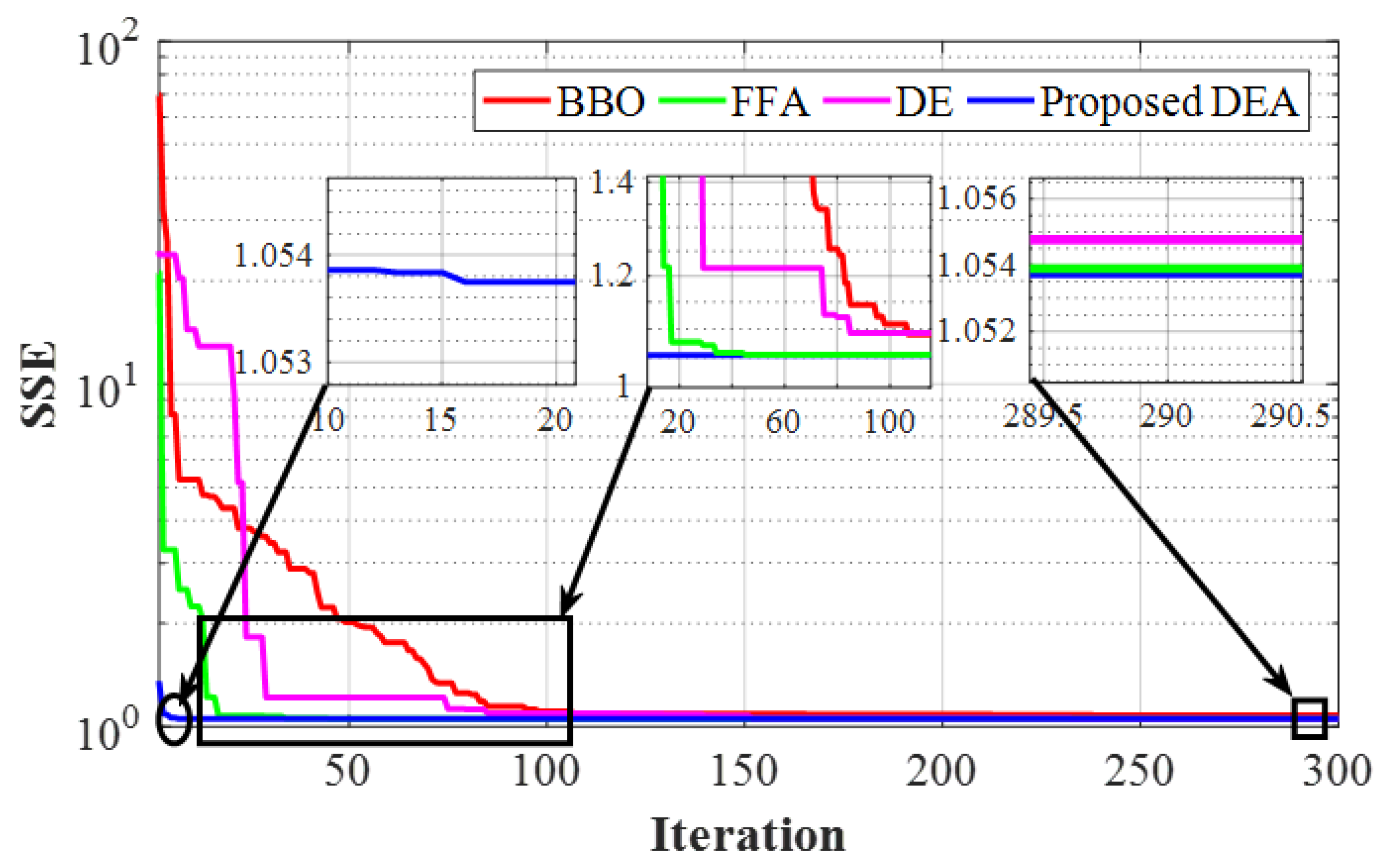
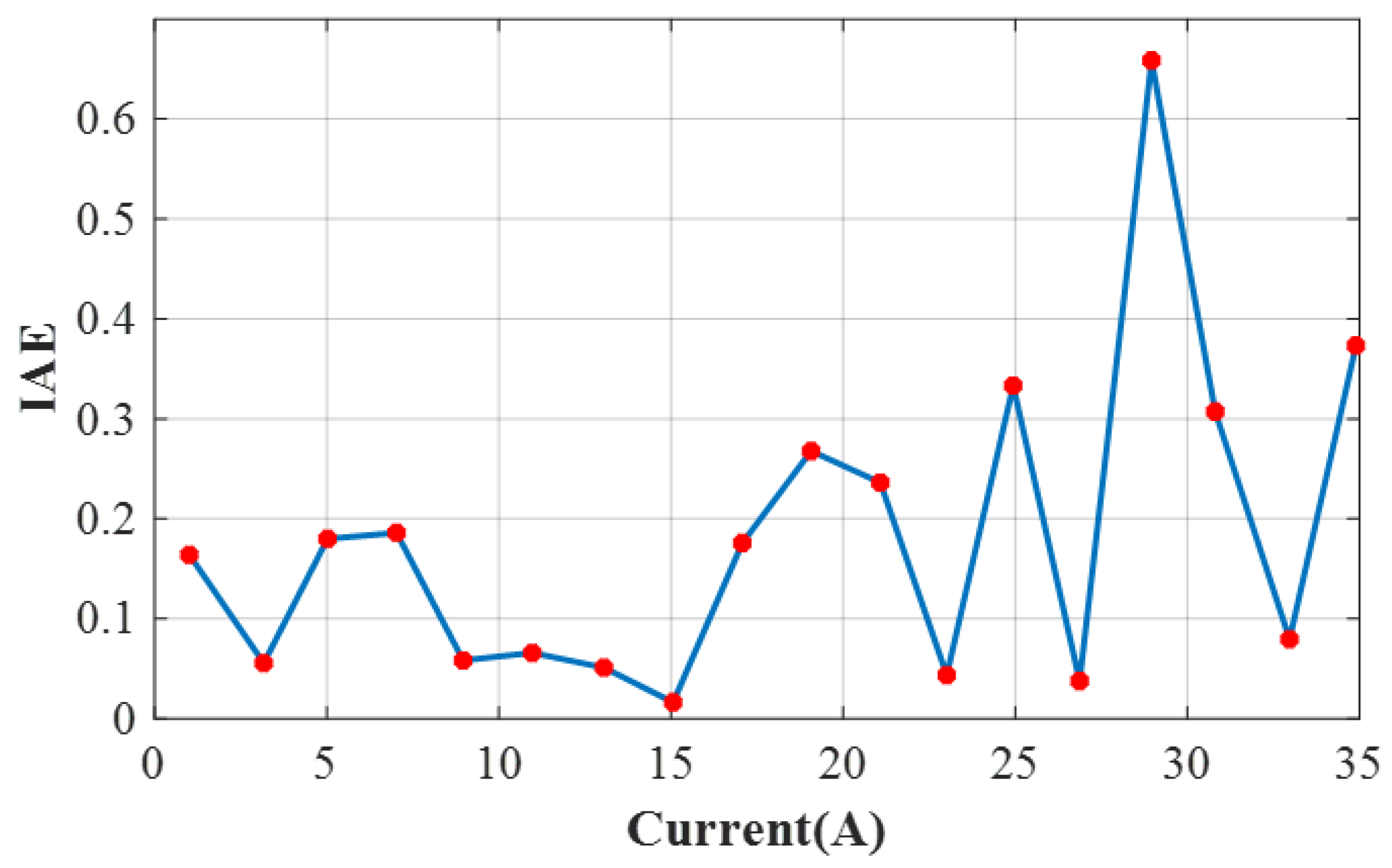
Figure 5 displays the convergence characteristics of all the methods specified in Table 5. The proposed DEA method demonstrates the most optimal convergence curve. Furthermore, Figure 6 displays the IAE values, with only one point exceeding 0.4. Figure 5 displays the convergence characteristics of all the methods specified in Table 5. The proposed DEA method demonstrates the most optimal convergence curve. Furthermore, Figure 6 displays the IAE values, with only one point exceeding 0.4 despite the non-linearity of the I/V curve and the lack of sufficient data points. The IEA for each data point is calculated and presented in Table 6.

The stability and accuracy of the suggested optimization technique are assessed by examining the impact of altering the cell temperature and reactant pressures. The polarization curves of SR-12 at various cell temperatures and the effects of H2 and O2 pressure changes are presented in Figure 7 and Figure 8, based on the optimum parameters delivered by DEA.

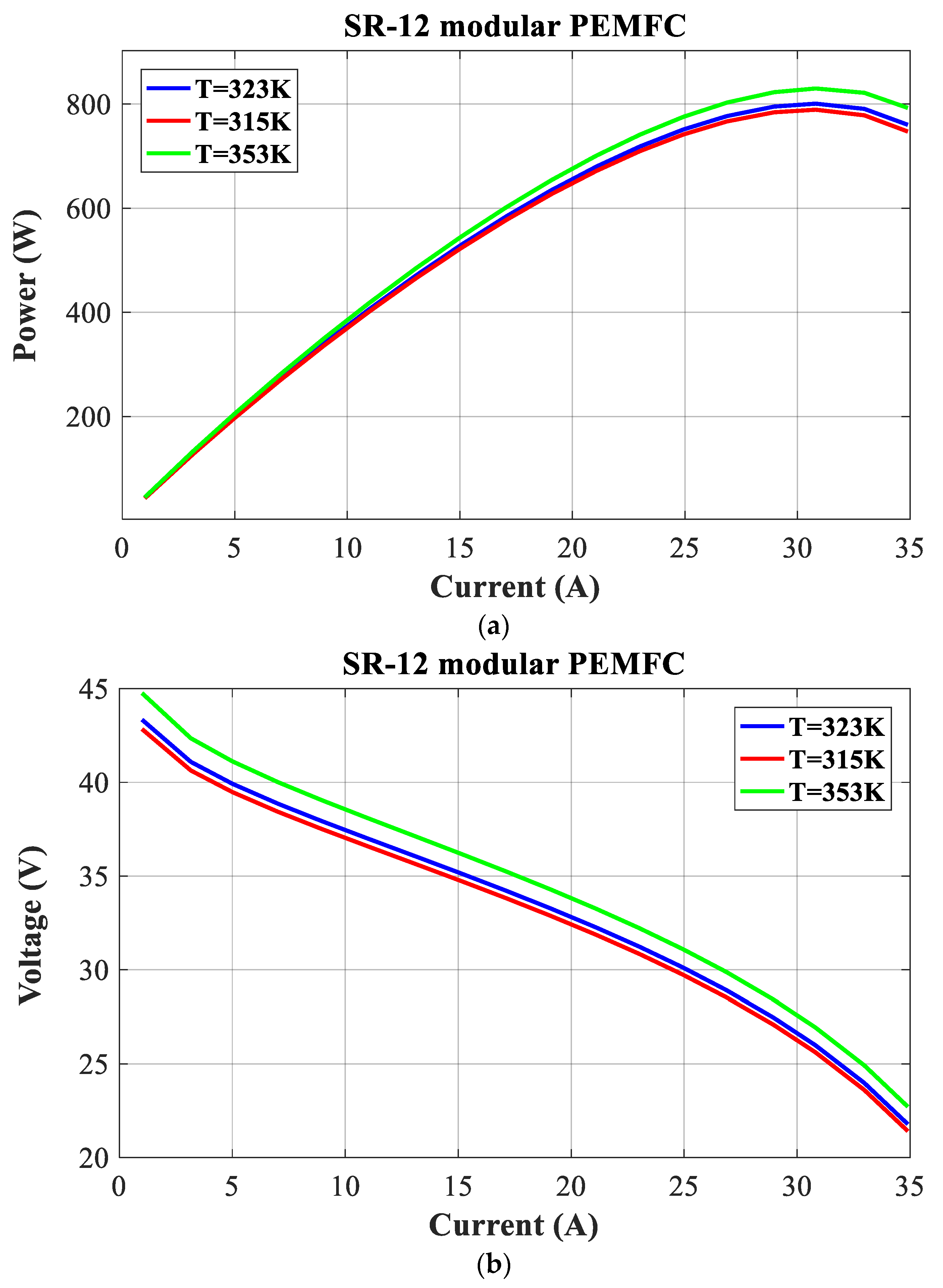
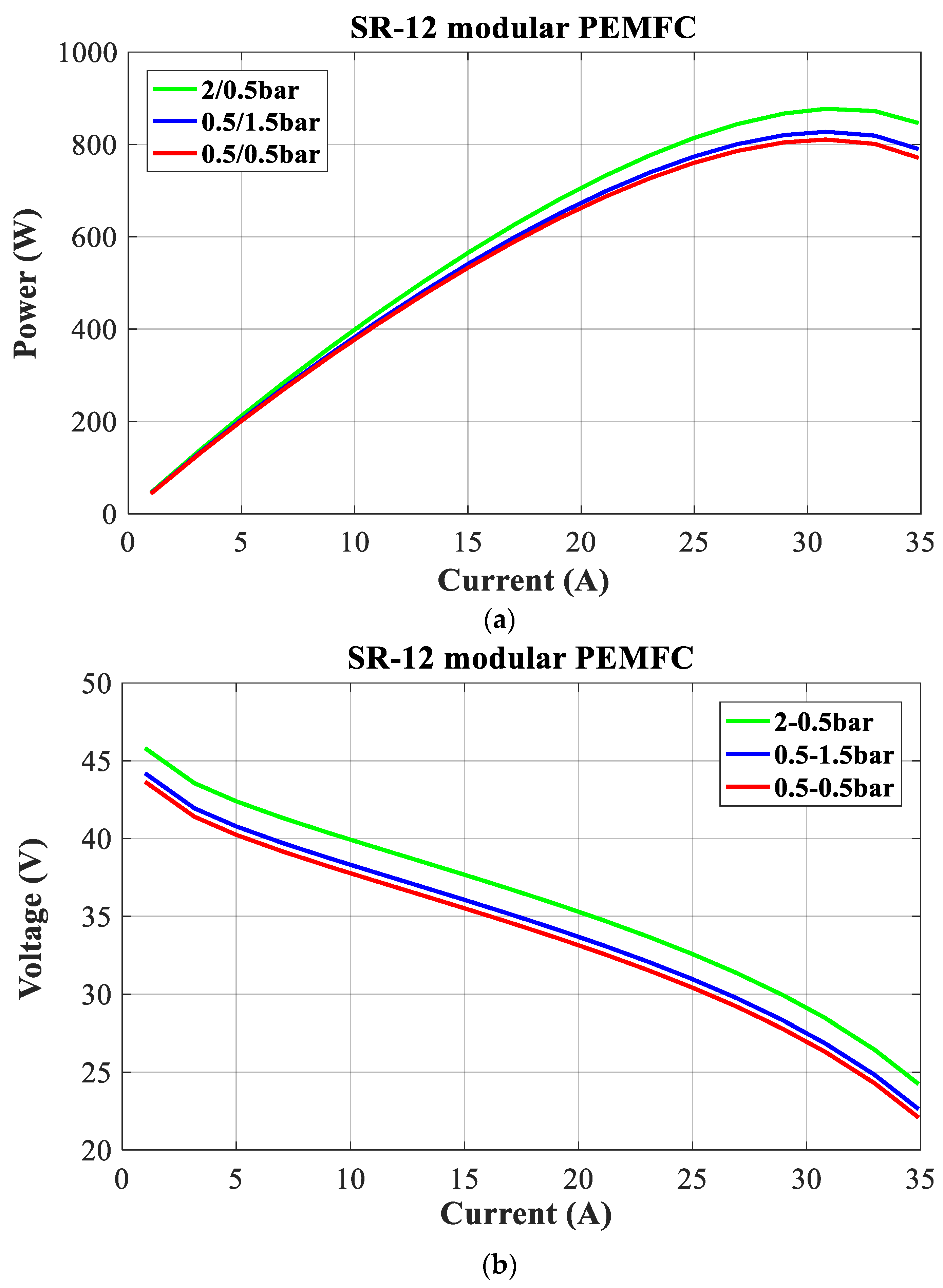
The polarization curves (P-I and V-I) of the SR-12 PEMFC stack at temperatures of 323 K, 315 K, and 353 K are shown in Figure 7. In this case, the pressures are maintained at the levels specified in the manufacturer’s datasheet. Furthermore, Figure 8 shows the polarization curves of the SR-12 PEMFC stack, which are measured at several pressures: 2/0.5 bar, 0.5/1.5 bar, 0.5/0.5 bar, and the constant temperature value specified in the manufacturer’s datasheet.

It is evident that the power and voltage of the SR-12 PEMFC increase as the reactant pressures and cell temperature rise.

5.2. Type 2: 250 W Stack

The objective of this section is to enhance the model parameters of the 250 W PEMFC based on the proposed DEA. The results and data obtained from this model are available in

Table 7. Comparative analysis of several algorithms for 250 W PEMFC.

	Algorithms
	Proposed DEA	BBO	FFA	DE	GOA [39]	RSA [39]	PDO [39]
SSE min	0.5063	0.5069	0.5063	0.5064	0.5940	0.5940	0.5940
SSE mean	0.5063	0.5117	0.5092	0.5071	0.5940	0.5940	0.5940
SSE max	0.5063	0.5185	0.5426	0.5079	0.5940	0.5940	0.5941
STD	1.7256 × 10−11	2.3847 × 10−3	0.0072	4.0580 × 10−04	1.7473 × 10−14	7.4732 × 10−14	0.0036
RMSE	7.8935 × 10−06	5.6538 × 10−3	2.8754 × 10−02	5.7100 × 10−02	2.1328 × 10−15	2.1328 × 10−15	4.1170 × 10−05
MEA	6.2307 × 10−11	3.1966 × 10−05	8.2680 × 10−04	3.2604 × 10−03	2.0058 × 10−15	2.0058 × 10−15	2.0273 × 10−05

,

Table 8. A comparative analysis of several algorithms for 250W PEMFC.

Algorithms	ζ1	ζ2 × 10−3	ζ3 × 10−5	ζ4 × 10−4	λ	RC × 10−4	β	SSE
Proposed DEA	−1.1018	3.4253	8.4411	−1.7515	10.0000	1.0000	0.0615	0.5062
BBO	−1.0000	3.0000	7.5811	−1.7302	11.7029	2.6832	0.0610	0.5069
FFA	−0.9349	2.3818	4.4615	−1.7506	11.4069	1.0000	0.0616	0.5063
DE	−1.0129	3.0553	7.6413	−1.7572	10.1458	1.0000	0.6129	0.5640
GOA [38]	−1.0694	2.6063	3.6000	−1.5543	24.0000	1.0000	0.0559	0.5940
RSA [38]	−1.0694	2.6063	3.6000	−1.5543	24.0000	1.0000	0.0559	0.5940
PDO [38]	−0.9112	2.1583	3.6000	−1.5543	24.0000	1.0000	0.0559	0.5940

and

Table 9. The absolute errors for the 250 W PEMFC stack, as well as the experimental and simulated stack voltages.

N0	Experimental Data		Simulated Data
	Iexp	Vexp	Vmod	IAE
1	0.4717	21.6300	21.6610	0.0310
2	2.1490	19.6800	19.3219	0.3580
3	2.8300	18.7800	18.8607	0.0807
4	3.9830	17.8800	18.2551	0.3751
5	5.7130	17.5800	17.5556	0.0243
6	7.0750	17.1200	17.0959	0.0240
7	8.0180	16.7700	16.8046	0.0346
8	11.1600	15.9200	15.9120	0.0079
9	13.7300	15.2200	15.1981	0.0218
10	16.5600	14.4000	14.3366	0.0833
11	17.5600	14.0200	13.9874	0.0325
12	19.0300	13.5200	13.3911	0.1288
13	20.3400	12.8200	12.7088	0.1111
14	22.0100	10.8600	11.2722	0.4122
15	22.9600	9.0580	8.91632	0.1416

.

The results detailed that the proposed DEA provides the lowest SSE (0.5063), surpassing the performance of other methods. Table 7 depicts a detailed statistical comparison of the proposed DEA with many conventional algorithms. Regarding standard STD, MAE, and RMSE, it is evident that the DEA algorithm is highly accurate compared to BBO, FFA, DE, GOA, RSA, and PDO. The optimized parameter values for several algorithms are listed in Table 8. It can be observed that the optimal result of the DEA algorithm is 1.05374, while the BBO, FFA, DE, GOA, RSA, and PDO algorithms yield the following optimal results: 1.0593, 1.0538, 1.0539, 1.05662, 1.0566, and 1.0566, respectively.

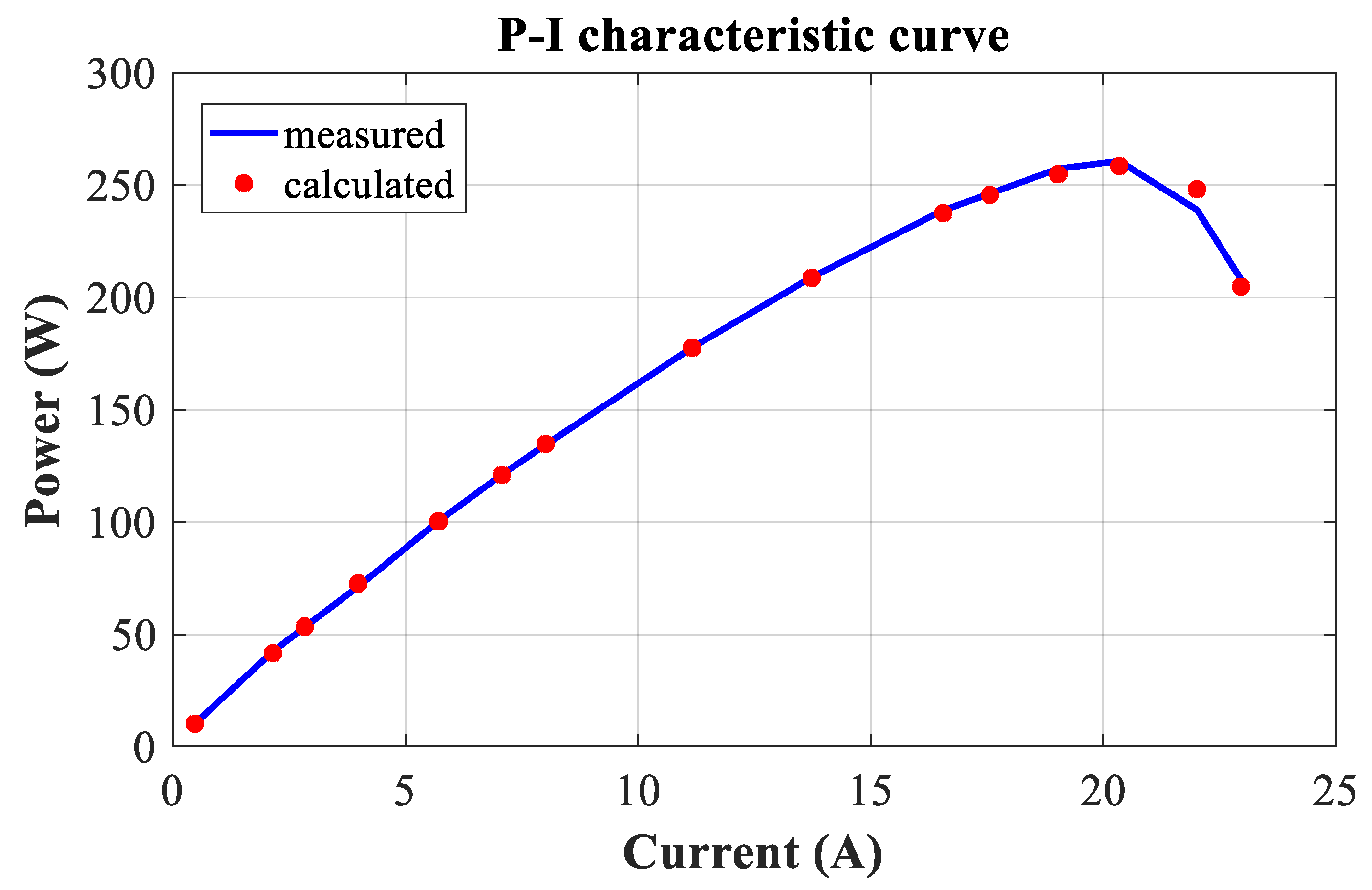
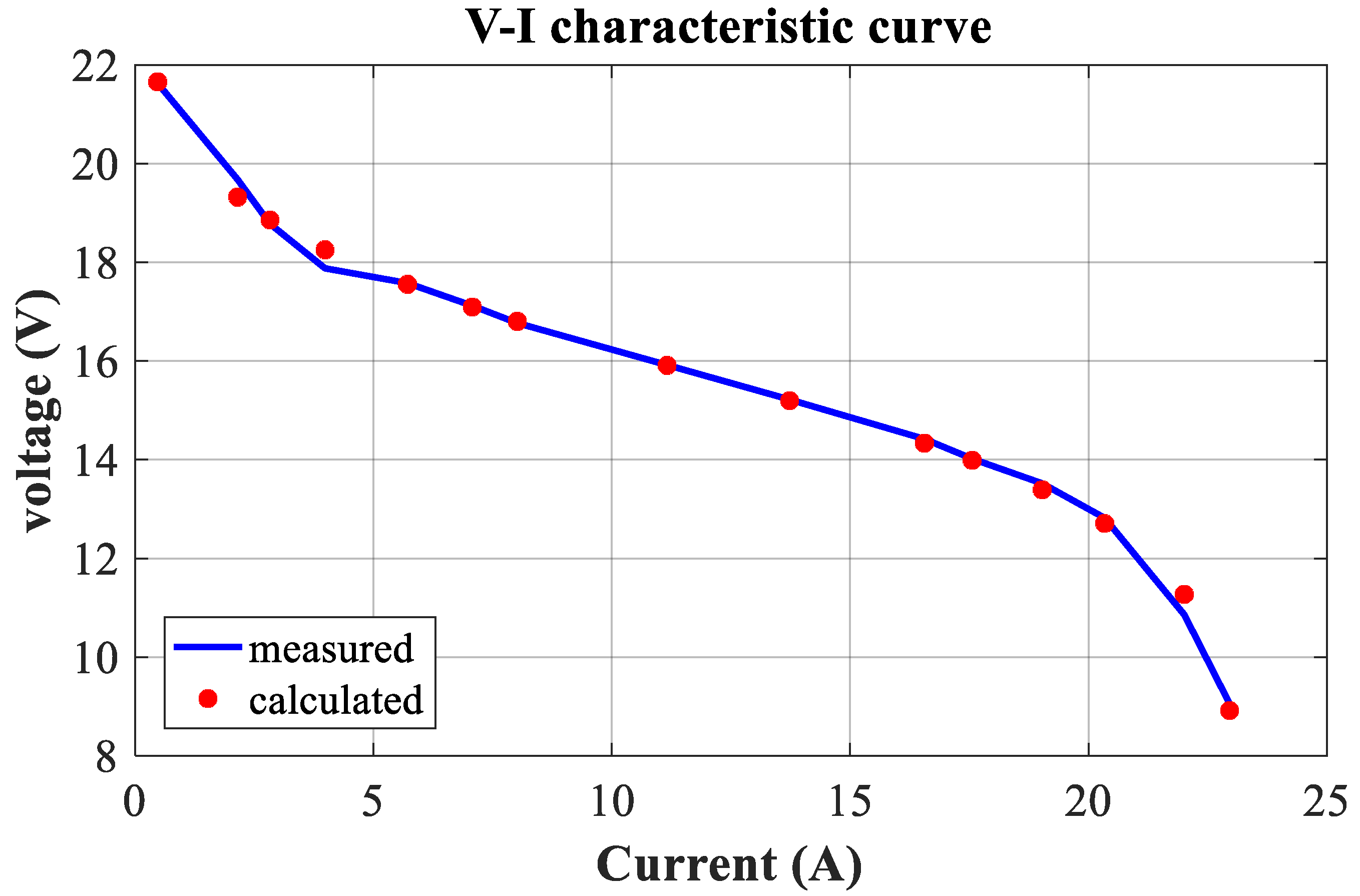
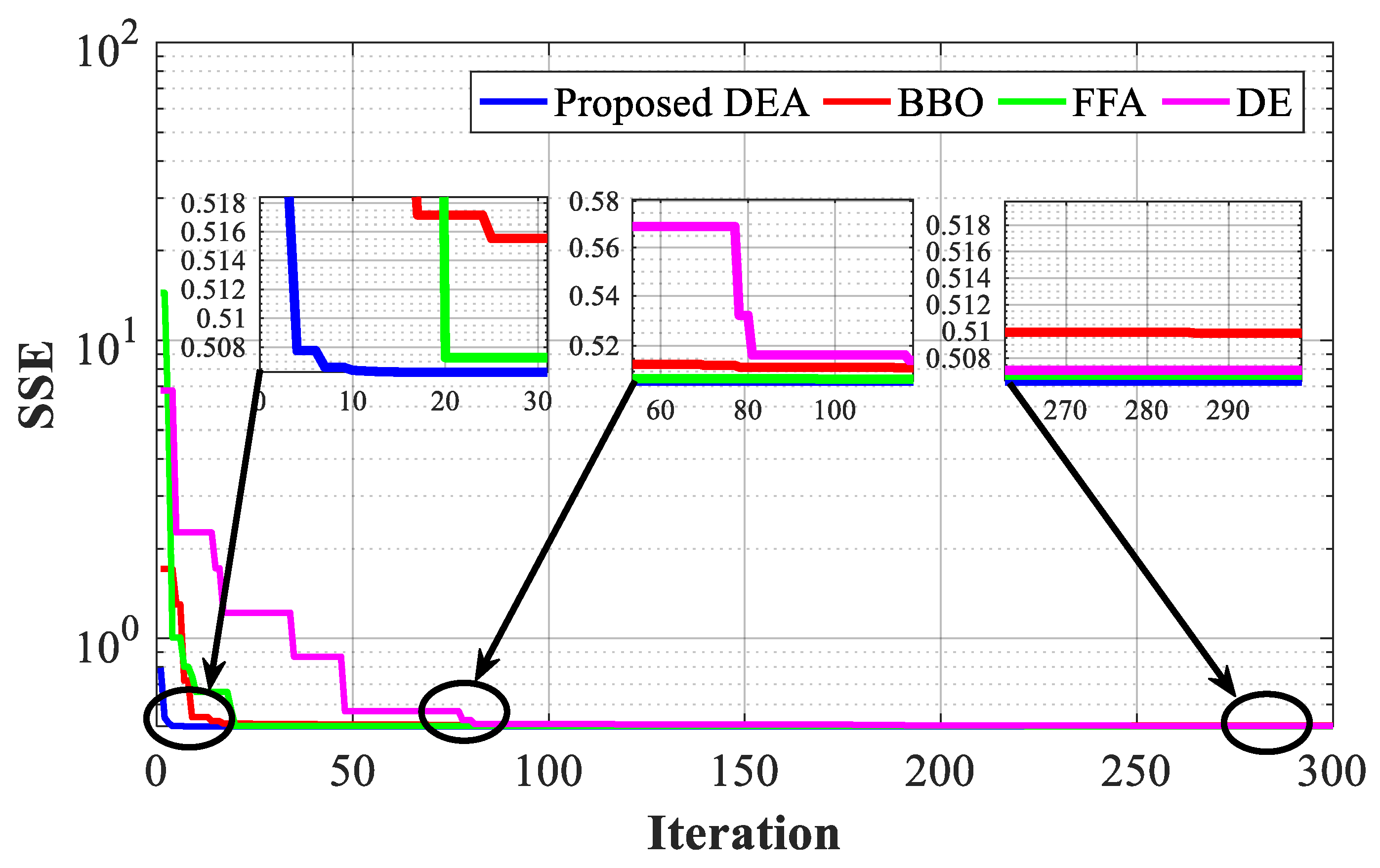
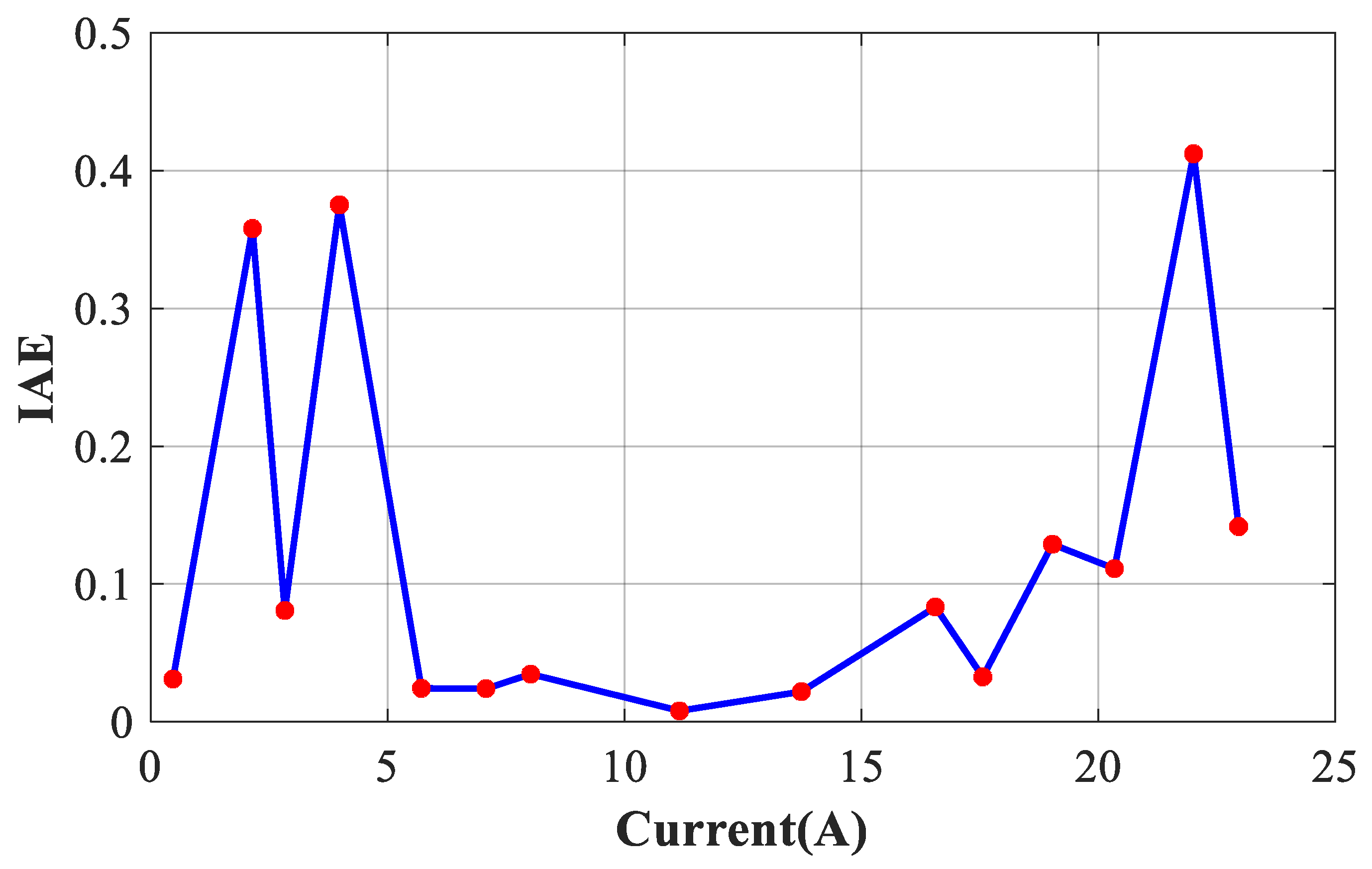
The V-I and P-I curves of the 250 W PEMFC are depicted in Figure 9 and Figure 10, respectively. These curves are drawn using experimental and measurement data generated by the DEA algorithm. Thus, the DEA V-I and P-I curves exhibit a high similarity to the relevant experimental curves. Figure 11 displays the convergence curves of DEA, BBO, and FFA algorithms in terms of iterations. The comparison graphs demonstrate that the proposed DEA outperforms other approaches in terms of convergence speed. Moreover, only one point exceeds 0.4 from the IAE values, despite the non-linearity of the I/V curve and the lack of sufficient data points, as presented in Figure 12. The IAE for each data point is computed and displayed in Table 6.

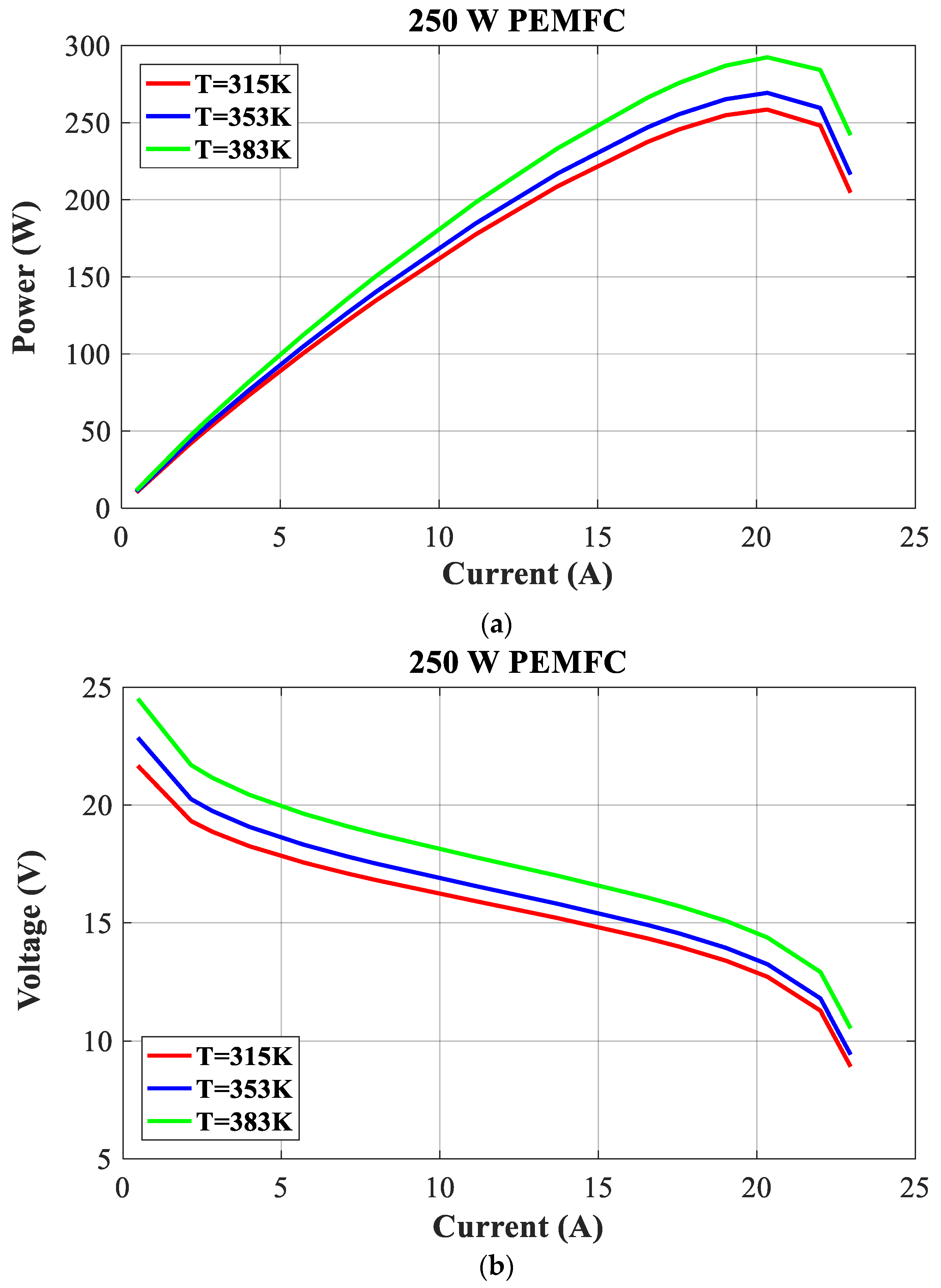
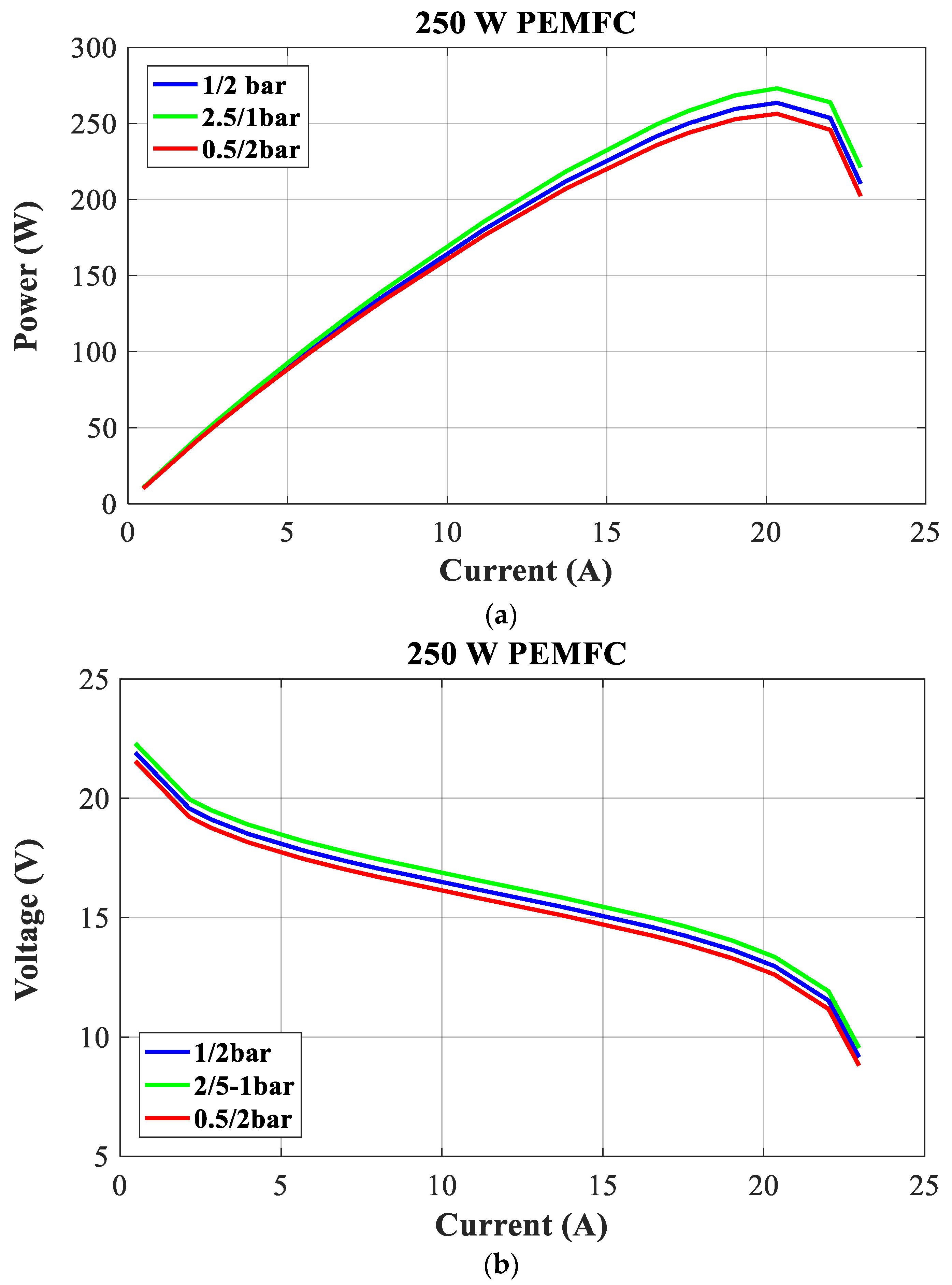
The stability and accuracy of the proposed optimization technique are evaluated by analyzing the effects of changing the cell temperature and reactant pressures. Figure 13 and Figure 14 show the polarization curves of a 250 W PEMFC at different cell temperatures and the effects of changes in H2 and O2 pressure. Figure 13 displays the polarization curves (P-I and V-I) of the 250 W PEMFC stack at various temperature values (315 K, 335 K, and 383 K) and constant pressures at the levels specified in the manufacturer’s datasheet. The pressures are maintained at the levels specified in the datasheet. Furthermore, the polarization curves of the 250 W PEMFC stack are drawn in Figure 14 at several pressure values (1/2 bar, 2.5/1 bar, and 0.5/2 bar) and constant temperature at a value specified in the datasheet.

The 250 W PEMFC’s power and voltage increase with reactant pressures and cell temperature.

6. Conclusions

A proton exchange membrane fuel cell (PEMFC) is a kind of electrochemical device that generates electrical energy. The mathematical model of PEMFC is non-linear, consists of seven parameters, and is used to fit the V-I and P-I characteristic curves under various operating situations. These parameters characterize the performance and operation of the model equations. A novel hybrid meta-heuristics technique, namely differential evolution ameliorated (DEA).

The unknown seven parameters of a PEMFC with accurate values were introduced in this study. The proposed DEA is a combination of differential evolution (DE) and Firefly (FA) algorithms. A detailed comparison analysis with previously published methods such as BBO, FFA, DE, GOA, RSA, and PDO was performed using MATLAB/Simulink^TM (R2016b, MathWorks, Natick, MA, USA) regarding system correctness and the convergence process to verify the proposed DEA-based parameter identification.

To determine the precise values of unknown model parameters for addressing the optimization issue, the fitness function is defined as the sum of squared errors (SSE) between the real models and the optimizing models. The suggested approach demonstrated a strong connection between the calculated and measured data under various operating situations, indicating excellent performance for all the PEMFC stacks investigated. The suggested DEA has achieved the best solution and is more efficient than previous algorithms discussed in the literature for all test types.

The findings indicate that the BBO, FFA, and DE algorithms exhibit low accuracy parameter values and slower convergence speeds. Hence, it is advisable to use the DEA method for resolving intricate and extensively interconnected optimization issues.