Abstract
Demand response management (DRM) plays a crucial role in the prospective development of smart grids. The precise estimation of electricity demand for individual houses is vital for optimizing the operation and planning of the power system. Accurate forecasting of the required components holds significance as it can substantially impact the final cost, mitigate risks, and support informed decision-making. In this paper, a forecasting approach employing neural networks for smart grid demand-side management is proposed. The study explores various enhanced artificial neural network (ANN) architectures for forecasting smart grid consumption. The performance of the ANN approach in predicting energy demands is evaluated through a comparison with three statistical models: a time series model, an auto-regressive model, and a hybrid model. Experimental results demonstrate the ability of the proposed neural network framework to deliver accurate and reliable energy demand forecasts.
1. Introduction
Smart grids (Figure 1) play a crucial role in ensuring the safe, efficient, and reliable operation of systems, contributing to the reduction of power loss in the electricity network. However, modern smart grids face various economic and technical challenges as they strive to deliver energy securely and cost-effectively to consumers. Among the most significant obstacles are load-flow analysis, scheduling, and electric energy system control. Achieving optimal operation and planning of the power system requires an accurate prediction model.
Over the past decade, load forecasting has emerged as a rapidly developing field of interest and research within smart grids. Numerous forecasting techniques for power system load have been proposed, with mathematical models demonstrating success. These techniques aim to minimize estimation errors between predicted and measured future values in energy demands.
The importance of smart grids’ demand forecasting is evident in several key aspects:
- Reducing unit production costs and preserving the efficiency of power facilities.
- Monitoring high-risk maintenance operations and managing energy reserves.
- Providing crucial data for planning and ensuring effective power delivery.
1.1. Literature Review on Forecasting Models for Load Forecasting
One of the most common forecasting models is categorization, which distinguishes between linear and non-linear models (Raza et al. [1]). Linear models are separated into statistic time series and dynamic time series models.
Figure 1.
Smart grid as a network of intelligent devices.
Time series forecasting is the analysis of time series data using statistics and modeling to generate predictions. The forecast is generally based on data with a historical time stamp. Time series forecasting techniques can be categorized according to numerous parameters [2]. Categorization according to the forecasting horizon distinguishes between the time frame of the forecast:
- Very short-term load forecasting (VSTLF): from a few seconds to several hours. These models are commonly used in flow management.
- Short-term load forecasting (STLF): ranging from hours to weeks. These models are commonly used to balance supply and demand.
- Medium-term and long-term load forecasting (MTLF and LTLF): between months and years normally. These models are used to plan resource usage.
The magnitude of the variables employed is the key distinction between these three forecasting horizons, not taking into consideration the model that was used (Hernandez et al. [3]). Meanwhile, there are some limitations on time series forecasting. For instance, time series are not useful for all situations, as not all models can fit all sets of data. It is up to data teams and analysts to understand the limits of their analysis and what their models can support.
Dynamic models are such that factors and random inputs are taken into consideration dynamically. They make use of time series for modeling dynamical behavior. They are divided into auto-regressive and moving average models and state-space models.
- Auto-regressive and moving average (ARMA) models combine auto-regressive and moving average models. Auto-regressive models use the previous values to forecast future values. Moving average (MA) models calculate the residuals or errors of previous values and determine future values. In ARMA models, residuals and the effects of previous values are taken into account when predicting future values. Many modifications to the ARMA model can be found in the literature under other names like Auto-Regressive Integrated Moving Average (ARIMA), which is quite similar to the ARMA model in the use of previous values and residuals to predict future values, other than the fact that it includes one more factor known as Integrated (I).
- State-space models are used when dealing with dynamic time series issues. They use a set of input, output, and state variables to represent a physical system mathematically. The state variables are employed to describe a system with a set of first-order differential equations. State–space models are commonly used to analyze ecological and biological time-series data.
A comprehensive table outlining the findings of the review of 47 publications detailing 264 forecasting models from 1997 to 2018 is presented in Czapaj et al. [4]. It summarizes the status of research on short-term power demand forecasting for power systems using auto-regressive and non-auto-regressive approaches and models. In addition, the authors provide a new method for creating literature reviews when choosing the most probable forecasting models. An analysis was conducted on the effectiveness of the forecasting models as determined by the Mean Average Percentage Error (MAPE) measure. Table 1 lists the top 10 forecasting techniques and models: DEA, FR, GRM, GA, ANFIS, ANN, FGRM, WANN, ANN, and FL, where the repeated ANN belongs to different models [4]. FGRM and GRM employ the explanatory variables, while the remaining eight models are auto-regressive.

Table 1.
Top 10 rank of the forecasting techniques and models.
The results of the reviews supported the auto-regressive approach’s great potential for forecasting power demand. The employment of auto-regressive models may assist the transmission system operator in achieving improved forecasting efficiency. The advantage of using the ARIMA model is that it is simple to use and offers good forecasts over a short period of time. It has two basic limitations, which are listed below (Khashei et al. [8]):
- Linear limitation: it is supposed that a variable’s future value will be a linear function of several previous data points and random errors. If the implicit mechanism is nonlinear, the ARIMA models’ estimation may be completely unsuitable. However, since non-linearity is a common feature of real-world systems (Zhang et al. [9]), it is illogical to assume that a given implementation of a time series is the result of a linear process.
- Data limitation: for ARIMA models to produce the desired results, a lot of historical data are required. Data limitation dictates that ARIMA models need at least 50, and preferably 100 or more, data points to get the required results.
Using hybrid models or combining multiple models can be an efficient strategy to enhance forecasting performance. The fundamental concept behind model combining in forecasting is to remove its limits in order to create a more comprehensive model with more accurate outcomes. The fundamental ideas of ARIMA, ANNs, and fuzzy regression models are used to formulate a new approach to forecasting. In that model, the special ability of ANNs in nonlinear estimating is employed to go over the ARIMA models’ linear limitations and create a more accurate model. Additionally, fuzzy logic is used to get beyond the ARIMA models’ data limitations and provide a model that is more adaptable [8].
1.2. Literature Review on ANN Approaches for Load Forecasting
Recently, Dewangan et al. [10] provided an extensive examination of load forecasting, encompassing the categorization, performance indicator calculation, data analysis procedures, and utilization of conventional meter data for load forecasting, alongside the technologies employed and associated challenges. This study delved into the significance of smart meter-based load forecasting, exploring various approaches available.
In particular, the application of ANN-based machine learning to estimate electricity consumption dates back to the 1990s, with ongoing research. Park et al. [11] demonstrated the superiority of ANN-based techniques over traditional forecasting methods. Amjady et al. [12] used the ANN modified harmony search algorithm for short-term load forecasting (STLF) with excellent accuracy. Macedo et al. [13] explored DRM in power systems using ANN. Baliyan et al. [14] conducted a survey on ANN applications for short-term load forecasting. Muralitharan et al. [15] proposed a neural-network-based optimization model for energy demand forecasting, employing genetic algorithms and particle swarm optimization. Li [16] utilized a machine learning-based forecasting model for short-term load forecasting, integrating data mining and de-noising methods. Jha et al. [17] employed the LSTM and random forest methodologies for electricity load forecasting. Through meticulous comparison with models employing analogous parameters, they ascertained the superior reliability and suitability of our model for long-term forecasting. Their model exhibits an exemplary performance, boasting an average overall accuracy of 96%. Sharadga et al. [18] compared various methods for predicting time series, including both statistical techniques and artificial intelligence-based approaches for forecasting phtovoltaic (PV) power output. Additionally, the study examines how altering the prediction time frame impacts the performance of these algorithms. The BI-LSTM algorithm proves to be a highly precise model for predicting power output in large-scale PV plants, surpassing various neural networks and statistical models in accuracy.
Da Silva et al. [19] proposed a solution employing a fuzzy-ARTMAP (FAM) artificial neural network (ANN). Historical databases are utilized to extract the fundamental knowledge necessary for training this ANN. In tandem with load forecasting, the FAM-ANN integrates a continuous learning (CL) mechanism, enabling incremental knowledge acquisition through real-time measurement system data. A rapid and highly precise load forecasting (with a mean absolute percentage error of around 2%) is achieved for extended forecast intervals, such as 96 h ahead. Tarmanini et al. [20] used two different forecasting models within machine learning (ML) techniques for load prediction: auto regressive integrated moving average (ARIMA) and artificial neural network (ANN). They evaluated the performance of both methods using mean absolute percentage error (MAPE). Utilizing daily electricity consumption data from 709 randomly selected households in Ireland over an 18-month duration, the study demonstrated that ANN outperforms ARIMA in handling non-linear load data.
1.3. Motivation and Novelties of Our Approach
The utilization of ML-based forecasting models continues to evolve, addressing various aspects of energy demand prediction with advancements in neural network approaches. In this context, this paper aims to identify the most accurate smart grid load forecasting models and neural network architectures.
The key challenges faced by artificial neural networks (ANN) involve obtaining precise results, achieving maximum performance during training, and minimizing overall prediction errors. The main innovation points in our current paper intend to address these challenges. To this aim, we explore three distinct models:
- Time series model, utilizing multiple input measurements (hour, period, day, season, month, number of appliances) to forecast energy consumption.
- Auto-regressive model, relying on past energy consumption (within a specific period range) to predict future energy consumption.
- Hybrid auto-regressive model, incorporating both input measurements and past energy consumption to forecast energy consumption.
The performance of these three models is assessed using various multi-layer neural network architectures. The proposed ANN framework undergoes testing on two real-life smart grid data sets to derive general recommendations.
Our paper introduces novelty through the comparison of three statistical models within various ANN architectures for smart grid load forecasting, a comparison that, to our knowledge, has not been conducted previously. The closest study to ours is by Tarmanini et al. [20], which compares the ARIMA model with an ANN model for short-term load forecasting. However, our work stands out notably as we integrate the time series model, the auto-regressive model, and the hybrid model within the ANN forecasting framework. To the best of our knowledge, this approach has not been published before. The chosen forecasting model and neural network are intended to contribute to energy conservation, aid in demand and supply management, and facilitate efficient financial planning for users venturing into power generation.
Section 2 outlines the data formatting and pre-processing methods employed in our context. Additionally, it provides a detailed account of the statistical models and the artificial neural network (ANN) approach for DRM. Section 3 presents the experimental results obtained with the three different models, utilizing various ANN architectures on two smart grid data sets. Finally, Section 4 summarizes and concludes the paper.
2. ANN Forecasting Approach for DRM
Neural network (NN) techniques constitute a subset of machine learning methods employed for diverse prediction problems. NNs excel at modeling non-linear data across various domains and can approximate complex functions with reasonable precision. In particular, recurrent neural networks (RNNs) employ training data to acquire knowledge. Their defining feature is their ability to retain and leverage information from previous inputs to influence current input-output relationships [21]. RNNs’ outputs are influenced by preceding elements within the sequence. In this paper, RNNs (Figure 2) are used to estimate the uncertain smart grid energy load . To do so, we utilize observed historical values , on previous observations of , input variables. The estimated of is then employed as the average value approximation for the smart grid demand. The activation function used in each layer l () of the ANN may be different. It approximates the output of each neuron in layer l. Each layer l may contain neurons. A composed function transforms the input into a predicted , such that:
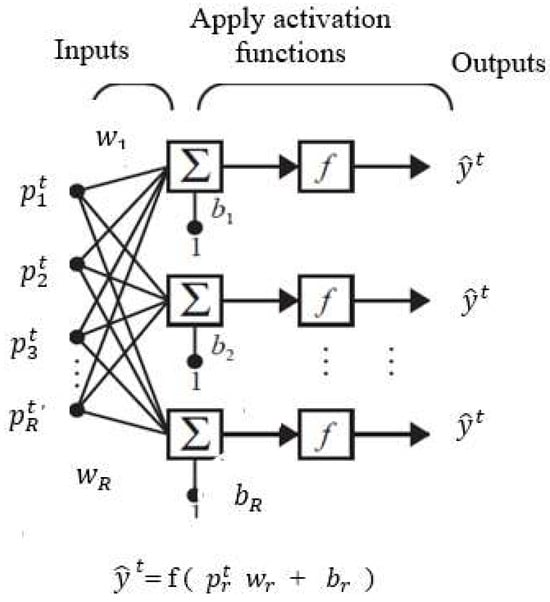
Figure 2.
Neural Network Sample Architecture.
2.1. Steepest Descent Methods
In a traditional steepest descent scheme, weight updates occur after each forward pass h, adhering to the following sequence:
Here, represents a predetermined parameter adjusted based on specific guidelines, while indicates the magnitude of . In vector form, the steepest gradient descent scheme is written as:
In the forthcoming Experimental Results Section 3, we employ a walk-forward optimization on the training set as we assess the effectiveness of our ANN utilizing various gradient optimizers, encompassing adaptive moment estimation (Adam) [22], adaptive gradient algorithm (Adagrad) [23], and Adamax [22] as a further development of Adam.
2.2. Data Sets, Data Formatting and Component Analysis
This paper investigates two real-life data sets: Toronto Data Set 1 and Data Set 2. Toronto Data Set 1 encompasses energy consumption information from 1082 households, collected daily over 36 consecutive months in the past 3 years: 2019, 2020, and 2021. The data include geographic coordinates of each household, its current index in the data set, the ‘number of electric appliances’ inventoried, the ‘day order’ within the current year, the ‘season’, the ‘day of the week’, and the ‘period’ of the ‘measurement’. Each household contributes only one observation.
Toronto Data Set 2 comprises over 30,000 observations from 6 selected residential areas. The energy consumption information was gathered daily over 60 consecutive months spanning the past 5 years: 2017, 2018, 2019, 2020, and 2021. Similar to Data Set 1, it includes details such as the ‘number of electric appliances’ inventoried, the ‘day order’ within the current year, the ‘season’, the ‘day of the week’, the ‘period’, and the ‘hour’ of the ‘measurement’.
The ‘day order’ represents the order of the measurement day in the corresponding year. Both data sets are segmented into three four-month seasons: Season 1 spans from November to February, Season 2 spans from March to June, and Season 3 spans from July to October. Days of the week are denoted by integers, with Monday assigned the value of 1, Tuesday assigned the value of 2, and so forth. Time periods are also represented by integers: 1 indicates the time between 0:00 and 5:59, 2 indicates the time between 6:00 and 11:59, 3 indicates the time between 12:00 and 17:59, and 4 indicates the time between 18:00 and 23:59. In Data Set 2, measurements are taken over six hours, ranging from 1 to 6, for each time period.
2.3. Data Formatting and Cleaning
The acquired data needed to undergo transformation into input-output time series samples for model training. Specifically, for data set 1, we had to address issues with 14 out of 1082 data entries. These 14 entries generally had a value of 0 in the (kilowatt per hour) KWH electricity consumption column, likely stemming from measurement errors. Subsequently, we replaced the entries in the corresponding cells with the average values observed for demand. This replacement took into consideration factors such as average demand on similar weekdays, seasons, and periods.
Data cleaning involves identifying and rectifying mistakes and discrepancies to enhance the quality of the data. Errors in data entry, information gaps, and other types of inaccuracies can lead to issues with data quality.
2.3.1. Correlation Analysis
The correlation matrix obtained for residential area 1, as shown in Table 2, indicates that the correlation between consumption (KWH) and the number of appliances is the highest. The correlation between consumption and the other features is lower than the correlation with the number of appliances. All the features have a similar positive effect on consumption, but their impact is smaller than the impact of the number of appliances.

Table 2.
Correlation matrix: residential area 1.
2.3.2. Trend and Seasonality
Trend and seasonality decomposition, whether additive or multiplicative, enables the identification of inherent data patterns specific to the problem at hand. An additive decomposition is applied when the variation around the trend cycle or the magnitude of seasonal fluctuations remains constant with the time series level. On the other hand, a multiplicative decomposition is preferred when such variance is found to be proportional to the time series level. The additive formula for time series decomposition is given by:
Meanwhile, the multiplicative formula is expressed as:
where represents the observed series, denotes the trend component, stands for the seasonal component, and represents the irregular component (residual) at period t.
For example, the additive seasonality decomposition shown in Figure 3 indicates a significant seasonal component for electricity consumption in data set 1. It also reveals a specific trend related to increased electricity consumption during the first season, corresponding to the harsh winter conditions in Canada. The Dickey-Fuller test, with a p-value of (more than ), conducted on electricity consumption confirms the presence of seasonality.
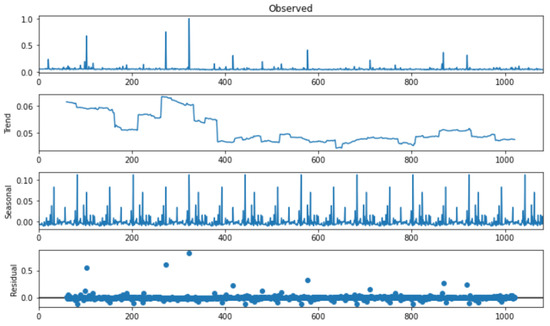
Figure 3.
Additive Trend-Seasonality Decomposition Results.
3. ANN Forecasting Experimental Results
We evaluate the performance of our neural network (NN) approach in predicting energy demands by comparing it with three statistical models: a time series model, an auto-regressive model, and a hybrid model. For this evaluation, we employ various network architectures, manipulating the number of neurons at each layer, using different activation function types, and employing diverse gradient descent methods, including Adam, Adagrad, or Adamax.
3.1. Time Series Model
Time series models serve as statistical tools for analyzing and predicting data collected over a specific period. Their applications span various fields, encompassing finance, economics, weather forecasting, and more. The main goal of time series modeling is to understand and characterize the inherent patterns and trends within the data, facilitating accurate predictions of future values.
The time series model undergoes testing on both data sets 1 and 2. In the first layer, we apply the activation function to the inputs of the data set. The output from the neurons in the first layer is subsequently used as input for the second layer, and this process continues until reaching the final layer, denoted as L. The computation is represented as follows:
3.2. Auto-Regressive Model
Auto-regressive models (AR) belong to the category of time series models that utilize the previous values of a variable to predict its future values. These models posit that the current value of the variable results from a combination of its past values and a random error term. The order of an AR model, denoted as ‘r’, indicates the number of preceding values used to forecast the present value. For example, an AR(1) model uses the previous value of the variable to predict the current value, while an AR(2) model incorporates the last two values. In this paper, our auto-regressive model is expressed as follows:
Here, r denotes the number of preceding values of y utilized, representing the time delay in hours between the last measurement and the output forecasting.
For data set 1, where only a single observation is recorded for each household, this model cannot be applied. Consequently, the auto-regressive model is exclusively tested on data set 2, with a maximum delay of h, corresponding to a complete period.
3.3. Hybrid Model
Hybrid models, also known as mixed models, are models that incorporate multiple types of models to formulate predictions. A hybrid time series model can integrate various models, such as combining an auto-regressive model with a moving average model or merging an auto-regressive integrated moving average (ARIMA) model with a neural network model. The purpose of a hybrid model is to leverage the strengths of different models and mitigate their respective limitations. For example, an auto-regressive model might perform well for short-term predictions but may fall short for long-term predictions. In such a case, a hybrid model that combines an auto-regressive model with a moving average model could yield superior results. Our hybrid model combines time series and auto-regressive models, considering:
Similar to the auto-regressive model, the hybrid model is exclusively tested on data set 2, with a maximum delay of h, corresponding to a complete period.
3.4. Experimental Results
Our experiments were conducted using Python 3 on Jupyter Notebook (Jupyter Project). The computations were executed on 64-bit workstations equipped with 2.9 GHz Intel Core i7-7600 processors and 8 GB RAM, running under MS Windows 11.
The accuracy results of the three-layer ANN are summarized in the following tables: The results were obtained by varying the number of neurons in each layer (, , and ) and the activation functions and . The entries in the table indicate the root mean squared error (RMSE) of the residuals calculated with a training set size that remains constant at of the entire data set while predicting household consumption.
Though the scientific community may not have definitively resolved the debate concerning the ideal size ratio between the training and validation sets, we opt to leave this question open for future exploration, as it does not align with the primary objectives of our current study.
RMSE is one of the most popular measures for assessing the accuracy of predictions. It represents the Euclidean distance between measured true values and forecasts. To compute RMSE, we first calculate the residual (the difference between prediction and true value) for each data point, then compute the norm of the residuals for each data point. Finally, we compute the mean of the residuals and take the square root of that mean using the formula:
All the results are obtained with a fixed number of epochs (50). An epoch refers to a single forward and backward pass through the entire training data set.
The results in Table 3 reveal that the last architecture, with : relu and : relu as activation functions, generally provides the best predictions and the lowest RMSE averages. In particular, the lowest RMSE () is obtained with neurons in the first layer, neurons in the second, and neurons in the third layer with the Adam optimizer. Adam is more stable than Adagrad and Adamax when varies from 32 to 256, varies from 16 to 128 neurons, and varies from 8 to 64 neurons across the four architectures. The third architecture, with : tanh and : log-sigmoid as activation functions, yields a larger RMSE on average. Its best RMSE () is slightly better than that obtained by the best accuracy provided by the first architecture. More detailed results are available upon request.

Table 3.
Three-Layer ANN Forecasting Results on Data Set 1.
Figure 4 depicts the consumption values in the y-axis (blue) against the corresponding predicted values (green) using the proposed three-layer ANN on data set 1. The neural network is configured with : relu, : relu, and the Adam optimizer. The x-axis represents the index of observations.
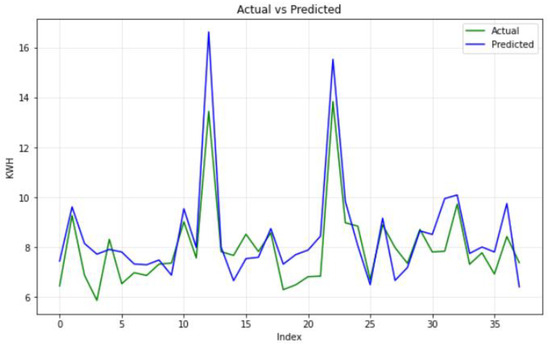
Figure 4.
Sample Measurement vs. Prediction on Data Set 1.
Table 4 showcases the results for residential area 1 in data set 2. In the time series model, the most effective architecture, featuring : relu and : relu as activation functions, achieves the lowest RMSE (). This result is obtained with neurons in the first layer, neurons in the second layer, neurons in the third layer, and the Adamax optimizer.

Table 4.
Forecasting Results on Residential 1.
For the auto-regressive model, utilizing : relu and : relu as activation functions, the minimum RMSE () is attained with neurons in the first layer, neurons in the second layer, and neurons in the third layer, with the Adam optimizer.
In the hybrid model, employing : relu and : relu as activation functions, the lowest RMSE () is achieved with neurons in the first layer, neurons in the second layer, neurons in the third layer, and the Adamax optimizer.
Across all three models and four architectures, both Adam and Adamax demonstrate greater stability than Adagrad. Notably, as varies from 32 to 256, ranges from 16 to 128 neurons, and varies from 8 to 64 neurons. Overall, the hybrid model consistently yields the lowest RMSE among the three models.
For residential area 4, the results presented in Table 5 indicate that the last architecture, featuring : relu and : relu as activation functions, generally offers the best predictions with the lowest average RMSE across all three models.

Table 5.
Forecasting Results on Residential 4.
In the time series model, the lowest RMSE achieved by the three-layer ANN is , obtained with neurons in the first layer, neurons in the second, and neurons in the third layer, utilizing the Adam optimizer.
In the auto-regressive model, the lowest RMSE, amounting to , is attained with neurons in the first layer, neurons in the second, and neurons in the third layer, employing the Adamax optimizer.
Concerning the hybrid model, the lowest RMSE, totaling , is achieved with neurons in the first layer, neurons in the second, and neurons in the third layer, utilizing the Adamax optimizer.
Across all four architectures and three models, both Adam and Adamax exhibit greater stability compared to Adagrad, as varies from 32 to 256, ranges from 16 to 128 neurons, and varies from 8 to 64 neurons. Overall, the hybrid model consistently yields the lowest RMSE among the three models.
3.5. Summary of Results
For both data sets 1 and 2, the optimal accuracy with our three-layer ANN is consistently achieved using the last architecture with : relu and : relu as activation functions. Specifically, for data set 1, this is typically realized with the Adam optimizer, while for data set 2, the preference is generally for the Adamax optimizer.
In the case of data set 2, within the time series model, the Adamax optimizer yields the most accurate results for residential areas 1, 2, 3, 5, and 6. Residential area 4, on the other hand, achieves the best accuracy with the Adam optimizer. In the auto-regressive model, the Adamax optimizer is superior in accuracy for residential areas 2, 3, 4, 5, and 6, while residential area 1 achieves the best accuracy with the Adam optimizer. For the hybrid model, the Adamax optimizer consistently provides the best accuracy across all residential areas. Notably, the hybrid model exhibits the highest accuracy (lowest RMSE value) among the three models.
Stochastic Gradient Descent (SGD) proves ineffective with both data sets 1 and 2. The underlying concept of SGD relies on random subsets of the gradient, but due to sparse gradients and numerous zeros in each gradient subset, it fails to perform effectively.
4. Conclusions
This paper proposed a neural network forecasting approach for demand-side management in smart grids. The presented neural network framework demonstrated the ability to accurately and reliably predict energy consumption, as evidenced by experimental results on two data sets. The paper explored diverse three-layer neural network architectures and three different statistical models.
The experimental results showed that the most effective architecture employs the relu activation function in all three layers. In addition, the Adamax optimizer consistently yielded the highest accuracy for the hybrid model across all residential areas. Notably, among the three models, the hybrid model demonstrated the greatest accuracy.
Regarding computational efficiency, the time series model emerges as the fastest among the three models, albeit with a compromise in accuracy. Conversely, the hybrid model requires more computational time but delivers superior accuracy.
The selected ANN, coupled with the most suitable statistical model chosen by energy providers, has the potential to contribute to energy conservation, demand and supply management, and the effective organization of financial support for individuals initiating power production.
Author Contributions
Methodology, S.B.; Validation, S.B.; Formal analysis, S.A.-A.; Investigation, S.A.-A.; Resources, S.B.; Data curation, S.A.-A.; Writing—original draft, S.A.-A.; Writing—review & editing, S.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Raza, M.Q.; Khosravi, A. A review on artificial intelligence based load demand forecasting techniques for smart grid and buildings. Renew. Sustain. Energy Rev. 2015, 50, 1352–1372. [Google Scholar] [CrossRef]
- Hippert, H.S.; Pedreira, C.E.; Souza, C.R. Neural Networks for Short-Term Load Forecasting: A review and Evaluation. IEEE Trans. Power Syst. 2001, 16, 44–51. [Google Scholar] [CrossRef]
- Hernandez, L.; Baladron, C.; Aguiar, J.; Belen, C.; Sanchez-Esguevillas, A.J.; Lloret, J.; Massana, J. A Survey on Electric Power Demand Forecasting: Future Trends in Smart Grids, Microgrids and Smart Buildings, A Survey on Electric Power Demand Forecasting: Future Trends in Smart Grids, Microgrids and Smart Buildings. IEEE Commun. Surv. Tutorials 2014, 16, 1460–1495. [Google Scholar] [CrossRef]
- Czapaj, J.S.M.; Kaminski, R. A review of auto-regressive methods applications to short-term demand forecasting in power systems. Energies 2022, 15, 6729. [Google Scholar] [CrossRef]
- Kheirkhah, A.; Azadeh, A.; Saberi, M.; Azaron, A.; Shakouri, H. Improved estimation of electricity demand function by using of artificial neural network, principal component analysis and data envelopment analysis. Comput. Ind. Eng. 2013, 64, 425–441. [Google Scholar] [CrossRef]
- Wang, Y.; Bielicki, J.M. Acclimation and the response of hourly electricity loads to meteorological variables. Energy 2018, 142, 473–485. [Google Scholar] [CrossRef]
- Rana, M.; Koprinska, I. Forecasting electricity load with advanced wavelet neural networks. Neurocomputing 2016, 182, 118–132. [Google Scholar] [CrossRef]
- Khashei, M.; Bijari, M.; Ardali, G.A.R. Improvement of auto- regressive integrated moving average models using fuzzy logic and artificial neural networks (anns). Neurocomputing 2009, 72, 956–967. [Google Scholar] [CrossRef]
- Zhang, G.; Patuwo, B.E.; Hu, M.Y. Forecasting with artificial neural networks: The state of the art. Int. J. Forecast. 1998, 14, 35–62. [Google Scholar] [CrossRef]
- Dewangan, F.; Abdelaziz, A.Y.; Biswal, M. Load Forecasting Models in Smart Grid Using Smart Meter Information: A Review. Energies 2023, 16, 1404. [Google Scholar] [CrossRef]
- Park, D.C.; El-Sharkawi, M.A.; Marks, R.J.I.I.; Atlas, L.E.; Damborg, M.J. Electric load forecasting using an artificial neural network. IEEE Trans. Power Eng. 1991, 6, 442–449. [Google Scholar] [CrossRef]
- Amjady, N.; Keynia, F. A New Neural Network Approach to Short Term Load Forecasting of Electrical Power Systems. Energies 2011, 4, 488–503. [Google Scholar] [CrossRef]
- Macedo, M.N.Q.; Galo, J.J.M.; de Almeida, L.A.L.; de CLima, A.C. Demand side management using artificial neural networks in a smart grid environment. Renew. Sustain. Energy Rev. 2015, 41, 128–133. [Google Scholar] [CrossRef]
- Baliyan, A.; Gaurav, K.; Mishra, K.S. A Review of Short Term Load Forecasting using Artificial Neural Network Models. Procedia Comput. Sci. 2015, 48, 121–125. [Google Scholar] [CrossRef]
- Muralitharan, K.; Sakthivel, R.; Vishnuvarthan, R. Neural network based optimization approach for energy demand prediction in smart grid. Neurocomputing 2018, 273, 199–208. [Google Scholar] [CrossRef]
- Li, C. Designing a short-term load forecasting model in the urban smart grid system. Appl. Energy 2020, 266, 114850. [Google Scholar] [CrossRef]
- Jha, N.; Prashar, D.; Rashid, M.; Gupta, S.K.; Saket, R.K. Electricity load forecasting and feature extraction in smart grid using neural networks. Comput. Electr. Eng. 2021, 96, 107479. [Google Scholar] [CrossRef]
- Sharadga, H.; Hajimirza, S.; Balog, R.S. Time series forecasting of solar power generation for large-scale photovoltaic plants. Renew. Energy 2020, 150, 797–807. [Google Scholar] [CrossRef]
- da Silva, M.A.; Abreu, T.; Santos-Junior, C.R.; Minussi, C.R. Load forecasting for smart grid based on continuous-learning neural network. Electr. Power Syst. Res. 2021, 201, 107545. [Google Scholar] [CrossRef]
- Tarmanini, C.; Sarma, N.; Gezegin, C.; Ozgonenel, O. Short term load forecasting based on ARIMA and ANN approaches. Energy Rep. 2023, 9, 550–557. [Google Scholar] [CrossRef]
- Hopfield, J.J. Neural Networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 1982, 79, 2554–2558. [Google Scholar] [CrossRef] [PubMed]
- Kingma, D.P.; Ba, J.L. Adam: A method for Stochastic Optimization. In Proceedings of the ICLR, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Duchi, J.; Hazan, E.; Singer, Y. Adaptive subgradient methods for online learning and stochastic optimization. J. Mach. Learn. Res. 2011, 12, 2121–2159. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).