1. Introduction
The rapid expansion of the global economy significantly influences various social, economic, and environmental aspects, resulting in a profound impact. This has compelled policymakers to establish goals and develop economic policies that align with sustainability objectives. The United Nations has introduced a framework called Sustainable Development Goals (SDGs) to address these challenges and promote sustainable development [
1]. The United Nations General Assembly devised seventeen global goals, known as Sustainable Development Goals (SDGs), aimed at fostering a sustainable future for everyone. These goals, established in 2015, are anticipated to be implemented on a global scale by the year 2030 [
2]. In relation to the SDGs, renewable energy development allows achieving energy security for transportation, environment, construction, economy, mechanical work, and industry [
3]. Renewable energies generated from solar [
4,
5] wind [
6], hydro [
7], tidal [
8], geothermal [
9,
10], and biomass [
11] Renewable energy contributes to meeting the global energy demand while facilitating community development and protecting the environment on a worldwide scale. In recent decades, renewable energy has emerged as a powerful and effective solution to address the energy crisis [
5,
12] offering the added benefit of mitigating adverse climate and nature-related consequences. Photovoltaic (PV) systems have emerged as a formidable solution to the global energy crisis, offering significant potential to address the increasing energy demand. While mitigating adverse climate and nature-related consequences. The integration of PV technology aligns with the Sustainable Development Goals (SDGs) proposed by the United Nations, which aims to ensure access to affordable and clean energy for all. By utilizing solar power, PV systems contribute to reducing greenhouse gas emissions and combating climate change [
13]. PV systems harness sunlight to directly convert it into electricity, providing a clean and renewable energy source [
14,
15]. However, one challenge associated with PV systems is their relatively low efficiency, on average, only around 15–20% of the incoming solar irradiation is converted into electricity [
16,
17,
18]. To further enhance the capabilities of PV systems, researchers and engineers have developed photovoltaic thermal PVT systems, which combines a cooling system and a PV panel, has emerged as a promising solution for simultaneously providing electricity and hot water, in order to enhancing the energy efficiency and improved space utilization. The electrical and thermal behavior of PVT collectors is forecasted through numerous research works. Furthermore, different PVT classifications are proposed according to several factors such as geometry, heat extraction mode, and cooling fluids; Common base fluids used in the PVT systems are water, ethylene glycol and oil [
19] in the quest to enhance the performance of PVT systems, recent studies have specifically explored the potential of nanofluids to improve the cooling process of PV cells. In a previous study by [
20], the electrical energy performance of a PVT panel was examined through both numerical (Num) simulations and experimental (Exp) investigations. The study focused on online monitoring and control of the PVT system to assess its effectiveness. [
21] A nanofluid (NF) is defined as an engineered colloidal suspension of nanoparticles (e.g., a metallic oxide, a carbide, or carbon materials) in a base fluid. Common base fluids used in the PVT systems are water, ethylene glycol and oil [
22]. The inclusion of nanoparticles in a base-fluid as a colloidal suspension result in a notable enhancement of the thermophysical properties of the base-fluid. These enhanced properties include improvements in density, dynamic viscosity, specific heat capacity, and thermal conductivity [
23]. Consequently, these improvements in thermophysical properties lead to an overall enhancement in the performance of the entire fluid system.
In a study conducted by [
24], the performance of a water-based PVT system with a rectangular tube absorber was experimentally evaluated using various types of nanofluids (SiO
2, TiO
2, and SiC) mixed with water. The findings of the study revealed that the PVT collector utilizing the SiC/water nanofluid exhibited the highest combined efficiency of 81.73% and an electrical efficiency of 13.52%. In [
25], the impact of using a SiC/water nanofluid, with a concentration of 3wt%, in a PV/T system was evaluated to assess the improvements in electrical and thermal efficiencies. The findings revealed that incorporating the 3wt% SiC/water nanofluid resulted in a significant increase in electrical efficiency (ɳ
ele), up to 24.1%, compared to the PV system operating with water alone. Additionally, the thermal efficiency (ɳ
th) showed a remarkable enhancement, up to 100.19%, when using the SiC/water nanofluid for cooling instead of water. In this study, an Al
2O
3/water nanofluid was utilized as the cooling fluid. The results also indicated that the total efficiency of the system increased with a higher Reynolds number, fin length, and volume fraction of the nanoparticles. In [
22], a study was conducted to experimentally investigate the impact of different nanoparticles on PV/T systems. Specifically, Al
2O
3, CuO, and multiwall carbon nanotube (MWCNT) were dispersed in water at varying volume fractions (0%, 0.5%, 1%, 2.5%, and 5%), using the ultrasonication procedure. The results demonstrated significant improvements in electrical efficiency when using MWCNT, Al
2O
3, and CuO nanofluids, with respective increases of 60%, 55%, and 52% compared to a traditional PV panel. Notably, the MWCNT nanofluid was identified as the most effective coolant for the PVT panel. One study [
26] was conducted to examine the impact of incorporating different nanoparticles, namely, Al
2O
3, CuO, and SiC, at varying volume fractions (0.5%, 1%, 2%, 3%, and 4%), into a PVT system. The findings indicated that the utilization of SiC/water nanofluid is particularly advantageous in enhancing the output of the PVT system. Up to this point, the evaluation of the electrical and thermal outputs of PVT systems has been conducted through a combination of experimental studies and the development of various numerical models. In recent years, researchers have increasingly utilized artificial intelligence (AI) techniques in various fields [
27,
28]. These AI-based methods offer the advantage of efficiently establishing relationships between inputs and outputs [
29]. However, when it comes to calculating the thermal efficiency of PVT systems using conventional solution methods, the process can be time-consuming due to solving complex mathematical differential equations. To overcome this challenge, the use of machine learning methods has been considered [
30]. Despite the potential benefits, it is worth noting that only a limited number of studies have applied these techniques to predict the performances of PVT systems [
31].
Si et al. (2023) [
32] utilized the random forest (RF) machine learning approach to develop a predictive model for thermal and electrical efficiency and exergy in terms of Re and nanoparticle concentrations. The results demonstrated that R
2 = 0.9856 and RMSE = 0.718 in terms of electrical efficiency and R
2 = 0.989 and RMSE = 0.001 in terms of thermal efficiency.
In the investigation by Shakibi et al. (2023), [
33] they designed and assessed an advanced solar photovoltaic–thermal (PVT) unit. The incorporation of multi-walled carbon nanotube (MWCNT) nanoparticles into the phase-change material (PCM) was employed to establish a homogeneous cooling medium. The researchers developed a 3D computational fluid dynamic (CFD) model to assess the overall performance of the system. Utilizing CFD simulations, a dataset was generated and subsequently employed for machine learning optimization. A substantial dataset was compiled and applied to an artificial-neural-network (ANN)-based deep learning approach, employing four distinct networks: long short-term memory (LSTM), extreme learning machine (ELM), radial basis function (RBF), and multilayer perceptron (MLP). The optimization process involved multiple aspects and employed a variety of algorithms and decision-making methods. For the training model, the R
2 values for MLP, RBF, ELM, and LSTM were found to be 0.976775, 0.990863, 0.999593, and 0.999856, respectively. These R
2 values serve as indicators of the models’ effectiveness in capturing and representing the variability present in the dataset during the training phase.
MLP-ANN, ANFIS, and LSSVM soft computational techniques were applied for forecasting the efficiency of a PV/T collector. [
30] The input variables for training and testing the machine learning models included sun heat, flow rate, inlet temperature, and solar radiation, while the output variable studied was the electrical efficiency yield. The results indicate that the proposed LSSVM model outperformed the other models. The R
2 (coefficient of determination) and MSE (mean squared error) values for the four models were as follows: 0.986 and 0.007 (MLP-ANN), 0.94 and 0.037 (ANFIS), 0.922 and 0.011 (LSSVM), and 0.987 and 0.004 (unspecified fourth model), respectively.
In the study of [
31] various artificial intelligence (AI) models, including ANFIS, MLP, CFF, RBF, GR neural networks, and LS SVR, were employed to model the electrical efficiency of a photovoltaic–thermal (PVT) system cooled by nanofluids. The study involved conducting trial-and-error scenarios and statistical analyses. The findings highlighted that ANFIS, trained with a subtractive clustering membership function using a hybrid algorithm, stood out as the most accurate predictor for the given task. The reported R
2 values for the different models were LS-SVR: R
2 = 0.9368, ANFIS: R
2 = 0.9534, CFF: R
2 = 0.9597, MLP: R
2 = 0.9511, GR: R
2 = 0.9535, RBF: R
2 = 0.9044, and MLP (second instance): R
2 = 0.97. These R
2 values serve as metrics indicating the accuracy of each model in capturing the variability in the electrical efficiency of the PVT system. Notably, the research underscores that ANFIS, with its specific training methodology, provides the most precise predictions for the specified task.
In the study of Barthwal and Rakshit (2021) [
34], an artificial neural network (ANN) was trained to forecast the annual energy and exergy output of a modeled system. The ANN incorporates six input parameters, encompassing design, operational, and application factors. To ascertain the optimal parameter combinations, a multi-criterion decision-making (MCDM) approach was applied, considering system outputs and efficiencies. The trained neural network exhibited remarkable accuracy, achieving an R
2 value surpassing 0.97. This high R
2 value signifies the effectiveness of the ANN in accurately predicting the annual energy and exergy output of the modeled system.
In this study [
35], experimental datasets for photovoltaic–thermal (PVT) systems are generated, and electrical efficiency values are calculated based on these datasets. Subsequently, two modeling techniques, Elastic.net regression and an artificial neural network (ANN), are employed to predict the efficiency values of PVT using the available datasets. Elastic.net regression is utilized to generate mathematical equations for calculating the electrical efficiency of PVT. The results obtained from the Elastic.net regression and ANN models are compared with the experimental results, revealing a strong agreement between the models and the experimental data, indicating that their effectiveness in predicting PVT electrical efficiency was about 0.997 and 0.912 of R
2 for ANN and Elastic.net, respectively.
In [
36], a novel approach is introduced to model a photovoltaic–thermal (PVT) nanofluid-based collector system. The researchers utilized a radial basis function artificial neural network (RBFANN), multilayer perceptron artificial neural network (MLPANN), and adaptive neuro-fuzzy inference system (ANFIS) to capture the complex non-linear relationship between the input and output parameters of the PVT system. The crucial output parameters chosen for analysis were the fluid outlet temperature of the collector and the electrical efficiency of the photovoltaic unit (PV). The results of the three models were compared and validated against measurements, revealing their reasonable capability in estimating the performance of the PVT system. The reported R
2 values for MLPANN, RBFANN, and ANFIS are approximately 0.9363, 0.9906, and 0.9896, respectively. These R
2 values indicate the models’ ability to capture and represent the variability in the PVT system’s performance, with higher values suggesting better predictive accuracy.
In [
37], the solar electrical efficiency of photovoltaic–thermal (PVT) systems based on nanofluid is modeled using the artificial neural network (ANN) technique. Three ANN methods—multilayer perceptron (MLP), self-organizing feature map (SOFM), and support vector machine (SVM)—were implemented based on experimental results. The findings indicate that the network output aligns well with both the experimental results and previously published works, demonstrating the effectiveness of the ANN approach in predicting the solar energy production of PVT systems. The reported R
2 values for MLP, SOFM, and SVM are approximately 0.54186, 0.90064, and 0.99109, respectively. These R
2 values serve as indicators of the models’ ability to capture and represent the variability in the solar electrical efficiency of PVT systems, with higher values suggesting better predictive accuracy.
In the context of recent studies exploring the performance of photovoltaic–thermal (PVT) systems cooled by nanofluids, it is crucial to acknowledge existing gaps in the literature. While advancements have been made in understanding the impact of various nanofluids on the electrical and thermal efficiency of PVT systems, there remains a notable knowledge gap regarding the application of artificial intelligence (AI) techniques for predictive modeling in this specific domain. Recognizing this gap, the current study aims to bridge the existing knowledge deficit by leveraging three prominent soft computing approaches, XGBoost (XGB), extra tree regressor (ETR), and k-nearest neighbors (KNNs), to develop accurate and efficient predictive models for estimating the electrical and thermal efficiency of PVT systems cooled by nanofluids. This novel approach not only contributes to the growing body of research on renewable energy systems but also pioneers the application of AI methodologies in predicting the intricate dynamics of PVT systems. The unique amalgamation of AI and nanofluid-enhanced PVT systems positions this study at the forefront of innovative research, offering valuable insights and paving the way for future advancements in sustainable energy technologies.
In addition, the study aims to predict new data that have not been utilized in the training phase and validate them against a previous experimental study. In summary, the results demonstrate the robust performance of the XGB and ETR models in accurately predicting both electrical and thermal efficiency. The XGB model consistently exhibits the highest R2 values of about 0.99999, indicating its superior predictive capabilities.
2. Materials and Methods
In this section, the machine learning techniques that were examined and employed to simulate the electrical and thermal efficiency of PVT collectors are described.
2.1. Extreme Gradient Boosting (XGB)
XGB is a prominent implementation of gradient-boosting machines (GBM), widely recognized as constituting one of the most powerful algorithms used in supervised learning. It excels in both regression and classification tasks, making it a versatile tool for various predictive problems [
38]. XGB operates in the following manner: if we have, for example, a dataset that has
m features and
n number of examples datasets
. Let
be the predicted output of an ensemble tree model generated from the following equation [
37]:
In the XGB model, the variable
k denotes the number of trees included in the model. Each tree is denoted as
, representing the
k-th tree in the ensemble. To solve the equation mentioned above, the goal is to find the optimal set of functions by minimizing the objective composed of the loss function and regularization terms. This optimization process aims to strike a balance between reducing the training error (loss) and preventing overfitting through regularization [
39].
In the XGB model, the loss function “
l” quantifies the difference between the predicted output
and the actual output
. The regularization term (represented as Ω) is a measure of the model’s complexity and helps to prevent overfitting. It is calculated using the following equation:
represents the number of leaves of the tree;
W is the weight of each leaf.
Boosting is utilized in the training of XGB models to minimize the objective function in decision trees. This process involves adding a new function, represented by a tree, during each iteration of the training process [
37]. Thus, in the
t-th iteration, a new function (tree) is added, as follows:
Table 1 summarizes the main results of literature studies based on machine learning applied to PVT-system-based nanofluids.
Table 1.
Literature review regarding machine learning utilized in PVT-system-based nanofluids.
Table 1.
Literature review regarding machine learning utilized in PVT-system-based nanofluids.
| | Data Type | Data Points | Fluid | Model | RMSE | MSE | R2 | Remarks |
|---|
| | Exp | Num | ɳele | ɳth | ɳele | ɳth | ɳele | ɳth | ɳele | ɳth |
|---|
| [32] | ⨯ | | - | - | NF | RF | 0.001 | 0.718 | - | - | 0.989 | 0.9856 | Random forest (RF) machine learning predicted thermal, electrical, and exergy efficiency based on Re and nanoparticle concentrations. The results showed acceptable accuracy, with superior overall energy and exergy efficiency precision compared to other targets. |
| [38] | | ⨯ | - | - | NF | ANN | | 0.1104 | - | 0.0122 | 0.9981 | 0.9998 | An advanced solar PVT unit was designed, incorporating MWCNT nanoparticles into the PCM for uniform cooling. A 3D computational fluid dynamic model was created to assess performance, generating data for machine learning optimization. Multi-aspect optimization employed diverse algorithms and decision-making techniques. |
| [39] | ⨯ | | 98 | - | W | LS-SVM | 0.055 | | 0.003 | | 0.991 | - | MLP-ANN, ANFIS, and LSSVM techniques forecasted PV/T collector efficiency using sun heat, flow rate, inlet temperature, and solar radiation as input variables. The LSSVM model outperformed others, with R2 and MSE of 0.987 and 0.004, respectively, surpassing MLP-ANN and ANFIS models, which scored 0.986 and 0.007 and 0.94 and 0.037, respectively. |
| ANFIS | 0.164 | - | 0.027 | | 0.918 | - |
| ANFIS | 0.089 | - | 0.008 | | 0.976 | - |
| RBF-ANN | 0.143 | - | 0.020 | | 0.937 | - |
| [40] | | ⨯ | 200 | - | NF | LS-SVR | 1.85 | - | 3.417 | - | 0.9368 | - | Various AI models, such as ANFIS, MLP, CFF, RBF, GR neural networks, and LS SVR, were used to simulate the electrical efficiency of a PVT system cooled by nanofluids. Research found that ANFIS, trained with a hybrid algorithm and the subtractive clustering membership function, offered the most accurate predictions. |
| ANFIS | 1.60 | - | 2.548 | - | 0.9534 | - |
| CFF | 1.48 | - | 2.191 | - | 0.9597 | - |
| MLP | 16.08 | - | 2.645 | - | 0.9511 | - |
| GR | 4.37 | - | 2.542 | - | 0.9535 | - |
| RBF | 21.04 | - | 5.037 | - | 0.9044 | - |
| [33] | ⨯ | | 69 120 | - | W | MLP | - | - | - | - | >0.97 | An ANN predicted the annual energy and exergy production of a modeled system using six input parameters, including various design, operational, and application factors. An MCDM approach was employed to select the best parameter combinations based on the system’s results and efficiencies. The trained neural network demonstrated high accuracy, with an R2 exceeding 0.97. |
| [41] | ⨯ | | 200 | - | air | ANN | - | - | - | - | 0.997 | - | Experimental data for PVT systems were used to calculate electrical efficiency. Two modeling techniques, Elastic.net regression and ANN, predicted PVT efficiency using these data. Elastic.net regression generated equations to calculate PVT electrical efficiency. Comparisons with experimental results showed strong agreement, indicating the effectiveness of both models in predicting PVT efficiency. |
| Elastic.net | - | - | - | - | 0.912 | - |
| [34] | ⨯ | | 130 | - | NF | MLPANN | 0.362 | - | - | - | 0.9363 | - | A novel method modelled a PVT system using RBFANN, MLPANN, and ANFIS to capture complex non-linear relationships. The fluid outlet temperature and electrical efficiency of the PV unit were key output parameters. Comparing the three models against measurements validated their reasonable performance in estimating PVT system performance. |
| RBFANN | 0.256 | - | - | - | 0.9906 | - |
| ANFIS | 0.267 | - | - | - | 0.9896 | - |
| [42] | ⨯ | | - | - | NF | MLP | 0.710 | - | - | - | 0.5418 | - | This study employed ANN techniques to model the solar electrical efficiency of PVT systems with nanofluid. Three ANN methods—MLP, SOFM, and SVM—were applied using experimental data. Results show good alignment between network output, experimental data, and previous works, indicating the effectiveness of ANN in predicting solar energy production in PVT systems. |
| SOFM | 0.190 | - | - | - | 0.9006 | - |
| SVM | 0.333 | - | - | - | 0.9910 | - |
| Present work | | ⨯ | 1006 | 370 | NF | XGB | 0.291 | 0.1772 | 0.085 | 0.0699 | 0.9894 | 0.99969 | This work compared AI models to predict PVT system efficiency with nanofluid cooling. XGB and ETR models demonstrated strong performance with R2 values near 0.99999. |
| ETR | 0.291 | 0.0810 | 0.087 | 1.6921 | 0.9894 | 0.99984 |
| KNN | 0.398 | 1.9413 | 0.162 | 27.584 | 0.9802 | 0.93711 |
ə likely represents the predicted value or output of the model at a certain iteration or step each step denoted by Å.(t−1).
2.2. Extra Tree Regression (ETR)
The extra tree regression (ETR) approach is a variant of the random forest (RF) model, which was initially proposed by [
40]. In the conventional top–down technique, the extra tree regression (ETR) algorithm builds a collection of unpruned decision or regression trees ([
40], p. 20). To conduct regression, the random forest (RF) model employs two steps: bootstrapping and bagging. In the bootstrapping step, each individual tree is grown using a random sample from the training dataset, resulting in a set of decision trees. The bagging step further divides the decision tree nodes in the ensemble by selecting random subsets of the training data. The decision-making process involves selecting the best subset and its corresponding value [
41,
42], defining the random forest (RF) model as a collection of decision trees, denoted as
, where
G represents the
G-th predicting tree and θ is a uniform independent distribution vector assigned prior to tree growth. The ensemble of trees, forming the forest, is combined and averaged according to Breiman’s equation [
42] to obtain the final prediction
.
The extra tree regression (ETR) algorithm differs from the random forest (RF) model in two main features. Firstly, the ETR utilizes all cutting points and randomly selects from these points to divide nodes. In contrast, the RF system typically considers a subset of cutting points. Secondly, the ETR uses the entire learning samples to grow the trees, aiming to minimize bias. This contrasts with RF, which often uses bootstrapped samples. These distinctions highlight the unique characteristics of the ETR approach [
40].
The splitting process in the extra tree regression (ETR) approach is governed by two important parameters: k and n
min. The parameter k determines the number of features randomly selected at each node for potential splits, while the n
min parameter defines the minimum sample size required to split a node further. These parameters play a crucial role in controlling the strength of attribute selection and noise reduction in the ETR model. By appropriately setting the values of k and n
min, the ETR model can enhance precision and mitigate the risk of overfitting [
43].
2.3. k-Nearest Neighbor (K-NN)
When using KNN regression, the object’s attribute value is simply set to be the average of that of its K closest neighbors. The neighbors’ contributions can be weighted so that the closer neighbors make a greater average contribution than the farther neighbors because of the KNN’s effectiveness, simplicity, and capacity to function effectively with enormous numbers of training data [
44].
The distance metric KNN forecasts outcomes based on the K-neighbors that are nearest to the location. Thus, it must design a measure for gauging the distance between instances from the example samples and the query point when using KNN to make predictions. Euclidean geometry is among the most widely used methods for measuring this distance. Cityblock:
Chebyshev
where
x and
y are, respectively, the topic of the inquiry and a case from the example sample.
Using
k-nearest-neighbor predictions after selecting the
K value, it is possible to create predictions using the KNN examples. In regression problems, the KNN prediction is the average of the
K-nearest-neighbor output:
Although the XGBoost (XGB), extra tree regressor (ETR), and k-nearest-neighbor (KNN) models represent powerful tools for predictive modelling, they come with their own set of limitations that can impact the accuracy of the results. The main limits that can be mentioned are the following:
Overfitting Risk: All three models are prone to overfitting, where they may capture noise or abnormalities in the training data, leading to poor generalization of unseen data. Proper regularization techniques and hyperparameter tuning are crucial in mitigating overfitting and reducing the overfitting risk.
Model Complexity: XGB, ETR, and KNN have different complexity, XGB and ETR being ensemble learning methods based on decision trees and KNN being a non-parametric algorithm based on similarity measures. While ensemble methods like XGB and ETR can capture complex relationships in the data, they may require more computational resources and longer training times compared to the simpler KNN.
Hyperparameter Sensitivity: The performance of these models heavily relies on hyperparameter settings, and finding the optimal combination can be challenging and time-consuming. Inadequate hyperparameter tuning can lead to suboptimal model performance and reduced accuracy.
Data Preprocessing Impact: The quality of data preprocessing, including feature scaling, handling missing values, and feature engineering, significantly affects the performance of these models. Proper preprocessing techniques are essential for improving model accuracy.
Outlier Sensitivity: Outliers in the data can distort decision boundaries and influence predictions, particularly for proximity-based methods like ETR and KNN. Robust preprocessing methods and outlier detection techniques are necessary to mitigate the impact of outliers on model performance.
Curse of Dimensionality: KNN is sensitive to the curse of dimensionality, where the algorithm’s performance deteriorates as the number of features increases. High-dimensional spaces can lead to sparsity and adversely affect distance calculations, reducing the effectiveness of KNN.
Assumption of Linearity: While KNN makes no assumptions about data distribution, XGB and ETR assume some degree of non-linearity in the data. If the relationship between features and the target variable is highly non-linear, then KNN may outperform XGB and ETR.
2.4. Processed Experimental Dataset from the Literature
In this study, machine learning approaches were utilized to analyze the electrical efficiency and thermal efficiency of a photovoltaic–thermal system cooled down by nanofluids starting from experimental data derived from various research articles to train the machine learning models. Python was utilized as the programming language to implement and execute these analyses. The algorithms are implemented using popular machine learning libraries in Python, such as scikit-learn and TensorFlow. These libraries provide a wide range of tools and functionalities for building, training, and evaluating machine learning models efficiently, using the libraries listed in
Figure 1 (which include pandas, numpy, matplotlib, etc.) for various data manipulation and visualization tasks.
The dataset used for electrical efficiency consisted of 1006 experimental datasets, reported in 13 different research articles: [
22,
24,
25,
27,
45,
46,
47,
48,
49,
50,
51]. and 370 experimental datasets for thermal efficiency, reported in seven different research articles: [
22,
23,
24,
25,
45,
48,
49,
51,
52,
53].
These datasets are divided into thirteen features as inputs to obtain the electrical or thermal efficiency as the output. Based on the article information, data used in this study are classified into two groups: features related to the PVT system and features related to the climate. Additionally, features specifically related to the nanofluid properties are considered.
Features related to the PVT system: PVT surface, time.
Features related to the weather data (i.e., solar radiation, ambient temperature, and wind speed).
Figure 2 and
Table 2 illustrate the countries and the climate type where the analyzed researches were carried out
Features related to nanofluid properties: nanoparticle size, volume fraction, mass flow rate, inlet temperature, thermal conductivity, specific heat, density.
The procedure involved finding the best model among XGB, ETR, and KNN regression techniques. Thus, the predictive performances of these three regression models were compared to identify which one of them provided the most accurate predictions for this specific problem.
Figure 2.
The geographic areas where the analyses were carried out.
Figure 2.
The geographic areas where the analyses were carried out.
Various statistical criteria, such as R-squared, root-mean-square error (RMSE), and mean squared error (MSE), were used to assess the confidence, reliability, and accuracy of the models [
54]. These criteria provided valuable insights into the performance of the models and helped in determining their effectiveness in capturing the underlying patterns and making accurate predictions.
Root-mean-squared error (RMSE)
Correlation coefficient (R
2)
Once the best machine learning (ML) technique was identified, it was employed to predict a new dataset that had not been used before. The selected ML approach would be validated by comparing its predictions with the experimental datasets from the study conducted in [
24].
Figure 3 shows this comparison.
Figure 4 depicts the PVT collector studied, which constituted a silicon monocrystalline glass–glass panel, a wooden frame for insulation, a copper plate used as the absorber, and copper pipes with 0.0085 kg/s of water with a 2% volume fraction of nanofluid flowing. The collector’s surface measures around 0.616 m
2, and a peak power of approximately 90.424 W is indicated. Further details on parameters such as electrical efficiency, thermal efficiency, optical efficiency, and loss coefficients would enhance comprehensive performance evaluation.
Figure 5 illustrates the flowchart of the algorithm employed, which encompasses essential steps developed through libraries and modules for efficient data processing and analysis. The process begins with the uploading of the dataset, followed by preparations for the input and output variables. Subsequently, the input features undergo normalization to ensure uniform scaling across the dataset. Next, the model studies commence, involving the definition and training of regression models. The core of the evaluation process lies in performing k-fold cross-validation, which systematically validates the model’s performance across multiple subsets of the dataset. Once trained, the models are deployed to make predictions on new data instances. Finally, the R
2 score is computed to quantitatively reckon the model’s predictive capability. This comprehensive approach ensures robust model development and evaluation, ultimately leading to reliable results.
3. Results and Discussion
The analysis carried out entailed two parts: firstly, machine learning approaches (XGB, ETR, and KNN) were applied to analyze the electrical and thermal efficiency of a PVT system. To train the machine learning models, experimental data from various research articles were utilized. In the second part, the XGB, ETR, and KNN models were validated using new data, derived from the experimental results obtained in [
55]. This validation process aimed to evaluate the performance and generalization capability of the models on unseen data.
3.1. The Dataset Split
The k-fold cross-validation method was chosen to evaluate the performance of the three models [
56]. By dividing the data into k subsets or folds, this method aided in evaluating the generalization and robustness of the models.
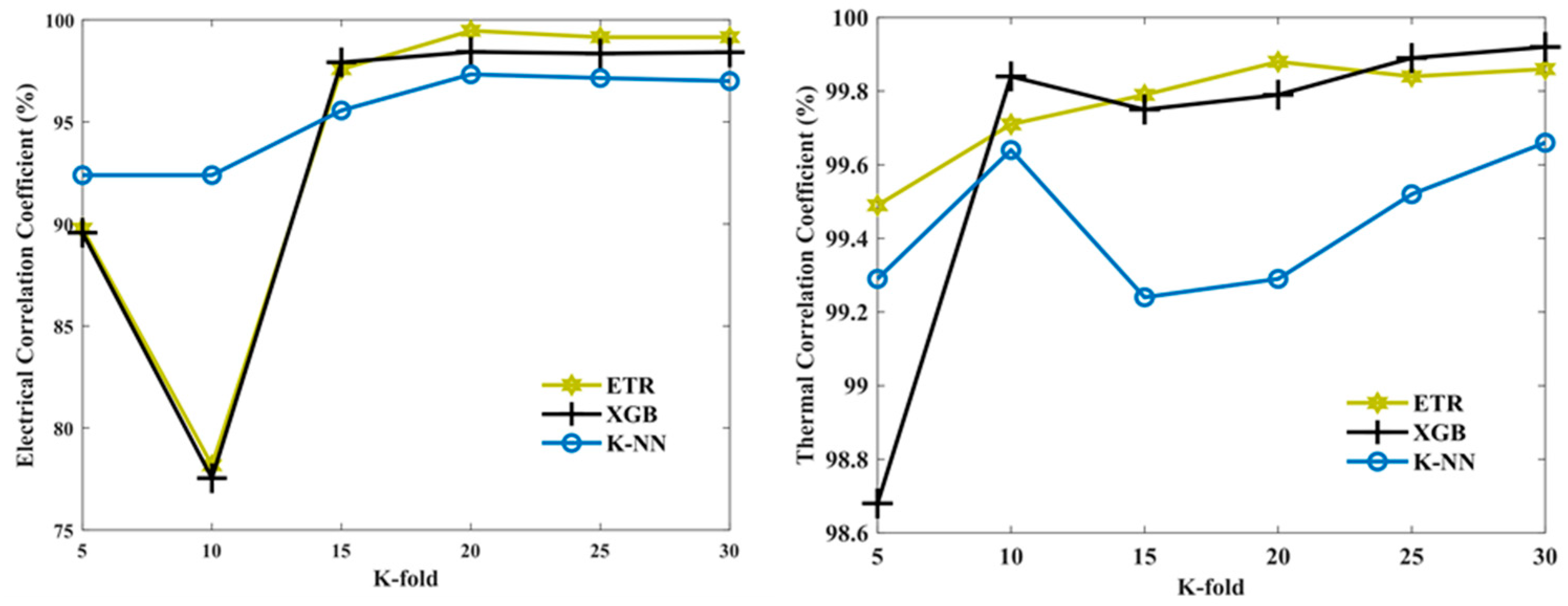
Figure 6 presents the correlation coefficient in the k-fold function for electrical and thermal efficiency.
These analyses suggest that the value of 30 can be used as the k-fold cross-validation value both for electrical and thermal efficiency. This means that the dataset is divided into 30 folds and the models are trained and tested on different combinations of these folds.
Figure 7 illustrates an extract of the first five splits for both the training and testing data in the k-fold cross-validation process for both electrical and thermal efficiency.
The data shown in
Figure 7 represent the partitioning of the dataset into training and testing subsets for the initial phase of k-fold cross-validation. This meticulous process is tailored to assess the performance of models concerning both electrical and thermal efficiency. The k-fold methodology involves systematically dividing the data into ‘k’ segments, allowing the model to undergo a series of training and validation cycles. By showcasing the initial splits, this visualization provides a glimpse into the iterative nature of this procedure, effectively portraying how the model’s competence is rigorously evaluated across diverse subsets of the data. In essence, this illustration underscores the significance of k-fold cross-validation in ensuring a robust assessment of models’ aptitude in predicting both electrical and thermal efficiency outcomes.
3.2. Assessment of Machine Learning Model Accuracy
Table 3 and
Table 4 provide the errors shown by the three presented intelligent models in the evaluation of electrical and thermal efficiency.
Two types of plots are generated: the regression plot of efficiency (experimental vs. estimated) and the relative deviations of efficiency (experimental vs. predicted).
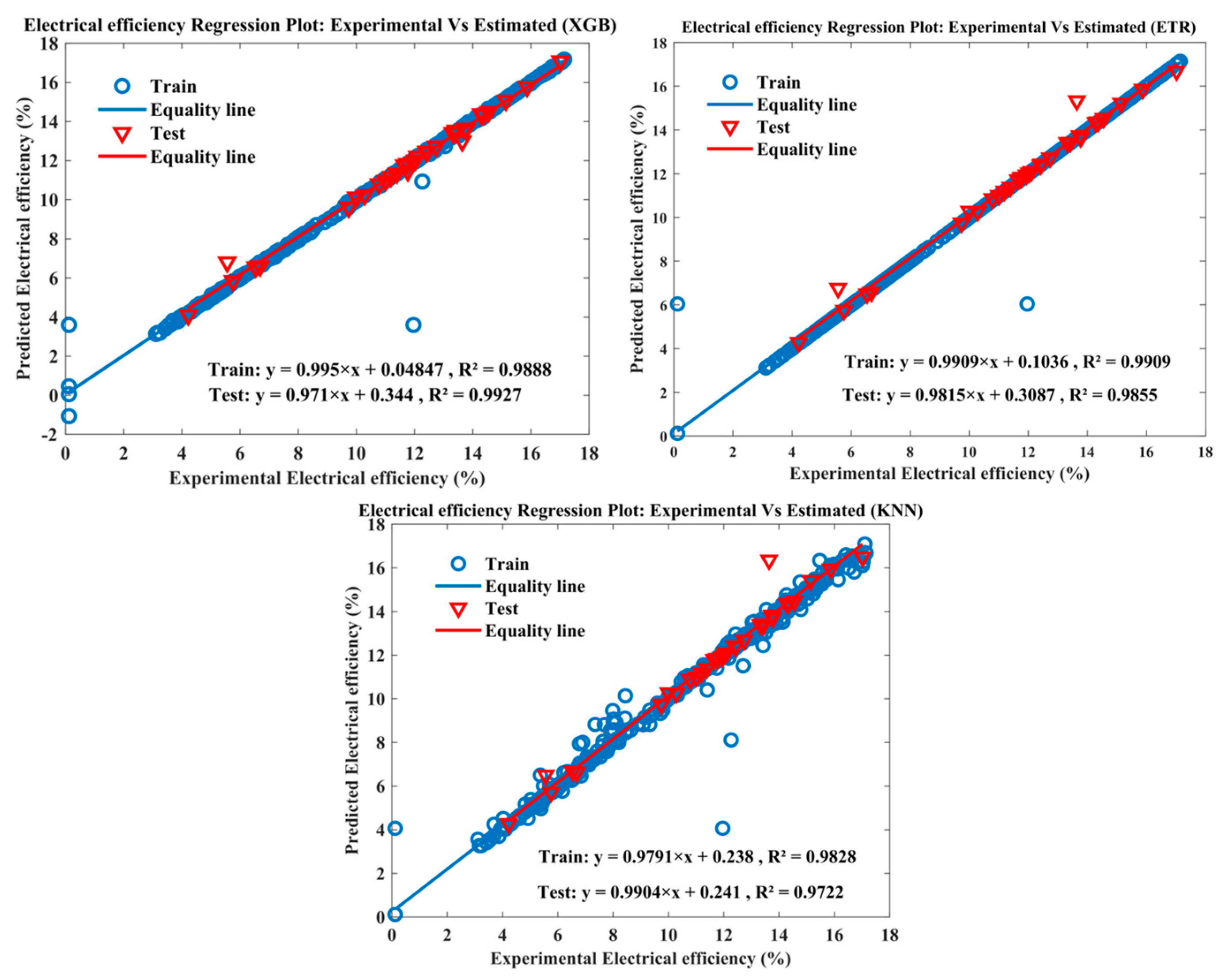
Figure 8 shows the regression plot of electrical efficiency, which compares the experimental values of efficiency with the corresponding estimated values obtained from the models. It gives a picture of how effectively the models are able to predict the efficiency values. Typically, the plot is made up of scatter points for the experimental efficiency values and a line for the estimated efficiency values. The scatter points’ alignment along the line indicates how well the scatter points’ predictions match the actual experimental data.
It is evident that a significant number of data points from the training and testing datasets closely align with the diagonal line, indicating a strong agreement between the model predictions and the experimental data. This alignment suggests that the models are effective in estimating the electrical efficiency of the PVT system. The R2 values further support this observation, with the XGB model achieving the perfect R2 of 0.99998 for training data and the high R2 of 0.99855 for testing data. Similarly, the ETR model demonstrates excellent performance with an R2 of 0.99999 for training data and an impressive R2 of 0.99927 for testing data. However, the KNN model exhibits the slightly lower R2 values of 0.92259 for training data and 0.99522 for testing data.
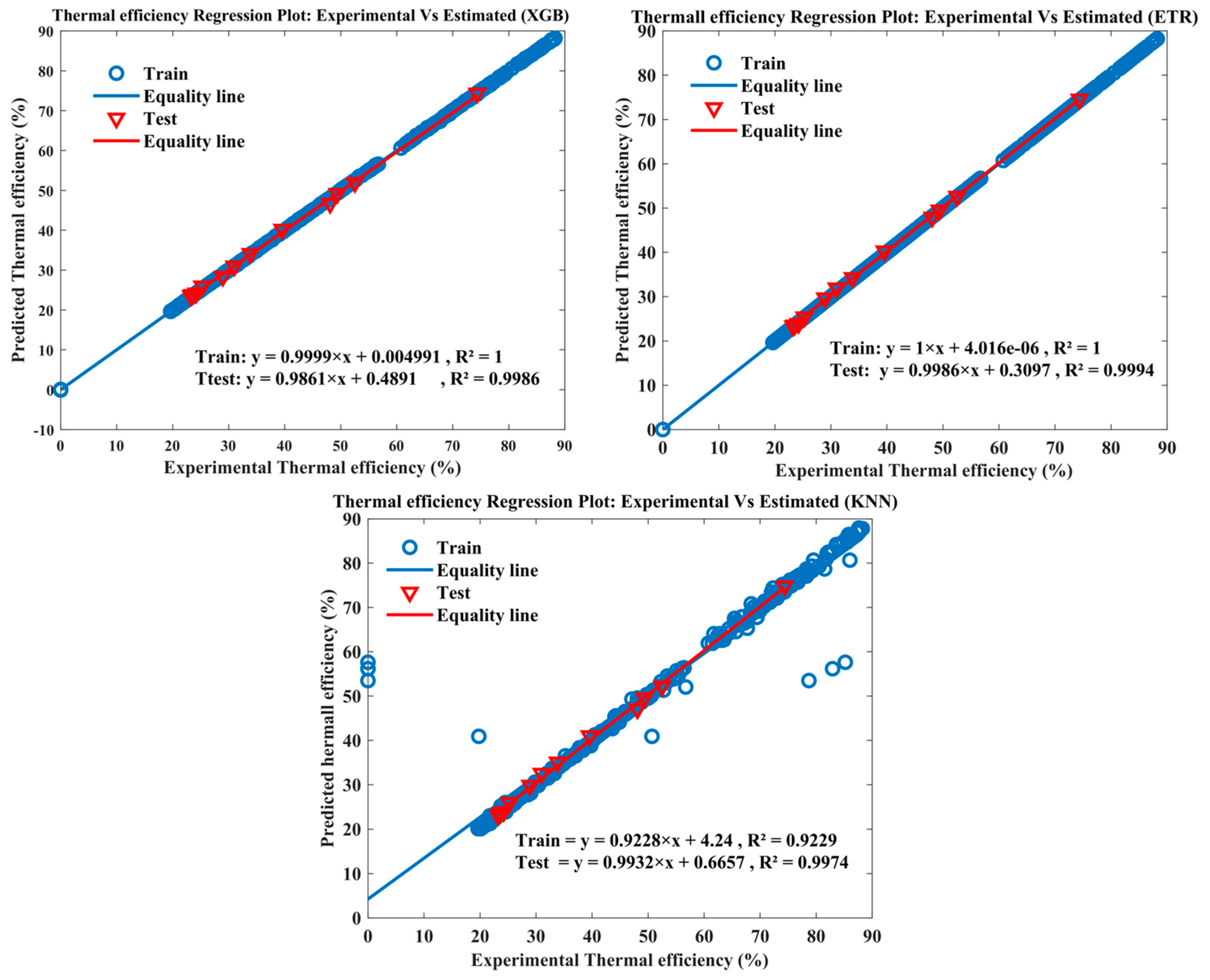
Figure 9 shows the thermal efficiency regression plot, which compares experimental data against estimated data from three different models for both training and testing set.
Once again, a substantial number of data points from the training and testing datasets closely align with the diagonal line, indicating a strong agreement between the model predictions and the experimental data for the thermal analysis. The R2 values further support the effectiveness of the models, indeed the XGB model, achieving the perfect R2 of 0.99998 for training data and the high R2 of 0.99855 for testing data. Similarly, the ETR model demonstrates excellent performance, with an R2 of 0.99999 for training data and an impressive R2 of 0.99927 for testing data. However, the KNN model exhibits the slightly lower R2 values of 0.92259 for training data and 0.99522 for testing data.
These results indicate that the XGB and ETR models excelled in estimating the thermal efficiency, with the XGB model displaying a slightly better performance based on the R2 values. The close alignment of the data points to the diagonal line in the regression plot further confirms the accuracy and reliability of the model predictions.
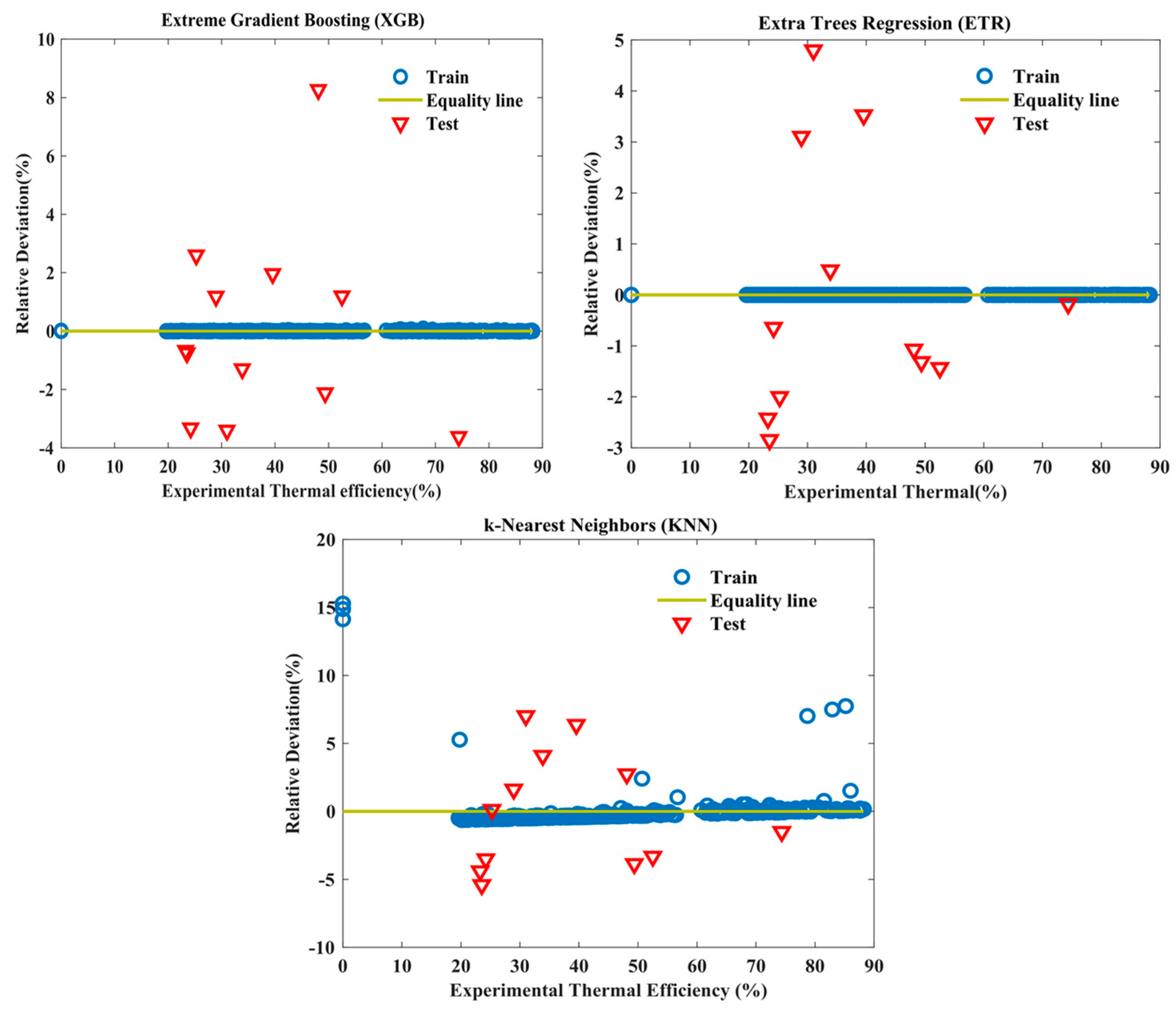
The relative deviations of efficiency is another index used to assess ML models. It shows the percentage differences or deviations between the experimental and predicted efficiency values. The plot typically consists of bars or scatter points that represent the relative deviations for each data point. A smaller deviation indicates a better agreement between the predicted and experimental efficiency values.
Figure 10 illustrates the values of observed relative deviation for the collected electrical experimental data points.
The mean relative deviation values for the training data are 0.00451, 0.00125, and 0.00999 for the XGB, ETR, and KNN models, respectively. These values represent the average deviations between the predicted and experimental electrical efficiency for the training data. On the other hand, the mean relative deviation values for the testing data are 0.39336, 0.40823, and 0.56770 for the XGB, ETR, and KNN models, respectively. These values represent the average deviations between the predicted and experimental electrical efficiency for the testing data. As previously mentioned, lower mean relative deviation values indicate a better agreement between the predicted and experimental electrical efficiency values. In this case, the XGB model performs the best with the lowest mean relative deviation for both training and testing data. The ETR model also shows good performance, particularly in the training data, while the KNN model exhibits relatively higher average deviations in both training and testing.
Figure 11 represents the mean relative deviation values, which offer insights into the agreement between the predicted and experimental values for each model for thermal efficiency.
On the training data, the XGB model demonstrated a mean relative deviation of 0.00002, indicating a relatively small average deviation between the predicted and experimental values. This suggests a good level of agreement and accuracy in capturing thermal efficiency trends. The ETR model exhibits an even lower mean relative deviation of 0.01676, indicating an even smaller average deviation between the predicted and experimental values. This signifies a higher level of agreement between the predicted and experimental values for the ETR model. On the other hand, the KNN model shows a mean relative deviation of 0.32539, suggesting a slightly larger average deviation between the predicted and experimental values compared to the XGB and ETR models. For the testing data, the relative deviation for the XGB, ETR, and KNN are 3.48655, 2.79772, and 5.93964, respectively. In summary, based on the given relative deviation values for the testing data, the ETR model performed the best in terms of agreement with the experimental electrical efficiency values, followed by the XGB model, while the KNN model showed the highest average deviation.
Table 5 summarizes the main results derived from the previous analyses.
3.3. Model Validation
In this part, the XGB, ETR, and KNN models were validated by introducing new data derived from the experimental results of [
55]. This validation process aimed to assess the performance and generalization capability of the models on unseen data.
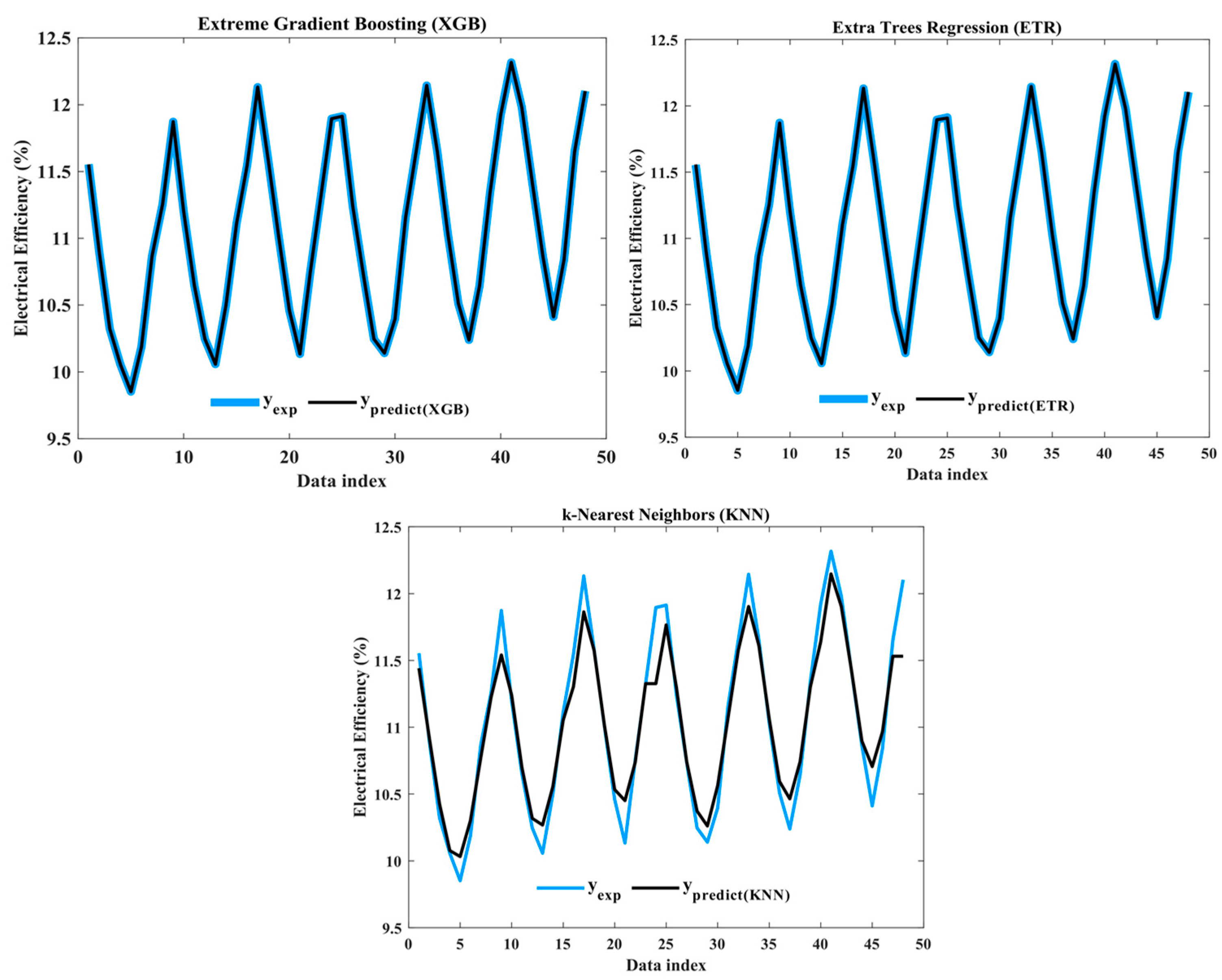
Figure 12 shows the comparison among the experimental and predicted electrical efficiency of the three models.
The results represented in
Figure 12 indicated that the XGB model achieved a high level of accuracy with an R
2 value of 0.99997, while the ETR model also performed exceptionally well, with an R
2 value of 0.99999. The KNN model exhibited a slightly lower accuracy, with an R
2 value of 0.92682.
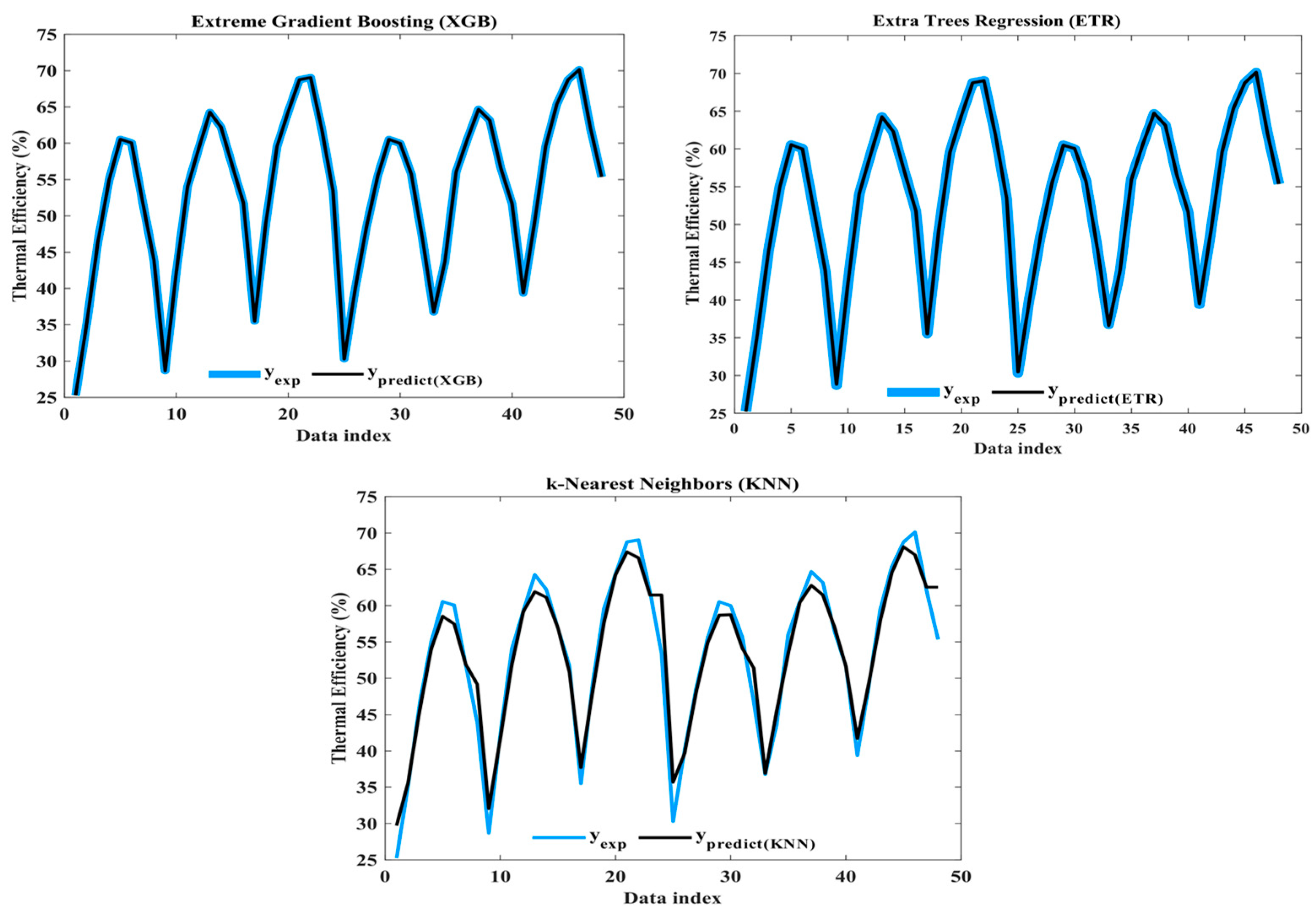
Figure 13 shows a comparison among the experimental and predicted thermal efficiency values from the three models.
In
Figure 13, the data points represent the thermal efficiency values predicted by the XGBoost (XGB), extra tree regressor (ETR), and k-nearest-neighbor (KNN) models. XGB and ETR show exceptionally high R
2 values (0.99995 and 0.99999), indicating strong agreement with the actual values. KNN, with an R
2 of 0.94726, also performed well. The ‘data index’ likely signifies individual data points. Overall,
Figure 13 confirms the accuracy and reliability of XGB, ETR, and KNN in predicting the thermal efficiency of the photovoltaic–thermal (PVT) system.
Table 6 and
Table 7 summarize the main results derived from the previous analyses.
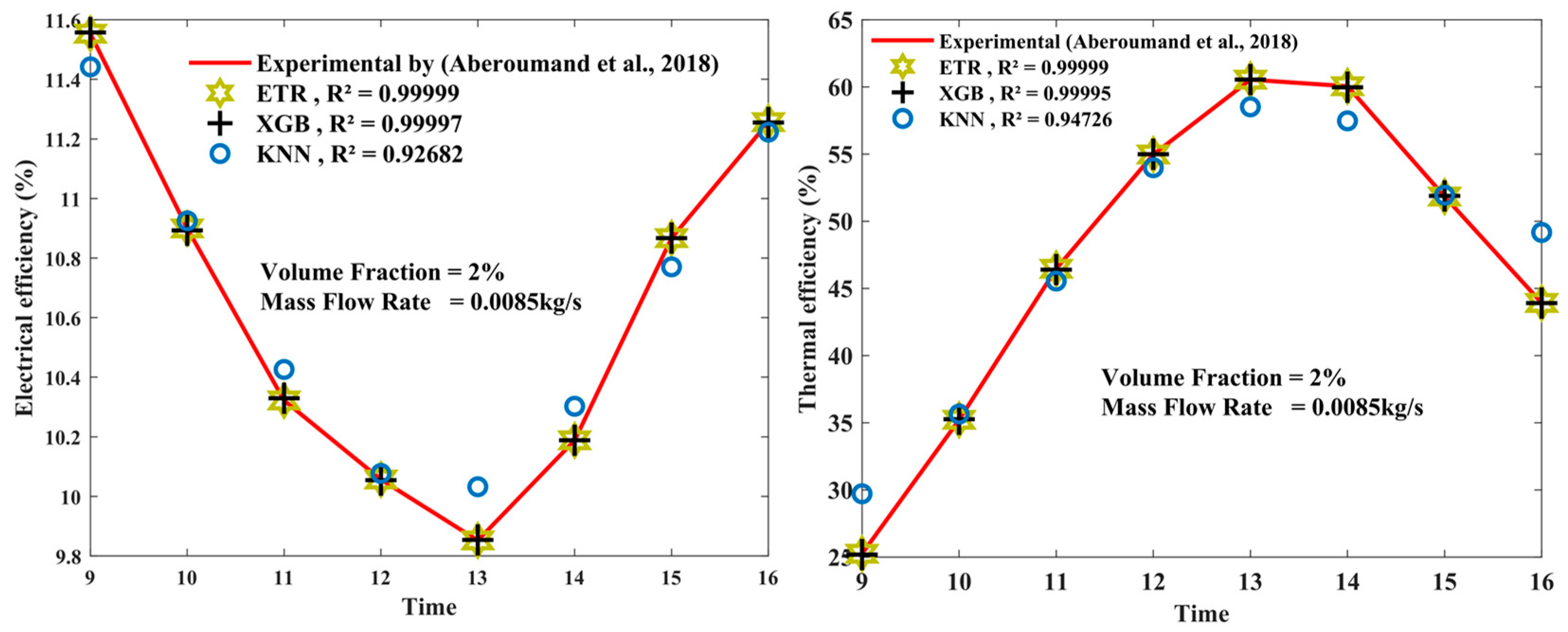
Figure 14 depicts the comparison between the experimental electrical and thermal efficiencies over time, as observed in the study conducted by Aberoumand et al. [
55], under conditions of 2% volume fraction and a mass flow rate of 0.0085 kg/s. This comparison is made against the predicted values obtained using the XGBoost (XGB), extra tree regression (ETR), and K-nearest-neighbor (KNN) models.
As regards electrical efficiency, the XGB model exhibits an R2 value of 0.99999, indicating the highly accurate prediction of the electrical efficiency over time. The ETR model also shows a strong performance, with an R2 value of 0.99997, closely following the XGB model. The KNN model, while still providing reasonable results, has a slightly lower R2 value of 0.92682, suggesting a relatively lower accuracy in predicting electrical efficiency compared to the other models.
Turning to thermal efficiency, all three models show excellent predictive capabilities. The XGB model achieves an outstanding R2 value of 0.99999, indicating a close agreement between the predicted and actual thermal efficiency values. The ETR model follows closely with an R2 value of 0.99995, demonstrating high accuracy, as well. The KNN model performs relatively slightly lower with an R2 value of 0.94726, indicating a still-satisfactory estimation of the thermal efficiency.
Overall, these figures highlight the strong performance of the XGB and ETR models in predicting both electrical and thermal efficiency, with the XGB model often achieving the highest R2 values. While the KNN model shows slightly lower accuracy, it still provides reasonable estimations for both efficiency metrics.
Table 8 summarizes the main results derived from the previous analyses.
4. Conclusions
This study systematically assessed the predictive performance of XGBoost (XGB), extra tree regressor (ETR), and k-nearest-neighbor (KNN) models for estimating the electrical and thermal efficiency of PVT systems. The evaluation, conducted through regression plots, relative deviations, and R2 values, revealed compelling insights.
Notably, the XGB model exhibited outstanding accuracy in estimating electrical efficiency, yielding the high R2 values of 0.98872 (training) and 0.99223 (testing). The ETR and KNN models also demonstrated commendable performances, achieving R2 values ranging from 0.98282 to 0.99090. In thermal efficiency predictions, both the XGB and ETR models excelled, attaining impressive R2 values, from 0.99855 to 0.99998.
Validation using additional data from Aberoumand et al. (2018) further substantiated the reliability of these models. The study’s findings underscore the transformative impact of advanced machine learning techniques on PVT system predictions, minimizing errors and deviations.
Importantly, our research highlights practical advantages. Employing sophisticated algorithms such as XGB, ETR, and KNN enhances prediction accuracy, facilitating informed decision-making and optimized PVT system designs. The emphasis on error minimization contributes to the precision of estimations, ensuring robust performance assessments.
Looking forward, this study serves as a foundation for future advancements. The potential exploration of more intricate algorithms and hybrid models, coupled with real-time data integration and advanced control strategies, holds promise for further improving predictive capabilities under diverse conditions.
In summary, the robust performance of XGB, ETR, and KNN models in predicting PVT system efficiency underscores the efficacy of advanced machine learning techniques. This study not only emphasizes the immediate benefits of enhanced prediction accuracy but also sets the stage for ongoing research and development in this dynamic field.