Accuracy of Simscape Solar Cell Block for Modeling a Partially Shaded Photovoltaic Module
Abstract
1. Introduction
- Thorough validation of the Simscape solar cell model in partially shaded conditions, considering a wide range of shading scenarios;
- Improved methodology for comprehensive model evaluation, based on comparison along entire I-V and P-V curves;
- Experimental validation using a half-cut PV module;
- Initial estimation of how different shading parameters influence the model’s error.
2. Materials and Methods
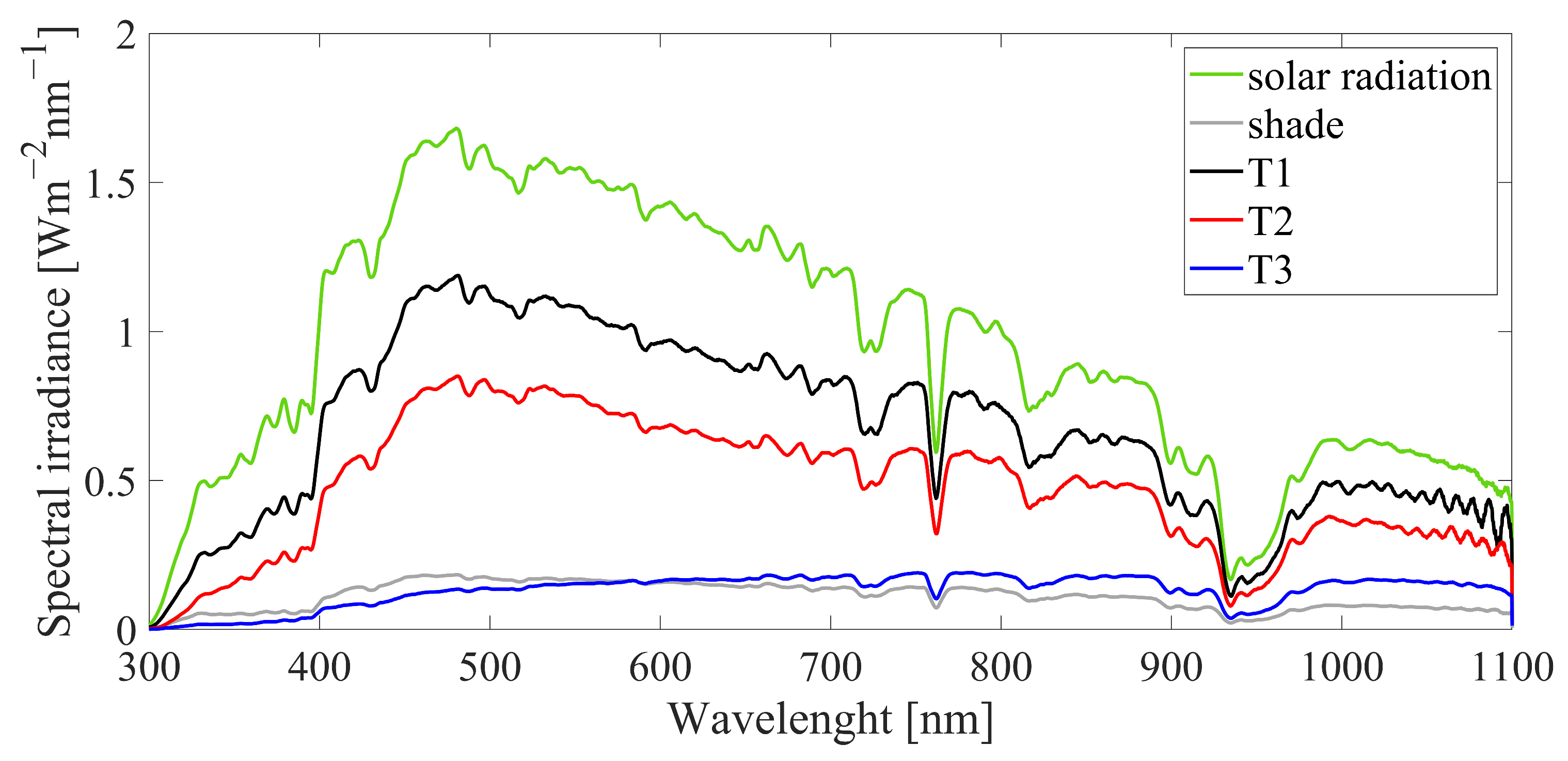
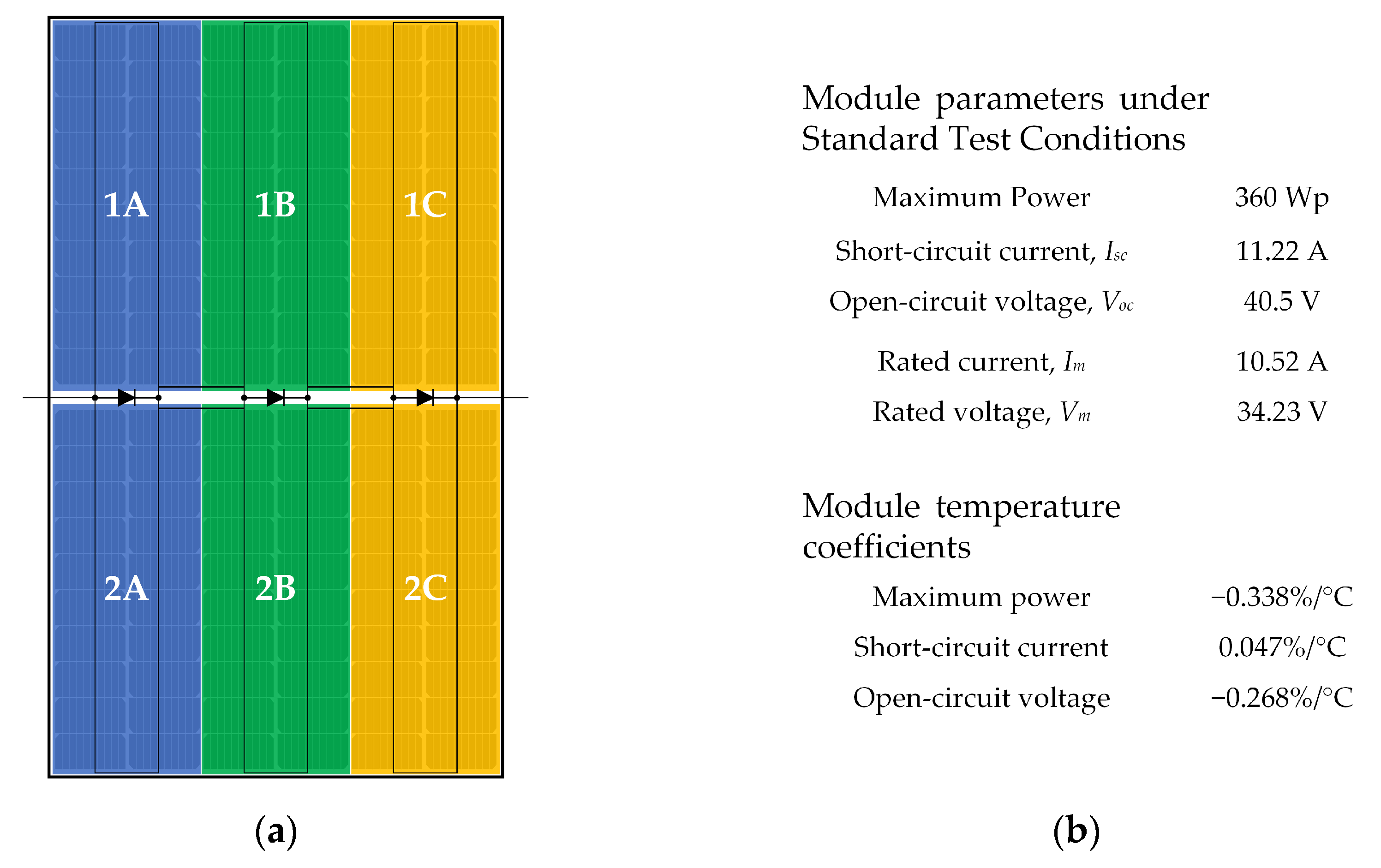
2.1. Experimental Details
2.2. Modeling and Simulation
- (a)
- 5 parameters using short-circuit current (Isc) and open-circuit voltage (Voc);
- (b)
- 5 parameters using parameters of an equivalent circuit model;
- (c)
- 8 parameters using parameters of a double-diode equivalent circuit model.
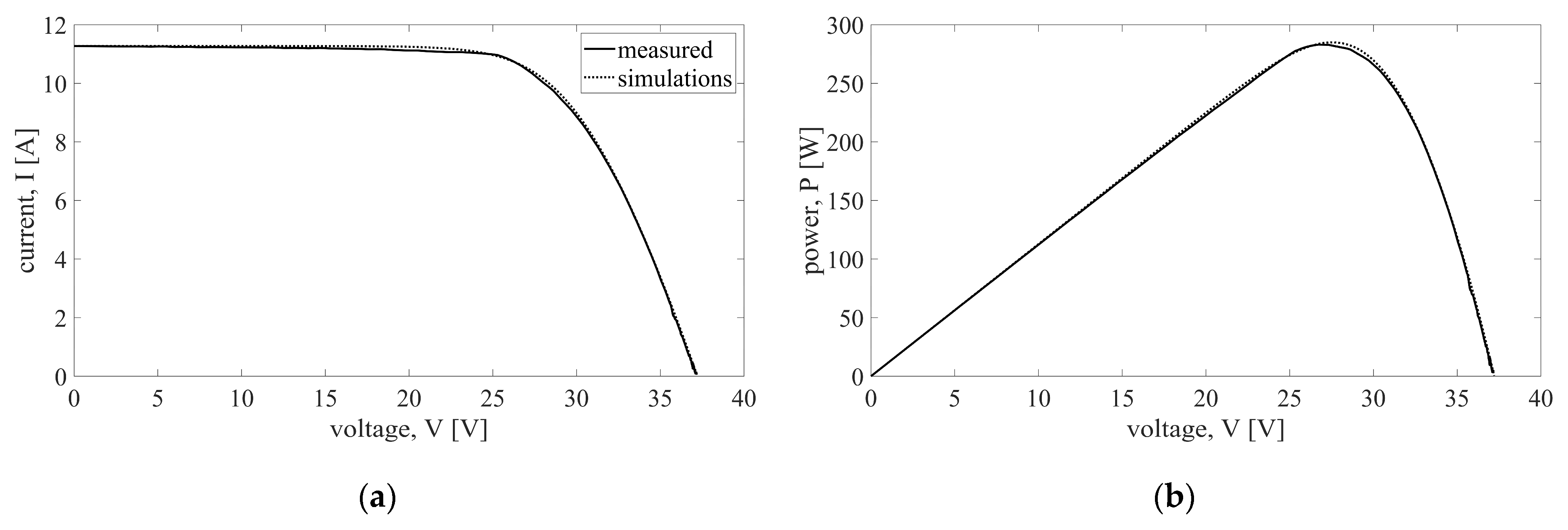
2.3. Metrics for Estimation of the Model Accuracy
3. Results
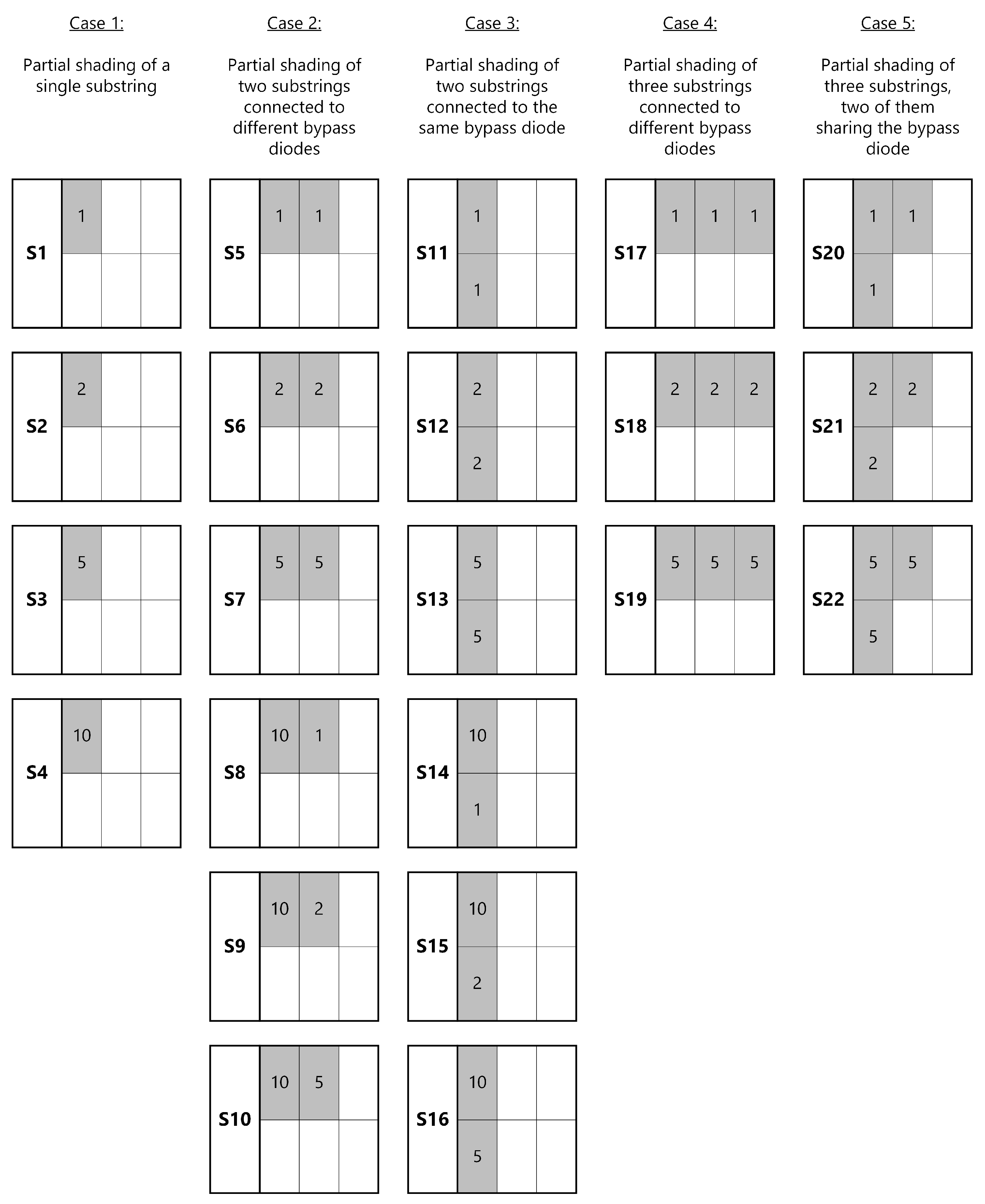
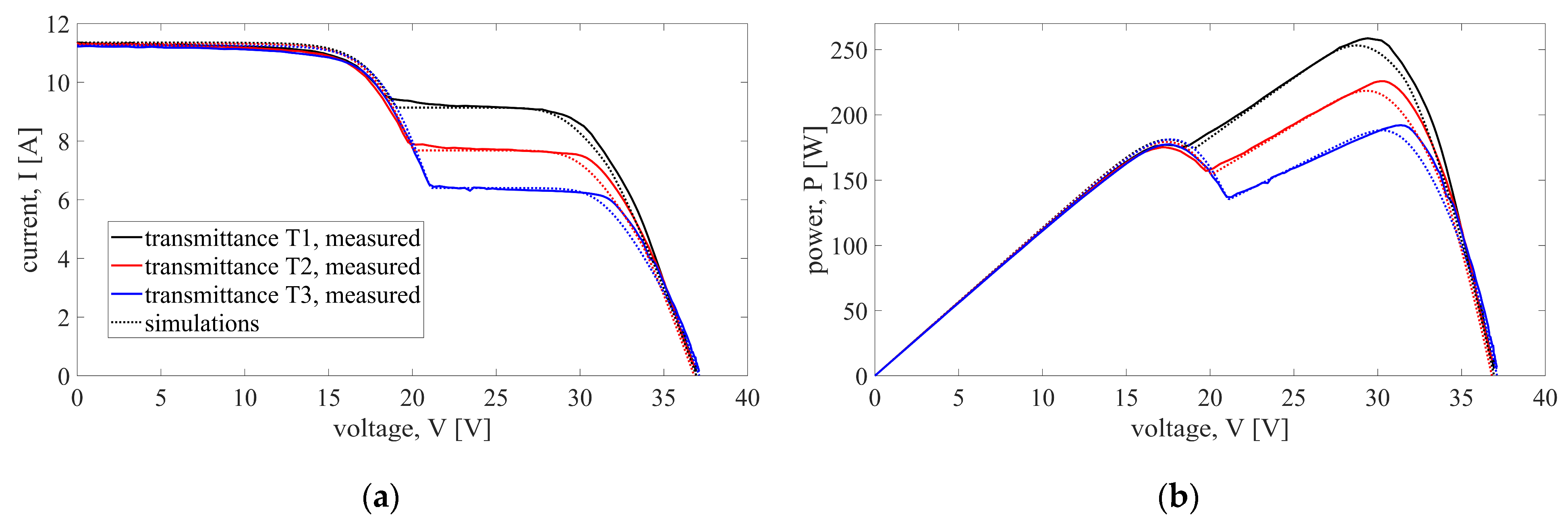
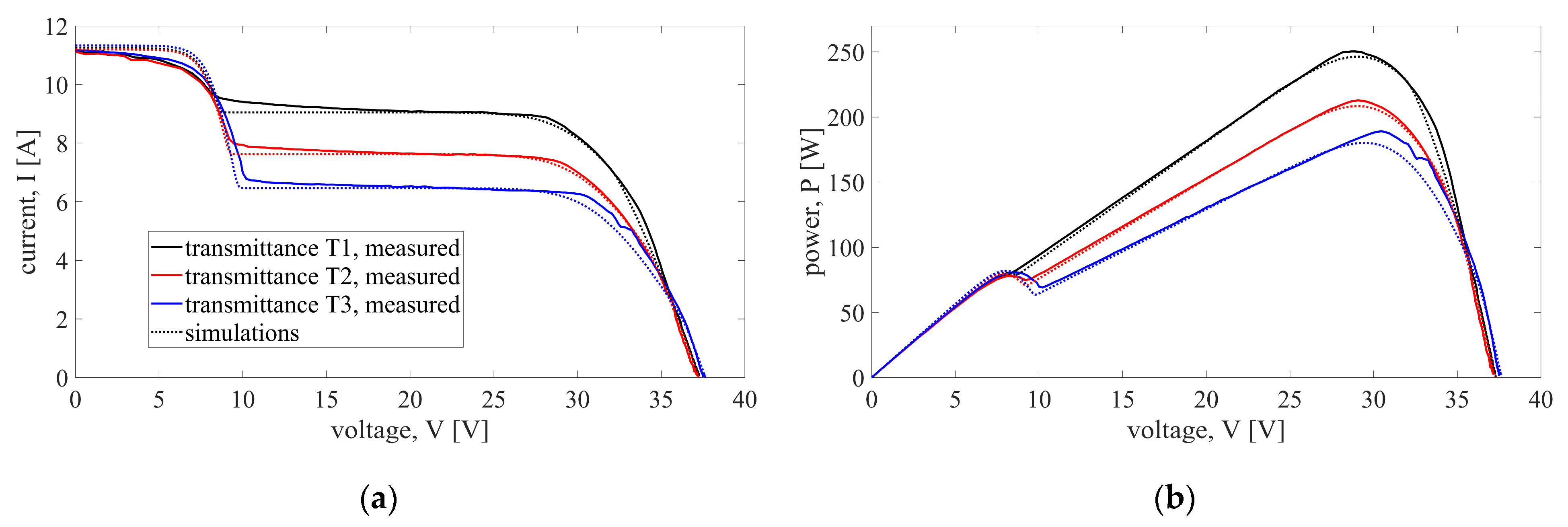
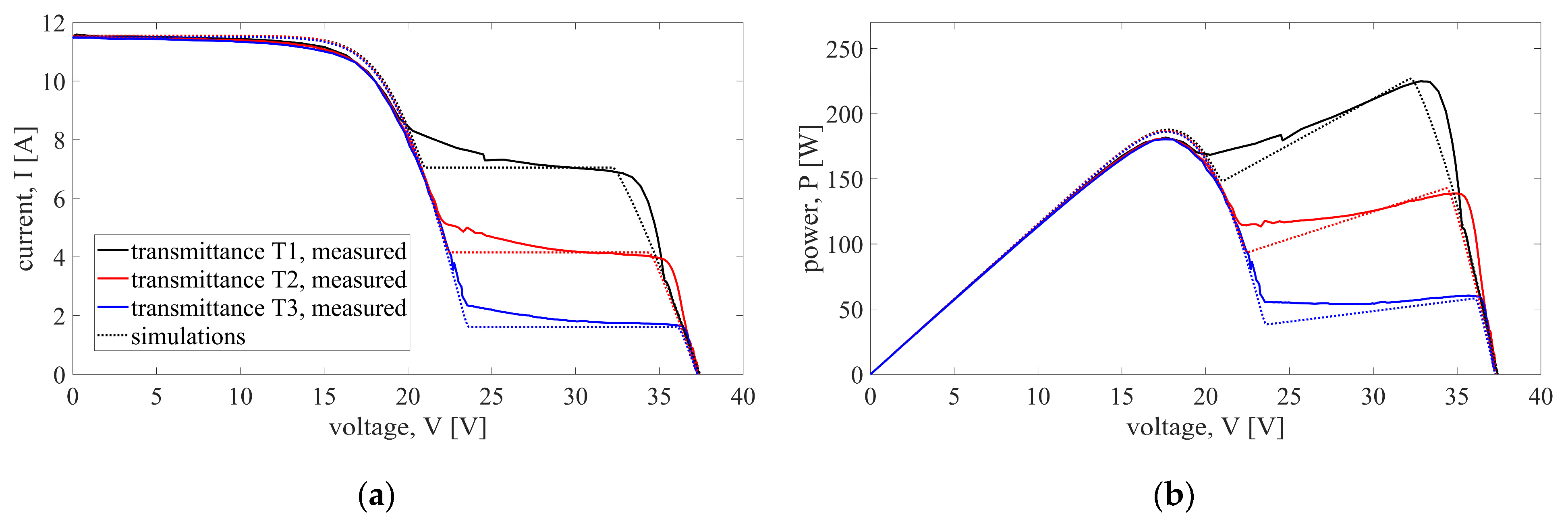
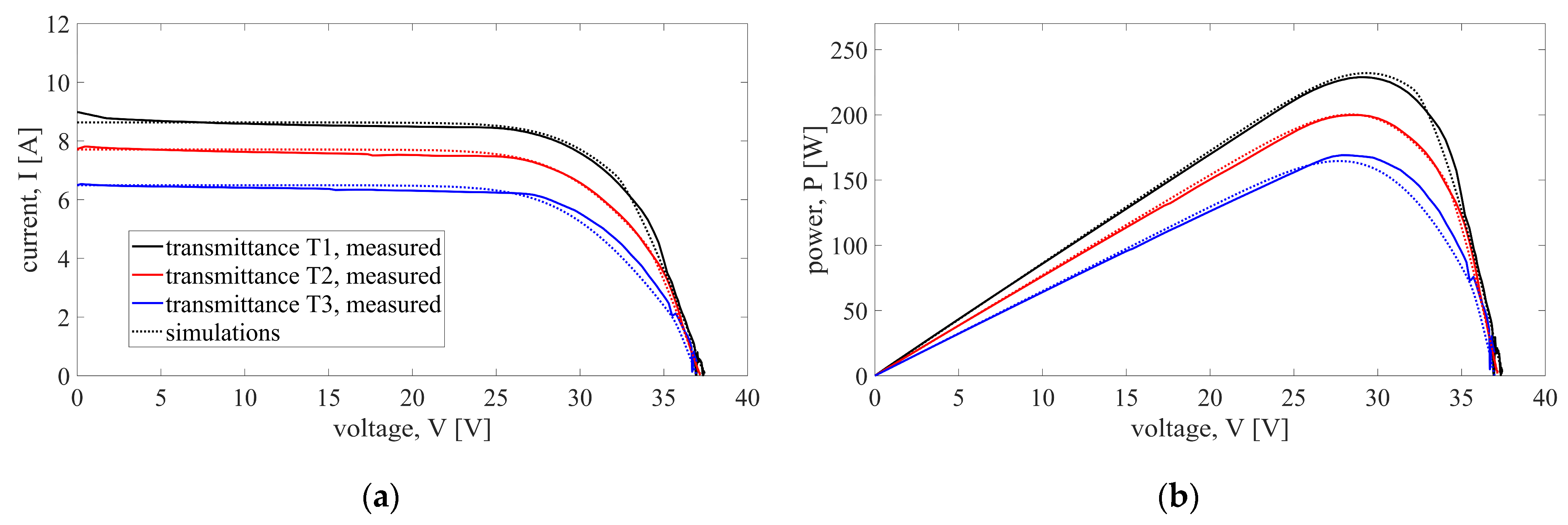
3.1. Partial Shading of a Single Substring (Case 1)
3.2. Partial Shading of Two Substrings (Cases 2 and 3)
3.3. Partial Shading of Three Substrings (Cases 4 and 5)
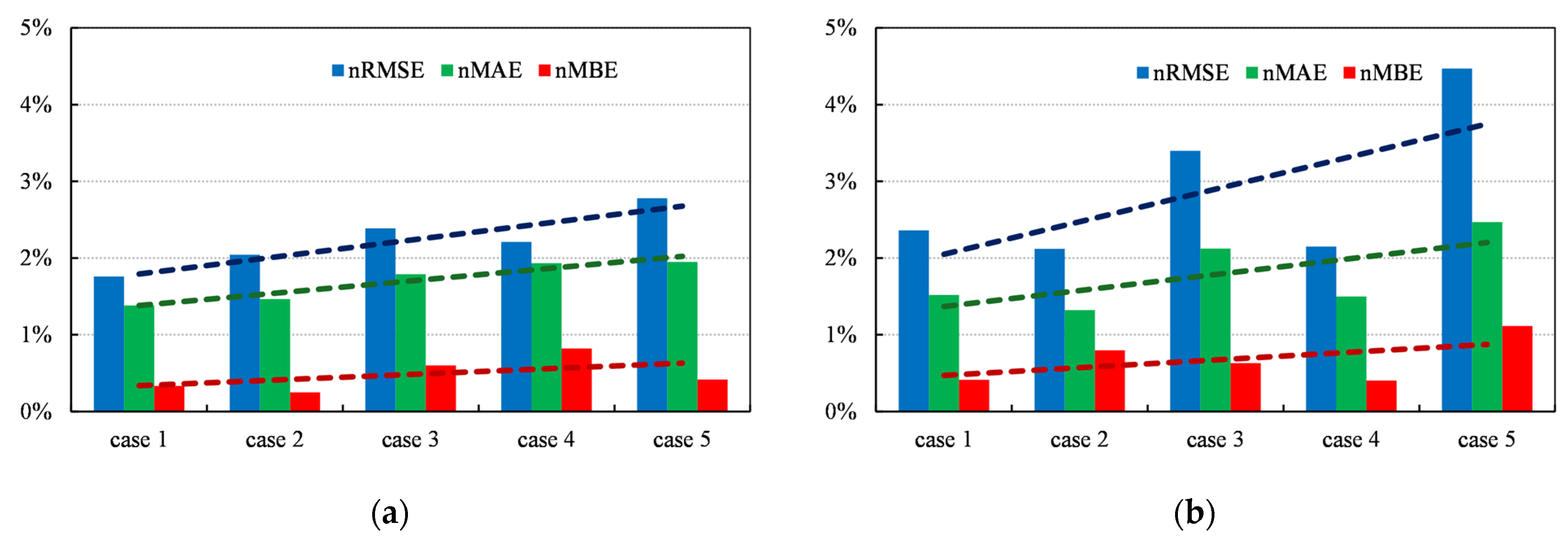
3.4. Additional Comparison of Studied Cases of Partial Shading
4. Discussion
5. Conclusions
- A great number of shading scenarios is taken into account, designed by varying
- -
- shaded module area corresponding to different numbers of shaded solar cells,
- -
- distribution of shaded area covering from one to three solar cell substrings in different configurations,
- -
- shading intensity.
In total, 66 unique shading conditions are considered. - Comprehensive error metrics for evaluation of the model’s accuracy are proposed that not only take into account the characteristic points (Pm, Isc, Voc), but also assess the accuracy of the whole I-V and P-V curves generated by the model for a given shading condition.
- The simulation results are compared to the measurements on a partially shaded half-cut PV module. Comparisons show a great level of agreement between simulations and measurements, with errors being limited to ±3% in most shading conditions and for most considered metrics.
- Comparisons of errors between different scenarios show that model errors depend mostly on the shadow distribution on the module (i.e., number and configuration of partially shaded substrings), while the variations in the number of shaded cells and shading intensity have limited influence on errors. However, more extensive simulations and measurements are needed to be able to statistically determine and quantify how the change in one of these parameters (shadow distribution, area, and intensity) influences the model’s accuracy.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Patel, H.; Agarwal, V. MATLAB-Based Modeling to Study the Effects of Partial Shading on PV Array Characteristics. IEEE Trans. Energy Convers. 2008, 23, 302–310. [Google Scholar] [CrossRef]
- Abdulmawjood, K.; Alsadi, S.; Refaat, S.S.; Morsi, W.G. Characteristic Study of Solar Photovoltaic Array under Different Partial Shading Conditions. IEEE Access 2022, 10, 6856–6866. [Google Scholar] [CrossRef]
- Nguyen, X.H. Matlab/Simulink Based Modeling to Study Effect of Partial Shadow on Solar Photovoltaic Array. Environ. Syst. Res. 2015, 4, 20. [Google Scholar] [CrossRef]
- Meyers, B.; Mikofski, M. Accurate Modeling of Partially Shaded PV Arrays. In Proceedings of the 2017 IEEE 44th Photovoltaic Specialist Conference (PVSC), Washington, DC, USA, 25–30 June 2017; pp. 3354–3359. [Google Scholar]
- Mäki, A.; Valkealahti, S.; Leppäaho, J. Operation of Series-Connected Silicon-Based Photovoltaic Modules under Partial Shading Conditions. Prog. Photovolt. Res. Appl. 2012, 20, 298–309. [Google Scholar] [CrossRef]
- Rauschenbach, H.S. Electrical Output of Shadowed Solar Arrays. IEEE Trans. Electron Devices 1971, 18, 483–490. [Google Scholar] [CrossRef]
- Bowden, S.; Honsberg, C. PVCDROM | PVEducation. Available online: https://www.pveducation.org (accessed on 28 April 2024).
- Petrone, G.; Ramos-Paja, C.A.; Spagnuolo, G. Photovoltaic Sources Modeling; John Wiley & Sons: Hoboken, NJ, USA, 2017; ISBN 978-1-118-67903-6. [Google Scholar]
- Mertens, K. Photovoltaics: Fundamentals, Technology, and Practice; John Wiley & Sons: Hoboken, NJ, USA, 2018; ISBN 978-1-119-40104-9. [Google Scholar]
- Cotfas, D.T.; Cotfas, P.A.; Kaplanis, S. Methods to Determine the Dc Parameters of Solar Cells: A Critical Review. Renew. Sustain. Energy Rev. 2013, 28, 588–596. [Google Scholar] [CrossRef]
- Jordehi, A.R. Parameter Estimation of Solar Photovoltaic (PV) Cells: A Review. Renew. Sustain. Energy Rev. 2016, 61, 354–371. [Google Scholar] [CrossRef]
- Oulcaid, M.; El Fadil, H.; Ammeh, L.; Yahya, A.; Giri, F. Parameter Extraction of Photovoltaic Cell and Module: Analysis and Discussion of Various Combinations and Test Cases. Sustain. Energy Technol. Assess. 2020, 40, 100736. [Google Scholar] [CrossRef]
- Gu, Z.; Xiong, G.; Fu, X. Parameter Extraction of Solar Photovoltaic Cell and Module Models with Metaheuristic Algorithms: A Review. Sustainability 2023, 15, 3312. [Google Scholar] [CrossRef]
- Batzelis, E.I.; Georgilakis, P.S.; Papathanassiou, S.A. Energy Models for Photovoltaic Systems under Partial Shading Conditions: A Comprehensive Review. IET Renew. Power Gener. 2015, 9, 340–349. [Google Scholar] [CrossRef]
- Gow, J.A.; Manning, C.D. Development of a Photovoltaic Array Model for Use in Power-Electronics Simulation Studies. IEE Proc.-Electr. Power Appl. 1999, 146, 193–200. [Google Scholar] [CrossRef]
- Boukenoui, R.; Salhi, H.; Bradai, R.; Mellit, A. A New Intelligent MPPT Method for Stand-Alone Photovoltaic Systems Operating under Fast Transient Variations of Shading Patterns. Sol. Energy 2016, 124, 124–142. [Google Scholar] [CrossRef]
- Chellaswamy, C.; Ramesh, R. Future Renewable Energy Option for Recharging Full Electric Vehicles. Renew. Sustain. Energy Rev. 2017, 76, 824–838. [Google Scholar] [CrossRef]
- Verma, D.; Nema, S.; Nema, R.K. Implementation of Perturb and Observe Method of Maximum Power Point Tracking in SIMSCAPE/MATLAB. In Proceedings of the 2017 International Conference on Intelligent Sustainable Systems (ICISS), Palladam, India, 7–8 December 2017; pp. 148–152. [Google Scholar]
- Brown, R.; Kamper, M.J.; Ockhuis, D.K. Utility-Scale PV-Powered Motor-Generator System with Model-Based MPPT Control. In Proceedings of the 2023 International Aegean Conference on Electrical Machines and Power Electronics (ACEMP) & 2023 International Conference on Optimization of Electrical and Electronic Equipment (OPTIM), Istanbul, Türkiye, 1–2 September 2023; pp. 1–8. [Google Scholar]
- Orta-Quintana, Á.A.; García-Chávez, R.E.; Silva-Ortigoza, R.; Marciano-Melchor, M.; Villarreal-Cervantes, M.G.; García-Sánchez, J.R.; García-Cortés, R.; Silva-Ortigoza, G. Sensorless Tracking Control Based on Sliding Mode for the “Full-Bridge Buck Inverter–DC Motor” System Fed by PV Panel. Sustainability 2023, 15, 9858. [Google Scholar] [CrossRef]
- Lu, F.; Guo, S.; Walsh, T.M.; Aberle, A.G. Improved PV Module Performance under Partial Shading Conditions. Energy Procedia 2013, 33, 248–255. [Google Scholar] [CrossRef]
- Brecl, K.; Bokalič, M.; Topič, M. Annual Energy Losses Due to Partial Shading in PV Modules with Cut Wafer-Based Si Solar Cells. Renew. Energy 2021, 168, 195–203. [Google Scholar] [CrossRef]
- Qian, J.; Thomson, A.; Blakers, A.; Ernst, M. Comparison of Half-Cell and Full-Cell Module Hotspot-Induced Temperature by Simulation. IEEE J. Photovolt. 2018, 8, 834–839. [Google Scholar] [CrossRef]
- Trends in PV Applications 2023. Available online: https://iea-pvps.org/trends_reports/trends-2023/ (accessed on 20 March 2024).
- Yang, Z.; Liao, K.; Chen, J.; Xia, L.; Luo, X. Output Performance Analysis and Power Optimization of Different Configurations Half-Cell Modules under Partial Shading. Optik 2021, 232, 166499. [Google Scholar] [CrossRef]
- Sarniak, M.T. Modeling the Functioning of the Half-Cells Photovoltaic Module under Partial Shading in the Matlab Package. Appl. Sci. 2020, 10, 2575. [Google Scholar] [CrossRef]
- Quaschning, V.; Hanitsch, R. Influence of Shading on Electrical Parameters of Solar Cells. In Proceedings of the Conference Record of the Twenty Fifth IEEE Photovoltaic Specialists Conference—1996, Washington, DC, USA, 13–17 May 1996; pp. 1287–1290. [Google Scholar]
- Wang, Y.; Pei, G.; Zhang, L. Effects of Frame Shadow on the PV Character of a Photovoltaic/Thermal System. Appl. Energy 2014, 130, 326–332. [Google Scholar] [CrossRef]
- Bharadwaj, P.; John, V. Subcell Modeling of Partially Shaded Photovoltaic Modules. IEEE Trans. Ind. Appl. 2019, 55, 3046–3054. [Google Scholar] [CrossRef]
- Moreira, H.S.; Lucas de Souza Silva, J.; Gomes dos Reis, M.V.; de Bastos Mesquita, D.; Kikumoto de Paula, B.H.; Villalva, M.G. Experimental Comparative Study of Photovoltaic Models for Uniform and Partially Shading Conditions. Renew. Energy 2021, 164, 58–73. [Google Scholar] [CrossRef]
- MS-711N Spectroradiometer. Available online: https://www.eko-instruments.com/cn/categories/products/spectroradiometers/ms-711n-spectroradiometer (accessed on 1 April 2024).
- Singh, A.; Umakanth, V.; Tyagi, N.; Baghel, A.K.; Kumar, S. Comparative Study of Commercial Crystalline Solar Cells. Results Opt. 2023, 11, 100379. [Google Scholar] [CrossRef]
- Solvis SV120 E HC9B Datasheet. Available online: https://solvis.hr/wp-content/uploads/2022/03/LQSOLVIS-DS-EN-SV120_E_HC9B-1755x1038x35-355-375-20210222.pdf (accessed on 29 April 2024).
- MP-11 Portable I–V Checker. Available online: https://www.eko-instruments.com/eu/categories/products/i-v-measurement-instruments/mp-11-portable-i-v-checker (accessed on 21 March 2024).
- Photovoltaic Solar Cell—MATLAB. Available online: https://www.mathworks.com/help/sps/ref/solarcell.html (accessed on 29 April 2024).
- Marion, B.; Kroposki, B.; Emery, K.; Cueto, J.; Myers, D.; Osterwald, C. Validation of a Photovoltaic Module Energy Ratings Procedure at NREL; NREL/TP-520-26909; NREL Technical Report; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 1999. [CrossRef]
- Cubas, J.; Pindado, S.; Sorribes-Palmer, F. Analytical Calculation of Photovoltaic Systems Maximum Power Point (MPP) Based on the Operation Point. Appl. Sci. 2017, 7, 870. [Google Scholar] [CrossRef]
- Jadli, U.; Thakur, P.; Shukla, R.D. A New Parameter Estimation Method of Solar Photovoltaic. IEEE J. Photovolt. 2018, 8, 239–247. [Google Scholar] [CrossRef]
- Peña, R.; Diez-Pascual, A.M.; Díaz, P.G.; Davoise, L.V. A New Method for Current–Voltage Curve Prediction in Photovoltaic Modules. IET Renew. Power Gener. 2021, 15, 1331–1343. [Google Scholar] [CrossRef]
- Alonso-García, M.C.; Ruiz, J.M.; Herrmann, W. Computer Simulation of Shading Effects in Photovoltaic Arrays. Renew. Energy 2006, 31, 1986–1993. [Google Scholar] [CrossRef]

| Relative Error Xrel | I-V Curve | P-V Curve | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pm | Vm | Im | Voc | Isc | nRMSE | nMAE | nMBE | nRMSE | nMAE | nMBE | ||
| S0 | 0.7 | 3.1 | 2.5 | 0.8 | 0.01 | 0.7 | 0.6 | 0.5 | 0.6 | 0.5 | 0.5 | |
| S1–S22 | Mean | 2.2 | 3.2 | 2.5 | 0.5 | 0.9 | 2.2 | 1.7 | 0.5 | 2.8 | 1.8 | 0.7 |
| Max | 5.1 | 80.5 | −43.4 | 1.9 | 3.5 | 4.5 | 4.2 | 1.8 | 5.8 | 3.5 | −2.3 | |
| Relative Error Xrel | I-V Curve | P-V Curve | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Scenario | Shading Level | Pm | Vm | Im | Voc | Isc | nRMSE | nMAE | nMBE | nRMSE | nMAE | nMBE |
| S1 | T1 | −2.1 | −2.3 | 0.1 | 0.8 | 0.1 | 1.7 | 1.3 | −0.2 | 2.1 | 1.3 | −0.7 |
| T2 | −3.3 | −3.1 | −0.2 | −0.3 | 0.1 | 1.9 | 1.5 | −0.2 | 2.8 | 1.7 | −0.9 | |
| T3 | −2.1 | −3.7 | 1.8 | −0.1 | 0.3 | 1.7 | 1.3 | 0.3 | 2.7 | 1.7 | −0.3 | |
| S2 | T1 | −2.5 | −1.6 | −0.9 | −1.3 | −0.1 | 1.5 | 1.0 | 0.1 | 1.6 | 1.0 | −0.3 |
| T2 | −1.4 | −3.3 | 2.0 | −0.1 | 0.2 | 1.7 | 1.3 | 0.5 | 2.0 | 1.4 | 0.1 | |
| T3 | −1.6 | −3.4 | 1.9 | −1.4 | 0.3 | 1.7 | 1.3 | 0.4 | 2.6 | 1.7 | −0.1 | |
| S3 | T1 | −2.3 | −2.4 | 0.1 | 0.0 | 0.2 | 1.4 | 1.0 | 0.1 | 1.5 | 0.9 | −0.3 |
| T2 | −2.8 | −2.8 | 0.0 | 1.0 | 0.6 | 1.9 | 1.5 | 0.2 | 2.5 | 1.6 | −0.5 | |
| T3 | −1.6 | −2.8 | 1.3 | 1.9 | 0.7 | 1.9 | 1.6 | 0.5 | 2.9 | 1.9 | −0.2 | |
| S4 | T1 | −2.2 | −2.7 | 0.5 | 0.4 | 0.7 | 2.1 | 1.6 | 0.1 | 2.5 | 1.5 | −0.6 |
| T2 | −0.4 | −2.5 | 2.1 | 0.3 | 0.8 | 1.7 | 1.4 | 1.0 | 1.7 | 1.3 | 0.6 | |
| T3 | −1.2 | −4.2 | 3.1 | 0.7 | −3.2 | 2.0 | 1.6 | 0.3 | 3.5 | 2.1 | −0.4 | |
| Relative Error Xrel | I-V Curve | P-V Curve | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Scenario | Shading Level | Pm | Vm | Im | Voc | Isc | nRMSE | nMAE | nMBE | nRMSE | nMAE | nMBE |
| S5 | T1 | −1.6 | 1.2 | −2.8 | 0.0 | 0.9 | 2.1 | 1.6 | −0.3 | 1.5 | 1.0 | −0.7 |
| T2 | −2.1 | −0.1 | −2.0 | −1.7 | 0.7 | 1.9 | 1.3 | 0.1 | 1.1 | 0.8 | −0.2 | |
| T3 | −4.7 | −3.4 | −1.3 | 0.4 | 1.4 | 2.6 | 1.9 | −0.5 | 3.0 | 1.9 | −1.4 | |
| S6 | T1 | −1.2 | 1.1 | −2.3 | −0.1 | −0.2 | 1.7 | 1.3 | 0.1 | 1.1 | 0.8 | −0.4 |
| T2 | −2.0 | −0.5 | −1.5 | −1.2 | −1.4 | 1.7 | 1.2 | −0.1 | 1.7 | 1.1 | −0.7 | |
| T3 | −4.7 | −2.5 | −2.2 | 0.1 | 1.4 | 2.8 | 1.9 | −0.5 | 3.3 | 2.0 | −1.5 | |
| S7 | T1 | −2.7 | −0.7 | −2.0 | −0.5 | 1.6 | 2.4 | 1.8 | −0.5 | 2.9 | 1.6 | −1.4 |
| T2 | −0.9 | 0.9 | −1.8 | 1.1 | 0.3 | 1.5 | 1.0 | 0.3 | 0.9 | 0.6 | −0.1 | |
| T3 | −2.8 | −2.2 | −0.6 | −0.7 | 1.5 | 2.7 | 2.0 | −0.1 | 3.5 | 2.2 | −1.1 | |
| S8 | T1 | −3.3 | −0.1 | −3.1 | −0.5 | 0.5 | 2.2 | 1.7 | −0.7 | 2.5 | 1.5 | −1.3 |
| T2 | −2.6 | −0.8 | −1.7 | −1.7 | −0.3 | 2.0 | 1.4 | −0.2 | 2.3 | 1.3 | −1.0 | |
| T3 | −3.1 | −2.6 | −0.5 | 0.1 | 0.7 | 1.9 | 1.4 | 0.1 | 2.0 | 1.4 | −0.6 | |
| S9 | T1 | −1.1 | 1.1 | −2.3 | −0.3 | −0.2 | 1.9 | 1.3 | 0.0 | 1.8 | 1.0 | −0.7 |
| T2 | −1.3 | −0.7 | −0.6 | −0.4 | −5.9 | 1.6 | 1.0 | 0.3 | 1.0 | 0.7 | −0.2 | |
| T3 | −4.0 | −3.3 | −0.6 | −0.4 | −0.1 | 2.3 | 1.6 | −0.4 | 3.5 | 2.1 | −1.3 | |
| S10 | T1 | −1.8 | 0.8 | −2.6 | −1.1 | −0.5 | 1.6 | 1.1 | 0.1 | 1.2 | 0.8 | −0.5 |
| T2 | −2.0 | −0.6 | −1.4 | 0.0 | −0.1 | 1.7 | 1.2 | −0.0 | 1.8 | 1.1 | −0.6 | |
| T3 | −3.3 | −2.8 | −0.6 | −0.4 | 0.6 | 2.1 | 1.7 | 0.1 | 3.0 | 2.0 | −0.8 | |
| Relative Error Xrel | I-V Curve | P-V Curve | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Scenario | Shading Level | Pm | Vm | Im | Voc | Isc | nRMSE | nMAE | nMBE | nRMSE | nMAE | nMBE |
| S11 | T1 | 0.9 | −1.9 | 2.8 | 0.2 | 0.1 | 3.3 | 2.2 | −0.7 | 4.6 | 2.6 | −1.4 |
| T2 | 3.2 | 0.9 | 2.2 | 0.0 | 0.3 | 3.0 | 2.2 | −0.3 | 5.2 | 3.0 | −1.3 | |
| T3 | 3.2 | 0.7 | 2.4 | 0.1 | 0.5 | 2.4 | 2.0 | −0.1 | 3.5 | 2.7 | −1.1 | |
| S12 | T1 | −1.1 | −2.6 | 1.6 | 0.3 | 0.4 | 2.6 | 1.8 | 0.1 | 3.8 | 2.0 | −0.6 |
| T2 | 3.5 | 4.3 | −0.7 | 0.4 | 0.3 | 2.0 | 1.5 | 0.5 | 3.4 | 1.9 | 0.0 | |
| T3 | 4.1 | 0.7 | 3.4 | −0.2 | 0.6 | 1.9 | 1.6 | 0.6 | 2.4 | 1.9 | 0.1 | |
| S13 | T1 | −2.2 | −3.3 | 1.2 | 0.0 | 0.1 | 2.8 | 1.8 | −0.6 | 4.6 | 2.3 | −1.5 |
| T2 | 4.0 | 1.5 | 2.5 | 0.7 | 0.2 | 2.0 | 1.5 | 0.5 | 3.4 | 1.9 | −0.1 | |
| T3 | 3.0 | 1.4 | 1.5 | −0.5 | 0.4 | 1.8 | 1.4 | 0.6 | 2.2 | 1.6 | 0.1 | |
| S14 | T1 | −0.3 | −3.1 | 2.9 | −0.3 | 0.7 | 2.9 | 2.3 | −0.1 | 3.9 | 2.6 | −0.9 |
| T2 | 4.3 | 1.8 | 2.4 | 0.7 | 0.6 | 2.7 | 2.1 | 0.4 | 3.7 | 2.7 | −0.2 | |
| T3 | 4.2 | 1.9 | 2.2 | −0.5 | 0.7 | 2.2 | 1.8 | 0.6 | 2.7 | 2.0 | 0.1 | |
| S15 | T1 | −1.9 | −3.2 | 1.3 | −0.2 | 0.6 | 2.5 | 1.8 | 0.4 | 3.3 | 1.9 | −0.3 |
| T2 | 3.2 | 1.0 | 2.2 | 0.3 | 0.6 | 2.0 | 1.5 | 0.8 | 3.1 | 1.9 | 0.3 | |
| T3 | 4.8 | 0.7 | 4.0 | 0.2 | 0.7 | 2.1 | 1.5 | 1.2 | 2.4 | 1.5 | 1.0 | |
| S16 | T1 | −0.6 | −3.1 | 2.5 | 0.6 | 0.8 | 2.5 | 1.9 | 0.7 | 3.5 | 2.0 | −0.1 |
| T2 | 5.1 | 4.4 | 0.7 | 0.6 | 0.7 | 2.5 | 1.8 | 1.6 | 3.2 | 2.1 | 1.6 | |
| T3 | 3.0 | 2.2 | 0.7 | 0.0 | 0.6 | 1.8 | 1.5 | 1.0 | 2.3 | 1.6 | 0.7 | |
| Relative Error Xrel | I-V Curve | P-V Curve | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Scenario | Shading Level | Pm | Vm | Im | Voc | Isc | nRMSE | nMAE | nMBE | nRMSE | nMAE | nMBE |
| S17 | T1 | 1.4 | 1.5 | −0.1 | 0.0 | −4.1 | 1.6 | 1.3 | 0.2 | 1.6 | 1.0 | 0.2 |
| T2 | 0.2 | −0.8 | 1.0 | −0.2 | −0.3 | 1.4 | 1.1 | 0.6 | 1.3 | 0.8 | 0.3 | |
| T3 | −2.7 | −0.5 | −2.2 | 0.2 | 0.0 | 3.0 | 2.3 | −0.3 | 3.5 | 2.3 | −1.0 | |
| S18 | T1 | 1.8 | 1.0 | 0.8 | 0.8 | 0.9 | 1.9 | 1.7 | 0.9 | 1.9 | 1.4 | 0.4 |
| T2 | 0.0 | −1.5 | 1.5 | −0.4 | 1.3 | 2.0 | 1.7 | 0.8 | 2.0 | 1.2 | 0.1 | |
| T3 | −1.9 | −1.8 | −0.1 | −0.6 | 1.4 | 2.7 | 2.5 | 0.6 | 2.7 | 2.0 | −0.4 | |
| S19 | T1 | 2.0 | 2.2 | −0.2 | 0.2 | 1.2 | 1.5 | 1.5 | 1.2 | 1.2 | 1.0 | 0.6 |
| T2 | 0.5 | −0.2 | 0.7 | 0.3 | 1.1 | 1.3 | 1.2 | 1.0 | 0.9 | 0.7 | 0.5 | |
| T3 | −0.9 | −1.5 | 0.6 | −1.0 | 3.5 | 4.5 | 4.2 | 1.8 | 4.2 | 3.0 | 0.0 | |
| Relative Error Xrel | I-V Curve | P-V Curve | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Scenario | Shading Level | Pm | Vm | Im | Voc | Isc | nRMSE | nMAE | nMBE | nRMSE | nMAE | nMBE |
| S20 | T1 | 0.9 | −4.1 | 5.1 | −1.3 | 0.9 | 4.1 | 2.9 | −1.0 | 5.8 | 3.2 | −2.3 |
| T2 | 2.1 | 80.5 | −43.4 | −0.1 | 0.4 | 2.8 | 2.1 | 0.2 | 5.0 | 3.2 | −1.0 | |
| T3 | −0.3 | −2.4 | 2.1 | −0.5 | 1.2 | 2.7 | 2.2 | −0.3 | 5.0 | 3.5 | −2.2 | |
| S21 | T1 | −0.9 | −3.7 | 2.8 | −1.9 | 2.5 | 3.1 | 2.1 | 0.3 | 4.2 | 2.0 | −0.9 |
| T2 | 1.2 | −1.0 | 2.3 | −0.5 | 1.3 | 2.3 | 1.6 | 0.6 | 4.3 | 2.0 | −0.4 | |
| T3 | −0.8 | −3.1 | 2.4 | −0.3 | −1.8 | 2.1 | 1.5 | 0.7 | 2.4 | 1.8 | 0.3 | |
| S22 | T1 | −2.4 | −4.6 | 2.3 | −2.2 | −0.4 | 3.1 | 1.9 | −0.2 | 4.9 | 2.2 | −1.5 |
| T2 | 0.1 | −2.3 | 2.4 | −0.8 | 2.1 | 2.7 | 1.8 | 0.1 | 5.7 | 2.5 | −1.3 | |
| T3 | 1.3 | −0.4 | 1.7 | −0.3 | 0.6 | 2.1 | 1.5 | 0.4 | 2.9 | 1.8 | −0.2 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Betti, T.; Kristić, A.; Marasović, I.; Pekić, V. Accuracy of Simscape Solar Cell Block for Modeling a Partially Shaded Photovoltaic Module. Energies 2024, 17, 2276. https://doi.org/10.3390/en17102276
Betti T, Kristić A, Marasović I, Pekić V. Accuracy of Simscape Solar Cell Block for Modeling a Partially Shaded Photovoltaic Module. Energies. 2024; 17(10):2276. https://doi.org/10.3390/en17102276
Chicago/Turabian StyleBetti, Tihomir, Ante Kristić, Ivan Marasović, and Vesna Pekić. 2024. "Accuracy of Simscape Solar Cell Block for Modeling a Partially Shaded Photovoltaic Module" Energies 17, no. 10: 2276. https://doi.org/10.3390/en17102276
APA StyleBetti, T., Kristić, A., Marasović, I., & Pekić, V. (2024). Accuracy of Simscape Solar Cell Block for Modeling a Partially Shaded Photovoltaic Module. Energies, 17(10), 2276. https://doi.org/10.3390/en17102276






