1. Introduction
The relentless pursuit of sustainable energy solutions has led to the widespread adoption of lithium-ion batteries (LiBs) as a primary energy storage technology in numerous applications, ranging from portable electronics to transportation and renewable energy systems [
1,
2,
3,
4]. The energy landscape is transitioning from traditional fossil fuel-based systems to distributed solutions powered by renewable sources, notably wind and photovoltaic energy [
5]. Nevertheless, the intermittent nature of renewable sources presents challenges to the reliable and stable operation of energy grids.
The primary drivers behind the LiBs being widespread are their exceptional technical characteristics, which include high energy and power densities, impressive efficiency, and minimal self-discharge rates in comparison to their counterparts, such as NiCd, NiMH, and Lead Acid batteries [
6,
7,
8]. To harness these advantages effectively, LiBs must operate under the supervision of a battery management system (BMS). The BMS plays a crucial role in ensuring that the battery operates safely within its designated temperature and state of charge (SOC) parameters. For LiBs, the temperature of the cells is not only influential in affecting the open circuit voltage (OCV), internal resistance, and available capacity, but it can also cause rapid battery degradation and even thermal runaway if the battery is operated beyond a specified temperature threshold. To maintain the battery within its safe operational range under all conditions, an electrothermal battery model is crucial. Such a model must comprehensively represent both the electrical and thermal behaviors of Li-ion cells, guaranteeing that the battery temperature remains well within acceptable limits throughout its operation [
9,
10,
11].
While LiBs have undoubtedly revolutionized the way we store and utilize energy, their long-term performance and reliability remain central challenges [
5]. Over time, LiBs inevitably degrade due to a multitude of complex factors, collectively referred to as aging phenomena. Understanding and identifying the key mechanisms behind LiB aging is fundamental to extend their lifespan, enhance their safety, and optimize their performance. Battery aging models can be classified according to the methodology adopted into three groups hereby listed in descending order of physical–chemical knowledge and computational effort, and in ascending order of experimental test requirement and applicability: electrochemical models, semi-empirical models, and data-driven models.
Electrochemical aging models require the knowledge of several physical and chemical parameters of the cell, different for each type of LiBs and very difficult to measure. However, they need a few experimental tests as the model is very detailed. In [
12], an aging formulation for NCA/graphite Li-ion cells that include heterogeneous dual-layer solid electrolyte interphase and lithium-plating aging mechanisms with porosity evaluation is proposed. The implemented model belongs to the category of electrochemical ones and requires an extensive knowledge of the chemical and physical aspects of the cell. More than 60 parameters are required to model the aging of the cell, of which 14 were not known and have been estimated bringing to End of Life (EoL) only one cell. The model captures the cell capacity fade with an accuracy of 98% goodness-of-fit error. Another example of an electrochemical aging model is [
13] which develops a single particle-based degradation model [
14] by including the physics of capacity and voltage degradation phenomena. The model has 35 parameters, and it captures the capacity fade and voltage profile as functions of cycle number with a Root Mean Square Error (RMSE) of 1.03%.
Data-driven aging models, on the contrary, do not require any physical and chemical knowledge of the battery, and can be extended to every type of LiB. Their major drawback is the extensive experimental campaign that has to be made in order to develop the model, which degrades several batteries, thus increasing the operational costs. In a set of two papers [
15,
16], a data-driven model to estimate the capacity degradation of lithium-ion cells is presented. The papers investigate calendar and cycling aging, and introduce a data-driven aging model for Li-ion batteries under the Gaussian process framework. To build the calendar aging model, 32 cells were tested, while the cycling aging model was built on the results of experiments on 124 cells. The calendar and cycling aging models returned a Mean Absolute Error (MAE) of 0.58% and 1.04%, respectively. In [
17], a feed-forward migration neural network is proposed to predict LiBs’ aging trajectories. First, a base model that describes the capacity decay over time is established from the existing battery aging data set. Then, the base model is transformed by an input–output slope and bias correction method structure to capture the degradation of the target cell. To enhance the model’s nonlinear transfer capability, the model is further integrated into a four-layer neural network. A total of eight batteries were utilized and brought to their EoL, and the model always returned a RMSE lower than 2.5%. In [
18], a multivariable fractional polynomial regression approach is proposed to model the degradation of LiBs. In [
19], a data-driven approach is proposed to forecast LiBs’ state of health (SOH) and SOC under constant current discharge conditions.
Semi-empirical aging models stand in the middle between electrochemical and data-driven models, balancing complexity, computational effort, applicability, and data requirements; furthermore, they can be applied to different types of LiBs [
20]. In [
21], a method to estimate the battery SOH and SOC with a semi-empirical approach is proposed. The developed model uses three parameters, two of which are time-variant. One battery is repeatedly charged and discharged till its EoL and three others undergo a dynamic stress test protocol, each one at a different temperature. The validation results show a correlation coefficient of 0.9. In [
22], a semi-empirical LiB degradation model assessing the battery cell life loss from operating profiles is proposed. The model takes as input the battery Depth of Discharge (DoD), SOC, and temperature, and provides an offline estimation of the SOH. Experiments were run on a total of eight batteries and the results showed a SOH estimation error near 3%. In [
20], a semi-empirical model for battery capacity and resistance degradations is proposed, based on physical equations from fatigue theory and equivalent cycle counting. The model takes as input the ambient temperature, the battery SOC, and current, and it is interfaced with an electrochemical model of a LiB that evaluates the battery temperature evolution from the working conditions and the ambient temperature [
11]. The model is validated using two types of Li-ion cells (LFP and NMC) and simulation results show an error within ±1.5% compared to experimental results.
Semi-empirical and data-driven aging models can be integrated to create hybrid models. An example of a semi-empirical/data-driven aging model is [
23], where a robust SOH estimation method is proposed. The developed model presents four parameters, of which two are estimated through curve fitting, one is predicted by training a neural network, and one is obtained through Gaussian process regression. Tests are run on five batteries (three LFPs with 32 cells each and two NMCs with 40 cells each) cycled according to four different categories of tests, i.e., (1) standard cycling at different C-rates and temperatures, (2) standard calendar at different SOCs, (3) combination of cycling and calendar, and (4) combination of realistic working conditions. For standard cycling tests, the RMSE is below 4% for most of the groups of batteries; for the standard calendar, the RMSE is lower than 2%; for the combination of cycling and testing, the average RMSE is 1.21%; for the combination of realistic working conditions, the average RMSE is 1.53%.
In this paper, we present a LiB electrothermal model (EM) that returns the battery voltage and capacity as functions of the battery temperature, and interfaces with a LiB semi-empirical aging model (AM) that forecasts online the battery capacity and resistance evolution. Moreover, we propose a method to identify the parameters of the two models and validate the results on cross-validating tests. The main contributions of this work can be summarized as follows:
Development of a comprehensive LiB model able to represent the battery voltage, capacity, and resistance according to battery temperature and degradation, to forecast their evolution over time and/or to be easily integrated with a BMS.
A suitably developed method to identify the parameters of the electrothermal and aging parameters of the LiB model.
An extensive experimental validation realized by using measurements collected from real Li-ion cells and real battery-use profiles.
It is worth noticing that the proposed LiB model is an enhanced version of existing electrothermal and aging models. Specifically, the EM is formulated based on the models in [
11,
24,
25], while the AM starts from the one presented in [
20]. However, as we will specifically clarify in
Section 3.3 and
Section 4.3, in this paper we introduce two main improvements: the formal inclusion of the relation between the maximum theoretical discharge capacity, used in the EM, and the battery nominal capacity, used in the AM; and the generalization of the aging parameter identification procedure to the case of multiple experimental measurements for each aging condition.
The remainder of this paper is organized as follows:
Section 2 introduces the problem and the experimental dataset,
Section 3 describes the LiBs models,
Section 4 presents the parameter identification methodology,
Section 5 presents the results, and
Section 6 summarizes the paper conclusions.
2. Problem Statement and Experimental Dataset
The principal objective of this paper is to experimentally validate a model able to reproduce the operation due to aging of LiBs. Among the observable aging-related phenomena, we focus on two aspects: capacity fade and internal resistance increase, two phenomena that lead to reduced availability of energy storage, power fade, and reduced round trip efficiency. To model these phenomena, we will introduce and validate a semi-empirical AM. In order to obtain a complete representation of the battery behavior, the AM has to face an EM that returns the battery voltage, capacity, and internal resistance in the function of the current and temperature. Therefore, we will also introduce and validate an EM. The final result will be the Whole Battery Model (WBM) obtained by coupling the EM and the AM.
The purpose of developing the WBM lies in several potential practical applications. Indeed, the WBM can be used in electric vehicles [
26,
27] or in stationary applications, such as microgrids [
28,
29] and grid-level storage systems [
30], to allow the real-time monitoring of the battery SOH or to be integrated into optimal battery management algorithms. Moreover, the WBM can also be used to perform simulations in the design phase of new devices employing LiBs.
Regardless of the final use of the WBM, this paper focuses on the offline preliminary phase, where the WBM is identified and validated using a properly defined set of experimental measurements on the same battery type that will be used in the real application. Any stage after the WBM validation is beyond the scope of the paper.
The proposed procedure to identify and validate the WBM is shown in
Figure 1. We design three sets of experimental tests: Experiment 1, to identify the parameters of the EM; Experiment 2, to identify the parameters of the AM; Experiment 3, to realize the validation. In
Section 2.1 we detail the three experiments. The EM and AM parameter identification procedures are described in
Section 4.1 and
Section 4.2, respectively. Finally, validation results are reported in
Section 5.
2.1. Experiment Description
To properly define the set of experimental tests, we considered that the following operating conditions have an impact on the LiBs’ electrothermal behavior and on the capacity fade and internal resistance growth [
31]:
Charge rate;
Discharge rate;
Battery temperature;
DoD.
The current rate affects the terminal voltage and internal potential, leading to side reactions that reduce battery life. Excessive current accelerates active material fatigue, damages the structure, and disrupts current distribution, potentially causing local lithium plating. Fast charging, in particular, can lead to lithium deposition, further affecting battery life. Temperature affects various reactions within the battery, with higher temperatures increasing side reactions and potentially causing thermal runaway (the optimal working range for most commercial LiBs is typically in the range of 15–35 °C). Finally, in LiBs, cycling within a certain DoD range is critical. Initially, increasing DoD improves battery life by lowering the average SOC and anode potential. However, high DoD leads to phase changes in cathode and anode materials, causing structural and volume changes and significantly reducing battery life.
Therefore, the three experimental tests detailed in the following have been designed and carried out taking into account the above-listed four operating conditions. During all tests, battery temperature, current, and voltage were constantly monitored and logged with a corresponding timestamp. Tests were carried out on Samsung INR21700-50E (Samsung SDI Co. Ltd., Yongin, Gyeonggi-do, Republic of Korea) lithium-ion cells [
32], assuming as given from the datasheet the cut-off voltage
(V), the full capacity voltage
(V), and the nominal capacity Q (Ah) in fresh battery conditions. However, it should be pointed out that the experimental discharge curves performed on these cells showed a lower capacity than the one declared in [
32].
It is finally worth remarking that all experimental data have been provided by Yanmar Holdings Co., Ltd. (Maibara, Japan) [
33] based on their experience in using LiBs in off-road vehicles and industrial applications.
2.1.1. Experiment 1
The purpose of Experiment 1 is to characterize the battery EM. To this end, a fresh battery was discharged three times from full capacity at constant current (CC) to reach the cut-off voltage () with the same C-rate. Each discharge was carried out at a different temperature, i.e., 0 °C, 25 °C, 50 °C, and at the 0.5C rate. Before discharging at CC, the battery was brought to 100% SOC (which the full capacity voltage is related to) and the test temperature was set. Then, the battery was discharged at the 0.5C rate, meaning that in two hours the whole battery nominal capacity Q was transferred and the output voltage was registered with a sampling time of 1 s. Once the cut-off voltage was reached, the battery was rested for 10 min before being charged at 0.5C to 100% SOC. Then, the temperature was updated for the following discharge (the second and the third ones).
2.1.2. Experiment 2
Experiment 2 is a set of cycle tests, detailed in
Table 1, suitably designed to investigate the effects of the four stress factors (charge rate, discharge rate, battery temperature, and DoD) on capacity fade and internal resistance increase. A cycle test consisted of repeating charge/discharge cycles at specific battery temperature conditions, with established charge and discharge rates, and within a specific SOC range. Every time the top and bottom ends of the SOC range were reached, the battery was rested for 10 min. To define the tests listed in
Table 1, a test matrix was organized with two charge rates (0.5C and 1C), two discharge rates (1C and 2C), two battery temperatures (25 °C and 40 °C), and two DoDs (100% and 80%). Considering one of the two test values for each of the four stress factors as reference, five cycle tests were carried out: one setting all stress factors at the reference values (cycle test #1) and four by setting one stress factor at a non-reference value (cycle tests #2–#5). Then, to further investigate the effect of the DoD at different starting SOCs, a sixth cycle test was realized (cycle test #6).
To monitor the battery degradation, at the beginning and every 50 cycles a capacity measurement and a resistance measurement were conducted during each cycle test. Furthermore, cycle tests #1 and #2 were conducted on three different battery cells each, while all the other cycle tests were conducted on just one battery cell. The data of one each of the three cells subject to cycle tests #1 and #2 were used for the validation, namely cycle test #1-3 and cycle test #2-3, whereas the data of the other two cells were used for the identification of the parameters. Each test was suspended after the battery hit the EoL, which in this work is defined as the condition at which the battery capacity reaches 80% of the battery capacity at the Beginning of Life (BoL). The capacity measurement consists of repeating the same discharge procedure of Experiment 1 with a discharge current of 0.98 A (approximately 0.2C rate) and monitoring the amount of extracted capacity to reach a voltage of from a voltage of .
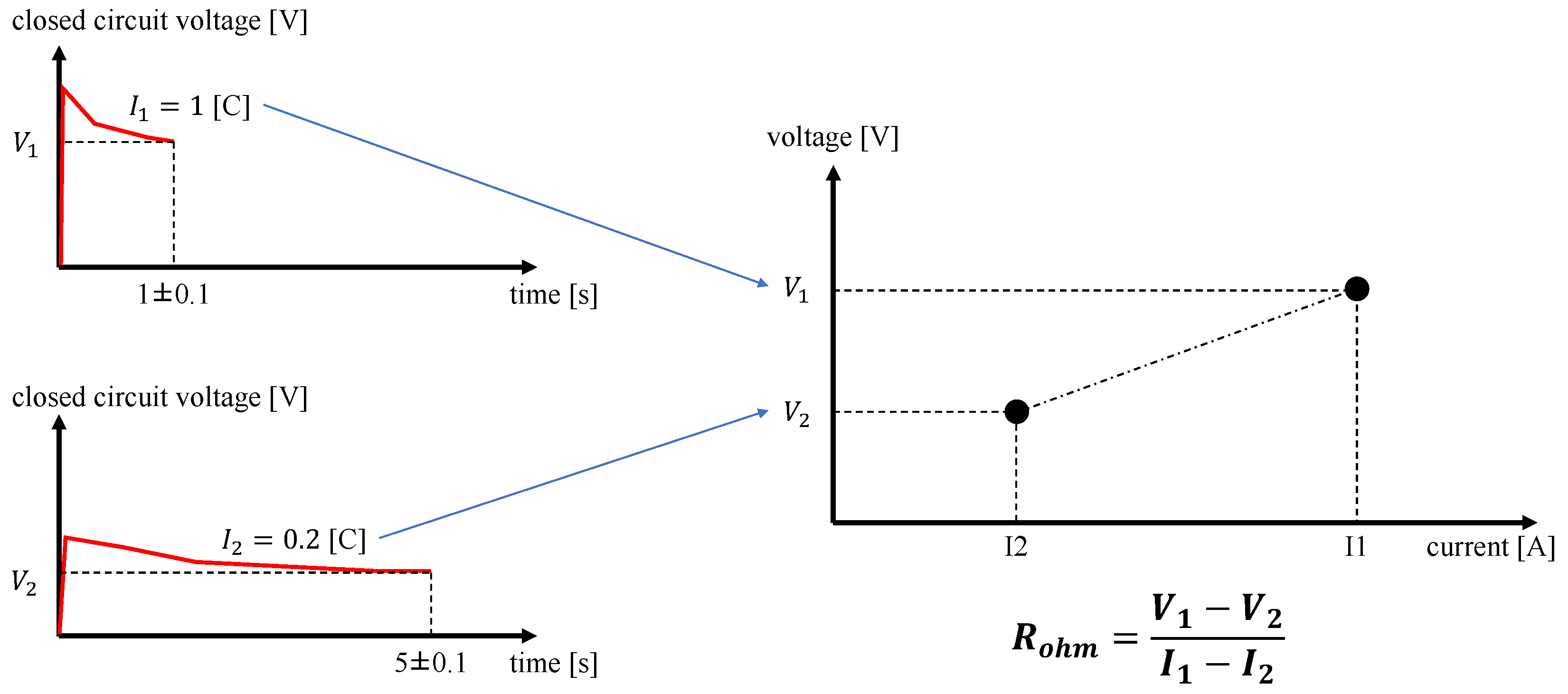
Figure 2 illustrates how the internal resistance was computed. Two discharge current steps were applied to the cell, i.e.,
at 1C for 1 s and
at 0.2C for 5 s, such that the extracted capacity was the same. The steady-state values of the terminal voltage were measured after the two current steps, i.e.,
after
and
after
. Then, the resistance was estimated as the ratio between the differences between voltage values and the difference between current values in the two testing conditions as follows:
2.1.3. Experiment 3
Experiment 3 is a set of tests used to validate the WBM. To this end, two real load cycles were designed, namely Pattern A, at 0 and 25 °C, and Pattern B, at 25 °C, to validate the AM model. Moreover, as anticipated in
Section 2.1.2, one each of the three cycle tests #1 and #2, i.e., #1-3 and #2-3, were also used to validate the battery AM parameters, together with a test that we referred to as Append 5, which consists of the same operations of cycle test #5 run at 40 °C. The validation of the EM was carried out using discharge tests identical to those in Experiment 1 and on discharge tests for battery capacity measurements performed during the Pattern A test, Pattern B test, cycle test #1-3, cycle test #2-3, and Append 5 test. In particular, the discharge tests identical to those of Experiment 1 were conducted at 0, 10, 25, 40, and 50 °C on fresh batteries at the 0.5C rate, while the other tests were also used to validate the battery EM parameters at different levels of battery age and to cross-validate the WBM. As previously mentioned in
Section 2.1.2, the capacity measurements consist of full discharge test at 0.98 A.
Regarding the validation of the AM, the details of Pattern A and Pattern B are given in the following.
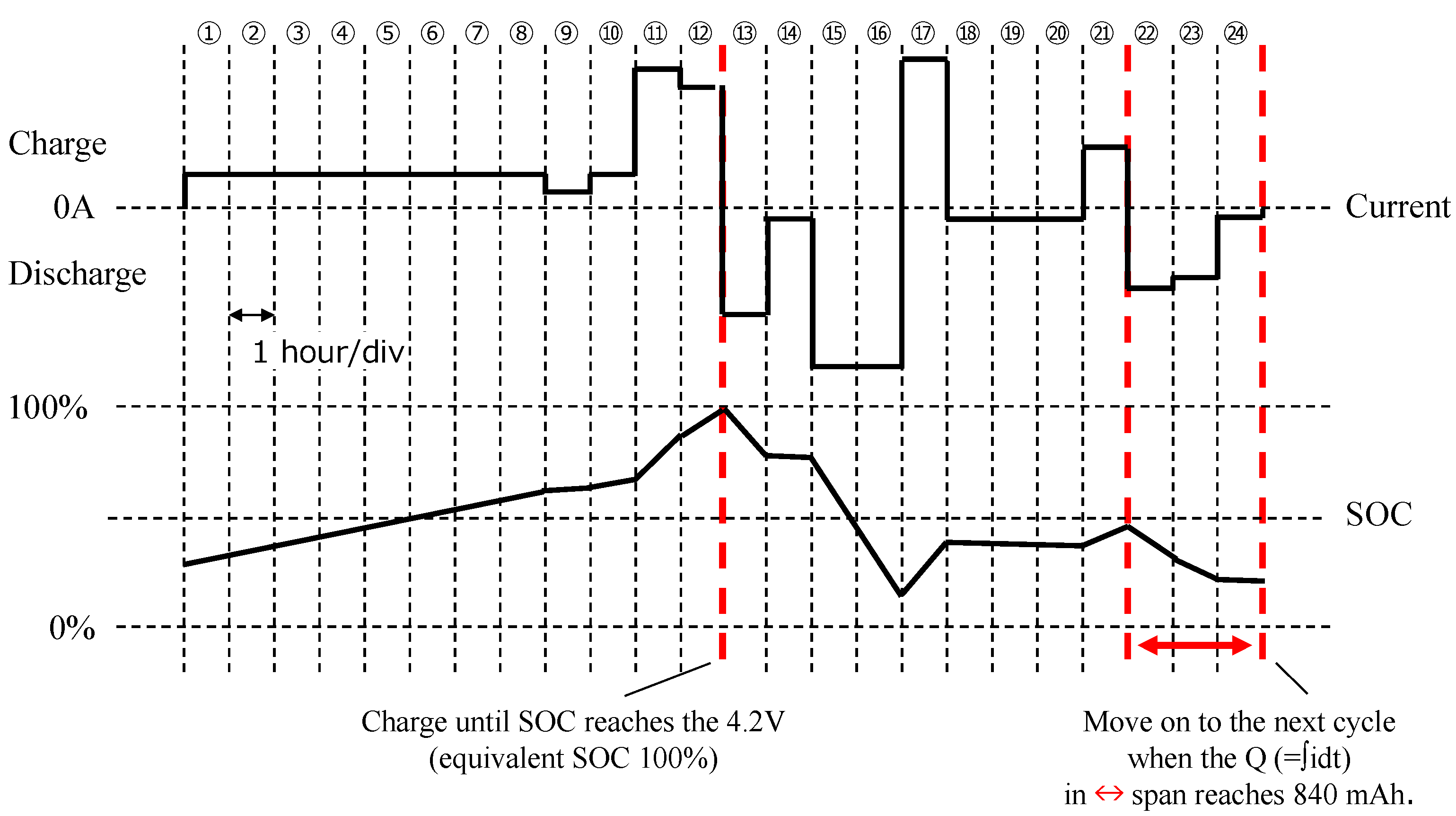
Figure 3 shows the diagram of Pattern A: the top graph is the profile current applied to the battery, with positive values meaning charging; on the bottom the estimated evolution of the battery SOC is shown. Each timestamp lasts 1 h, except for the 12th that lasts the time needed to reach the voltage
, and for the 24th timestamp that lasts the necessary time to discharge 840 mAh along the 22nd, 23rd, and 24th timestamps. Pattern B is shown in
Figure 4.
Figure 4a describes the general cycle that lasts around 19 h: on top we have the current applied to the battery cell, with positive values referring to charge operations; on the bottom the estimated SOC evolution is given. The discharges highlighted in
Figure 4a are not operated under CC conditions and consist of the repetition of the pattern detailed in
Figure 4b; in particular, the same pattern, lasting 20 min, is repeated along test Pattern B once for 2.5 h and, later, once for the necessary time to reach
. The cycle composing Pattern B ends with a full CC-CV charge to be repeated.
3. Battery Model
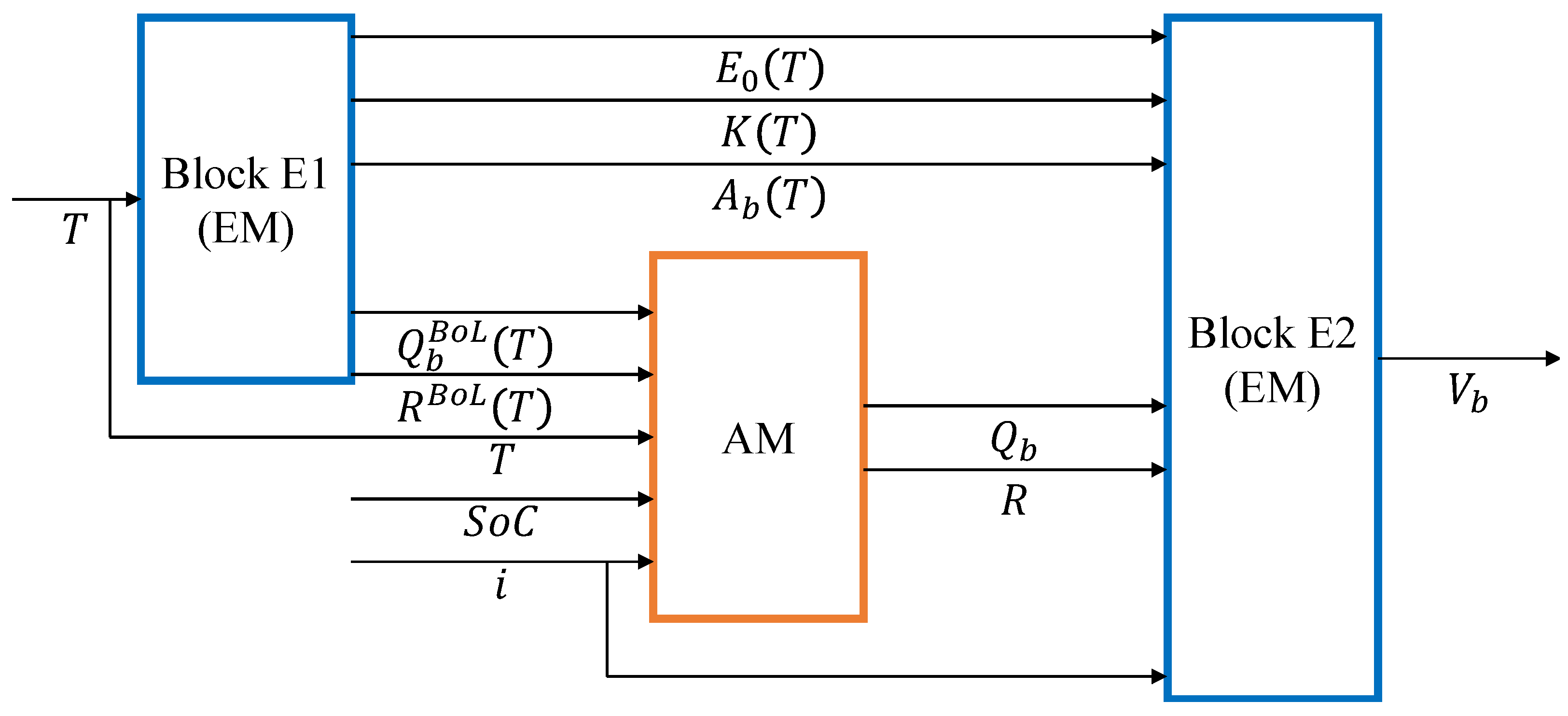
This section presents the WBM, whose basic diagram is shown in
Figure 5. It consists of two sub-models, the EM and the AM. The EM in turn consists of two main blocks: Block E1 and Block E2.
Block E2 is the electrothermal sub-model, which computes the battery voltage (V), given the battery current i (A), positive if charging, and the actual values of: battery maximum capacity (Ah); battery resistance R (); and three other model parameters, , K, and , introduced in the following.
Block E1 is the thermal sub-model, which computes the battery maximum capacity and resistance at BoL, , and , and the values of , K, and , in the function of the battery temperature T.
The AM quantifies the ongoing battery degradation and returns and R from their corresponding values at BoL, as functions of the four stress variables: charge rate, discharge rate, battery temperature, and DoD.
3.1. Battery Electrothermal Model
The proposed EM model is based on the modified Shepherd curve fitting mode [
34,
35], where an additional term (voltage polarization) is added to the battery voltage formulation to better represent the effect of SOC on the battery open circuit voltage. Also, to represent the battery dynamics, the battery current is delayed through a low-pass filter accounting for the polarization resistance. As mentioned before and shown in
Figure 5, the EM is composed of Block E1 and Block E2. In the following, we detail these two blocks, starting with Block E2.
3.1.1. Block E2
For a LiB type, the battery voltage
is expressed as follows:
where
is the battery thermodynamics voltage (V);
K is the polarization constant (V/Ah);
is the battery maximum capacity (Ah);
is the filtered battery current (A);
denotes the time integral of the extracted current (Ah), i.e., meaning that is the actual battery charge (Ah);
is the exponential zone amplitude (V);
B is the exponential zone time constant inverse 1/(Ah);
C is the polarization voltage slope V/(Ah);
R is the battery internal resistance ();
is the polarization resistance ().
The polarization resistance changes if the battery is discharging or charging according to the next relation:
where
u is a binary variable, equal to one when
, i.e., charging, and
K is intended as a polarization resistance constant with the same value as the one in the second term in (
2) but measured in
.
Model (
2) in discharging mode is valid for
. At
, there is a vertical negative asymptote. Moreover, given a (negative) discharge current
, we have that, at fully charged condition (
):
where
is the fully charged voltage.
The battery maximum capacity
is the maximum theoretical discharge capacity. However, batteries are operated in a range of voltage that goes from
to the cut-off voltage
(V), which are parameters usually provided on the battery datasheet. Let us indicate with
Q (Ah) the battery nominal capacity, which corresponds to the discharged capacity from
to
at the nominal discharge current
(A).
Figure 6 helps to make clear the difference between
and
Q.
The battery cut-off voltage
and
Q are related by the following equation:
From (
5), it is possible to find a direct relation between
and
Q:
Note that the capacity that can be measured with an experimental full discharge cycle is actually
Q; then, the battery capacity
can be computed using (
6). Hereafter, we will refer to
Q simply as the battery capacity. As demonstrated in
Appendix A, relation (
5) can also be solved with respect to
Q and the relation
obtained.
The filtered battery current is computed as follows:
where
is the inverse Laplace transform,
is the Laplace transform of the battery current, and
(s) is the battery response time.
3.1.2. Block E1
In Block E1, to account for the impact of the battery temperature on the EM, the thermodynamics voltage
, the polarization constant
K, the internal resistance
R, and the exponential zone amplitude
are calculated according to Nernst and Arrhenius laws as follows [
36]:
where
T (K) is the battery temperature,
(K) is the reference battery temperature,
is the open circuit temperature coefficient (V/K),
and
are the Arrhenius constants for the polarization resistance and internal resistance, respectively, and
is a parameter that models the linear dependence of the exponential zone amplitude from the temperature. In the literature, it is common to find battery models such as the one in (
2); however, none of them considers a temperature dependence of the parameter
. The choice of modeling the exponential zone amplitude
as a temperature-linear function was made by carefully looking at the experimental results. This alternative turned out to outperform the option in which
is constant. In Block E2 the impact of the battery temperature on the battery maximum capacity at BoL
is also accounted for as follows:
where
is the battery capacity temperature coefficient (Ah/K).
3.2. Battery Aging Model
The battery AM modifies the battery capacity and resistance R based on ongoing aging and consists of four main blocks:
Block A1, which determines the DoD, and average C-rates and battery temperature during each cycle;
Block A2, which evaluates the battery stress arising during any cycle in the function of DoD, C-rates, and temperature;
Block A3, which computes the aging index , based on the concept of equivalent number of cycles;
Block A4, which adjusts the battery capacity and resistance according to the actual value of the aging index.
The interconnections among these four blocks are highlighted in
Figure 7, which shows the detailed WBM scheme.
3.2.1. Block A1
Block A1 works on a discrete time base, assuming that
and
are the measures of SOC (p.u.) and battery current at the discrete time step
,
. Using these measurements, Block A1 updates the DoD, the average C-rates
and
during discharge and charge, respectively, and the average battery temperature
, when the battery transits from charge to discharge or vice versa. These updates are therefore indexed by the transition number
n. A new transition is detected by monitoring the change in sign of the variation of the SOC defined as
Therefore, the update of the DoD and the average C-rates and battery temperature is carried out by executing Algorithm 1.
| Algorithm 1 DoD, C-rates and battery temperature update. |
- 1.
initialize the transition number, , the DoD, , where is the battery initial SOC, the C-rates, , , where is the battery initial current, and the previous transition time step ; - 2.
at every time step k, - 3.
evaluate as in ( 13); - 4.
if : - 5.
1; - 6.
calculate DoD as ; - 7.
calculate and using ( 14) and ( 15); - 8.
calculate using ( 16); - 9.
; - 10.
end if
|
3.2.2. Block A2
In Block A2, the battery stress factor at transition n is computed. This factor must measure the degradation of the battery due to its use between transition and transition n. Such a battery use is characterized by the DoD, the average C-rates, and the average temperature, computed by Block A1, which influence the battery stress as modeled in the following.
The stress factor
due to temperature is computed using the Arrhenius equation:
where
is the model reference temperature and
is the Arrhenius rate constant. By analogy with Miner’s rule, using Wöhler approximation, the stress factors associated with the discharge and charge currents are computed as follows:
where
and
are the peak stress amplitudes for the discharge and charge current, respectively, and both are positive;
and
are the stress exponents for the discharge and charge current, respectively.
Similarly, the stress factor
associated with a given DoD can be computed as follows:
where
is the stress exponent for the DoD.
The final combined stress factor is given by
Based on the experimental results, the accuracy of the overall AM drops if the same stress factor is used for both capacity and resistance, as usually carried out in literature papers such as [
20]. Therefore, in this paper, we define two different stress factors
and
for capacity and resistance, respectively. This means that the relations in (
17)–(
21) must be considered as defined twice, one for capacity and one for resistance. In particular:
is obtained by applying (
21) starting from (
17)–(
20) with
,
,
, and
;
is obtained by applying (
21) starting from (
17)–(
20) with
,
,
, and
.
3.2.3. Block A3
Block A3 computes the aging index . Such an index represents the contribution of the battery use between transition and transition n to the total aging of the battery.
Let us define first
as the number of cycles from BoL to EoL in reference use conditions, i.e., when the battery use is with DoD = 1 and with reference C-rates and battery temperature. Under reference conditions, the aging index after one cycle (two transitions) is given by
Knowing that, in real load profiles, charging and discharging cycles do not always cover the entire battery capacity (DoD < 1), the equivalent number of full cycles
is computed at each transition
n as follows:
Then, given
, the aging index
is updated as follows:
Since we have two different stress factors for capacity and resistance, we also have two different aging indices
and
computed by applying (
24) with
and
, respectively.
3.2.4. Block A4
Finally, in Block A4, the battery capacity and internal resistance are updated based on ongoing degradation through the computation of the aging index
. In particular, the maximum capacity
Q and the internal resistance
R are expressed as
where
and are the battery capacity (Ah) at BoL and EoL, respectively;
and are the battery resistance () at BoL and EoL, respectively;
and are the aging exponents for the battery maximum capacity and internal resistance, respectively.
3.3. Novelty Aspects
We remark that the battery models introduced in this section build upon existing electrothermal and aging Li-ion cell models. Specifically, the EM is formulated based on the models in [
11,
24,
25], while the AM originates from the framework presented in [
20]. However, in this paper, we formalize the integration of the EM and the AM, depicted in
Figure 7, by including the relation between the maximum theoretical discharge capacity
and the battery nominal capacity
Q. Indeed, in [
20], this relation is not explicitly taken into account. Moreover, differently from [
20] and from other literature approaches, in this paper we differentiate the computation of the aging index for capacity and resistance.
6. Conclusions
This paper presents a comprehensive Li-ion battery semi-empirical model able to represent the electrothermal dynamics taking into account aging degradation due to operations. Moreover, a suitable procedure to identify both electrothermal and aging parameters is introduced. This method does not require expensive thermal test chambers and calorimeters, since it requires simple cycling and discharge tests. In more detail, the presented model is an integration of two sub-models, the EM, which models the electrical and thermal behavior of the battery, and the AM, which models the aging of the battery through operations. The resulting WBM allows evaluating the battery state of health and resistance temporal evolution as functions of battery temperature, state of charge, and current. Therefore, it can be easily interfaced with a battery management system for the online evaluation of battery conditions.
It is worth remarking that the WBM builds upon existing electrothermal and aging Li-ion cell models. Specifically, the EM is formulated based on the models in [
11,
24,
25], while the AM originates from the framework presented in [
20]. However, as already clarified in
Section 3.3 and
Section 4.3, in this paper we introduce two main improvements: the formal inclusion of the relation between the maximum theoretical discharge capacity
, used in the EM, and the battery nominal capacity
Q, used in the AM; and the generalization of the aging parameter identification procedure to the case of multiple experimental measurements for each aging condition.
The proposed method is validated through experimental tests carried out on real Li-ion battery cells, subject to real load profiles. The identified AM is validated by measuring its capability to estimate the battery state of heath in terms of capacity decrease and internal resistance increase. In particular, the results show a MAPE lower than 1% for battery capacity and a maximum absolute error of 0.14 m for the internal resistance. The identified EM is validated by measuring its capability in reproducing the battery voltage profile both in a fresh battery and at different levels of aging. The results show a MAPE for voltage reproduction lower than 1%.
Notice that the analysis of the performance of the EM at different levels of aging represents a validation of the integration EM-AM in the WBM. This actually addresses a gap in the existing literature, where EM and AM are usually identified and validated separately.
Future works will consider the integration of SOH estimation with a procedure to estimate the battery SOC. Further developments may examine the performance of an adaptive model that updates the parameters during the actual battery operation or consider the design of parameter identification procedures based on a digital-twin approach.