Monte Carlo Simulation of the CO2 Flooding Efficiency at a Core Scale for Different Oil Compositions
Abstract
1. Introduction
2. Problem Statement
2.1. Overview
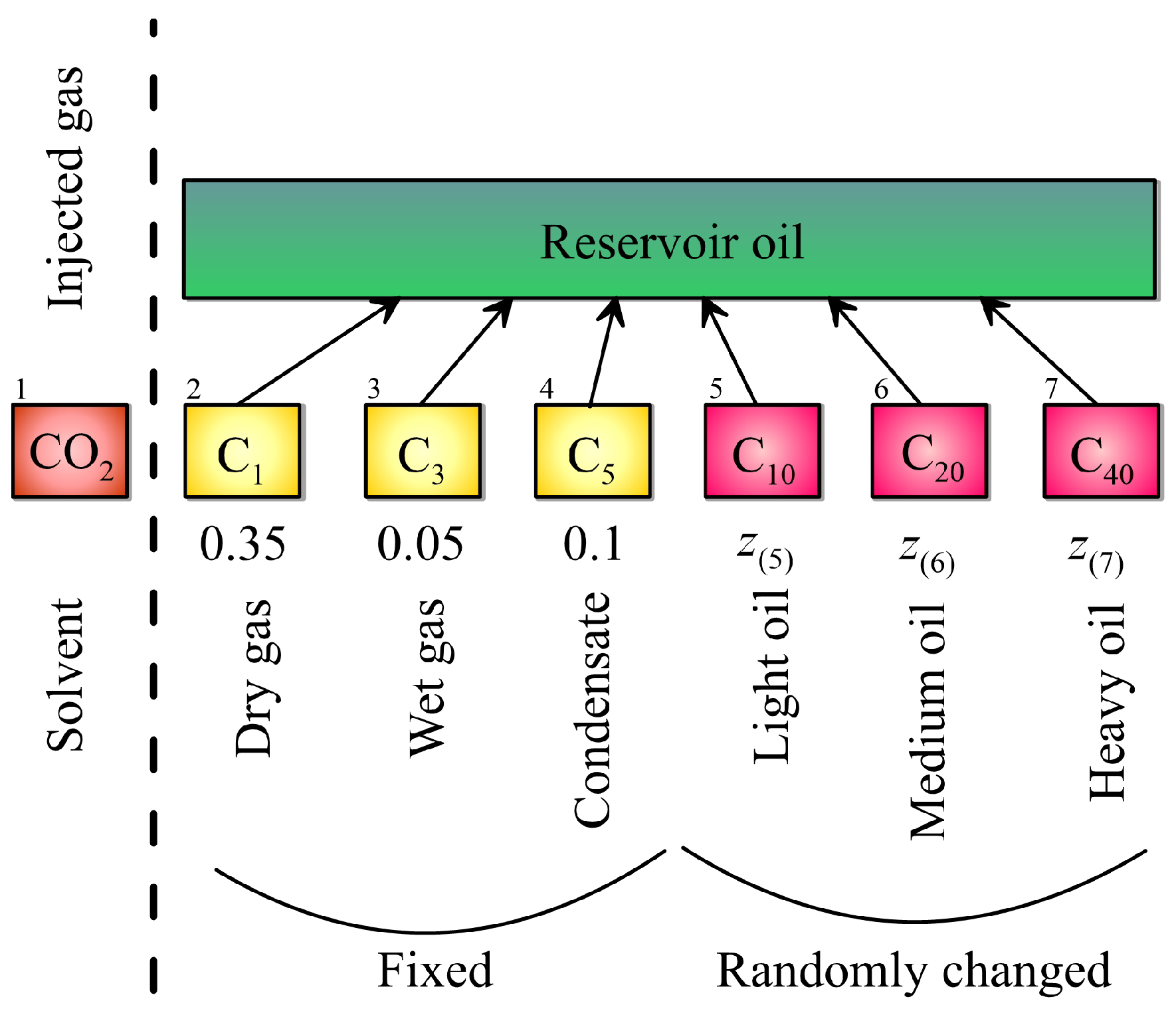
2.2. Oil Composition
2.3. Injection Strategies
3. The Governing Equations
3.1. Balance Equations
3.2. Equations of State
3.3. Economic Model
3.4. Dimensionless Variables
4. Methods
5. Results
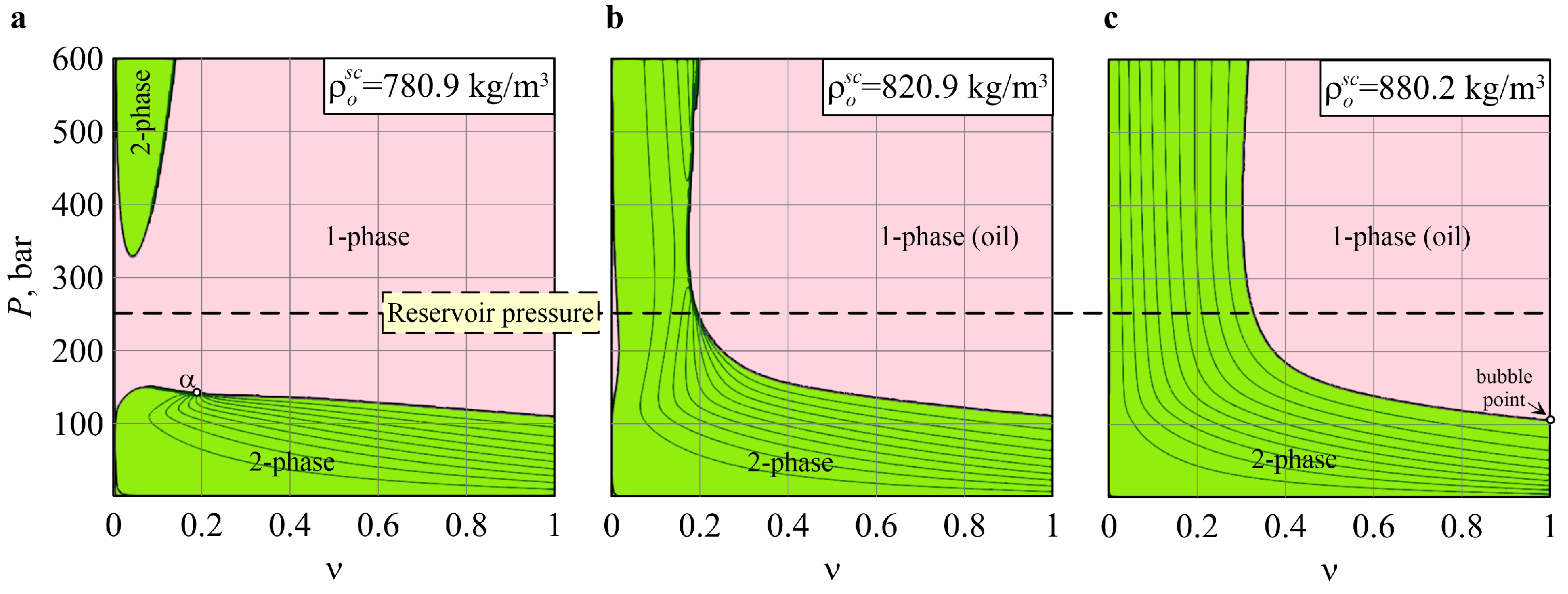
5.1. Simulated Oil Properties
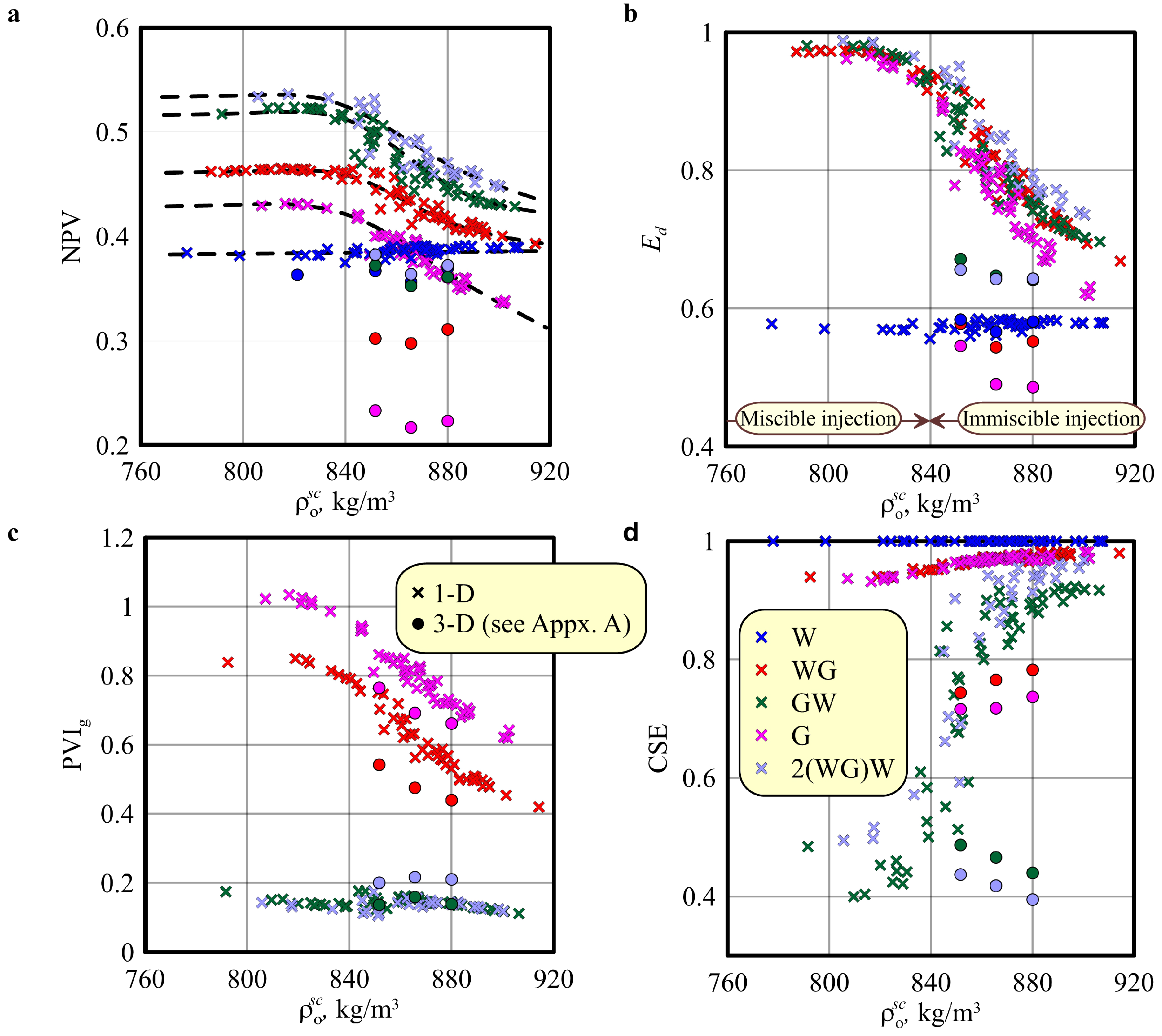
5.2. Base Study at
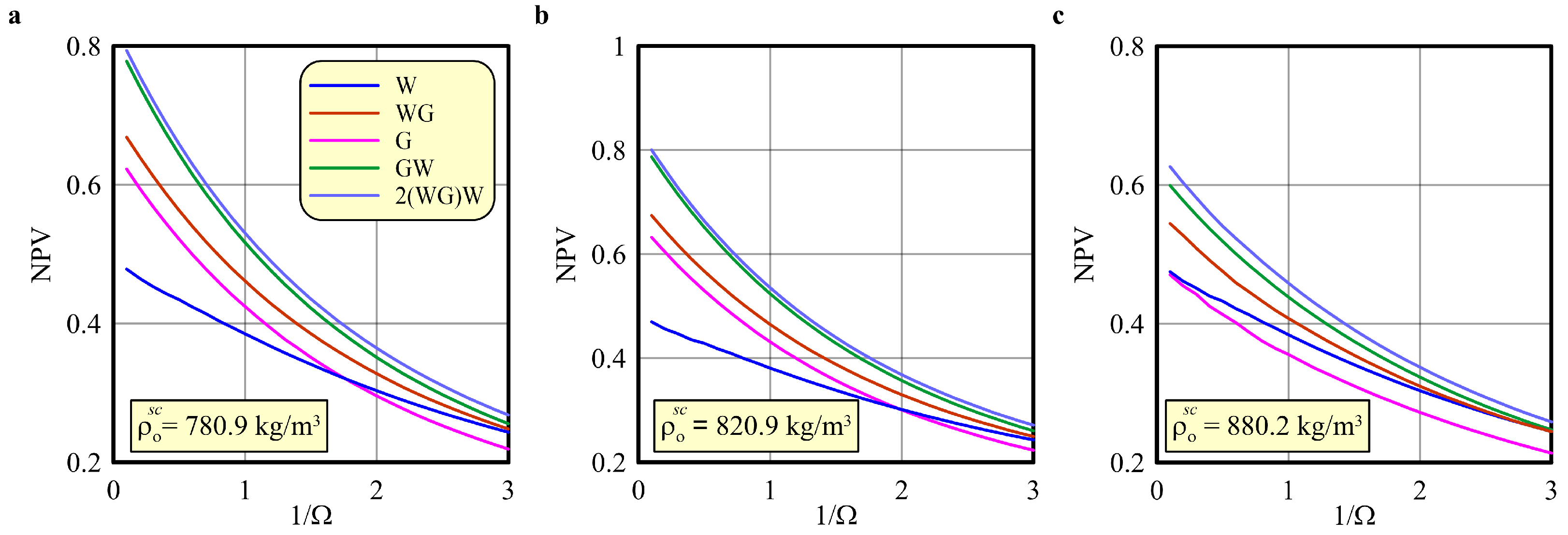
5.3. Influence of the Injection Rate
5.4. Influence of the Light Hydrocarbon Components
6. Discussion and Conclusions
- We validated that the conclusions of our previous study [34] are still valid for reservoirs saturated with various light and heavy oils. The concept of the dimensionless injection rate is working for oils of different compositions and in the cases of both miscible and immiscible injections.
- The parameters of optimized WAG injection strategies and their efficiency depend mainly on the injection rate and the oil density at surface conditions . Neither bubble point pressure nor MMP can be used in the characterization of the optimal WAG parameters.
- The CO2–EOR method applied to a reservoir characterized by a less dense oil results in a higher microscopic displacement efficiency and NPV, but it also causes the CO2 storage potential to be lower. Thus, implementing the CO2–EOR method at a reservoir that has more light oil can generally increase the oil recovery efficiency but at the cost of larger volumes of CO2 being extracted back to the surface with the produced oil.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CSE | Carbon storage efficiency |
| EOR | Enhanced oil recovery |
| EoS | Equation of state |
| MMP | Minimum miscibility pressure |
| NPV | Net present value |
| PVI | Pore volumes injected |
| WAG | Water-alternating-gas |
Appendix A. 3-D Scenario
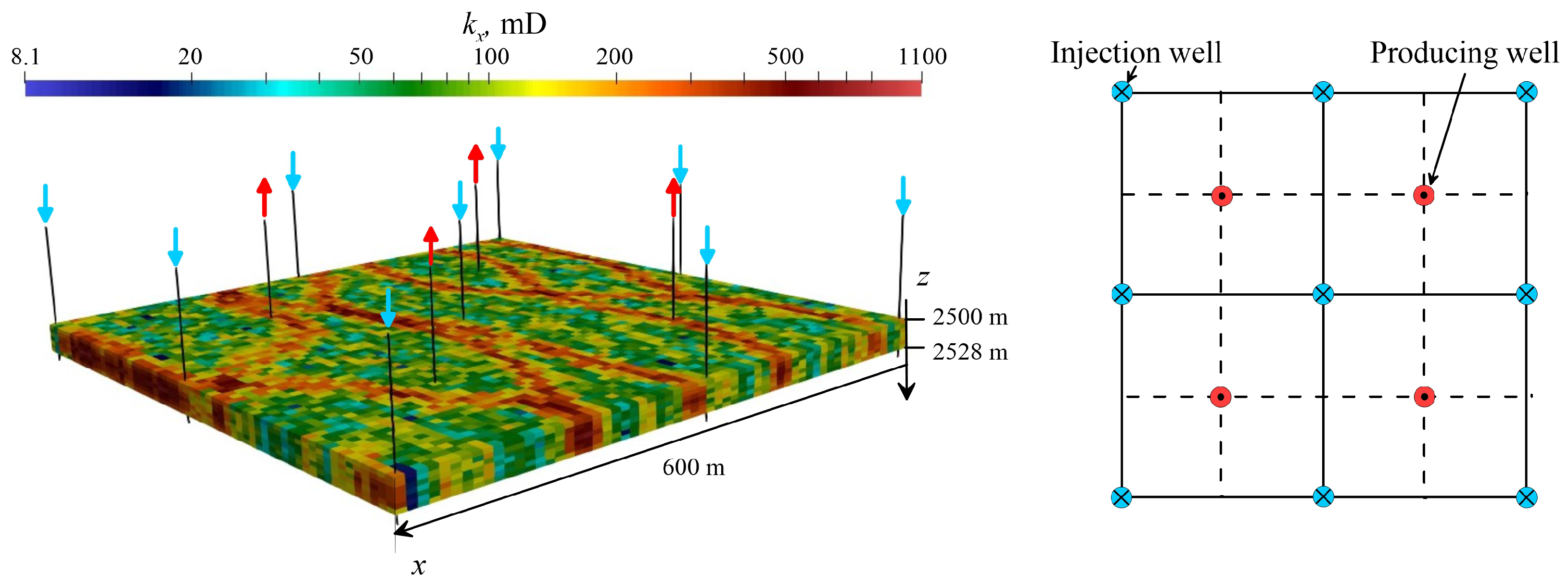
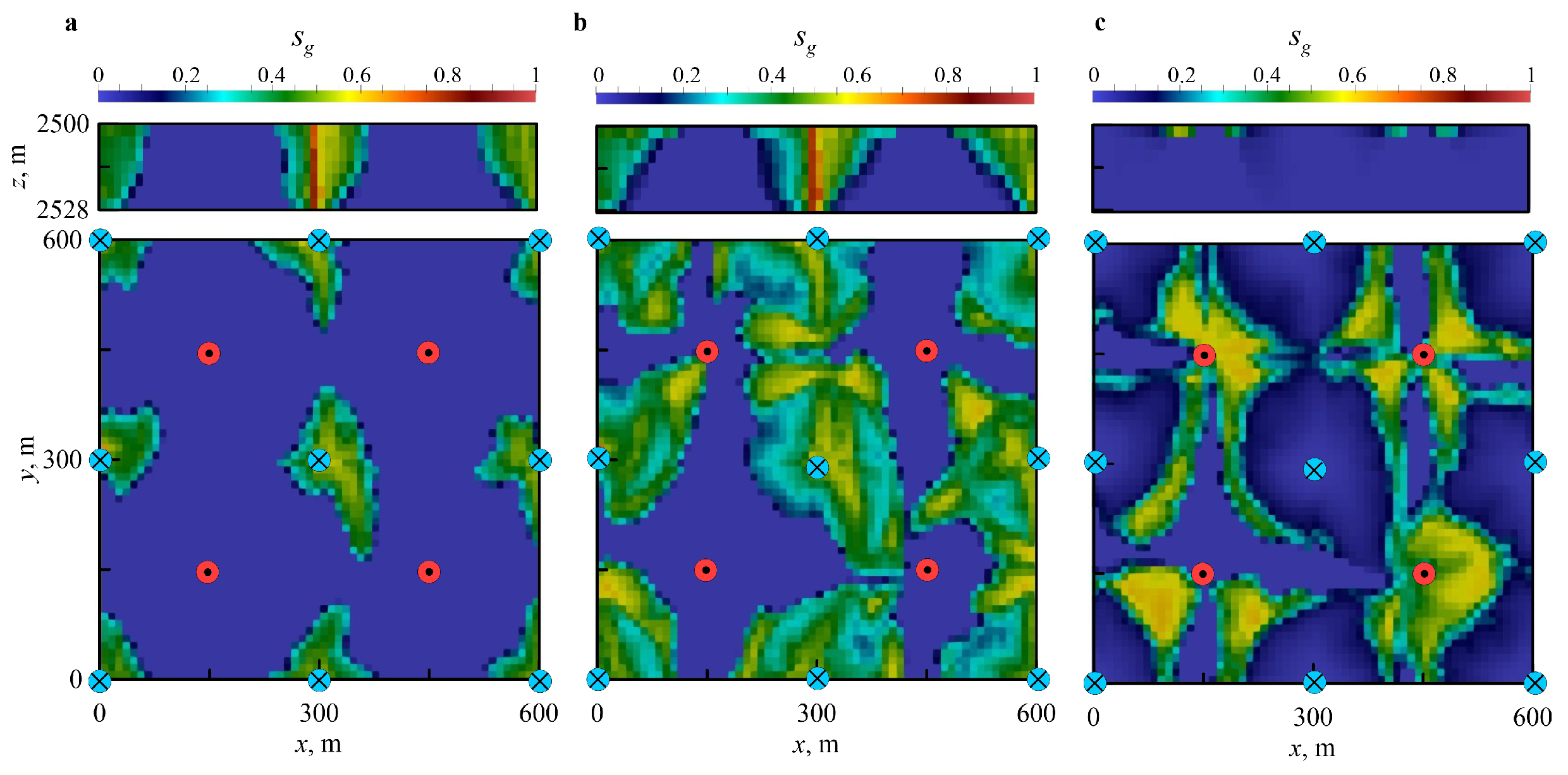
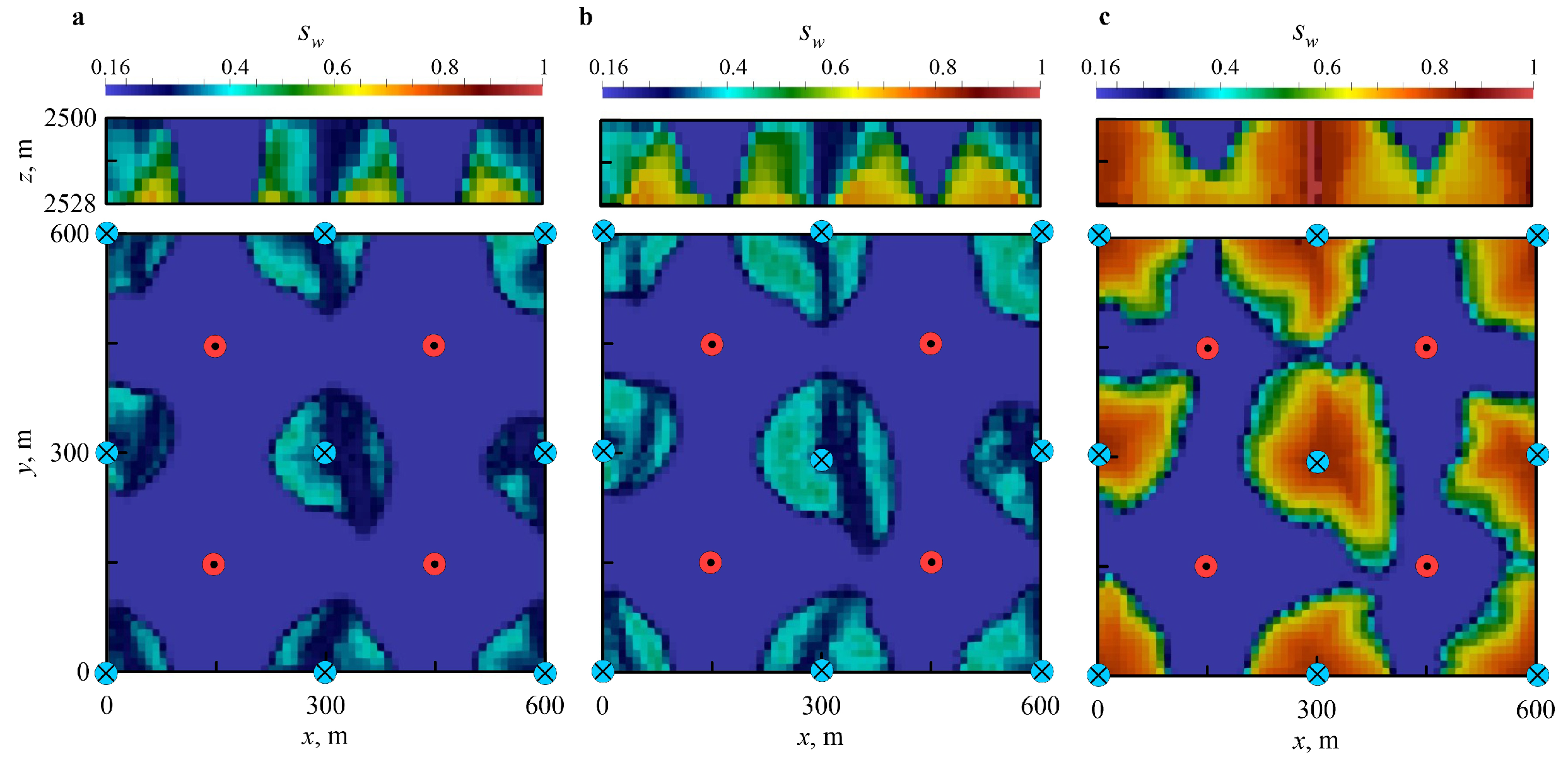
References
- Jessen, K.; Kovscek, A.R.; Orr, F.M. Increasing CO2 storage in oil recovery. Energy Convers. Manag. 2005, 46, 293–311. [Google Scholar] [CrossRef]
- Kovscek, A.; Cakici, M. Geologic storage of carbon dioxide and enhanced oil recovery. II. Cooptimization of storage and recovery. Energy Convers. Manag. 2005, 46, 1941–1956. [Google Scholar] [CrossRef]
- Holt, T.; Lindeberg, E.; Wessel-Berg, D. EOR and CO2 disposal—Economic and capacity potential in the North Sea. Energy Procedia 2009, 1, 4159–4166. [Google Scholar] [CrossRef]
- Mon, M.T.; Tansuchat, R.; Yamaka, W. CCUS Technology and Carbon Emissions: Evidence from the United States. Energies 2024, 17, 1748. [Google Scholar] [CrossRef]
- Cao, J.; Gao, M.; Liu, Z.; Yu, H.; Liu, W.; Yin, H. Research and Application of Carbon Capture, Utilization, and Storage–Enhanced Oil Recovery Reservoir Screening Criteria and Method for Continental Reservoirs in China. Energies 2024, 17, 1143. [Google Scholar] [CrossRef]
- Lake, L.W. Enhanced Oil Recovery; Prentice Hall: Hoboken, NJ, USA, 1989. [Google Scholar]
- Christensen, J.; Stenby, E.; Skauge, A. Review of WAG Field Experience. SPE Reserv. Eval. Eng. 2001, 4, 97–106. [Google Scholar] [CrossRef]
- Thomas, S. Enhanced Oil Recovery—An Overview. Oil Gas Sci. Technol. -Rev. L’IFP 2008, 63, 9–19. [Google Scholar] [CrossRef]
- Alvarado, V.; Manrique, E. Enhanced Oil Recovery: An Update Review. Energies 2010, 3, 1529–1575. [Google Scholar] [CrossRef]
- Yao, J.; Yuan, W.; Peng, X.; Chen, Z.; Gu, Y. A Novel Multi-Phase Strategy for Optimizing CO2 Utilization and Storage in an Oil Reservoir. Energies 2023, 16, 5289. [Google Scholar] [CrossRef]
- Ettehadtavakkol, A.; Lake, L.W.; Bryant, S.L. CO2-EOR and storage design optimization. Int. J. Greenh. Gas Control 2014, 25, 79–92. [Google Scholar] [CrossRef]
- Rodrigues, H.; Mackay, E.; Arnold, D. Impact of WAG Design on Calcite Scaling Risk in Coupled CO2-EOR and Storage Projects in Carbonate Reservoirs. In Proceedings of the SPE Reservoir Simulation Conference, Galveston, TX, USA, 10–11 April 2019. [Google Scholar] [CrossRef]
- Orr, F.M.; Dindoruk, B.; Johns, R.T. Theory of Multicomponent Gas/Oil Displacements. Ind. Eng. Chem. Res. 1995, 34, 2661–2669. [Google Scholar] [CrossRef]
- Orr, F.M. Theory of Gas Injection Processes; Tie-Line Publications: Holte, Denmark, 2007. [Google Scholar]
- Pritchard, D.; Nieman, R. Improving Oil Recovery Through WAG Cycle Optimization in a Gravity-Overide-Dominated Miscible Flood. In Proceedings of the SPE/DOE Enhanced Oil Recovery Symposium. Society of Petroleum Engineers, Tulsa, OK, USA, 22–24 April 1992. [Google Scholar] [CrossRef]
- Johns, R.; Leonardo, B.; Harshad, P. WAG Optimization for Gas Floods above the MME. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 5–8 October 2003; Society of Petroleum Engineers: Kuala Lumpur, Malaysia, 2003. [Google Scholar] [CrossRef]
- Johns, R.T.; Dindoruk, B. Gas Flooding. In Enhanced Oil Recovery Field Case Studies; Elsevier: Amsterdam, The Netherlands, 2013; pp. 1–22. [Google Scholar] [CrossRef]
- Li, D.; Saraji, S.; Jiao, Z.; Zhang, Y. An experimental study of CO2 injection strategies for enhanced oil recovery and geological sequestration in a fractured tight sandstone reservoir. Geoenergy Sci. Eng. 2023, 230, 212166. [Google Scholar] [CrossRef]
- Huang, X.; Li, X.; Zhang, Y.; Li, T.; Zhang, R. Microscopic production characteristics of crude oil in nano-pores of shale oil reservoirs during CO2 huff and puff. Pet. Explor. Dev. 2022, 49, 636–643. [Google Scholar] [CrossRef]
- Tang, W.; Peng, Z.; Sheng, J.J. Evaluation of CO2 utilization and storage potential in the Jimsar shale play from an optimization study. Geoenergy Sci. Eng. 2023, 224, 211607. [Google Scholar] [CrossRef]
- Massarweh, O.; Abushaikha, A.S. A review of recent developments in CO2 mobility control in enhanced oil recovery. Petroleum 2022, 8, 291–317. [Google Scholar] [CrossRef]
- Hassanzadeh, A.; Katiyar, A.; Kalaei, H.; Pecore, D.; Schofield, E.; Nguyen, Q.P. A novel foam process with CO2 dissolved surfactant for improved sweep efficiency in EVGSAU field. Geoenergy Sci. Eng. 2023, 231, 212310. [Google Scholar] [CrossRef]
- LaForce, T.; Jessen, K. Analytical and numerical investigation of multicomponent multiphase WAG displacements. Comput. Geosci. 2010, 14, 745–754. [Google Scholar] [CrossRef]
- Ghaderi, S.M.; Clarkson, C.R.; Chen, S. Optimization of WAG Process for Coupled CO2 EOR-Storage in Tight Oil Formations: An Experimental Design Approach. In Proceedings of the SPE Canadian Unconventional Resources Conference, Calgary, AB, Canada, 30 October–1 November 2012. [Google Scholar] [CrossRef]
- Mirzaei-Paiaman, A.; Santos, S.M.; Schiozer, D.J. Optimization of design variables and control rules in field development under uncertainty: A case of intelligent wells and CO2 water alternating gas injection. Geoenergy Sci. Eng. 2023, 227, 211854. [Google Scholar] [CrossRef]
- Ghedan, S.G. Global Laboratory Experience of CO2-EOR Flooding. In Proceedings of the SPE/EAGE Reservoir Characterization and Simulation Conference, Abu Dhabi, United Arab Emirates, 19–21 October 2009; Society of Petroleum Engineers: Kuala Lumpur, Malaysia, 2009. [Google Scholar] [CrossRef]
- Verma, M.K. Fundamentals of Carbon Dioxide-Enhanced Oil Recovery (CO2-EOR): A Supporting Document of the Assessment Methodology for Hydrocarbon Recovery Using CO2-EOR Associated with Carbon Sequestration; Technical Report; U.S. Geological Survey: Reston, VA, USA, 2015. [Google Scholar] [CrossRef]
- Bermudez, L.; Johns, R.T.; Parakh, H. Parametric Investigation of WAG Floods Above the MME. SPE J. 2007, 12, 224–234. [Google Scholar] [CrossRef]
- Namani, M.; Kleppe, J. Investigation of the Effect Of Some Parameters In Miscible WAG Process Using Black-Oil And Compositional Simulators. In Proceedings of the SPE Enhanced Oil Recovery Conference, Kuala Lumpur, Malaysia, 19–20 July 2011; Society of Petroleum Engineers: Kuala Lumpur, Malaysia, 2011. [Google Scholar] [CrossRef]
- Asante, J.; Ampomah, W.; Tu, J.; Cather, M. Data-driven modeling for forecasting oil recovery: A timeseries neural network approach for tertiary CO2 WAG EOR. Geoenergy Sci. Eng. 2024, 233, 212555. [Google Scholar] [CrossRef]
- Al-Khdheeawi, E.A. Optimizing CO2-Water Injection Ratio in Heterogeneous Reservoirs: Implications for CO2 Geo-Storage. Energies 2024, 17, 678. [Google Scholar] [CrossRef]
- Fathinasab, M.; Shahbazi, K. A new correlation for estimation of minimum miscibility pressure (MMP) during hydrocarbon gas injection. J. Pet. Explor. Prod. Technol. 2020, 10, 2349–2356. [Google Scholar] [CrossRef]
- Chen, B.; Pawar, R. Capacity assessment of CO2 storage and enhanced oil recovery in residual oil zones. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 24–26 September 2018. [Google Scholar] [CrossRef]
- Afanasyev, A.; Andreeva, A.; Chernova, A. Influence of oil field production life on optimal CO2 flooding strategies: Insight from the microscopic displacement efficiency. J. Pet. Sci. Eng. 2021, 205, 108803. [Google Scholar] [CrossRef]
- Kulkarni, M.; Rao, D. Experimental Investigation of Miscible Secondary Gas Injection. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 9–12 October 2005; Society of Petroleum Engineers: Kuala Lumpur, Malaysia, 2005. [Google Scholar] [CrossRef]
- Fatemi, S.M.; Sohrabi, M.; Jamiolahmady, M.; Ireland, S.; Robertson, G. Experimental Investigation of Near-Miscible Water-Alternating-Gas WAG Injection Performance in Water-wet and Mixed-wet Systems. In Proceedings of the SPE Offshore Europe Oil and Gas Conference and Exhibition, Aberdeen, UK, 6–8 September 2011. [Google Scholar] [CrossRef]
- Alkhazmi, B.; Sohrabi, M.; Farzaneh, S.A. An Experimental Investigation of the Effect of Gas and Water Slug Size and Injection Order on the Performance of Immiscible WAG Injection in a Mixed-Wet System. In Proceedings of the SPE Kuwait Oil & Gas Show and Conference, Kuwait City, Kuwait, 15–18 October 2017. [Google Scholar] [CrossRef]
- Sun, L.; Hao, X.; Dou, H.; Daniel Adenutsi, C.; Li, Z.; Zhang, Y. Co-optimization of oil recovery and CO2 storage for cyclic CO2 flooding in ultralow permeability reservoirs. Oil Gas Sci. Technol. Rev. D’IFP Energies Nouv. 2018, 73, 42. [Google Scholar] [CrossRef]
- Li, G.; Yao, J. Snap-Off during Imbibition in Porous Media: Mechanisms, Influencing Factors, and Impacts. Eng 2023, 4, 2896–2925. [Google Scholar] [CrossRef]
- Wang, T.; Wang, L.; Meng, X.; Chen, Y.; Song, W.; Yuan, C. Key parameters and dominant EOR mechanism of CO2 miscible flooding applied in low-permeability oil reservoirs. Geoenergy Sci. Eng. 2023, 225, 211724. [Google Scholar] [CrossRef]
- Kulkarni, M.; Rao, D. Experimental Investigation of Various Methods of Tertiary Gas Injection. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 26–29 September 2004; Society of Petroleum Engineers: Kuala Lumpur, Malaysia, 2004. [Google Scholar] [CrossRef]
- Poling, B.E.; Prausnitz, J.M.; O’Connell, J.P. Properties of Gases and Liquids, 5th ed.; McGraw-Hill Education: New York, NY, USA, 2001. [Google Scholar]
- Peng, D.Y.; Robinson, D.B. A New Two-Constant Equation of State. Ind. Eng. Chem. Fundam. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Péneloux, A.; Rauzy, E.; Fréze, R. A consistent correction for Redlich-Kwong-Soave volumes. Fluid Phase Equilibria 1982, 8, 7–23. [Google Scholar] [CrossRef]
- Coats, K.H. An Equation of State Compositional Model. Soc. Pet. Eng. J. 1980, 20, 363–376. [Google Scholar] [CrossRef]
- Afanasyev, A.; Andreeva, A.; Chernova, A. Numerical optimisation of CO2 flooding using a hierarchy of reservoir models. Adv. Geosci. 2021, 56, 19–31. [Google Scholar] [CrossRef]
- Galindo, M.E.; Lacerda, I.V.; Galindez-Ramirez, G.; Lyra, P.R.; Carvalho, D.K. A very high order Flux Reconstruction (FR) method for the numerical simulation of 1-D compositional fluid flow model in petroleum reservoirs. Geoenergy Sci. Eng. 2023, 229, 212056. [Google Scholar] [CrossRef]
- Brock, W.; Bryan, L. Summary Results of CO2 EOR Field Tests, 1972–1987. In Proceedings of the Low Permeability Reservoirs Symposium, Denver, CO, USA, 6–8 March 1989; Society of Petroleum Engineers: Kuala Lumpur, Malaysia, 1989. [Google Scholar] [CrossRef]
- Kenyon, D.; Behie, A. Third SPE Comparative Solution Project: Gas Cycling of Retrograde Condensate Reservoirs. J. Pet. Technol. 1987, 39, 981–997. [Google Scholar] [CrossRef]
- Lohrenz, J.; Bray, B.G.; Clark, C.R. Calculating Viscosities of Reservoir Fluids From Their Compositions. J. Pet. Technol. 1964, 16, 1171–1176. [Google Scholar] [CrossRef]
- Tzimas, E.; Georgakaki, A.; Garcia Cortes, C.; Peteves, S.D. Enhanced Oil Recovery Using Carbon Dioxide in the European Energy System; Technical Report; European Commission: Brussels, Belgium, 2005. [Google Scholar]
- Salem, S.; Moawad, T. Economic Study of Miscible CO2 Flooding in a Mature Waterflooded Oil Reservoir. In Proceedings of the SPE Saudi Arabia Section Technical Symposium and Exhibition, Al-Khobar, Saudi Arabia, 19–22 May 2013. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Afanasyev, A.; Vedeneeva, E. Compositional modeling of multicomponent gas injection into saline aquifers with the MUFITS simulator. J. Nat. Gas Sci. Eng. 2021, 94, 103988. [Google Scholar] [CrossRef]
- Afanasyev, A. Hydrodynamic Modelling of Petroleum Reservoirs using Simulator MUFITS. Energy Procedia 2015, 76, 427–435. [Google Scholar] [CrossRef]
- Liu, X.; Qin, J.; Han, H.; Li, S.; Ji, Z. Multiphase boundary of C16+ heavy n-alkanes and CO2 systems. Pet. Explor. Dev. 2017, 44, 105–110. [Google Scholar] [CrossRef]
- Jansen, J.D.; Fonseca, R.M.; Kahrobaei, S.; Siraj, M.M.; Van Essen, G.M.; Van den Hof, P.M.J. The egg model—A geological ensemble for reservoir simulation. Geosci. Data J. 2014, 1, 192–195. [Google Scholar] [CrossRef]




| Abbreviation | Description |
|---|---|
| W | Waterflooding |
| G | Continuous gas injection |
| WG | Gas injection after waterflooding |
| GW | CO2 slug followed by continuous water injection |
| 2(WG)W | Two identical WAG cycles followed by continuous water injection |
| 20.27 USD/bbl | 150 USD/ton | |
| 2 USD/bbl | 12.5 USD/ton | |
| 1.5 USD/bbl | 9.5 USD/ton | |
| 2.55 USD/Mscf | 45 USD/ton | |
| 1.33 USD/Mscf | 23.5 USD/ton |
| Sample | , bar | MMP, bar | ||||
|---|---|---|---|---|---|---|
| l | 0.456 | 0.032 | 0.012 | 780.9 | 108.9 | 148.8 |
| m | 0.279 | 0.194 | 0.027 | 820.9 | 110.7 | 337.4 |
| h | 0.031 | 0.286 | 0.183 | 880.2 | 105.2 | 268 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andreeva, A.; Afanasyev, A. Monte Carlo Simulation of the CO2 Flooding Efficiency at a Core Scale for Different Oil Compositions. Energies 2024, 17, 2259. https://doi.org/10.3390/en17102259
Andreeva A, Afanasyev A. Monte Carlo Simulation of the CO2 Flooding Efficiency at a Core Scale for Different Oil Compositions. Energies. 2024; 17(10):2259. https://doi.org/10.3390/en17102259
Chicago/Turabian StyleAndreeva, Anna, and Andrey Afanasyev. 2024. "Monte Carlo Simulation of the CO2 Flooding Efficiency at a Core Scale for Different Oil Compositions" Energies 17, no. 10: 2259. https://doi.org/10.3390/en17102259
APA StyleAndreeva, A., & Afanasyev, A. (2024). Monte Carlo Simulation of the CO2 Flooding Efficiency at a Core Scale for Different Oil Compositions. Energies, 17(10), 2259. https://doi.org/10.3390/en17102259







