Optimized Dynamic Vehicle-to-Vehicle Charging for Increased Profit
Abstract
1. Introduction
2. Literature Review
3. Routing Problem Modeling
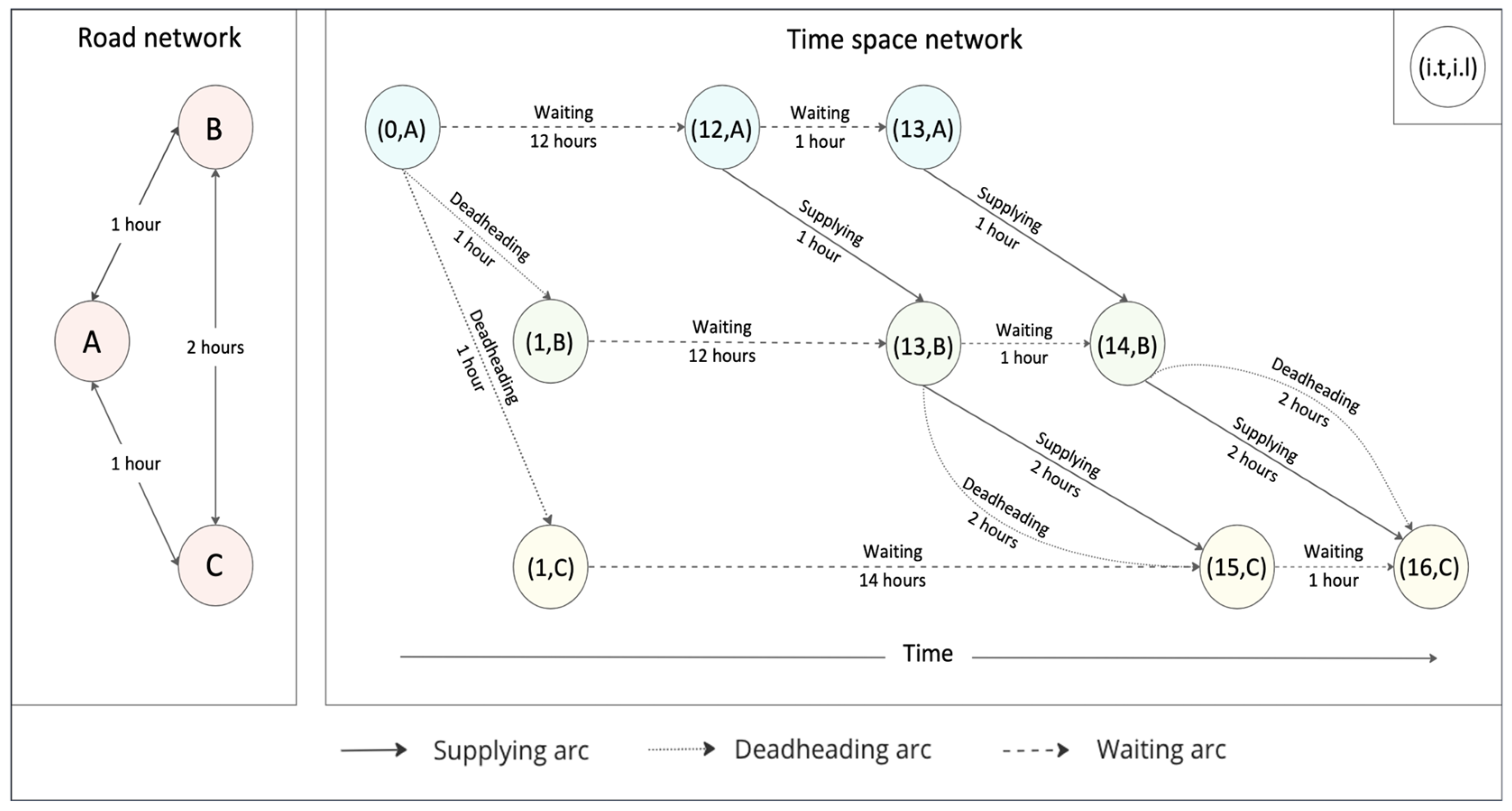
3.1. Construction of the Time–Space Network
- signifies the set of supplying arcs associated with an ER , where ;
- reflects the set of supplying arcs for a requester with a tail node . Specifically, where is the start time at the tail node and is the arrival time at the head node;
- represents the set of supplying arcs of ER with departure time It is defined as , with and as previously defined. Again .
3.2. Time–Space Network Formulation
4. Optimization Formulation and Solution
4.1. Shortest-Path Problem
- The path can only contain supplying arcs of a given requester that belong to the same departure time:This ensures that we select only one departure time for each ER that receives energy.
- If the path contains supplying arcs associated with a given ER, this set of arcs must be a path:i.e., the set of arcs on the left side is a path. This ensures that the charging process of any ER cannot be interrupted.
- The path cannot contain supplying arcs that overcharge the ER battery:This ensures that the energy balance of each ER does not exceed its battery capacity at any node along its route.
- If the path contains one or more supplying arcs of a given ER, there must be sufficient supplying arcs in the path so that the ER receives at least as much as energy as the minimum threshold.Particularly, we do not need any synchronization constraints since: (i) the ERs start their routes within the allowed time windows by the definition of the supplying arcs, and (ii) a path in the TSN already defines the timing of the ES.
4.2. Dynamic-Programming Solution Methodology
- The node is associated with (commonly called the resident node of the path).
- A reference to the predecessor label . Chaining labels to their predecessors in that way is an efficient way to keep track of the paths [53].
- The total consumed energy of the ES’s battery up to the current node, .
- The total costs up to the current node, .
- The set of ERs that have been served, , where only ERs from which the ES has disconnected already are included.
- If the ES is currently connected to an ER, then the ER identity is stored in, .
- is a mapping stores the departure time of all ERs. If an ER has not received any energy yet, it takes on an arbitrary value.
- is a mapping that stores the total received energy of all ERs. If an ER has not received any energy yet, it takes on the value zero.
- The set records fulfilled requests, which can occur in two scenarios: (i) if the current ER remains connected, implying , or (ii) if the demand of the current ER is fulfilled, resulting in the ER no longer being in platooning with the ES, i.e., .
- The set maintains potential start times for an ER which can vary based on two scenarios: (i) the ER has begun charging and the new departure time for this specific ER is added, i.e., , where , or (ii) the ER has not commenced charging, hence there are no changes in start times, i.e., .
- represents the total energy received from supplying arcs. If a supplying arc is traversed, is to be augmented with the energy received by the ER that is being currently served, i.e., . Otherwise, no change is made, i.e., .
5. Numerical Study
5.1. Experiment Setting
5.2. Travel Time and Distance
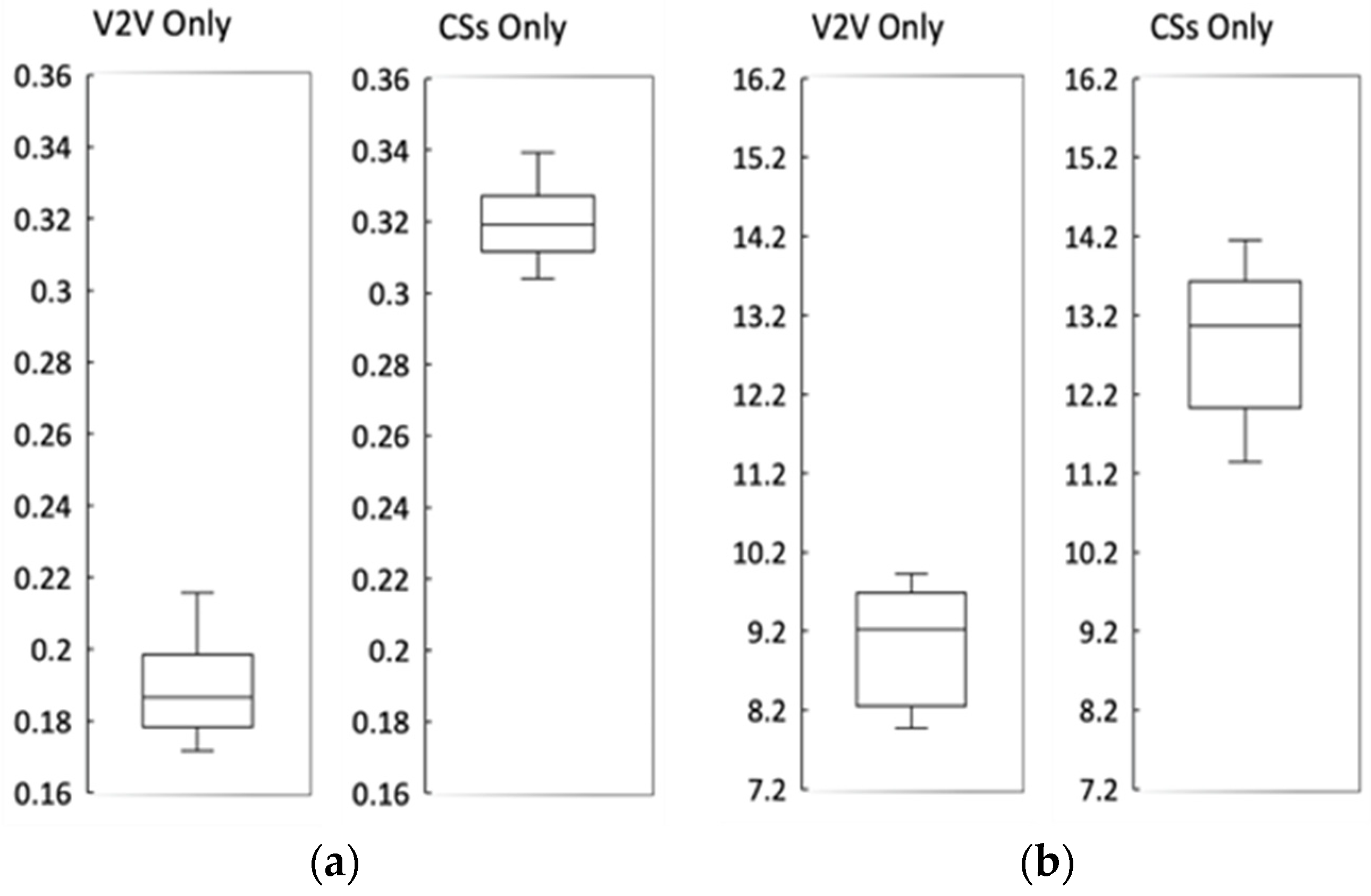
5.3. Energy and Charging Time
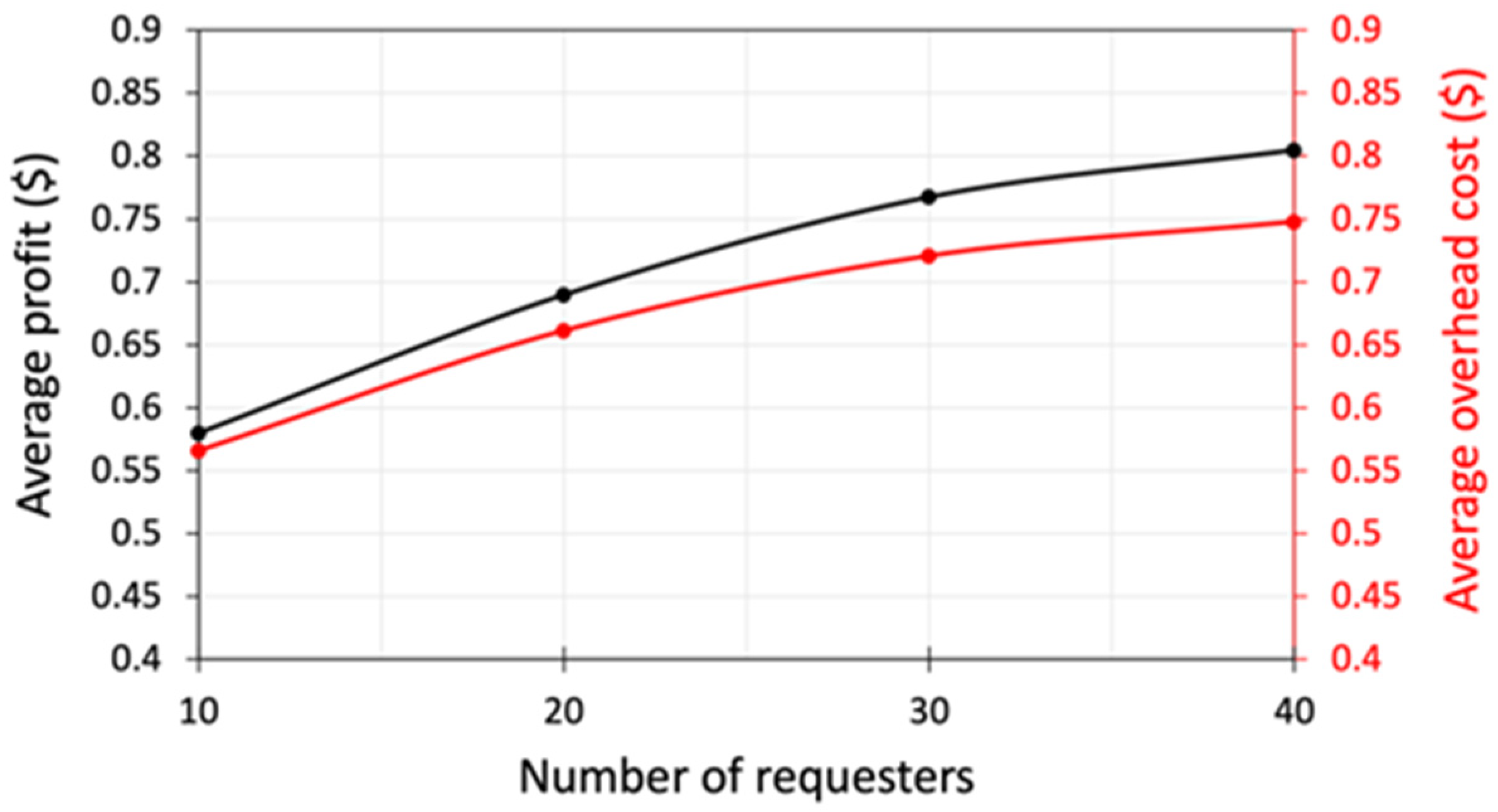
5.4. Profit and Overhead
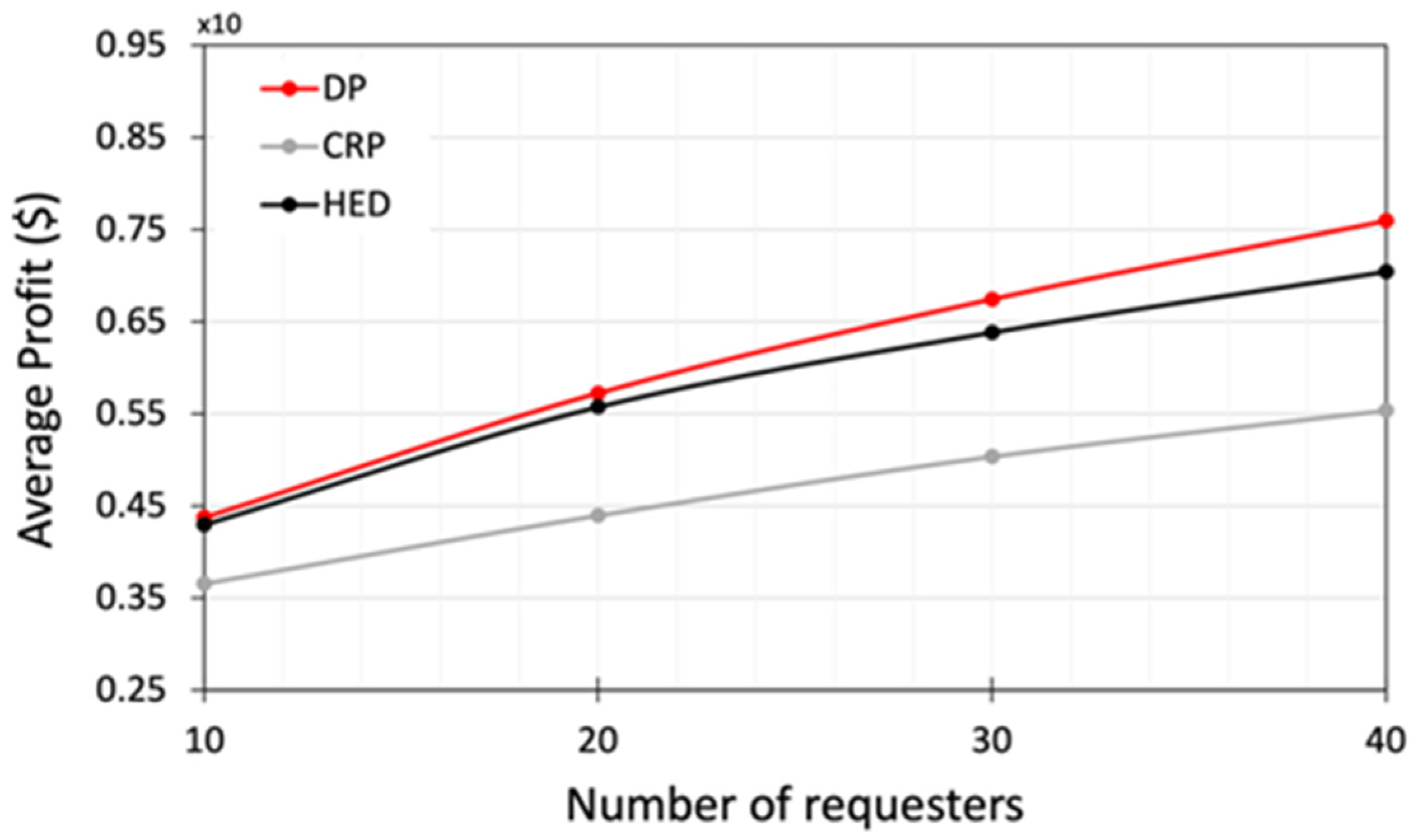
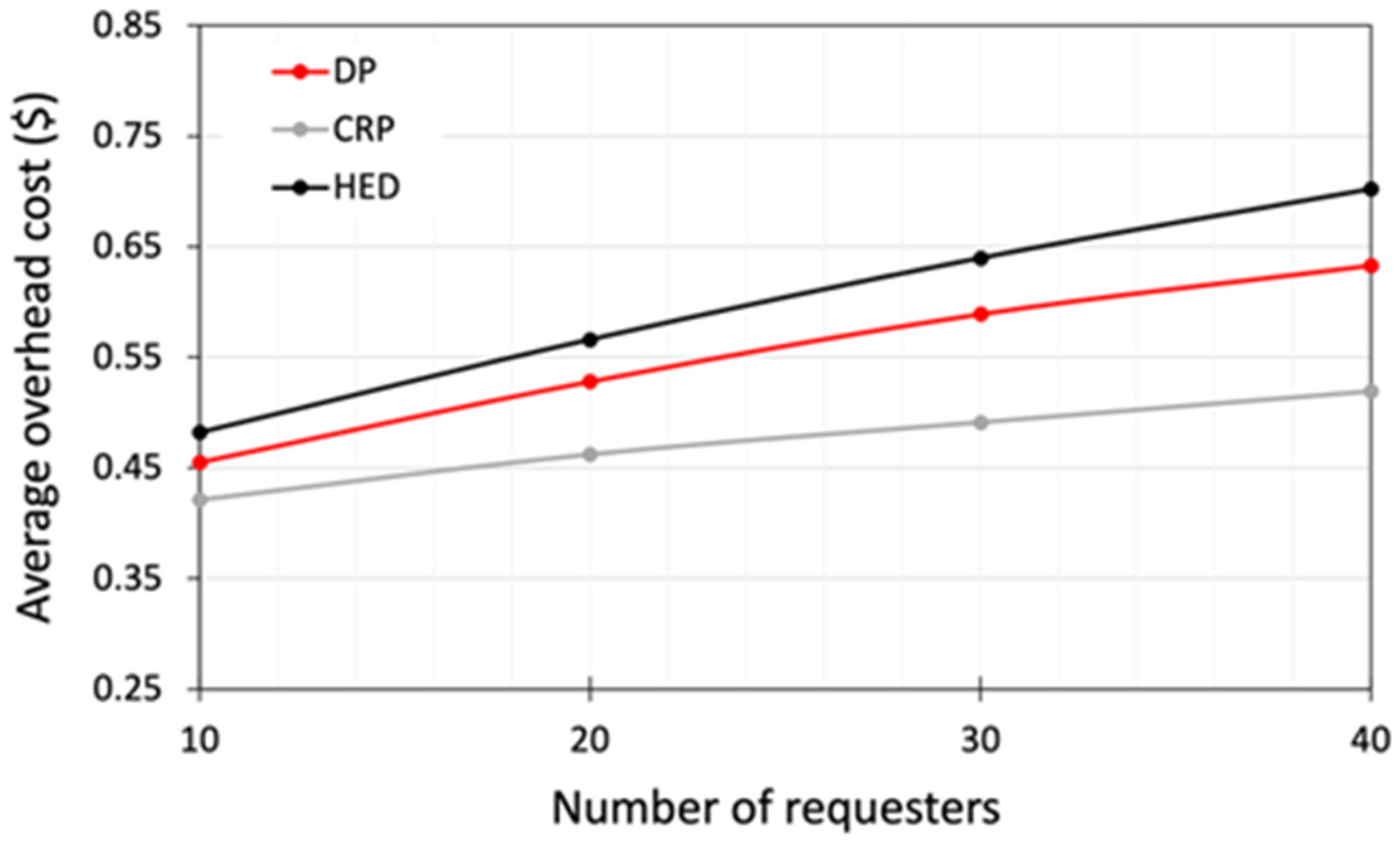
5.4.1. Comparison with a Baseline Approach
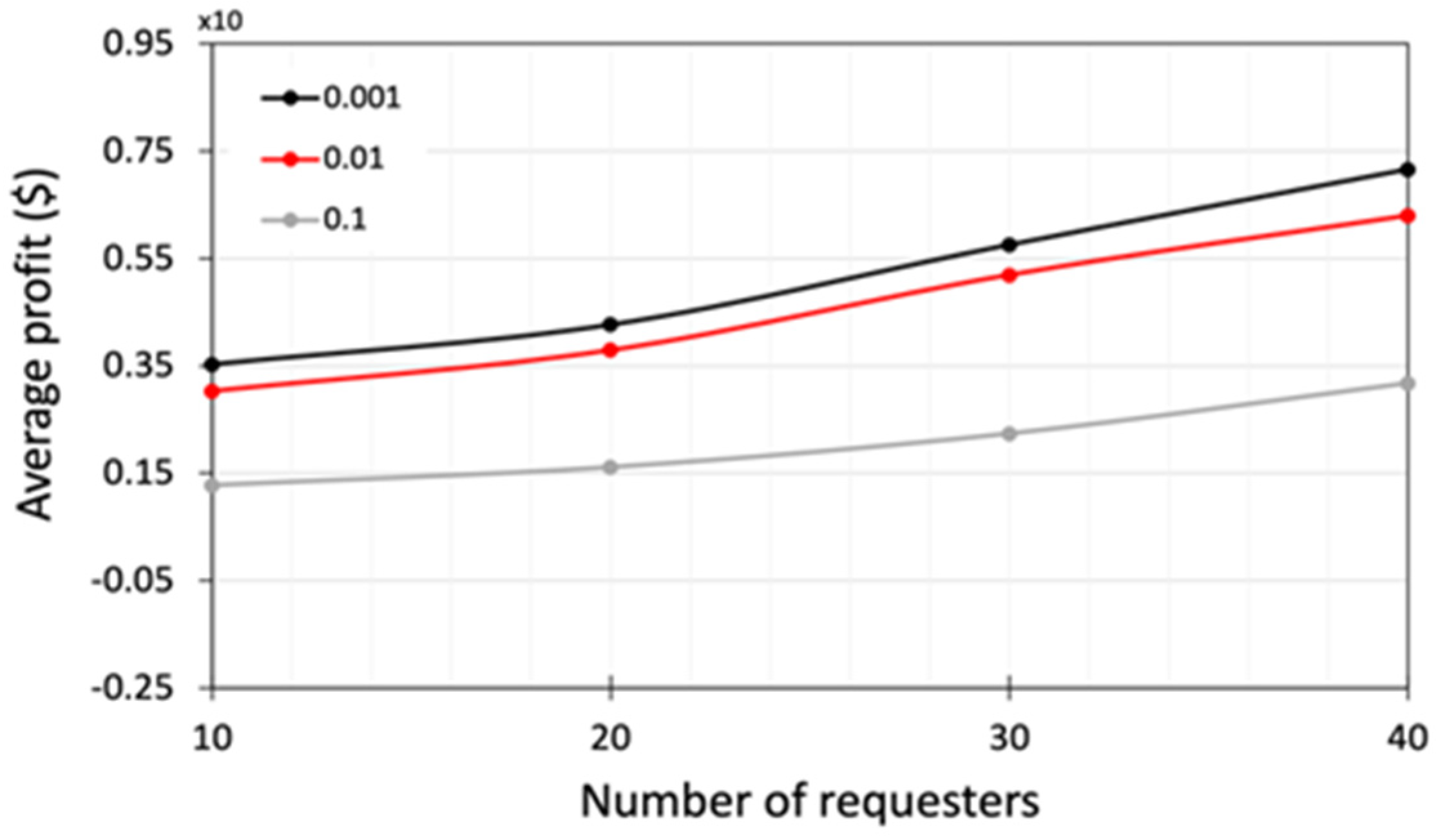
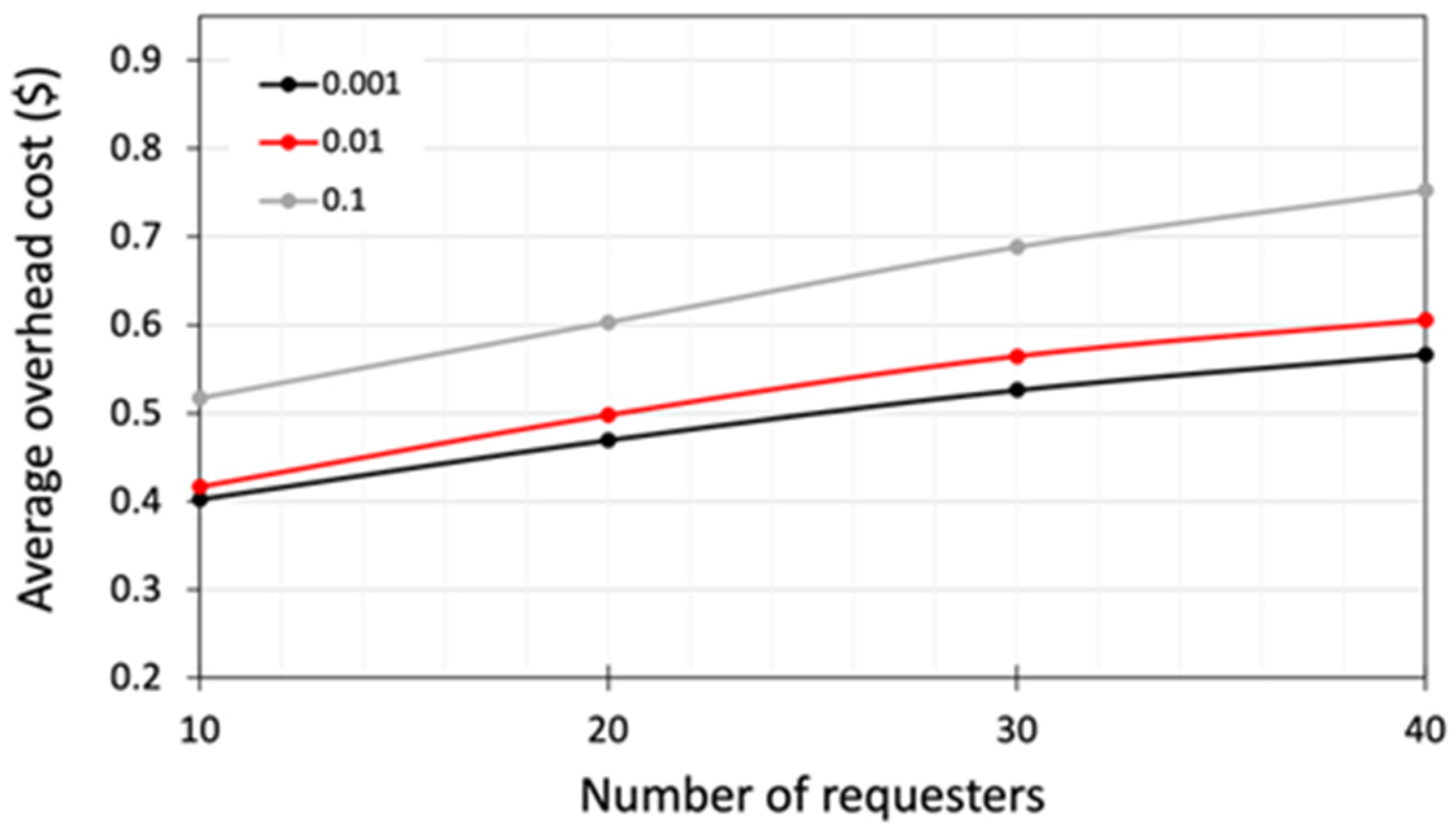
5.4.2. Waiting-Cost Analysis
5.5. Computational Complexity Comparison
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Table of Notations
| Symbol | Description |
|---|---|
| Set of nodes | |
| Set of arcs | |
| Set of ERs | |
| Set of nodes of the time-space network | |
| Set of arcs of the time-space network, where | |
| Set of supplying arcs of the time-space network | |
| Set of deadheading arcs of the time-space network | |
| Set of waiting arcs of the time-space network | |
| Set pf supplying arcs associated with ER and the index of the tail node, | |
| Set of supplying arcs associated with ER and departure time | |
| Time of node in the time-space network | |
| Location of node in the time-space network | |
| Length of the route of ER (i.e., number of arcs) | |
| Route of ER (along of which charging can take place) | |
| Energy consumption when traversing arc | |
| Energy consumption when traversing arc | |
| Total energy consumption of a shortest path (in terms of travel time) from node to node | |
| Travel time for traversing arc | |
| Total travel time of a shortest path (in terms of travel time) from node to node | |
| Total travel time for the route | |
| Energy transfer if platooning is performed on arc | |
| Energy transfer if platooning is performed over the link sequence | |
| transmission power during platooning in kW | |
| Cost of traversing | |
| Cost of driving a shortest path (in terms of travel time) from node to node | |
| Total cost of traversing (including all relevant cost factors) | |
| Earliest departure time of ER at its origin node | |
| Latest arrival time of ER at its destination node | |
| Discrete set of start times of ER at its initial location | |
| Possible departure times at the node with index of the route of ER | |
| Minimum share of the battery capacity that must be charged per request | |
| Initial location of the ES | |
| Destination location of the ES | |
| Total battery capacity of the ES. | |
| Initial energy ES’s battery. | |
| Initial energy ER’s battery. | |
| Battery capacity of ER | |
| Purchase price per unit of energy | |
| Sell price per unit of energy | |
| Cost for the supplier to wait one time unit | |
| Set of arcs incident to node where is the tail node | |
| Set of arcs incident to node j where is the head node | |
| Charging coefficient (to account for energy loss during transmission) | |
| Battery replacement cost | |
| Degradation coefficient | |
| A sufficiently large number | |
| Binary decision variable that is 1, if the ES traverses arc , and 0 otherwise. | |
| Binary decision variable that is 1, if ER receives energy and starts its tour at time , and zero otherwise. |
Appendix B
| Algorithm A1. DP Algorithm |
 |
References
- IPCC. Global Warming of 1.5C. An IPCC Special Report on the Impacts of Global Warming of 1.5C Above Pre-Industrial Levels and Related Global Greenhouse Gas Emission Pathways. 2018. Available online: https://www.ipcc.ch/ (accessed on 15 June 2023).
- The White House. FACT SHEET: President Biden Announces Steps to Drive American Leadership Forward on Clean Cars and Trucks. Available online: https://www.whitehouse.gov/briefing-room/statements-releases/2021/08/05/fact-sheet-president (accessed on 15 June 2023).
- IEA. Global EV Outlook 2020, IEA, Paris. 2020. Available online: https://www.iea.org/reports/global-ev-outlook-2020 (accessed on 15 June 2023).
- Luo, S.; Tian, Y.; Zheng, W.; Zhang, X.; Zhang, J.; Zhou, B. Large-Scale Electric Vehicle Energy Demand Considering Weather Conditions and Onboard Technology. In Advances in Green Energy Systems and Smart Grid; Springer: Berlin/Heidelberg, Germany, 2018; pp. 81–93. [Google Scholar]
- Yong, J.Y.; Ramachandaramurthy, V.K.; Tan, K.M.; Mithulananthan, N. A review on the state-of-the-art technologies of electric vehicle, its impacts and prospects. Renew. Sustain. Energy Rev. 2015, 49, 365–385. [Google Scholar] [CrossRef]
- Berckmans, G.; Messagie, M.; Smekens, J.; Omar, N.; Vanhaverbeke, L.; Van Mierlo, J. Cost Projection of State of the Art Lithium-Ion Batteries for Electric Vehicles Up to 2030. Energies 2017, 10, 1314. [Google Scholar] [CrossRef]
- Buja, G.; Rim, C.-T.; Mi, C.C. Dynamic Charging of Electric Vehicles by Wireless Power Transfer. IEEE Trans. Ind. Electron. 2016, 63, 6530–6532. [Google Scholar] [CrossRef]
- Luo, X.; Qiu, R. Electric vehicle charging station location towards sustainable cities. Int. J. Environ. Res. Public Health 2020, 17, 2785. [Google Scholar] [CrossRef]
- Huang, Y.; Kockelman, K.M. Electric vehicle charging station locations: Elastic demand, station congestion, and network equilibrium. Transp. Res. Part D Transp. Environ. 2020, 78, 102179. [Google Scholar] [CrossRef]
- Schneider, F.; Thonemann, U.W.; Klabjan, D. Optimization of Battery Charging and Purchasing at Electric Vehicle Battery Swap Stations. Transp. Sci. 2018, 52, 1211–1234. [Google Scholar] [CrossRef]
- Ban, M.; Zhang, Z.; Li, C.; Li, Z.; Liu, Y. Optimal scheduling for electric vehicle battery swapping-charging system based on nanogrids. Int. J. Electr. Power Energy Syst. 2021, 130, 106967. [Google Scholar] [CrossRef]
- He, J.; Yang, H.; Tang, T.-Q.; Huang, H.-J. Optimal deployment of wireless charging lanes considering their adverse effect on road capacity. Transp. Res. Part C Emerg. Technol. 2020, 111, 171–184. [Google Scholar] [CrossRef]
- Tran, C.Q.; Keyvan-Ekbatani, M.; Ngoduy, D.; Watling, D. Dynamic wireless charging lanes location model in urban networks considering route choices. Transp. Res. Part C Emerg. Technol. 2022, 139, 103652. [Google Scholar] [CrossRef]
- Hannon, K. Could roads recharge electric cars? The technology may be close. New York Times, 29 November 2021. [Google Scholar]
- Bi, Z.; Keoleian, G.A.; Lin, Z.; Moore, M.R.; Chen, K.; Song, L.; Zhao, Z. Life cycle assessment and tempo-spatial optimization of deploying dynamic wireless charging technology for electric cars. Transp. Res. Part C Emerg. Technol. 2019, 100, 53–67. [Google Scholar] [CrossRef]
- Chen, X.; Xing, K.; Ni, F.; Wu, Y.; Xia, Y. An electric vehicle battery-swapping system: Concept, architectures, and implementations. IEEE Intell. Transp. Syst. Mag. 2021, 14, 175–194. [Google Scholar] [CrossRef]
- Ulrich, L. How Is This A Good Idea?: EV Battery Swapping. 2021. Available online: https://spectrum.ieee.org/ev-battery-swapping-how-is-this-a-good-idea (accessed on 15 June 2023).
- Adegbohun, F.; von Jouanne, A.; Lee, K.Y. Autonomous Battery Swapping System and Methodologies of Electric Vehicles. Energies 2019, 12, 667. [Google Scholar] [CrossRef]
- Tesla, N. Apparatus for Transmitting Electrical Energy. U.S. Patent 1,119,732, 12 December 1914. [Google Scholar]
- Deb, S.; Gao, X.-Z.; Tammi, K.; Kalita, K.; Mahanta, P. Nature-Inspired Optimization Algorithms Applied for Solving Charging Station Placement Problem: Overview and Comparison. Arch. Comput. Methods Eng. 2019, 28, 91–106. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Y.; Li, F.; Wu, B.; Chiang, Y.Y.; Zhang, X. Efficient deployment of electric vehicle charging infrastructure: Simultaneous optimization of charging station placement and charging pile assignment. IEEE Trans. Intell. Transp. Syst. 2020, 22, 6654–6659. [Google Scholar] [CrossRef]
- Conrad, R.G.; Figliozzi, M.A. The Recharging Vehicle Routing Problem. In Proceedings of the 2011 Industrial Engineering Research Conference, Singapore, 6–9 December 2011; IISE Norcross: Peachtree Corners, GA, USA, 2011; Volume 8. [Google Scholar]
- Jing, W.; Kim, I.; Ramezani, M.; Liu, Z. Stochastic traffic assignment of mixed electric vehicle and gasoline vehicle flow with path distance constraints. Transp. Res. Procedia 2017, 21, 65–78. [Google Scholar] [CrossRef]
- Zhang, K.; Lu, L.; Lei, C.; Zhu, H.; Ouyang, Y. Dynamic operations and pricing of electric unmanned aerial vehicle systems and power networks. Transp. Res. Part C Emerg. Technol. 2018, 92, 472–485. [Google Scholar] [CrossRef]
- Sun, Z.; Gao, W.; Li, B.; Wang, L. Locating charging stations for electric vehicles. Transp. Policy 2020, 98, 48–54. [Google Scholar] [CrossRef]
- Zhang, S.; Gajpal, Y.; Appadoo, S.; Abdulkader, M. Electric vehicle routing problem with recharging stations for minimizing energy consumption. Int. J. Prod. Econ. 2018, 203, 404–413. [Google Scholar] [CrossRef]
- Guo, F.; Yang, J.; Lu, J. The battery charging station location problem: Impact of users’ range anxiety and distance convenience. Transp. Res. Part E Logist. Transp. Rev. 2018, 114, 1–18. [Google Scholar] [CrossRef]
- You, P.; Yang, Z. Efficient Optimal Scheduling of Charging Station with Multiple Electric Vehicles via V2V. In Proceedings of the 2014 IEEE International Conference on Smart Grid Communications (SmartGridComm), Venice, Italy, 3–6 November 2014; IEEE: Piscataway, NJ, USA, 2014. [Google Scholar]
- Koufakis, A.M.; Rigas, E.S.; Bassiliades, N.; Ramchurn, S.D. Towards an Optimal EV Charging Scheduling Scheme with V2G and V2V Energy Transfer. In Proceedings of the 2016 IEEE International Conference on Smart Grid Communications (SmartGridComm), Sydney, NSW, Australia, 6–9 November 2016; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar]
- Zhang, R.; Cheng, X.; Yang, L. Flexible Energy Management Protocol for Cooperative EV-to-EV Charging. IEEE Trans. Intell. Transp. Syst. 2018, 20, 172–184. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, X.; Wei, W.; Peng, T.; Hong, G.; Meng, C. Mobile charging: A novel charging system for electric vehicles in urban areas. Appl. Energy 2020, 278, 115648. [Google Scholar] [CrossRef]
- Kabir, M.E.; Sorkhoh, I.; Moussa, B.; Assi, C. Joint Routing and Scheduling of Mobile Charging Infrastructure for V2V Energy Transfer. IEEE Trans. Intell. Veh. 2021, 6, 736–746. [Google Scholar] [CrossRef]
- Behl, M.; DuBro, J.; Flynt, T.; Hameed, I.; Lang, G.; Park, F. Autonomous Electric Vehicle Charging System. In Proceedings of the 2019 Systems and Information Engineering Design Symposium (SIEDS), Charlottesville, VA, USA, 26 April 2019; IEEE: Piscataway, NJ, USA, 2019. [Google Scholar]
- Kong, P.-Y. Autonomous robot-like mobile chargers for electric vehicles at public parking facilities. IEEE Trans. Smart Grid 2019, 10, 5952–5963. [Google Scholar] [CrossRef]
- Abdolmaleki, M.; Masoud, N.; Yin, Y. Vehicle-to-vehicle wireless power transfer: Paving the way toward an electrified transportation system. Transp. Res. Part C Emerg. Technol. 2019, 103, 261–280. [Google Scholar] [CrossRef]
- Nezamuddin, O.; dos Santos, E.C. Vehicle-to-Vehicle in-Route Wireless charging SYSTEM. In Proceedings of the 2020 IEEE Transportation Electrification Conference & Expo (ITEC), Chicago, IL, USA, 23–26 June 2020; IEEE: Piscataway, NJ, USA, 2020. [Google Scholar]
- Chakraborty, P.; Parker, R.; Hoque, T.; Cruz, J.; Du, L.; Wang, S.; Bhunia, S. Addressing the range anxiety of battery electric vehicles with charging en route. Sci. Rep. 2022, 12, 5588. [Google Scholar] [CrossRef]
- Chakraborty, P.; Dizon-Paradis, R.N.; Bhunia, S. SAVIOR: A Sustainable Network of Vehicles with Near-Perpetual Mobility. IEEE Internet Things Mag. 2023, 6, 108–114. [Google Scholar] [CrossRef]
- Guanetti, J.; Kim, Y.; Borrelli, F. Control of connected and automated vehicles: State of the art and future challenges. Annu. Rev. Control. 2018, 45, 18–40. [Google Scholar] [CrossRef]
- Ma, H.; Chu, L.; Guo, J.; Wang, J.; Guo, C. Cooperative Adaptive Cruise Control Strategy Optimization for Electric Vehicles Based on SA-PSO With Model Predictive Control. IEEE Access 2020, 8, 225745–225756. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, G.; Barth, M.J. A Review on Cooperative Adaptive Cruise Control (CACC) Systems: Architectures, Controls, and Applications. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; IEEE: Piscataway, NJ, USA, 2018. [Google Scholar]
- Kosmanos, D.; Maglaras, L.A.; Mavrovouniotis, M.; Moschoyiannis, S.; Argyriou, A.; Maglaras, A.; Janicke, H. Route Optimization of Electric Vehicles Based on Dynamic Wireless Charging. IEEE Access 2018, 6, 42551–42565. [Google Scholar] [CrossRef]
- Moschoyiannis, S.; Maglaras, L.; Jiang, J.; Topalis, F.; Maglaras, A. Dynamic wireless charging of electric vehicles on the move with mobile energy disseminators. Int. J. Adv. Comput. Sci. Appl. (IJACSA) 2015, 6, 239–251. [Google Scholar]
- Liu, P.; Wang, C.; Fu, T.; Guan, Z. Efficient Electric Vehicles Assignment for Platoon-Based Charging. In Proceedings of the 2019 IEEE Wireless Communications and Networking Conference (WCNC), Marrakesh, Morocco, 15–18 April 2019; IEEE: Piscataway, NJ, USA, 2019. [Google Scholar]
- Qiu, J.; Lili, D. Optimal dispatching of electric vehicles for providing charging on-demand service leveraging charging-on-the-move technology. Transp. Res. Part C Emerg. Technol. 2023, 146, 103968. [Google Scholar] [CrossRef]
- Gambella, C.; Naoum-Sawaya, J.; Ghaddar, B. The Vehicle Routing Problem with Floating Targets: Formulation and Solution Approaches. Inf. J. Comput. 2018, 30, 554–569. [Google Scholar] [CrossRef]
- Zhang, W.; Jacquillat, A.; Wang, K.; Wang, S.; Geometric Optimization for Routing with Floating Targets. TSL Second. Trienn. Conf. 2020. Available online: https://www.informs.org/Publications/Proceedings-of-the-TSL-Second-Triennial-Conference (accessed on 15 May 2023).
- Ozbaygin, G.; Karasan, O.E.; Savelsbergh, M.; Yaman, H. A branch-and-price algorithm for the vehicle routing problem with roaming delivery locations. Transp. Res. Part B Methodol. 2017, 100, 115–137. [Google Scholar] [CrossRef]
- Wu, D.; Zeng, H.; Lu, C.; Boulet, B. Two-Stage Energy Management for Office Buildings with Workplace EV Charging and Renewable Energy. IEEE Trans. Transp. Electrif. 2017, 3, 225–237. [Google Scholar] [CrossRef]
- Desrosiers, J.; Soumis, F.; Desrochers, M. Routing with time windows by column generation. Networks 1984, 14, 545–565. [Google Scholar] [CrossRef]
- Desrochers, M.; Soumis, F. A Generalized Permanent Labelling Algorithm for The Shortest Path Problem with Time Windows. INFOR: Inf. Syst. Oper. Res. 1988, 26, 191–212. [Google Scholar] [CrossRef]
- Irnich, S.; Guy, D. Shortest Path Problems with Resource Constraints. In Column Generation; Springer: Boston, MA, USA, 2005; pp. 33–65. [Google Scholar]
- Ahuja, R.K.; Thomas, L.M.; James, B.O. Network Flows: Theory, Algorithms and Applications; Pearson: London, UK, 2013. [Google Scholar]
- Transportation Networks for Research Core Team. Transportation Networks for Research. Available online: https://github.com/bstabler/TransportationNetworks (accessed on 15 May 2023).
- PlugShare. 2023. Available online: https://www.plugshare.com/ (accessed on 15 July 2023).


| Battery Capacity (kWh) | Max Range (km) | |
|---|---|---|
| Tesla Model S | 85 | 482 |
| Nissan Leaf | 24 | 161 |
| BMW i3 | 19 | 161 |
| Mitsubishi i-MiEV | 16 | 161 |
| Ford Focus | 23 | 161 |
| Honda Fit | 20 | 199 |
| Volkswagen e-Golf | 26.5 | 151 |
| BYD e6 | 57 | 302 |
| BYD Qin | 35 | 201 |
| DFM Venucia e30 | 24 | 175 |
| Energy Consumption Rate (Watt) | Supplied Energy (Watt) | Lost Energy (Watt) | Charging Time at CSs (Min) | |
|---|---|---|---|---|
| V2V Only | 1825.77 | 9363.047 | 463.84 | - |
| CSs Only | 2146.01 | 14,210.07 | - | 8.90 |
| Deadheading Time (%) | Supplying Time (%) | Waiting Time (%) | |
|---|---|---|---|
| DP | 39.90 | 47.86 | 12.24 |
| CRP | 36.77 | 38.28 | 24.95 |
| HED | 50.40 | 42.13 | 7.48 |
| Requester Count | DP | CBC | Greedy | |
|---|---|---|---|---|
| Runtime (ms) | Runtime (ms) | Runtime (ms) | Deviation from Optimal Solution (%) | |
| 10 | 115.66 | 210.32 | 0.095 | 11.23 |
| 20 | 338.90 | 427.66 | 0.645 | 9.19 |
| 30 | 532.89 | 597.80 | 0.132 | 25.74 |
| 40 | 994.92 | 1162.98 | 0.200 | 45.24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alaskar, S.; Younis, M. Optimized Dynamic Vehicle-to-Vehicle Charging for Increased Profit. Energies 2024, 17, 2243. https://doi.org/10.3390/en17102243
Alaskar S, Younis M. Optimized Dynamic Vehicle-to-Vehicle Charging for Increased Profit. Energies. 2024; 17(10):2243. https://doi.org/10.3390/en17102243
Chicago/Turabian StyleAlaskar, Shorooq, and Mohamed Younis. 2024. "Optimized Dynamic Vehicle-to-Vehicle Charging for Increased Profit" Energies 17, no. 10: 2243. https://doi.org/10.3390/en17102243
APA StyleAlaskar, S., & Younis, M. (2024). Optimized Dynamic Vehicle-to-Vehicle Charging for Increased Profit. Energies, 17(10), 2243. https://doi.org/10.3390/en17102243








