Advances in Short-Term Solar Forecasting: A Review and Benchmark of Machine Learning Methods and Relevant Data Sources
Abstract
:1. Introduction
- The available open-source data enabling the comparison and benchmarking of different forecasting methods. Today, there is a significant body of work describing different ML methods and explaining the benefits of applying them to specific case studies. However, in most of the papers, the dataset is unavailable and unknown in terms of the number of data and quality of the data, as well as availability to produce the results from the published paper. We find that such an approach hinders future development, as each researcher/developer needs to self-test all available methods to learn about their advantages and disadvantages. Our goal is to list the open available data and to assist in creating an open-source community where transparency of newly developed tools/solutions is key to quality research.
- The relevant metrics to benchmark the effectiveness of a certain ML method as well as what is the range of the values for those metrics in previously published papers. Our goal is to provide a framework for future researchers to use adequate metrics and to understand the quality of their proposed method.
- New sources of data, previously less or not utilized, that could improve the existing or new ML methods. Here again, we focus on open sets of data that are transparent and available to everyone, and as such can serve as a unified benchmark of the proposed method.
2. Research Area Overview
- Goal—goal of the paper: PV power or solar irradiance forecasting;
- Horizon (Step)— forecast horizon with the granularity of the forecast (step);
- Test size—it is important to highlight this feature, as a larger test set provides a more statistically significant sample of the data, indicates robustness, reduces risk of overfitting and gives more credibility to solutions tested on larger datasets;
- Error term—measure of performance used to compare methods;
- Method—ML method employed in the paper;
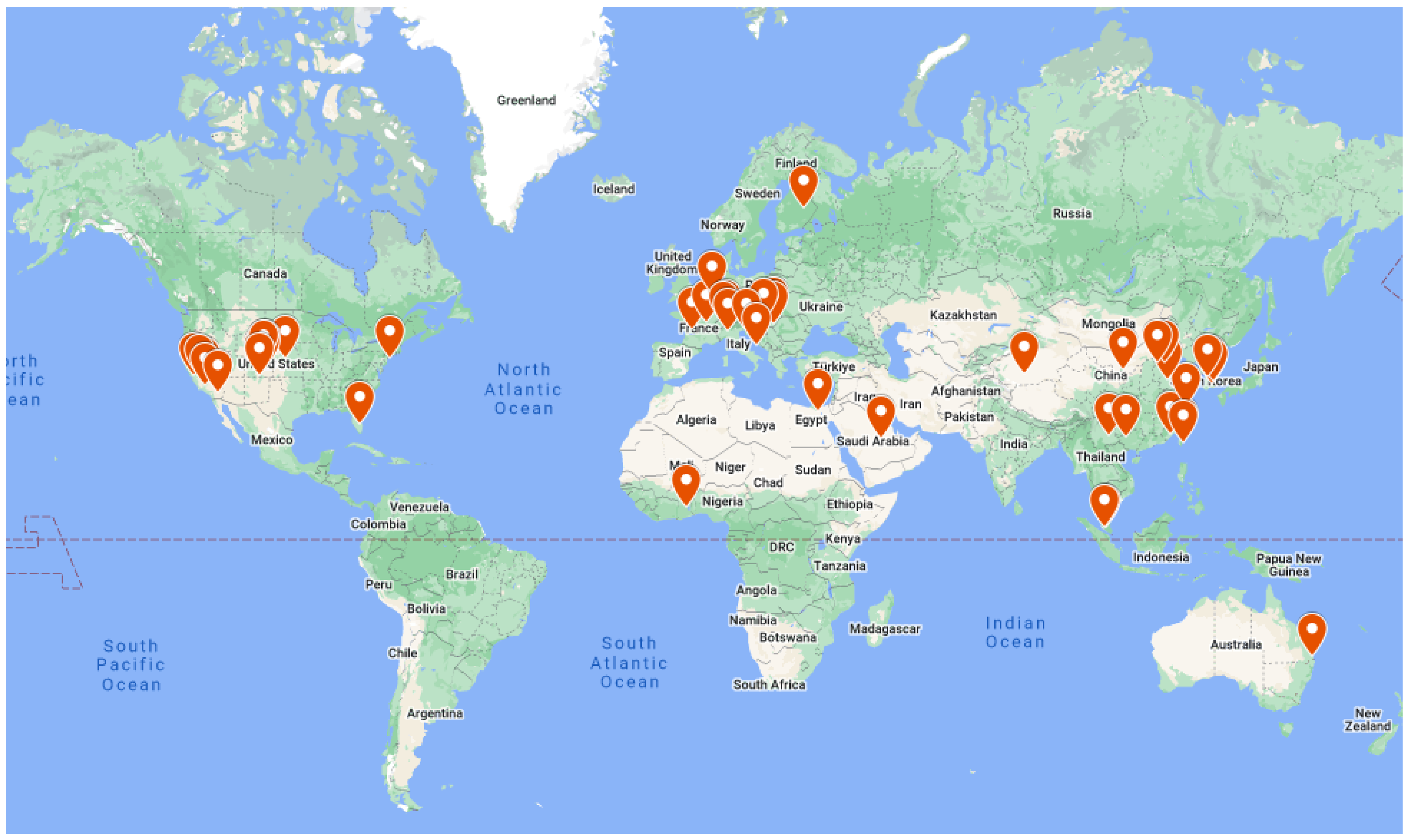
- Location—geographical location of the PV power plant(s); all locations referred to in the analysed literature are shown on the world map in Figure 1.
Performance Measures
3. Machine Learning Methods
3.1. Classical Machine Learning
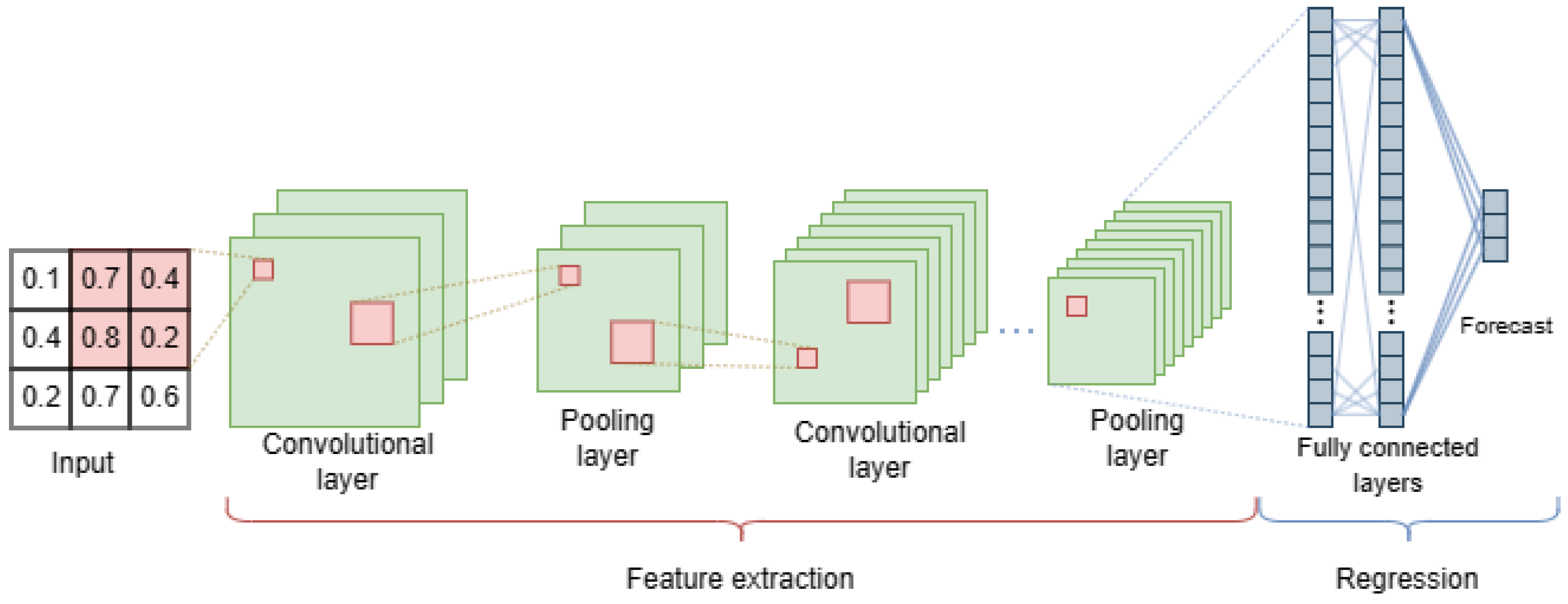
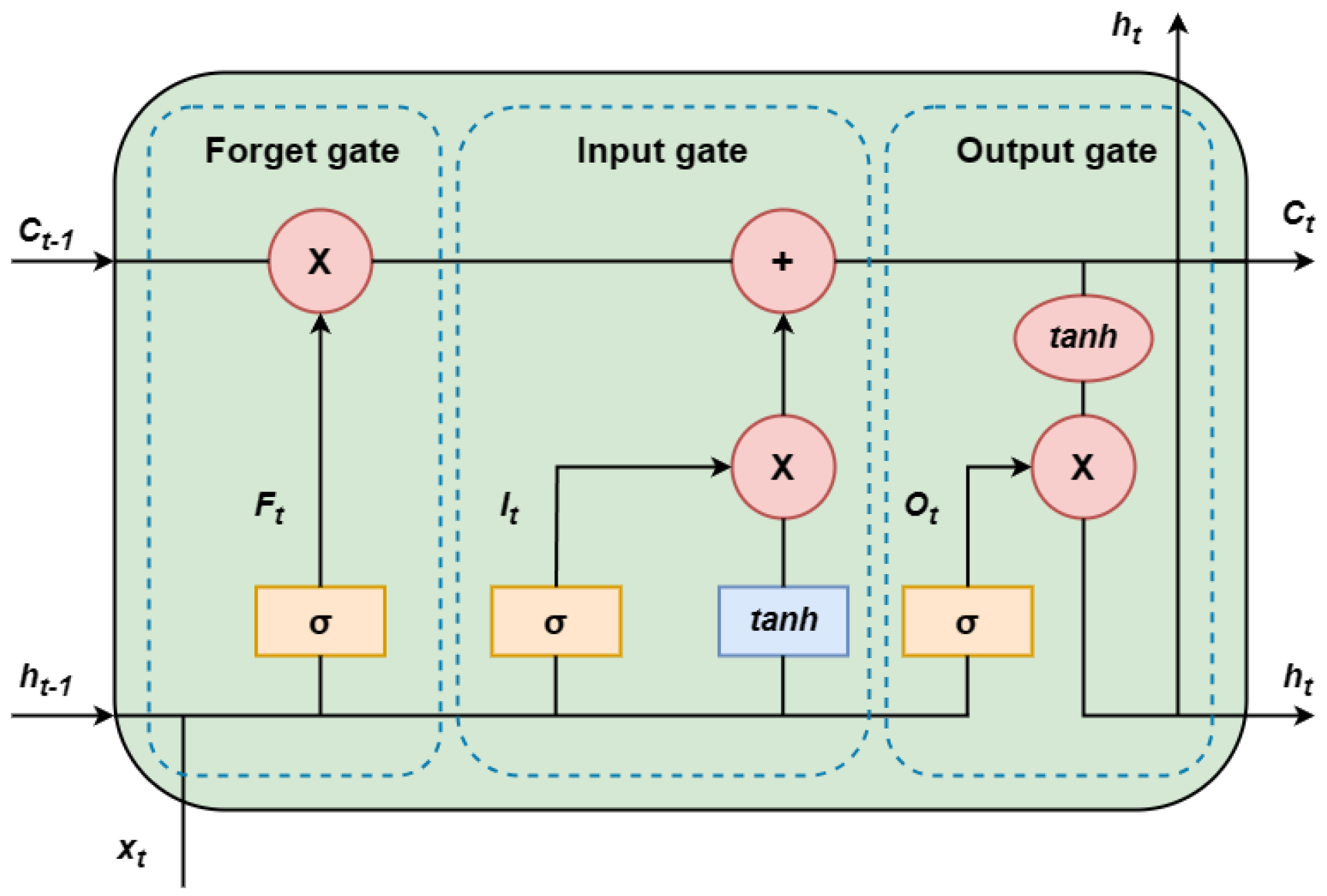
3.2. Neural Networks (Deep Learning)
4. Open-Source Data
4.1. Sources
4.2. Benchmark
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| ANN | Artificial Neural Network |
| SVM | Support Vector Machine |
| BPNN | Backpropagation Neural Network |
| MLR | Multiple Linear Regression |
| (Bi)LSTM | (Bidirectional) Long Short-Term Memory |
| CNN | Convolutional Neural Network |
| ConvNet | Convolutional Neural Network |
| SVR | Support Vector Regression |
| DT | Decision Tree |
| MLP | Multiple Layer Perceptron |
| RF | Random Forest |
| AR | Autoregressive Model |
| DNN | Deep Neural Network |
| FNN | Feedforward Neural Network |
| DXNN | Direct Explainable Neural Network |
| GB(D)T | Gradient Boosting (Decision) Trees |
| (L)GBM | (Light) Gradient Boosting Machine |
| XGB | Extreme Gradient Boosting |
| NGBoost | Natural Gradient Boosting |
| ReLU | Rectified Linear Unit |
| Dense | Fully connected feedforward layer |
| (S)AR(I)MA | (Seasonal) Autoregressive (Integrated) Moving Average |
| ResNet | Residual Neural Network |
| GRU | Gated Recurrent Unit |
| QR | Quantile Regression |
| ANFIS | Adaptive Neuro-Fuzzy Inference System |
| GP(R) | Gaussian Process (Regression) |
| KNN | K-Nearest Neighbors |
| LR | Linear Regression |
| AdaBoost | Adaptive Boosting |
| ETR | Extra Trees Regressor or Extremely Randomized Trees |
| EDLSTM | Encoder-Decoder Long Short Term Memory |
| STCNN | Space-Time Convolutional Neural Network |
| NLSTM | Multi-Task Multi-Channel Nested Long Short Term Memory |
| SSA | Salp-Swarm Algorithm |
| PSO | Particle Swarm Algorithm |
| ENN | Elman Neural Network |
| NAR(X) | Autoregressive Neural Network (with Exogenous Inputs) |
| PHANN | Physical Hybrid Artificial Neural Network |
| GCLSTM | Graph Convolutional Long Short Term Memory |
| STAR | Spatio-Temporal Autoregressive Model |
| GCTrafo | Graph Convolutional Transformer |
| MR-ESN | Multiple Reservoirs Echo State Network |
| ELM | Extreme Learning Machine |
| DRL | Deep Reinforcement Learning |
| KS test | Kolmogorov–Smirnov test |
| IAE | Individual Absolute Error |
| SSIM | Structural Similarity |
| Coefficient of correlation | |
| PIAW | Prediction Interval Average Width |
| PICP | Prediction Interval Coverage Probability |
| CRPS | Continuous Ranked Probability Score |
| CWC | Coverage Width Calculation |
| TSM-GAT | Temporal-Spatial Multi-Windows Graph Attention Network |
| Lasso | Least Absolute Shrinkage and Selection Operator |
| ST-Lasso | Spatio Temporal model with Least Absolute Shrinkage and Selection Operator |
References
- International Energy Agency. Share of Cumulative Power Capacity by Technology. 2022. Available online: https://www.iea.org/data-and-statistics/charts/share-of-cumulative-power-capacity-by-technology-2010-2027 (accessed on 7 September 2023).
- Alcañiz, A.; Grzebyk, D.; Ziar, H.; Isabella, O. Trends and gaps in photovoltaic power forecasting with machine learning. Energy Rep. 2023, 9, 447–471. [Google Scholar] [CrossRef]
- Liu, C.; Li, M.; Yu, Y.; Wu, Z.; Gong, H.; Cheng, F. A review of multitemporal and multispatial scales photovoltaic forecasting methods. IEEE Access 2022, 10, 35073–35093. [Google Scholar] [CrossRef]
- Gupta, P.; Singh, R. PV power forecasting based on data-driven models: A review. Int. J. Sustain. Eng. 2021, 14, 1733–1755. [Google Scholar] [CrossRef]
- Mellit, A.; Massi Pavan, A.; Ogliari, E.; Leva, S.; Lughi, V. Advanced methods for photovoltaic output power forecasting: A review. Appl. Sci. 2020, 10, 487. [Google Scholar] [CrossRef]
- Benavides Cesar, L.; Amaro e Silva, R.; Manso Callejo, M.Á.; Cira, C.I. Review on spatio-temporal solar forecasting methods driven by in situ measurements or their combination with satellite and numerical weather prediction (NWP) estimates. Energies 2022, 15, 4341. [Google Scholar] [CrossRef]
- Mohamad Radzi, P.N.L.; Akhter, M.N.; Mekhilef, S.; Mohamed Shah, N. Review on the Application of Photovoltaic Forecasting Using Machine Learning for Very Short-to Long-Term Forecasting. Sustainability 2023, 15, 2942. [Google Scholar] [CrossRef]
- Jung, Y.; Jung, J.; Kim, B.; Han, S. Long short-term memory recurrent neural network for modeling temporal patterns in long-term power forecasting for solar PV facilities: Case study of South Korea. J. Clean. Prod. 2020, 250, 119476. [Google Scholar] [CrossRef]
- Haider, S.A.; Sajid, M.; Sajid, H.; Uddin, E.; Ayaz, Y. Deep learning and statistical methods for short-and long-term solar irradiance forecasting for Islamabad. Renew. Energy 2022, 198, 51–60. [Google Scholar] [CrossRef]
- Ofori-Ntow Jnr, E.; Ziggah, Y.Y.; Rodrigues, M.J.; Relvas, S. A New Long-Term Photovoltaic Power Forecasting Model Based on Stacking Generalization Methodology. Nat. Resour. Res. 2022, 31, 1265–1287. [Google Scholar] [CrossRef]
- Ghimire, S.; Deo, R.C.; Downs, N.J.; Raj, N. Self-adaptive differential evolutionary extreme learning machines for long-term solar radiation prediction with remotely-sensed MODIS satellite and Reanalysis atmospheric products in solar-rich cities. Remote. Sens. Environ. 2018, 212, 176–198. [Google Scholar] [CrossRef]
- Han, S.; Qiao, Y.; Yan, J.; Liu, Y.; Li, L.; Wang, Z. Mid-to-long term wind and photovoltaic power generation prediction based on copula function and long short term memory network. Appl. Energy 2019, 239, 181–191. [Google Scholar] [CrossRef]
- Wang, F.; Lu, X.; Mei, S.; Su, Y.; Zhen, Z.; Zou, Z.; Zhang, X.; Yin, R.; Duić, N.; Shafie-khah, M.; et al. A satellite image data based ultra-short-term solar PV power forecasting method considering cloud information from neighboring plant. Energy 2022, 238, 121946. [Google Scholar] [CrossRef]
- Pothineni, D.; Oswald, M.R.; Poland, J.; Pollefeys, M. Kloudnet: Deep learning for sky image analysis and irradiance forecasting. In Proceedings of the Pattern Recognition: 40th German Conference, GCPR 2018, Stuttgart, Germany, 9–12 October 2018; Proceedings 40. Springer: Berlin/Heidelberg, Germany, 2019; pp. 535–551. [Google Scholar]
- Zhen, Z.; Liu, J.; Zhang, Z.; Wang, F.; Chai, H.; Yu, Y.; Lu, X.; Wang, T.; Lin, Y. Deep learning based surface irradiance mapping model for solar PV power forecasting using sky image. IEEE Trans. Ind. Appl. 2020, 56, 3385–3396. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, Z.; Chai, H.; Yu, Y.; Lu, X.; Wang, T.; Lin, Y. Deep learning based irradiance mapping model for solar PV power forecasting using sky image. In Proceedings of the 2019 IEEE Industry Applications Society Annual Meeting, Baltimore, MD, USA, 29 September 2019–3 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–9. [Google Scholar]
- Wang, F.; Xuan, Z.; Zhen, Z.; Li, Y.; Li, K.; Zhao, L.; Shafie-khah, M.; Catalão, J.P. A minutely solar irradiance forecasting method based on real-time sky image-irradiance mapping model. Energy Convers. Manag. 2020, 220, 113075. [Google Scholar] [CrossRef]
- Bauer, P.; Thorpe, A.; Brunet, G. The quiet revolution of numerical weather prediction. Nature 2015, 525, 47–55. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.G.; Huang, X.Y.; Wang, W.; Powers, J.G. A description of the advanced research WRF version 3. NCAR Tech. Note 2008, 475, 113. [Google Scholar]
- Pandžić, F.; Sudić, I.; Capuder, T. Cloud Effects on Photovoltaic Power Forecasting: Initial Analysis of a Single Power Plant Based on Satellite Images and Weather Forecasts. In Proceedings of the 8th International Conference on Advances on Clean Energy Research, Barcelona, Spain, 28–30 April 2023. [Google Scholar]
- AlShafeey, M.; Csáki, C. Evaluating neural network and linear regression photovoltaic power forecasting models based on different input methods. Energy Rep. 2021, 7, 7601–7614. [Google Scholar] [CrossRef]
- Huang, C.J.; Kuo, P.H. Multiple-input deep convolutional neural network model for short-term photovoltaic power forecasting. IEEE Access 2019, 7, 74822–74834. [Google Scholar] [CrossRef]
- Si, Z.; Yang, M.; Yu, Y.; Ding, T. Photovoltaic power forecast based on satellite images considering effects of solar position. Appl. Energy 2021, 302, 117514. [Google Scholar] [CrossRef]
- Agoua, X.G.; Girard, R.; Kariniotakis, G. Photovoltaic power forecasting: Assessment of the impact of multiple sources of spatio-temporal data on forecast accuracy. Energies 2021, 14, 1432. [Google Scholar] [CrossRef]
- Venugopal, V.; Sun, Y.; Brandt, A.R. Short-term solar PV forecasting using computer vision: The search for optimal CNN architectures for incorporating sky images and PV generation history. J. Renew. Sustain. Energy 2019, 11, 066102. [Google Scholar] [CrossRef]
- Lago, J.; De Brabandere, K.; De Ridder, F.; De Schutter, B. Short-term forecasting of solar irradiance without local telemetry: A generalized model using satellite data. Sol. Energy 2018, 173, 566–577. [Google Scholar] [CrossRef]
- Feng, C.; Zhang, J. SolarNet: A sky image-based deep convolutional neural network for intra-hour solar forecasting. Sol. Energy 2020, 204, 71–78. [Google Scholar] [CrossRef]
- Sharadga, H.; Hajimirza, S.; Balog, R.S. Time series forecasting of solar power generation for large-scale photovoltaic plants. Renew. Energy 2020, 150, 797–807. [Google Scholar] [CrossRef]
- Yang, D. Choice of clear-sky model in solar forecasting. J. Renew. Sustain. Energy 2020, 12, 026101. [Google Scholar] [CrossRef]
- Wen, H.; Du, Y.; Chen, X.; Lim, E.; Wen, H.; Jiang, L.; Xiang, W. Deep learning based multistep solar forecasting for PV ramp-rate control using sky images. IEEE Trans. Ind. Inform. 2020, 17, 1397–1406. [Google Scholar] [CrossRef]
- Nie, Y.; Li, X.; Scott, A.; Sun, Y.; Venugopal, V.; Brandt, A. SKIPP’D: A SKy Images and Photovoltaic Power Generation Dataset for short-term solar forecasting. Sol. Energy 2023, 255, 171–179. [Google Scholar] [CrossRef]
- Kuo, W.C.; Chen, C.H.; Chen, S.Y.; Wang, C.C. Deep learning neural networks for short-term PV Power Forecasting via Sky Image method. Energies 2022, 15, 4779. [Google Scholar] [CrossRef]
- Hossain, M.S.; Mahmood, H. Short-term photovoltaic power forecasting using an LSTM neural network and synthetic weather forecast. IEEE Access 2020, 8, 172524–172533. [Google Scholar] [CrossRef]
- Mayer, M.J.; Yang, D. Probabilistic photovoltaic power forecasting using a calibrated ensemble of model chains. Renew. Sustain. Energy Rev. 2022, 168, 112821. [Google Scholar] [CrossRef]
- Dai, Y.; Wang, Y.; Leng, M.; Yang, X.; Zhou, Q. LOWESS smoothing and Random Forest based GRU model: A short-term photovoltaic power generation forecasting method. Energy 2022, 256, 124661. [Google Scholar] [CrossRef]
- Fu, Y.; Chai, H.; Zhen, Z.; Wang, F.; Xu, X.; Li, K.; Shafie-Khah, M.; Dehghanian, P.; Catalão, J.P. Sky image prediction model based on convolutional auto-encoder for minutely solar PV power forecasting. IEEE Trans. Ind. Appl. 2021, 57, 3272–3281. [Google Scholar] [CrossRef]
- Brester, C.; Kallio-Myers, V.; Lindfors, A.V.; Kolehmainen, M.; Niska, H. Evaluating neural network models in site-specific solar PV forecasting using numerical weather prediction data and weather observations. Renew. Energy 2023, 207, 266–274. [Google Scholar] [CrossRef]
- Mayer, M.J. Benefits of physical and machine learning hybridization for photovoltaic power forecasting. Renew. Sustain. Energy Rev. 2022, 168, 112772. [Google Scholar] [CrossRef]
- Markovics, D.; Mayer, M.J. Comparison of machine learning methods for photovoltaic power forecasting based on numerical weather prediction. Renew. Sustain. Energy Rev. 2022, 161, 112364. [Google Scholar] [CrossRef]
- Yu, D.; Lee, S.; Lee, S.; Choi, W.; Liu, L. Forecasting photovoltaic power generation using satellite images. Energies 2020, 13, 6603. [Google Scholar] [CrossRef]
- Abdellatif, A.; Mubarak, H.; Ahmad, S.; Ahmed, T.; Shafiullah, G.M.; Hammoudeh, A.; Abdellatef, H.; Rahman, M.M.; Gheni, H.M. Forecasting photovoltaic power generation with a stacking ensemble model. Sustainability 2022, 14, 11083. [Google Scholar] [CrossRef]
- Harrou, F.; Kadri, F.; Sun, Y. Forecasting of photovoltaic solar power production using LSTM approach. In Advanced Statistical Modeling, Forecasting, and Fault Detection in Renewable Energy Systems; Intech Open: London, UK, 2020; pp. 3–18. [Google Scholar]
- Simeunović, J.; Schubnel, B.; Alet, P.J.; Carrillo, R.E.; Frossard, P. Interpretable temporal-spatial graph attention network for multi-site PV power forecasting. Appl. Energy 2022, 327, 120127. [Google Scholar] [CrossRef]
- Jeong, J.; Kim, H. Multi-site photovoltaic forecasting exploiting space-time convolutional neural network. Energies 2019, 12, 4490. [Google Scholar] [CrossRef]
- Guo, X.; Mo, Y.; Yan, K. Short-term photovoltaic power forecasting based on historical information and deep learning methods. Sensors 2022, 22, 9630. [Google Scholar] [CrossRef]
- Aprillia, H.; Yang, H.T.; Huang, C.M. Short-term photovoltaic power forecasting using a convolutional neural network–salp swarm algorithm. Energies 2020, 13, 1879. [Google Scholar] [CrossRef]
- Simeunović, J.; Schubnel, B.; Alet, P.J.; Carrillo, R.E. Spatio-temporal graph neural networks for multi-site PV power forecasting. IEEE Trans. Sustain. Energy 2021, 13, 1210–1220. [Google Scholar] [CrossRef]
- Gao, M.; Li, J.; Hong, F.; Long, D. Day-ahead power forecasting in a large-scale photovoltaic plant based on weather classification using LSTM. Energy 2019, 187, 115838. [Google Scholar] [CrossRef]
- Liu, W.; Liu, C.; Lin, Y.; Ma, L.; Xiong, F.; Li, J. Ultra-short-term forecast of photovoltaic output power under fog and haze weather. Energies 2018, 11, 528. [Google Scholar] [CrossRef]
- Yao, X.; Wang, Z.; Zhang, H. A novel photovoltaic power forecasting model based on echo state network. Neurocomputing 2019, 325, 182–189. [Google Scholar] [CrossRef]
- Han, Y.; Wang, N.; Ma, M.; Zhou, H.; Dai, S.; Zhu, H. A PV power interval forecasting based on seasonal model and nonparametric estimation algorithm. Sol. Energy 2019, 184, 515–526. [Google Scholar] [CrossRef]
- Dolara, A.; Grimaccia, F.; Leva, S.; Mussetta, M.; Ogliari, E. Comparison of training approaches for photovoltaic forecasts by means of machine learning. Appl. Sci. 2018, 8, 228. [Google Scholar] [CrossRef]
- Louzazni, M.; Mosalam, H.; Khouya, A.; Amechnoue, K. A non-linear auto-regressive exogenous method to forecast the photovoltaic power output. Sustain. Energy Technol. Assess. 2020, 38, 100670. [Google Scholar] [CrossRef]
- Lee, D.; Kim, K. Recurrent neural network-based hourly prediction of photovoltaic power output using meteorological information. Energies 2019, 12, 215. [Google Scholar] [CrossRef]
- Son, J.; Park, Y.; Lee, J.; Kim, H. Sensorless PV power forecasting in grid-connected buildings through deep learning. Sensors 2018, 18, 2529. [Google Scholar] [CrossRef]
- Mellit, A.; Pavan, A.M.; Lughi, V. Deep learning neural networks for short-term photovoltaic power forecasting. Renew. Energy 2021, 172, 276–288. [Google Scholar] [CrossRef]
- Dolatabadi, A.; Abdeltawab, H.; Mohamed, Y.A.R.I. Deep reinforcement learning-based self-scheduling strategy for a CAES-PV system using accurate sky images-based forecasting. IEEE Trans. Power Syst. 2022, 38, 1608–1618. [Google Scholar] [CrossRef]
- Pérez, E.; Pérez, J.; Segarra-Tamarit, J.; Beltran, H. A deep learning model for intra-day forecasting of solar irradiance using satellite-based estimations in the vicinity of a PV power plant. Sol. Energy 2021, 218, 652–660. [Google Scholar] [CrossRef]
- Zhen, Z.; Pang, S.; Wang, F.; Li, K.; Li, Z.; Ren, H.; Shafie-khah, M.; Catalao, J.P. Pattern classification and PSO optimal weights based sky images cloud motion speed calculation method for solar PV power forecasting. IEEE Trans. Ind. Appl. 2019, 55, 3331–3342. [Google Scholar] [CrossRef]
- Akhter, M.N.; Mekhilef, S.; Mokhlis, H.; Almohaimeed, Z.M.; Muhammad, M.A.; Khairuddin, A.S.M.; Akram, R.; Hussain, M.M. An hour-ahead PV power forecasting method based on an RNN-LSTM model for three different PV plants. Energies 2022, 15, 2243. [Google Scholar] [CrossRef]
- Wang, H.; Cai, R.; Zhou, B.; Aziz, S.; Qin, B.; Voropai, N.; Gan, L.; Barakhtenko, E. Solar irradiance forecasting based on direct explainable neural network. Energy Convers. Manag. 2020, 226, 113487. [Google Scholar] [CrossRef]
- Mitrentsis, G.; Lens, H. An interpretable probabilistic model for short-term solar power forecasting using natural gradient boosting. Appl. Energy 2022, 309, 118473. [Google Scholar] [CrossRef]
- Sun, Y.; Venugopal, V.; Brandt, A.R. Short-term solar power forecast with deep learning: Exploring optimal input and output configuration. Sol. Energy 2019, 188, 730–741. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. PeerJ Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef]
- Hodson, T.O. Root-mean-square error (RMSE) or mean absolute error (MAE): When to use them or not. Geosci. Model Dev. 2022, 15, 5481–5487. [Google Scholar] [CrossRef]
- Koutsandreas, D.; Spiliotis, E.; Petropoulos, F.; Assimakopoulos, V. On the selection of forecasting accuracy measures. J. Oper. Res. Soc. 2022, 73, 937–954. [Google Scholar] [CrossRef]
- Arya, D.; Maeda, H.; Ghosh, S.K.; Toshniwal, D.; Mraz, A.; Kashiyama, T.; Sekimoto, Y. Transfer learning-based road damage detection for multiple countries. arXiv 2020, arXiv:2008.13101. [Google Scholar]
- Madiniyeti, J.; Chao, Y.; Li, T.; Qi, H.; Wang, F. Concrete Dam Deformation Prediction Model Research Based on SSA–LSTM. Appl. Sci. 2023, 13, 7375. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, CA, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Grinsztajn, L.; Oyallon, E.; Varoquaux, G. Why do tree-based models still outperform deep learning on typical tabular data? Adv. Neural Inf. Process. Syst. 2022, 35, 507–520. [Google Scholar]
- Munawar, U.; Wang, Z. A framework of using machine learning approaches for short-term solar power forecasting. J. Electr. Eng. Technol. 2020, 15, 561–569. [Google Scholar] [CrossRef]
- Bhatt, U.; Xiang, A.; Sharma, S.; Weller, A.; Taly, A.; Jia, Y.; Ghosh, J.; Puri, R.; Moura, J.M.; Eckersley, P. Explainable machine learning in deployment. In Proceedings of the 2020 Conference on Fairness, Accountability, and Transparency, Barcelona, Spain, 27–30 January 2020; pp. 648–657. [Google Scholar]
- Burkart, N.; Huber, M.F. A survey on the explainability of supervised machine learning. J. Artif. Intell. Res. 2021, 70, 245–317. [Google Scholar] [CrossRef]
- Linardatos, P.; Papastefanopoulos, V.; Kotsiantis, S. Explainable ai: A review of machine learning interpretability methods. Entropy 2020, 23, 18. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Murzakhanov, I.; Chatzivasileiadis, S. Neural network interpretability for forecasting of aggregated renewable generation. In Proceedings of the 2021 IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids (SmartGridComm), Aachen, Germany, 25–28 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 282–288. [Google Scholar]
- Blanc, P.; Gschwind, B.; Lefèvre, M.; Wald, L. The HelioClim project: Surface solar irradiance data for climate applications. Remote Sens. 2011, 3, 343–361. [Google Scholar] [CrossRef]
- Vernay, C.; Blanc, P.; Pitaval, S. Characterizing measurements campaigns for an innovative calibration approach of the global horizontal irradiation estimated by HelioClim-3. Renew. Energy 2013, 57, 339–347. [Google Scholar] [CrossRef]
- Terrén-Serrano, G.; Bashir, A.; Estrada, T.; Martínez-Ramón, M. Girasol, a sky imaging and global solar irradiance dataset. Data Brief 2021, 35, 106914. [Google Scholar] [CrossRef]
- Terrén-Serrano, G. Intra-Hour Solar Forecasting Using Cloud Dynamics Features Extracted from Ground-Based Infrared Sky Images. Ph.D. Thesis, The University of New Mexico, Albuquerque, NM, USA, 2022. [Google Scholar]
- Augustine, J.A.; DeLuisi, J.J.; Long, C.N. SURFRAD–A national surface radiation budget network for atmospheric research. Bull. Am. Meteorol. Soc. 2000, 81, 2341–2358. [Google Scholar] [CrossRef]
- Holben, B.N.; Eck, T.F.; Slutsker, I.a.; Tanré, D.; Buis, J.; Setzer, A.; Vermote, E.; Reagan, J.A.; Kaufman, Y.; Nakajima, T.; et al. AERONET—A federated instrument network and data archive for aerosol characterization. Remote Sens. Environ. 1998, 66, 1–16. [Google Scholar] [CrossRef]
- Amillo, A.; Taylor, N.; Fernandez, A.; Dunlop, E.; Mavrogiorgios, P.; Fahl, F.; Arcaro, G.; Pinedo, I. Adapting PVGIS to trends in climate, technology and user needs. In Proceedings of the 38th European Photovoltaic Solar Energy Conference and Exhibition, Online, 6–10 September 2021; pp. 6–10. [Google Scholar]
- Hersbach, H. The ERA5 Atmospheric Reanalysis. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 12–16 December 2016; Volume 2016, p. NG33D–01. [Google Scholar]
- European Space Agency and European Organisation for the Exploitation of Meteorological Satellites. Meteosat Second Generation. Available online: https://www.eumetsat.int/meteosat-second-generation (accessed on 21 September 2023).
- European Centre for Medium-Range Weather Forecasts. Atmospheric Model High Resolution 10-Day Forecast (Set I-HRES). Available online: https://www.ecmwf.int/en/forecasts/datasets/set-i (accessed on 21 September 2023).
- European Centre for Medium-Range Weather Forecasts. Copernicus Climate Change Service-C3S. Available online: https://cds.climate.copernicus.eu/cdsapp#!/search?type=dataset (accessed on 21 September 2023).
- Surface Radiation Budget Network. Surface Radiation Budget Network. Available online: https://gml.noaa.gov/grad/surfrad/overview.html (accessed on 21 September 2023).
- National Centers for Environtmental Prediction (NCEP). Global Forecasting System. Available online: https://www.ncei.noaa.gov/products/weather-climate-models/global-forecast (accessed on 21 September 2023).
- Mahammad, S.S.; Ramakrishnan, R. GeoTIFF-A standard image file format for GIS applications. Map India Image Process. Interpret. 2003, 2023, 28–31. [Google Scholar]
- Finnish Meteorological Institute. Open Data Sets. Available online: https://en.ilmatieteenlaitos.fi/open-data-sets-available (accessed on 21 September 2023).
| Reference | Goal | Horizon (Step) | Test Size | Error Term | Methods | Location |
|---|---|---|---|---|---|---|
| [21] | PV power forecasting | 24 h (15 min) | 5 months | MAE, MSE, R, RMSE, Error | MLR, ANN | Hungary |
| [22] | PV power forecasting | 24 h (1 h) | not specified | RMSE, MAE | CNN, SVM, DT, MLP, LSTM, RF | Taiwan |
| [23] | PV power forecasting | 15, 30, 60 min (15 min) | 4 months | nMAE, nRMSE, 1- | Conv-LSTM, CNN | China |
| [24] | PV power forecasting | 15 min, 1 h, 3 h, 6 h (15 min) | not specified | nRMSE, nMAE | ST-Lasso, AR | France |
| [25] | PV power forecasting | 15 min | 20 days | RMSE, FS | CNN, AR | USA |
| [26] | Irradiance forecasting | 6 h (1 h) | 1 year | rRMSE, MBE, FS | DNN (FNN), AR, GBT | Netherlands |
| [27] | Irradiance forecasting | 1 h (10 min) | 2 years | RMSE, MBE, FS | ANN, GBM, RF, Conv ReLU + Dense | USA |
| [28] | PV power forecasting | 1, 2, 3 h (1 h) | 23 days | RMSE, MSE, | BiLSTM, ARMA, ARIMA, SARIMA | China |
| [29] | Irradiance forecasting | 24 h (15 min) | 3 years | MSE, FS | Clear sky models | USA |
| [15] | Irradiance forecasting | 15 min | 36 days | RMSE, MAE, | CNN-LSTM, CNN-ANN | USA |
| [30] | Irradiance forecasting | 10 min (1 min) | 1 month | RMSE, MAE, nRMSE, nMAE, FS | ResNet | USA |
| [31] | PV power forecasting | 15 min (1 min) | 20 days | RMSE, MAE, FS | CNN + Dense | USA |
| [32] | PV power forecasting | 1 h (1 min) | 1 week | RMSE, MAE, MAPE | LSTM, ANN, GRU | Taiwan (*) |
| [33] | PV power forecasting | 6, 12, 24 h (1 h) | 100 days | RMSE, MAE, MAPE, MRE, MBE | LSTM, ANN, GRU | USA |
| [16] | Irradiance forecasting | 15 min | 70 days | RMSE, MAE, , nPIAW, PICP, CWC | CNN-QR, LSTM-QR, ANN | USA |
| [17] | Irradiance forecasting | 10 min (1 min) | 30 days | MAPE, RMSE, MBE | SVM, BPNN, ARIMA | USA |
| [14] | Irradiance forecasting | 5, 10 min | 5 months | Accuracy | ResNet | Italy, Switzerland |
| [34] | PV power forecasting | 24 h (15 min) | 1 year | CRPS, MARE, PIAW | QR | Hungary |
| [35] | PV power forecasting | 24 h | 31 days | RMSE, MSE, MAE, MAPE, nRMSE, R | GRU, RF | China |
| [36] | PV power forecasting | 5 min (0.5 min) | 1 day | SSIM, MSE | Conv-AutoEncoder | USA |
| [37] | PV power forecasting | 24 h | 5 weeks | MAE, RMSE, nMAE, nRMSE, IA, Error | MLP | Finland |
| [38] | PV power forecasting | 24 h (15 min) | 1 year | nRMSE, nMAE, nMBE | ANN + Physical Model | Hungary |
| [39] | PV power forecasting | 24 h (15 min) | 2 years | nRMSE, nMAE, nMBE, FS, | LR, SVM, CatBoost, MLP, RF, LGBM, XGB | Hungary |
| [40] | PV power forecasting | 5 h (1 h) | 4 months | MAPE, MAE, RMSE, nMAE | LSTM, CNN, FNN | South Korea |
| [41] | PV power forecasting | 24 h | 10 months | RMSE, MSE, MAE, | XGB, AdaBoost, RF, ETR | Kuala Lumpur |
| [42] | PV power forecasting | 24 h (15 min) | 1.5 months | RMSE, MAPE, MAE, | LSTM | Saudi Arabia (*) |
| [43] | PV power forecasting | 6 h (15 min) | 4 months, 1 year | nMAE, nRMSE | GCLSTM, GCTrafo, TSM-GAT, STCNN | Switzerland, USA |
| [44] | PV power forecasting | 2, 6 h (1 h) | 2.5 months | nRMSE, MAPE, Error | AR, FNN, LSTM, STCNN | USA |
| [45] | PV power forecasting | 7.5, 15 min, (0.05 min) | 4 days | MAE, RMSE, adj R, Accuracy | DT, RF, SVR, MLP, LSTM, BiLSTM, NLSTM | China |
| [46] | PV power forecasting | 24 h (1 h) | 3.5 months | MAPE, MRE | SVM-SSA, CNN-SSA, LSTM-SSA | Taiwan |
| [47] | PV power forecasting | 6 h (15 min) | 1 year | nMAE, nRMSE | STAR, GCLSTM, GCTrafo, STCNN, SVR, EDLSTM | Switzerland |
| [48] | PV power forecasting | 16 h (15 min) | not specified | RMSE, MAD | LSTM, Wavelet NN, SVM, BPNN | China |
| [49] | PV power forecasting | 72 h (1 h) | 2 months | MAE, MSE | BPNN | China |
| [50] | PV power forecasting | 10 h (1 h) | 500 samples | MAPE, Error | MR-ESN | USA |
| [51] | Irradiance forecasting | not specified | not specified | MAE, RMSE, PICP, PINAW, Accuracy | ELM | China |
| [20] | PV power forecasting | 1 h (1 h) | 3.5 months | MSE | Ridge | Croatia |
| [52] | PV power forecasting | 24 h (1 h) | 22 days | MAPE, nMAE, wMAE, eMAE, nRMSE, , Error | PHANN | Italy |
| [53] | PV power forecasting | 24, 72 h (1 h) | 1 month | IAE, RMSE, MSE, R | NARX | Egypt |
| [54] | PV power forecasting | 14 h (1 h) | 4 months | MAE, RMSE | ANN, DNN, LSTM, ARIMA, SARIMA | South Korea |
| [55] | PV power forecasting | 24 h | 4 months | MAE, RMSE, MAPE, Error, | MLP (DNN) | South Korea |
| [56] | PV power forecasting | 1, 5, 30, 60 min (1 min) | 1 month | MAE, RMSE, MAPE, | LSTM, ENN, NAR | Italy |
| [57] | Irradiance forecasting | 17 h (1 h) | 1 year | MAE, MAPE, RMSE | DRL + CNN-BiLSTM | USA |
| [13] | PV power forecasting | 4 h (15 min) | 30 days | nMAE, nRMSE | SVM, GBDT, ARMA | USA |
| [58] | Irradiance forecasting | 6 h (15 min) | 6 months | MAE, rMAE, RMSE, rRMSE | ConvNet + Dense | France |
| [59] | PV power forecasting | 1 min | 200 samples | K-means, PSO | China | |
| [60] | PV power forecasting | 1 h | 1 year | RMSE, R | LSTM, SVR, ANN, ANFIS, GPR | Kuala Lumpur |
| [61] | Irradiance forecasting | 1 min | not specified | RMSE, MAE, R | SVR, BPNN, XGB, DXNN | France |
| [62] | PV power forecasting | 36 h (15 min) | 1 month | RMSE, MAE, MBE, CRPS, PIAW, PICP | NGBoost, GP | Germany |
| Measure of Performance | Equation |
|---|---|
| Root Mean Squared Error (RMSE) * | |
| Mean Squared Error (MSE) | |
| Mean Absolute Error (MAE) * | |
| Mean Absolute Percentage Error (MAPE) | |
| Mean Absolute Deviation (MAD) | |
| Mean Bias Error (MBE) * | |
| Index of Agreement (IA) | |
| Correlation Coefficient () | |
| Coefficient of Determination (R) | |
| Continuous Ranked Probability Score (CRPS) | |
| Prediction Interval Average Width (PIAW) * | |
| Prediction Interval Coverage Probability (PICP) | |
| Coverage Width Calculation (CWC) | |
| Forecast Skill (FS) | |
| Envelope Weighted Mean Absolute Error (eMAE) |
| Source/Name | Data Type | Link | References |
|---|---|---|---|
| NREL | Irradiance, satellite images | https://midcdmz.nrel.gov/apps/sitehome.pl?site=BMS | [15,16,27,33,43,44,57] |
| HelioClim3 | Irradiance | https://www.soda-pro.com/help/helioclim/helioclim-3-overview | [24,76,77] |
| EUMETSAT | Satellite images | https://www.eumetsat.int/eumetsat-data-centre | [20] |
| Girasol | Irradiance | https://datadryad.org/stash/dataset/doi:10.5061/dryad.zcrjdfn9m | [78,79] |
| ECMWF | Irradiance | https://www.ecmwf.int/en/forecasts/datasets/set-i | [11,26] |
| SURFRAD | Satellite images | https://gml.noaa.gov/grad/surfrad/ | [29,80] |
| SKIPP’D | Satellite images | https://github.com/yuhao-nie/Stanford-solar-forecasting-dataset | [31] |
| AERONET | Aerosol optical depth (AOD) | https://aeronet.gsfc.nasa.gov/new_web/data.html | [49,81] |
| GFS | Irradiance | global_weather_forecast | [47] |
| SARAH-2 | Irradiance | pvgis_sarah-2 | [82] |
| C3S | Irradiance | https://cds.climate.copernicus.eu/cdsapp#!/search?type=dataset | [83] |
| Source/Ref. | Period (Training) | Testing | Goal | Horizon (Step) | Best Method | Error |
|---|---|---|---|---|---|---|
| NREL/[57] | (1 January 2015–31 December 2018) | 1 January 2020–31 December 2020 | Irradiance forecasting | 17 h (1 h) | DRL + CNN-BiLSTM | RMSE = 80.02 W/m MAE = 51.95 W/m MAPE = 7.64% |
| NREL/[27] | (1 January 2012–31 December 2014) | 1 January 2016–31 December 2017 | Irradiance forecasting | 1 h (10 min) | SolarNet | FS = 34.02 RMSE = 81.03 W/m MBE = −0.44 W/m |
| NREL/[15] | (1 July 2017–19 April 2018) | 25 May 2018–30 June 2018 | Irradiance forecasting | 15 min | CNN-LSTM CNN-ANN | = 0.97 RMSE = 80.48 W/m MAE = 51.89 W/m |
| NREL/[33] | (1 January 2016–22 September 2018) | 22 September 2018–31 December 2018 | PV power forecasting | 24 h (1 h) | LSTM-NN | MAE = 0.36 MW RMSE = 0.71 MW MAPE = 22.31% MRE = 1.44% MBE = 0.01 MW |
| NREL/[16] | 1 July 2017–30 June 2018 | 5-fold CV∼70 days | Irradiance forecasting | 15 min | CNN-QR LSTM-QR | MAE = 68.84 W/m RMSE = 98.94 W/m nPIAW = 0.09% PICP = 0.92% CWC = 0.16 = 0.96 |
| NREL/[43] | (1 January 2006–31 August 2006) | 1 September 2006–31 December 2006 | PV power forecasting | 6 h (15 min) | TSM-GAT | nMAE = 14.78% nRMSE = 10.37% |
| SKIPP’D/[31] | 1 March 2017–1 December 2019 | ∼20 days (4% of data) | PV power forecasting | 15 min (1 min) | ConvNet | FS = 16.44 RMSE = 0.0024 MW MAE = 0.0015 MW |
| SURFRAD/[29] | 1 January 2015–31 December 2018 | not specified | Irradiance forecasting | 24 h (15 min) | Ineichen-Perez clear sky model | FS = 14.3 RMSE = 120 W/m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pandžić, F.; Capuder, T. Advances in Short-Term Solar Forecasting: A Review and Benchmark of Machine Learning Methods and Relevant Data Sources. Energies 2024, 17, 97. https://doi.org/10.3390/en17010097
Pandžić F, Capuder T. Advances in Short-Term Solar Forecasting: A Review and Benchmark of Machine Learning Methods and Relevant Data Sources. Energies. 2024; 17(1):97. https://doi.org/10.3390/en17010097
Chicago/Turabian StylePandžić, Franko, and Tomislav Capuder. 2024. "Advances in Short-Term Solar Forecasting: A Review and Benchmark of Machine Learning Methods and Relevant Data Sources" Energies 17, no. 1: 97. https://doi.org/10.3390/en17010097
APA StylePandžić, F., & Capuder, T. (2024). Advances in Short-Term Solar Forecasting: A Review and Benchmark of Machine Learning Methods and Relevant Data Sources. Energies, 17(1), 97. https://doi.org/10.3390/en17010097







