Multi-Objective Short-Term Optimal Dispatching of Cascade Hydro–Wind–Solar–Thermal Hybrid Generation System with Pumped Storage Hydropower
Abstract
:1. Introduction
- (1)
- This paper proposes a multi-objective optimal dispatching model of a cascade hydro–wind–solar–thermal hybrid generation system with pumped storage hydropower, which takes into account the complex restrictions of cascade hydropower and the flexibility of the PSH.
- (2)
- In order to improve the computational speed of the initialization process, the discharge of each cascade hydropower station is selected as the bottom decision variable to form the feasible region, and the dispatch output of every station is chosen as the upper variable to participate in the genetic variation in the population.
- (3)
- Based on the dispatching operation strategy proposed in this paper, the optimization results under four different scenarios are compared. As a result, PSH can exert the advantage of peak load shifting to significantly reduce the operation cost and the residual load fluctuation while improving the renewable energy consumption rate.
2. Short-Term Optimal Dispatching Model of the Hybrid Generation System
2.1. Objective Functions
2.1.1. Objective Function F1: The Lowest Operation Costs
- Fuel cost of thermal power units Cf
- Penalty cost for pollutant emissions Cp
- The maintenance cost of the power stations Cs
- The penalty cost of power abandonment Cd
- Start-up and shutdown loss cost of PSH Ch
2.1.2. Objective Function F2: The Smallest Residual Load Fluctuation
2.2. Constraints
2.2.1. System Power Balance Constraints
2.2.2. Operational Constraints of Thermal Power Units
2.2.3. Operational Constraints of Cascade Hydropower
- Unit output constraints
- Hydropower output characteristic constraints
- Water discharge and reservoir volume constraints
- Water balance constraints
2.2.4. Renewable Energy Output Constraints
2.2.5. Operation Constraints of PSH
- Unit output constraints
- Unique operating condition constraints
- Reservoir capacity and energy balance constraints
- Maximum start–stop times constraint of units
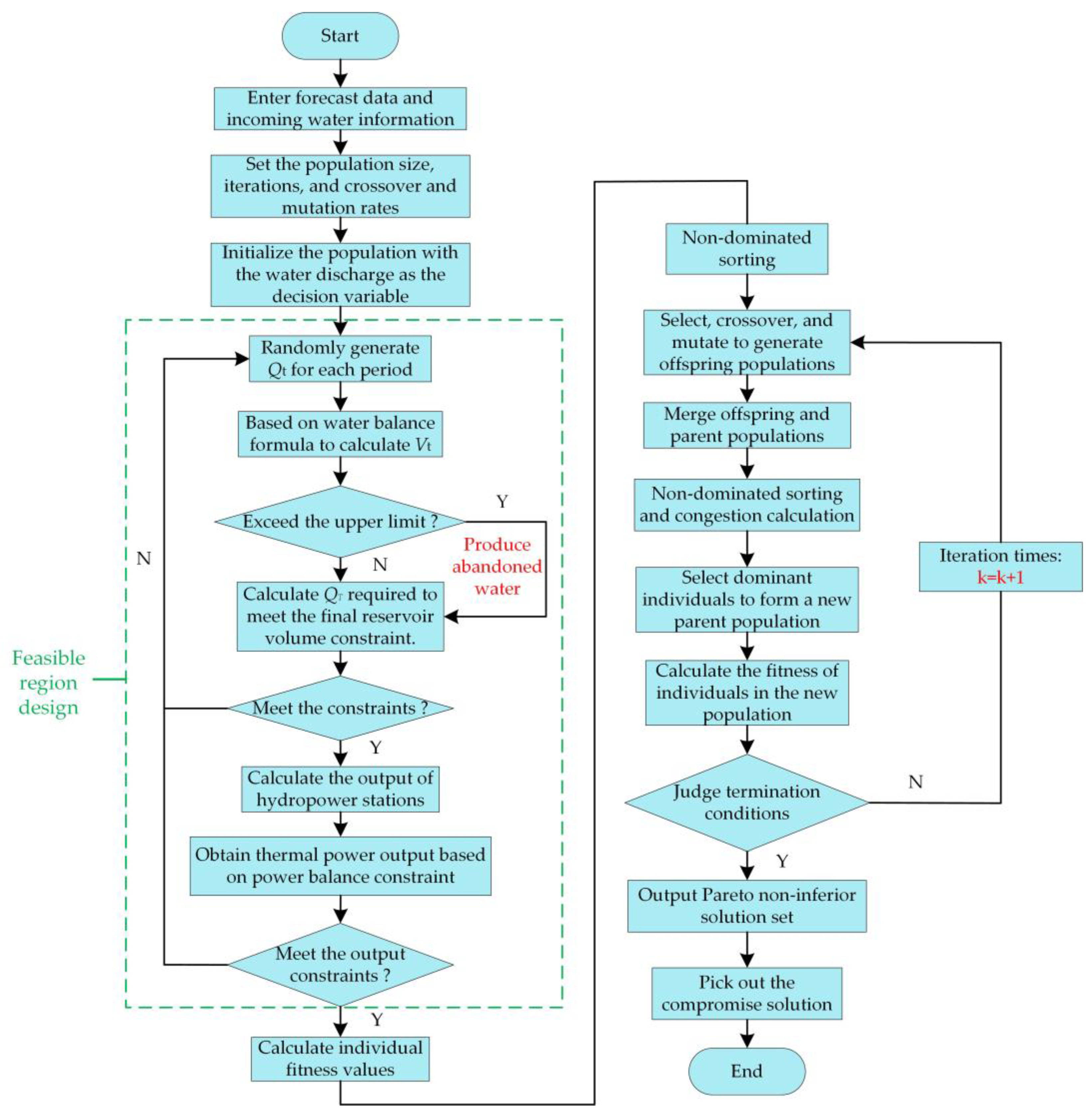
3. Solution and Scheduling Strategy
3.1. Multi-Objective Optimization Method Based on NSGA-II Algorithm
3.2. Operation Strategy of Hybrid Generation System
4. Case Study
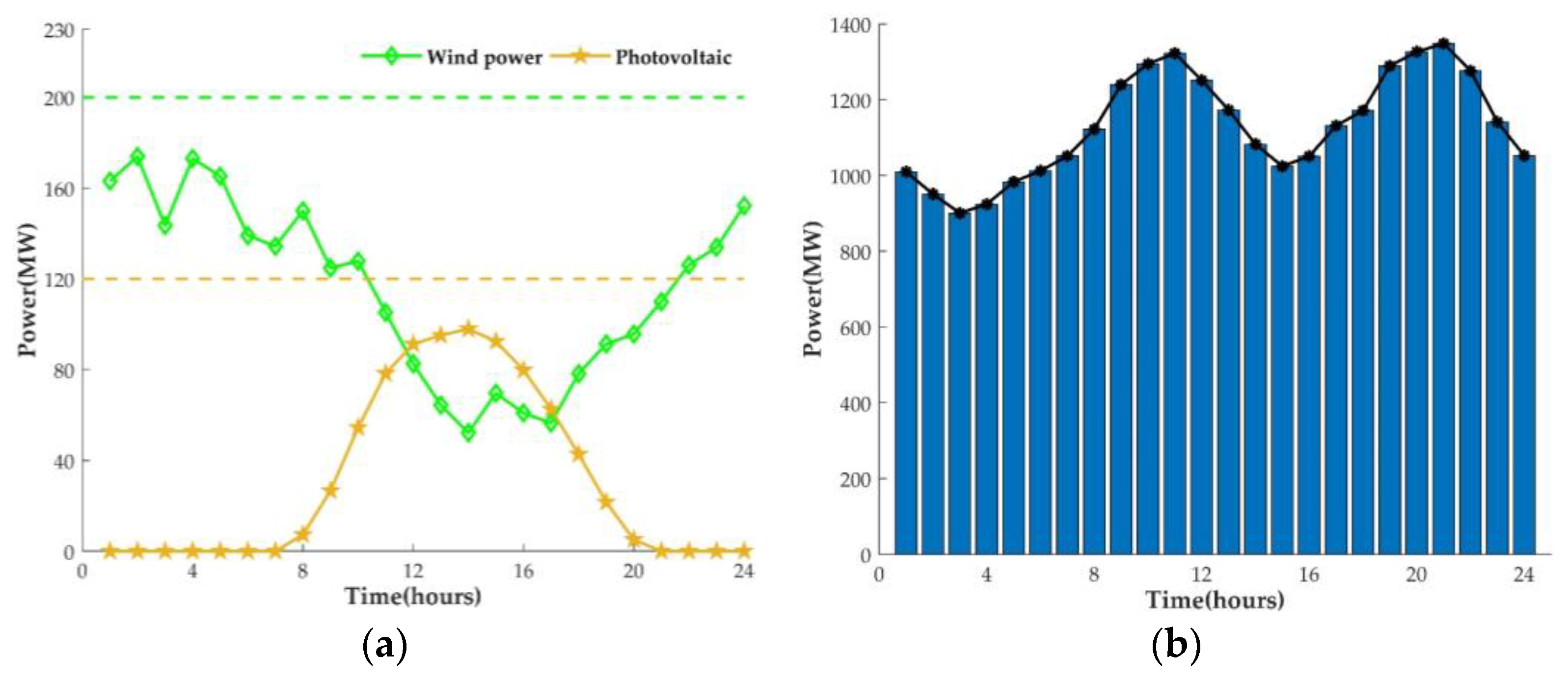
4.1. Basic Data
4.2. Scheduling Scenarios
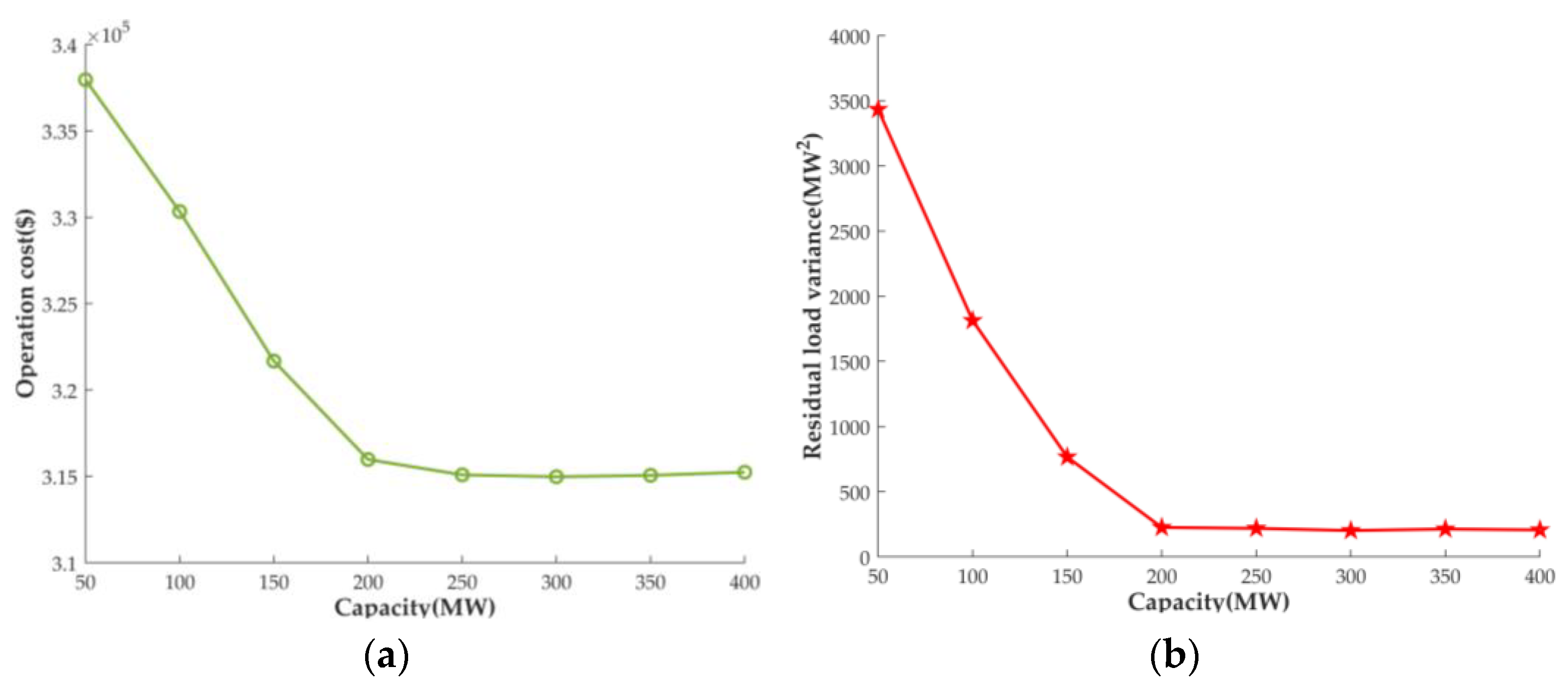
5. Results and Discussion
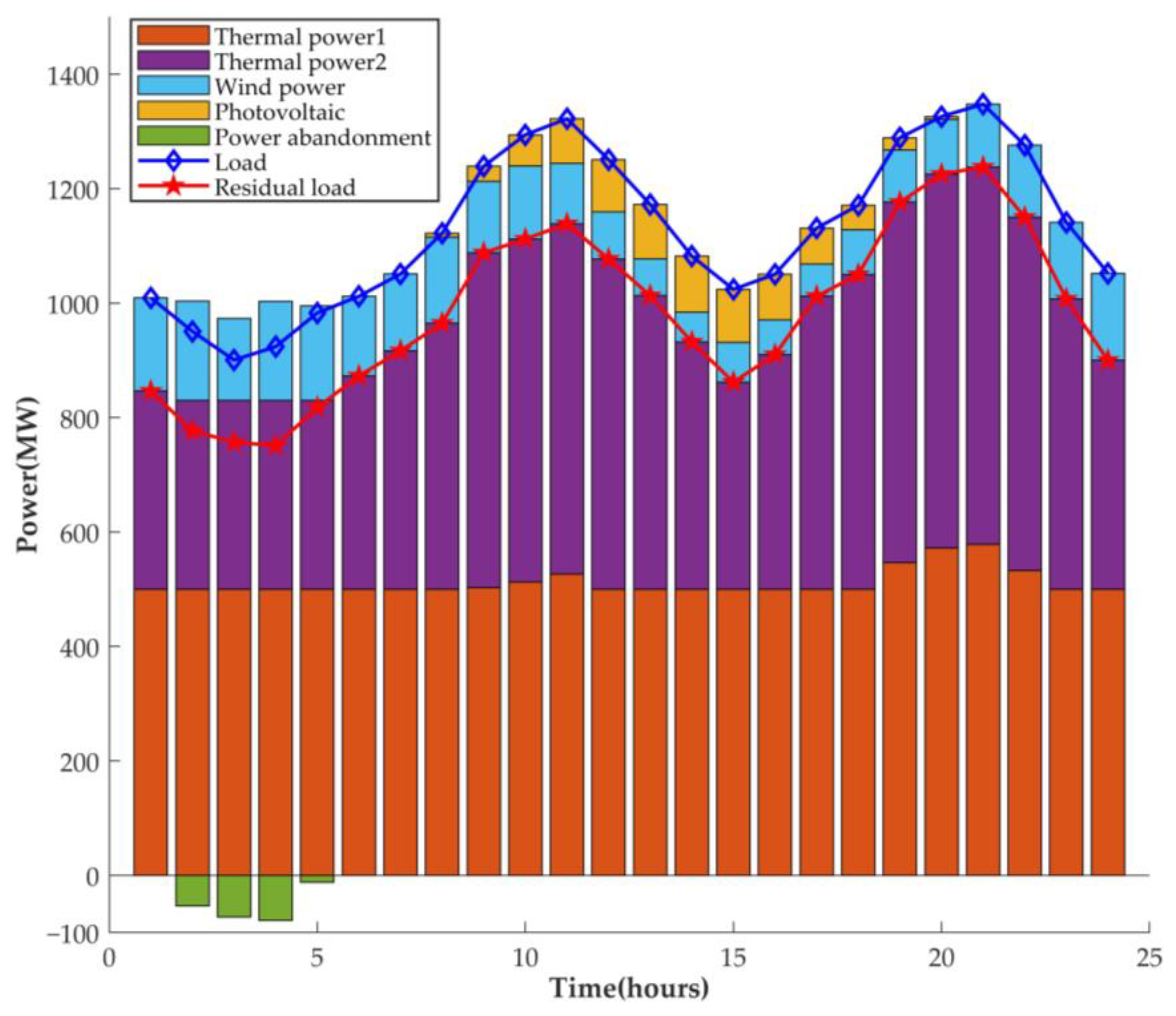
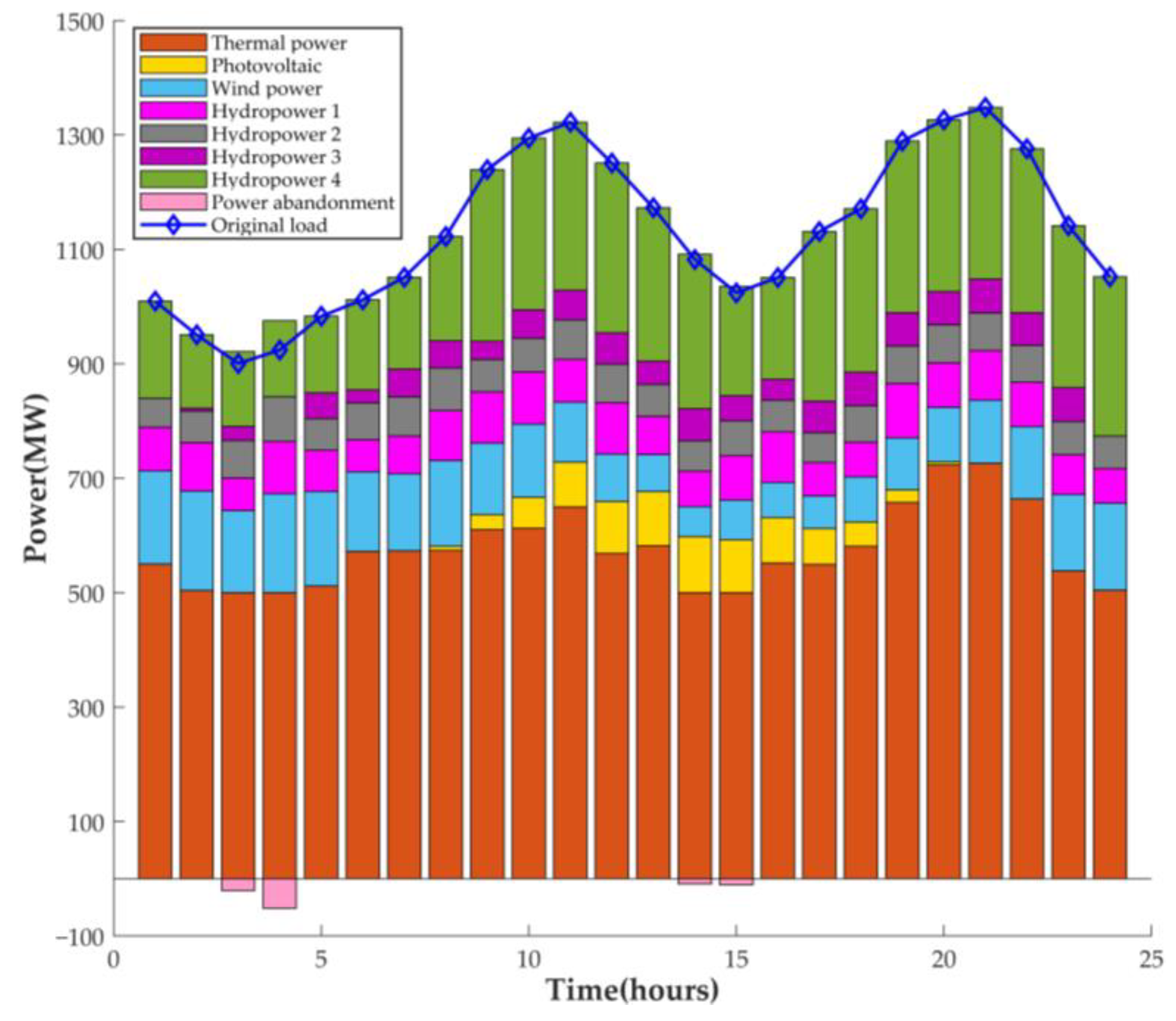
5.1. Results
5.2. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Z.G.; Kang, C.Q. Challenges and prospects for constructing the new-type power system towards a carbon neutrality future. Proc. CSEE 2022, 42, 2806–2819. [Google Scholar] [CrossRef]
- Zhang, L.Q.; Xie, J.; Chen, X.Y.; Zhan, Y.S.; Zhou, L. Cooperative Game-Based Synergistic Gains Allocation Methods for Wind-Solar-Hydro Hybrid Generation System with Cascade Hydropower. Energies 2020, 13, 3890. [Google Scholar] [CrossRef]
- Xie, J.; Zheng, Y.M.; Pan, X.P.; Zheng, Y.; Zhang, L.Q. A Short-Term Optimal Scheduling Model for Wind-Solar-Hydro Hybrid Generation System with Cascade Hydropower Considering Regulation Reserve and Spinning Reserve Requirements. IEEE ACCESS 2021, 9, 10765–10777. [Google Scholar] [CrossRef]
- Gilberto, P.; Arno, K.; Fausto, A.C. Complementarity Maps of Wind and Solar Energy Resources for Rio Grande do Sul, Brazil. Energy Power Eng. 2017, 9, 489–504. [Google Scholar] [CrossRef]
- Han, X.Y.; Ding, L.J.; Chen, G. Key Technologies and Research Prospects for Cascaded Hydro-Photovoltaic-Pumped Storage Hybrid Power Generation System. Trans. China Electrotech. Soc. 2020, 35, 2711–2722. [Google Scholar] [CrossRef]
- Li, F.; Li, X.S. Short-term optimal scheduling of multi-energy combined generation systems based on the regulation of cascade hydropower stations. Power Syst. Prot. Control. 2022, 50, 11–20. [Google Scholar] [CrossRef]
- Petrakopoulou, F.; Robinson, A.; Loizidou, M. Simulation and analysis of a stand-alone solar-wind and pumped-storage hydro power plant. Energy 2016, 96, 676–683. [Google Scholar] [CrossRef]
- Gupta, A.; Kumar, A.; Khatod, D.K. Optimized scheduling of hydropower with increase in solar and wind installations. Energy 2019, 183, 716–732. [Google Scholar] [CrossRef]
- Shen, J.J.; Wang, Y.; Chen, C.T. Research Status and Prospect of Generation Scheduling for Hydropower-wind-solar Energy Complementary System. Proc. CSEE 2022, 42, 3871–3885. [Google Scholar] [CrossRef]
- Beluco, A.; Souza, P.K.D.; Krenzinger, A. A method to evaluate the effect of complementarity in time between hydro and solar energy on the performance of hybrid hydro PV generating plants. Renew. Energy 2012, 45, 24–30. [Google Scholar] [CrossRef]
- Chaima, E.; Lian, J.J.; Ma, C.; Zhang, Y.S.; Kavwenje, S. Complementary Optimization of Hydropower with Pumped Hydro Storage–Photovoltaic Plant for All-Day Peak Electricity Demand in Malawi. Energies 2021, 14, 4948. [Google Scholar] [CrossRef]
- Bayόn, L.; Grau, J.M.; Ruiz, M.M.; Suarez, P.M. A comparative economic study of two configurations of hydro–wind power plants. Energy 2016, 112, 8–16. [Google Scholar] [CrossRef]
- Wang, X.X.; Mei, Y.D.; Cai, H.; Cong, X.Y. A New Fluctuation Index: Characteristics and Application to Hydro-Wind Systems. Energies 2016, 9, 114. [Google Scholar] [CrossRef]
- Hu, W.; Zhang, H.X.; Dong, Y.; Wang, Y.T. Short-term optimal operation of hydro-wind-solar hybrid system with improved generative adversarial networks. Appl. Energy 2019, 250, 389–403. [Google Scholar] [CrossRef]
- Huang, K.D.; Liu, P.; Ming, B.; Kim, J.S.; Gong, Y. Economic operation of a wind-solar-hydro complementary system considering risks of output shortage, power curtailment and spilled water. Appl. Energy 2021, 290, 116805. [Google Scholar] [CrossRef]
- Luo, B.; Chen, Y.C.; Liu, Z.W. Short-term Optimal Dispatch Model for Maximizing Expectation of Consumption Power of Cascade Hydro-Photovoltaic Complementary System. Autom. Electr. Power Syst. 2023, 47, 66–75. [Google Scholar] [CrossRef]
- Li, F.F.; Qiu, J. Multi-objective optimization for integrated hydro–photovoltaic power system. Appl. Energy 2016, 167, 377–384. [Google Scholar] [CrossRef]
- Xiao, X.; Zhou, Y.H.; He, S.Y.; Zhang, L. Optimal joint operation of hydro-thermal-wind hybrid power system with cascaded hydro power. Electr. Power Autom. Equip. 2018, 38, 100–108. [Google Scholar] [CrossRef]
- Wang, K.Y.; Luo, X.J.; Wu, L.; Liu, X.C. Optimal Dispatch of Wind-hydro-thermal Power System with Priority Given to Clean Energy. Proc. CSEE 2013, 33, 27–38. [Google Scholar] [CrossRef]
- Ye, L.; Qu, X.X.; Yao, Y.X. Analysis on Intraday Operation Characteristics of Hybrid Wind-solar-hydro Power Generation System. Autom. Electr. Power Syst. 2018, 42, 66–75. [Google Scholar] [CrossRef]
- Zhang, X.S.; Ma, G.W.; Huang, W.B.; Chen, S.J. Short-Term Optimal of a Wind-PV-Hydro Complementary Installation: Yalong River, Sichuan Province, China. Energies 2018, 11, 868. [Google Scholar] [CrossRef]
- Wei, M.K.; Cai, S.R.; Li, J. Peak-shaving co-optimization strategies of cascaded hydropower and wind-photovoltaic generation in system with high penetration of hydropower. J. Electr. Power Sci. Technol. 2021, 36, 199–208. [Google Scholar] [CrossRef]
- Yin, Y.; Liu, T.Q.; He, C. Day-ahead stochastic coordinated scheduling for thermal-hydro-wind-photovoltaic systems. Energy 2019, 187, 115944–115956. [Google Scholar] [CrossRef]
- Wang, J.H.; Niu, Y.G.; Chen, Y.; Li, X.W. Research on Day-ahead Optimal Dispatching of High-proportion Renewable Energy Power System considering Deep Peak Load Regulation of the Thermal Power. Acta Energiae Solaris Sin. 2023, 44, 493–499. [Google Scholar] [CrossRef]
- Zhang, S.; Yang, W.; Li, X.; Zhao, Z.; Wang, R.; Li, Y. Economic Evaluation of Wind–PV–Pumped Storage Hybrid System Considering Carbon Emissions. Energy Rep. 2022, 8, 1249–1258. [Google Scholar] [CrossRef]
- Luo, Y.X.; Wang, Y.H.; Liu, C.; Fan, L.D. Two-Stage Optimal Dispatching of Wind Power-Photovoltaic-Thermal Power-Pumped Storage Combined System. Acta Energiae Solaris Sin. 2023, 44, 500–508. [Google Scholar] [CrossRef]
- Zhang, G.B.; Chen, Y.; Zhang, J.H.; Tang, N.N. Research on Optimization of Day-ahead Dispatching of Wind Power-Photovoltaic-Hydropower-Thermal Power-Pumped Storage Combined Power Generation System. Acta Energiae Solaris Sin. 2020, 41, 79–85. [Google Scholar]
- Zhang, Q.W.; Wang, X.L.; Li, Y. Optimal Scheduling of Hybrid Wind-Photovoltaic-Hydro-Pumped Storage Power System. Electr. Energy 2017, 38, 581–586. [Google Scholar]
- Zhu, L.; Zhou, X.Y.; Tang, L.J.; Lao, C.S. Multi-Objective Optimal Operation for Microgrid Considering Interruptible Loads. Power Syst. Technol. 2017, 41, 1847–1854. [Google Scholar] [CrossRef]
- Weng, J.M.; Liu, D.; He, W.G.; Yang, B.; Huang, Y.H. Multi-objective Optimization of Distribution Network Operation Mode Based On AHP. Autom. Electr. Power Syst. 2012, 36, 56–61. [Google Scholar] [CrossRef]
- Shi, R.F.; Liang, Z.H.; Ma, Y. TOPSIS Method Based Orderly Charging Strategy for Electric Vehicles in Residential Area. Autom. Electr. Power Syst. 2018, 42, 104–110+159. [Google Scholar] [CrossRef]
- Xu, X.T.; Zou, W.J.; Ma, G. Research on Comprehensive Evaluation of Regional Integrated Energy System Based on BWM-CRITIC Determination. Electr. Autom. 2023, 45, 78–81. [Google Scholar] [CrossRef]
- Sun, H.J.; Gong, L.; Peng, C.H.; Wen, Z.Z. Multi-objective Dynamic Decomposition Optimal Dispatch Considering Wind-photovoltaic-hydro Multiple Uncertainty Confidence Risk. Power Syst. Technol. 2022, 46, 3416–3428. [Google Scholar] [CrossRef]
- Bognár, F.; Szentes, B.; Benedek, P. Development of the PRISM Risk Assessment Method Based on a Multiple AHP-TOPSIS Approach. Risks 2022, 10, 213. [Google Scholar] [CrossRef]
- Zeng, W.; Fan, J.; Ren, Z.; Liu, X.; Lv, S.; Cao, Y.; Xu, X.; Liu, J. Economic Evaluation Method of Modern Power Transmission System Based on Improved Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) and Best-Worst Method-Anti-Entropy Weight. Energies 2023, 16, 7242. [Google Scholar] [CrossRef]
- Hassan, I.; Alhamrouni, I.; Azhan, N.H. A CRITIC–TOPSIS Multi-Criteria Decision-Making Approach for Optimum Site Selection for Solar PV Farm. Energies 2023, 16, 4245. [Google Scholar] [CrossRef]
- Xu, J. Peak Shaving Strategy and Benefit Evaluation of Thermal Power Units under the Consumption of New Energy; Nanjing University of Posts and Telecommunications: Nanjing, China, 2021. [Google Scholar]
- Yan, S.L.; Gu, B.; Ai, S.J. The Environmental Cost Accounting and Sensitivity Analysis for Thermal Power Plants. Electr. Power Sci. Eng. 2016, 32, 62–67. [Google Scholar] [CrossRef]
- Zhao, C.; Dai, C.H.; Yuan, S. Multi-Objective Optimization of Wind Power Planning considering Economy-Social Benefit of Wind Power and Thermal Power. Acta Energiae Solaris Sin. 2019, 40, 1125–1132. [Google Scholar]
- Lin, L.; Yue, X.Y.; Xu, B.Q.; Sun, Y. Sequence and Strategy of Pumped Storage-thermal Combined Peak Shaving Considering Benefits of Pumped Storage and Deep Regulation of Thermal Power. Power Syst. Technol. 2021, 45, 20–32. [Google Scholar] [CrossRef]
- Basu, M. An interactive fuzzy satisfying method based on evolutionary programming technique for multiobjective short-term hydrothermal scheduling. Electr. Power Syst. Res. 2003, 69, 277–285. [Google Scholar] [CrossRef]
- Zeng, X.T.; Liu, T.Q.; Li, Q.; Wang, F.J. Short-Term Complementary Optimal Dispatch Model of Multi-Source Hybrid Power System Based on Virtual Power Configuration Strategy. Power Syst. Technol. 2016, 40, 1386–1397. [Google Scholar] [CrossRef]
- Liu, Z.F.; Zhang, Z.; Zhuo, R.Q.; Wang, X.Y. Optimal operation of independent regional power grid with multiple wind solar-hydro-battery power. Appl. Energy 2019, 235, 1541–1550. [Google Scholar] [CrossRef]




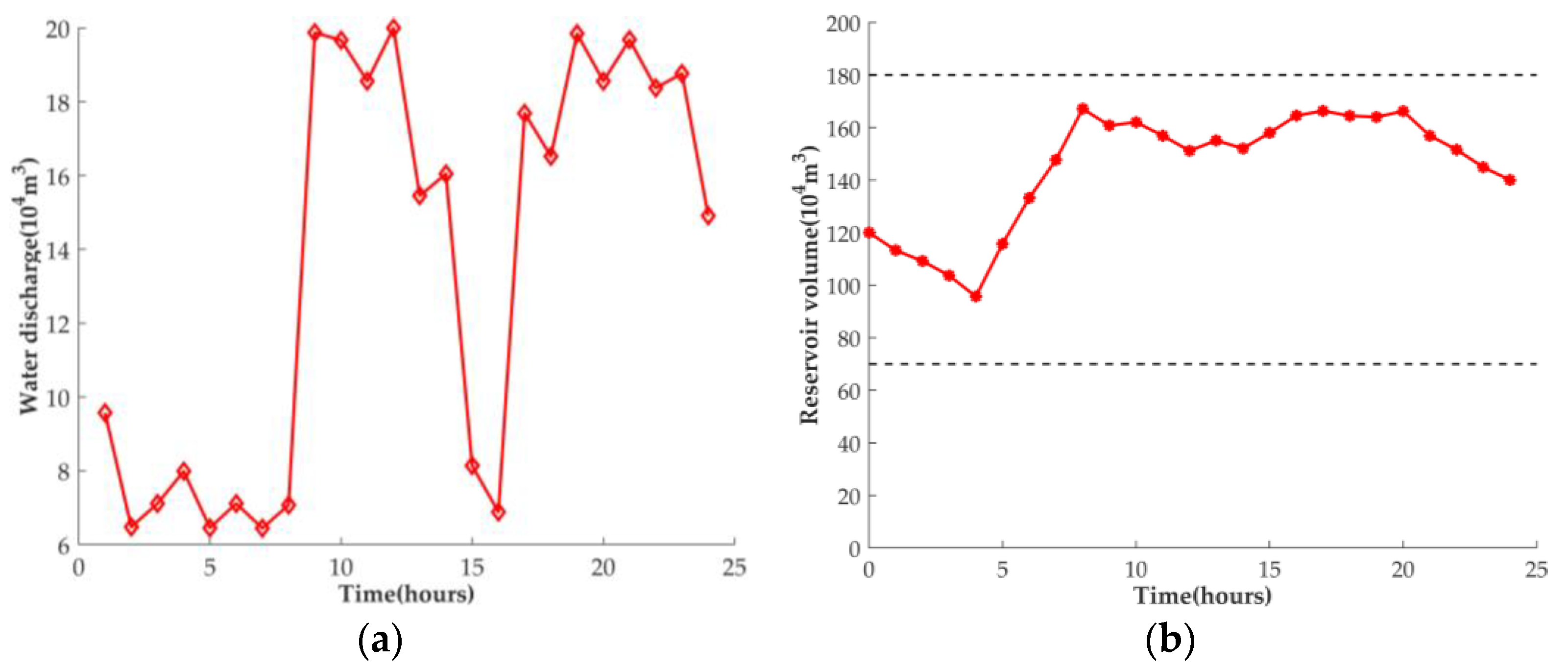
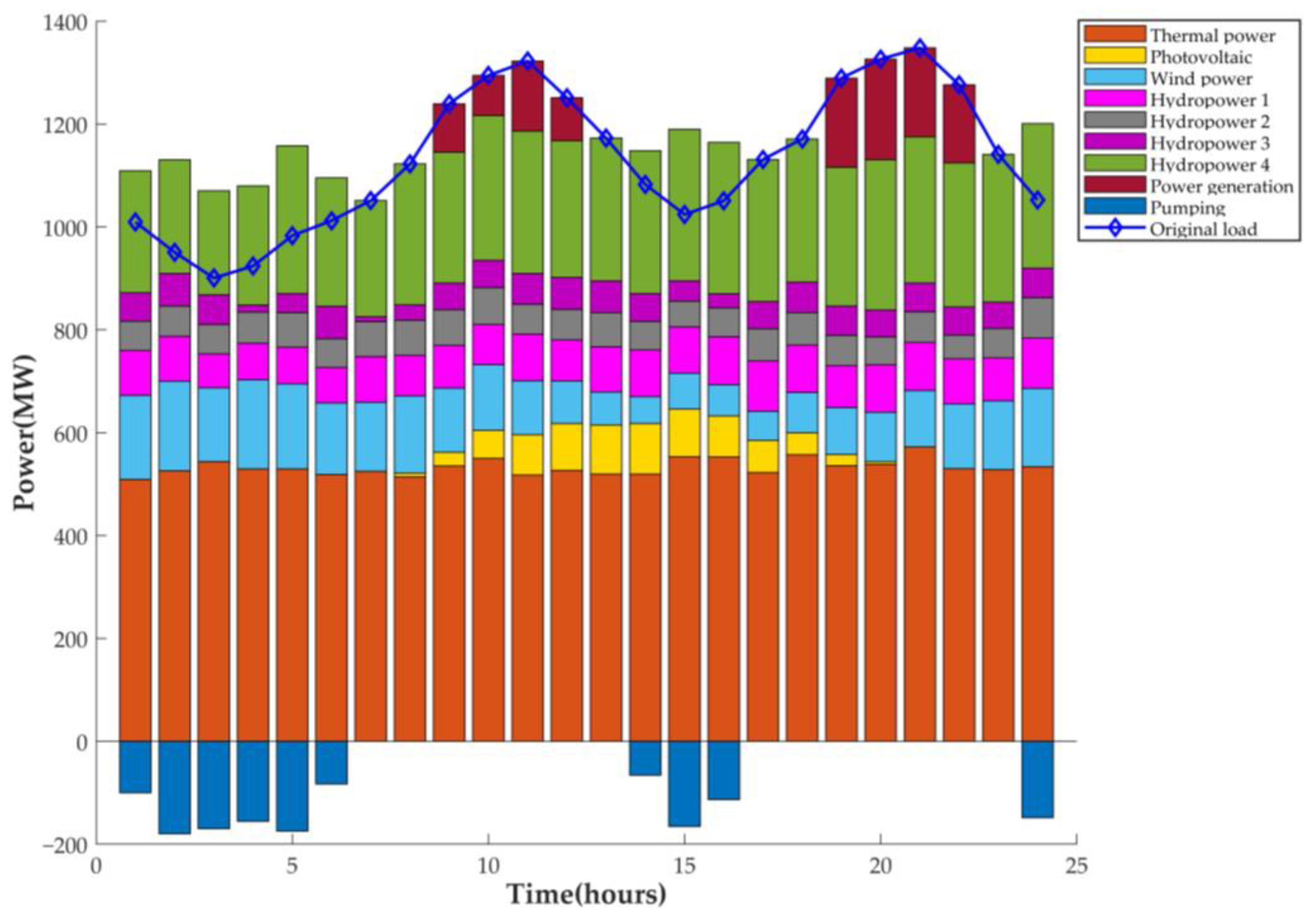
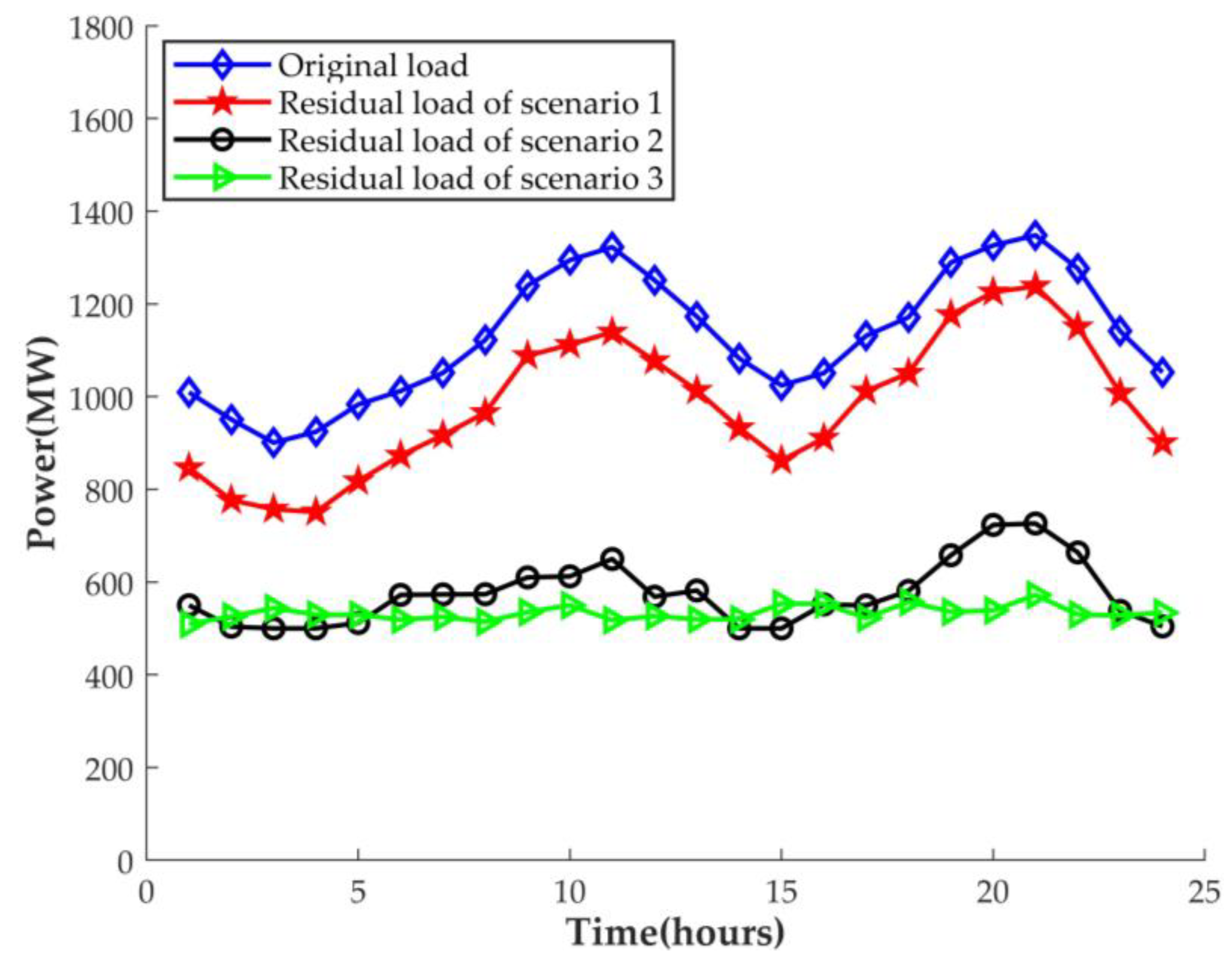
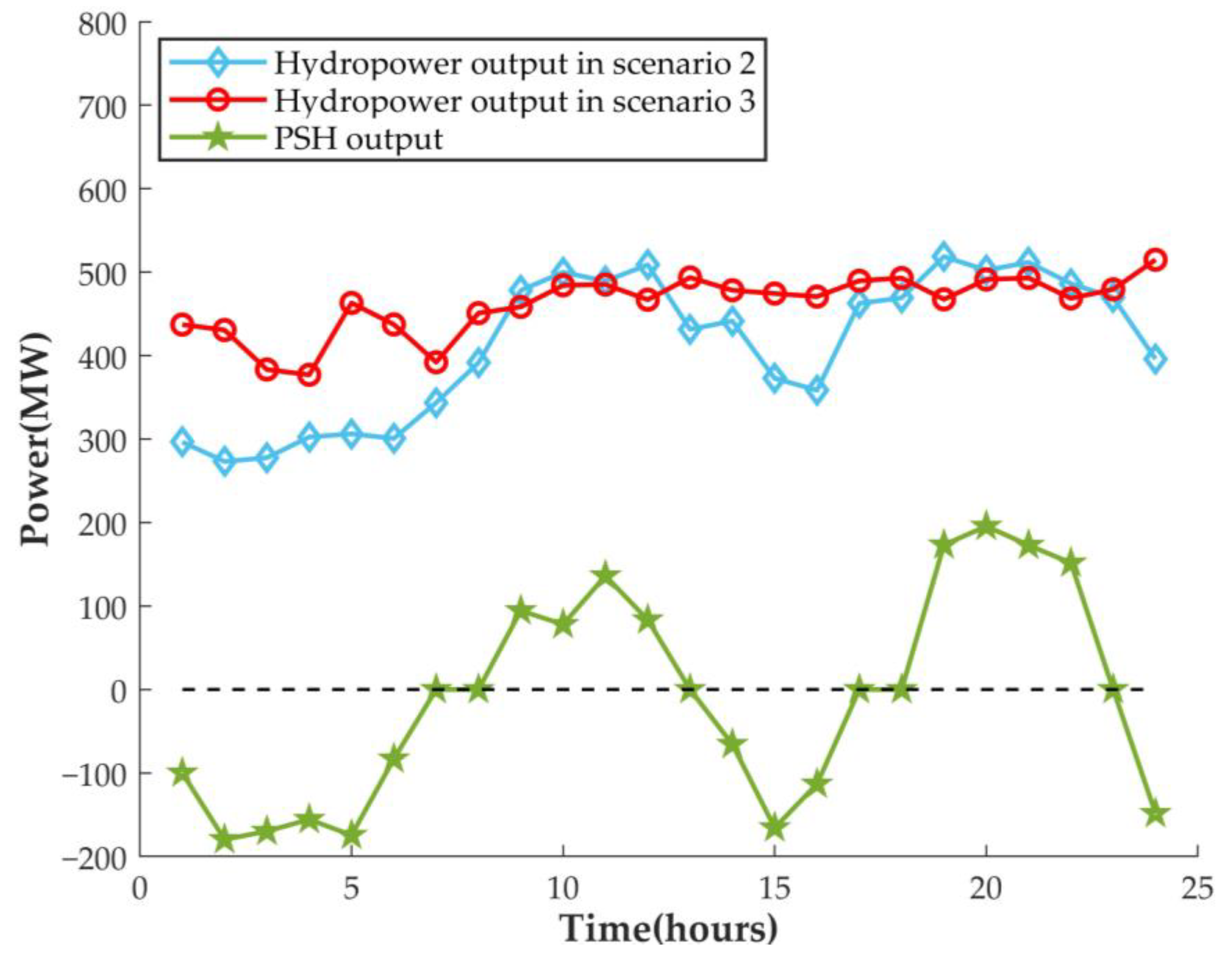
| Plant | Qmin | Qmax | Vini | Vend | Vmin | Vmax | Time Delay |
|---|---|---|---|---|---|---|---|
| h1 | 5 | 15 | 100 | 120 | 80 | 150 | 2 |
| h2 | 6 | 15 | 80 | 70 | 60 | 120 | 3 |
| h3 | 10 | 30 | 170 | 170 | 100 | 240 | 4 |
| h4 | 6 | 20 | 120 | 140 | 70 | 180 | 0 |
| Scenarios | Residual Load Variance (MW2) | Residual Load Peak–Valley Difference (MW) | Operation Cost (Thousand Dollars) | Renewable Energy Curtailment Rate |
|---|---|---|---|---|
| Scenario 1 | 20,681.67 | 487.04 | 540.17 | 6.16% |
| Scenario 2 | 4487.80 | 226.26 | 347.10 | 2.60% |
| Scenario 3 | 225.36 | 62.95 | 315.97 | 0% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Shi, L.; Fu, H. Multi-Objective Short-Term Optimal Dispatching of Cascade Hydro–Wind–Solar–Thermal Hybrid Generation System with Pumped Storage Hydropower. Energies 2024, 17, 98. https://doi.org/10.3390/en17010098
Li J, Shi L, Fu H. Multi-Objective Short-Term Optimal Dispatching of Cascade Hydro–Wind–Solar–Thermal Hybrid Generation System with Pumped Storage Hydropower. Energies. 2024; 17(1):98. https://doi.org/10.3390/en17010098
Chicago/Turabian StyleLi, Jie, Linjun Shi, and Hao Fu. 2024. "Multi-Objective Short-Term Optimal Dispatching of Cascade Hydro–Wind–Solar–Thermal Hybrid Generation System with Pumped Storage Hydropower" Energies 17, no. 1: 98. https://doi.org/10.3390/en17010098
APA StyleLi, J., Shi, L., & Fu, H. (2024). Multi-Objective Short-Term Optimal Dispatching of Cascade Hydro–Wind–Solar–Thermal Hybrid Generation System with Pumped Storage Hydropower. Energies, 17(1), 98. https://doi.org/10.3390/en17010098








