Heat Extraction Evaluation of CO2 and Water Flow through Different Fracture Networks for Enhanced Geothermal Systems
Abstract
:1. Introduction
2. Model Descriptions
2.1. Hydraulic–Thermal–Mechanical Coupled Modeling
- The rock matrix is isotropic, and the permeability of the rock matrix is very small compared to that of the fractures, which means that the rock matrix is assumed to be impermeable;
- The working fluid (water/CO2) remains in a liquid or supercritical state under reservoir conditions;
- Darcy’s law is applicable to fluids flowing in the reservoir;
- The fluids that originally existed in the reservoir are the same as those in the working fluid.
2.2. Heat Transfer Simulation and Evaluation
2.3. Discrete Fracture Network Generation
3. Numerical Simulations
3.1. Discrete Fracture Network Generation
3.2. Material Properties and Boundary Conditions
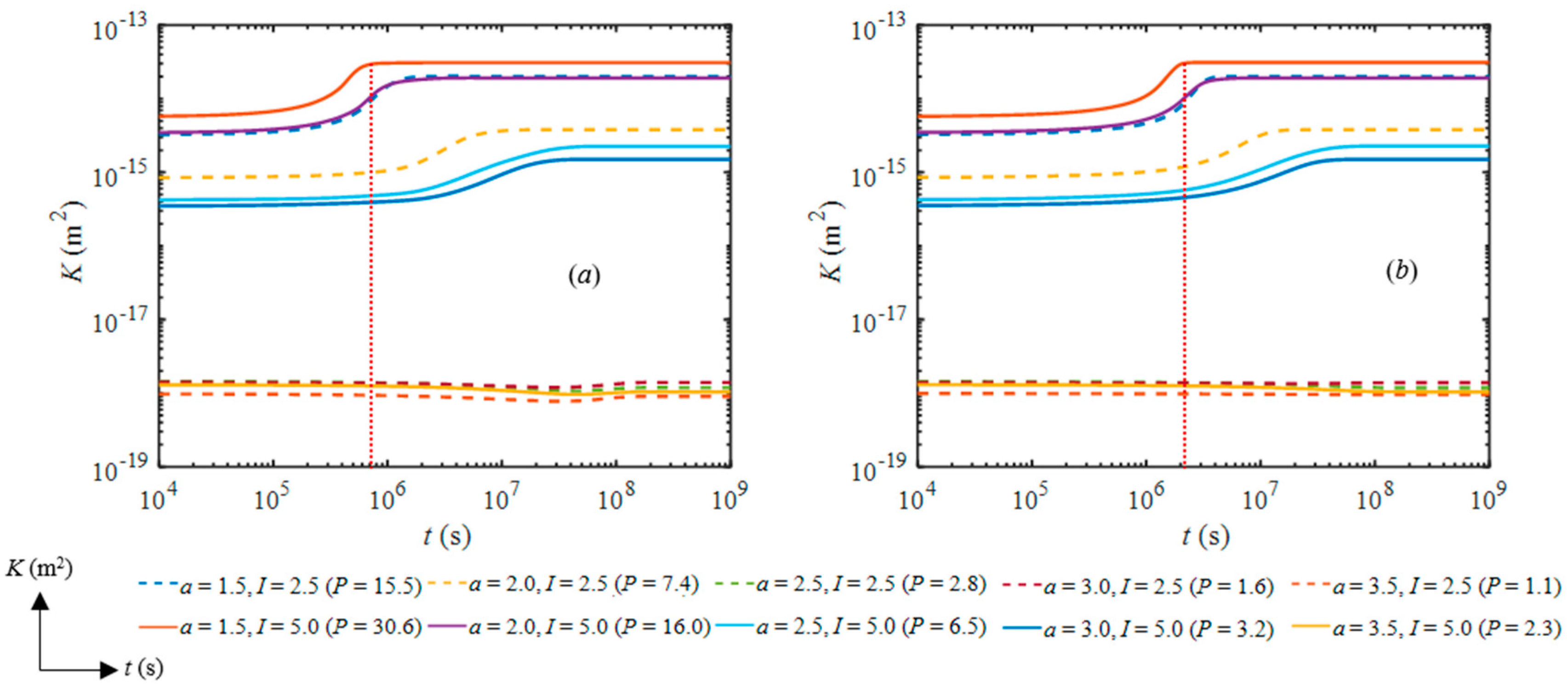
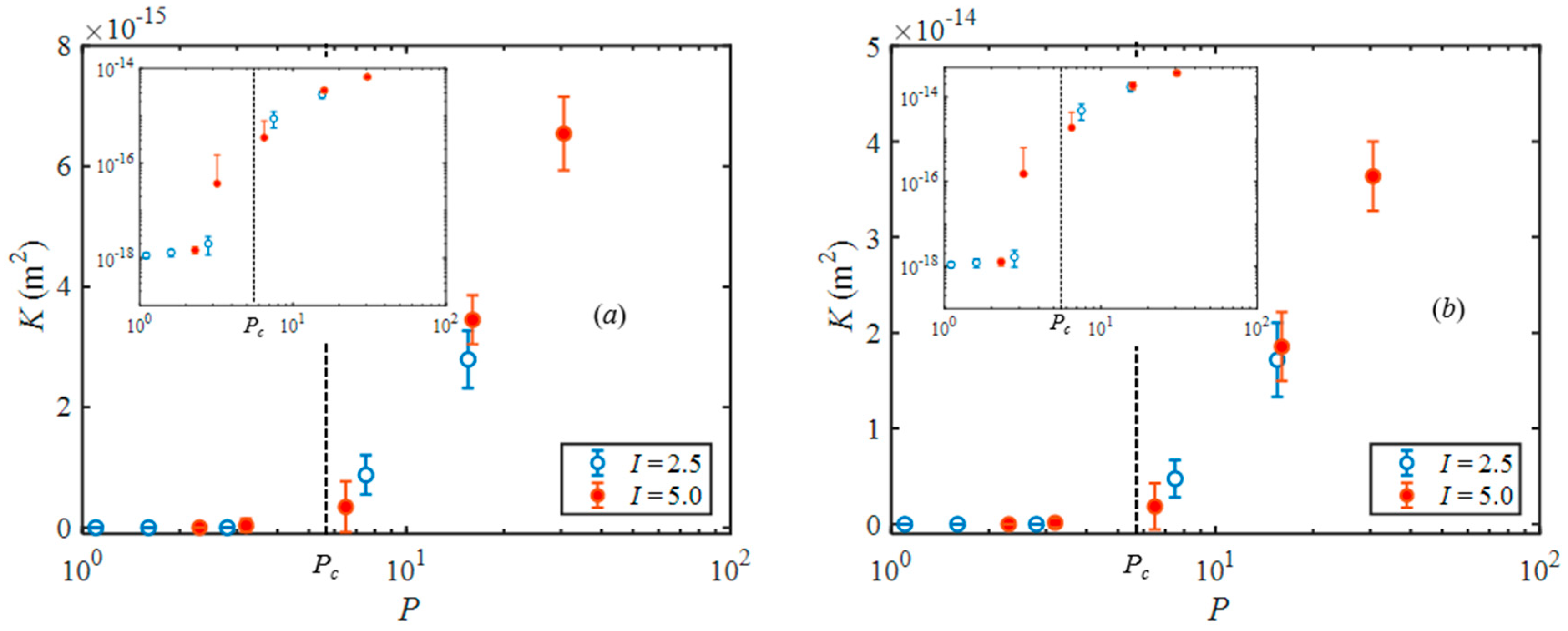
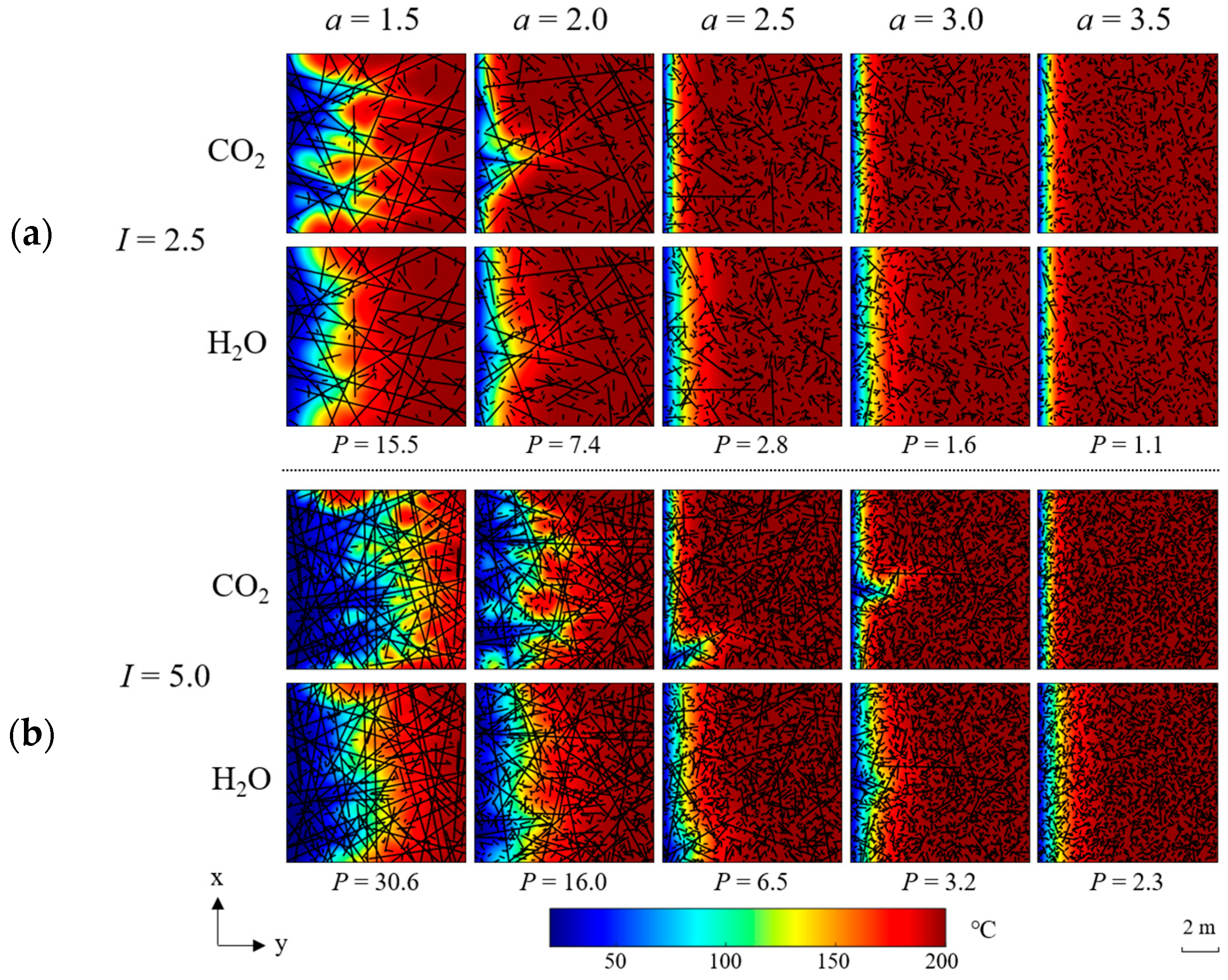
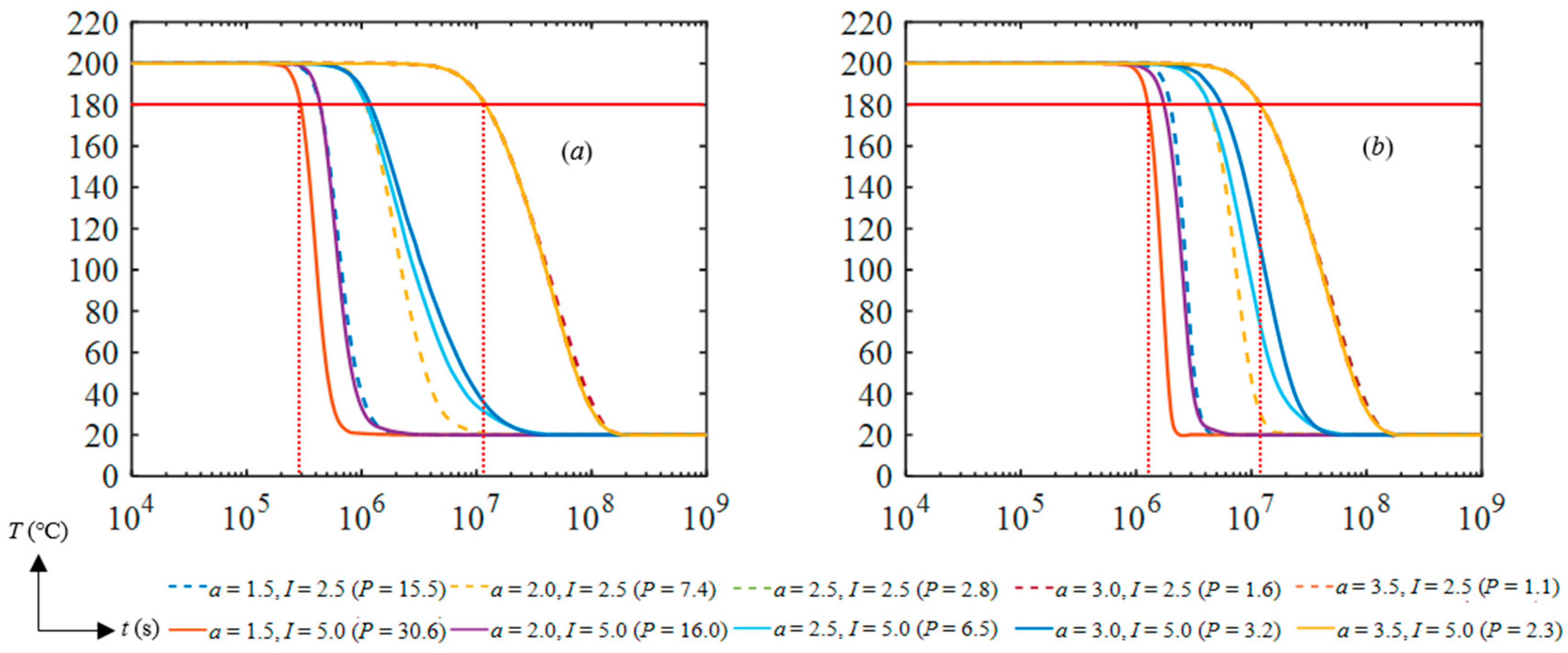
4. Results and Analysis
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Johnston, I.W.; Narsillo, G.A.; Colls, S. Emerging geothermal energy technologies. KSCE J. Civ. Eng. 2011, 15, 643–653. [Google Scholar] [CrossRef]
- William, E.G. Geothermal Energy: Renewable Energy and the Environment; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- BP plc. Statistical Review of World Energy; BP: London, UK, 2021. [Google Scholar]
- Xu, T.; Zhang, Y.; Zeng, Z.; Bao, X. Technology Progress in an Enhanced Geothermal System (Hot Dry ROCK). Sci. Technol. Rev. 2012, 30, 42–45. [Google Scholar]
- Wang, X.; Wu, N.; Su, Z.; Zeng, Y. Progress of the enhanced geothermal systems (EGS) development technology. Prog. Geophys. 2012, 27, 15–22. [Google Scholar]
- Kelkar, S.; Woldegabriel, G.; Rehfeldt, K. Lessons learned from the pioneering hot dry rock project at Fenton. Geothermics 2016, 63, 5–14. [Google Scholar] [CrossRef]
- Buscheck, T.A.; Bielicki, J.M.; Chen, M.; Sun, Y.W.; Hao, Y.; Edmunds, T.A.; Randolph, J.B.; Saar, M.O. Multi-fluid sedimentary geothermal energy systems for dispatchable renewable electricity. In Proceedings of the World Geothermal Congress, Melbourne, Australia, 19–25 April 2015. [Google Scholar]
- Xu, T.F.; Pruess, K.; Apps, J. Numerical studies of fluid-rock interactions in Enhanced Geothermal Systems (EGS) with CO2 as working fluid. In Proceedings of the Thirty-Third Workshop on Geothermal Reservoir Engineering, Stanford University, Stanford, CA, USA, 28–30 January 2008. SGP-TR-185. [Google Scholar]
- Olasolo, P.; Juarez, M.C.; Morales, M.P.; Sebastiano, D.A.; Liarte, I.A. Enhanced geothermal systems (EGS): A review. Renew. Sustain. Energy Rev. 2016, 56, 133–144. [Google Scholar] [CrossRef]
- Zhang, F.Z.; Jiang, P.X.; Xu, R.N. System thermodynamic performance comparison of CO2-EGS and water-EGS systems. Appl. Therm. Eng. 2013, 61, 236–244. [Google Scholar] [CrossRef]
- Borgia, A.; Oldenburg, C.M.; Zhang, R.; Pan, L.H.; Daley, T.M.; Finsterle, S.; Ramakrishnan, T.S. Simulation of CO2 injection into fractures and faults for improving their geophysical characterization at EGS sites. Geothermics 2017, 69, 189–201. [Google Scholar] [CrossRef]
- Fox, D.B.; Koch, D.L.; Tester, J.W. An analytical thermos hydraulic model for discretely fractured geothermal reservoirs. Water Resour. Res. 2016, 52, 6792–6817. [Google Scholar] [CrossRef]
- Sun, Z.; Zhang, X.; Xu, Y.; Yao, J.; Wang, H.; Lv, S.; Sun, Z.; Huang, Y.; Cai, M.; Huang, X. Numerical simulation of the heat extraction in EGS with thermal-hydraulic-mechanical coupling method based on discrete fractures model. Energy 2017, 120, 20–33. [Google Scholar] [CrossRef]
- Borgia, A.; Pruess, K.; Kneafsey, T.J.; Oldenburg, C.M. Pan l. Numerical simulation of salt precipitation in a fractured CO2-Enhanced geothermal system. Geothermics 2012, 44, 13–22. [Google Scholar] [CrossRef]
- Juliusson, E.; Horne, R.N. Optimization of injection scheduling in fractured geothermal reservoirs. Geothermics 2013, 48, 80–92. [Google Scholar] [CrossRef]
- Li, J.W.; Sun, Z.X.; Jiang, C.Y.; Cherubini, C.; Scheuermann, A.; Galindo Torres, S.A.; Li, L. Investigations of heat extraction for water and CO2 flow based on the rough-walled discrete fracture network. Energy 2019, 189, 116184. [Google Scholar] [CrossRef]
- Asai, P.; Panja, P.; Velasco, R.; Mclennan, J.; Moore, J. Fluid flow distribution in fractures for a doublet system in Enhanced Geothermal Systems (EGS). Geothermics 2018, 75, 171–179. [Google Scholar] [CrossRef]
- Pruess, K. Enhanced geothermal systems (EGS) using CO2 as working fluid—A novel approach for generating renewable energy with simultaneous sequestration of carbon. Geothermics 2006, 35, 351–367. [Google Scholar] [CrossRef]
- Jiang, F.; Chen, J.; Huang, W.; Luo, L. A three-dimensional transient model for EGS subsurface thermo-hydraulic process. Energy 2014, 72, 300–310. [Google Scholar] [CrossRef]
- Talybov, M.A.; Abdulagatov, M.I. High-temperature and high-pressure PVT measurements and derived thermodynamics properties of geothermal fluids from East Turkey. Geothermics 2021, 95, 102125. [Google Scholar] [CrossRef]
- Pruess, K. On production behavior of enhanced geothermal systems with CO2 as working fluid. Energy Convers. Manag. 2008, 49, 1446–1454. [Google Scholar] [CrossRef]
- Remoroza, A.; Doroodchi, E.; Behdad, M. CO2-EGS in hot dry rock: Preliminary results from CO2-Rock interaction experiments. In Proceedings of the Thirty-Seventh Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 30 January–1 February 2012. [Google Scholar]
- Wang, C.L.; Cheng, W.L.; Nian YLe Yang, L.; Han, B.B.; Liu, M.H. Simulation of heat extraction from CO2-based enhanced geothermal systems considering CO2 sequestration. Energy 2018, 142, 157–167. [Google Scholar] [CrossRef]
- Jiang, P.X.; Zhang, L.; Xu, R.N. Experimental study of convective heat transfer of carbon dioxide at supercritical pressures in a horizontal rock fracture and its application to enhanced geothermal systems. Appl. Therm. Eng. 2017, 117, 39–49. [Google Scholar] [CrossRef]
- Zhang, L.; Jiang, P.X.; Wang, Z.; Xu, R.N. Convective heat transfer of supercritical CO2 in a rock fracture for enhanced geothermal systems. Appl. Therm. Eng. 2017, 115, 923–936. [Google Scholar] [CrossRef]
- Duan, X.-Y.; Huang, D.; Lei, W.-X.; Chen, S.-C.; Huang, Z.-Q.; Zhu, C.-Y. Investigation of Heat Extraction in an Enhanced Geothermal System Embedded with Fracture Networks Using the Thermal–Hydraulic–Mechanical Coupling Model. Energies 2023, 16, 3758. [Google Scholar] [CrossRef]
- Yin, H. Theoretical and Experimental Study on Sustainable Heat Extraction from Hydrothermal Geothermal Based on Multi-Scale Entropy; Tianjin University: Tianjin, China, 2022. [Google Scholar]
- Yuan, X. Numerical Simulation of Seepage Heat Transfer in Deep Artificial Fissures Based on Discrete Elements; Jilin University: Changchun, China, 2022. [Google Scholar]
- Zhao, Y. Performance Analysis of Water and CO2 Heat Extraction from Supercritical Geothermal System; Jilin University: Changchun, China, 2023. [Google Scholar]
- Saeid, S.; Al-Khoury, R.; Barends, F. An efficient computational model for deep low-enthalpy geothermal systems. Comput. Geosci. 2013, 51, 400–409. [Google Scholar] [CrossRef]
- Chen, B.G.; Song, E.X.; Cheng, X.H. A numerical method for discrete fracture network model for flow and heat transfer in two-dimensional fractured rocks. Chin. J. Rock Mech. Eng. 2014, 33, 43–51. (In Chinese) [Google Scholar]
- Xu, C.; Dowd, P.A.; Tian, Z.F. A simplified coupled hydro-thermal model for enhanced geothermal systems. Appl. Energy 2015, 140, 135–145. [Google Scholar] [CrossRef]
- Louis, C. Rock Hydraulics in Rock Mechanics; Springer: New York, NY, USA, 1974; pp. 299–387. [Google Scholar]
- Yao, J.; Zhang, X.; Sun, Z.; Huang, Z.; Liu, J.; Li, Y.; Xin, Y.; Yan, X.; Liu, W. Numerical simulation of the heat extraction in 3D-EGS with thermal-hydraulic-mechanical coupling method based on discrete fractures model. Geothermics 2018, 74, 19–34. [Google Scholar] [CrossRef]
- Bour, O.; Davy, P. Connectivity of random fault networks following a power law fault length distribution. Water Resour. Res. 1997, 33, 1567–1584. [Google Scholar] [CrossRef]
- Darcel, C. Stereological analysis of fractal fracture networks. J. Geophys. Res. 2003, 108, 2451. [Google Scholar] [CrossRef]
- Watanabe, K.; Takahashi, H. Fractal geometry characterization of geothermal reservoir fracture networks. J. Geophys. Res. Solid Earth 1995, 100, 521–528. [Google Scholar] [CrossRef]
- Tester, J.W.; Anderson, B.J.; Batchelor, A.S.; Blackwell, D.D.; DiPippo, R.; Drake, E.M.; Garnish, J.; Livesay, B.; Moore, M.C.; Nichols, K.; et al. The Future of Geothermal Energy: Impact of Enhanced Geothermal Systems (EGS) on the United States in the 21st Century; MIT: Cambridge, MA, USA, 2006. [Google Scholar]
- Elsworth, D. A Comparative-Evaluation of the Parallel Flow and Spherical Reservoir Models of Hdr Geothermal Systems. J. Volcanol. Geotherm. Res. 1990, 44, 283–293. [Google Scholar] [CrossRef]

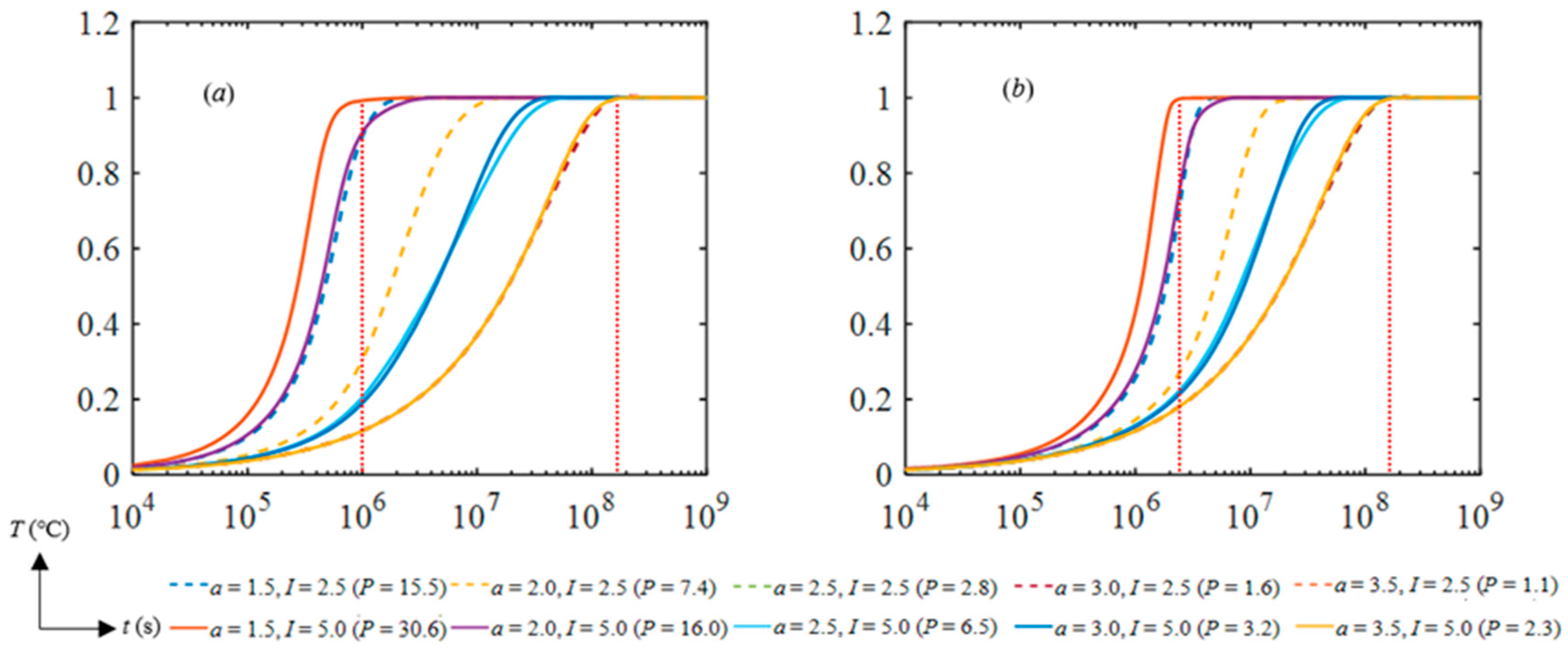
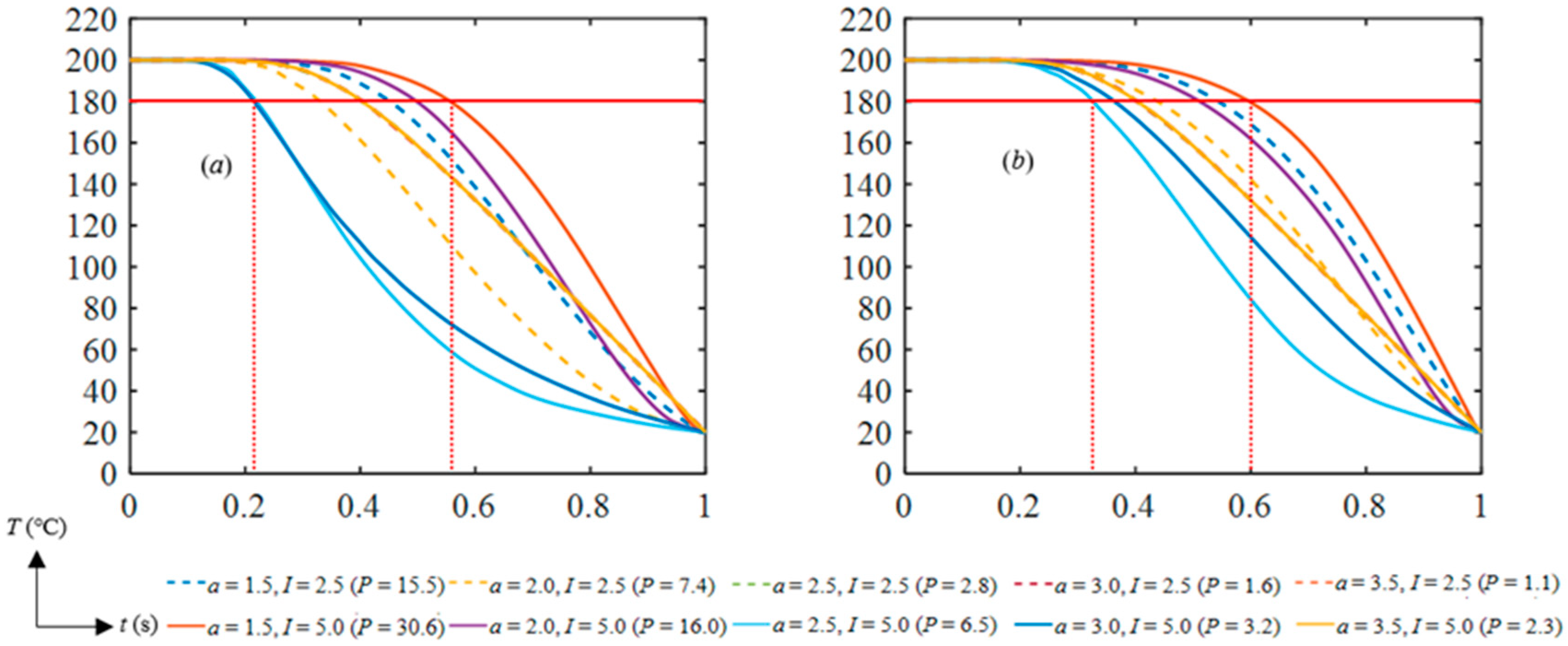
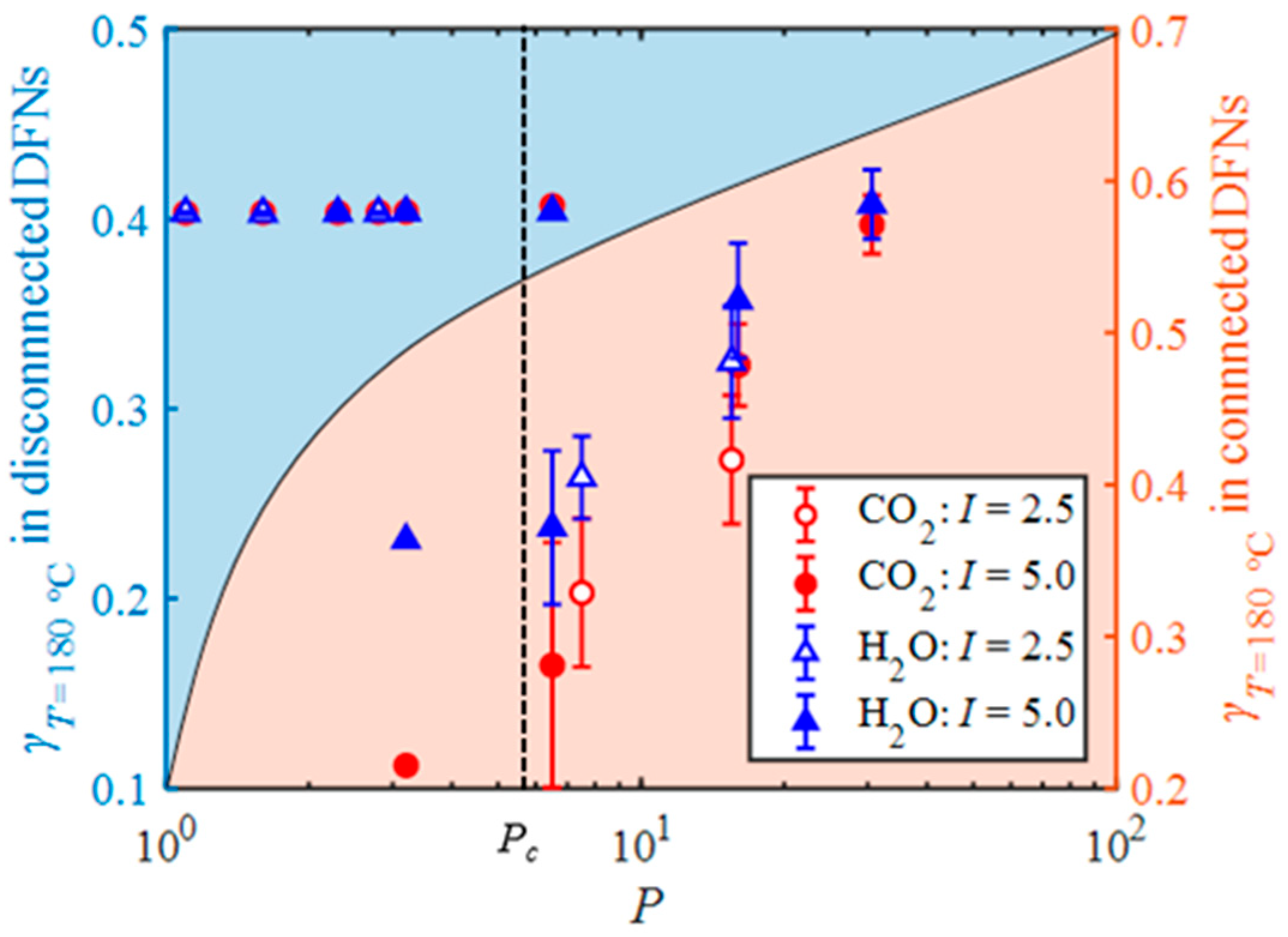
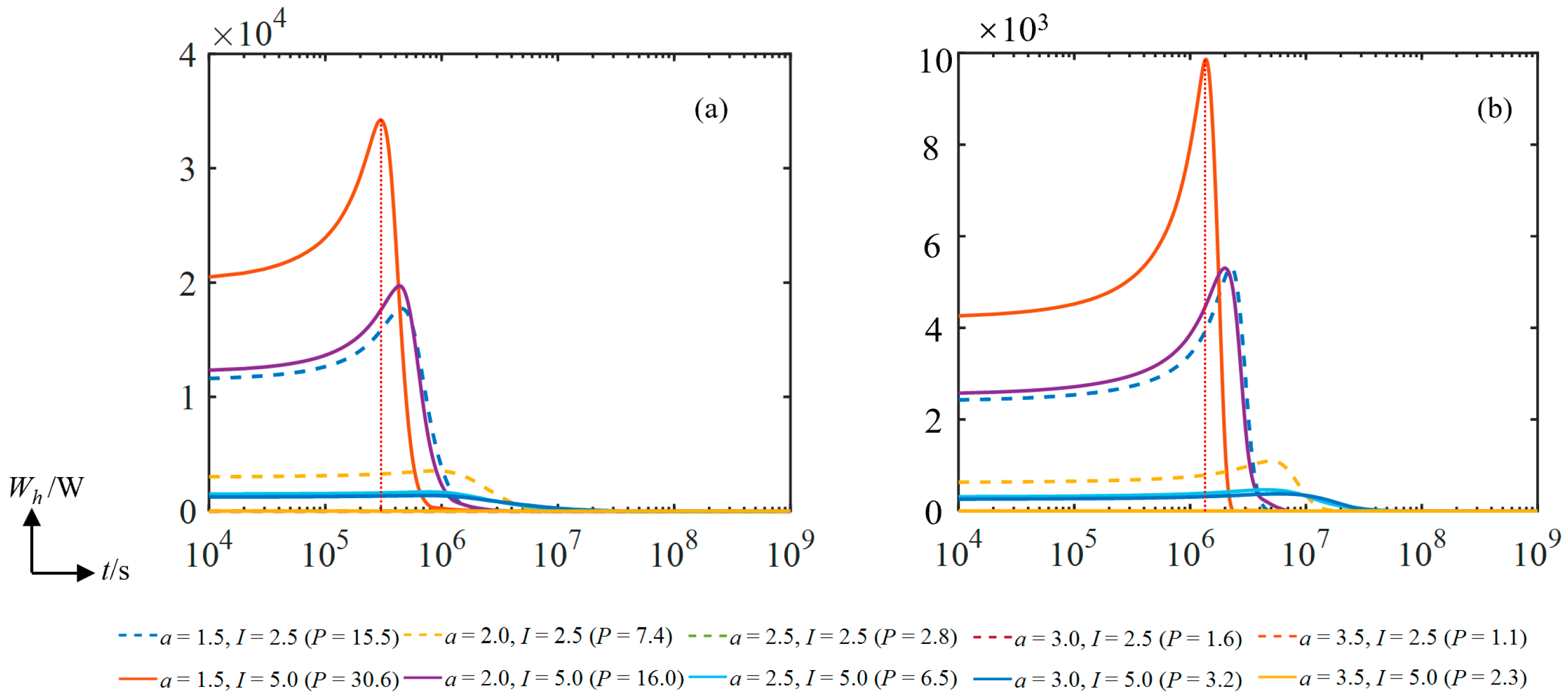
| I = 2.5 m−1 | I = 5.0 m−1 | ||||
|---|---|---|---|---|---|
| a | P | Proportion% | a | P | Proportion% |
| 1.5 | 15.5 | 100 | 1.5 | 30.6 | 100 |
| 2.0 | 7.4 | 100 | 2.0 | 16.0 | 100 |
| 2.5 | 2.8 | 0 | 2.5 | 6.5 | 50 |
| 3.0 | 1.6 | 0 | 3.0 | 3.2 | 10 |
| 3.5 | 1.1 | 0 | 3.5 | 2.3 | 0 |
| Parameters | Value |
|---|---|
| Water thermal conductivity , W/m/K | 0 |
| CO2 thermal conductivity , W/m/K | 0 |
| Rock density , kg/m3 | 2700 |
| Rock heat capacity , J/kg/K | 1000 |
| Rock thermal conductivity , W/m/K | 3 |
| Rock matrix porosity | 0.0001 |
| Rock matrix permeability km, m2 | 1.0 × 10−18 |
| Convection heat transfer coefficient , W/m2/K | 3000 |
| Gravity acceleration , m/s2 | 9.8 |
| Elastic modulus , GPa | 30 |
| Poisson ratio | 0.25 |
| Thermal expansion coefficient , K−1 | 1.0 × 106 |
| Biot’s constant | 1 |
| Normal stiffness , GPa/m | 1200 |
| Tangential stiffness , GPa/m | 400 |
| Matrix storage coefficient , 1/Pa | 1.0 × 10−8 |
| Fracture storage coefficient , 1/Pa | 1.0 × 10−9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Z.; Song, W.; Zhang, H.; Li, X.; Xie, S.; Nie, H. Heat Extraction Evaluation of CO2 and Water Flow through Different Fracture Networks for Enhanced Geothermal Systems. Energies 2024, 17, 86. https://doi.org/10.3390/en17010086
Sun Z, Song W, Zhang H, Li X, Xie S, Nie H. Heat Extraction Evaluation of CO2 and Water Flow through Different Fracture Networks for Enhanced Geothermal Systems. Energies. 2024; 17(1):86. https://doi.org/10.3390/en17010086
Chicago/Turabian StyleSun, Zhixue, Wentong Song, Hao Zhang, Xueyuan Li, Shuang Xie, and Haifeng Nie. 2024. "Heat Extraction Evaluation of CO2 and Water Flow through Different Fracture Networks for Enhanced Geothermal Systems" Energies 17, no. 1: 86. https://doi.org/10.3390/en17010086
APA StyleSun, Z., Song, W., Zhang, H., Li, X., Xie, S., & Nie, H. (2024). Heat Extraction Evaluation of CO2 and Water Flow through Different Fracture Networks for Enhanced Geothermal Systems. Energies, 17(1), 86. https://doi.org/10.3390/en17010086






