Analysis of Flexibility Potential of a Cold Warehouse with Different Refrigeration Compressors
Abstract
:1. Introduction
2. Definition of Flexibility
2.1. Literature Review
2.2. A Comprehensive Definition for Flexibility
Flexibility is the capability of an energy system to undergo temporary, reversible, and expectable changes, over a certain period, in reaction to an external signal to fulfill a specific goal.
3. Quantification of Flexibility
3.1. Literature Review
3.2. Aspects of Quantification of Flexibility
3.3. Developed Methodology to Quantify Flexibility
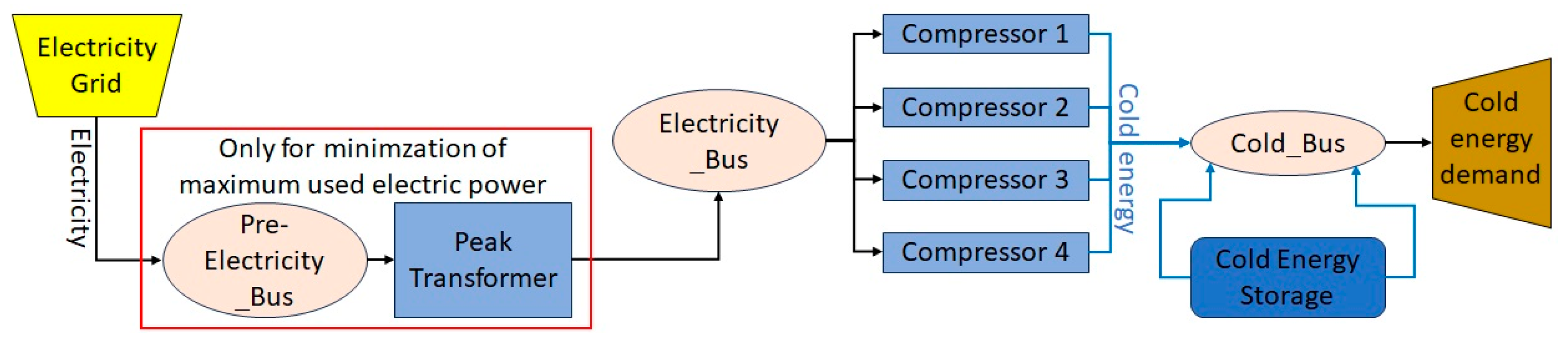
4. Goal-Oriented Optimization Models
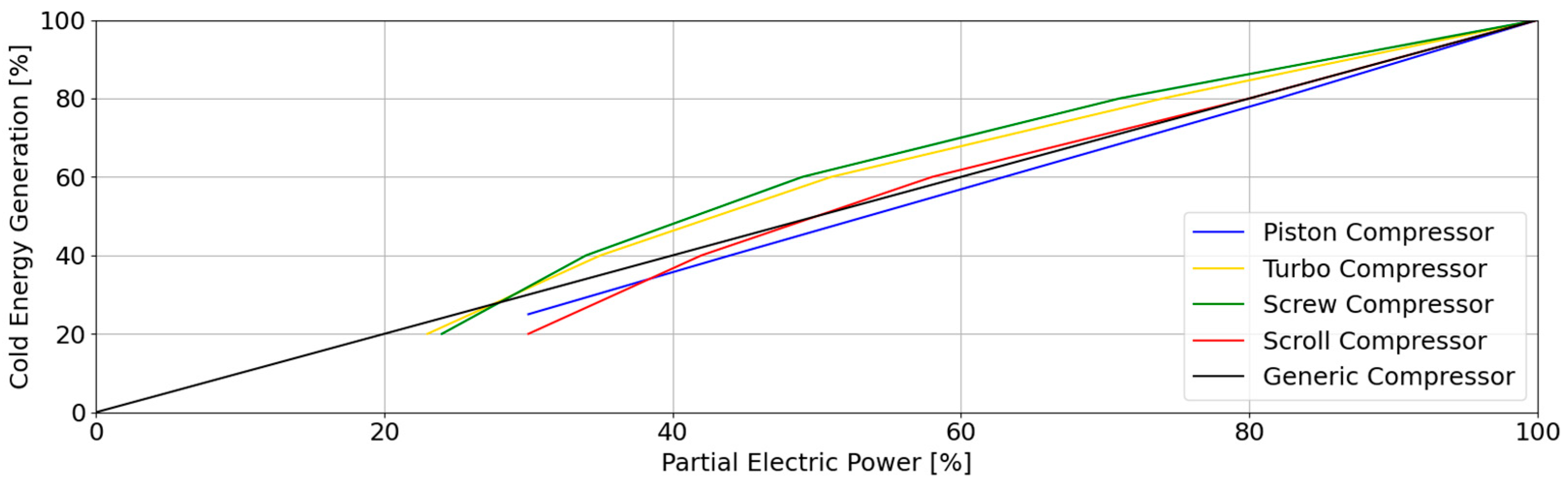
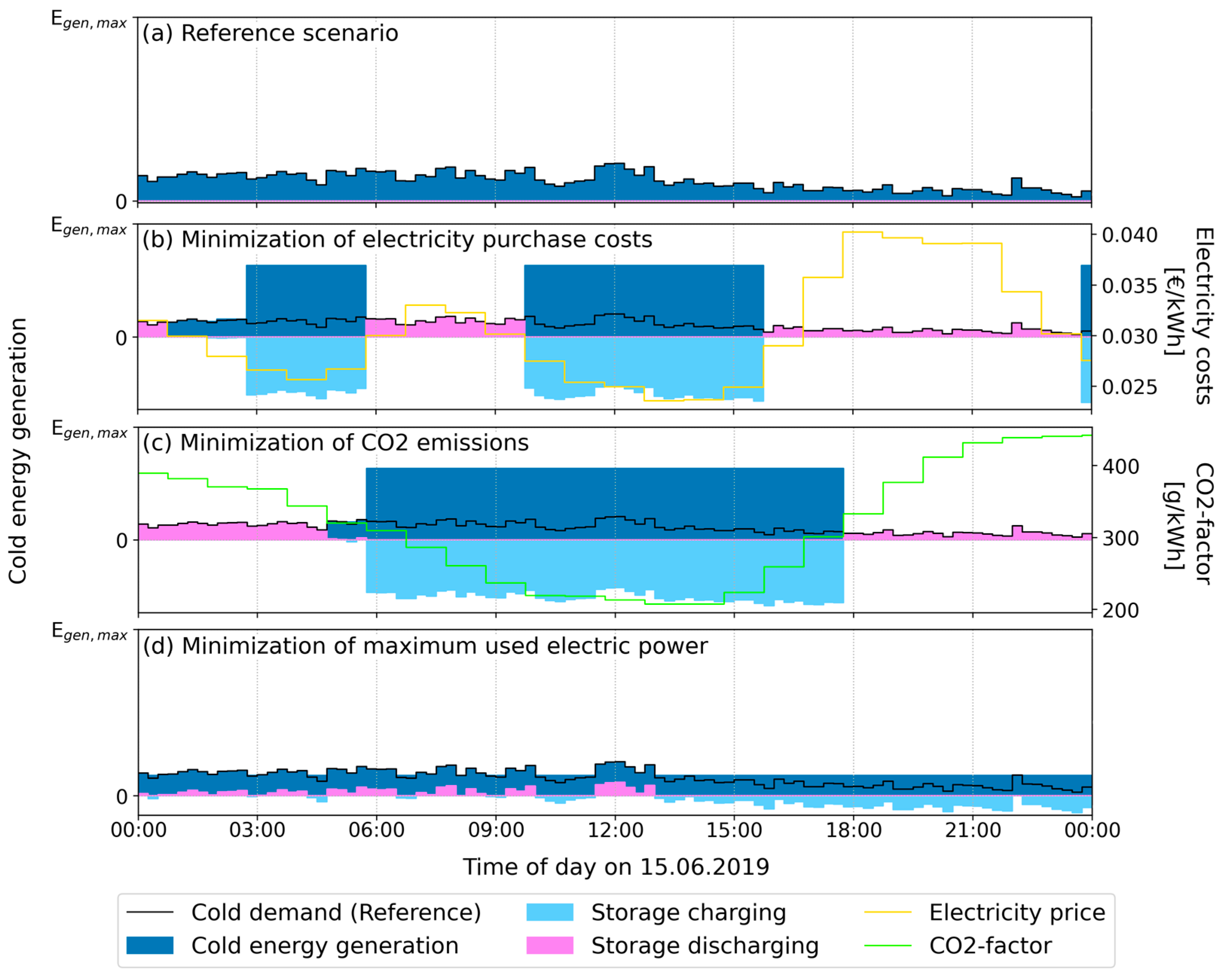
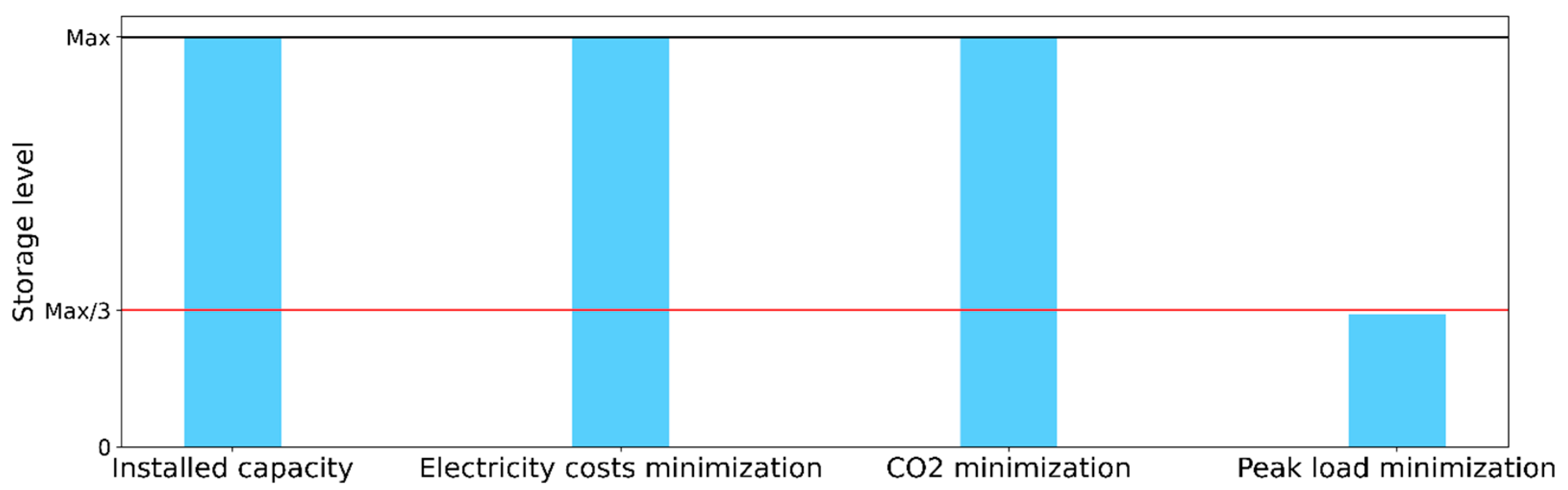
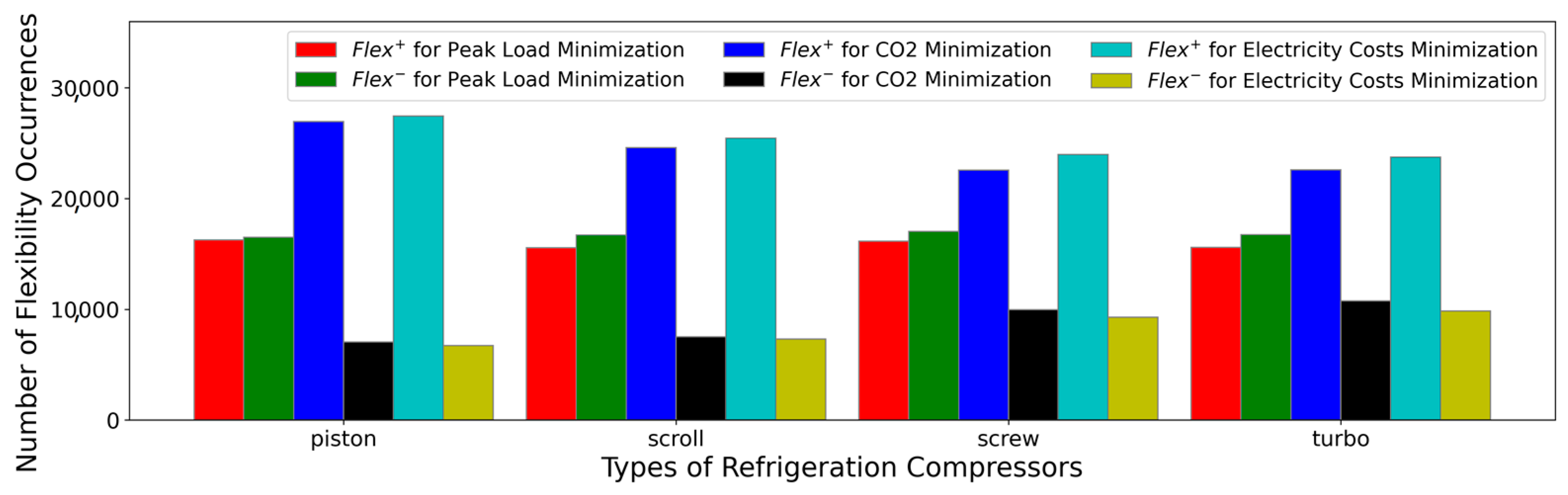
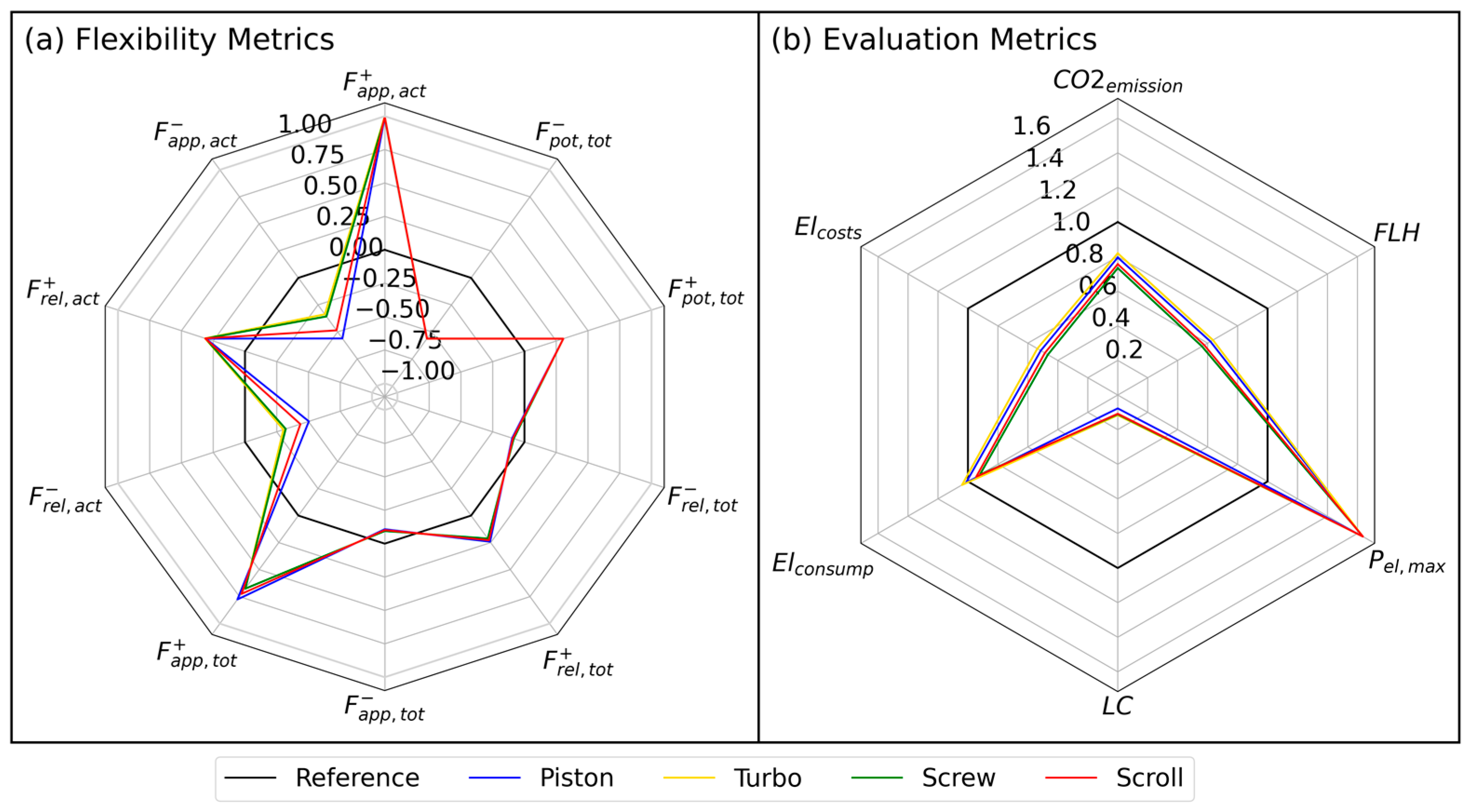
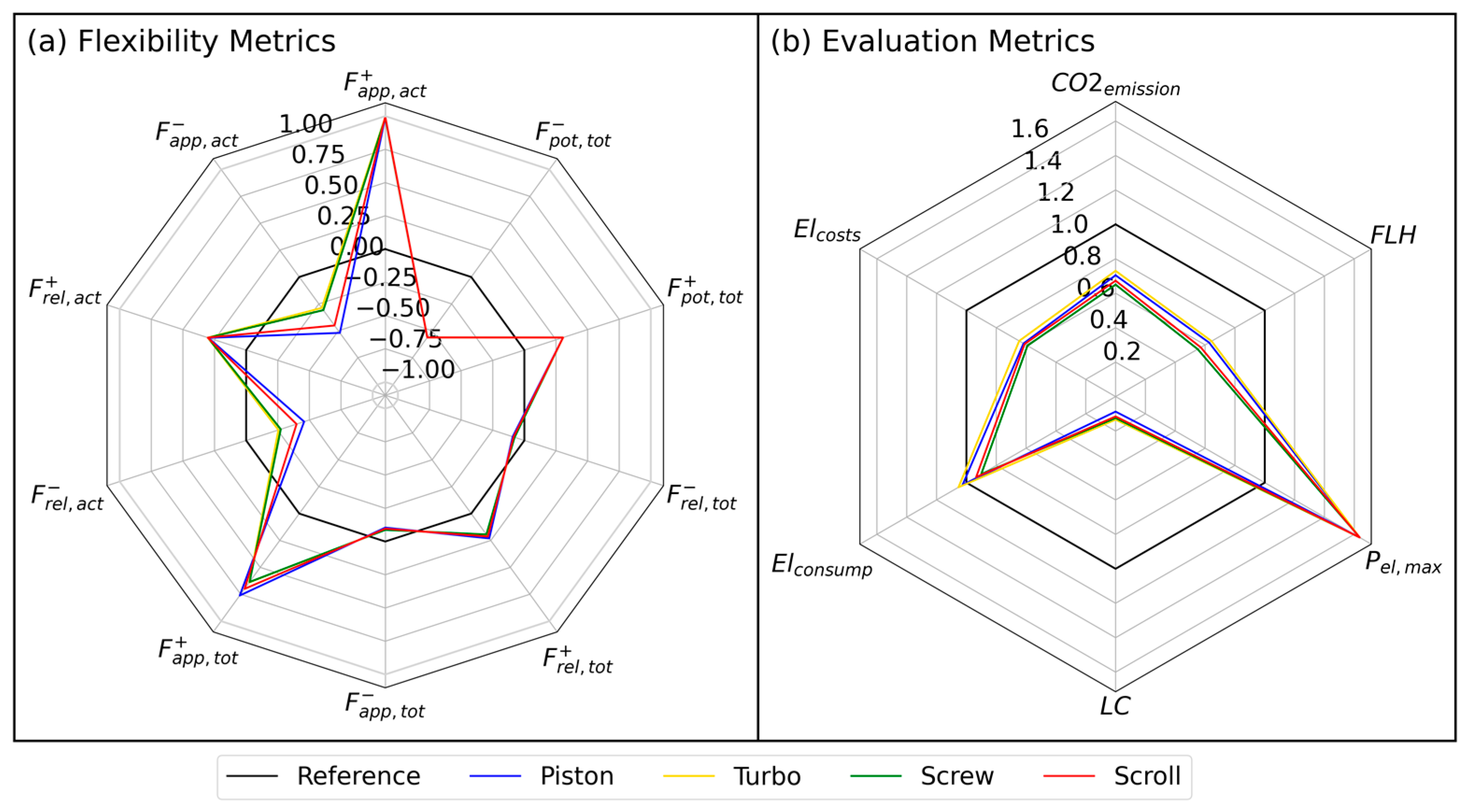
5. Results and Discussion
6. Conclusions
- -
- Reduction of electricity purchase costs up to 50%;
- -
- Reduction of CO2 emissions between 25–30%;
- -
- Reduction of electric peak load about 50%;
- -
- Screw compressors are the most favorable refrigeration compressor type for a goal-oriented flexible operation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Basit, M.A.; Dilshad, S.; Badar, R.; Sami ur Rehman, S.M. Limitations, challenges, and solution approaches in grid-connected renewable energy systems. Int. J. Energy Res. 2020, 44, 4132–4162. [Google Scholar] [CrossRef]
- Reynders, G.; Amaral Lopes, R.; Marszal-Pomianowska, A.; Aelenei, D.; Martins, J.; Saelens, D. Energy flexible buildings: An evaluation of definitions and quantification methodologies applied to thermal storage. Energy Build. 2018, 166, 372–390. [Google Scholar] [CrossRef]
- Osička, J.; Černoch, F. European energy politics after Ukraine: The road ahead. Energy Res. Social. Sci. 2022, 91, 102757. [Google Scholar] [CrossRef]
- Ashok, S.; Banerjee, R. An optimization mode for industrial load management. IEEE Trans. Power Syst. 2001, 16, 879–884. [Google Scholar] [CrossRef]
- Sinsel, S.R.; Riemke, R.L.; Hoffmann, V.H. Challenges and solution technologies for the integration of variable renewable energy sources—A review. Renew. Energy 2020, 145, 2271–2285. [Google Scholar] [CrossRef]
- Denholm, P.; Hand, M. Grid flexibility and storage required to achieve very high penetration of variable renewable electricity. Energy Policy 2011, 39, 1817–1830. [Google Scholar] [CrossRef]
- Moslehi, K.; Kumar, R. A Reliability Perspective of the Smart Grid. IEEE Trans. Smart Grid 2010, 1, 57–64. [Google Scholar] [CrossRef]
- Strbac, G. Demand side management: Benefits and challenges. Energy Policy 2008, 36, 4419–4426. [Google Scholar] [CrossRef]
- Grein, A.; Pehnt, M. Load management for refrigeration systems: Potentials and barriers. Energy Policy 2011, 39, 5598–5608. [Google Scholar] [CrossRef]
- D’hulst, R.; Labeeuw, W.; Beusen, B.; Claessens, S.; Deconinck, G.; Vanthournout, K. Demand response flexibility and flexibility potential of residential smart appliances: Experiences from large pilot test in Belgium. Appl. Energy 2015, 155, 79–90. [Google Scholar] [CrossRef]
- Stinner, S.; Huchtemann, K.; Müller, D. Quantifying the operational flexibility of building energy systems with thermal energy storages. Appl. Energy 2016, 181, 140–154. [Google Scholar] [CrossRef]
- Lund, P.D.; Lindgren, J.; Mikkola, J.; Salpakari, J. Review of energy system flexibility measures to enable high levels of variable renewable electricity. Renew. Sustain. Energy Rev. 2015, 45, 785–807. [Google Scholar] [CrossRef]
- Lopes, R.A.; Chambel, A.; Neves, J.; Aelenei, D.; Martins, J. A Literature Review of Methodologies Used to Assess the Energy Flexibility of Buildings. Energy Procedia 2016, 91, 1053–1058. [Google Scholar] [CrossRef]
- Arteconi, A.; Hewitt, N.J.; Polonara, F. State of the art of thermal storage for demand-side management. Appl. Energy 2012, 93, 371–389. [Google Scholar] [CrossRef]
- Eisenhauer, S.; Marmullaku, D.; Reichart, M.; Sauer, A. Simulationsgestützte Analyse der Energetischen Flexibilisierbarkeit Industrieller Kompressionskälteanlagen; Universität Stuttgart, Institut für Energieeffizienz in der Produktion, Deutsche Kälte- und Klimatagung (DKV-Tagung): Bremen, Germany, 2017. [Google Scholar]
- Altwies, J.E.; Reindl, D.T. Passive thermal energy storage in refrigerated warehouses. Int. J. Refrig. 2002, 25, 149–157. [Google Scholar] [CrossRef]
- Tassou, S.A.; Ge, Y.; Hadawey, A.; Marriott, D. Energy consumption and conservation in food retailing. Appl. Therm. Eng. 2011, 31, 2–3. [Google Scholar] [CrossRef]
- Arteconi, A.; Polonra, F. Demand side management in refrigeration applications. IJHT 2017, 35, S58–S63. [Google Scholar] [CrossRef]
- Plaum, F.; Ahmadiahangar, R.; Rosin, A.; Kilter, J. Aggregated demand-side energy flexibility: A comprehensive review on characterization, forecasting and market prospects. Energy Rep. 2022, 8, 9344–9362. [Google Scholar] [CrossRef]
- Kouzelis, K.; Diaz de Cerio Mendaza, I.; Bak-Jensen, B. Probabilistic quantification of potentially flexible residential demand. In Proceedings of the 2014 IEEE PES General Meeting|Conference & Exposition, National Harbor, MD, USA, 27–31 July 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1–5. [Google Scholar]
- Groppi, D.; Pfeifer, A.; Garcia, D.A.; Krajačić, G.; Duić, N. A review on energy storage and demand side management solutions in smart energy islands. Renew. Sustain. Energy Rev. 2021, 135, 110–183. [Google Scholar] [CrossRef]
- Le Dréau, J.; Heiselberg, P. Energy flexibility of residential buildings using short term heat storage in the thermal mass. Energy 2016, 111, 991–1002. [Google Scholar] [CrossRef]
- Reynders, G.; Nuytten, T.; Saelens, D. Potential of structural thermal mass for demand-side management in dwellings. Build. Environ. 2013, 64, 187–199. [Google Scholar] [CrossRef]
- Nuytten, T.; Claessens, B.; Paredis, K.; van Bael, J.; Six, D. Flexibility of a combined heat and power system with thermal energy storage for district heating. Appl. Energy 2013, 104, 583–591. [Google Scholar] [CrossRef]
- Tahersima, F.; Stoustrup, J.; Meybodi, S.A.; Rasmussen, H. Contribution of domestic heating systems to smart grid control. In Proceedings of the IEEE Conference on Decision and Control and European Control Conference, Orlando, FL, USA, 12–15 December 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 3677–3681. [Google Scholar]
- Weiß, T.; Rüdisser, D.; Reynders, G. Tool to Evaluate the Energy Flexibility in Buildings—A Short Manual: IEA EBC Annex 67 Project Energy Flexible Buildings; AEE INTEC: Gleisdorf, Austria, 2019. [Google Scholar]
- De Coninck, R.; Helsen, L. Quantification of flexibility in buildings by cost curves—Methodology and application. Appl. Energy 2016, 162, 653–665. [Google Scholar] [CrossRef]
- Junker, R.G.; Azar, A.G.; Lopes, R.A.; Lindberg, K.B.; Reynders, G.; Relan, R.; Madsen, H. Characterizing the energy flexibility of buildings and districts. Appl. Energy 2018, 225, 175–182. [Google Scholar] [CrossRef]
- Vandermeulen, A.; van der Heijde, B.; Helsen, L. Controlling district heating and cooling networks to unlock flexibility: A review. Energy 2018, 151, 103–115. [Google Scholar] [CrossRef]
- Jin, X.; Wu, Q.; Jia, H. Local flexibility markets: Literature review on concepts, models and clearing methods. Appl. Energy 2020, 261, 114387. [Google Scholar] [CrossRef]
- Graßl, M.A. Bewertung der Energieflexibilität in der Produktion. Ph.D. Thesis, Universität München, Munich, Germany, 2014. [Google Scholar]
- Ulbig, A.; Andersson, G. Analyzing operational flexibility of electric power systems. Int. J. Electr. Power Energy Syst. 2015, 72, 155–164. [Google Scholar] [CrossRef]
- Kondziella, H.; Bruckner, T. Flexibility requirements of renewable energy based electricity systems—A review of research results and methodologies. Renew. Sustain. Energy Rev. 2016, 53, 10–22. [Google Scholar] [CrossRef]
- Nalini, B.K.; Eldakadosi, M.; You, Z.; Zade, M.; Tzscheutschler, P.; Wagner, U. Towards Prosumer Flexibility Markets: A Photovoltaic and Battery Storage Model. In Proceedings of the 2019 IEEE PES Innovative Smart Grid Technologies Europe (ISGT-Europe), Bucharest, Romania, 29 September–2 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–5. [Google Scholar]
- Li, R.; Satchwell, A.J.; Finn, D.; Christensen, T.H.; Kummert, M.; Le Dréau, J.; Lopes, R.A.; Madsen, H.; Salom, J.; Henze, G.; et al. Ten questions concerning energy flexibility in buildings. Build. Environ. 2022, 223, 109461. [Google Scholar] [CrossRef]
- Huber, M.; Dimkova, D.; Hamacher, T. Integration of wind and solar power in Europe: Assessment of flexibility requirements. Energy 2014, 69, 236–246. [Google Scholar] [CrossRef]
- Fischer, D.; Wolf, T.; Wapler, J.; Hollinger, R.; Madani, H. Model-based flexibility assessment of a residential heat pump pool. Energy 2017, 118, 853–864. [Google Scholar] [CrossRef]
- Oldewurtel, F.; Sturzenegger, D.; Andersson, G.; Morari, M.; Smith, R.S. Towards a standardized building assessment for demand response. In Proceedings of the 52nd IEEE Conference on Decision and Control, Florence, Italy, 10–13 December 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 7083–7088. [Google Scholar]
- Brouwer, A.S.; van den Broek, M.; Seebregts, A.; Faaij, A. Operational flexibility and economics of power plants in future low-carbon power systems. Appl. Energy 2015, 156, 107–128. [Google Scholar] [CrossRef]
- Saarinen, L.; Dahlbäck, N.; Lundin, U. Power system flexibility need induced by wind and solar power intermittency on time scales of 1–14 days. Renew. Energy 2015, 83, 339–344. [Google Scholar] [CrossRef]
- Finck, C.; Li, R.; Kramer, R.; Zeiler, W. Quantifying demand flexibility of power-to-heat and thermal energy storage in the control of building heating systems. Appl. Energy 2018, 209, 409–425. [Google Scholar] [CrossRef]
- Riaz, S.; Mancarella, P. Modelling and Characterisation of Flexibility from Distributed Energy Resources. IEEE Trans. Power Syst. 2022, 37, 38–50. [Google Scholar] [CrossRef]
- Reynders, G.; Diriken, J.; Saelens, D. Generic characterization method for energy flexibility: Applied to structural thermal storage in residential buildings. Appl. Energy 2017, 198, 192–202. [Google Scholar] [CrossRef]
- oemof. A Modular Open Source Framework to Model Energy Supply Systems. 2022. Available online: https://oemof.org/ (accessed on 14 November 2023).
- Market Data|EPEX SPOT. 2022. Available online: https://www.epexspot.com/en/market-data (accessed on 14 November 2023).
- Agorameter. 2023. Available online: https://www.agora-energiewende.de/service/agorameter/chart/power_generation/28.02.2023/03.03.2023/today/ (accessed on 12 February 2023).
- Sprenger, E.; Recknagel, H.; Albers, K.-J. Taschenbuch für Heizung + Klimatechnik; RECKNAGEL: Munich, Germany, 2015. [Google Scholar]
- IKET (Ed.) Pohlmann Taschenbuch der Kältetechnik: Grundlagen, Anwendungen, Arbeitstabellen und Vorschriften; VDE VERLAG: Berlin, Germany, 2018; ISBN 978-3-8007-4149-6. [Google Scholar]
- Hu, S.-C.; Yang, R.-H. Development and testing of a multi-type air conditioner without using AC inverters. Energy Convers. Manag. 2005, 46, 373–383. [Google Scholar] [CrossRef]
- Sensfuß, F.; Ragwitz, M.; Genoese, M. The merit-order effect: A detailed analysis of the price effect of renewable electricity generation on spot market prices in Germany. Energy Policy 2008, 36, 3086–3094. [Google Scholar] [CrossRef]

| Parameter | Description | Domain |
|---|---|---|
| Number of all timesteps in the operational period | ||
| Number of timesteps with positive flexibility | ||
| Number of timesteps with negative flexibility | ||
| Set of all timesteps | ||
| Timestep index of set | ; | |
| Maximum capacity of the storage | ||
| Fill level of storage at timestep | ||
| Remaining capacity of the storage at timestep | ||
| Initial fill level of the storage | ||
| Maximum possible level of energy generation | ||
| Level of energy generation at timestep | ||
| Initial level of energy generation | ||
| Maximum energy demand in the entire horizon | ||
| Minimum energy demand in the entire horizon | ||
| Energy demand at timestep | ||
| Potential flexibility | ||
| Positive potential flexibility at timestep | ||
| Negative potential flexibility at timestep | ||
| Applied flexibility | ||
| Positive applied flexibility at timestep | ||
| Negative applied flexibility at timestep | ||
| Relative flexibility | ||
| Positive relative flexibility at timestep | ||
| Negative relative flexibility at timestep | ||
| Positive total flexibility of the whole period | ||
| Negative total flexibility of the whole period | ||
| Positive actual flexibility of the whole period | ||
| Negative actual flexibility of the whole period |
| Constraint | Piston Compressor | Turbo Compressor | Screw Compressor | Scroll Compressor |
|---|---|---|---|---|
| Maximum hourly starts | ||||
| Minimum up-time | 20 min | |||
| Minimum down-time | ||||
| Minimum load |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khorsandnejad, E.; Malzahn, R.; Oldenburg, A.-K.; Mittreiter, A.; Doetsch, C. Analysis of Flexibility Potential of a Cold Warehouse with Different Refrigeration Compressors. Energies 2024, 17, 85. https://doi.org/10.3390/en17010085
Khorsandnejad E, Malzahn R, Oldenburg A-K, Mittreiter A, Doetsch C. Analysis of Flexibility Potential of a Cold Warehouse with Different Refrigeration Compressors. Energies. 2024; 17(1):85. https://doi.org/10.3390/en17010085
Chicago/Turabian StyleKhorsandnejad, Ehsan, Robert Malzahn, Ann-Katrin Oldenburg, Annedore Mittreiter, and Christian Doetsch. 2024. "Analysis of Flexibility Potential of a Cold Warehouse with Different Refrigeration Compressors" Energies 17, no. 1: 85. https://doi.org/10.3390/en17010085
APA StyleKhorsandnejad, E., Malzahn, R., Oldenburg, A.-K., Mittreiter, A., & Doetsch, C. (2024). Analysis of Flexibility Potential of a Cold Warehouse with Different Refrigeration Compressors. Energies, 17(1), 85. https://doi.org/10.3390/en17010085







