Analysis of the Influence of the 6-Pulse Thyristor-Bridge Input Reactor Size on the Shunt Active Power Filter Work Efficiency: A Case Study
Abstract
1. Introduction
2. Simulation Study
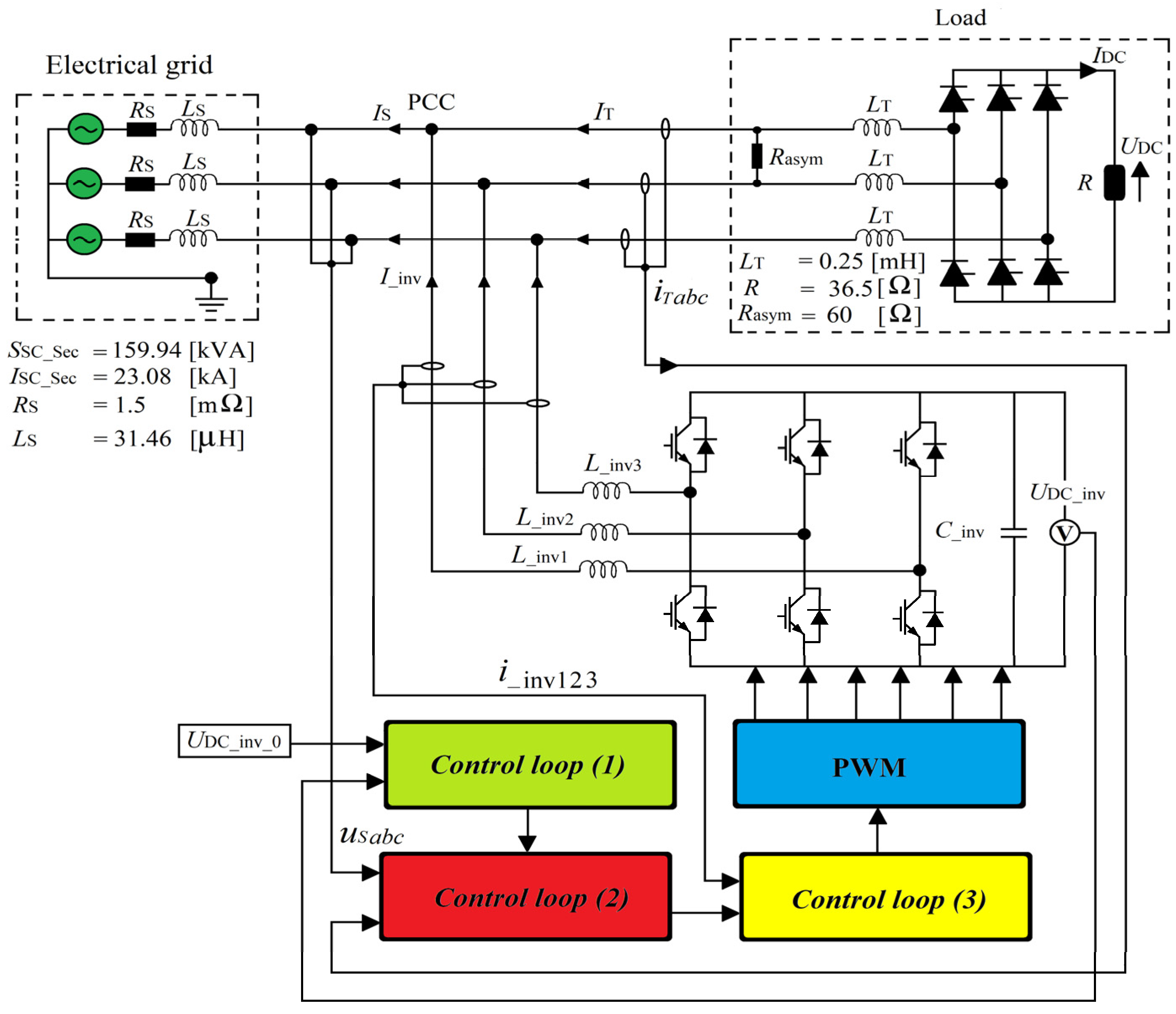
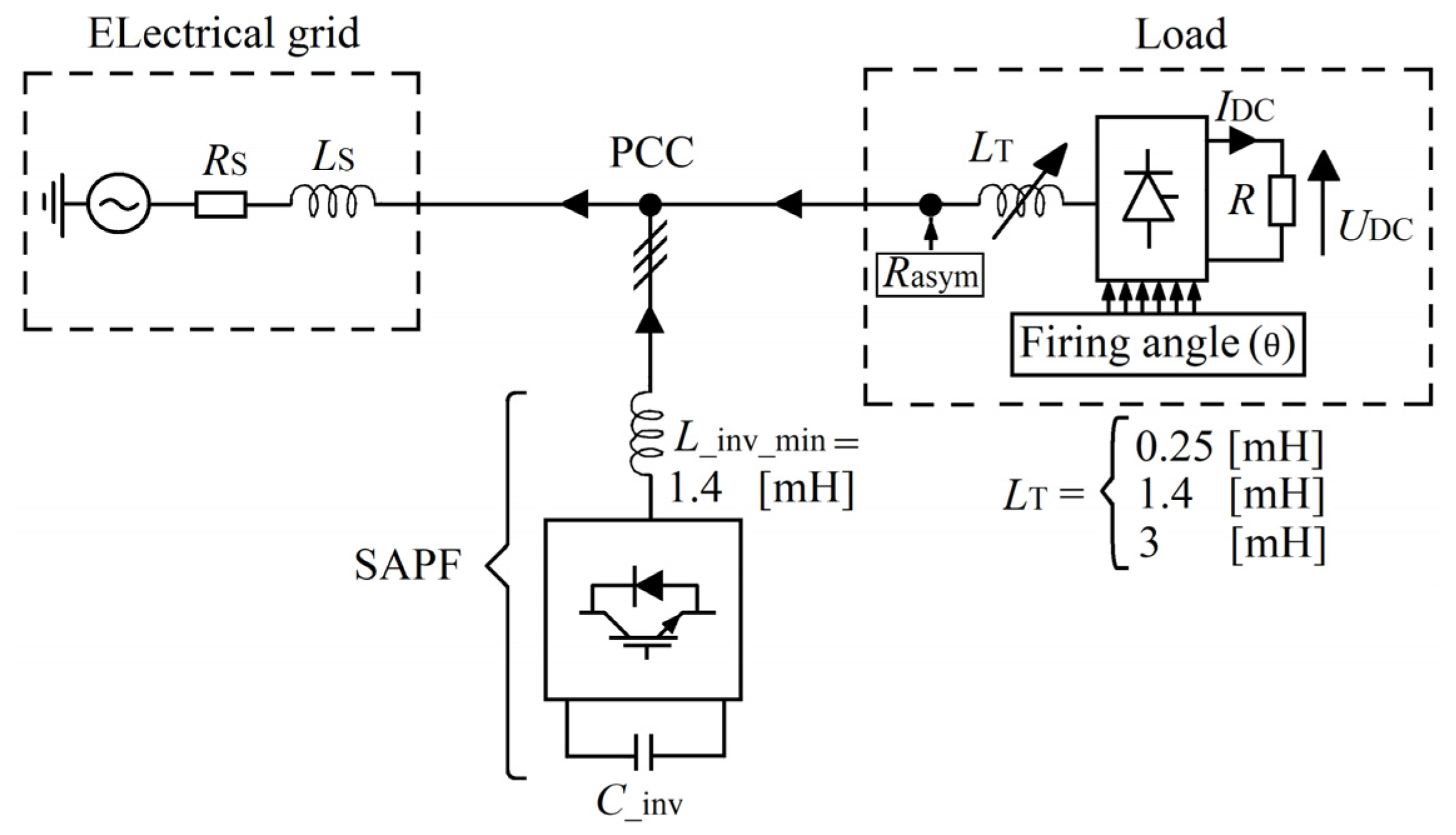
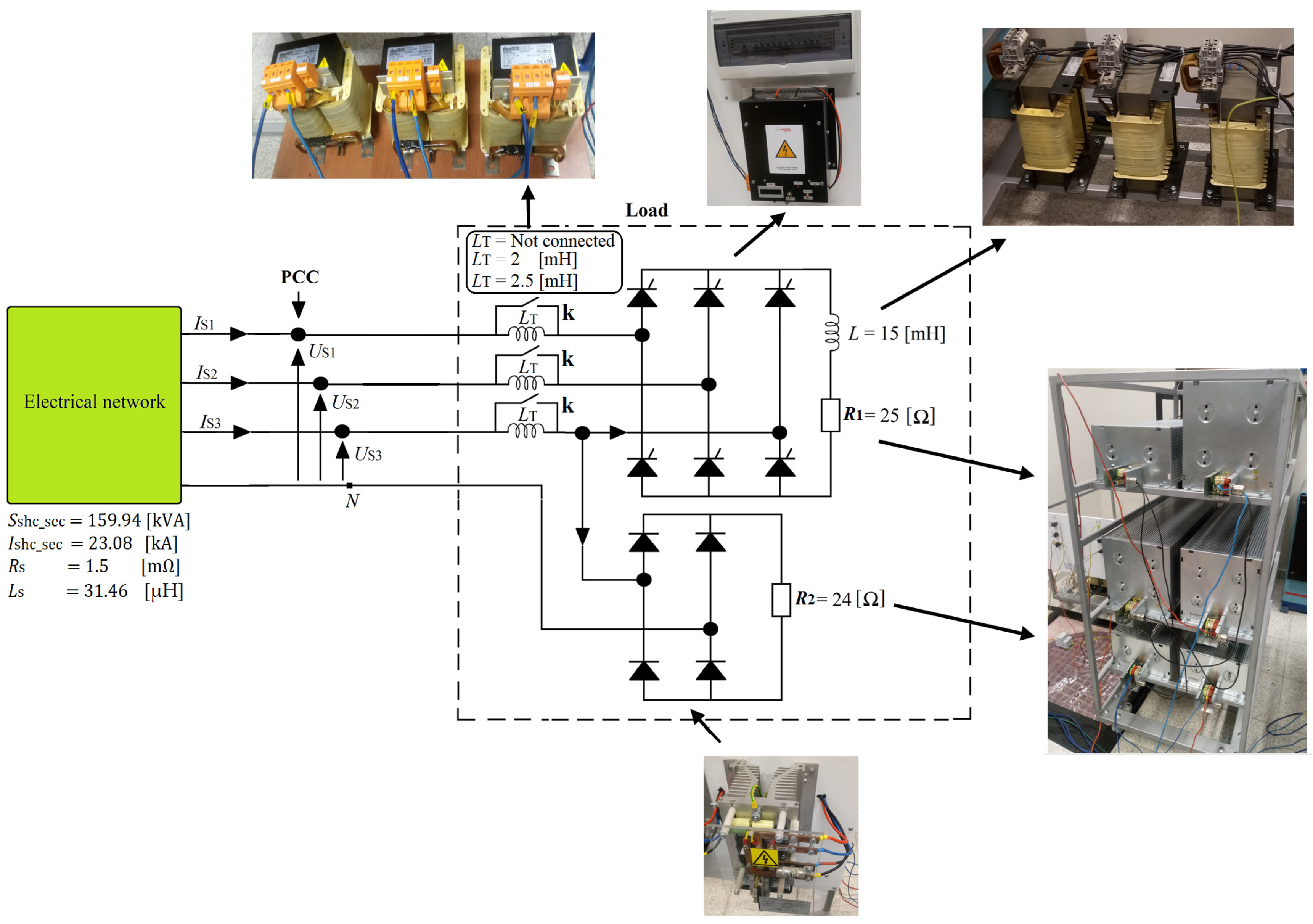
2.1. Presentation of the Simulated Power System
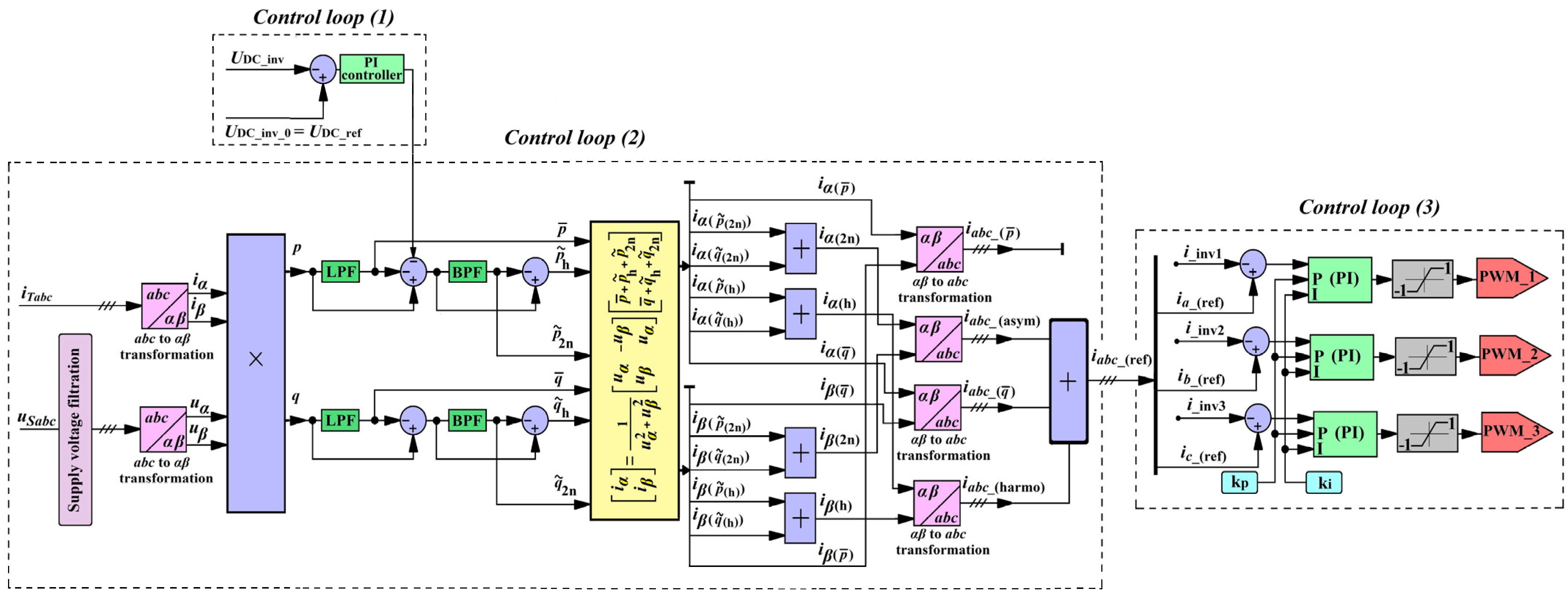
2.1.1. Description of the Proposed Control System
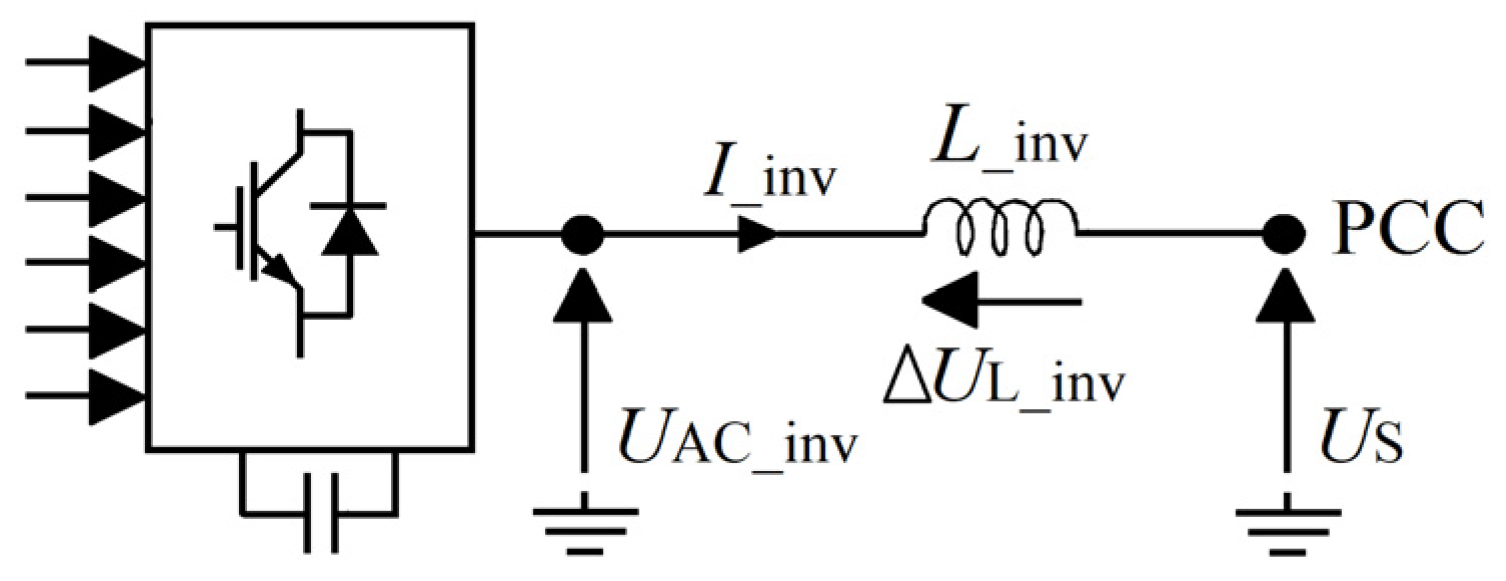
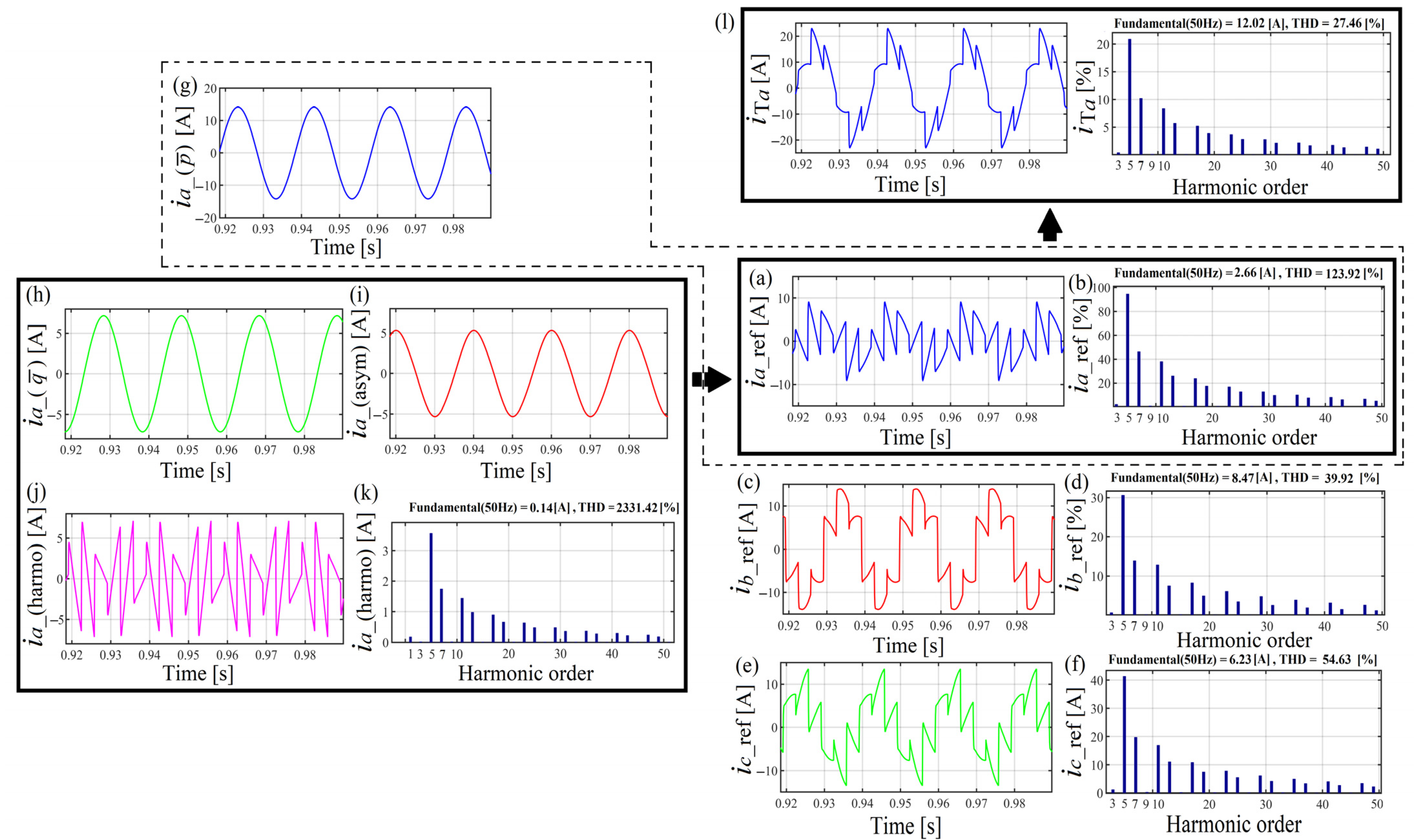
2.1.2. Proposed Expressions for the SAPF Parameters Computation
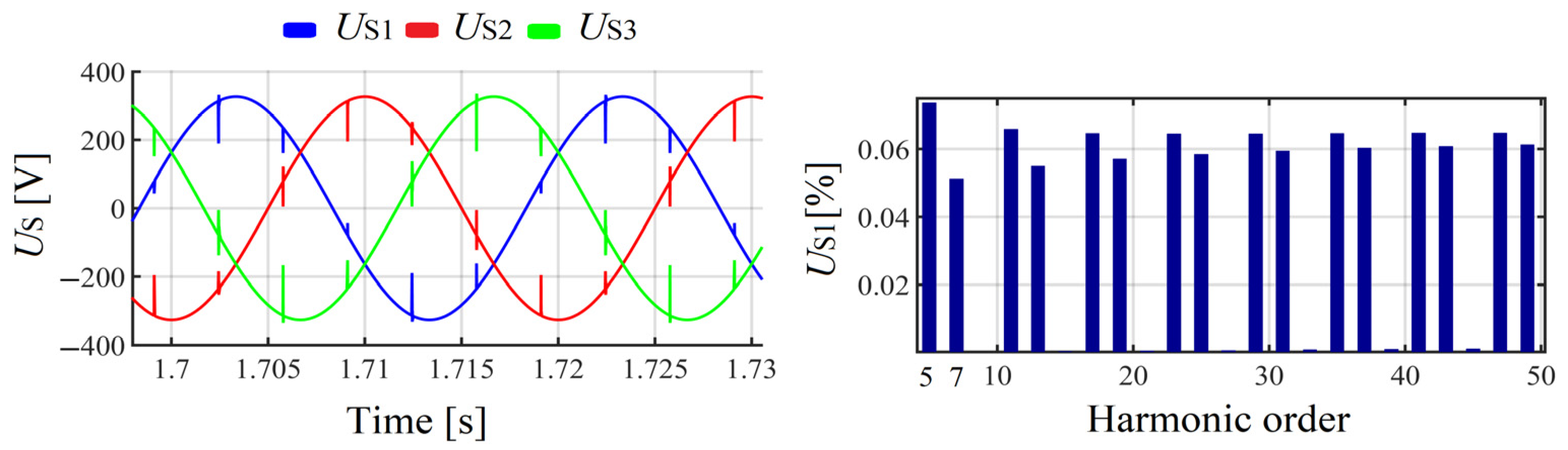
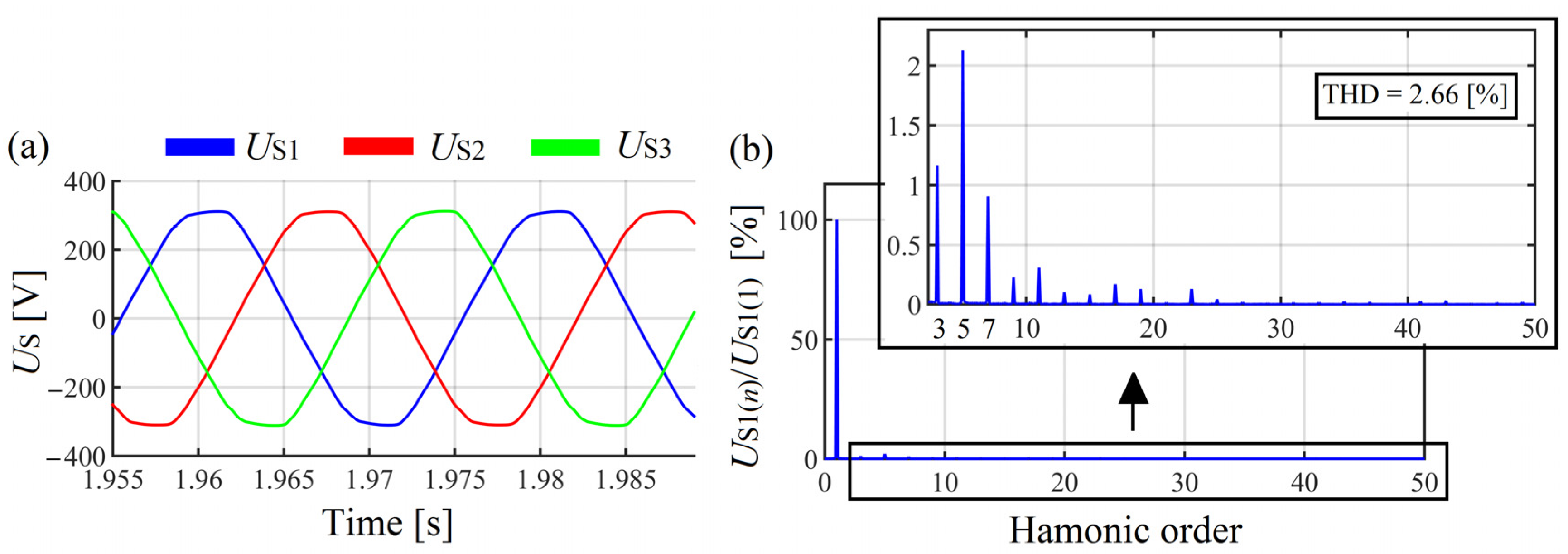
2.2. Simulation Assumption
2.3. Simulation Results
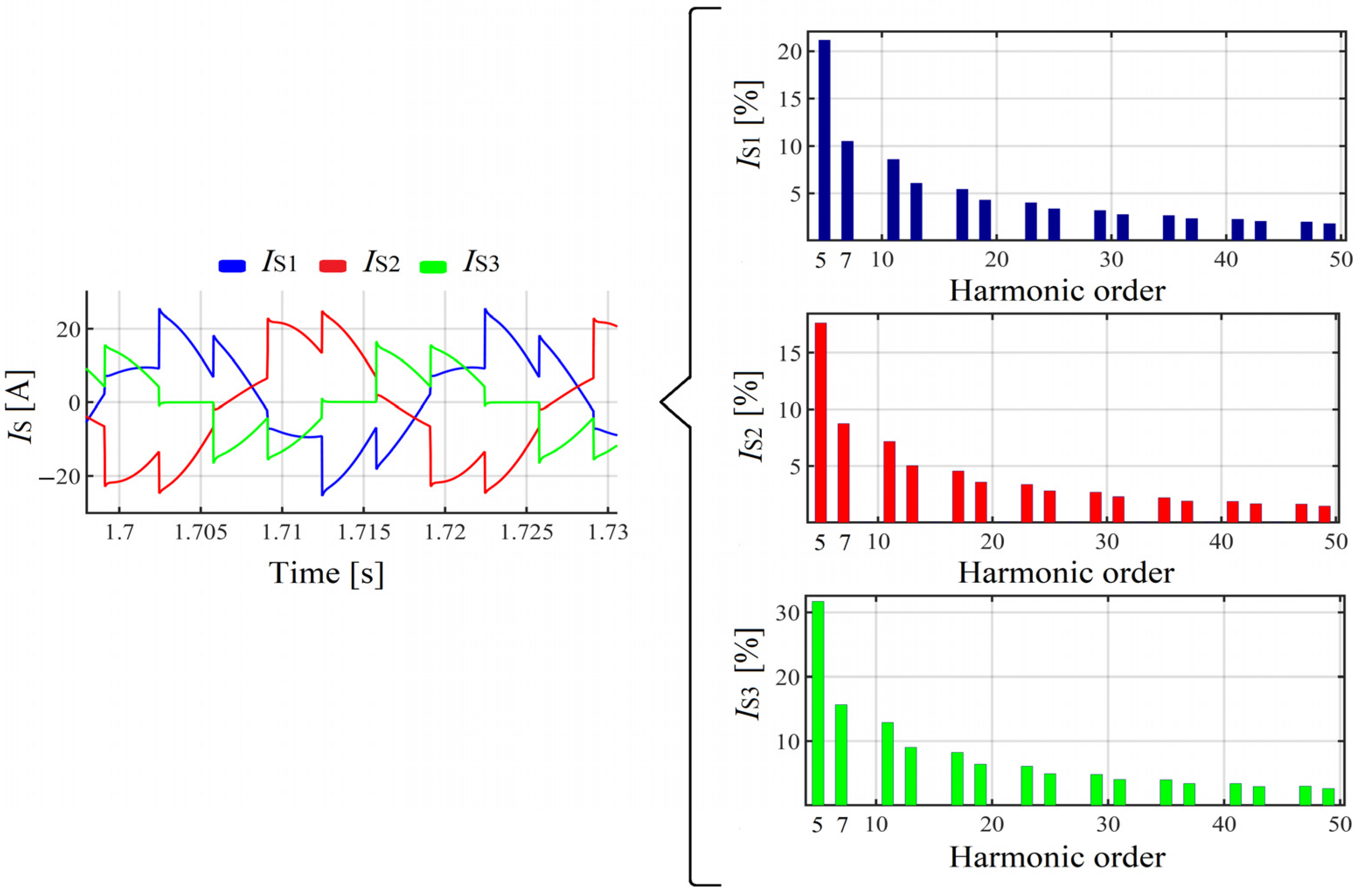
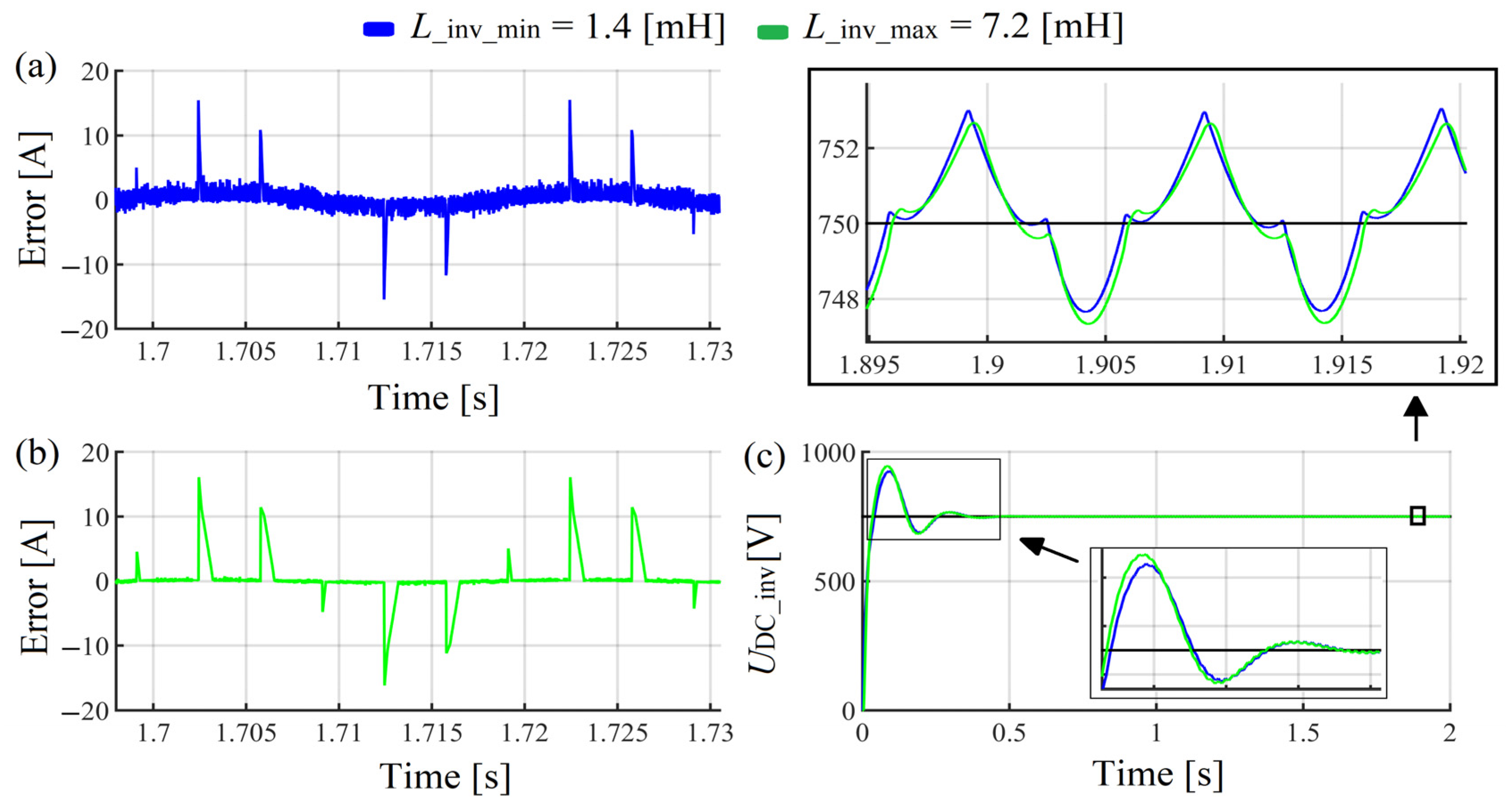
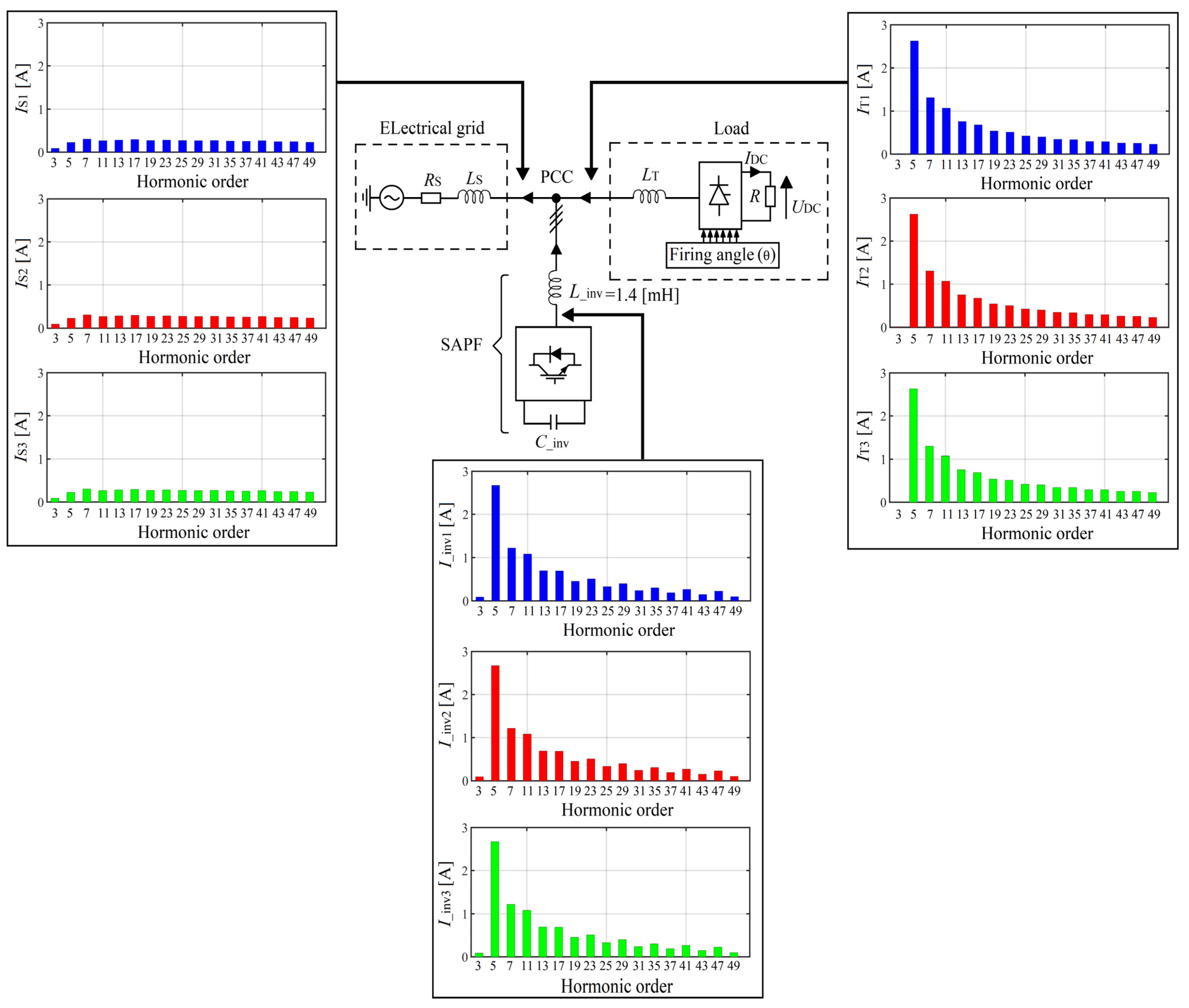
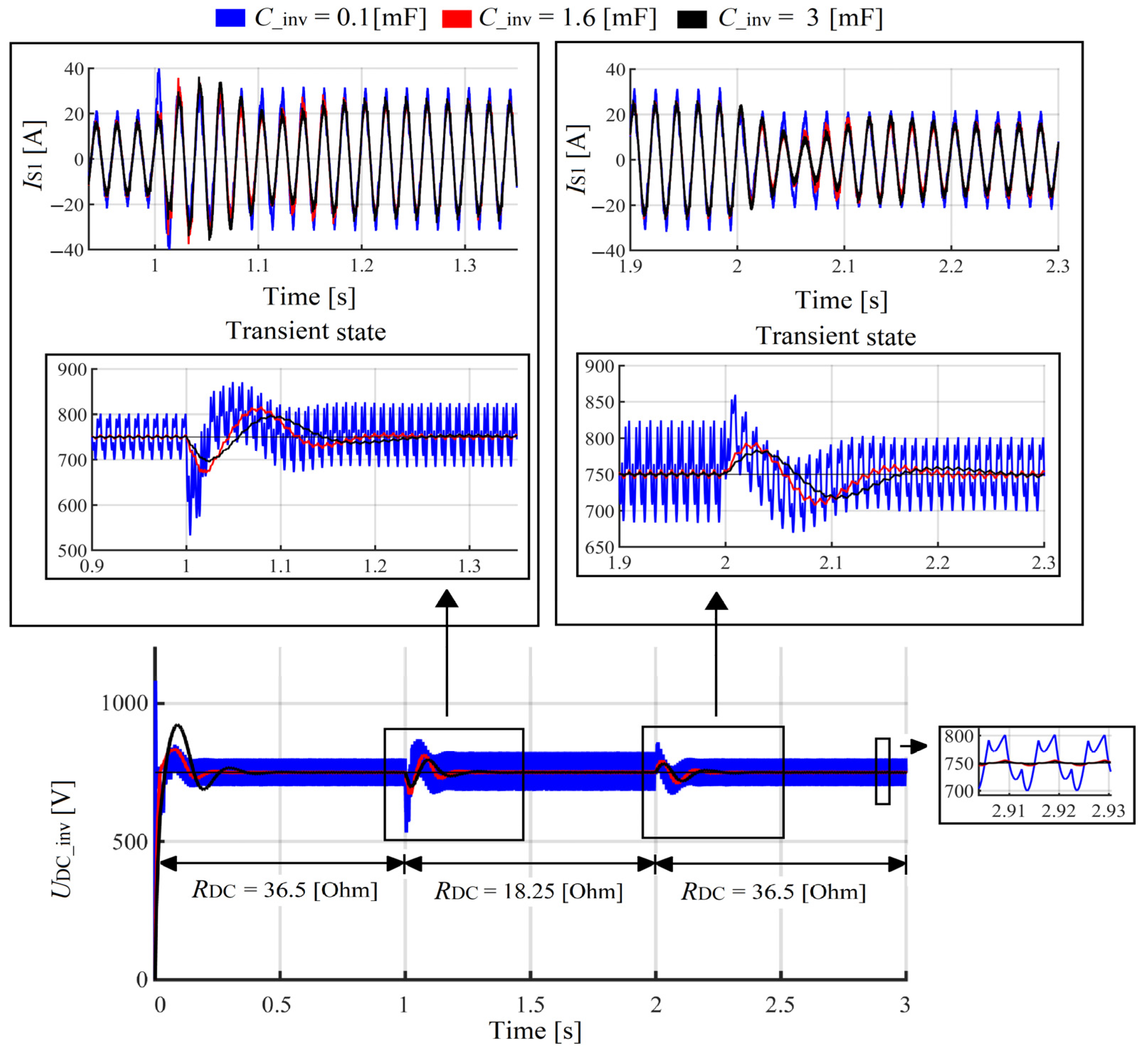
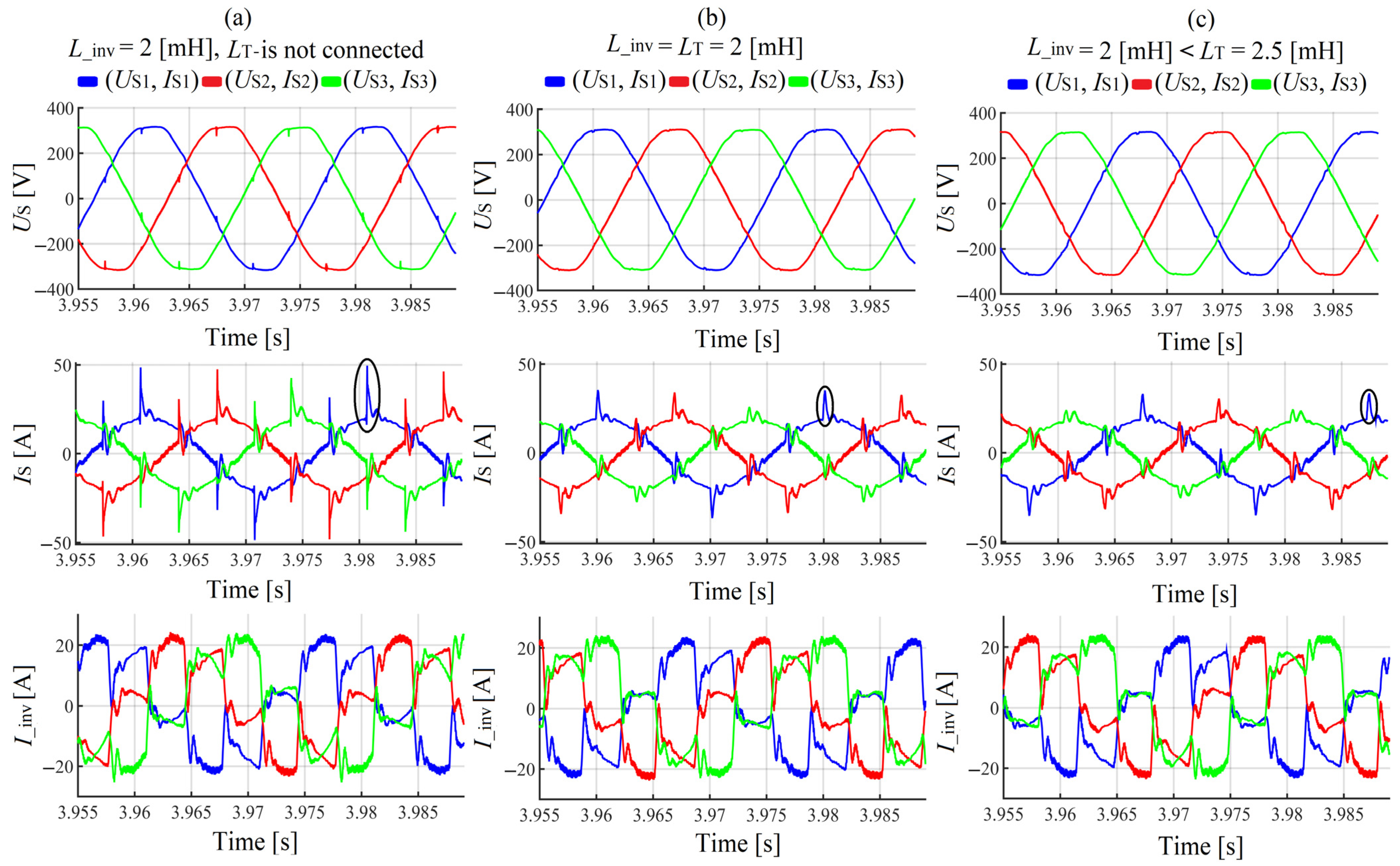
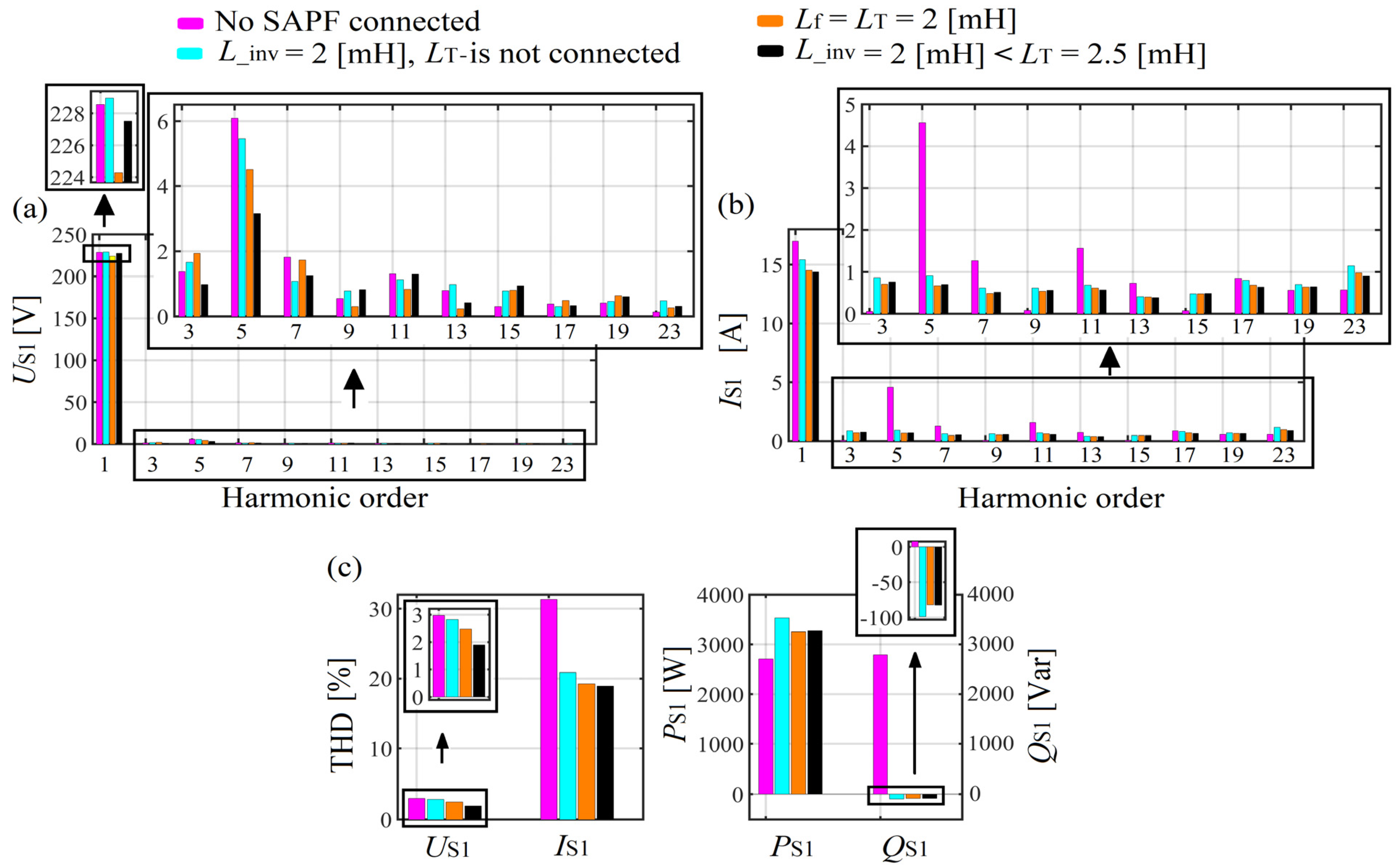
2.4. First Simulation Results
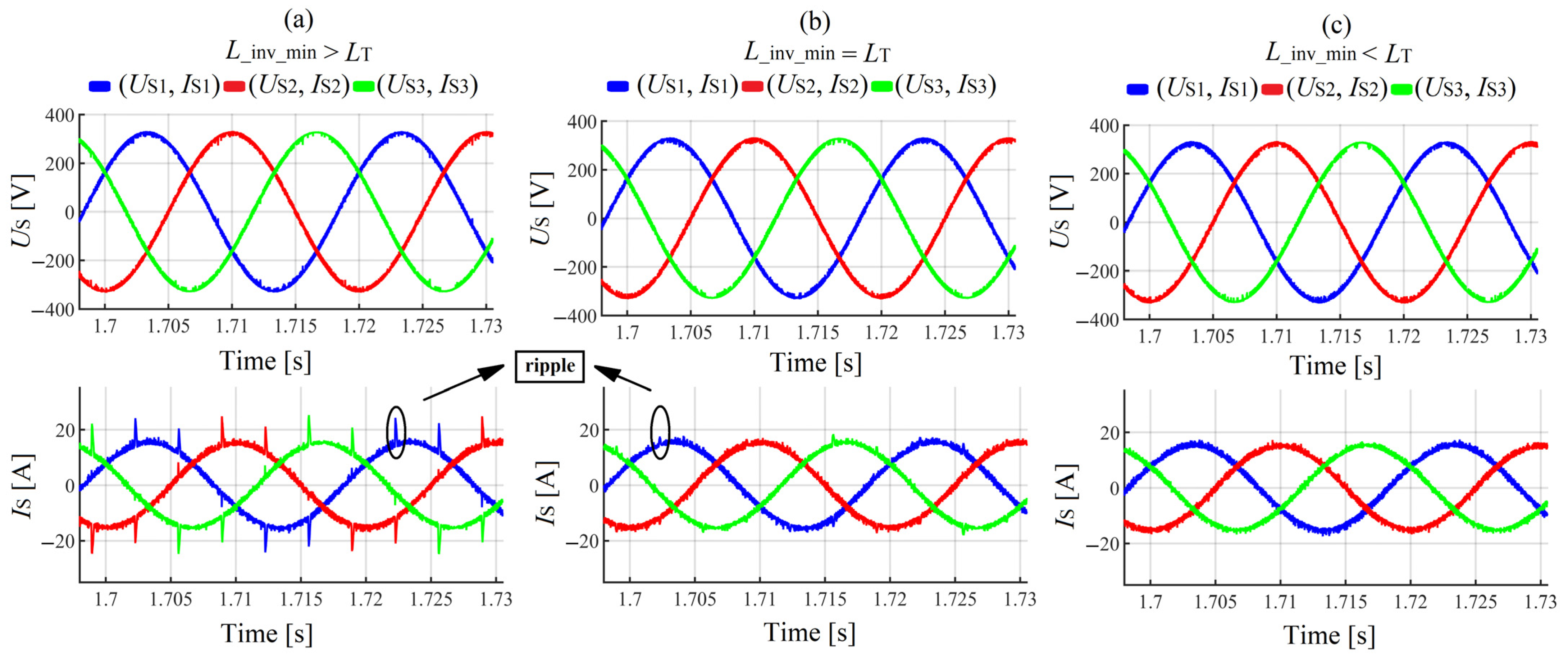
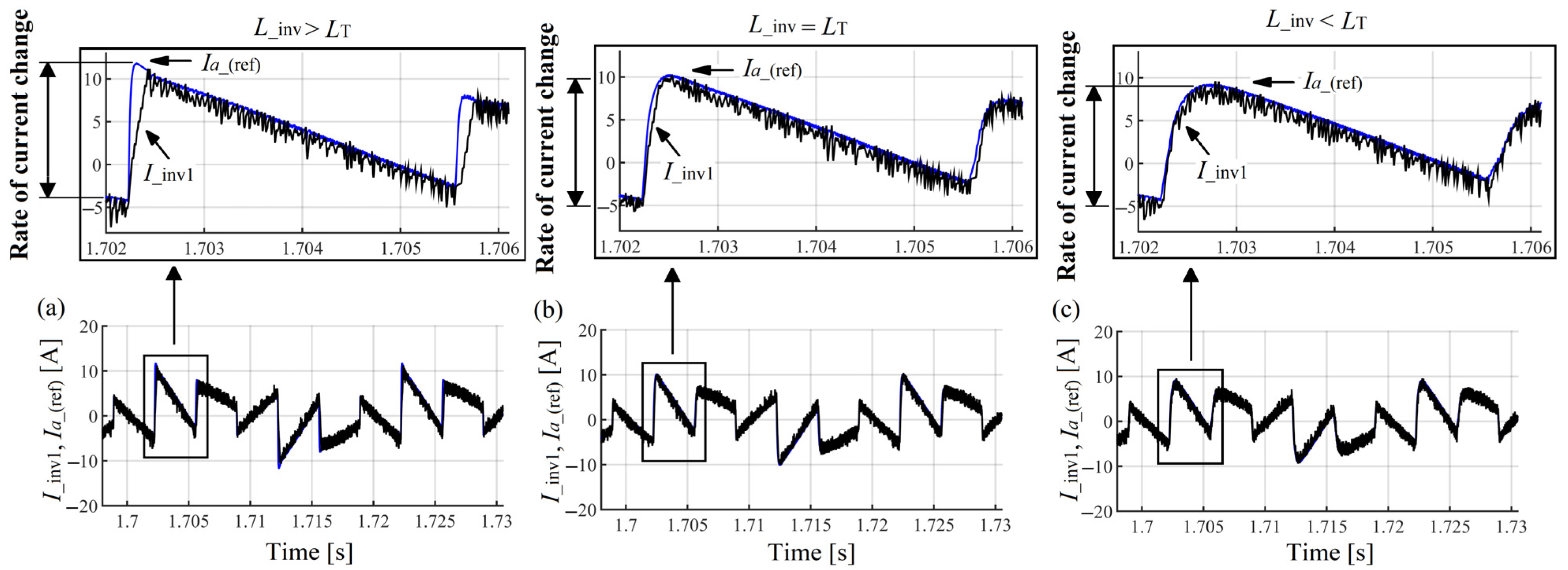
Influence of the Inverter Input Reactor Size on the SAPF Work Efficiency
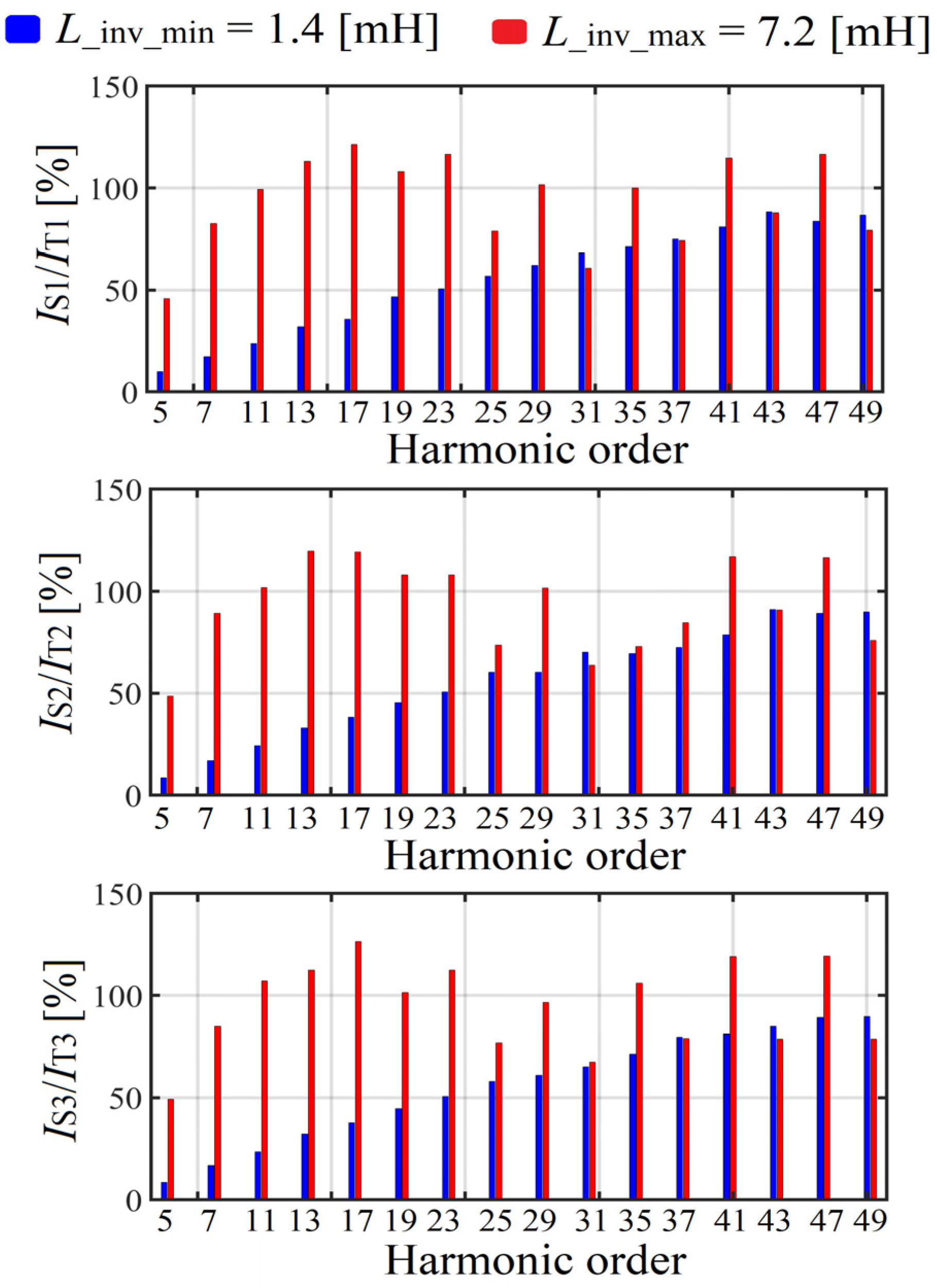
2.5. Second Simulation Results
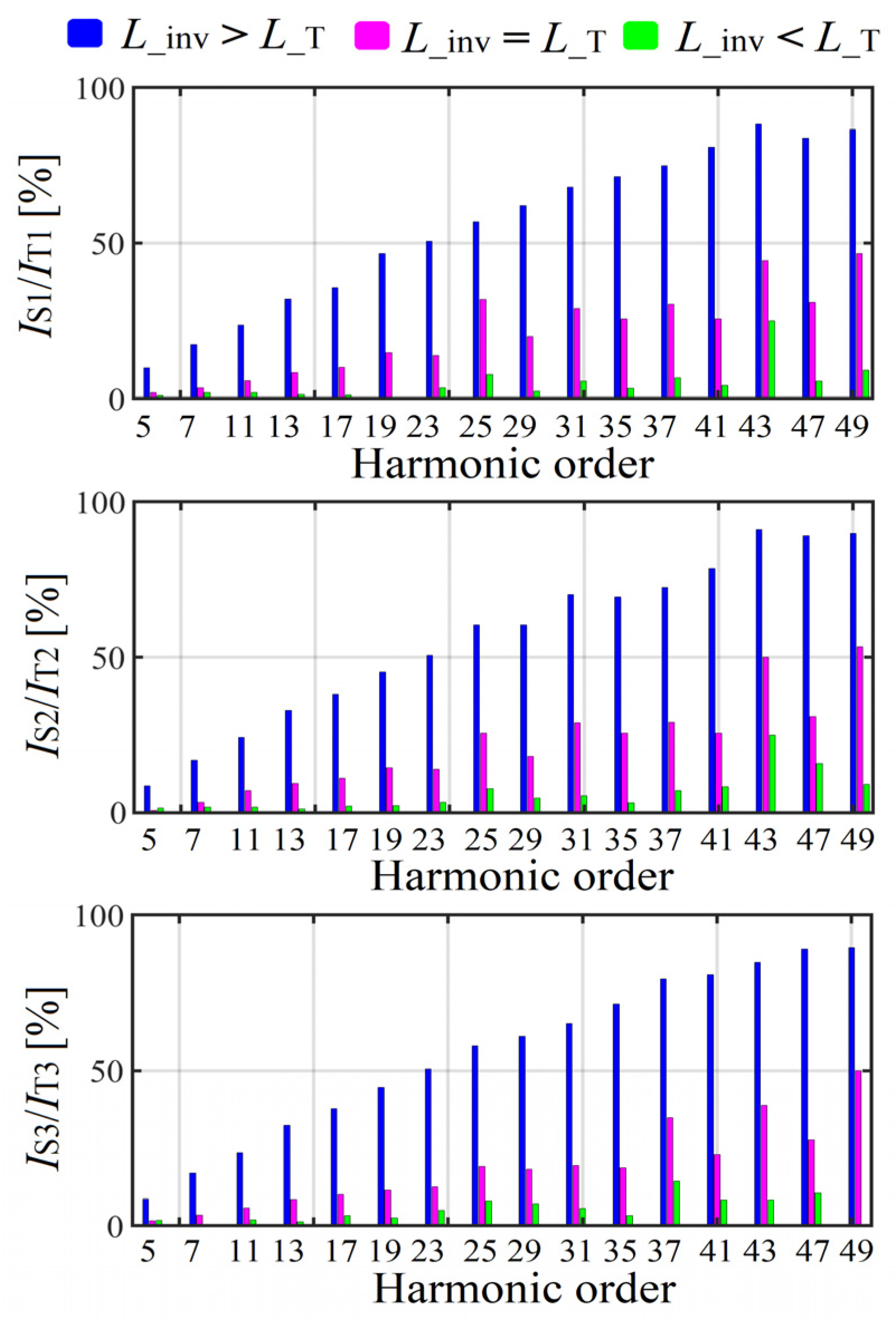
Influence of the Thyristor-Bridge Input Reactor Size on the SAPF Work Efficiency
3. Laboratory Experiments
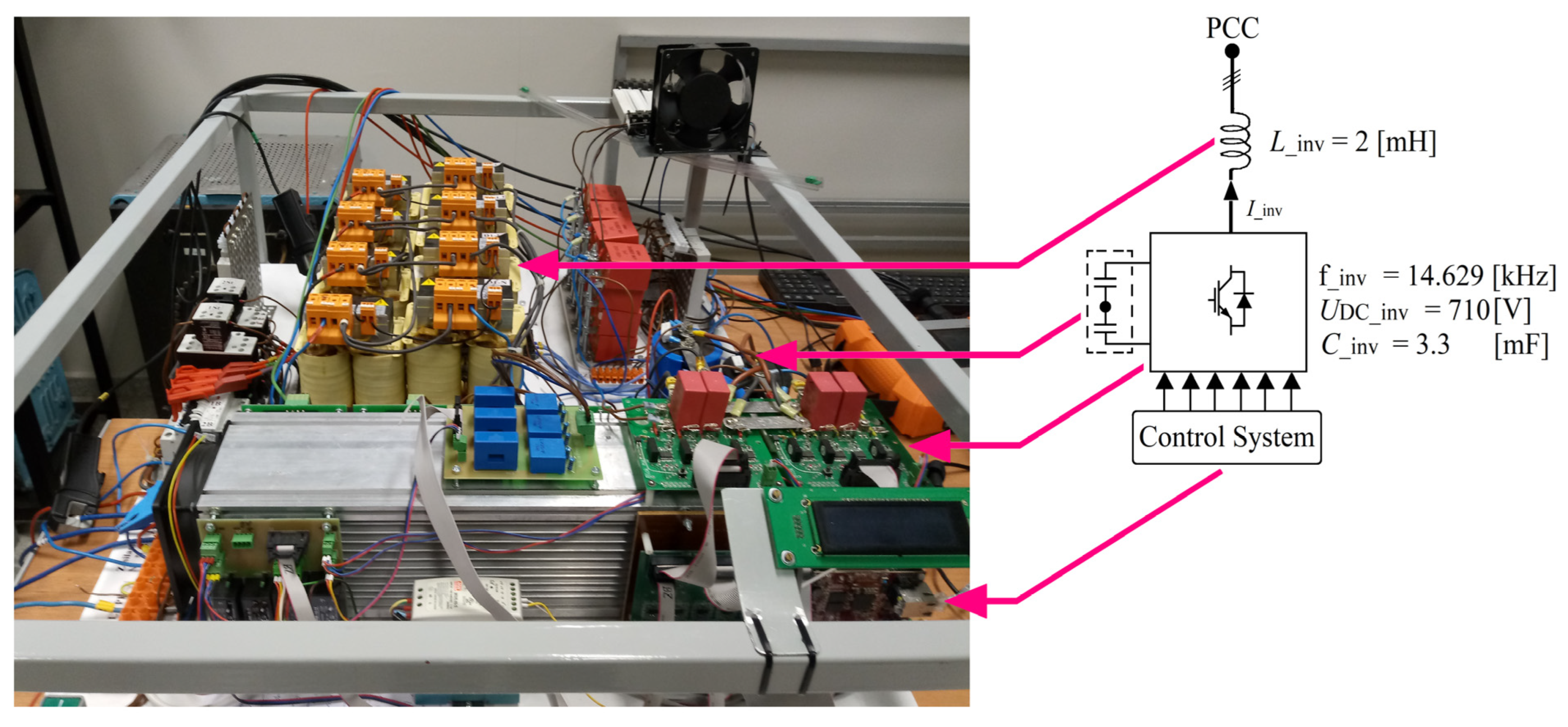
3.1. Laboratory Model Description
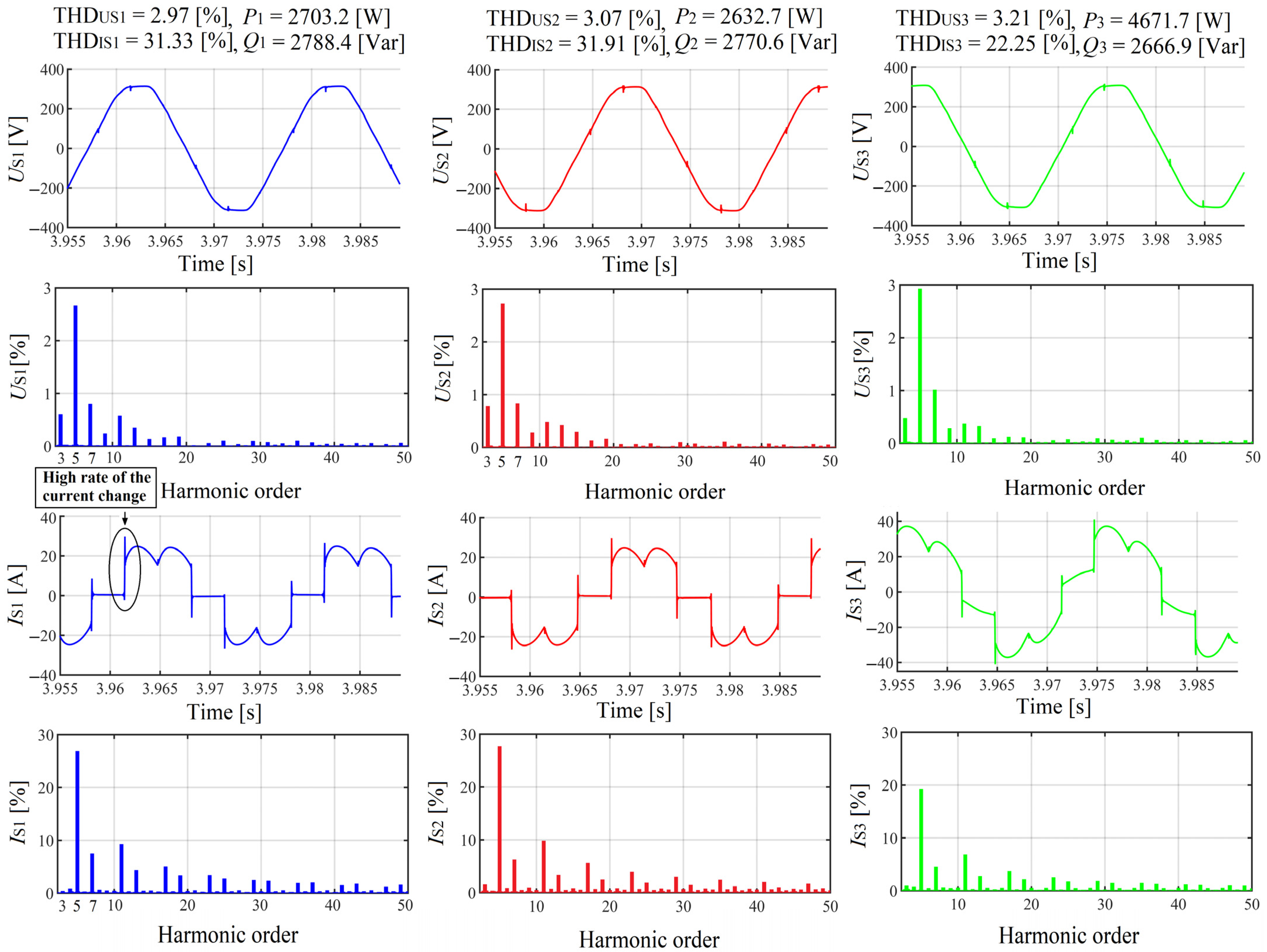
3.2. Laboratory Results
4. Conclusions
- -
- if the SAPF input reactor parameters are computed (chosen) based only on the criteria of a better reduction in the switching ripples (which means a large size of that reactor), the SAPF work efficiency in terms of reactive power, harmonics and reactive power mitigation may be reduced.
- -
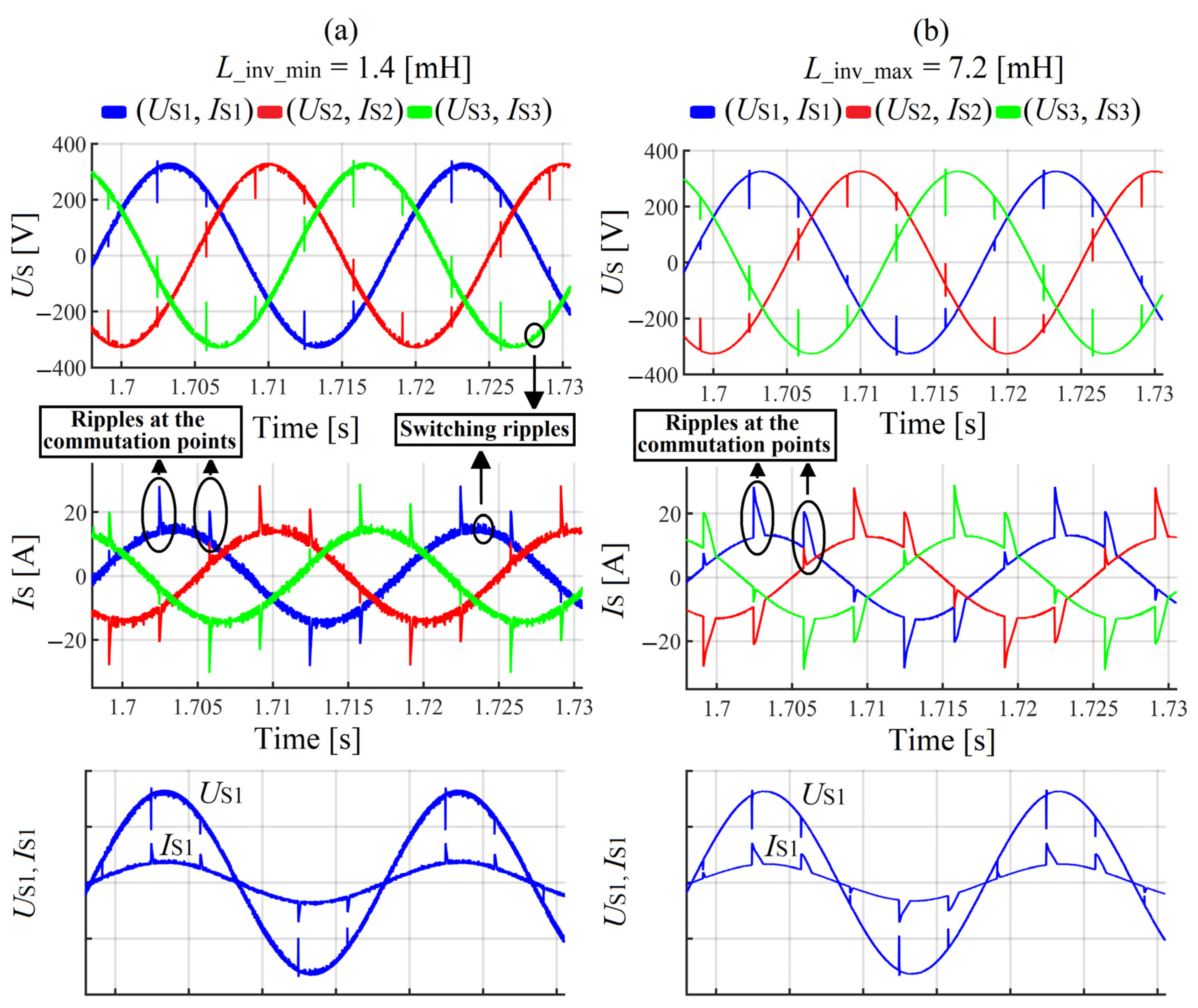
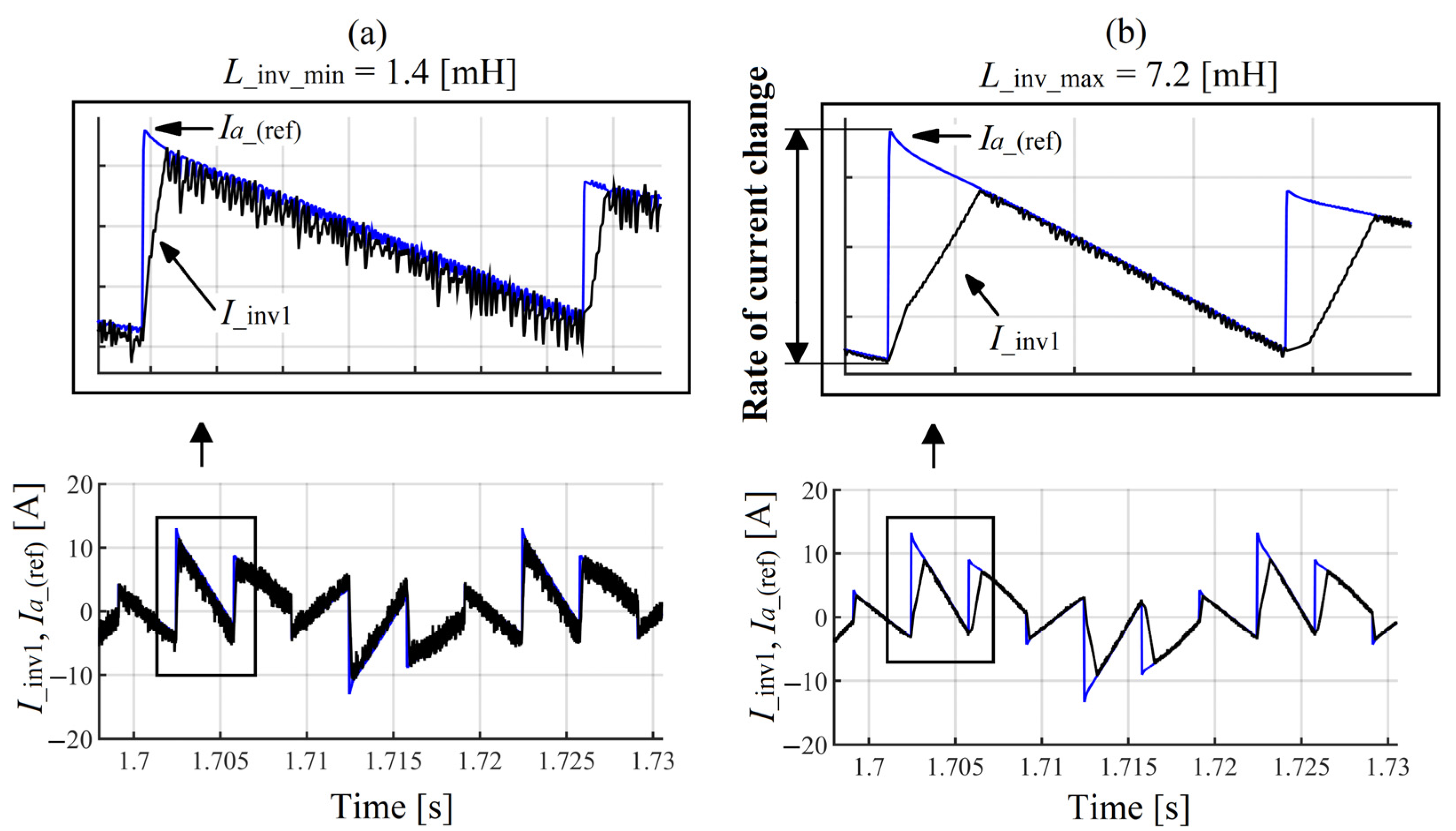
- The SAPF with an input reactor inductance higher than the input reactor inductance of the thyristor-bridge is less efficient in terms of ripples mitigation at the points of commutation notches because at those points the compensating current has difficulties in tracking the reference current.
- -
- The SAPF with an input reactor inductance equal or smaller than the input reactor inductance of the thyristor-bridge is more efficient in terms of ripples mitigation at the points of commutation notches because at those points the compensating current can easily track the reference current.
- -
- The SAPF with an input reactor inductance equal or smaller than the input reactor inductance of the thyristor-bridge is more efficient in terms of reactive power, harmonics and asymmetry mitigation than the one with an input reactor inductance higher than the input reactor inductance of the thyristor-bridge.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bhattacharyya, S.; Myrzik, J.M.A.; Kling, W.L. Consequences of poor power quality—An overview. In Proceedings of the IEEE 42nd International Universities Power Engineering Conference, Brighton, UK, 4–6 September 2007. [Google Scholar]
- Bhattacharyya, S.; Lumig, M.V.; Cobben, S.; Myrzik, J.; Kling, W. Consequences of poor power quality for grid operators. In Proceedings of the IEEE 20th International Conference and Exhibition on Electricity Distribution—Part 2, Prague, Czech Republic, 8–11 June 2009. [Google Scholar]
- Tazky, M.; Regula, M.; Otcenasova, A. Impact of changes in a distribution network nature on the capacitive reactive power flow into the transmission network in Slovakia. Energies 2021, 14, 5321. [Google Scholar] [CrossRef]
- Shawon, M.H.; Hanzelka, Z.; Dziadecki, A. Voltage-current and harmonic characteristic analysis of different FC-TCR based SVC. In Proceedings of the IEEE Conference Eindhoven PowerTech, Eindhoven, The Netherlands, 29 June–2 July 2015. [Google Scholar]
- AbdElhafez, A.A.; Alruways, S.H.; Alsaif, Y.A.; Althobaiti, M.F.; Alotaibi, A.B.; Alotaibi, N.A. Reactive power problem and solutions: An overview. J. Power Energy Eng. 2017, 5, 40–54. [Google Scholar] [CrossRef][Green Version]
- Kuldeep, K.S.; Saquib, S.; Nanand, V.P. Harmonics & its mitigation technique by passive shunt filter. Int. J. Soft Comput. Eng. (IJSCE) 2013, 3, 325–331. [Google Scholar]
- Singh, G.K. Power System Harmonic Research: A Survey. Eur. Trans. Electr. Power 2009, 19, 151–172. [Google Scholar] [CrossRef]
- Wagner, V.E. Effects of harmonics on equipment. IEEE Trans. Power Deliv. 1993, 8, 672–680. [Google Scholar] [CrossRef]
- Bennett, P.C.; Darley, V.; Abbott, S.M. The effects of harmonic distortion on equipments. In Proceedings of the IEEE Colloquium on Sources and Effects of Harmonic Distortion in Power Systems, London, UK, 5 March 1997. [Google Scholar]
- Buzdugan, M.I.; Balan, H. Power system harmonics issues in some end. In Proceedings of the 52nd IEEE International Universities Power Engineering Conference (UPEC), Heraklion, Greece, 28–31 August 2017. [Google Scholar]
- Plummer, I. Assymmetry in Distribution Systems: Causes, Harmful Effects and Remedies. LSU Master’s Thesis. Available online: https://digitalcommons.lsu.edu/cgi/viewcontent.cgi?referer=&httpsredir=1&article=2489&context=gradschool_theses (accessed on 1 March 2023).
- Jouanne, A.V.; Banerjee, B. Assessment of voltage unbalance. IEEE Trans. Power Deliv. 2001, 16, 782–790. [Google Scholar] [CrossRef]
- Lee, K.; Jahns, T.M.; Lipo, T.A.; Venkataramanan, G.; Berkopec, W.E. Impact of input sag and unbalance on DC-link inductor and capacitor stress in adjustable-speed drives. IEEE Trans. Ind. Appl. 2008, 44, 1825–1833. [Google Scholar] [CrossRef]
- Horia, G.B.; Sorin, G.P.; Iulian, M.T.B.; Anca, M.; Pompei, C.D.; Mohammed, S. Effects of voltage unbalance and harmonics on drive systems with induction motor. J. Taibah Univ. Sci. 2022, 16, 1. [Google Scholar] [CrossRef]
- Driesen, J.; Craenenbroeck, T.V. Voltage Disturbances Introduction to Unbalance. Power Quality Application Guide, Katholieke Universiteit Leuven, May 2002. Available online: https://studylib.net/doc/18037296/5.1.3-introduction-to-unbalance (accessed on 7 October 2023).
- Osahenvemwen, O.A.; Okhumeode, M.E.; Emakpor, S. The Effects of Unbalance Load in Power Distribution Sub—Station Network. Am. J. Sci. Eng. Res. 2020, 3, 1–11. Available online: https://www.researchgate.net/publication/344188516 (accessed on 13 March 2023).
- Arghavani, H.; Peyravi, M. Unbalanced current based tariff. In Proceedings of the CIRED 24th International Conference on Electricity Distribution, Glasgow, Scotland, 12–15 June 2017. [Google Scholar]
- Kahingala, T.D.; Perera, S.; Agalgaonkar, A.P.; Jayatunga, U. Statcom based network voltage unbalance mitigation for sub-transmission networks. In Proceedings of the IEEE Innovative Smart Grid Technologies—Asia (ISGT Asia), Chengdu, China, 21–24 May 2019. [Google Scholar]
- Singh, A.K.; Singh, G.K.; Mitra, R. Impact of source voltage unbalance on AC-DC rectifier performance. In Proceedings of the IEEE 2nd International Conference on Power Electronics Systems and Applications, Hong Kong, China, 12–14 November 2006. [Google Scholar]
- EIC 61000-2-4. Electromagnetic Compatibility (EMC) Part 2-4: Environment Levels in Industry Plants for Low-Frequency Conducted Disturbances.Second edition 2002-06. Available online: https://www.vde-verlag.de/iec-normen/preview-pdf/info_iec61000-2-4%7Bed2.0%7Db.pdf (accessed on 21 December 2020).
- Klempka, R. Design of C-type passive filter for arc furnaces. Metalurgia 2017, 56, 161–163. [Google Scholar]
- Azebaze, M.C.S.; Hanzelka, Z. Passive harmonic filters. In Power Quality in Future Electrical Power Systems, 1st ed.; Zobaa, A.F., Shady, H.E.A.A., Eds.; IET the Institution of Engineering and Technology: London, UK, 2017. [Google Scholar]
- Klempka, R. Optimal Double-Tuned Filter Efficiency analysis. IEEE Trans. Power Deliv. 2020, 36, 1079–1088. [Google Scholar] [CrossRef]
- Firlit, A.; Kołek, K.; Piątek, K. Heterogeneous active power filter controller. In Proceedings of the IEEE International Symposium ELMAR, Zadar, Croatia, 18–20 September 2017. [Google Scholar]
- Azebaze, M.C.S.; Hanzelka, Z. Different approaches for designing the passive power filters. Przegląd Elektrotechniczny 2015, 91, 102–108. [Google Scholar]
- Piątek, K. A new approach of DVR control with minimized energy injection. In Proceedings of the IEEE 12th International conference on Power Electronics and motion Control, Portoroz, Slovenia, 30 August–1 September 2006. [Google Scholar]
- Azebaze, M.C.S.; Hanzelka, Z. Hybrid passive harmonic filter: Group of two parallel connected single-tuned filters and the series passive filter. In Polish-Hybrydowy Filtr Pasywny: Grupa Dwóch Jednogałęziowych Filtrów Równoległych Połączonych z Filtrem Szeregowym; Grupa MEDIUM Sp. z o.o. Sp.k.-a: Cracow, Poland, 2022; pp. 64–70. [Google Scholar]
- Ehsan, P.; Masood, A.A. Efficient procedures to design and characterize passive harmonic filters in low power applications. In Proceedings of the IEEE International Symposium on Industrial Electronics (ISIE), Bari, Italy, 4–7 July 2010. [Google Scholar]
- Reynaldo, R.; Gregory, A.F. Optimal harmonic filter topology applied in HV and EHV networks using particle swarm optimization. In Proceedings of the IEEE Electrical Power and Energy Conference (EPEC), Ottawa, ON, Canada, 12–14 October 2016. [Google Scholar]
- Gumilar, L.; Afandi, A.N.; Aripriharta; Habibi, M.A.; Kusumawardana, A.; Baskoro, A. Performance of combination shunt passive harmonic filter and detuned reactor at high voltage level. In Proceedings of the IEEE 7th International Conference on Electrical, Electronics and Information Engineering (ICEEIE), Malang, Indonesia, 2 October 2021. [Google Scholar]
- Tupsa-ard, J.; Chamchoy, C.; Tayjasanant, T. High-voltage passive harmonic filter design. In Proceedings of the IEEE 8th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI) Association of Thailand, Khon Kaen, Thailand, 11 July 2011. [Google Scholar]
- Azebaze, M.C.S. Investigation on the work efficiency of the LC passive harmonic filter chosen topologies. Electronics 2021, 10, 896. [Google Scholar] [CrossRef]
- Azebaze, M.C.S.; Hanzelka, Z.; Firlit, A. Analysis of the factor having an influence on the LC passive harmonic filter work efficiency. Energies 2022, 15, 1894. [Google Scholar] [CrossRef]
- Fujita, H.; Yamasaki, T.; Akagi, H. A hybrid active filter for damping of harmonic resonance in industrial power systems. IEEE Trans. Power Electron. 2000, 15, 215–222. [Google Scholar] [CrossRef]
- Gonzatti, R.B.; Ferreira, S.C.; da Silva, C.H.; Pereira, R.R.; da Silva, L.E.B.; Lambert-Torres, G. Smart Impedance: A New Way to Look at Hybrid Filters. IEEE Trans. Smart Grid 2016, 7, 837–846. [Google Scholar] [CrossRef]
- Swain, S.D.; Ray, P.K.; Mohanty, K.B. Improvement of power quality using a robust hybrid series active power filter. IEEE Trans. Power Electron. 2017, 32, 3490–3498. [Google Scholar] [CrossRef]
- Lee, T.; Wang, Y.C.; Li, J.C.; Guerrero, J.M. Hybrid active filter with variable conductance for harmonic resonance suppression in industrial power systems. IEEE Trans. Ind. Electron. 2015, 62, 746–756. [Google Scholar] [CrossRef]
- Jalil, M.; Amiri, A. An effective structure of three-phase parallel hybrid active power filter to accurate harmonic elimination. In Proceedings of the IEEE 15th International Conference on Protection and Automation of power Systems (IPAPS), Shiraz, Iran, 30–31 December 2020. [Google Scholar]
- Cleary-Balderas, A.; Medina-Rios, A.; Cruz-Hernéndez, O. Hybrid active power filter based on the IRP theory for harmonic current mitigation. In Proceedings of the IEEE International Autumn Meeting on Power, Electronics and Computing (ROPEC), Ixtapa, Mexico, 26 January 2017. [Google Scholar]
- Daftary, D.; Shah, M.T. Design and analysis of the hybrid active power filter for current harmonics mitigation. In Proceedings of the IEEE 16th India Council International Conference (INDICON), Rajkot, India, 13–15 December 2019. [Google Scholar]
- Akagi, H.; Tamai, Y. Comparisons in Circuit Configuration and Filtering Performance between Hybrid and Pure Shunt Active Filters, In Proceedings of the IEEE 38th IAS Annual Meeting on Conference Record of the Industry Applications, Salt Lake City, UT, USA, 12–16 October 2003.
- Lee, H.; Shon, J. Sensorless AC capacitor voltage monitoring method for HAPF. IEEE Access 2023, 11, 15514–15524. [Google Scholar] [CrossRef]
- Azebaze, M.C.S.; Hanzelka, Z. Hybrid power active filter—Effectiveness of passive filter on the reduction of voltage and current distortion. In Proceedings of the IEEE International Conference on Electric Power Quality and Supply Reliability, Estonia, Tallinn, 29–31 August 2016. [Google Scholar]
- Singh, B.; Chandra, A.; Al-Haddad, K. Power Quality: Problems and Mitigation Techniques; John Wiley & Sons Ltd.: Chichester, UK, 2015. [Google Scholar]
- Firlit, A.; Kołek, K.; Piątek, K. Rapid controller development for a dynamic voltage restorer. In Proceedings of the IEEE International Symposium ELMAR, Zadar, Croatia, 18–20 September 2017. [Google Scholar]
- Jacek, K. Practical application of series active compensators. In Power Theories for Improved Power Quality; Grzegorz, B., Pasko, M., Eds.; Springer: London, UK, 2012; pp. 13–47. [Google Scholar]
- Kwak, S.; Toliyat, H.A. Design and rating comparison of PWM voltage source rectifiers and active power filters for AC drives with unity power factor. IEEE Trans. Power Electron. 2015, 20, 1133–1142. [Google Scholar] [CrossRef]
- Abdelmadjid, C.; Jean-Paul, G.; Fateh, K.; Laurent, R. On the design of shunt active filter for improving power quality. In Proceedings of the IEEE International Symposium on Industrial Electronics, Cambridge, UK, 30 June–2 July 2008. [Google Scholar]
- Chiang, S.J.; Chang, J.M. Design and implementation of the parallelable active power filter. In Proceedings of the 30th Annual IEEE Power Electronics Specialists Conference, Charleston, SC, USA, 1 July 1999. [Google Scholar]
- Juan, W.D.; Contardo, J.M.; Moran, L.A. A Fuzzy-controlled active front-end rectifier with current harmonic filtering characteristics and minimum sensing variables. IEEE Trans. Power Electron. 1999, 14, 724–729. [Google Scholar]
- Sut-Ian, H.; Chi-Seng, L.; Man-Chung, W. Comparison among PPF, APF, HAPF and a combined system of a shunt HAPF and a Shunt Thyristor controlled LC. In Proceedings of the IEEE Region 10 Conference TENCON, Macao, China, 1–4 November 2015. [Google Scholar]
- Bing, Y.; Jiang, D.; Liang, Y.; Jiang, C.; He, T.; Yang, L.; Hu, P. Modified modeling and system stabilization of shunt active power filter compensation loads with μF capacitance. Energies 2019, 12, 2084. [Google Scholar] [CrossRef]
- Yap, H.; Mohd, A.M.R.; Muhammad, A.A.M.Z.; Mohamad, A.M.Z. Shunt active power filter: A review on phase synchronization control techniques. Electronics 2019, 8, 791. [Google Scholar] [CrossRef]
- Helder, J.A.; José, M.F.; António, P.M.; Adriano, S.C. Direct Current Control of an Active Power Filter for Harmonic Elimination, Power Factor Correction and Load Unbalancing Compensation. Available online: https://core.ac.uk/reader/143395357 (accessed on 29 October 2023).
- António, M.; José, F.; Helder, A. Active power filters for harmonic elimination and power quality improvement. In Power Quality; Eberhard, A., Ed.; InTech: Rijeka, Croatia, 2011; pp. 161–182. [Google Scholar]
- Saifullah, K.; Bharti, D.; Mishra, V.M. Constant instantaneous power based controller for a shunt active power filter under balanced, unbalanced, and distorted supply conditions. In Proceedings of the IEEE International Conference on Computing, Communication and Automation (ICCCA2015), Greater Noida, India, 15–16 May 2015. [Google Scholar]
- Prasanta, K.B.; Gauri, S.; Pradeepta, K.S.; Rajvikram, M.E.; Sachin, K.; Federico, M.I.; Mohamad, A.H.; Ankit, K.S.; Vladimir, T. A novel negative feedback phase locked loop-based reference current generation technique for shunt active power filter. Electr. Power Energy Syst. 2023, 153, 109389. [Google Scholar] [CrossRef]
- Debendra, D.; Rabi, N.M.; Ramaprasad, P. Power quality enhancement by shunt active power filter employing different control strategies. In Proceedings of the IEEE International Conference on Circuits, Power and Intelligent Systems (CCPIS), Bhubaneswar, India, 1–3 September 2023. [Google Scholar]
- Sabir, O.; Heinrich, S.; Mohamed, B.; Frede, B. Robust DPC-SVM control strategy for shunt active power filter based on H∞ regulators. Electr. Power Energy Syst. 2020, 117, 105699. [Google Scholar] [CrossRef]
- Salem, S.; Rabeh, A.; Souad, C. Fuzzy logic controller for three-level shunt active filter compensating harmonics and reactive power. Int. J. Adapt. Control Signal Process. 2016, 30, 809–823. [Google Scholar] [CrossRef]
- Sabir, O.; Mohamed, M.; Frede, B.; Achour, B.; Heinrich, S. Direct power control of shunt active power filter using space vector modulation based on supertwisting sliding mode control. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 3243–3253. [Google Scholar]
- Mousavi, M.S.; Jalilian, A.; Asadi, M. A sliding mode control method of dc-link capacitor voltage used in active power filter. In Proceedings of the IEEE 2015 30th International Power Systems Conference (PSC), Tehran, Iran, 23–25 November 2015. [Google Scholar]
- Chi, J.; Yi, T.; Peng, W.; Xiong, L.; Dexuan, Z.; Frede, B. Reduction of Dc-Link capacitance for three-phase three-wire shunt active power filters. In Proceedings of the IEEE IECON 2013—39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10 November 2013. [Google Scholar]
- Bitoleanu, A.; Popescu, M.; Matin, D.; Dobriceanu, M. LCL interface filter design for shunt active power filters. In Proceedings of the 3rd international Symposium on Electrical Engineering and Energy Converters, Suceava, Romania, 24–25 September 2009; Available online: https://www.academia.edu/45369198/LCL_Interface_Filter_Design_for_Shunt_Active_Power_Filters (accessed on 29 October 2023).
- Lorzadeh, I.; Savaghebi, M.; Askarian, A.; Guerrero, M.J. Active damping technique for LCL-filtered inverters-based microgrids. In Proceedings of the IEEE 10th international Symposium on Diagnostics for Electrical Machines, Power Electronics and Drives (SDEMPED), Guarda, Portugal, 1–4 September 2015. [Google Scholar]
- Yang, L.; Liu, D.; Zhang, Z.; Yang, M.; Zhao, L.; Chen, X.; Xu, L.; Fu, Y.; Ma, C. Improving the current control performance of LCL type shunt active power filters with high-pass inverter-side current feedback active damping. In Proceedings of the 2023 IEEE 6th International Electrical and Energy Conference (CIEEC), Hefei, China, 12–14 May 2023. [Google Scholar]
- Büyük, M.; Tan, A.; Çağatay, B.K.; Tümay, M. Analysis and comparison of passive damping methods for shunt active power filter with output LCL filter. In Proceedings of the IEEE 2015 Intl Aegean Conference on Electrical Machines & Power Electronics (ACEMP), 2015 Intl Conference on Optimization of Electrical & Electronic Equipment (OPTIM) & 2015 Intl Symposium on Advanced Electromechanical Motion Systems (ELECTROMOTION), Side, Turkey, 2–4 September 2015. [Google Scholar]
- Bitoleanu, A.; Popescu, M.; Linca, M. Limitation of LCL filter for three-phase shunt active power filters in active traction substations. In Proceedings of the IEEE 2016 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Capri, Italy, 22–24 June 2016. [Google Scholar]
- Yu, N.; Yang, J.; Chen, S.; Ye, M. Design of LCL-filter based three-level active power filters. Telkomnika Indones. J. Electr. Eng. 2014, 12, 48–56. Available online: https://ijeecs.iaescore.com/index.php/IJEECS/article/view/2976/987 (accessed on 29 October 2023). [CrossRef]
- Li, L.; Guo, Y.; Zhang, X. Analysis and application of passive damping LLCL filter in active filter. In Proceedings of the 5th Annual IEEE International Conference on Cyber Technology in Automation, Control and Intelligent Systems, Shenyang, China, 8–12 June 2015. [Google Scholar]
- Azebaze, M.C.S.; Firlit, A. Investigation of the line-reactor influence on the active power filter and hybrid active power filter efficiency: Practical approach. Przegląd Elektrotech. 2021, 97, 39–44. [Google Scholar]
- Abu-Rubu, H.; Iqbal, A.; Guzinski, J. High Performance Control of AC Drives with Matlab/Simulink Models; John Wiley & Sons: Chichester, UK, 2012. [Google Scholar] [CrossRef]
- Akagi, H.; Kanazawa, Y.; Nabea, A. Instantaneous reactive power compensators comprising switching devices without Energy storage components. IEEE Trans. Ind. Appl. 1984, IA-20, 625–630. [Google Scholar] [CrossRef]
- Akagi, H.; Kanazawa, Y.; Fujita, K.; Nabae, A. Generalized theory of instantaneous reactive power and its application. Electr. Eng. Jpn. 1983, 103, 483–490. [Google Scholar] [CrossRef]
- Akagi, H.; Watanabe, H.E.; Aredes, M. Instantaneous Power Theory and Application to Power Conditioning; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007. [Google Scholar]
- Moran, L.M.; Dixon, J.W.; Wallace, R.R. A three-phase active power filter operating with fixed switching frequency for reactive power and current harmonic compensation. IEEE Trans. Ind. Electron. 1995, 42, 402–408. [Google Scholar] [CrossRef]
- Hanzelka, Z. High Harmonics of Voltage and Current (in Polish—Wyższe Harmoniczne Napięć i Prądów). Available online: http://www.twelvee.com.pl/42767005.php?c=%D0%B5 (accessed on 29 October 2023).
- Piróg, S. Power Electronics—Network communication and hard commutation systems. In Polish—Energoelektronika—Układ o Komunikacji Sieciowej i o Komutacji Twardej; AGH: Krakow, Poland, 2006. [Google Scholar]
- The Mobile Power Quality Meter for Experts PQ-Box 200. Available online: https://www.a-eberle.de/en/products/mobile-power-quality-analyzer-pq-box-200/ (accessed on 29 October 2023).
- Hanzelka, Z. Quality of the Electricity Supply-Disturbances of the Voltage RMS Value. In Polish–Jakość Dostawy Energii Elektrycznej—Zaburzenia Wartości Skutecznej Napięcia; AGH: Krakow, Poland, 2013. [Google Scholar]





[V] | [A] | [A] | [A] | [mH] | [mH] | [V] | [V] | [J] | [V] | [F] | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 4.46 | 9.38 | 7.34 | 1.4 | - | 1.32 | 400 | 750 | 11 | 5 | 3 |
| 16 | 4.46 | 9.38 | 7.34 | - | 7.2 |
| kp | ki | |
|---|---|---|
| Control loop (1) | 40,000 | 43.75 |
| Control loop (3) | 250 | 0.0001 |
| THDUS (%) | THDIS (%) | QS(1) (Var) | PS(1) (W) | SS(1) (VA) | kasym (%) | |
|---|---|---|---|---|---|---|
| L1 | 0.25 | 28.07 | 414.08 | 2838.4 | 2868.5 | 33.25 |
| L2 | 0.25 | 23.41 | 1954.5 | 2833.1 | 3441.9 | |
| L3 | 0.25 | 42.07 | 1181.8 | 1507.2 | 1915.2 | |
| Us1(1) = 230.8 ej30° | Is1(1) = 12.43 ej21.7° | |||||
| Us2(1) = 230.7 ej270° | Is2(1) = 14.92 ej235.4° | |||||
| Us3(1) = 230.7 ej150° | Is3(1) = 8.29 ej111.90° | |||||
| L_inv_min = 1.4 (mH) | L_inv_max = 7.2 (mH) | |||||
|---|---|---|---|---|---|---|
| THDUS (%) | THDIS (%) | kasym (%) | THDUS (%) | THDIs (%) | kasym (%) | |
| L1 | 0.18 | 10.34 | 0.59 | 0.25 | 26.7 | 0.75 |
| L2 | 0.19 | 10.99 | 0.25 | 27.92 | ||
| L3 | 0.18 | 10.93 | 0.25 | 27.7 | ||
| Us1(1) = 230.8 ej30° | Is1(1) = 10.45 ej28.9° | Us1(1) = 230.80 ej30° | Is1(1) = 10.36 ej27.8° | |||
| Us2(1) = 230.8 ej270° | Is2(1) = 10.99 ej268.7° | Us2(1) = 230.80 ej270° | Is2(1) = 10.48 ej267.7° | |||
| Us3(1) = 230.8 ej150° | Is3(1) = 10.93 ej149.1° | Us3(1) = 230.80 ej150° | Is3(1) = 10.4 ej147.2° | |||
| After the SAPF Connection | ||||
|---|---|---|---|---|
| L_inv_min = 1.4 (mH) | L_inv_max = 7.2 (mH) | |||
| TTHDUS (%) | TTHDIS (%) | TTHDUS (%) | TTHDIS (%) | |
| L1 | 3.57 | 16.31 | 1.70 | 27.09 |
| L2 | 2.93 | 16.19 | 1.50 | 27.59 |
| L3 | 3.60 | 16.20 | 2.13 | 27.89 |
| (L_inv_min = 1.4 (mH)) | (L_inv_max = 7.2 (mH)) | ||||||
|---|---|---|---|---|---|---|---|
| PCC | Load | SAPF | PCC | Load | SAPF | ||
| P(1) [W] | L1 | 2411.4 | 2838.8 | 427.40 | 2389.3 | 2838.8 | 449.82 |
| L2 | 2535.8 | 2837.9 | 438.19 | 2416.8 | 2837.9 | 421.33 | |
| L3 | 2522.3 | 1505.7 | −890.35 | 2397.5 | 1505.7 | −891.61 | |
| Q(1) [Var] | L1 | 46.30 | 414.13 | 370.22 | 91.78 | 414.13 | 323.23 |
| L2 | 57.54 | 1950.4 | 1898 | 97.07 | 1950.4 | 1854.5 | |
| L3 | 39.62 | 1180.6 | 1143.7 | 117.25 | 1180.6 | 1062.6 | |
| S(1) [VA] | L1 | 2411.9 | 2868.8 | 565.46 | 2391.1 | 2868.8 | 553.92 |
| L2 | 2536.5 | 3443.5 | 1948 | 2418.8 | 3443.5 | 1.901.8 | |
| L3 | 2522.6 | 1913.3 | 1449.4 | 2400.3 | 1913.3 | 1387.1 | |
| IT1(1) = 12.43 ej21.7° | I_inv1(1) = 2.45 ej−10.9° | IT1(1) = 12.43 ej21.7° | I_inv1(1) = 2.40 ej−5.7° | ||||
| IT2(1) = 14.92 ej235.5° | I_inv2(1) = 8.44 ej193.0° | IT2(1) = 14.92 ej235.5° | I_inv2(1) = 8.24 ej192.8° | ||||
| IT3(1) = 8.29 ej111.9° | I_inv3(1) = 6.28 ej22.1° | IT3(1) = 8.29 ej111.9° | I_inv3(1) = 6.01 ej20° | ||||
| Before the SAPF Connection LT = 1 nH | After the SAPF Connection | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| L_in_min > LT | L_inv_min = LT | L_inv_min < LT | ||||||||||||||
| US(1) (V) | IS(1) (A) | US(1) (V) | IS(1) (A) | US(1) (V) | IS(1) (A) | US(1) (V) | IS(1) (A) | |||||||||
| RMS | Phase | RMS | Phase | RMS | Phase | RMS | Phase | RMS | Phase | RMS | Phase | RMS | Phase | RMS | Phase | |
| L1 | 230.8 | 30° | 12.43 | 21.7° | 230.8 | 30° | 10.41 | 29.4° | 230.8 | 30° | 10.29 | 29.4° | 230.8 | 30° | 10.14 | 29.5° |
| L2 | 230.7 | 270° | 14.92 | 235.4° | 230.7 | 270° | 10.4 | 269.2° | 230.7 | 270° | 10.3 | 269.3° | 230.8 | 270° | 10.14 | 269.3° |
| L3 | 230.7 | 150° | 8.29 | 111.90° | 230.7 | 150° | 10.37 | 149.3° | 230.7 | 150° | 10.28 | 149.3° | 230.8 | 150° | 10.11 | 149.4° |
| Before the SAPF Connection | After the SAPF Connection | |||||||||
| LT = 1 nH | L_inv_min > LT | |||||||||
| THDUS (%) | THDIS (%) | QS(1) (Var) | PS(1) (W) | kasym (%) | THDUS (%) | THDIS (%) | QS(1) (Var) | PS(1) (W) | kasym (%) | |
| L1 | 0.25 | 28.07 | 414.08 | 2838.4 | 33.25 | 0.15 | 8.77 | 25.15 | 2402.5 | 0.30 |
| L2 | 0.25 | 23.41 | 1954.5 | 2833.1 | 0.15 | 8.75 | 33.51 | 2400.1 | ||
| L3 | 0.25 | 42.07 | 1181.8 | 1507.2 | 0.15 | 8.77 | 29.24 | 2393.2 | ||
| After the SAPF Connection | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| L_inv_min = LT | L_inv_min < LT | |||||||||
| THUS (%) | THDIS (%) | QS(1) (Var) | PS(1) (W) | kasym (%) | THDUS (%) | THDIS (%) | QS(1) (Var) | PS(1) (W) | kasym (%) | |
| L1 | 0.04 | 2.47 | 24.86 | 2374.8 | 0.30 | 0.02 | 1.22 | 20.42 | 2340.2 | 0.20 |
| L2 | 0.05 | 2.91 | 29.04 | 2377.1 | 0.02 | 1.49 | 28.59 | 2340.1 | ||
| L3 | 0.05 | 2.79 | 28.98 | 2372.4 | 0.02 | 1.22 | 24.43 | 2333.3 | ||
| After the SAPF Connection | ||||||
|---|---|---|---|---|---|---|
| L_inv_min > LT | L_inv_min = LT | L_inv_min < LT | ||||
| TTHDUS (%) | TTHDIS (%) | TTHDUS (%) | TTHDIS (%) | TTHDUS (%) | TTHDIS (%) | |
| L1 | 3.12 | 12.60 | 3.18 | 7.16 | 3.30 | 6.59 |
| L2 | 2.77 | 13.77 | 2.85 | 8.08 | 2.92 | 6.82 |
| L3 | 3.12 | 13.40 | 3.23 | 7.20 | 3.29 | 6.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azebaze Mboving, C.S.; Hanzelka, Z. Analysis of the Influence of the 6-Pulse Thyristor-Bridge Input Reactor Size on the Shunt Active Power Filter Work Efficiency: A Case Study. Energies 2024, 17, 80. https://doi.org/10.3390/en17010080
Azebaze Mboving CS, Hanzelka Z. Analysis of the Influence of the 6-Pulse Thyristor-Bridge Input Reactor Size on the Shunt Active Power Filter Work Efficiency: A Case Study. Energies. 2024; 17(1):80. https://doi.org/10.3390/en17010080
Chicago/Turabian StyleAzebaze Mboving, Chamberlin Stéphane, and Zbigniew Hanzelka. 2024. "Analysis of the Influence of the 6-Pulse Thyristor-Bridge Input Reactor Size on the Shunt Active Power Filter Work Efficiency: A Case Study" Energies 17, no. 1: 80. https://doi.org/10.3390/en17010080
APA StyleAzebaze Mboving, C. S., & Hanzelka, Z. (2024). Analysis of the Influence of the 6-Pulse Thyristor-Bridge Input Reactor Size on the Shunt Active Power Filter Work Efficiency: A Case Study. Energies, 17(1), 80. https://doi.org/10.3390/en17010080







