A Novel Voltage Sensorless Estimation Method for Modular Multilevel Converters with a Model Predictive Control Strategy
Abstract
:1. Introduction
- (1)
- The DOB realizes the estimation of the ac-side and dc bus voltages of the MMC system without sacrificing the performance of the original MPC. It is a simple structure with minimal order and low computational cost.
- (2)
- Using the ac-side and dc bus voltages estimated by the DOB and estimating the SM capacitor voltages through the ANN algorithm, the computational effort of this method does not significantly increase with the number of SMs.
- (3)
- Based on the MPC, the combination of the DOB and the ANN algorithm achieves voltage sensorless control for the MMC.
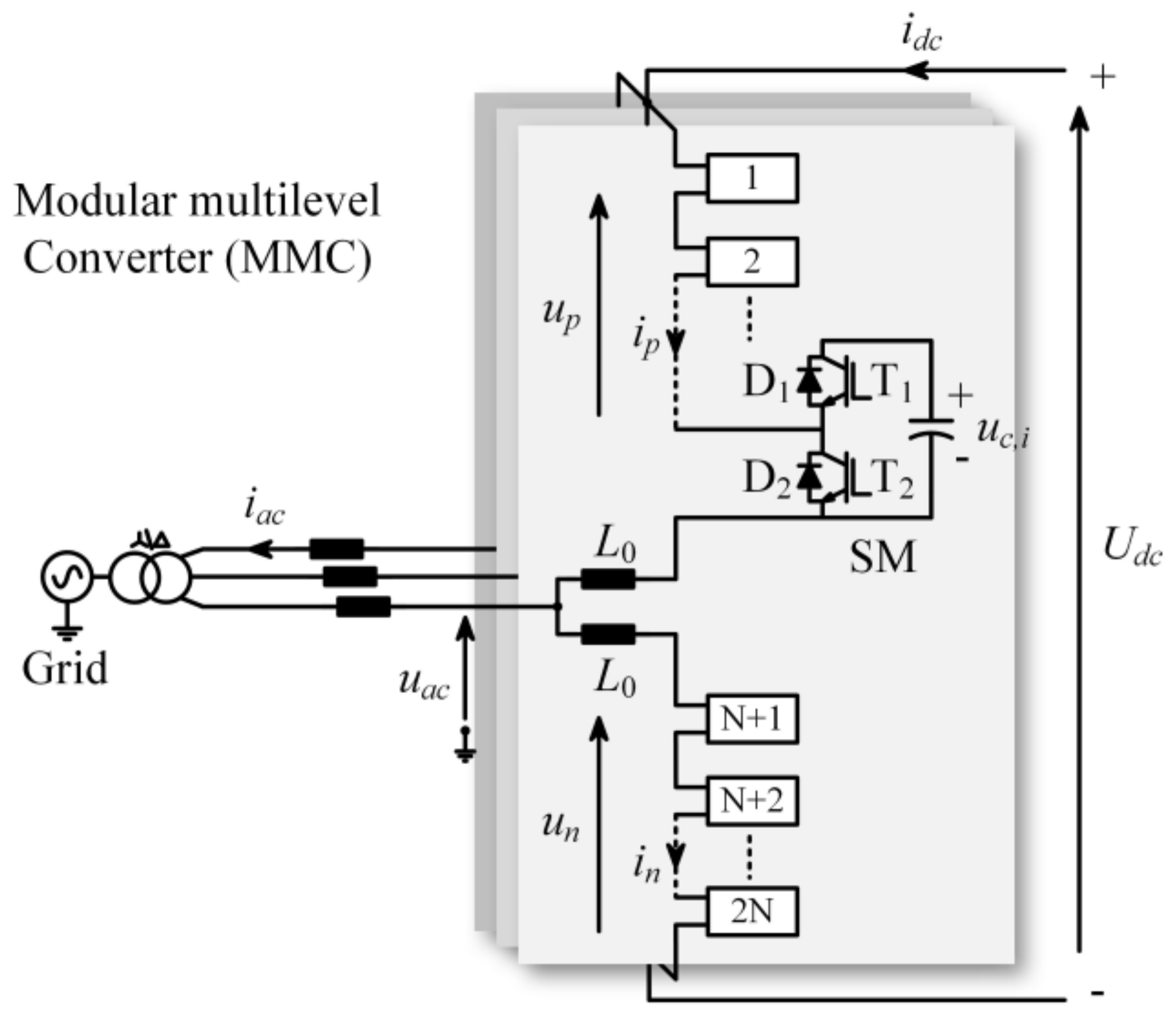
2. MPC Strategy of the MMC
3. The Proposed Voltage Estimation Scheme
3.1. AC-Side and DC Bus Voltage Estimation Based on DOB
3.2. SM Capacitor Voltage Estimation Based on ANN
4. Simulation and Experimental Verification
4.1. Simulation Verification
4.1.1. Simulation Results of DOB-Based ac-Side and dc Bus Voltage Estimation
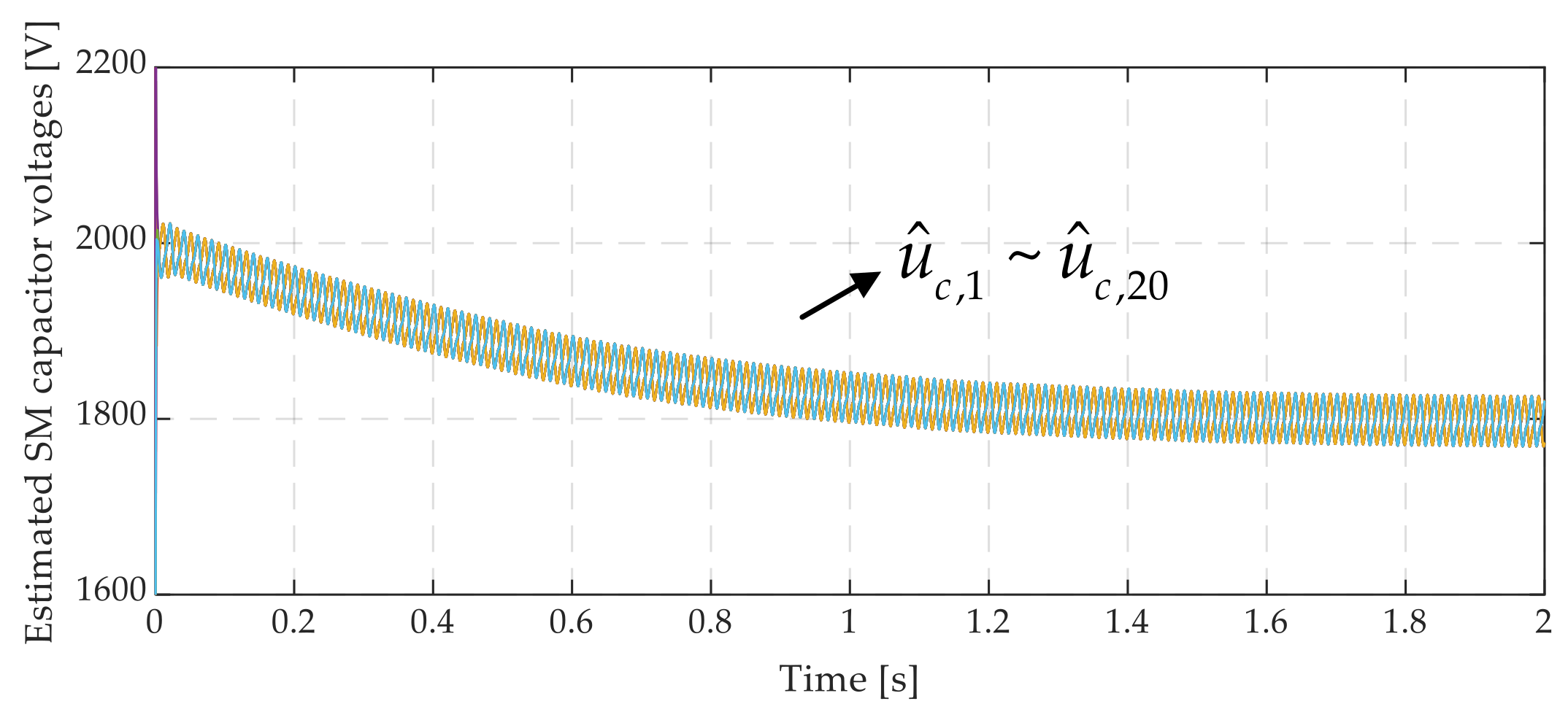
4.1.2. Simulation Results of ANN-Based SM Capacitor Voltage Estimation
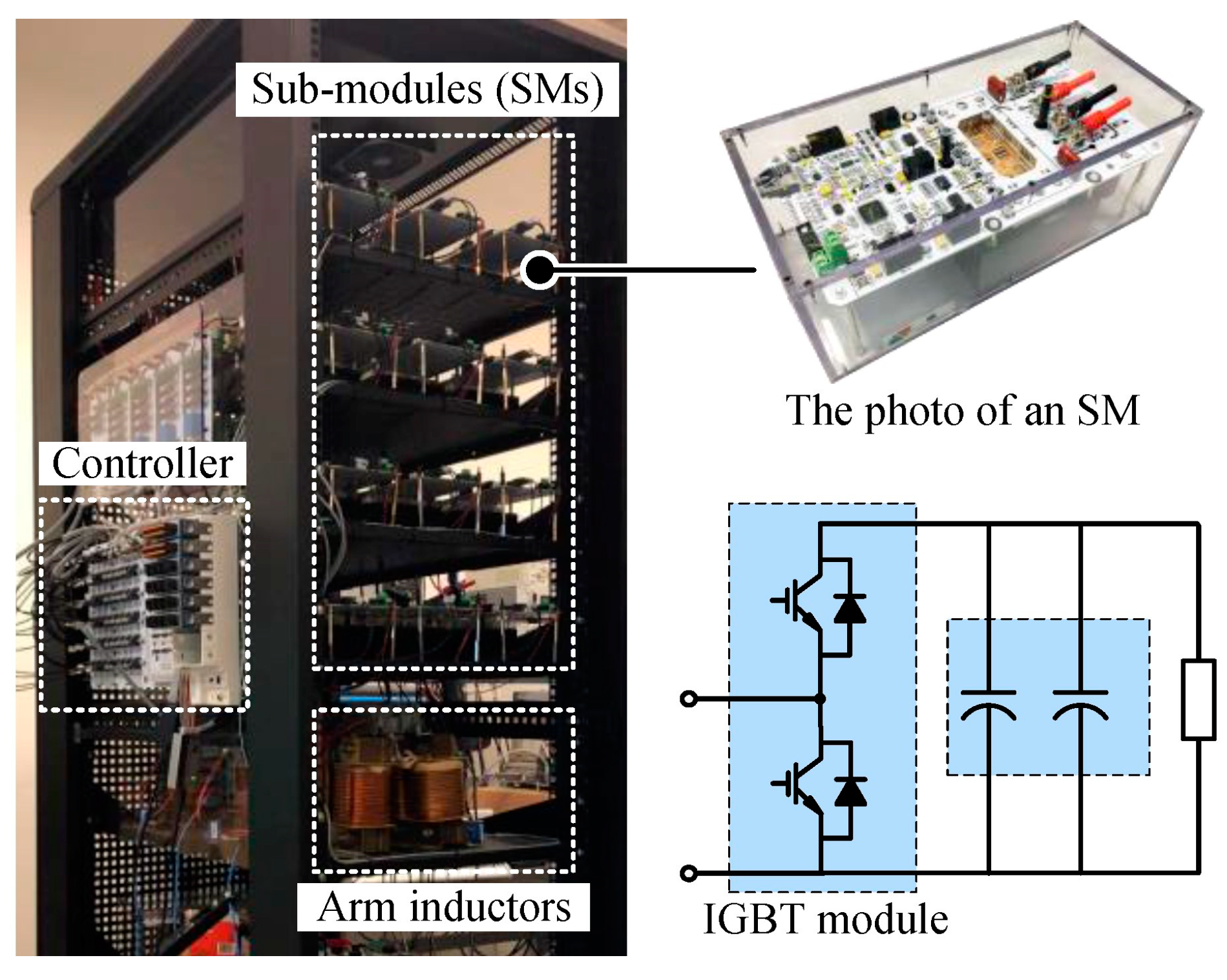
4.2. Experimental Verification
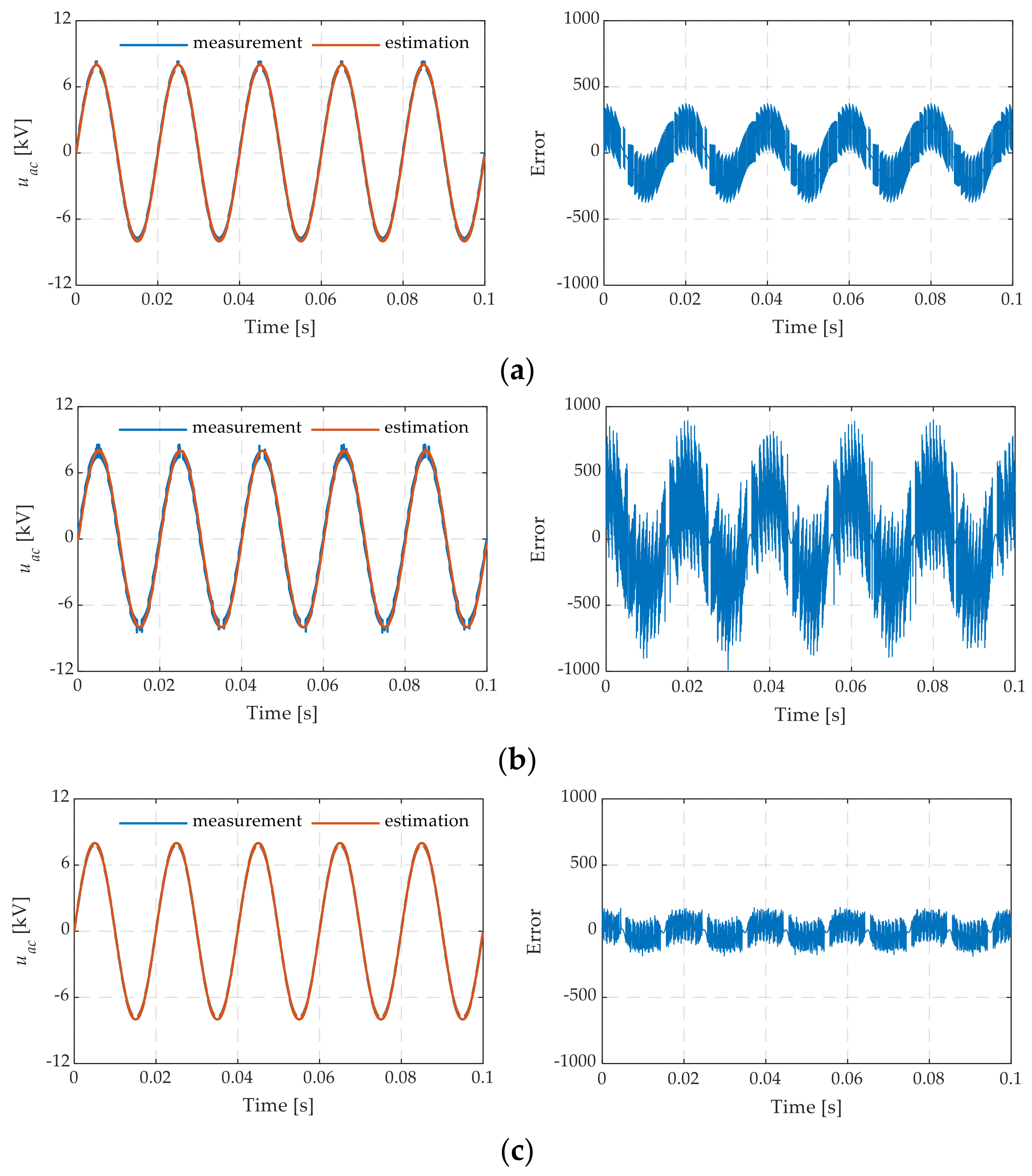
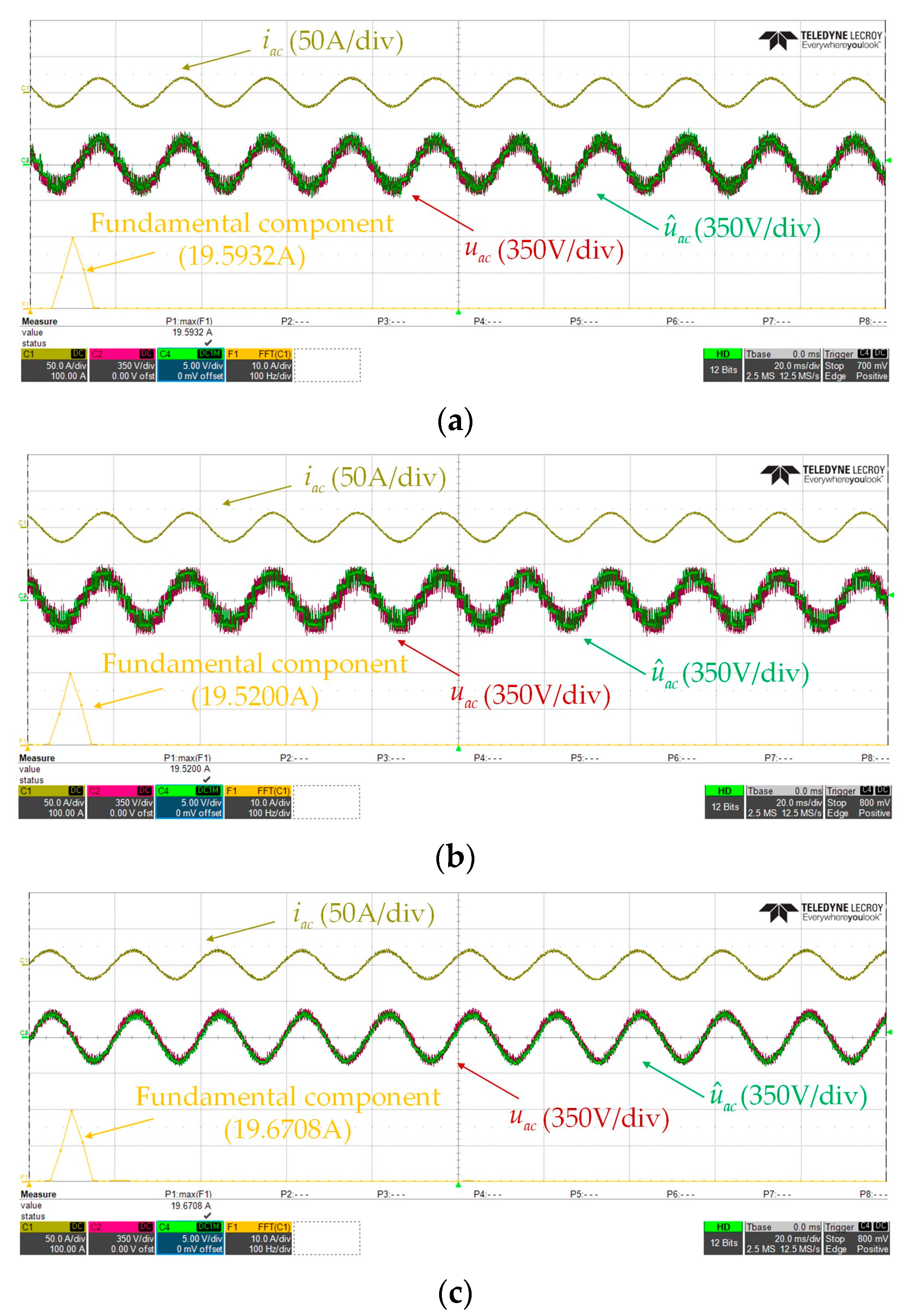
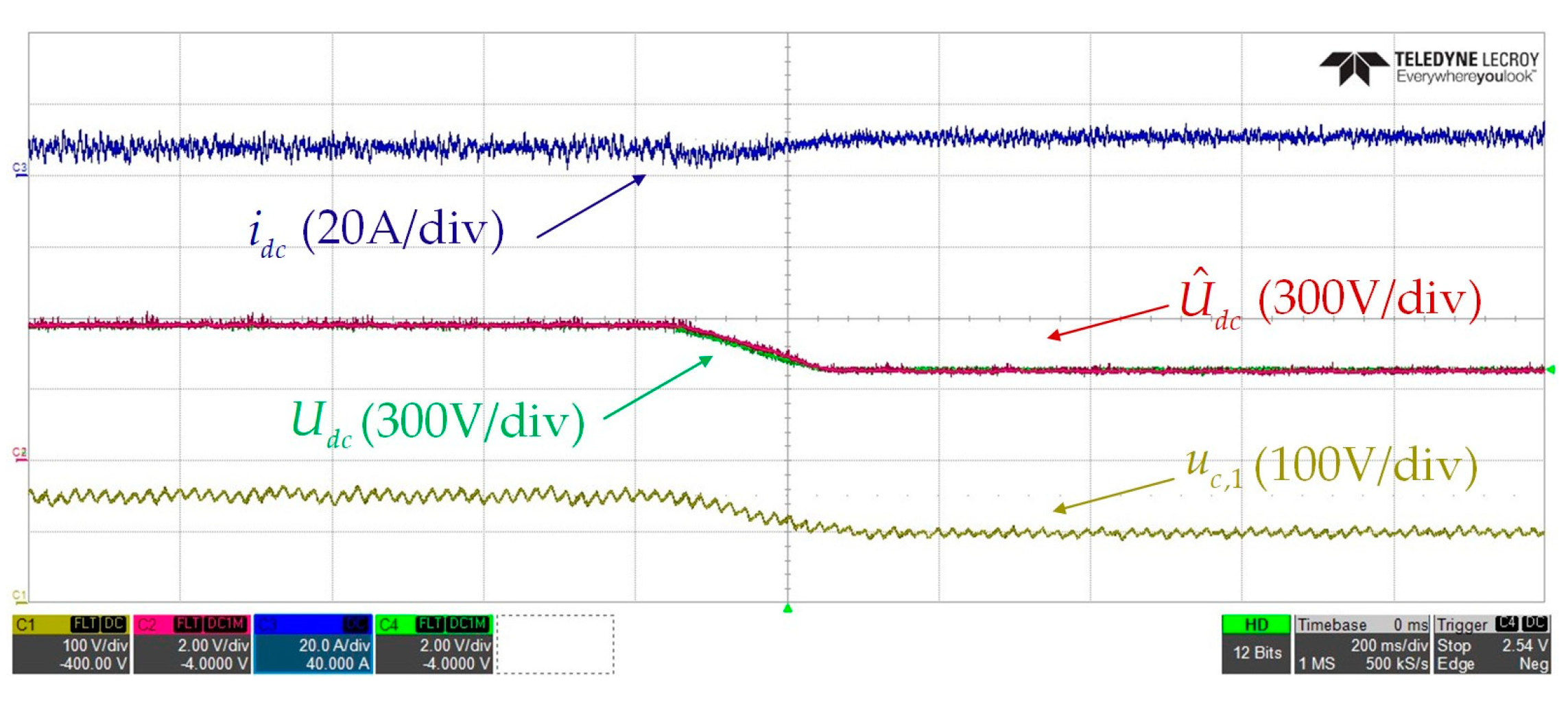
4.2.1. Experimental Results of DOB-Based ac-Side and dc Bus Voltage Estimation
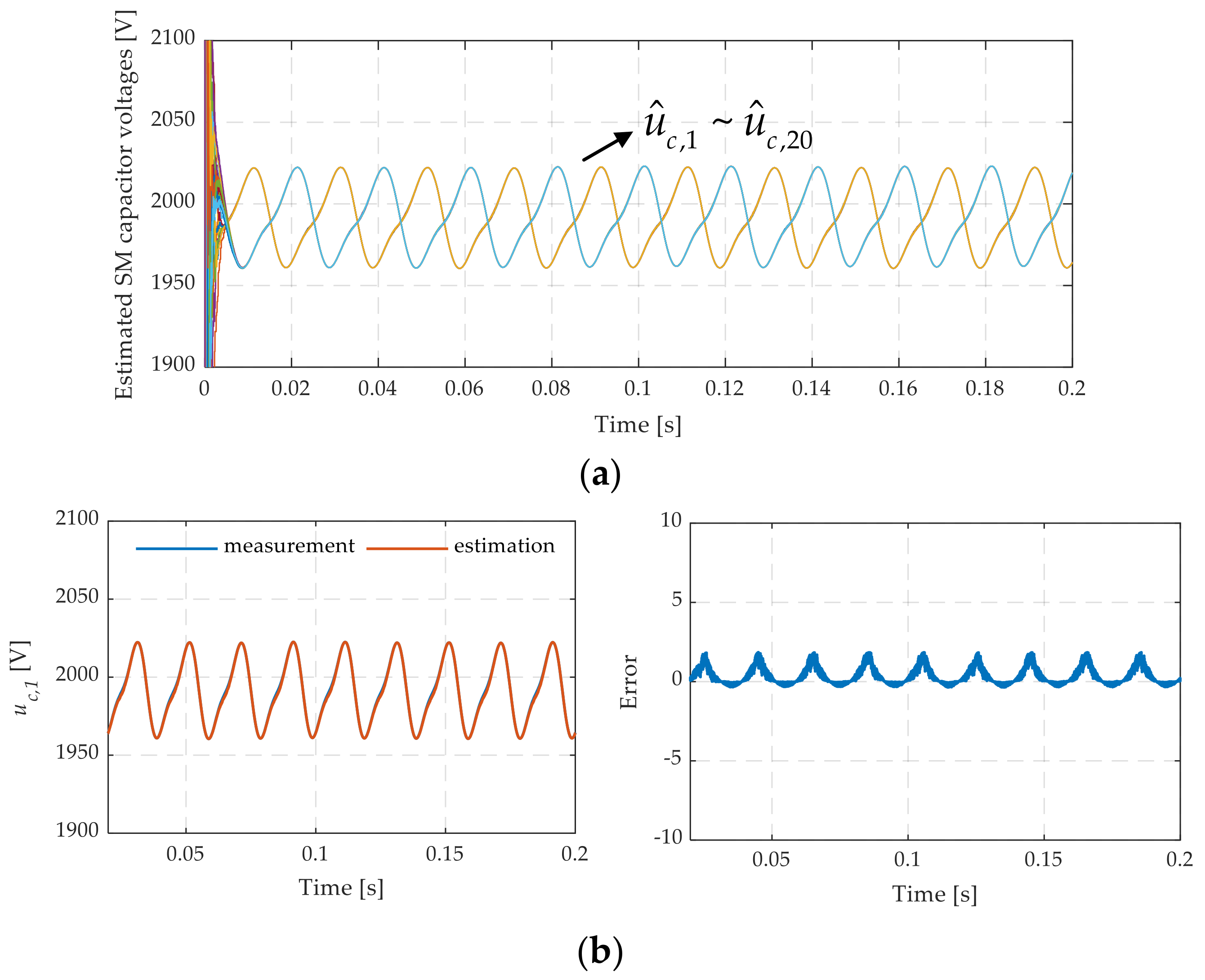
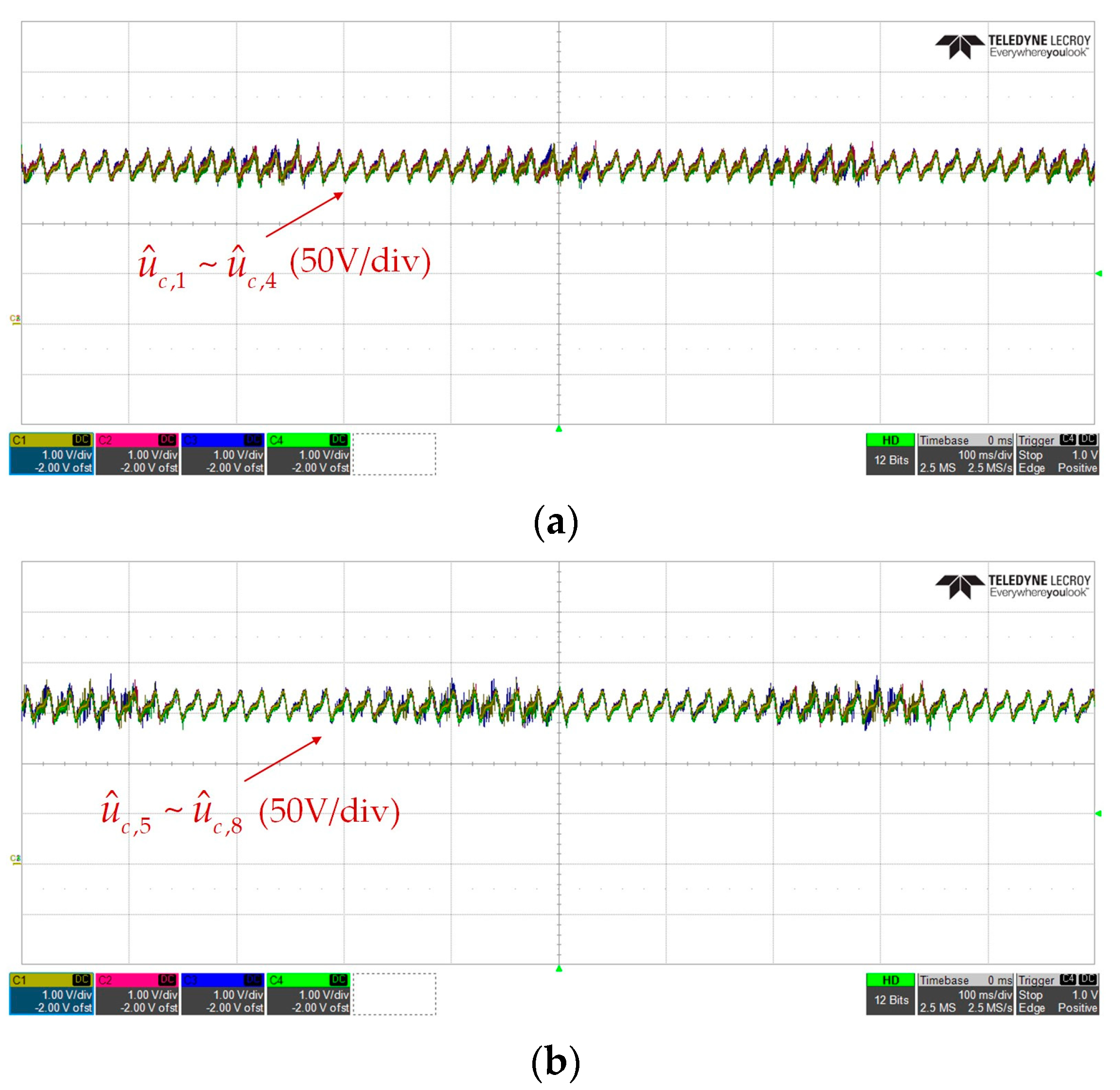
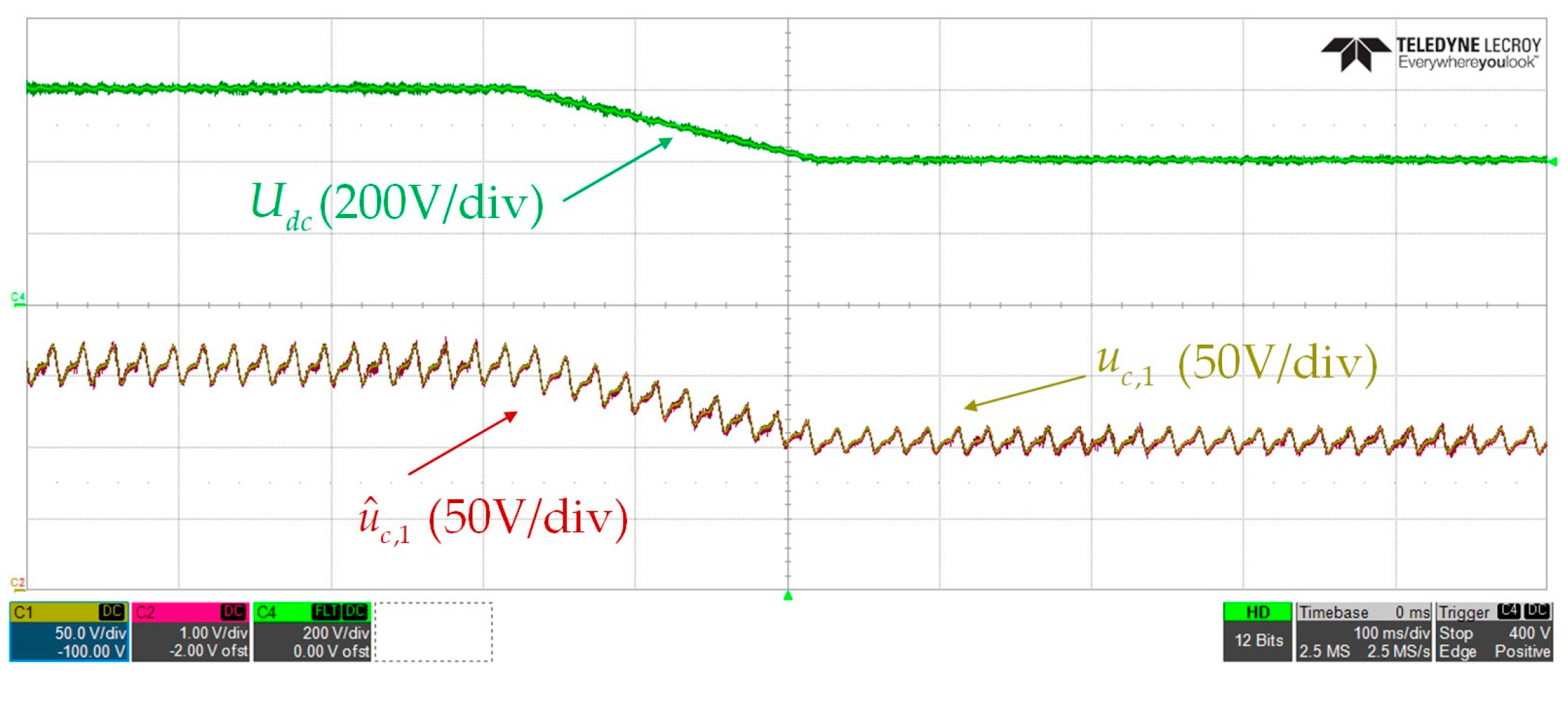
4.2.2. Experimental Results of ANN-Based SM Capacitor Voltage Estimation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Arias-Esquivel, Y.; Cárdenas, R.; Tarisciotti, L.; Díaz, M.; Mora, A. A Two-Step Continuous-Control-Set MPC for Modular Multilevel Converters Operating with Variable Output Voltage and Frequency. IEEE Trans. Power Electron. 2023, 38, 12091–12103. [Google Scholar] [CrossRef]
- Huang, M. Submodule Capacitor Voltage Ripple Reduction of Full-Bridge Submodule-Based MMC (FBSM-MMC) with Non-Sinusoidal Voltage Injection. Energies 2023, 16, 4305. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Z.; Li, Z.; Babayomi, O. Predictive Control of Modular Multilevel Converters: Adaptive Hybrid Framework for Circulating Current and Capacitor Voltage Fluctuation Suppression. Energies 2023, 16, 5772. [Google Scholar] [CrossRef]
- Yang, Q.F.; Ding, T.; He, H.X.; Chen, X.; Tao, F.B.; Zhou, Z.C.; Xu, Y.; Chen, S. Model predictive control of MMC-UPFC under unbalanced grid conditions. Int. J. Electr. Power Energy Syst. 2020, 117, 105637.1–105637.11. [Google Scholar] [CrossRef]
- Wang, C.; Xu, J.X.; Pan, X.W.; Gong, W.M.; Zhu, Z.; Xu, S.K. Impedance Modeling and Analysis of Series-Connected Modular Multilevel Converter (MMC) and its Comparative Study with Conventional MMC for HVDC Applications. IEEE Trans. Power Deliv. 2022, 37, 3270–3281. [Google Scholar] [CrossRef]
- Vural, A.M.; Wirsiy, E.N. Three-phase modular multilevel converter based unified power flow controller. Eng. Sci. Technol. Int. J. 2020, 23, 299–306. [Google Scholar] [CrossRef]
- Viatkin, A.; Ricco, M.; Mandrioli, R.; Kerekes, T.; Teodorescu, R.; Grandi, G. A Novel Modular Multilevel Converter Based on Interleaved Half-Bridge Submodules. IEEE Trans. Ind. Electron. 2023, 70, 125–136. [Google Scholar] [CrossRef]
- Liao, Y.; You, J.; Yang, J.; Wang, Z.; Jin, L. Disturbance-observer-based model predictive control for battery energy storage system modular multilevel converters. Energies 2018, 11, 2285. [Google Scholar] [CrossRef]
- Li, P.K.; Wang, Y.; Liu, Y.; Zhu, Q.L.; Xue, Y.L.; Li, X.; Feng, B.L.; Li, R.T. Impedance Modeling and Mechanism Analysis of Low-Frequency Oscillations in Single-Phase MMC-RPC Integrated Vehicle-Grid Coupling System. IEEE Trans. Power Electron. 2023, 38, 4820–4839. [Google Scholar] [CrossRef]
- Liu, H.; Ma, K.; Loh, P.C.; Blaabjerg, F. Online fault identification based on an adaptive observer for modular multilevel converters applied to wind power generation systems. Energies 2015, 8, 7140–7160. [Google Scholar] [CrossRef]
- Moon, J.W.; Gwon, J.S.; Park, J.W.; Kang, D.W.; Kim, J.M. Model predictive control with a reduced number of considered states in a modular multilevel converter for HVDC system. IEEE Trans. Power Deliv. 2015, 30, 608–617. [Google Scholar] [CrossRef]
- Sztykiel, M.; Silva, R.D.; Teodorescu, R.; Zeni, L.; Kjaer, P.C. Modular multilevel converter modelling, control and analysis under grid frequency deviations. In Proceedings of the 2013 15th European Conference on Power Electronics and Applications (EPE), Lille, France, 2–6 September 2013; pp. 1–11. [Google Scholar]
- Rohner, S.; Bernet, S.; Hiller, M.; Sommer, R. Modulation, losses, and semiconductor requirements of modular multilevel converters. IEEE Trans. Ind. Electron. 2010, 57, 2633–2642. [Google Scholar] [CrossRef]
- Guan, M.; Xu, Z. Modeling and control of a modular multilevel converter-based HVDC system under unbalanced grid conditions. IEEE Trans. Power Electron. 2012, 27, 4858–4867. [Google Scholar] [CrossRef]
- Rahoui, A.; Bechouche, A.; Seddiki, H.; Abdeslam, D.O. Grid voltages estimation for three-phase PWM rectifiers control without ac voltage sensors. IEEE Trans. Power Electron. 2018, 33, 859–875. [Google Scholar] [CrossRef]
- Ketzer, M.B.; Jacobina, C.B. Sensorless control technique for PWM rectifiers with voltage disturbance rejection and adaptive power factor. IEEE Trans. Ind. Electron. 2015, 62, 1140–1151. [Google Scholar] [CrossRef]
- Kukkola, J.; Hinkkanen, M. State observer for grid-voltage sensorless control of a converter equipped with an LCL filter: Direct discrete-time design. IEEE Trans. Ind. Appl. 2016, 52, 3133–3145. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, F.; Bai, T.; Guo, H.; Feng, X. A Sensorless Control Method for MMC Based on Sliding Mode Observer. In Proceedings of the 2018 IEEE International Power Electronics and Application Conference and Exposition (PEAC), Shenzhen, China, 4–7 November 2018; pp. 1–6. [Google Scholar]
- Chakraborty, R.; Samantaray, J.; Dey, A.; Chakrabarty, S. Capacitor Voltage Estimation of MMC Using a Discrete-Time Sliding Mode Observer Based on Discrete Model Approach. IEEE Trans. Ind. Appl. 2022, 58, 494–504. [Google Scholar] [CrossRef]
- Abdelsalam, M.; Tennakoon, S.; Diab, H.; Marei, M.I. An ADALINE based capacitor voltage estimation algorithm for modular multilevel converters. In Proceedings of the 2016 19th International Symposium on Electrical Apparatus and Technologies (SIELA), Bourgas, Bulgaria, 29 May–1 June 2016; pp. 1–4. [Google Scholar]
- Ke, Z.; Pan, J.; Sabbagh, M.A.; Na, R.; Zhang, J.; Wang, J.; Xu, L. Capacitor Voltage Ripple Estimation and Optimal Sizing of Modular Multi-Level Converters for Variable-Speed Drives. IEEE Trans. Power Electron. 2020, 35, 12544–12554. [Google Scholar] [CrossRef]
- Wang, Z.; Peng, L. Grouping Capacitor Voltage Estimation and Fault Diagnosis with Capacitance Self-Updating in Modular Multilevel Converters. IEEE Trans. Power Electron. 2021, 36, 1532–1543. [Google Scholar] [CrossRef]
- Abushafa, O.S.H.M.; Dahidah, M.S.A.; Gadoue, S.M.; Atkinson, D.J. Submodule Voltage Estimation Scheme in Modular Multilevel Converters with Reduced Voltage Sensors Based on Kalman Filter Approach. IEEE Trans. Ind. Electron. 2018, 65, 7025–7035. [Google Scholar] [CrossRef]
- Abushafa, O.S.H.M.; Gadoue, S.M.; Dahidah, M.S.A.; Atkinson, D.J.; Missailidis, P. Capacitor Voltage Estimation Scheme with Reduced Number of Sensors for Modular Multilevel Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 2086–2097. [Google Scholar] [CrossRef]
- Islam, M.D.; Razzaghi, R.; Bahrani, B. Arm-sensorless sub-module voltage estimation and balancing of modular multilevel converters. IEEE Trans. Power Deliv. 2020, 35, 957–967. [Google Scholar] [CrossRef]
- Wang, K.; Jin, L.; Li, G.; Deng, Y.; He, X. Online Capacitance Estimation of Submodule Capacitors for Modular Multilevel Converter With Nearest Level Modulation. IEEE Trans. Power Electron. 2020, 35, 6678–6681. [Google Scholar] [CrossRef]
- Purkayastha, B.; Bhattacharya, T. Simplified Approach for Acquisition of Submodule Capacitor Voltages of the Modular Multilevel Converter Using Low Sampling Rate Sensing and Estimation. IEEE Trans. Power Electron. 2022, 37, 13428–13438. [Google Scholar] [CrossRef]
- Tormo, D.; Vidal-Albalate, R.; Idkhajine, L.; Monmasson, E.; Blasco-Gimenez, R. Embedded Real-Time Simulator for Sensorless Control of Modular Multi-Level Converters. Electronics 2022, 11, 719. [Google Scholar] [CrossRef]
- Sun, Y.; Li, Z.; Zhang, Y.; Li, Y.; Zhang, Z. A time-domain virtual-flux based predictive control of modular multilevel converters for offshore wind energy integration. IEEE Trans. Energy Convers. 2022, 37, 1803–1814. [Google Scholar] [CrossRef]
- Liu, X.; Qiu, L.; Ma, J.; Fang, Y.; Wu, W.; Peng, Z.; Wang, D. A fast finite-level-state model predictive control strategy for sensorless modular multilevel converter. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 3570–3581. [Google Scholar] [CrossRef]
- Nademi, H.; Norum, L.E.; Wersland, S. An accurate MPPT scheme for photovoltaic modular-based conversion units: A robust sensorless predictive approach. In Proceedings of the 2017 IEEE 18th Workshop on Control and Modeling for Power Electronics (COMPEL), Stanford, CA, USA, 9–12 July 2017; pp. 1–6. [Google Scholar]
- Kim, K.S.; Rew, K.H. Reduced order disturbance observer for discrete-time linear systems. Automatica 2013, 49, 968–975. [Google Scholar] [CrossRef]
- Nguyen, H.X.; Tran, N.C.; Park, J.W.; Jeon, J.W. An adaptive linear-neuron-based third-order PLL to improve the accuracy of absolute magnetic encoders. IEEE Trans. Ind. Electron. 2019, 66, 4639–4649. [Google Scholar] [CrossRef]
- Young, H.A.; Perez, M.A.; Rodriguez, J. Analysis of finite-control-set model predictive current control with model parameter mismatch in a three-phase inverter. IEEE Trans. Ind. Electron. 2016, 63, 3100–3107. [Google Scholar] [CrossRef]
- Rodriguez, J.; Cortes, P. Predictive Control of Power Converters and Electrical Drives; Wiley-IEEE Press: Hoboken, NJ, USA, 2012. [Google Scholar]



| Parameter | Simulation | Experiment |
|---|---|---|
| Nominal power | 1.2 MVA | 8 kVA |
| The ac-side current peak | 100 A | 20 A |
| The dc bus voltage | 20 kV | 600 V |
| Arm inductance | 20 mH | 8 mH |
| Line frequency | 50 Hz | 50 Hz |
| Number of SMs per arm | 10 | 4 |
| SM capacitance | 2000 μF | 1640 μF |
| SM capacitor voltage | 2000 V | 150 V |
| Sampling and control period | 20 μs | 50 μs |
| Inductance Mismatch | Fundamental Component (A) | THD (%) | ||
|---|---|---|---|---|
| without DOB | with DOB | without DOB | with DOB | |
| 19.6087 | 19.5932 | 5.09 | 5.45 | |
| 19.5139 | 19.5200 | 6.79 | 6.06 | |
| 19.6701 | 19.6708 | 4.72 | 5.38 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, Y.; Jin, L.; You, J.; Xu, Z.; Liu, K.; Zhang, H.; Shen, Z.; Deng, F. A Novel Voltage Sensorless Estimation Method for Modular Multilevel Converters with a Model Predictive Control Strategy. Energies 2024, 17, 61. https://doi.org/10.3390/en17010061
Liao Y, Jin L, You J, Xu Z, Liu K, Zhang H, Shen Z, Deng F. A Novel Voltage Sensorless Estimation Method for Modular Multilevel Converters with a Model Predictive Control Strategy. Energies. 2024; 17(1):61. https://doi.org/10.3390/en17010061
Chicago/Turabian StyleLiao, Yantao, Long Jin, Jun You, Zhike Xu, Kaiyuan Liu, Hongbin Zhang, Zhan Shen, and Fujin Deng. 2024. "A Novel Voltage Sensorless Estimation Method for Modular Multilevel Converters with a Model Predictive Control Strategy" Energies 17, no. 1: 61. https://doi.org/10.3390/en17010061
APA StyleLiao, Y., Jin, L., You, J., Xu, Z., Liu, K., Zhang, H., Shen, Z., & Deng, F. (2024). A Novel Voltage Sensorless Estimation Method for Modular Multilevel Converters with a Model Predictive Control Strategy. Energies, 17(1), 61. https://doi.org/10.3390/en17010061






