Radiation Force Modeling for a Wave Energy Converter Array

Abstract

The motivation and focus of this work is to generate passive transfer function matrices that model the radiation forces for an array of WECs. Multivariable control design is often based on linear time-invariant (LTI) systems such as state-space or transfer function matrix models. The intended use is for designing real-time control strategies where knowledge of the model’s poles and zeros is helpful. This work presents a passivity-based approach to estimate radiation force transfer functions that accurately replace the convolution operation in the Cummins equation while preserving the physical properties of the radiation function. A two-stage numerical optimization approach is used, the first stage uses readily available algorithms for fitting a radiation damping transfer function matrix to the system’s radiation frequency response. The second stage enforces additional constraints on the form of the transfer function matrix to increase its passivity index. After introducing the passivity-based algorithm to estimate radiation force transfer functions for a single WEC, the algorithm was extended to a WEC array. The proposed approach ensures a high degree of match with the radiation function without degrading its passivity characteristics. The figures of merit that will be assessed are (i) the accuracy of the LTI systems in approximating the radiation function, as measured by the normalized root mean squared error (NRMSE), and (ii) the stability of the overall system, quantified by the input passivity index, $\nu$, of the radiation force transfer function matrix.

1. Introduction

Real-time motion control of a wave energy converter (WEC) requires a model that captures the system’s hydrodynamic interactions. Time-domain dynamics for a marine structure can be described using the Cummins equation [1,2]. A WEC array emanates a radiation wave field when excited by an incoming wave field, resulting in radiation forces. Modeling motion dynamics using the Cummins equation requires a convolution operation to calculate the radiation forces. The convolution operation can be replaced by a linear time-invariant (LTI) system [3]. However, estimating a numerically stable LTI system, that can accurately replicate the radiation force convolution can be difficult [4]. The radiated forces dissipate energy away from the system—a physical property that this work exploits to estimate numerically stable LTI systems. LTI systems that represent dissipative systems, that cannot generate energy, are characterized as passive systems [5]. The proposed LTI system estimation algorithm requires the estimated LTI systems to be passive—thereby imposing numerical stability and the physical properties of the radiation forces.

This work presents a time-domain modeling framework for hydrodynamically coupled multibody dynamics in floating body clusters. The proposed algorithm can be used for heterogeneous WEC arrays that may not have the same geometry. The transfer function array models developed here are an important step towards designing motion control strategies that can respond to changing ocean conditions in real time.

1.1. Main Contributions of the Proposed Approach

This paper focuses on developing linear, passive models for the radiation force effects in WECs, that can be used for model-based control strategies. This approach can be considered a frequency-domain method because the initial reference function is the radiation function $H_r\left(j\omega \right)$. This approach incorporates an optimization routine that enforces the physical properties of the radiation function while minimizing the error between the magnitudes and phases of the estimated transfer functions and the $H_r\left(j\omega \right)$. The multibody dynamics involved in a multiple input multiple output (MIMO) system can be more conveniently modeled using the estimation of transfer function arrays. This paper will demonstrate a passivity-based estimation algorithm for $G\left(s\right)$ that is applicable to MIMO systems such as WEC arrays.

1.2. Overview of Frequency- and Time-Domain Estimation Methods

Duarte et al. present a thorough comparison of different approaches taken by researchers over the years [6]. Their comparative review is expanded here with recent developments since their publication. The main approaches for finding an approximate replacement to the convolution-based calculation of the radiation force ${\overrightarrow{F}}_R\left(t\right)$ can be classified as:

• Frequency-domain methods, which use the radiation function $H_r\left(j\omega \right)$ itself to estimate state-space or transfer function models. The main routes taken are:

  –

  Identifying continuous-time filter parameters from frequency response data [4,6,7,8];

  –

  The moment matching method [9,10,11,12], including maintaining passivity.

• Time-domain methods, which numerically calculate the radiation IRF $h_r\left(t\right)$ and then use the IRFs to estimate state-space or transfer function models. The main routes taken for this approach are:

  –

  Curve fitting methods based on least squares curve fitting of the IRFs [13,14];

  –

  The realization theory method, which is based on Hankel singular value decomposition (SVD) followed by order reduction strategies such as balanced-realization order reduction.

1.3. Frequency-Domain Estimation Methods

1.3.1. Identifying Continuous-Time Filter Parameters from Frequency Response Data

Duarte et al. summarize the least-squares methods [6]. These methods minimize the least-squares error between the radiation function and the estimated LTI system. Some of these optimization-based approaches use the invfreqs() command in MATLAB. The invfreqs() command is based on Gauss–Newton iterative search optimization. The estimation process can be weighted or biased by incorporating a fitted polynomial using a weighting function. Originally developed for ship motions, this approach was developed at Norges Teknisk-Naturvitenskapelige Universitet—NTNU and is packaged as the Marine Systems Simulator (MSS toolbox). The MSS toolbox is based on Taghipour et al., and Perez, T. and T. I. Fossen [4,7].

The MSS toolbox has the FDI (frequency-domain identification) utility, approximating LTI models using the frequency-dependent radiation function $H_r\left(j\omega \right)$. The FDI utility first filters out the frequencies with discontinuous points owing to numerical errors in the hydrodynamic coefficients data from WAMIT or any other BEM solver. The process also rejects zero frequency lines in the estimation process. The estimation process starts from a second-order system, and then the order is increased to improve the match in the frequency response of the estimated system and the radiation function $H_r\left(j\omega \right)$. The package then iteratively reduces the error between the radiation IRF, $h_r\left(t\right)$, and the approximated transfer function. This step is followed by the MATLAB command ss() to generate a state-space model.

The estimation process then checks for unstable poles (poles in the right-hand plane of the Laplace plane). If unstable poles are found, they are reflected about the imaginary axis by multiplying the positive real parts by $-1$, and the estimation process is reinitialized with the reflected pole. The rejection of zero frequency points and ‘wild points’, and the weighting process itself, risks losing the physical nuances of the marine system, especially for multiple bodies in WEC arrays. The iterative increase in orders also risks the overestimating issue discussed by Perez and Fossen [7]. The process requires the user to pick a frequency range to be used for estimation. As pointed out by Perez and Fossen, the matches with this method work best for low frequency ranges, and it does not guarantee stability and passivity [7]. Taghipour et al. also observe that the improper scaling of the input data can result in numerical instability [4].

Forehand et al. also generate a transfer function and a state-space model, with the added feature that their code package can be used for a WEC array [8]. They estimate the transfer function using the invfreqs() command in MATLAB. They also minimize the root mean square error between the frequency response of the estimated transfer function and the frequency response of the radiation impedance function using the freqreqs() command in MATLAB. These estimations are performed for different orders, and the estimated transfer function with the least error is chosen. The order of the transfer function system is then minimized further to estimate the state-space model. The stability and conditionality for the estimated system are checked but not enforced in the estimation process.

1.3.2. The Moment Matching Method

Recently, some very promising developments have been made in frequency-domain estimation methods. Faedo et al. at Maynooth University developed a novel approach using moment matching to estimate LTI systems [9]. In this context, a moment refers to the radiation function $H_r\left(j\omega \right)$ at some specific frequency. The method uses a few points or moments of the $H_r\left(j\omega \right)$. Faedo et al. then used these estimated models to devise an energy maximizing controller model [10]. They also extended this approach for a multiple-degrees-of-freedom (MDOFs) problem [11].

The moment matching method shows good results, with very low normalized root mean squared error (NRMSE) between body motions calculated using their estimated system and those from the convolution [15,16,17]. However, this method relies on choosing the moments correctly. In their case studies, Faedo et al. point out that the frequencies used for the chosen moments correspond to the radiation function $H_r\left(j\omega \right)$ peaks. However, this becomes difficult to judge if the $H_r\left(j\omega \right)$ has a multi-lobed frequency response, especially for multibody MDOFs systems. Although regular geometries like spheres and cylinders usually have a single-lobed $H_r\left(j\omega \right)$, disparate marine structures or innovative WECs will have multi-lobed $H_r\left(j\omega \right)$, making it difficult to choose the moments, especially in situations where coupled modes exist.

Similarly, WEC arrays, especially compact WEC arrays, are challenging systems for a moment-matching-based method. When marine structures are in close proximity, such as in a compact WEC array, the velocity field within the area occupied by the structures is modified. This results in a trapping effect which introduces additional local minima in the hydrodynamic coefficients. These trapping effects are extensively discussed in work by Eatock Taylor et al. [12]. Wolgamot et al. also described the effect of trapping effects in WEC arrays [18,19]. These phenomena show that each frequency is coded with critical hydrodynamic information about the system. Faedo et al. remarked that an additional constraint could introduce passivity to their optimization [9]. More recently, the same authors have proposed a passivity preserving method [20]. In that work, Faedo et al. introduced the conditions needed to guarantee passivity for a single body. In the numerical example shown in that paper, the authors selected a new set of moments for a passive model. This shows that the selection criteria for moments in an MDOFs and/or multiple body system becomes difficult. The accuracy for coupled modes, whose radiation damping characteristics usually have multiple local minima, can therefore be enforced only in a limited bandwidth [21,22].

1.4. Time-Domain Estimation Methods

Time-domain estimation methods are carried out in two stages: the numerical integration for the radiation IRF, $h_r\left(t\right)$, followed by estimating an LTI system based on this radiation IRF, $h_r\left(t\right)$. The general approach for the numerical integration for the cosine transform is to use either Euler integration or trapezoidal integration methods. For instance, NEMOH, developed by LHEEA Centrale Nantes, uses Euler integration [13,14]. Whereas the WEC-Sim package, developed by the National Renewable Energy Laboratory (NREL) and Sandia National Laboratories, uses the trapezoidal integration method by calling the trapz() function in MATLAB [23]. Prony’s method can also be used to calculate the radiation IRF $h_r\left(t\right)$ [24]. However, Prony’s method only works for single bodies. It does not work for arrays because of the shape of the impulse response functions. WAMIT uses a tool called the $f2t$ utility to output radiation IRFs using Filon’s trapezoidal numerical integration (see chapter 13 of the WAMIT manual for a description of the $f2t$ utility) [23]. The $f2t$ description recognizes that the Fourier transform (and more specifically the cosine transform for the radiation IRF) is more accurately calculated using Filon’s integration method, especially for large values of the time variable.

The following two subsections describe the main approaches taken over the years by researchers.

1.4.1. The Least Squares (LS) Curve Fitting Method

Yu and Falnes presented their, in some ways, pioneering work, outlining the different ways the real-time convolution could be circumvented [3]. They proposed that the estimated system may need a higher-order approach to describe the radiation IRF, $h_r\left(t\right)$. Yu and Falnes used numerical integration to form companion form matrices for the radiation and excitation forces. However, the stability and passivity properties of the estimated state-space models were not considered. Taghipour et al. point out that the LS methods result in LTI systems whose frequency responses have very poor matches with the respective radiation function $H_r\left(j\omega \right)$ [4].

Another notable example of an LS curve fitting model was presented by Alves et al. [25]. They used the MATLAB function $prony$ to find a discrete transfer function. However, this method does not ensure stability, especially for higher-order radiation functions [6].

1.4.2. The Realization Theory Method Using the SVD Hankel Decomposition

Unneland et al. and Kristiansen et al. performed a state-space realization using the Markovian property of state-space models [26,27,28]. The MATLAB function $imp2ss$ can be used to perform the SVD Hankel decomposition. Additionally, Taghipour, Perez, and Fossen showed that the overfitting could be mitigated by a balanced order reduction using the $balmr$ command in MATLAB [4,24]. This approach does not enforce stability or passivity, although Taghipour et al. and Perez et al. recognize that the approximation process should ideally result in a passive LTI system. Perez and Fossen point out that the realization theory method does not necessarily satisfy the low-frequency asymptotic values and the relative degree requirements of the radiation function $H_r\left(j\omega \right)$ [4,24]. This approach has been widely cited and was incorporated in the WEC-Sim package developed by Sandia National Laboratories and the National Renewable Energy Laboratory (NREL) [23]. Subsequent reports published by Sandia National Laboratories highlight the difficulty of ensuring stability for a complete dynamics model that has the radiation force as the negative feedback [29]. However, this approach becomes difficult to implement for a multibody MDOFs system.

Lecuyer-Le Bris et al. also used SVD Hankel decomposition and demonstrated the need for the numerical calculations of the radiation function to be zero at $t\le 0$, and of the convergence to zero at $t=\infty$ [30]. They ensured that the radiation function was zero at $t\le 0$ by incorporating the radiation function evaluated at $t\le 0$. They extrapolated their radiation function coefficients to a frequency high enough that it converged to zero, thereby mitigating the high-frequency numerical artifacts. They demonstrated their findings by using a modified kernel of the radiation damping by comparing the effect of their modified kernel on the response amplitude operators (RAOs) of the motion dynamics. They concluded that their formulation ensured the radiation function was zero at $t\le 0$ and its asymptotic convergence to zero at $t=\infty$. They asserted that their proposed kernel incorporated the passivity of the radiation function. From a system identification perspective, the work by Lecuyer-Le Bris et al. also satisfies the properties listed in Section 3. In the Laplace domain, their considerations ensure phase relationships at zero frequency and describe the need for the estimated LTI systems to have a zero at the origin.

1.5. Article Organization

The rest of the paper is organized as follows. Section 2 describes the pertinent equations of motion and develops a time-domain model for a WEC. Section 3 introduces the need for passivity in estimated LTI systems and outlines the physical properties of the radiation function that the LTI system is supposed to emulate. Section 4 outlines the algorithm for the proposed approach. The efficacy of the proposed approach is demonstrated using some examples in Section 5. The estimated system’s accuracy is quantified in terms of its frequency response function (FRF) and passivity using the input passivity index ($\nu$). Section 6 describes the motion simulation using the estimated transfer functions and compares its performance to direct convolution. Following this, Section 7 analyzes the results and discusses the observations. Finally, Section 8 presents the overall conclusions.

2. Equations of Motion and Development of a Time-Domain Model

This paper focuses on developing linear, stable models for the radiation force effects in single and multiple floating marine structures, such as wave energy converter (WEC) arrays, that can be used for model-based control strategies. The viscous drag forces can be ignored for the compact and sparse arrays analyzed in this work as they are small compared to radiation damping [31]. The equations of motion shown here can be used for both hydrodynamically coupled and uncoupled arrays. A WEC array is hydrodynamically coupled when the motion of a WEC is affected by the motion of other WECs in the array. An array can be considered hydrodynamically uncoupled when its members are far enough apart to have minimal mode-couplings, the motion of any WEC in the array is independent of the motion of any other WEC.

The motion of WECs is commonly described by Equation (1), which is the Cummins equation [1,2]. The viscous drag forces can be ignored for large marine structures as they are small compared to radiation damping [2].

$$(\mathbf{M}+{\mathbf{a}}_{\infty })\overrightarrow{\ddot{q}}\left(t\right)+{\int }_0^t{\mathbf{h}}_{\mathbf{r}}(t-\tau )\overrightarrow{\dot{q}}\left(\tau \right)d\tau +\mathbf{K}\overrightarrow{q}\left(t\right)=\overrightarrow{Q}\left(t\right)$$

(1)

where the $\overrightarrow{q}\left(t\right)$ are generalized motion coordinates, and the coefficient of $\overrightarrow{\ddot{q}}\left(t\right)$ is the summation of the inertia of the system and the asymptotic added mass. That is, for an n degrees-of-freedom system, $\mathbf{M}\in {\mathbb{R}}^{nxn}$ is the inertia matrix, and ${\mathbf{a}}_{\infty }\in {\mathbb{R}}^{nxn}$ is the added mass matrix at infinite frequency. The second term is the convolution operation needed to calculate the radiation force, ${\overrightarrow{F}}_R\left(t\right)$. Also, $\mathbf{K}\in {\mathbb{R}}^{nxn}$ is the hydrostatic and gravitational stiffness matrix, and the $\overrightarrow{Q}\left(t\right)$ contains the Froude–Krylov, diffraction, PTO, and friction generalized forces. For a rigid body moving in six DOFs (degrees of freedom), the $\overrightarrow{q}\left(t\right)$ are surge, sway, heave, roll, pitch, and yaw modes, and the matrices $\mathbf{M},{\mathbf{a}}_{\infty },{\mathbf{h}}_{\mathbf{r}}\left(t\right)$, and $\mathbf{K}$ are $6\times 6$ matrices. For multiple bodies forming an array of N rigid bodies, each moving in six DOFs, these matrices become $6N\times 6N$ matrices, and the off-diagonal terms contain the appropriate coupling terms.

The linear assumptions entail that the incoming waves have small amplitude and steepness and that the body motions are also small. For the dynamics model discussed in later sections, it is assumed that no PTO or control forces are acting on the system, so the right-hand side of Equation (1), $\overrightarrow{Q}\left(t\right)$, will be replaced with just the excitation force, ${\overrightarrow{F}}_{exc}\left(t\right)$, for the remainder of this paper. Note, in this section the excitation force coefficients and the radiation function are represented as $H_{exc}\left(j\omega \right)$ and $H_r\left(j\omega \right)$ to emphasize that they are complex functions.

The excitation force is the input to the system, as shown in Equation (2). The excitation force impulse response function (IRF) is expressed as Equation (3). Therefore, the convolution in Equation (2) models the excitation force acting on the system for a known wave elevation time history $\eta$, as shown in Equation (4). The excitation force can be calculated in advance without affecting the real-time dynamic model because the excitation force depends on the incoming wave profile. However, for irregular wave inputs, with wave profiles changing in real time, prediction of the incoming wave profile becomes critical.

$${\overrightarrow{F}}_{exc}\left(t\right)={\int }_{-\infty }^{\infty }\left[h_{exc}\left(\tau \right)\eta (t-\tau )\right]d\tau$$

(2)

where

$$h_{exc}\left(t\right)=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }\left[H_{exc}\left(j\omega \right)e^{j\omega t}\right]d\omega$$

(3)

and

$$\eta \left(t\right)=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }\left[\eta \left(j\omega \right)e^{j\omega t}\right]d\omega$$

(4)

The second term in Equation (1), together with the ${\mathbf{a}}_{\infty }\ddot{\overrightarrow{q}}\left(t\right)$ term, corresponds to the radiation force. This term is the convolution of the radiation force IRF with the body’s velocity. This follows from defining the radiation FRF $H_r\left(j\omega \right)$, using the hydrodynamic radiation effects of the body, i.e., added mass $\mathbf{a}\left(\omega \right)$ and radiation damping $\mathbf{b}\left(\omega \right)$, which are obtained using numerical solvers like WAMIT. The radiation FRF can therefore be expressed as

$$H_r\left(j\omega \right)=[j\omega \tilde{\mathbf{a}}\left(\omega \right)+\mathbf{b}\left(\omega \right)],$$

(5)

where $\tilde{\mathbf{a}}\left(\omega \right)=\mathbf{a}\left(\omega \right)-{\mathbf{a}}_{\infty }\left(\omega \right)$, such that the asymptotic added mass that converges to a constant ${\mathbf{a}}_{\infty }$ at higher frequencies is subtracted from the radiation function $H_r\left(j\omega \right)$ and added to the inertia matrix $\mathbf{M}$, as shown in Equation (1). The inverse Fourier transform of $H_r\left(j\omega \right)$ in Equation (5) results in the radiation IRF, as shown in Equation (6):

$$h_r\left(t\right)=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }\left[H_r\left(j\omega \right)e^{j\omega t}\right]d\omega$$

(6)

which becomes

$$h_r\left(t\right)=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }\left[[j\omega \tilde{\mathbf{a}}\left(\omega \right)+\mathbf{b}\left(\omega \right)](cos\left(\omega t\right)+jsin\left(\omega t\right))\right]d\omega$$

(7)

Note, the radiation function $H_r\left(j\omega \right)$ itself is a complex function; however, the corresponding IRF is a real function. This is physically justified by associating the added mass with local, evanescent, and non-propagating modes, represented by the imaginary part of the complex radiation function; while the radiation damping part propagates with the real part such that the radiation force, $\overrightarrow{F_r}\left(t\right)$, is a causal real force experienced in the vicinity. This can be shown mathematically by observing that sine is an odd function, while cosine is an even function, and that both the $\tilde{\mathbf{a}}\left(\omega \right)$ and $\mathbf{b}\left(\omega \right)$ are even functions [2]. Therefore, the imaginary part of Equation (7) is an odd function, thus vanishes, while the real part, being an even function, is twice its value when the lower limit is $zero$ and the upper limit is ∞. Changing the lower limit of Equation (7) to $zero$ and doubling the real part gives

$$h_r\left(t\right)=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }\left[\mathbf{b}\left(\omega \right)cos\left(\omega t\right)-\omega \tilde{\mathbf{a}}\left(\omega \right)sin\left(\omega t\right)\right]d\omega$$

(8)

The Kramers–Kronig relations relate the added mass $\mathbf{a}\left(\omega \right)$ and radiation damping $\mathbf{b}\left(\omega \right)$. The Ogilvie equations use the Kramers–Kronig relations to simplify (8) such that $h_r\left(t\right)$ can be expressed as either a cosine transform of the radiation damping FRF $\mathbf{b}\left(\omega \right)$ or the sine transform of the FRF of the added mass $\mathbf{a}\left(\omega \right)$ [32].

$$\begin{array}{c}\hfill h_r\left(t\right)=\frac{2}{\pi }{\int }_0^{\infty }\left[\mathbf{b}\left(\omega \right)cos\left(\omega t\right)\right]d\omega \\ \hfill =-\frac{2}{\pi }{\int }_0^{\infty }\left[\omega \tilde{\mathbf{a}}\left(\omega \right)sin\left(\omega t\right)\right]d\omega \end{array}$$

(9)

Therefore, the radiation IRF is real-valued and causal. Motion-dynamics modeling of a marine structure requires the convolution of Equation (9) with the body velocity to calculate the radiation force in real time. Physically, this means the body will only experience the radiation force after a wave has hit it, and the body generates a radiation field around it that, in turn, becomes the radiation force experienced by the body. The expression for the radiation force in the time domain can, therefore, be expressed as

$${\overrightarrow{F}}_R\left(t\right)={\mathbf{a}}_{\infty }\ddot{\overrightarrow{q}}\left(t\right)+{\int }_0^t\left[h_r(t-\tau )\overrightarrow{\dot{q}}\left(\tau \right)\right]d\tau$$

(10)

such that $h_r\left(\tau \right)=0,$ for $\tau <0$. When numerically integrating Equation (10), the limits of the integral can go from the $max(0,t-t_d)$ to t, where $t_d$ is the duration of the radiation IRF (i.e., the radiation IRF is zero for $t>t_d$).

3. Passivity Properties of the Radiation Function, ${\mathit{H}}_{\mathit{r}}\mathbf{\left(}\mathit{j}\mathit{\omega }\mathbf{\right)}$, Radiation IRF, ${\mathit{h}}_{\mathit{r}}\mathbf{\left(}\mathit{t}\mathbf{\right)}$, and Estimated LTI System, $\mathit{G}\mathbf{\left(}\mathit{s}\mathbf{\right)}$

In its simplest high-level form, the Cummins equation is analogous to a mass–spring–damper system, where the hydrostatic forces act as a spring force while the radiation forces contribute to the damping force and the overall inertia of the system. Equation (11) shows the equation of motion for such a 1-DOF system:

$$m_0\ddot{z}+k_{0}z+{\int }_0^{t}g(t-\tau )\dot{z}\left(\tau \right)d\tau =f_{ext}$$

(11)

where $m_0$ represents the system’s effective inertia, z represents motion in some arbitrary mode, $k_0$ the hydrostatic stiffness, followed by the convolution integral used to calculate the radiation forces, in which $g(t-\tau )$ is the impulse response function of the wave field radiated by the system. The right-hand side of the equation encapsulates all external forces, such as the power take-off (PTO) forces and the excitation forces. The focus of this work is identifying a linear time-invariant system that can replicate the convolution integral needed to calculate the radiation forces. This equivalent LTI system is represented hereafter as the transfer function $G\left(s\right)$, where $s=j\omega$. The Laplace transform of Equation (11) is

$$Z\left(s\right)\left(m_0{s}^2+k_0+sG\left(s\right)\right)=F_{ext}\left(s\right)$$

(12)

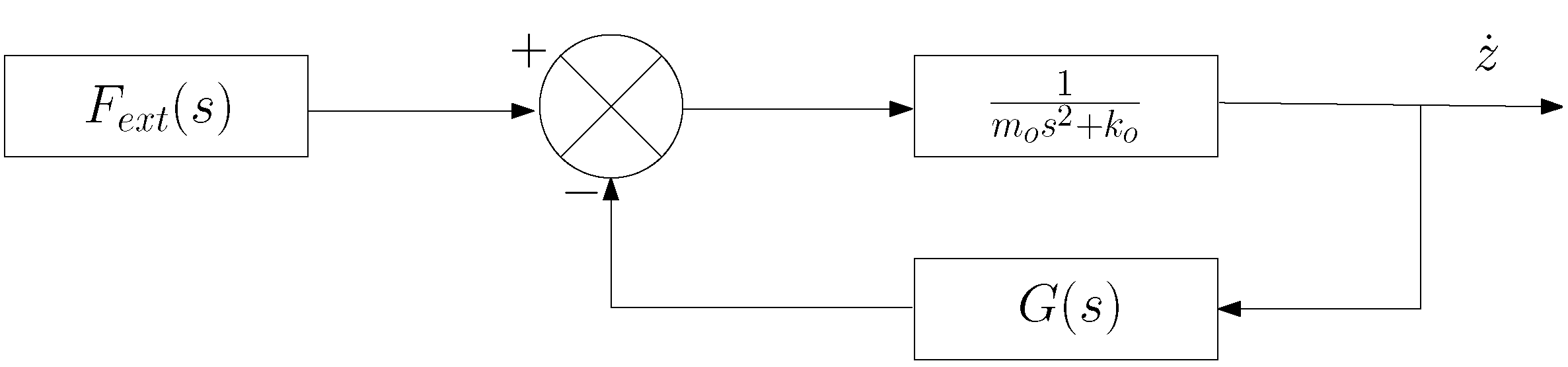
In Equation (12), and the block diagram shown in Figure 1, the WEC is represented as $\frac{1}{m_0{s}^2+k_0}$, and is the plant of the system composed of a mass–spring system, such that $m_0$ represents the mass of the simplified WEC model and $k_0$ is the hydrostatic coefficient. The radiation forces serve as the negative feedback to the system, and are represented as $G\left(s\right)$. The external forces, shown as $F_{ext}\left(s\right)$, represent the excitation forces composed of the incident Froude–Krylov forces and the diffraction forces that serve as the input to the system, and the WEC’s velocity is the output. The computation of the radiation forces requires the convolution of the body’s velocity and the radiation force impulse response function (IRF).

The radiation force is causal and needs the body’s velocity information in real time for the convolution. The radiation force in the time domain is calculated using the frequency-domain hydrodynamic coefficients, solved using a boundary element method (BEM) solver, such as commercial software packages like Wave Analysis MIT (WAMIT v7.4). The frequency-domain hydrodynamic coefficients are then used to calculate an IRF. Convolving the IRFs with the buoy velocity gives the radiation force in real time. This convolution operation makes model-based motion control difficult because motion control of a dynamic system requires the knowledge of its poles and zeros [4,24].

This work circumvents the convolution operation by proposing an algorithm to generate a transfer function between the radiation force and body velocity. Modeling the dynamics using a linear time-invariant (LTI) model provides the knowledge of the system’s dynamical characteristics and facilitates various motion-control strategies based on the system’s motion dynamics. Note that the model-based control schemes, whether for analysis or implementation, often rely on reduced-order models, which further necessitate system identification of the radiation forces. For instance, model-predictive control (MPC) of a WEC array is computed based on running an optimization problem at each control update step.

The motion dynamics matrices need to encapsulate all possible mode couplings. A time-domain model of a multibody system is a multiple input multiple output (MIMO) system. Estimating a linear time-invariant (LTI) MIMO system is challenging in terms of accuracy and stability. The estimated radiation force transfer function array (hereafter $G\left(s\right)$) has to ensure the stability of the closed-loop multibody dynamics system. The $G\left(s\right)$ is in the negative feedback of the overall dynamics model. A passivity-based estimation algorithm for $G\left(s\right)$ can, therefore, ensure the stability of the overall dynamics model. A passivity-based approach also ensures fidelity to the physical system because radiation forces are dissipative in nature. The Nyquist stability criteria used for single input single output (SISO) systems can be extended to a multiple intput multiple output (MIMO) system by assessing the input passivity index ($\nu$) of $G\left(s\right)$.

The properties of radiation effects are encapsulated in the radiation function $H_r\left(j\omega \right)$; therefore, the estimated LTI system, $G\left(s\right)$, should preserve the physical phenomenon being approximated. The boundary conditions of the radiation function $H_r\left(j\omega \right)$, and its time-domain counterpart radiation IRF, $h_r\left(t\right)$, are summarized in

Table 1. Properties of the radiation function $H_r\left(j\omega \right)$, radiation IRF, $h_r\left(t\right)$, and estimated LTI system, $G\left(s\right)$; see [6,33].

Property	Implications
1. $li{m}_{\omega \to 0}{H}_r\left(j\omega \right)=0$	There are zeros at $s=0$
2. $li{m}_{\omega \to \infty }{H}_r\left(j\omega \right)=0$	Strictly proper
3. $li{m}_{t\to 0^{+}}{h}_r\left(t\right)\ne 0$	Relative degree 1
4. $li{m}_{t\to \infty }{h}_r\left(t\right)=0$	Bounded input bounded output (BIBO) stability
5. The mapping, $\dot{x}\to {\overrightarrow{F}}_R\left(t\right)$ is passive	$H_r\left(j\omega \right)$, therefore, $G\left(s\right)$ is positive real (PR)

. Table 1 is similar to the properties discussed by Duarte et al. and Perez and Fossen [6,33].

In Table 1, properties $1,2$, and 3 are a consequence of the Riemann–Lebesgue lemma, while the BIBO stability condition in property 4 establishes the input–output stability of the convolution for radiation forces [4,33].

Property 5 in Table 1 entails the dissipativity property of the radiation function $H_r\left(j\omega \right)$, since it starts as 0 and then converges to 0 since the radiation forces are dissipative. The Ogilvie equations indicate that the radiation IRF, $h_r\left(t\right)$, can be calculated using the radiation damping coefficients $\mathbf{b}\left(\omega \right)$ [32]. The $\mathbf{b}\left(\omega \right)$ also starts from 0 and converges to 0 since the hydrodynamic theory dictates that the $\mathbf{b}\left(\omega \right)$$>0,\forall \omega$. It can be therefore said that the radiation forces are passive, since radiation forces are dissipative and they generate no energy. For linear systems, the passivity property is equivalent to positive realness [4,5].

The estimated transfer functions are used to calculate the radiation force and are used in the negative feedback of the complete dynamic system. A challenging property of linear systems is that even if a system such as a transfer function is stable on its own when used in the closed loop of the complete system, it can result in making the overall system unstable. Therefore, system stability can be assessed by looking into its passivity property. Passivity implies that the physical system does not generate energy and can only store or dissipate energy. Therefore, the estimated transfer function array should be passive, i.e., positive real. This stability criterion has been recognized by various researchers, such as in [4,6,14,24,27].

The passivity condition essentially requires that the estimated LTI system, $G\left(s\right)$, or the radiation force transfer function array, populated by transfer functions between body velocity and radiation force, ${\overrightarrow{F}}_R\left(t\right)$, is positive semi-definite, which implies that the real part of the transfer function array is positive. Formally, the passivity condition for a transfer function array, which is a multiple input multiple output (MIMO) system, can be stated as discussed by Khalil [5].

Lemma 1. 

Let G(s) be a $p\times p$ proper rational transfer function matrix, and suppose $det[G\left(s\right)+G{(-s)}^T]$ is not identically zero. Then, G(s) is strictly positive real if and only if:

1. 

G(s) is Hurwitz; that is, the poles of G(s) have negative real parts;

2. 

$G\left(s\right)+G{(-s)}^T$ is positive definite for all $\omega \in R$;

3. 

Either $G(\infty )+G{(\infty )}^T$ is positive definite; or it is positive semi-definite and the terms $li{m}_{\omega \to \infty }{\omega }^2{M}^T[G\left(j\omega \right)+G{(-j\omega )}^T]M$ are positive definite for any $p\times (p-q)$ full-rank matrix M, such that the term $M^T[G(\infty )+G{(\infty )}^T]M=0$, where $q=rank[G(\infty )+G{(\infty )}^T]$. Additionally, if $G(\infty )+G{(\infty )}^T=0$, then $M=I$, which is the case for radiation damping.

The passivity of the estimated radiation transfer functions using the input passivity index, $\nu$, is such that $\nu =\frac{1}{2}mi{n}_{\omega }{\lambda }_{min}(G\left(j\omega \right)+G(-j\omega ))$, where ${\lambda }_{min}$ are the minimum eigenvalues of the magnitude of $\left(G\right(j\omega )+G(-j\omega \left)\right)$. For SISO LTI systems, the input passivity index corresponds to the horizontal distance of the Nyquist plot from the imaginary axis, or in other words, the real part of the Nyquist plot, since for a SISO LTI system, $\left(G\right(j\omega )+G(-j\omega \left)\right)$ results in $2Re\left(G\right(j\omega \left)\right)$, making $\nu =Re\left(G\right(j\omega \left)\right)$. Note, the passivity corresponds to the Nyquist criterion for feedback systems, requiring the phase of the LTI system in question to be within $[-\pi /2,+\pi /2]$ $rad$.

Classical control methods such as the Nyquist plot can be used to assess the robustness of stability and passivity. However, assessing stability through a passivity-index-based approach, as proposed here, has certain advantages, including:

• Satisfying robust stability criteria such as ${\mathcal{L}}_2$ stability, and more generally, dissipativity;
• Using passivity ensures mapping the estimated LTI system to the physical properties of the system being modeled;
• Passivity-based stability analysis can be extended to a MIMO system, such as a multiple-degrees-of-freedom (MDOFs) analysis of a single-body or multiple-body arrays.

Note, the evaluation of stability is based on a real quantity—the input passivity index. Interestingly, the analytic property of the radiation function is preserved when using the passivity-index-based system estimation because the estimation method matches both the magnitude and phase of the radiation function. The estimated system does eventually converge because a passive system is also dissipative, thereby preserving the analytic property of the radiation function [34,35]. There is, however, a trade-off between the stability of the estimated models and their fidelity to the physical system. While estimating, it must be kept in mind that, in general, increasing the order of the estimated model may result in a better fit but sacrifice passivity (and thus, stability) and also risk overfitting. Overfitting results in the estimated system having high-frequency poles (typically higher than 10 $rad/s$) that do not correspond to the actual physical system because marine systems are relatively very slow (typically operate within 0 to 4 rad/s). On the contrary, reducing the order of the estimated system will enhance passivity but sacrifice fidelity to the physical system being estimated.

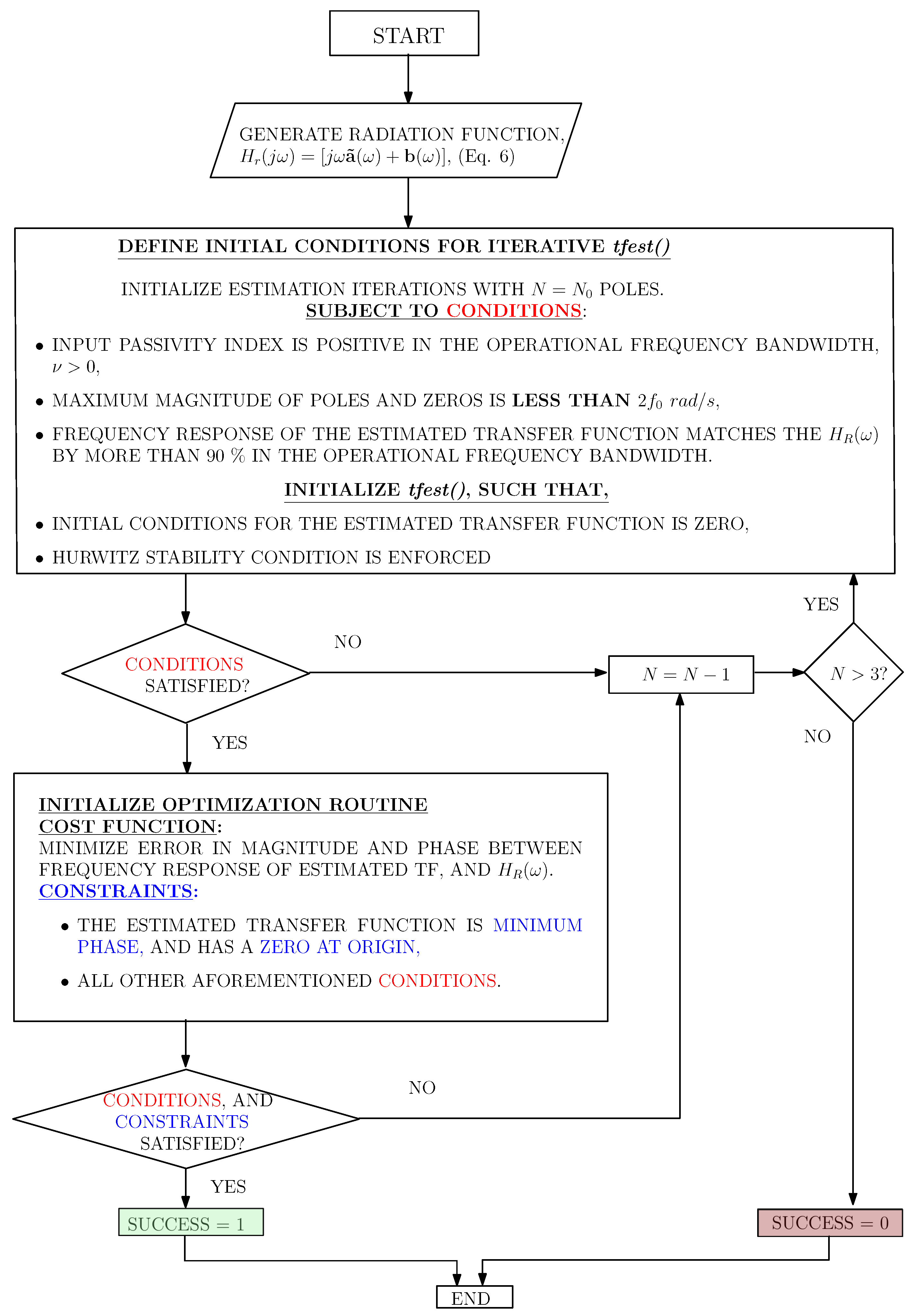
It is proposed that the passivity property can be checked for, and the orders of the estimated transfer functions can be chosen through iterations, as discussed in [4,24]. Many researchers, therefore, start with the smallest order possible, i.e., relative degree 1, and then increase the order while checking for model fidelity and passivity [4,24]. The current state-of-the-art methods, therefore, check for passivity but do not enforce or guarantee the passivity in the estimated transfer functions [4,9,20,24].

4. The Algorithm

This section will describe the proposed algorithm and the scaling scheme that can be used to generalize the estimated transfer function, so that it can be scaled up or down corresponding to the body geometry as long as its dimensions maintain geometric similarity, i.e., have the same ratios with respect to each other. The radiation force estimation strategy follows three stages:

• Generation of a reference for the radiation transfer function;
• Iteration to obtain a low-order, accurate, and passive transfer function;
• Final tuning to ensure minimum phase, such that at least one zero of the estimated radiation transfer function is at the origin (i.e., $s=0$ is a zero).

4.1. Generation of a Reference for the Radiation Transfer Function

For the frequency-domain approach, the radiation function $H_r\left(j\omega \right)$ is generated using WAMIT, as shown in Equation (5). This function is then used as the reference function for the iterative estimation of radiation transfer functions. Since the radiation function is dissipative, it asymptotically approaches zero. In the discussion that follows, the frequency at which the radiation function is less than $5\%$ of its maximum ($f_{0}rad/s$ is greater than the frequency at the maximum) will be referred to as $f_{0}rad/s$.

4.2. Iterative Estimation of Radiation Transfer Functions

This stage corresponds to the iterative loop initialized with $N_0$ poles in Figure 2. The initial number of poles, $N_0$, is the highest order desired by the user. The algorithm then iteratively decreases the number of poles—balancing the trade-offs between stability and accuracy because it can be observed empirically that estimated systems with a higher number of poles sacrifice stability for accuracy, and vice-versa. The estimation process is performed using the tfest() command in MATLAB. This function uses iterative optimization to curve-fit either impulse response data or frequency response data. The function has options that let the user enforce Hurwitz stability. This is achieved by reflecting poles estimated in the right-hand plane about the imaginary axis and starting the estimating optimization again. The estimated transfer function is then further refined using non-linear search optimization to obtain the best possible fit. The tfest() command by default estimates a $strictly-proper$ transfer function. The estimation process is carried out for each mode combination, resulting in a transfer function array, $G\left(s\right)$. For MDOFs systems such as WEC arrays, mode couplings include both intra-body and inter-body interactions, while for single-body MDOFs systems, mode couplings include implying intra-body mode couplings. When estimating transfer function matrices, $G\left(s\right)$, the input passivity index ($\nu$) characteristics correspond to the positive definiteness of the transfer function matrix. The matrix of magnitudes of each individual transfer function in $G\left(s\right)$ can be seen as a Toeplitz matrix. It was observed that the $\nu$ of the entire transfer function matrix could be enhanced if the $\nu$ of the Toeplitz matrices making up the transfer function array increased [36]. Therefore, iterating on the order of the individual transfer functions in $G\left(s\right)$ to achieve more positive $\nu$ for each transfer function helps in estimating more positive $\nu$ for the transfer function array $G\left(s\right)$.

The iterative estimation process using the tfest() command is initiated with the highest expected order, $N_0$. At each iteration, the tfest() command estimates a transfer function array $G\left(s\right)$. This $G\left(s\right)$ should then satisfy the following criteria:

• $G\left(s\right)$ is bandwidth-limited passive, such that the input passivity index is positive ($\nu >0$) for a defined frequency bandwidth;
• $G\left(s\right)$ has accurate frequency response, such that the percentage $fit$ between the frequency response of $G\left(s\right)$ and the radiation function $H_r\left(j\omega \right)$ is greater than $90\%$ for a defined frequency bandwidth;
• Finally, $G\left(s\right)$ should not have pole frequencies higher than $2f_0$$rad/s$ in the Laplace domain. This is necessary to avoid overfitting and avoiding poles that do not correspond to the physical phenomenon $G\left(s\right)$ is supposed to replicate. This upper bound was empirically set to about two times the frequency at which the radiation function converges to 0.

If the estimation process fails to find a $G\left(s\right)$ that satisfies these three criteria, the algorithm re-iterates by reducing the expected order by one. This iterative process is deemed to fail if the estimated order has to be reduced below the third order. Note, that regardless of the initial reference function being the radiation IRF, $h_r\left(t\right)$, or the radiation function $H_r\left(j\omega \right)$, the iterative process compares the frequency response of $G\left(s\right)$ with the radiation function $H_r\left(j\omega \right)$, ensuring fidelity with the hydrodynamics radiation damping data.

4.3. Final Optimization Routine

The estimated $G\left(s\right)$ from the previous step serves as a very good initial guess for the final optimization. The estimated $G\left(s\right)$ from the iterative tfest() routine has very high accuracy and positive input passivity index $\nu$. However, the $G\left(s\right)$ estimated from the iterative routine in the previous step often generates transfer functions that do not have a zero at the origin. The $G\left(s\right)$ is then subjected to optimization to enhance the accuracy and passivity index characteristics while ensuring that the properties listed in Table 1 are exhibited by the estimated transfer function array $G\left(s\right)$.

The final optimization is set up so that the cost function is a weighted function formed by the sum of the absolute squared difference between the frequency response magnitude and phase of the transfer function array $G\left(s\right)$ and the radiation function $H_r\left(j\omega \right)$, such that

$$J=\alpha \sum {\left(|H_r\left(j\omega \right)|-|G\left(j\omega \right)|\right)}^2+\beta \sum {\left(\angle \left(H_r\left(j\omega \right)\right)-\angle \left(G\left(j\omega \right)\right)\right)}^2,$$

(13)

where J is the cost function to be minimized by optimization, $\alpha$ is the weight for the magnitude difference, and $\beta$ is the weight for the phase difference. The weights of the cost function are so chosen that both phase and magnitude of the optimized $G\left(s\right)$ are more accurately matched with the radiation function $H_r\left(j\omega \right)$. Additionally, the frequency range over which the optimization is performed can also be chosen such that the accuracy and passivity characteristics are further improved.

The optimization is further subject to constraints such that the estimated $G\left(s\right)$ satisfies the properties laid out in Table 1 and meets the following criteria:

• $G\left(s\right)$ must be minimum-phase and have a zero at the origin;
• $G\left(s\right)$ must be strictly proper, i.e., has a relative degree of 1;
• The input passivity index is positive, such that $\nu >0$, for a defined frequency bandwidth;
• All poles are less than $2f_0$$rad/s$;
• The accuracy of the optimized $G\left(s\right)$ exceeds $90\%$ for a defined frequency bandwidth.

Figure 3 shows the effect of optimization on the estimated $G\left(s\right)$ for the case of a single heaving cylinder with a radius of 1 m and draft of 1 m. It can be observed that the optimized $G\left(s\right)$ has resolved the non-minimum-phase issue in the $G\left(s\right)$ before optimization. The zero-at-the-origin constraint helped in significantly enhancing the accuracy of the optimized $G\left(s\right)$ with respect to $H_r\left(j\omega \right)$ at low frequencies. The optimized $G\left(s\right)$ satisfied the properties listed in Table 1 for the frequency bandwidth in which hydrodynamic data were available.

The final optimization ensured that the $G\left(s\right)$ had a minimum phase. This also helped increase the input passivity index $\nu$, as shall be demonstrated in the case studies in Section 5. As shown in Figure 2, should the optimization fail in satisfying all of the aforementioned conditions, further iteration is performed by reducing the initial estimation order. Further refinement is subject to the empirical inverse relationship between the accuracy and the stability such that an increase in the accuracy typically decreases the passivity index and vice versa.

4.4. Scaling Scheme

Scalability of the estimated transfer functions is desirable for consistency in modeling the WECs at prototype scale and deployment scale. The algorithm can be scaled up or down by first normalizing the estimated transfer function using wave frequency, water density, and the characteristic length, and then performing Froude scaling using the characteristic length for wave frequency and the pertinent hydrodynamic coefficients. The normalizing scheme for the added mass, radiation damping, and the wave frequency can be expressed as [37]

$$\begin{array}{c}{\overline{\mathbf{a}}}_{i,j}\left(\omega \right)=\frac{{\mathbf{a}}_{i,j}\left(\omega \right)}{\rho g{L}^k};{\overline{\mathbf{b}}}_{i,j}\left(\omega \right)=\frac{{\mathbf{b}}_{i,j}\left(\omega \right)}{\rho g\omega L^k};\hfill \\ \mathrm{where},\\ k=3\mathrm{for}(i,j=1,2,3)\\ k=4\mathrm{for}(i=1,2,3,j=4,5,6)\mathrm{or}(i=1,2,3,j=4,5,6)\\ k=5\mathrm{for}(i,j=4,5,6)\end{array}$$

(14)

Consider a system with a characteristic length $L=L_0$ and radiation function $H_{r0}\left(j{\omega }_0\right)$, and another system with a characteristic length $L=L_1$ and radiation function $H_{r1}\left(j{\omega }_1\right)$, where ${\omega }_0$ represents the frequency at $L_0$ scale, and ${\omega }_1$ represents the frequency at $L_1$ scale. The radiation function as shown in Equation (5), $H_r\left(j\omega \right)=[j\omega \tilde{\mathbf{a}}\left(\omega \right)+\mathbf{b}\left(\omega \right)]$, for $H_{r0}\left(j{\omega }_0\right)$ and $H_{r1}\left(j{\omega }_1\right)$, can be expressed in terms of the normalized hydrodynamic coefficients shown in Equation (14), such that

$$H_{r0}\left(j{\omega }_0\right)=[j{\overline{\mathbf{a}}}_{i,j}\left({\omega }_0\right)+{\overline{\mathbf{b}}}_{i,j}\left({\omega }_0\right)]{\omega }_0\rho g{L}_0^k;H_{r1}\left(j{\omega }_1\right)=[j{\overline{\mathbf{a}}}_{i,j}\left({\omega }_1\right)+{\overline{\mathbf{b}}}_{i,j}\left({\omega }_1\right)]{\omega }_1\rho g{L}_1^k$$

(15)

Note, Froude-scaling the characteristic length of the system also scales its frequency, such that ${\omega }_1={\omega }_0{\left(\frac{L_1}{L_0}\right)}^{-\frac{1}{2}}$. Then, these radiation functions can be related using the ratio of the two characteristic lengths $L_{sc}=\frac{L_1}{L_0}$, such that

$$H_{r1}\left(j{\omega }_1\right)=H_{r0}\left(j{\omega }_0\right)L_{sc}^{\left(k-\frac{1}{2}\right)}$$

(16)

while all other physical parameters will be scaled using Froude-scaling. Therefore, the estimated transfer functions can be scaled as

$$G_1\left(s\right)=G_0\left(s\right)L_{sc}^{\left(k-\frac{1}{2}\right)}$$

(17)

5. Case Studies

The proposed algorithm is demonstrated using a single cylindrical buoy and a nine-buoy WEC array. The cylindrical WEC buoy represents a prototype that can be tested at a typical wave-tank facility. The incoming waves were set parallel to the $+x$-direction. An axisymmetric body makes for a good candidate for a simpler hydrodynamic analysis. This section compares the accuracy and passivity characteristics of the estimated transfer function’s frequency response function (FRF). Falnes et al. and Folley used the non-dimensionalized hydrodynamic coefficients while discussing the radiation FRF and IRF characteristics [31,38]. The cylindrical WEC discussed here was modeled as a cylinder of radius 1 m and draft 1 m, such that the radius to draft ratio was unity. Therefore, for a cylinder of similar radius-to-draft ratio, the estimated transfer function can be scaled by a factor of $L^{k-\frac{1}{2}}$ if the characteristic length for the cylinder of radius 1 m and draft 1 m is set to unity.

For a single WEC, the estimation process generates a $6\times 6$ transfer function matrix $G\left(s\right)$, whose diagonal elements correspond to self-interacting modes and off-diagonal elements correspond to coupled modes. This work shows the heave mode only, but similar analyses can be carried out for other modes and mode couplings. For the single WEC case, the proposed algorithm is demonstrated using a frequency-domain route and two time-domain routes (see Section 4.1). Henceforth, the estimated transfer function matrix will be denoted by $G_{H_r}\left(s\right)$. The accuracy of the estimated transfer function matrix, $G\left(s\right)$, is demonstrated by comparing its FRF with the radiation function $H_r\left(\omega \right)$ matrix constructed purely with the heave modes and their couplings. The passivity characteristics are quantified using the input passivity index $\nu$, such that $\nu =\frac{1}{2}mi{n}_{\omega }{\lambda }_{min}(G\left(j\omega \right)+G(-j\omega ))$, where ${\lambda }_{min}$ are the minimum eigenvalues of $\left(G\right(j\omega )+G(-j\omega \left)\right)$. The accuracy of the FRF is assessed using the normalized root mean square error (NRMSE) fitness percentage, such that

$$\mathit{NRMSE}(\%)=100\times \left(1-\frac{\left|\right|y-\widehat{y}\left|\right|}{\left|\right|y-\mathit{mean}\left(y\right)\left|\right|}\right),$$

(18)

where y is the validation data, which is the magnitude of the radiation function $H_r\left(j\omega \right)$, while $\widehat{y}$ is the FRF of the $G\left(s\right)$ being assessed.

5.1. A Single WEC

The single WEC was modeled as a cylinder of radius of 1 m and draft of 1 m, such that the radius-to-draft ratio is unity. The algorithm was initiated with $N_0=10$ poles (see Section 4.2 and Figure 2). The higher-order transfer functions had high accuracy but did not satisfy the passivity requirements, while the converse was true for lower-order transfer functions. The final estimated transfer functions had satisfactory accuracy and had a positive input passivity index, $\nu$, for the frequency bandwidth in which radiation damping data from WAMIT were greater than 0.

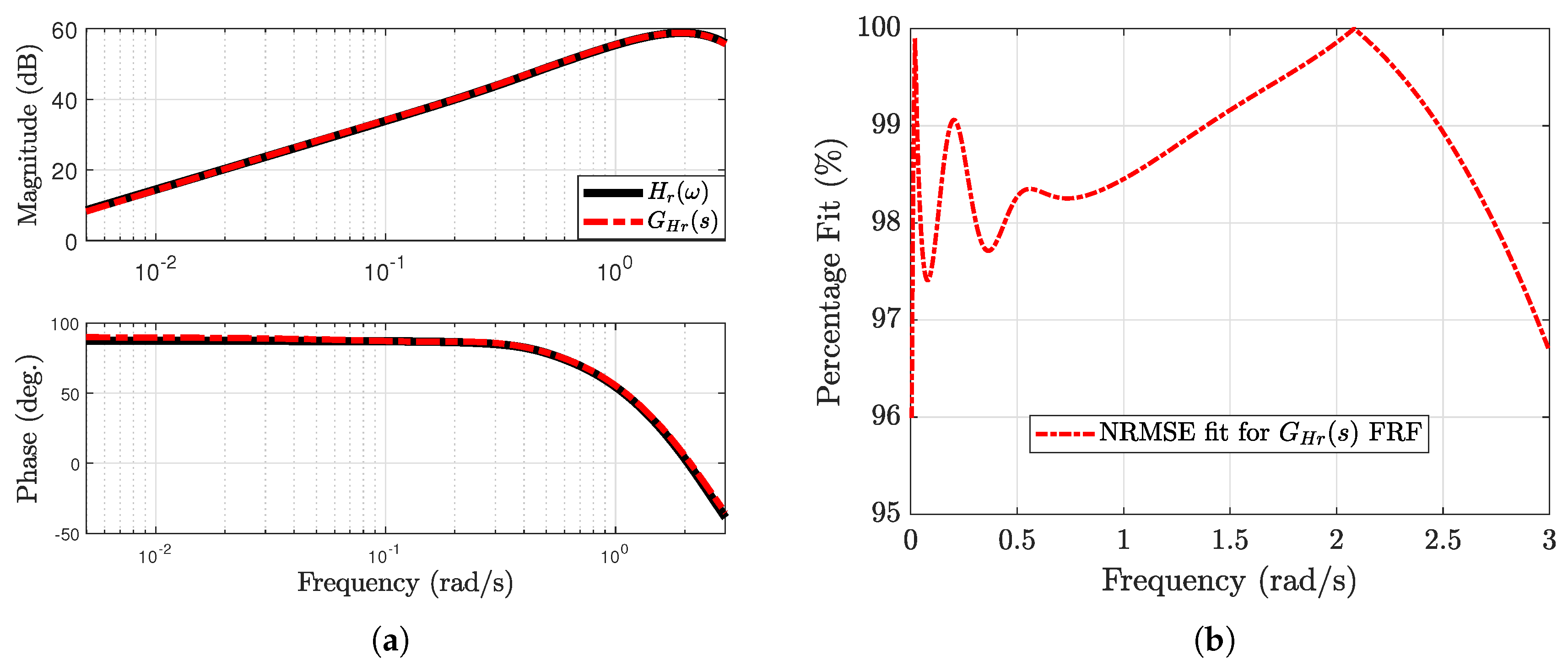
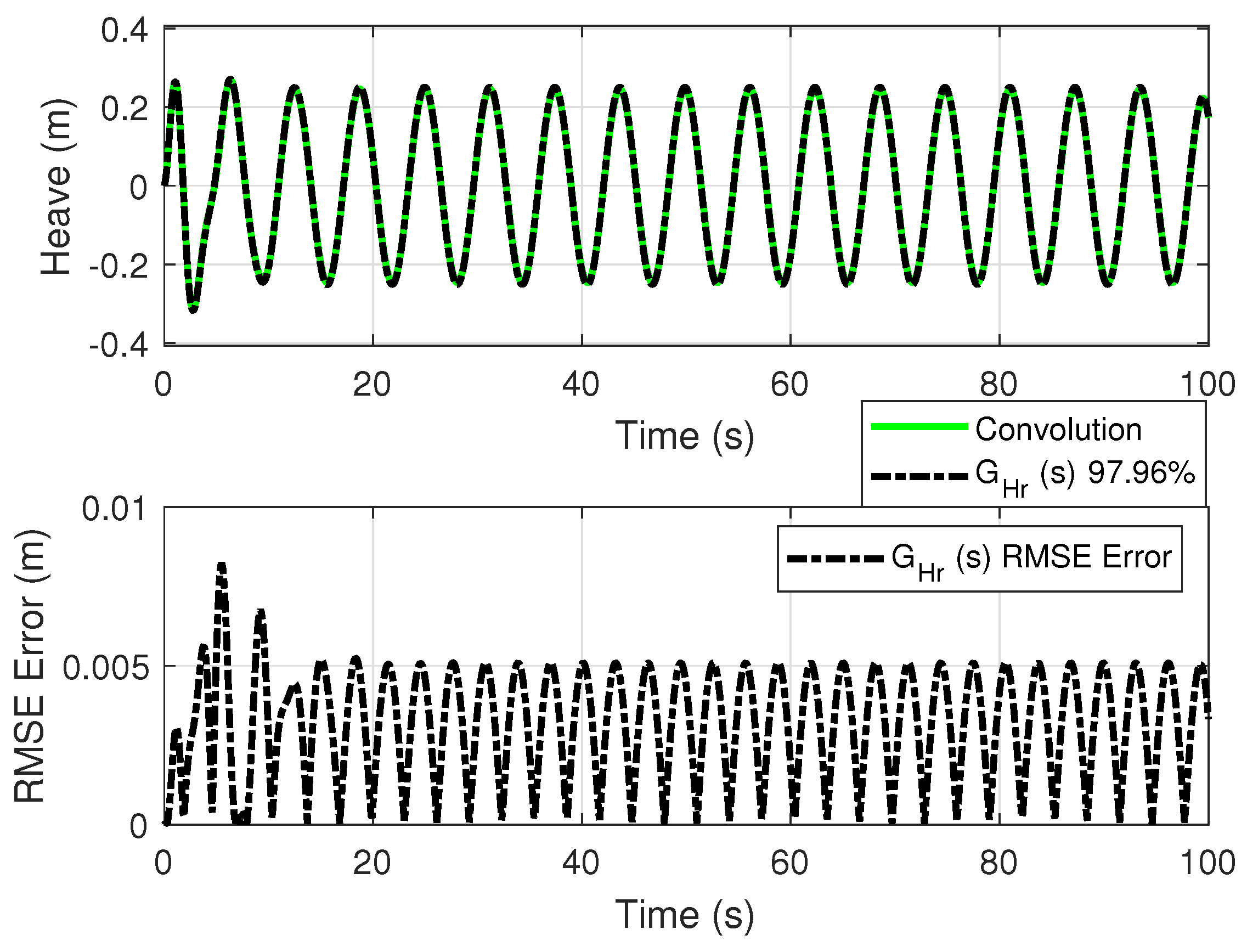
5.1.1. Comparison of Frequency Response of Estimated Transfer Functions

Figure 4 shows the comparison of the frequency response characteristics of $G_{H_r}\left(s\right)$. Notice that the estimated transfer function is minimum-phase. The phase plot shows that the phase for the transfer functions stays between $\pm \pi /2$, which suggests positive realness and passivity. This corresponds to the Nyquist plot being in the right-hand plane for a SISO system. The FRF of the estimated transfer functions is compared to the $H_r\left(\omega \right)$. Also, the estimated transfer function has its phase plot between $\pm \pi /2$$rad$. The NRMSE fit percentage as a function of frequency was calculated by comparing the radiation function $H_r\left(\omega \right)$ and the FRF of $G_{H_r}\left(s\right)$.

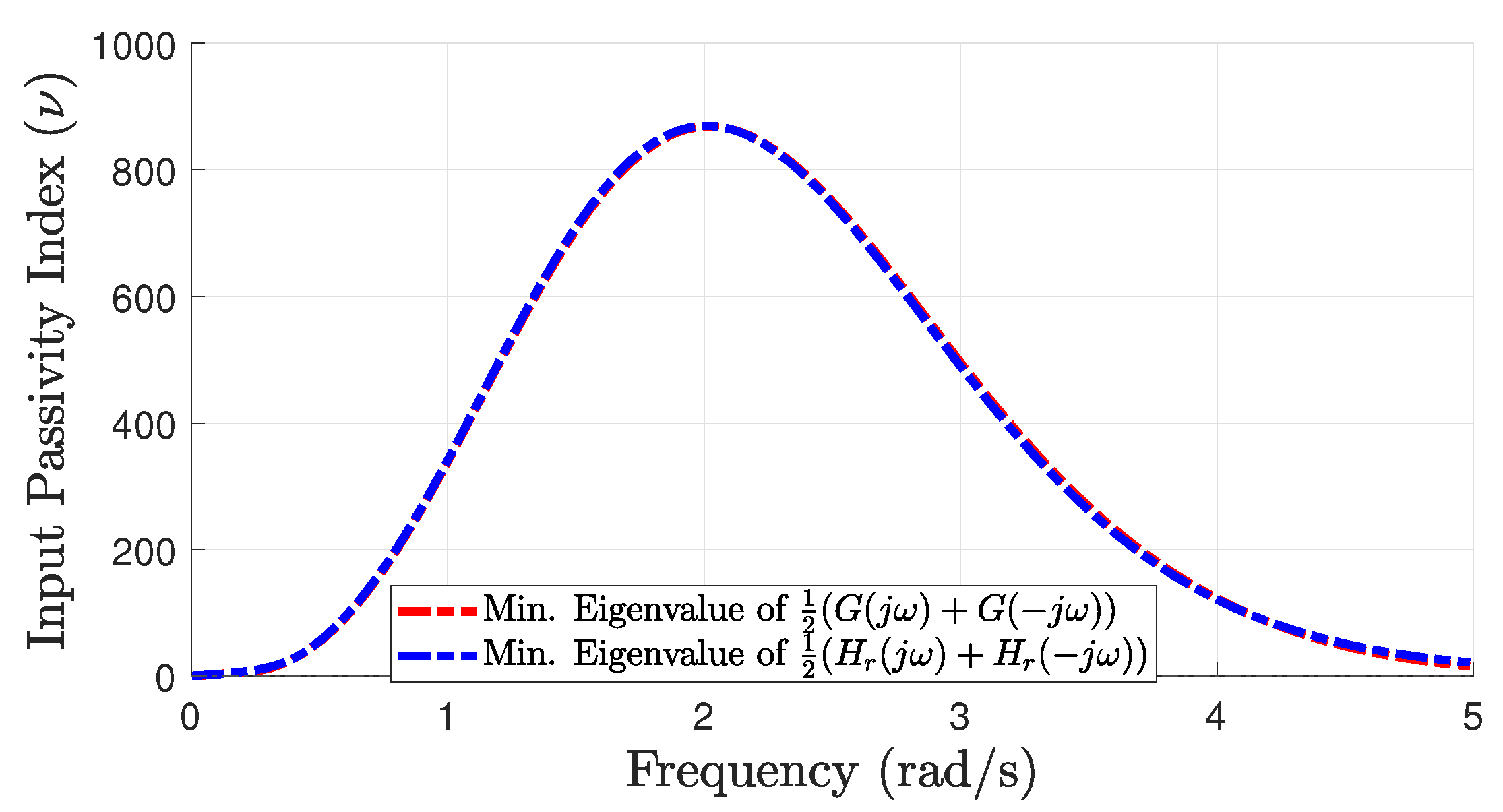
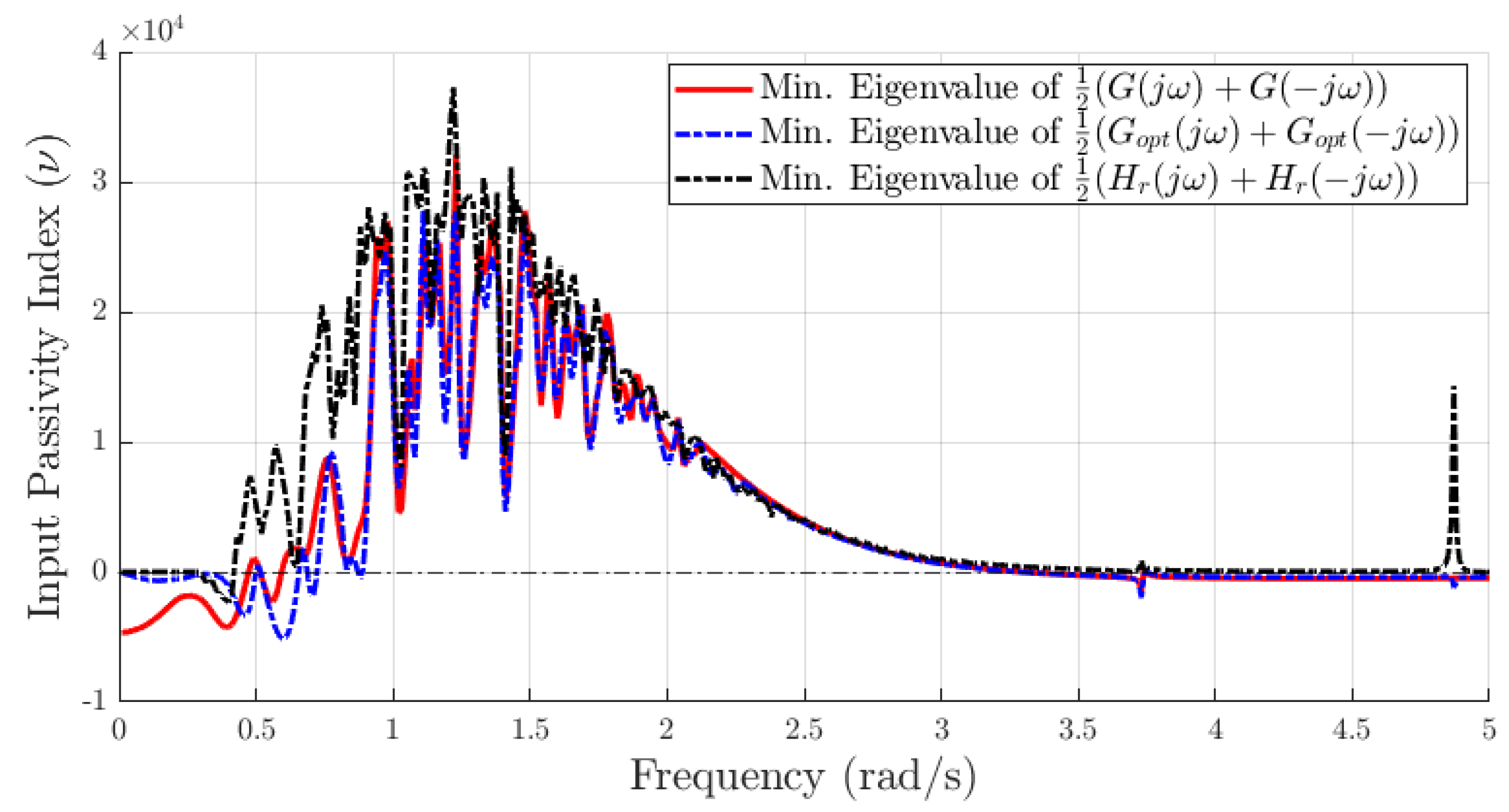
5.1.2. Comparison of Input Passivity Index of Estimated Transfer Functions

Figure 5 shows that the estimated transfer functions have a positive input passivity index between 0 and 5 rad/s. Therefore, the estimated transfer functions will have passivity for the frequency bandwidths where $\nu$ is positive. Since this work is only using the heave mode, the transfer function system is a single transfer function corresponding to that mode, and therefore, the input passivity index reduces to the FRF of the corresponding estimated $G\left(s\right)$. In other words, $\nu =\frac{1}{2}mi{n}_{\omega }{\lambda }_{min}(G\left(j\omega \right)+G(-j\omega ))=\frac{1}{2}\left(2G\left(j\omega \right)\right)$ for SISO LTI systems. Note that for multi-mode analyses such as MDOFs systems or multibody systems, the transfer function system will be a MIMO transfer function matrix and, therefore, will not reduce to $G\left(s\right)$. As discussed in Section 3, stability analyses can also be performed using the Nyquist criterion; however, it is limited to SISO systems. As described in Section 4, the final optimization routine ensured that the estimated transfer function had a positive input passivity index in the operational bandwidth, had high accuracy with respect to the corresponding radiation function, and had a zero at the origin (see Table 1). The input passivity index analyses shown here make the stability analyses simpler, especially for MDOFs and multibody systems, as shown in the following subsection.

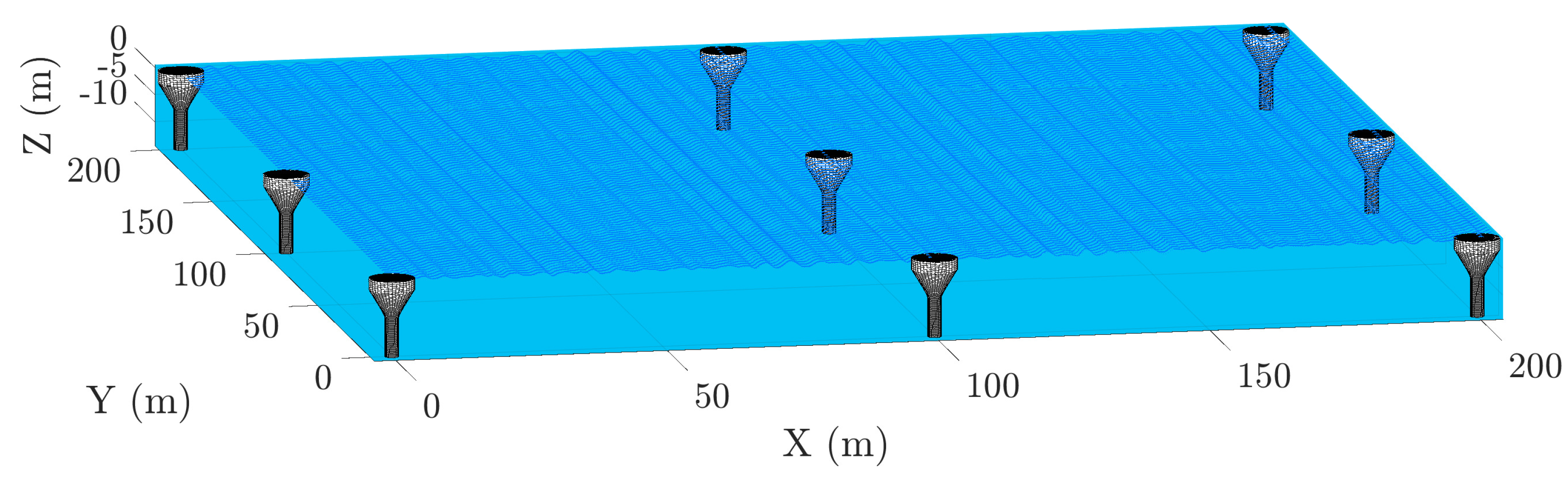
5.2. A Homogeneous WEC Array of CorPower Devices

The algorithm will now be demonstrated using a homogeneous array comprised of nine CorPower devices laid out in a square array of three rows and three columns (see Figure 6). The CorPower is a heaving point absorber device being developed by the Swedish company CorPower Ocean and its device specifications can be found at [39]. The device can be described as a combination of three shapes: a cylinder of diameter $8.4$ m and height $4.6$ m over an inverted-truncated cone with top radius $8.4$ m, bottom radius $1.25$ m, and height $5.08$ m. The third and bottom-most part of the device extends as a cylinder of radius $1.25$ m for a length of $7.32$ m. The draft of the device is $14.5$ m.

This homogeneous WEC array was designed to represent a realistic deployable compact array. The distance between any two neighboring bodies was 100 m along the $X\mathrm{and}Y$ directions. The hydrodynamics were calculated assuming plane-progressive waves propagating along the positive X-axis. Figure 6 shows the homogeneous WEC array’s spatial layout. For a WEC array, the self-interacting modes and their mutual couplings result in a $6N\times 6N$ radiation function matrix (where $N=9$ for the current array). For this work, only the heave modes and their mutual couplings are considered, such that the radiation function matrix was an $N\times N$ matrix.

5.3. Passivity Index, $\nu$, for the Homogeneous WEC Array

The WECs in the homogeneous array had a much higher volume (16 times that of the cylinder in the previous case), and the WECs in the array interacted with each other such that the motion of one WEC affected another due to hydrodynamic coupling. The multiple peaks in the passivity index of the homogeneous array in Figure 7 indicate hydrodynamic couplings in the system.

It can be observed in Figure 7 that the optimized transfer function matrix represented by $G_{opt}\left(s\right)$ shows an increase in the input passivity index, especially at lower frequencies. The optimization also ensured that the phase at 0 rad/s was ${90}^{\circ }$ for all transfer functions in the transfer function matrix. Note, a phase of ${90}^{\circ }$ at 0 rad/s indicates a zero at the origin. All estimated transfer functions matched with the corresponding reference radiation function by more than 90 % in terms of NRMSE error defined in the previous case. The asymptotic convergence to zero indicates that the estimated transfer function matrix represents a dissipative system. The input passivity index characteristics shown can be used to inform WEC array design and optimize a control strategy that can maximize the energy extracted. The properties mentioned in Table 1 were, therefore, achieved by the proposed system identification algorithm.

6. Motion Simulations

A motion simulation model was created based on the Cummins equation discussed in Section 2. Only the heave mode is presented here, such that the generalized motion coordinates $\overrightarrow{q}\left(t\right)$ can be replaced by heave displacements, $\overrightarrow{x}\left(t\right)$. Also, the generalized external forces $\overrightarrow{Q}\left(t\right)$ can be replaced by the excitation force, ${\overrightarrow{F}}_{exc}\left(t\right)$, and control force, ${\overrightarrow{F}}_c\left(t\right)$.

Rewriting the Cummins Equation (1) gives

$$\overrightarrow{\ddot{x}}\left(t\right)=\frac{1}{\mathbf{M}+{\mathbf{a}}_{\infty }}\left[{\overrightarrow{F}}_{exc}\left(t\right)+{\overrightarrow{F}}_c\left(t\right)-{\overrightarrow{F}}_R\left(t\right)-\mathbf{K}\overrightarrow{x}\left(t\right)\right]$$

(19)

The incoming wave elevation profile was calculated using the Pierson–Moskowitz (PM) spectrum, that uses an energy distribution as a function of frequency [40]. It is defined as [23,40]

$$S_{PM}\left(f\right)=\frac{{H_{m0}}^2}{4}{\left(1.057f_p\right)}^4{f}^{-5}exp\left[-\frac{5}{4}{\left(\frac{f_p}{f}\right)}^4\right]$$

(20)

whose coefficients in general form are

$$\begin{array}{cc}\hfill A_{ws}& =\frac{{H_{m0}}^2}{4}{\left(1.057f_p\right)}^4\approx \frac{5}{16}{H_{m0}}^2{f_p}^4\approx \frac{B_{ws}}{4}{H_{m0}}^2\hfill \\ \hfill B_{ws}& ={\left(1.057f_p\right)}^4\approx \frac{5}{4}{f_p}^4\hfill \end{array}$$

(21)

where $H_{m0}$ is the significant wave height, $f_p$ is the peak wave frequency (=1/$T_p$), and f is the wave frequency, while the coefficients $A_{ws}$ and $B_{ws}$ vary depending on the wave spectrum, which in this case, define the spectrum to represent the Pierson–Moskowitz (PM) spectrum.

In recent years, WEC motion simulations have been increasingly modeled using WEC-Sim, an open-source MATLAB Simulink based simulation software [23]. WEC-Sim uses customized Simulink blocks and the multi-physics capabilities of the Simscape. In the results that follow, the motion simulations were verified against a WEC-Sim model that used the convolution integral to calculate the radiation forces.

6.1. The Single-Cylinder Case

The dynamics equation shown in (19) is used to simulate the complete dynamics model in the time domain. The complete dynamics model was set up in MATLAB-Simulink. The hydrodynamic coefficients were calculated for a water depth of 100 m. The excitation force was calculated offline prior to the simulations. The cylinder was approached by a regular wave of amplitude $0.25$ m and wave period $6.22$ s. For these motion simulations, no control force was applied, and the cylindrical body only experienced the excitation force as an input.

Figure 8 shows the heave motion characteristics for a time period of 100 s. The simulation was first run with the radiation force calculated using direct convolution and then by using the estimated transfer functions. These body-motion simulations were performed in Simulink.

The simulations were run for only the heave mode but can be easily run for any other mode or mode combination, using the appropriate estimated transfer function matrices. Figure 8 shows the heave motion for a single regular wave. The models can be easily used for irregular waves if the excitation force inputs can be calculated in advance.

Note that in Figure 8, at the beginning of the time history, the motion simulation shows some fluctuating behavior. The transient behavior seen at the start of the top figures in Figure 8 is physical and not numerical. It is the result of the buoys being released from rest at $t=0$, while the fluctuating behavior seen at the start of the bottom figure in Figure 8 is numerical. This fluctuating behavior can be mitigated by using a $ramp$ function, as is performed in the WEC simulator package WEC-Sim [23]. However, such pre-processing or truncation was not used here to show the initial transient behavior. The overall NRMSE matches for all estimated transfer functions and the agreement approaches 99% if the initial 40 s of the data is truncated. Note that the dynamics model shown here used a linearized model, but the analyses shown here can be easily adapted for a model that uses non-linear Froude–Krylov forces as the external forces acting on the body.

6.2. The Homogeneous WEC Array Case

A transfer function matrix $G\left(s\right)$ was formed using the body-only heave modes and the inter-body heave mode couplings. The dynamics equation of motion in (19) was used to simulate the complete dynamics model in the time-domain using MATLAB-Simulink. The excitation force was calculated offline to the simulation. Figure 9 shows the heave motion characteristics such that the simulation was first run by calculating the radiation force using real-time convolution and then run again by calculating the radiation force using the estimated transfer function matrix. These simulations were run for only the heave mode but can be easily run for any other mode or mode combination, using the appropriate estimated transfer function matrices.

The percentages shown in Figure 9 are the NRMSE fit percentage between the body motion when the radiation force is calculated using the estimated transfer function arrays, compared to the body motion when the radiation force is calculated using the convolution of radiation IRF, $h_r\left(t\right)$, and body velocity. As discussed for the single-cylinder case, an initial transient in the time histories for the WEC array buoys was observed. For this case, a ramp function was used to mitigate this initial transient. The accuracy percentages in Figure 9 show the comparison between 10 s and 50 s. Note that the WEC array modeled here did not incorporate the contributions of non-heave modes to heave time histories due to hydrodynamic coupling. A more realistic WEC array model would include the contributions of the support structure and moorings that would maintain the WEC array layout. This would further introduce forces and couplings of the dynamics modes of WEC buoys.

7. Discussion

The frequency domain was used to estimate transfer functions between body velocity and radiation forces. Frequency-domain estimation methods are the most direct route to generate the desired time-domain models. Marine systems operate at relatively low-frequency bandwidths. For instance, JONSWAP and Bretschneider wave spectra have most of their energy concentrated between 0 and $1.5$ rad/s [1,2,31]. Due to the relatively slow nature of marine dynamics and very narrow bandwidth of marine systems, the FRF of a marine system encapsulates critical information about the said marine system’s dynamics at each data point in the FRF. Direct estimation methods, like the frequency-domain estimation method shown here, can reduce the potential numerical artifacts that multi-stage time-domain estimation methods may have due to truncation and round-off errors. The proposed algorithm can achieve highly accurate transfer functions using the direct estimation or frequency-domain route despite its sensitivity, while having a positive input passivity index across most of the operational bandwidth.

As discussed in Section 4.2, the proposed algorithm tries to strike a balance between the accuracy of the estimated transfer function and its passivity characteristics by iterating upon the order of the estimated transfer function system. Empirically, increasing the order of the estimated transfer function system increases its accuracy while decreasing its passivity and vice versa.

The estimated models were assessed based on two metrics; firstly, how well the estimated models replicated the FRF of the radiation functions, and secondly, how well was the body motion replicated when the radiation force was calculated using the estimated models as opposed to calculating the radiation force using the convolution approach. Significantly, the estimated LTI systems presented here did not have high-frequency poles, despite being high-order systems. Low-order estimation methods compromise the fidelity of fit in favor of stability and robustness, resulting in underfitting, as was the case in [4,24]. Conversely, high-order estimation methods compromise guaranteeing stability and robustness because they have poles faster than the physical system’s properties due to overfitting [4,24]. The proposed estimation algorithm succeeded in preventing underfitting and overfitting while guaranteeing Hurwitz stability and ensuring passivity. Although Taghipour et al. observed that the body motions tend to be less sensitive to the otherwise sensitive LTI system estimation process [4], an effective and optimal motion-control design requires that the model-based controller be based on the physical phenomenon’s most accurate representation. Therefore, sacrificing accuracy in favor of passivity should be assessed based on the particular case being considered.

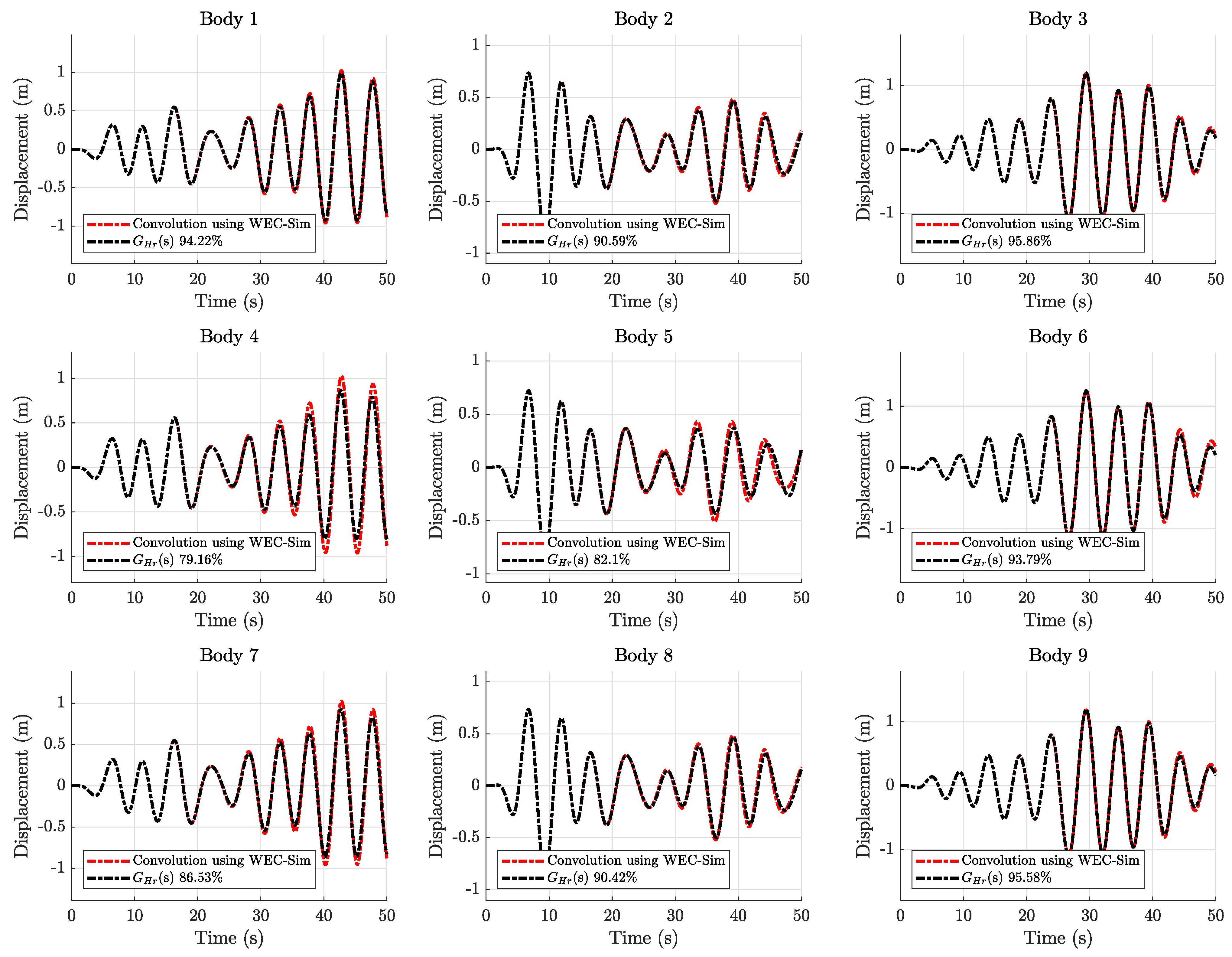
The case studies that are shown here demonstrate that the proposed algorithm can model accurate and stable motion-dynamics models of MDOFs marine systems with various degrees of hydrodynamic coupling. The off-diagonal terms representing the coupled modes of the radiation function are highly oscillating but have relatively low magnitudes. These terms were modeled with relatively higher-order transfer functions due to the sensitivity of the coupled modes. Their low magnitude and highly oscillatory behavior make the transfer function estimation more challenging. It could be argued that the low magnitude and highly oscillatory behavior of these terms is non-physical and due to numerical issues in the calculation of the hydrodynamic coefficients corresponding to the inter-body hydrodynamic couplings.

The motion time histories from the models using the convolution-based radiation forces were used as the reference for the time-domain performance of the models using the estimated transfer function array to calculate the radiation force. Ultimately, the body motion characteristics should replicate the motion characteristics calculated using Cummins’ equation. As shown in Section 6, all cases resulted in very accurate motion characteristics while staying stable. A numerically stable time-domain model that can be analyzed in the Laplace domain using the estimated LTI systems can eventually be used to investigate the multibody dynamics of more complicated models with the necessary control.

8. Conclusions

The real-time convolution operation needed to calculate radiation forces can be circumvented using estimated LTI systems. Motion control of floating marine structures requires the Cummins equation to be modified such that the radiation force is calculated using an LTI system. This work presents an algorithm to calculate radiation forces experienced by floating marine structures using an LTI system. The proposed algorithm enforces the stability of the complete dynamics model by ensuring the passivity of the estimated LTI system. The passivity of estimated transfer functions and the complete dynamics model is assessed using the input passivity index. The passivity-based proposed algorithm facilitates motion control analyses of floating marine structures. The passivity criteria are more stringent than mere gain margin criteria by ensuring the stability of the complete dynamic models. Also, the passivity-based approach, unlike the Nyquist-plot-based approach, can be extended to MDOFs systems with multiple modes and bodies. The modeling architecture presented here can serve as a base dynamics model for marine hydrokinetics simulations. Such a base model can then integrate and compute control forces for a model-based controller deployed on sea-worthy devices.

Although closely related, both stability and hydrodynamic couplings can be characterized using the passivity index. Not only does the passivity index ensure numerical stability, but it also indicates the degree of stability quantified as the input passivity index. Motion simulations further confirmed that the estimated transfer function array could replace the convolution operation for MDOFs floating marine structures. Further work on passivity-based control can be explored. The passivity-based time-domain methods presented here can help develop a robust model-based framework for motion control and establishment of marine energy grids, especially for power management and power control. For the hydrodynamically coupled MDOFs systems, the input passivity index is an important criterion for model robustness and can be a crucial design parameter guiding the WEC array layout design, motion modeling, and control.