Piecewise Linear Power Flow Algorithm of DC Distribution Networks Considering Automatic Adjustment of VSC Control Strategy
Abstract
:1. Introduction
- The critical point of the VSC hitting the capacity limit can be directly determined through one linear calculation according to the VSC power balance. Compared with the bisection algorithm, the proposed PLPF algorithm has the same computational accuracy and less calculation time;
- The proposed PLPF algorithm is more straightforward and effective for the situation with multiple overloaded VSCs.
2. Linear Power Flow Model
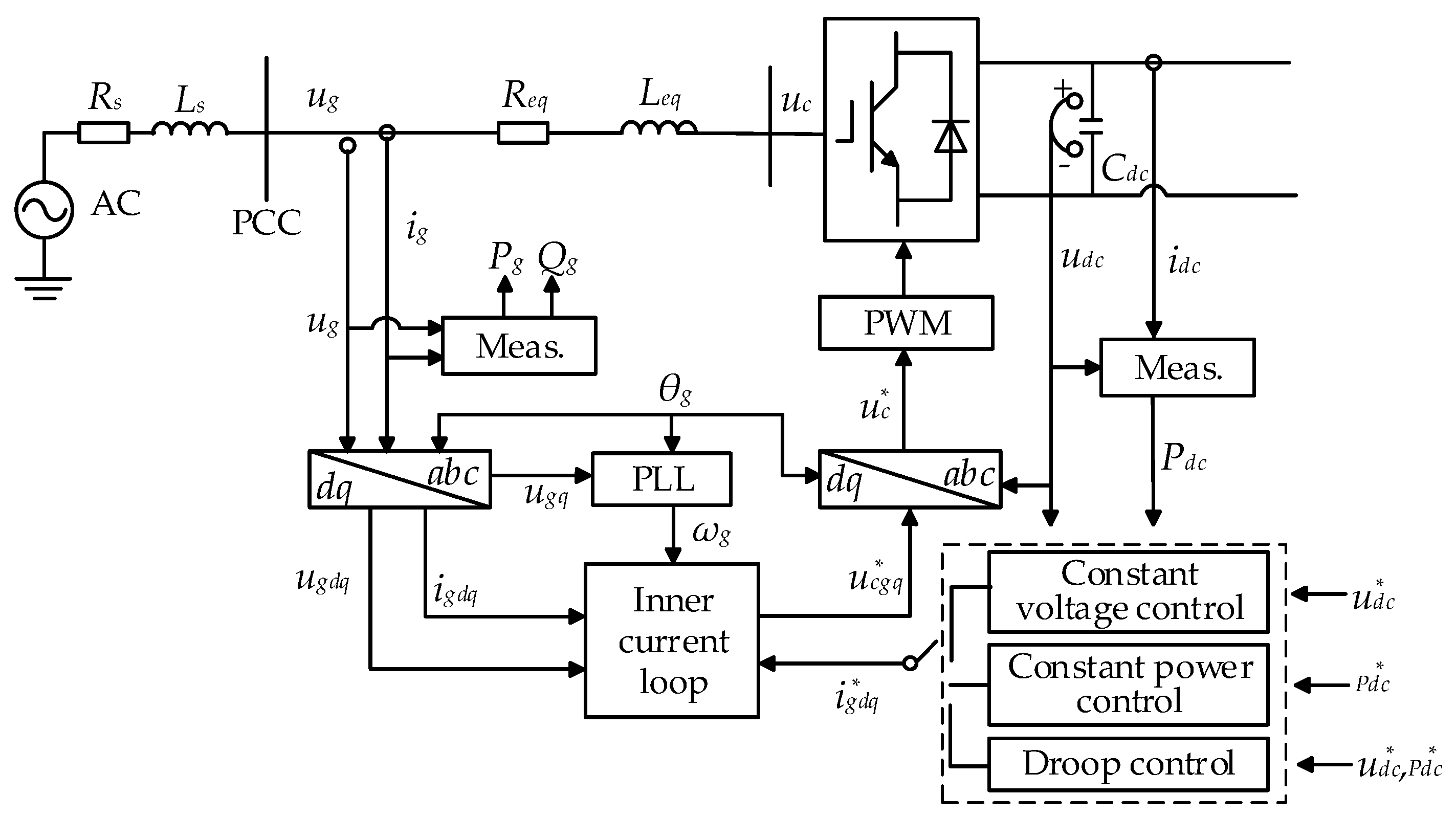
2.1. Control Strategies of DCDNs
2.2. Generalized Power Flow Model for VSC with Different Control Strategies
2.3. Linear Power Flow Model for Nodal Voltages
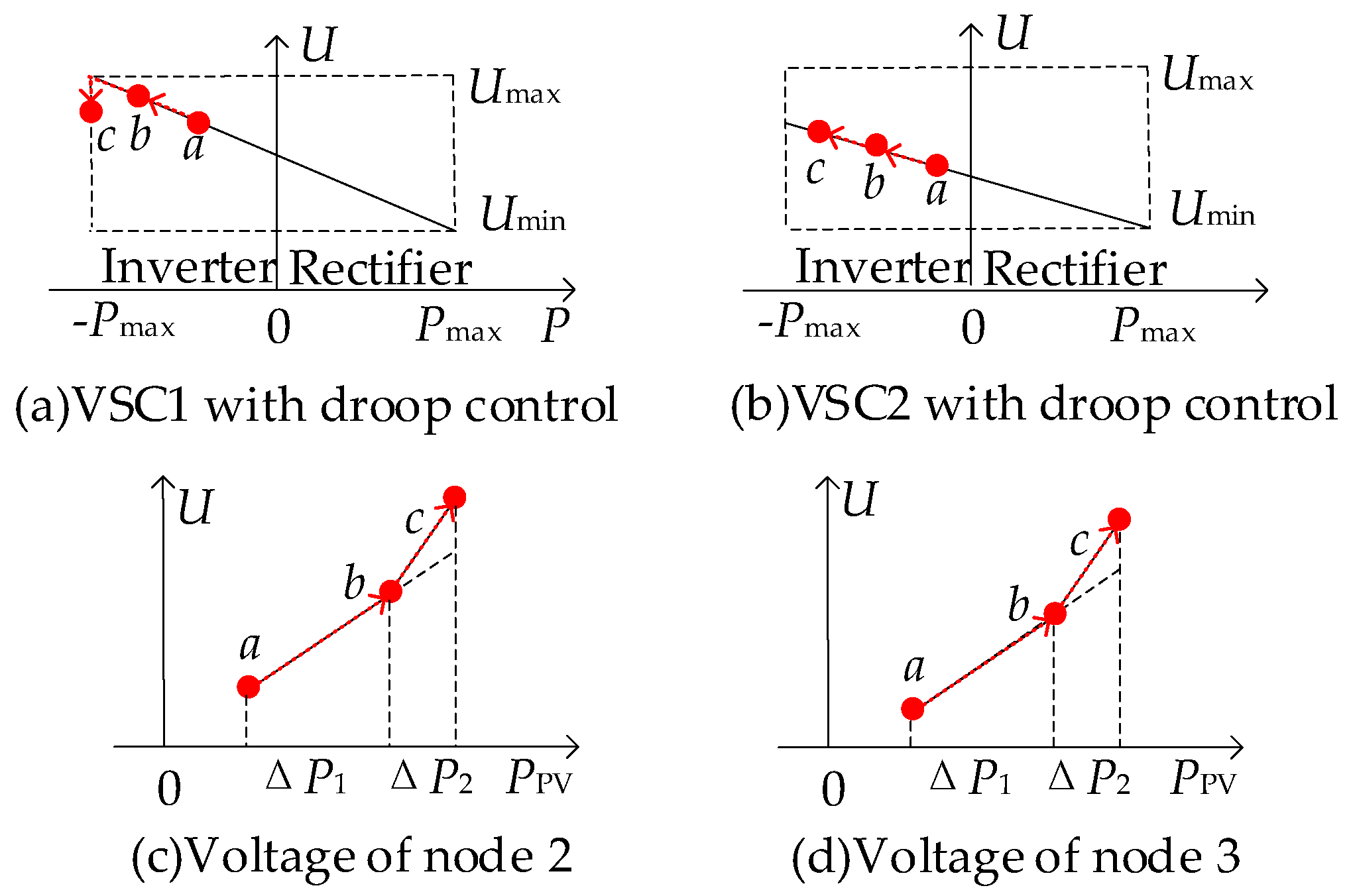
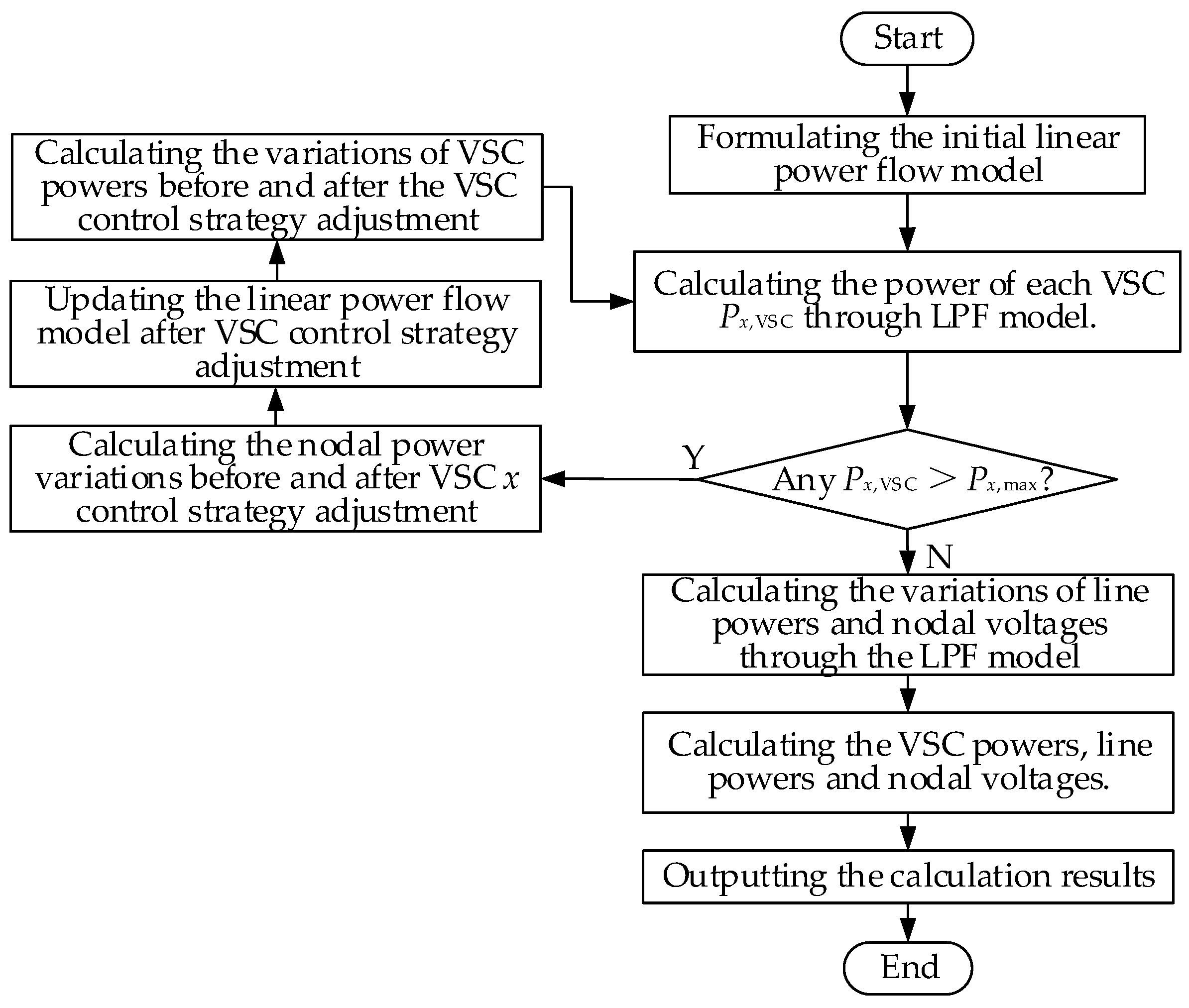
3. Piecewise Linear Power Flow Model to Represent the VSC Control Strategy Adjustment
3.1. Power Flow Analysis Considering VSC Control Strategy Adjustment
3.2. Piecewise Linear Power Flow Model
3.3. Multiple Overloaded Converters
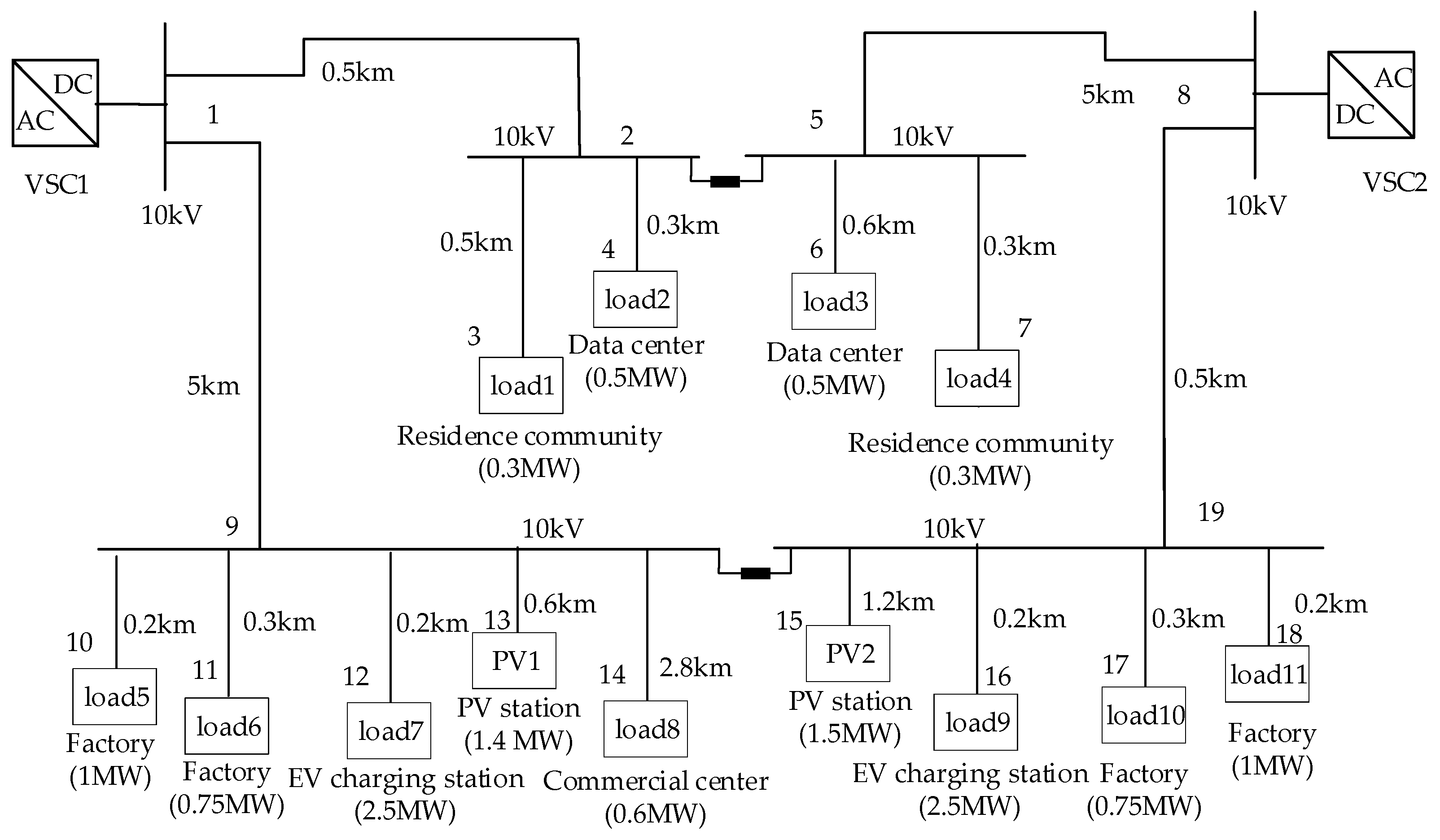
4. Numerical Examples
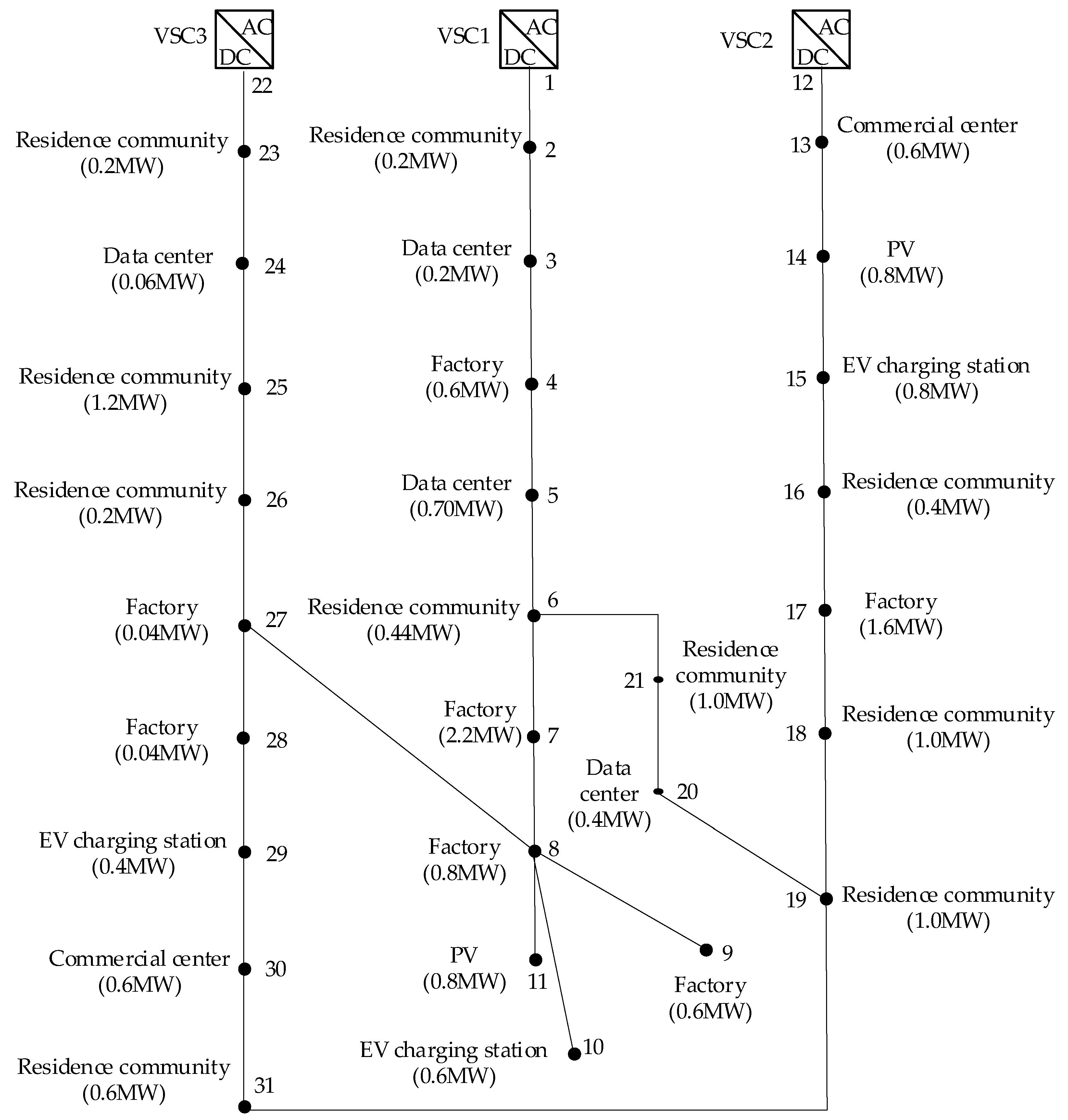
4.1. Test System 1
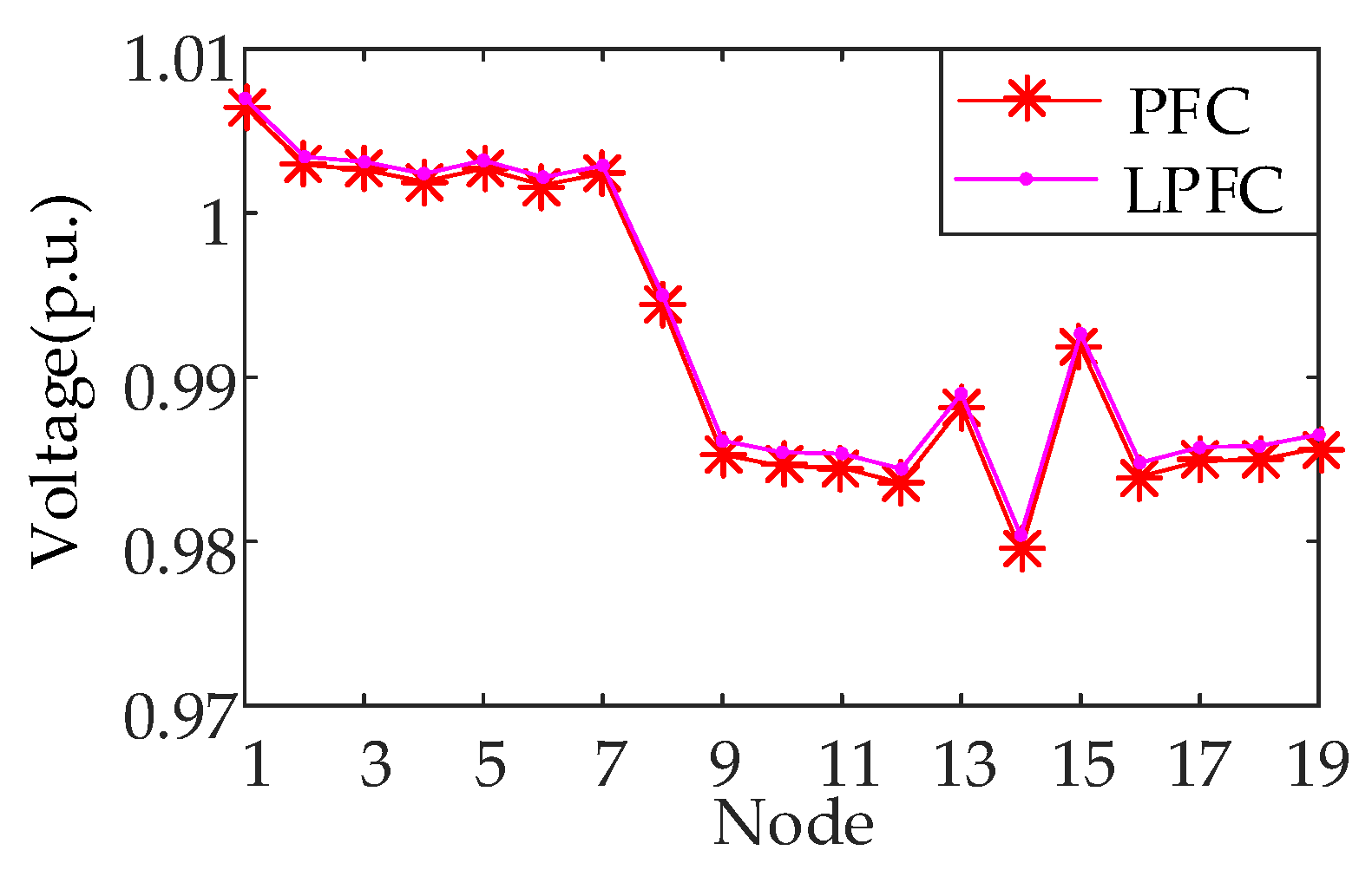
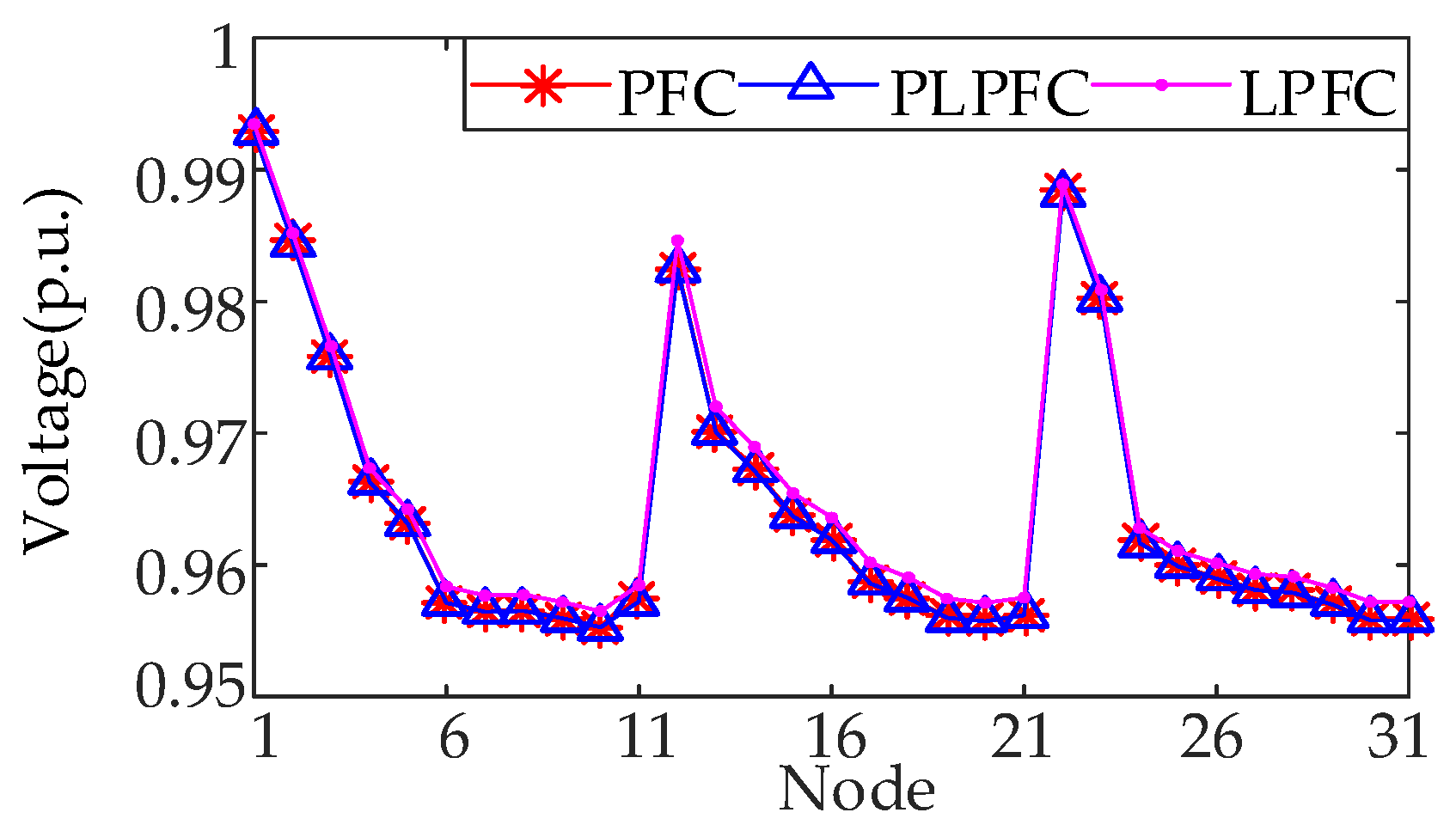
4.2. Accuracy Test of the Improved LPF Model
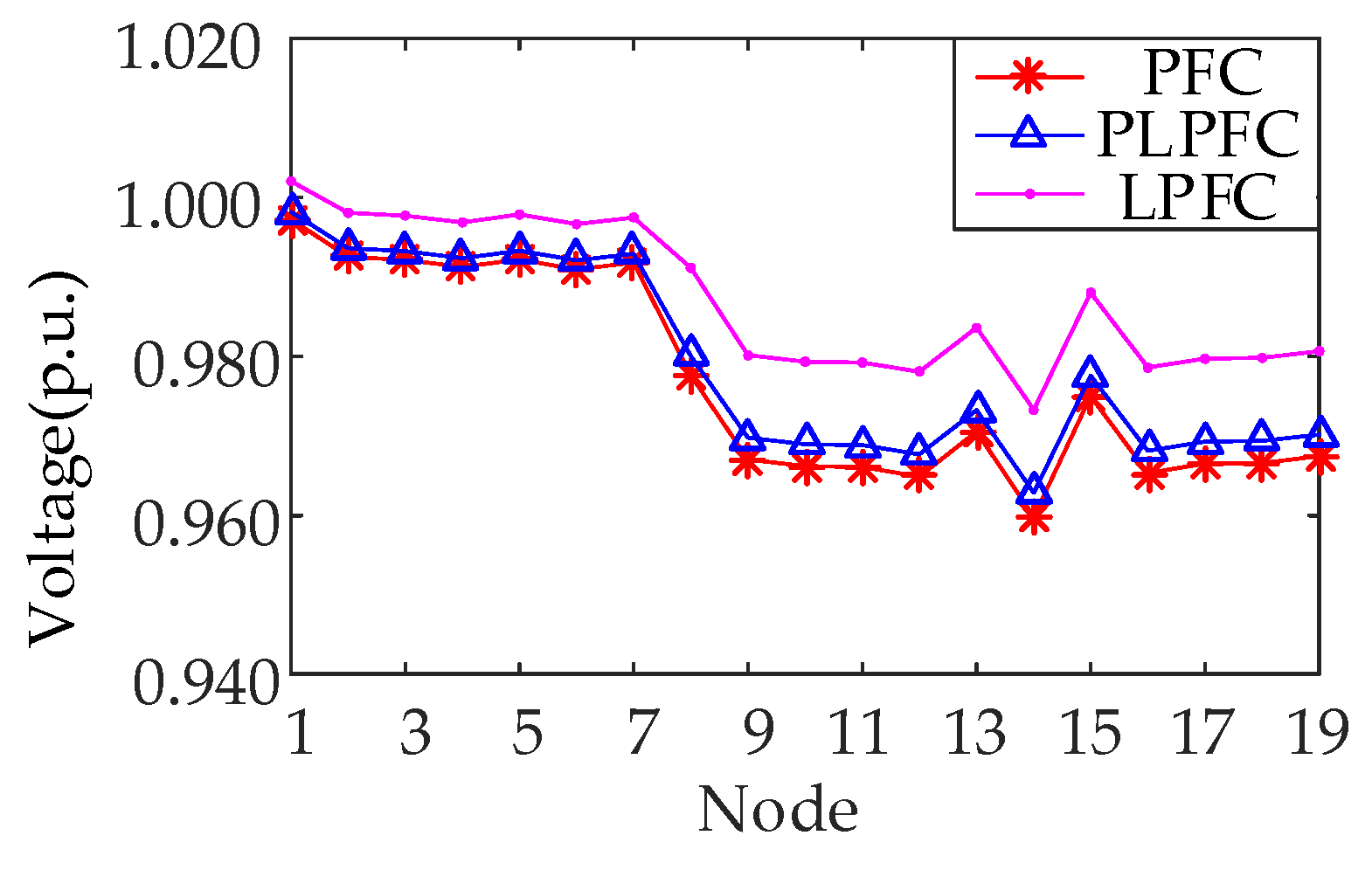
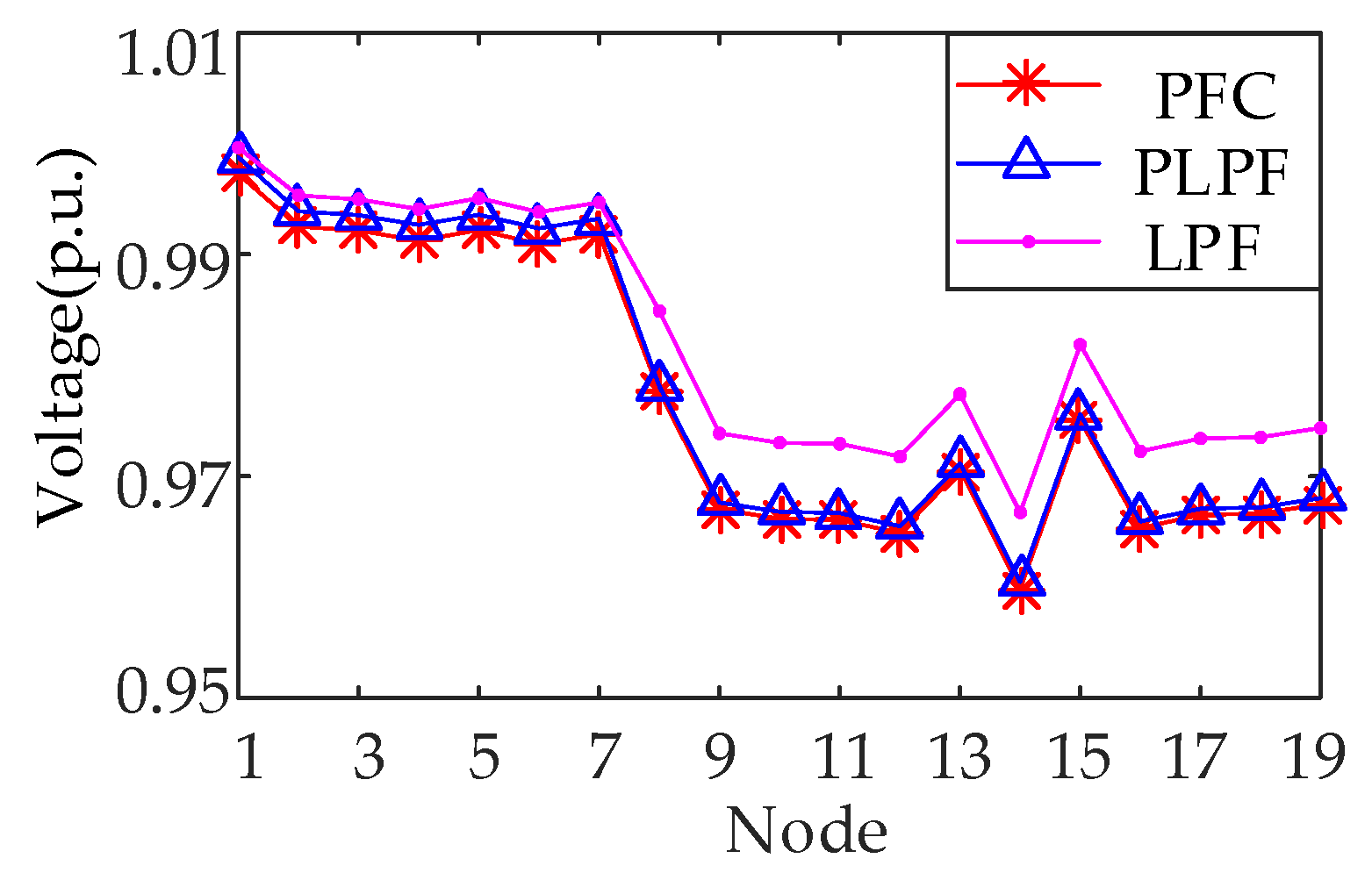
4.3. Test System 2
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Un,ref | Reference voltage of the VSC at node n | W | Sensitivity matrix of nodal injection power to VSC power |
| Pn,ref | Reference power of the VSC at node n | Px,ini | Initial power of the VSC at node x |
| kn | Droop coefficient of the VSC at node n | ΔPx | VSC power variation in the VSC at node x |
| Pi,PV | PV output power of node i | ΔPi | Nodal power variation at node i |
| Pi,L | Load power of node i | Wi,x | Sensitivity of power variation at node i to the VSC power at node x |
| gij | Admittance of the line from node i to node j | Ti,l | Sensitivity of transmission power of line l to nodal injection power at node i |
| Ui | Voltage of node i | Si,j | Sensitivity of voltage of node j to nodal injection power at node i |
| ML | Set of load nodes | α | Proportion of the power variation before the VSC control strategy adjustment |
| MD | Set of droop nodes | Px,max | Capacity of the VSC at node x |
| S | Nodal voltage sensitivity matrix | Pl,ini | Initial power of line l |
| ΔP | Change in nodal injection power | Uj,ini | Initial voltage of node j |
| ΔU | Change in nodal injection power | Wi,x,s2 | Sensitivity of transmission power of VSC x to nodal injection power at node i after VSC control strategy change |
| ΔPL | Change in line power | Ti,l,s2 | Sensitivity of transmission power of line l to nodal injection power at node i after VSC control strategy change |
| T | Sensitivity matrix of nodal injection power to line transmission power | Si,j,s2 | Sensitivity of voltage of node j to nodal injection power at node i after VSC control strategy change |
| G | Derivative of voltage with respect to line power | β | Proportion of the power variation before the VSC at node y control strategy adjustment |
| Si,j,s3 | Sensitivity of voltage of node j to nodal injection power at node i after the VSC control strategy is changed | Px,max | Capacity of the VSC at node x |
| VSC | Voltage source converter | PV | Photovoltaic |
| DCDN | DC distribution network | EV | Electric vehicle |
| PLPF | Piecewise linear power flow | PFC | Power flow calculation |
| HVDC | High-voltage direct current |
Appendix A
| Head Node | End Node | Line Resistance (Ω) | Head Node | End Node | Line Resistance (Ω) |
|---|---|---|---|---|---|
| 1 | 2 | 0.1708 | 9 | 12 | 0.0683 |
| 2 | 3 | 0.1025 | 9 | 13 | 0.2050 |
| 2 | 4 | 0.2050 | 9 | 14 | 0.9567 |
| 2 | 5 | 0.0170 | 9 | 15 | 0.0170 |
| 5 | 6 | 0.2050 | 19 | 15 | 0.4100 |
| 5 | 7 | 0.1025 | 19 | 16 | 0.0683 |
| 5 | 8 | 1.7080 | 19 | 17 | 0.1025 |
| 1 | 9 | 1.7080 | 19 | 18 | 0.0683 |
| 9 | 10 | 0.0680 | 19 | 8 | 0.1708 |
| 9 | 11 | 0.1025 |
| Head Node | End Node | Line Resistance (Ω) | Head Node | End Node | Line Resistance (Ω) |
|---|---|---|---|---|---|
| 1 | 2 | 0.1944 | 17 | 18 | 0.0786 |
| 2 | 3 | 0.2096 | 18 | 19 | 0.0393 |
| 3 | 4 | 0.2358 | 19 | 20 | 0.0786 |
| 4 | 5 | 0.0917 | 20 | 21 | 0.0524 |
| 5 | 6 | 0.2096 | 22 | 23 | 0.2268 |
| 6 | 7 | 0.0393 | 24 | 25 | 0.5371 |
| 7 | 8 | 0.0405 | 25 | 26 | 0.0524 |
| 8 | 9 | 0.1048 | 26 | 27 | 0.0405 |
| 8 | 10 | 0.2358 | 27 | 28 | 0.0393 |
| 8 | 11 | 0.1048 | 28 | 29 | 0.0262 |
| 12 | 13 | 0.2430 | 29 | 30 | 0.1048 |
| 13 | 14 | 0.0655 | 30 | 31 | 0.2358 |
| 14 | 15 | 0.0655 | 6 | 21 | 0.1310 |
| 15 | 16 | 0.0655 | 19 | 31 | 0.0393 |
| 16 | 17 | 0.0393 | 8 | 27 | 0.1310 |
References
- Nami, A.; Rodriguez-Amenedo, J.L.; Arnaltes, S.; Cardiel-Álvarez, M.Á.; Baraciarte, R.A. Control of the parallel operation of DR-HVDC and VSC-HVDC for offshore wind power transmission. IEEE Trans. Power Deliv. 2022, 37, 1682–1691. [Google Scholar] [CrossRef]
- Gomis-Bellmunt, O.; Sau-Bassols, J.; Prieto-Araujo, E.; Cheah-Mane, M. Flexible converters for meshed HVDC grids: From flexible AC transmission systems (FACTS) to flexible DC grids. IEEE Trans. Power Deliv. 2020, 35, 2–15. [Google Scholar] [CrossRef]
- Obradović, D.; Oluić, M.; Eriksson, R.; Ghandhari, M. Supplementary power control of an HVDC system and its impact on electromechanical dynamics. IEEE Trans. Power Syst. 2021, 36, 4599–4610. [Google Scholar] [CrossRef]
- Li, X.; Li, Z.; Zhao, B.; Lu, C.; Song, Q.; Zhou, Y.; Rao, H.; Xu, S.; Zhu, Z. HVDC reactor reduction method based on virtual reactor fault current limiting control of MMC. IEEE Trans. Ind. Electron. 2020, 67, 9991–10000. [Google Scholar] [CrossRef]
- Tang, G.; He, Z.; Pang, H.; Huang, X.; Zhang, X.-P. Basic topology and key devices of the five-terminal DC grid. CSEE J. Power Energy Syst. 2015, 1, 22–35. [Google Scholar] [CrossRef]
- Yang, R.; Shi, G.; Cai, X.; Zhang, C.; Li, G.; Liang, J. Autonomous synchronizing and frequency response control of multi-terminal DC systems with wind farm integration. IEEE Trans. Sustain. Energy 2020, 11, 2504–2514. [Google Scholar] [CrossRef]
- Chai, Y.; Guo, L.; Wang, C.; Zhao, Z.; Du, X.; Pan, J. Network partition and voltage coordination control for distribution networks with high penetration of distributed PV units. IEEE Trans. Power Syst. 2018, 33, 3396–3407. [Google Scholar] [CrossRef]
- Zhang, L.; Liang, J.; Tang, W.; Li, G.; Cai, Y.; Sheng, W. Converting AC distribution lines to DC to increase transfer capacities and DG penetration. IEEE Trans. Smart Grid 2019, 10, 1477–1487. [Google Scholar] [CrossRef]
- Dastgeer, F.; Gelani, H.E.; Anees, H.M.; Paracha, Z.J.; Kalam, A. Analyses of efficiency/energy-savings of DC power distribution systems/microgrids: Past, present and future. Int. J. Electr. Power Energy Syst. 2019, 104, 89–100. [Google Scholar] [CrossRef]
- Xie, X.; Quan, X.; Wu, Z.; Cao, X.; Dou, X.; Hu, Q. Adaptive master-slave control strategy for medium voltage DC distribution systems based on a novel nonlinear droop controller. IEEE Trans. Smart Grid 2021, 12, 4765–4777. [Google Scholar] [CrossRef]
- Cao, X.; Han, M.; Nee, H.-P.; Yan, W. A new method for simplifying complex DC systems and obtaining the controller droop coefficients. IEEE Trans. Power Syst. 2022, 37, 996–1006. [Google Scholar] [CrossRef]
- Wang, W.; Barnes, M. Power flow algorithms for multi-terminal VSC-HVDC with droop control. IEEE Trans. Power Syst. 2014, 29, 1721–1730. [Google Scholar] [CrossRef]
- Zeng, L.; Chiang, H.-D. Toward an online minimum number of controls for relieving overloads. IEEE Trans. Power Syst. 2018, 33, 1882–1890. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Vasquez, J.C.; Matas, J.; de Vicuna, L.G.; Castilla, M. Hierarchical control of droop-controlled AC and DC microgrids—A general approach toward standardization. IEEE Trans. Ind. Electron. 2011, 58, 158–172. [Google Scholar] [CrossRef]
- Haileselassie, T.M.; Uhlen, K. Impact of DC line voltage drops on power flow of MTDC using droop control. IEEE Trans. Power Syst. 2012, 27, 1441–1449. [Google Scholar] [CrossRef]
- Yuan, Z.; Wang, Y.; Yi, Y.; Wang, C.; Zhao, Y.; Wen, W. Fast linear power flow algorithm for the study of steady-state performance of DC grid. IEEE Trans. Power Syst. 2019, 34, 4240–4248. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, N.; Zhang, Y.; Liao, J.; Tan, S.; Liu, X.; Guo, C.; Wang, Q. Linearized power flow calculation of bipolar DC distribution network with multiple flexible equipment. Int. J. Electr. Power Energy Syst. 2024, 155, 109568. [Google Scholar] [CrossRef]
- Beerten, J.; Belmans, R. Analysis of power sharing and voltage deviations in droop-controlled DC grids. IEEE Trans. Power Syst. 2013, 28, 4588–4597. [Google Scholar] [CrossRef]
- Xiao, L.; Xu, Z.; An, T.; Bian, Z. Improved analytical model for the study of steady state performance of droop-controlled VSC-MTDC systems. IEEE Trans. Power Syst. 2017, 32, 2083–2093. [Google Scholar] [CrossRef]
- Zhang, S.; Fang, Y.; Zhang, H.; Cheng, H.; Wang, X. Maximum hosting capacity of photovoltaic generation in SOP-based power distribution network integrated with electric vehicles. IEEE Trans. Ind. Inform. 2022, 18, 8213–8224. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, Y.; Wang, S.; Liang, D.; Zhao, Q.; Zhao, X. Voltage regulation strategy for DC distribution networks based on coordination of centralized control and adaptive droop control. IEEE Trans. Power Deliv. 2022, 37, 3730–3739. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, S.; Zhao, Q.; Wang, K. Interval power flow calculation algorithm for multi-terminal DC distribution networks considering distributed generation output uncertainties. IET Gener. Transm. Distrib. 2021, 15, 986–996. [Google Scholar] [CrossRef]
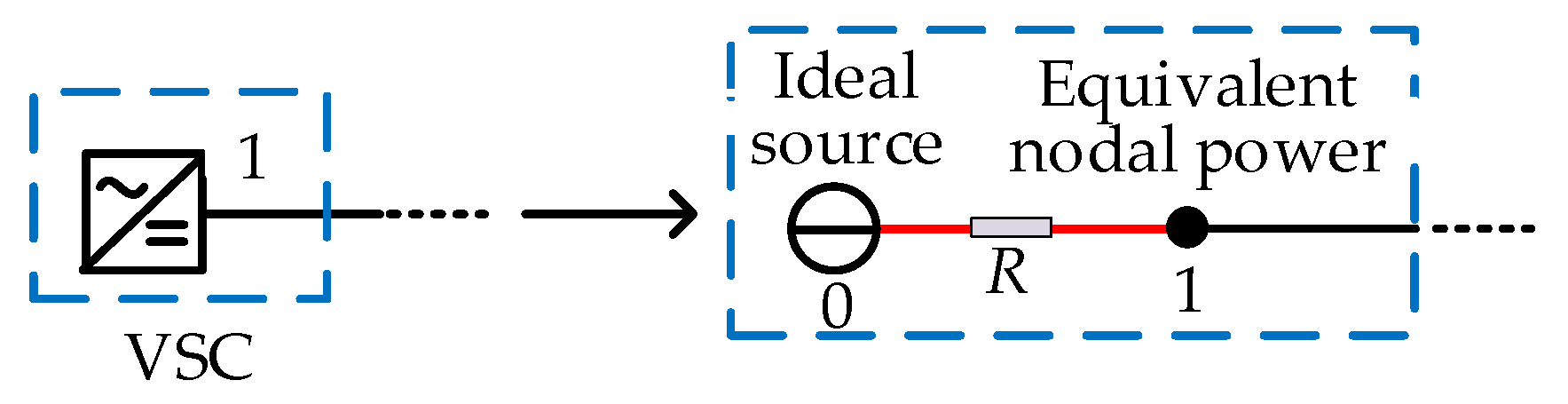



| Control Mode | Voltage of Ideal Source | Line Resistance | Equivalent Nodal Power |
|---|---|---|---|
| Droop control | Reference voltage | Product of droop coefficient and reference voltage | Negative reference power |
| Constant-voltage control | Reference voltage | 0 | Negative maximum power |
| Constant-power control | Reference voltage | ∞ | Negative reference power |
| Scenario | No Overloaded VSCs | Only VSC1 Overload | VSC1 and VSC2 Overload |
|---|---|---|---|
| Conditions | P1 < P1,max, P2 < P2,max, P3 < P3,max | P1 = P1,max, P2 < P2,max, P3 < P3,max | P1 = P1,max, P2 = P2,max, P3 < P3,max |
| Algorithm | VSC1 | VSC2 | ||
|---|---|---|---|---|
| Power (MW) | Error (%) | Power (MW) | Error (%) | |
| PFC | 3.3457 | - | 4.5612 | - |
| LPFC | 3.3065 | 1.17 | 4.5005 | 1.33 |
| Algorithm | VSC1 | VSC2 | |||
|---|---|---|---|---|---|
| Power (MW) | Error (%) | Power (MW) | Error (%) | ||
| PFC | 4.5461 | - | 5.0000 | - | |
| LPF in [16] | 3.9610 | 12.87 | 5.4025 | 8.50 | |
| PLPF | First round | 3.9610 | 12.87 | 5.4025 | 8.50 |
| Second round | 4.3641 | 4.03 | 5.0000 | 0 | |
| Algorithm | VSC1 | VSC2 | |||
|---|---|---|---|---|---|
| Power (MW) | Error (%) | Power (MW) | Error (%) | ||
| PFC | 4.5461 | - | 5.0000 | - | |
| LPF in [16] | 3.6687 | 19.3 | 5.8391 | 16.78 | |
| PLPF | First round | 3.6687 | 19.3 | 5.8391 | 16.78 |
| Second round | 4.5462 | 0.0021 | 5.0000 | 0 | |
| Algorithm | Proportion of Power Variation in Stage 1 | Number of Iterations | Calculation Time |
|---|---|---|---|
| Proposed PLPF | 0.3421 | 15 | 0.032 s |
| Bisection algorithm in [19] | 0.3421 | 2 | 0.057 s |
| VSC | Droop Coefficient | Reference Power | VSC Capacity |
|---|---|---|---|
| VSC1 | 0.1 kV/MW | 6 MW | 10 MW |
| VSC2 | 0.1 kV/MW | 6 MW | 10 MW |
| VSC3 | 0.1 kV/MW | 4 MW | 10 MW |
| Algorithm | VSC1 | VSC2 | VSC3 | ||||
|---|---|---|---|---|---|---|---|
| Power (MW) | Error (%) | Power (MW) | Error (%) | Power (MW) | Error (%) | ||
| PFC | 8.6128 | - | 10.0000 | - | 7.1297 | - | |
| LPF | 8.5060 | 1.24% | 10.0273 | 5.46 | 7.0220 | 1.51 | |
| PLPF | First round | 8.5060 | 1.24% | 10.0273 | 5.46 | 7.0220 | 1.51 |
| Second round | 8.6335 | 0.24 | 10.0000 | 0 | 7.1508 | 0.29 | |
| Algorithm | VSC1 | VSC2 | VSC3 | ||||
|---|---|---|---|---|---|---|---|
| Power (MW) | Error (%) | Power (MW) | Error (%) | Power (MW) | Error (%) | ||
| PFC | 10.0000 | - | 10.0000 | - | 8.6450 | - | |
| LPF | 9.6087 | 3.91% | 11.5966 | 15.97% | 7.4282 | 14.07 | |
| PLPF | First round | 9.6087 | 3.91% | 11.5966 | 15.97% | 7.4282 | 14.07 |
| Second round | 10.1031 | 0 | 10.0000 | 0 | 8.5972 | 0.55 | |
| Third round | 10.0000 | 0 | 10.0000 | 0 | 8.6820 | 0.42 | |
| Algorithm | Proportion of Power Variation in Stage 1 | Proportion of Power Variation in Stage 2 | Number of Iterations | Calculation Time |
|---|---|---|---|---|
| PLPF | 0.6211 | 0.3588 | 3 | 0.143 s |
| Bisection algorithm in [19] | 0.6211 | 0.3588 | 27 | 0.293 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, R.; Wang, Y.; Yu, S.; Chen, Y.; Cheng, X. Piecewise Linear Power Flow Algorithm of DC Distribution Networks Considering Automatic Adjustment of VSC Control Strategy. Energies 2024, 17, 41. https://doi.org/10.3390/en17010041
Yang R, Wang Y, Yu S, Chen Y, Cheng X. Piecewise Linear Power Flow Algorithm of DC Distribution Networks Considering Automatic Adjustment of VSC Control Strategy. Energies. 2024; 17(1):41. https://doi.org/10.3390/en17010041
Chicago/Turabian StyleYang, Ruixiong, Yizhen Wang, Songtao Yu, Yong Chen, and Xu Cheng. 2024. "Piecewise Linear Power Flow Algorithm of DC Distribution Networks Considering Automatic Adjustment of VSC Control Strategy" Energies 17, no. 1: 41. https://doi.org/10.3390/en17010041
APA StyleYang, R., Wang, Y., Yu, S., Chen, Y., & Cheng, X. (2024). Piecewise Linear Power Flow Algorithm of DC Distribution Networks Considering Automatic Adjustment of VSC Control Strategy. Energies, 17(1), 41. https://doi.org/10.3390/en17010041







