A New Double-Switch SEPIC-Buck Topology for Renewable Energy Applications
Abstract
1. Introduction
- When compared to the conventional SEPIC-Buck converter, the suggested converter has an additional transistor (MOS2).
- When compared to the duty cycle of the first switch (MOS1), the duty cycle of the second transistor (MOS2), which is used for the converter bucking regime, is shifted by T/2.
- The proposed converter employs more capacitive/inductive components than the previous DC-DC conventional converters in order to discharge its stored energy into the load while the switches are off and to boost the voltage gain of the converter.
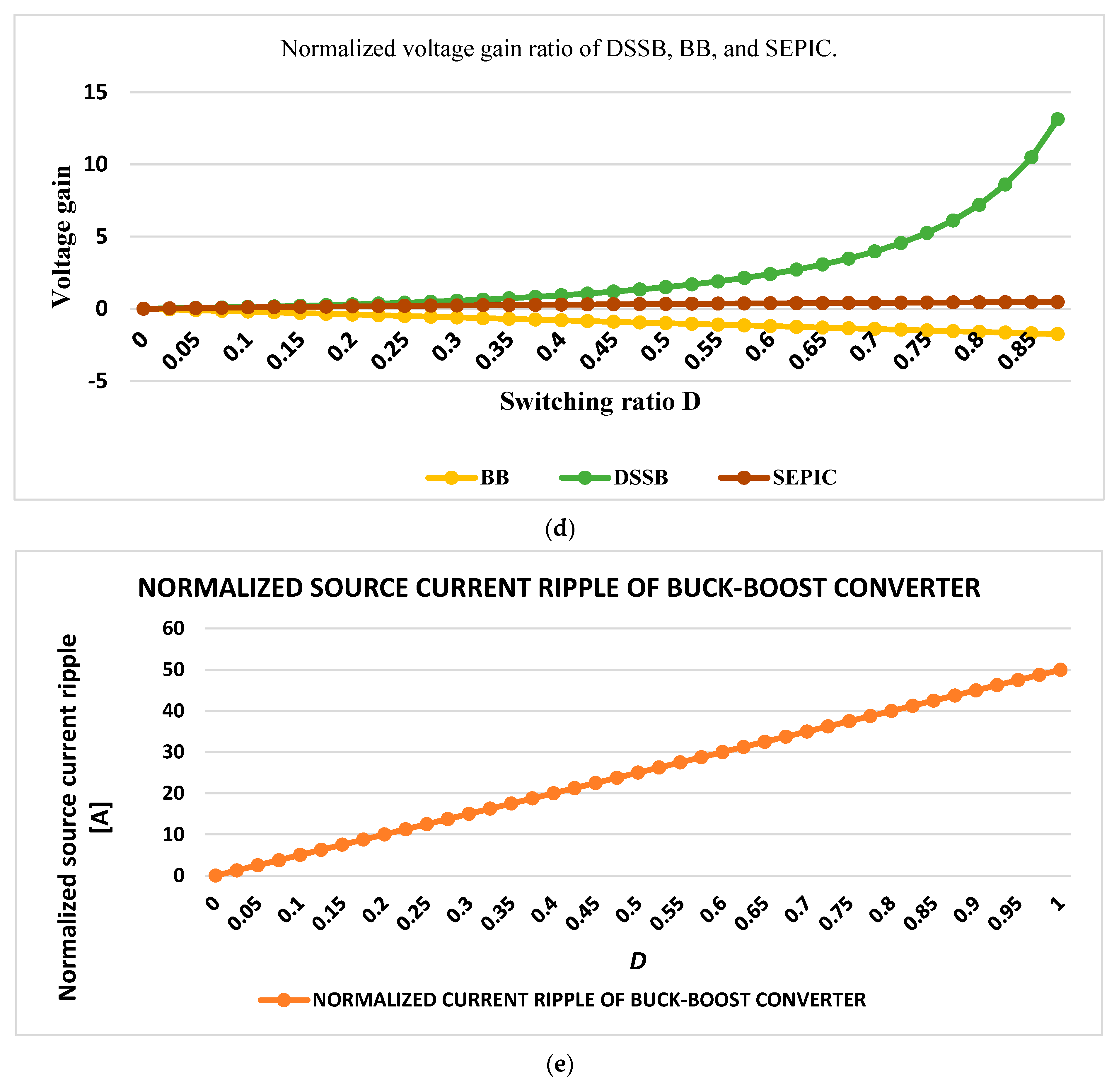
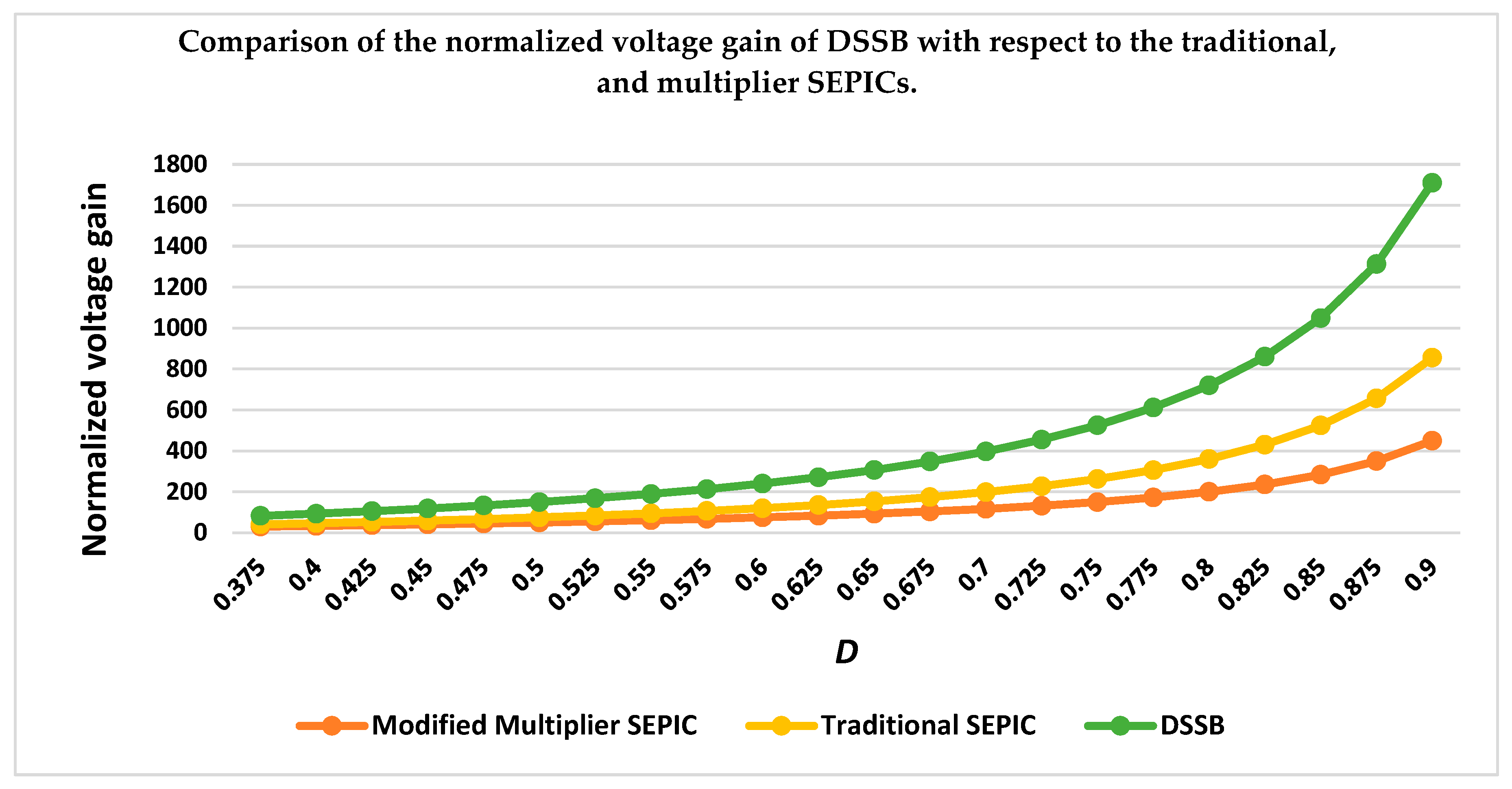
- The proposed converter’s normalized voltage gain is larger than traditional boost, modified Sepic, buck-boost, and other DC-DC converters.
- Furthermore, the proposed design can lower the harmonic content generated at the output and input, resulting in a larger DC output voltage range and higher efficiency when compared to the current SEPIC, boost, and buck converter circuits.
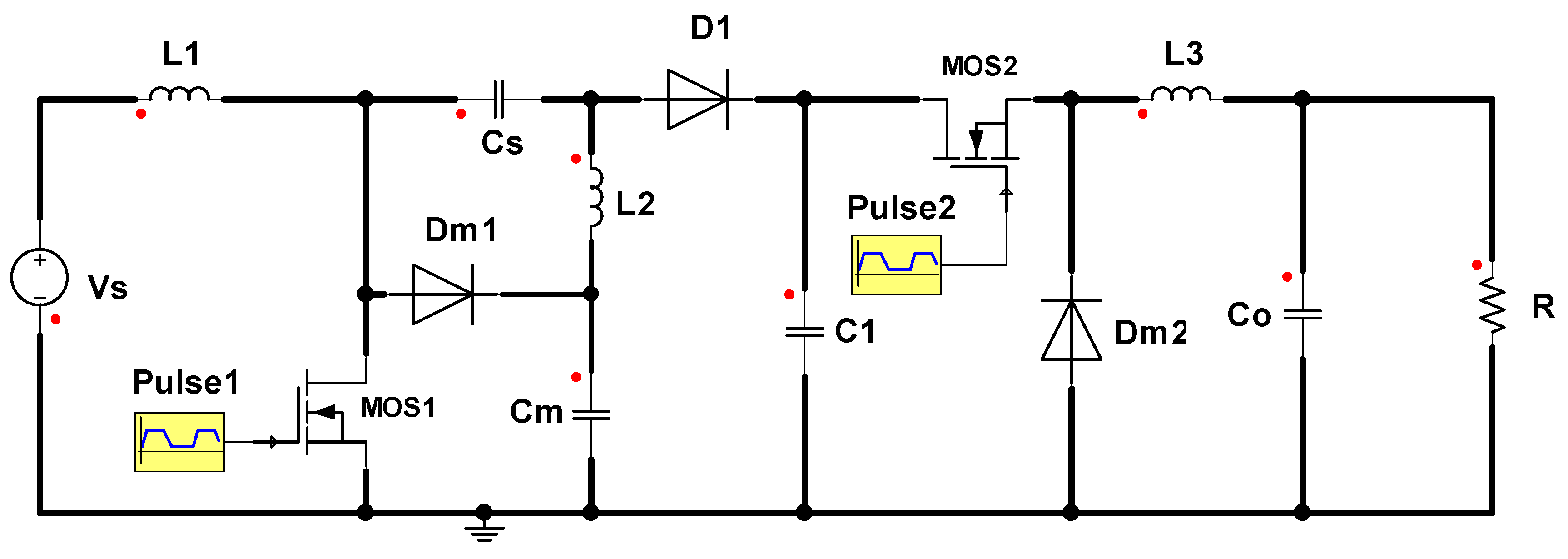
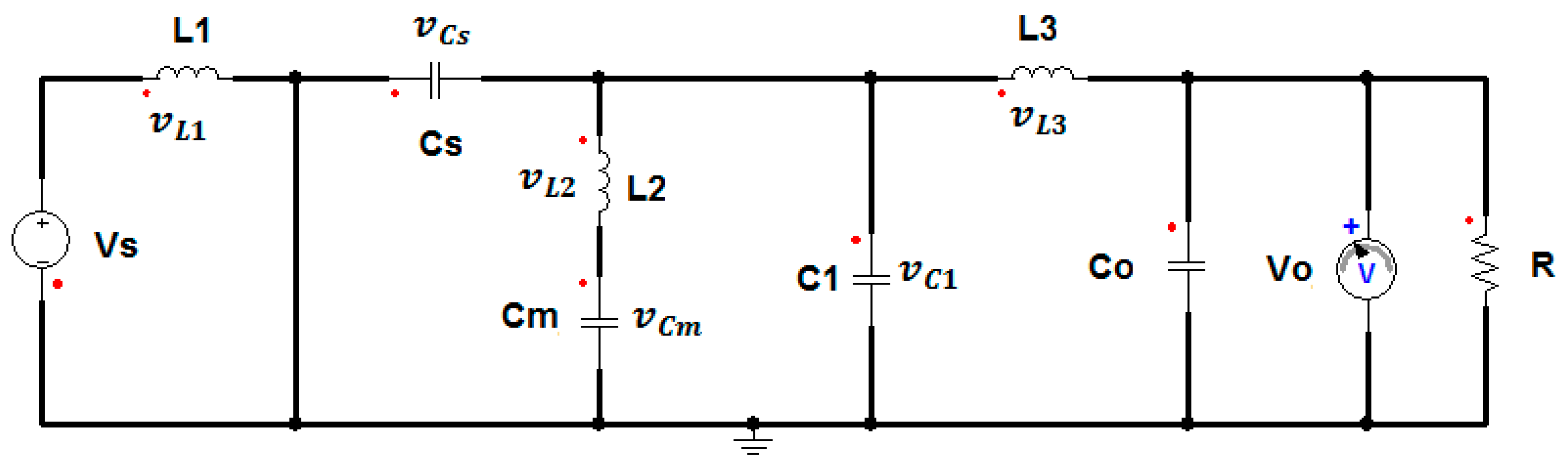
2. The Essentials of the DSSB Converter Analysis
2.1. Working Principle of the DSSB
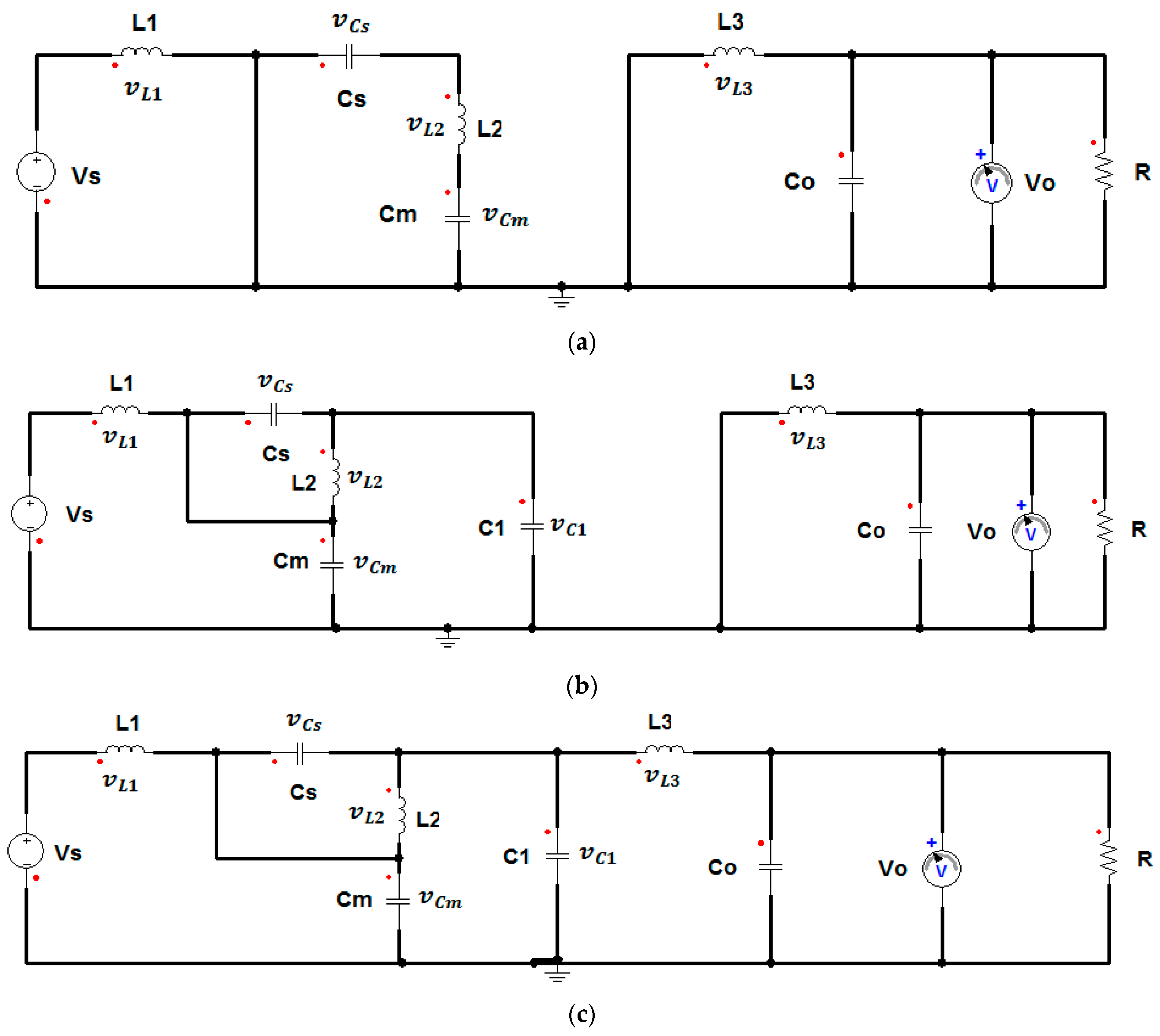
2.1.1. Quasi-Stationary State of the DSSB
2.1.2. Buck Regime of the DSSB
2.1.3. Boost-Regime of the DSSB
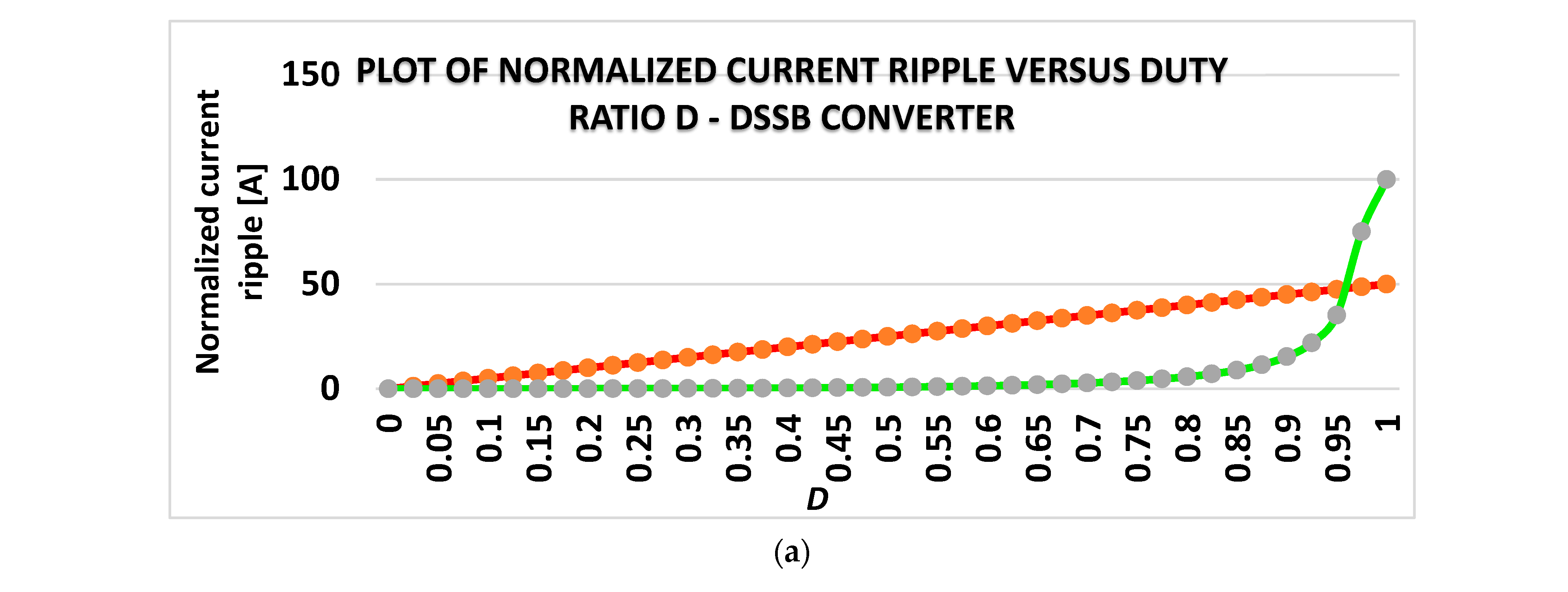
2.1.4. The Inductor Current Ripple
2.2. Normalized Voltage Stress of the DSSB Main Switches, MOS1 and MOS2
3. Comparison of the DSSB Performance with That of Other DC-DC Converters
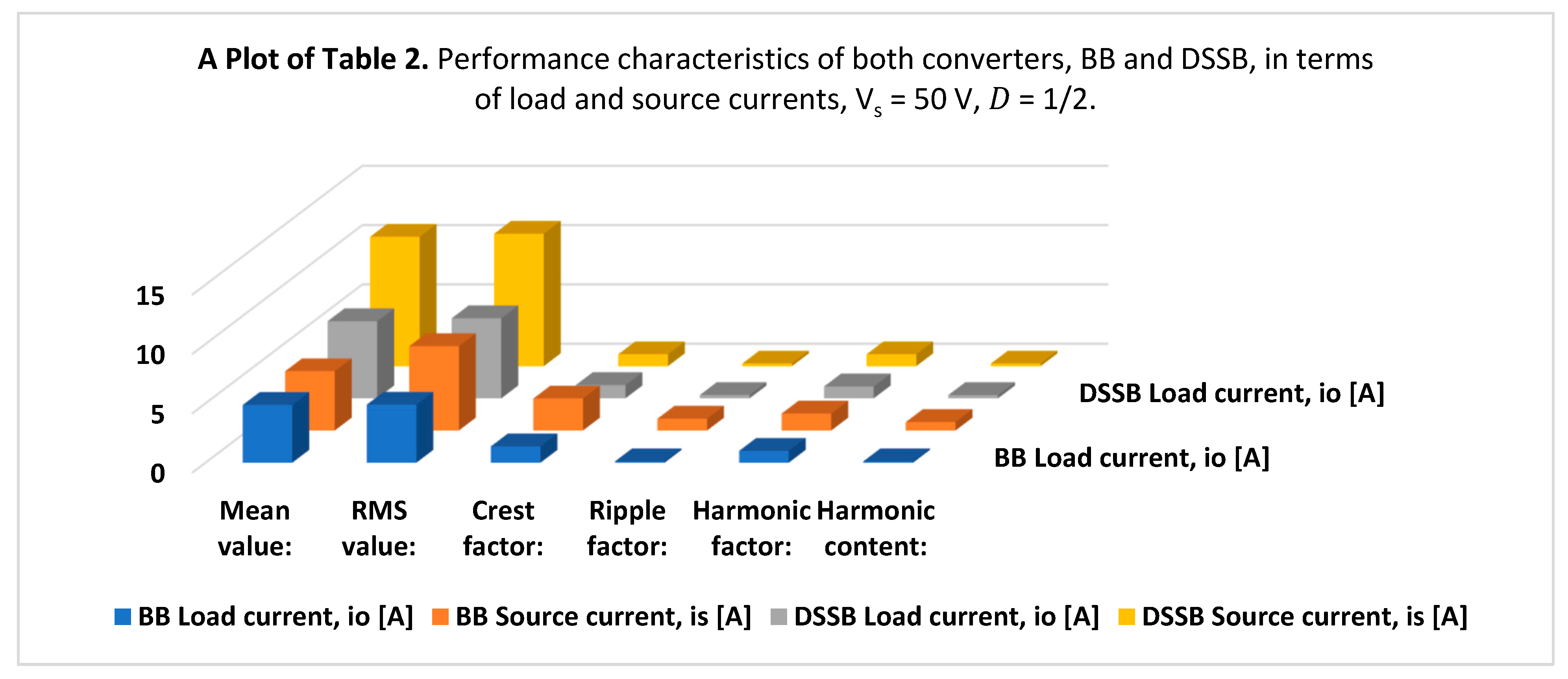
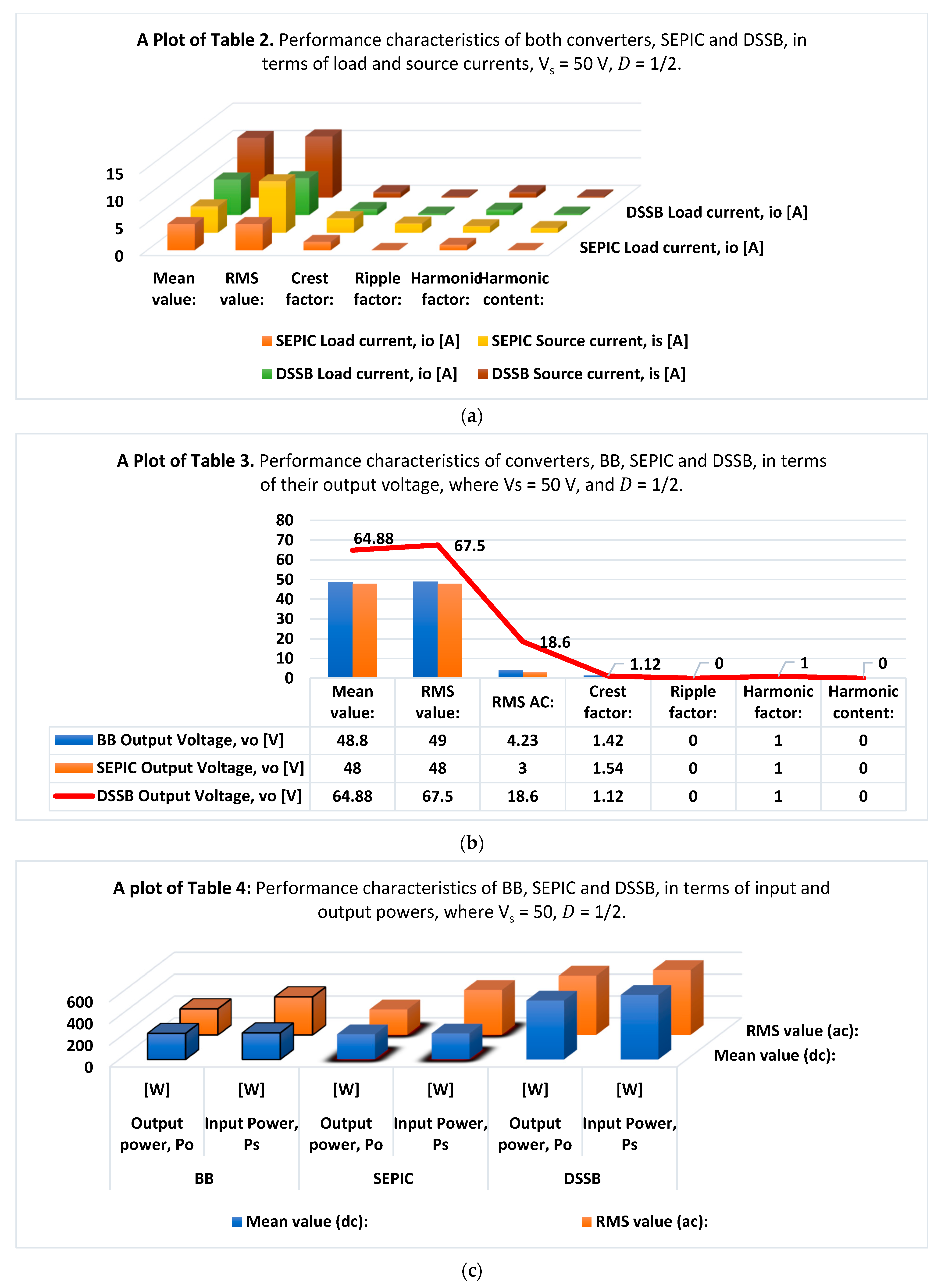
3.1. In Comparison to SEPIC and BB Converters
3.2. In Comparison to Other SEPIC Converter Topologies
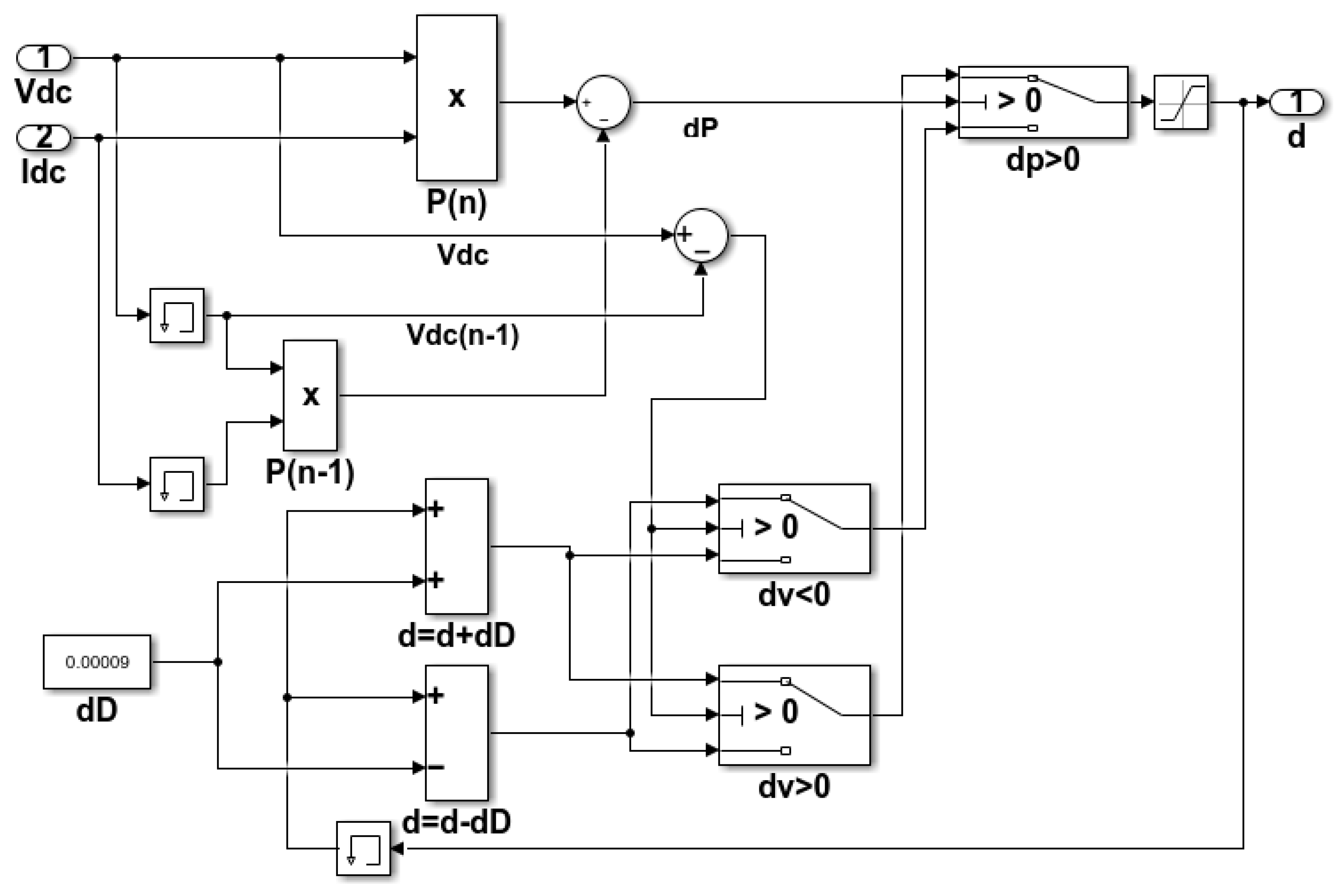
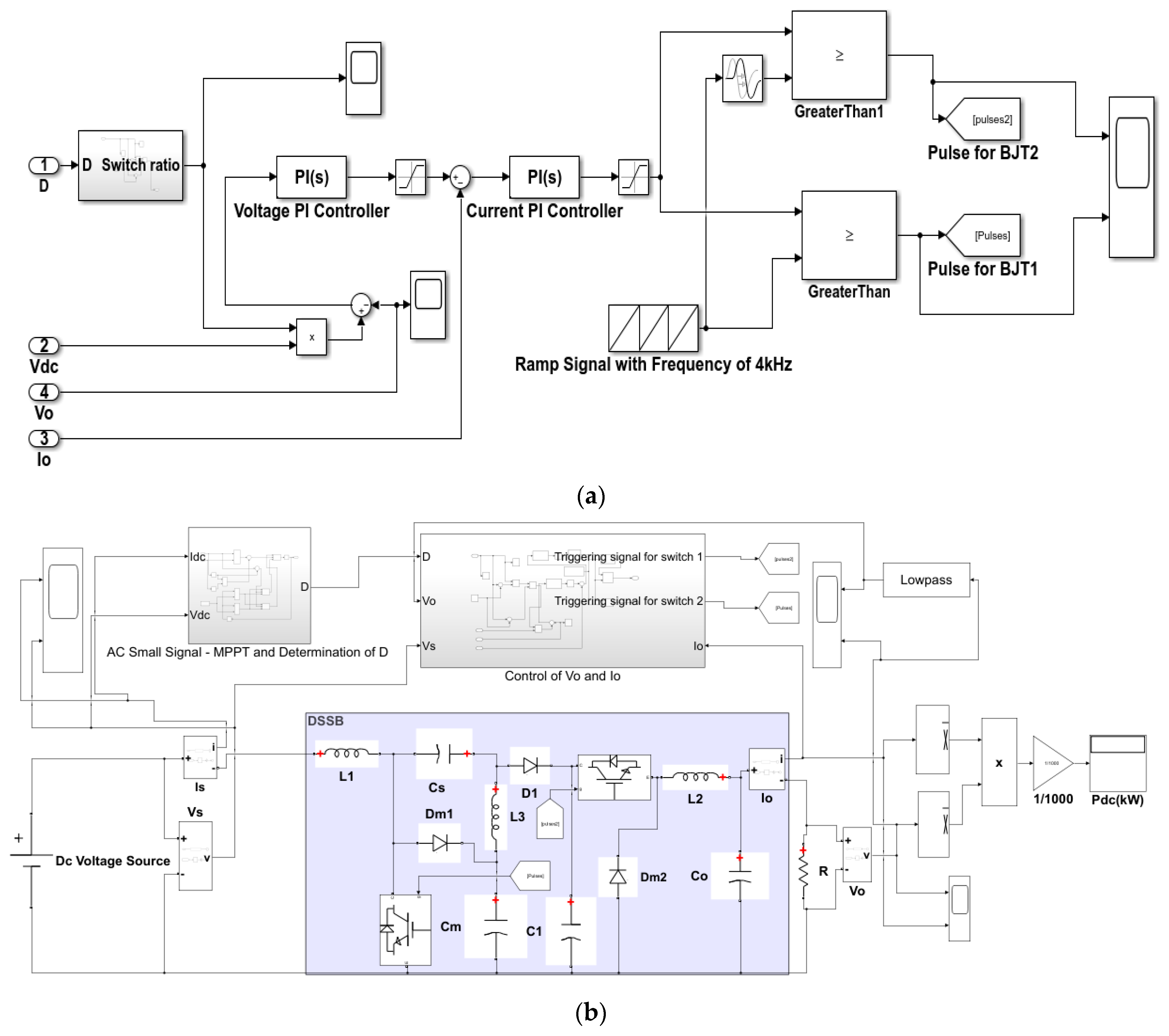
4. Control Method of DSSB Converter
4.1. AC Small-Signal Analysis Technique
- Several perturbation input voltages and currents are selected to perform the DSSB small-signal analysis.
- A compensator for the resulting linear model is designed and tuned using techniques such as automatic PI tuning or interactive loop shaping, with the original locus and Bode plots.
- A programmed gain compensator is created to operate the power electronic system under all possible operating conditions.
- The design of the controller is verified and tried by simulating it against the non-linear power electronic system model.
- Instead, a simulation built using the non-linear DSSB model is used to verify and validate the implementation of the controller design.
- A MATLAB and Simplorer 7 models are automatically generated for rapid prototyping and production control system implementation.
4.2. Current-Mode Technique Based on AC Small-Signal Analysis
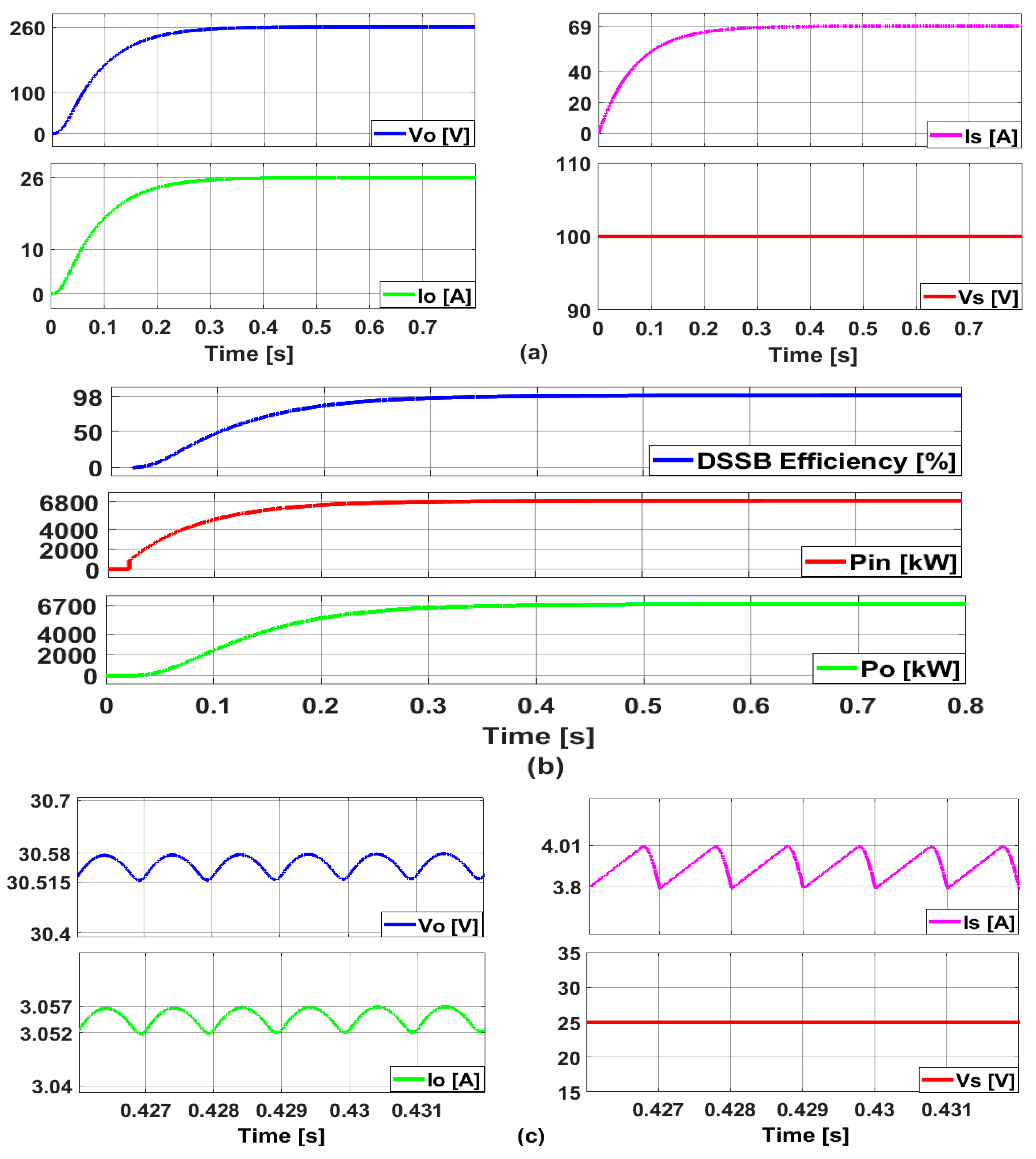
5. Simulation Results
| Parameter | Symbol | Real value | Type |
|---|---|---|---|
| Input Voltage | Vs | 50 V | DC power source |
| Input Inductor | L1 | (100–400) mH | Core NEE-65/33 by Thornton, NL1 = 180 turns − 4 × AWG 27 |
| Input inductor current ripple | ∆iL1 | 0.12 A | - |
| Output inductor current ripple | ∆iL3 | 0.08 A | - |
| Shunt Inductor | L3 | 20 mH | Core NEE-65/33 by Thornton, NL2 = 180 turns − 4 × AWG 27 |
| Output Inductor | L2 | 20 mH | core NEE-65/33 by Thornton, NL3 = 45 turns − 5 × AWG 24 |
| Smoothing capacitor | Cs | 940 uF | Electrolytic capacitor by Hitano |
| Shunt capacitor | Cm | 940 uF | Electrolytic capacitor by Nichicon |
| Shunt capacitor | C1 | 940 uF | Electrolytic capacitor by Nichicon |
| Output capacitor | Co | 3.33 mF | Electrolytic capacitor by Hitano |
| Switching ratio | D | 0.4 | - |
| Output voltage: | Vo | 25 V | - |
| Load resistance: | R | 10 Ω | Ceramic resistor by LW |
| Switching frequency: | f | 4 kHz | Signal generator |
6. Conclusions
- Using the current-mode control technique, it is possible to regulate the inductor current’s peak-to-peak ripple as well as its mean value, which is an advantage of the current-mode control technique based on small-signal analysis.
- Another advantage is that the higher-order system control used to produce the frequency response of such a converter is reduced to the second-order frequency response.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hart, D.W. Power Electronics, International Edition; McGraw Hill: New York, NY, USA, 2011. [Google Scholar]
- Rahbar, K.; Xu, J.; Zhang, R. Real-time energy storage management for renewable integration in microgrid: An off-line optimization approach. IEEE Trans. Smart Grid 2014, 6, 124–134. [Google Scholar] [CrossRef]
- Rahbar, K.; Chai, C.C.; Zhang, R. Energy cooperation optimization in microgrids with renewable energy integration. IEEE Trans. Smart Grid 2016, 9, 1482–1493. [Google Scholar] [CrossRef]
- Vadivel, S.; Ragupathy, U.S. Modeling and Design of High-Performance Converters for Optimal Utilization of Interconnected Renewable Energy Resources to Micro Grid with GOLRS Controller. Int. J. Control Autom. Syst. 2021, 19, 63–75. [Google Scholar] [CrossRef]
- Li, H.; Liu, C.; Zhang, X.; Guo, Z.; Zheng, T.Q. Stability Analysis for Two-Stage Cascaded DC-DC Converters System Based on Describing Function Method. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; pp. 4141–4147. [Google Scholar] [CrossRef]
- Azer, P.; Emadi, A. Generalized State Space Average Model for Multi-Phase Interleaved Buck, Boost and Buck-Boost DC-DC Converters: Transient, Steady-State and Switching Dynamics. IEEE Access 2020, 8, 77735–77745. [Google Scholar] [CrossRef]
- Yalçin, F.; Yazici, İ. Robust Discrete-Time Hybrid Controller for Non-Inverting Buck-Boost DC-DC Converter. Sak. Univ. J. Sci. 2023, 27, 68–82. [Google Scholar] [CrossRef]
- Wu, J.; Mo, M.; Li, J.; Zhang, Y.; Zhang, X.; Fan, X. Inverse decoupling internal model control for multilevel buck converter with constant power load. Energy Rep. 2023, 9 (Suppl. 7), 1181–1189. [Google Scholar] [CrossRef]
- Hao, Y.; Guo, K.; Liu, L.; Cai, W.; Liu, F. improved cubic boost converter based on voltage closed-loop control. Energy Rep. 2022, 8 (Suppl. 6), 87–95. [Google Scholar] [CrossRef]
- Vinay Kumar, C.; Rao, G.M.; Raghu Ram, A.; Prasanna Kumar, Y. Designing of Neuro-Fuzzy Controllers for Brushless DC Motor Drives Operating with Multiswitch Three-Phase Topology. J. Electr. Comput. Eng. 2022, 2022, 7001448. [Google Scholar] [CrossRef]
- Al Attar, H.; Hamida, M.A.; Ghanes, M.; Taleb, M. Review on Modeling and Control Strategies of DC–DC LLC Converters for Bidirectional Electric Vehicle Charger Applications. Energies 2023, 16, 3946. [Google Scholar] [CrossRef]
- Solis-Rodriguez, J.; Rosas-Caro, J.C.; Alejo-Reyes, A.; Valdez-Resendiz, J.E. Optimal Selection of Capacitors for a Low Energy Storage Quadratic Boost Converter (LES-QBC). Energies 2023, 16, 2510. [Google Scholar] [CrossRef]
- Kalimuthu; Ramkumar, M.S.; Amudha, A.; Balachander, K.; Krishnan, M.S. A High Gain Input-Parallel Output-Series Dc/Dc Converter with Dual Coupled-Inductors. Math. Comput. For. Nat. Resour. Sci. 2019, 11, 242–246. [Google Scholar]
- Dagal, I.; Akın, B.; Akboy, E. MPPT mechanism based on novel hybrid particle swarm optimization and salp swarm optimization algorithm for battery charging through simulink. Sci. Rep. 2022, 12, 2664. [Google Scholar] [CrossRef] [PubMed]
- Seyezhai, R.; Mathur, B.L. A Comparison of Three-Phase Uncoupled and Directly Coupled Interleaved Boost Converter for Fuel Cell Applications. Int. J. Electr. Eng. Inform. 2011, 3, 394–407. [Google Scholar] [CrossRef]
- Reatti, A.; Corti, F.; Tesi, A.; Torlai, A.; Kazimierczuk, M.K. Effect of Parasitic Components on Dynamic Performance of Power Stages of DC-DC PWM Buck and Boost Converters in CCM. In Proceedings of the 2019 IEEE International Symposium on Circuits and Systems (ISCAS), Sapporo, Japan, 26–29 May 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, Y.; Li, Z.; Zhang, X. The dynamic Power Loss analysis in Buck Converter. In Proceedings of the 2009 IEEE 6th International Power Electronics and Motion Control Conference, Wuhan, China, 17–20 May 2009; pp. 362–367. [Google Scholar] [CrossRef]
- Trakuldit, S.; Tattiwong, K.; Bunlaksananusorn, C. Design and evaluation of a quadratic Buck Converter. Energy Rep. 2022, 8 (Suppl. 1), 536–543. [Google Scholar] [CrossRef]
- Emar, W.; Huneiti, Z.; Hayajneh, S. Analysis, Synthesis and Simulation of Compact Two-channel Boost Converter for Portable Equipments Operating with a Battery or Solar Cell. Procedia Comput. Sci. 2015, 65, 241–248. [Google Scholar] [CrossRef]
- Emar, W. Analysis, modeling and simulation of step-up converter using Matlab-Simulink and simplorer. Int. J. Model. Simul. Sci. Comput. 2016, 7, 1650004:1–1650004:13. [Google Scholar] [CrossRef]
- de Dieu Nguimfack-Ndongmo, J.; Ngoussandou, B.P.; Goron, D.; Asoh, D.A.; Kidmo, D.K.; Nfah, E.M.; Kenné, G. Nonlinear neuro-adaptive MPPT controller and voltage stabilization of PV Systems under real environmental conditions. Energy Rep. 2022, 8 (Suppl. 9), 1037–1052. [Google Scholar] [CrossRef]
- Zaid, M.; Khan, S.; Mahmood, A.; Ali, M.; Sarwar, A.; Khalid, M. A New High Gain Boost Converter with Common Ground for Solar-PV Application and Low Ripple Input Current. Arab. J. Sci. Eng. 2023, 48, 14655–14669. [Google Scholar] [CrossRef]
- Raj, T.A.B.; Ramesh, R.; Maglin, J.R.; Vaigundamoorthi, M.; Christopher, I.W.; Gopinath, C.; Yaashuwanth, C. Grid Connected Solar PV System with SEPIC Converter Compared with Parallel Boost Converter Based MPPT. Int. J. Photoenergy 2014, 2014, 385720. [Google Scholar] [CrossRef]
- Attar, H.; Kamarposhti, M.A.; Solyman, A.A.A. Impacts of integration of wind farms on voltage stability margin. Int. J. Electr. Comput. Eng. (IJECE) 2022, 12, 4623–4631. [Google Scholar] [CrossRef]
- Iqteit, N.A.; Yahya, K.; Makahleh, F.M.; Attar, H.; Amer, A.; Solyman, A.A.A.; Qudaimat, A.; Tamizi, K. Simple Mathematical and Simulink Model of Stepper Motor. Energies 2022, 15, 6159. [Google Scholar] [CrossRef]
- Bairabathina, S.; S, B. Design and Validation of a SEPIC-Based Novel Multi-Input DC-DC Converter for Grid-Independent Hybrid Electric Vehicles. Energies 2022, 15, 5663. [Google Scholar] [CrossRef]
- Iqbal, D.; Siddique, M.; Chaudhary, A.; Liaqat Bhatti, K.; Abrar, M.; Hussain, M. Novel Concept of Reducing OVR at the Output of SEPIC Converter using Programmable Capacitors. Int. J. Electr. Eng. Inform. 2021, 13, 477–494. [Google Scholar] [CrossRef]
- Komathi, C.; Umamaheswari, M.G. Analysis, and design of genetic algorithm-based cascade control strategy for improving the dynamic performance of interleaved DC–DC SEPIC PFC converter. Neural Comput. Appl. 2020, 32, 5033–5047. [Google Scholar] [CrossRef]
- Senthilkumar, R.; Justin Sunil Dhas, G. Fractional order controller design for SEPIC converter using metaheuristic algorithm. J. Intell. Fuzzy Syst. 2018, 35, 6269–6276. [Google Scholar] [CrossRef]
- Kwon, J.-M.; Choi, W.-Y.; Lee, J.-J.; Kim, E.-H.; Kwon, B.-H. Continuous-conduction-mode SEPIC converter with low reverse-recovery loss for power factor correction. IEE Proc. Electr. Power Appl. 2006, 153, 673–681. [Google Scholar] [CrossRef]
- Dalimunthe, A.M.A.; Sara, I.D.; Tarmizi. Adaptive Control for SEPIC Converter. In Proceedings of the 2020 4rd International Conference on Electrical, Telecommunication and Computer Engineering (ELTICOM), Medan, Indonesia, 3–4 September 2020; pp. 92–96. [Google Scholar] [CrossRef]
- Hu, J.; Sagneri, A.D.; Rivas, J.M.; Han, Y.; Davis, S.M.; Perreault, D.J. High-Frequency Resonant SEPIC Converter with Wide Input and Output Voltage Ranges. IEEE Trans. Power Electron. 2012, 27, 189–200. [Google Scholar] [CrossRef]
- Weitz, N.; Utzelmann, S.; Ditze, S.; März, M. A Resonant Push–Pull DC–DC Converter With an Intrinsic Current Source Behavior for Radio Frequency Power Conversion. IEEE Trans. Power Electron. 2022, 37, 7001–7012. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, Y.; Zhao, Y.; Liu, J.; Zhu, B. High frequency and high-power density bipolar DC–DC converter with GaN HEMT. Energy Rep. 2023, 9 (Suppl. 7), 617–624. [Google Scholar] [CrossRef]
- Amer, A.; Attar, H.; As’ad, S.; Alsaqoor, S.; Colak, I.; Alahmer, A.; Alali, M.; Borowski, G.; Hmada, M.; Solyman, A. Floating Photovoltaics: Assessing the Potential, Advantages, and Challenges of Harnessing Solar Energy on Water Bodies. J. Ecol. Eng. 2023, 24, 324–339. [Google Scholar] [CrossRef]

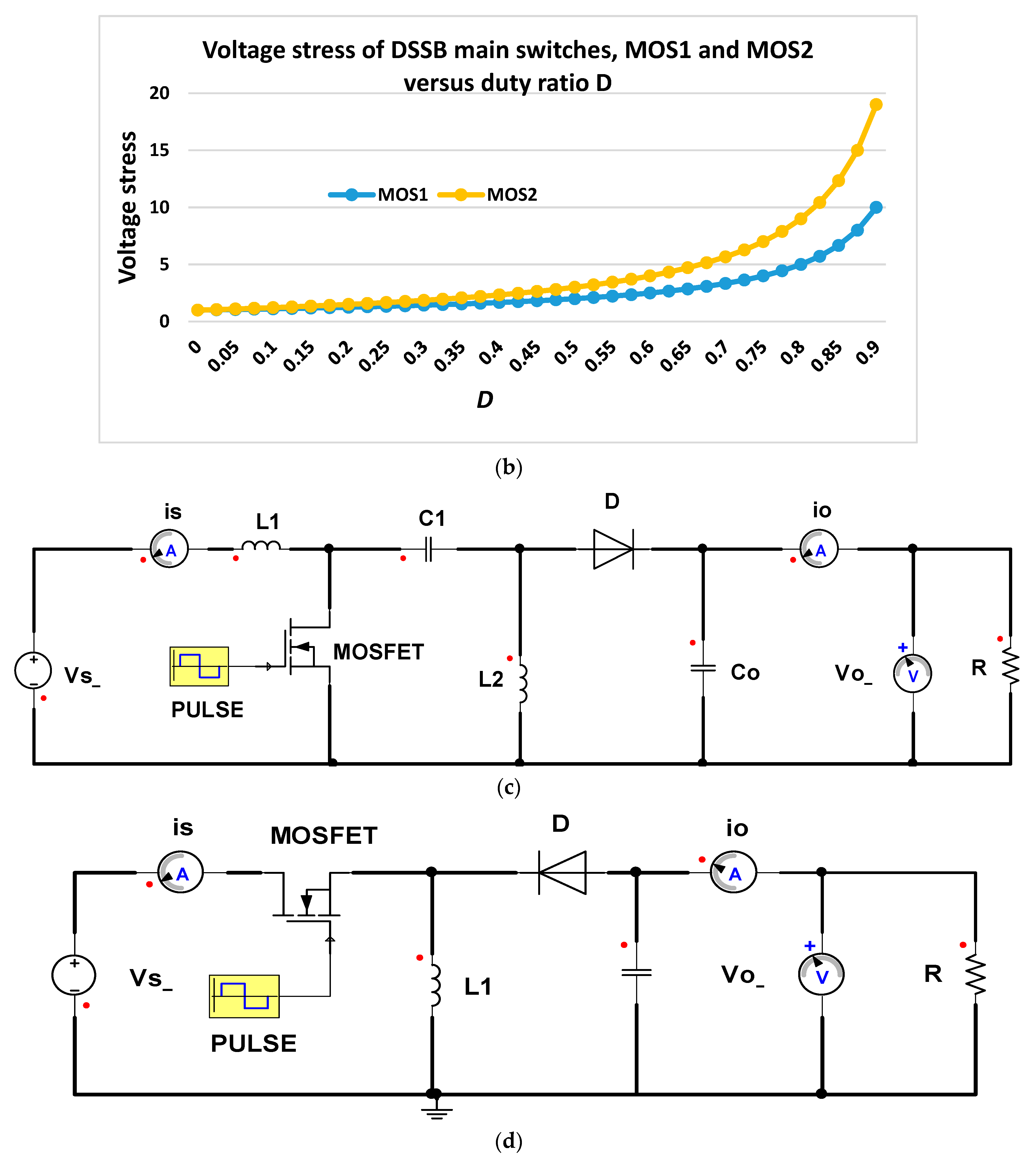
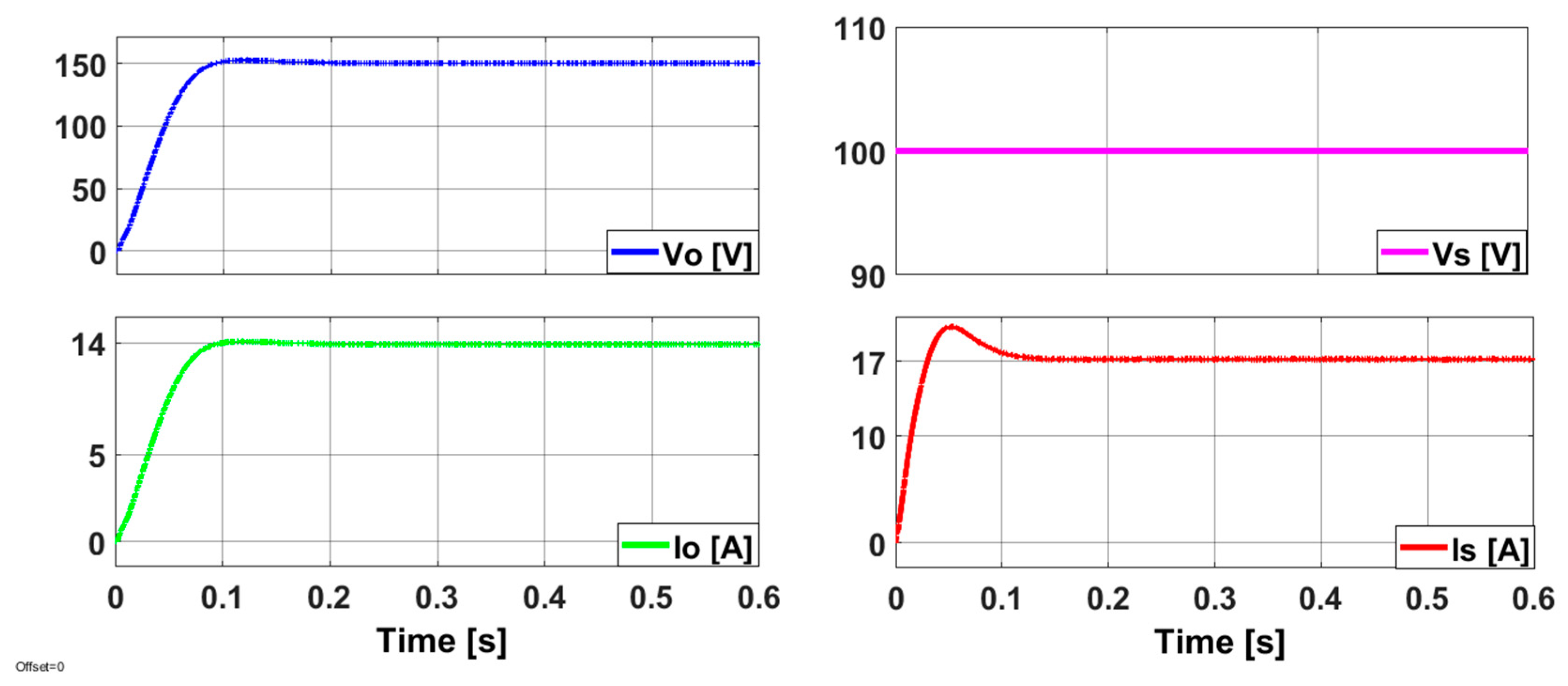

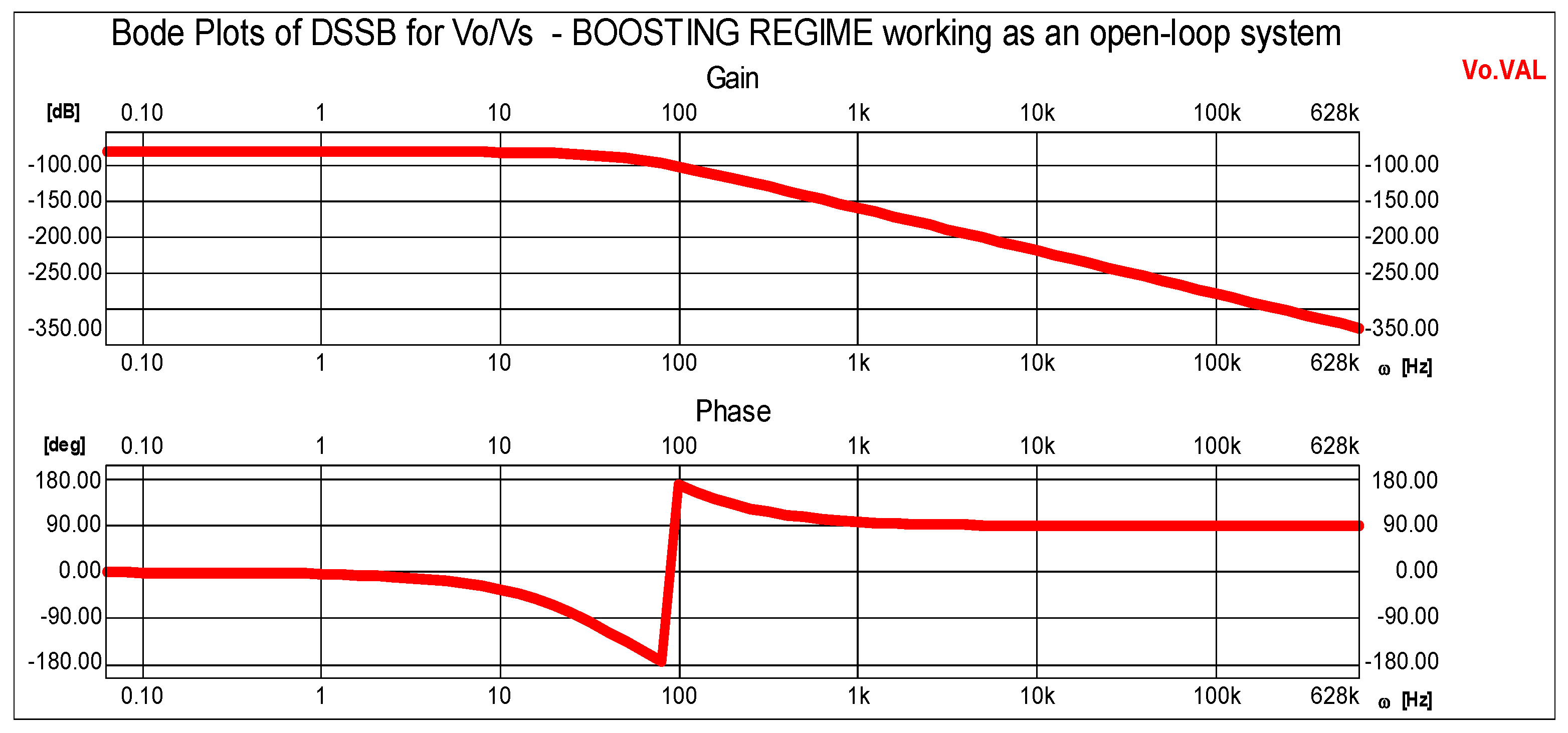
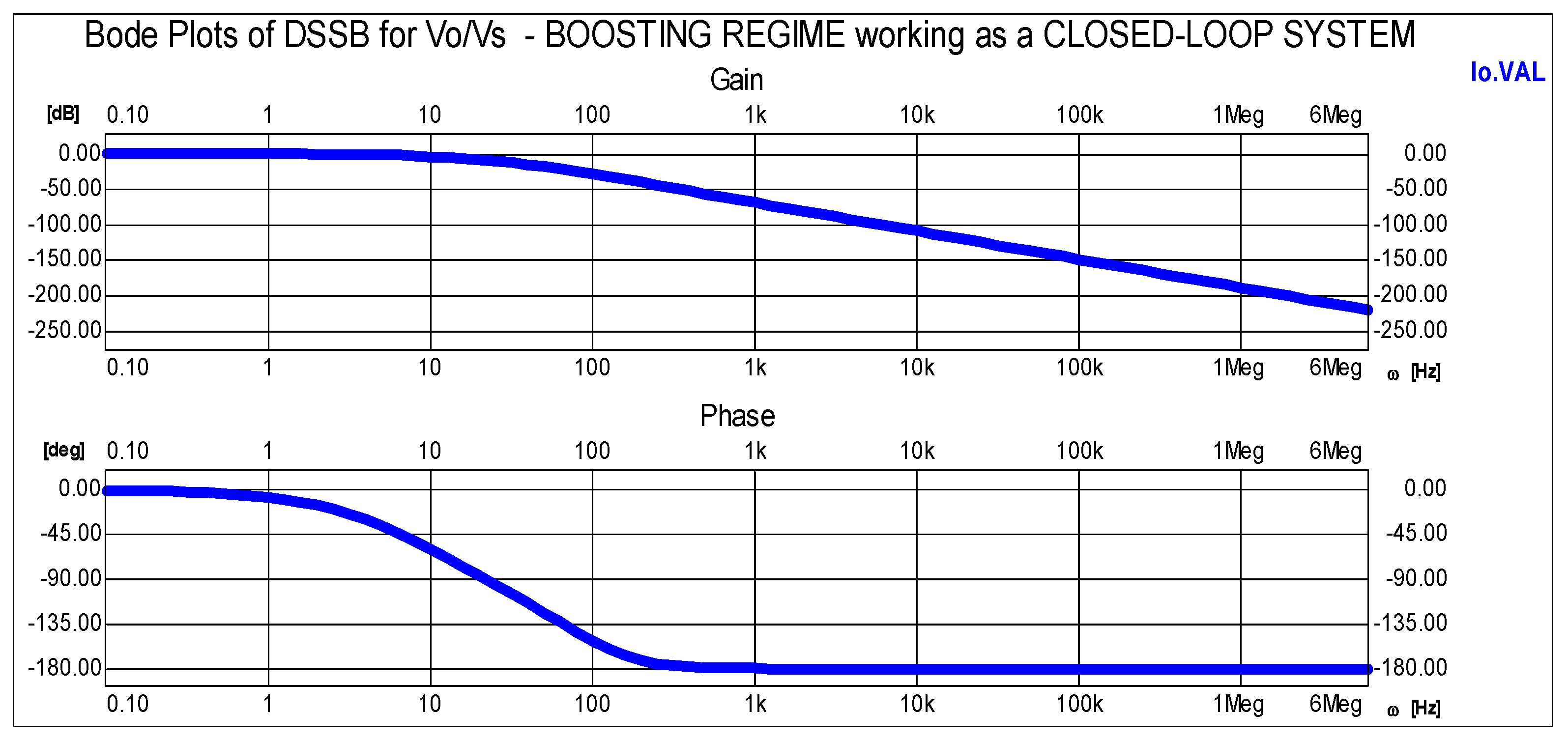
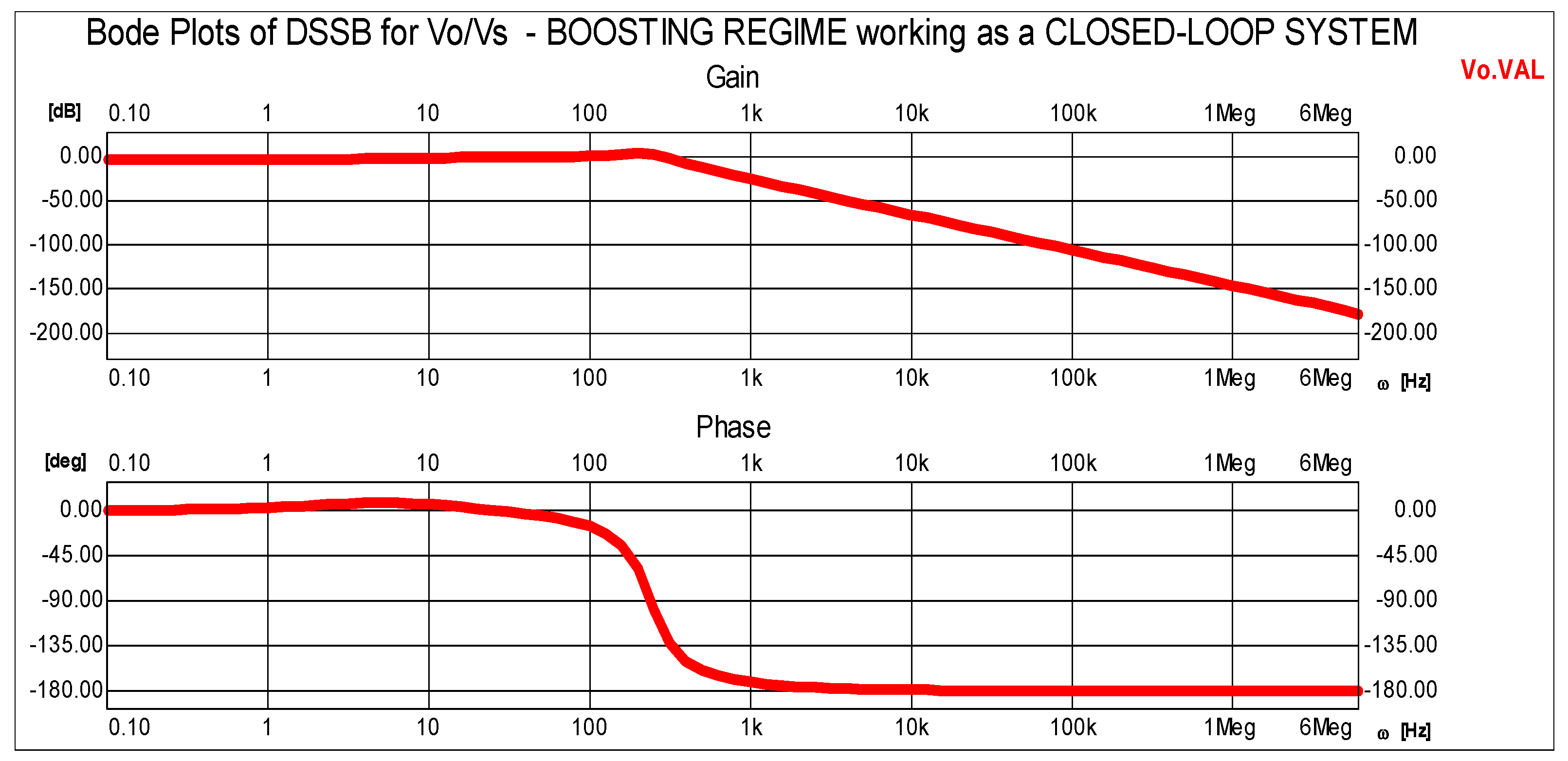
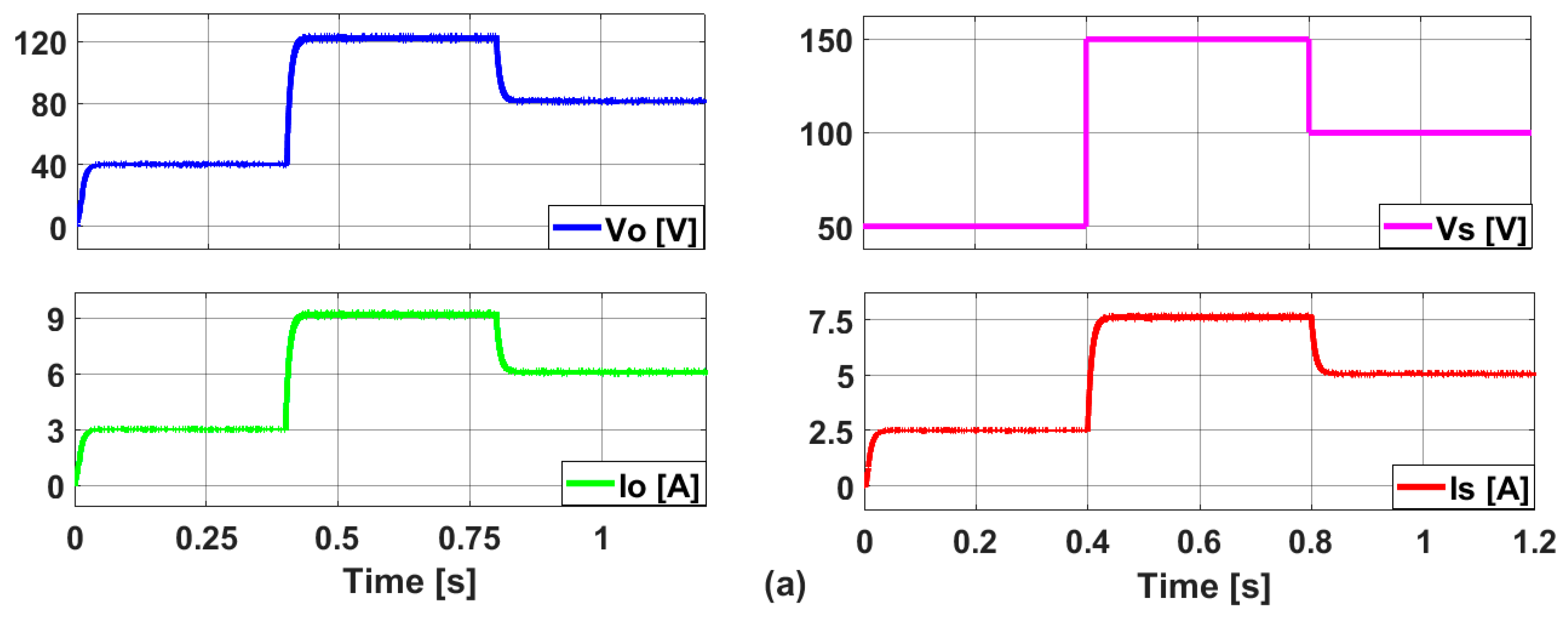
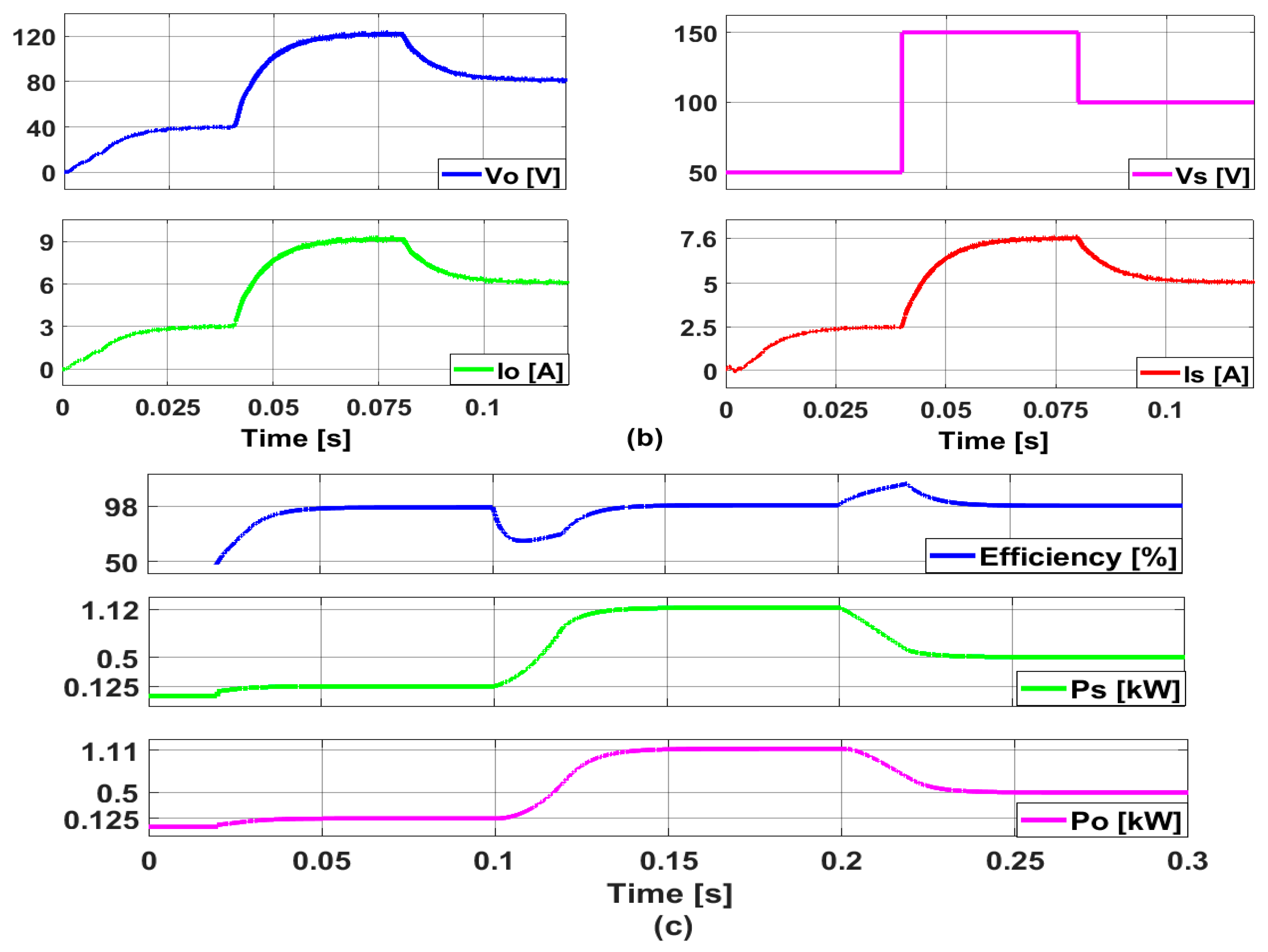
| Parameter | Symbol | Real Value |
|---|---|---|
| Smoothing Inductors | L | 30 mH |
| Solar cell supply voltage: | Vs | 50 V |
| Load resistance: | R | 10 Ω |
| The capacitance of all capacitors: | C | 1 mF |
| Switching frequency: | f | 4 kHz |
| Converter Type | BB | SEPIC | DSSB | |||
|---|---|---|---|---|---|---|
| Parameter | Load Current io [A] | Source Current is [A] | Load Current io [A] | Source Current is [A] | Load Current io [A] | Source Current is [A] |
| Mean value: | 4.87 | 5 | 4.8 | 4.8 | 6.5 | 10.9 |
| RMS value: | 4.9 | 7.11 | 4.8 | 9.4 | 6.75 | 11.16 |
| Crest factor: | 1.38 | 2.7 | 1.54 | 2.65 | 1.12 | 1 |
| Ripple factor: | 118 m | 1 | 62.5 m | 1.69 | 286.5 m | 221.8 m |
| Harmonic factor: | 1 | 1.43 | 1 | 1.2 | 1 | 1 |
| Harmonic content: | 117 m | 715.24 m | 62.4 m | 860 m | 275.4 m | 216.5 m |
| Converter Type | BB | SEPIC | DSSB |
|---|---|---|---|
| Parameter | Output Voltage [V] | Output Voltage [V] | Output Voltage [V] |
| Mean value: | 48.8 | 48 | 64.88 |
| RMS value: | 49 | 48 | 67.5 |
| RMS AC: | 4.23 | 3 | 18.6 |
| Crest factor: | 1.42 | 1.54 | 1.12 |
| Ripple factor: | 86.74 m | 62.48 m | 286.5 m |
| Harmonic factor: | 1 | 1 | 1 |
| Harmonic content: | 86.42 m | 62.36 m | 275.4 m |
| Converter Type | BB | SEPIC | DSSB | |||
|---|---|---|---|---|---|---|
| Parameter | Output Power, Po | Input Power, Ps | Output Power, Po | Input Power, Ps | Output Power, Po | Input Power, Ps |
| [W] | [W] | [W] | [W] | [W] | [W] | |
| Mean value (dc): | 240 | 244 | 232 | 240 | 542 | 594 |
| RMS value (ac): | 240 | 350 | 234 | 414 | 544 | 595 |
| Power factor = Po(dc + ac)/Ps(dc + ac)% | 82% | 92% | 92% | |||
| Efficiency = Po(dc)/Ps(dc)% | 98% | 92% | 92% | |||
| Performance | Type of SEPIC | ||
|---|---|---|---|
| Traditional Sepic as Explained in [4] | Modified Multiplier [4] | DSSB Figure 1 | |
| Normalized voltage gain: | |||
| Example: | … this topology of SEPIC is an up/down converter if D < 0.5 or D > 0.5, respectively. | … this topology of SEPIC is an up/down converter if D < 0.618 or D > 0.618, respectively. | … this topology of SEPIC is an up/down converter if D < 0.414 or D > 0.414 respectively, with a much greater value of step-up voltage than others. |
| Normalized inductor source current ripple: | for all values of duty ratio D. | for all values of duty ratio D. | for all values of duty ratio D. |
| Number of Capacitors and Power Electronic Devices | One transistor, one diode, two capacitors, and two inductors | One transistor, three diodes, three capacitors, and three inductors | Two transistors, three diodes, four capacitors, and three inductors |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Emar, W.; Issa, H.; Kanaker, H.; Fares, O.; Attar, H. A New Double-Switch SEPIC-Buck Topology for Renewable Energy Applications. Energies 2024, 17, 238. https://doi.org/10.3390/en17010238
Emar W, Issa H, Kanaker H, Fares O, Attar H. A New Double-Switch SEPIC-Buck Topology for Renewable Energy Applications. Energies. 2024; 17(1):238. https://doi.org/10.3390/en17010238
Chicago/Turabian StyleEmar, Walid, Haitham Issa, Hasan Kanaker, Osama Fares, and Hani Attar. 2024. "A New Double-Switch SEPIC-Buck Topology for Renewable Energy Applications" Energies 17, no. 1: 238. https://doi.org/10.3390/en17010238
APA StyleEmar, W., Issa, H., Kanaker, H., Fares, O., & Attar, H. (2024). A New Double-Switch SEPIC-Buck Topology for Renewable Energy Applications. Energies, 17(1), 238. https://doi.org/10.3390/en17010238








