Testing and Numerical Analysis of Abnormal Pressure Pulsations in Francis Turbines

Abstract

During the flood season, Francis turbines often operate under low-head and full-load conditions, frequently experiencing significant pressure pulsations, posing potential threats to the safe and stable operation of the units. However, the factors contributing to substantial pressure pulsations in Francis turbines are multifaceted. This paper focuses on a mixed-flow hydroelectric generating unit at a specific hydropower station. Field tests were conducted to investigate abnormal vibrations and hydraulic pressure pulsations under low-head and full-load conditions. Utilizing the Navier–Stokes equations and the RNG k-ε turbulence model, the unsteady flow field within the turbine under these conditions was calculated. The results indicate that the abnormal pressure pulsations detected in the bladeless zone between the wicket gates and the turbine inlet are due to operational points deviating from the normal operating range of the turbine. When water flows at a large inflow angle, striking the turbine blade heads, it leads to significant flow separation and vortex formation at the back of the blade inlet edges, causing severe vibrations in the hydroelectric generating unit. These findings provide a basis and assurance for the safe and stable operation of the power station.

1. Introduction

Stability has always been a key research focus in the operation of hydroelectric generating units, particularly the stability of large hydropower stations, which draws significant attention from researchers. In China, hydropower stations are often required to operate at full or even overload capacity during the flood season, in accordance with grid regulation demands, especially those equipped with Francis turbines. However, many of these stations experience abnormal pressure pulsations during full-load operation. For instance, domestic projects such as the Yantan and Xiaolangdi Hydropower Stations have exhibited abnormal vibrations under full-load conditions, with some stations even unable to sustain long-term operation under these conditions [1,2,3]. Prolonged self-excited or excessive vibrations in hydroelectric units can lead to component deformation, loosening, or even fracturing, thereby posing a threat to the safety of the entire unit and the power station [4,5,6].

Recently, the occurrence of abnormal vibrations during the operation of Francis turbines has become increasingly frequent, and the stability of these units has turned into a pressing concern in the industry. However, the factors inducing abnormal hydraulic vibrations in turbines are diverse [7,8]. Tian Shutang, based on the low-head operation experience of the Longyangxia Hydropower Station, conducted a series of model and prototype turbine tests and analyzed the impact of head variations on different types of hydraulic vibrations [9]. Qiao Liangliang and others studied the pressure pulsations in the cover area caused by flow separation and the formation of Karman vortices and blade passage vortices, which is due to the worsening flow conditions around the blades when the operation area of Francis turbine units deviates from the optimal operating range [10]. Feng Jinhai and others, aiming to study the stability of Francis turbines under off-design conditions, performed static and modal analyses on turbines under three typical off-design conditions [11]. Furthermore, Feng Yanmin and others researched the stability characteristics of units with large head variations, suggesting that stability tests should be conducted under multiple characteristic heads to further determine the vibration zones of the units at different heads, thereby improving the safety and stability of unit operations [12]. Additionally, Wu Daoping analyzed the problem of large vibrations under certain conditions. To ensure the stable operation of the units, the Francis turbine units at the Youshui River Hydropower Station were taken as the test subjects, and field tests on the vibration, noise, and hydraulic pressure pulsation of these units were conducted [13].

While the above research outcomes have provided some explanation for the causes of abnormal vibrations in turbines, the factors leading to these vibrations are complex. The results of on-site tests of turbines often result from a combination of multiple factors, and relying solely on field test methods to investigate the root causes of abnormal turbine vibrations clearly has its limitations.

In the past decade or so, fruitful research outcomes have been achieved in analyzing the internal flow field of turbines using CFD software 2021. Numerical simulations enable the dissection of local details in the turbine flow field, further revealing the causes of abnormal vibrations. Lu Lei and others applied numerical simulation methods to analyze the intense vibrations and noise emitted by turbines under full and overload conditions, concluding that the hydraulic instability at the station was caused by blade passage vortices in the turbine [14]. Dekterev et al. further investigated the evolution of vortex cores in turbine blade passages based on hydrodynamic models of hydraulic units [15]. Luo Xingqi and others summarized that the root cause of turbine vibrations lies in the vortex structures of unsteady flows within the turbine, which can lead to large pressure fluctuations, significant unit vibrations, and fatigue of turbine components [16]. Sun L and others conducted unsteady numerical calculations and visualization experiments of turbine flow fields, researching the evolution and pressure pulsation characteristics of blade passage cavitation vortices under partial-load conditions. The results indicated that changes in the volume of cavitation vortices primarily occur near the junction of the trailing edge of the turbine blade back and the lower ring, subsequently inducing local amplification of pressure pulsation magnitudes [17].

The phenomenon of abnormal vibrations in Francis turbines during full-load operation is a widespread issue in the industry. However, the factors causing abnormal hydraulic vibrations in turbines are complex, and particularly, the relationship between the unsteady flow field structure and unstable pressure pulsations under low-head, full-load conditions is still unclear.

At a specific hydropower station in Guizhou, Unit 4 operated at the historically lowest gross head of 110.19 m due to the rise in downstream water levels during the flood season. The turbine of this station was stable and operated normally with the wicket gates at a relative opening of 78% and an active power of 215.57 MW. However, when the relative opening of the wicket gates further increased to 80.449% and the active power rose to 218.863 MW, operating at full load, the unit experienced severe abnormal vibrations accompanied by noticeable noise.

This paper systematically investigates the full-load abnormal vibrations of Unit 4’s turbine at a specific hydropower station. Using numerical simulation methods, the unsteady internal flow field of the turbine was calculated for the full-load operating conditions (a wicket gate relative opening of 80.449%, an active power of 218.863 MW, and a gross head of 110.19 m). The study initially involved solving three-dimensional turbulent flow equations to perform unsteady calculations of the flow field in the bladeless zone between the wicket gates and the turbine inlet, obtaining the pressure pulsation curves at computational monitoring points. Additionally, by combining field test data, the root causes of the unit’s severe vibrations were analyzed, providing references to improve the operating conditions with abnormal pressure pulsations and to ensure the stable operation of the unit.

2. Unsteady Calculation and Testing of the Internal Flow Field in the Turbine

To dissect the flow conditions within the internal flow field of Unit 4’s turbine at a specific hydropower station under full-load conditions, this paper established a geometric model of the turbine’s internal flow passages using the three-dimensional geometric modeling software Unigraphics (UG) 2021. This was followed by mesh division, and then, numerical analysis and the calculation of the unsteady flow within the turbine unit were conducted using numerical simulation software.

2.1. Control Equations [18,19,20]

When applying the principle of mass conservation to incompressible fluids, the continuity equation is:

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0$$

(1)

In the equation: t—time, s; u, v, w—components of fluid velocity in different directions; ρ—fluid density.

Motion Equation (Navier–Stokes Equation) [21]:

$$\begin{array}{l}\nabla \cdot \overrightarrow{u}=0\\ \frac{\partial \overrightarrow{u}}{\partial t}+\left(\overrightarrow{u}\cdot \nabla \right)\overrightarrow{u}=-\frac{\nabla p}{\rho }+{\nabla }^2\cdot \overrightarrow{u}+\overrightarrow{F}\end{array}$$

(2)

where $\overrightarrow{u}$ is the flow velocity, a vector field; ρ is the fluid density, p is the pressure, v is the kinematic viscosity, and $\overrightarrow{F}$ represents external force (per unit of mass in a volume) acting on the fluid. Let us also choose the Ox axis that coincides with the main direction of flow propagation. Moreover, we assume here the external force $\overrightarrow{F}$ above to be the force, which has a potential $\Phi$ represented by $\overrightarrow{F}=-\nabla \Phi$.

The Re-Normalization Group (RNG) k-ε turbulence model is an advanced version of the standard k-ε model used in computational fluid dynamics (CFD) for simulating turbulence. The RNG model modifies the standard k-ε model by including additional terms derived from statistical mechanics. These modifications enhance the model’s accuracy for a wider range of flows, especially those involving rapid strain rates, swirling, and complex flows. The equations for the RNG k-ε model are as follows [22]:

Turbulent Kinetic Energy (k) Equation:

$$\frac{\partial (\rho k)}{\partial t}+\frac{\partial (\rho u_{i}k)}{\partial x_i}=\frac{\partial }{\partial x_j}[(\mu +\frac{{\mu }_t}{{\sigma }_k})\frac{\partial k}{\partial x_j}]+P_k+P_b-\rho \epsilon -Y_M+S_k$$

(3)

where P_k is the production of turbulence kinetic energy due to mean velocity gradients, P_b is the production of turbulence kinetic energy due to buoyancy, Y_M is the contribution of the fluctuating dilatation in compressible turbulence to the overall dissipation rate, and S_k is a user-defined source term.

Turbulent Dissipation Rate (ε) Equation:

$$\frac{\partial (\rho \epsilon )}{\partial t}+\frac{\partial (\rho u_i\epsilon )}{\partial x_i}=\frac{\partial }{\partial x_j}[(\mu +\frac{{\mu }_t}{{\sigma }_{\epsilon }})\frac{\partial \epsilon }{\partial x_j}]+C_{1\epsilon }\frac{\epsilon }{k}(P_k+C_{3\epsilon }{P}_b)-C_{2\epsilon }\rho \frac{{\epsilon }^2}{k}+S_{\epsilon }$$

(4)

where C_1ε, C_2ε, and C_3ε are constants; ${\sigma }_k$ and ${\sigma }_{\epsilon }$ are the turbulent Prandtl numbers for k and ε, respectively; and S_ε is a user-defined source term.

The RNG k-ε model introduces additional terms and constants into the ε equation that improve its accuracy for complex flows. The model also uses an analytical formula for turbulent Prandtl numbers, which enhances its performance over the standard k-ε model under certain flow conditions.

2.2. Hydroelectric Turbine 3D Modeling and Grid Generation

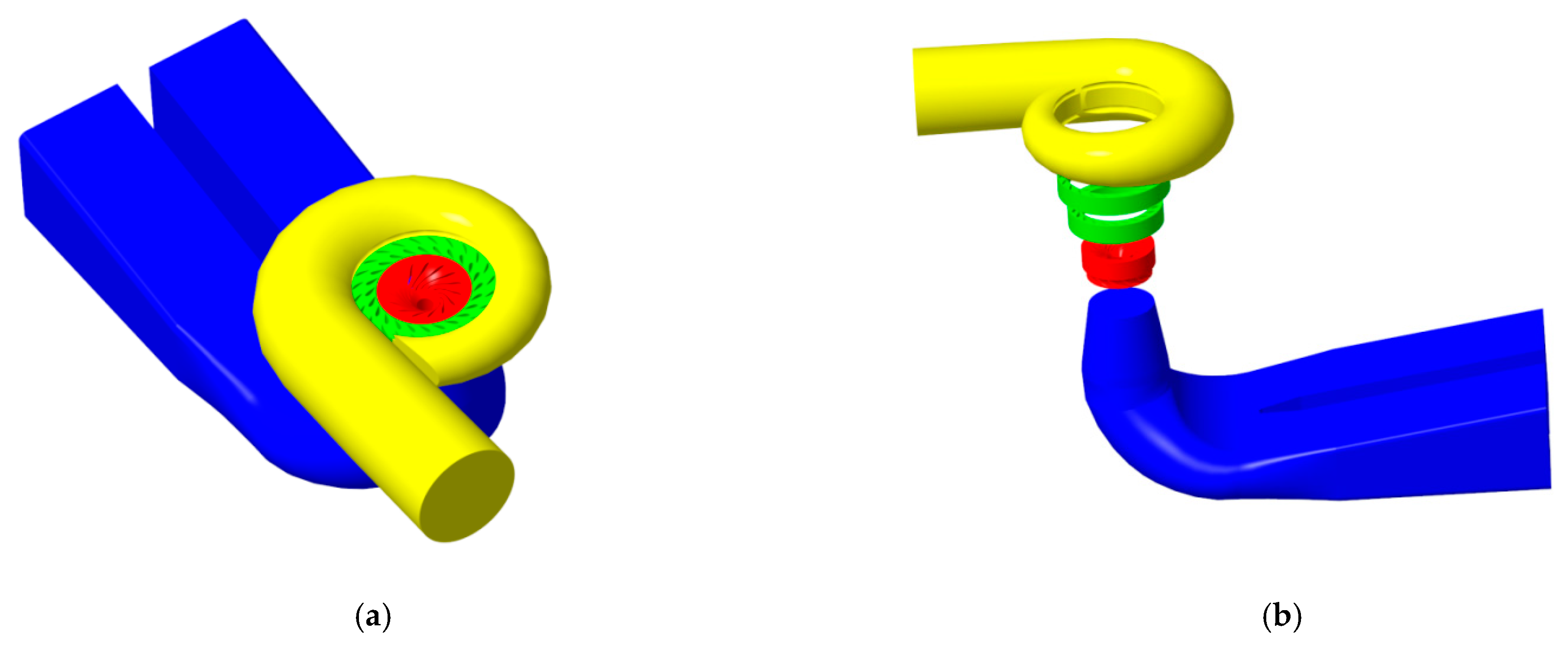
2.2.1. 3D Modeling

After making the corresponding spatial adjustments in the 3D modeling software UG, the guide vanes of the hydroelectric turbine were reconstructed using the spline surface method, and a mathematical model for surface fitting of the Francis turbine blades was provided. Geometric models for other flow components, such as the volute casing and tailpipe, were also established. The geometric modeling of the entire flow passage of the hydroelectric turbine, as shown in Figure 1, is divided into four parts: the volute casing, guide vanes (including fixed guide vanes and adjustable guide vanes), runner, and tailpipe. Figure 1a represents the overall 3D model of the hydroelectric turbine, and Figure 1b shows an exploded view of the complete 3D model.

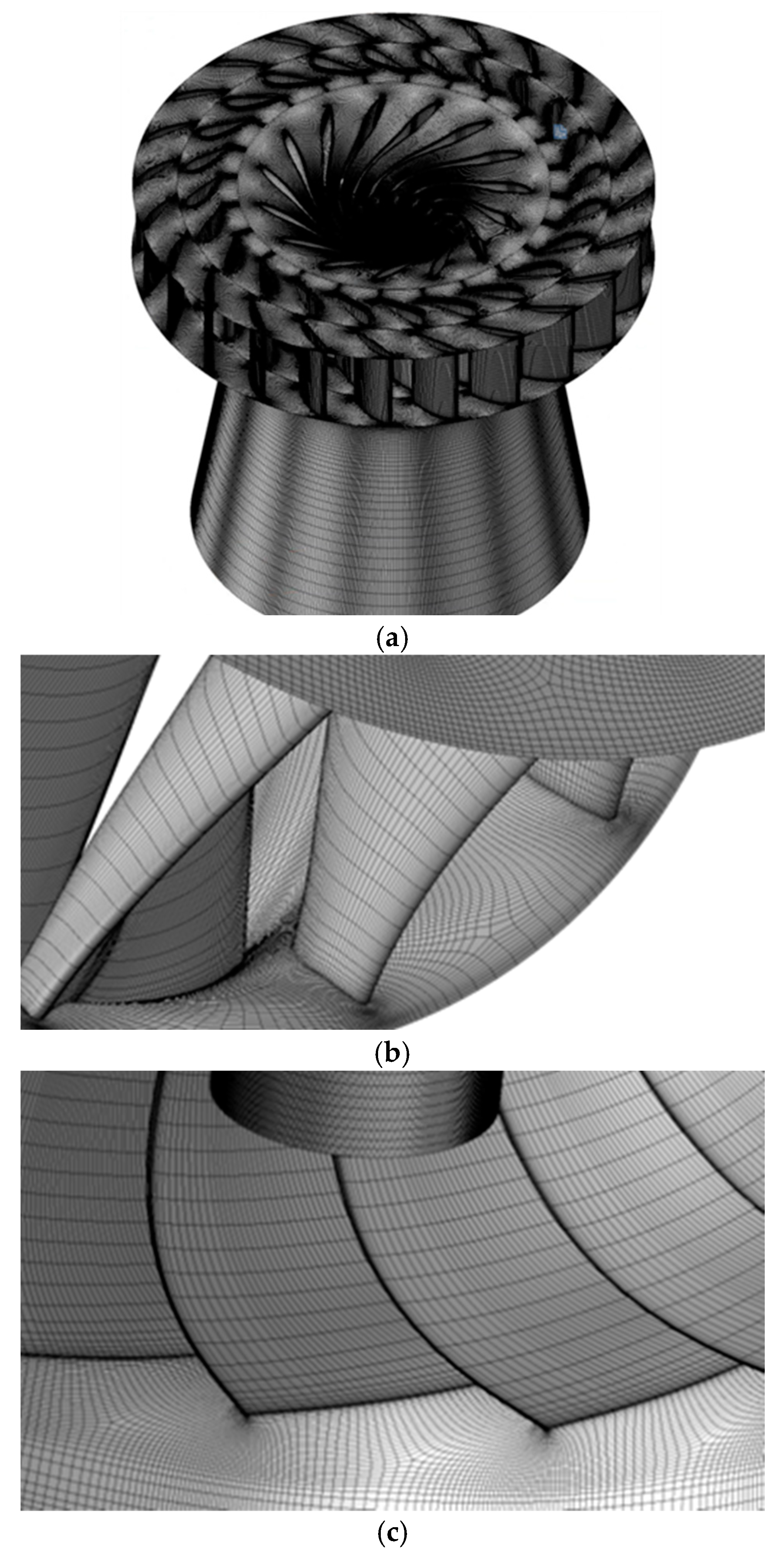
2.2.2. Grid Partitioning

In CFD simulations, to achieve higher accuracy, it often becomes necessary to refine the computational grid and, thus, determine the appropriate size of the near-wall mesh. For rapid solutions near the wall, it is essential to use a turbulence model in conjunction with wall function methods that incorporate accurate empirical data. For example, when using the standard k-ε turbulence model with wall function modeling, the closest internal node to the wall must be within the logarithmic layer of turbulence, meaning y+ must be greater than 11.63 (ideally between 30 and 500). This sets a range for the distance from the closest grid to the wall and the grid size. Using NUMECA’s IGG software 2021 [23], the geometric model was partitioned into grids. After grid independence testing, a final grid partitioning scheme was selected, with a total number of grid elements of approximately 150 million. The grid model is shown in Figure 2.

2.3. Boundary Conditions

We set the volume flow rate as the inlet boundary condition and absolute static pressure at the tailrace outlet as the outlet boundary condition, and choose the no-slip wall condition for the wall. The specific numerical values are given in

Table 1. Boundary condition parameters.

Boundary Conditions for Calculation	Parameters
Flow rate (m3/s)	232.77
Outlet absolute pressure At the tailrace (kPa)	307.26
Rotation speed (r/min)	166.7

.

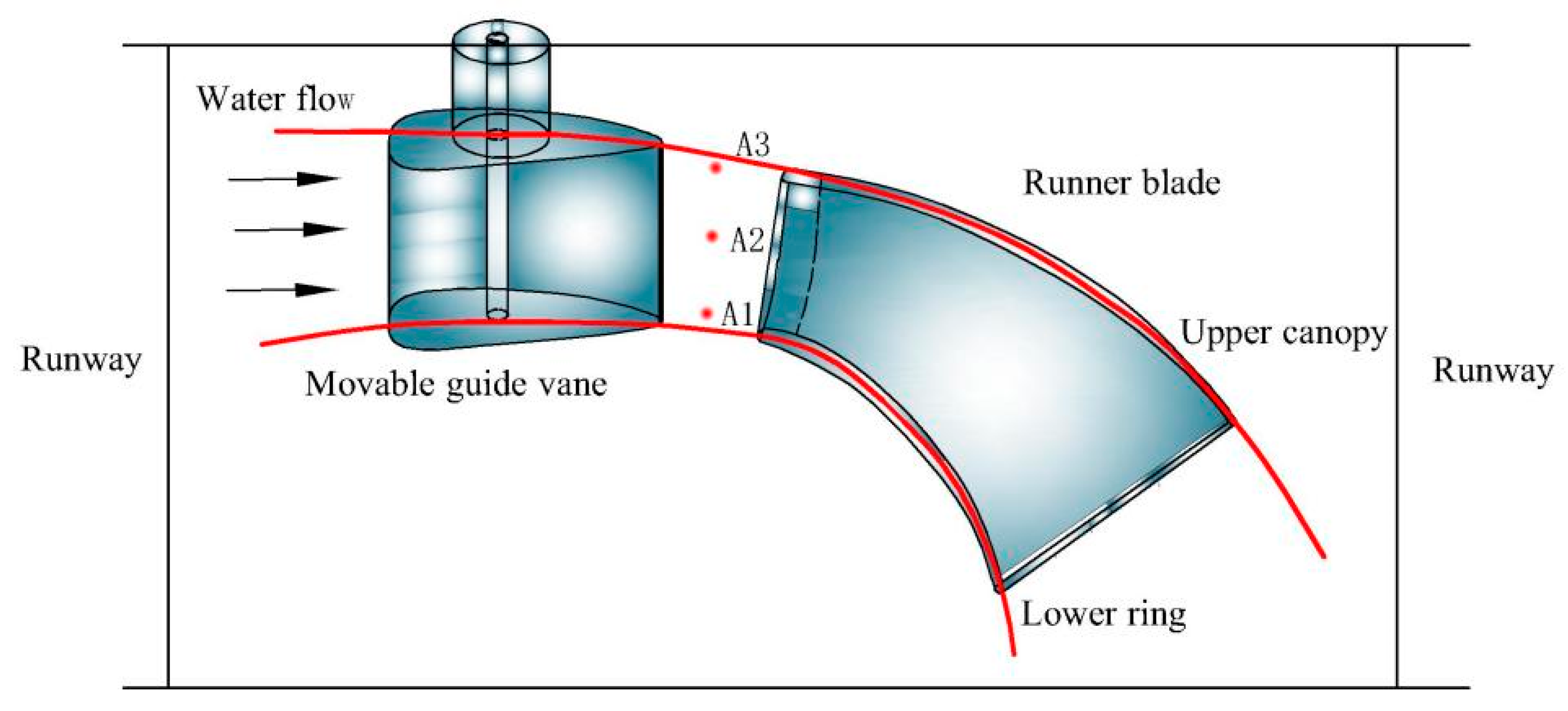
2.4. Configuration of Monitoring Points for Pressure Pulsation Calculation

To facilitate comparison with measured data, three computational monitoring points (A1, A2, and A3) were strategically placed within the bladeless region between the active guide vane and the runner inlet of the turbine. Point A3 was positioned at the top cover of the stay ring, which coincided with the sensor location. Additionally, two more computational monitoring points, A1 and A2, were introduced to further monitor pressure pulsations in the central region of the bladeless area. These points were located at 50% of the blade height and near the lower stay ring, as illustrated in Figure 3. This configuration allows us to observe and compare pressure variations within the entire bladeless region with greater precision, enabling a more accurate assessment of the turbine’s operational state. Additionally, this level of attention to detail and careful setup underscores our high standards and expertise in equipment monitoring and maintenance.

2.5. Field Testing

2.5.1. Test Methodology

The vibration monitoring system consists of three main components, including sensors, a signal acquisition unit, and a data processing unit. The signal acquisition unit is composed of intelligent data acquisition devices and DC power supply devices, responsible for collecting sensor signals and other data inputs. The data processing unit is managed by the main control workstation, which handles the real-time monitoring, analysis, and diagnostic applications of the system. Vibration sensors installed at designated locations convert vibration signals generated during the turbine’s operation into electrical signals. These signals are then transmitted to the intelligent data acquisition devices. The main control workstation retrieves the acquisition data from the intelligent data acquisition devices via Ethernet. After processing through software algorithms and data processing, various characteristic parameters reflecting the turbine’s operational status are obtained.

2.5.2. Sensor Measurement Point Arrangement

The selection and arrangement of sensor measurement points during on-site testing are presented in

Table 2. Selection and arrangement of sensor measurement point serial.

Serial Number	Signal Type	Measurement Point Name	Sensor Type
1	Vibration	Upper frame X-axis horizontal vibration	Low-frequency velocity vibration sensor
2		Upper frame Y-axis horizontal vibration	Low-frequency velocity vibration sensor
3		Upper frame vertical vibration	Low-frequency velocity vibration sensor
4		Lower frame X-axis horizontal vibration	Low-frequency velocity vibration sensor
5		Lower frame Y-axis horizontal vibration	Low-frequency velocity vibration sensor
6		Lower frame vertical vibration	Low-frequency velocity vibration sensor
7		Top cover X-axis horizontal vibration	Low-frequency velocity vibration sensor
8		Top cover Y-axis horizontal vibration	Low-frequency velocity vibration sensor
8		Top cover vertical vibration	Low-frequency velocity vibration sensor
10	Pressure pulsation	Guide vane outlet pressure pulsation	Pressure pulsation sensor
11		Top cover bottom pressure pulsation	Pressure pulsation sensor

.

3. Results and Analysis

3.1. Numerical Calculation Results

The flow distribution within the runner and guide vanes at three different blade heights under the operating conditions of relative opening at 80.449%, an active power of 218.863 MW, and a gross head of 110.19 m was obtained through numerical simulations, as shown in Figure 4, Figure 5 and Figure 6. At different time instants, the flow patterns within the flow field vary, and flow separation occurs as the water flows through the active guide vanes. From the figures, it can be observed that a Karman vortex appears at the rear of the active guide vanes, leading to turbine vibrations.

Under these operating conditions, the kinetic energy at the inlet region of the fixed guide vanes remains stable. However, significant flow separation occurs from the runner inlet to the outlet region. This is because the water jet impacts the leading edge of the runner blades at a large angle of attack, causing a noticeable flow separation vortex to form as the water flows from the runner blade inlet edge toward the blade’s backside. This results in an increase in vortex energy between the blades, generating significant turbulence. It is this flow separation that induces unstable flow within the turbine, leading to severe vibrations in the hydroelectric generator unit.

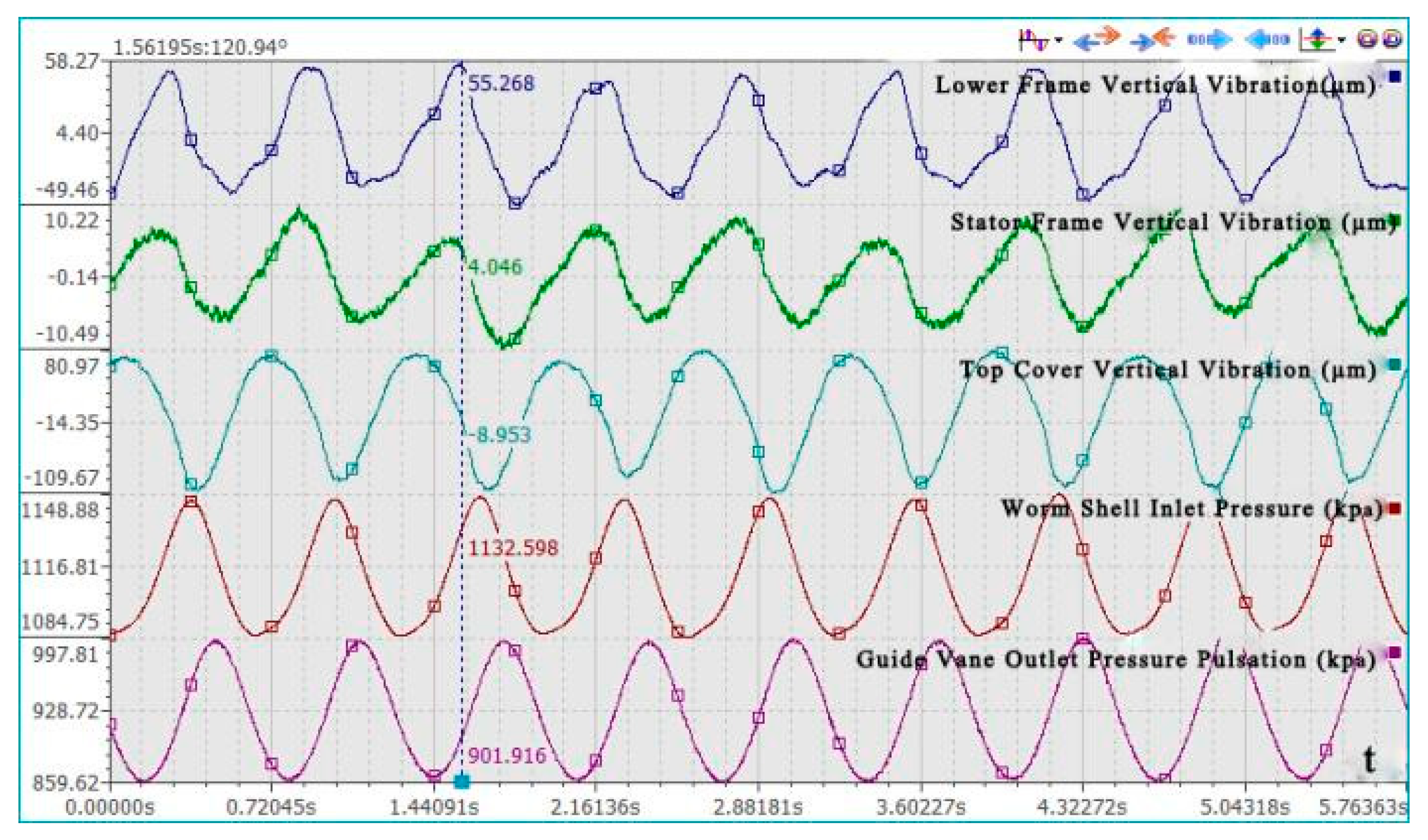
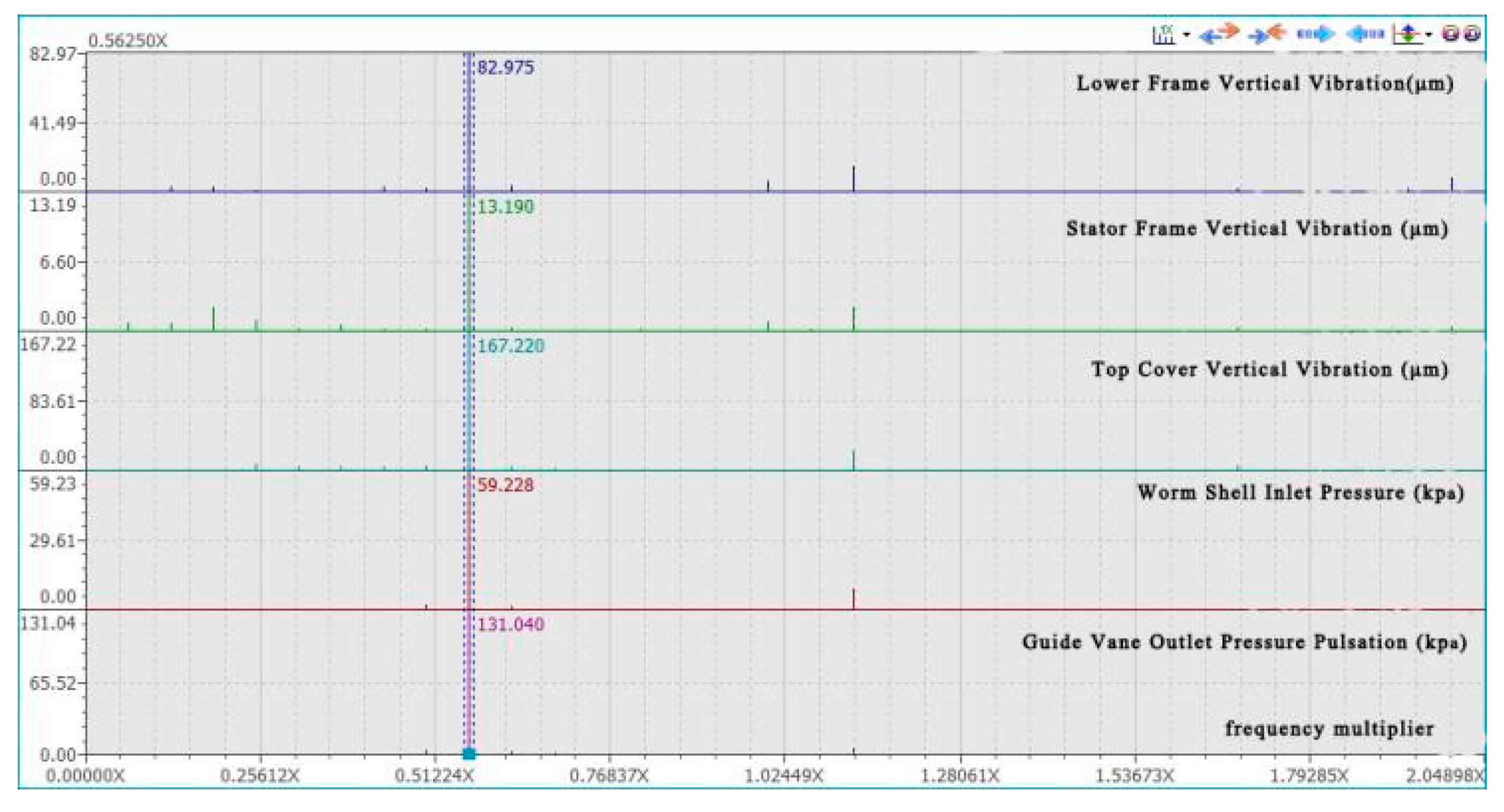
3.2. Field Test Results

The specific test data for severe abnormal vibrations of the unit under this operating condition are shown in

Table 3. Comparison table between unit swinging alarms and normal data.

Serial Number	Guide Vane Opening (%)	Active Power (MW)	Top Cover Vertical Vibration (μm)	Lower Frame Vertical Vibration (μm)	Spiral Casing Inlet Pressure Pulsation (kPa)	Guide Vane Outlet Pressure Pulsation (kPa)	Remarks
1	80.449	218.863	378	139	93.2	131.04	Alarm value
2	78	215.57	19	18	6.0	9.3	Normal Operating value

. From Table 3, it can be observed that during the abnormal operation of the unit, both the vertical vibration amplitude of the top cover and the vertical vibration amplitude of the lower frame have significantly exceeded the standard values. According to the standards [24], the vertical vibration displacement of the top cover should not exceed 90 μm, and the vertical vibration displacement of the lower frame should not exceed 70 μm.

Figure 7 and Figure 8 show the waveform and order ratio plots of some monitoring points obtained from the on-site online monitoring system during the abnormal vibration of the unit. It can be seen from the figures that the reason for the excessive vibration of the unit is the very clear 0.56250× low-frequency component present in both the unit’s vibration and pressure pulsation signals. Regarding the frequency components causing the excessive vibration amplitude, this frequency is mainly generated by hydraulic factors. Its source mainly originates from the instability of water flow in the bladeless area at the outlet of the unit’s guide vane, leading to a significant increase in pressure pulsation. This, in turn, generates a huge hydraulic force in the axial direction of the unit, resulting in excessive vertical vibrations of the top cover and lower frame.

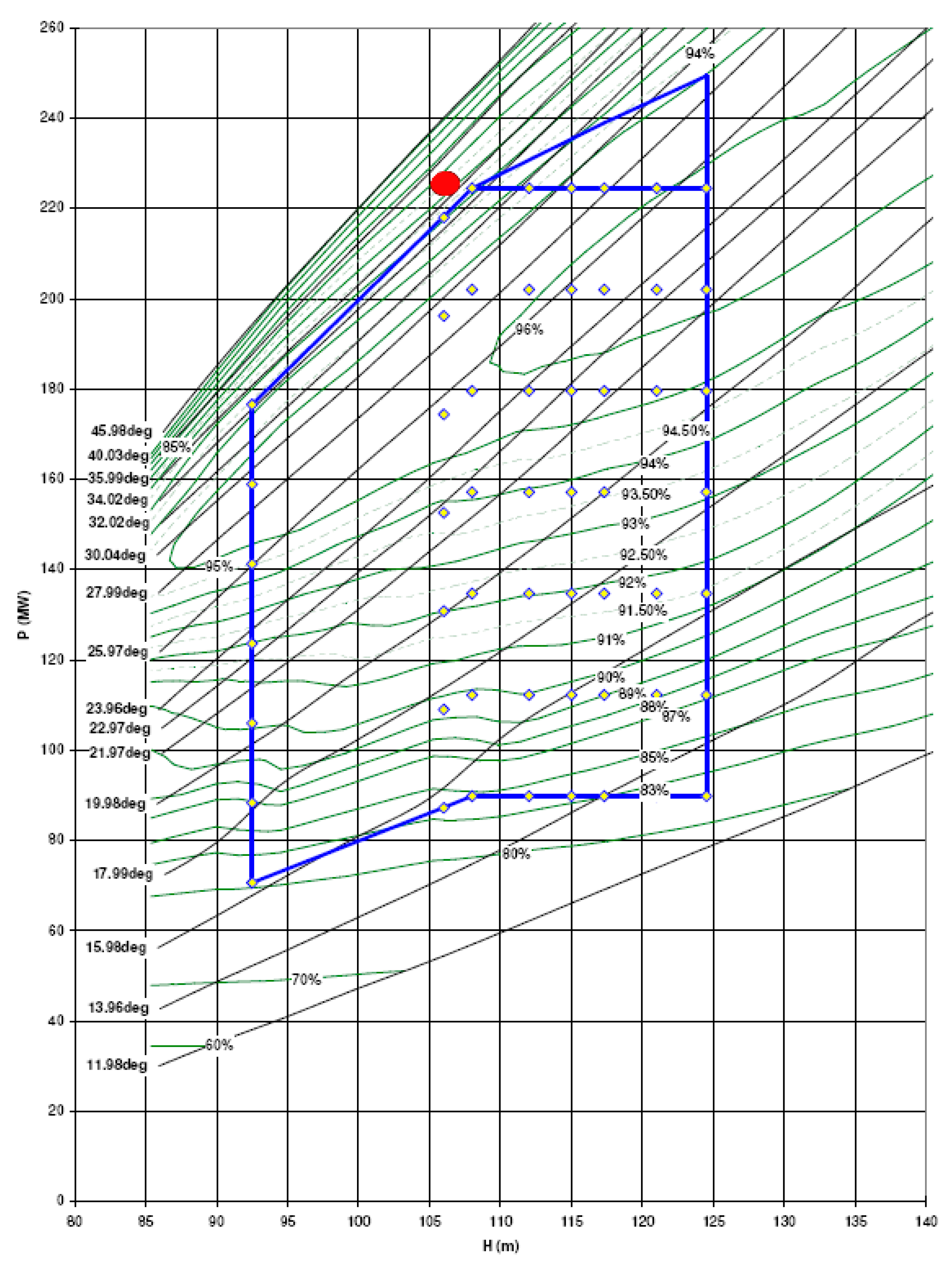
3.3. Verification Calculation of Working Head under Operating Conditions

After calculating the working head of the No.4 unit of Dongqing Hydropower Station operating at a relative openness of 80.449%, with an active power of 218.863 MW, and a gross head of 110.19 m, it was found that the operating condition points of severe vibration in the hydro-turbine generator set deviate from the safe operating range specified by the turbine manufacturer. The following details the specific calculation process [25,26,27].

Based on the field test data, including upstream and downstream water levels, gross head, active power, and generator efficiency, the output calculation formula for the hydro-turbine can be established as:

$$N=\rho \cdot \mathrm{g}\cdot Q\cdot H\cdot {\eta }_w\cdot {\eta }_e$$

(5)

In the formula, ρ represents the density of water; g is the acceleration due to gravity, a variable parameter; Q is the flow rate of water in the pipeline; H is the working head of the hydropower station; η_e is the efficiency of the generator; and η_w is the efficiency of the turbine.

Using the trial calculation method, and initially assuming the working efficiency of the turbine at this condition based on the turbine test report, with η_w = 92.3% and η_e = 98%, the flow rate of the turbine is calculated as:

$$Q=\frac{P}{\rho \cdot \mathrm{g}\cdot H\cdot {\eta }_w\cdot {\eta }_e}$$

(6)

From this, the total head loss in the water diversion system of the hydropower station can be calculated as:

$$\Delta H=\left({\displaystyle \sum S_{0}L}+{\displaystyle \sum T_0}\right)Q^2$$

(7)

In the formula, $T_0=\frac{8\zeta }{{\pi }^2\mathrm{g}{d}^4}$ represents the local specific resistance, S₀ is the pipe-specific resistance, L is the length of the pipe section, ζ is the coefficient of local head loss, and d is the hydraulic diameter.

Finally, $H=H_{\mathrm{g}}-\Delta H$ is calculated as the working head of the turbine, where H_g represents the gross head.

Based on the pressure pipeline layout diagram of the power station, the working head for the No.4 unit of the hydropower station operating at a relative openness of 80.449%, with an active power of 218.863 MW, and a gross head of 110.19 m, was calculated. The results are presented in

Table 4. Parameters of the turbine under full-load operating conditions.

Parameter Name	Parameter Values
Relative guide vane opening (%)	80.449
Flow rate (m³/s)	232.77
Gross head (m)	110.19
Head loss (m)	4.00
Working head (m)	106.19
Active power (MW)	218.863

.

The operating condition values from Table 4 are marked on the comprehensive characteristic curve diagram of the turbine operation for the station, as shown by the red circle in Figure 9. It was observed that the operating condition point (a relative openness of 80.449%, an active power of 218.863 MW, and a gross head of 110.19 m, corresponding to a working head of 106.19 m) has deviated from the normal operating range provided by the turbine manufacturer.

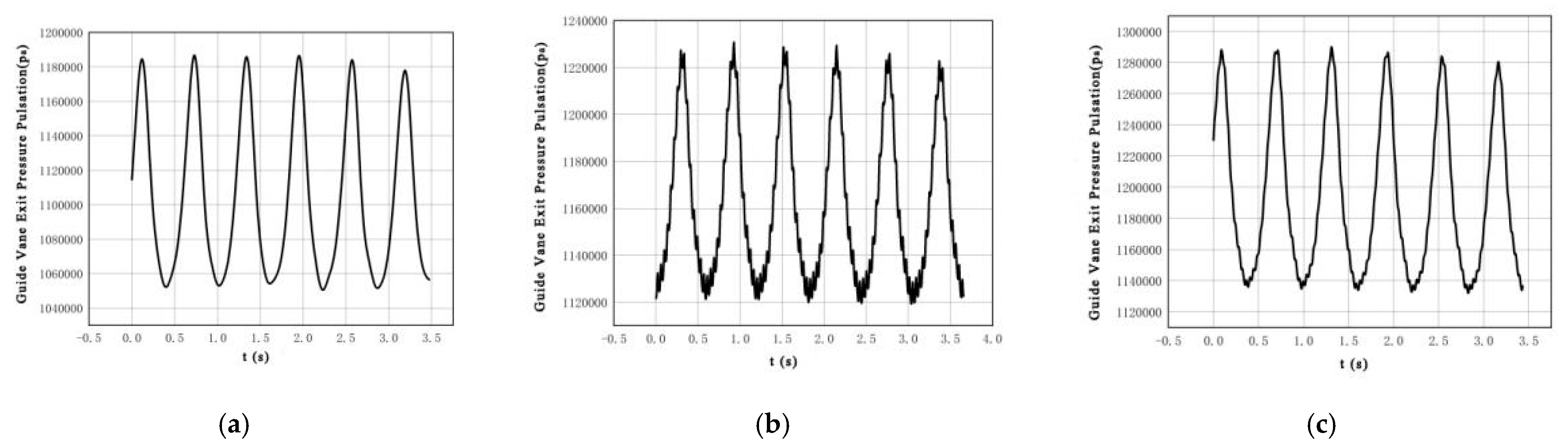
3.4. Calculation Results of Pressure Pulsation and Frequency at Monitoring Points

Through unsteady numerical simulations of the flow field, pressure pulsation curves and frequency curves at monitoring points were obtained. The results are presented in Figure 10 and Figure 11, which show the time-domain and frequency-domain diagrams of pressure pulsations at three computational monitoring points located at the exit of the movable guide vanes of the turbine under this abnormal operating condition. As shown in Figure 10, although there are minor differences in the pressure fluctuation amplitudes at the three different blade height positions at the monitoring points near the exit of the movable guide vanes, the pattern of pressure pulsation is essentially the same across these points, with similar main frequencies and amplitudes of pressure pulsation. Moreover, the amplitude of fluctuations is very large, exceeding 10 m of the water column, with the results at point A3 closely matching the field-measured data (as shown in Figure 7). Applying Fast Fourier Transform (FFT) spectral analysis, the frequency of pressure pulsations at the monitoring points was found to be 0.56250X (as shown in Figure 8), which is consistent with the calculated and measured values, as shown in Figure 11. This indicates that the numerical simulation method used in this paper can accurately predict the hydraulic performance of the turbine, with the amplitude and frequency of the main vibration sources obtained through numerical simulation corresponding well with the actual flow field test data under this operating condition.

Figure 12 shows the pressure distribution inside the turbine and guide vanes at a 50% blade height under 80% operating conditions of the hydro-turbine. The diagram reveals that under 80% operating conditions, the water pressure is relatively high around the guide vanes and lower in the turbine area. The pressure is stable at the inlet of the guide vanes but fluctuates significantly at the outlet. Additionally, the pressure inside the guide vanes exhibits good circumferential symmetry. At the turbine inlet, due to the impact of the water flow, the pressure increases noticeably compared to the surrounding water, and within the turbine flow field, the pressure first decreases, then increases, and decreases again from top to bottom. Due to the influence of the Karman vortex, significant flow separation occurs at the exit of the movable guide vanes, resulting in the boundary layer that was originally adhering to the wall at the front of the blade separating from the wall.

At a relative openness of 80%, the pattern of pressure pulsation amplitude changes at the three measurement points at the exit of the movable guide vanes is similar, with the pressure pulsation amplitudes being essentially the same and several times higher than the pressure pulsation values at the same points under normal operating conditions. With the increase in load, the flow rate of the unit increases, leading to higher head losses, resulting in a mismatch between the water flow characteristics and the guide vane profiles. This results in increased pressure pulsation at the exit of the movable guide vanes as the water flows around them, ultimately reducing the efficiency of the turbine.

3.5. Analysis of Abnormal Pressure Pulsation Formation

The experimental tests and computational results indicate that the high-amplitude pressure pulsations occurring under full-load conditions in the power station are directly related to the deviation of the turbine operating point from the operating region. The calculations and simulations have demonstrated that the hydraulic vibrations occurring in the Dongjing Hydropower Station’s turbine under the condition of a 222.8 MW load, a gross head of 110.19 m, and a relative opening of 80.449% are due to the operating point being outside the turbine output limit line on the comprehensive characteristic curve provided by the manufacturer. This deviation of the operating point leads to a detached flow in the moving guide vanes within the internal flow field, resulting in the generation of low-frequency Kármán vortex streets.

The coupling of the Kármán vortices at the exit of the moving guide vanes with the detached vortices occurring in the backside region of the turbine blade inlet leads to an abnormal increase in the amplitude of pressure pulsations in the vaneless space.

4. Conclusions

This paper, utilizing CFD software, conducted unsteady flow computations for the internal flow field of the No.4 unit of a hydropower station in Guizhou, and compared these with on-site experimental test data. Applying FFT spectrum analysis, the study investigated the pressure pulsation frequencies at monitoring points and arrived at the following conclusions:

• The generation of low-frequency, large-amplitude pressure pulsations at 0.56250X in the vaneless space of the turbine at the Guizhou Hydropower Station is due to the operating point deviating from the operational range. This deviation led to significant detached vortices in the backside area of the turbine blade inlets, causing low-frequency vibrations in the vaneless space and inducing unstable flows in the turbine.
• The coupling of the detached vortices from the trailing edge of the moving guide vanes with those formed in the backside area of the turbine blade inlets led to a dramatic increase in pressure pulsation amplitudes in the vaneless space, reaching 1.29 MPa, thus causing excessive vertical vibration amplitudes in the top cover and lower frame.
• These findings suggest that employing fluid simulation technology combined with experimental testing to analyze hydraulic vibrations in turbines is an effective approach. Simultaneously, by reducing the opening of the movable guide vanes and lowering the load, the abnormal vibrations of the turbine were eliminated.