Application of Fuzzy Neural Networks in Combustion Process Diagnostics
Abstract
:1. Introduction
2. Materials and Methods
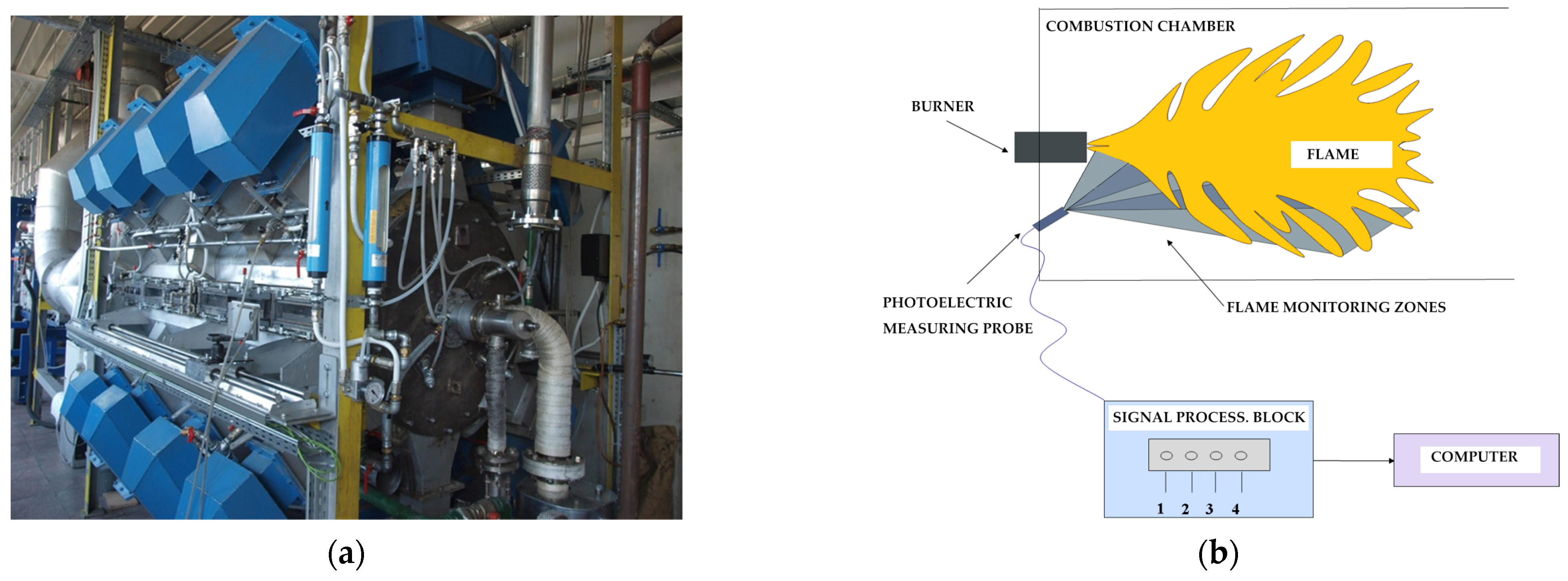
2.1. Measurement System
2.2. Analysis of Measurement Data
2.3. Flame Time Series Predictions Using the ARMA Model
- -
- p—the number of autoregression parameters,
- -
- q—the number of parameters of the moving average.
2.4. Classification of Flame States
- 0—stable,
- 1—flame with a rising exponential trend,
- 2—flame with an exponential downward trend,
- 3—flame with an increasing linear trend,
- 4—flame with a descending linear trend,
- 5—state of fading flame.
- True Positive Rate (TPR)—a measure of the probability of correct classification for the class “stable” if the case belongs to this class. It is expressed by the relation:
- True Negative Rate (TNR)—a measure of the probability of correct classification for the class “unstable” if the case belongs to this class. It is expressed as follows: True Negative (TN) is the number of unstable cases classified as unstable, and False Positive (FP) is the number of unstable cases classified as stable.
- Accuracy (ACC)—a parameter that evaluates what the probability of correct classification of cases is that belong to both classes, e.g., stable and unstable. It is calculated from the equation:
- Precision (PRE)—a parameter that evaluates what number of selected observations is accurate. It is calculated from the equation:
- F1 Score—a value based on precision and sensitivity parameters; it is calculated as follows:
3. Results and Discussion
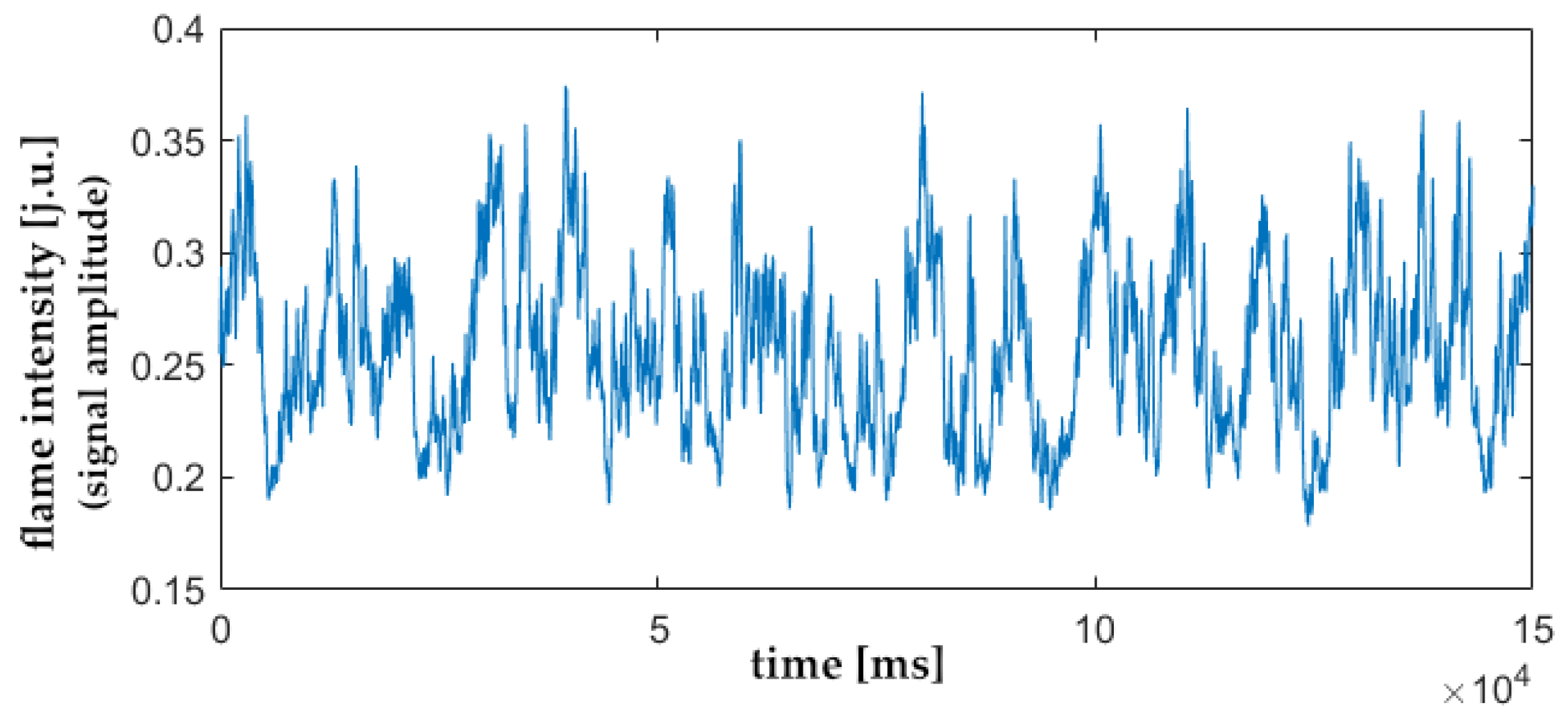
3.1. Statistical Analysis of Flame Signals
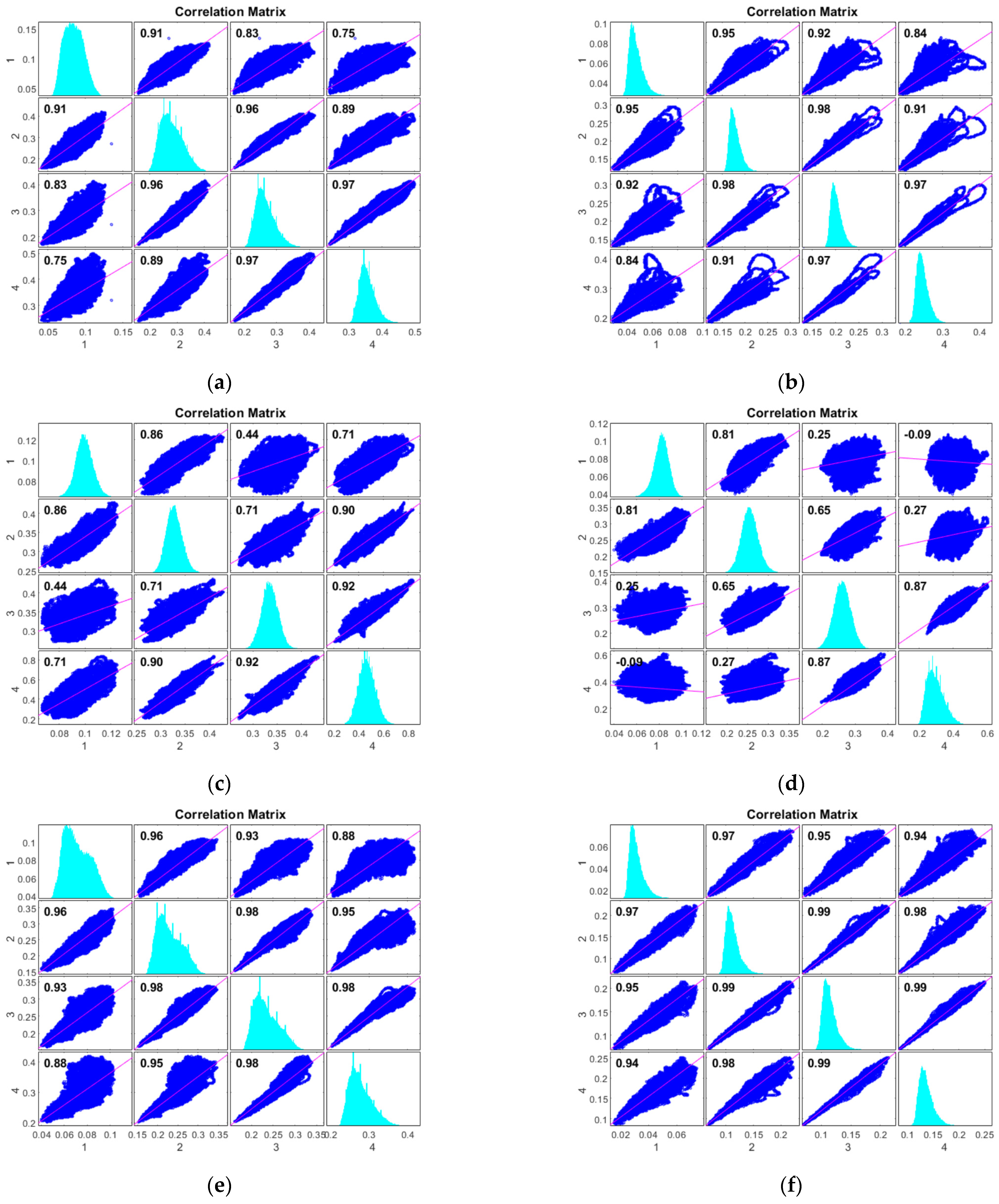
3.2. Correlation Coefficient
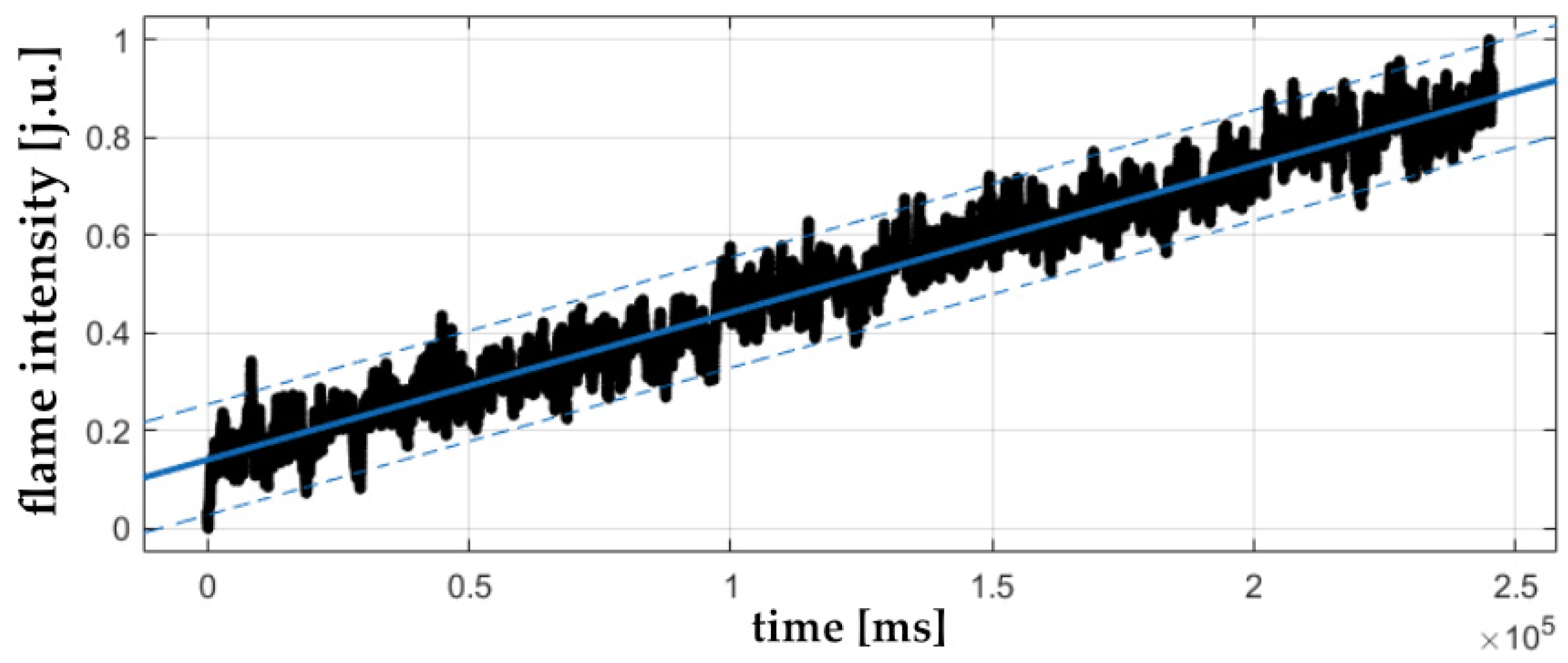
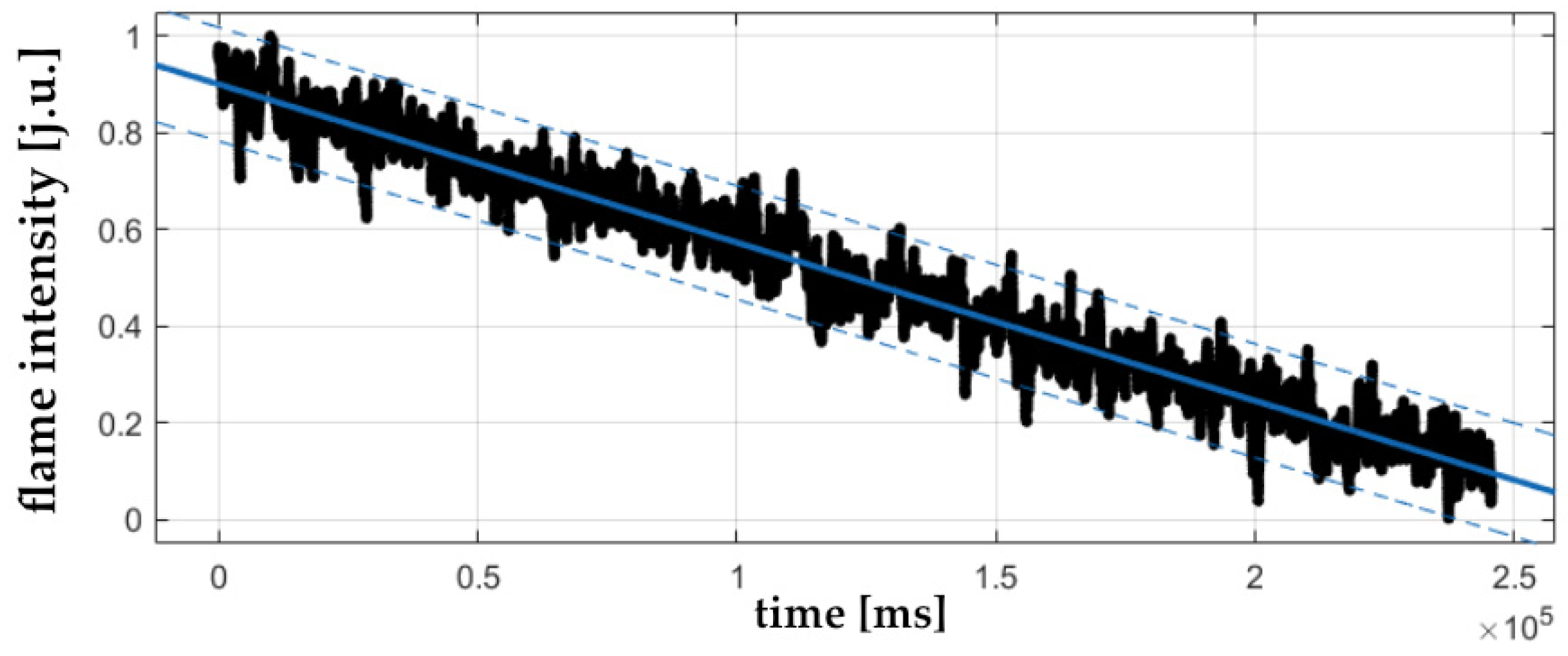
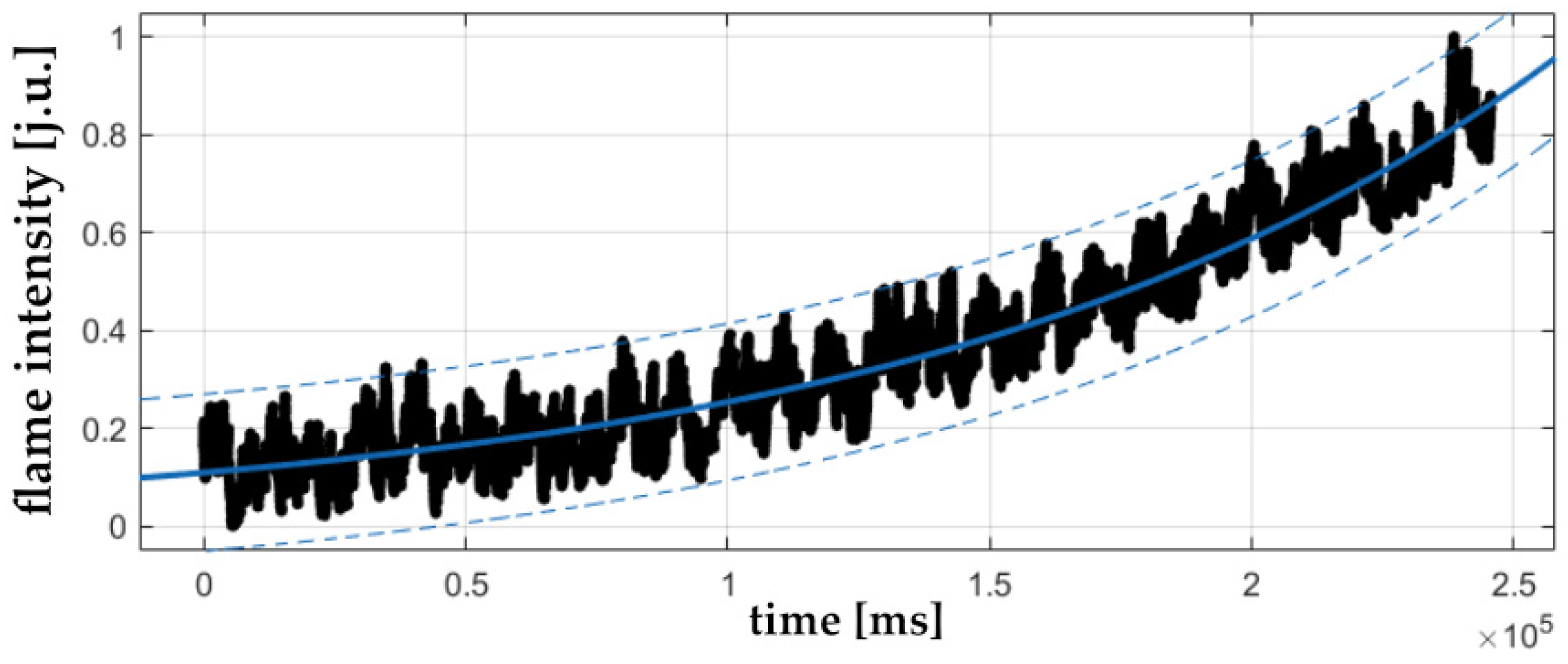
3.3. Determining Trends in Flame Signals
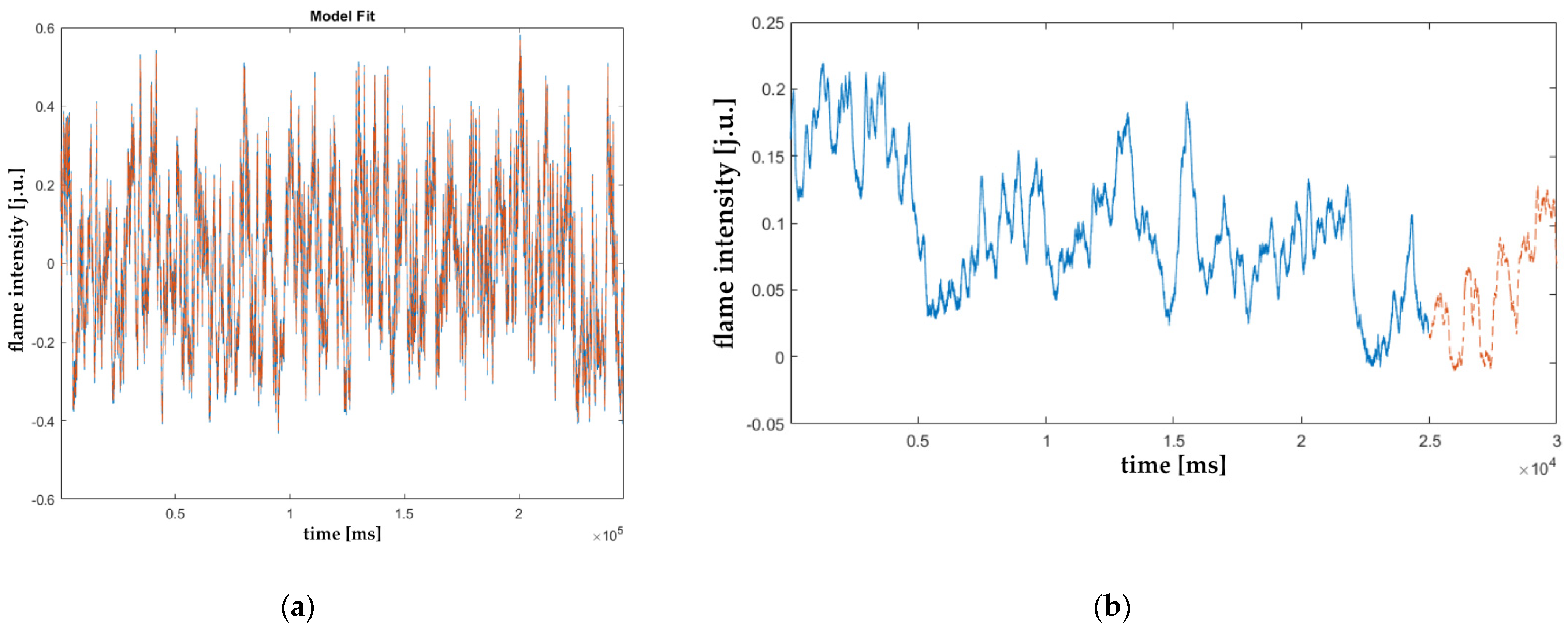
3.4. Flame Time Series Predictions Using the ARMA Model
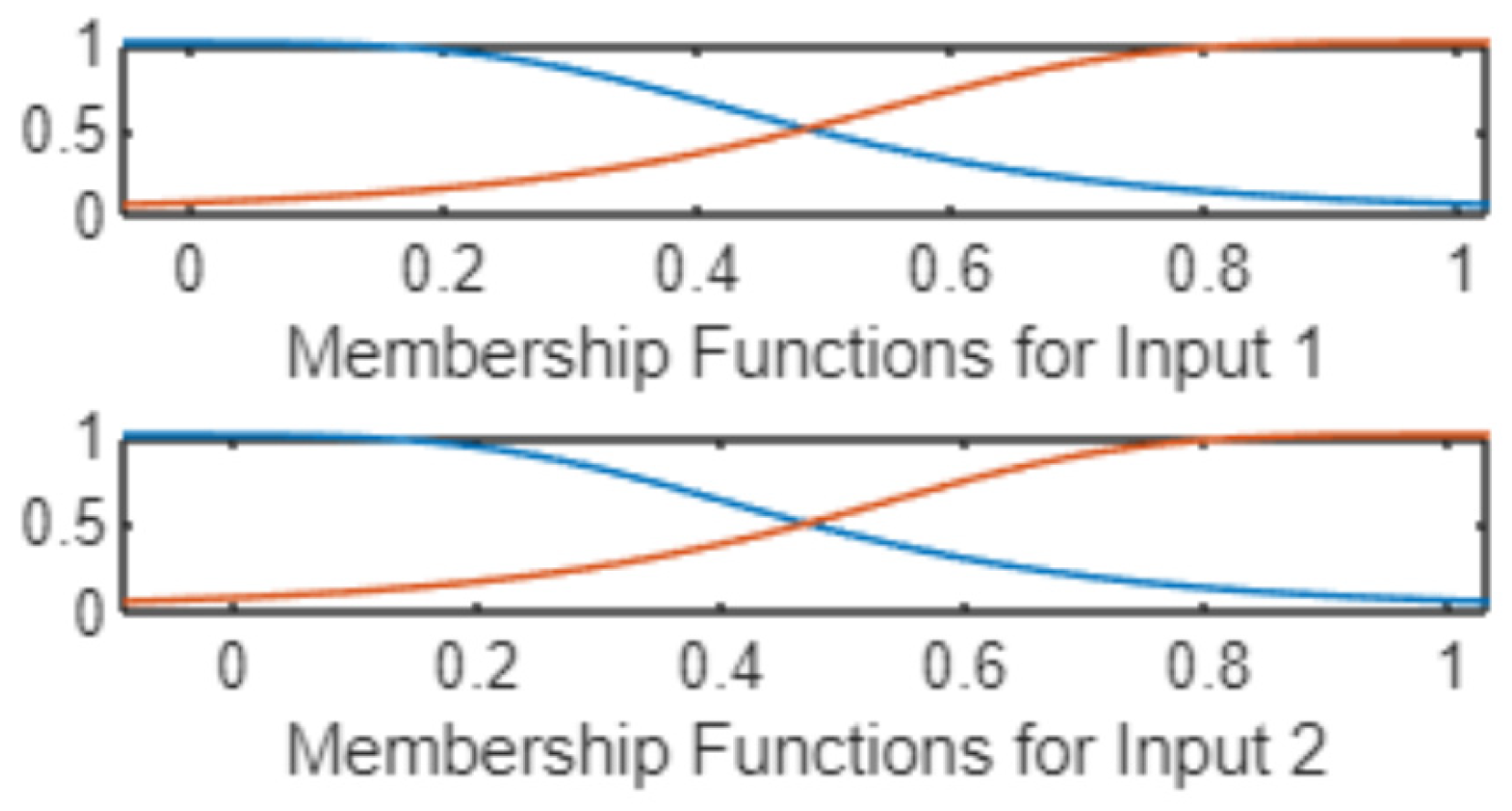
3.5. Classification of Flame States Using Fuzzy Neural Networks
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ministerstwo Klimatu i Środowiska. Polityka Energetyczna Polski do 2040 r; Ministerstwo Klimatu i Środowiska: Warsaw, Poland, 2021.
- Ministerstwo Klimatu i Środowiska, Surowce Strategiczne i Krytyczne dla Polski i UE. Available online: https://www.gov.pl/web/klimat/surowce-strategiczne-ikrytyczne-dla-polski-i-ue (accessed on 2 July 2022).
- Tainaka, K.; Hashimoto, N.; Umemoto, S.; Nakatsuka, N.; Hayashi, J.; Watanabe, H.; Akamatsu, F.; Makino, H. Measurement techniques for soot in pulverized coal combustion fields. J. Soc. Powder Technol. Jpn. 2018, 55, 275–281. [Google Scholar] [CrossRef]
- Idris, M.; Renz, U. Two colour pyrometer technique for coal particle temperature measurements in pressurised pulverised coal flame. J. Energy Inst. 2007, 80, 185–191. [Google Scholar] [CrossRef]
- Tian, F.; Zhang, H.; Tian, Y. Design and implementation of furnace temperature measurement system for power plant coal-fired boiler in acoustic method. MATEC Web Conf. 2018, 232, 04031. [Google Scholar] [CrossRef]
- Xu, W.; Yan, Y.; Huang, X.; Hu, Y. Quantitative measurement of the stability of a pulverized coal-fired flame through digital image processing and statistical analysis. Measurement 2023, 206, 112328. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, X.; Xu, M. Online measurement of soot formation distribution along time and axial in the volatile flames of coal and biomass using light scattering. J. Energy Inst. 2022, 105, 33–41. [Google Scholar] [CrossRef]
- Matthes, J.; Waibel, P.; Kollmer, M.; Aleksandrov, K.; Gehrmann, H.-J.; Stapf, D.; Vogelbacher, M. Camera based flame stability monitoring and control of multi-burner systems using deep learning based flame detection. Therm. Sci. Eng. Prog. 2023, 41, 101859. [Google Scholar] [CrossRef]
- Ma, P.; Huang, Q.; Wu, Z.; Lyu, J.; Li, S. Optical diagnostics on coal ignition and gas-phase combustion in co-firing ammonia with pulverized coal on a two-stage flat flame burner. Proc. Combust. Inst. 2023, 39, 3457–3466. [Google Scholar] [CrossRef]
- Kordylewski, W. Spalanie i Paliwa; Oficyna Wydawnicza Politechniki Wrocławskiej: Wrocław, Poland, 2008. [Google Scholar]
- Kordylewski, W. Niskoemisyjne Techniki Spalania w Energetyce; Oficyna Wydawnicza Politechniki Wrocławskiej: Wrocław, Poland, 2000. [Google Scholar]
- Li, S.; Xu, T.; Sun, P.; Zhou, Q.; Tan, H.; Hui, S. NOx and SOx emissions of a high sulfur self–retention coal during air-staged combustion. Fuel 2008, 87, 723–731. [Google Scholar] [CrossRef]
- Mollo, M.; Kolesnikov, A.; Makgato, S. Simultaneous reduction of NOx emission and SOx emission aided by improved efficiency of a Once-Through Benson Type Coal Boiler. Energy 2022, 248, 123551. [Google Scholar] [CrossRef]
- Wang, C.; Liu, Y.; Zheng, S.; Jiang, A. Optimizing combustion of coal-fired boilers for reducing NOx emission using Gaussian Process. Energy 2018, 153, 149–158. [Google Scholar] [CrossRef]
- Zheng, L.G.; Zhou, H.; Cen, K.F.; Wang, C.L. A comparative study of optimization algorithms for low NOx combustion modification at a coal-fired utility boiler. Expert Syst. Appl. 2009, 36, 2780–2793. [Google Scholar] [CrossRef]
- Ma, L.; Fang, Q.; Yin, C.; Wang, H.; Zhang, C.; Chen, G. A novel corner-fired boiler system of improved efficiency and coal flexibility and reduced NOx emissions. Appl. Energy 2019, 238, 453–465. [Google Scholar] [CrossRef]
- Li, S.; Xu, T.; Hui, S.; Wei, X. NOx emission and thermal efficiency of a 300 MWe utility boiler retrofitted by air staging. Appl. Energy 2009, 86, 1797–1803. [Google Scholar] [CrossRef]
- Hosseini, S.E. Fundamentals of Low Emission Flameless Combustion and Its Applications; Elsevier: Amsterdam, The Netherlands, 2022; pp. 1–652. [Google Scholar]
- Zhou, C.; Wang, Y.; Jin, Q.; Chen, Q.; Zhou, Y. Mechanism analysis on the pulverized coal combustion flame stability and NOx emission in a swirl burner with deep air staging. J. Energy Inst. 2019, 92, 298–310. [Google Scholar] [CrossRef]
- Minkyu, J.; Eunsong, L.; Minsu, K.; Hyunwook, J.; Sangbin, P.; Jun, H.C.; Sehyun, B.; Jongmin, L.; Sang-In, K. Nitric oxide (NO) and nitrous oxide (N2O) emissions during selective non-catalytic reduction and selective catalytic reduction processes in a pulverized coal/Ammonia Co-fired boiler. J. Environ. Chem. Eng. 2023, 11, 109398. [Google Scholar]
- Feng, D.; Shang, Q.; Dong, H.; Zhang, Y.; Wang, Z.; Li, D.; Sun, S. Catalytic mechanism of Na on coal pyrolysis–derived carbon black formation: Experiment and DFT simulation. Fuel Process. Technol. 2021, 224, 107011. [Google Scholar] [CrossRef]
- Choi, M.; Kim, K.; Li, X.; Deng, K.; Park, Y.; Seo, M.; Choi, G. Strategic combustion technology with exhaust tube vortex flame: Combined effect of biomass co–firing and air–staged combustion on combustion characteristics and ash deposition. Energy 2020, 203, 117839. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, Z.; Liu, J.; Zhuang, P.; Evrendilek, F.; Huang, S.; Sun, S. Optimizing co-combustion synergy of soil remediation biomass and pulverized coal toward energetic and gas-to-ash pollution controls. Sci. Total Environ. 2023, 857, 159585. [Google Scholar] [CrossRef]
- Hu, F.; Li, P.; Zhang, T.; Wang, F.; Cheng, P.; Liu, Y.; Liu, Z. MILD combustion of co–firing biomass and pulverized coal fuel blend for heterogeneous fuel NO and PM2.5 emission reduction. Fuel Process. Technol. 2022, 230, 107222. [Google Scholar] [CrossRef]
- Ma, P.; Huang, Q.; Si, T.; Yang, Y.; Li, S. Experimental investigation of NOx emission and ash–related issues in ammonia/coal/biomass co-combustion in a 25 kW down–fired furnace. Proc. Combust. Inst. 2023, 39, 3467–3477. [Google Scholar] [CrossRef]
- Xing, J.; Luo, K.; Kurose, R.; Fan, J. An extended flamelet/progress variable model for coal/biomass co-firing flame. Proc. Combust. Inst. 2023, 39, 3227–3237. [Google Scholar] [CrossRef]
- Molcan, P.; Lu, G.; Le Bris, T.; Yan, Y.; Taupin, B.; Caillat, S. Characterisation of biomass and coal co-firing on a 3 MWth Combustion Test Facility using flame imaging and gas/ash sampling techniques. Fuel 2009, 88, 2328–2334. [Google Scholar] [CrossRef]
- Seidel, T.; Krishnamoorthy, G.; Seames, W.S. Characterizing flame stability and radiative heat transfer in non-swirling oxy-coal flames using different multiphase modeling frameworks. Fuel 2019, 256, 115948. [Google Scholar] [CrossRef]
- Moroń, W.; Rybak, W. Ignition behaviour and flame stability of different ranks coals in oxy fuel atmosphere. Fuel 2015, 161, 174–181. [Google Scholar] [CrossRef]
- Santos, S.O.; Chen, S.; Zheng, C. A numerical investigation on flame stability of oxy–coal combustion: Effects of blockage ratio, swirl number, recycle ratio and partial pressure ratio of oxygen. Int. J. Greenh. Gas Control 2017, 57, 63–72. [Google Scholar]
- Corrêa Da Silva, R.; Kangwanpongpan, T.; Krautz, H.J. Flame pattern, temperatures and stability limits of pulverized oxy-coal combustion. Fuel 2014, 115, 507–520. [Google Scholar] [CrossRef]
- Lu, G.; Yan, Y.; Cornwell, S.; Whitehouse, M.; Riley, G. Impact of co-firing coal and biomass on flame characteristics and stability. Fuel 2008, 87, 1133–1140. [Google Scholar] [CrossRef]
- Su, S.; Pohl, J.H.; Holcombe, D.; Hart, J.A. Techniques to determine ignition, flame stability and burnout of blended coals in p.f. power station boilers. Prog. Energy Combust. Sci. 2001, 27, 75–98. [Google Scholar] [CrossRef]
- Yadav, S.; Yu, P.; Tanno, K.; Watanabe, H. Large eddy simulation of coal-ammonia flames with varied ammonia injection locations using a flamelet-based approach. Energy 2023, 276, 127546. [Google Scholar] [CrossRef]
- Zhao, D. Meso- and micro-scale combustion instability and flame characteristics. Thermoacoustic Combust. Instab. Control 2023, 741–829. [Google Scholar]
- Shaddix, C.; Molina, A. Ignition, flame stability, and char combustion. In Oxy-Fuel Combustion for Power Generation and Carbon Dioxide (CO2) Capture; Woodhead Publishing: Sawston, UK, 2011; pp. 101–124. [Google Scholar]
- Malmgren, A.; Riley, G. Biomass Power Generation. Compr. Renew. Energy 2012, 27–53. [Google Scholar]
- Wójcik, W.; Kotyra, A.; Smolarz, A.; Gromaszek, K. Modern Methods of Monitoring and Controlling Combustion of Solid Fuels in Order to Reduce Its Environmental Impact. Rocz. Ochr. Środowiska 2011, 13, 1559–1576. [Google Scholar]
- Sawicki, D.; Kotyra, A. Monitoring combustion process using image classification. Przegląd Elektrotechniczny 2014, 90, 130–132. [Google Scholar]
- Smolarz, A.; Wójcik, W.; Kotyra, A.; Wojciechowski, C.; Komada, P. Fibre optic monitoring system. Proc. SPIE Light. Their Appl. 2001, 4239, 129–132. [Google Scholar]
- Hotra, O.; Kovtun, S.; Dekusha, O.; Grądz, Ż. Prospects for the application of wavelet analysis to the results of thermal conductivity express control of thermal insulation materials. Energies 2021, 14, 5223. [Google Scholar] [CrossRef]
- Hotra, O.; Kovtun, S.; Dekusha, O.; Grądz, Ż.; Babak, V.; Styczeń, J. Analysis of Low-Density Heat Flux Data by the Wavelet Method. Energies 2023, 16, 430. [Google Scholar] [CrossRef]
- Grądz, Ż.; Klimek, J.; Kozak, C. Flame analysis by selected methods in the frequency domain. Inform. Autom. Pomiary w Gospod. i Ochr. Środowiska 2023, 12, 87–89. [Google Scholar] [CrossRef]
- Gradz, Ż.; Wojcik, W.; Kotyra, A. Analysis of changes in flame luminosity for process diagnostics. In Proceedings of the 2019 International Interdisciplinary PhD Workshop (IIPhDW), Wismar, Germany, 15–17 May 2019; pp. 84–88. [Google Scholar]
- Yadav, V.; Casel, M.; Ghani, A. Physics-informed recurrent neural networks for linear and nonlinear flame dynamics. Proc. Combust. Inst. 2023, 39, 1597–1606. [Google Scholar] [CrossRef]
- Sujatha, K.; Bhavani, N.P.G.; Srividhya, V.; Karthikeyan, V.; Jayachitra, N. Soft sensor with shape descriptors for flame quality prediction based on LSTM regression. Real-Time Data Anal. Large Scale Sens. Data 2020, 6, 115–138. [Google Scholar]
- ElSaid, A.E.R.; Benson, S.; Patwardhan, S.; Stadem, D.; Desell, T. Evolving recurrent neural networks for time series data prediction of coal plant parameters. In Proceedings of the Applications of Evolutionary Computation: 22nd International Conference, EvoApplications 2019, Held as Part of EvoStar 2019, Leipzig, Germany, 24–26 April 2019; pp. 488–503. [Google Scholar]
- Lyu, Z.; Jia, X.; Yang, Y.; Hu, K.; Zhang, F.; Wang, G. A comprehensive investigation of LSTM–CNN deep learning model for fast detection of combustion instability. Fuel 2021, 303, 121300. [Google Scholar] [CrossRef]
- Jadidi, M.; Di Liddo, L.; Dworkin, S.B. A Long Short-Term Memory Neural Network for the Low-Cost Prediction of Soot Concentration in a Time-Dependent Flame. Energies 2021, 14, 1394. [Google Scholar] [CrossRef]
- Ren, J.; Wang, H.; Chen, G.; Luo, K.; Fan, J. Predictive models for flame evolution using machine learning: A priori assessment in turbulent flames without and with mean shear. Phys. Fluids 2021, 33, 55113. [Google Scholar] [CrossRef]
- Bhattacharya, C.; Ray, A. Thresholdless Classification of chaotic dynamics and combustion instability via probabilistic finite state automata. Mech. Syst. Signal Process. 2022, 164, 108213. [Google Scholar] [CrossRef]
- Omiotek, Z.; Smolarz, A. Combustion process monitoring based on flame intensity time series. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2020, 235, 809–822. [Google Scholar] [CrossRef]
- Choi, O.; Choi, J.; Kim, N.; Lee, M.C. Combustion Instability Monitoring through Deep-Learning-Based Classification of Sequential High-Speed Flame Images. Electronics 2020, 9, 848. [Google Scholar] [CrossRef]
- Ronquillo-Lomeli, G.; Romero, C.E.; Yao, Z.; Si, F.; Coria-Silva, R.; Hernandez-Rosales, F.; Trejo-Morales, A. On-line flame signal time series analysis for oil-fired burner optimization. Fuel 2015, 158, 416–423. [Google Scholar] [CrossRef]
- Wang, Y.; Bao, D.; Qin, S.J. A novel bidirectional DiPLS based LSTM algorithm and its application in industrial process time series prediction. Chemom. Intell. Lab. Syst. 2023, 240, 104878. [Google Scholar] [CrossRef]
- Gangopadhyay, T.; Tan, S.Y.; LoCurto, A.; Michael, J.B.; Sarkar, S. Interpretable Deep Learning for Monitoring Combustion Instability. IFAC-PapersOnLine 2020, 53, 832–837. [Google Scholar] [CrossRef]
- Chaudhry, Q.; Chrétien, J.; Craciun, M.; Guo, G.; Lemke, F.; Müller, J.A.; Neagu, D.; Piclin, N.; Pintore, M.; Trundle, P. Chapter 4—Algorithms for (Q)SAR model building. In Quantitative Structure-Activity Relationships (QSAR) for Pesticide Regulatory Purposes; Benfenati, E., Ed.; Elsevier: Amsterdam, The Netherlands, 2007; pp. 111–147. [Google Scholar]
- Zadeh, L. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Riza, L.; Bergmeir, C.; Herrera, F.; Benitez, J. FRBS: Fuzzy rule-based systems for classication and regression in r. J. Stat. Softw. 2015, 65, 1–30. [Google Scholar] [CrossRef]
- Quteishat, A.; Lim, C.P. A modified fuzzy min–max neural network with rule extraction and its application to fault detection and classification. Appl. Soft Comput. 2008, 8, 985–995. [Google Scholar] [CrossRef]
- Qiao, L.; Yang, P.; Leng, Q.; Xu, L.; Bi, Y.; Xu, J.; Wang, Z.; Liu, J.; Yin, W.; Zhang, L.; et al. Exploring ANFIS application based on actual data from wastewater treatment plant for predicting effluent removal quality of selected major pollutants. J. Water Process Eng. 2023, 56, 104247. [Google Scholar] [CrossRef]
- Smolarz, A.; Wójcik, W.; Gromaszek, K. Fuzzy Modeling for Optical Sensor for Diagnostics of Pulverized Coal Burner. Procedia Eng. 2012, 47, 1029–1032. [Google Scholar] [CrossRef]
- Smolarz, A.; Kotyra, A.; Wójcik, W.; Ballester, J. Advanced diagnostics of industrial pulverized coal burner using optical methods and artificial intelligence. Exp. Therm. Fluid Sci. 2012, 43, 82–89. [Google Scholar] [CrossRef]
- Wójcik, W. Optical fibre system for flame monitoring in energetic boilers. Technol. Appl. Light. Proc. SPIE 1997, 3189, 74–82. [Google Scholar]
- Grądz, Ż. Research on the combustion process using time series. Inform. Autom. Pomiary w Gospod. i Ochr. Środowiska 2020, 10, 52–55. [Google Scholar] [CrossRef]
- Wójcik, W. Nowoczesne Technologie Paliw i Spalania; Monografie Komitetu Inżynierii Środowiska PAN: Lublin, Poland, 2011. [Google Scholar]
- Mathworks. Available online: https://uk.mathworks.com/ (accessed on 5 May 2023).
- Bronsztejn, I.N.; Muhlig, H.; Musiol, G.; Siemiendiajew, K.A. Nowoczesne Kompendium Matematyki; Wydawnictwo Naukowe PWN: Warszawa, Poland, 2009. [Google Scholar]
- Box, G.E.P.; Jenkins, G.M. Analiza Szeregów Czasowych—Prognozowanie i Sterowanie; Państwowe Wydawnictwo Naukowe: Warszawa, Poland, 1983. [Google Scholar]
- StatSoft. Electronic Textbook StatSoft—Analiza Szeregów Czasowych. Available online: https://www.statsoft.pl/textbook/stathome_stat.html?https%3A%2F%2Fwww.statsoft.pl%2Ftextbook%2Fsttimser.html (accessed on 1 March 2023).




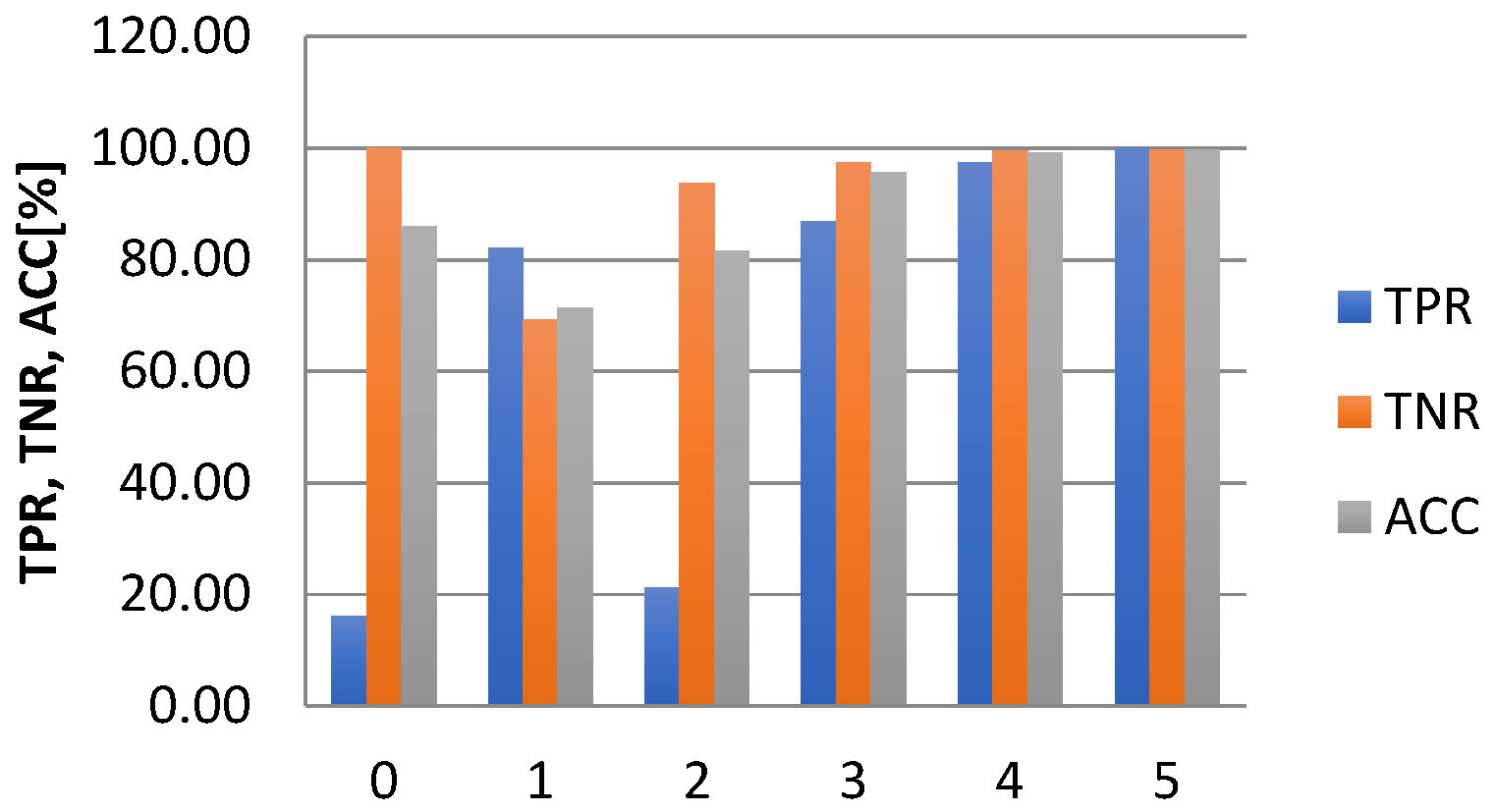

| Flame Signal Number | Fuel | Minimum Value | Maximum Value | Average Value | Root Mean Square Value | Standard Deviation | Coefficient of Variation [%] |
|---|---|---|---|---|---|---|---|
| 1_channel1 | 100% pulverized coal | 0.0413 | 0.1345 | 0.0785 | 0.0798 | 0.0143 | 18.2172 |
| 1_channel2 | 0.1574 | 0.4186 | 0.2578 | 0.2578 | 0.0395 | 15.4895 | |
| 1_channel3 | 0.1696 | 0.4153 | 0.2524 | 0.2545 | 0.0328 | 12.98,04 | |
| 1_channel4 | 0.2391 | 0.5000 | 0.3252 | 0.3269 | 0.0327 | 10.0675 | |
| 2_channel1 | 0.0282 | 0.0849 | 0.0403 | 0.0407 | 0.0057 | 14.1211 | |
| 2_channel2 | 0.1184 | 0.2946 | 0.1520 | 0.1529 | 0.0157 | 10.3252 | |
| 2_channel3 | 0.1315 | 0.2982 | 0.1656 | 0.1663 | 0.0153 | 9.2587 | |
| 2_channel4 | 0.1850 | 0.4130 | 0.2281 | 0.2289 | 0.0192 | 8.4217 | |
| 3_channel1 | 0.0666 | 0.1250 | 0.0950 | 0.0953 | 0.0069 | 7.2773 | |
| 3_channel2 | 0.2585 | 0.4285 | 0.3277 | 0.3282 | 0.0185 | 5.6302 | |
| 3_channel3 | 0.2713 | 0.4347 | 0.3364 | 0.3369 | 0.0185 | 5.4973 | |
| 3_channel4 | 0.3441 | 0.5866 | 0.4238 | 0.4247 | 0.0277 | 6.5352 | |
| 4_channel1 | 80% pulverized coal with 20% biomass | 0.0400 | 0.1069 | 0.0773 | 0.0776 | 0.0170 | 21.9923 |
| 4_channel2 | 0.1843 | 0.3477 | 0.2597 | 0.2604 | 0.0192 | 7.3835 | |
| 4_channel3 | 0.1948 | 0.3904 | 0.2782 | 0.2792 | 0.0241 | 8.6503 | |
| 4_channel4 | 0.2418 | 0.6034 | 0.3470 | 0.3500 | 0.0462 | 13.3201 | |
| 5_channel1 | 0.0396 | 0.1036 | 0.0648 | 0.0658 | 0.0114 | 17.5534 | |
| 5_channel2 | 0.1522 | 0.3461 | 0.2191 | 0.2214 | 0.0322 | 14.6776 | |
| 5_channel3 | 0.1604 | 0.3389 | 0.2234 | 0.2254 | 0.0300 | 13.4112 | |
| 5_channel4 | 0.2017 | 0.4186 | 0.2710 | 0.2731 | 0.0338 | 12.4776 | |
| 6_channel1 | 0.0154 | 0.0744 | 0.0284 | 0.0291 | 0.0062 | 21.9591 | |
| 6_channel2 | 0.0682 | 0.2227 | 0.1033 | 0.1046 | 0.0160 | 15.5302 | |
| 6_channel3 | 0.0711 | 0.2142 | 0.1051 | 0.1062 | 0.0148 | 14.0935 | |
| 6_channel4 | 0.0859 | 0.2506 | 0.1252 | 0.1263 | 0.0171 | 13.6292 |
| Flame Signal Number | SSE | R2 | RMSE | Number of Coefficients |
|---|---|---|---|---|
| 1 | 6424 | 0.0250 | 0.1617 | 2 |
| 7 | 475.3125 | 0.9594 | 0.0440 | 2 |
| 13 | 512.7889 | 0.9628 | 0.0457 | 2 |
| 19 | 949.7369 | 0.9202 | 0.0622 | 2 |
| 25 | 2010 | 0.7615 | 0.0904 | 2 |
| Flame Signal Number | Model Parameter | Value | Standard Error | Statistics t |
|---|---|---|---|---|
| 1 | Constant value | –6.7588 × 10−7 | 6.4078 × 10−6 | –0.1055 |
| AR{1} | 0.9999 | 3.3437 × 10−5 | 2.9903 × 10−4 | |
| MA{1} | –0.5775 | 0.0015 | –373.9257 | |
| Variance | 5.6424 × 10−5 | 1.4437 × 10−7 | 390.8195 | |
| 7 | Constant value | 9.9979 × 10−8 | 3.7923 × 10−6 | 0.0264 |
| AR{1} | 0.9992 | 0.8581 × 10−4 | 1.1644 × 10−4 | |
| MA{1} | –0.5058 | 0.0020 | –251.4473 | |
| Variance | 1.3065 × 10−5 | 3.0852 × 10−8 | 423.4724 | |
| 13 | Constant value | –1.0662 × 10−7 | 4.0297 × 10−6 | –0.0265 |
| AR{1} | 0.9992 | 8.6789 × 10−5 | 1.1513 × 10−4 | |
| MA{1} | –0.5481 | 0.0019 | –281.4230 | |
| Variance | 1.7332 × 10−5 | 4.4769 × 10−8 | 387.1379 | |
| 19 | Constant value | 1.4874 × 10−6 | 1.5015 × 10−6 | 0.9906 |
| AR{1} | 1 | 1.7996 × 10−5 | 5.5567 × 10−4 | |
| MA{1} | –0.5787 | 0.0015 | –375.9948 | |
| Variance | 3.1232 × 10−6 | 1.6239 × 10−8 | 192.3328 | |
| 25 | Constant value | 3.2273 × 10−7 | 2.0362 × 10−6 | 0.1585 |
| AR{1} | 0.9999 | 1.9903 × 10−5 | 50240 | |
| MA{1} | –0.4067 | 0.0015 | –265.2504 | |
| Variance | 2.9296 × 10−6 | 1.4723 × 10−8 | 198.9732 |
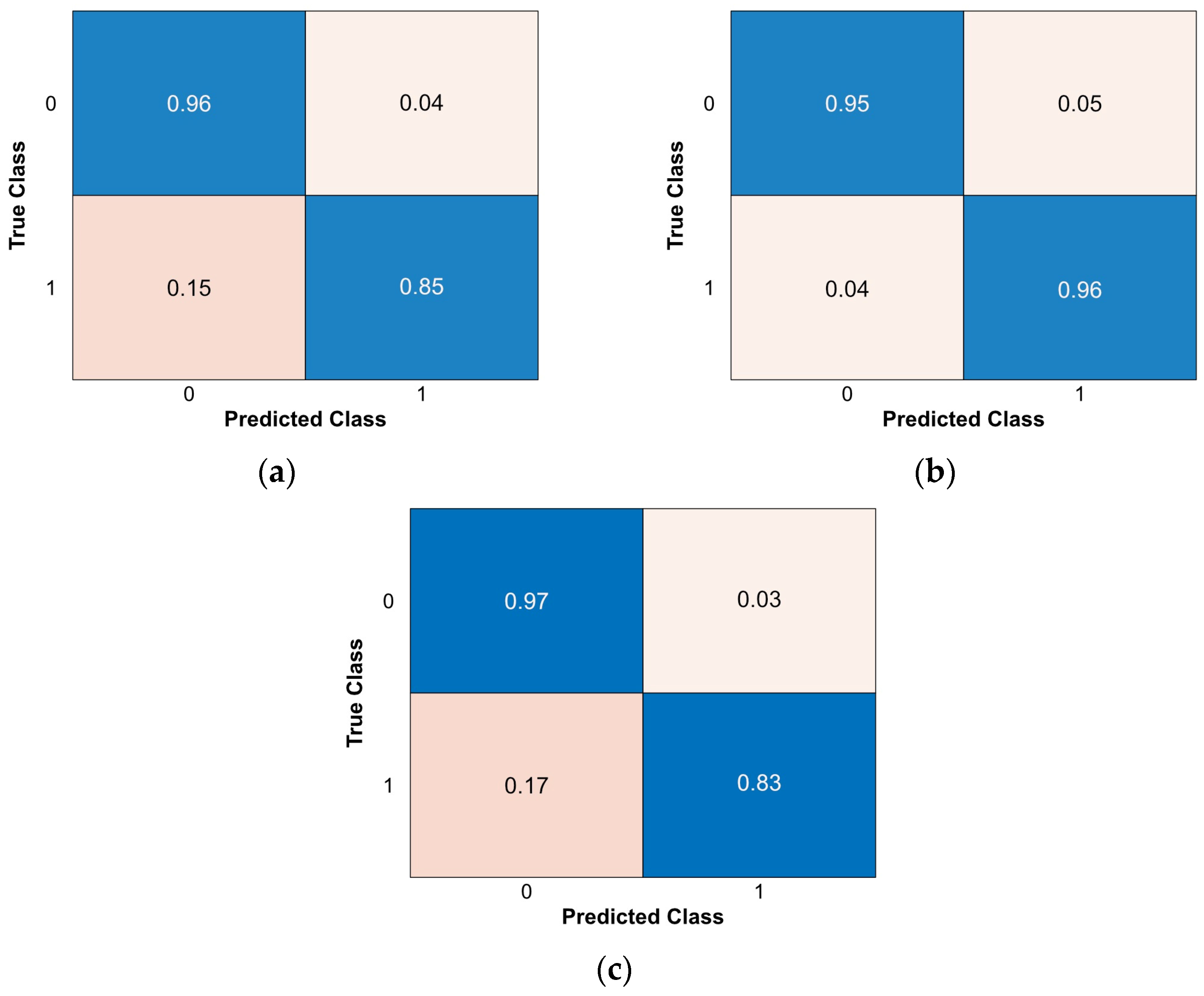
| Model | Sensitivity | Precision | F1 Score | Accuracy [%] |
|---|---|---|---|---|
| ANFIS_FCM | 0.96 | 0.86 | 0.91 | 90.43 |
| ANFIS_GP | 0.95 | 0.96 | 0.95 | 95.46 |
| ANFIS_SC | 0.97 | 0.85 | 0.91 | 89.96 |
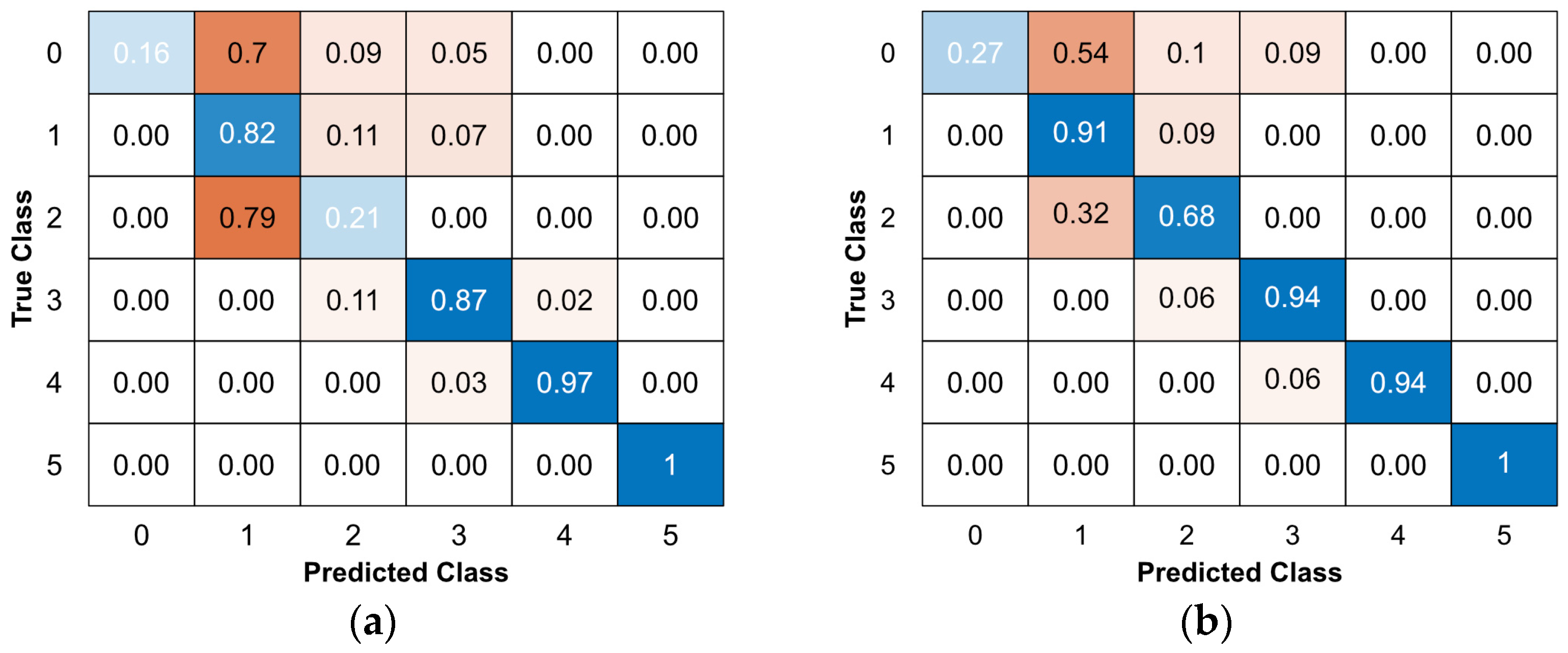
| Model | Class | Sensitivity | Precision | F1 Score | Accuracy [%] |
|---|---|---|---|---|---|
| ANFIS_FCM | 0 | 0.16 | 1.00 | 0.28 | 67.07 |
| 1 | 0.82 | 0.36 | 0.50 | ||
| 2 | 0.21 | 0.40 | 0.28 | ||
| 3 | 0.87 | 0.87 | 0.87 | ||
| 4 | 0.97 | 0.98 | 0.98 | ||
| 5 | 1.00 | 0.99 | 0.99 | ||
| ANFIS_GP | 0 | 0.27 | 1.00 | 0.43 | 79.08 |
| 1 | 0.91 | 0.52 | 0.66 | ||
| 2 | 0.68 | 0.74 | 0.71 | ||
| 3 | 0.94 | 0.93 | 0.93 | ||
| 4 | 0.94 | 1.00 | 0.97 | ||
| 5 | 1.00 | 1.00 | 1.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grądz, Ż.; Wójcik, W.; Gromaszek, K.; Kotyra, A.; Smailova, S.; Iskakova, A.; Yeraliyeva, B.; Kumargazhanova, S.; Imanbek, B. Application of Fuzzy Neural Networks in Combustion Process Diagnostics. Energies 2024, 17, 212. https://doi.org/10.3390/en17010212
Grądz Ż, Wójcik W, Gromaszek K, Kotyra A, Smailova S, Iskakova A, Yeraliyeva B, Kumargazhanova S, Imanbek B. Application of Fuzzy Neural Networks in Combustion Process Diagnostics. Energies. 2024; 17(1):212. https://doi.org/10.3390/en17010212
Chicago/Turabian StyleGrądz, Żaklin, Waldemar Wójcik, Konrad Gromaszek, Andrzej Kotyra, Saule Smailova, Aigul Iskakova, Bakhyt Yeraliyeva, Saule Kumargazhanova, and Baglan Imanbek. 2024. "Application of Fuzzy Neural Networks in Combustion Process Diagnostics" Energies 17, no. 1: 212. https://doi.org/10.3390/en17010212
APA StyleGrądz, Ż., Wójcik, W., Gromaszek, K., Kotyra, A., Smailova, S., Iskakova, A., Yeraliyeva, B., Kumargazhanova, S., & Imanbek, B. (2024). Application of Fuzzy Neural Networks in Combustion Process Diagnostics. Energies, 17(1), 212. https://doi.org/10.3390/en17010212






