A Case Study on the CO2 Sequestration in Shenhua Block Reservoir: The Impacts of Injection Rates and Modes
Abstract
:1. Introduction
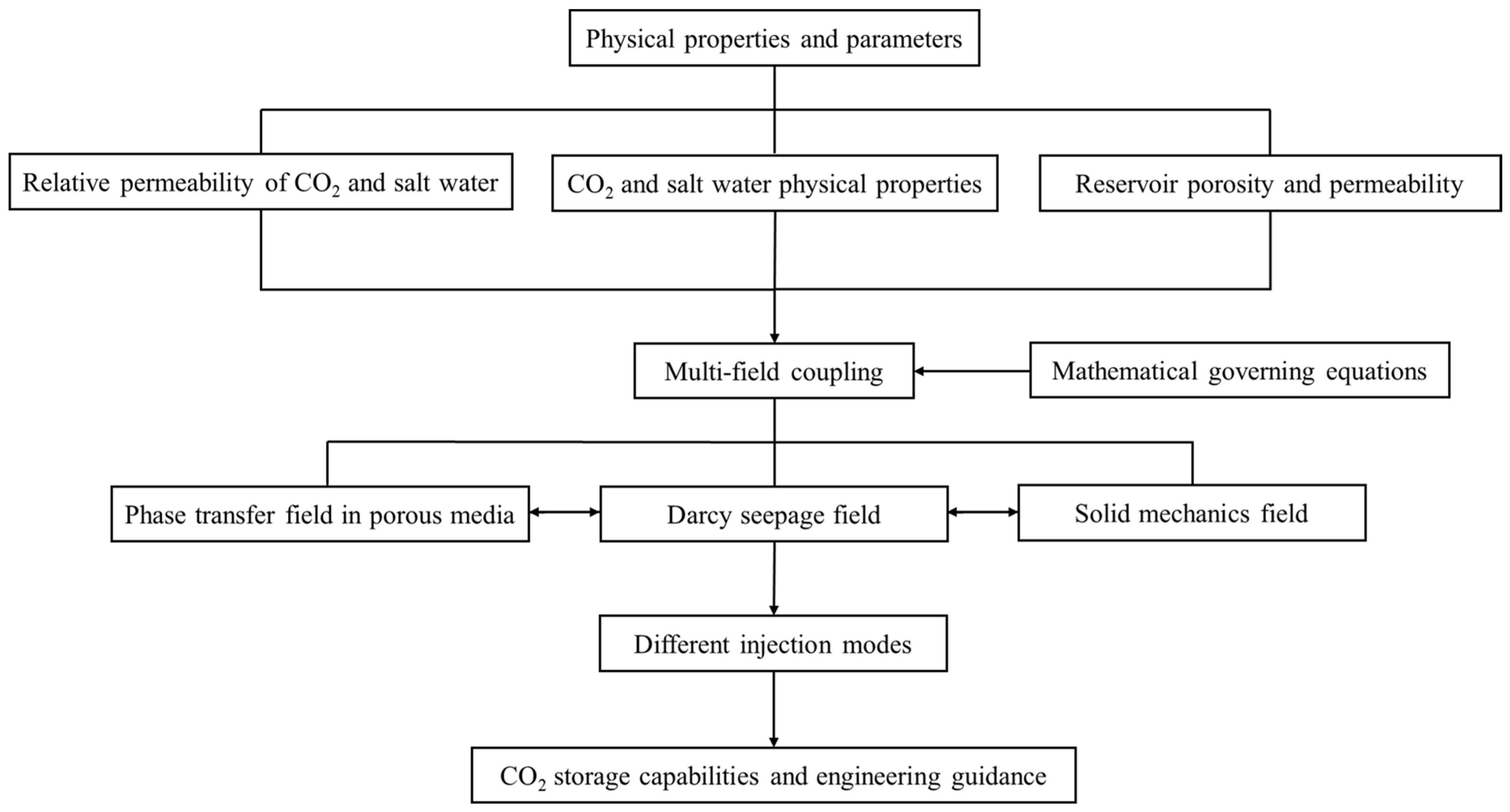
2. Methodology
2.1. Mathematical Model
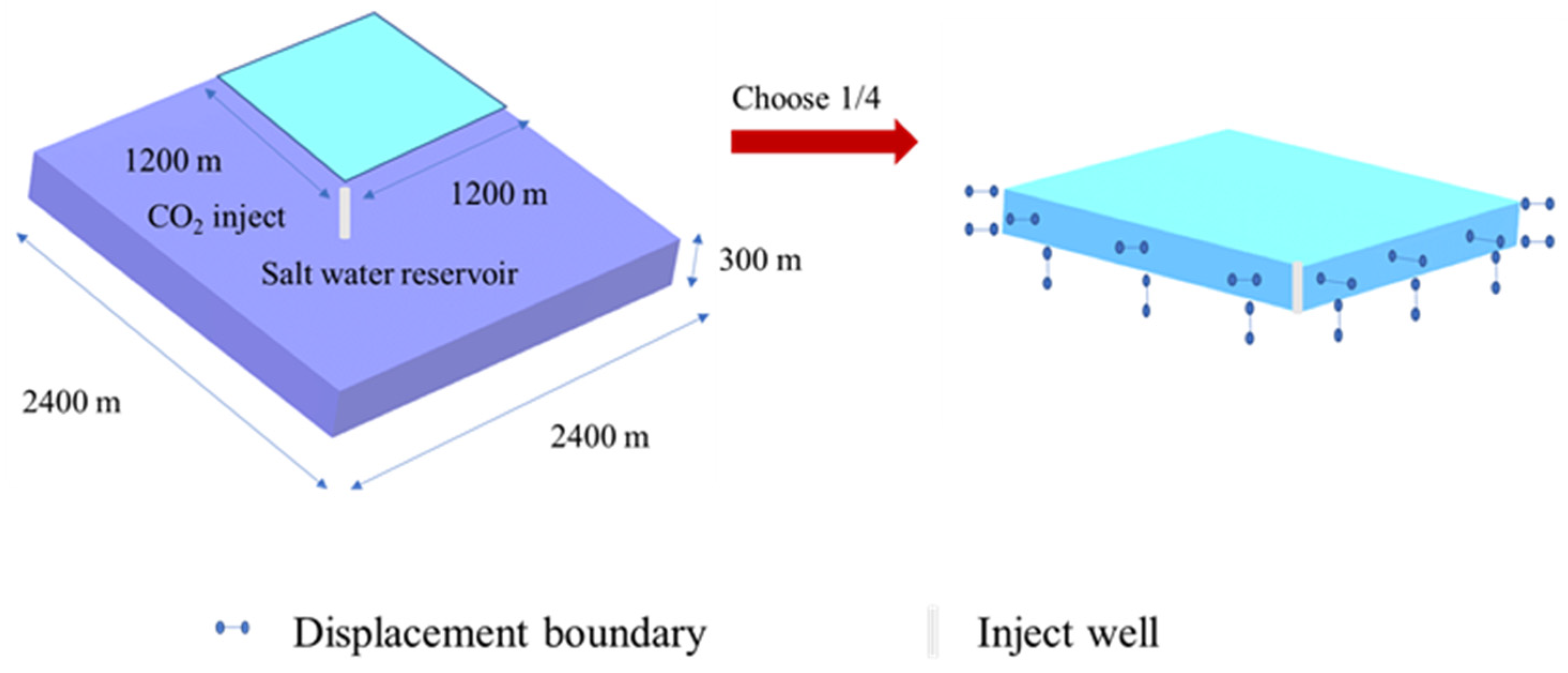
2.2. Physical Models and Numerical Methods
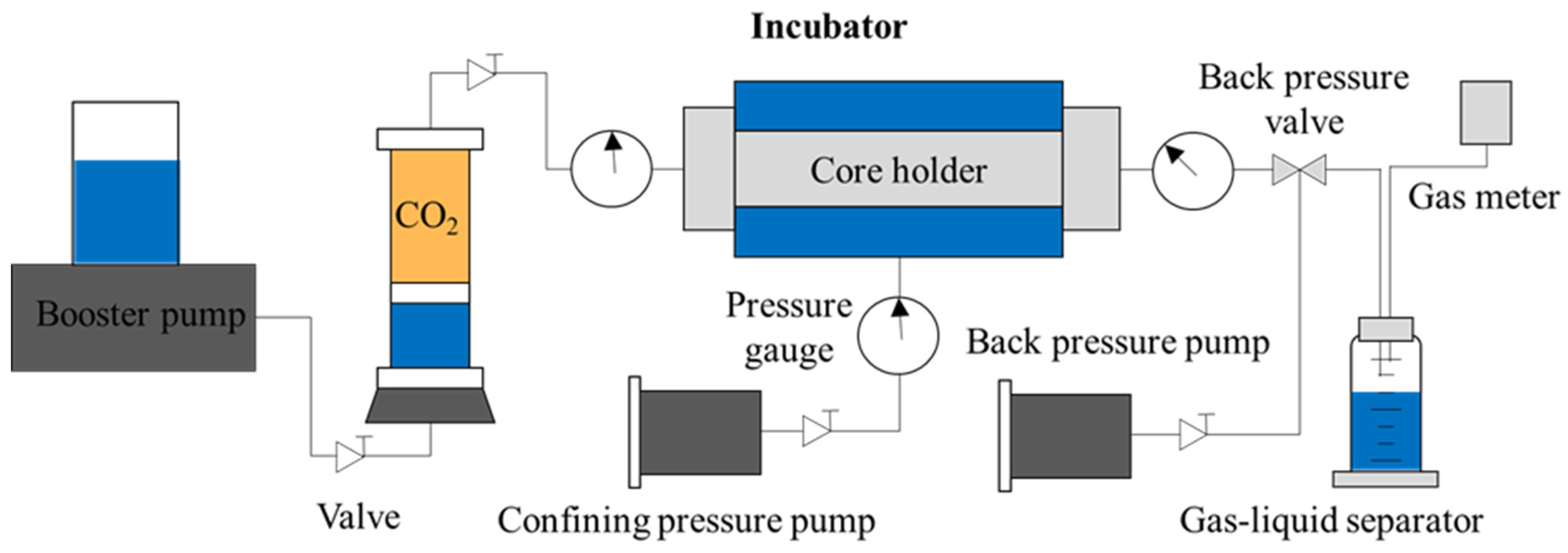
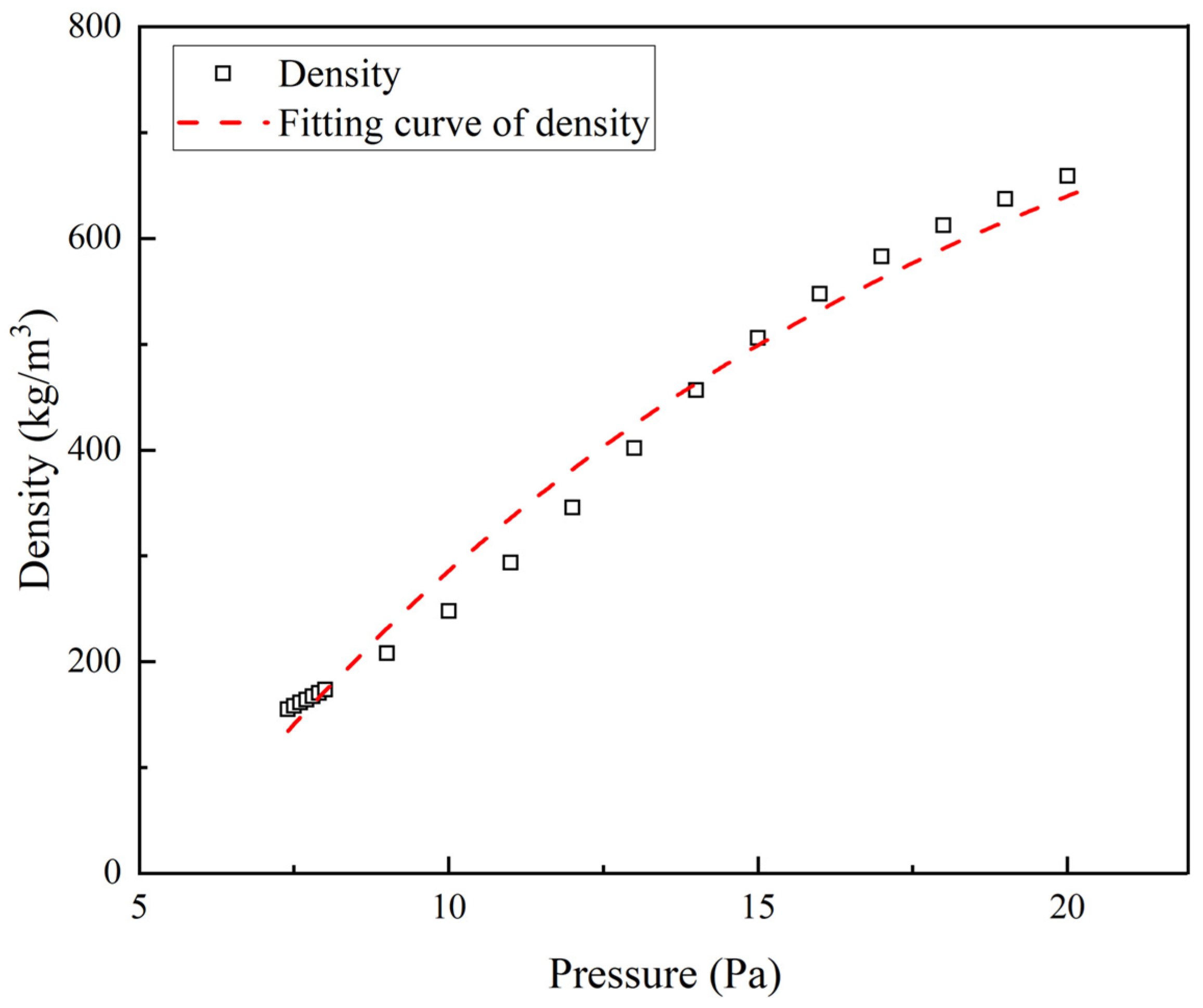
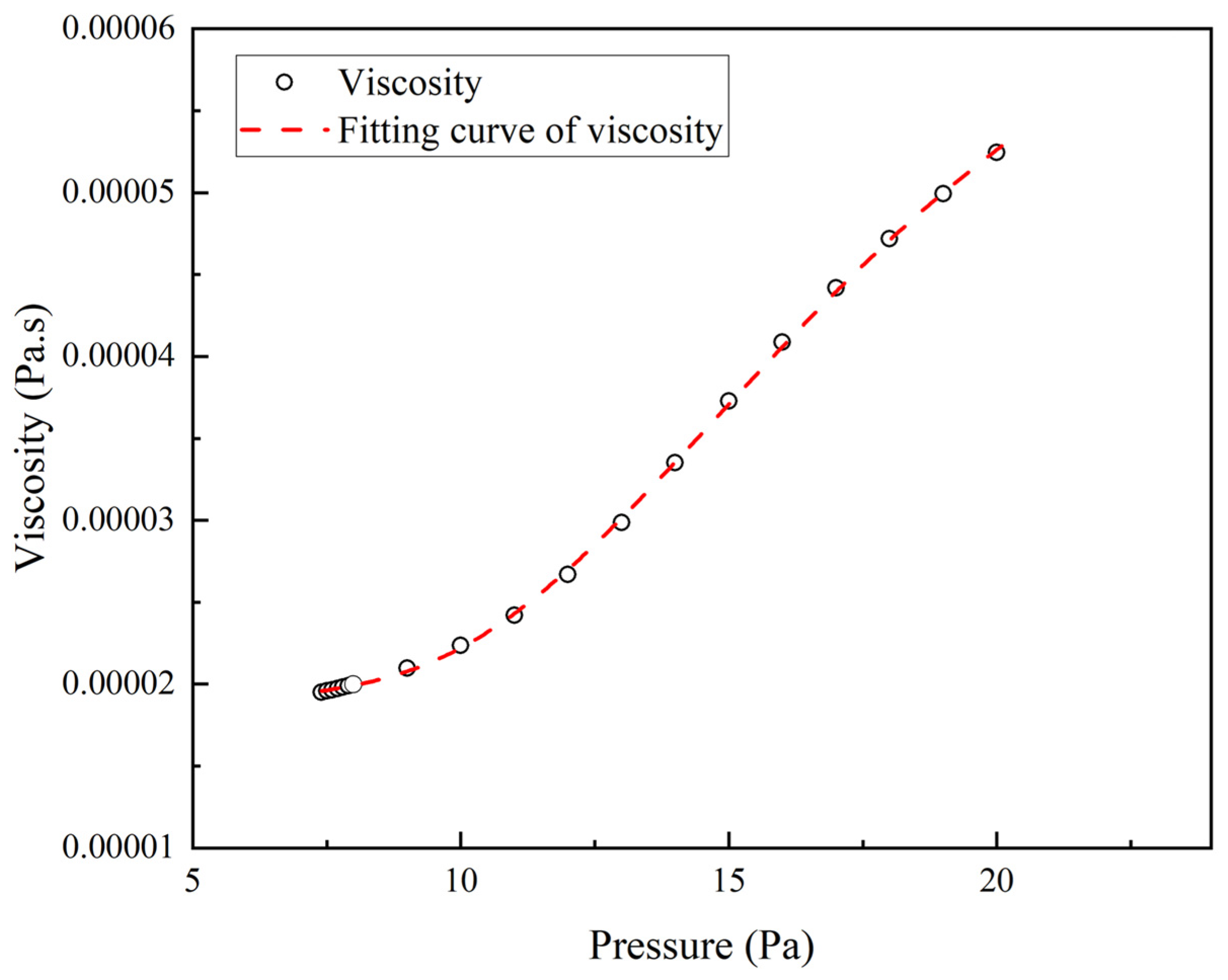
2.3. Physical Properties and Seepage Characteristic Parameters
2.4. Introduction to Injection Methods
2.5. Block Introduction
3. Results and Discussion
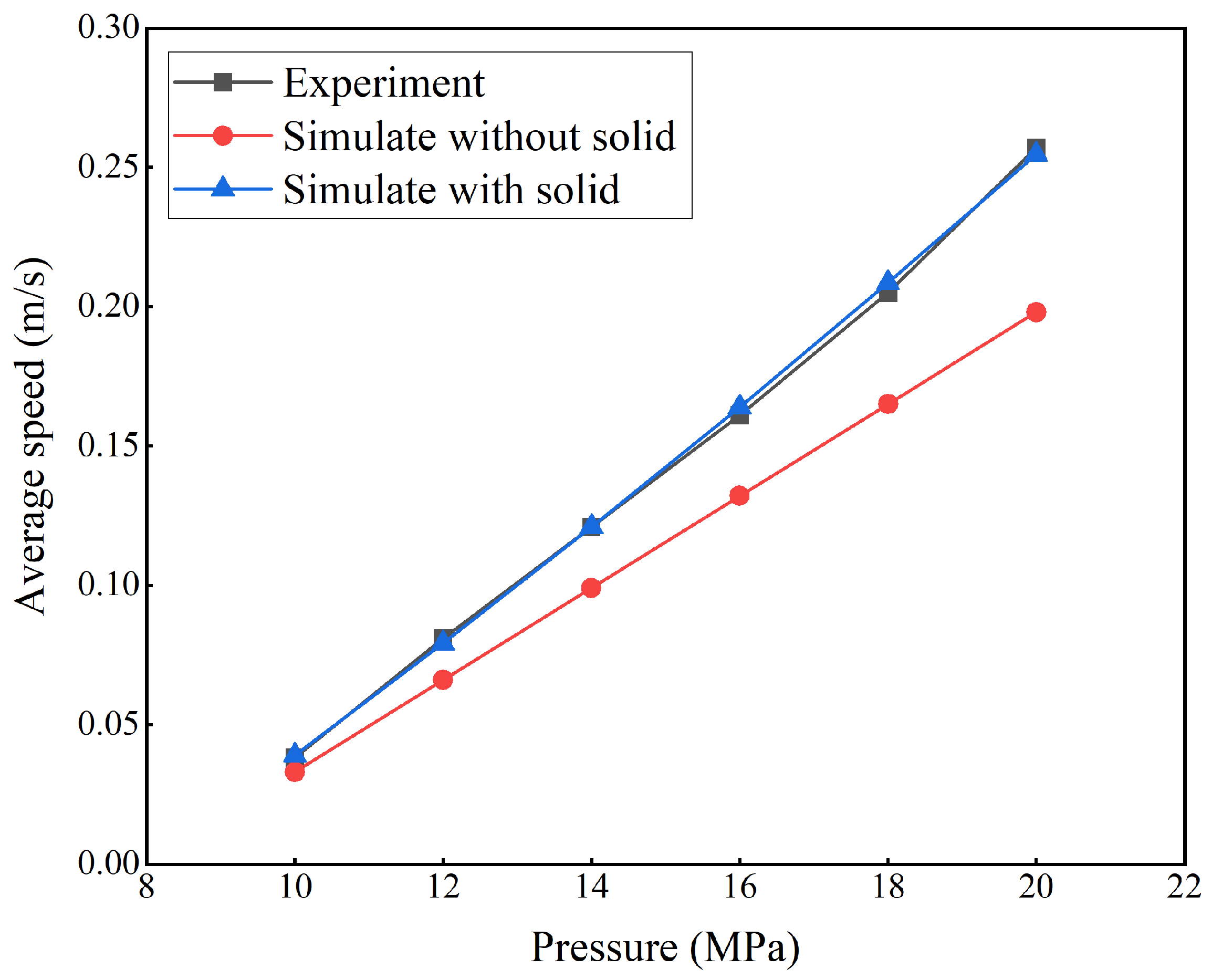
3.1. Model Validation
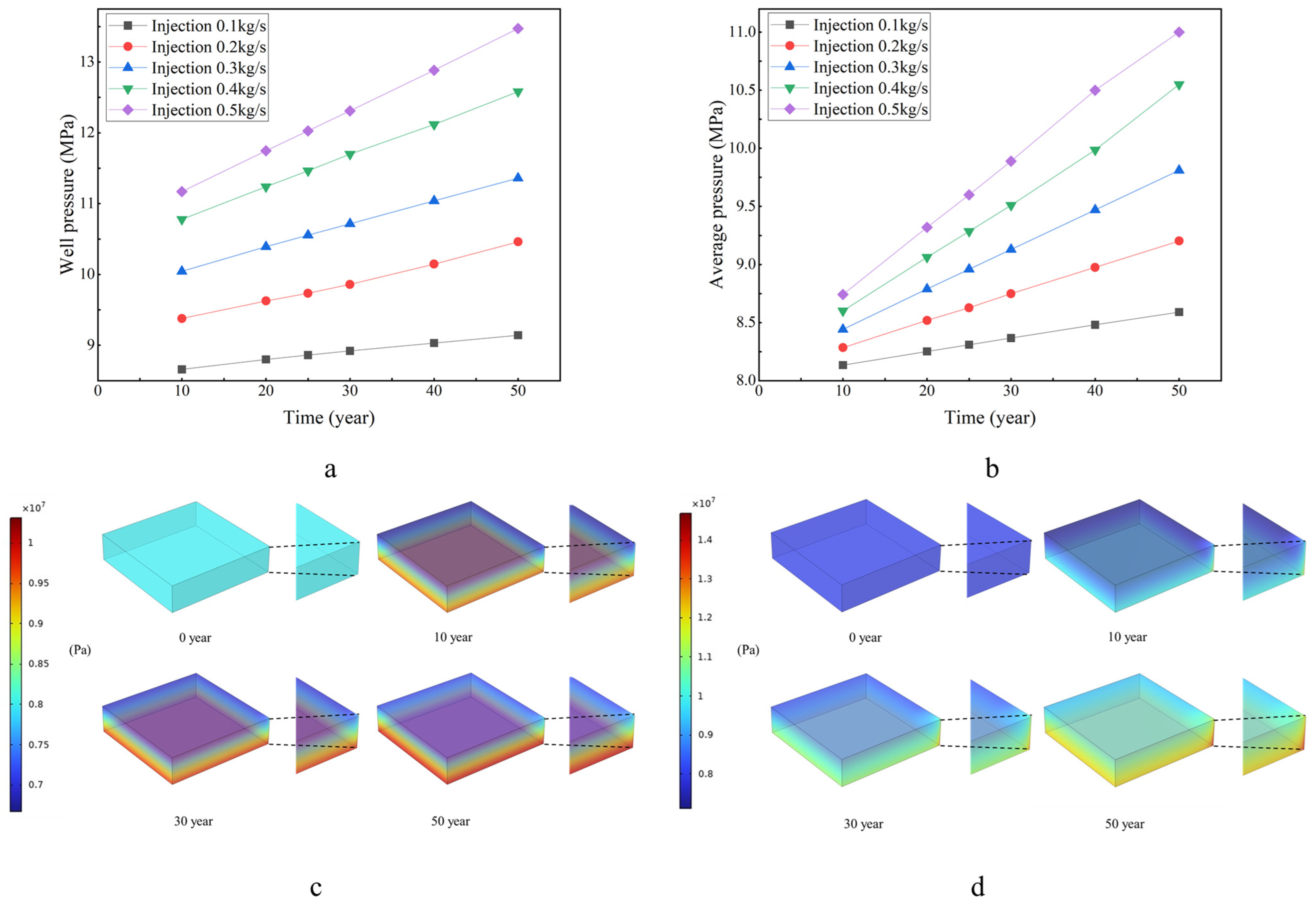
3.2. Reservoir Pressure Comparison
- 0.1 k g/s: Average max formation pressure is about 8.6 MPa (7% higher), and max wellbore pressure is about 9.1 MPa (14% higher, the average pressure value of the wellbore).
- 0.2 kg/s: Average max formation pressure is about 9.2 MPa (15% higher), and max wellbore pressure is about 10.4 MPa (30% higher).
- 0.3 kg/s: Average max formation pressure is about 9.8 MPa (23% higher), and max wellbore pressure is about 11.4 MPa (42% higher).
- 0.4 kg/s: Average max formation pressure is about 10.6 MPa (32% higher), and max wellbore pressure is about 12.6 MPa (57% higher).
- 0.5 kg/s: Average max formation pressure is about 11.0 MPa (38% higher), and max wellbore pressure is about 13.5 MPa (68% higher).
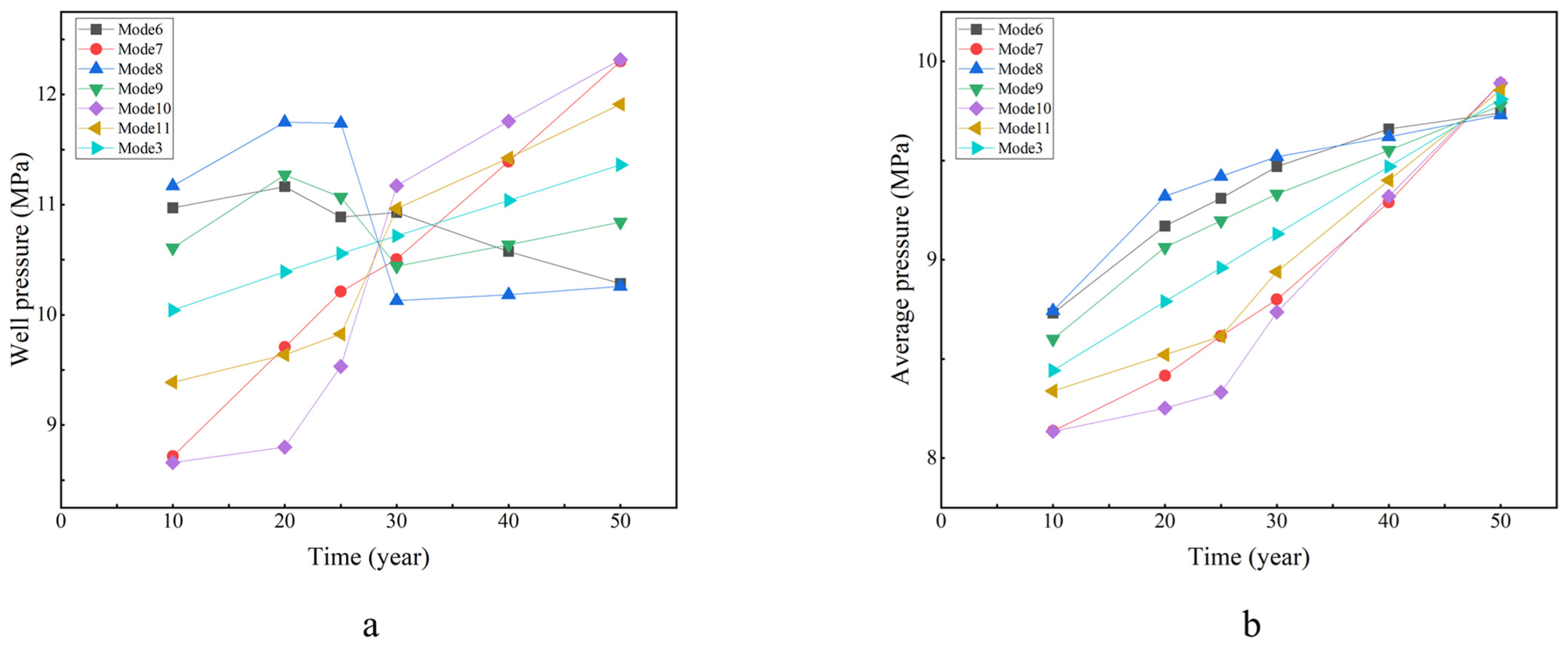
- Average Formation Pressure: It increases with injection time, peaking at 50 years for various injection modes. The maximum values at 50 years are 9.74, 9.89, 9.73, 9.77, 9.89, and 9.86 MPa. These values are relatively close to the case of a constant injection rate of 0.3 kg/s, which reaches 9.81 MPa after 50 years.
- Wellbore Pressure: The pressure around the well does not exhibit a simple monotonic change over time. The maximum value occurs at different times for various injection modes, and there is a considerable gap between these maximum values. It is worth noting that Mode 6, Mode 8, and Mode 9 each experienced a decrease in wellbore pressure in different years, which was due to their reduced injection rates. The pressure around the well is affected by both the injection time and injection rate. The pressure around the well becomes higher as the injection time and injection rate increase.
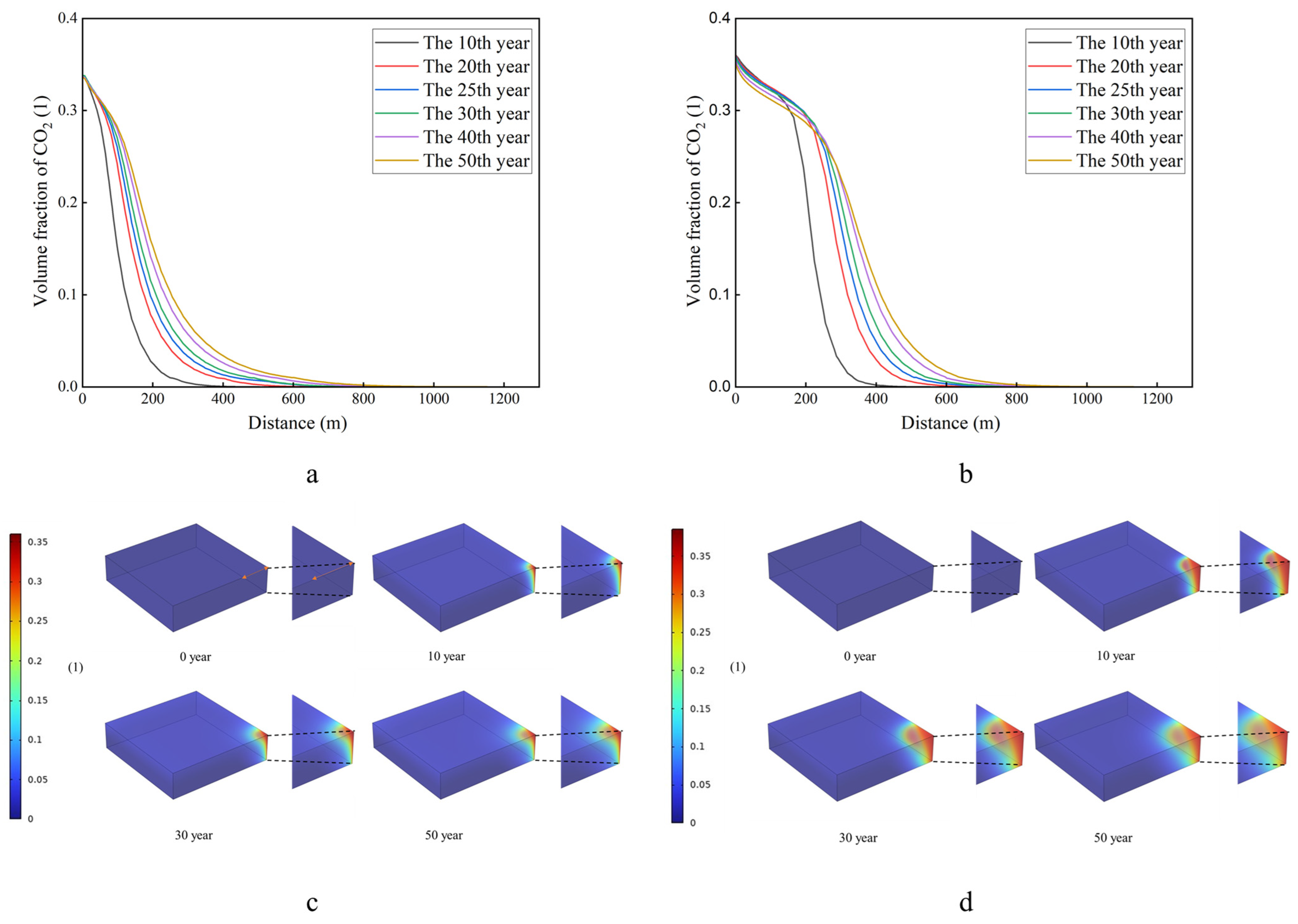
3.3. CO2 Distribution Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CCS | Carbon capture and storage |
| CO2 | Carbon dioxide |
| CT | Computed tomography |
| SEM | Scanning electron microscopy |
| CFD | Computational fluid dynamics |
| VOF | Volume of Fluid |
| FEM | Finite element method |
| NIST | National Institute of Standards and Technology |
| Nomenclature | |
| The following variables are used in this manuscript: | |
| Variable | Meaning |
| porosity | |
| permeability | |
| fluid density | |
| volume fraction | |
| fluid velocity | |
| diffusion coefficient | |
| normal stress component | |
| shear stress component | |
| body force component | |
| gravity | |
| elastic modulus | |
| Poisson’s ratio | |
| displacement component | |
| effective stress component | |
| reservoir pressure | |
| strain component | |
| volume strain | |
| α | Biot coefficient |
| water relative permeability | |
| gas relative permeability | |
Appendix A

References
- Song, Y.; Jun, S.; Na, Y.; Kim, K.; Jang, Y.; Wang, J. Geomechanical challenges during geological CO2 storage: A review. Chem. Eng. J. 2023, 456, 140968. [Google Scholar] [CrossRef]
- Agaton, C.B. Application of real options in carbon capture and storage literature: Valuation techniques and research hotspots. Sci. Total Environ. 2021, 795, 148683. [Google Scholar] [CrossRef] [PubMed]
- Zuch, M.; Ladenburg, J. Navigating the information pathway to carbon capture and storage acceptance: Patterns and insights from a literature review. Energy Res. Soc. Sci. 2023, 105, 103283. [Google Scholar] [CrossRef]
- Li, M.; He, N.; Xu, L.; Peng, C.; Chen, H.; Yu, G. Eco-CCUS: A cost-effective pathway towards carbon neutrality in China. Renew. Sustain. Energy Rev. 2023, 183, 113512. [Google Scholar] [CrossRef]
- Marbun, B.; Sinaga, S.Z.; Purbantanu, B.; Santoso, D.; Kadir, W.; Sule, R.; Prasetyo, D.E.; Prabowo, H.; Susilo, D.; Firmansyah, F.R. Lesson learned from the assessment of planned converted CO2 injection well integrity in Indonesia-CCUS project. Heliyon 2023, 9, e18505. [Google Scholar] [CrossRef]
- Li, X.; Li, Q.; Bai, B.; Wei, N.; Yuan, W. The geomechanics of Shenhua carbon dioxide capture and storage (CCS) demonstration project in Ordos Basin, China. J. Rock. Mech. Geotech. 2016, 8, 948–966. [Google Scholar] [CrossRef]
- Tan, Y.; Nookuea, W.; Li, H.; Thorin, E.; Yan, J. Property impacts on Carbon Capture and Storage (CCS) processes: A review. Energy Convers. Manag. 2016, 118, 204–222. [Google Scholar] [CrossRef]
- Vatalis, K.I.; Laaksonen, A.; Charalampides, G.; Benetis, N.P. Intermediate technologies towards low-carbon economy. The Greek zeolite CCS outlook into the EU commitments. Renew. Sustain. Energy Rev. 2012, 16, 3391–3400. [Google Scholar] [CrossRef]
- Lai, N.; Yap, E.H.; Lee, C.W. Viability of CCS: A broad-based assessment for Malaysia. Renew. Sustain. Energy Rev. 2011, 15, 3608–3616. [Google Scholar] [CrossRef]
- Shaw, R.; Mukherjee, S. The development of carbon capture and storage (CCS) in India: A critical review. Carbon Capture Sci. Technol. 2022, 2, 100036. [Google Scholar] [CrossRef]
- Rodrigues, H.W.; Mackay, E.J.; Arnold, D.P. Multi-objective optimization of CO2 recycling operations for CCUS in pre-salt carbonate reservoirs. Int. J. Greenh. Gas Control 2022, 119, 103719. [Google Scholar] [CrossRef]
- Leonzio, G.; Bogle, D.; Foscolo, P.U.; Zondervan, E. Optimization of CCUS supply chains in the UK: A strategic role for emissions reduction. Chem. Eng. Res. Des. 2020, 155, 211–228. [Google Scholar] [CrossRef]
- Vulin, D.; Mocilac, I.K.; Jukic, L.; Arnaut, M.; Vodopic, F.; Saftic, B.; Sedlar, D.K.; Cvetkovic, M. Development of CCUS clusters in Croatia. Int. J. Greenh. Gas Control 2023, 124, 103857. [Google Scholar] [CrossRef]
- Bazhenov, S.; Chuboksarov, V.; Maximov, A.; Zhdaneev, O. Technical and economic prospects of CCUS projects in Russia. Sustain. Mater. Technol. 2022, 33, e00452. [Google Scholar] [CrossRef]
- Yuan, J.; Lyon, T.P. Promoting global CCS RDD&D by stronger U.S.-China collaboration. Renew. Sustain. Energy Rev. 2012, 16, 6746–6769. [Google Scholar]
- Maheen, R.; Cai, L.; Zhang, Y.S.; Zhao, M. Quantitative analysis of carbon dioxide emission reduction pathways: Towards carbon neutrality in China’s power sector. Carbon Capture Sci. Technol. 2023, 7, 100112. [Google Scholar] [CrossRef]
- Liu, Z.; Gao, M.; Zhang, X.; Liang, Y.; Guo, Y.; Liu, W.; Bao, J. CCUS and CO2 injection field application in abroad and China: Status and progress. Geoenergy Sci. Eng. 2023, 229, 212011. [Google Scholar] [CrossRef]
- Jiang, K.; Ashworth, P.; Zhang, S.; Liang, X.; Sun, Y.; Angus, D. China’s carbon capture, utilization and storage (CCUS) policy: A critical review. Renew. Sustain. Energy Rev. 2020, 119, 109601. [Google Scholar] [CrossRef]
- Terwel, B.W.; Harinck, F.; Ellemers, N.; Daamen, D.D. Going beyond the properties of CO2 capture and storage (CCS) technology: How trust in stakeholders affects public acceptance of CCS. Int. J. Greenh. Gas Control 2011, 5, 181–188. [Google Scholar] [CrossRef]
- Tcvetkov, P.; Cherepovitsyn, A.; Fedoseev, S. Public perception of carbon capture and storage: A state-of-the-art overview. Heliyon 2019, 5, e02845. [Google Scholar] [CrossRef]
- van Os, H.W.; Herber, R.; Scholtens, B. Not Under Our Back Yards? A case study of social acceptance of the Northern Netherlands CCS initiative. Renew. Sustain. Energy Rev. 2014, 30, 923–942. [Google Scholar] [CrossRef]
- Jiang, K.; Ashworth, P.; Zhang, S.; Hu, G. Print media representations of carbon capture utilization and storage (CCUS) technology in China. Renew. Sustain. Energy Rev. 2022, 155, 111938. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, B.; Chen, Y.; Lu, S. Public perceived risks and benefits of carbon capture, utilization, and storage (CCUS): Scale development and validation. J. Environ. Manag. 2023, 347, 119109. [Google Scholar] [CrossRef] [PubMed]
- Storrs, K.; Lyhne, I.; Drustrup, R. A comprehensive framework for feasibility of CCUS deployment: A meta-review of literature on factors impacting CCUS deployment. Int. J. Greenh. Gas Control 2023, 125, 103878. [Google Scholar] [CrossRef]
- Berrezueta, E.; Kovacs, T.; Herrera-Franco, G.; Mora-Frank, C.; Caicedo-Potosi, J.; Carrion-Mero, P.; Carneiro, J. Laboratory studies on CO2-brine-rock interaction: An analysis of research trends and current knowledge. Int. J. Greenh. Gas Control 2023, 123, 103842. [Google Scholar] [CrossRef]
- Xie, J.; Yang, X.; Qiao, W.; Peng, S.; Yue, Y.; Chen, Q.; Cai, J.; Jiang, G.; Liu, Y. Investigations on CO2 migration and flow characteristics in sandstone during geological storage based on laboratory injection experiment and CFD simulation. Gas Sci. Eng. 2023, 117, 205058. [Google Scholar] [CrossRef]
- Hu, Y.; Yan, X.; Chen, L.; Yu, S.; Liu, C.; Yu, J. Leakage hazard distance of supercritical CO2 pipelines through experimental and numerical studies. Int. J. Greenh. Gas Control 2022, 119, 103730. [Google Scholar] [CrossRef]
- Tutolo, B.M.; Kong, X.; Seyfried, W.E., Jr.; Saar, M.O. High performance reactive transport simulations examining the effects of thermal, hydraulic, and chemical (THC) gradients on fluid injectivity at carbonate CCUS reservoir scales. Int. J. Greenh. Gas Control 2015, 39, 285–301. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, J.; Wang, J.; Zhang, Q.; Yao, J. Pore-scale numerical simulation of supercritical CO2-brine two-phase flow based on VOF method. Nat. Gas Ind. B 2023, 10, 466–475. [Google Scholar] [CrossRef]
- Cai, M.; Li, X.; Zhang, K.; Su, Y.; Wang, D.; Yang, S.; Liu, S. Coupled hydro-mechanical-chemical simulation of CCUS-EOR with static and dynamic microscale effects in tight reservoirs. Fuel 2024, 357, 129888. [Google Scholar] [CrossRef]
- Ratnakar, R.R.; Chaubey, V.; Dindoruk, B. A novel computational strategy to estimate CO2 solubility in brine solutions for CCUS applications. Appl. Energy 2023, 342, 121134. [Google Scholar] [CrossRef]
- Omosebi, O.A.; Oldenburg, C.M.; Reagan, M. Development of lean, efficient, and fast physics-framed deep-learning-based proxy models for subsurface carbon storage. Int. J. Greenh. Gas Control 2022, 114, 103562. [Google Scholar] [CrossRef]
- Du, S.; Wang, J.; Wang, M.; Yang, J.; Zhang, C.; Zhao, Y.; Song, H. A systematic data-driven approach for production forecasting of coalbed methane incorporating deep learning and ensemble learning adapted to complex production patterns. Energy 2023, 263, 126121. [Google Scholar] [CrossRef]
- Du, S.; Wang, M.; Yang, J.; Zhao, Y.; Wang, J.; Yue, M.; Xie, C.; Song, H. An enhanced prediction framework for coalbed methane production incorporating deep learning and transfer learning. Energy 2023, 282, 128877. [Google Scholar] [CrossRef]
- Xie, C.; Du, S.; Wang, J.; Lao, J.; Song, H. Intelligent modeling with physics-informed machine learning for petroleum engineering problems. Adv. Geo-Energy Res. 2023, 8, 71–75. [Google Scholar] [CrossRef]
- Xie, C.; Zhu, J.; Yang, H.; Wang, J.; Liu, L.; Song, H. Relative permeability curve prediction from digital rocks with variable sizes using deep learning. Phys. Fluids 2023, 35, 096605. [Google Scholar] [CrossRef]
- Nassan, T.H.; Amro, M. Finite Element Simulation of Multiphase Flow in Oil Reservoirs-Comsol Multiphysics as Fast Prototyping Tool in Reservoir Simulation. Gorn. Nauk. I Tekhnologii Min. Sci. Technol. 2020, 4, 220–226. [Google Scholar] [CrossRef]
- Sharafi, M.S.; Ghasemi, M.; Ahmadi, M.; Kazemi, A. An experimental approach for measuring carbon dioxide diffusion coefficient in water and oil under supercritical conditions. Chin. J. Chem. Eng. 2021, 34, 160–170. [Google Scholar] [CrossRef]
- Mase, G.T.; Smelser, R.E.; Mase, G.E. Continuum Mechanics for Engineers; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Ebrahiminejadhasanabadi, M.; Nelson, W.M.; Naidoo, P.; Mohammadi, A.H.; Ramjugernath, D. Experimental measurements of CO2 solubility, viscosity, density, sound velocity and evaporation rate for 2-(2-aminoethoxy) ethanol (DGA)+ 1-methylpyrrolidin-2-one (NMP)/water+ ionic liquid systems. Fluid Phase Equilibria 2022, 559, 113475. [Google Scholar] [CrossRef]






| 0–10 Years | 10–20 Years | 20–25 Years | 25–30 Years | 30–40 Years | 40–50 Years | |
|---|---|---|---|---|---|---|
| Mode 1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| Mode 2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 |
| Mode 3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 |
| Mode 4 | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 |
| Mode 5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| Mode 6 | 0.5 | 0.4 | 0.3 | 0.3 | 0.2 | 0.1 |
| Mode 7 | 0.1 | 0.2 | 0.3 | 0.3 | 0.4 | 0.5 |
| Mode 8 | 0.5 | 0.5 | 0.5 | 0.1 | 0.1 | 0.1 |
| Mode 9 | 0.4 | 0.4 | 0.4 | 0.2 | 0.2 | 0.2 |
| Mode 10 | 0.1 | 0.1 | 0.1 | 0.5 | 0.5 | 0.5 |
| Mode 11 | 0.2 | 0.2 | 0.2 | 0.4 | 0.4 | 0.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, L.; Ding, G.; Song, S.; Wang, H.; Xie, W.; Wang, J. A Case Study on the CO2 Sequestration in Shenhua Block Reservoir: The Impacts of Injection Rates and Modes. Energies 2024, 17, 122. https://doi.org/10.3390/en17010122
Tang L, Ding G, Song S, Wang H, Xie W, Wang J. A Case Study on the CO2 Sequestration in Shenhua Block Reservoir: The Impacts of Injection Rates and Modes. Energies. 2024; 17(1):122. https://doi.org/10.3390/en17010122
Chicago/Turabian StyleTang, Ligen, Guosheng Ding, Shijie Song, Huimin Wang, Wuqiang Xie, and Jiulong Wang. 2024. "A Case Study on the CO2 Sequestration in Shenhua Block Reservoir: The Impacts of Injection Rates and Modes" Energies 17, no. 1: 122. https://doi.org/10.3390/en17010122
APA StyleTang, L., Ding, G., Song, S., Wang, H., Xie, W., & Wang, J. (2024). A Case Study on the CO2 Sequestration in Shenhua Block Reservoir: The Impacts of Injection Rates and Modes. Energies, 17(1), 122. https://doi.org/10.3390/en17010122





