Optimal Placement of Battery Swapping Stations for Power Quality Improvement: A Novel Multi Techno-Economic Objective Function Approach

Abstract

In recent years, battery swapping stations have become increasingly popular in smart energy networks. Its advantages include reducing the time required for recharging energy, balancing the grid’s load, and extending the battery’s lifespan. Despite efforts focused on the placement and operation of battery swapping stations (BSSs), there is still a lack of a comprehensive and systematic examination that covers all aspects of both the economic and technical aspects of the power network. This encompasses considerations such as power quality and reliability, particularly in terms of where these stations should be located. This paper introduces a novel framework for strategically positioning BSS within smart microgrids that integrate distributed energy resources (DERs). It takes into account various technical factors (such as reliability and power quality) and economic factors (like the cost of generation and operation), which have been overlooked in the previous research. To achieve this goal, a unique hybrid optimization strategy is developed, incorporating a combination of epsilon-constraint and lexicographic (DECL) optimization methods. This approach tackles a multi-objective challenge, treating factors like the number, locations, and sizes of BSS as independent variables, while operational costs and technical power quality metrics are considered dependent variables. To validate this approach, it is tested on standard benchmark distribution power networks such as IEEE 33, 69, and 118 bus systems. The simulation results, showcasing the strengths and capabilities of this innovative strategy, are compared to the findings of previous research studies.

1. Introduction

1.1. Importance and Motivations

In modern smart distribution networks, BSSs have been developed to enhance the efficient functioning of the network, reduce carbon emissions, and optimize the use of DERs [1]. BSSs charge their batteries using their own renewable energy sources like solar panels and wind turbines or they can also draw power from the power grid/microgrid (MG). In the latter scenario, they have the ability to exchange power with the grid/MG. BSSs are capable of charging their stored batteries during periods of low electricity prices. They bring benefits to power grids/MGs as well. By employing battery-to-grid (B2G) capabilities, BSSs lower the operational costs of the grid/MG and can even provide spinning reserves for these systems [1]. The location of BSSs in a power system is a vital factor that affects the system’s operational expenses. It is crucial to identify the best position for BSSs. Furthermore, the placement of BSSs in the network can impact power quality and network reliability. However, it is noteworthy that the previous research studies have not extensively explored this aspect [2]. Therefore, the location of BSSs within a power system is a critical factor that affects operational costs. Identifying the optimal location for BSSs is essential, as it can impact power quality and network reliability. However, the previous research has not extensively investigated this aspect. Consequently, this study aims to evaluate the most appropriate locations for BSSs in the distribution network, considering technical factors such as power quality standards and reliability measures, as well as economic objectives. The subsequent section provides a comprehensive review of the previous studies conducted in this area.

1.2. Literature Review

The prevailing body of research on BSSs primarily focuses on using diverse methodologies to optimize the costs associated with charging operations. Among the first works devoted to BSS was one [2] that established an optimization model for the method. When modeling the optimization issue, the authors took into account both the unpredictability of swap demand and the need to look forward by one day. Minimizing the cost of BSS operations was the goal of an optimization problem addressed in [3]. The authors provide a model in [1,2,3,4] that examines the battery swap patterns of electric vehicle (EV) owners using data from survey research. The model also suggests an optimal charging method for EVs. The authors provided the operating strategy for a prosumer BSS in [5,6], which takes into account service availability and self-consumption of photovoltaic (PV) electricity. The optimal charging schedule of BSSs catering to electric buses (EBs) was investigated in [7,8]. Furthermore, the objective of [9,10] is to reduce the overall cost of a BSSs facility that caters to EVs within a single day. Demand response is a factor in achieving this. In a further study [11], the impact of substituting charging stations with BSSs on the power system is investigated within a 32-bus system. The ideal approach of a MG and BSS as two distinct stakeholders with competing objectives, was outlined in the study referenced as [12], The authors in [12] proposed a bi-level optimization framework aimed at maximizing the profit of the BSS at a lower level, while simultaneously minimizing the cost of the MG at a higher level. In another paper [13], researchers provided a two-tiered model in which a solution system was implemented to simultaneously minimize the cost of the BSS and maximize the performance of the island MG. For real-time energy management of a BSS-based MG, reference [14] suggested a Lyapunov optimization methodology based on queuing theory. Furthermore, in [15,16], the BSS was used for a grid-connected MG with PV and wind turbines to reduce operating costs for the MG. The optimal location and size of BSSs have only been the subject of a few studies. Charging stations have been the focus of most of the research on optimal location and size. Scientists, however, have learned a lot from these investigations. The charging station sitting challenge in a system with renewable generating and storage assets was resolved in reference [17]. Detailed network restrictions were taken into account in an optimal site analysis that was completed in [18]. Additionally, the literature has a number of studies on the optimal location of charging stations within distribution networks [14,19,20,21]. One of the first investigations into the ideal location for BSSs is documented in reference [22]. Using an artificial bee colony, the scientists identified the optimal site for BSS and calculated its optimal size. The goal of the research was to pinpoint the spot where network power loss was minimal. Only one research study [23] has looked at BSSs as a potential answer to the MG sitting issue. In a microgrid system, the authors placed the BSS in the most advantageous spot possible. However, a MG is the only way to tackle the seating issue. Furthermore, no study of swap demand was carried out for the BSS. The goal of the project was to find ways to make MGs more cost-effective to run. Last but not least, none of the research has ever performed an economic examination of BSS placement issues. Differential evolution (DE) with a fitness-sharing method was used in [23] to find the best location and size for BSSs from the owner’s point of view. Additionally, the study considered the security restrictions of the power system. The BSS planning issue was mathematically expressed as a non-convex mixed-integer nonlinear programming (MINLP) model. The objective is to minimize the net present value (NPV) of the BSS project, taking into account the life cycle cost criteria. The progression of EV adoption was represented mathematically as a geometric Brownian motion function, and to address uncertainties, Monte Carlo Simulation (MCS) was used. The findings indicate that the integration of BSSs leads to a more uniform demand profile for the power system. On the other hand, the presence of battery charging stations (BCSs) introduces additional peaks in the demand profile. The grasshopper optimization method was used in a study [24] to determine the best placement and dimensions of BSSs inside power systems. The formulation of the planning issue was approached as a multi-objective optimization problem, with the goals being energy loss and voltage stability. However, the temporal fluctuations in power prices have not been taken into account. The use of a linear weighted sum (LWS) was employed as a means to convert the multi-objective optimization issue into a single-objective optimization problem. To enable the charging of EVs at BSSs, the power infrastructure was divided into several zones. The findings indicate that the grasshopper optimization method exhibits superior performance compared to the particle swarm optimization (PSO), gravitational search algorithms, and artificial bee colony. The determination of the route and placement of the BSSs for a fleet of EVs is conducted in order to minimize the investment cost of the BSSs and the shipping cost of the EVs, as shown in reference [25]. The purpose of EVs is to facilitate the transportation of products to various destinations for client delivery. A single EV must be the only one to visit each individual client. The specified optimization issue is solved using CPLEX, which serves as a mixed-integer programming (MIP) solver, as well as Tabu search. In contemporary times, the prevailing trend is the decentralization of power systems and the proliferation of MGs, resulting in the widespread connection of BSSs to the MGs located within their vicinity. Based on an analysis of the existing literature, it is important to note that the ideal positioning of BSS in MGs has not been well explored from the specific standpoint of MGs. Because of this, the main goal of this study is to find the best place for base station stations BSSs in an MG that has micro PHS, PV, wind, and geothermal DG units. This investigation takes into account all network limitations and reactive power dispatch. It is often assumed that the ownership of all facilities, with the exception of thermal DGs, is with the MG owner. Consequently, the optimization process is conducted from the viewpoint of MG. The DICOPT solver, implemented in the general algebraic mathematical system (GAMS), was used to solve the mixed-integer nonlinear optimization problem, as stated in references [26,27]. In

Table 1. Comparison of the features of the proposed method and the recent previous methods.

Criterion	[2]	[3]	[1,4]	[5,6]	[7,8]	[10]	[12,14]	[15]	[21]	[23]	[24,25,27]	This Paper
Operation cost	✓	✓	✓	✓	✓	✗	✓	✓	✓	✓	✓	✓
Power loss or energy loss	✗	✓	✓	✓	✓	✓	✗	✓	✓	✓	✓	✓
PLSF	✗	✗	✗	✗	✗	✓	✗	✓	✗	✓	✗	✓
Pollution reduction	✓	✗	✗	✓	✗	✗	✗	✓	✗	✗	✓	✓
VSI	✗	✗	✗	✗	✗	✗	✗	✗	✓	✓	✓	✓
EENS	✗	✗	✗	✗	✗	✗	✓	✓	✗	✓	✓	✓
VD	✗	✓	✓	✗	✓	✓	✗	✓	✗	✗	✓	✓
SCL	✗	✗	✗	✗	✗	✗	✗	✗	✗	✗	✗	✓

, the problems with the earlier research and studies are listed. These problems include economic goals; technical indicators like losses, voltage deviation, and reliability; and power quality indicators like unsupplied energy (EENS) and the loss and voltage sensitivity factor.

1.3. Contributions

After addressing the limitations identified in the prior research, this paper introduces an innovative approach for strategically situating BSSs in the distribution network. The objective is to determine the ideal quantity, precise positioning, and optimal capacity of these BSSs. This comprehensive framework considers economic, technical, as well as network reliability and power quality factors. By incorporating the following objectives, this study sets itself apart from earlier investigations:

• Suggesting an innovative mixed multi-objective framework for resolving optimal placement challenges, this framework relies on the combination of elitist non-dominated sorting and the crowding distance mechanism. The multi-objective approach introduced can handle numerous and contradictory objectives during the process of optimizing problems. Its formulation employs the principles of elitist, non-dominated sorting and the crowding distance mechanism. Moreover, this approach effectively addresses unconstrained, constrained, and engineering design problems, encompassing a wide range of linear, nonlinear, continuous, and discrete characteristics that define Pareto front problems.
• This study aims to determine the optimal location for BSSs in a distribution network, considering both technical and economic factors. This study differs from the previous research by incorporating a comprehensive framework that considers multiple objectives, such as network reliability and power quality. The approach involves strategically placing BSSs based on their quantity, positioning, and capacity while also considering technical metrics associated with MG, such as preventing alterations in short-circuit levels to maintain protective configurations.
• Incorporating reliability measures such as the anticipated energy shortage (EENS) and voltage sensitivity indices of the system, alongside economic aims.
• Accounting for power quality aspects of the network, such as voltage deviations, losses, and loss sensitivity indices, within the context of an optimal placement problem.

1.4. Organization

The structure of this paper is outlined as follows: Commencing with an introductory section that provides an overview, the subsequent sections delve into specific aspects. Section 2 elaborates on the conceptual model, followed by Section 3, which outlines the mathematical formulation of the proposed technique. Additionally, Section 4 encompasses the incorporation of the proposed approach into a multi-objective optimization framework, illustrated through a flowchart. Moving on, Section 5 centers on the simulation and discourse of the results derived from the conducted simulations. Concluding the paper, the primary findings of this article are summarized in the Section 6.

2. Conceptual Framework

Figure 1 presents the proposed conceptual framework for strategically positioning BSSs within the power distribution network, incorporating DG, and addressing both the economic and technical aspects of the challenge. As depicted in this diagram, a comprehensive multi-objective framework model should be capable of enhancing technical aspects of the power grid, such as power quality metrics, reliability, and short-circuit levels, while simultaneously aligning with the economic objectives of its operation. Therefore, as evident from the research background, this study distinguishes itself from the previous research by integrating the following objectives:

• Proposing a groundbreaking mixed multi-objective framework to address the challenges of optimal placement. This framework combines elitist non-dominated sorting with the crowding distance mechanism.The multi-objective approach introduced is capable of handling multiple and often conflicting objectives during the optimization process. Its formulation incorporates the principles of elitist, non-dominated sorting and the crowding distance mechanism. Furthermore, this approach effectively addresses a wide range of problems, including unconstrained, constrained, and engineering design problems, encompassing various linear, nonlinear, continuous, and discrete characteristics that define Pareto front problems.
• Considering technical metrics related to MGs, such as maintaining protective configurations by preventing changes in short-circuit levels, alongside economic objectives when determining the best placement for BESS units.
• Incorporating reliability measures, including the anticipated energy shortage (EENS) and voltage sensitivity indices of the system, in addition to economic goals.
• Accounting for power quality aspects of the network, including voltage deviations, losses, and loss sensitivity indices, as part of the optimal placement problem.

3. Mathematical Problem Formulations

In this section, the mathematical formulation of the proposed multi-objective framework is designed for the optimal placement of BSSs within distribution networks, taking into account the presence of DG units. This approach places a strong emphasis on achieving both optimal and secure energy management scheduling and enhancing various technical metrics, with a particular focus on power quality factors and system reliability. The optimization of the multi-objective mathematical function is carried out using a developed multi-objective optimization algorithm, which is discussed in detail in the fourth section of this paper. Initially, the discussion centers around the modeling of cost functions related to distributed generation resources, specifically BSSs, as well as other technical indices and network reliability considerations. In this framework, the process unfolds as follows:

• The initial data of the power network, including factors such as the load profile, DG units generation, electricity pricing, and the initial configuration of the power network under normal operating conditions, are retrieved by the central processing system.
• In the subsequent stage, the power flow analysis is conducted, taking into account the initial techno-economic indices of the power system.
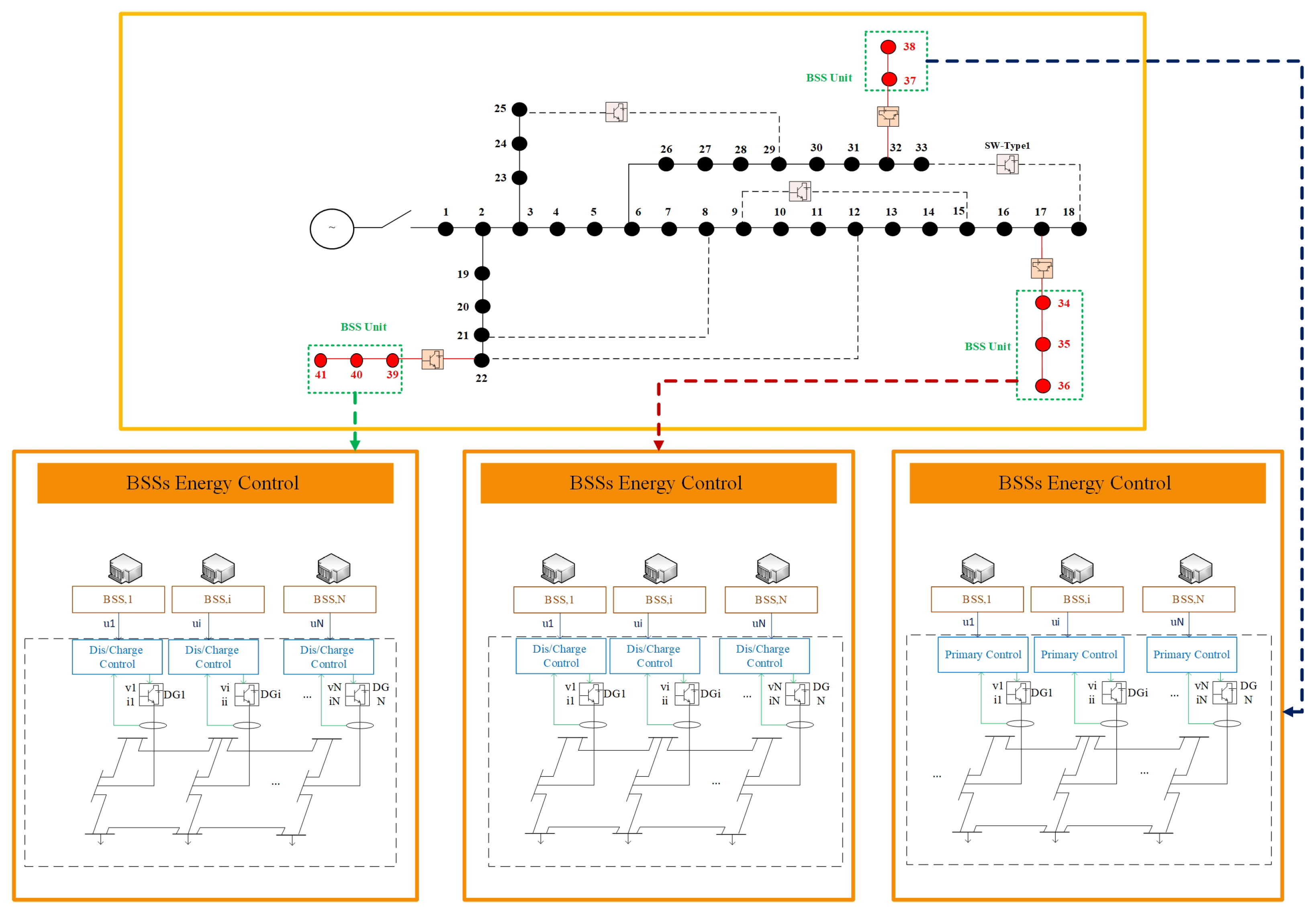
• Following the power flow analysis, the proposed multi-objective framework is invoked. Its purpose is to determine the optimal quantity, ideal locations, and appropriate sizes for the BSS units, ultimately optimizing the objective function. This objective function encompasses various techno-economic indices of the power system and is compared against the initial normal operation of the power system. These steps collectively form the core of our proposed approach for optimizing the placement of BSSs within distribution networks, contributing to improved energy management, enhanced technical performance, and increased system reliability.

Furthermore, the present paper proposes an innovative mixed multi-objective framework to address the challenges of optimal placement. This framework relies on a combination of elitist non-dominated sorting and the crowding distance mechanism. The introduced multi-objective approach demonstrates its capability to handle a multitude of conflicting objectives during the optimization process. Its formulation incorporates the principles of elitist non-dominated sorting and the crowding distance mechanism. Furthermore, this approach effectively deals with a diverse set of problems, whether they are unconstrained, constrained, or related to engineering design. It encompasses a wide spectrum of linear, nonlinear, continuous, and discrete characteristics that are associated with defining Pareto front problems. The flowchart depicting the process stages of the proposed multi-objective framework for BSSs is illustrated in Figure 2.

3.1. Cost Modeling of Distributed Generation Units (PV and Wind Generation)

The availability of essential energy sources like wind velocity and sunlight plays a crucial role in determining the power generated by renewable energy systems. The electricity generated by solar panels is directly linked to the quantity of sunlight received on the Earth’s surface, and this is greatly influenced by factors like the installation site, weather patterns, and daylight duration. Consequently, the power output of solar arrays hinges on factors such as cell temperature and the intensity of solar radiation at the point where maximum power is generated. These values can be calculated using Equations (1) and (2) [28].

$${\mathrm{P}}_{\mathrm{PV}}\left(\mathrm{t}\right)=\left[{\mathrm{P}}_{(\mathrm{PV},\mathrm{STC})}·\frac{{\mathrm{G}}_{\mathrm{T}}\left(\mathrm{t}\right)}{1000}·\left(1-\gamma ({\mathrm{T}}_{\mathrm{j}}-25)\right)\right]·{\mathrm{N}}_{\mathrm{PVs}}·{\mathrm{N}}_{\mathrm{PVp}}.$$

(1)

$${\mathrm{T}}_{\mathrm{j}}={\mathrm{T}}_{\mathrm{amp}}+\frac{{\mathrm{G}}_{\mathrm{T}}}{{\mathrm{G}}_{\mathrm{T},\mathrm{STC}}}·(\mathrm{NOCT}-20).$$

(2)

where in Equations (1) and (2), ${\mathrm{P}}_{\mathrm{PV}}$${\mathrm{P}}_{\mathrm{PV},\mathrm{STC}}$, ${\mathrm{G}}_{\mathrm{T}}$,$\gamma$, ${\mathrm{T}}_{\mathrm{j}}$, ${\mathrm{N}}_{\mathrm{PVs}}$, ${\mathrm{N}}_{\mathrm{PVp}}$, and $\mathrm{NOCT}$ represent the rated power of the photovoltaic system at the maximum power point and standard conditions, the amount of radiation under standard conditions, the temperature coefficient of power at the maximum power point, the temperature of solar cells, the nominal operating cell temperature, and the number of modules in series and parallel, respectively. In this regard, the operation cost of the PV systems can be defined with the following equation:

$${\mathrm{C}}_{\mathrm{PV}}=\left\{\begin{array}{cc}{\alpha }_{\mathrm{PV}}{\mathrm{P}}_{\mathrm{PV}}+{\mathrm{c}}_{\mathrm{PV}}^{\mathrm{cte}}\hfill & \mathrm{if}0<{\mathrm{P}}_{\mathrm{PV}}<{\mathrm{P}}_{\mathrm{PV}}^{max},\hfill \\ 0\hfill & \mathrm{if}{\mathrm{P}}_{\mathrm{PV}}=0\hfill \end{array}\right.$$

(3)

where ${\mathrm{c}}_{\mathrm{PV}}^{\mathrm{cte}}$ and ${\alpha }_{\mathrm{PV}}$ are constant and variable cost of PV generation units and ${\mathrm{P}}_{\mathrm{PV}}^{\max }$ is the maximum output power pf PV units. Furthermore, the output power of wind turbines depends on wind speed. The wind speed variations can occur on an instantaneous, hourly, daily, and seasonal basis. Therefore, Equation (4) is used to model the actual power generated by a wind turbine [29].

$${\mathrm{P}}_{\mathrm{wt}}\left(\mathrm{v}\right)=\left\{\begin{array}{cc}0:\hfill & \mathrm{if}\mathrm{v}<{\mathrm{V}}_{\mathrm{ci}},\hfill \\ {\mathrm{P}}_{\mathrm{R}}(\mathrm{A}+\mathrm{Bv}+{\mathrm{Cv}}^2):\hfill & \mathrm{if}{\mathrm{V}}_{\mathrm{ci}}<\mathrm{v}<{\mathrm{V}}_{\mathrm{r}},\hfill \\ {\mathrm{P}}_{\mathrm{R}}:\hfill & \mathrm{if}{\mathrm{V}}_{\mathrm{r}}<\mathrm{v}<{\mathrm{V}}_{\mathrm{co}},\hfill \\ 0:\hfill & \mathrm{if}{\mathrm{V}}_{\mathrm{co}}<\mathrm{v},\hfill \end{array}\right.$$

(4)

where in Equation (4), ${\mathrm{V}}_{\mathrm{ci}}$,${\mathrm{V}}_{\mathrm{co}}$, ${\mathrm{V}}_{\mathrm{r}}$, ${\mathrm{P}}_{\mathrm{R}}$, A, B, and C represent the cut-in, cut out and rated wind speeds, rated power of the wind turbine, and coefficients associated with the turbine, respectively. Also like the PV generation unit the operation cost of wind turbine generation unit can be calculated using the Equation (5).

$${\mathrm{C}}_{\mathrm{wt}}=\left\{\begin{array}{cc}{\alpha }_{\mathrm{wt}}{\mathrm{P}}_{\mathrm{wt}}+{\mathrm{c}}_{\mathrm{wt}}^{\mathrm{cte}}\hfill & \mathrm{if}0<{\mathrm{P}}_{\mathrm{wt}}<{\mathrm{P}}_{\mathrm{wt}}^{max},\hfill \\ 0\hfill & \mathrm{if}{\mathrm{P}}_{\mathrm{wt}}=0.\hfill \end{array}\right.$$

(5)

where ${\mathrm{c}}_{\mathrm{wt}}^{\mathrm{cte}}$ and ${\alpha }_{\mathrm{wt}}$ are constant and variable cost of wind turbine generation units and ${\mathrm{P}}_{\mathrm{wt}}^{\max }$ is the maximum output power pf WT units.

3.2. Cost Modeling of the Traditional Generation Units

Equation (6) represents the expenses associated with running conventional distributed power generation systems like micro-turbines and diesel generators, encompassing both operational expenditures and the costs linked to environmental pollution [29].

$${\mathrm{C}}_{\mathrm{DG},\mathrm{t}}={\mathrm{C}}_{\mathrm{DG},\mathrm{t}}^{\mathrm{OP}}+{\mathrm{C}}_{\mathrm{DG},\mathrm{t}}^{\mathrm{EM}}.$$

(6)

where in Equation (6), ${\mathrm{C}}_{\mathrm{DG},\mathrm{t}}^{\mathrm{OP}}$ presents the cost of operating, and ${\mathrm{C}}_{\mathrm{DG},\mathrm{t}}^{\mathrm{EM}}$ is the cost associated with the pollution of the units in each time interval t, which can be defined as follows:

$${\mathrm{C}}_{\mathrm{DG},\mathrm{t}}^{\mathrm{op}}=\left\{\begin{array}{cc}{\mathrm{a}}_{\mathrm{Dg}}{\mathrm{P}}_{\mathrm{Dg}}^2+{\mathrm{b}}_{\mathrm{Dg}}{\mathrm{P}}_{\mathrm{Dg}}+{\mathrm{c}}_{\mathrm{Dg}}:\hfill & \mathrm{if}0<{\mathrm{P}}_{\mathrm{Dg}}<{\mathrm{P}}_{\mathrm{Dg}}^{\mathrm{rated}},\hfill \\ 0:\hfill & \mathrm{if}{\mathrm{P}}_{\mathrm{Dg}}=0.\hfill \end{array}\right.$$

(7)

$${\mathrm{CF}}_{\mathrm{Dg},\mathrm{t}}^{\mathrm{EMI}}=\left({\mathrm{C}}_{{\mathrm{CO}}_2}\times {\mathrm{CO}}_2+{\mathrm{C}}_{{\mathrm{SO}}_2}\times {\mathrm{SO}}_2+{\mathrm{C}}_{{\mathrm{NO}}_{\mathrm{x}}}\times {\mathrm{NO}}_{\mathrm{x}}\right)\times {\mathrm{P}}_{\mathrm{Dg}}.$$

(8)

The parameters in Equation (8) are defined as follows:

• ${\mathrm{C}}_{{\mathrm{CO}}_2}$: Penalty factor for CO₂ production.
• ${\mathrm{C}}_{{\mathrm{SO}}_2}$: Penalty factor for SO₂ production.
• ${\mathrm{C}}_{{\mathrm{NO}}_{\mathrm{x}}}$: Penalty factor for NO_x production.

3.3. Battery Swapping Station Modeling

With the increasing integration of renewable energy sources and electric vehicles in contemporary hybrid systems, maintaining the desired frequency levels has become a significant challenge. Additional energy sources play a vital role in ensuring a stable supply–demand balance, thereby averting voltage and frequency fluctuations in real time. One solution to address this issue is the utilization of a BSS as an auxiliary power reserve. This BSS can compensate for voltage fluctuations caused by sudden changes in power generation from renewable sources. The operational parameters governing a BSS are influenced by various factors, including the arrangement of battery units, backup duration, temperature, battery lifespan, discharge depth, power reserve requirements, and the level of renewable energy generation on the grid, among others. The charging and discharging schedule for a BSS unit is detailed in reference [30]:

$${\mathrm{P}}_{\mathrm{BSS}}\left(\mathrm{t}\right)={\mathrm{P}}_{\mathrm{ch}}\left(\mathrm{t}\right):\mathrm{if}\left\{\sum {\mathrm{P}}_{\mathrm{G}}\left(\mathrm{t}\right)-{\mathrm{P}}_{\mathrm{D}}\left(\mathrm{t}\right)\right\}\ge 0.$$

(9)

$${\mathrm{P}}_{\mathrm{BSS}}\left(\mathrm{t}\right)={\mathrm{P}}_{\mathrm{dch}}\left(\mathrm{t}\right):\mathrm{if}\left\{\sum {\mathrm{P}}_{\mathrm{G}}\left(\mathrm{t}\right)-{\mathrm{P}}_{\mathrm{D}}\left(\mathrm{t}\right)\right\}<0.$$

(10)

where ${\mathrm{P}}_{\mathrm{BSS}}$$\left(\mathrm{t}\right)$, $\sum {\mathrm{P}}_{\mathrm{G}}\left(\mathrm{t}\right)$, and ${\mathrm{P}}_{\mathrm{D}}\left(\mathrm{t}\right)$ are the powers of BSS, total generation of the system, and load demand, respectively. Furthermore, ${\mathrm{P}}_{\mathrm{ch}\left(\mathrm{t}\right)}$ and ${\mathrm{P}}_{\mathrm{dch}\left(\mathrm{t}\right)}$ are charging and discharging powers of BSS. Fundamentally, a BSS unit can operate in just one mode at any given time, which is either charging or discharging. The calculation for the power of the BSS during the charging state is as follows:

$${\mathrm{E}}_{\mathrm{ch}}\left(\mathrm{t}\right)=\left(\frac{\sum {\mathrm{P}}_{\mathrm{G}}\left(\mathrm{t}\right)-{\mathrm{P}}_{\mathrm{D}}\left(\mathrm{t}\right)}{{\eta }_{\mathrm{Conv}}}\right)\times \Delta \mathrm{t}\times {\eta }_{\mathrm{ch}}.$$

(11)

$$SOC\left(\mathrm{t}\right)=SOC(\mathrm{t}-1)(1-\sigma )+{\mathrm{E}}_{\mathrm{c}\mathrm{h}}\left(\mathrm{t}\right).$$

(12)

Discharging state:

$${\mathrm{E}}_{\mathrm{dch}}\left(\mathrm{t}\right)=\left(\frac{-\left(\sum {\mathrm{P}}_{\mathrm{G}}\left(\mathrm{t}\right)-{\mathrm{P}}_{\mathrm{D}}\left(\mathrm{t}\right)\right)}{{\eta }_{\mathrm{Conv}}}\right)\times \Delta \mathrm{t}\times {\eta }_{\mathrm{dch}}.$$

(13)

$$SOC\left(\mathrm{t}\right)=SOC(\mathrm{t}-1)(1-\sigma )-{\mathrm{E}}_{\mathrm{ch}}\left(\mathrm{t}\right).$$

(14)

where $\mathrm{SOC}\left(\mathrm{t}\right)$, ${\mathrm{E}}_{\mathrm{ch}}\left(\mathrm{t}\right)$, ${\mathrm{E}}_{\mathrm{dch}}\left(\mathrm{t}\right)$, $\sigma$, ${\eta }_{\mathrm{ch}}$, ${\eta }_{\mathrm{dch}}$, and ${\eta }_{\mathrm{Conv}}$ denote the battery charge state, charging energy, discharging energy, self-discharge rate, charging/ discharging efficiency, and converter efficiency, respectively. In the following, constraints as in Equations (15) and (16) serve to limit the energy level and the charging/discharging power of a BSS. Meanwhile, Equation (17) enforces that the BSS’s energy level remains consistent, ensuring it is the same at both the beginning and the end of the scheduling horizon.

$${\mathrm{E}}_{\mathrm{BSS}}^{min}\left(\mathrm{t}\right)\le {\mathrm{E}}_{\mathrm{BSS}}\left(\mathrm{t}\right)\le {\mathrm{E}}_{\mathrm{BSS}}^{max}\left(\mathrm{t}\right).$$

(15)

$${\mathrm{P}}_{\mathrm{BSS}}^{min}\left(\mathrm{t}\right)\le {\mathrm{P}}_{\mathrm{BSS}}\left(\mathrm{t}\right)\le {\mathrm{P}}_{\mathrm{BSS}}^{max}\left(\mathrm{t}\right).$$

(16)

$${\mathrm{E}}_{\mathrm{BSS}}^{\mathrm{initial}}\left(\mathrm{t}\right)={\mathrm{P}}_{\mathrm{BSS}}^{\mathrm{final}}\left(\mathrm{t}\right).$$

(17)

The operating cost of the $\mathrm{PSS}$$\left({\mathrm{C}}_{\mathrm{b}}\mathrm{w}\right)$ units can be described as

$${\mathrm{C}}_{\mathrm{BSS}}={\mathrm{N}}_{\mathrm{batt}}\frac{{\mathrm{C}}_{\mathrm{rep},\mathrm{batt}}}{\sqrt{\eta \mathrm{rt}}}+{\mathrm{C}}_{\mathrm{BSS}}^{\mathrm{constant}}.$$

(18)

where ${\mathrm{C}}_{\mathrm{rep},\mathrm{batt}}$, ${\eta }_{\mathrm{rt}}$, and ${\mathrm{C}}_{\mathrm{BSS}}^{\mathrm{constant}}$ are storage replacement cost, the round-trip efficiency of storage, and the constant cost of the BSS, respectively.

3.4. Power Losses and Loss Sensitivity Factor

The losses in power networks are an unavoidable problem that restricts the transmission capacity of the lines and continually incurs additional expenses for the network. Hence, the primary objective of microgrid planners and smart distribution networks is to minimize these losses. This article examines the losses in the distribution networks as a factor in the objective function. These losses are determined using Equations (19) and (20) [31]:

$$\mathrm{Active}\mathrm{Losses}={\left(\frac{{\left|\mathrm{V}\right|}^2}{{\mathrm{R}}_{{\mathrm{Z}}_{\mathrm{i}}}}\right)}_{\mathrm{end}}-{\left(\frac{{\left|\mathrm{V}\right|}^2}{{\mathrm{R}}_{{\mathrm{Z}}_{\mathrm{j}}}}\right)}_{\mathrm{start}}.$$

(19)

$$\mathrm{Reactive}\mathrm{Losses}={\left(\frac{{\left|\mathrm{V}\right|}^2}{{\mathrm{X}}_{{\mathrm{Z}}_{\mathrm{i}}}}\right)}_{\mathrm{end}}-{\left(\frac{{\left|\mathrm{V}\right|}^2}{{\mathrm{X}}_{{\mathrm{Z}}_{\mathrm{j}}}}\right)}_{\mathrm{start}}.$$

(20)

On the other side, the power loss sensitivity factor (PLSF) evaluates the vulnerability of a bus in the system to variations in active power injection and the subsequent effect on the total power loss in the system, as described in Equation (21). This statistic is used to assess the most suitable bus sites for deploying DG in a RDS. The algorithm evaluates the sensitivity of each bus, and buses with a high PLSF are deemed optimal sites for DG installations.

$$\mathrm{PLSF}=\sum _{\mathrm{i}=1}^{\mathrm{N}}\frac{\partial {\mathrm{P}}_{\mathrm{loss}(\mathrm{i},\mathrm{i}+1)}}{\partial {\mathrm{P}}_{\mathrm{i}+1}}=\sum _{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{R}}_{\mathrm{i}}\left(\frac{2{\mathrm{P}}_{\mathrm{i}+1}}{{\left|{\mathrm{V}}_{\mathrm{i}+1}\right|}^2}\right).$$

(21)

3.5. Voltage Deviations Formulations

The primary objective of this research article is to reduce voltage variations in the distribution network through the use of BSS. The magnitude of the voltage deviation can be determined by employing the formula shown in Equation (22) [31]:

$$\begin{array}{cc}\hfill \mathrm{VD}& =\sqrt{\sum _{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{b}}}{\left(\frac{{\mathrm{V}}_{\mathrm{standard}}}{{\mathrm{V}}_{\mathrm{Base}}}-\frac{{\mathrm{V}}_{\mathrm{i}}}{{\mathrm{V}}_{\mathrm{Base}}}\right)}^2}.\hfill \end{array}$$

(22)

3.6. Short Circuit Level Criteria Modeling

One of the most critical technical parameters in a network, which undergoes direct variations due to changes in generation, consumption, and network structure, is the short-circuit level at different network points and within connected microgrids. This vital measure has a substantial impact on protection settings and network planning, ultimately influencing the network’s safety and optimal operation. Therefore, when strategically placing BSSs from a technical and economic standpoint, it is imperative to consider this significant parameter, which has been overlooked in the prior studies. Failure to consider the short-circuit level can result in damages caused by insufficient performance of the protection system during BSS charge and discharge cycles, as well as power generation from various sources. The detriments resulting from optimal generation distribution may significantly surpass the advantages realized. Therefore, it is crucial to accurately determine the short-circuit level in a complete energy management plan to maintain stability even when there are variations in the generation capacity and network layout. The short-circuit level is specified in the present study report as follows: [32]:

$$\mathrm{SCLI}=\left(\sum _{\mathrm{k}=1}^{\mathrm{n}\mathrm{b}}\left(1-\frac{{\mathrm{I}}_{\mathrm{k}}^{*}\left(\mathrm{F}\right)}{{\mathrm{I}}_{\mathrm{k}}\left(\mathrm{F}\right)}\right)\right)$$

(23)

$${\mathrm{I}}_{\mathrm{k}}\left(\mathrm{F}\right)=\frac{{\mathrm{V}}_{\mathrm{k}}}{{\mathrm{Z}}_{\mathrm{kk}}+{\mathrm{Z}}_{\mathrm{f}}}.$$

(24)

$${\mathrm{I}}_{\mathrm{k}}^{*}\left(\mathrm{F}\right)=\frac{{\mathrm{V}}_{\mathrm{k}}^{*}}{{\mathrm{Z}}_{\mathrm{kk}}+{\mathrm{Z}}_{\mathrm{f}}}.$$

(25)

where, ${\mathrm{V}}_{\mathrm{k}}$ and ${\mathrm{V}}_{\mathrm{k}}^{*}$ represent the voltage of each bus in the network before and after any changes in the network. ${\mathrm{Z}}_{\mathrm{kk}}$ and ${\mathrm{Z}}_{\mathrm{f}}$ represent the impedance of the bus and the impedance of the fault that occurred at the bus in the network, respectively.

3.7. Voltage Sensitivity Index

Another crucial factor within the realm of security and power quality in power distribution networks and microgrids is the voltage sensitivity index (VSI). This indicator evaluates the power distribution network’s capacity to maintain voltage levels within a secure range in response to increasing customer demands, indicating the overall safety of the power system. Consequently, in this study article, the VSI of the power distribution network is specified as one of the aims for strengthening network security. The specification is formulated so that the VSI diminishes as the system load escalates, ultimately reaching zero when the network is on the verge of failure and the maximum sustainable system load is attained [33]:

$$\mathrm{VSI}=\sum _{\mathrm{i}=1}^{\mathrm{N}}\left({\left|{\mathrm{V}}_{\mathrm{i}}\right|}^4-4{\left|{\mathrm{V}}_{\mathrm{i}}\right|}^2\left({\mathrm{R}}_{\mathrm{e}\mathrm{q},\mathrm{i}}{\mathrm{P}}_{\mathrm{L}\mathrm{m},\mathrm{i}}+{\mathrm{X}}_{\mathrm{e}\mathrm{q},\mathrm{i}}{\mathrm{Q}}_{\mathrm{L}\mathrm{m},\mathrm{i}}\right)-4{\left({\mathrm{X}}_{\mathrm{e}\mathrm{q},\mathrm{i}}{\mathrm{P}}_{\mathrm{L}\mathrm{m},\mathrm{i}}-{\mathrm{R}}_{\mathrm{e}\mathrm{q},\mathrm{i}}{\mathrm{Q}}_{\mathrm{L}\mathrm{m},\mathrm{i}}\right)}^2\right)$$

(26)

where in Equation (26), $|{\mathrm{V}}_{\mathrm{i}}|$ represents the voltage magnitude at the bus $\mathrm{i}$, ${\mathrm{R}}_{\mathrm{eq},\mathrm{i}}$ and ${\mathrm{X}}_{\mathrm{eq},\mathrm{i}}$ are the equivalent resistance and reactance of the line; moreover, ${\mathrm{P}}_{\mathrm{Lm},\mathrm{i}}$ and ${\mathrm{Q}}_{\mathrm{Lm},\mathrm{i}}$ represent the total active and reactive power of all nodes, respectively.

3.8. Expected Energy Not Served (EENS) Criteria

In the realm of planning and operational studies for power distribution networks and microgrids, assessing network reliability stands out as a paramount concern. Multiple indices are scrutinized to gauge network reliability, yet the most practical one for assessing reliability across various levels of energy generation and transmission is the EENS index, a measure also employed in this paper. To calculate the EENS index, it is necessary to acquire the forced outage probability for each equipment component, such as producing units and power distribution lines. This study aims to quantify the unmet demand resulting from the forced shutdowns of power generation units and distribution lines, taking into account the existence of a virtual power generator at each bus. A deterministic model is used to produce continuous occurrences and their corresponding probabilities. The EENS index is calculated using the following Equation [34]:

$${\mathrm{F}}_{\mathrm{i}}=\mathrm{EENS}={\mathrm{EENS}}_G+{\mathrm{EENS}}_{\mathrm{L}}.$$

(27)

subjected to:

$${\mathrm{EENS}}_G=\sum _{\mathrm{i}=1}^{\mathrm{NG}}{\rho }_{\mathrm{i}}^{\mathrm{G}}{\mathrm{E}}_{\mathrm{i},{\mathrm{P}}_{{\mathrm{G}}_{\mathrm{i}}}^{\mathrm{Outage}}G...}$$

$${\mathrm{EENS}}_{\mathrm{L}}=\sum _{j=1}^{NL}{\rho }_{\mathrm{j}}^L{E}_{\mathrm{i},{\mathrm{L}}_{\mathrm{i}}^{\mathrm{Outage}}}^L.$$

3.9. Objective Function Formulation

The optimization model presented in the current paper is designed to address a complex problem with multiple conflicting objectives. Unlike traditional optimization problems, it lacks a single unique solution. Instead, any solution that adheres to the defined constraints can be considered optimal. To achieve the desired objectives of ensuring both safety and efficiency in the placement of BSSs while meeting specified constraints, various factors such as unit commitment, controllable distributed generation unit capacities, and power exchange with the upstream network must be determined for each hour in advance. The overarching aim of this comprehensive planning is to achieve optimal and safe operation, taking into account all technical network parameters while accommodating the charging and discharging states of BSSs over time. To accomplish this goal, a novel multi-objective optimization approach is employed, combining the epsilon-constraint and lexicographic optimization methods. The planning problem is formulated with a multi-objective function represented by Equation (28).

$$min\left\{{\mathrm{F}}_{\mathrm{i}}({\mathrm{N}}_{\mathrm{BSS}},\mathrm{i},{\mathrm{L}}_{\mathrm{BSS}},\mathrm{i},{\mathrm{C}}_{\mathrm{BSS}},\mathrm{i})\right\}.$$

(28)

In the above equation, ${\mathrm{N}}_{\mathrm{BSS},\mathrm{i}}$ and ${\mathrm{L}}_{\mathrm{BSS},\mathrm{i}}$ represent the number and location of the BSSs, respectively; furthermore, the ${\mathrm{C}}_{\mathrm{BSS},\mathrm{i}}$ represents the capacity of the BSSs in objective functions of the mentioned planning problem. Therefore, the desired objective functions in this problem can be formulated as follows:

$${\mathrm{F}}_1({\mathrm{N}}_{\mathrm{BSS}},\mathrm{i},{\mathrm{L}}_{\mathrm{BSS}},\mathrm{i},{\mathrm{C}}_{\mathrm{BSS}},\mathrm{i})=\mathrm{Total}\mathrm{Cost}$$

$$\begin{array}{cc}\hfill & {\mathrm{F}}_1\left({\mathrm{N}}_{\mathrm{B}\mathrm{S}\mathrm{S}},\mathrm{i},{\mathrm{L}}_{\mathrm{B}\mathrm{S}\mathrm{S}},\mathrm{i},{\mathrm{C}}_{\mathrm{B}\mathrm{S}{\mathrm{S}}_{\mathrm{r}}}\mathrm{i}\right)=\mathrm{Total}\mathrm{Cost}=\hfill \\ \hfill & =\left\{\begin{array}{c}\underset{\mathrm{PV}\mathrm{Cost}}{\underbrace{C_{\mathrm{P}\mathrm{V}}\left({\mathrm{P}}_{\mathrm{P}\mathrm{V}}\right)}}+\underset{\mathrm{Wind}\mathrm{Turbine}\mathrm{Cost}}{\underbrace{{\mathrm{C}}_{\mathrm{wt}}\left({\mathrm{P}}_{\mathrm{wt}}\right)}}+\underset{\mathrm{Traditional}\mathrm{Unit}\mathrm{Cost}}{\underbrace{C_{{\mathrm{D}}_{\mathrm{g}}}\left({\mathrm{P}}_{\mathrm{D}\mathrm{g}}\right)}}\hfill \\ +\underset{\mathrm{Utility}\mathrm{Cost}}{\underbrace{C_{\mathrm{utility}}\left(P_{\mathrm{utility}}\right)}}+\underset{\mathrm{Battery}\mathrm{Cost}}{\underbrace{C_{\mathrm{battery}}\left(P_{\mathrm{Battery}}\right)}}\hfill \end{array}\right\}\hfill \end{array}.$$

(29)

$$\begin{array}{cc}\hfill {\mathrm{F}}_2({\mathrm{N}}_{\mathrm{BSS}},\mathrm{i},{\mathrm{L}}_{\mathrm{BSS}},\mathrm{i},{\mathrm{C}}_{\mathrm{BSS}},\mathrm{i})& =\mathrm{Losses}\hfill \\ \hfill & =\underset{\mathrm{Active}\mathrm{Losses}}{\underbrace{\left({\left|\frac{{\mathrm{V}}^2}{{\mathrm{R}}_{{\mathrm{Z}}_{\mathrm{i}}}}\right|}_{\mathrm{end}}-{\left|\frac{{\mathrm{V}}^2}{{\mathrm{R}}_{{\mathrm{Z}}_{\mathrm{j}}}}\right|}_{\mathrm{start}}\right)}}\hfill \\ \hfill & +\underset{\mathrm{Reactive}\mathrm{Losses}}{\underbrace{\left({\left|\frac{{\mathrm{V}}^2}{{\mathrm{X}}_{{\mathrm{Z}}_{\mathrm{i}}}}\right|}_{\mathrm{end}}-{\left|\frac{{\mathrm{V}}^2}{{\mathrm{X}}_{{\mathrm{Z}}_{\mathrm{j}}}}\right|}_{\mathrm{start}}\right)}}.\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill {\mathrm{F}}_3({\mathrm{N}}_{\mathrm{BSS}},\mathrm{i},{\mathrm{L}}_{\mathrm{BSS}},\mathrm{i},{\mathrm{C}}_{\mathrm{BSS}},\mathrm{i})& =\mathrm{PLSF}\hfill \\ \hfill & =\sum _{\mathrm{i}=1}^{\mathrm{N}}\frac{\partial {\mathrm{P}}_{\mathrm{loss}(\mathrm{i},\mathrm{i}+1)}}{\partial {\mathrm{P}}_{\mathrm{i}+1}}\hfill \\ \hfill & =\sum _{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{R}}_{\mathrm{i}}\left(\frac{2{\mathrm{P}}_{\mathrm{i}+1}}{|{\mathrm{V}}_{\mathrm{i}+1}{|}^2}\right).\hfill \end{array}$$

(31)

$$\begin{array}{c}\hfill {\mathrm{F}}_4({\mathrm{N}}_{\mathrm{BSS}},\mathrm{i},{\mathrm{L}}_{\mathrm{BSS}},\mathrm{i},{\mathrm{C}}_{\mathrm{BSS}},\mathrm{i})=\\ \hfill \mathrm{VD}=\sqrt{\sum _{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{b}}}{\left(\frac{{\mathrm{V}}_{\mathrm{standard}}}{{\mathrm{V}}_{\mathrm{Base}}}-\frac{{\mathrm{V}}_{\mathrm{i}}}{{\mathrm{V}}_{\mathrm{Base}}}\right)}^2}.\end{array}$$

(32)

$${\mathrm{F}}_5({\mathrm{N}}_{\mathrm{BSS}},\mathrm{i},{\mathrm{L}}_{\mathrm{BSS}},\mathrm{i},{\mathrm{C}}_{\mathrm{BSS}},\mathrm{i})=\mathrm{VSI}.$$

(33)

$${\mathrm{F}}_6({\mathrm{N}}_{\mathrm{BSS}},\mathrm{i},{\mathrm{L}}_{\mathrm{BSS}},\mathrm{i},{\mathrm{C}}_{\mathrm{BSS}},\mathrm{i})=\left(1-\sum _{\mathrm{k}=1}^{\mathrm{nb}}\frac{{\mathrm{I}}_{\mathrm{k}}^{*}\left(\mathrm{F}\right)}{{\mathrm{I}}_{\mathrm{k}}\left(\mathrm{F}\right)}\right).$$

(34)

$${\mathrm{F}}_7({\mathrm{N}}_{\mathrm{BSS},\mathrm{i}},{\mathrm{L}}_{\mathrm{BSS},\mathrm{i}},{\mathrm{C}}_{\mathrm{BSS},\mathrm{i}})=\mathrm{EENS}.$$

(35)

In the distribution network that encompasses all power generation, consumption resources, and interconnected microgrids, there exists the potential for energy to flow in both directions between the network, microgrids, and generation/consumption sources. Each objective function in this context seeks to maximize its own advantages when dealing with multiple objectives simultaneously. As a result, when accounting for various operational scenarios for the microgrids, the multi-objective function for achieving optimal and secure energy management across the entire network can be mathematically represented as follows:

$$min\left\{{\mathrm{OF}}_{\mathrm{Total}}\right\}=\left[\begin{array}{cccc}{\chi }_{12}& {\chi }_{12}& \cdots & {\chi }_{pk}\end{array}\right]\left[\begin{array}{c}{\mathrm{OF}}_1\\ {\mathrm{OF}}_2\\ ⋮\\ {\mathrm{OF}}_{\mathrm{k}}\end{array}\right].$$

(36)

Equation (36), ${\chi }_{pk}$ represents the weight coefficient of the objective functions. Adjusting the weights for each objective function should take into account specific events and system characteristics, such as different system states during maintenance, replacement schedules, the likelihood of component failures, and various error events within the system, each leading to distinct system performance conditions. These weights are tuned to accurately represent the significance of these events and characteristics within the overall optimization framework. By assigning higher weights to particular objective functions, their influence on the optimization process is heightened, signifying their relative importance in attaining the desired system performance. The weight adjustment procedure entails a meticulous evaluation of each event and system attribute to ensure an optimal and well-balanced solution for the multi-objective optimization challenge.

4. Multi-Objective Optimization Method

Typically, a mathematical representation of an optimization problem involving two or more objective functions can be expressed as follows:

$$\min ,\mathrm{F}={\left[\begin{array}{c}{f}_1\left(\chi \right)f_2\left(\chi \right)f_3\left(\chi \right)\cdots f_{\mathrm{p}}\left(\chi \right)\end{array}\right]}^T.$$

(37)

Subjected to

$$\left\{\begin{array}{c}\begin{array}{cc}{\mathrm{g}}_{\mathrm{i}}\left(x\right)⪯0,\hfill & \hfill \mathrm{i}=1,2,3,\dots ,{\mathrm{N}}_{\mathrm{ueq}}.\\ {\mathrm{h}}_{\mathrm{i}}\left(x\right)⪯0,\hfill & \hfill \mathrm{i}=1,2,3,\dots ,{\mathrm{N}}_{\mathrm{eq}}.\end{array}\hfill \end{array}\right.$$

(38)

where p represents the number of objective functions, ${\mathrm{N}}_{\mathrm{ueq}}$ designates the count of inequality constraints, and ${\mathrm{N}}_{\mathrm{eq}}$ signifies the number of equality constraints. Furthermore, the decision vector is denoted by X. It is crucial to observe that the objective functions are purposed to be either minimized or maximized, contingent upon the problem’s application and the specific definition of the objective function. It is of paramount significance to recognize that the resolution of a multi-objective optimization problem results in the derivation of a collection of optimal solutions, while a single-objective optimization problem culminates in a singular optimal solution. In fact, within this assortment, each constituent comprises a pair of values when addressing a bi-objective problem. From this perspective, every component within the ensemble of optimal solutions is referred to as a Pareto optimal (non-dominated or non-inferior) solution. The fundamental concept behind the Pareto optimal front lies in the impossibility of improving the value of one objective function without adversely affecting the values of other objective functions. Among the numerous multi-objective optimization techniques introduced to date, the epsilon-constraint method has demonstrated itself as a highly efficient approach, especially when compared to the weighting-sum method. With the weighting-sum method, all objective functions are assigned weights and combined into a single objective function. Nonetheless, a renowned optimization method such as the epsilon-constraint technique also presents two significant drawbacks that require careful consideration. When dealing with P objective functions, it becomes imperative to define the range of P-1 objective functions as these objectives will be treated as constraints in the problem. In this paper, addressing these challenges involves the utilization of the lexicographic optimization technique to effectively determine the range for each objective function, which addresses the first shortcoming of this multi-objective optimization method. As for the second shortcoming, concerning the efficiency and quality of the obtained solutions, the modified epsilon-constraint technique is applied to overcome this limitation. Therefore, this paper combines the hybrid techniques of the developed epsilon-constraint and the lexicographic optimization methods to resolve the proposed multi-objective optimization problem characterized by conflicting objective functions. The core principle of this method revolves around designating one of the objective functions, as the primary focus and treating all others as constraints within the problem, as follows:

$$\left\{\begin{array}{c}min,f_1\left(\overline{\chi }\right)\hfill \\ f_2\left(\overline{\chi }\right)\le e_2,f_3\left(\overline{\chi }\right)\le e_3,\dots f_{\mathrm{p}}\left(\overline{\chi }\right)\le e_{\mathrm{p}}.\hfill \end{array}\right.$$

(39)

where, $\mathrm{p}$ represents the number of objective functions, and x denotes the vector of decision variables. As evident from the expression above, all the objective functions are set to be minimized. As previously discussed, it is crucial to establish the ranges for the $(p-1)$ objective functions. To achieve this, the payoff matrix can be employed to calculate these values. To construct the payoff matrix, the problem is initially solved as a single-objective optimization problem to find optimal values for each $f_i$ for p objective function. These values are then used to calculate the single optimum values of the other objective functions $f_i^{*}\left({\overline{\chi }}_i^{*}\right)$ and ${\overline{\chi }}_i^{*}$, respectively. The resultant payoff matrix is structured with rows representing various combinations of objective function values. For a more comprehensive understanding and access to the associated equations, please consult the provided reference. It should be noted that the remaining objective functions possess a single optimal value:

$$f_{\mathrm{i}}\left({\overline{\chi }}_{\mathrm{i}}^{*}\right),f_2\left({\overline{\chi }}_{\mathrm{i}}^{*}\right),f_{\mathrm{i}-1}^{*}\left({\overline{\chi }}_{\mathrm{i}}^{*}\right),f_{\mathrm{i}+1}\left({\overline{\chi }}_{\mathrm{i}}^{*}\right),\dots f_{\mathrm{p}}\left({\overline{\chi }}_{\mathrm{i}}^{*}\right).$$

(40)

the payoff matrix is created by arranging the elements of each row i in a specific manner:

$$f_1\left({\overline{\chi }}_{\mathrm{i}}^{*}\right),f_2\left({\overline{\chi }}_{\mathrm{i}}^{*}\right),\dots f_{\mathrm{i}}\left({\overline{\chi }}_{\mathrm{i}}^{*}\right),f_{\mathrm{p}}\left({\overline{\chi }}_{\mathrm{i}}^{*}\right).$$

(41)

$$Q=\left[\begin{array}{ccccc}{f}_1^{*}\left({\overline{\chi }}_1^{*}\right)& \cdots & f_{\mathrm{i}}\left({\overline{\chi }}_1^{*}\right)& \cdots & f_{\mathrm{p}}\left({\overline{\chi }}_1^{*}\right)\\ ⋮& \\ f_1\left({\overline{\chi }}_{\mathrm{i}}^{*}\right)& \cdots & f_{\mathrm{i}}^{*}\left({\overline{\chi }}_{\mathrm{i}}^{*}\right)& \cdots & f_{\mathrm{p}}\left({\overline{\chi }}_{\mathrm{i}}^{*}\right)\\ ⋮& \\ f_1\left({\overline{\chi }}_{\mathrm{p}}^{*}\right)& \cdots & f_{\mathrm{i}}\left({\overline{\chi }}_{\mathrm{p}}^{*}\right)& \cdots & f_{\mathrm{p}}^{*}\left({\overline{\chi }}_{\mathrm{p}}^{*}\right)\end{array}\right].$$

(42)

The payoff matrix is a square one $(\mathrm{p}\times \mathrm{q})$ where each column n represents the optimum value of an objective function $f_n$, bounded by minimum and maximum values, while the Utopia point $f^U$ represents the best values of all objectives in an infeasible region.

$$\begin{array}{c}\hfill f^{\mathrm{U}}=[f_1^{\mathrm{U}},\dots ,f_{\mathrm{i}}^{\mathrm{U}},\dots ,f_{\mathrm{p}}^{\mathrm{U}}]=[f_1^{*}\left({\overline{\chi }}_1^{*}\right),\dots ,f_{\mathrm{i}}^{*}\left({\overline{\chi }}_{\mathrm{i}}^{*}\right),\dots ,f_{\mathrm{p}}^{*}\left({\overline{\chi }}_{\mathrm{p}}^{*}\right)].\end{array}$$

(43)

Conversely, the Nadir point $\left(f^N\right)$ refers to the point in the objective region where all objective functions attain their worst values.

$$f^{\mathrm{N}}=[f_1^{\mathrm{N}},\dots ,f_{\mathrm{i}}^{\mathrm{N}},\dots ,f_{\mathrm{p}}^N].$$

(44)

where:

$$\left\{\begin{array}{cc}{f}_{\mathrm{i}}^{\mathrm{N}}=(Max/\overline{\chi })f_{\mathrm{i}}\left(\overline{\chi }\right).\hfill & \\ \mathrm{Compliance}\mathrm{with}:\overline{x}\in \mathsf{\Omega }.\hfill \end{array}\right.$$

(45)

The feasible region $\mathsf{\Omega }$ contains the Pseudo-Nadir point, which closely resembles the Nadir point, and it is presented as

$$f^{\mathrm{SN}}=[f_1^{\mathrm{SN}},\dots ,f_{\mathrm{i}}^{\mathrm{SN}},\dots ,f_{\mathrm{p}}^{\mathrm{SN}},\dots ].$$

(46)

$$f_{\mathrm{i}}^{\mathrm{SN}}=max\{f_{\mathrm{i}}\left({\overline{\chi }}_1^{*}\right),\dots ,f_{\mathrm{i}}^{*}\left({\overline{\chi }}_{\mathrm{i}}^{*}\right),\dots ,f_{\mathrm{i}}\left({\overline{\chi }}_{\mathrm{p}}^{*}\right)\}.$$

(47)

The objective functions range is determined using the Utopia and pseudo-Nadir points according to the following formula:

$$f_{\mathrm{i}}^{\mathrm{U}}\le f_{\mathrm{i}}\left(\overline{\chi }\right)\le f_{\mathrm{i}}^{\mathrm{SN}}.$$

(48)

The objective space, which is shown in Figure 3, is determined by the dimension of objective functions, and the Utopia, Pseudo-Nadir, and Nadir points help depict the Pareto frontier while dividing the objective function ranges into equal intervals using intermediate grid points $(q_2-1),\dots ,(q_p-1)$. Moreover, this results in the requirement of solving ${\prod }_{\mathrm{i}=2}^p\left(q_{\mathrm{i}+1}\right)$ subproblems.

$$min{f}_1\left(\overline{\chi }\right).$$

so that

$$f_2\left(\overline{\chi }\right)\le e_{2,\mathrm{n}2},\dots ,f_{\mathrm{p}}\left(\overline{\chi }\right)\le e_{\mathrm{p},\mathrm{np}}.$$

(49)

where

$$e_{2,\mathrm{n}2}=f_2^{\mathrm{SN}}-\left(\frac{f_2^{\mathrm{SN}}-f_2^{\mathrm{U}}}{{\mathrm{q}}_2})\right)\times \mathrm{n}2,\mathrm{n}2=0,1,\dots ,{\mathrm{q}}_2.$$

$$e_{2,\mathrm{n}2}=f_{\mathrm{p}}^{\mathrm{SN}}-\left(\frac{f_{\mathrm{p}}^{\mathrm{SN}}-f_{\mathrm{p}}^{\mathrm{U}}}{{\mathrm{q}}_{\mathrm{p}}})\right)\times \mathrm{np},\mathrm{np}=0,1,\dots ,{\mathrm{q}}_{\mathrm{p}}.$$

(50)

The technique involves solving sub-problems using Equation (50) constraints, along with the main problem constraints, to obtain the Pareto optimal front and eliminate infeasible solutions, with the objective function constraints transformed into equalities using the slack variable method.

$$\left\{\begin{array}{c}Min,\left(f_1\left(\overline{\chi }\right)-{\mathrm{r}}_1\sum _{\mathrm{i}=2}^{\mathrm{P}}\left(\frac{{\mathrm{s}}_{\mathrm{i}}}{{\mathrm{r}}_{\mathrm{i}}}\right)\right).\hfill \\ \mathrm{Subject}\mathrm{to}\hfill \\ f_{\mathrm{i}}\left(\overline{\chi }\right)+{\mathrm{s}}_{\mathrm{i}},{\mathrm{n}}_{\mathrm{i}}={\mathrm{e}}_{\mathrm{i}},{\mathrm{n}}_{\mathrm{i}},\to \mathrm{i}=2,\dots ,\mathrm{p}{\mathrm{s}}_{\mathrm{i}},{\mathrm{n}}_{\mathrm{i}}\in {\mathrm{R}}^{+}.\hfill \\ \overline{\chi }\in \mathsf{\Omega }.\hfill \end{array}\right.$$

(51)

The method ${\mathrm{s}}_2,\dots ,{\mathrm{s}}_{\mathrm{p}}$ addresses scaling issues by introducing slack variables based on the Equation (51) formula and includes ${\mathrm{r}}_1({\mathrm{s}}_{\mathrm{i}}/{\mathrm{r}}_{\mathrm{i}})$, a term in the objective function to handle objective scale discrepancies, while the ranges of objective functions are determined using the payoff matrix $({\mathrm{r}}_{\mathrm{i}}={\mathrm{f}}_{\mathrm{i}}^{\mathrm{S}}\mathrm{N}-{\mathrm{f}}_{\mathrm{i}}^{\mathrm{U}})$. The augmented epsilon-constraint method is used, and the flowchart in Figure 4 presents the multi-objective optimization process where the decision maker selects the most desirable solution based on linear membership functions defined for each objective function using the fuzzy satisfying method.

$${\mu }_{\mathrm{F}\mathrm{i}}\left(\chi \right)=\left\{\begin{array}{cc}1\hfill & {\mathrm{F}}_{\mathrm{i}}\left(\chi \right)\le {\mathrm{F}}_{\mathrm{i}}^{min}.\hfill \\ \frac{{\mathrm{F}}_{\mathrm{i}}^{max}-{\mathrm{F}}_{\mathrm{i}}\left(\chi \right)}{{\mathrm{F}}_{\mathrm{i}}^{max}-{\mathrm{F}}_{\mathrm{i}}^{min}}\hfill & {\mathrm{F}}_{\mathrm{i}}^{min}\le {\mathrm{F}}_{\mathrm{i}}\left(\chi \right)\le {\mathrm{F}}_{\mathrm{i}}^{max}.\hfill \\ 0\hfill & {\mathrm{F}}_{\mathrm{i}}\left(\chi \right)\ge {\mathrm{F}}_{\mathrm{i}}^{max}.\hfill \end{array}\right.$$

(52)

The membership function evaluates the satisfaction level of the objective function condition with 1 indicating satisfaction and 0 representing no satisfaction, ${\mathrm{F}}_{\mathrm{i}}^{\mathrm{k}}$ represents the value of each objective function, and ${\mu }_{\mathrm{i}}^{\mathrm{k}}$ is the membership value in the Pareto solution k. This membership function is designed for minimizing objective functions. The overall membership value ${\mu }^{\mathrm{k}}$ determines the most compromised solution.

$${\mu }^{\mathrm{k}}=\frac{{\sum }_{\mathrm{i}=1}^{\mathrm{P}}{w}_{\mathrm{i}}{\mu }_{\mathrm{i}}^{\mathrm{k}}}{{\sum }_{\mathrm{k}=1}^{\mathrm{M}}{\sum }_{\mathrm{i}=1}^{\mathrm{P}}{w}_{\mathrm{i}}{\mu }_{\mathrm{i}}^{\mathrm{k}}}.$$

(53)

The weighting factor $w_{\mathrm{i}}$ determines the importance of each objective function $\left(\mathrm{i}\right)$ as the decision maker selects the optimal expansion plan based on system requirements, with the solution having the highest ${\mu }^{\mathrm{k}}$ value chosen as the most compromised solution considering the weighted membership values.

5. Simulation Results and Discussion

This section focuses on examining a suggested approach for thoroughly evaluating the most advantageous placement of BSSs in intelligent distribution networks like IEEE 118, 69, and 33-bus systems, along with their corresponding subnetworks. This assessment is conducted under typical load conditions, as well as under various load patterns, ranging from 20% to 150% of the rated load. To investigate this further, this setup serves as a test bed to validate the proposed methodology: designating a 118-bus network inclusive of its interconnected microgrids, as illustrated in Figure 5, to conduct the test. This structure supports the efficacy and soundness of the proposed methodology, and it is compared with other recent methods in the field. For a detailed understanding of the load data and network lines mentioned here, please refer to [35]. In this study, as depicted in Figure 5, three microgrids were positioned at nodes 1, 42, and 110 within the mentioned distribution networks. Moreover, within this study, the distributed generation resources in these microgrids comprised a combination of wind turbines, photovoltaic systems, microturbines, and diesel generators to supply operational power, while the optimal placement of BSSs is carried out during system operation. Following the introduction of the study’s input parameters, the proposed method was assessed and evaluated in comparison with other recent methods, taking into account both the consideration and non-consideration of network security and reliability indicators. Additionally, to optimize the multi-objective function mentioned in the previous section, a developed multi-objective optimization algorithm was employed, and its outcomes were compared with other optimization algorithms under discussion.

5.1. Input Parameters of the System

As indicated in Figure 5, the sophisticated distribution network, in conjunction with its interconnected microgrids, employs distributed generation sources such as wind turbines and photovoltaic systems to generate power. In this context, Figure 6, Figure 7 and Figure 8 present the profiles of solar radiation, ambient temperature, wind speed, and load consumption at various time intervals during the load variations in the network.

5.2. Results Analysis

In the first stage, a comprehensive examination of the optimal placement of BSSs in the IEEE 118-bus distribution network, along with its connected sub-networks, was undertaken using the proposed method, which considered both the technical and economic aspects of the problem in comparison to other recent approaches. In this context, the performance of the proposed optimization method was compared with that of the previous methods during the load variation period. The results of optimizing the objective function using the proposed algorithm and other previous methods are presented in

Table 2. Comparison of the proposed optimization algorithm with other optimization methods.

		Indexes
		CPU	Operation	Losses	Voltage	(EENS)	VSI	PLSF	SCLI
Optimization	Iterations	Times	Cost	(KW)	Deviation
Method		(s)	($)		(pu)	(KWh)	(pu)	(pu)	(pu)
(PM)	20	1380	20,589.31	2.08	1.06	80.48	110.26	16.32	0.24
P(PSO)	30	1420	66581.51	4.12	5.31	158.62	97.19	14.26	0.45
(MOGA)	110	1480	55164.43	3.74	5.21	145.46	87.52	15.33	0.39
(MODE)	56	2541	47412.74	5.46	5.01	154.82	154.54	14.88	0.29
(MOBE-PSO)	40	3024	34718.87	3.48	5	150.18	117.73	15.61	0.28

. As was evident, the proposed optimization algorithm has consistently outperformed other optimization methods in all the desired indicators, clearly demonstrating its superior performance. Table 2 compare the results of the proposed method with those of other optimization methods under the same conditions and objective function. The simulation results in Table 2 confirm that the proposed method is superior to other methods in terms of accuracy and acceleration. The table shows that the proposed method has the best CPU time performance with minimum iteration, and it also provides the lowest operating cost, voltage deviation, and system losses. Moreover, the proposed method has the minimum EENS, which is desirable for a system. Additionally, the PM has found the maximum PLSF and VSI for the benchmark network case studies, indicating better technical performance of a distribution power network. The PM also has the minimum change in the short circuit level of the system.

Continuing further, after applying the proposed method to determine the optimal location and optimal states of the ch/discharge of the BSSs in the IEEE 118, 69, and 33 bus systems within the different percentages of nominal load with the aim of improving both the economic and technical aspects of the problem using the proposed multi-objective optimization algorithm, the resulting optimal solution can be described as follows. Figure 9, Figure 10 and Figure 11 showcase the optimal power generation profiles for each energy source during load variations in the IEEE 118, 69, and 33 bus systems, respectively. Additionally, Figure 12, Figure 13 and Figure 14 depict the optimal location and optimal states of ch/discharge of the BSSs within the IEEE 118, 69, and 33 power networks, respectively, for each analyzed time interval. In addition to delivering the lowest operating cost, voltage variation, and system losses, Figure 15 demonstrates that the suggested solution achieves the highest CPU time performance with minimal iteration. Additionally, the suggested approach has the lowest EENS, which is an excellent quality in a system. Furthermore, the PM has determined the highest PLSF and VSI for the benchmark network case studies, suggesting that a distribution power network has higher technical performance. Additionally, the PM has the system’s lowest short circuit level change.

Furthermore,

Table 3. Comparisonof the proposed method with other recent past methods in the IEEE 118−bus.

	Indexes	Operating Cost ($)	Losses (kW)	Voltage Deviation (pu)	(EENS) (kWh)	VSI (pu)	Sum of Short Circuit-Level Changes (pu)
Consideration Status
Proposed Method		2804.55	0.84	2.21	118.32	9.91	0.52
[7,8]		2856.39	1.24	3.21	215.21	1.22	7.98
[12,14]		2934.41	9.87	4.35	110.21	3.73	5.21
[24,25,27]		3654.61	1.94	2.35	125.64	1.32	11.32

,

Table 4. Comparisonof the proposed method with other recent past methods in the IEEE−69 bus.

	Indexes	Operating Cost ($)	Losses (kW)	Voltage Deviation (pu)	(EENS) (kWh)	VSI (pu)	Sum of Short Circuit-Level Changes (pu)
Consideration Status
Proposed Method		20,589.31	2.08	1.06	80.48	110.26	0.24
[7,8]		20,474.76	2.28	5.45	334.91	78.21	5.23
[12,14]		19,643.21	11.34	6.28	78.25	65	4.12
[24,25,27]		2392.14	3.67	5.21	91.21	131.21	12.34

and

Table 5. Comparisonof the proposed method with other recent past methods in the IEEE−33 bus.

	Indexes	Operating Cost ($)	Losses (kW)	Voltage Deviation (pu)	(EENS) (kWh)	VSI (pu)	Sum of Short Circuit-Level Changes (pu)
Consideration Status
Proposed Method		4224.24	0.28	0.43	15.35	67.52	0.000
[7,8]		4321.69	1.021	1.31	65.28	21.62	2.84
[12,14]		4223.89	7.34	9.31	18.21	62.38	6.96
[24,25,27]		4721.33	0.97	2.10	19.94	63.46	8.32

were prepared to display the outcomes of comparing the performance of the proposed method against the previous approaches across a range of economic, power quality, reliability, and network security indicators within the context of executing the optimal BSS placement program throughout the studied time period in the IEEE 118, 69, and 33 bus networks, respectively. The following accurate results of the optimal location and optimal states of ch/discharge of BSSs for IEEE 118, 69 and 33 bus are reported in the Table 6, Table 7 and Table 8, respectively.

As demonstrated in Table 6, Table 7 and Table 8, upon evaluating the output simulation results of the three case studies involving the IEEE118, 69, and 33 bus test systems, it is evident that the proposed method has surpassed the previous approaches in various economic and technical network indicators. This achievement is notable, especially considering that reliability and network power quality indicators were overlooked in the prior studies. The proposed method effectively harnesses the full potential of distributed generation control within the distribution network and intelligent MGs, specifically in terms of optimizing the operation, including the charge and discharge of BSSs in strategically chosen locations. For instance, as observed in Figure 12, Figure 13 and Figure 14 (or Table 6, Table 7 and Table 8), the energy storage system within the IEEE 118, 69, and 33 bus networks was charged during the hours of low demand (20% to 50% p.u of the nominal load). This occurred at the juncture where technical functions (reliability and power quality) and economic functions (operation and generation cost) intersect.

In Figure 13, for instance, the proposed method identified the optimal location for BSSs (in charge mode) in the IEEE 69 bus system near buses 40, 42, and 48, coinciding with the presence of generation units at these buses during off-peak time intervals (ranging from 20% to 50% of nominal load). Conversely, the proposed method recommended the optimal location for BSSs in discharge mode near consumer load centers and away from generation units. This scenario recurred in the simulation results for the IEEE 33 bus network, where the proposed method sought to strike a balance between technical and economic considerations. As shown in Figure 12, Figure 13 and Figure 14 (or Table 6, Table 7 and Table 8), this optimized management approach enables the efficient utilization of BSSs in the networks to store low-cost energy generated by other microgrids. During these hours, as depicted in Figure 11, the system operated under low-load conditions, with zero energy obtained from the power company via the bus connected to the upper-level network. Consequently, to ensure safe and cost-effective network operation, the microgrid loads needed to be supplied by local distributed generation. Furthermore, this optimal management strategy allowed the energy for the loads to be supplied through shorter paths, resulting in improved network indices such as reduced losses, enhanced short-circuit levels, minimized voltage deviations, and increased network capacity. To investigate the impact of considering or neglecting the technical factors of the IEEE 118-bus network, such as different indices of power qualities and reliability factors, specifically, Figure 16a–e depict the total voltage deviation, total losses, total generation and operation costs, total SCL changing index, and total EENS for the IEEE 118 bus power network (the most difficult benchmark case study) at different percentages of the load for two scenarios. The first scenario considers the optimal placement of BSSs while taking into account technical factors such as voltage deviation, losses, SCL changing, VSI, and PLSF, as well as economic factors like generation and operation costs. The second scenario involves the optimal placement of BSSs based solely on economic factors without considering the aforementioned technical factors of the network.

The findings of the vital indices obtained after applying the two scenarios (without and with an account of the technical aspects) such as voltage variation, total losses, short-circuit level, and EENS were also statistically analyzed. As a consequence, Figure 17, Figure 18, Figure 19 and Figure 20 were added to extend the scope of clarity and emphasize the importance of the results produced using the proposed approach. The efficacy, as well as the durability of the proposed approach in determining the number, size, and location of BSS within the distribution network, is evident in Figure 17, Figure 18, Figure 19 and Figure 20. The approach attained the lowest values for all important metrics, ensuring an improvement in the quality of the electrical power. This outcome aligns with our objectives and is advantageous from both technical and economic perspectives.

When Figure 16a–e were analyzed, the following results were obtained:

• In Figure 16a,b, it is evident that during most hours of the day, the voltage deviation and network loss graphs displayed lower values when the BSSs were optimally placed within the power network. However, when considering the presence of optimally located BSSs, additional factors such as reliability and short-circuit levels were also taken into consideration, introducing extra constraints in the quest for the best solution. Conversely, as indicated by Figure 16a, there was only an increase in voltage deviation during the states of more than 50% of the nominal load, compared to scenarios where the technical factor capability was not factored in. This increase was a result of improvements in other economic and security indicators within the network, contributing to the overall optimal solutions. Additionally, during these hours, as illustrated in Figure 12, the BSSs adjusted their charge states to redirect power flow in a manner that optimized all objective functions indicators. Moreover, according to Table 3, Table 4 and Table 5, the summation of the total losses from 20% to 150% of the nominal load is less than the states without considering the technical factors.
• Figure 16c and the results of Table 3, Table 4 and Table 5 show the operating cost of the system in the state of the optimal placement of batteries by considering that the technical parameters of the network in most cases of load changes are slightly higher than the case of not considering the technical parameters of the network in some cases, like in 20% of freight where the operating cost is also lower. This is while the technical parameters of the network are in a more favorable condition in all cases.
• As previously mentioned, one of the pivotal indicators to be taken into account when optimizing the placement of BSSs in power distribution networks is the short-circuit level variation index. This index holds immense importance as alterations in the short-circuit level, stemming from changes in production and network topology, have the potential to disrupt the protective system configurations, resulting in substantial damages and costs to the system. Consequently, as depicted in Figure 16d, the short-circuit level variation index approaches less than 0.5 when it is considered in the optimal placement of BSSs within the network. This capability plays a crucial role in averting disruptions to the protective system configurations through the optimal charging and discharging of BSSs during the operation of the power network.
• Through an analysis of Figure 16e, it becomes evident that the network’s reliability status, as assessed by the total energy not supplied to the network indicator, exhibits notably reduced values in all states of changing load (20% to 150%). Nevertheless, when looking at Table 3, Table 4 and Table 5 in a broader context, it can be concluded that the utilization of the reliability indices (EENS index) in optimal placement of BSSs in the network and control of the states of charge/discharge for BSSs within the network results in substantially lower total energy supplied to the entire system, in sharp contrast to scenarios where the capability of reliability is not taken into consideration.
• The problem of optimal placement of BSSs is a complex one that involves various objectives and constraints. To make informed decisions, it is crucial to prioritize these objectives and constraints effectively. Here are some key considerations:
  • Coverage and Quality of Technical Service (QoS)
    Prioritize ensuring comprehensive coverage of the MG area to provide reliable services to all consumers. QoS parameters, such as voltage sensitivity, voltage deviations, short circuit level, losses, and loss sensitivity factor, should be prioritized to meet the specific consumers’ needs of different applications within the MG.
  • Cost
    Cost considerations are essential, as deploying BSSs can be expensive. Prioritize minimizing the deployment and operational costs, which may include equipment costs, power consumption, maintenance expenses, and backhaul connectivity costs.
  • Energy Efficiency
    In MGs, energy conservation is critical. Therefore, it is necessary to prioritize the deployment of BSSs in a way that minimizes their energy consumption, as excessive power usage can strain the microgrid’s resources.
  • Reliability and Redundancy
    Prioritize ensuring high reliability and redundancy in supply energy to consumers. Redundant BSSs placement can be prioritized to ensure backup connectivity in case of failures.
  • Environmental Impact
    Given the increasing focus on sustainability, prioritize solutions that minimize the environmental impact of BSSs deployment, such as reducing carbon emissions or avoiding disruption to local ecosystems.
  • Voltage Security
    Prioritize the security concerns, such as VSI within the MG. Secure BSSs placement can help reduce vulnerabilities.

6. Conclusions

Today, smart distribution microgrids are comprised of autonomous units that serve as both energy consumers and generators, playing a crucial role in enhancing economic efficiency and ensuring the safe operation of smart distribution networks. The dynamic ability to charge and discharge BSSs within the power networks can transform these units into intelligent network nodes. A substantial proportion of the energy is generated locally, and all generators and consumers are managed with intelligence. However, recent power networks have been operated with a focus on maximum capacity and low power quality, driven by economic goals. Failure to promptly address the consequences of such operational conditions can lead to irreparable damage to the network. The present paper proposes a solution for the optimal placement of BSSs in power networks, taking into account both the technical aspects of the power system (power quality and reliability) and economic factors simultaneously. This solution, while controlling resource generation, leverages the charge and discharge capabilities of BSSs within the power distribution network. By harnessing the potential within energy transfer and transformation pathways in the network, it seeks to mitigate the damages resulting from purely economic exploitation. In this context, when formulating the objective function of a comprehensive BSS placement program for the network, it becomes crucial to consider not only economic metrics but also indicators related to reliability and network security. Neglecting these indicators can sometimes overshadow all the benefits of optimal distribution generations. Therefore, this paper presents a framework that incorporates not only economic metrics but also other reliability and security indicators, such as EENS and the absence of changes in short-circuit connection levels, in the formulation of a multi-objective optimization algorithm for the optimal placement of the BSSs in power network. This ensures that concerns related to anticipated energy shortages and disruptions in protection settings are effectively addressed during the economic operation of the distribution network and connected MGs, particularly under conditions of maximum capacity. These objectives can be achieved through the utilization of the charge and discharge capabilities of the MG networks, coupled with optimal energy management. In this context, a comparison of the results obtained from the proposed method with the previous approaches reveals consistent and significant improvements in both technical and economic indicators, underscoring the efficacy of considering reliability and security indicators in the formulation of the BSS placement problem.

Finally, the proposed algorithm exhibits certain limitations, which are suggested as potential avenues for future works. First and foremost, there is a need to prioritize the minimization of interference between BSSs and other FACTS devices within the MG. This prioritization is essential for maintaining the quality of consumer services. Additionally, it is imperative to give due consideration to compliance with local regulations and legal constraints when implementing the algorithm. Ensuring that BSS placement aligns with spectrum licensing, zoning laws, and other relevant regulations should be of paramount importance. Furthermore, it is important to address the issue of cybersecurity within the MG context. This includes preventing unauthorized access and safeguarding data transmissions. Regrettably, these aspects were not covered in the present paper. Enhancing the security of BSS placement can significantly reduce vulnerabilities and enhance the overall effectiveness of the system.

Table 6. Detailed results of optimal location and optimal states of ch/discharge of the BSSs within the IEEE-118 bus network.

Bus Number	Optimal State of ch/discharge (kWh) of BSSs at Different Percentages of Nominal Load				Bus Number	Optimal State of ch/discharge (kWh) of BSSs at Different Percentages of Nominal Load
	20%	50%	100%	150%		20%	50%	100%	150%
1	138.56	0.00	0.00	−197.20	60	0.00	239.05	−250.00	−250.00
2	−250.00	157.67	0.00	−15.82	61	0.00	0.00	0.00	250.00
3	0.00	0.00	250.00	250.00	62	0.00	0.00	−250.00	−250.00
4	0.00	0.00	−250.00	0.00	63	0.00	−191.86	0.00	222.32
5	250.00	0.00	−250.00	0.00	64	0.00	182.76	−250.00	−190.80
6	−250.00	111.11	−250.00	0.00	65	0.00	183.32	−250.00	250.00
7	0.00	0.00	−250.00	0.00	66	113.71	0.00	0.00	−55.50
8	87.61	−34.94	0.00	250.00	67	250.00	0.00	0.00	0.00
9	0.00	−250.00	−250.00	0.00	68	60.14	0.00	0.00	72.03
10	7.31	−197.36	0.00	0.00	69	−193.79	58.49	0.00	0.00
11	0.00	−11.42	0.00	0.00	70	0.00	0.00	−250.00	−177.43
12	−236.30	−236.46	0.00	−81.55	71	0.00	166.56	0.00	−250.00
13	0.00	211.92	0.00	0.00	72	0.00	250.00	0.00	−169.07
14	−250.00	111.12	0.00	250.00	73	0.00	−148.41	250.00	0.00
15	0.00	−136.37	0.00	0.00	74	84.17	0.00	−250.00	250.00
16	250.00	−240.31	0.00	0.00	75	0.00	207.96	−250.00	0.00
17	190.02	−92.16	−250.00	0.00	76	0.00	77.16	0.00	−214.39
18	0.00	0.00	0.00	−183.53	77	250.00	0.00	0.00	−250.00
19	0.00	0.00	250.00	0.00	78	0.00	−250.00	0.00	0.00
20	−140.01	0.00	0.00	−39.10	79	250.00	−250.00	−250.00	49.23
21	−250.00	−213.98	−250.00	202.38	80	0.00	0.00	0.00	0.00
22	0.00	−52.04	−250.00	250.00	81	0.00	0.00	0.00	0.00
23	250.00	101.51	0.00	118.48	82	0.00	−76.59	0.00	−250.00
24	0.00	−250.00	0.00	0.00	83	178.44	250.00	−250.00	−250.00
25	0.00	0.00	0.00	0.00	84	0.00	−0.26	0.00	0.00
26	0.00	250.00	0.00	0.00	85	0.00	0.00	0.00	0.00
27	184.44	−250.00	0.00	0.00	86	0.00	0.00	0.00	−187.20
28	0.00	−250.00	0.00	−135.23	87	0.00	−222.40	0.00	0.00
29	−242.27	140.61	−250.00	0.00	88	236.89	28.63	−250.00	−250.00
30	0.00	−32.37	−250.00	0.00	89	0.00	−83.06	0.00	−166.05
31	0.00	−250.00	0.00	0.00	90	−239.91	139.69	−250.00	49.34
32	−88.75	0.00	0.00	−67.77	91	0.00	0.00	0.00	−250.00
33	0.00	−250.00	−250.00	0.00	92	0.00	230.36	0.00	0.00
34	250.00	0.00	0.00	0.00	93	−121.41	−248.28	−250.00	0.00
35	0.00	0.00	−250.00	0.00	94	−250.00	0.00	0.00	250.00
36	0.00	−250.00	0.00	−55.74	95	250.00	167.54	250.00	0.00
37	0.00	−190.92	0.00	0.00	96	0.00	0.00	0.00	246.84
38	−182.08	0.00	0.00	0.00	97	−27.63	78.52	−248.75	0.00
39	0.00	185.55	0.00	0.00	98	−43.60	0.00	0.00	0.00
40	0.00	223.58	−250.00	145.84	99	181.41	250.00	0.00	0.00
41	0.00	−250.00	−250.00	0.00	100	−85.70	0.00	0.00	213.07
42	0.00	−232.40	0.00	0.00	101	0.00	0.00	0.00	0.00
43	0.00	0.00	0.00	−223.53	102	0.00	0.00	0.00	0.00
44	10.31	85.34	0.00	0.00	103	0.00	−122.32	250.00	0.00
45	0.00	0.00	0.00	0.00	104	126.18	−250.00	−250.00	142.39
46	0.00	174.10	0.00	0.00	105	0.00	223.13	0.00	−250.00
47	0.00	48.79	−250.00	0.00	106	−240.53	−92.01	0.00	87.27
48	0.00	−61.71	−245.94	−34.96	107	−250.00	0.00	−250.00	0.00
49	0.00	0.00	−250.00	248.17	108	250.00	−250.00	−250.00	−241.45
50	216.91	0.00	0.00	0.00	109	0.00	20.70	0.00	0.00
51	−140.79	−222.31	0.00	0.00	110	250.00	0.00	0.00	−250.00
52	0.00	−250.00	0.00	46.76	111	233.10	0.00	−250.00	−250.00
53	0.00	0.00	0.00	72.88	112	0.00	0.00	0.00	240.12
54	0.00	0.00	−250.00	250.00	113	−250.00	172.46	0.00	−128.91
55	0.00	107.88	0.00	0.00	114	0.00	−250.00	139.28	0.00
56	0.00	214.91	0.00	249.82	115	207.51	0.00	0.00	−250.00
57	0.00	0.00	0.00	−250.00	116	0.00	0.00	0.00	−243.65
58	0.00	0.00	−250.00	250.00	117	217.48	168.68	0.00	29.62
59	0.00	0.00	0.00	0.00	118	−250.00	0.00	0.00	0.00

Table 6. Detailed results of optimal location and optimal states of ch/discharge of the BSSs within the IEEE-118 bus network.

Bus Number	Optimal State of ch/discharge (kWh) of BSSs at Different Percentages of Nominal Load				Bus Number	Optimal State of ch/discharge (kWh) of BSSs at Different Percentages of Nominal Load
	20%	50%	100%	150%		20%	50%	100%	150%
1	138.56	0.00	0.00	−197.20	60	0.00	239.05	−250.00	−250.00
2	−250.00	157.67	0.00	−15.82	61	0.00	0.00	0.00	250.00
3	0.00	0.00	250.00	250.00	62	0.00	0.00	−250.00	−250.00
4	0.00	0.00	−250.00	0.00	63	0.00	−191.86	0.00	222.32
5	250.00	0.00	−250.00	0.00	64	0.00	182.76	−250.00	−190.80
6	−250.00	111.11	−250.00	0.00	65	0.00	183.32	−250.00	250.00
7	0.00	0.00	−250.00	0.00	66	113.71	0.00	0.00	−55.50
8	87.61	−34.94	0.00	250.00	67	250.00	0.00	0.00	0.00
9	0.00	−250.00	−250.00	0.00	68	60.14	0.00	0.00	72.03
10	7.31	−197.36	0.00	0.00	69	−193.79	58.49	0.00	0.00
11	0.00	−11.42	0.00	0.00	70	0.00	0.00	−250.00	−177.43
12	−236.30	−236.46	0.00	−81.55	71	0.00	166.56	0.00	−250.00
13	0.00	211.92	0.00	0.00	72	0.00	250.00	0.00	−169.07
14	−250.00	111.12	0.00	250.00	73	0.00	−148.41	250.00	0.00
15	0.00	−136.37	0.00	0.00	74	84.17	0.00	−250.00	250.00
16	250.00	−240.31	0.00	0.00	75	0.00	207.96	−250.00	0.00
17	190.02	−92.16	−250.00	0.00	76	0.00	77.16	0.00	−214.39
18	0.00	0.00	0.00	−183.53	77	250.00	0.00	0.00	−250.00
19	0.00	0.00	250.00	0.00	78	0.00	−250.00	0.00	0.00
20	−140.01	0.00	0.00	−39.10	79	250.00	−250.00	−250.00	49.23
21	−250.00	−213.98	−250.00	202.38	80	0.00	0.00	0.00	0.00
22	0.00	−52.04	−250.00	250.00	81	0.00	0.00	0.00	0.00
23	250.00	101.51	0.00	118.48	82	0.00	−76.59	0.00	−250.00
24	0.00	−250.00	0.00	0.00	83	178.44	250.00	−250.00	−250.00
25	0.00	0.00	0.00	0.00	84	0.00	−0.26	0.00	0.00
26	0.00	250.00	0.00	0.00	85	0.00	0.00	0.00	0.00
27	184.44	−250.00	0.00	0.00	86	0.00	0.00	0.00	−187.20
28	0.00	−250.00	0.00	−135.23	87	0.00	−222.40	0.00	0.00
29	−242.27	140.61	−250.00	0.00	88	236.89	28.63	−250.00	−250.00
30	0.00	−32.37	−250.00	0.00	89	0.00	−83.06	0.00	−166.05
31	0.00	−250.00	0.00	0.00	90	−239.91	139.69	−250.00	49.34
32	−88.75	0.00	0.00	−67.77	91	0.00	0.00	0.00	−250.00
33	0.00	−250.00	−250.00	0.00	92	0.00	230.36	0.00	0.00
34	250.00	0.00	0.00	0.00	93	−121.41	−248.28	−250.00	0.00
35	0.00	0.00	−250.00	0.00	94	−250.00	0.00	0.00	250.00
36	0.00	−250.00	0.00	−55.74	95	250.00	167.54	250.00	0.00
37	0.00	−190.92	0.00	0.00	96	0.00	0.00	0.00	246.84
38	−182.08	0.00	0.00	0.00	97	−27.63	78.52	−248.75	0.00
39	0.00	185.55	0.00	0.00	98	−43.60	0.00	0.00	0.00
40	0.00	223.58	−250.00	145.84	99	181.41	250.00	0.00	0.00
41	0.00	−250.00	−250.00	0.00	100	−85.70	0.00	0.00	213.07
42	0.00	−232.40	0.00	0.00	101	0.00	0.00	0.00	0.00
43	0.00	0.00	0.00	−223.53	102	0.00	0.00	0.00	0.00
44	10.31	85.34	0.00	0.00	103	0.00	−122.32	250.00	0.00
45	0.00	0.00	0.00	0.00	104	126.18	−250.00	−250.00	142.39
46	0.00	174.10	0.00	0.00	105	0.00	223.13	0.00	−250.00
47	0.00	48.79	−250.00	0.00	106	−240.53	−92.01	0.00	87.27
48	0.00	−61.71	−245.94	−34.96	107	−250.00	0.00	−250.00	0.00
49	0.00	0.00	−250.00	248.17	108	250.00	−250.00	−250.00	−241.45
50	216.91	0.00	0.00	0.00	109	0.00	20.70	0.00	0.00
51	−140.79	−222.31	0.00	0.00	110	250.00	0.00	0.00	−250.00
52	0.00	−250.00	0.00	46.76	111	233.10	0.00	−250.00	−250.00
53	0.00	0.00	0.00	72.88	112	0.00	0.00	0.00	240.12
54	0.00	0.00	−250.00	250.00	113	−250.00	172.46	0.00	−128.91
55	0.00	107.88	0.00	0.00	114	0.00	−250.00	139.28	0.00
56	0.00	214.91	0.00	249.82	115	207.51	0.00	0.00	−250.00
57	0.00	0.00	0.00	−250.00	116	0.00	0.00	0.00	−243.65
58	0.00	0.00	−250.00	250.00	117	217.48	168.68	0.00	29.62
59	0.00	0.00	0.00	0.00	118	−250.00	0.00	0.00	0.00

Table 7. Detailed results of optimal location and optimal states of ch/discharge of the BSSs within the IEEE 69-bus network.

Bus Number	Optimal State of ch/discharge (kWh) of BSSs at Different Percentages of Nominal Load				Bus Number	Optimal State of ch/discharge (kWh) of BSSs at Different Percentages of Nominal Load
	20%	50%	100%	150%		20%	50%	100%	150%
1	250.00	−250.00	−248.94	−250.00	36	0.00	−250.00	−246.32	0.00
2	0.00	0.00	−250.00	−250.00	37	0.00	−114.73	0.00	0.00
3	8.35	0.00	0.00	−234.99	38	0.00	0.00	0.00	0.00
4	250.00	0.00	250.00	−250.00	39	0.00	−250.00	0.00	61.04
5	0.00	−250.00	−250.00	−250.00	40	0.00	92.64	−250.00	−148.97
6	−250.00	0.00	0.00	−250.00	41	−67.04	−250.00	−250.00	0.00
7	0.00	−233.59	0.00	−250.00	42	0.00	0.00	−250.00	0.00
8	0.00	0.00	250.00	54.75	43	250.00	−250.00	−250.00	−250.00
9	53.16	−250.00	0.00	−86.19	44	0.00	0.00	0.00	0.00
10	88.13	−250.00	0.00	0.00	45	−250.00	250.00	−226.55	0.00
11	216.89	0.00	0.00	26.12	46	141.07	0.00	0.00	0.00
12	0.00	193.30	−250.00	250.00	47	0.00	0.00	0.00	−250.00
13	−249.68	0.00	0.00	250.00	48	0.00	−250.00	0.00	0.00
14	0.00	0.00	250.00	0.00	49	−250.00	−235.73	−250.00	0.00
15	−178.35	250.00	0.00	0.00	50	−250.00	0.00	0.00	0.00
16	−116.50	0.00	0.00	0.00	51	−250.00	0.00	250.00	0.00
17	127.34	−250.00	0.00	0.00	52	−250.00	250.00	0.00	208.60
18	0.00	0.00	250.00	0.00	53	−195.82	−250.00	0.00	0.00
19	149.81	250.00	−250.00	0.00	54	0.00	−250.00	−250.00	0.00
20	0.00	−250.00	−250.00	0.00	55	0.00	250.00	0.00	27.40
21	0.00	−250.00	0.00	−250.00	56	250.00	−250.00	0.00	250.00
22	0.00	0.00	0.00	0.00	57	0.00	0.00	−250.00	−250.00
23	0.00	0.00	250.00	125.61	58	250.00	0.00	−250.00	−157.86
24	0.00	−250.00	0.00	250.00	59	0.00	0.00	−250.00	−126.82
25	0.00	250.00	134.92	0.00	60	−243.24	0.00	250.00	0.00
26	250.00	219.69	0.00	−196.83	61	0.00	45.91	250.00	−228.69
27	0.00	245.24	0.00	250.00	62	131.48	−250.00	0.00	0.00
28	250.00	0.00	−250.00	0.00	63	−214.27	0.00	0.00	−94.50
29	0.00	0.00	0.00	−246.37	64	−216.12	0.00	−221.01	0.00
30	−129.95	−250.00	−250.00	0.00	65	−250.00	235.54	250.00	250.00
31	0.00	172.76	0.00	234.15	66	0.00	−250.00	0.00	0.00
32	−250.00	0.00	0.00	−250.00	67	0.00	0.00	0.00	0.00
33	0.00	0.00	0.00	0.00	68	0.00	0.00	−250.00	−222.88
34	−250.00	250.00	250.00	−13.57	69	250.00	−250.00	−250.00	−250.00
35	0.00	250.00	250.00	250.00

Table 7. Detailed results of optimal location and optimal states of ch/discharge of the BSSs within the IEEE 69-bus network.

Bus Number	Optimal State of ch/discharge (kWh) of BSSs at Different Percentages of Nominal Load				Bus Number	Optimal State of ch/discharge (kWh) of BSSs at Different Percentages of Nominal Load
	20%	50%	100%	150%		20%	50%	100%	150%
1	250.00	−250.00	−248.94	−250.00	36	0.00	−250.00	−246.32	0.00
2	0.00	0.00	−250.00	−250.00	37	0.00	−114.73	0.00	0.00
3	8.35	0.00	0.00	−234.99	38	0.00	0.00	0.00	0.00
4	250.00	0.00	250.00	−250.00	39	0.00	−250.00	0.00	61.04
5	0.00	−250.00	−250.00	−250.00	40	0.00	92.64	−250.00	−148.97
6	−250.00	0.00	0.00	−250.00	41	−67.04	−250.00	−250.00	0.00
7	0.00	−233.59	0.00	−250.00	42	0.00	0.00	−250.00	0.00
8	0.00	0.00	250.00	54.75	43	250.00	−250.00	−250.00	−250.00
9	53.16	−250.00	0.00	−86.19	44	0.00	0.00	0.00	0.00
10	88.13	−250.00	0.00	0.00	45	−250.00	250.00	−226.55	0.00
11	216.89	0.00	0.00	26.12	46	141.07	0.00	0.00	0.00
12	0.00	193.30	−250.00	250.00	47	0.00	0.00	0.00	−250.00
13	−249.68	0.00	0.00	250.00	48	0.00	−250.00	0.00	0.00
14	0.00	0.00	250.00	0.00	49	−250.00	−235.73	−250.00	0.00
15	−178.35	250.00	0.00	0.00	50	−250.00	0.00	0.00	0.00
16	−116.50	0.00	0.00	0.00	51	−250.00	0.00	250.00	0.00
17	127.34	−250.00	0.00	0.00	52	−250.00	250.00	0.00	208.60
18	0.00	0.00	250.00	0.00	53	−195.82	−250.00	0.00	0.00
19	149.81	250.00	−250.00	0.00	54	0.00	−250.00	−250.00	0.00
20	0.00	−250.00	−250.00	0.00	55	0.00	250.00	0.00	27.40
21	0.00	−250.00	0.00	−250.00	56	250.00	−250.00	0.00	250.00
22	0.00	0.00	0.00	0.00	57	0.00	0.00	−250.00	−250.00
23	0.00	0.00	250.00	125.61	58	250.00	0.00	−250.00	−157.86
24	0.00	−250.00	0.00	250.00	59	0.00	0.00	−250.00	−126.82
25	0.00	250.00	134.92	0.00	60	−243.24	0.00	250.00	0.00
26	250.00	219.69	0.00	−196.83	61	0.00	45.91	250.00	−228.69
27	0.00	245.24	0.00	250.00	62	131.48	−250.00	0.00	0.00
28	250.00	0.00	−250.00	0.00	63	−214.27	0.00	0.00	−94.50
29	0.00	0.00	0.00	−246.37	64	−216.12	0.00	−221.01	0.00
30	−129.95	−250.00	−250.00	0.00	65	−250.00	235.54	250.00	250.00
31	0.00	172.76	0.00	234.15	66	0.00	−250.00	0.00	0.00
32	−250.00	0.00	0.00	−250.00	67	0.00	0.00	0.00	0.00
33	0.00	0.00	0.00	0.00	68	0.00	0.00	−250.00	−222.88
34	−250.00	250.00	250.00	−13.57	69	250.00	−250.00	−250.00	−250.00
35	0.00	250.00	250.00	250.00

Table 8. Detailed results of optimal location and optimal states of ch/discharge of the BSSs within the IEEE 33-bus network.

Bus Number	Optimal State of ch/discharge (kWh) of BSSs at Different Percentages of Nominal Load				Bus Number	Optimal State of ch/discharge (kWh) of BSSs at Different Percentages of Nominal Load
	20%	50%	100%	150%		20%	50%	100%	150%
1	0.00	0.00	50.00	0.00	18	50.00	10.63	−13.04	−50.00
2	−50.00	35.00	0.00	0.00	19	0.00	0.00	0.00	0.00
3	0.00	50.00	0.00	0.00	20	0.00	50.00	0.00	0.00
4	−50.00	−50.00	−46.46	0.00	21	0.00	−50.00	0.00	−50.00
5	−50.00	0.13	50.00	37.14	22	50.00	−50.00	50.00	0.00
6	0.00	0.00	−36.11	0.00	23	0.00	16.62	0.00	0.00
7	0.00	−50.00	19.59	−50.00	24	−50.00	0.00	0.00	0.00
8	−50.00	−50.00	0.00	0.00	25	50.00	0.00	50.00	−42.50
9	−50.00	−4.33	−11.62	0.00	26	0.00	50.00	0.00	−50.00
10	0.00	0.00	−50.00	−50.00	27	−50.00	0.00	−50.00	−17.09
11	−50.00	−50.00	−50.00	0.00	28	50.00	−14.10	0.00	0.00
12	−50.00	−50.00	0.00	0.00	29	0.00	−50.00	0.00	−50.00
13	0.00	0.00	−42.63	−50.00	30	50.00	0.00	0.00	0.00
14	−50.00	−50.00	−50.00	0.00	31	48.48	0.00	0.00	0.00
15	0.00	−50.00	−50.00	−50.00	32	35.63	−30.84	−50.00	−50.00
16	0.00	23.07	0.00	−50.00	33	0.00	50.00	0.00	−50.00
17	0.00	50.00	−19.54	−11.99

Table 8. Detailed results of optimal location and optimal states of ch/discharge of the BSSs within the IEEE 33-bus network.

Bus Number	Optimal State of ch/discharge (kWh) of BSSs at Different Percentages of Nominal Load				Bus Number	Optimal State of ch/discharge (kWh) of BSSs at Different Percentages of Nominal Load
	20%	50%	100%	150%		20%	50%	100%	150%
1	0.00	0.00	50.00	0.00	18	50.00	10.63	−13.04	−50.00
2	−50.00	35.00	0.00	0.00	19	0.00	0.00	0.00	0.00
3	0.00	50.00	0.00	0.00	20	0.00	50.00	0.00	0.00
4	−50.00	−50.00	−46.46	0.00	21	0.00	−50.00	0.00	−50.00
5	−50.00	0.13	50.00	37.14	22	50.00	−50.00	50.00	0.00
6	0.00	0.00	−36.11	0.00	23	0.00	16.62	0.00	0.00
7	0.00	−50.00	19.59	−50.00	24	−50.00	0.00	0.00	0.00
8	−50.00	−50.00	0.00	0.00	25	50.00	0.00	50.00	−42.50
9	−50.00	−4.33	−11.62	0.00	26	0.00	50.00	0.00	−50.00
10	0.00	0.00	−50.00	−50.00	27	−50.00	0.00	−50.00	−17.09
11	−50.00	−50.00	−50.00	0.00	28	50.00	−14.10	0.00	0.00
12	−50.00	−50.00	0.00	0.00	29	0.00	−50.00	0.00	−50.00
13	0.00	0.00	−42.63	−50.00	30	50.00	0.00	0.00	0.00
14	−50.00	−50.00	−50.00	0.00	31	48.48	0.00	0.00	0.00
15	0.00	−50.00	−50.00	−50.00	32	35.63	−30.84	−50.00	−50.00
16	0.00	23.07	0.00	−50.00	33	0.00	50.00	0.00	−50.00
17	0.00	50.00	−19.54	−11.99