Review of Hysteresis Models for Magnetic Materials
Abstract
1. Introduction
2. What Is Hysteresis?
2.1. Rate-Independency and Rate-Dependency
2.2. Phenomenological or Physical Models?
3. History Dependence and Independence
3.1. History Dependency
3.2. History Independency
3.3. Other Types of History Dependency
4. Algebraic, Differential and Integral Models
5. Duhem Models
5.1. Increasing and Decreasing Curves
5.2. Classical Approach to Duhem Models
5.3. Anhysteresis Curve and Limiting Boundaries
5.4. Examples of Duhem Models
5.5. The Model in Duhem’s Work
5.6. Linked to Energy Losses
5.7. Coenergy Expression
6. Coleman–Hodgdon Model
Inverse Coleman–Hodgdon Model
7. Jiles–Atherton Model
7.1. Phenomenological Anhysteresis Function
7.2. Illustrating That It Is a Duhem Model
7.3. Anisotropic Versions of the Models
7.4. Inverse Adoptions of the Model
7.5. Vector Adoptions of the Model
7.6. Dynamic Generalizations of the Model
8. Describing Minor Loops
8.1. Major Loop and Reversal Curves
8.2. Concentric Cycling
8.3. Reversal Curves
9. Scaling Type Models
9.1. Functional Transforming
9.2. Transplantation Type Models
9.3. Functional Transform by Shrinking Curves
9.4. Scaling Models as Duhem Models
9.5. Scaling Curve Models
9.6. Talukdar–Bailey Model
9.7. Rewriting as Differential Equations
9.8. Problems with Curves Leaving the Hysteresis Area
9.9. Tellinen Model
9.10. Flatley–Henretty Model
9.11. Other Transplantation Models
10. Curve Shapes of Magnetization
10.1. Functions and Curve Fitting
10.2. Frölich Equation
10.3. Law of Approach to Saturation
10.4. Rayleigh’s Law and Polynomial Models
10.5. Exponential Functions
10.6. Phenomenological Sigmoid Functions
10.7. Statistical Distributions
10.8. Fourier Series Models
11. History Dependent Models
11.1. Madelung’s Phenomenological Model of Hysteresis and Reversal Curves
- Each curve , which runs inside the hysteresis area, is clearly defined by the reversal point , from which it emerges.
- If one makes any point of this curve itself to a new reversal point , the curve defined by leads back again to the starting point of the curve .
- If the magnetization curve originating in to continues beyond , it continues as a continuation of the curve on which had originally arrived at , as if the cycle -- had not been present.
11.2. Other Forms of Madelung’s Rules
11.3. History by Reversal Points
12. Preisach Type Models
12.1. Congruency and Wiping out Properties
12.2. Congruency by Everett Functions
12.3. Congruency of Prandtl–Ishlinskii Models
12.4. Models Considering Accommodation
12.5. Avoiding Congruency Properties
12.6. Methods to Change the Congruency
- Moving model: The moving model by Della Torre [55,416,417] has a skewed linear congruency by [78,79,418]. It has the input of the Preisach model depending on the current magnetization M, (as in the effective field ) which changes the description of minor loops for different magnitudes of magnetization M. Since the effective field is phenomenological, it is possible to generalize with other functions .
- Restricted model: The Preisach model depends on past extreme values of M [426]. The method is thereby dependent on past reversal points, and not just the last reversal point.
- Inverse model: An inverse Preisach model is expressed as or [429,430]. In this case, the congruency is then changed, so that it will be congruent for intervals of B, rather than H [379]. Because the inverse Preisach model has another congruency than a common Preisach model [379], the Prandtl–Ishlinskii model can be an alternative since that model could be written with an inverse model with the same congruency [379,406].
12.7. Inverse Models
13. Scaling Models with History Dependence
13.1. Models Based on Reversal Curves
13.2. Scaling Models Considering History of Reversal Points
13.3. Preisach Models Generated by Scaled Major Loop Curves
13.4. Jiles–Atherton Models with History Dependence
13.5. Coleman–Hodgdon Models with History Dependence
13.6. Comparing Scaling of a Reversal Curves with Congruency of Reversal Curves
13.7. Other Similar Models
14. Comparing History Dependence
14.1. Comparison Duhem Models and the Preisach Type Models
14.2. Hysterons and Prehysterons
14.3. Other Names for Types of History Dependency
15. Phasor Model with Complex Permeability
15.1. Including Eddy Currents
15.2. Written as Functions
16. Dynamic Models
17. Chua Model
Model with Canceled Frequency Dependence
18. Dynamic Hysteresis Models
18.1. Addition of Models
18.2. Nitzan Model
18.3. Hysteresis Model with Frequency Dependency
18.4. Duhem Model with a Dynamic Model
19. Dynamic Models and Preisach Models
Dynamic Preisach Model with Frequency-Dependent Hysteron
20. Transfer Function of Linear Model
20.1. Hysteresis Model Series Connected with Dynamic Model
20.2. Addition of Preisach Model and Dynamic Model
21. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jiles, D. Hysteresis models: Non-linear magnetism on length scales from the atomistic to the macroscopic. J. Magn. Magn. Mater. 2002, 242–245, 116–124. [Google Scholar] [CrossRef]
- Jiles, D.C.; Fang, X.; Zhang, W. Modeling of Hysteresis in Magnetic Materials. In Handbook of Advanced Magnetic Materials; Liu, Y., Sellmyer, D.J., Shindo, D., Eds.; Springer: Boston, MA, USA, 2006; pp. 745–779. [Google Scholar] [CrossRef]
- Liorzou, F.; Phelps, B.; Atherton, D.L. Macroscopic models of magnetization. IEEE Trans. Magn. 2000, 36, 418–428. [Google Scholar] [CrossRef]
- Andrei, P.; Caltun, O.; Stancu, A. Differential phenomenological models for the magnetization processes in soft MnZn ferrites. IEEE Trans. Magn. 1998, 34, 231–241. [Google Scholar] [CrossRef]
- Cardelli, E. Chapter 4—Advances in Magnetic Hysteresis Modeling. InHandbook of Magnetic Materials; Elsevier: Amsterdam, The Netherlands, 2015; Volume 24, pp. 323–409. [Google Scholar] [CrossRef]
- Bavendiek, G.J. A Contribution to the Electromagnetic Finite Element Analysis of Soft and Hard Magnetic Materials in Electrical Machines; Shaker Verlag: Herzogenrath, Germany, 2020. [Google Scholar]
- Takach, M.D.; Lauritzen, P.O. Survey of magnetic core models. In Proceedings of the 1995 IEEE Applied Power Electronics Conference and Exposition (APEC’95), Dallas, TX, USA, 5–9 March 1995; Volume 2, pp. 560–566. [Google Scholar] [CrossRef]
- Petrun, M.; Steentjes, S.; Hameyer, K.; Dolinar, D. Comparison of static hysteresis models subject to arbitrary magnetization waveforms. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2017, 36, 774–790. [Google Scholar] [CrossRef]
- Steentjes, S.; Hameyer, K.; Dolinar, D.; Petrun, M. Iron-Loss and Magnetic Hysteresis Under Arbitrary Waveforms in NO Electrical Steel: A Comparative Study of Hysteresis Models. IEEE Trans. Ind. Electron. 2017, 64, 2511–2521. [Google Scholar] [CrossRef]
- Ewing, J.A. Experimental Researches in Magnetism. Philos. Trans. R. Soc. Lond. 1885, 176, 523–640. [Google Scholar] [CrossRef]
- Tan, X.; Iyer, R.V. Modeling and control of hysteresis. IEEE Control Syst. Mag. 2009, 29, 26–28. [Google Scholar] [CrossRef]
- Morris, K.A. What is Hysteresis? Appl. Mech. Rev. 2012, 64, 050801. [Google Scholar] [CrossRef]
- Bertotti, G. Chapter 2—Types of Hysteresis. In Hysteresis in Magnetism; Bertotti, G., Ed.; Electromagnetism, Academic Press: San Diego, CA, USA, 1998; pp. 31–70. [Google Scholar] [CrossRef]
- Mayergoyz, I.D. Mathematical Models of Hysteresis and their Applications; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Bernstein, D.S. Ivory Ghost [Ask The Experts]. IEEE Control Syst. Mag. 2007, 27, 16–17. [Google Scholar] [CrossRef]
- Visintin, A. Chapter 1—Mathematical Models of Hysteresis. In The Science of Hysteresis; Bertotti, G., Mayergoyz, I.D., Eds.; Academic Press: Oxford, UK, 2006; pp. 1–123. [Google Scholar] [CrossRef]
- Vaiana, N.; Sessa, S.; Rosati, L. A generalized class of uniaxial rate-independent models for simulating asymmetric mechanical hysteresis phenomena. Mech. Syst. Signal Process. 2021, 146, 106984. [Google Scholar] [CrossRef]
- Vaiana, N.; Rosati, L. Classification and unified phenomenological modeling of complex uniaxial rate-independent hysteretic responses. Mech. Syst. Signal Process. 2023, 182, 109539. [Google Scholar] [CrossRef]
- Della Torre, E. Problems in physical modeling of magnetic materials. Phys. B Condens. Matter 2004, 343, 1–9. [Google Scholar] [CrossRef]
- Della Torre, E. Modeling of magnetizing processes. Proc. IEEE 1990, 78, 1017–1026. [Google Scholar] [CrossRef]
- Alatawneh, N.; Pillay, P. Modeling of the interleaved hysteresis loop in the measurements of rotational core losses. J. Magn. Magn. Mater. 2016, 397, 157–163. [Google Scholar] [CrossRef]
- Fidler, J.; Schrefl, T. Micromagnetic modelling - the current state of the art. J. Phys. D Appl. Phys. 2000, 33, R135–R156. [Google Scholar] [CrossRef]
- Van de Wiele, B.; Olyslager, F.; Dupré, L. Fast numerical three-dimensional scheme for the simulation of hysteresis in ferromagnetic grains. J. Appl. Phys. 2007, 101, 073909. [Google Scholar] [CrossRef]
- Stancu, A.; Pike, C.; Stoleriu, L.; Postolache, P.; Cimpoesu, D. Micromagnetic and Preisach analysis of the First Order Reversal Curves (FORC) diagram. J. Appl. Phys. 2003, 93, 6620–6622. [Google Scholar] [CrossRef]
- Toman, M.; Stumberger, G.; Dolinar, D. Parameter Identification of the Jiles–Atherton Hysteresis Model Using Differential Evolution. IEEE Trans. Magn. 2008, 44, 1098–1101. [Google Scholar] [CrossRef]
- Rosenbaum, S.; Ruderman, M.; Strohla, T.; Bertram, T. Use of Jiles–Atherton and Preisach Hysteresis Models for Inverse Feed-Forward Control. IEEE Trans. Magn. 2010, 46, 3984–3989. [Google Scholar] [CrossRef]
- Armin, M.; Roy, P.N.; Das, S.K. A Survey on Modelling and Compensation for Hysteresis in High Speed Nanopositioning of AFMs: Observation and Future Recommendation. Int. J. Autom. Comput. 2020, 17, 479. [Google Scholar] [CrossRef]
- Melo, P.; Araújo, R.E. An Overview on Preisach and Jiles–Atherton Hysteresis Models for Soft Magnetic Materials. In Proceedings of the Technological Innovation for Smart Systems; Camarinha-Matos, L.M., Parreira-Rocha, M., Ramezani, J., Eds.; Springer: Cham, Switzerland, 2017; pp. 398–405. [Google Scholar] [CrossRef]
- Naidu, S. Simulation of the hysteresis phenomenon using Preisach’s theory. IEE Proc. A Phys. Sci. Meas. Instrum. Manag. Educ. 1990, 137, 73–79. [Google Scholar] [CrossRef]
- Hussain, S.; Lowther, D.A. Establishing a Relation between Preisach and Jiles–Atherton Models. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef]
- Van de Wiele, B.; Vandenbossche, L.; Dupré, L.; De Zutter, D. Energy considerations in a micromagnetic hysteresis model and the Preisach model. J. Appl. Phys. 2010, 108, 103902. [Google Scholar] [CrossRef]
- Stancu, A.; Pǎpuşoi, C.; Spînu, L. Mixed-type models of hysteresis. J. Magn. Magn. Mater. 1995, 150, 124–130. [Google Scholar] [CrossRef]
- Hamimid, M.; Feliachi, M.; Mimoune, S. Modified Jiles–Atherton model and parameters identification using false position method. Phys. B Condens. Matter 2010, 405, 1947–1950. [Google Scholar] [CrossRef]
- Lederer, D.; Igarashi, H.; Kost, A.; Honma, T. On the parameter identification and application of the Jiles–Atherton hysteresis model for numerical modelling of measured characteristics. IEEE Trans. Magn. 1999, 35, 1211–1214. [Google Scholar] [CrossRef]
- Leite, J.V.; Sadowski, N.; Kuo-Peng, P.; Batistela, N.J.; Bastos, J.P.A.; de Espindola, A.A. Inverse Jiles–Atherton vector hysteresis model. IEEE Trans. Magn. 2004, 40, 1769–1775. [Google Scholar] [CrossRef]
- Andrei, P.; Oniciuc, L.; Stancu, A.; Stoleriu, L. Identification techniques for phenomenological models of hysteresis based on the conjugate gradient method. J. Magn. Magn. Mater. 2007, 316, e330–e333. [Google Scholar] [CrossRef]
- He, X.Q.; Lozito, G.M.; Riganti Fulginei, F.; Salvini, A. On the Generalization Capabilities of the Ten-Parameter Jiles–Atherton Model. Math. Probl. Eng. 2015, 2015, 715018. [Google Scholar] [CrossRef]
- Shiming, L.; Ruisheng, L.; Liang, D.; Yu, G. Identification of a Hysteresis Model Parameters Using the Differential Evolution Algorithm. IOP Conf. Ser. Mater. Sci. Eng. 2017, 199, 012145. [Google Scholar] [CrossRef]
- Annakkage, U.; McLaren, P.; Dirks, E.; Jayasinghe, R.; Parker, A. A current transformer model based on the Jiles–Atherton theory of ferromagnetic hysteresis. IEEE Trans. Power Deliv. 2000, 15, 57–61. [Google Scholar] [CrossRef]
- Zirka, S.E.; Moroz, Y.I.; Marketos, P.; Moses, A.J. Congruency-based hysteresis models for transient simulation. IEEE Trans. Magn. 2004, 40, 390–399. [Google Scholar] [CrossRef]
- Wang, X.; Thomas, D.; Sumner, M.; Paul, J.; Cabral, S. Numerical determination of Jiles–Atherton model parameters. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2009, 28, 493–503. [Google Scholar] [CrossRef]
- Melikhov, Y.; Hadimani, R.L.; Raghunathan, A. Phenomenological modelling of first order phase transitions in magnetic systems. J. Appl. Phys. 2014, 115, 183902. [Google Scholar] [CrossRef]
- Gentili, G. A history-differential model for ferromagnetic hysteresis. Math. Comput. Model. 2001, 34, 1459–1482. [Google Scholar] [CrossRef]
- Gentili, G.; Giorgi, C. A new model for rate-independent hysteresis in permanent magnets. Int. J. Eng. Sci. 2001, 39, 1057–1090. [Google Scholar] [CrossRef]
- Hornung, U. The mathematics of hysteresis. Bull. Aust. Math. Soc. 1984, 30, 271–287. [Google Scholar] [CrossRef]
- Vaiana, N.; Capuano, R.; Rosati, L. Evaluation of path-dependent work and internal energy change for hysteretic mechanical systems. Mech. Syst. Signal Process. 2023, 186, 109862. [Google Scholar] [CrossRef]
- Zirka, S.E.; Moroz, Y.I.; Harrison, R.G.; Chiesa, N. Inverse Hysteresis Models for Transient Simulation. IEEE Trans. Power Deliv. 2014, 29, 552–559. [Google Scholar] [CrossRef]
- Krasnosel’skii, M.A.; Pokrovskii, A.V. Systems with Hysteresis, 1st ed.; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar] [CrossRef]
- de Almeida, L.A.L.; Deep, G.S.; Lima, A.M.N.; Neff, H. Limiting Loop Proximity Hysteresis Model. IEEE Trans. Magn. 2003, 39, 523–528. [Google Scholar] [CrossRef]
- Hauser, H. Energetic model of ferromagnetic hysteresis. J. Appl. Phys. 1994, 75, 2584. [Google Scholar] [CrossRef]
- Hauser, H.; Groessinger, R. Directional Dependence and Minor Loops of Magnetization of Ba- and Sr-Ferrites. IEEE Trans. Magn. 2003, 39, 2887–2889. [Google Scholar] [CrossRef]
- Hauser, H. Energetic model of ferromagnetic hysteresis: Isotropic magnetization. J. Appl. Phys. 2004, 96, 2753–2767. [Google Scholar] [CrossRef]
- Takacs, J. Analytical way to model magnetic transients and accommodation. Phys. B Condens. Matter 2007, 387, 217–221. [Google Scholar] [CrossRef]
- van Bree, P.J.; van Lierop, C.M.M.; van den Bosch, P.P.J. Control-Oriented Hysteresis Models for Magnetic Electron Lenses. IEEE Trans. Magn. 2009, 45, 5235–5238. [Google Scholar] [CrossRef]
- Della Torre, E. A Preisach model for accommodation. IEEE Trans. Magn. 1994, 30, 2701–2707. [Google Scholar] [CrossRef]
- Zirka, S.E.; Moroz, Y.I.; Della Torre, E. Combination hysteresis model for accommodation magnetization. IEEE Trans. Magn. 2005, 41, 2426–2431. [Google Scholar] [CrossRef]
- Dimian, M.; Andrei, P. Chapter 1: Mathematical models of hysteresis. In Noise-Driven Phenomena in Hysteretic Systems, 1st ed.; Springer: New York, NY, USA, 2014; pp. 1–63. [Google Scholar] [CrossRef]
- Vaiana, N.; Sessa, S.; Marmo, F.; Rosati, L. A class of uniaxial phenomenological models for simulating hysteretic phenomena in rate-independent mechanical systems and materials. Nonlinear Dyn. 2018, 93, 1647–1669. [Google Scholar] [CrossRef]
- Gan, J.; Zhang, X. A review of nonlinear hysteresis modeling and control of piezoelectric actuators. AIP Adv. 2019, 9, 040702. [Google Scholar] [CrossRef]
- Duhem, P. Chapter IV—De l’Hysteresis Magnétique. In Sur les DéFormations Permanentes et L’Hysteresis; Bibliothèque nationale de France; Impr. de Hayez: Bruxelles, Belgium, 1894–1902; pp. 51–60. Available online: http://catalogue.bnf.fr/ark:/12148/cb30370663w (accessed on 5 March 2023).
- Duhem, P. Die dauernden Änderungen und die Thermodynamik. I. Z. Für Phys. Chem. Stöchiometrie Und Verwandtschaftslehre 1897, 22, 545–589. [Google Scholar] [CrossRef]
- Duhem, P. Die dauernden Änderungen und die Thermodynamik. II. Z. Für Phys. Chem. Stöchiometrie Und Verwandtschaftslehre 1897, 23, 193–266. [Google Scholar] [CrossRef]
- Duhem, P. Die dauernden Änderungen und die Thermodynamik. III. Z. Für Phys. Chem. Stöchiometrie Und Verwandtschaftslehre 1897, 23, 497–541. [Google Scholar] [CrossRef]
- Duhem, P. Die dauernden Änderungen und die Thermodynamik. IX. Z. Für Phys. Chem. 1903, 43U, 695–700. [Google Scholar] [CrossRef]
- Takagi, J. On a mathematical expression of the hysteresis curves. Mem. Fac. Sci. Eng. Waseda Univ. Jpn. 1952, 10, 9–11. [Google Scholar]
- Sequenz, H. Beiträge zur Gleichung der Hystereseschleife. Arch. für Elektrotechnik 1935, 29, 387–394. [Google Scholar] [CrossRef]
- Rivas, J.; Zamarro, J.; Martin, E.; Pereira, C. Simple approximation for magnetization curves and hysteresis loops. IEEE Trans. Magn. 1981, 17, 1498–1502. [Google Scholar] [CrossRef]
- Battistelli, L.; Gentile, G.; Piccolo, A. Representation of hysteresis loops by rational fraction approximations. Phys. Scr. 1989, 40, 502–507. [Google Scholar] [CrossRef]
- Coleman, B.D.; Hodgdon, M.L. A constitutive relation for rate-independent hysteresis in ferromagnetically soft materials. Int. J. Eng. Sci. 1986, 24, 897–919. [Google Scholar] [CrossRef]
- Hodgdon, M.L. Applications of a theory of ferromagnetic hysteresis. IEEE Trans. Magn. 1988, 24, 218–221. [Google Scholar] [CrossRef]
- Hodgdon, M.L. Mathematical theory and calculations of magnetic hysteresis curves. IEEE Trans. Magn. 1988, 24, 3120–3122. [Google Scholar] [CrossRef]
- Jiles, D.C.; Atherton, D.L. Theory of ferromagnetic hysteresis (invited). J. Appl. Phys. 1984, 55, 2115–2120. [Google Scholar] [CrossRef]
- Jiles, D.; Atherton, D. Theory of ferromagnetic hysteresis. J. Magn. Magn. Mater. 1986, 61, 48–60. [Google Scholar] [CrossRef]
- Cisotti, U. Sull’isteresi magnetica. Rend. Accad. Dei Lincei (5a) 1908, 17, 413–420. [Google Scholar]
- Gans, R. Zur Theorie des Ferromagnetismus. 2. Mitteilung: Die reversible longitudinale Permeabilität. Ann. Der Phys. 1908, 332, 1–42. [Google Scholar] [CrossRef]
- Gans, R. Zur Theorie des Ferromagnetismus. 3. Mitteilung: Die reversible longitudinale und transversale Permeabilität. Ann. Der Phys. 1909, 334, 301–315. [Google Scholar] [CrossRef]
- Everett, D.H.; Smith, F.W. A general approach to hysteresis. Part 2: Development of the domain theory. Trans. Faraday Soc. 1954, 50, 187–197. [Google Scholar] [CrossRef]
- Janssens, N. Mathematical modelling of Magnetic Hysteresis. In Proceedings of the 1st Compumag Conference, Compumag, Oxford, UK, 31 March–2 April 1976; pp. 190–195. [Google Scholar]
- Janssens, N. Static models of magnetic hysteresis. IEEE Trans. Magn. 1977, 13, 1379–1381. [Google Scholar] [CrossRef]
- Hannalla, A.Y.; MacDonald, D.C. Representation of soft magnetic materials. IEE Proc. A Phys. Sci. Meas. Instrum. Manag. Educ. 1980, 127, 386–391. [Google Scholar] [CrossRef]
- Barker, J.A.; Schreiber, D.E.; Huth, B.G.; Everett, D.H. Magnetic hysteresis and minor loops: Models and experiments. Proc. R. Soc. A 1983, 386, 251–261. [Google Scholar] [CrossRef]
- Visintin, A. Models of hysteresis. Rend. Del Semin. Mat. E Fis. Di Milano 1988, 58, 221–238. [Google Scholar] [CrossRef]
- Visintin, A. Differential Models of Hysteresis; Series: Applied Mathematical Sciences; Springer: Berlin/Heidelberg, Germany, 1994; Chapter V5. [Google Scholar] [CrossRef]
- Ohteru, S. On Expressions of Magnetic Hysteresis Characteristics. Trans. Am. Inst. Electr. Eng. Part III Power Appar. Syst. 1959, 78, 1809–1815. [Google Scholar] [CrossRef]
- Babuška, I. Die nichtlineare Theorie der inneren Reibung. In Aplikace Matematiky; Czech Academy of Sciences Library: Staré Město, Czechia, 1959; pp. 303–321. [Google Scholar]
- Babuška, I. Die nichtlineare theorie der inneren reibung. Apl. Mat. 1959, 4, 303–321. [Google Scholar] [CrossRef]
- Ikhouane, F. A Survey of the Hysteretic Duhem Model. Arch. Comput. Methods Eng. 2018, 25, 965–1002. [Google Scholar] [CrossRef]
- Ikhouane, F. On babuška’s model for asymmetric hysteresis. Commun. Nonlinear Sci. Numer. Simul. 2021, 95, 105650. [Google Scholar] [CrossRef]
- Bouc, R. A Mathematical Model for Hysteresis, Modèle mathèmatique d’hystèrèsis. Acta Acust. United Acust. 1971, 24, 16–25. [Google Scholar]
- Macki, J.W.; Nistri, P.; Zecca, P. Mathematical models for hysteresis. SIAM Rev. 1993, 35, 94–123. [Google Scholar] [CrossRef]
- Ivshin, Y.; Pence, T. A constitutive model for hysteretic phase transition behavior. Int. J. Eng. Sci. 1994, 32, 681–704. [Google Scholar] [CrossRef]
- JinHyoung, O.; Bernstein, D.S. Semilinear Duhem model for rate-independent and rate-dependent hysteresis. IEEE Trans. Autom. Control 2005, 50, 631–645. [Google Scholar] [CrossRef]
- Madelung, E. Über Magnetisierung durch schnellverlaufende Ströme und die Wirkungsweise des Rutherford-Marconischen Magnetdetektors. Ann. Der Physic 1905, 322, 861–890. [Google Scholar] [CrossRef]
- Madelung, E. Über eine analytische Darstellung von Magnetisierungskurven. Phys. Z. 1912, 13, 436–440. [Google Scholar]
- Gans, R. Die Gleichung der Kurve der reversiblen Suszeptibilität. Phys. Z. 1911, 12, 1053–1054. [Google Scholar]
- Dahl, P.R. A Solid Friction Model; SAMSO Technical Rept. TR-77-131, U.S. DTIC: ADA041920; Aerospace Corp.: El Segundo, CA, USA, 1968. [Google Scholar]
- Dahl, P.R. Solid Friction Damping of Mechanical Vibrations. AIAA J. 1976, 14, 1675–1682. [Google Scholar] [CrossRef]
- Padthe, A.K.; Drincic, B.; Oh, J.; Rizos, D.D.; Fassois, S.D.; Bernstein, D.S. Duhem modeling of friction-induced hysteresis. IEEE Control Syst. Mag. 2008, 28, 90–107. [Google Scholar] [CrossRef]
- Canudas de Wit, C.; Olsson, H.; Åström, K.J.; Lischinsky, P. A new model for control of systems with friction. IEEE Trans. Autom. Control 1995, 40, 419–425. [Google Scholar] [CrossRef]
- Åström, K.J.; Canudas de Wit, C. Revisiting the LuGre friction model. IEEE Control Syst. Mag. 2008, 28, 101–114. [Google Scholar] [CrossRef]
- Wen, Y.K. Stochastic response and damage analysis of inelastic structures. Probab. Eng. Mech. 1986, 1, 49–57. [Google Scholar] [CrossRef]
- Ismail, M.; Ikhouane, F.; Rodellar, J. The Hysteresis Bouc-Wen Model, a Survey. Arch. Comput. Methods Eng. 2009, 16, 161–188. [Google Scholar] [CrossRef]
- Capuano, R.; Vaiana, N.; Pellecchia, D.; Rosati, L. A Solution Algorithm for a Modified Bouc-Wen Model Capable of Simulating Cyclic Softening and Pinching Phenomena. IFAC-PapersOnLine 2022, 55, 319–324. [Google Scholar] [CrossRef]
- Laudani, A.; Fulginei, F.R.; Salvini, A. Comparative analysis of Bouc-Wen and Jiles–Atherton models under symmetric excitations. Phys. B Condens. Matter 2014, 435, 134–137. [Google Scholar] [CrossRef]
- Warburg, E. Magnetische Untersuchungen. Ann. Der Phys. 1881, 249, 141–164. [Google Scholar] [CrossRef]
- Warburg, E.; Hönig, L. Ueber die Wärme, welche durch periodisch wechselnde magnetisirende Kräfte im Eisen erzeugt wird. Ann. Der Phys. 1883, 256, 814–835. [Google Scholar] [CrossRef]
- Guggenheim, E.A.; Darwin, C.G. The thermodynamics of magnetization. Proc. R. Soc. A Math. Phys. Eng. Sci. 1936, 155, 70–101. [Google Scholar] [CrossRef]
- Ossart, F.; Phung, T.A.; Meunier, G. Comparison between various hysteresis models and experimental data. J. Appl. Phys. 1990, 67, 5379–5381. [Google Scholar] [CrossRef]
- Voros, J. Modeling and identification of hysteresis using special forms of the Coleman-Hodgdon model. J. Electr. Eng. 2009, Vol. 60, 100–105. [Google Scholar]
- Feng, Y.; Rabbath, C.A.; Chai, T.; Su, C. Robust adaptive control of systems with hysteretic nonlinearities: A Duhem hysteresis modelling approach. In Proceedings of the AFRICON 2009, Nairobi, Kenya, 23–25 September 2009; 2009; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, C.; Yu, Y.; Xu, J.; Han, Z.; Zhou, M. Duhem Hysteresis Modeling of Magnetic Shape Memory Alloy Actuator via Takagi-Sugeno Fuzzy Neural Network. In Proceedings of the 2020 IEEE 15th International Conference on Nano/Micro Engineered and Molecular System (NEMS), San Diego, CA, USA, 27–30 September 2020; pp. 77–82. [Google Scholar] [CrossRef]
- Vörös, J. Identification of nonlinear cascade systems with output hysteresis based on the key term separation principle. Appl. Math. Model. 2015, 39, 5531–5539. [Google Scholar] [CrossRef]
- Vörös, J. Modeling and Identification of Discrete-Time Nonlinear Dynamic Cascade Systems with Input Hysteresis. Math. Probl. Eng. 2015, 2015, 393572. [Google Scholar] [CrossRef]
- Esguerra, M. Computation of minor hysteresis loops from measured major loops. J. Magn. Magn. Mater. 1996, 157–158, 366–368. [Google Scholar] [CrossRef]
- Sieber, A.V.; Romero, M. A collection of definitions and fundamentals for a design-oriented inductor model. In Proceedings of the 2020 Argentine Conference on Automatic Control (AADECA), Buenos Aires, Argentina, 28–30 October 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Lewis, L.H.; Gao, J.; Jiles, D.C.; Welch, D.O. Modeling of permanent magnets: Interpretation of parameters obtained from the Jiles—Atherton hysteresis model. J. Appl. Phys. 1996, 79, 6470–6472. [Google Scholar] [CrossRef]
- Gao, Z.; Jiles, D.C.; Branagan, D.J.; McCallum, R.W. Dependence of energy dissipation on annealing temperature of melt–spun NdFeB permanent magnet materials. J. Appl. Phys. 1996, 79, 5510–5512. [Google Scholar] [CrossRef]
- Zhang, D.; Kim, H.J.; Li, W.; Koh, C.S. Analysis of Magnetizing Process of a New Anisotropic Bonded NdFeB Permanent Magnet Using FEM Combined With Jiles–Atherton Hysteresis Model. IEEE Trans. Magn. 2013, 49, 2221–2224. [Google Scholar] [CrossRef]
- Jiles, D.; Ramesh, A.; Shi, Y.; Fang, X. Application of the anisotropic extension of the theory of hysteresis to the magnetization curves of crystalline and textured magnetic materials. IEEE Trans. Magn. 1997, 33, 3961–3963. [Google Scholar] [CrossRef]
- Gyselinck, J.; Dular, P.; Sadowski, N.; Leite, J.; Bastos, J. Incorporation of a Jiles–Atherton vector hysteresis model in 2D FE magnetic field computations: Application of the Newton-Raphson method. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2004, 23, 685–693. [Google Scholar] [CrossRef]
- Guérin, C.; Jacques, K.; Sabariego, R.V.; Dular, P.; Geuzaine, C.; Gyselinck, J. Using a Jiles–Atherton vector hysteresis model for isotropic magnetic materials with the finite element method, Newton–Raphson method, and relaxation procedure. Int. J. Numer. Model. Electron. Netw. Devices Fields 2017, 30, e2189. [Google Scholar] [CrossRef]
- Brachtendorf, H.; Eck, C.; Laur, R. Macromodeling of hysteresis phenomena with SPICE. IEEE Trans. Circuits Syst. II Analog. Digit. Signal Process. 1997, 44, 378–388. [Google Scholar] [CrossRef]
- Dimitropoulos, P.; Stamoulis, G.; Hristoforou, E. A 3-D hybrid Jiles–Atherton/Stoner-Wohlfarth magnetic hysteresis model for inductive sensors and actuators. IEEE Sens. J. 2006, 6, 721–736. [Google Scholar] [CrossRef]
- Emami, Z.; Karimi, M.; Motahari, S.R. Simulation and modeling of high voltage nano crystallinecore toroid pulse transformer for pulse modulator. In Proceedings of the 2015 23rd Iranian Conference on Electrical Engineering, Tehran, Iran, 10–14 May 2015; pp. 1551–1555. [Google Scholar] [CrossRef]
- Lacerda Ribas, J.; Lourenço, E.M.; Leite, J.; Batistela, N. Modeling Ferroresonance Phenomena With a Flux-Current Jiles–Atherton Hysteresis Approach. IEEE Trans. Magn. 2013, 49, 1797–1800. [Google Scholar] [CrossRef]
- Benabou, A.; Clénet, S.; Piriou, F. Comparison of Preisach and Jiles–Atherton models to take into account hysteresis phenomenon for finite element analysis. J. Magn. Magn. Mater. 2003, 261, 139–160. [Google Scholar] [CrossRef]
- Deane, J. Modeling the dynamics of nonlinear inductor circuits. IEEE Trans. Magn. 1994, 30, 2795–2801. [Google Scholar] [CrossRef]
- Padilha, J.; Kuo-Peng, P.; Sadowski, N.; Leite, J.; Batistela, N. Restriction in the determination of the Jiles–Atherton hysteresis model parameters. J. Magn. Magn. Mater. 2017, 442, 8–14. [Google Scholar] [CrossRef]
- Jiles, D.; Thoelke, J. Theory of ferromagnetic hysteresis: Determination of model parameters from experimental hysteresis loops. IEEE Trans. Magn. 1989, 25, 3928–3930. [Google Scholar] [CrossRef]
- Cao, S.; Wang, B.; Yan, R.; Huang, W.; Yang, Q. Optimization of hysteresis parameters for the Jiles–Atherton model using a genetic algorithm. IEEE Trans. Appl. Supercond. 2004, 14, 1157–1160. [Google Scholar] [CrossRef]
- Li, H.; Li, Q.; Zhang, J. Calculation of Jiles–Atherton hysteresis model’s parameters using mix of chaos optimization algorithm and simulated annealing algorithm. In Proceedings of the 2009 International Conference on Microwave Technology and Computational Electromagnetics (ICMTCE 2009), Beijing, China, 3–6 November 2009; pp. 471–474. [Google Scholar] [CrossRef]
- Cong, H.; Zou, L.; Zhang, L.; Li, Q. Parameters determination of the modified J–A model with an optimization algorithm. Int. J. Appl. Electromagn. Mech. 2013, 41, 259–266. [Google Scholar] [CrossRef]
- Upadhaya, B.; Martin, F.; Rasilo, P.; Handgruber, P.; Belahcen, A.; Arkkio, A. Modelling anisotropy in non-oriented electrical steel sheet using vector Jiles–Atherton model. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2017, 36, 764–773. [Google Scholar] [CrossRef]
- Rubežić, V.; Lazović, L.; Jovanović, A. Parameter identification of Jiles–Atherton model using the chaotic optimization method. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2018, 37, 2067–2080. [Google Scholar] [CrossRef]
- Vijn, A.R.P.J.; Baas, O.; Lepelaars, E. Parameter Estimation for the Jiles–Atherton Model in Weak Fields. IEEE Trans. Magn. 2020, 56, 1–10. [Google Scholar] [CrossRef]
- Aboura, F.; Touhami, O. Modeling and Analyzing Energetic Hysteresis Classical Model. In Proceedings of the 2018 International Conference on Electrical Sciences and Technologies in Maghreb (CISTEM), Algiers, Algeria, 28–31 October 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Zirka, S.E.; Moroz, Y.I.; Harrison, R.G.; Chwastek, K. On physical aspects of the Jiles–Atherton hysteresis models. J. Appl. Phys. 2012, 112, 043916. [Google Scholar] [CrossRef]
- Takács, J. A phenomenological mathematical model of hysteresis. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2001, 20, 1002–1015. [Google Scholar] [CrossRef]
- Steentjes, S.; Eggers, D.; Hameyer, K. Application and Verification of a Dynamic Vector-Hysteresis Model. IEEE Trans. Magn. 2012, 48, 3379–3382. [Google Scholar] [CrossRef]
- Jastrzebski, R.; Jakubas, A.; Chwastek, K. A Comparison of Two Phenomenological Descriptions of Magnetization Curves Based on T(x) Model. In Proceedings of the 13th Symposium of Magnetic Measurements and Modeling SMMM’2018, Wieliczka, Poland, 8–10 October 2018. [Google Scholar] [CrossRef]
- Raghunathan, A.; Melikhov, Y.; Snyder, J.E.; Jiles, D.C. Generalized form of anhysteretic magnetization function for Jiles–Atherton theory of hysteresis. Appl. Phys. Lett. 2009, 95, 172510. [Google Scholar] [CrossRef]
- Kokornaczyk, E.; Gutowski, M.W. Anhysteretic Functions for the Jiles–Atherton Model. IEEE Trans. Magn. 2015, 51, 1–5. [Google Scholar] [CrossRef]
- Chwastek, K.; Szczygłowski, J.; Wilczyński, W. Modelling dynamic hysteresis loops in steel sheets. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2009, 28, 603–612. [Google Scholar] [CrossRef]
- Chwastek, K. Modelling magnetic properties of MnZn ferrites with the modified Jiles–Atherton description. J. Phys. D Appl. Phys. 2009, 43, 015005. [Google Scholar] [CrossRef]
- Chwastek, K. Modelling offset minor hysteresis loops with the modified Jiles–Atherton description. J. Phys. D Appl. Phys. 2009, 42, 165002. [Google Scholar] [CrossRef]
- Carpenter, K.H.; Warren, S. A wide bandwidth, dynamic hysteresis model for magnetization in soft ferrites. IEEE Trans. Magn. 1992, 28, 2037–2041. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, Y.; Liu, S.; Lin, F. Application of Jiles–Atherton model in description of temperature characteristics of magnetic core. Rev. Sci. Instrum. 2018, 89, 104702. [Google Scholar] [CrossRef]
- Messal, O.; Sixdenier, F.; Morel, L.; Burais, N. Temperature Dependent Extension of the Jiles–Atherton Model: Study of the Variation of Microstructural Hysteresis Parameters. IEEE Trans. Magn. 2012, 48, 2567–2572. [Google Scholar] [CrossRef]
- Wilson, P.; Ross, J.; Brown, A. Simulation of magnetic component models in electric circuits including dynamic thermal effects. IEEE Trans. Power Electron. 2002, 17, 55–65. [Google Scholar] [CrossRef]
- Hussain, S.; Benabou, A.; Clénet, S.; Lowther, D.A. Temperature Dependence in the Jiles–Atherton Model for Non-Oriented Electrical Steels: An Engineering Approach. IEEE Trans. Magn. 2018, 54, 1–5. [Google Scholar] [CrossRef]
- Birčáková, Z.; Kollár, P.; Füzer, J.; Bureš, R.; Fáberová, M. Magnetic properties of selected Fe-based soft magnetic composites interpreted in terms of Jiles–Atherton model parameters. J. Magn. Magn. Mater. 2020, 502, 166514. [Google Scholar] [CrossRef]
- Bergqvist, A. A Simple Vector Generalization of the Jiles–Atherton Model of Hysteresis. IEEE Trans. Magn. 1996, 32, 4213–4215. [Google Scholar] [CrossRef]
- Ramesh, A.; Jiles, D.; Roderick, J. A model of anisotropic anhysteretic magnetization. IEEE Trans. Magn. 1996, 32, 4234–4236. [Google Scholar] [CrossRef]
- Ramesh, A.; Jiles, D.C.; Bi, Y. Generalization of hysteresis modeling to anisotropic materials. J. Appl. Phys. 1997, 81, 5585–5587. [Google Scholar] [CrossRef]
- Szewczyk, R. Validation of the Anhysteretic Magnetization Model for Soft Magnetic Materials with Perpendicular Anisotropy. Materials 2014, 7, 5109–5116. [Google Scholar] [CrossRef] [PubMed]
- Sablik, M.; Jiles, D. Coupled magnetoelastic theory of magnetic and magnetostrictive hysteresis. IEEE Trans. Magn. 1993, 29, 2113–2123. [Google Scholar] [CrossRef]
- Li, J.; Xu, M. Modified Jiles–Atherton-Sablik model for asymmetry in magnetomechanical effect under tensile and compressive stress. J. Appl. Phys. 2011, 110, 063918. [Google Scholar] [CrossRef]
- Jakubas, A.; Chwastek, K. A Simplified Sablik’s Approach to Model the Effect of Compaction Pressure on the Shape of Hysteresis Loops in Soft Magnetic Composite Cores. Materials 2020, 13, 170. [Google Scholar] [CrossRef] [PubMed]
- Sadowski, N.; Batistela, N.J.; Bastos, J.P.A.; Lajoie-Mazenc, M. An Inverse Jiles–Atherton Model to Take Into Account Hysteresis in Time-Stepping Finite-Element Calculations. IEEE Trans. Magn. 2002, 38, 797–800. [Google Scholar] [CrossRef]
- Andrei, P.; Dimian, M. Clockwise Jiles–Atherton Hysteresis Model. IEEE Trans. Magn. 2013, 49, 3183–3186. [Google Scholar] [CrossRef]
- Koltermann, P.; Righi, L.; Bastos, J.; Carlson, R.; Sadowski, N.; Batistela, N. A modified Jiles method for hysteresis computation including minor loops. Phys. B Condens. Matter 2000, 275, 233–237. [Google Scholar] [CrossRef]
- Vaseghi, B.; Mathekga, D.; Rahman, S.; Knight, A. Parameter Optimization and Study o Inverse J–A Hysteresis Model. IEEE Trans. Magn. 2013, 49, 1637–1640. [Google Scholar] [CrossRef]
- Miljavec, D.; Zidarič, B. Introducing a domain flexing function in the Jiles–Atherton hysteresis model. J. Magn. Magn. Mater. 2008, 320, 763–768. [Google Scholar] [CrossRef]
- Araneo, R.; Celozzi, S. Analysis of the shielding performance of ferromagnetic screens. IEEE Trans. Magn. 2003, 39, 1046–1052. [Google Scholar] [CrossRef]
- Steentjes, S.; Chwastek, K.; Petrun, M.; Dolinar, D.; Hameyer, K. Sensitivity Analysis and Modeling of Symmetric Minor Hysteresis Loops Using the GRUCAD Description. IEEE Trans. Magn. 2014, 50, 1–4. [Google Scholar] [CrossRef]
- Steentjes, S.; Petrun, M.; Dolinar, D.; Hameyer, K. Effect of Parameter Identification Procedure of the Static Hysteresis Model on Dynamic Hysteresis Loop Shapes. IEEE Trans. Magn. 2016, 52, 1–4. [Google Scholar] [CrossRef]
- Jastrzȩbski, R.; Jakubas, A.; Chwastek, K. Modeling of DC-biased Hysteresis Loops with the GRUCAD Description. Int. J. Appl. Electromagn. Mech. 2019, 61, S151–S157. [Google Scholar] [CrossRef]
- Ivanyi, A. Hysteresis in rotation magnetic field. Phys. B Condens. Matter 2000, 275, 107–113. [Google Scholar] [CrossRef]
- Upadhaya, B.; Rasilo, P.; Perkkiö, L.; Handgruber, P.; Belahcen, A.; Arkkio, A. A constraint-based optimization technique for estimating physical parameters of Jiles–Atherton hysteresis model. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2020, 39, 1281–1298. [Google Scholar] [CrossRef]
- Upadhaya, B.; Perkkiö, L.; Rasilo, P.; Belahcen, A.; Handgruber, P.; Arkkio, A. Representation of anisotropic magnetic characteristic observed in a non-oriented silicon steel sheet. AIP Adv. 2020, 10, 065222. [Google Scholar] [CrossRef]
- Upadhaya, B.; Rasilo, P.; Perkkiö, L.; Handgruber, P.; Benabou, A.; Belahcen, A.; Arkkio, A. Alternating and rotational loss prediction accuracy of vector Jiles–Atherton model. J. Magn. Magn. Mater. 2021, 527, 167690. [Google Scholar] [CrossRef]
- Appino, C.; Ragusa, C.; Fiorilloa, F. Can rotational magnetization be theoretically assessed? Int. J. Appl. Electromagn. Mech. 2014, 44, 355–370. [Google Scholar] [CrossRef]
- Bergqvist, A. Magnetic vector hysteresis model with dry friction-like pinning. Phys. B Condens. Matter 1997, 233, 342–347. [Google Scholar] [CrossRef]
- Iyer, R.; Krishnaprasad, P. On a low-dimensional model for ferromagnetism. Nonlinear Anal. Theory Methods Appl. 2005, 61, 1447–1482. [Google Scholar] [CrossRef]
- Cheng, P.; Szewczyk, R. Modified Description of Magnetic Hysteresis in Jiles–Atherton Model. In Proceedings of the Automation 2018; Szewczyk, R., Zieliński, C., Kaliczyńska, M., Eds.; Springer: Cham, Switzerland, 2018; pp. 648–654. [Google Scholar] [CrossRef]
- Hamel, M.; Nait Ouslimane, A.; Hocini, F. A study of Jiles–Atherton and the modified arctangent models for the description of dynamic hysteresis curves. Phys. B Condens. Matter 2022, 638, 413930. [Google Scholar] [CrossRef]
- Jiles, D.C. Frequency dependence of hysteresis curves in conducting magnetic materials. J. Appl. Phys. 1994, 76, 5849–5855. [Google Scholar] [CrossRef]
- Du, R.; Robertson, P. Dynamic Jiles–Atherton Model for Determining the Magnetic Power Loss at High Frequency in Permanent Magnet Machines. IEEE Trans. Magn. 2015, 51, 1–10. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, L.; Zhu, J. Core Loss Calculation Based on Finite-Element Method With Jiles–Atherton Dynamic Hysteresis Model. IEEE Trans. Magn. 2018, 54, 1–5. [Google Scholar] [CrossRef]
- Lin, D.; Zhou, P.; Lu, C.; Chen, N.; Rosu, M. Construction of magnetic hysteresis loops and its applications in parameter identification for hysteresis models. In Proceedings of the 2014 International Conference on Electrical Machines (ICEM), Berlin, Germany, 2–5 September 2014; pp. 1050–1055. [Google Scholar] [CrossRef]
- Takahashi, S.; Zhang, L. Minor Hysteresis Loop in Fe Metal and Alloys. J. Phys. Soc. Jpn. 2004, 73, 1567–1575. [Google Scholar] [CrossRef]
- Takahashi, S.; Zhang, L.; Kobayashi, S.; Kamada, Y.; Kikuchi, H.; Ara, K. Analysis of minor hysteresis loops in plastically deformed low carbon steel. J. Appl. Phys. 2005, 98, 033909. [Google Scholar] [CrossRef]
- Dick, E.; Watson, W. Transformer Models for Transient Studies Based on Field Measurements. IEEE Trans. Power Appar. Syst. 1981, PAS-100, 409–419. [Google Scholar] [CrossRef]
- Zirka, S.; Moroz, Y.I. Hysteresis modeling based on transplantation. IEEE Trans. Magn. 1995, 31, 3509. [Google Scholar] [CrossRef]
- Milovanovic, A.M.; Koprivica, B.M. Mathematical Model of Major Hysteresis Loop and Transient Magnetizations. Electromagnetics 2015, 35, 155–166. [Google Scholar] [CrossRef]
- Zirka, S.; Moroz, Y. Hysteresis modeling based on similarity. IEEE Trans. Magn. 1999, 35, 2090. [Google Scholar] [CrossRef]
- Ossart, F.; Meunier, G. Results on modeling magnetic hysteresis using the finite-element methoda). J. Appl. Phys. 1991, 69, 4835–4837. [Google Scholar] [CrossRef]
- Potter, R.; Schmulian, R. Self-consistently computed magnetization patterns in thin magnetic recording media. IEEE Trans. Magn. 1971, 7, 873–880. [Google Scholar] [CrossRef]
- Williams, M.L.; Comstock, R.L. An analytical model of the write process in digital magnetic recording. AIP Conf. Proc. 1972, 5, 738–742. [Google Scholar] [CrossRef]
- Potter, R.I. Analysis of Saturation Magnetic Recording Based on Arctangent Magnetization Transitions. J. Appl. Phys. 1970, 41, 1647–1651. [Google Scholar] [CrossRef]
- Portigal, D. A magnetic recording simulation program having an improved fit to actual hysteresis loops. IEEE Trans. Magn. 1975, 11, 934–941. [Google Scholar] [CrossRef]
- Liu, H.; Lin, H.; Zhu, Z.Q.; Huang, M.; Jin, P. Permanent Magnet Remagnetizing Physics of a Variable Flux Memory Motor. IEEE Trans. Magn. 2010, 46, 1679–1682. [Google Scholar] [CrossRef]
- Teape, J.; Simpson, R.; Slater, R.; Wood, W. Representation of magnetic characteristic, including hysteresis, by exponential series. Proc. Inst. Electr. Eng. 1974, 9, 1019–1020. [Google Scholar] [CrossRef]
- Thompson, W. Mathematical model for nonlinear magnetic cores at low frequencies. IEEE Trans. Magn. 1974, 10, 332–337. [Google Scholar] [CrossRef]
- Thompson, W.; Munk, P. Mathematical model of nonlinear magnetic cores. IEEE Trans. Magn. 1970, 6, 523. [Google Scholar] [CrossRef]
- Wong, C.C. A dynamic hysteresis model. IEEE Trans. Magn. 1988, 24, 1966–1968. [Google Scholar] [CrossRef]
- Chan, J.H.; Vladimirescu, A.; Gao, X.; Liebmann, P.; Valainis, J. Nonlinear transformer model for circuit simulation. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 1991, 10, 476–482. [Google Scholar] [CrossRef]
- Talukdar, S.N.; Bailey, J. Hysteresis models for system studies. IEEE Trans. Power Appar. Syst. 1976, 95, 1429–1434. [Google Scholar] [CrossRef]
- Zaher, F.A.A.; Shobeir, A.I. Analog Simulation of the Magnetic Hysteresis. IEEE Trans. Power Appar. Syst. 1983, PAS-102, 1235–1239. [Google Scholar] [CrossRef]
- Zaher, F.A.A.; Shobeir, A.I. Analog Simulation of the Magnetic Hysteresis. IEEE Power Eng. Rev. 1983, PER-3, 39–40. [Google Scholar] [CrossRef]
- Xu, Q.F.; Refsum, A. Analysis of some numerical models of hysteresis loops. In Proceedings of the 1993 2nd International Conference on Advances in Power System Control, Operation and Management (APSCOM-93), Hong Kong, China, 7–10 December 1993; Volume 2, pp. 734–737. [Google Scholar]
- Faiz, J.; Saffari, S. Inrush Current Modeling in a Single-Phase Transformer. IEEE Trans. Magn. 2010, 46, 578–581. [Google Scholar] [CrossRef]
- Faiz, J.; Saffari, S. A New Technique for Modeling Hysteresis Phenomenon in Soft Magnetic Materials. Electromagnetics 2010, 30, 376–401. [Google Scholar] [CrossRef]
- Guerra, F.; Mota, W.S. Current Transformer Model. IEEE Trans. Power Deliv. 2007, 22, 187–194. [Google Scholar] [CrossRef]
- Mukherjee, A.; Mukhopadhyay, S.C.; Iwahara, M.; Yamada, S.; Dawson, F.P. A numerical method for analyzing a passive fault current limiter considering hysteresis. IEEE Trans. Magn. 1998, 34, 2048–2050. [Google Scholar] [CrossRef]
- Herceg, D.; Chwastek, K.; Herceg, D. The Use of Hypergeometric Functions in Hysteresis Modeling. Energies 2020, 13, 6500. [Google Scholar] [CrossRef]
- Herceg, D.; Herceg, D. Improved accuracy hysteresis model based on hypergeometric functions. AIP Adv. 2020, 10, 105321. [Google Scholar] [CrossRef]
- Zeinali, R.; Krop, D.; Lomonova, E. Anisotropic Congruency-Based Vector Hysteresis Model Applied to Non-Oriented Laminated Steels. IEEE Trans. Magn. 2021, 57, 1–4. [Google Scholar] [CrossRef]
- Mousavi, S.A.; Engdahl, G. Differential Approach of Scalar Hysteresis Modeling Based on the Preisach Theory. IEEE Trans. Magn. 2011, 47, 3040–3043. [Google Scholar] [CrossRef]
- Frame, J.G.; Mohan, N.; Liu, T. Hysteresis Modeling in An Electro-Magnetic Transients Program. IEEE Trans. Power Appar. Syst. 1982, PAS-101, 3403–3412. [Google Scholar] [CrossRef]
- Tellinen, J. A simple scalar model for magnetic hysteresis. IEEE Trans. Magn. 1998, 34, 2200–2206. [Google Scholar] [CrossRef]
- Ziske, J.; Ehle, F.; Neubert, H.; Price, A.D.; Lienig, J. A Simple Phenomenological Model for Magnetic Shape Memory Actuators. IEEE Trans. Magn. 2015, 51, 1–8. [Google Scholar] [CrossRef]
- Glehn, G.; Steentjes, S.; Hameyer, K. Pulsed-Field Magnetometer Measurements and Pragmatic Hysteresis Modeling of Rare-Earth Permanent Magnets. IEEE Trans. Magn. 2018, 54, 1–4. [Google Scholar] [CrossRef]
- Kühn, J.; Bartel, A.; Putek, P. A thermal extension and loss model for Tellinen’s hysteresis model. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2020, 40, 126–141. [Google Scholar] [CrossRef]
- Li, Y.; Chen, R.; Cheng, Z.; Zhang, C.; Liu, L. Dynamic Hysteresis Loops Modeling of Electrical Steel With Harmonic Components. IEEE Trans. Ind. Appl. 2020, 56, 4804–4811. [Google Scholar] [CrossRef]
- Ray, S. Digital simulation of B/H excursions for power system studies. Inst. Electr. Eng. IEE Proc. Part C 1988, 135, 202–209. [Google Scholar] [CrossRef]
- Bastos, J.P.A.; Hoffmann, K.; Leite, J.V.; Sadowski, N. A New and Robust Hysteresis Modeling Based on Simple Equations. IEEE Trans. Magn. 2018, 54, 1–4. [Google Scholar] [CrossRef]
- Flatley, T.W.; Henretty, D.A. A Magnetic Hysteresis Model; N95-27801; NASA Technical Reports Server: Washington, DC, USA, 1995.
- Mészáros, I. Magnetization curve modelling of soft magnetic alloys. J. Phys. Conf. Ser. 2011, 268, 012020. [Google Scholar] [CrossRef]
- O’Kelly, D. Simulation of transient and steady-state magnetisation characteristics with hysteresis. Proc. Inst. Electr. Eng. 1977, 124, 578–582. [Google Scholar] [CrossRef]
- Zirka, S.E.; Moroz, Y.I.; Chiesa, N.; Harrison, R.G.; Høidalen, H.K. Implementation of Inverse Hysteresis Model into EMTP—Part I: Static Model. IEEE Trans. Power Deliv. 2015, 30, 2224–2232. [Google Scholar] [CrossRef]
- Trutt, F.C.; Erdelyi, E.A.; Hopkins, R.E. Representation of the Magnetization Characteristic of DC Machines for Computer Use. IEEE Trans. Power Appar. Syst. 1968, PAS-87, 201–213. [Google Scholar] [CrossRef]
- Fischer, J.; Moser, H. Die nachbildung von Magnetisierungskurven durch einfache algebraische oder transzendente Funktionen. Arch. Für Elektrotechnik 1956, 42, 286–299. [Google Scholar] [CrossRef]
- Böning, W. Analytische Darstellung der Kennlinien nichtlinearer Zweipole. Arch. Für Elektrotechnik 1960, 45, 265–278. [Google Scholar] [CrossRef]
- Dadić, M.; Jurčević, M.; Malarić, R. Approximation of the Nonlinear B-H Curve by Complex Exponential Series. IEEE Access 2020, 8, 49610–49616. [Google Scholar] [CrossRef]
- Curland, N.; Speliotis, D. An iterative hysteretic model for digital magnetic recording. IEEE Trans. Magn. 1971, 7, 538–543. [Google Scholar] [CrossRef]
- Motoasca, S.; Scutaru, G.; Gerigan, C. Improved analytical method for hysteresis modelling of soft magnetic materials. In Proceedings of the 2015 International Aegean Conference on Electrical Machines Power Electronics (ACEMP), 2015 International Conference on Optimization of Electrical Electronic Equipment (OPTIM), 2015 International Symposium on Advanced Electromechanical Motion Systems (ELECTROMOTION), Side, Turkey, 2–4 September 2015; pp. 558–563. [Google Scholar] [CrossRef]
- Everatt, J.S. Computer simulation of nonlinear inductors with hysteresis. Electron. Lett. 1970, 6, 833–834. [Google Scholar] [CrossRef]
- Gallicchio, G.; Nardo, M.D.; Palmieri, M.; Cupertino, F. Analysis, Design and Optimization of Hysteresis Clutches. IEEE Open J. Ind. Appl. 2020, 1, 258–269. [Google Scholar] [CrossRef]
- Frölich, O. Versuche mit dynamoelektrischen Maschinen und elektrischer Kraftübertragung und theoretische Folgerungen aus denselben. Elektrotechn. Z. 1881, 2, 134–141. [Google Scholar]
- Kennelly, A.E. Magnetic Reluctance. Trans. Am. Inst. Electr. Eng. 1891, VIII, 485–533. [Google Scholar] [CrossRef]
- Jiles, D.C. Introduction to Magnetism and Magnetic Materials, 3rd ed.; Taylor and Francis: New York, NY, USA, 1998; p. 113. [Google Scholar]
- Bozorth, R.M. Ferromagnetism; Van Nostrand: Toronto, ON, Canada, 1951; p. 484 ff. [Google Scholar]
- Ewing, J.A. Magnetic Induction in Iron and Other Metals; The Electricians: London, UK, 1892; p. 320. [Google Scholar]
- Woods, E.J. Eddy Current Losses in Solid Iron With DC Offset. IEEE Trans. Power Appar. Syst. 1981, PAS-100, 2241–2248. [Google Scholar] [CrossRef]
- Mahmoud, M.O.; Whitehead, R.W. Piecewise Fitting Function for Magnetisation Charateristics. IEEE Trans. Power Appar. Syst. 1985, PAS-104, 1822–1824. [Google Scholar] [CrossRef]
- Gupta, T.; Yoshino, Y.S. Finite element solution of permanent magnetic field. IEEE Trans. Magn. 1990, 26, 383–386. [Google Scholar] [CrossRef]
- Tuohy, E.J.; Panek, J. Chopping of Transformer Magnetizing Currents Part I: Single Phase Transformers. IEEE Trans. Power Appar. Syst. 1978, PAS-97, 261–268. [Google Scholar] [CrossRef]
- Jufer, M.; Apostolides, A. An analysis of eddy current and hysteresis losses in solid iron based upon simulation of saturation and hysteresis characteristics. IEEE Trans. Power Appar. Syst. 1976, 95, 1786–1794. [Google Scholar] [CrossRef]
- Rahman, M.; Poloujadoff, M.; Jackson, R.; Perard, J.; Gowda, S. Improved algorithms for digital simulation of hysteresis processes in semi hard magnetic materials. IEEE Trans. Magn. 1981, 17, 3253–3255. [Google Scholar] [CrossRef]
- Watson, E. Permanent magnets, and the relation of their properties to the constitution of magnet steels. J. Inst. Electr. Eng. 1923, 61, 641–660. [Google Scholar] [CrossRef]
- Hornfeck, A.J.; Edgar, R.F. The output and optimum design of permanent magnets subjected to demagnetizing forces. Electr. Eng. 1940, 59, 1017–1024. [Google Scholar] [CrossRef]
- Roshen, W. Ferrite core loss for power magnetic components design. IEEE Trans. Magn. 1991, 27, 4407–4415. [Google Scholar] [CrossRef]
- Roshen, W. Magnetic loss in AC motors in transportation. In Proceedings of the Power Electronics in Transportation (IEEE Cat. No.04TH8756), Novi, MI, USA, 21–22 October 2004; pp. 103–108. [Google Scholar] [CrossRef]
- Grössinger, R. A critical examination of the law of approach to saturation. I. Fit procedure. Phys. Status Solidi A 1981, 66, 665–674. [Google Scholar] [CrossRef]
- Zhang, X.; Tan, Y. A hybrid model for rate-dependent hysteresis in piezoelectric actuators. Sens. Actuators A Phys. 2010, 157, 54–60. [Google Scholar] [CrossRef]
- Wang, L.; Ding, F.; Yang, D.; Wang, K.; Jiao, B.; Chen, Q. A fitting-extrapolation method of B-H curve for magnetic saturation application. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2022, 29, 494–505. [Google Scholar] [CrossRef]
- Sivaranjani, K.S.; Jacob, G.A.; Joseyphus, R.J. Comprehensive Law-of-Approach-to-Saturation for the Determination of Magnetic Anisotropy in Soft Magnetic Materials. Phys. Status Solidi B 2022, 259, 2200050. [Google Scholar] [CrossRef]
- Akulov, N. Zur Theorie der Magnetisierungskurve von Einkristallen. Z. Phys. 1931, 67, 794–807. [Google Scholar] [CrossRef]
- Bitter, F. Introduction to Ferromagnetism, 1st ed.; McGraw-Hill Book Company: New York, NY, USA, 1937. [Google Scholar]
- Kaufmann, A.R. The Approach to Saturation of Iron and Nickel. Phys. Rev. 1939, 55, 1142. [Google Scholar]
- Kaufmann, A.R. Approach to magnetic saturation of nickel under torsional strain. Phys. Rev. 1940, 57, 1089. [Google Scholar]
- Polley, H. Das Einmünden der Magnetisierung in die Sättigung bei Nickel zwischen +135C und -253C. Temperaturabhängigkeit der Kristallenergie. Ann. Der Phys. 1939, 428, 625–650. [Google Scholar] [CrossRef]
- Brown, W.F. Theory of the Approach to Magnetic Saturation. Phys. Rev. 1940, 58, 736–743. [Google Scholar] [CrossRef]
- Brown, W.F. Dislocations, Cavities, and the Approach to Magnetic Saturation. Phys. Rev. 1951, 82, 94. [Google Scholar] [CrossRef]
- Rayleigh, L. XXV. Notes on electricity and magnetism.—III. On the behaviour of iron and steel under the operation of feeble magnetic forces. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1887, 23, 225–245. [Google Scholar] [CrossRef]
- Kachniarz, M.; Szewczyk, R. Study on the Rayleigh Hysteresis Model and its Applicability in Modeling Magnetic Hysteresis Phenomenon in Ferromagnetic Materials. Acta Phys. Pol. A 2017, 131, 1244–1249. [Google Scholar] [CrossRef]
- Canova, A.; Freschi, F.; Giaccone, L.; Repetto, M. Numerical Modeling and Material Characterization for Multilayer Magnetically Shielded Room Design. IEEE Trans. Magn. 2018, 54, 1–4. [Google Scholar] [CrossRef]
- Baldwin, J. Rayleigh hysteresis-A new look at an old law. IEEE Trans. Magn. 1978, 14, 81–84. [Google Scholar] [CrossRef]
- Baldwin, J.A.; Revol, J.; Milstein, F. Failure of the Rayleigh hysteresis law in low magnetic fields. Phys. Rev. B 1977, 15, 426–428. [Google Scholar] [CrossRef]
- Koller, A.; Pfrenger, E.; Stierstadt, K. New Interpretation of the Rayleigh Law. J. Appl. Phys. 1968, 39, 869–870. [Google Scholar] [CrossRef]
- Dietzmann, G.; Schaefer, M. Rayleigh hysteresis with sinusoidal wave form of magnetic induction. J. Magn. Magn. Mater. 1992, 110, 151–160. [Google Scholar] [CrossRef]
- Zapperi, S.; Magni, A.; Durin, G. Microscopic foundations of the Rayleigh law of hysteresis. J. Magn. Magn. Mater. 2002, 242-245, 987–992. [Google Scholar] [CrossRef]
- Ponomarev, Y.F. On the Rayleigh Law of Magnetization: A New Mathematical Model of Hysteresis Loops. Phys. Met. Metallogr. 2007, 104, 469–477. [Google Scholar] [CrossRef]
- Ponomarev, Y. On the Rayleigh law of magnetization. Symmetrical and asymmetric hysteresis loops. Experiment. Phys. Met. Metallogr. 2008, 105, 263–274. [Google Scholar] [CrossRef]
- Bintachitt, P.; Jesse, S.; Damjanovic, D.; Han, Y.; Reaney, I.M.; Trolier-McKinstry, S.; Kalinin, S.V.; Nattermann, T. Collective dynamics underpins Rayleigh behavior in disordered polycrystalline ferroelectrics. Proc. Natl. Acad. Sci. USA 2010, 107, 7219–7224. [Google Scholar] [CrossRef] [PubMed]
- Kaido, C. Modeling of magnetization curves in nonoriented electrical steel sheets. Electr. Eng. Jpn. 2012, 180, 1–8. [Google Scholar] [CrossRef]
- Paesano, A., Jr.; Ferreira, R.F.; Schafer, D.; Alves, T.J.B.; Fortunato, J.; Ivashita, F.F. Application of the modified Rayleigh model in the mathematical analysis of Alnico II minor loops. Phys. B Condens. Matter 2021, 612, 412629. [Google Scholar] [CrossRef]
- Néel, L. Théorie des lois d’aimantation de Lord Rayleigh et les déplacements d’une paroi isolée. Cah. De Phys. 1942, 12, 1–20. [Google Scholar]
- Néel, L. Some theoretical aspects of rock-magnetism. Adv. Phys. 1955, 4, 191–243. [Google Scholar] [CrossRef]
- Nakamura, K.; Saito, K.; Watanabe, T.; Ichinokura, O. A new nonlinear magnetic circuit model for dynamic analysis of interior permanent magnet synchronous motor. J. Magn. Magn. Mater. 2005, 290-291, 1313–1317. [Google Scholar] [CrossRef]
- Peterson, E. Harmonic production in ferromagnetic materials at low frequencies and low flux densities. Bell Syst. Tech. J. 1928, 7, 762–796. [Google Scholar] [CrossRef]
- Michaelides, A.; Simkin, J.; Kirby, P.; Riley, C. Permanent magnet (de-)magnetization and soft iron hysteresis effects: A comparison of FE analysis techniques. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2010, 29, 1090–1096. [Google Scholar] [CrossRef]
- Zhilichev, Y.; Campbell, P.; Miller, D. In situ magnetization of isotropic permanent magnets. IEEE Trans. Magn. 2002, 38, 2988–2990. [Google Scholar] [CrossRef]
- Ruoho, S. A mathematical method to describe recoil behavior of Nd-Fe-B-material. In Proceedings of the Seminar on Advanced Magnetic Materials and Their Applications 2007, Pori, Finland, 10–11 October 2007. [Google Scholar]
- Ossart, F.; Meunier, G. Comparison between various hysteresis models and experimental data. IEEE Trans. Magn. 1990, 26, 2837–2839. [Google Scholar] [CrossRef]
- Roberts, A.P.; Pike, C.R.; Verosub, K.L. First-order reversal curve diagrams: A new tool for characterizing the magnetic properties of natural samples. J. Geophys. Res. Solid Earth 2000, 105, 28461–28475. [Google Scholar] [CrossRef]
- Carvallo, C.; Dunlop, D.J.; Özdemir, Ö. Experimental comparison of FORC and remanent Preisach diagrams. Geophys. J. Int. 2005, 162, 747–754. [Google Scholar] [CrossRef]
- Cao, Y.; Xu, K.; Jiang, W.; Droubay, T.; Ramuhalli, P.; Edwards, D.; Johnson, B.R.; McCloy, J. Hysteresis in single and polycrystalline iron thin films: Major and minor loops, first order reversal curves, and Preisach modeling. J. Magn. Magn. Mater. 2015, 395, 361–375. [Google Scholar] [CrossRef]
- Poljak, M.; Kolibas, N. Computation of current transformer transient performance. IEEE Trans. Power Deliv. 1988, 3, 1816–1822. [Google Scholar] [CrossRef]
- Santesmases, J.G.; Ayala, J.; Cachero, A.H. Analytical approximation of dynamic hysteresis loop and its application to a series ferroresonant circuit. Proc. Inst. Electr. Eng. 1970, 117, 234–240. [Google Scholar] [CrossRef]
- De Leon, F.; Semlyen, A. A simple representation of dynamic hysteresis losses in power transformers. IEEE Trans. Power Deliv. 1995, 10, 315–321. [Google Scholar] [CrossRef]
- Greene, J.D.; Gross, C.A. Nonlinear modeling of transformers. IEEE Trans. Ind. Appl. 1988, 24, 434–438. [Google Scholar] [CrossRef]
- Prusty, S.; Rao, M. A novel approach for predetermination of magnetization characteristics of transformers including hysteresis. IEEE Trans. Magn. 1984, 20, 607–612. [Google Scholar] [CrossRef]
- Lucas, J.R.; McLaren, P.G. B-H Loop Representation for Transient Studies. Int. J. Electr. Eng. Educ. 1991, 28, 261–270. [Google Scholar] [CrossRef]
- Lucas, J.R. Representation of Magnetisation Curves over a Wide Region Using a Non-Integer Power Series. Int. J. Electr. Eng. Educ. 1988, 25, 335–340. [Google Scholar] [CrossRef]
- Mayergoyz, I.D.; Abdel-Kader, F.M.; Emad, F.P. On penetration of electromagnetic fields into nonlinear conducting ferromagnetic media. J. Appl. Phys. 1984, 55, 618–629. [Google Scholar] [CrossRef]
- Mayergoyz, I.D. Mathematical models of hysteresis. IEEE Trans. Magn. 1986, 22, 603–608. [Google Scholar] [CrossRef]
- Widger, G. Representation of magnetisation curves over extensive range by rational-fraction approximations. Proc. Inst. Electr. Eng. 1969, 116, 156–160. [Google Scholar] [CrossRef]
- Ruoho, S.; Dlala, E.; Arkkio, A. Comparison of Demagnetization Models for Finite-Element Analysis of Permanent-Magnet Synchronous Machines. IEEE Trans. Magn. 2007, 43, 3964–3968. [Google Scholar] [CrossRef]
- Ruoho, S.; Arkkio, A. Partial Demagnetization of Permanent Magnets in Electrical Machines Caused by an Inclined Field. IEEE Trans. Magn. 2008, 44, 1773–1778. [Google Scholar] [CrossRef]
- Mazgaj, W.; Sierzega, M.; Szular, Z. Approximation of Hysteresis Changes in Electrical Steel Sheets. Energies 2021, 14, 4110. [Google Scholar] [CrossRef]
- Gonda, P.; Marcely, P.; Macko, J.; Pavlovič, M. Computerized evaluation of magnetic properties. J. Magn. Magn. Mater. 1984, 41, 241–243. [Google Scholar] [CrossRef]
- Šigut, Z.; Zemčík, T. Hysteresis loop analytical approximation. J. Magn. Magn. Mater. 1988, 73, 193–198. [Google Scholar] [CrossRef]
- Brauer, J. Simple equations for the magnetization and reluctivity curves of steel. IEEE Trans. Magn. 1975, 11, 81. [Google Scholar] [CrossRef]
- El-Sherbiny, M. Representation of the magnetization characteristic by a sum of exponentials. IEEE Trans. Magn. 1973, 9, 60–61. [Google Scholar] [CrossRef]
- MacFadyen, W.; Simpson, R.; Slater, R.; Wood, W. Representation of magnetisation curves by exponential series. Proc. Inst. Electr. Eng. 1973, 120, 902–904. [Google Scholar] [CrossRef]
- Coulson, M.A.; Slater, R.D.; Simpson, R.R.S. Representation of magnetic characteristic, including hysteresis, using Preisach’s theory. Proc. Inst. Electr. Eng. 1977, 124, 895–898. [Google Scholar] [CrossRef]
- Takács, J. Approximations for Brillouin and its reverse function. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2016, 35, 2095–2099. [Google Scholar] [CrossRef]
- Gans, R. Die reversible Permeabilität auf der idealen Magnetisierungskurve. Ann. Der Phys. 1920, 366, 379–395. [Google Scholar] [CrossRef]
- Szpunar, B.; Atherton, D.; Schonbachler, M. An extended Preisach model for hysteresis processes. IEEE Trans. Magn. 1987, 23, 3199–3201. [Google Scholar] [CrossRef]
- Szpunar, J.; Atherton, D.; Szpunar, B. Analysis of the irreversible processes of magnetization in steel. IEEE Trans. Magn. 1987, 23, 300–304. [Google Scholar] [CrossRef]
- Harrison, R.G. A physical model of spin ferromagnetism. IEEE Trans. Magn. 2003, 39, 950–960. [Google Scholar] [CrossRef]
- Harrison, R.G. Physical Theory of Ferromagnetic First-Order Return Curves. IEEE Trans. Magn. 2009, 45, 1922–1939. [Google Scholar] [CrossRef]
- Henrotte, F.; Hameyer, K. A dynamical vector hysteresis model based on an energy approach. IEEE Trans. Magn. 2006, 42, 899–902. [Google Scholar] [CrossRef]
- Henrotte, F.; Nicolet, A.; Hameyer, K. An energy-based vector hysteresis model for ferromagnetic materials. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2006, 25, 71–80. [Google Scholar] [CrossRef]
- Chwastek, K.; Baghel, A.P.S.; Ram, B.S.; Borowik, B.; Daniel, L.; Kulkarni, S.V. On some approaches to model reversible magnetization processes. J. Phys. D Appl. Phys. 2018, 51, 145003. [Google Scholar] [CrossRef]
- DośpiaŁ, M.; Nabiałek, M.; Szota, M.; Pietrusiewicz, P.; Gruszka, K.; Błoch, K. Modeling the Hysteresis Loop in Hard Magnetic Materials Using T(x) Model. Acta Phys. Pol. Ser. A 2014, 126, 170–171. [Google Scholar] [CrossRef]
- Nova, I.; Havlicek, V.; Zemanek, I. Dynamic Hysteresis Loops Modeling by Means of Extended Hyperbolic Model. IEEE Trans. Magn. 2013, 49, 148–151. [Google Scholar] [CrossRef]
- Fuzi, J. Analytical approximation of Preisach distribution functions. IEEE Trans. Magn. 2003, 39, 1357–1360. [Google Scholar] [CrossRef]
- Zhou, P.; Lin, D.; Xiao, Y.; Lambert, N.; Rahman, M.A. Temperature-Dependent Demagnetization Model of Permanent Magnets for Finite Element Analysis. IEEE Trans. Magn. 2012, 48, 1031. [Google Scholar] [CrossRef]
- Wilhelm, J.; Renhart, W. Exploiting the T(x) function in fast hysteresis models for transient circuit simulations. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2019, 38, 1427–1440. [Google Scholar] [CrossRef]
- Bavendiek, G.; Müller, F.; Steentjes, S.; Hameyer, K. Modeling of history-dependent magnetization in the finite element method on the example of a postassembly rotor magnetizer. Int. J. Numer. Model. Electron. Netw. Devices Fields 2020, 33, e2674. [Google Scholar] [CrossRef]
- Bullingham, J.; Bernal, M. Investigation of the effect of nonlinear B/H loops on the calculation of eddy-current losses. Proc. Inst. Electr. Eng. 1967, 114, 1174–1176. [Google Scholar] [CrossRef]
- Varga, L.; Kovács, G.; Takács, J. Modeling the overlapping, simultaneous magnetization processes in ultrasoft nanocrystalline alloys. J. Magn. Magn. Mater. 2008, 320, L26–L29. [Google Scholar] [CrossRef]
- Varga, L.; Kovac, J. Minor Loop Scaling Rules for Finemet Type Soft Magnetic Cores. Acta Phys. Pol. A 2014, 126, 156–157. [Google Scholar] [CrossRef]
- Sokalski, K. An Approach to Modeling and Scaling of Hysteresis in Soft Magnetic Materials. I Magnetization Curve. Acta Phys. Pol. A 2015, 127. [Google Scholar] [CrossRef]
- Karlqvist, O. Calculation of the magnetic field in the ferromagnetic layer of a magnetic drum. KTH Trans. R. Inst. Technol. 1954. [Google Scholar]
- Middleton, F.H. Analytic Hysteresis Function. J. Appl. Phys. 1961, 32, S251–S252. [Google Scholar] [CrossRef]
- Perez-Rojas, C. Fitting saturation and hysteresis via arctangent functions. IEEE Power Eng. Rev. 2000, 20, 55–57. [Google Scholar] [CrossRef]
- Wilson, P.; Ross, J.; Brown, A.; Kazmierski, T.; Baranowski, J. Efficient mixed-domain behavioural modelling of ferromagnetic hysteresis implemented in VHDL-AMS. In Proceedings of the Design, Automation and Test in Europe Conference and Exhibition, Paris, France, 16–20 February 2004; Volume 1, pp. 742–743. [Google Scholar] [CrossRef]
- Petrescu, L.; Cazacu, E.; Petrescu, C. Sigmoid functions used in hysteresis phenomenon modeling. In Proceedings of the 2015 9th International Symposium on Advanced Topics in Electrical Engineering (ATEE), Bucharest, Romania, 7–9 May 2015; pp. 521–524. [Google Scholar] [CrossRef]
- Jesenik, M.; Mernik, M.; Trlep, M. Determination of a Hysteresis Model Parameters with the Use of Different Evolutionary Methods for an Innovative Hysteresis Model. Mathematics 2020, 8, 201. [Google Scholar] [CrossRef]
- Sari, Z.; Ivanyi, A. Statistical approach of hysteresis. Phys. B Condens. Matter 2006, 372, 45–48. [Google Scholar] [CrossRef]
- Basso, V.; Berlotti, G.; Infortuna, A.; Pasquale, M. Preisach model study of the connection between magnetic and microstructural properties of soft magnetic materials. IEEE Trans. Magn. 1995, 31, 4000–4005. [Google Scholar] [CrossRef]
- Azzerboni, B.; Cardelli, E.; Della Torre, E.; Finocchio, G. Reversible magnetization and Lorentzian function approximation. J. Appl. Phys. 2003, 93, 6635–6637. [Google Scholar] [CrossRef]
- Dupré, L.R.; Van Keer, R.; Melkebeek, J.A.A. Identification of the relation between the material parameters in the Preisach model and in the Jiles–Atherton hysteresis model. J. Appl. Phys. 1999, 85, 4376–4378. [Google Scholar] [CrossRef]
- de Wulf, M.; Vandevelde, L.; Maes, J.; Dupre, L.; Melkebeek, J. Computation of the Preisach distribution function based on a measured Everett map. IEEE Trans. Magn. 2000, 36, 3141–3143. [Google Scholar] [CrossRef]
- Consolo, G.; Finocchio, G.; Carpentieri, M.; Cardelli, E.; Azzerboni, B. About identification of Scalar Preisach functions of soft magnetic materials. IEEE Trans. Magn. 2006, 42, 923–926. [Google Scholar] [CrossRef]
- Sutor, A.; Rupitsch, S.; Lerch, R. A Preisach-based hysteresis model for magnetic and ferroelectric hysteresis. Appl. Phys. A 2010, 100, 425–430. [Google Scholar] [CrossRef]
- J. Eichler, M.N.; Kosek, M. Experimental Determination of the Preisach Model for Grain Oriented Steel. In Proceedings of the 13th Symposium of Magnetic Measurements and Modeling (SMMM’2018), Wieliczka, Poland, 8–10 October 2018; Volume 136. [Google Scholar] [CrossRef]
- Stancu, A.; Stoleriu, L.; Postolache, P.; Tanasa, R. New Preisach model for structured particulate ferromagnetic media. J. Magn. Magn. Mater. 2005, 290-291, 490–493. [Google Scholar] [CrossRef]
- Vajda, F.; Della Torre, E. Measurements of output-dependent Preisach functions. IEEE Trans. Magn. 1991, 27, 4757–4762. [Google Scholar] [CrossRef]
- Henze, O.; Rucker, W.M. Identification procedures of Preisach model. IEEE Trans. Magn. 2002, 38, 833–836. [Google Scholar] [CrossRef]
- Pruksanubal, P.; Binner, A.; Gonschorek, K.H. Determination of distribution functions and parameters for the Preisach hysteresis model. In Proceedings of the 2006 17th International Zurich Symposium on Electromagnetic Compatibility, Singapore, 27 February–3 March 2006; pp. 258–261. [Google Scholar] [CrossRef]
- Zeinali, R.; Krop, D.C.J.; Lomonova, E.; Ertan, H.B. Improved Preisach Model for Modelling Magnetic Hysteresis Effect in Non-Oriented Steels. In Proceedings of the 2018 XIII International Conference on Electrical Machines (ICEM), Alexandroupoli, Greece, 3–6 September 2018; pp. 1031–1036. [Google Scholar] [CrossRef]
- Wallace, J.L. Real-time fast-Fourier-transform analysis of M-H hysteresis loops. J. Appl. Phys. 1993, 73, 6849–6851. [Google Scholar] [CrossRef]
- Thompson, S.P. On Hysteresis Loops and Lissajous’ Figures, and on the Energy wasted in a Hysteresis Loop. Proc. Phys. Soc. Lond. 1909, 22, 454–476. [Google Scholar] [CrossRef]
- Udpa, S.; Lord, W. A Fourier descriptor model of hysteresis loop phenomena. IEEE Trans. Magn. 1985, 21, 2370–2373. [Google Scholar] [CrossRef]
- Mohammed, I.A.; Al-Hashemy, B.A.R.; Tawfik, M.A. A Fourier descriptor model of hysteresis loops for sinusoidal and distorted waveforms. IEEE Trans. Magn. 1997, 33, 686–691. [Google Scholar] [CrossRef]
- Davis, N. Derivation and application of an equation to the B-H loop. J. Phys. D Appl. Phys. 1971, 4, 1034–1039. [Google Scholar] [CrossRef]
- Willcock, S.; Tanner, B. Harmonic analysis of B-H loops of constructional steel. IEEE Trans. Magn. 1983, 19, 2145–2147. [Google Scholar] [CrossRef]
- Willcock, S.; Tanner, B. Harmonic analysis of B-H loops. IEEE Trans. Magn. 1983, 19, 2265–2270. [Google Scholar] [CrossRef]
- Josephs, R.; Crompton, D.; Krafft, C. Characterization of magnetic oxide recording media using fourier analysis of static hysteresis loops. IEEE Trans. Magn. 1986, 22, 653–655. [Google Scholar] [CrossRef]
- Yamada, S.; Bessho, K.; Lu, J. Harmonic balance finite element method applied to nonlinear AC magnetic analysis. IEEE Trans. Magn. 1989, 25, 2971–2973. [Google Scholar] [CrossRef]
- Yamada, S.; Biringer, P.; Bessho, K. Calculation of nonlinear eddy-current problems by the harmonic balance finite element method. IEEE Trans. Magn. 1991, 27, 4122–4125. [Google Scholar] [CrossRef]
- Rupanagunta, P.; Hsu, J.; Weldon, W. Determination of iron core losses under influence of third-harmonic flux component. IEEE Trans. Magn. 1991, 27, 768–777. [Google Scholar] [CrossRef]
- Abuelman’atti, M. Modeling of magnetization curves for computer-aided design. IEEE Trans. Magn. 1993, 29, 1235–1239. [Google Scholar] [CrossRef]
- Goev, G.; Masheva, V.; Mikhov, M. Fourier analysis of AC hysteresis loops. IEEE Trans. Magn. 2003, 39, 1993–1996. [Google Scholar] [CrossRef]
- Takács, J. Fourier analysis of hysteretic distortions. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2003, 22, 273–284. [Google Scholar] [CrossRef]
- Takács, J. Laplace transform of waveforms with hysteretic distortion. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2004, 23, 305–315. [Google Scholar] [CrossRef]
- Kuhnen, K. Modeling, Identification and Compensation of Complex Hysteretic Nonlinearities: A Modified Prandtl-Ishlinskii Approach. Eur. J. Control. 2003, 9, 407–418. [Google Scholar] [CrossRef]
- Harrison, R.G. Positive-Feedback Theory of Hysteretic Recoil Loops in Hard Ferromagnetic Materials. IEEE Trans. Magn. 2011, 47, 175–191. [Google Scholar] [CrossRef]
- Pierce, M.S.; Buechler, C.R.; Sorensen, L.B.; Kevan, S.D.; Jagla, E.A.; Deutsch, J.M.; Mai, T.; Narayan, O.; Davies, J.E.; Liu, K.; et al. Disorder-induced magnetic memory: Experiments and theories. Phys. Rev. B 2007, 75, 144406. [Google Scholar] [CrossRef]
- Astorino, A.; Swaminathan, M.; Antonini, G. A New Approach for Magneto-Static Hysteresis Behavioral Modeling. IEEE Trans. Magn. 2016, 52. [Google Scholar] [CrossRef]
- Farrokh, M.; Dizaji, M.S.; Dizaji, F.S.; Moradinasab, N. Universal Hysteresis Identification Using Extended Preisach Neural Network. arXiv 2019, arXiv:2001.01559. [Google Scholar]
- Cao, K.; Li, R. Modeling of Rate-Independent and Symmetric Hysteresis Based on Madelung’s Rules. Sensors 2019, 19, 352. [Google Scholar] [CrossRef] [PubMed]
- Brokate, M.; Sprekels, J. Hysteresis and Phase Transitions, 1st ed.; Springer: New York, NY, USA, 1996. [Google Scholar] [CrossRef]
- Prandtl, L. Ein Gedankenmodell zur kinetischen Theorie der festen Körper. ZAMM J. Appl. Math. Mech. Z. Angew. Math. Mech. 1928, 8, 85–106. [Google Scholar] [CrossRef]
- Enderby, J.A. The domain model of hysteresis. Part 1.-Independent domains. Trans. Faraday Soc. 1955, 51, 835–848. [Google Scholar] [CrossRef]
- Everett, D.H. A general approach to hysteresis. Part 4. An alternative formulation of the domain model. Trans. Faraday Soc. 1955, 51, 1551–1557. [Google Scholar] [CrossRef]
- Egorov, D.; Petrov, I.; Pyrhönen, J.; Link, J.; Stern, R. Hysteresis Loss in Ferrite Permanent Magnets in Rotating Electrical Machinery. IEEE Trans. Ind. Electron. 2018, 65, 9280–9290. [Google Scholar] [CrossRef]
- Preisach, F. Über die magnetische Nachwirkung. Z. Für Phys. 1935, 94, 277–302. [Google Scholar] [CrossRef]
- Preisach, F. On the Magnetic Aftereffect. IEEE Trans. Magn. 2017, 53, 1–11. [Google Scholar] [CrossRef]
- Visintin, A. On the Preisach model for hysteresis. Nonlinear Anal. Theory Methods Appl. 1984, 8, 977–996. [Google Scholar] [CrossRef]
- Mayergoyz, I.D.; Adly, A.A.; Friedman, G. New Preisach-type models of hysteresis and their experimental testing. J. Appl. Phys. 1990, 67, 5373–5375. [Google Scholar] [CrossRef]
- Brokate, M. Some mathematical properties of the Preisach model for hysteresis. IEEE Trans. Magn. 1989, 25, 2922–2924. [Google Scholar] [CrossRef]
- Bertotti, G. Hysteresis in Magnetism; For Physicists, Materials Scientists, and Engineers; a volume in Electromagnetism, 1st ed.; Academic Press: Cambridge, MA, USA, 1998. [Google Scholar] [CrossRef]
- Bergqvist, A.; Engdahl, G. A phenomenological differential-relation-based vector hysteresis model. J. Appl. Phys. 1994, 75, 5484–5486. [Google Scholar] [CrossRef]
- Bobbio, S.; Milano, G.; Serpico, C.; Visone, C. Models of magnetic hysteresis based on play and stop hysterons. IEEE Trans. Magn. 1997, 33, 4417. [Google Scholar] [CrossRef]
- Matsuo, T. Magnetic Hysteresis Represented by Play Model. In Motor Drive System and Magnetic Material; Fujisaki, K., Ed.; Springer: Singapore, 2019; pp. 191–202. [Google Scholar] [CrossRef]
- Matsuo, T.; Osaka, Y.; Shimasaki, M. Eddy-current analysis using vector hysteresis models with play and stop hysterons. IEEE Trans. Magn. 2000, 36, 1172–1177. [Google Scholar] [CrossRef]
- Matsuo, T.; Terada, Y.; Shimasaki, M. Stop Model With Input-Dependent Shape Function and Its Identification Methods. IEEE Trans. Magn. 2004, 40, 1776–1783. [Google Scholar] [CrossRef]
- Jiang, C.; Deng, M.; Inoue, A. Operator based robust control for nonlinear systems with hysteresis. In Proceedings of the SICE Annual Conference 2007, Takamatsu, Japan, 17–20 September 2007; pp. 2292–2295. [Google Scholar] [CrossRef]
- Deng, M.; Jiang, C.; Inoue, A.; Su, C.Y. Operator-based robust control for nonlinear systems with Prandtl–Ishlinskii hysteresis. Int. J. Syst. Sci. 2011, 42, 643–652. [Google Scholar] [CrossRef]
- Bergqvist, A.; Lundgren, A.; Engdahl, G. Experimental testing of an anisotropic vector hysteresis model. IEEE Trans. Magn. 1997, 33, 4152–4154. [Google Scholar] [CrossRef]
- Krejčí, P. On Maxwell equations with the Preisach hysteresis operator: The one-dimensional time-periodic case. Apl. Mat. 1989, 34, 364–374. [Google Scholar] [CrossRef]
- Krejčí, P.; Lovicar, V. Continuity of hysteresis operators in Sobolev spaces. Apl. Mat. 1990, 35, 60–66. [Google Scholar] [CrossRef]
- Visone, C. Hysteresis modelling and compensation for smart sensors and actuators. J. Phys. Conf. Ser. 2008, 138, 012028. [Google Scholar] [CrossRef]
- Al-Janaideh, M.; Visone, C.; Davino, D.; Krejčí, P. The generalized Prandtl-Ishlinskii model: Relation with the preisach nonlinearity and inverse compensation error. In Proceedings of the 2014 American Control Conference, Portland, OR, USA, 4–6 June 2014; pp. 4759–4764. [Google Scholar] [CrossRef]
- Al-Janaideh, M.; Davino, D.; Krejčí, P.; Visone, C. Comparison of Prandtl–Ishlinskii and Preisach modeling for smart devices applications. Phys. B Condens. Matter 2016, 486, 155–159. [Google Scholar] [CrossRef]
- Nierla, M.; Loeffler, M.; Kaltenbacher, M.; Rupitsch, S.J. Comparison of different vector Preisach models for the simulation of ferromagnetic materials. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2019, 38, 1696–1710. [Google Scholar] [CrossRef]
- Everett, D.H. A general approach to hysteresis. Part 3. A formal treatment of the independent domain model of hysteresis. Trans. Faraday Soc. 1954, 50, 1077–1096. [Google Scholar] [CrossRef]
- Pescetti, D. Some remarks on Preisach modeling. J. Appl. Phys. 1991, 69, 4605. [Google Scholar] [CrossRef]
- Everett, D.H.; Whitton, W.I.A. A general apporach to hysteresis. Trans. Faraday Soc. 1952, 48, 749–757. [Google Scholar] [CrossRef]
- Del Vecchio, R. An efficient procedure for modeling complex hysteresis processes in ferromagnetic materials. IEEE Trans. Magn. 1980, 16, 809–811. [Google Scholar] [CrossRef]
- Park, G.-S.; Hahn, S.-Y.; Lee, K.-S.; Jung, H.-K. Implementation of hysteresis characteristics using the Preisach model with M-B variables. IEEE Trans. Magn. 1993, 29, 1542–1545. [Google Scholar] [CrossRef]
- Stenzel, J.; Weber, T. Model representing the nonlinear behaviour of three-phase transformers. Arch. Elektrotech. 1994, 77, 143–150. [Google Scholar] [CrossRef]
- Enderby, J.A. The domain model of hysteresis. Part 2.—Interacting domains. Trans. Faraday Soc. 1956, 52, 106–120. [Google Scholar] [CrossRef]
- Mörée, G.; Leijon, M. Review of Play and Preisach Models for Hysteresis in Magnetic Materials. Materials 2023, 16, 2422. [Google Scholar] [CrossRef] [PubMed]
- Pescetti, D. Hysteresis Modelling. J. Phys. Colloq. 1988, 49, C8–1923–C8–1924. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Ueda, F.; Yamamoto, E. Simulation of Hysteresis Characteristics of Core Materials Using the Everett Function. IEEE Transl. J. Magn. Jpn. 1989, 4, 353–359. [Google Scholar] [CrossRef]
- Sjöström, M. Differentiation and power loss computation of classical Preisach model. Phys. B Condens. Matter 2004, 343, 96–100. [Google Scholar] [CrossRef]
- Atherton, D.; Szpunar, B.; Szpunar, J. A new approach to Preisach diagrams. IEEE Trans. Magn. 1987, 23, 1856–1865. [Google Scholar] [CrossRef]
- Parker, S.; Faunce, C.; Grundy, P.; Maylin, M.; Ludlow, J.; Lane, R. Preisach modelling of magnetisation changes in steel. J. Magn. Magn. Mater. 1995, 145, 51–56. [Google Scholar] [CrossRef]
- Stoleriu, L.; Stancu, A. Using Experimental FORC Distribution as Input for a Preisach-Type Model. IEEE Trans. Magn. 2006, 42, 3159–3161. [Google Scholar] [CrossRef]
- Finocchio, G.; Carpentieri, M.; Cardelli, E.; Azzerboni, B. Analytical solution of Everett integral using Lorentzian Preisach function approximation. J. Magn. Magn. Mater. 2006, 300, 451–470. [Google Scholar] [CrossRef]
- Włodarski, Z. Modeling hysteresis by analytical reversal curves. Phys. B Condens. Matter 2007, 398, 159–163. [Google Scholar] [CrossRef]
- Renhart, W.; Bíró, O.; Magele, C.; Preis, K.; Rabel, A. Inrush current computations using an optimised analytical hysteresis model. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2017, 36, 1568–1576. [Google Scholar] [CrossRef]
- Hejda, P.; Zelinka, T. Modelling of hysteresis processes in magnetic rock samples using the Preisach diagram. Phys. Earth Planet. Inter. 1990, 63, 32–40. [Google Scholar] [CrossRef]
- Pike, C.R.; Roberts, A.P.; Verosub, K.L. Characterizing interactions in fine magnetic particle systems using first order reversal curves. J. Appl. Phys. 1999, 85, 6660–6667. [Google Scholar] [CrossRef]
- Pike, C.R. First-order reversal-curve diagrams and reversible magnetization. Phys. Rev. B 2003, 68, 104424. [Google Scholar] [CrossRef]
- Newell, A.J. A high-precision model of first-order reversal curve (FORC) functions for single-domain ferromagnets with uniaxial anisotropy. Geochem. Geophys. Geosyst. 2005, 6, Q05010. [Google Scholar] [CrossRef]
- Zeinali, R.; Krop, D.C.J.; Lomonova, E.A. Comparison of Preisach and Congruency-Based Static Hysteresis Models Applied to Non-Oriented Steels. IEEE Trans. Magn. 2020, 56, 1–4. [Google Scholar] [CrossRef]
- Krejci, P.; Kuhnen, K. Inverse control of systems with hysteresis and creep. IEE Proc. Control Theory Appl. 2001, 148, 185–192. [Google Scholar] [CrossRef]
- Al-Janaideh, M.; Rakotondrabe, M.; Al-Janaideh, O. Further Results on Hysteresis Compensation of Smart Micropositioning Systems With the Inverse Prandtl–Ishlinskii Compensator. IEEE Trans. Control. Syst. Technol. 2016, 24, 428–439. [Google Scholar] [CrossRef]
- Thompson, P.J.; Street, R. Viscosity, reptation and tilting effects in permanent magnets. J. Phys. D Appl. Phys. 1997, 30, 1273–1284. [Google Scholar] [CrossRef]
- Bottoni, G. The reptation of the magnetization cycles in particulate recording media. J. Magn. Magn. Mater. 1991, 95, 14–16. [Google Scholar] [CrossRef]
- Winter, C. Effect of fine-particle interactions on minor loops: Magnetic flip-flop. IEEE Trans. Magn. 1982, 18, 1586–1588. [Google Scholar] [CrossRef]
- Thompson, P.J.; Street, R. Reptation and magnetic viscosity effects in a permanent magnet. J. Phys. D Appl. Phys. 1996, 29, 2789–2795. [Google Scholar] [CrossRef]
- Benda, O. Possibilities and limits of the Preisach model. J. Magn. Magn. Mater. 1992, 112, 443–446. [Google Scholar] [CrossRef]
- Hauser, H.; Melikhov, Y.; Jiles, D.C. Examination of the Equivalence of Ferromagnetic Hysteresis Models Describing the Dependence of Magnetization on Magnetic Field and Stress. IEEE Trans. Magn. 2009, 45, 1940–1949. [Google Scholar] [CrossRef]
- Mayergoyz, I.D. The classical Preisach model of hysteresis and reversibility. J. Appl. Phys. 1991, 69, 4602. [Google Scholar] [CrossRef]
- Carnevale, D.; Nicosia, S.; Zaccarian, L. A Differential Hysteresis Model. IFAC Proc. Vol. 2005, 38, 301–306. [Google Scholar] [CrossRef]
- Stancu, A.; Andrei, P.; Stoleriu, L. Magnetic characterization of samples using first- and second-order reversal curve diagrams. J. Appl. Phys. 2006, 99, 08D702. [Google Scholar] [CrossRef]
- Della Torre, E. Effect of interaction on the magnetization of single-domain particles. IEEE Trans. Audio Electroacoust. 1966, 14, 86–92. [Google Scholar] [CrossRef]
- Della Torre, E.; Kadar, G. Hysteresis modeling: II. Accommodation. IEEE Trans. Magn. 1987, 23, 2823–2825. [Google Scholar] [CrossRef]
- Della Torre, E. Existence of magnetization-dependent Preisach models. IEEE Trans. Magn. 1991, 27, 3697–3699. [Google Scholar] [CrossRef]
- Mayergoyz, I.D.; Friedman, G. Generalized Preisach model of hysteresis. IEEE Trans. Magn. 1988, 24, 212–217. [Google Scholar] [CrossRef]
- Mayergoyz, I. Dynamic Preisach models of hysteresis. IEEE Trans. Magn. 1988, 24, 2925–2927. [Google Scholar] [CrossRef]
- Ben Mrad, R.; Hu, H. Dynamic modeling of hysteresis in piezoceramics. In Proceedings of the 2001 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (Cat. No.01TH8556), Como, Italy, 8–12 July 2001; Volume 1, pp. 510–515. [Google Scholar] [CrossRef]
- Ben Mrad, R.; Hu, H. A model for voltage-to-displacement dynamics in piezoceramic actuators subject to dynamic-voltage excitations. IEEE/ASME Trans. Mechatron. 2002, 7, 479–489. [Google Scholar] [CrossRef]
- Kadar, G.; Torre, E. Hysteresis modeling: I. Non-congruency. IEEE Trans. Magn. 1987, 23, 2820–2822. [Google Scholar] [CrossRef]
- Vajda, F.; Della Torre, E. Relationship between the moving and the product Preisach models. IEEE Trans. Magn. 1991, 27, 3823–3826. [Google Scholar] [CrossRef]
- Kádár, G. On the product Preisach model of hysteresis. Phys. B Condens. Matter 2000, 275, 40–44. [Google Scholar] [CrossRef]
- Wiesen, K.; Charap, S.H. A better scalar Preisach algorithm. IEEE Trans. Magn. 1988, 24, 2491–2493. [Google Scholar] [CrossRef]
- Basso, V.; Bertotti, G. Hysteresis models for the description of domain wall motion. IEEE Trans. Magn. 1996, 32, 4210–4212. [Google Scholar] [CrossRef]
- Basso, V. Hysteresis models for magnetization by domain wall motion. IEEE Trans. Magn. 1998, 34, 2207–2212. [Google Scholar] [CrossRef]
- Takahashi, N.; Miyabara, S.H.; Fujiwara, K. Problems in practical finite element analysis using Preisach hysteresis model. IEEE Trans. Magn. 1999, 35, 1243–1246. [Google Scholar] [CrossRef]
- Dlala, E.; Saitz, J.; Arkkio, A. Inverted and Forward Preisach Models for Numerical Analysis of Electromagnetic Field Problems. IEEE Trans. Magn. 2006, 42, 1963–1973. [Google Scholar] [CrossRef]
- Bernard, Y.; Mendes, E.; Santandrea, L.; Bouillault, F. Inverse Preisach model in finite elements modelling. Eur. Phys. J. AP 2000, 12, 117–121. [Google Scholar] [CrossRef]
- Harrison, R.G. Modeling High-Order Ferromagnetic Hysteretic Minor Loops and Spirals Using a Generalized Positive-Feedback Theory. IEEE Trans. Magn. 2012, 48, 1115–1129. [Google Scholar] [CrossRef]
- Nishimoto, K.; Nagao, M.; Suganuma, Y.; Tanaka, H. Computer simulation of high-density multiple transitions in magnetic disc recording. IEEE Trans. Magn. 1974, 10, 769–772. [Google Scholar] [CrossRef]
- Cortial, F.; Ossart, F.; Albertini, J.B.; Aid, M. An improved analytical hysteresis model and its implementation in magnetic recording modeling by the finite element method. IEEE Trans. Magn. 1997, 33, 1592–1595. [Google Scholar] [CrossRef]
- Lee, C.; Miyata, K.; Kaido, C.; Matsuo, T. Phenomenological Hysteresis Modeling Based on Asymmetric Transition Probability of Magnetization. IEEE Trans. Magn. 2014, 50, 1–4. [Google Scholar] [CrossRef]
- Morita, T.; Ishii, Y.; Fukai, I. Hysteresis model using distribution of susceptibility. J. Appl. Phys. 1993, 73, 7025–7029. [Google Scholar] [CrossRef]
- Gans, R. Magnetisch korrespondierende Zustände. Phys. Z. 1910, 11, 988–991. [Google Scholar]
- Takahashi, S.; Kobayashi, S.; Shishido, T. A scaling power-law relation in magnetic minor hysteresis loops in Fe and Ni metals. J. Phys. Condens. Matter 2007, 20, 035217. [Google Scholar] [CrossRef]
- Takahashi, S.; Kobayashi, S.; Kamada, Y.; Shishido, T. Similarity rules of magnetic minor hysteresis loops in Fe and Ni metals. J. Magn. Magn. Mater. 2008, 320, 2056–2061. [Google Scholar] [CrossRef]
- Zeinali, R.; Krop, D.; Lomonova, E. Weight-Function Identification for the Preisach Model of Laminated Steels Using Concentric Hysteresis Loops. In ELECTRIMACS 2019. Lecture Notes in Electrical Engineering; Springer: Cham, Switzerland, 2020; Volume 697, pp. 389–397. [Google Scholar] [CrossRef]
- Hamimid, M.; Mimoune, S.; Feliachi, M.; Atallah, K. Non centered minor hysteresis loops evaluation based on exponential parameters transforms of the modified inverse Jiles–Atherton model. Phys. B Condens. Matter 2014, 451, 16–19. [Google Scholar] [CrossRef]
- Jiles, D. A Self Consistent Generalized Model for the Calculation of Minor Loop Excursions in Theory of Hysteresis. IEEE Trans. Magn. 1992, 28, 2602–2604. [Google Scholar] [CrossRef]
- Carpenter, K.H. A differential equation approach to minor loops in the Jiles–Atherton hysteresis model. IEEE Trans. Magn. 1991, 27, 4404–4406. [Google Scholar] [CrossRef]
- Leite, J.V.; Benabou, A.; Sadowski, N.E.D. Accurate minor loops calculation with a modified Jiles-Atherton hysteresis model. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2009, 28, 741–749. [Google Scholar] [CrossRef]
- Mohan Unniachanparambil, G.; Kulkarni, S.V. Use of a scaling power law to incorporate asymmetrical minor loops in the inverse Jiles–Atherton model. IET Electr. Power Appl. 2019, 13, 2090–2095. [Google Scholar] [CrossRef]
- Pasquale, M.; Basso, V.; Bertotti, G.; Jiles, D.C.; Bi, Y. Domain-wall motion in random potential and hysteresis modeling. J. Appl. Phys. 1998, 83, 6497–6499. [Google Scholar] [CrossRef]
- Pasquale, M.; Bertotti, G.; Jiles, D.C.; Bi, Y. Application of the Preisach and Jiles–Atherton models to the simulation of hysteresis in soft magnetic alloys. J. Appl. Phys. 1999, 85, 4373–4375. [Google Scholar] [CrossRef]
- Philips, D.A.; Dupre, L.R.; Melkebeek, J.A. Comparison of Jiles and Preisach hysteresis models in magnetodynamics. IEEE Trans. Magn. 1995, 31, 3551–3553. [Google Scholar] [CrossRef]
- O’Kelly, D. Hysteresis and eddy-current losses in steel plates with nonlinear magnetisation characteristics. Proc. Inst. Electr. Eng. 1972, 119, 1675–1676. [Google Scholar] [CrossRef]
- Zaher, F. An analytical solution for the field of a hysteresis motor based on complex permeability. IEEE Trans. Energy Convers. 1990, 5, 156–163. [Google Scholar] [CrossRef]
- Tavakoli, H.; Bormann, D.; Ribbenfjärd, D.; Engdahl, G. Comparison of a simple and a detailed model of magnetic hysteresis with measurements on electrical steel. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2009, 28, 700–710. [Google Scholar] [CrossRef]
- Goodenough, J. Summary of losses in magnetic materials. IEEE Trans. Magn. 2002, 38, 3398–3408. [Google Scholar] [CrossRef]
- Arkadiew, W. Die Theorie des elektromagnetischen Feldes in ferromagnetischen Metallen und die Berechnungen von R. Gans. Ann. Der Phys. 1921, 370, 643–656. [Google Scholar] [CrossRef]
- Feldtkeller, R. Zur Theorie der Wirbelstrom-Anomalie. Freq. Z. Für Schwing.-Und Schwachstromtechnik 1949, 3, 229–237. [Google Scholar] [CrossRef]
- Latour, M. Note on Losses in Sheet Iron at Radio Frequencies. Proc. Inst. Radio Eng. 1919, 7, 61–71. [Google Scholar] [CrossRef]
- Hamilton, N.C. Ferrites: Magnetic and electric equivalent circuits and the complex permeability spectra. In Proceedings of the Active and Passive RF Devices Seminar, London, UK, 17 February 2016; pp. 1–8. [Google Scholar] [CrossRef]
- Lazan, B.J. Damping of Materials and Members in Structural Mechanics, 1st ed.; Pergamon Press: Oxford, UK, 1968. [Google Scholar]
- Chua, L.O.; Stromsmoe, K.A. Lumped-Circuit Models for Nonlinear Inductors Exhibiting Hysteresis Loops. IEEE Trans. Circuit Theory 1970, 17, 564–574. [Google Scholar] [CrossRef]
- Swift, G.W. Power Transformer Core Behavior Under Transient Conditions. IEEE Trans. Power Appar. Syst. 1971, PAS-90, 2206–2210. [Google Scholar] [CrossRef]
- Gu, G.; Zhu, L. High-speed tracking control of piezoelectric actuators using an ellipse-based hysteresis model. Rev. Sci. Instrum. 2010, 81, 085104. [Google Scholar] [CrossRef]
- Lin, D.; Zhou, P.; Fu, W.N.; Badics, Z.; Cendes, Z.J. A Dynamic Core Loss Model for Soft Ferromagnetic and Power Ferrite Materials in Transient Finite Element Analysis. IEEE Trans. Magn. 2004, 40, 1318–1321. [Google Scholar] [CrossRef]
- Nakamura, K.; Yamada, Y.; Ohinata, T.; Arimatsu, K.; Kojima, T.; Yamada, M.; Matsumoto, R.; Takiguchi, M.; Ichinokura, O. Iron Loss Calculation for Concentric-Winding Type Three-Phase Variable Inductor based on Reluctance Network Analysis. J. Magn. Soc. Jpn. 2016, 40, 67–70. [Google Scholar] [CrossRef]
- Chua, L.O.; Stromsmoe, K.A. Mathematical model for dynamic hysteresis loops. Int. J. Eng. Sci. 1971, 9, 435–450. [Google Scholar] [CrossRef]
- Chua, L.O.; Bass, S.C. A generalized hysteresis model. IEEE Trans. Circuit Theory 1972, 19, 36–48. [Google Scholar] [CrossRef]
- Saito, Y.; Fukushima, K.; Hayano, S.; Tsuya, N. Application of a Chua type model to the loss and skin effect calculations. IEEE Trans. Magn. 1987, 23, 2227–2229. [Google Scholar] [CrossRef]
- Saito, Y. Three-dimensional analysis of magnetodynamic fields in electromagnetic devices taken into account the dynamic hysteresis loops. IEEE Trans. Magn. 1982, 18, 546–551. [Google Scholar] [CrossRef]
- Saito, Y.; Saotome, H.; Hayano, S.; Yamamura, T. Modelling of nonlinear inductor exhibiting hysteresis loops and its application to the single phase parallel inverters. IEEE Trans. Magn. 1983, 19, 2189–2191. [Google Scholar] [CrossRef]
- Saito, Y.; Saotome, H.; Yamamura, T. A lumped circuit model for a nonlinear inductor exhibiting dynamic hysteresis loops and its application to the electric circuits. Comput. Methods Appl. Mech. Eng. 1983, 38, 185–202. [Google Scholar] [CrossRef]
- Yoon, H.; Kim, I.; Shin, P.S.; Koh, C.S. Finite Element Implementation Of A Generalized Chua-Type Vector Hysteresis model and application to iron loss analysis of three-phase transformer. In Proceedings of the Digests of the 2010 14th Biennial IEEE Conference on Electromagnetic Field Computation, Chicago, IL, USA, 9–12 May 2010. [Google Scholar] [CrossRef]
- Kawashima, T.; Enokizono, M. Magnetic field analysis of ferrite core by using Chua-type-model. IEEE Trans. Magn. 2003, 39, 1558–1561. [Google Scholar] [CrossRef]
- Malczyk, R.; Izydorczyk, J. The frequency-dependent Jiles–Atherton hysteresis model. Phys. B Condens. Matter 2015, 463, 68–75. [Google Scholar] [CrossRef]
- Santesmases, J.; Ayala, J.; Cachero, A. Analog simulation of a ferroresonant system including analysis of hysteresis loop. Math. Comput. Simul. 1967, 9, 76–80. [Google Scholar] [CrossRef]
- Charap, S. Magnetic hysteresis model. IEEE Trans. Magn. 1974, 10, 1091–1096. [Google Scholar] [CrossRef]
- Javora, R.; Iwahara, M.; Yamada, S. Effect of dynamic core losses on ferroresonance phenomena. J. Mater. Process. Technol. 2005, 161, 156–161. [Google Scholar] [CrossRef]
- Carpenter, K. Simple models for dynamic hysteresis which add frequency-dependent losses to static models. IEEE Trans. Magn. 1998, 34, 619–622. [Google Scholar] [CrossRef]
- Nitzan, D. Computation of flux switching in magnetic circuits. IEEE Trans. Magn. 1965, 1, 222–234. [Google Scholar] [CrossRef]
- Zirka, S.E.; Moroz, Y.I.; Marketos, P.; Moses, A.J. Viscosity-based magnetodynamic model of soft magnetic materials. IEEE Trans. Magn. 2006, 42, 2121–2132. [Google Scholar] [CrossRef]
- Zirka, S.E.; Moroz, Y.I.; Marketos, P.; Moses, A.J. A viscous-type dynamic hysteresis model as a tool for loss separation in conducting ferromagnetic laminations. IEEE Trans. Magn. 2005, 41, 1109–1111. [Google Scholar] [CrossRef]
- Zirka, S.; Moroz, Y.; Marketos, P.; Moses, A. Dynamic hysteresis modelling. Phys. B Condens. Matter 2004, 343, 90–95. [Google Scholar] [CrossRef]
- Street, R.; Woolley, J.C. A Study of Magnetic Viscosity. Proc. Phys. Soc. Sect. A 1949, 62, 562–572. [Google Scholar] [CrossRef]
- Givord, D.; Lienard, A.; Tenaud, P.; Viadieu, T. Magnetic viscosity in Nd-Fe-B sintered magnets. J. Magn. Magn. Mater. 1987, 67, L281–L285. [Google Scholar] [CrossRef]
- Chevalier, T.; Kedous-Lebouc, A.; Cornut, B.; Cester, C. A new dynamic hysteresis model for electrical steel sheet. Phys. B Condens. Matter 2000, 275, 197–201. [Google Scholar] [CrossRef]
- Steentjes, S.; Zirka, S.E.; Moroz, Y.E.; Moroz, E.Y.; Hameyer, K. Dynamic Magnetization Model of Nonoriented Steel Sheets. IEEE Trans. Magn. 2014, 50, 1–4. [Google Scholar] [CrossRef]
- Zirka, S.E.; Moroz, Y.I.; Chiesa, N.; Harrison, R.G.; Høidalen, H.K. Implementation of Inverse Hysteresis Model Into EMTP—Part II: Dynamic Model. IEEE Trans. Power Deliv. 2015, 30, 2233–2241. [Google Scholar] [CrossRef]
- Hamzehbahmani, H. Static hysteresis modeling for grain-oriented electrical steels based on the phenomenological concepts of energy loss mechanism. J. Appl. Phys. 2021, 130, 055102. [Google Scholar] [CrossRef]
- Bertotti, G. General properties of power losses in soft ferromagnetic materials. IEEE Trans. Magn. 1988, 24, 621–630. [Google Scholar] [CrossRef]
- Steentjes, S.; Boehmer, S.; Hameyer, K. Permanent Magnet Eddy-Current Losses in 2-D FEM Simulations of Electrical Machines. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef]
- Bertotti, G. Dynamic generalization of the scalar Preisach model of hysteresis. IEEE Trans. Magn. 1992, 28, 2599–2601. [Google Scholar] [CrossRef]
- Steinmetz, C.P. On the Law of Hysteresis. Trans. Am. Inst. Electr. Eng. 1892, IX, 1–64. [Google Scholar] [CrossRef]
- Steinmetz, C.P. On the Law of Hysteresis (Part II.) and Other Phenomena of the Magnetic Circuit. Trans. Am. Inst. Electr. Eng. 1892, IX, 619–758. [Google Scholar] [CrossRef]
- Steinmetz, C.P. On the Law of Hysteresis (Part III), and the Theory of Ferric Inductances. Trans. Am. Inst. Electr. Eng. 1894, XI, 570–616. [Google Scholar] [CrossRef]
- Cannas, B.; Cincotti, S.; Daneri, I. A generalization of a piece-wise linear circuit model of hysteresis. IEEE Trans. Magn. 2002, 38, 901–904. [Google Scholar] [CrossRef]
- Wills, A.; Schön, T.B.; Ljung, L.; Ninness, B. Identification of Hammerstein–Wiener models. Automatica 2013, 49, 70–81. [Google Scholar] [CrossRef]
- Brouri, A.; Giri, F.; Ikhouane, F.; Chaoui, F.; Amdouri, O. Identification Of Hammerstein-Wiener Systems With Backlash Input Nonlinearity Bordered By Straight Lines. IFAC Proc. Vol. 2014, 47, 475–480. [Google Scholar] [CrossRef]
- Hsu, J.T.; Ngo, K. A Hammerstein-based dynamic model for hysteresis phenomenon. IEEE Trans. Power Electron. 1997, 12, 406–413. [Google Scholar] [CrossRef]
- Gu, G.; Li, C.; Zhu, L.; Su, C. Modeling and Identification of Piezoelectric-Actuated Stages Cascading Hysteresis Nonlinearity with Linear Dynamics. IEEE/ASME Trans. Mechatron. 2016, 21, 1792–1797. [Google Scholar] [CrossRef]
- Zhang, X.; Tan, Y.; Su, M. Modeling of hysteresis in piezoelectric actuators using neural networks. Mech. Syst. Signal Process. 2009, 23, 2699–2711. [Google Scholar] [CrossRef]
- Zeinali, R.; Krop, D.; Lomonova, E. A Mesh-Free Dynamic Magnetic Model Applied to Non-Oriented Laminated Steels. In Proceedings of the 2019 19th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering (ISEF), Nancy, France, 29–31 August 2019; pp. 1–2. [Google Scholar] [CrossRef]
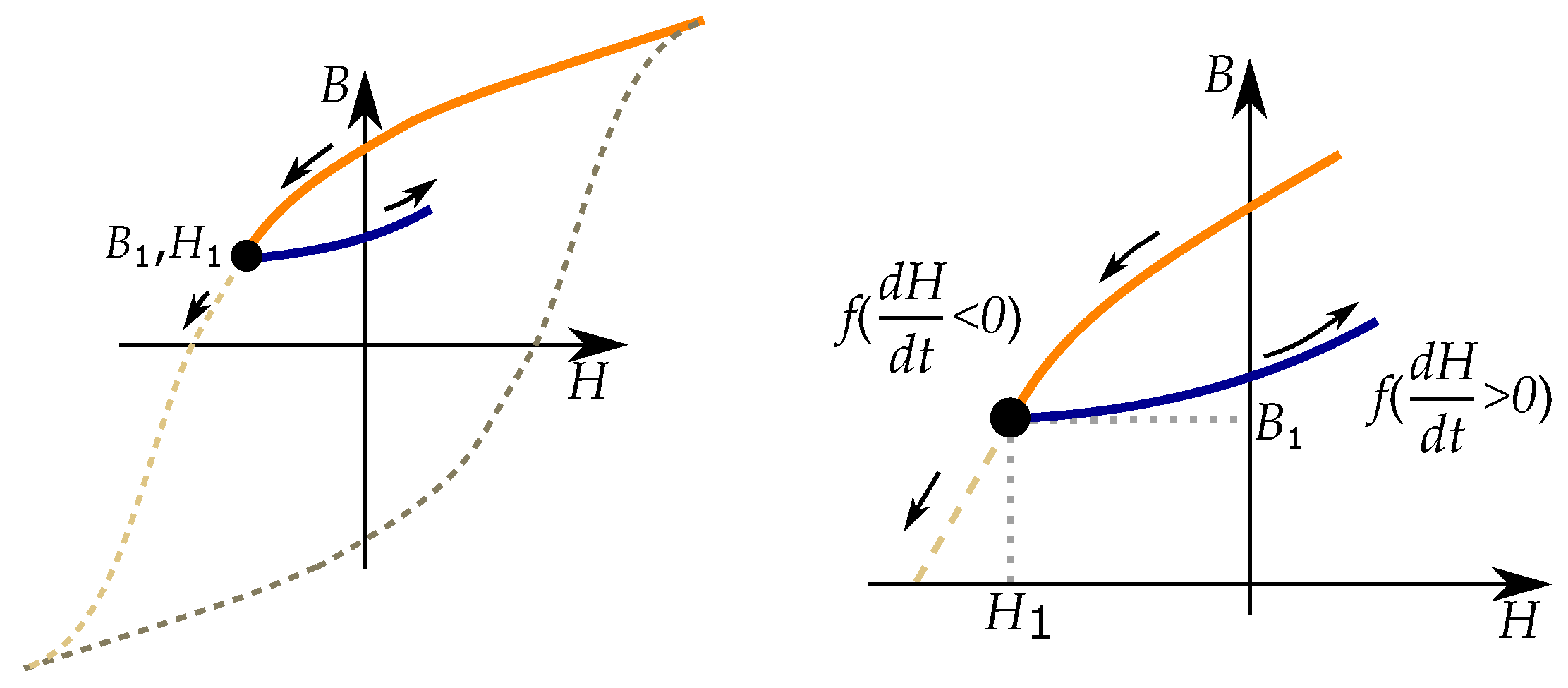

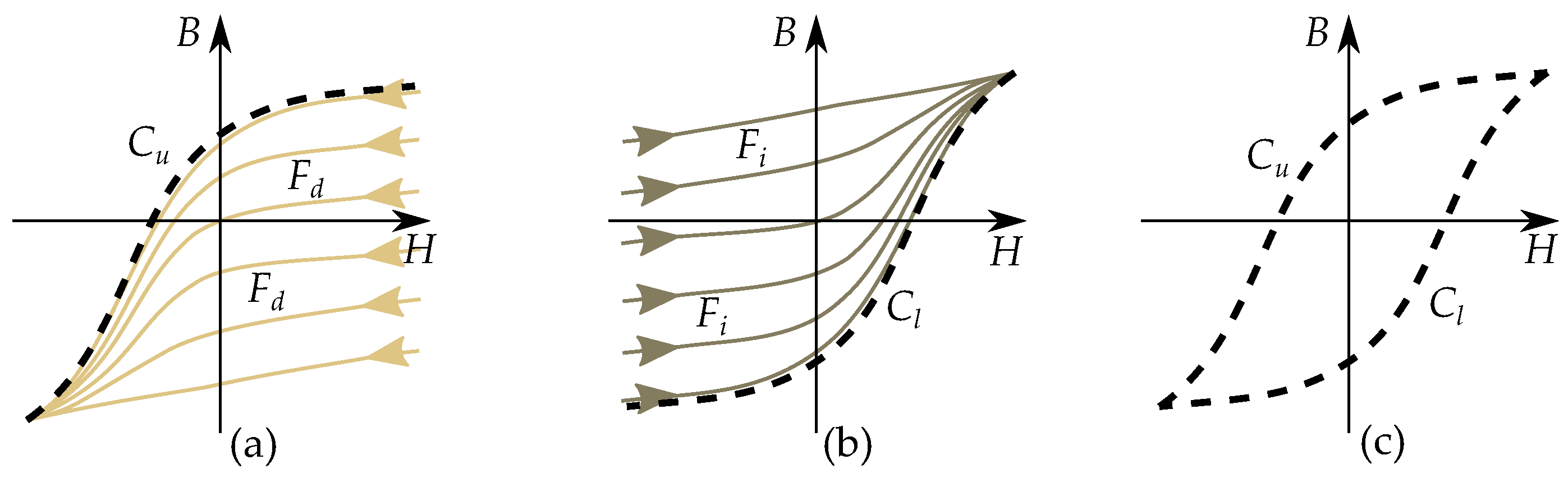


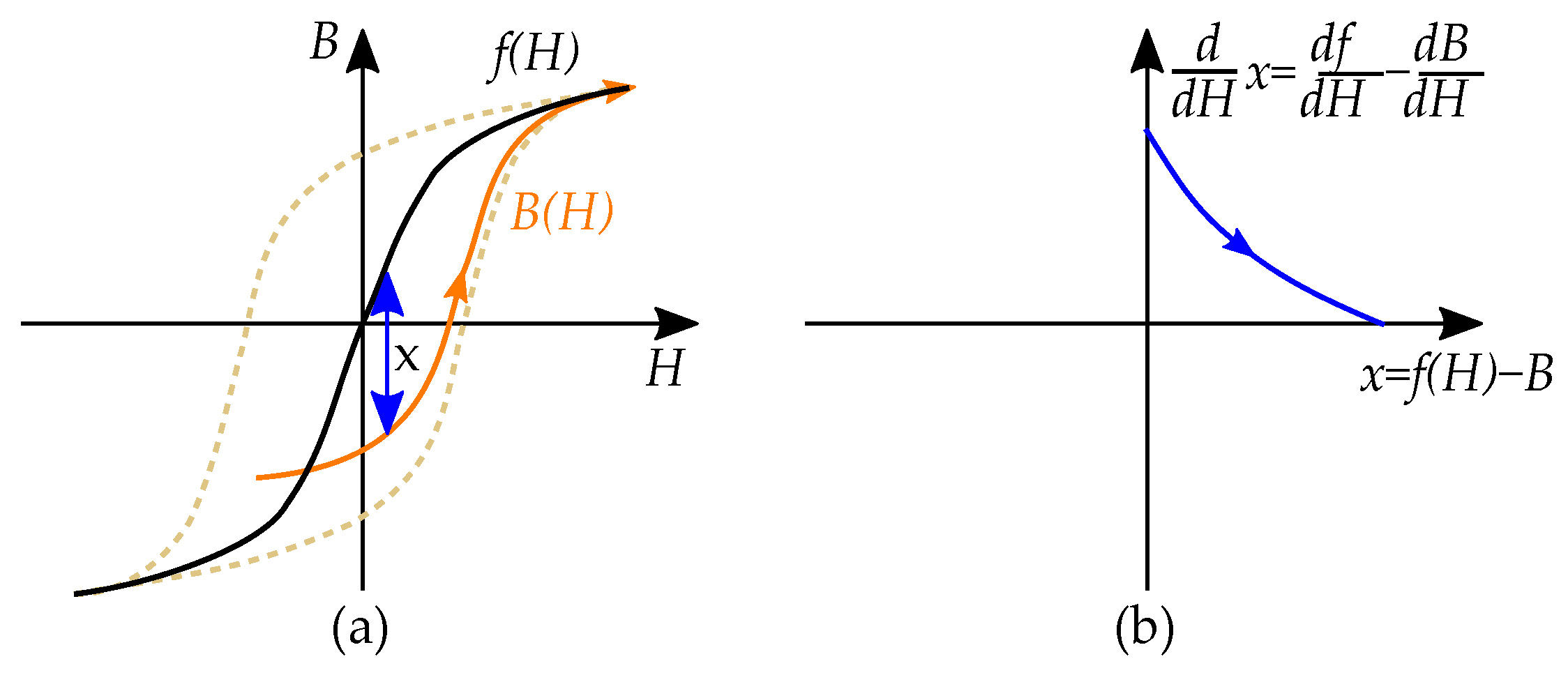
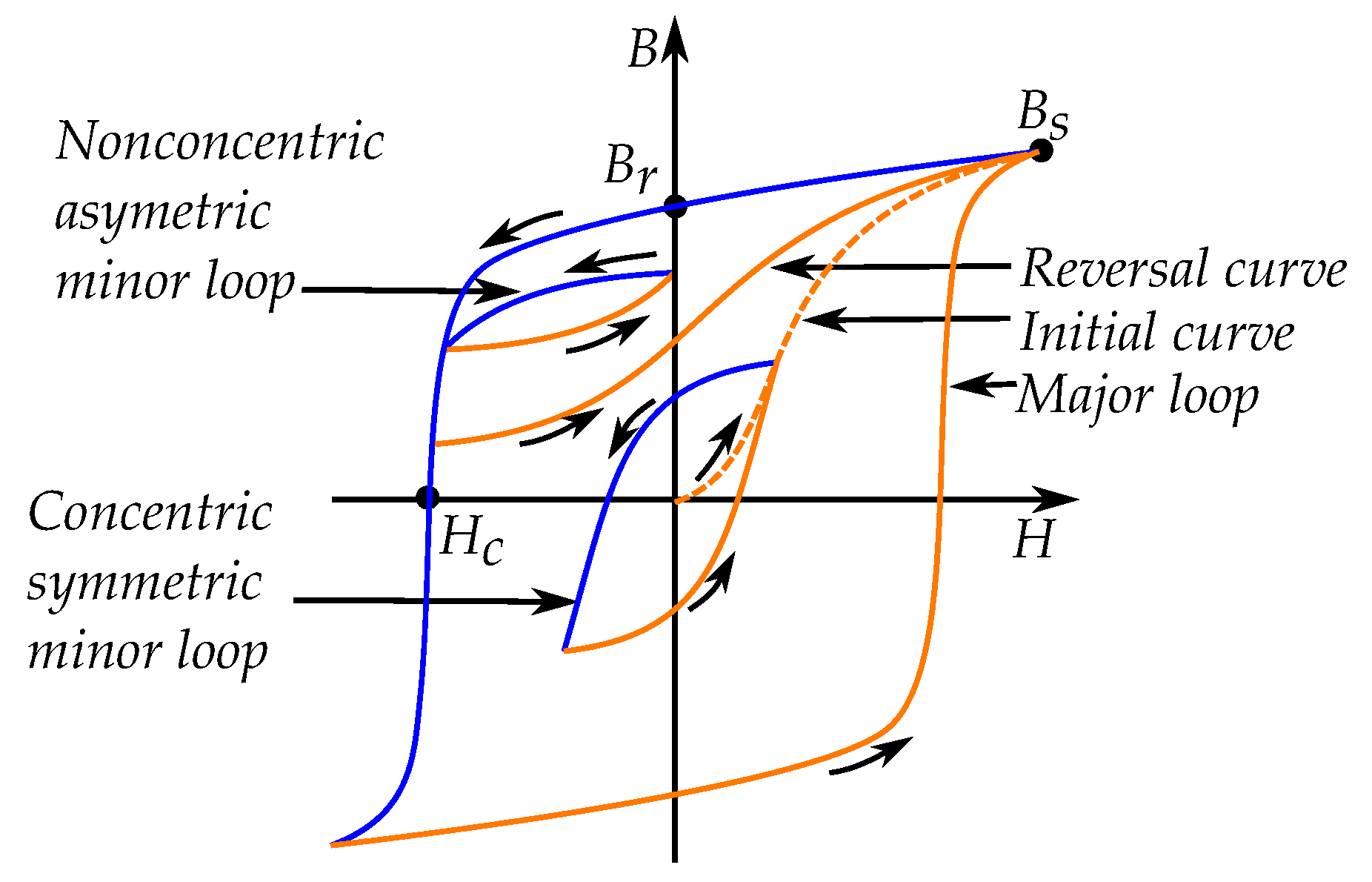
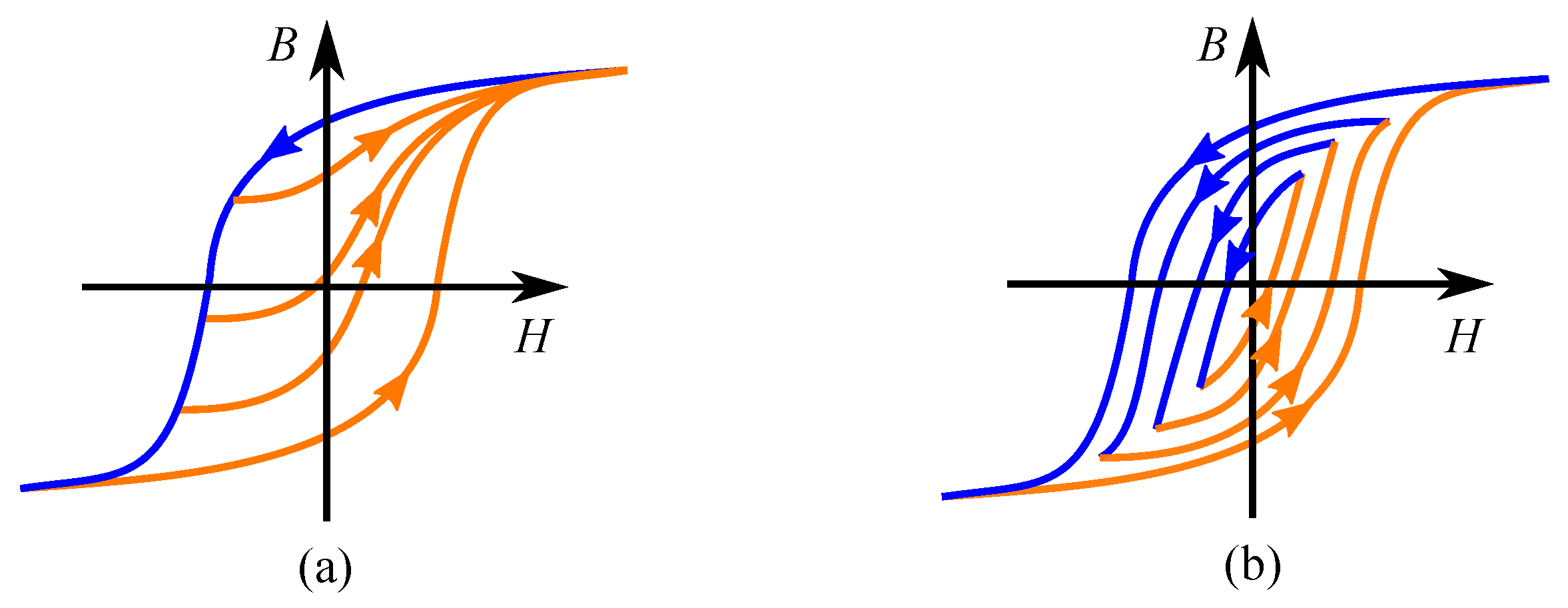

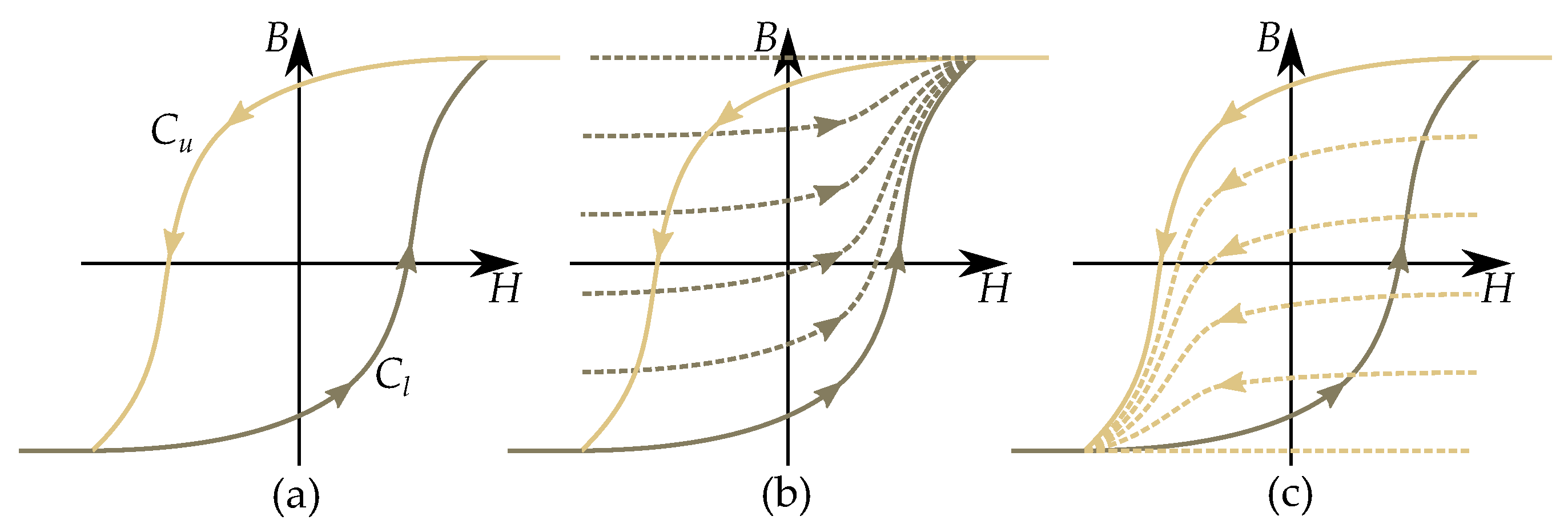

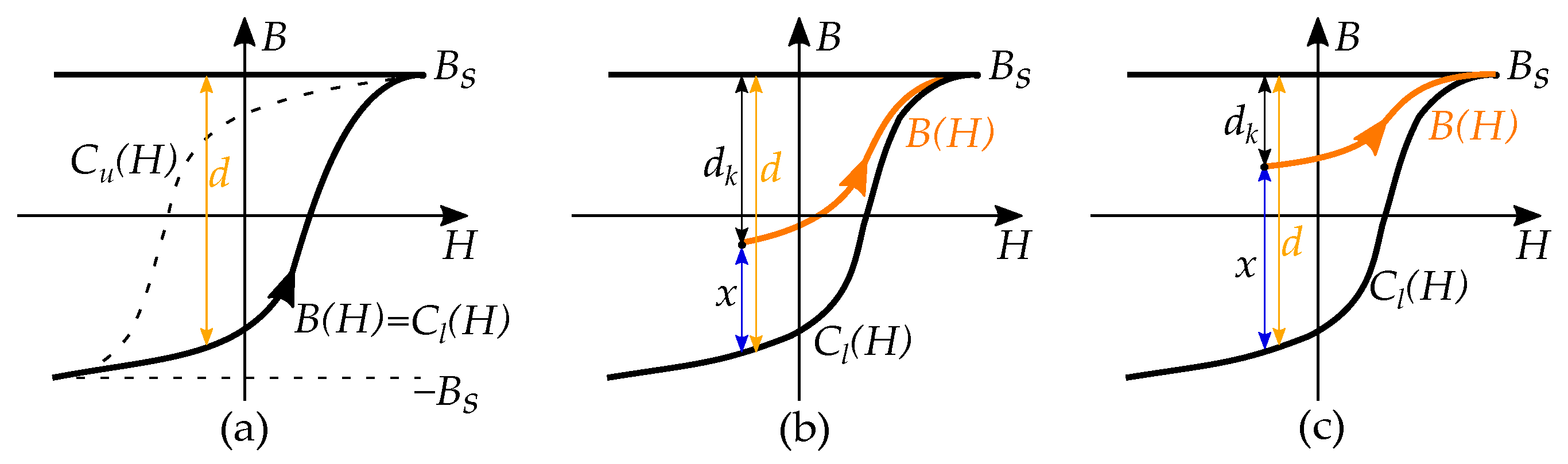

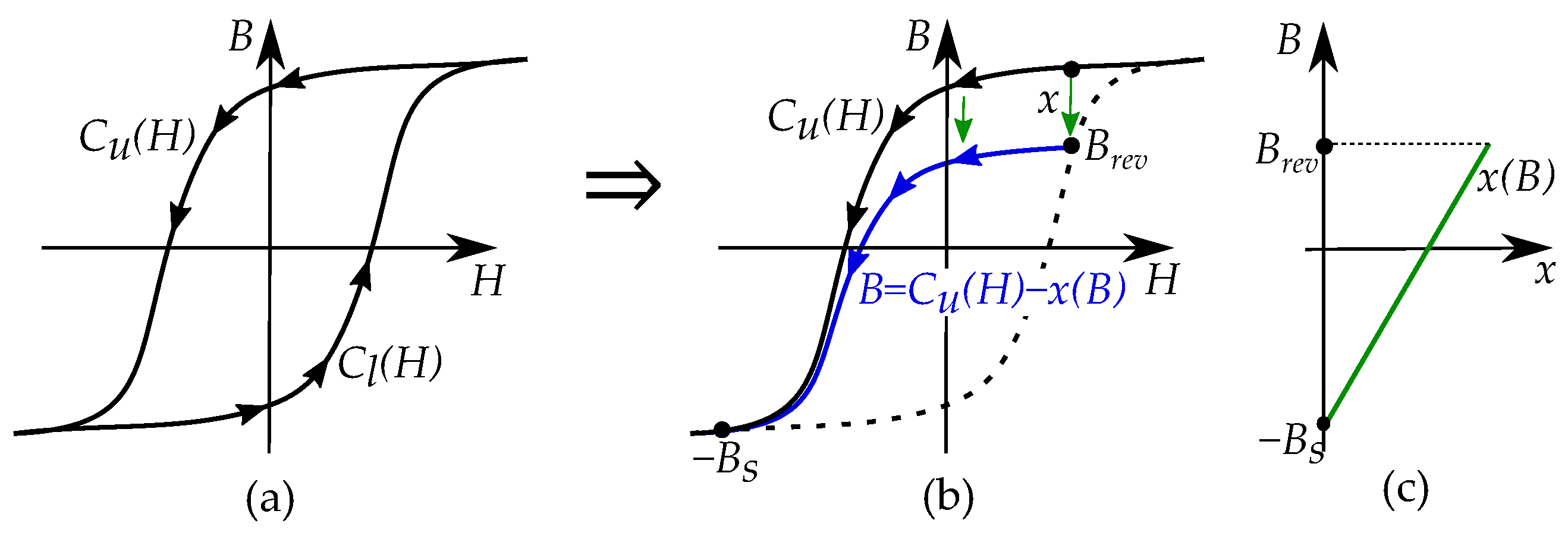
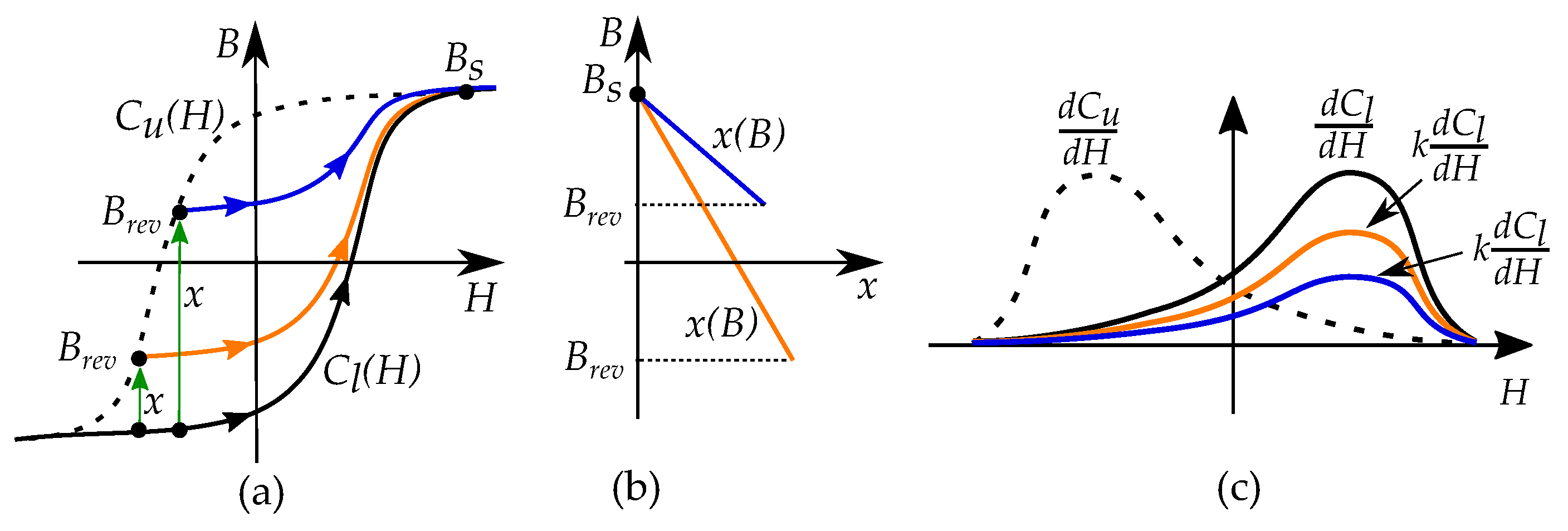
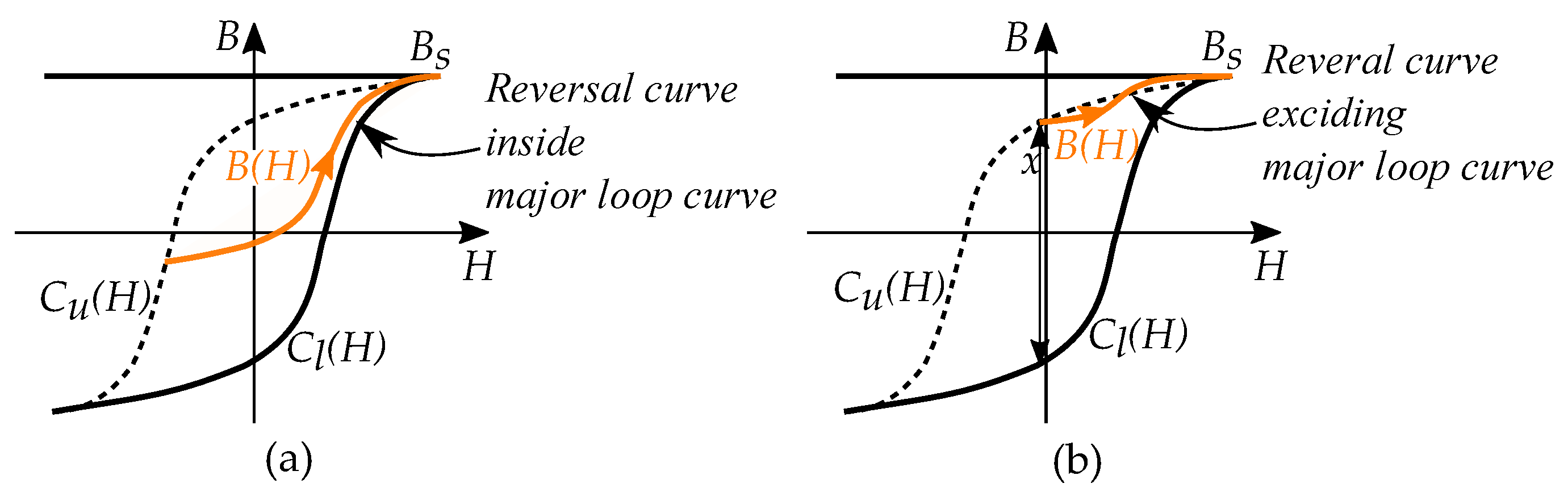
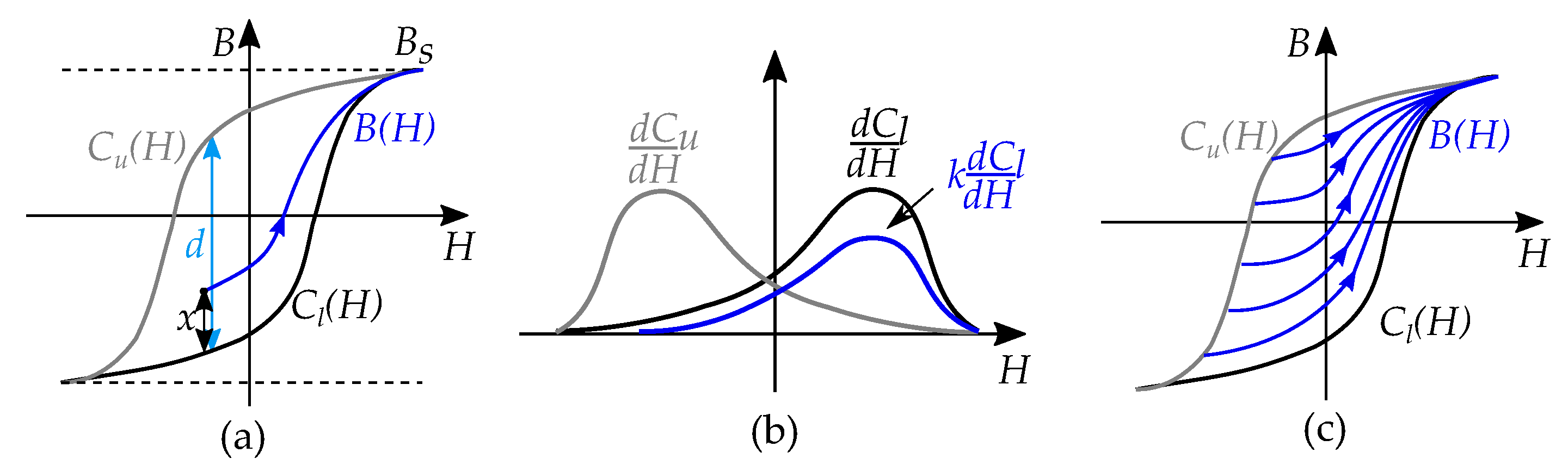
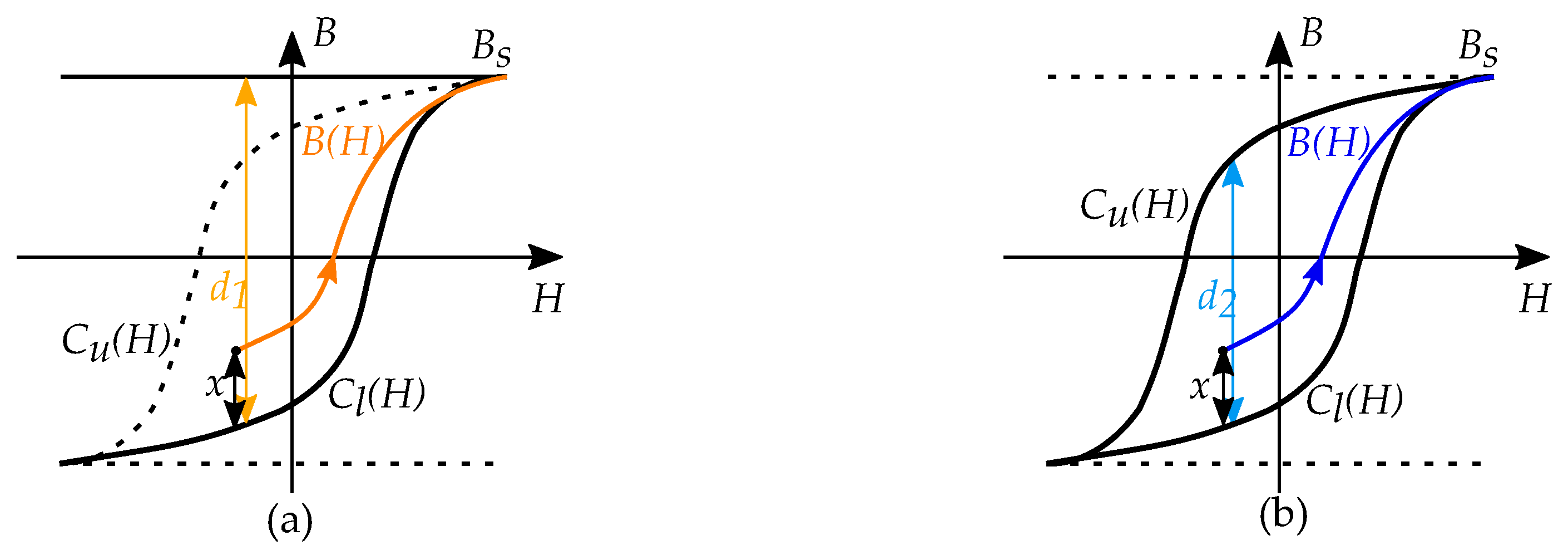




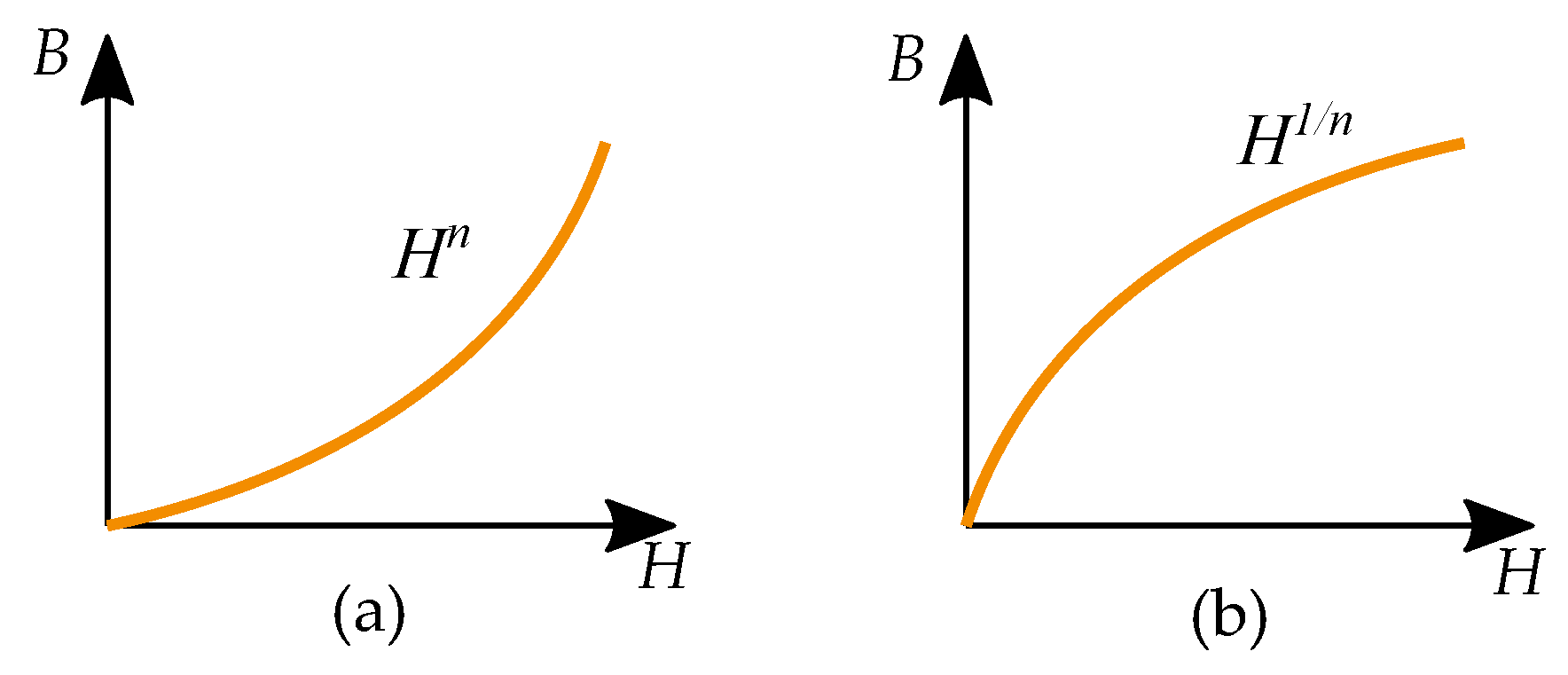
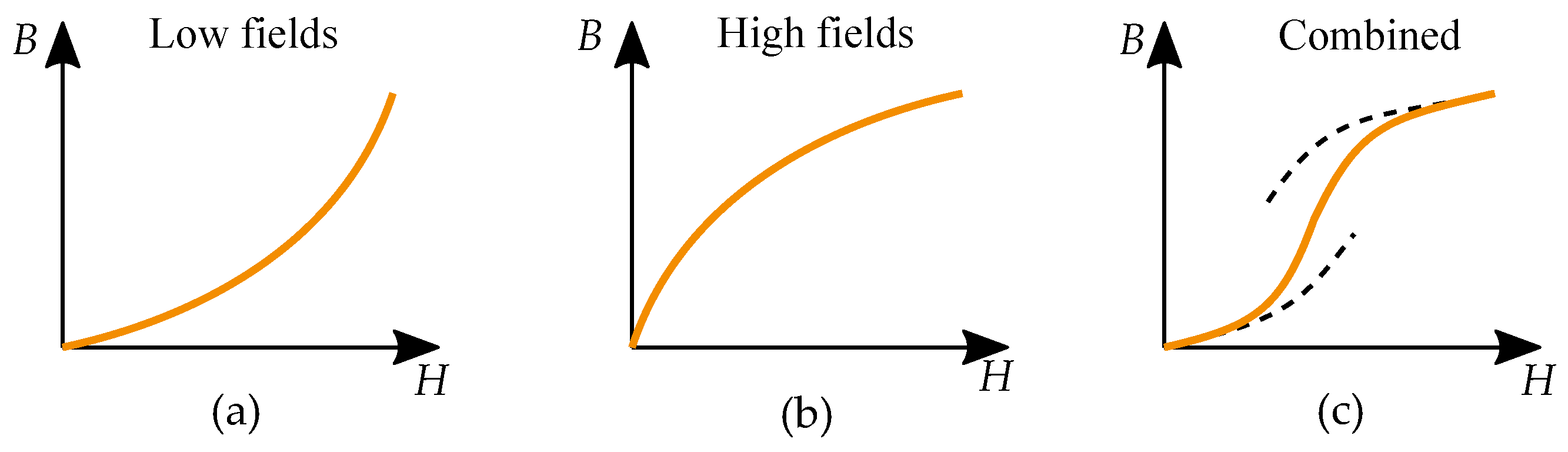

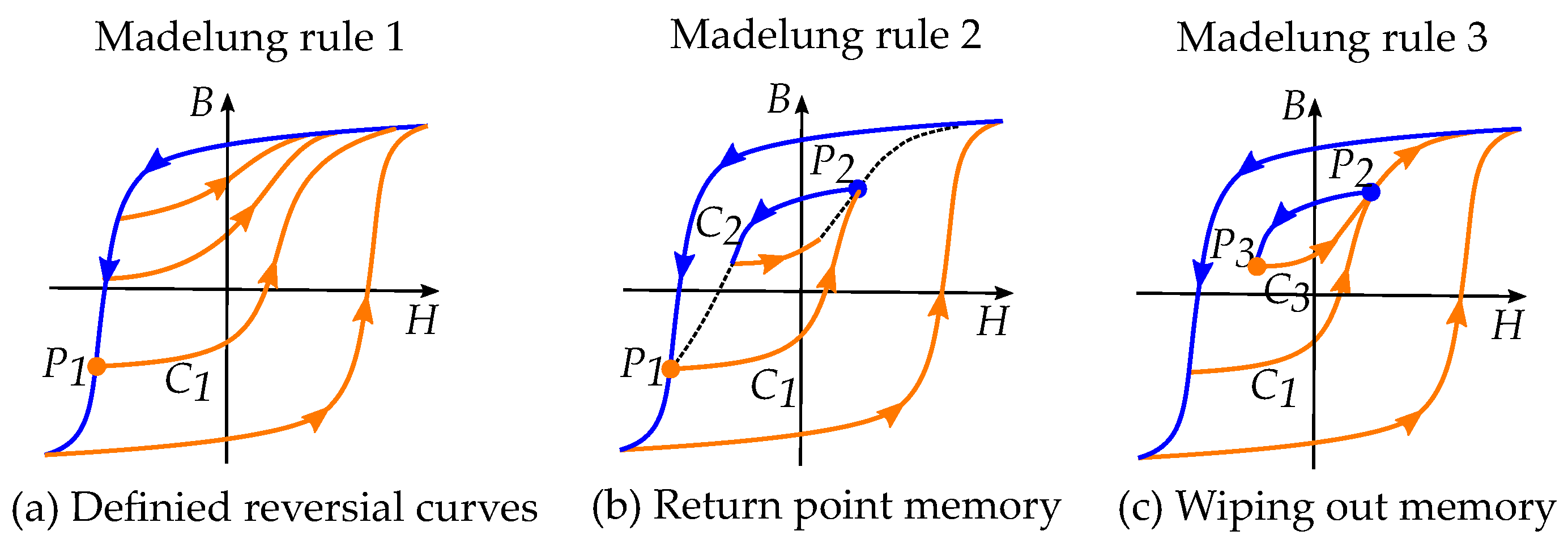


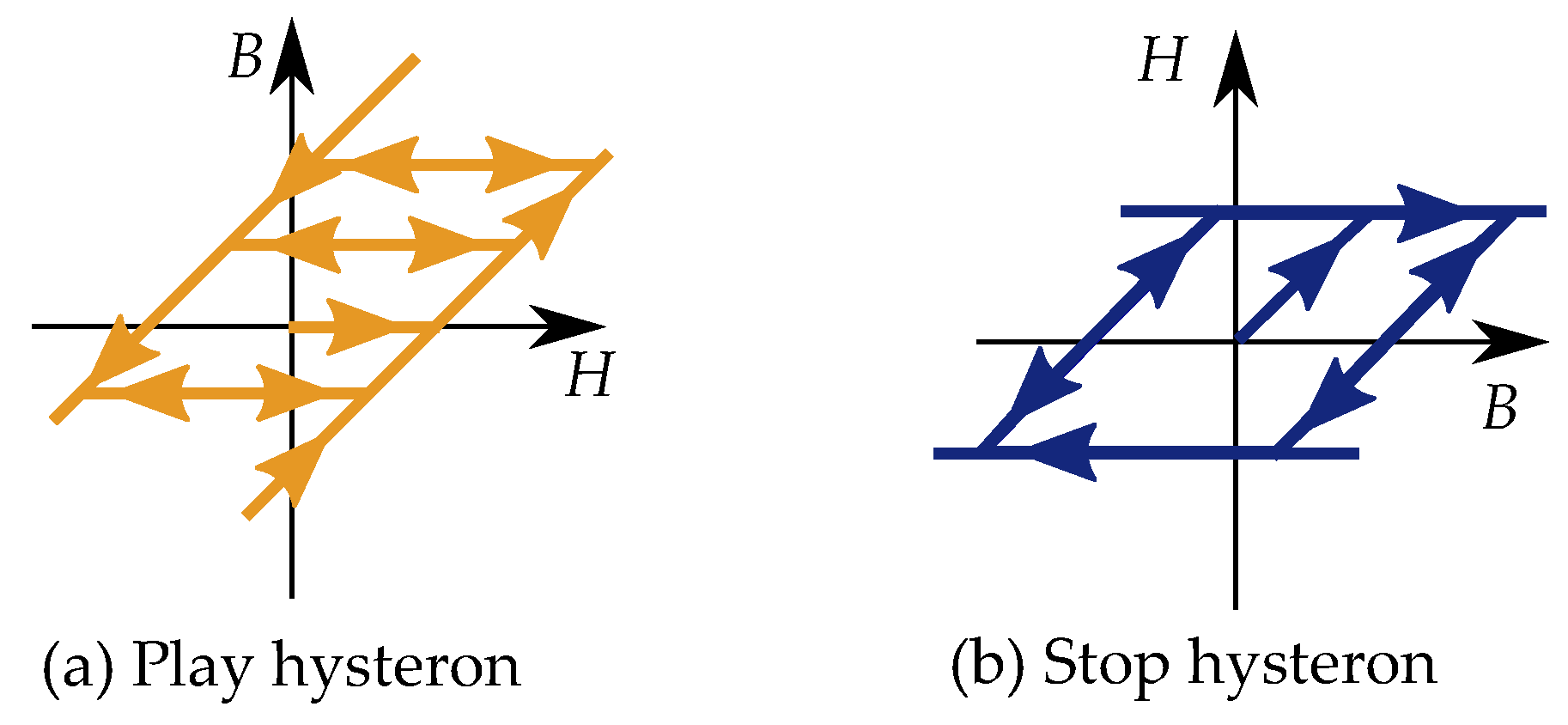
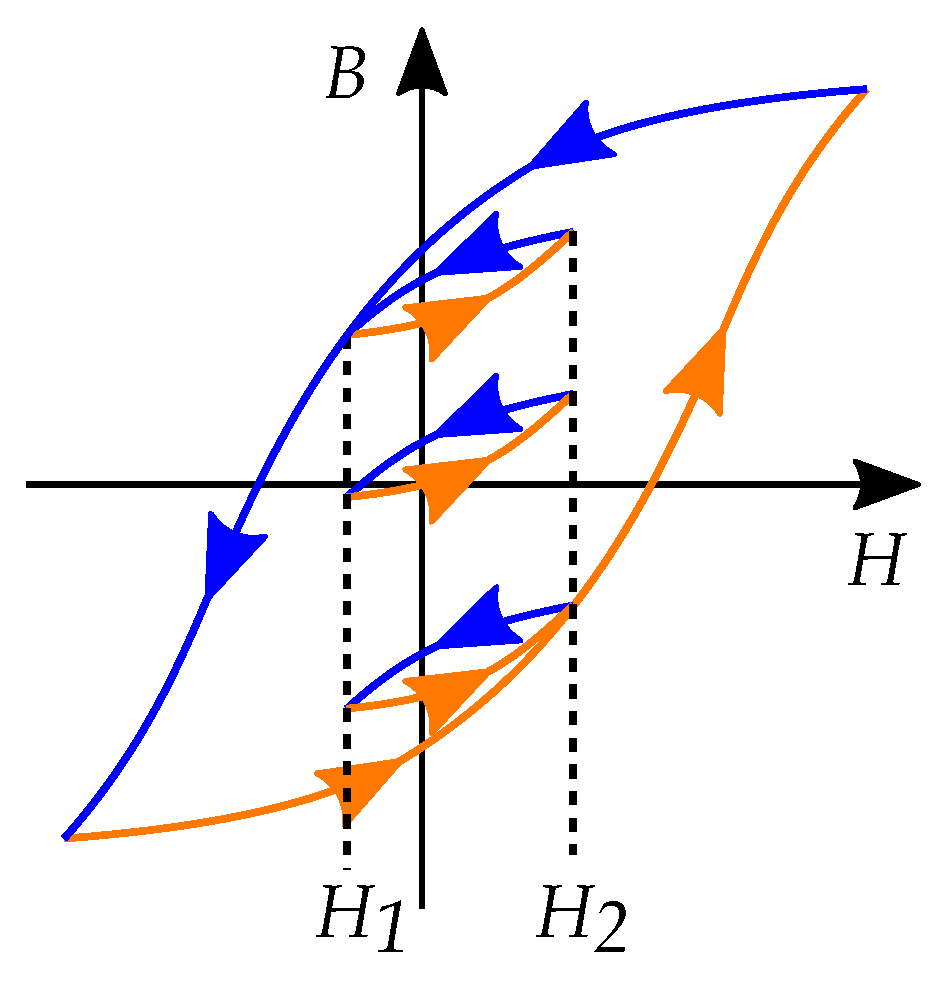
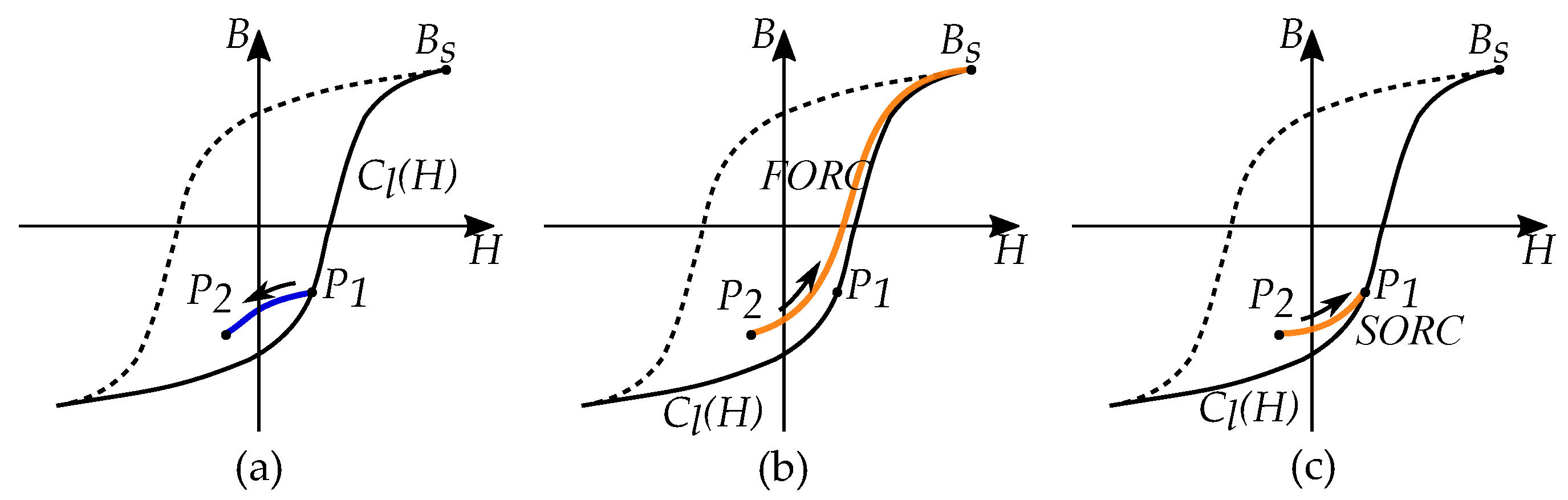
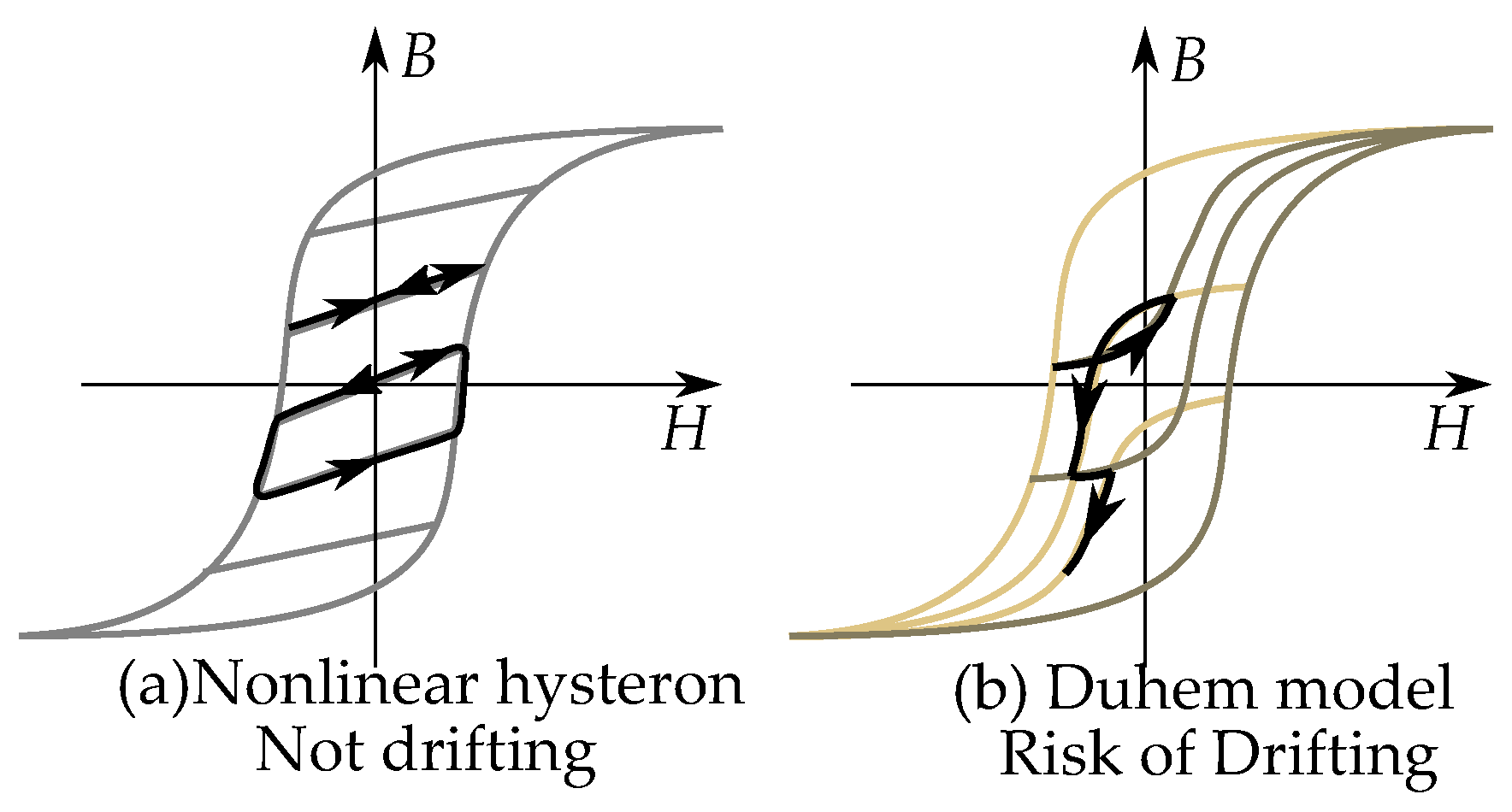

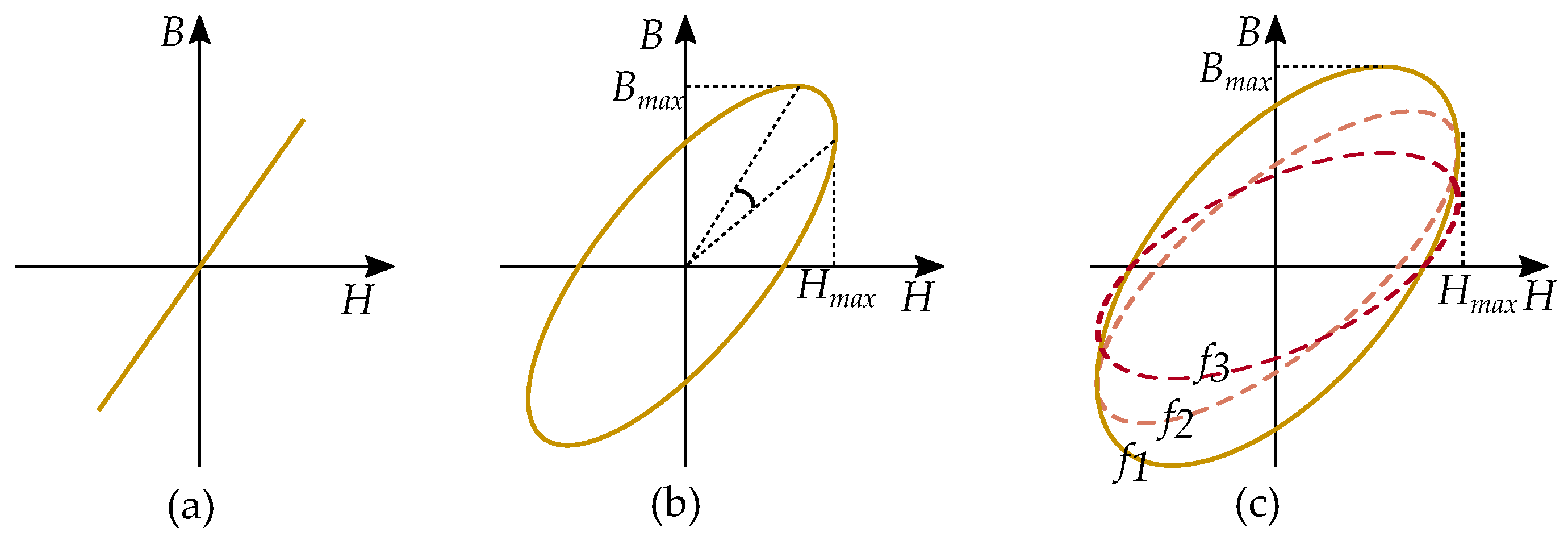
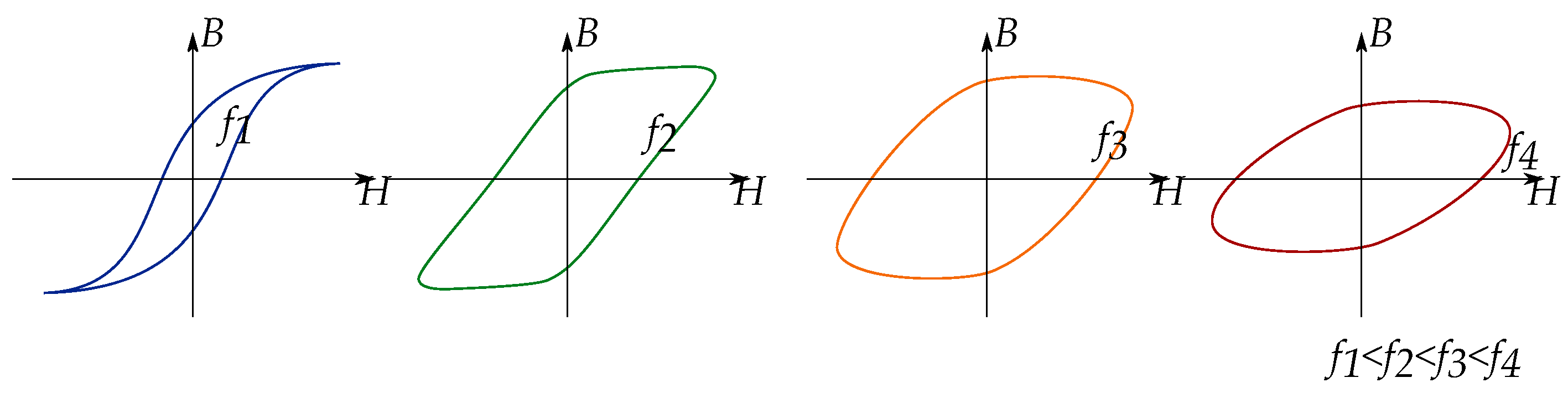

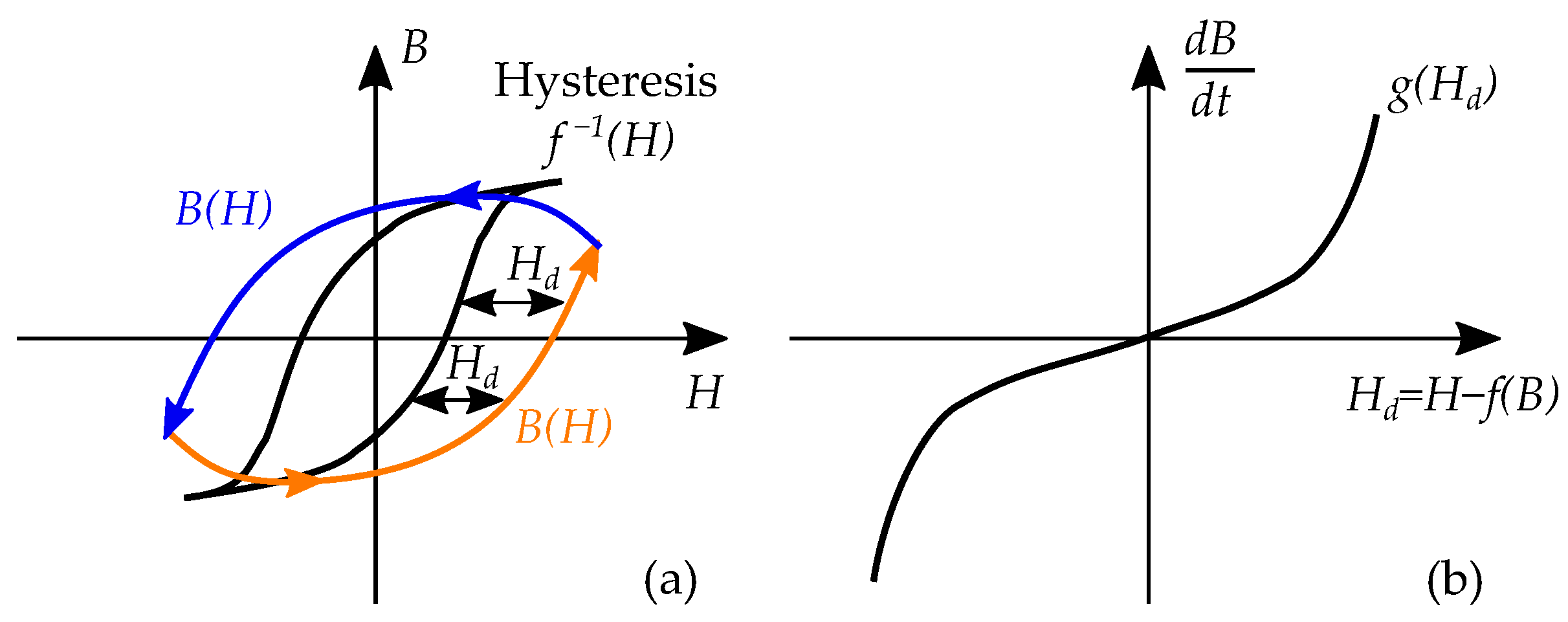
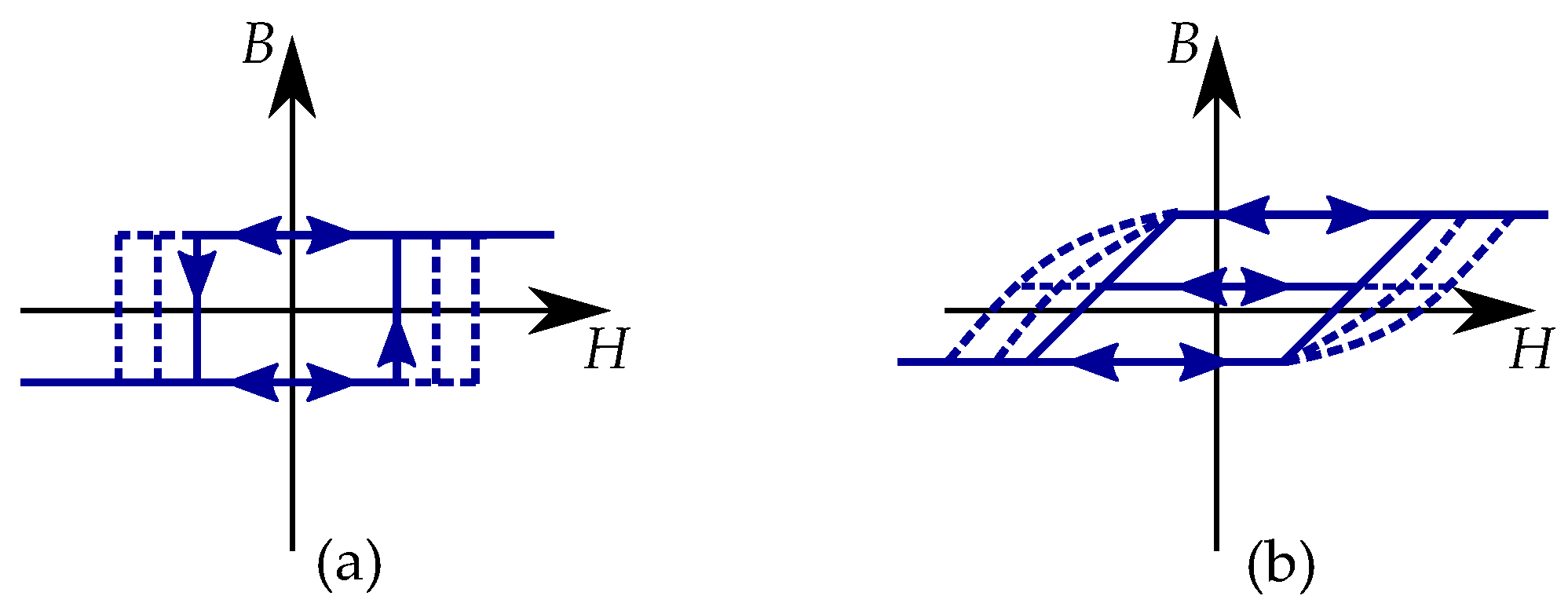
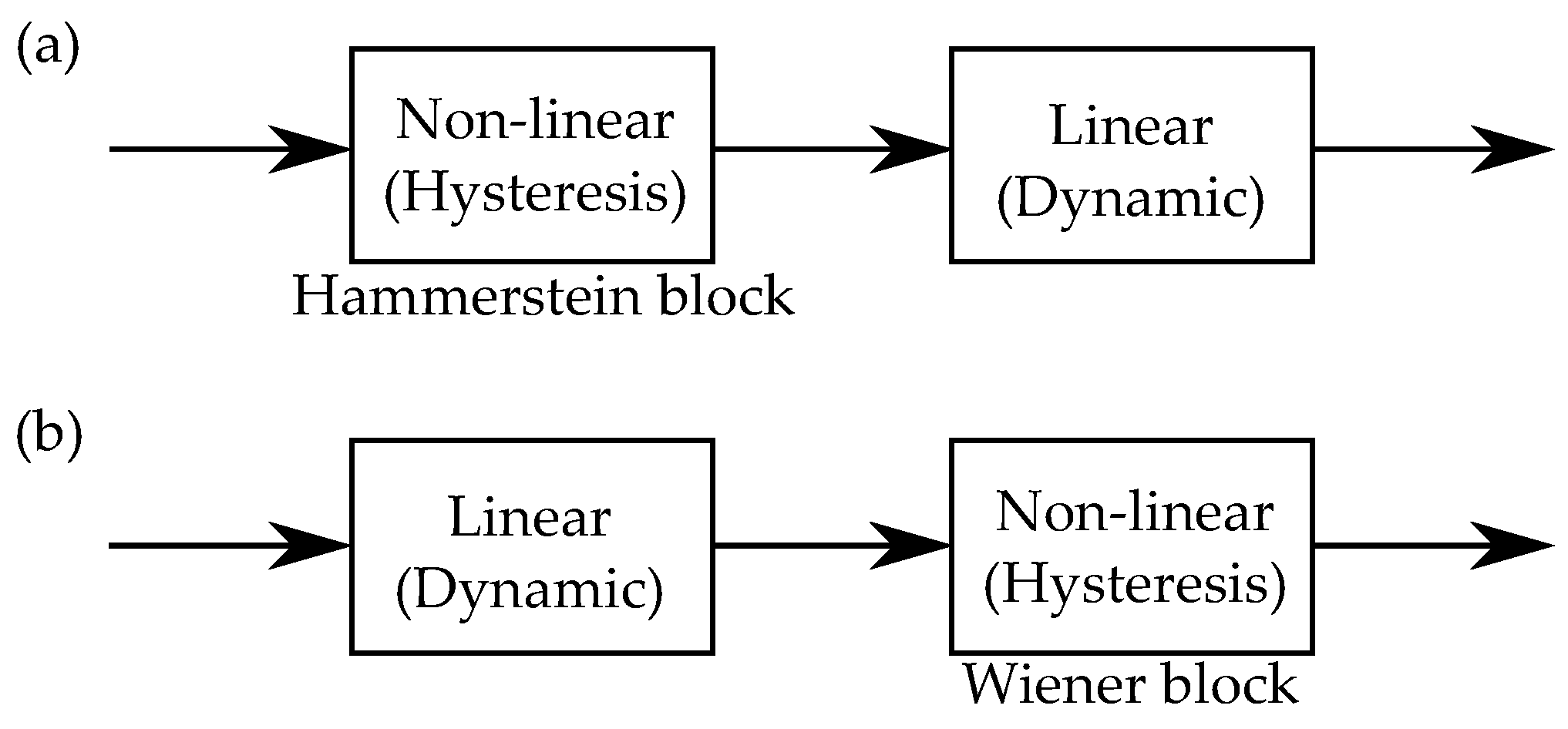
| Parameter | Explanation |
|---|---|
| Saturation magnetization | |
| Effective field parameter, linked to magnetization | |
| a | Shape parameter, for anhysteretic curve |
| c | Reversibility coefficient |
| k | Linked to hysteresis loss |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mörée, G.; Leijon, M. Review of Hysteresis Models for Magnetic Materials. Energies 2023, 16, 3908. https://doi.org/10.3390/en16093908
Mörée G, Leijon M. Review of Hysteresis Models for Magnetic Materials. Energies. 2023; 16(9):3908. https://doi.org/10.3390/en16093908
Chicago/Turabian StyleMörée, Gustav, and Mats Leijon. 2023. "Review of Hysteresis Models for Magnetic Materials" Energies 16, no. 9: 3908. https://doi.org/10.3390/en16093908
APA StyleMörée, G., & Leijon, M. (2023). Review of Hysteresis Models for Magnetic Materials. Energies, 16(9), 3908. https://doi.org/10.3390/en16093908







