Abstract
Reducing energy consumption and increasing operational efficiency are currently among the leading research topics in the design of hydraulic systems. In recent years, hydraulic system modeling and design techniques have rapidly expanded, especially using artificial intelligence methods. Due to the variety of algorithms, methods, and tools of artificial intelligence, it is possible to consider the prospects and directions of their further development. The analysis of the most recent publications allowed three leading technologies to be indicated, including artificial neural networks, evolutionary algorithms, and fuzzy logic. This article summarizes their current applications in the research, main advantages, and limitations, as well as expected directions for further development.
1. AI in Research on Hydraulic Systems
Hydraulic systems are now widely used in industrial equipment and work machines. Their undoubted advantages include obtaining a high force or torque with the compact design of actuators, the ability to work under various environmental conditions, durability and reliability, and a high level of fire safety. On the other hand, phenomena related to the flow of the working fluid, such as turbulence, hydrodynamic forces, deviation of jet angle, changes in the state of the medium, formation of boundary layers, cavitation, etc., can be difficult to describe using traditional mathematical models. Additionally, in the field of control of hydraulic systems, there are numerous problems related to non-linearities, such as dead zone, hysteresis, or saturation.
In the beginning, publications indexed in the Scopus and Web of Science (WoS) databases were analyzed [1,2]. The following phrase was searched: “artificial AND intelligence AND hydraulic” in relation to documents, including articles, conference papers, conference reviews, reviews, and book chapters from all existing subject areas. At first, the publication year boundaries were set between 2013 and 2023. The number of publications in particular years until 2022 is shown in Figure 1. During the first five weeks of 2023, Scopus indexed eighteen publications in the considered field, and WoS indexed six.
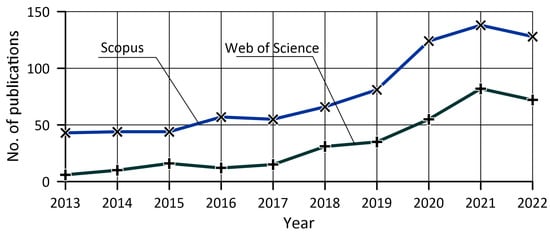
Figure 1.
Number of Scopus- and WoS-indexed publications on AI methods in hydraulic.
Further analyses concern the Scopus database due to the greater number of publications and the fact that almost all WoS articles are also indexed by Scopus. The graph clearly shows the increase in interest in the subject under consideration since 2015, which resulted in more than triple the number of publications in 2020 compared to 2015. As for the most recent period, there have been 408 items in total since 2020. The classifications of these publications according to selected criteria are shown in the following figures, including the country or region of origin of the authors in Figure 2, while document types and subject areas are shown in Figure 3a,b, respectively.
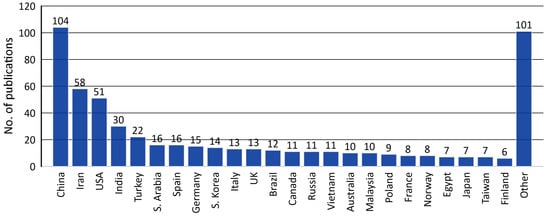
Figure 2.
Publications from different countries or regions (Scopus, 2020-23).
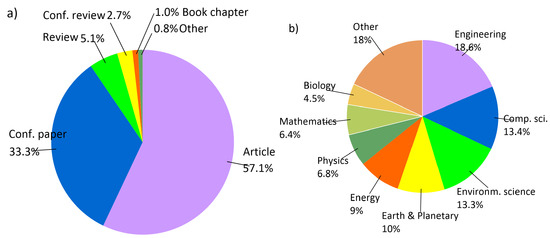
Figure 3.
Document classifications: (a) types, (b) subject areas (Scopus, 2020-23).
As shown in the figure, the number of declared countries/regions exceeds the number of publications since there are some articles with authors from different countries.
Among the document types, articles and conference materials definitely prevail, with a total share of over 90%. The large variety of scientific disciplines is also worth noting. However, the most significant number of publications concerns Engineering and Computer Science. In addition, Environmental Science, Earth Science, and Energy also make considerable contributions. The diversity of disciplines implies the usage of various AI-related technologies. The prospects for their development in the very near future are also different. Therefore, in the next chapter, an attempt will be made to classify the leading AI techniques and methods according to their types and applications.
2. State-of-the-Art and Prospects for Development
Classification of the considered techniques of artificial intelligence can be carried out from many different points of view. Within the general architectures of AI models and objects, three main directions of development can be distinguished, including artificial neural networks (ANN), evolutionary algorithms (EA), and fuzzy logic (FL) (Figure 4). The following sections present a more detailed analysis of the development perspectives of the individual directions.
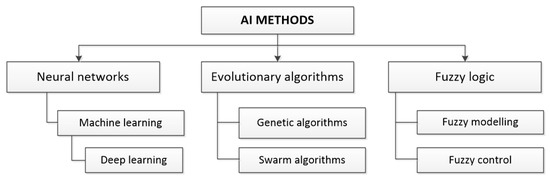
Figure 4.
Main directions of AI techniques development in hydraulic system design.
Neural networks belong to the class of learning systems, i.e., they are capable of modifying their parameters in the training process to obtain the desired response to a given extortion. Currently, this process is most often referred to as machine learning. Its specific variety is deep learning, which uses multi-layer networks with a more complex structure, the training of which is usually longer. In turn, a typical application of evolutionary algorithms is the solution of optimization problems, especially multi-criteria, where standard techniques are unable to determine the required values. Genetic algorithms (GA) and other types of swarm methods are often distinguished here, including ACO (Ant Colony Optimization), Particle Swarm Optimization (PSO), Differential Evolution (DE), Artificial Bee Colony (ABC), Glowworm Swarm Optimization (GSO). The third group includes algorithms related to fuzzy logic. Their typical applications include modeling and control, especially related to non-linear systems, making them particularly helpful in research on hydraulic systems characterized by numerous non-linearities.
2.1. Utilization of Neural Networks
The topic of neural networks is one of the most frequently discussed AI topics in publications. Various classification criteria can be used, including kinds of network architecture, types and methods of training, and practical applications. In this study, it was decided to group the publications according to practical applications primarily.
2.1.1. Neural Prediction
Publications on the neural network prediction related to hydraulic systems are presented below, while the main network parameters are summarized in Table 1. Neural networks designed for hydraulic systems are commonly used for forecasting future parameter values, such as flow rate and pressure. Su [3] proposed an accurate data-based flow rate prediction method for a four-spool independent-metering valve. Eight data-based estimation models, including machine learning and deep learning, were built and trained. The results indicated the best performance of the Support Vector Regression (SVR) and Deep Neural Network (DNN) with three hidden layers, where the Mean Absolute Percentage Error was close to 4%. Guan [4] carried out experimental studies on the hydraulic dynamic behaviors of a common rail injection system. The studies included the development of a multi-layer feed-forward artificial neural network (Figure 5) trained by the back-propagation algorithm to predict dynamic parameters, with particular attention paid to pressure fluctuations.
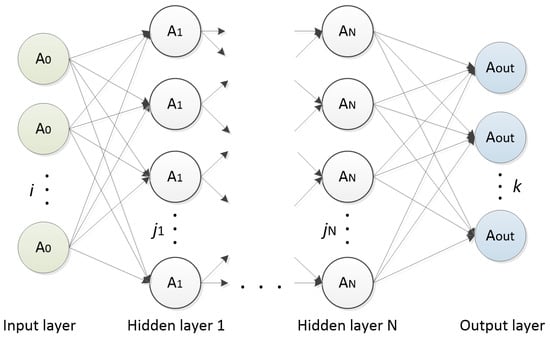
Figure 5.
Diagram of a multi-layer feed-forward BP neural network; , , , —activation functions, N—number of hidden layers, i, , , k— numbers of neurons in layers.
Lu [5] used a multi-layer feed-forward neural network to predict the in situ hydraulic fracture initiation pressure in a borehole considering a physic-based plastic critical distance. The data set built within numerical simulations was divided into a training set (249 samples) and a testing set (100 samples). A deep neural network model with three hidden layers of 12, 10, and 12 neurons was designed, and the sigmoid activation function was applied to all the neurons. The back-propagation algorithm was used in the training process. Comprehensive studies on neural network prediction related to the pressure drop in a two-phase flow in microchannels were carried out by Haghighi [6]. Different network structures were tested, including a multilayer perceptron (MLP), radial basis function (RBF), general regression (GR), and cascade feedforward (CF). Next, a committee neural network (CmNN) was created by averaging the MLP, GR, and CF outputs to improve prediction accuracy. Moreover, a genetic algorithm was used to optimize the averaged CmNN output. In turn, the prediction of thermo-hydraulic attributes of a nano-fluid flow with a simple neural network consisting of one hidden layer of seven neurons was realized by Bahiraei [7]. A neural network designed and trained to predict the flowing discharge from various geometrical and flow parameters was proposed by Tawfik [8]. A multi-layer network containing two hidden layers with the hyperbolic tangent (tanh) activation function and an output layer with a purelin function, respectively, was proposed.

Table 1.
Parameters of neural networks designed for prediction.
Table 1.
Parameters of neural networks designed for prediction.
| Ref. | Hidden Layers | No. of Neurons | Activation Function | Training | Quality Factor |
|---|---|---|---|---|---|
| [3] | DNN—1 layer | 5 | tanh | supervised | MAPE = 8.0% |
| [3] | DNN—3 layers | 6, 11, 1 | tanh | supervised | MAPE = 4.5% |
| [5] | 3 layers | 12, 10, 12 | sigmoid | supervised | rel. error < 1.0% |
| [7] | 1 layer | 7 | unknown | supervised | unknown |
| [8] | 2 layers | 11, 11 | tanh | supervised | rel. error ≤ 3.7% |
| [9] | 1 layer | 7 | Gaussian | self − org + superv. | rel. error ≤ 6.7% |
| [10] | Convolutional | 3 × 3 + 2 × 2 | RELU | supervised | RMSE = 0.63 |
| [11] | 3 layers | 128, 64, 64 | unknown | supervised | rel. error < 10% |
| [12] | LSTM-type | unknown | tanh | supervised | rel. error < 1.6% |
| [13] | recur.-LSTM | complex | tanh | supervised | MAPE = 0.2 – 3.0% |
| [14] | 2 layers | 6, 6 | tanh | superv. LM | rel. error = 2.94% |
| [15] | 3 layers | 15, 15, 15 | unknown | supervised | det.coeff. = 0.828 |
Another application of neural networks in the field of prediction is the estimation of the values of operational parameters or characteristics of hydraulic components. Huo applied an RBF neural network for intelligent prediction for the digging load of hydraulic excavators [9], according to the flowchart shown in Figure 6. Guo [10] investigated the use of four different neural network types, including convolutional, BP, T-S, and Elman, to predict the internal leakage of a hydraulic cylinder, and Neunzig utilized machine learning methods to predict internal leakage of hydraulic valves [11].

Figure 6.
Flowchart of a hydraulic excavator load prediction process by [9].
Nie [12] developed a remaining useful life (RUL) prediction method for a high-speed on/off valve by combining the autoregressive integrated moving average (ARIMA) model and the long short-term memory (LSTM) neural network and Li carried out the research on the RUL prediction of a hydraulic pump [16] based on kernel principal component analysis (KPCA) and just in time learning (JITL) (Figure 7). The LSTM recurrent network was also used by Ryu [13] to obtain more accurate predictions of the nuclear power plant’s thermal–hydraulic dynamics. The results were compared to the base Recurrent Neural Network model achieving 75% and 79% lower values of the MAPE and MSE indexes, respectively. Han [14] combined the Levenberg–Marquardt (LM) training algorithm and a double hidden layer backpropagation neural network to predict a centrifugal pump performance. In turn, Gregov [17] proposed a new approach for modeling and predictive analysis of the GEROLER hydraulic motor based on two types of multi-layer ANNs: static feed-forward and dynamic NARX. A toy model concept applicable to machine learning models, including neural networks, was proposed by Brahma [18]. Functional capabilities of the concept in the example of a hydraulic turbine efficiency prediction were presented. In addition, Guo designed a network with three hidden layers, 15 neural nodes each, to predict the hydraulic performance of free water surface constructed wetlands [15], while Albalasmeh [19] used a generalized regression neural network (GRNN) to predict saturated hydraulic conductivity, Jardani developed a convolutional network to predict the inverse operator of hydraulic tomography [20], and Ye proposed a method of physics-informed neural network formulation (PINN) to predict transient pressures at given locations of the pipelines [21].
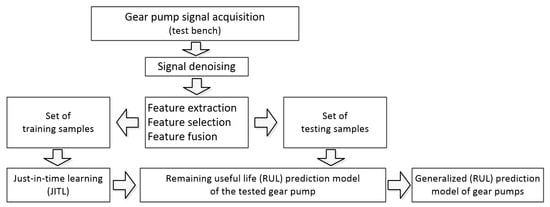
Figure 7.
Flow diagram of a hydraulic gear pump remaining useful life prediction by [16].
The main difficulties reported in publications on ANN prediction include the limited possibility of accuracy estimation and problems with the acquisition of training data samples for the whole domain of consideration. The following directions for future research may be formulated:
- developing of feed-forward ANNs with a greater number of hidden layers;
- searching for novel network structures, e.g., combining multiple sub-networks of different types (FNN, RBFNN, LSTM) into one ANN.
2.1.2. Neural Identification
The neural networks used for identification are presented in this section, and their parameters are summarized in Table 2. Wu [22] designed a convolutional neural network (CNN) for the identification of stall flow patterns occurring in pump turbines, obtaining an accuracy of near 100%. The created CNN structure is shown in Figure 8.

Table 2.
Parameters of neural networks designed for identification.
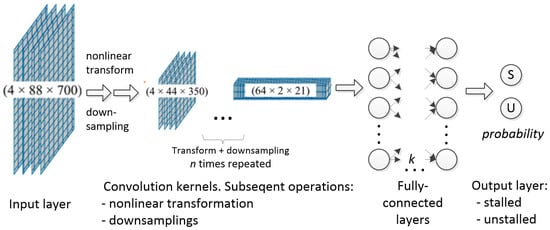
Figure 8.
Structure of the CNN for identification of stall flow patterns in pump turbines by [22].
Haldar [23] attempted to identify the rheological properties of hydraulic oil nano-lubricants using a traditional feed-forward multi-layer network. Banaszek carried out a series of experiments on neural identification, including optimal efficiency exploitation conditions of axial-piston hydraulic motor [24] and flow rate assessment of submerged hydraulic ballast pumps [25]. A standard network with one hidden layer of 10 neurons was used in both cases. The extension of a standard pipeline leak identification method (TFR) was proposed by Liao [26] by introducing a deep learning method into the TFR-based leak identification framework. A fully-linear DenseNet was designed and trained to identify a leak to a pipe in the suspected leak area. In turn, Pan [27] applied a convolutional network for inverse estimation of hydraulic conductivity field, Guo and Vu [28,29] proposed the applications of convolutional neural networks for solving hydraulic tomography issues.
The main difficulties reported in publications on neural identification include the complexity of the Convolutional NN structure which is most commonly used, and the limited range of use resulting in the identification ability of only one specific hydraulic element, e.g., a particular pump model or an ON-OFF valve of a given type. The following directions for future research may be formulated:
- development of ANN structures and training methods for widening the identification range (e.g., one ANN for a group of pumps or valves);
- searching for new identification methodologies;
- using semi-supervised training methods instead of classic fully-supervised ones, which could help to generalize the CNN’s identification abilities.
2.1.3. Neural Control
Articles related to neural network applications in control systems are presented in this section, and the summarized parameters are shown in Table 3. In control systems, neurons with transfer functions of the RBF type are often used. Tran in [30] presented an adaptive robust control system for the equilibrium position of an electrohydraulic elastic manipulator under the presence of variable stiffness. The proposed control strategy (Figure 9) includes sliding mode controls (SMCs), radial basis function neural network (RBFNN), and a backstepping technique. The proposed system allowed the reduction in absolute tracking error by 3–4 times compared to the classic PID algorithm. A similar application of the RBF-type network to control the hydraulic manipulator was presented by Tran [31], while Feng [32] and Nguyen [33] developed adaptive control methods based on the same type of neural network to control the servo valve under conditions of uncertainty and disturbance. All authors demonstrated the advantages of the proposed approach compared to standard regulators. In turn, Homayoun [34] utilized the RBF network to control an active suspension system with hydraulic actuators.

Table 3.
Parameters of neural networks designed for neural control.
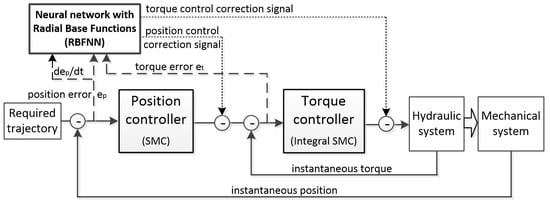
Figure 9.
Control strategy of an electro-hydraulic elastic manipulator with the use of RBFNN by [30].
Proposals for adaptive neural networks to control several various hydraulic components were presented by Yang. These include a multilayer neuro-adaptive force controller of load simulators driven by single-rod electro-hydraulic actuators [37], an adaptive sliding mode controller based on a neural network for precise position-tracking control of a hydraulic rotary drive joint [38], and a disturbance observer-based adaptive neural network control for a hydraulic knee exoskeleton [39]. An interesting paper on the neural controller for the piston-cylinder positioning system of the tank shooting barrel was published by Yakut [35]. In particular, the network was used to determine the required barrel elevation angle. Moreover, Zhang [36] proposed a computational flow feedback control method using a flow inferential measurement method and a PI controller, with the help of an AdaBoost neural network used to learn flow change regulation affected by spool displacement, pressure differential, and temperature with high accuracy and low over-fitting (Figure 10).
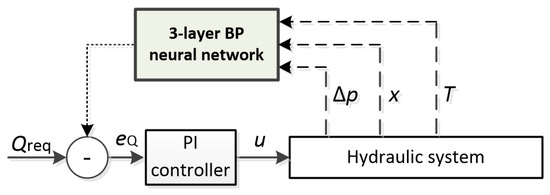
Figure 10.
Flow control system of a proportional valve by [36]; —required flow rate, —control error, u—control signal, —pressure drop, x—valve spool position, T—temperature.
The main difficulties reported in publications on neural control include the limited accuracy of an ANN’s output and problems with stability estimation (usually, the authors try to use multiple variants of the Lyapunov method). Moreover, obtaining a complete set of training samples is often necessary, which requires conducting previous measurements of the existing system during operation and extensive expert knowledge. Directions for future development:
- searching for new criteria for estimating the stability and robustness of ANN controllers (e.g., extensions of the Lyapunov approach);
- development of novel, adaptive ANN-based controllers for hydraulic systems under the condition of limited knowledge about the system’s dynamic;
- research on adaptive ANN-based controllers for compensating non-linearities of hydraulic systems.
2.1.4. Neural Estimation and Classification
A machine-learning method of rapid estimation of the void fraction and temperature in a steam generator using the reduced-order model was proposed by He [40]. A feed-forward ANN with three hidden layers of six neurons each was created and trained based on the CFD results. The void fraction and temperature field orders were reduced by % and %, respectively. The maximum absolute errors of void fraction and temperature were and K with an estimation speed-up of the order of . A case study related to hydraulic flow unit classification and prediction using machine learning techniques was carried out by Man [41]. Multiple AI algorithms were used in the research, including both unsupervised and supervised machine learning methods for hydraulic flow unit clustering and the prediction of hydraulic parameters.
As for the future directions of research on neural estimation and classification, the following suggestions can be made:
- development of innovative methods of parameter sensitivity analysis of hydraulic systems;
- design of neural estimators and classifiers using the methods of unsupervised ANN training.
2.1.5. Neural Parameter Monitoring and Fault Diagnosis
Real-time monitoring and fault diagnosis are also common topics of ANN research. The most recent publications in this field are presented, while the network architectures and parameters are summarized in Table 4. Makansi [42] developed a procedure for the data-driven condition monitoring of a hydraulic press using supervised learning and neural networks. The proposed method involves feature extraction as well as feature selection. A three-hidden-layer ANN was built and trained to monitor the condition of six selected parameters, obtaining an accuracy of 89–99%, depending on the parameter. A novel deep-learning data augmentation (jittering) designed for increasing the amount of hydraulic system condition monitoring data using a convolutional network was proposed by Kim [43]. The system monitored the state of four hydraulic components, including the cooler, valve, pump, and accumulator. The accuracy with the raw data was near 80% while using the jittering increased it to %. Several versions of an adaptive convolutional network for fault diagnosis of a piston pump were developed by Tang. In the first work [44], an improved intelligent method based on a convolutional neural network with adapting the training rate was constructed, obtaining the accuracy of 97–99%. The diagram of the designed CNN is shown in Figure 11.
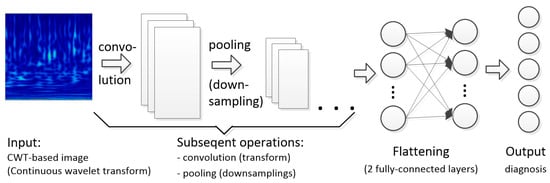
Figure 11.
Structure of the CNN for fault diagnosis of a piston pump by [44].
The following studies of the same author concern constructing an analogous system based on CNNs using pressure signal analysis [45] or a synchrosqueezed wavelet transform [46]. A flowchart of the fault diagnosis process is presented in Figure 12.
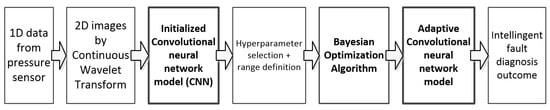
Figure 12.
Flowchart of a piston pump fault diagnosis based on a pressure signal by [45].
Other approaches [47,48] were related to employing the Bayesian optimization for adaptive hyper-parameter training and establishing an improved convolutional neural network for fault feature extraction and classification. The results confirmed higher accuracy (98.2–98.9%, average %) and better robustness of Convolutional–Bayesian network in fault diagnosis. Keleko [49] proposed a concept of a detailed framework for Condition Monitoring of complex hydraulic systems and multi-sensor data based on a deep neural network and other technologies such as Deep SHapley Additive exPlanations to ensure the reliability of the results. Ebrahimzadeh [50] introduced a new method based on thermal-hydraulic simulation and feed-forward neural networks (FFNN) for detecting faults of sensors in nuclear power plants.

Table 4.
Parameters of neural networks designed for fault diagnosis.
Table 4.
Parameters of neural networks designed for fault diagnosis.
| Ref. | Hidden Layers | No. of Neurons | Activation Function | Training | Quality Factor |
|---|---|---|---|---|---|
| [42] | 3 layers | max. 512, 256, 128 | sigmoid | supervised | acc. 89–99% |
| [43] | Convolutional | 3 × 1 kernel | ReLU | supervised | acc. 80.3–91.8% |
| [44] | Convolutional | 5 × 5 k1, 3 × 3 k2 | ReLU | supervised | acc. 97–99% |
| [47] | Convolutional | max. 7 × 7 | ReLU | supervised | acc. 98.7% |
| [49] | 9 layers | 25 × 8 each | ReLU | supervised | acc. 88.6–99.9% |
| [51] | Convolutional | complex | sigmoid | semi-superv. | acc. 99.0–99.7% |
| [52] | ELM—1 layer | unknown | sigmoid | supervised | near 100% |
Another fault diagnosis system based on a novel semi-supervised training method designed for a hydraulic valve was presented by Zhong [51]. A similar approach for a hydraulic pump based on the extreme learning machine was proposed by Ding [52] with the declared accuracy close to 100%.
The difficulties reported in publications on neural fault diagnosis include multiple issues. There is a need for earlier, sometimes long-term, acquisition of the operating parameters of a given element or device to obtain data on emergencies since training data must consider all the possibilities of faults. In more complex systems, there are difficulties with properly extracting all the parameters affecting the failure rate. There is also an issue resulting from various data types (numeric integers or floats, enumerations, logical, descriptive, etc.). Moreover, it is often necessary to install numerous sensors and transducers connected to the DAQ system and long-term signal recording and processing in a continuous mode. Directions for future development:
- research on systems based on convolutional ANNs for comprehensive condition monitoring, fault prediction, and fault diagnosis of the hydraulic system as a whole;
- combining fault monitoring and prediction systems with maintenance planning and business decision-making (development and implementation of the prescriptive maintenance methodology);
- the use of semi-supervised training methods could extend the operation of ANNs by providing the ability to detect damage or fault even if not included in the set of training samples.
2.2. Evolutionary Algorithms
Evolutionary algorithms are mainly used in optimizing hydraulic system parameters and, to a lesser extent, in fault detection. They are particularly useful in the case of complex, multi-criteria problems for which it is difficult or even impossible to find the optimal solution using standard deterministic methods. Genetic algorithms, swarm methods, and simulated annealing play the most important role; however, studies on different algorithms developed to solve a particular problem can also be found.
2.2.1. Genetic Algorithm Optimization
Xu used a multi-objective genetic algorithm to optimize the structure of jet fish pumps [53]. The obtained reduction in the internal radial pressure gradient, exposure strain rate, and danger zone to 40%, %, and 50%, respectively, compared to the pre-optimization level. This significantly reduces the risk of fish injuries, keeping the pump efficiency high. Qingtong [54] conducted a multi-objective optimization of a high-speed on–off valve designed for water hydraulic manipulators. The optimization method used a non-dominated sorting genetic algorithm shown in Figure 13. As a result, the opening and closing response times were reduced by 17% and 9%, respectively. Sun [55] presented a multi-objective optimization design of step-less flow control system parameters, while Yang [56] provided high dynamic optimal matching of the electro-hydraulic servo pump control system, and Li [57] conducted research on the optimization of vacuum pump shell profile. In all the mentioned studies, a double optimization scheme based on a non-dominated genetic algorithm with elite strategy (NSGA-II) was used. Due to the optimization, the compressor flow control error was reduced to less than 5%, the thermal power loss of the pump was significantly reduced, and the shell profile maximum suction capacity was increased by %. In turn, Zhang [58] used the genetic algorithm to optimize rectangular staggered fin heat exchangers for miniaturized hydraulic power units. Compared to the base solution, the weight of the exchanger was reduced by %, and its heat transfer capacity increased by %.
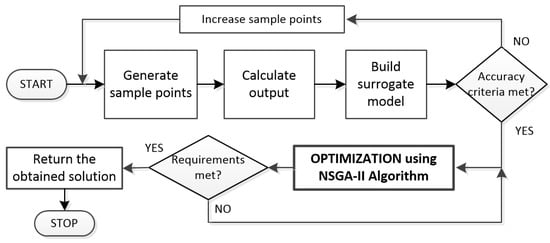
Figure 13.
Algorithm of multi-objective genetic optimization of an on-off valve by [54].
The next group includes optimization methods that combine genetic algorithms with other technologies, such as CFD analysis and neural networks. Nie [59] used a combination of surrogate model and multi-island genetic algorithm (MIGA) to optimize and compensate steady-state flow force on water hydraulic high-speed on-off valve, achieving a 15% reduction in energy consumption. The algorithm is shown in Figure 14. Moreover, Zhou [60] optimized a microporous ceramic emitter using CFD, ANN, and a multi-objective genetic algorithm. Ntiri [61] used multiple AI techniques, including an adaptive neuro-fuzzy inference system (ANFIS), ANN, and Pareto-based genetic algorithm (PBGA) for the multi-objective optimization of pump-as-turbine technology. Chen [62] proposed an optimization strategy for geometrical parameters of a hydraulic turbine in turbine mode (TMHT) with the help of CFD analysis.
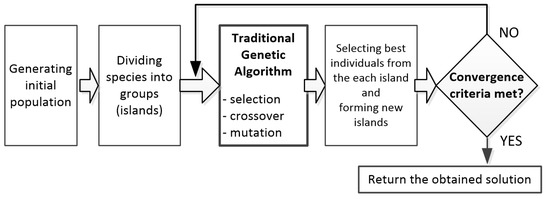
Figure 14.
Combination of a surrogate model and multi-island genetic algorithm to optimize a high-speed valve by [59].
2.2.2. Swarm and Neural Optimization
Geometrical or operational parameters of hydraulic systems can also be optimized through multiple swarm methods. Xu [63] used twelve multi-objective and many-objective evolutionary algorithms to solve the optimization problem of a hydraulic shovel. The optimization resulted in designing a TriRocker hydraulic shovel and building an 85-ton prototype. Incebay [64] combined a constrained Bees algorithm with fuzzy-based modeling and CFD analysis to optimize a centrifugal blood pump. The optimization aimed at shear stress minimization together with efficiency maximization.
In terms of neural network applications, Li designed a tree-like micro-channel heat sink [65] utilizing a three-layer feed-forward artificial neural network (ANN) and response surface methodology (RSM). The combined methods allowed him to obtain multiple optimal design configurations for different criteria, including heat sink longevity, maximization, and efficiency index maximization. In contrast, Yan [66] developed a recurrent neural network to optimize the electro-hydraulic braking control system of electric vehicles. The carried-out optimization increased the overall regenerative energy by 15%.
2.2.3. Swarm Fault Diagnosis
Fault diagnosis of hydraulic systems occupies a significant position among particle swarm optimization practical applications. An intelligent fault diagnosis for a hydraulic piston pump based on a standard LeNet convolutional neural network with the help of particle swarm optimization (PSO) was developed by Zhu [67,68]. Results indicated that the proposed PSO-Improve-CNN system had the highest fault-recognition accuracy reaching %. Another solution proposed by Jose [69] uses the Support Vector Machine (SVM) classifier with Particle Swarm Optimization (PSO) for early detection and classification of internal leakage in the boom actuator of a mobile hydraulic machine. The PSO was used for feature selection. The trained classifier was able to detect and classify internal leakage faults with more than 95% accuracy. The problem of optimal placement of sensors for fault diagnosis of hydraulic systems was investigated by Kong [70]. He proposed a sensor placement methodology of the hydraulic control system to determine the optimal number and position of sensors based on a discrete particle swarm algorithm. The developed procedure was used on an existing subsea blowout preventer system, increasing its diagnostic efficiency by more than 10%.
2.2.4. Simulated Annealing Optimization
Simulated annealing is a specific optimization technique. However, some applications for hydraulic systems can also be found. Pan [71] utilized a modified simulated annealing optimization to search for optimum operational parameters of a hydraulic variable valve actuation system (HVVA). Optimization aimed at reducing power consumption, improving the volumetric efficiency, and increasing control valve seating speed. Moreover, Meira [72] focused on scheduling pumping and delivery operations on straight multiproduct pipeline systems connecting a single source to multiple destinations. The allocation and sequencing activity (ASM) model was formulated, and a simulated annealing meta-heuristic was used to provide more robust input data for the ASM model.
2.2.5. Further Development of Evolutionary Methods in Hydraulic System Optimization
The current state includes the usage of a standard GA algorithm to find the Pareto-optimal state in a multi-criterion optimization process. Some modifications of the standard GA algorithm to solve a specific optimization problem (multi-island GA, non-dominated sorting GA) can also be found. Swarm methods (Bee Colony Algorithm, BCA) and other algorithms (simulated annealing, SA) are used more rarely.
The reported limitations and difficulties include the need to repeat the optimization process multiple times due to the lack of certainty in obtaining the global optimum and problems in scaling and normalizing different types of signals to store them in a single chromosome. The formulated directions for future development include:
- combining GA optimization with techniques of flow modeling and simulation methods, such as CFD, could extend the possibilities of defining the objective function in the optimization process;
- research on the algorithms of the significance test and sensitivity analysis, which gives the possibility of reducing or extending the number of optimized parameters;
- utilizing different evolutionary algorithms which currently are not used in hydraulic system optimization, such as Ant Colony System (ACS), Cuckoo Search (CS), or Particle Swarm Optimization (PSO);
- combining evolutionary algorithms with ANNs in the form of a neuro-evolution process.
2.3. Fuzzy Logic Systems
Fuzzy logic, concerning scientific research on hydraulic systems, is mainly used in two main areas, including developing fuzzy controllers and creating fuzzy logic-based fault detection and risk assessment systems.
2.3.1. Fuzzy Logic Controllers
Yang [73] developed a driving control strategy for a novel mechatronics-electro-hydraulic power coupling system. The created fuzzy controller with vehicle speed and pressure of the accumulator as variables was used to optimize the logic threshold control strategy, obtaining a reduction in a battery consumption rate by 14–21%. Similarly, Li [74] proposed a similar mechanical-electro-hydraulic power coupling system for electric vehicles to increase the transient power limit and reduce the impact of operating condition changes on the battery. The verification results showed a reduction in battery power consumption by %, and the obtained energy recovery rate %. A rule-based fuzzy PID controller for differential steering of tracked vehicles driven independently using a dual hydraulic motor system was proposed by Han [75]. Wrat [76] focused work on the increase in energy efficiency along with position control of the linear actuator in heavy earth moving equipment. With the usage of a PID controller tuned by the fuzzy logic controller, the % reduction in energy consumption was obtained. Jin [77] also proposed a fuzzy PID controller for a hydraulic transplanting manipulator, achieving a 56% reduction in step response time. The obtained control system is shown in Figure 15.
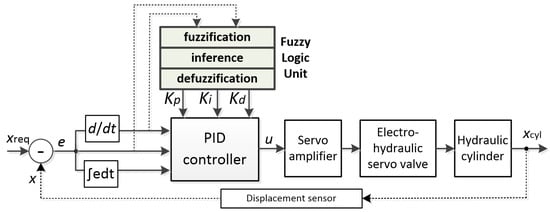
Figure 15.
Fuzzy PID controller diagram of a hydraulic transplanting manipulator by [77]; , —required and actual position of hydraulic cylinder, , , —PID controller parameters.
In turn, Jiang [78] studied the fuzzy-logic-based finite-time output–feedback control problem on electro-hydraulic systems with unknown states and subjected to actuator faults. The developed fuzzy adaptive control scheme is characterized by fast convergence and strong robustness against uncertainties. Moreover, Ma conducted research on the development of a Takagi–Sugeno fuzzy logic controller for a hydraulic turbine. He proposed multiple solutions, including a finite-time H-infinity control system with time delay [79] and a delay fractional-order system with elastic water hammer via a frequency distributed model [80]. In both cases, the achieved results outperformed the conventional methods.
The main difficulties related to fuzzy logic controllers include problems resulting from various available arithmetic and relational operators, membership functions, and defuzzification algorithms; thus, there is usually a need to perform numerous comparative studies. Moreover, there are no clear general guidelines for dividing the computational domain into fuzzy sets; sometimes, modeling is done by trial and error. Directions formulated for future research include:
- developing stricter guidelines for constructing FLC systems for individual types of hydraulic control elements, e.g., proportional relief valves, proportional flow regulators, servo valves, variable-capacity pumps, etc.;
- research on dedicated methods for assessing the stability of FLC units;
- exploring the possibility of developing stand-alone FLC systems instead of supporting PID controllers;
- development of FLCs and fuzzy-PID controllers operating under conditions of uncertainty and time-varying delays.
2.3.2. Fuzzy Fault Detection and Risk Assessment
Hu [81] conducted a fuzzy fault tree analysis based on a fault tree comprising 45 basic events on a hydraulic fracturing flow-back water storage. The fuzzy rules used to estimate the occurrence possibilities of the events were formulated through the human operator’s knowledge. The issue of risk assessment using fuzzy logic tree analysis was the subject of research by Kagar [82] in relation to mobile crane overturning in asymmetric tandem lifting operation, while Yu [83] used the fuzzy probabilistic Petri net method for the risk assessment of submarine pipeline leakage failure. Finally, Milton–Thompson [84] developed a fuzzy-logic-based risk framework utilizing data for quantitative numerical analysis and expert knowledge for qualitative analysis, focusing on hydraulically fractured wells during the stimulation stage. The created framework was applied to scenarios in the UK and Canada, resulting in the estimation of failure probability.
Problems and limitations of the fuzzy logic-based risk assessment and fault detection systems are similar to those defined for FLC units. Moreover, in systems with many parameters, the number of fuzzy rules used in the inferencing process increases dramatically (the total number of fuzzy rules is the Cartesian product of all fuzzy sets defined for all parameters). Directions for future research:
- creating fuzzy-neural systems, e.g., using an ANN in a defuzzification part of the fuzzy logic model;
- research on the possibilities of using fuzzy-based rules in the commonly used fault tree analysis methods;
- cooperation of fuzzy logic algorithms with other methods used for risk assessment and fault detection of hydraulic elements, such as Failure Mode and Effects Analysis (FMEA).
3. Summarization of Leading AI Techniques
The great variety of AI techniques determines their numerous practical applications. The primary fields of application distinguished based on the literature analysis are summarized in Figure 16.
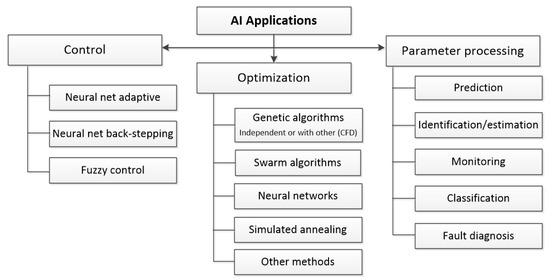
Figure 16.
Main fields of AI applications in hydraulic system design.
In terms of practical applications of AI methods, three main areas have been distinguished: control, optimization, and broadly understood parameter processing. The control uses mainly adaptive neural networks, back-stepping and fuzzy logic. Genetic algorithms and swarm algorithms are primarily used for optimization. Attempts are also made to combine them with CFD flow analysis methods and to develop new algorithms, usually to solve specific complex tasks. The broadest topic is the use of AI methods in various types of parameter processing. Due to the specificity of operation, different neural network architectures are usually used in tasks such as prediction, identification, estimation, monitoring, classification, and fault diagnosis. However, fuzzy logic can also be used in risk assessment and fault detection, e.g., by the Fuzzy FMEA method.
The most diverse applications concern neural networks. Hence, different architectures and topologies of ANNs are used in the research. The list prepared based on the analyzed publications in the field of hydraulic systems testing is presented in Figure 17.
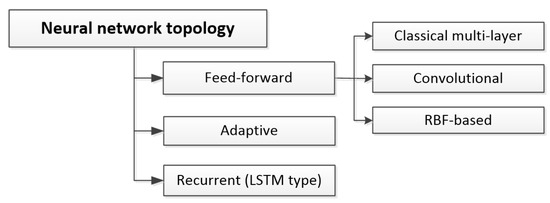
Figure 17.
Neural network topologies in research on hydraulic systems.
As is evident from the figure, the most commonly used topologies are feed-forward topologies, including multi-layer networks built of neurons with classical transfer functions or radial base functions and complex convolutional structures. However, there are also studies that utilize adaptive or recurrent architectures.
4. Conclusions
This perspective article is devoted to the vital issue of developing artificial intelligence (AI) techniques in scientific studies related to hydraulic systems and components. According to the statistics of leading databases of publications such as Scopus, recently, there has been a significant increase in interest in this subject. Hence, it is essential to conduct an analysis to identify leading development directions and technologies with prospects for the fastest growth. Based on the analyzed publications, the following detailed conclusions can be formulated:
- the technique of artificial neural networks (ANN) is used to the broadest extent, primarily for prediction, identification, control, and fault diagnosis. However, applications for classification, identification, and estimation can also be found;
- in the tasks of prediction, estimation, and classification, multi-layer feed-forward networks with classic transfer functions, such as sigmoid and hyperbolic tangent (tanh), are most often used;
- radial base neurons (RBF) with the Gaussian activation function are most often used for neural control;
- fault diagnosis, and to some extent identification, is most often implemented in the form of a complex convolutional neural network; in these cases, the ReLU-type transfer functions are particularly usable;
- training in the vast majority of cases is conducted using the traditional supervised method using the error backpropagation (BP) algorithm; however, there is a broad field here for the development of semi-supervised and non-supervised techniques;
- genetic algorithms and evolutionary swarm algorithms are used primarily to solve complex problems of multi-criteria optimization; the authors point to much better optimization results obtained by a properly designed population compared to traditional deterministic methods;
- other developing applications of evolutionary algorithms include fault diagnosis, while optimization is also performed using techniques such as neural networks and simulated annealing;
- fuzzy logic has the most remarkable development potential in the field of intelligent control systems, which can be standalone fuzzy units or combined with a traditional PID algorithm; however, there are also publications on the construction of fuzzy systems for fault detection or risk assessment.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
References
- Scopus Database. Available online: https://www.scopus.com/home.uri (accessed on 6 February 2023).
- WoS Database. Available online: https://www.webofscience.com/wos/woscc/basic-search (accessed on 10 February 2023).
- Su, W.; Ren, W.; Sun, H.; Liu, C.; Lu, X.; Hua, Y.; Wei, H.; Jia, H. Data-Based Flow Rate Prediction Models for Independent Metering Hydraulic Valve. Energies 2022, 15, 7699. [Google Scholar] [CrossRef]
- Guan, C.; Duan, Y.; Zhai, J.; Han, D. Hydraulic dynamics in split fuel injection on a common rail system and their artificial neural network prediction. Fuel 2019, 255, 115792. [Google Scholar] [CrossRef]
- Lu, Z.; Lai, H.; Zhou, L.; Shen, Z.; Ren, X.; Li, X. Prediction of hydraulic fracture initiation pressure in a borehole based on a neural network model considering plastic critical distance. Eng. Fract. Mech. 2022, 274, 108779. [Google Scholar] [CrossRef]
- Haghighi, A.; Shadloo, M.S.; Maleki, A.; Abdollahzadeh Jamalabadi, M.Y. Using Committee Neural Network for Prediction of Pressure Drop in Two-Phase Microchannels. Appl. Sci. 2020, 10, 5384. [Google Scholar] [CrossRef]
- Bahiraei, M.; Mazaheri, N.; Hosseini, S. Neural network modeling of thermo-hydraulic attributes and entropy generation of an ecofriendly nanofluid flow inside tubes equipped with novel rotary coaxial double-twisted tape. Powder Technol. 2020, 369, 162–175. [Google Scholar] [CrossRef]
- Tawfik, A.M. Hydraulic solutions of pipeline systems using artificial neural networks. Ain Shams Eng. J. 2023, 14, 101896. [Google Scholar] [CrossRef]
- Huo, D.; Chen, J.; Zhang, H.; Shi, Y.; Wang, T. Intelligent prediction for digging load of hydraulic excavators based on RBF neural network. Measurement 2023, 206, 112210. [Google Scholar] [CrossRef]
- Guo, Y.; Xiong, G.; Zeng, L.; Li, Q. Modeling and Predictive Analysis of Small Internal Leakage of Hydraulic Cylinder Based on Neural Network. Energies 2021, 14, 2456. [Google Scholar] [CrossRef]
- Neunzig, C.; Fahle, S.; Schulz, J.; Möller, M.; Kuhlenkötter, B. Model Selection for Predictive Quality in Hydraulic Testing. Proc. CIRP 2022, 107, 320–325. [Google Scholar] [CrossRef]
- Nie, S.; Liu, Q.; Ji, H.; Hong, R.; Nie, S. Integration of ARIMA and LSTM Models for Remaining Useful Life Prediction of a Water Hydraulic High-Speed On/Off Valve. Appl. Sci. 2022, 12, 8071. [Google Scholar] [CrossRef]
- Ryu, S.; Kim, H.; Kim, S.G.; Jin, K.; Cho, J.; Park, J. Probabilistic deep learning model as a tool for supporting the fast simulation of a thermal–hydraulic code. Expert Syst. Appl. 2022, 200, 116966. [Google Scholar] [CrossRef]
- Han, W.; Nan, L.; Su, M.; Chen, Y.; Li, R.; Zhang, X. Research on the Prediction Method of Centrifugal Pump Performance Based on a Double Hidden Layer BP Neural Network. Energies 2019, 12, 2709. [Google Scholar] [CrossRef]
- Guo, C.; Cui, Y. Utilizing artificial neural network to simulate and predict the hydraulic performance of free water surface constructed wetlands. J. Environ. Manag. 2022, 305, 114334. [Google Scholar] [CrossRef]
- Li, Z.; Jiang, W.; Zhang, S.; Xue, D.; Zhang, S. Research on Prediction Method of Hydraulic Pump Remaining Useful Life Based on KPCA and JITL. Appl. Sci. 2021, 11, 9389. [Google Scholar] [CrossRef]
- Gregov, G. Hydraulic GEROLER motor based on artificial neural network. Eng. Rev. 2022, 42, 91–100. [Google Scholar] [CrossRef]
- Brahma, I.; Jennings, R.; Freid, B. Using physics to extend the range of machine learning models for an aerodynamic, hydraulic and combusting system: The toy model concept. Energy AI 2021, 6, 100113. [Google Scholar] [CrossRef]
- Albalasmeh, A.; Mohawesh, O.; Gharaibeh, M.; Deb, S.; Slaughter, L.; El Hanandeh, A. Artificial neural network optimization to predict saturated hydraulic conductivity in arid and semi-arid regions. CATENA 2022, 217, 106459. [Google Scholar] [CrossRef]
- Jardani, A.; Vu, T.; Fischer, P. Use of convolutional neural networks with encoder-decoder structure for predicting the inverse operator in hydraulic tomography. J. Hydrol. 2022, 604, 127233. [Google Scholar] [CrossRef]
- Ye, J.; Do, N.C.; Zeng, W.; Lambert, M. Physics-informed neural networks for hydraulic transient analysis in pipeline systems. Water Res. 2022, 221, 118828. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, X. Convolutional Neural Network Identification of Stall Flow Patterns in Pump-Turbine Runners. Energies 2022, 15, 5719. [Google Scholar] [CrossRef]
- Haldar, A.; Chatterjee, S.; Kotia, A.; Kumar, N.; Ghosh, S.K. Analysis of rheological properties of MWCNT/SiO2 hydraulic oil nanolubricants using regression and artificial neural network. Int. Commun. Heat Mass Transf. 2020, 116, 104723. [Google Scholar] [CrossRef]
- Banaszek, A. Identification of optimal efficiency exploitation conditions of axial-piston hydraulic motor A2FM type using Artificial Neural Network algorithms. Proc. Comput. Sci. 2021, 192, 1532–1540. [Google Scholar] [CrossRef]
- Banaszek, A. Methodology of flow rate assessment of submerged hydraulic ballast pumps on modern product and chemical tankers with use of neural network methods. Proc. Comput. Sci. 2021, 192, 1894–1903. [Google Scholar] [CrossRef]
- Liao, Z.; Yan, H.; Tang, Z.; Chu, X.; Tao, T. Deep learning identifies leak in water pipeline system using transient frequency response. Process Saf. Environ. Prot. 2021, 155, 355–365. [Google Scholar] [CrossRef]
- Pan, Z.; Lu, W.; Wang, H.; Bai, Y. Fast inverse estimation of hydraulic conductivity field based on a deep convolutional-cycle generative adversarial neural network. J. Hydrol. 2022, 613, 128420. [Google Scholar] [CrossRef]
- Guo, Q.; Zhao, Y.; Lu, C.; Luo, J. High-dimensional inverse modeling of hydraulic tomography by physics informed neural network (HT-PINN). J. Hydrol. 2023, 616, 128828. [Google Scholar] [CrossRef]
- Vu, M.; Jardani, A. Mapping of hydraulic transmissivity field from inversion of tracer test data using convolutional neural networks. CNN-2T. J. Hydrol. 2022, 606, 127443. [Google Scholar] [CrossRef]
- Tran, D.T.; Nguyen, M.N.; Ahn, K.K. RBF Neural Network Based Backstepping Control for an Electrohydraulic Elastic Manipulator. Appl. Sci. 2019, 9, 2237. [Google Scholar] [CrossRef]
- Tran, D.T.; Truong, H.V.A.; Ahn, K.K. Adaptive Backstepping Sliding Mode Control Based RBFNN for a Hydraulic Manipulator Including Actuator Dynamics. Appl. Sci. 2019, 9, 1265. [Google Scholar] [CrossRef]
- Feng, H.; Song, Q.; Ma, S.; Ma, W.; Yin, C.; Cao, D.; Yu, H. A new adaptive sliding mode controller based on the RBF neural network for an electro-hydraulic servo system. ISA Trans. 2022, 129, 472–484. [Google Scholar] [CrossRef]
- Nguyen, M.H.; Dao, H.V.; Ahn, K.K. Adaptive Robust Position Control of Electro-Hydraulic Servo Systems with Large Uncertainties and Disturbances. Appl. Sci. 2022, 12, 794. [Google Scholar] [CrossRef]
- Homayoun, B.; Arefi, M.M.; Vafamand, N.; Yin, S. Neural minimal learning backstepping control of stochastic active suspension systems with hydraulic actuator saturation. J. Frankl. Inst. 2020, 357, 13687–13706. [Google Scholar] [CrossRef]
- Yakut, O. Implementation of hydraulically driven barrel shooting control by utilizing artificial neural networks. Math. Comput. Simul. 2021, 190, 1206–1223. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, D.; Xu, B.; Su, Q.; Lu, Z.; Wang, W. Flow control of a proportional directional valve without the flow meter. Flow Meas. Instrum. 2019, 67, 131–141. [Google Scholar] [CrossRef]
- Yang, G.; Yao, J. Multilayer neuroadaptive force control of electro-hydraulic load simulators with uncertainty rejection. Appl. Soft Comput. 2022, 130, 109672. [Google Scholar] [CrossRef]
- Yang, M.; Zhang, X.; Xia, Y.; Liu, Q.; Zhu, Q. Adaptive neural network-based sliding mode control for a hydraulic rotary drive joint. Comput. Electr. Eng. 2022, 102, 108189. [Google Scholar] [CrossRef]
- Yang, Y.; Li, Y.; Liu, X.; Huang, D. Adaptive neural network control for a hydraulic knee exoskeleton with valve deadband and output constraint based on nonlinear disturbance observer. Neurocomputing 2022, 473, 14–23. [Google Scholar] [CrossRef]
- He, S.; Wang, M.; Zhang, J.; Tian, W.; Qiu, S.; Su, G. A deep-learning reduced-order model for thermal hydraulic characteristics rapid estimation of steam generators. Int. J. Heat Mass Transf. 2022, 198, 123424. [Google Scholar] [CrossRef]
- Man, H.Q.; Hien, D.H.; Thong, K.D.; Dung, B.V.; Hoa, N.M.; Hoa, T.K.; Kieu, N.V.; Ngoc, P.Q. Hydraulic Flow Unit Classification and Prediction Using Machine Learning Techniques: A Case Study from the Nam Con Son Basin, Offshore Vietnam. Energies 2021, 14, 7714. [Google Scholar] [CrossRef]
- Makansi, F.; Schmitz, K. Data-Driven Condition Monitoring of a Hydraulic Press Using Supervised Learning and Neural Networks. Energies 2022, 15, 6217. [Google Scholar] [CrossRef]
- Kim, K.; Jeong, J. Deep Learning-based Data Augmentation for Hydraulic Condition Monitoring System. Proc. Comput. Sci. 2020, 175, 20–27. [Google Scholar] [CrossRef]
- Tang, S.; Zhu, Y.; Yuan, S. An improved convolutional neural network with an adaptable learning rate towards multi-signal fault diagnosis of hydraulic piston pump. Adv. Eng. Inform. 2021, 50, 101406. [Google Scholar] [CrossRef]
- Tang, S.; Zhu, Y.; Yuan, S. An adaptive deep learning model towards fault diagnosis of hydraulic piston pump using pressure signal. Eng. Fail. Anal. 2022, 138, 106300. [Google Scholar] [CrossRef]
- Tang, S.; Zhu, Y.; Yuan, S. Intelligent fault identification of hydraulic pump using deep adaptive normalized CNN and synchrosqueezed wavelet transform. Reliab. Eng. Syst. Saf. 2022, 224, 108560. [Google Scholar] [CrossRef]
- Tang, S.; Zhu, Y.; Yuan, S. A novel adaptive convolutional neural network for fault diagnosis of hydraulic piston pump with acoustic images. Adv. Eng. Inform. 2022, 52, 101554. [Google Scholar] [CrossRef]
- Tang, S.; Zhu, Y.; Yuan, S. Intelligent fault diagnosis of hydraulic piston pump based on deep learning and Bayesian optimization. ISA Trans. 2022, 129, 555–563. [Google Scholar] [CrossRef]
- Keleko, A.T.; Kamsu-Foguem, B.; Ngouna, R.H.; Tongne, A. Health condition monitoring of a complex hydraulic system using Deep Neural Network and DeepSHAP explainable XAI. Adv. Eng. Softw. 2023, 175, 103339. [Google Scholar] [CrossRef]
- Ebrahimzadeh, A.; Ghafari, M.; Moshkbar-Bakhshayesh, K. Detection and estimation of faulty sensors in NPPs based on thermal-hydraulic simulation and feed-forward neural network. Ann. Nucl. Energy 2022, 166, 108726. [Google Scholar] [CrossRef]
- Zhong, Q.; Xu, E.; Shi, Y.; Jia, T.; Ren, Y.; Yang, H.; Li, Y. Fault diagnosis of the hydraulic valve using a novel semi-supervised learning method based on multi-sensor information fusion. Mech. Syst. Signal Process. 2023, 189, 110093. [Google Scholar] [CrossRef]
- Ding, Y.; Ma, L.; Wang, C.; Tao, L. An EWT-PCA and Extreme Learning Machine Based Diagnosis Approach for Hydraulic Pump. IFAC-PapersOnLine 2020, 53, 43–47. [Google Scholar] [CrossRef]
- Xu, M.; Zeng, G.; Wu, D.; Mou, J.; Zhao, J.; Zheng, S.; Huang, B.; Ren, Y. Structural Optimization of Jet Fish Pump Design Based on a Multi-Objective Genetic Algorithm. Energies 2022, 15, 4104. [Google Scholar] [CrossRef]
- Qingtong, L.; Fanglong, Y.; Songlin, N.; Ruidong, H.; Hui, J. Multi-objective optimization of high-speed on-off valve based on surrogate model for water hydraulic manipulators. Fusion Eng. Des. 2021, 173, 112949. [Google Scholar] [CrossRef]
- Sun, X.; Wang, Y.; Zhang, J.; Lei, F.; Zhao, D.; Hong, H. Multi-Objective Optimization Design of Key Parameters of a Stepless Flow Control System with Multi-System Coupling Characteristics. Appl. Sci. 2022, 12, 1301. [Google Scholar] [CrossRef]
- Yang, M.; Yan, G.; Zhang, Y.; Zhang, T.; Ai, C. Research on high efficiency and high dynamic optimal matching of the electro-hydraulic servo pump control system based on NSGA-II. Heliyon 2023, 9, e13805. [Google Scholar] [CrossRef]
- Li, C.; Zhao, G.; Zhao, Y.; Fu, W.; Zheng, Z. Research on hydraulic loss of liquid ring vacuum pump and optimization of shell profile for high efficiency and energy saving. Vacuum 2023, 207, 111633. [Google Scholar] [CrossRef]
- Zhang, Y.; Peng, J.; Yang, R.; Yuan, L.; Li, S. Weight and performance optimization of rectangular staggered fins heat exchangers for miniaturized hydraulic power units using genetic algorithm. Case Stud. Therm. Eng. 2021, 28, 101605. [Google Scholar] [CrossRef]
- Nie, S.; Hong, R.; Ji, H.; Liu, Q.; Nie, S. A hybrid of surrogate model and MIGA method for optimization and compensation of steady-state flow force on water hydraulic HSV. Flow Meas. Instrum. 2022, 86, 102176. [Google Scholar] [CrossRef]
- Zhou, W.; Zhang, L.; Wu, P.; Cai, Y.; Zhao, X.; Yao, C. Hydraulic performance and parameter optimisation of a microporous ceramic emitter using computational fluid dynamics, artificial neural network and multi-objective genetic algorithm. Biosyst. Eng. 2020, 189, 11–23. [Google Scholar] [CrossRef]
- Ntiri Asomani, S.; Yuan, J.; Wang, L.; Appiah, D.; Adu-Poku, K.A. The Impact of Surrogate Models on the Multi-Objective Optimization of Pump-As-Turbine (PAT). Energies 2020, 13, 2271. [Google Scholar] [CrossRef]
- Chen, J.; Zheng, Y.; Zhang, L.; He, G.; Zou, Y.; Xiao, Z. Optimization of geometric parameters of hydraulic turbine runner in turbine mode based on the orthogonal test method and CFD. Energy Rep. 2022, 8, 14476–14487. [Google Scholar] [CrossRef]
- Xu, G.; Feng, Z.; Guo, E.; Cai, C.; Ding, H. Multi-objective optimization of hydraulic shovel using evolutionary algorithm. Autom. Constr. 2022, 142, 104486. [Google Scholar] [CrossRef]
- Incebay, O.; Onder, A.; Arif Sen, M.; Yapici, R.; Kalyoncu, M. Fuzzy-based modeling and speed optimization of a centrifugal blood pump using a modified and constrained Bees algorithm. Comput. Methods Programs Biomed. 2022, 221, 106867. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Kumar, T.C.A.; Elmasry, Y.; Singh, P.K.; Abed, A.M.; Algarni, A.D.; Nguyen, V.N.; Wae-hayee, M.; Phong Nguyen, P.Q.; Galal, A.M. Response Surface Methodology and Artificial Neural Network modelings on hydraulic and thermal performances of a disk-shaped heat sink with tree-like microchannels. Case Stud. Therm. Eng. 2022, 40, 102539. [Google Scholar] [CrossRef]
- Yan, J.; Kong, H.; Man, Z. Recurrent Neural Network-Based Nonlinear Optimization for Braking Control of Electric Vehicles. Energies 2022, 15, 9486. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, G.; Tang, S.; Wang, R.; Su, H.; Wang, C. Acoustic signal-based fault detection of hydraulic piston pump using a particle swarm optimization enhancement CNN. Appl. Acoust. 2022, 192, 108718. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, G.; Wang, R.; Tang, S.; Su, H.; Cao, K. Intelligent fault diagnosis of hydraulic piston pump combining improved LeNet-5 and PSO hyperparameter optimization. Appl. Acoust. 2021, 183, 108336. [Google Scholar] [CrossRef]
- Jose, J.T.; Das, J.; Mishra, S.K.; Wrat, G. Early detection and classification of internal leakage in boom actuator of mobile hydraulic machines using SVM. Eng. Appl. Artif. Intell. 2021, 106, 104492. [Google Scholar] [CrossRef]
- Kong, X.; Cai, B.; Liu, Y.; Zhu, H.; Liu, Y.; Shao, H.; Yang, C.; Li, H.; Mo, T. Optimal sensor placement methodology of hydraulic control system for fault diagnosis. Mech. Syst. Signal Process. 2022, 174, 109069. [Google Scholar] [CrossRef]
- Pan, J.; Khajepour, A.; Li, Y.; Yang, J.; Liu, W. Performance and power consumption optimization of a hydraulic variable valve actuation system. Mechatronics 2021, 73, 102479. [Google Scholar] [CrossRef]
- Meira, W.H.T.; Magatão, L.; Neves-Jr, F.; Arruda, L.V.; Vaqueiro, J.P.; Relvas, S.; Barbosa-Póvoa, A.P. Scheduling of a single-source multiproduct pipeline system by a matheuristic approach: Combining simulated annealing and MILP. Comput. Chem. Eng. 2020, 136, 106784. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, T.; Hong, J.; Zhang, H.; Zhao, Q.; Meng, Z. Research on driving control strategy and Fuzzy logic optimization of a novel mechatronics-electro-hydraulic power coupling electric vehicle. Energy 2021, 233, 121221. [Google Scholar] [CrossRef]
- Li, L.; Zhang, T.; Hong, J.; Zhang, H.; Yang, J.; Zhang, Z.; Wu, K. Energy management strategy of a novel mechanical–electro–hydraulic power coupling electric vehicle under smooth switching conditions. Energy Rep. 2022, 8, 8002–8016. [Google Scholar] [CrossRef]
- Han, J.; Wang, F.; Wang, Y. A Control Method for the Differential Steering of Tracked Vehicles Driven Independently by a Dual Hydraulic Motor. Appl. Sci. 2022, 12, 6355. [Google Scholar] [CrossRef]
- Wrat, G.; Bhola, M.; Ranjan, P.; Mishra, S.K.; Das, J. Energy saving and Fuzzy-PID position control of electro-hydraulic system by leakage compensation through proportional flow control valve. ISA Trans. 2020, 101, 269–280. [Google Scholar] [CrossRef] [PubMed]
- Jin, X.; Chen, K.; Zhao, Y.; Ji, J.; Jing, P. Simulation of hydraulic transplanting robot control system based on fuzzy PID controller. Measurement 2020, 164, 108023. [Google Scholar] [CrossRef]
- Jiang, C.; Sui, S.; Tong, S. Finite-time fuzzy adaptive output feedback control of electro-hydraulic system with actuator faults. Inf. Sci. 2023, 623, 577–591. [Google Scholar] [CrossRef]
- Ma, T.; Wang, B.; Zhang, Z.; Ai, B. A Takagi-Sugeno fuzzy-model-based finite-time H-infinity control for a hydraulic turbine governing system with time delay. Int. J. Electr. Power Energy Syst. 2021, 132, 107152. [Google Scholar] [CrossRef]
- Ma, T.; Wang, B. Disturbance observer-based Takagi-Sugeno fuzzy control of a delay fractional-order hydraulic turbine governing system with elastic water hammer via frequency distributed model. Inf. Sci. 2021, 569, 766–785. [Google Scholar] [CrossRef]
- Hu, G.; Phan, H.; Ouache, R.; Gandhi, H.; Hewage, K.; Sadiq, R. Fuzzy fault tree analysis of hydraulic fracturing flowback water storage failure. J. Nat. Gas Sci. Eng. 2019, 72, 103039. [Google Scholar] [CrossRef]
- Kargar, V.; Jahangiri, M.; Alimohammadlu, M.; Kamalinia, M.; Mirazahossieninejad, M. Risk assessment of mobile crane overturning in Asymmetric Tandem Lifting (ATL) operation based on fuzzy fault tree analysis (FFTA). Results Eng. 2022, 16, 100755. [Google Scholar] [CrossRef]
- Yu, J.; Zeng, Q.; Yu, Y.; Wu, S.; Ding, H.; Gao, H.; Yang, J. An intuitionistic fuzzy probabilistic Petri net method for risk assessment on submarine pipeline leakage failure. Ocean. Eng. 2022, 266, 112788. [Google Scholar] [CrossRef]
- Milton-Thompson, O.; Javadi, A.A.; Kapelan, Z.; Cahill, A.G.; Welch, L. Developing a fuzzy logic-based risk assessment for groundwater contamination from well integrity failure during hydraulic fracturing. Sci. Total Environ. 2021, 769, 145051. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).