Second-Life Battery Capacity Estimation and Method Comparison
Abstract
:1. Introduction
- Nearly all the published techniques start with a new battery and assume its end of useful life is 80%, whereas second-life batteries start with an 80% remaining capacity battery [1,2,3]. There are, therefore, very few published records of how batteries degrade below 80% of remaining capacity [4,5,6].
- Nearly all the published data assumed the cycling is from 0% to 100% DOD with no variations. Second-life batteries will undergo different cycling depending on their application and, therefore, they will not be following just a 100% charge/discharge curve. Some of the published methods are adaptable to deal with varying DOD, but it is by no means clear if the adjustments are valid [2].
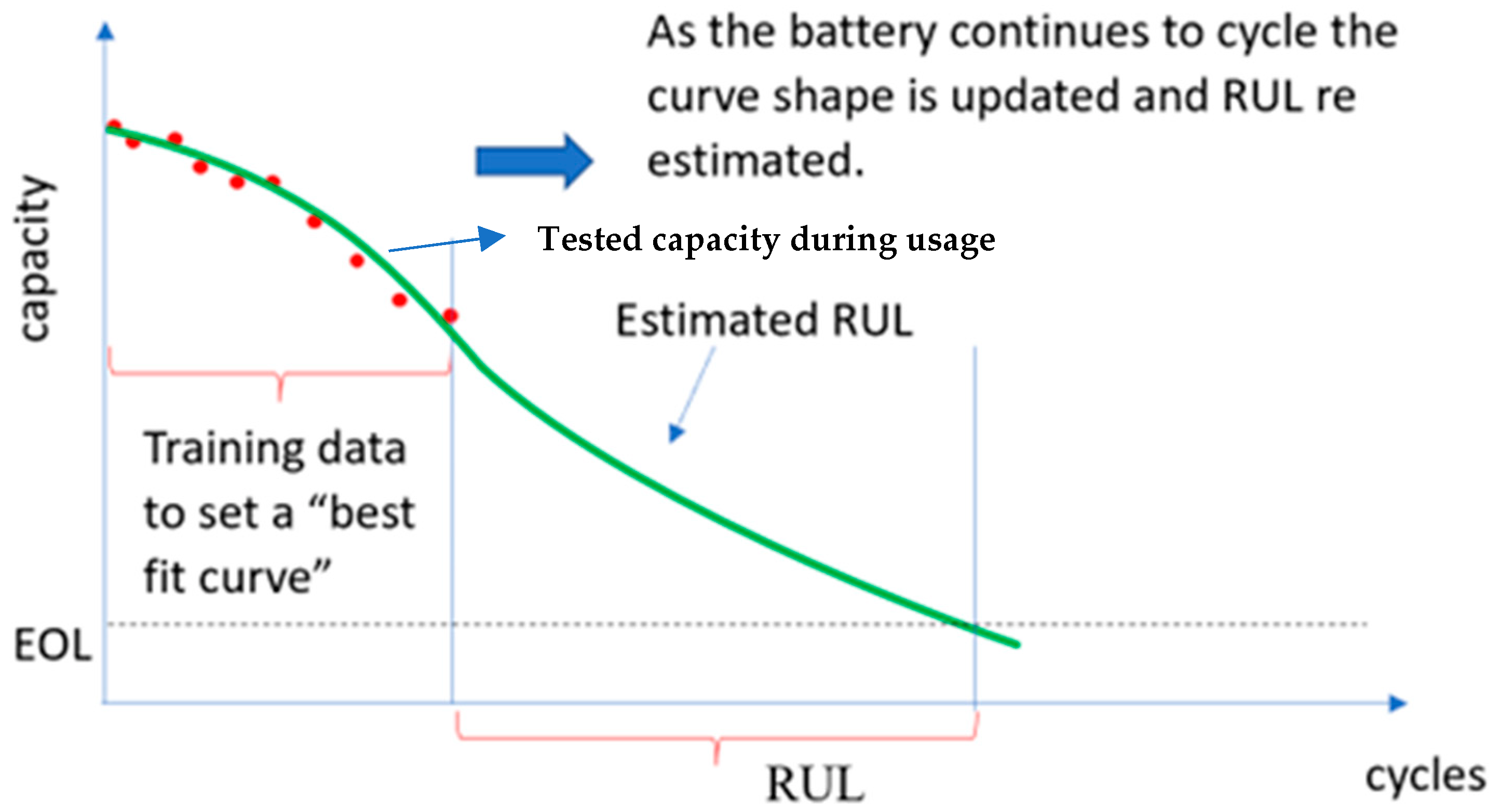
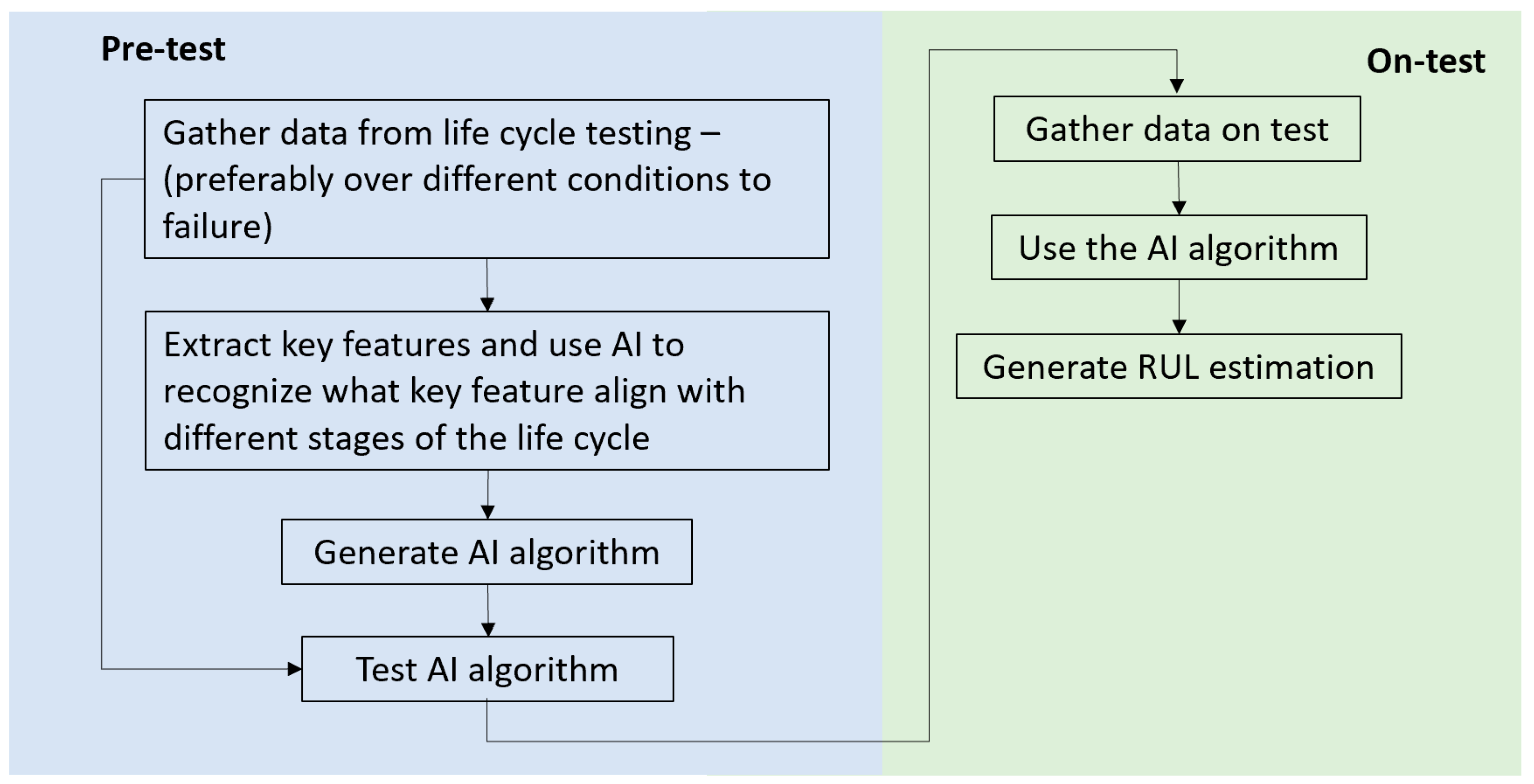
2. Remaining Useful Life Estimation
| Ref. | Chemistry | Cycling |
|---|---|---|
| [1] | LiFePO4 in cylindrical packaging | Capacity range: 100% to 80% of life Cycling conditions: Nine batteries with varying temperature, cycle depth, and number of cycles. |
| [2] | LiFePO4 in cylindrical packaging (2.2 Ah) | Capacity range: 100% to 80% of life Cycling conditions: Two batteries under each condition below. temperature (−30 °C, 0 °C, 15 °C, 25 °C, 45 °C, 60 °C), DOD (90%, 80%, 50%, 20%, 10%) and charge/discharge rate (C/2, 2C, 6C, and 10C) |
| [4] | LiMn2O4 in prismatic package (40 Ah and 80 Ah) | Capacity range: 100% to 30% of life Cycling conditions: Capacity tests with trickle charge rest periods, up to 1600 days testing. Cycle charge/discharge number and process are not clear as the results are in test days only |
| [7] | LiNiCoMnO2 in a cylindrical package | Capacity range: 95% to 75% Cycling conditions: Two (small) batteries cycled to 100% DOD (with over charge and over discharge to aid degradation) for around 100 cycles. Life estimation based on curve fitting an equation to the data. |
| [3,5,6,14,16,17,18] | LiCoO2 | Nasa dataset (all or part of) [28] Capacity range: 100% to 70% Cycling conditions: Li-ion 18,650 sized rechargeable batteries were cycled to 100% DOD from new to 70% capacity (2 Ah to 1.4 Ah). Life estimation based on curve fitting an equation to the data. |
| [3,14,16,17] | LiCoO2 | Maryland data set [29] Capacity range: 100% to 80% capacity range |
| [15] | LiCoO2 (probably) | Capacity range: 100–50% Cycling conditions: Two types of small cells with four of each, full charge and discharge cycle for around 200–800 cycles depending on type. |
| [11] | NiMH | Capacity range: 50–0% Cycling conditions: Two small cells full charge and discharge cycle for around 85 cycles. |
| [30] | Li Ion | Oxford university data set [31] Cycling conditions: Up to 3600 charging cycles, looking for changes in the incremental capacity data as a function of probability. |
| [12] | LiFePO4 | Cycling conditions: Four small cells, full charge and discharge cycle for between 363 to 1549 cycles, undertaken during charging above 70% SOC. |
| [32] | LiCoO2 | Capacity range: 100–70% Cycling conditions: At least seven small cells at discharge rates of 10% to 90% DOD with up to 4000+ cycles recorded at 50% DOD. |
| [33] | Lithium Ion | Capacity range: 100%-70% Cycling conditions: Small cells at 0.5C discharge for 1000 cycles. |
| [18] | Li(NiCoMn)1/3O2 | Capacity range: 100–80% Cycling conditions: Six small cells over 840 cycles undertaken at high temperature to speed aging. |
| [34] | Li(NiCoAl)O2 Panasonic cylindrical | Capacity range: 100% to about 60–70% Cycling conditions: 18 small cells undertaking 100% DOD charge and discharge cycles at cycle rates of 0.5C, 1C, and 2C at different temperatures. Up to 800 cycles recorded. |
| [22] | Lithium Ion | Capacity range: 100–80% Cycling conditions: Two small groups of cells, between 2500 cycles, one set with mechanical vibration. |
| [23] | Li(NiCoAl)O2 cylindrical batteries | Capacity range: 100–80% (approx.) Cycling conditions: 0-100% DOD cycles at different charge rates (1C, 2C and 3.5C) and temperature (25 °C and 40 °C) to around 600 cycles. |
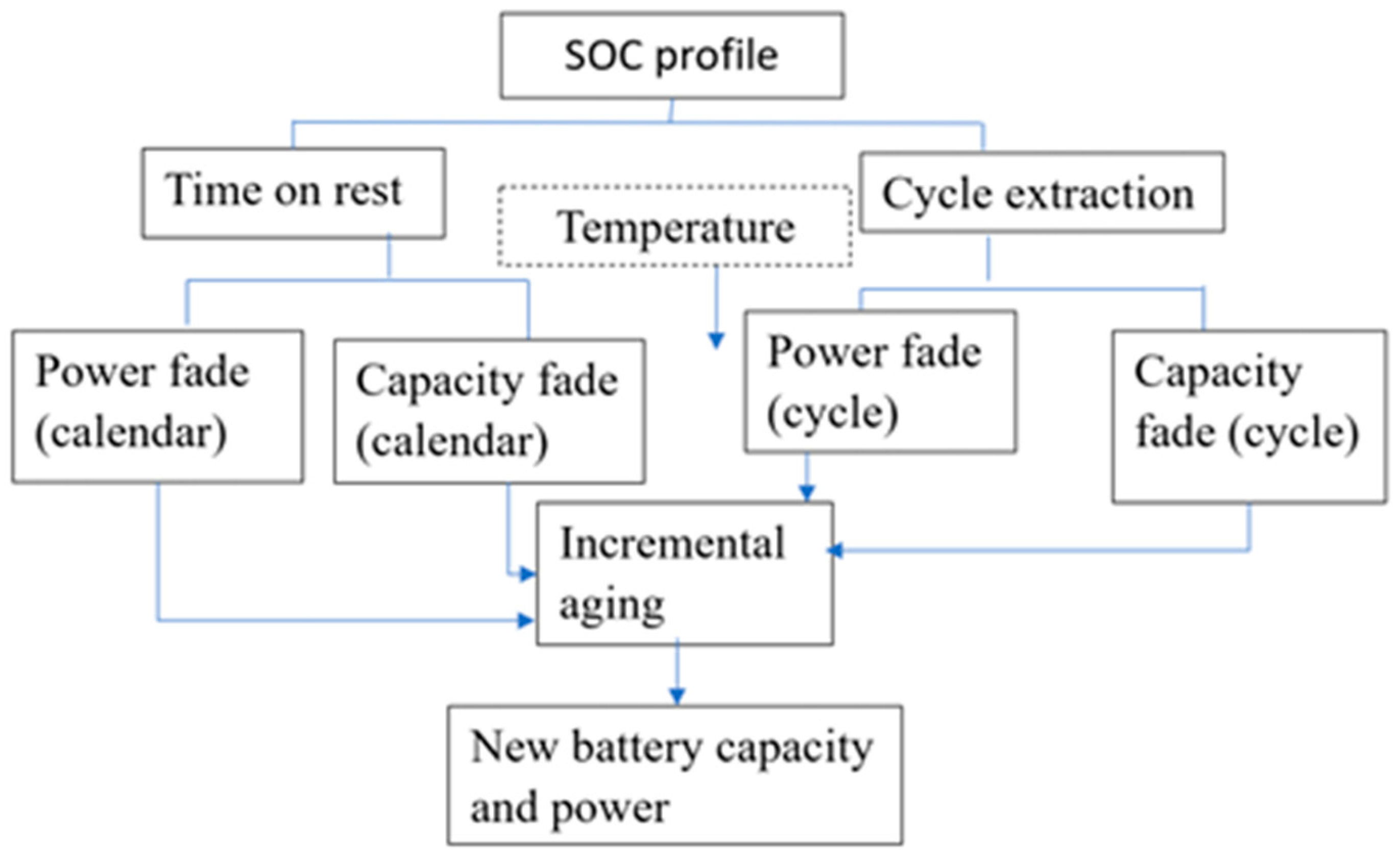
2.1. Method Used by Swierczynski et al.
- is the estimate of power fade (calendric);
- is the state of charge the battery is stored at (%);
- T is the temperature of storage in °C;
- t is the storage time;
- is the capacity fade (calendric);
- is the estimate of power fade (cyclic);
- is the cycle depth (%);
- nc is the number of cycles;
- is the capacity fade (cyclic).
2.2. Method Used by Wang et al.
- , is the percentage of capacity loss;
- B is the pre-exponential factor;
- Ea is the activation energy in J mol−1;
- R is the gas constant;
- T is the temperature in Kelvin;
- Ah is the Ah throughput, which is expressed as Ah = (cycle number) × (DOD) × (full cell capacity), and z is the power law factor.
2.3. Method Used by Matsushima et al.
- is the rate constant;
- t is time to reach 70% capacity;
- correlates with temperature and satisfies the relationship for cells between 100–70% degradation;
- is the rate constant;
- T is temperature in K.
2.4. Method Used by He et al.
- is the capacity at the kth cycle.
2.5. Method Used by Dogger et al.
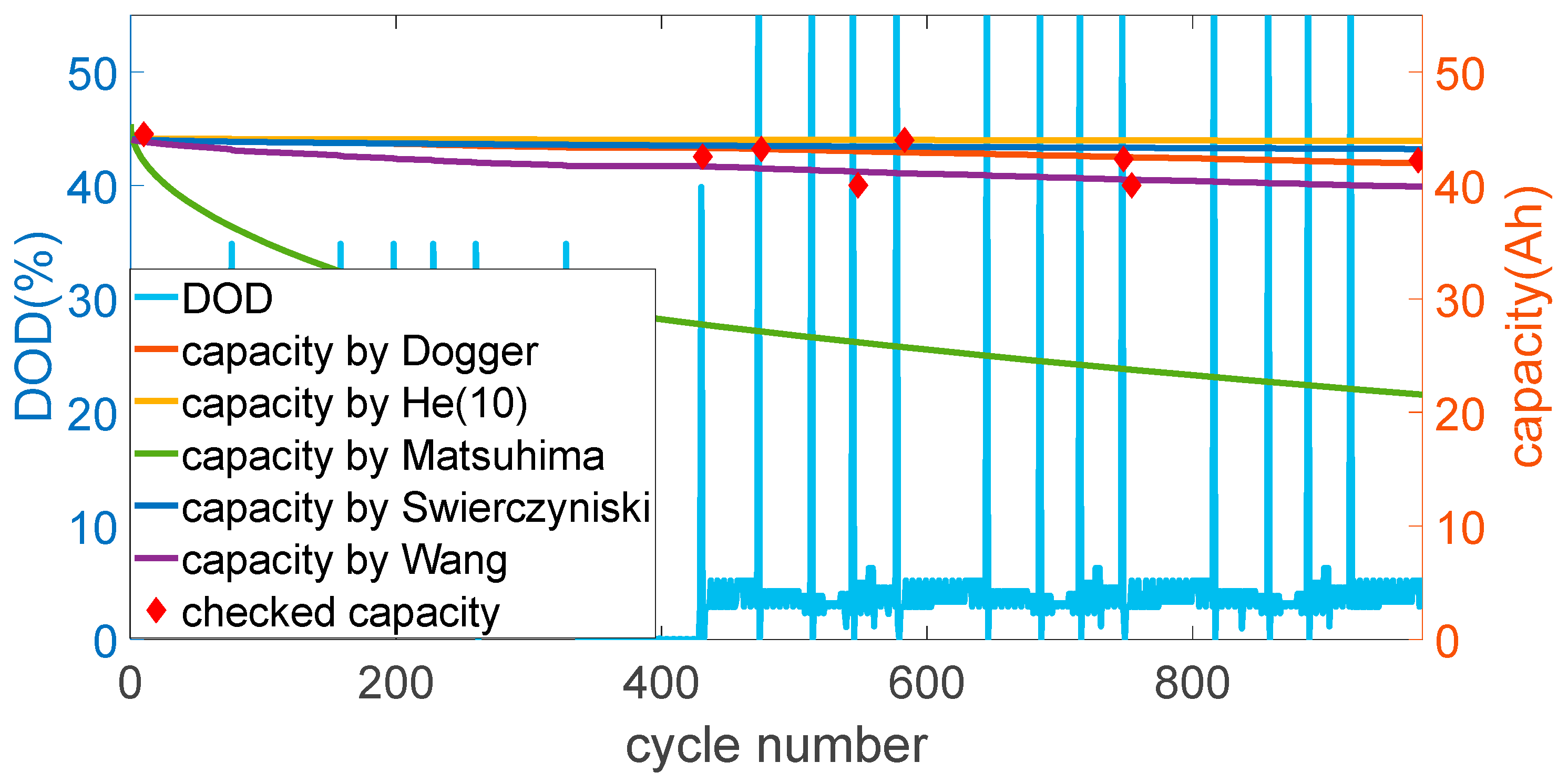
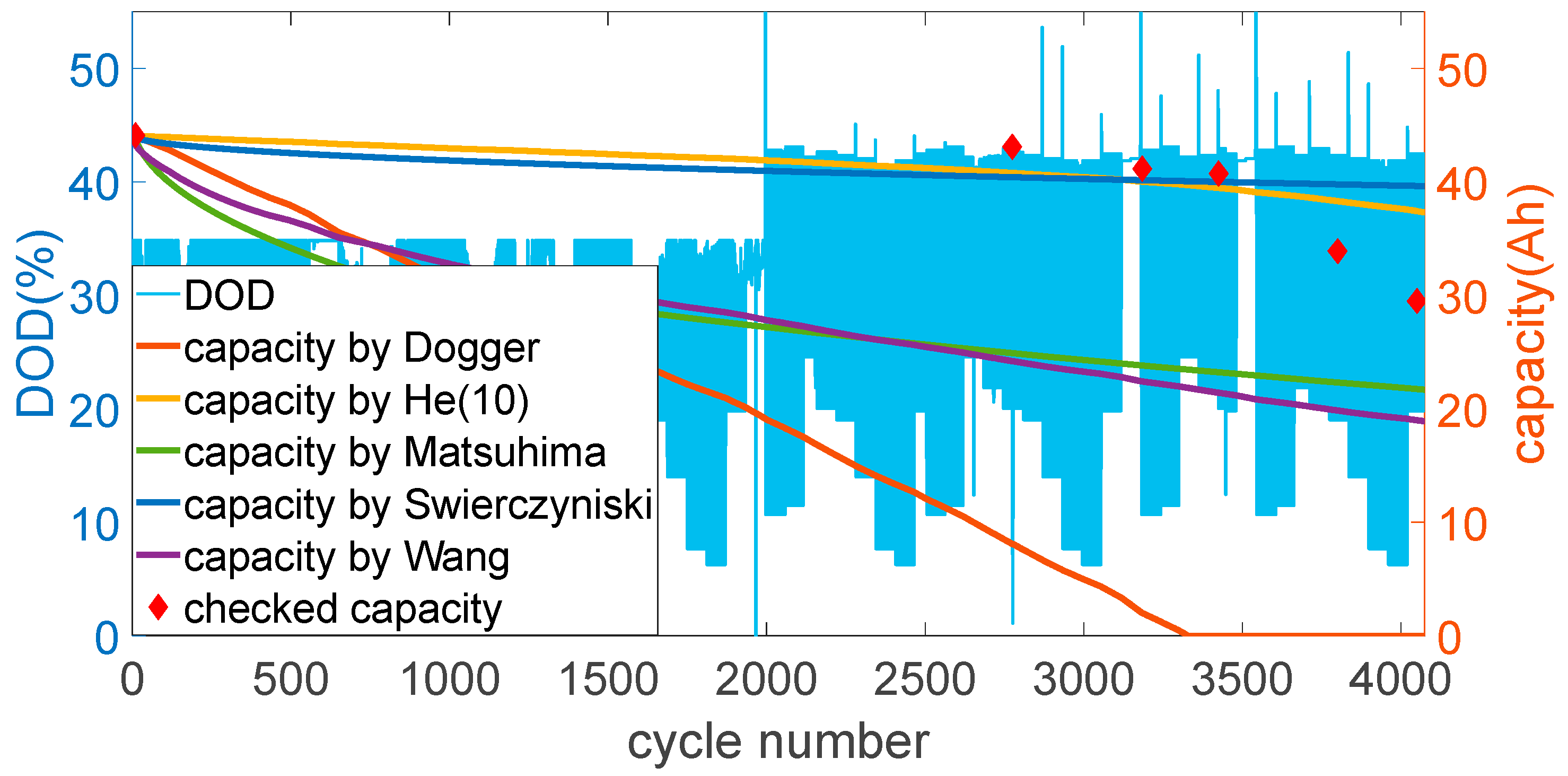
3. Cycle Testing
- Min cell voltage 5 V/module
- Nominal cell voltage 7.5 V/module
- Max cell voltage 8.3 V/module
- Capacity at new 66 Ah
- Q is the charge being estimated in Ah;
- I is the discharging current in A;
- T is discharging time in hour.
- A house with four people and a solar panel using the battery to absorb extra energy when the PV panel is producing more power than is absorbed in the house, releasing this energy afterwards.
- A house with four people and PV panels on a time-of-use tariff, where the battery is used to absorb extra energy from the PV panel and release this when the tariff is highest.
- A house with four people and no PV on a time-of-use tariff—where the battery is charged at low tariff and discharged on high tariff.
- The battery is operating as part of an aggregated static frequency response system performing on the UK Fast Frequency Response (FFR) market.
- The battery is operating as part of an aggregated dynamic frequency response system performing on the UK Enhanced Frequency Response (EFR) market.
- The battery is operating as part of an aggregated system looking to compete in the day ahead market.
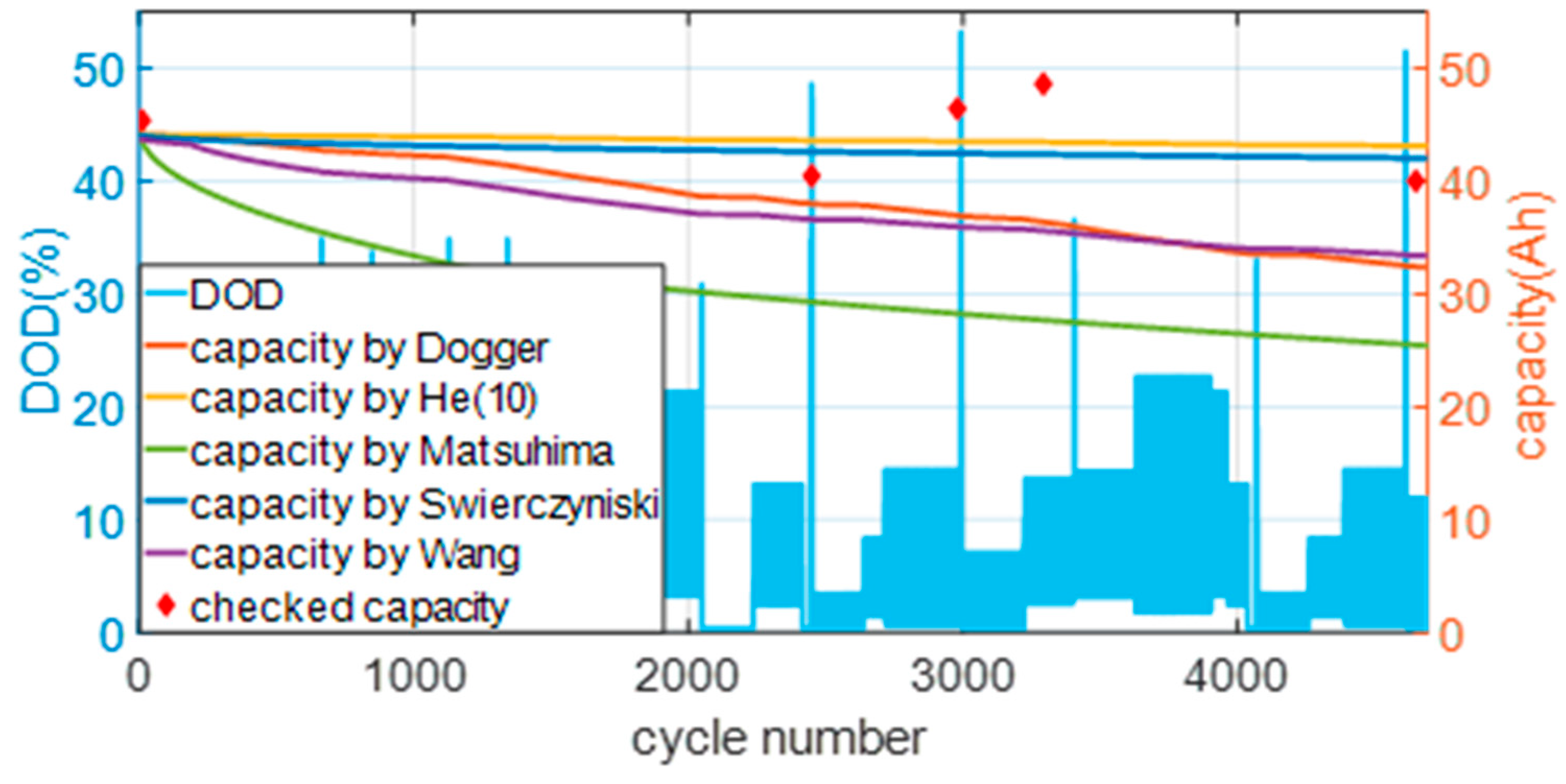
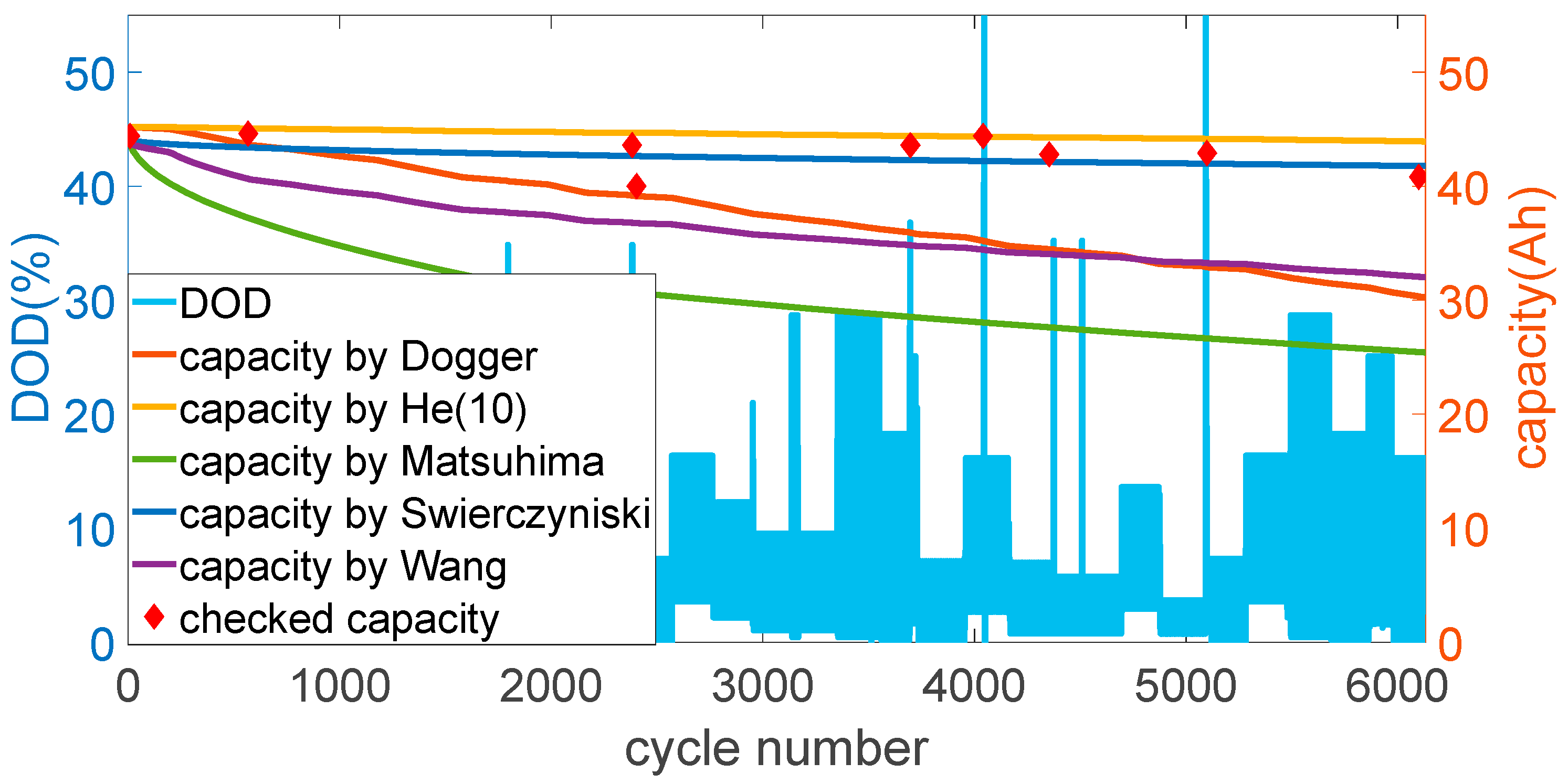
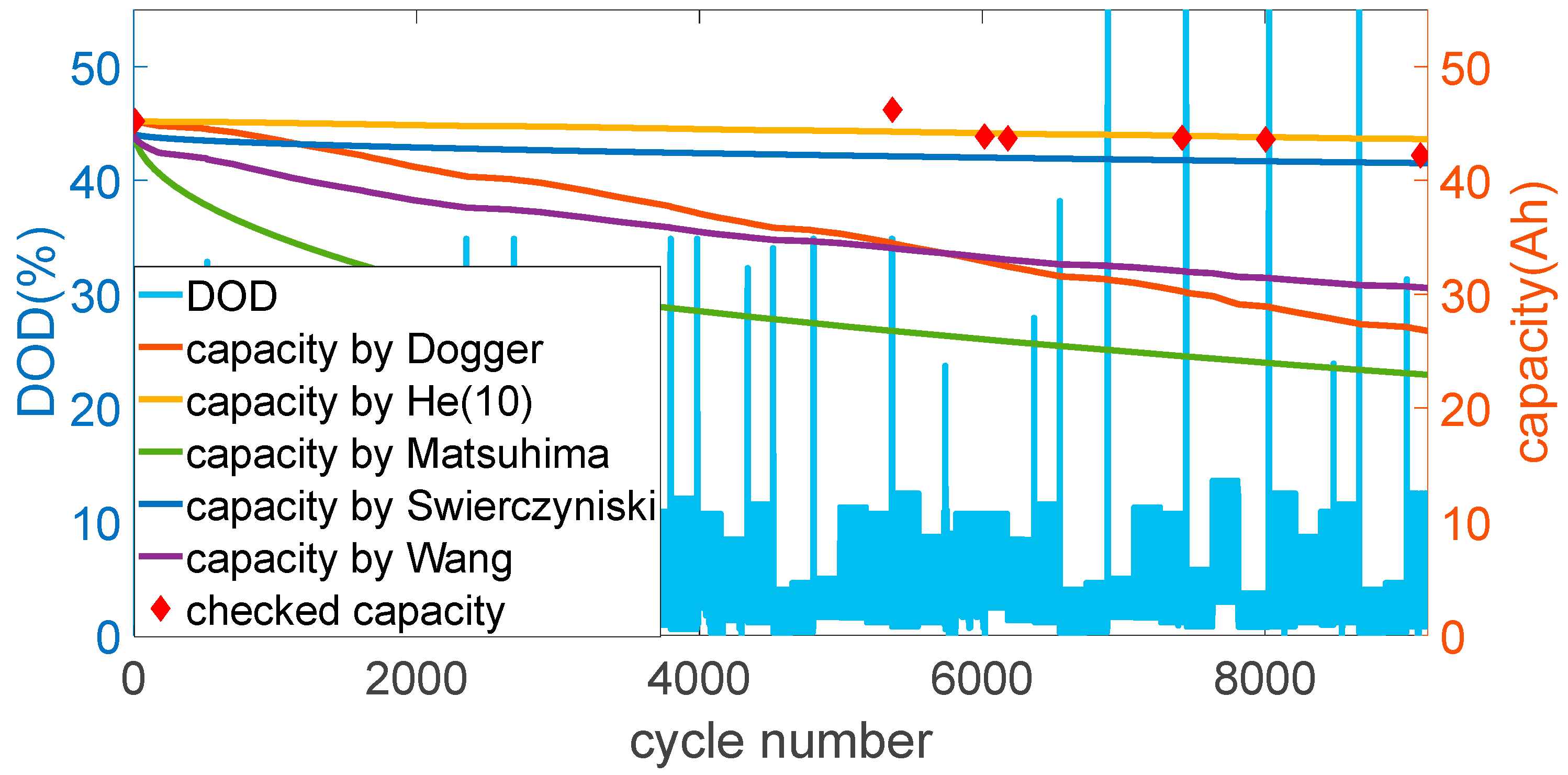
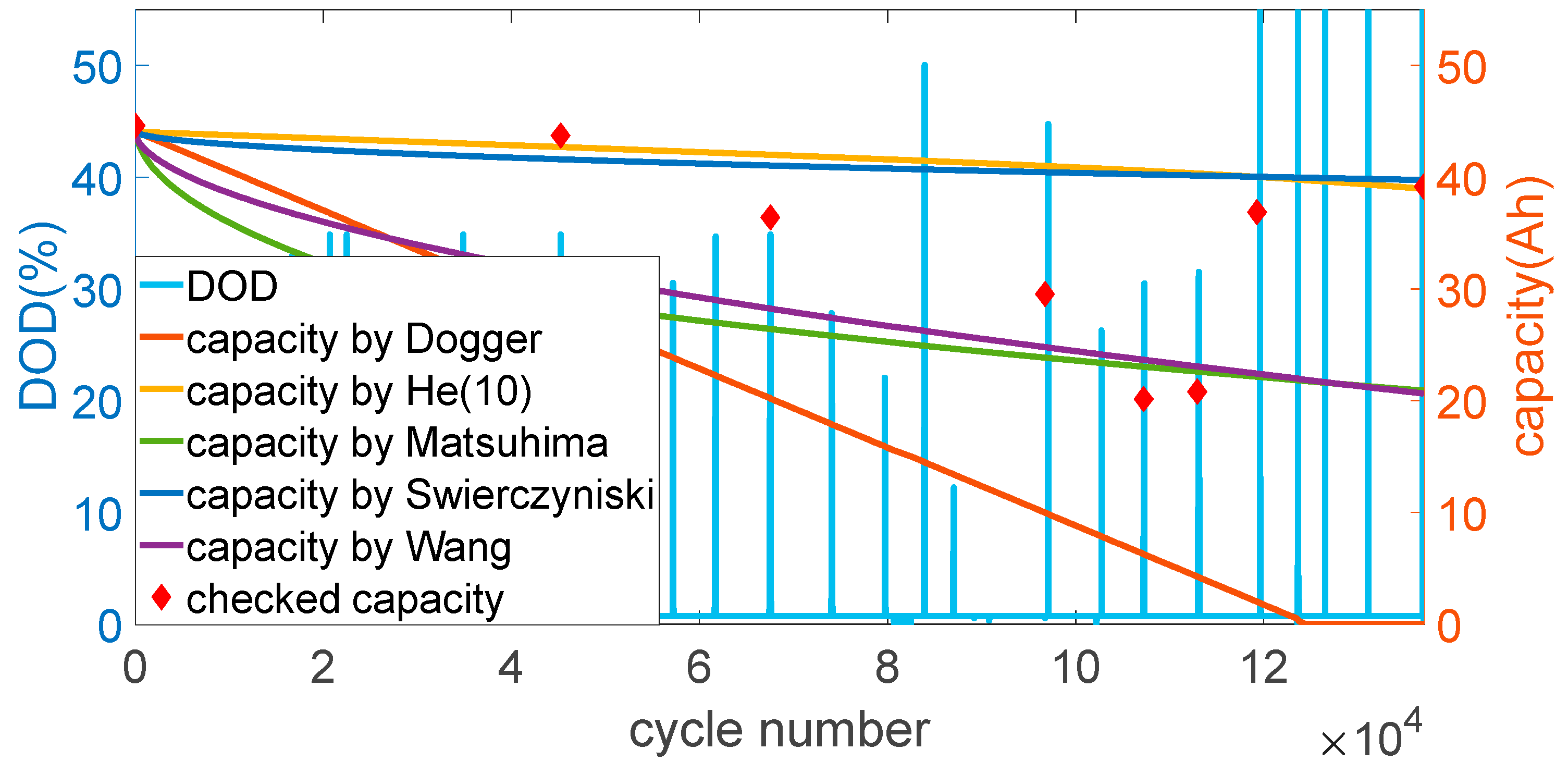
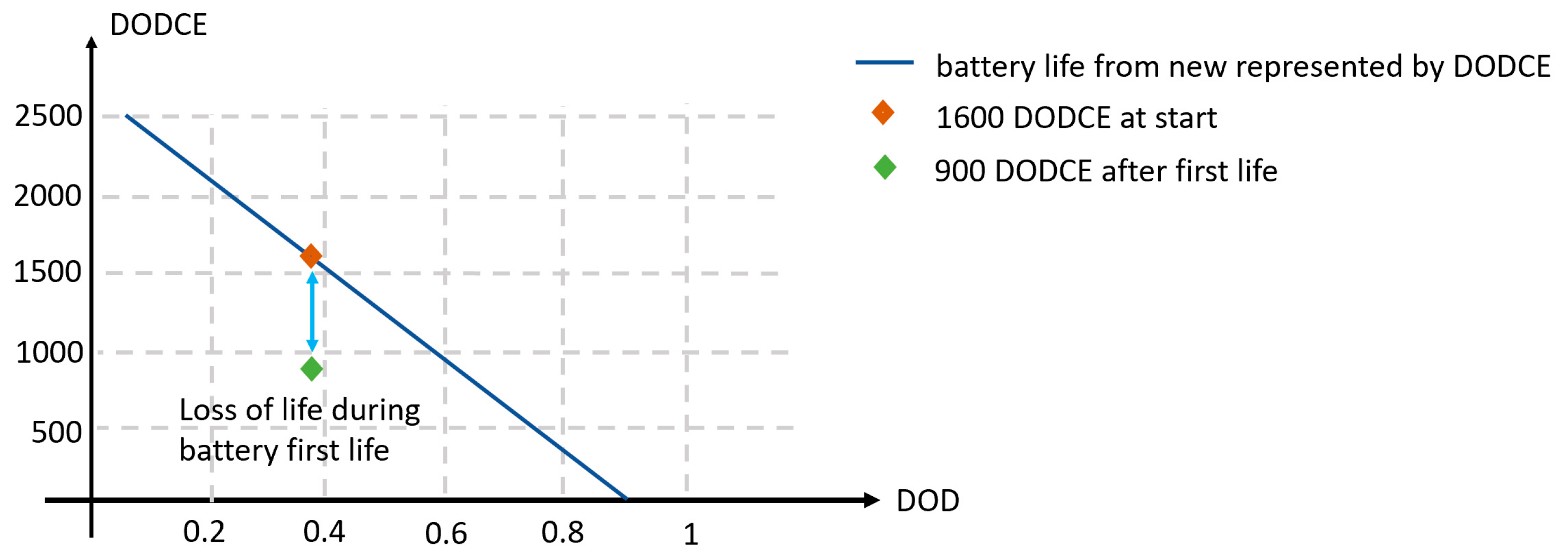
4. Life Cycle Modelling
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation | Meaning |
| DOD | Depth of discharge |
| RUL | Remaining useful life |
| EOL | End of life |
| AI | Artificial Intelligence |
| SVM | Support vector machine |
| SOC | State of charge |
| DODCE | DoD cycle equivalent |
| CC-CV | Constant current-Constant voltage |
| PV | Photovoltaics |
References
- Swierczynski, M.; Stroe, D.-I.; Stan, A.-I.; Teodorescu, R.; Kaer, S.K. Lifetime Estimation of the Nanophosphate LiFePO4C Battery Chemistry Used in Fully Electric Vehicles. IEEE Trans. Ind. Appl. 2015, 51, 3453–3461. [Google Scholar] [CrossRef]
- Wang, J.; Liu, P.; Hicks-Garner, J.; Sherman, E.; Soukiazian, S.; Verbrugge, M.; Tataria, H.; Musser, J.; Finamore, P. Cycle-life model for graphite-LiFePO4 cells. J. Power Sources 2011, 196, 3942–3948. [Google Scholar] [CrossRef]
- Long, B.; Xian, W.; Jiang, L.; Liu, Z. An improved autoregressive model by particle swarm optimization for prognostics of lithium-ion batteries. Microelectron. Reliab. 2013, 53, 821–831. [Google Scholar] [CrossRef]
- Matsushima, T. Deterioration estimation of lithium-ion cells in direct current power supply systems and characteristics of 400-Ah lithium-ion cells. J. Power Sources 2009, 189, 847–854. [Google Scholar] [CrossRef]
- Li, F.; Xu, J. A new prognostics method for state of health estimation of lithium-ion batteries based on a mixture of Gaussian process models and particle filter. Microelectron. Reliab. 2015, 55, 1035–1045. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiong, R.; He, H.; Pecht, M.G. Lithium-Ion Battery Remaining Useful Life Prediction With Box–Cox Transformation and Monte Carlo Simulation. IEEE Trans. Ind. Electron. 2018, 66, 1585–1597. [Google Scholar] [CrossRef]
- Pan, C. Lithium-ion Battery Remaining Useful Life Prediction Based on Exponential Smoothing and Particle Filter. Int. J. Electrochem. Sci. 2019, 14, 9537–9551. [Google Scholar] [CrossRef]
- Si, X.-S.; Wang, W.; Hu, C.-H.; Zhou, D.-H. Remaining useful life estimation—A review on the statis-tical data driven approaches. Eur. J. Oper. Res. 2011, 213, 1–14. [Google Scholar] [CrossRef]
- Shunli, W.; Siyu, J.; Dan, D.; Carlos, F. A Critical Review of Online Battery Remaining Useful Lifetime Prediction Methods. Front. Mech. Eng. 2021, 7, 719718. [Google Scholar]
- Wu, L.; Fu, X.; Guan, Y. Review of the Remaining Useful Life Prognostics of Vehicle Lithium-Ion Batteries Using Data-Driven Methodologies. Appl. Sci. 2016, 6, 166. [Google Scholar] [CrossRef] [Green Version]
- Micea, M.V.; Ungurean, L.; Carstoiu, G.N.; Groza, V. Online State-of-Health Assessment for Battery Management Systems. IEEE Trans. Instrum. Meas. 2011, 60, 1997–2006. [Google Scholar] [CrossRef]
- Wang, L.; Pan, C.; Liu, L.; Cheng, Y.; Zhao, X. On-board state of health estimation of LiFePO4 battery pack through differential voltage analysis. Appl. Energy 2016, 168, 465–472. [Google Scholar] [CrossRef]
- Liu, W.; Xu, Y. Data-Driven Online Health Estimation of Li-Ion Batteries Using A Novel Energy-Based Health Indicator. IEEE Trans. Energy Convers. 2020, 35, 1715–1718. [Google Scholar] [CrossRef]
- Chen, Y.; He, Y.; Li, Z.; Chen, L.; Zhang, C. Remaining Useful Life Prediction and State of Health Diagnosis of Lithium-Ion Battery Based on Second-Order Central Difference Particle Filter. IEEE Access 2020, 8, 37305–37313. [Google Scholar] [CrossRef]
- He, W.; Williard, N.; Osterman, M.; Pecht, M. Prognostics of lithium-ion batteries based on Dempster–Shafer theory and the Bayesian Monte Carlo method. J. Power Sources 2011, 196, 10314–10321. [Google Scholar] [CrossRef]
- Dong, G.; Chen, Z.; Wei, J.; Ling, Q. Battery Health Prognosis Using Brownian Motion Modeling and Particle Filtering. IEEE Trans. Ind. Electron. 2018, 65, 8646–8655. [Google Scholar] [CrossRef]
- Xu, X.; Yu, C.; Tang, S.; Sun, X.; Si, X.; Wu, L. Remaining Useful Life Prediction of Lithium-Ion Batteries Based on Wiener Processes with Considering the Relaxation Effect. Energies 2019, 12, 1685. [Google Scholar] [CrossRef] [Green Version]
- Tang, S.; Yu, C.; Wang, X.; Guo, X.; Si, X. Remaining Useful Life Prediction of Lithium-Ion Batteries Based on the Wiener Process with Measurement Error. Energies 2014, 7, 520–547. [Google Scholar] [CrossRef] [Green Version]
- Patil, M.A.; Tagade, P.; Hariharan, K.S.; Kolake, S.M.; Song, T.; Yeo, T.; Doo, S. A novel multistage Support Vector Machine based approach for Li ion battery remaining useful life estimation. Appl. Energy 2015, 159, 285–297. [Google Scholar] [CrossRef]
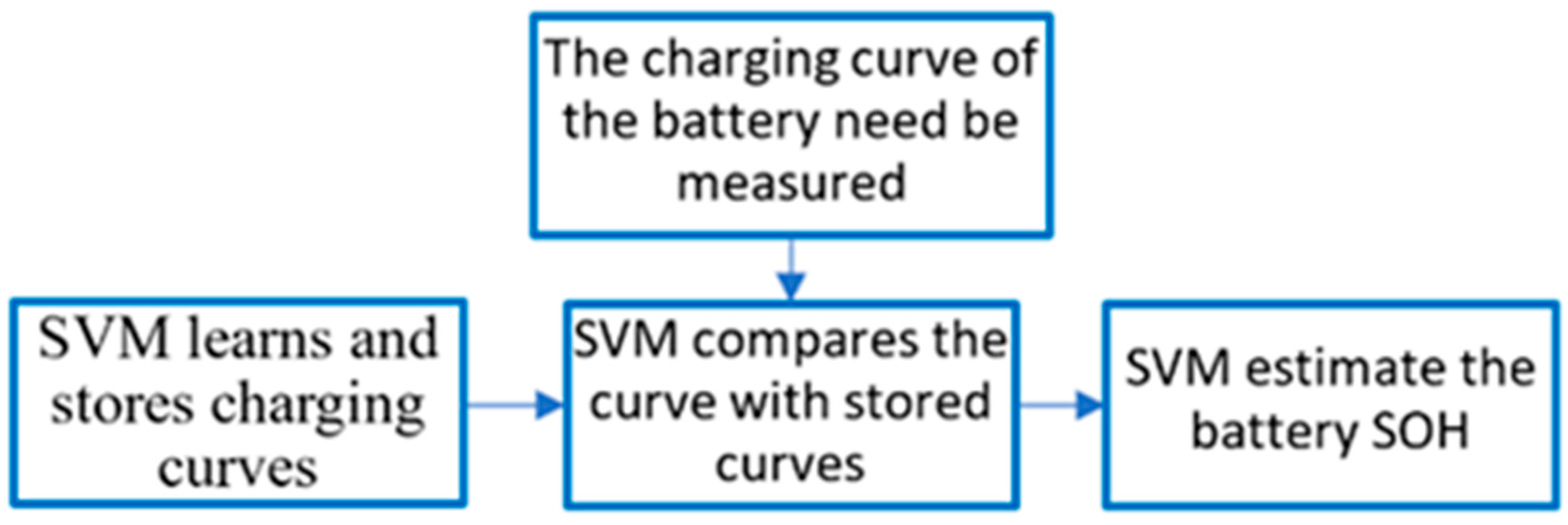
- Feng, X.; Weng, C.; He, X.; Han, X.; Lu, L.; Ren, D.; Ouyang, M. Online State-of-Health Estimation for Li-Ion Battery Using Partial Charging Segment Based on Support Vector Machine. IEEE Trans. Veh. Technol. 2019, 68, 8583–8592. [Google Scholar] [CrossRef]
- Liu, D.; Zhou, J.; Liao, H.; Peng, Y.; Peng, X. A Health Indicator Extraction and Optimization Framework for Lithium-Ion Battery Degradation Modeling and Prognostics. IEEE Trans. Syst. Man, Cybern. Syst. 2015, 45, 915–928. [Google Scholar] [CrossRef]
- Li, W.; Jiao, Z.; Du, L.; Fan, W.; Zhu, Y. An indirect RUL prognosis for lithium-ion battery under vibration stress using Elman neural network. Int. J. Hydrogen Energy 2019, 44, 12270–12276. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiong, R.; He, H.; Pecht, M.G. Long Short-Term Memory Recurrent Neural Network for Remaining Useful Life Prediction of Lithium-Ion Batteries. IEEE Trans. Veh. Technol. 2018, 67, 5695–5705. [Google Scholar] [CrossRef]
- Pang, X.; Huang, R.; Wen, J.; Shi, Y.; Jia, J.; Zeng, J. A Lithium-ion Battery RUL Prediction Method Considering the Capacity Regeneration Phenomenon. Energies 2019, 12, 2247. [Google Scholar] [CrossRef] [Green Version]
- Ren, L.; Zhao, L.; Hong, S.; Zhao, S.; Wang, H.; Zhang, L. Remaining Useful Life Prediction for Lithium-Ion Battery: A Deep Learning Approach. IEEE Access 2018, 6, 50587–50598. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, Y.; Cheng, J. A Hybrid Method for Remaining Useful Life Estimation of Lithium-Ion Battery with Regeneration Phenomena. Appl. Sci. 2019, 9, 1890. [Google Scholar] [CrossRef] [Green Version]
- Cadini, F.; Sbarufatti, C.; Cancelliere, F.; Giglio, M. State-of-life prognosis and diagnosis of lithium-ion batteries by data-driven particle filters. Appl. Energy 2018, 235, 661–672. [Google Scholar] [CrossRef]
- NASA’s Open Data Portal: Li-ion Battery Aging Datasets. data.nasa.gov. 14 July 2022. Available online: https://data.nasa.gov/dataset/Li-ion-Battery-Aging-Datasets/uj5r-zjdb (accessed on 3 October 2022).
- CALCE. Center for Advanced Life Cycle Engineering Battery Research Group. Available online: https://web.calce.umd.edu/batteries/data.htm (accessed on 1 March 2022).
- Kuznietsov, A.; Happek, T.; Guefack, F.L.T. On-board state of health estimation of Li-Ion batteries packs using incremental capacity analysis with principal components. In Proceedings of the 2018 IEEE International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference (ESARS-ITEC), Nottingham, UK, 7–9 November 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Oxford Battery Degradation Dataset. Oxford University Research Archive. 2017. Available online: https://ora.ox.ac.uk/objects/uuid:03ba4b01-cfed-46d3-9b1a-7d4a7bdf6fac (accessed on 3 October 2022).
- Dogger, J.D.; Roossien, B.; Nieuwenhout, F.D.J. Characterization of Li-Ion Batteries for Intelligent Management of Distributed Grid-Connected Storage. IEEE Trans. Energy Convers. 2010, 26, 256–263. [Google Scholar] [CrossRef] [Green Version]
- Yang, A.; Wang, Y.; Tsui, K.L.; Zi, Y. Lithium-ion Battery SOH Estimation and Fault Diagnosis with Missing Data. In Proceedings of the 2019 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Auckland, New Zealand, 20–23 May 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, W.; Mi, C.C. Compensation Topologies of High-Power Wireless Power Transfer Systems. IEEE Trans. Veh. Technol. 2015, 65, 4768–4778. [Google Scholar] [CrossRef]
- Strickland, D.; Chittock, L.; Stone, D.A.; Foster, M.P.; Price, B. Estimation of Transportation Battery Second Life for Use in Electricity Grid Systems. IEEE Trans. Sustain. Energy 2014, 5, 795–803. [Google Scholar] [CrossRef] [Green Version]
- IEEE 1661-2019; IEEE Guide for Test and Evaluation of Lead-Acid Batteries Used in Photovoltaic (PV) Hybrid Power Systems. IEEE: Piscataway, NJ, USA, 2019. [CrossRef]
- Varnosfaderani, M.A.; Strickland, D.; Ruse, M.; Castillo, E.B. Sweat Testing Cycles of Batteries for Different Electrical Power Applications. IEEE Access 2019, 7, 132333–132342. [Google Scholar] [CrossRef]



| Scenario | Total Charge over a Year (kWh) | Energy Balance |
|---|---|---|
| Use case 1—PV and maximizing FIT payment | 890 | Energy in battery balanced at the end of each day |
| Use case 2—PV maximizing FIT payment and TOU tariff | 838 | |
| Use case 3—no PV, but maximizing TOU tariff | 609 | |
| Use case 4—FFR market participation | 1120 | Energy in battery balanced over the course of a year |
| Use case 5—EFR market participation | 202 | |
| Use case 6—Day ahead market participation | 1404 |
| Scenario | Measured Terminal Voltage before Test (V) | Use Remaining Capacity (%) | Measured Impedance before Test (Hioki) mΩ |
|---|---|---|---|
| Use case 1—PV | 7.76 | 68.74 | 2.10 |
| Use case 2—PV—TOU | 7.7 | 67.25 | 2.23 |
| Use case 3—TOU | 7.9 | 68.5 | 2.23 |
| Use case 4—FFR | 7.8 | 67.58 | 2.1 |
| Use case 5—EFR | 7.8 | 67.44 | 2.15 |
| Use case 6—Day ahead | 7.8 | 66.84 | 2.14 |
| PV | PV-TOU | TOU | FFR | EFR | Day Ahead | |
|---|---|---|---|---|---|---|
| Swiercznski [1] | 43 | 43 | 43 | 40 | 44 | 40 |
| Wang 2011 [2] | 34 | 33 | 31 | 21 | 40 | 20 |
| Matsuhima | 26 | 26 | 23 | 21 | 30 | 22 |
| He: y2 = 1/10 | 44 | 44 | 44 | 39 | 44 | 38 |
| He: y2 = 1/3.9 | 43 | 42 | 40 | 0 | 44 | 0 |
| He: y2 = 1/1.5 | 16 | 0 | 0 | 0 | 43 | 0 |
| Dogger [32] | 33 | 30 | 27 | 0 | 42 | 0 |
| Experimental | 40 Ah | 43 Ah | 43 Ah | 40 Ah | 44 Ah | 29.5 Ah |
| Years of testing | 3y 1m | 3y 7m | 5y | 6y | 6y 4m | 7y |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Beatty, M.; Strickland, D.; Abedi-Varnosfaderani, M.; Warren, J. Second-Life Battery Capacity Estimation and Method Comparison. Energies 2023, 16, 3244. https://doi.org/10.3390/en16073244
Yang J, Beatty M, Strickland D, Abedi-Varnosfaderani M, Warren J. Second-Life Battery Capacity Estimation and Method Comparison. Energies. 2023; 16(7):3244. https://doi.org/10.3390/en16073244
Chicago/Turabian StyleYang, Jingxi, Matthew Beatty, Dani Strickland, Mina Abedi-Varnosfaderani, and Joe Warren. 2023. "Second-Life Battery Capacity Estimation and Method Comparison" Energies 16, no. 7: 3244. https://doi.org/10.3390/en16073244
APA StyleYang, J., Beatty, M., Strickland, D., Abedi-Varnosfaderani, M., & Warren, J. (2023). Second-Life Battery Capacity Estimation and Method Comparison. Energies, 16(7), 3244. https://doi.org/10.3390/en16073244