Analysis of Cantilever Triple-Layer Piezoelectric Harvester (CTLPH): Non-Resonance Applications
Abstract
1. Introduction
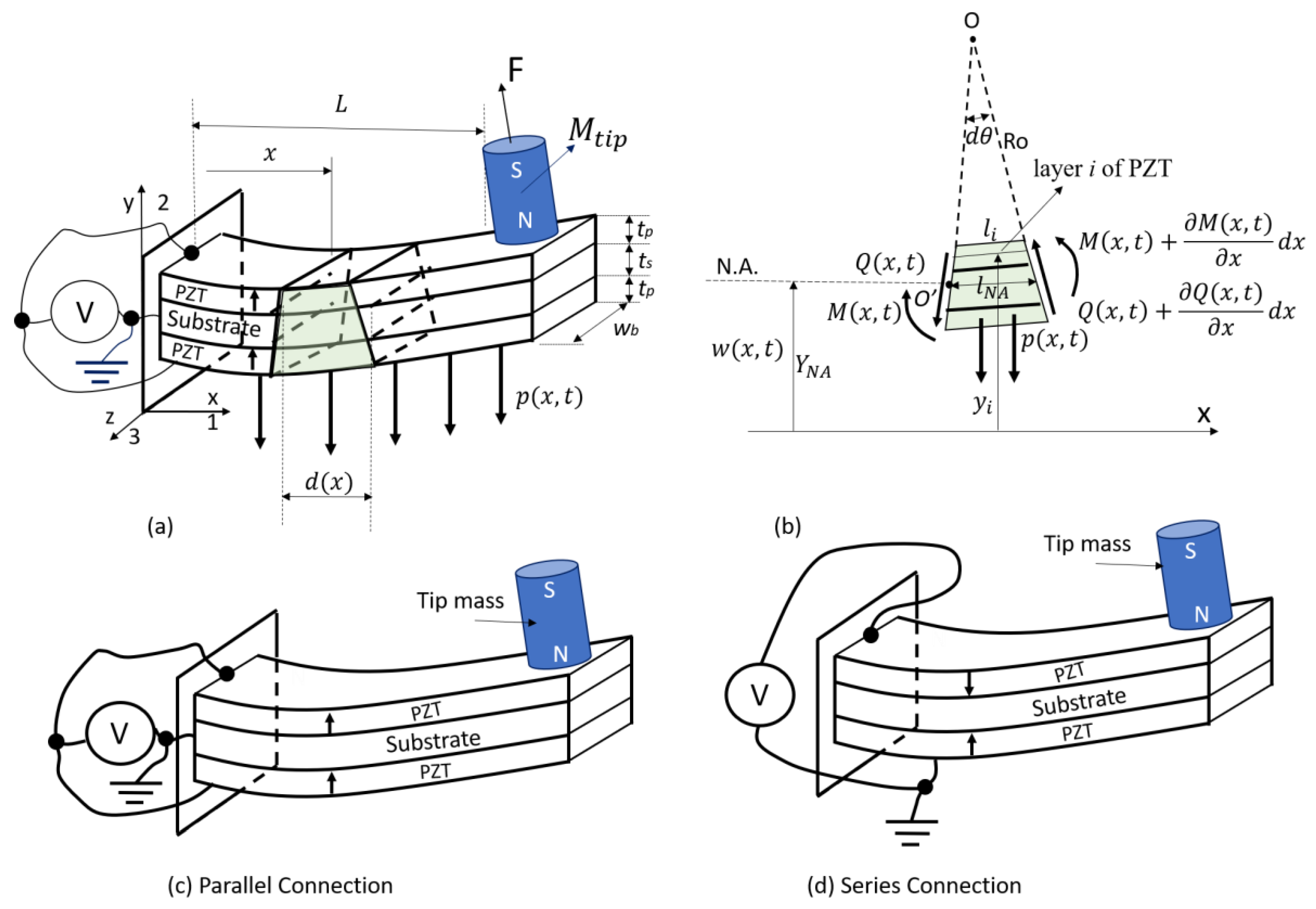
2. Principle of Operation
3. Theoretical Analysis
3.1. Assumptions and Constitutive Equations
3.2. Bending Stiffness
3.3. Output Voltage and Power
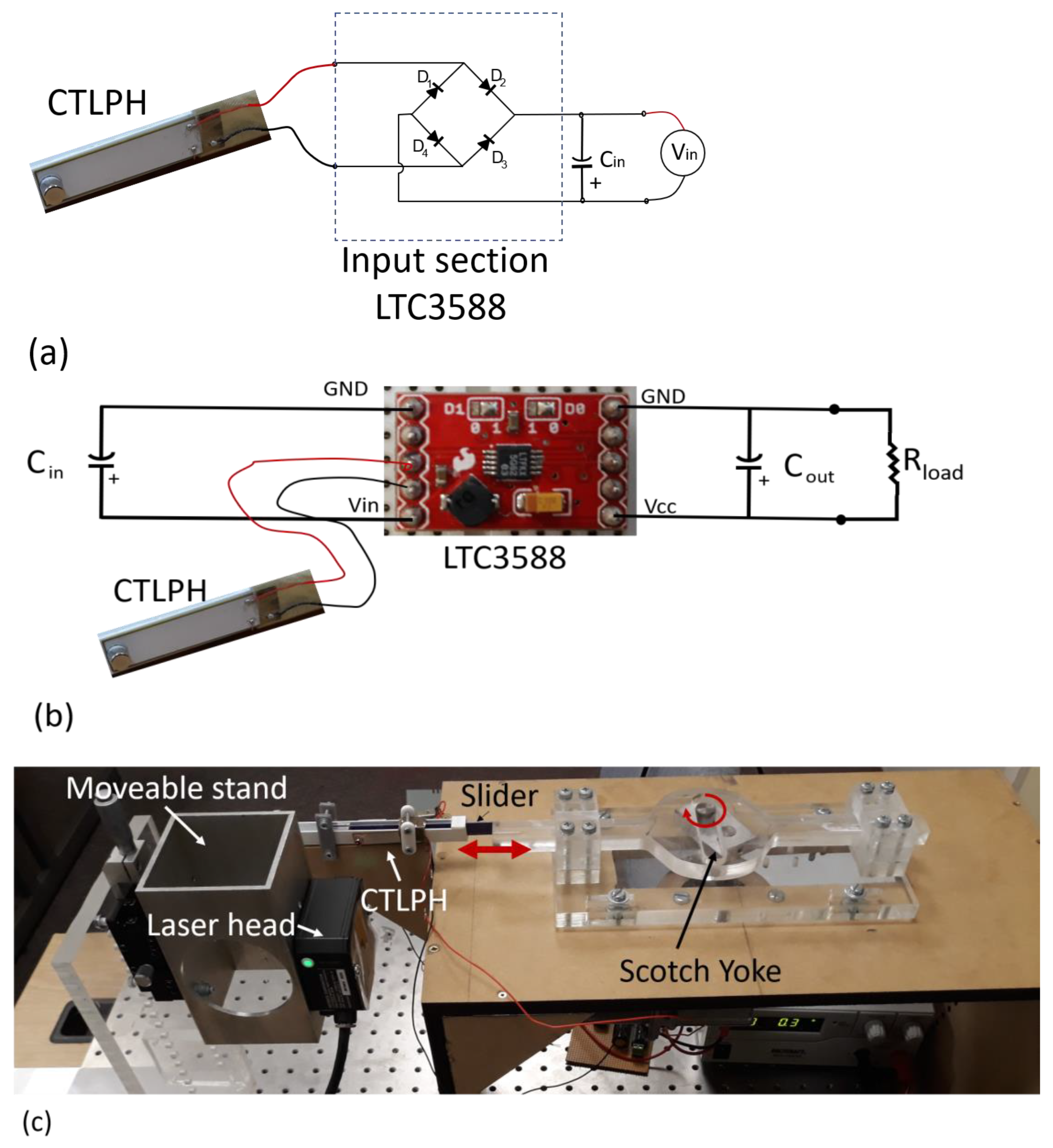
4. Methodology
5. Results and Discussion
5.1. Tip Force
5.2. Storage or Input Voltage
5.3. Output Voltage and Power with LTC3588
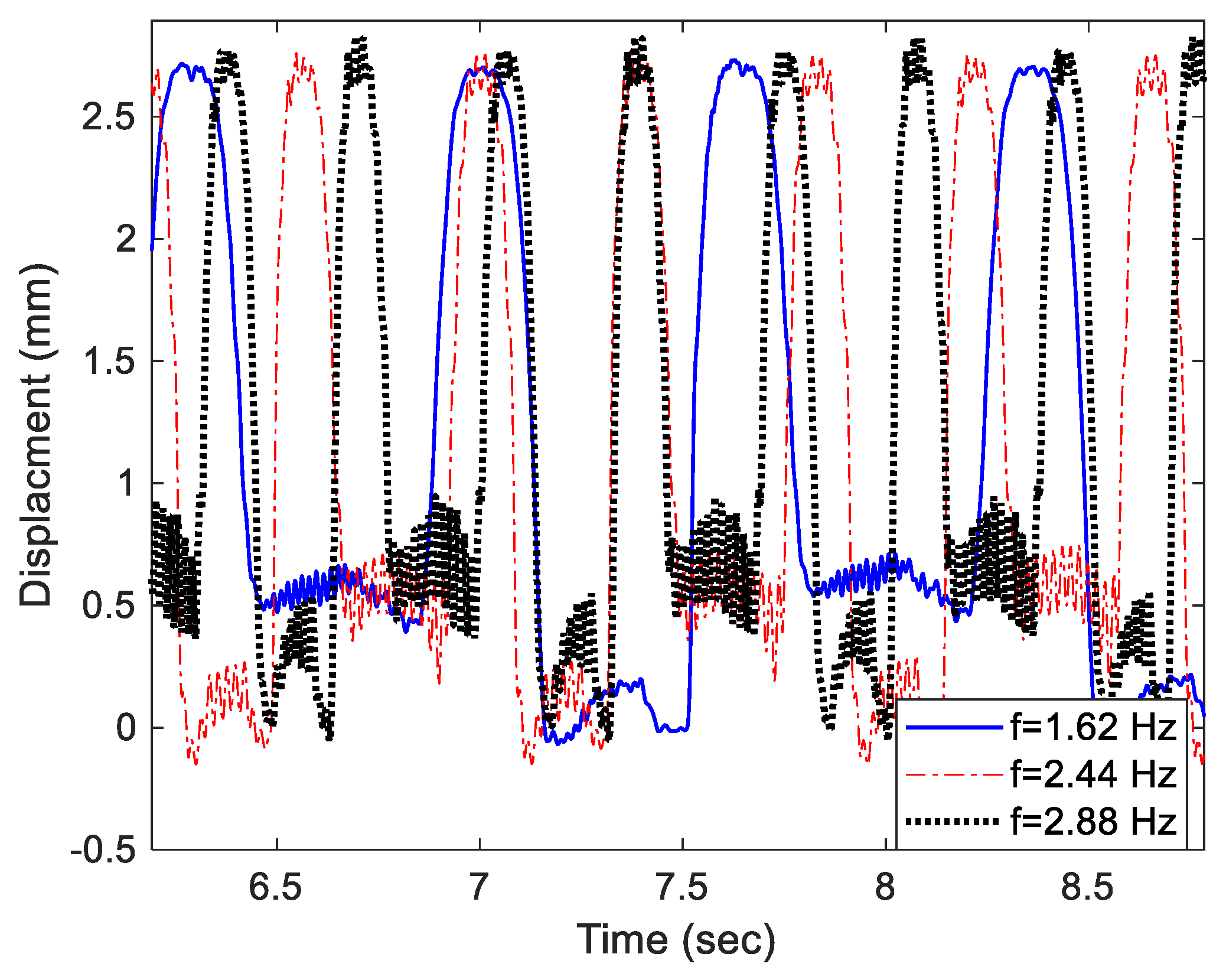
5.3.1. Effect of Frequency
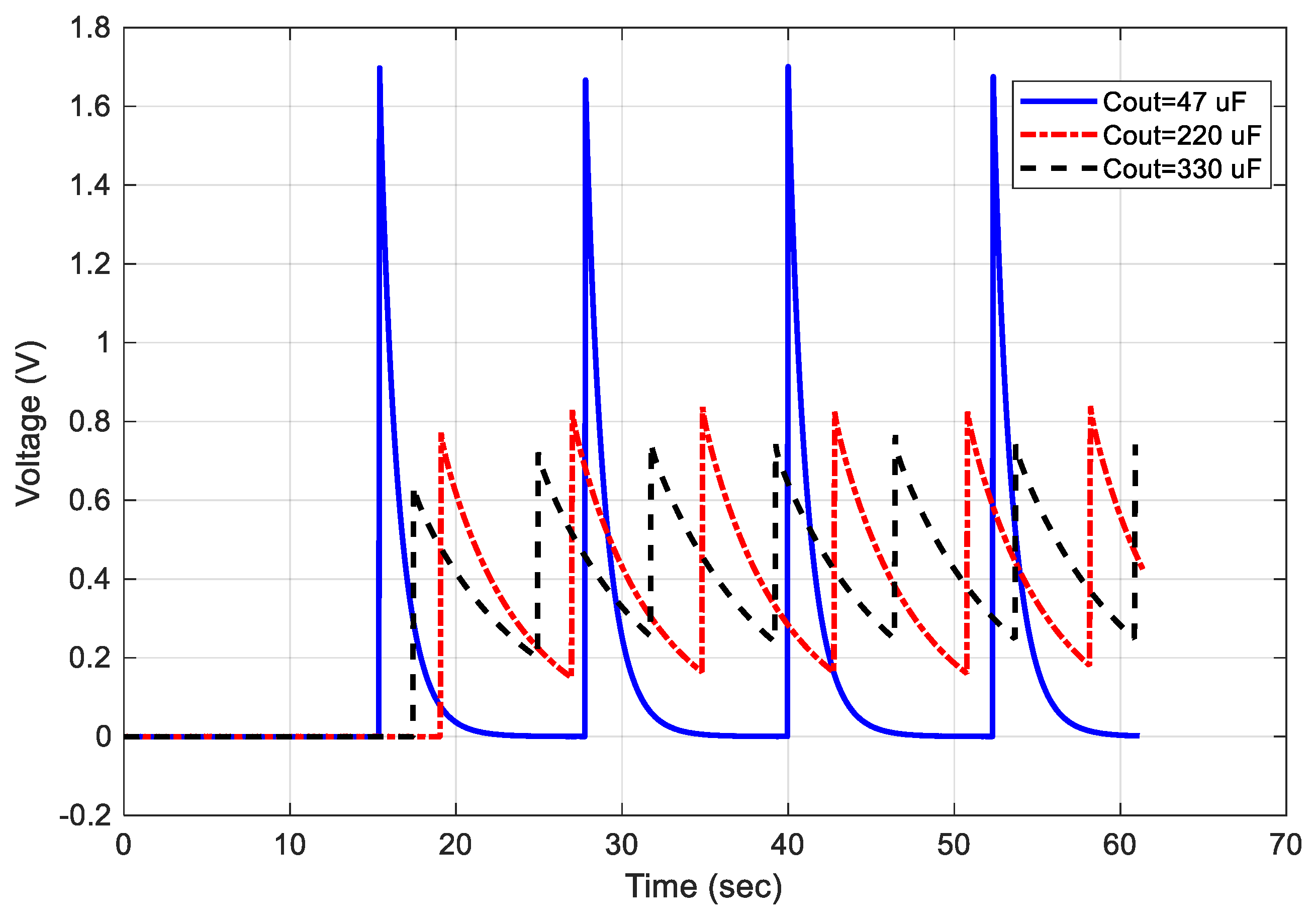
5.3.2. Effect of Storage and Output Capacitors
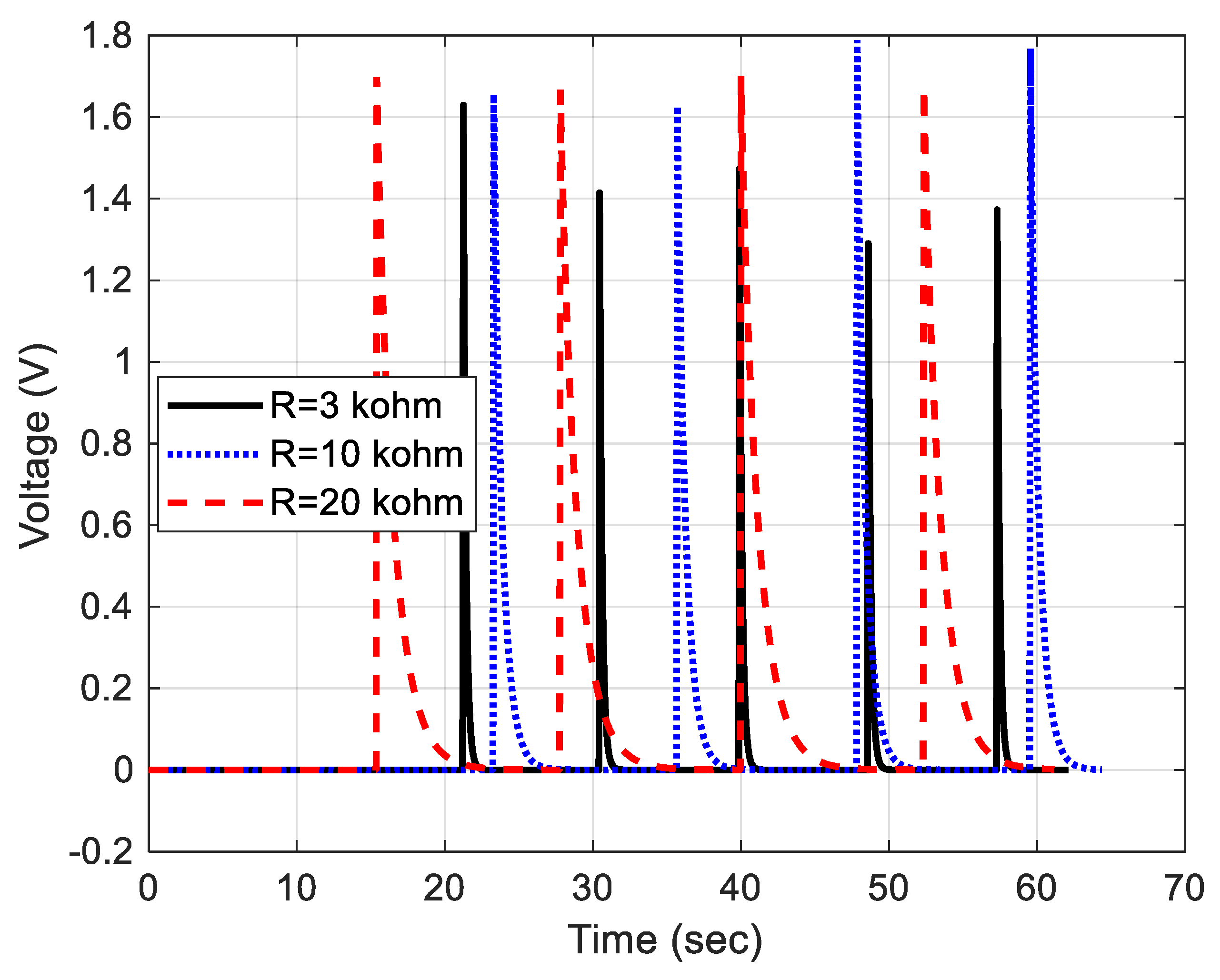
5.3.3. Effect of Resistive Load
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hoshyarmanesh, H.; Ghodsi, M.; Kim, M.; Cho, H.H.; Park, H.-H. Temperature effects on electromechanical response of deposited piezoelectric sensors used in structural health monitoring of aerospace structures. Sensors 2019, 19, 2805. [Google Scholar] [CrossRef] [PubMed]
- Du, S.; Jia, Y.; Zhao, C.; Amaratunga, G.A.; Seshia, A.A. A nail-size piezoelectric energy harvesting system integrating a mems transducer and a CMOS SSHI circuit. IEEE Sens. J. 2019, 20, 277–285. [Google Scholar] [CrossRef]
- Zhang, M.; Cai, W.; Wang, Z.; Fang, S.; Zhang, R.; Lu, H.; Aliev, A.E.; Zakhidov, A.A.; Huynh, C.; Gao, E. Mechanical energy harvesters with tensile efficiency of 17.4% and torsional efficiency of 22.4% based on homochirally plied carbon nanotube yarns. Nat. Energy 2023, 8, 203–213. [Google Scholar] [CrossRef]
- Adhikari, P.R.; Tasneem, N.T.; Reid, R.C.; Mahbub, I. Electrode and electrolyte configurations for low frequency motion energy harvesting based on reverse electrowetting. Sci. Rep. 2021, 11, 5030. [Google Scholar] [CrossRef]
- Li, M.; Luo, A.; Luo, W.; Wang, F. Recent progress on mechanical optimization of mems electret-based electrostatic vibration energy harvesters. J. Microelectromech. Syst. 2022, 31, 726–740. [Google Scholar] [CrossRef]
- Miao, G.; Fang, S.; Wang, S.; Zhou, S. A low-frequency rotational electromagnetic energy harvester using a magnetic plucking mechanism. Appl. Energy 2022, 305, 117838. [Google Scholar] [CrossRef]
- Tasneem, N.T.; Biswas, D.K.; Adhikari, P.R.; Gunti, A.; Patwary, A.B.; Reid, R.C.; Mahbub, I. A self-powered wireless motion sensor based on a high-surface area reverse electrowetting-on-dielectric energy harvester. Sci. Rep. 2022, 12, 3782. [Google Scholar] [CrossRef]
- Mohammadzaheri, M.; Soltani, P.; Ghodsi, M. Micro/nanopositioning systems with piezoelectric actuators and their role in sustainability and ecosystems. In Ecomechatronics: Challenges for Evolution, Development and Sustainability; Springer: Berlin/Heidelberg, Germany, 2022; pp. 233–250. [Google Scholar]
- Lim, C.; He, L. Three-dimensional exact solutions for the electromechanical response of triple-layer piezoelectric actuators. Smart Mater. Struct. 2004, 13, 1050. [Google Scholar] [CrossRef]
- Soltani, P.; Kerschen, G.; Tondreau, G.; Deraemaeker, A. Piezoelectric vibration damping using resonant shunt circuits: An exact solution. Smart Mater. Struct. 2014, 23, 125014. [Google Scholar] [CrossRef]
- Soltani, P.; Kerschen, G. The nonlinear piezoelectric tuned vibration absorber. Smart Mater. Struct. 2015, 24, 075015. [Google Scholar] [CrossRef]
- Makowski, M.; Knap, L. Study of a controlled piezoelectric damper. Sensors 2021, 21, 3509. [Google Scholar] [CrossRef]
- Marakakis, K.; Tairidis, G.K.; Koutsianitis, P.; Stavroulakis, G.E. Shunt piezoelectric systems for noise and vibration control: A review. Front. Built Environ. 2019, 5, 64. [Google Scholar] [CrossRef]
- Fang, S.; Chen, K.; Lai, Z.; Zhou, S.; Liao, W.-H. Analysis and experiment of auxetic centrifugal softening impact energy harvesting from ultra-low-frequency rotational excitations. Appl. Energy 2023, 331, 120355. [Google Scholar] [CrossRef]
- Dong, L.; Closson, A.B.; Oglesby, M.; Escobedo, D.; Han, X.; Nie, Y.; Huang, S.; Feldman, M.D.; Chen, Z.; Zhang, J.X. In Vivo cardiac power generation enabled by an integrated helical piezoelectric pacemaker lead. Nano Energy 2019, 66, 104085. [Google Scholar] [CrossRef]
- Shi, G.; Tong, D.; Xia, Y.; Jia, S.; Chang, J.; Li, Q.; Wang, X.; Xia, H.; Ye, Y. A piezoelectric vibration energy harvester for multi-directional and ultra-low frequency waves with magnetic coupling driven by rotating balls. Appl. Energy 2022, 310, 118511. [Google Scholar] [CrossRef]
- Qin, W.; Liu, Q.; Wang, Y.; Xie, Z.; Zhou, Z. Increase output of vibration energy harvester by a different piezoelectric mode and branch structure design. J. Phys. D Appl. Phys. 2022, 56, 034001. [Google Scholar] [CrossRef]
- Smits, J.G.; Dalke, S.I.; Cooney, T.K. The constituent equations of piezoelectric bimorphs. Sens. Actuators A Phys. 1991, 28, 41–61. [Google Scholar] [CrossRef]
- DeVoe, D.L.; Pisano, A.P. Modeling and optimal design of piezoelectric cantilever microactuators. J. Microelectromech. Syst. 1997, 6, 266–270. [Google Scholar] [CrossRef]
- Weinberg, M.S. Working equations for piezoelectric actuators and sensors. J. Microelectromech. Syst. 1999, 8, 529–533. [Google Scholar] [CrossRef]
- Wang, Q.-M.; Cross, L.E. Constitutive equations of symmetrical triple layer piezoelectric benders. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1999, 46, 1343–1351. [Google Scholar] [CrossRef]
- Tadmor, E.B.; Kósa, G. Electromechanical coupling correction for piezoelectric layered beams. J. Microelectromech. Syst. 2003, 12, 899–906. [Google Scholar] [CrossRef]
- Ismail, M.R.; Omar, F.K.; Ajaj, R.; Ghodsi, M. Correction factor of lumped parameter model for linearly tapered piezoelectric cantilever. J. Intell. Mater. Syst. Struct. 2022, 33, 474–488. [Google Scholar] [CrossRef]
- Lu, Q.; Liu, L.; Scarpa, F.; Leng, J.; Liu, Y. A novel composite multi-layer piezoelectric energy harvester. Compos. Struct. 2018, 201, 121–130. [Google Scholar] [CrossRef]
- Meirovitch, L. Fundamentals of Vibrations; Waveland Press: Long Grove, IL, USA, 2010. [Google Scholar]
- Inman, D.J. Engineering Vibration, 4th ed.; Pearson Education Ltd.: London, UK, 2014. [Google Scholar]
- ANSI/IEEE Std 176-1987; IEEE Standard on Piezoelectricity. The Institute of Electrical and Electronics Engineers: New York, NY, USA, 1988.
- Ghodsi, M.; Ziaiefar, H.; Mohammadzaheri, M.; Omar, F.K.; Bahadur, I. Dynamic analysis and performance optimization of permendur cantilevered energy harvester. Smart Struct. Syst. 2019, 23, 421–428. [Google Scholar]
- Available online: https://www.steminc.com (accessed on 6 June 2022).
- Wu, Y.; Qiu, J.; Zhou, S.; Ji, H.; Chen, Y.; Li, S. A piezoelectric spring pendulum oscillator used for multi-directional and ultra-low frequency vibration energy harvesting. Appl. Energy 2018, 231, 600–614. [Google Scholar] [CrossRef]
- Wei, X.; Zhao, H.; Yu, J.; Zhong, Y.; Liao, Y.; Shi, S.; Wang, P. A tower-shaped three-dimensional piezoelectric energy harvester for low-level and low-frequency vibration. Int. J. Precis. Eng. Manuf.-Green Technol. 2021, 8, 1537–1550. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, Z.; Jiang, X.; Peng, Y.; Zhu, C.; Li, Z. Experimental investigation on performance improvement of cantilever piezoelectric energy harvesters via escapement mechanism from extremely low-frequency excitations. Sustain. Energy Technol. Assess. 2022, 53, 102591. [Google Scholar] [CrossRef]
- Li, M.; Zhou, J.; Jing, X. Improving low-frequency piezoelectric energy harvesting performance with novel x-structured harvesters. Nonlinear Dyn. 2018, 94, 1409–1428. [Google Scholar] [CrossRef]







| Substrate Layer | Piezoelectric Layer | Tip Mass | Tiple-Layer Beam | |
|---|---|---|---|---|
| Material | Brass | PZT-5H | NdFeB-N35 | PZT-Brass-PZT |
| Dimensions (mm) | 40 × 10 × 0.11 | 40 × 10 × 0.225 | 5 × 5 | 40 × 10 × 0.56 |
| Elastic modulus (GPa) | 110 | 60 | 38 | ---- |
| Density (kg/m3) | 7800 | 6500 | 7500 | ---- |
| Mass (kg) | 0.00034 | 0.00058 | 0.00075 | 0.0015 |
| Ref. | Dimensions (mm) | Material | Frequency (Hz) | Power (µW) | Resistance (MΩ) | Power Density (µW/cm3) |
|---|---|---|---|---|---|---|
| [30] | 160 × 85 × 85 | Unknow PZT | 2.03 | 13290 | 0.54 | 11.5 |
| [31] | 40 × 70 × 35 | PVDF | 3.4 | 65.8 | 15 | 0.67 |
| [32] | 48 × 10 × 65 | Unknow PZT | 1 | 35 | 3 | 1.12 |
| [33] | 300 × 200 × 250 | PZT 5J | 2.5 | 146 | 0.5 | 0.00973 |
| This work | 40 ×10 × 0.56 | PZT-5H | 3.2 | 17.31 | 0.02 | 77.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghodsi, M.; Mohammadzaheri, M.; Soltani, P. Analysis of Cantilever Triple-Layer Piezoelectric Harvester (CTLPH): Non-Resonance Applications. Energies 2023, 16, 3129. https://doi.org/10.3390/en16073129
Ghodsi M, Mohammadzaheri M, Soltani P. Analysis of Cantilever Triple-Layer Piezoelectric Harvester (CTLPH): Non-Resonance Applications. Energies. 2023; 16(7):3129. https://doi.org/10.3390/en16073129
Chicago/Turabian StyleGhodsi, Mojtaba, Morteza Mohammadzaheri, and Payam Soltani. 2023. "Analysis of Cantilever Triple-Layer Piezoelectric Harvester (CTLPH): Non-Resonance Applications" Energies 16, no. 7: 3129. https://doi.org/10.3390/en16073129
APA StyleGhodsi, M., Mohammadzaheri, M., & Soltani, P. (2023). Analysis of Cantilever Triple-Layer Piezoelectric Harvester (CTLPH): Non-Resonance Applications. Energies, 16(7), 3129. https://doi.org/10.3390/en16073129








