Effects of Numerical Schemes of Contact Angle on Simulating Condensation Heat Transfer in a Subcooled Microcavity by Pseudopotential Lattice Boltzmann Model

Abstract

Various numerical schemes of contact angle are widely used in pseudopotential lattice Boltzmann model to simulate substrate contact angle in condensation. In this study, effects of numerical schemes of contact angle on condensation nucleation and heat transfer simulation are clarified for the first time. The three numerical schemes are pseudopotential-based contact angle scheme, pseudopotential-based contact angle scheme with a ghost fluid layer constructed on the substrate with weighted average density of surrounding fluid nodes, and the geometric formulation scheme. It is found that the subcooling condition destabilizes algorithm of pseudopotential-based contact angle scheme. However, with a ghost fluid layer constructed on the substrate or using geometric formulation scheme, the algorithm becomes stable. The subcooling condition also decreases the simulated contact angle magnitude compared with that under an isothermal condition. The fluid density variation near a microcavity wall simulated by pseudopotential-based contact angle scheme plays the role of the condensation nucleus and triggers “condensation nucleation”. However, with a ghost fluid layer constructed on the substrate or using geometric formulation scheme, the simulated fluid density distribution near the wall is uniform so that no condensation nucleus appears in the microcavity. Thus, “condensation nucleation” cannot occur spontaneously in the microcavity unless a thin liquid film is initialized as a nucleus in the microcavity. The heat flux at the microcavity wall is unphysical during the “condensation nucleation” process, but it becomes reasonable with a liquid film formed in the microcavity. As a whole, it is recommended to use pseudopotential-based contact angle scheme with a ghost fluid layer constructed on the substrate or use the geometric formulation scheme to simulate condensation under subcooling conditions. This study provides guidelines for choosing the desirable numerical schemes of contact angle in condensation simulation by pseudopotential lattice Boltzmann model so that more efficient strategies for condensation heat transfer enhancement can be obtained from numerical simulations.

1. Introduction

Condensation is a highly efficient heat transfer method, which has been applied in many energy industries, e.g., power plant, desalination, electronic thermal management, etc. [1]. Promoting condensation heat transfer helps in saving energy consumption in industrial applications. Compared with a hydrophobic substrate, condensed droplets prefer nucleating on a hydrophilic substrate [2]. However, condensed droplets on a hydrophilic substrate coalesce into liquid film more easily than those on a hydrophobic substrate. The liquid film on a substrate increases thermal resistance, deteriorating condensation heat transfer coefficient. To enhance condensation heat transfer, microstructures were introduced to increase hydrophobicity of a substrate in the past, which led to highly efficient self-propelled jumping of condensate droplets [3,4]. However, if the interval spacings between microstructures are too wide, condensation nucleation occurs inside the interval spacings [5]. This leads to wetting mode transition of condensed droplets and the loss efficacy of a droplet self-cleaning microstructural substrate.

As can be seen, the microstructure and wettability have significant effects on condensation heat transfer. However, condensation nucleation occurs in the microscopic scale and it is hard to investigate for detail by using traditional experimental techniques. Numerical simulation is a flexible and less expensive approach to investigate condensation heat transfer. Lattice Boltzmann method (LBM) is a mesoscopic numerical method governed by lattice Boltzmann equation, which can be recovered to macroscopic fluid dynamic governing equations. LBM retains microscopic fluid particle interaction characteristics, e.g., surface tension, phase separation, solid wall wettability, etc. [6,7,8,9]. Due to its mesoscopic characteristics, LBM has been applied widely to investigate dynamics of condensed droplets as well as condensation heat transfer in the past [10,11,12,13,14]. The pseudopotential lattice Boltzmann model proposed by Shan and Chen [15] is the simplest multiphase LB model and it is widely used in simulating multiphase flow and heat transfer problems with great success due to its computational efficiency. In the pseudopotential LB model, the “effective mass” (or “pseudopotential”) of fluid nodes is introduced to mimic fluid–fluid interaction force. In the pseudopotential LB model, condensation occurs due to phase separation induced by the fluid–fluid interaction force. Substrate wettability is incorporated in pseudopotential LB model by introducing a fluid–solid interaction force to mimic solid substrates’ affinity on liquid. There are different numerical schemes for incorporating fluid–solid interaction force in the pseudopotential LB model: density-based contact angle scheme [16], pseudopotential-based contact angle scheme [17], modified pseudopotential-based contact angle scheme [18], improved-virtual density contact angle scheme [19] and geometric formulation contact angle scheme [20,21].

The density-based contact angle scheme is the earliest proposed contact angle scheme, which was given by Martys and Chen [16]. In this scheme, the fluid–solid interaction strength is proportional to the fluid density so that the scheme is called a density-based contact angle scheme. Subsequently, Sukop and Throne proposed another contact angle scheme [17], in which the fluid–solid interaction strength is proportional to the “effective mass” (or “pseudopotential”) of fluid. This scheme is called a pseudopotential-based contact angle scheme. It was later demonstrated by Li et al. [18] that, with the application of density-based contact angle scheme in simulating a sessile droplet on a plate substrate, the minimum or maximum fluid density in the simulation deviated from the bulk equilibrium fluid density significantly. Li et al. [18] proposed the modified pseudopotential-based contact angle scheme and they showed that the pseudopotential-based contact angle scheme or the modified pseudopotential-based contact angle scheme have better performance than the density-based contact angle scheme in terms of fluid density deviation. Essentially, the fluid density deviation in the simulation comes from the fluid density variation near the solid wall due to the introduction of fluid–solid interaction force, as pointed out by Hu et al. [22]. To diminish such fluid density variation near the wall, Li et al. [19] proposed the improved virtual-density contact angle scheme, in which the fluid–solid interaction strength is determined by the “effective mass” of fluid nodes and the virtual “effective mass” of solid wall nodes. Based on geometric formulation, Ding and Spelt [21] proposed the geometric formulation contact angle scheme. The geometric formulation scheme recently was proved to be of good accuracy in predicting fluid density distribution near the wall [23]. Recently, it has been demonstrated that, when using the pseudopotential-based scheme or the modified pseudopotential-based scheme, a special ghost fluid layer should be necessarily constructed on the substrate to ensure temperature distribution accuracy in simulating droplet evaporation [24]. Such a special ghost fluid layer is constructed by using weighted average density of surrounding fluid nodes.

From the literature review above, it can be seen that different contact angle schemes have different numerical accuracy in predicting fluid density distribution near a solid wall. It was also demonstrated in molecular simulation previously [25] that the fluid density distribution near a solid substrate has significant effects on condensation nucleation physically. As a result, different numerical schemes of contact angle applied in condensation simulation have vital influences on the accuracy of predicting condensation behavior indirectly, which was rarely paid attention to in the past. This problem not only bothers investigators on choosing the desirable numerical scheme of contact angle in simulation condensation by pseudopotential LB model, but also leads to inconsistent simulation results. In addition, we have previously proved that superheating condition during droplet evaporation destabilizes the numerical schemes [24], but how the subcooling condition affects numerical stability of the schemes is unknown. This also brings about inconvenience in simulation condensation. In this paper, the most widely used numerical scheme of contact angle (i.e., pseudopotential-based scheme) [17], the recently proposed corrected numerical scheme of contact angle (i.e., pseudopotential-base scheme with a ghost fluid layer constructed on the substrate with weighted average density of surrounding fluid nodes) [24] and the recently proved most accurate numerical scheme of contact angle (i.e., geometric formulation scheme) [20,21] are used to simulate condensation on a substrate with a square microcavity. The microcavity of the square shape is chosen to investigate in the present study for the reasons that the square shape microcavity is the basic component constituting many complex microstructures and the boundaries of a square microcavity are straight lines where fluid flow and heat transfer can be accurately simulated without using complicated boundary condition implementation strategies. The effects of subcooling condition on numerical stability and the magnitude of simulated contact angle are investigated. The effects of fluid density variation near the wall in different numerical schemes on condensation nucleation and heat transfer at a microcavity wall are clarified.

2. Pseudopotential Lattice Boltzmann Model

2.1. Fluid Dynamics Description

In the pseudopotential LBM, the fluid dynamics are described by the evolution of micro fluid particles’ density distribution functions $f_i\left(x,t\right)$. The evolution of fluid density distribution function $f_i\left(x,t\right)$ is governed by lattice Boltzmann equation with the Bhatnagar–Gross–Krook (BGK) collision operator [26] as follows:

$$f_i\left(x+e_i\Delta t,t+\Delta t\right)-f_i\left(x,t\right)=-\frac{1}{\tau }\left[f_i\left(x,t\right)-f_i^{eq}\left(x,t\right)\right]+\Delta f_i\left(x,t\right)$$

(1)

where x is position in Cartesian co-ordinates and t is simulation time, $\Delta t$ is time spacing equaling 1, $\tau$ is the dimensionless relaxation time, $f_i^{eq}\left(x,t\right)$ is the equilibrium density distribution function, $e_i$ is the discrete velocity (the index $i=0,1,2\dots 8$ represents different directions in D2Q9 model) and $\Delta f_i\left(x,t\right)$ is the force term. $f_i^{eq}\left(x,t\right)$ is expressed as follows, given by Qian et al. [27], so that the macroscopic governing equations for fluid flow can be recovered:

$$f_i^{eq}\left(x,t\right)=\rho {\omega }_i\left[1+\frac{e_i\cdot u}{c_s^2}+\frac{{\left(e_i\cdot u\right)}^2}{2c_s^4}-\frac{u\cdot u}{2c_s^2}\right]$$

(2)

where $\rho$ is fluid density, u is equilibrium fluid velocity, ${\omega }_i$ is the weighting coefficient with ${\omega }_0=4/9$, ${\omega }_{1-4}=1/9$ and ${\omega }_{5-8}=1/36$ and $c_s$ is sound speed equaling $1/\sqrt{3}$, and the discrete velocity $e_i$ is given as follows [28]:

$$e_i=\left\{\begin{array}{ll}\left(0,0\right),\hfill & i=0\hfill \\ c\left(\cos \frac{\pi \left(i-1\right)}{2},\sin \frac{\pi \left(i-1\right)}{2}\right),\hfill & i=1,2,3,4\hfill \\ \sqrt{2}c\left(\cos \frac{\pi \left(2i-9\right)}{4},\sin \frac{\pi \left(2i-9\right)}{4}\right),\hfill & i=5,6,7,8\hfill \end{array}\right.$$

(3)

Fluid density and equilibrium fluid velocity are obtained from density distribution function as follows:

$$\rho ={\displaystyle \sum _i{f}_i}\left(x,t\right)$$

(4)

$$\rho u={\displaystyle \sum _i{e}_i{f}_i}\left(x,t\right)$$

(5)

The dimensionless relaxation time $\tau$ is related with fluid viscosity $\upsilon$ as follows:

$$\upsilon =\left(\tau -0.5\right)c_s^2\Delta t$$

(6)

The exact difference method (EDM) [29] is used to incorporate fluid–solid interaction force $F_{\mathrm{ads}}$ and fluid–fluid interaction force $F_{\mathrm{int}}$ into Equation (1) so that the force term $\Delta f_i\left(x,t\right)$ is expressed as follows:

$$\Delta f_i\left(x,t\right)=f_i^{eq}\left[\rho \left(x,t\right),u\left(x,t\right)+\Delta u\right]-f_i^{eq}\left[\rho \left(x,t\right),u\left(x,t\right)\right]$$

(7)

where $\Delta u=F\cdot \Delta t/\rho$ is the velocity change because of fluid–solid/fluid–fluid interaction force and $F=F_{\mathrm{ads}}+F_{\mathrm{int}}$. The fluid–fluid interaction force $F_{\mathrm{int}}$ is expressed as [30,31]:

$$F_{\mathrm{int}}\left(x\right)=-\beta \psi \left(x\right){\displaystyle \sum _{x^{\prime }}G\left(x,x^{\prime }\right)}\psi \left(x^{\prime }\right)\left(x^{\prime }-x\right)-\frac{1-\beta }{2}{\displaystyle \sum _{x^{\prime }}G\left(x,x^{\prime }\right){\psi }^2\left(x^{\prime }\right)\left(x^{\prime }-x\right)}$$

(8)

where $\psi \left(x\right)$ is “effective mass” of the fluid node x in pseudopotential lattice Boltzmann model [15], $G\left(x,x^{\prime }\right)$ is the Green function satisfying $G\left(x,x^{\prime }\right)=G\left(x^{\prime },x\right)$ and $\beta$ is a weighting factor depending on equation of state (EOS) [31]. $\psi \left(x\right)$ has the following form, as given by Yuan and Schaefer [32]:

$$\psi \left(x\right)=\sqrt{\frac{2\left(p-\rho \left(x\right)c_s^2\right)}{c_{0}g}}$$

(9)

where p is pressure, $c_0=6$ in D2Q9 model and g is the constant which ensures the term in the square root is positive. The Green function is expressed as follows [33]:

$$G\left(x,x^{\prime }\right)=\left\{\begin{array}{l}{g}_1,\left|x-x^{\prime }\right|=1\hfill \\ g_2,\left|x-x^{\prime }\right|=\sqrt{2}\hfill \\ 0,\mathrm{otherwise}\hfill \end{array}\right.$$

(10)

where g₁ = 2g and g₂ = g/2 in 2D simulation. The P-R EOS is used to calculate pressure p in Equation (9) as follows:

$$p_{EOS}=\frac{\rho RT}{1-b\rho }-\frac{a{\rho }^2\epsilon \left(T\right)}{1+2b\rho -b^2{\rho }^2}$$

(11a)

$$\epsilon \left(T\right)={\left[1+\left(0.3746+1.5423\omega -0.2699{\omega }^2\right)\left(1-\sqrt{T/T_c}\right)\right]}^2$$

(11b)

where $\omega$ is the acentric factor, which is 0.344 for water, $a=0.4572R^2{T}_c^2/p_c$ and $b=0.0778R{T}_c/p_c$. $T_c$ and $p_c$ are the critical temperature and critical pressure of water, respectively. According to Yuan and Schaefer [32], a = 2/49, b = 2/21 and R = 1.

As for calculating the fluid–solid interaction force $F_{\mathrm{ads}}$, three numerical schemes of contact angle are used to compare their effects on simulating condensation heat transfer. They are listed in the following

Table 1. Numerical schemes of contact angle calculating $F_{\mathrm{ads}}$.

Scheme	Description
#1	Pseudopotential-based scheme [17]
#2	Pseudopotential-based scheme with a special ghost fluid layer [24]
#3	Geometric formulation scheme [20,21]

.

In the pseudopotential-based scheme (Scheme #1), the fluid–solid interaction force $F_{\mathrm{ads}}$ is expressed as follows, given by Sukop and Thorne [17]:

$$F_{\mathrm{ads}}\left(x\right)=-G_s\psi \left(x\right){\displaystyle \sum _i{\omega }_{i}s\left(x+e_i\right)e_i}$$

(12)

where $G_s$ is the fluid–solid interaction strength controlling contact angle and $s\left(x+e_i\right)$ is the indicator function equaling 1 for solid nodes and 0 for fluid nodes. In the pseudopotential-based scheme with a ghost fluid layer constructed on the substrate by using weighted average density of surrounding fluid nodes (Scheme #2), the ghost fluid density or temperature are expressed as follows [24,34]:

$${\Phi }_{\mathrm{ghost}}\left(x^{\prime }\right)={\displaystyle \sum _i{\omega }_i\Phi \left(x^{\prime }+e_i\right)\left[1-s\left(x^{\prime }+e_i\right)\right]}/{\displaystyle \sum _i{\omega }_i\left[1-s\left(x^{\prime }+e_i\right)\right]}$$

(13)

where $x^{\prime }$ is the solid node and $\Phi \left(x^{\prime }+e_i\right)$ is the surrounding fluid node densities or temperatures. After constructing the ghost fluid density and temperature at the substrate, the “effective mass” of the ghost fluid node at substrate can be evaluated from Equation (9). In Scheme #2, the fluid–solid interaction force $F_{\mathrm{ads}}$ is the sum of fluid–solid interaction force according to Equation (12) and the fluid–ghost fluid interaction force according to Equation (8). In the geometric formulation scheme (Scheme #3), the solid node temperature at the substrate is constructed according to Equation (13) when calculating the “effective mass” of the solid node at substrate. The solid node density at the substrate is constructed according to the geometric formulation scheme at curved surface, given by Qin et al. [20] as follows:

$${\rho }_s\left(x^{\prime }\right)=\left\{\begin{array}{c}\max \left(\rho \left(D_1\right),\rho \left(D_2\right)\right),\theta \le \pi /2\\ \min \left(\rho \left(D_1\right),\rho \left(D_2\right)\right),\theta >\pi /2\end{array}\right.$$

(14)

where $x^{\prime }$ is the solid node, $\theta$ is the contact angle and $D_1$ and $D_2$ are the possible intersections between liquid–vapor interface and the grid. The unit direction vectors of $D_1-x^{\prime }$ and $D_2-x^{\prime }$ are $I_1$ and $I_2$, respectively. The unit normal vector of the curved surface at $x^{\prime }$ toward fluid is $n_s$, which can be calculated as:

$$n_s=-\frac{{\displaystyle \sum _i{\omega }^{\prime }\left({\left|v_i\right|}^2\right)s\left(x^{\prime }+v_i\right)v_i}}{\left|{\displaystyle \sum _i{\omega }^{\prime }\left({\left|v_i\right|}^2\right)s\left(x^{\prime }+v_i\right)v_i}\right|}$$

(15)

where ${\omega }^{\prime }\left({\left|v_i\right|}^2\right)$ is the weight for eighth-order isotropic discretization as follows:

$${\omega }^{\prime }\left({\left|v_i\right|}^2\right)=\left\{\begin{array}{cc}4/21& ,{\left|v_i\right|}^2=1\\ 4/45& ,{\left|v_i\right|}^2=2\\ 1/60& ,{\left|v_i\right|}^2=4\\ 2/315& ,{\left|v_i\right|}^2=5\\ 1/5040& ,{\left|v_i\right|}^2=8\end{array}\right.$$

(16)

The unit direction vectors of $I_1$ and $I_2$ are determined by $n_s$ and $\theta$ as follows:

$$\left\{\begin{array}{c}{I}_1=\left(n_{s,1}\cos \left(\pi /2-\theta \right)-n_{s,2}\sin \left(\pi /2-\theta \right),n_{s,1}\sin \left(\pi /2-\theta \right)+n_{s,2}\cos \left(\pi /2-\theta \right)\right)\\ I_2=\left(n_{s,1}\cos \left(\pi /2-\theta \right)+n_{s,2}\sin \left(\pi /2-\theta \right),-n_{s,1}\sin \left(\pi /2-\theta \right)+n_{s,2}\cos \left(\pi /2-\theta \right)\right)\end{array}\right.$$

(17)

With the known $I_1$ and $I_2$, the intersections between liquid–vapor interface and the grid $D_1$ and $D_2$ can be determined. Subsequently, the fluid density $\rho \left(D_1\right),\rho \left(D_2\right)$ at the intersections can be extrapolated by their surrounding fluid node densities and the solid node density at substrate is obtained from Equation (14). Then, the “effective mass” of solid nodes is calculated according to Equation (9) and the fluid–solid interaction force $F_{\mathrm{ads}}$ is evaluated from Equation (8). It is noted that, with the incorporation of force $F$ in LBM, the macroscopic velocity U is given as:

$$U=\frac{{\displaystyle \sum _i{f}_i}\left(x,t\right)e_i}{\rho }+\frac{\Delta tF}{2\rho }$$

(18)

2.2. Heat Transfer Description

A temperature distribution function $g_i\left(x,t\right)$ is introduced in LBM to simulate heat transfer and vapor–liquid condensation phase change, and the evolution equation of temperature distribution function is as follows in D2Q9 lattice structure [35]:

$$g_i\left(x+e_i\Delta t,t+\Delta t\right)-g_i\left(x,t\right)=-\frac{1}{{\tau }_g}\left(g_i\left(x,t\right)-g_i^{eq}\left(x,t\right)\right)+\Delta t{C}_i+\Delta t\left(G_i+\frac{\Delta t}{2}\cdot \frac{\partial G_i}{\partial t}\right)$$

(19)

where ${\tau }_g$ is the dimensionless relaxation time, $g_i^{eq}\left(x,t\right)$ is the equilibrium temperature distribution function, $C_i$ is the correction term and $G_i={\omega }_i\varphi$, where $\varphi$ is the liquid–vapor phase-change source term [33,35,36] and it is expressed as follows:

$$\varphi =T\left[1-\frac{1}{\rho c_{\mathrm{v}}}{\left(\frac{\partial p_{\mathrm{EOS}}}{\partial T}\right)}_{\rho }\right]\nabla \cdot U+\frac{\nabla \cdot \left(\lambda \nabla T\right)}{\rho c_{\mathrm{v}}}-\nabla \cdot \left(\alpha \nabla T\right)$$

(20)

where $c_{\mathrm{v}}$ is the specific heat at constant volume, $\lambda$ is the thermal conductivity of fluid and $\alpha =\lambda /\left(\rho c_p\right)$ is the thermal diffusivity of fluid. The fluid temperature $T\left(x\right)$ and thermal diffusivity of fluid $\alpha$ are given as:

$$T\left(x\right)={\displaystyle \sum _i{g}_i}\left(x,t\right)$$

(21)

$$\alpha =\left({\tau }_g-0.5\right)c_s^2\Delta t$$

(22)

The fluid properties $\chi$ at liquid–vapor interface are expressed as follows [33]:

$$\chi ={\chi }_l·\frac{\rho -{\rho }_v}{{\rho }_l-{\rho }_v}+{\chi }_v·\frac{{\rho }_l-\rho }{{\rho }_l-{\rho }_v}$$

(23)

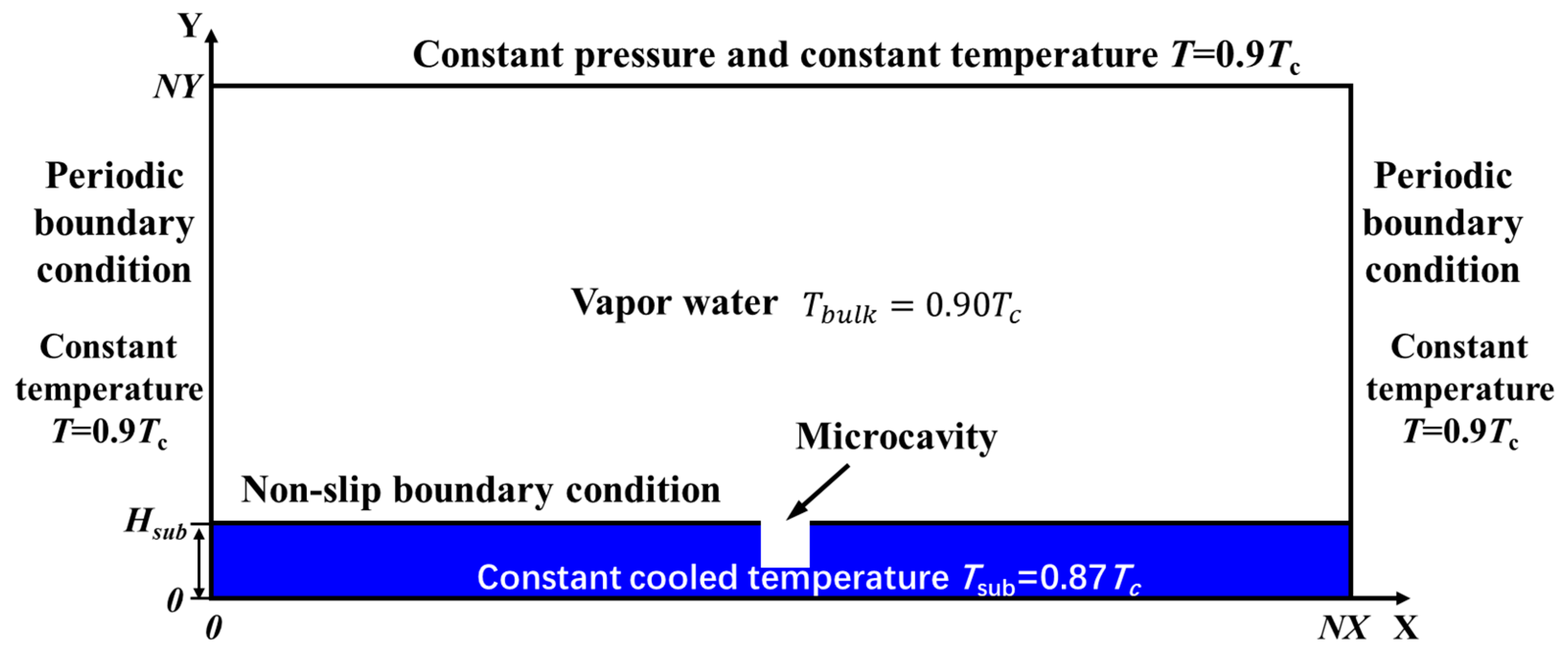
3. Simulation Settings

Firstly, a 2D sessile droplet (a spherical cap shape at a radius of R = 50 in lattice unit) initialized on a plate substrate with a microcavity in saturated vapor is simulated under an isothermal condition for simulation time $t\le 30,000$ (in lattice unit) to reach equilibrium status. Then, condensation on the sessile droplet is simulated for $t>30,000$ to investigate effects of subcooling condition on numerical schemes of contact angle. On the other hand, for the purpose of identifying effects of fluid density variation near the microcavity wall on simulating condensation behavior, no liquid is initialized or only a thin liquid film (thickness of 4$\Delta y$) is initialized in the microcavity to simulate condensation in the subcooled microcavity by different numerical schemes of contact angle.

Figure 1 shows the sketch for simulating settings of a plate substrate in saturated vapor ($T_{bulk}=0.9T_c$ in lattice unit) in a simulation domain size of $NX\times NY=200\times 200$. The plate substrate thickness is H = 20$\Delta y$ and the depth and width of the microcavity are 8$\Delta y$ and 10$\Delta y$, respectively. The saturated liquid density and vapor density are initialized as 5.91 and 0.58 in lattice unit according to the water liquid–vapor coexistence curve by Maxwell construction at 0.9T_c. It is noted that all the fluid properties in simulation are in lattice unit, so that the reduced fluid properties (${\chi }_{liquid}/{\chi }_{vapor}$) in lattice unit in the simulation are chosen to be equal to those of reduced fluid properties of water at 0.9T_c in real unit. The kinematic viscosities of saturated liquid and vapor are given as 0.17 and 1.00. The thermal diffusivities of the liquid phase and vapor phase are given as 0.10 and 0.17, respectively. The thermal conductivities of liquid phase and vapor phase are given as 1.00 and 0.08. A constant temperature of $T_{sub}=0.87T_c$ is imposed at the substrate to simulate a subcooling condition for $t>30,000$. No-slip condition is applied at the substrate, a constant pressure condition is applied at the top boundary and periodic conditions are applied at the left and right boundaries. Constant temperature boundaries of $T=0.9T_c$ are applied at the left boundary, right boundary and top boundary of the simulation domain.

The mesh independence analysis is carried out by using a pseudopotential-based scheme (Scheme #1) to simulate condensation nucleation in a subcooled microcavity based on four groups of meshes ($NX\times NY=100\times 100$, $200\times 200$, $300\times 300$ and $400\times 400$). The nucleation times t_n obtained at different meshes are listed in

Table 2. Condensation nucleation times t_n obtained at different meshes.

$\mathit{N}\mathit{X}\times \mathit{N}\mathit{Y}$	$100\times 100$	$200\times 200$	$300\times 300$	$400\times 400$
tn	36,400	36,400	36,300	36,300

. It is shown that the nucleation times t_n vary only slightly (no more than 0.3%) with the mesh refinement, so that the mesh of $NX\times NY=200\times 200$ is chosen in this study for saving computational resources and ensuring simulation accuracy.

4. Results and Discussions

4.1. Effects of Subcooling Condition on Numerical Schemes of Contact Angle

We first simulate a sessile droplet initialized on a substrate with an acute contact angle under isothermal condition ($T_{sub}=T_{bulk}$ for t < 30,000) and under a subcooling condition ($T_{sub}<T_{bulk}$ for t > 30,000) by using different numerical schemes of contact angle, as shown in Figure 2. Figure 2a shows that the substrate contact angle simulated by Scheme #1 at t = 30,000 under isothermal condition ${\theta }_{s,i}={60}^{\circ }$ equals that under subcooling condition at t = 31,000 ${\theta }_{s,c}={60}^{\circ }$, which indicates that the magnitude of the simulated acute contact angle by Scheme #1 is not affected by subcooling condition. However, Figure 2b shows that the substrate contact angle simulated by Scheme #2 at t = 30,000 under isothermal condition is ${\theta }_{s,i}={76}^{\circ }$, which is larger than the simulated substrate contact angle at t > 30,000 under subcooling condition ${\theta }_{s,c}={60}^{\circ }$. Figure 2c also shows similar results with Figure 2b for Scheme #3 (${\theta }_{s,i}={80}^{\circ }$ at t = 30,000 and ${\theta }_{s,c}={60}^{\circ }$ at t > 30,000). This means that the subcooling condition makes the simulated contact angle by Scheme #2 or #3 decreased compared with that under an isothermal condition. Similar temperature dependence of numerical schemes of contact angle has also been identified in our previous papers [24,37], where the superheating condition enlarges the simulated contact angle.

Figure 2a also shows that the droplet shape distorts at t = 32,800 under a subcooling condition and the algorithm collapses by using Scheme #1, which indicates that the subcooling condition destabilizes the algorithm incorporated with Scheme #1. The possible reason for the droplet shape distortion is due to the increasing spurious velocity as simulation time increases. It can be seen from Figure 2a that the maximum spurious velocity is only $0.003\ll c_s$ for t < 32,800. However, the maximum spurious velocity increases significantly to $0.6>c_s$ at t = 32,800 and the fluid becomes compressible under such large spurious velocity so that the droplet shape distorts. On the other hand, Figure 2b,c show that, by using Scheme #2 or Scheme #3, the droplet grows reasonably on the substrate under subcooling condition for t > 30,000 and the algorithm is stable.

As for obtuse contact angle simulated by using Scheme #1, #2 and #3, Figure 3 also shows that the substrate contact angle under subcooling condition (t > 30,000) ${\theta }_{s,c}$ is smaller than that under isothermal condition (t = 30,000) ${\theta }_{s,i}$ for any of the three numerical schemes. However, the discrepancy between ${\theta }_{s,c}$ and ${\theta }_{s,i}$ is only $\Delta \theta ={\theta }_{s,i}-{\theta }_{s,c}=7^{\circ }$ in Scheme #1, as shown in Figure 3a, $\Delta \theta ={\theta }_{s,i}-{\theta }_{s,c}={21}^{\circ }$ in Scheme #2, as shown in Figure 3b, and $\Delta \theta ={\theta }_{s,i}-{\theta }_{s,c}={11}^{\circ }$ in Scheme #3, as shown in Figure 3c. This indicates that the subcooling condition has the least effect on the magnitude of the simulated contact angle by Scheme #1. It is also noted that, by using any of the three numerical schemes to simulate an obtuse contact angle, the droplet grows reasonably due to condensation under subcooling condition (t > 30,000) and the algorithm is stable.

4.2. Effects of Fluid Density Variation near Wall on Condensation

Since Scheme #1 cannot simulate acute contact angle stable under the subcooling condition as discussed in Section 4.1, the rest of the results are obtained by using Scheme #1, #2 and #3 to simulate a substrate with a microcavity with ${\theta }_{s,c}\approx {95}^{\circ }$. Figure 4a shows that using Scheme #1 to simulate the substrate contact angle causes the vapor density near the substrate microcavity wall to be larger than the bulk vapor density under the isothermal condition. However, there is no fluid density variation near the substrate microcavity wall if using Scheme #2 or #3 to simulate the substrate contact angle under the isothermal condition, as Figure 4b,c shows.

The fluid density variation near the microcavity wall in Scheme #1 (shown in Figure 4a) has significant effects on condensation nucleation. Figure 5a shows that, in Scheme #1, due to vapor density variation near the microcavity wall, the bulk vapor condenses into liquid in the microcavity under subcooling condition at t = 40,000. Such a process should be taken as “condensation nucleation”, as liquid appears spontaneously in the microcavity but not given artificially. However, Figure 5b shows that, in Scheme #2 and #3, the vapor density distribution near the microcavity wall is uniform so that the bulk vapor cannot condense into liquid in the microcavity under subcooling condition at t = 40,000. It is speculated that the vapor density variation near the microcavity wall in Scheme #1 plays the role of condensation nuclei. In Scheme #2 and #3, the vapor density is uniform near the microcavity wall so that condensation hardly occurs even under the subcooling condition.

To supply a condensation nucleus for Scheme #2 and #3, a thin liquid film of thickness $4\Delta y$ is initialized in the microcavity, as shown in Figure 6a,b, at t = 0. Due to the saturated vapor pressure difference inside the microcavity and in the bulk vapor environment, the initialized liquid film grows and the liquid–vapor interface curvature changes continuously to equilibrium status at the simulation time t = 10,000 before subcooling condition is applied at the substrate. After the subcooling boundary condition (T_sub < T_bulk) is applied at the microcavity wall (t > 30,000), condensation occurs in the microcavity subsequently in Scheme #2 and #3, as shown in Figure 6a,b, at t = 33,000 and t = 40,000. Thus, it is demonstrated from Figure 5 and Figure 6 that the numerical schemes of contact angle have significant effects on vapor density distribution near the wall, which plays the role of the condensation nucleus and determines whether condensation occurs.

4.3. Effects of Numerical Schemes on Condensation Heat Transfer in a Microcavity

To investigate temperature variation with time inside the microcavity during condensation under different initial conditions in different numerical schemes (i.e., with/without a liquid film initialized inside the microcavity), the dimensionless temperature distributions (T*(x,t) = T(x,t)/T_c) along the horizontal line y = 18 inside the microcavity from x = 95 to x = 105 at different times with ${\theta }_{s,c}\approx {95}^{\circ }$ as shown in Figure 7a are simulated by different numerical schemes as shown in Figure 7b,c,d. It is shown that, under any initial condition, the dimensionless temperature near the microcavity wall is lower than that at the center of the microcavity due to the subcooled microcavity wall. Figure 7b shows that, without the liquid film initialized in the microcavity in Scheme #1, the dimensionless temperature in the microcavity and the dimensionless temperature gradient $\partial T^{*}\left(x,t\right)/\partial n_s$ near the wall decrease with time t from t = 31,000 to t = 33,000. Subsequently, the dimensionless temperature in the microcavity and the dimensionless temperature gradient $\partial T^{*}\left(x,t\right)/\partial n_s$ near the wall increase from t = 33,000 to t = 39,000. However, Figure 7c,d show that, with the liquid film initialized in the microcavity in Scheme #2 and #3, the dimensionless temperature in the microcavity and the dimensionless temperature gradient $\partial T^{*}\left(x,t\right)/\partial n_s$ near the wall decrease monotonically from t = 31,000 to t = 39,000. The different variation trend of dimensionless temperature distribution as well as dimensionless temperature gradient $\partial T^{*}\left(x,t\right)/\partial n_s$ near the wall with time under different initialized conditions is attributed to the effects of numerical schemes and the corresponding initial conditions, as will be discussed in Figure 8 and Figure 9.

To further investigate effects of numerical schemes and the corresponding initial conditions on condensation heat transfer, we evaluated the heat flux at the microcavity wall $Q$ during condensation at different times t, as Figure 8 shows. The heat flux at the microcavity wall can be evaluated as: $Q={\displaystyle \underset{\Omega }{\int }{q}^{″}}d\Omega$, where $\Omega$ is the microcavity wall boundary and $q^{″}=-{\lambda }_f{\left.\frac{\partial T_f}{\partial n_s}\right|}_{\Omega }$ is the local heat flux density, the direction of which is perpendicular to the local microcavity wall. ${\lambda }_f$ is the thermal conductivity of fluid, $T_f$ is the fluid temperature and $n_s$ is the unit normal vector of the microcavity wall. Q reflects the heat transfer rate from the saturated vapor to the subcooled substrate.

The evaluated heat flux at the microcavity wall Q versus time t during condensation simulated by different numerical schemes of contact angle without/with a liquid film initialized in the microcavity are shown in Figure 9. It is shown that, without a liquid film initialized in the microcavity in Scheme #1, there is an increasing trend of Q with t for t = 33,000 to t = 40,000. However, with a liquid film initialized in the microcavity, Q decreases with t monotonically for t > 30,000 in Scheme #1, #2 and #3. It is noted that, without a liquid film initialized in the microcavity for the time t = 33,000 to t = 40,000 in Scheme #1, the vapor in the microcavity condenses into liquid, as Figure 5a shows, i.e., “condensation nucleation”. However, the increasing Q in this period of time cannot be latent heat releasing, otherwise Q will continue to increase for t > 40,000. It is inferred that the increasing trend of Q with time t during “condensation nucleation” in Scheme #1 without a liquid film initialized in the microcavity is unphysical due to vapor density variation near the wall, as discussed in Figure 4 and Figure 5. If there is a liquid film inside the microcavity, either by initialization in Scheme #1, #2 and #3 or through “condensation nucleation” in Scheme #1 without a liquid film initialized in the microcavity for t > 40,000, the heat flux at the microcavity wall Q decreases monotonically with time t. Such a phenomenon is reasonable, because the thermal resistance between the saturated vapor and the subcooled wall increases with the continuous growing of condensed liquid.

5. Conclusions

In this paper, we have used three numerical schemes of contact angle in pseudopotential lattice Boltzmann model to simulate condensation in a subcooled microcavity. It is found that the numerical schemes have significant effects on condensation nucleation and heat flux at the microcavity wall. The main conclusions are summarized as follows:

• The simulated contact angle of a subcooled substrate is smaller than that of an isothermal substrate by using different numerical schemes of contact angle in pseudopotential lattice Boltzmann model. The subcooling condition also destabilizes the algorithm incorporated with the pseudopotential-based scheme (Scheme #1) so that only an obtuse contact angle can be simulated by Scheme #1. However, such destabilization effect is eliminated by constructing a ghost fluid layer with weighted average density of surrounding fluid nodes (Scheme #2) or by using the geometric formulation scheme (Scheme #3).
• The fluid density near the wall simulated by the pseudopotential-based scheme (Scheme #1) fluctuates and deviates from the bulk fluid density, which plays the role of condensation nucleus. However, the simulated fluid density near the wall is uniform by constructing a ghost fluid layer with weighted average density of surrounding fluid nodes (Scheme #2) or by using the geometric formulation scheme (Scheme #3), so that condensation nucleation cannot occur spontaneously unless with a liquid film initialized in the microcavity.
• In the pseudopotential-based scheme (Scheme #1) the heat flux at the microcavity wall is unphysical before a liquid film is formed in the microcavity through “condensation nucleation”. Only after a liquid film forms in the microcavity, the temperature distribution and heat flux at the microcavity wall become reasonable in LB simulation by using the three numerical schemes of contact angle.
• Since an unphysical heat transfer phenomenon may occur in condensation simulation by pseudopotential LB model with the application of Scheme #1, it is recommended to use Scheme #2 or Scheme #3 in simulation. This study provides guidelines for researchers choosing the desirable numerical schemes of contact angle to ensure simulation accuracy on simulating the condensation process, so that much more efficient strategies or mechanisms for condensation heat transfer enhancement are expected to be revealed in the future from LB simulation.