Abstract
Solid oxide electrolysis cells (SOECs) have great application prospects because of their excellent performance, but the long-term applications of the stacks are restricted by the structural degradation under the high-temperature conditions. Therefore, an SOEC degradation model is developed and embedded in a process model of the high-temperature steam electrolysis (HTSE) system to investigate the influence of the stack degradation at the system level. The sensitivity analysis and optimization were carried out to study the influence factors of the stack degradation and system hydrogen production efficiency and search for the optimal operating conditions to improve the hydrogen production efficiency and mitigate the stack degradation. The analysis results show that the high temperature and large current density can accelerate the stack degradation but improve the hydrogen production efficiency, while the high temperature gradually becomes unfavorable in the late stage. The low air-to-fuel feed ratio is beneficial to both the degradation rate and hydrogen production efficiency. The results show that the optimization method can improve the hydrogen production efficiency and inhibit the stack degradation effectively. Moreover, part of the hydrogen production efficiency has to be sacrificed in order to obtain a lower stack degradation rate.
1. Introduction
With the increasing prominent global environmental problems and fossil fuel depletion issues, there is an urgent need for sustainable and environmentally friendly hydrogen production technologies [1]. Among the many hydrogen production technologies, the steam electrolysis vian SOECs has attracted much attention due to the high electrolysis efficiency and low energy consumption [2,3]. At present, with the various applications of SOECs as a high-efficiency energy conversion technology, numerous studies on their long-term durability have been performed. One of the challenges for long-term operation of SOECs is the degradation of cell materials [4]. The high-temperature operating environment not only leads to the high efficiency of SOECs but also exacerbates the degradation of cell materials.
The factors resulting in degradation have been found by the investigation on the degradation of SOEC components. In the study on the causes of electrolyte degradation, Hattori et al. [5] investigated the electrical conductivity change of YSZ system at 1000 °C and found that the cubic phase transformation led to the conductivity drop of electrolyte YSZ. In order to investigate the degradation mechanism of oxygen and fuel electrodes, Yan et al. [6] and Zheng et al. [7] conducted tests using LSC-YSZ, LSCF-YSZ and LSM-YSZ as the oxygen electrodes during the long-term electrolytic operation at 700–800 °C with current density of 0.5 Am−2, respectively. The delamination of oxygen electrodes and the agglomeration of Ni in fuel electrodes were observed, which reduced the TPB length and increased the polarization resistance. Wolf et al. [8] studied the degradation behavior using NiO-YSZ/YSZ/GDC/LSC single cells under steam electrolysis and coelectrolysis conditions and found Ni-depletion and agglomeration in the fuel electrode in all cells. Vibhu et al. [9] investigated the degradation process of an electrolyte-supported single cell composed of Mo-Au-Ni/GDC fuel electrode and LSCF oxygen electrode under the steam electrolysis condition and found the Sr-segregation and cobalt oxide formation at the oxygen electrode side as well as the Ni-particle coarsening and depletion at the fuel electrode side were the main reasons for the degradation.
In addition, some studies also focused on the influence of the operating conditions on SOEC degradation, such as current density, electrolysis temperature and inlet steam content. Kim Lohsoontorn et al. [10] performed durability studies of cells at different electrolytic current densities at periods of over 20 h and found increasing the electrolysis current density accelerated performance degradation. Zhang et al. [11] carried out an experimental investigation on the performance and durability of three different solid oxide cells, and the results demonstrated stable performance in the fuel cell mode but rapid degradation in the electrolysis mode, especially at the high current density. Hoerlein et al. [12] conducted 1000 h degradation experiments with NiO-YSZ/YSZ/LSCF cells to study the effect of fuel electrode inlet gas humidity on the long-term stability of SOEC, and the results demonstrated that increasing humidity may slow down the overall degradation process despite the initial degradation being fast. Further study of the influence factors of SOEC degradation was conducted using numerical simulations. Jacobsen and Mogensen [13] and Virkar [14] developed an electrochemical model of the degraded SOEC indicating that the degradation was caused by the delamination of the oxygen electrode due to the high oxygen partial pressure near the oxygen electrode and electrolyte interface. Jensen et al. [15] used the Ni/YSZ fuel electrode impedance model to simulate the increase in the electrochemical reaction resistance caused by the decrease of the TPB length. Kamkeng et al. [16] developed a more detailed SOEC degradation model to analyze the effects of current density and temperature on degradation.
Compared with the studies on the degradation mechanism of the SOEC stack, few studies focus on the HTSE system. The heat efficiency and hydrogen production efficiency are the research emphasis. AlZahrani et al. [17] carried out a thermodynamic simulation of an SOEC system for hydrogen and oxygen production and performed an optimization for the system exergy efficiency. Xing et al. [18] developed an energy flow model for the HTSE system and established an optimizing strategy to maximize the hydrogen yield. Using high-fidelity and empirical-based system component models, Min et al. [19] performed a thermodynamic optimization of a coelectrolysis cell system. Li et al. [20] carried out the system simulation of the solid oxide electrolysis system and made assessments of the thermodynamic performance using the exergy analysis method.
Some studies have focused on the integrated energy system with the HTSE system. Prabhakaran et al. [21] proposed a dynamic pricing model of the Power to Gas system via SOECs used for seasonal energy storage. The energy storage time is optimized to minimize system costs. Cai et al. [22] performed an optimization of an integrated energy system coupling the SOEC system with intermittent renewable energy to maximize hydrogen production and minimize the SOEC energy consumption and compressor energy consumption. Chen et al. [23] proposed a photovoltaic hydrogen production system integrating SOECs with ammonia and performed an optimization to obtain the optimal solar to hydrogen efficiency. Sun et al. [24] used the genetic algorithm to optimize an integrated energy system including SOECs and the intermittent renewable energy. The double-objective optimization in electrolytic efficiency and conversion rate were carried out. Mohammadpour et al. [25] proposed an optimized integrated energy system including SOECs that considered the sustainable index and the total cost rate.
As mentioned above, there have been many studies and modeling work on the degradation mechanism of SOECs. However, there are few studies that consider reactor degradation at the system level, and there is still no system optimization that takes degradation into consideration. Therefore, in order to study the influence of reactor structure degradation on the hydrogen production system, this work carried out parameter analysis and optimization of the HTSE system considering SOEC stack degradation, aiming to find an effective strategy to slow down the SOEC degradation and extend its life span. The goals of this paper can be summarized as follows:
- A pseudo-dynamic model of SOEC degradation is established and embedded in the HTSE system, which takes into account the high-temperature degradation of typical SOEC materials.
- The effects of the key operating conditions on the hydrogen production efficiency and degradation were studied such as the operating temperature, current density, air-to-fuel feed ratio, etc.
- An optimization was carried out to propose the operation strategies to balance the hydrogen production efficiency and the stack life span.
2. Model Development of SOEC Degradation
For the 1D pseudo-dynamic SOEC model developed in this work, the following assumptions were considered:
- All gas flows are considered as the ideal gases.
- Only the degradation due to the stack materials changes at the high temperature condition is considered, while the mass or heat accumulation inside the cell is not considered.
- The governing equations to describe the structural degradation are only available for specified SOEC materials.
- A planar SOEC stack consists of many single cells, which are regarded as unit cells with the same performance.
A single cell is modeled on behalf of the SOEC stack. Each cell contains an anode channel, a cathode channel, a solid structure and two interconnected plates [17]. The four zones are distinguished to facilitate heat balance calculations.
The operating potential of a single cell can be written as
where
is the equilibrium voltage;
is the overpotential of the cathode sides;
is the overpotential of the anode side and
is the overpotential of the electrolyte.
2.1. Equilibrium Potential
The equilibrium potential is defined by the Nernst equation as follows [26]:
where stands for the standard potential; F is the Faraday constant, 96,485 C/mol; , and are the partial pressures of hydrogen, oxygen and steam on the electrode surfaces, respectively; and R is the universal gas constant, 8.3145 J/(mol K).
2.2. Cathode Overpotentials
The cathode overpotentials is expressed by the following equation:
where is the concentration overpotential is the activation overpotential and is ohmic overpotential.
The concentration overpotential of the cathode side can be obtained by adopting the Fick’s model [17]:
where (i = H2 and H2O) represents the concentrations of the species at the TPB and in the bulk flow, respectively.
The degradation process is considered in the activation overpotential and the ohmic overpotential. The initial activation overpotential can be described by the Butler–Volmer equation as follows [26]:
where represents the initial exchange current density of the cathode side; is the initial current density of the cell; ɑ is the charge transfer coefficient and is the number of electrons produced per reaction. For water electrolysis, and are set as 0.5 and 2, respectively. Thus, Equation (5) can be expressed as [26]:
In the high-temperature environment, the degradation of the cathode materials is mainly caused by Ni-particle coarsening [16]. It is assumed that Ni will agglomerate with H2O by forming Ni2-OH; thus, the size growth of Ni particles can be expressed by the following equation [14]:
where t is the degradation time; and are the radii of Ni particles at the initial condition and at the degradation time t, respectively; C is the temperature-independent constant; and are the weight fraction of Ni and YSZ; is the YSZ surface area; and are the mole fractions of H2O and H2; and is the activation energy for sintering.
Ni-particle coarsening in the cathode can reduce the TPB length. The relationship between the TPB length and Ni particle growth can be described by [27]
According to the Butler–Volmer equation [27], Equation (5) can be approximately expressed as
Integration of Equation (10) gives Equation (11), establishing the relationship between the activation overpotentials at the initial condition and at the degradation time:
where is the activation overpotentials at the degradation time t; J is the electrolysis current density at the degradation time t and is the exchange current density at the degradation time t.
Considering Equation (8) and the exchange current density is proportional to the TPB length [27], Equation (11) can be deduced to Equation (12):
The ohmic overpotential of the cathode can be expressed as follows [16]:
where is the thickness of Ni-YSZ composite; is the electronic conductivity of Ni-YSZ composite; and are the electronic conductivity of Ni particle and YSZ particle, respectively; and and are the volume fractions of Ni and YSZ in the cathode, respectively. Since is so low compared to that it can be negligible, can be calculated by the following equations based on the percolation theory [16]:
where is the Ni volume fraction at percolation; Φ is the porosity.
2.3. Anode Overpotentials
The anode overpotentials is expressed by the following equation:
where is the concentration overpotential; is the activation overpotential and is ohmic overpotential.
The concentration overpotential of the anode side can also be obtained by adopting the Fick’s model [16]:
where are the concentrations of the species at the TPB and in the bulk flow, respectively; and are the average temperature of the solid structure and the anode gas stream, respectively.
Under the high-temperature conditions, the structural degradation of the anode is mainly caused by the coarsening of LSM-YSZ particles, the formation of lanthanum zirconate (LZO) and chromium oxide scale (COS) layer.
Like the Ni coarsening in the cathode side, the coarsening of LSM-YSZ particles also reduces the TPB length on the anode side. The activation overpotential at the degradation time t can be expressed as
where and are the activation overpotentials at the initial condition and the degradation time t, respectively. is the LSM surface diffusion, which represents the initial exchange current density of the anode side.
The formation of the lanthanum zirconate (LZO) and chromium oxide scale (COS) layer will increase the ohmic resistance of the anode side due to the poor conductive of the LZO and COS. The ohmic overpotential of the anode side can be expressed as follows:
where and are the thicknesses of the LZO layer and COS layer, respectively. and are the electronic conductivity of the LZO layer and COS layer, respectively.
Using Wagner’s law for parabolic oxidation, the growth of LZO and COS can be written as follows [28]:
In Equations (22) and (23), and are the weight gain rates for the LZO and COS layer growth, respectively. and are the weight ratios of oxygen in the LZO and COS layers, respectively. and are the LZO and COS densities, respectively. and are the activation energies for the LZO and COS layer growth, respectively.
2.4. Electrolyte Overpotentials
The YSZ crystal structure changes due to the cation diffusion under high temperature and reducing conditions, leading to a decrease in the YSZ ionic conductivity. The ohmic overpotential of the electrolyte can be expressed as follows [16]:
where is the thickness of YSZ electrolyte; is the electronic conductivity of YSZ electrolyte; is the pre-exponential factor for electrolyte; is the electrolyte activation energy; is the electrolyte fitting parameter; is the time constant and is the ionic radius.
2.5. Mass and Heat Balance
The average temperatures at the anode channel, the cathode channel, the solid structure and the interconnect plate are calculated by the mass and heat balance equations as follows:
where and are the enthalpies of the outlet and inlet gas of the cathode side, respectively. and are the enthalpies of the outlet and inlet gas of the anode side, respectively. and are the heat generated or lost by gas diffusion at the cathode and anode sides, respectively. and are the heat by the convective heat transfer at the cathode and anode flow channels, respectively. and are the heat by the convective heat transfer at the solid structure and the interconnect plate, respectively. is the reaction heat; is the heat by the radiant heat transfer; and Num denotes the number of the single cells in the stack.
3. Simulation
3.1. Process Description and Simulation
The flow diagram of the HTSE system in this work is shown in Figure 1. In the cathode side, the purified water is transferred to the steam generator by a feed pump and turns into steam. After being mixed with a certain proportion of hydrogen, the gas mixture is further heated by the cathode heat exchanger and electric heater before entering the cathode of the SOEC stack. In the anode side, the air is pressurized by the air compressor and heated by the anode heat exchanger and electric heater before entering the stack. In the SOEC stack, the steam is electrolyzed into hydrogen and oxygen, which flow out from the cathode and anode sides, respectively. The oxygen-rich gas at the anode outlet is directly vented after exchanging heat with the anode inlet gas. The hydrogen-containing gas is cooled by exchanging heat with the cathode inlet gas and then further cooled to remove water at a flash tank. The produced high-purity hydrogen is then compressed into the cylinders for storage.
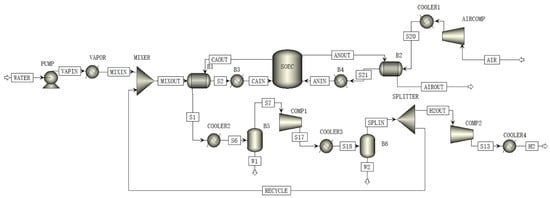
Figure 1.
The process model of HTSE system established by Aspen Plus.
The process model of the HTSE system is established in Aspen Plus software. The SOEC degradation model was developed via Aspen Custom Modeler and embedded in Aspen Plus for the process simulation. The HTSE system is assumed to operate under steady state conditions in the simulation. On the contrary, the SOEC degradation model considers the dynamic degradation process by the structural parameters, which are defined by the time-dependent functions, such as , and . The values of some parameters for the calculation of the SOEC stack degradation are provided in Table 1.

Table 1.
Some parameters used in SOEC modeling.
3.2. Optimization
The degradation rate is a key indicator reflecting the stack performance, while the hydrogen production efficiency is a key indicator reflecting the system performance. Both the degradation rate and the hydrogen production efficiency should be considered for a long-term, highly efficient operation. Thus, the degradation rate of SOEC stack and the hydrogen production efficiency of the HTSE system are taken as optimization objectives.
The degradation rate of SOEC stack is calculated by
where and are the SOEC stack voltages at the degradation time t and t0, respectively.
The hydrogen production efficiency used to evaluate HTSE system can be expressed by
where is the hydrogen production. is the low heating value of H2. denotes the power and heat energy demands of the system, respectively. contains the electrical power demands of the SOEC stack, pump, steam generator, electric heaters and compressors.
According to the mechanism analysis, the high temperature leads to the serious structural damages of the SOEC stack as well as the lower impedance of the stack [29]. In addition, the stack temperature can be effectively controlled by adjusting the air flow at the anode inlet [30]. Therefore, the inlet temperatures of cathode and anode, current density and air-to-fuel feed ratio were selected as the decision variables. The upper and lower bound values of the decision variables are given in Table 2.

Table 2.
The value ranges of the decision variables in optimization.
In this work, the optimization program based on the Multiobjective Particle Swarm Optimization (MOPSO) algorithm was developed in MATLAB to optimize the system process model in Aspen Plus. The flowchart of the optimization procedure is shown in Figure 2. As shown in Figure 2, the optimization method is as follows:
- Update the structural parameters of the SOEC stack. The structural parameters (i.e., , and ) at the end of the previous degradation period should be assigned as the structural parameters of the SOEC stack in the current period.
- Perform the optimization. The optimal decision variables for the new degradation period are solved by the MOPSO algorithm.
- Carry out the simulation of the next period. The simulation of the new degradation period is carried out by the new decision variables and structural parameters, and the new structural parameters for the succeeding period are calculated. Repeat steps 1 to 2 until the optimization process is over.
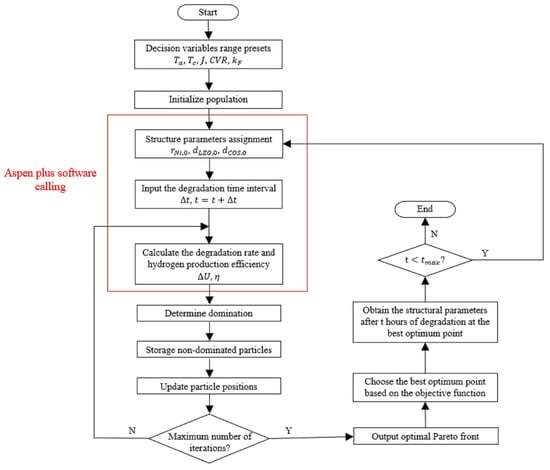
Figure 2.
The flowchart for the online optimization procedure of the SOEC hydrogen production.
4. Results and Discussion
4.1. Model Validation and Analysis
The simulation results were validated by the experimental data reported by Brisse et al. [31]. The J-V curves at two different temperatures are selected for the model validation. As shown in Figure 3, a good agreement between the simulation results and experimental data was found. The maximum and minimum relative errors at 800 °C are 6.7% and 0.7%, respectively. Moreover, the large error occurs at low temperature and high current density. In general, the SOEC model developed in this work is feasible for simulating the HTSE system from in terms of accuracy.
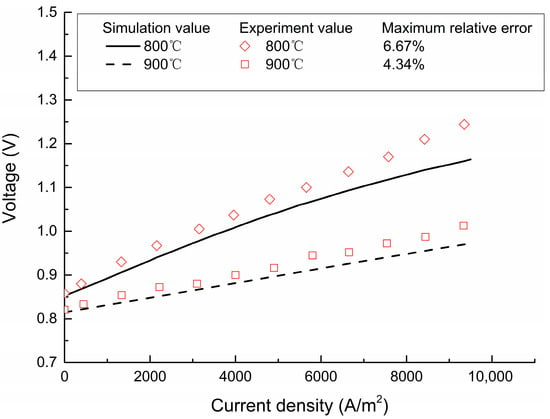
Figure 3.
The result of model validation for SOECs.
Figure 4 shows the contributions of the anode, electrolyte and cathode sides to the overpotentials of a single cell at conditions of 750 °C, 5000 A/m2 and air-to-fuel feed ratio of 3. As shown in Figure 4, the proportion of the anode overpotentials is the largest followed by that of the cathode overpotentials, and both of them account for far more than the proportion of the electrolyte overpotential. It can also be found that the proportion of the anode overpotentials increases with the degradation, time while those of the cathode overpotentials and electrolyte overpotentials decrease. This can be explained by the fact that, in the degradation model, the formation of LZO and COS layers and coarsening of LSM-YSZ are considered in the anode part, resulting in the increase of activation overpotential and ohmic overpotential, while only Ni-particle coarsening is considered in the cathode part, and only the conductivity reduction caused by the electrolyte crystal structure change is considered in the electrolyte part.
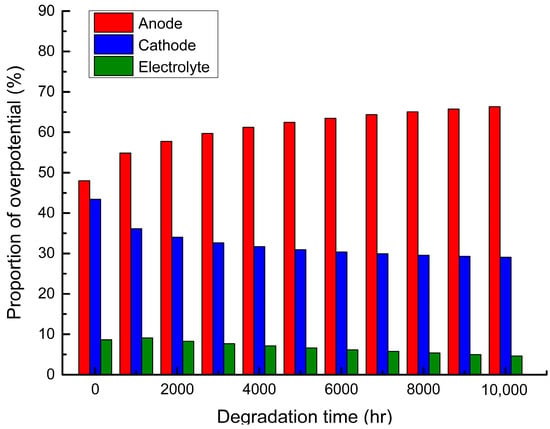
Figure 4.
The proportion of overpotential at each part of a single cell during degradation.
4.2. Sensitivity Analysis
To obtain a more detailed understanding of the behavior of the developed system, the sensitivity analysis of the hydrogen production efficiency of the system and the degradation rate of the SOEC stack was performed at different inlet temperatures, current densities and air-to-fuel feed ratios. The effects of various operating variables on the degradation rate, stack voltage and hydrogen production efficiency are further discussed.
4.2.1. Effect of Inlet Temperature
Figure 5 shows the variation of the degradation rate, stack voltage and hydrogen production efficiency with the different inlet temperatures at the fixed current density of 5000 A/m2, air-to-fuel feed ratio of 3. Three different temperatures of 700 °C, 750 °C and 800 °C were selected. Figure 5a shows that the degradation rate increases gradually, which leads to an increase in the overpotential at the fixed current density. Therefore, it can be found in Figure 5b that the stack voltage also increases gradually over time. In Figure 5c, the increasing stack voltage increases the electrolytic power, which results in a gradual decrease in the hydrogen production efficiency.
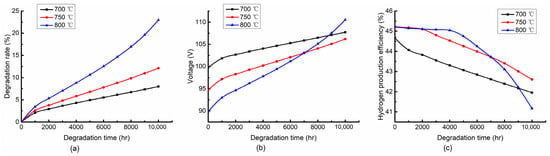
Figure 5.
Variation trends of (a) degradation rate, (b) stack voltage and (c) hydrogen production efficiency with degradation time at 700 °C, 750 °C and 800 °C. (Operating at 5000 A/m2 and air-to-fuel feed ratio of 3).
In Figure 5a, the degradation rate increases with the increase of inlet temperature. Especially at the end of the period, the rise rate of the curve at a high temperature is more obvious. The effect of the degradation rate is reflected in the distribution of the stack voltage. As can be seen from Figure 5b, the stack voltage decreases with the increase of inlet temperature, while the trend changes at the end of the period where the higher temperature leads to a larger voltage. This is because the rise rate of the degradation rate at the end of the period under the higher temperature is larger than that under the lower temperature. Figure 5c shows the distribution of the hydrogen production efficiency at the different temperatures. Moreover, it can be found that the distribution of the hydrogen production efficiency is opposite to that of the stack voltage.
In general, the inlet temperatures of the cathode and anode sides have a significant effect on the degradation rate, stack voltage and hydrogen production efficiency. Moreover, it can be found that the impact trends of the inlet temperatures on the stack voltage and hydrogen production efficiency are different at different time periods.
4.2.2. Effect of Current Density
Figure 6 shows the variation of the degradation rate, stack voltage and hydrogen production efficiency with the different current densities at the fixed inlet temperature of 750 °C and air-to-fuel feed ratio of 3. Three current densities of 2000 A/m2, 5000 A/m2, and 8000 A/m2 are selected. The variation trends of the degradation rate, stack voltage and hydrogen production efficiency with the degradation time are the same as those in Section 4.2.1. As shown in Figure 6a, a large current density results in a large degradation rate. Especially at the end of the period, the rise rate of the degradation rate under the higher current density increases dramatically. This is because the larger current density increases the reaction temperature, which can promote the stack degradation. From Figure 6b, the higher current density leads to the larger stack voltage. It can be explained by the electrochemical mechanism of the SOEC stack that the higher current density increases the overpotentials of the stack. As shown in Figure 6c, the current density has a significant effect on the hydrogen production efficiency. The increase of the current density results in the increase of the steam conversion rate, which greatly improves the hydrogen production efficiency of the system. However, the hydrogen production efficiency drops dramatically at the high current density due to the sharp rise in the degradation rate.
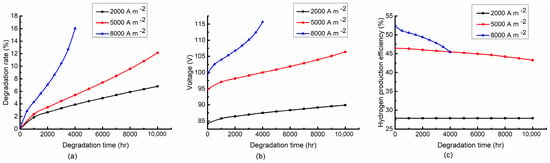
Figure 6.
Variation trends of (a) degradation rate, (b) stack voltage and (c) hydrogen production efficiency with degradation time at 2000 A/m2, 5000 A/m2 and 8000 A/m2. (Operating at 750 °C and air−to−fuel feed ratio of 3).
In general, the high current density can improve the hydrogen production efficiency while accelerating the stack degradation. Thus, the high current density should be adopted at the beginning of the degradation period for high hydrogen production efficiency and then decrease in the middle and late stages of the degradation period for a long operating life.
4.2.3. Effect of Air-to-Fuel Feed Ratio
Figure 7 shows that the variation of the degradation rate, stack voltage and hydrogen production efficiency with different air-to-fuel feed ratios at the fixed inlet temperature of 750 °C and current density of 5000 A/m2. From Figure 7a, it can be seen that the air-to-fuel feed ratio has a little effect on the degradation rate. A larger air-to-fuel feed ratio results in a larger degradation rate. The reason is that the stack is in an endothermic state at the inlet temperature of 750 °C and the current density of 5000 A/m2; the larger air flow can increase the reaction temperature, which leads to a larger degradation rate. Figure 7b shows the distribution of the stack voltage. It can be found that a larger air-to-fuel feed ratio leads to a lower stack voltage within 1000 h. This is because the reaction temperature with a large air-to-fuel feed ratio will be higher under the endothermic operation of the stack, which reduces the irreversible loss of the stack. However, a higher temperature also leads to a larger degradation rate, and the stack voltage increases faster. Therefore, a larger stack voltage with a larger air-to-fuel feed ratio occurs after 1000 h. Figure 7c shows the distribution of the hydrogen production efficiency. It can be seen that the hydrogen production efficiency decreases with the increase of the air-to-fuel feed ratio. This is because the large air flow not only increases the power consumption of the air compressor but also increases the stack voltage.
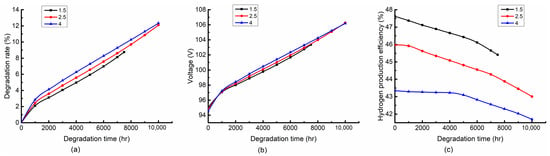
Figure 7.
Variation trends of (a) degradation rate, (b) stack voltage and (c) hydrogen production efficiency with degradation time at air-to-fuel feed ratio of 1.5, 2.5 and 4. (Operating at 750 °C and 5000 A/m2).
In general, the air-to-fuel feed ratio has a slight effect on the degradation rate and stack voltage while having a significant effect on the hydrogen production efficiency. A low air-to-fuel feed ratio is beneficial to the degradation rate and hydrogen production efficiency.
4.3. Multiobjective Optimization
The decision variables and objective functions of multiobjective optimization are described in Section 3.2. The decision variables are optimized every 100 h, and the degradation period is set for 2000 h. In this process, the structural parameters after the previous degradation are used as the structural parameters of the SOEC stack for the next optimization. Since the optimal solution solved by the multiobjective optimization is a set of Pareto solutions, it is necessary to select a point from the optimal solution set. Therefore, the hydrogen production efficiency is prioritized to select the optimal point in the first 1100 h, while the point with the smallest distance from the ideal point is selected as the optimal point in the last 900 h. Taking the Pareto solution set at the time of degradation 1200 h as an example, the red point a is selected as the optimal point which is the closest to the ideal point shown in Figure 8.
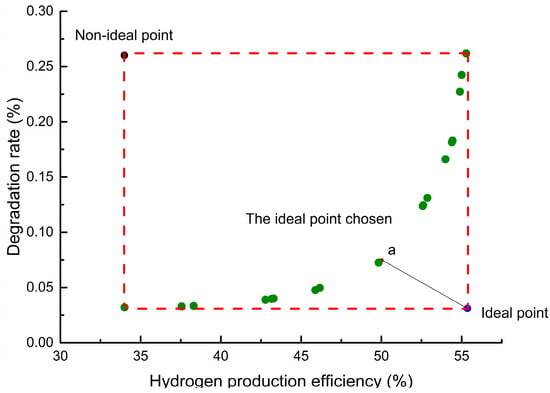
Figure 8.
Pareto solution set at degradation for 1200 h.
The optimal point records selected during the optimization process are listed in Table 3. As shown in Table 3, the decision variables at the optimum point are all on the boundary except for the inlet temperatures in the first 1100 h. This is because the hydrogen production efficiency is prioritized to select the optimal point within 1100 h. As discussed in Section 4.2.2 and Section 4.2.3, the large current density and low air-to-fuel feed ratio is more beneficial to the hydrogen production efficiency. After 1100 h, both the degradation rate and hydrogen production efficiency are taken into consideration. As shown in Figure 5c, although the higher temperature leads to a higher hydrogen production efficiency, it has a slight effect in the hydrogen production efficiency within 2000 h. The floating valve of the hydrogen production efficiency within 2000 h is lower than 1.5%. However, the low temperature can reduce the degradation rate significantly. Moreover, the low air-to-fuel feed ratio is beneficial to both the degradation rate and hydrogen production efficiency. Therefore, the minimum temperature and air-to-fuel feed ratio are obtained in the last 900 h.

Table 3.
The optimal point selection records during optimization.
The variations of the optimization objectives in the optimization process are shown in Figure 9. In the optimization process, the hydrogen production efficiency of the system is given priority at the first 1100 h, and both the hydrogen production efficiency and degradation rate are taken into consideration after 1100 h. As shown in Figure 9a, as the hydrogen production efficiency of the system is given priority, the hydrogen production efficiency after the optimization is significantly larger than that without the optimization, while it decreases dramatically after taking both the hydrogen production efficiency and degradation rate into consideration at 1100 h. This can be explained by the fact that the temperature, current density and air-to-fuel feed ratio have a limited effect on the degradation rate but have a significant effect on the hydrogen production efficiency at the first 1100 h. Thus, as shown by Figure 9b, the distributions of the degradation rate before and after optimization in the first 1100 h are very close. When the degradation rate is considered after 1100 h, the lower temperature and lower current density are desired, which have an adverse effect on the hydrogen production efficiency, so the hydrogen production efficiency drops dramatically at 1100 h, and the degradation rate decreases significantly compared with the nonoptimization, as shown in Figure 9b. In general, partial hydrogen production efficiency has to be sacrificed to obtain a lower degradation rate.
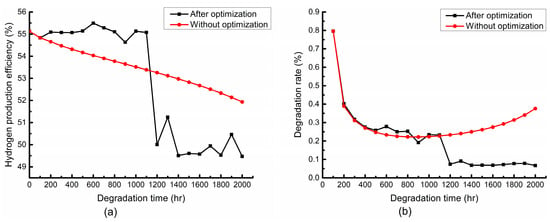
Figure 9.
Variation trends of (a) hydrogen production efficiency and (b) stack degradation rate in the optimization process.
Figure 10 shows the distributions of the Ni radius and the thickness of LZO and COS with and without the optimization. From Figure 10, it can be seen that in the first 1100 h the Ni radius, the thicknesses of LZO and COS are larger than those without optimization. In the last 900 h, the growth of the structural parameters slowed down, and the Ni radius and the thicknesses of LZO and COS are lower than those without the optimization after 1800 h. This is because the optimal selection takes both hydrogen production efficiency and stack degradation rate into account, and the stack degradation is significantly inhibited.
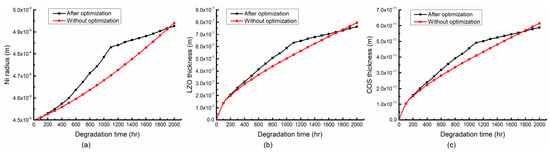
Figure 10.
Variation trends of structural parameters (a) Ni radius, (b) LZO thickness and (c) COS thickness over time during optimization.
5. Conclusions
An optimization program was developed in this work to mitigate the degradation of the SOEC stack and improve the hydrogen production efficiency for the HTSE system. The degradation process was modeled by a custom-developed SOEC model embedded into a system model of the HTSE system, and the effects of some decision variables (i.e., the inlet temperature, current density and air-to-fuel feed ratio) on the hydrogen production efficiency and stack degradation rate of the system were studied. The main conclusions of this work are listed as follows:
- (1)
- The high temperature accelerates the stack degradation. However, it is favorable to the hydrogen production efficiency at the early stage of the degradation process and gradually becomes unfavorable in the late stage. The high current density can improve the hydrogen production efficiency while accelerating the stack degradation. The air-to-fuel feed ratio has a slight effect on the degradation rate and stack voltage, while it has a significant effect on the hydrogen production efficiency. A low air-to-fuel feed ratio is beneficial to the degradation rate and hydrogen production efficiency.
- (2)
- Compared with the nonoptimization, the hydrogen production efficiency after the optimization is significantly larger when taking the hydrogen production efficiency as the objective in the early stage. The degradation rate is significantly lower than that without the optimization when taking the degradation rate into consideration in the late stage. Part of the hydrogen production efficiency has to be sacrificed in order to obtain a lower stack degradation rate.
- (3)
- Compared with the nonoptimization, the structural degradation after the optimization is more obvious when taking the hydrogen production efficiency as the objective in the early stage, while it decreases to be less than those without the optimization when taking the degradation rate into consideration in the late stage.
Author Contributions
Conceptualization, J.Y., T.L. and J.-Q.W.; methodology, J.Y. and B.Y.; software, T.L.; validation, G.X., T.L. and J.-Q.W.; formal analysis, B.Y. and G.X.; investigation, J.Y. and B.Y.; resources, G.X., T.L. and J.-Q.W.; data curation, Z.L.; writing—original draft preparation, J.Y.; writing—review and editing, B.Y. and G.X.; visualization, J.Y. and B.Y.; supervision, T.L. and J.-Q.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Transformational Technologies for Clean Energy and Demonstration Strategic Priority Research Program of the Chinese Academy of Sciences, XDA2100000, and the Young Potential Program of Shanghai Institute of Applied Physics, Chinese Academy of Sciences, E155041031.
Data Availability Statement
Not applicable.
Acknowledgments
This work was partly supported by the Transformational Technologies for Clean Energy and Demonstration Strategic Priority Research Program of the Chinese Academy of Sciences and the Young Potential Program of Shanghai Institute of Applied Physics, Chinese Academy of Sciences.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, N.; Wang, M.; Shen, Q.; Teng, Y.; Wang, D.; Chen, C.; Zhan, Z. Reduced concentration polarization and enhanced steam throughput conversion with a solid oxide electrolysis cell supported on an electrode with optimized pore structure. Int. J. Hydrogen Energy 2022, 47, 21673–21680. [Google Scholar] [CrossRef]
- Navasa, N.; Yuan, J.; Sundén, B. Computational fluid dynamics approach for performance evaluation of a solid oxide electrolysis cell for hydrogen production. Appl. Energy 2015, 137, 867–876. [Google Scholar] [CrossRef]
- Laguna-Bercero, M.A. Recent advances in high temperature electrolysis using solid oxide fuel cells: A review. J. Power Sources 2012, 203, 4–16. [Google Scholar] [CrossRef]
- Hauch, A.; Küngas, R.; Blennow, P.; Hansen, A.B.; Hansen, J.B.; Mathiesen, B.V.; Mogensen, M.B. Recent advances in solid oxide cell technology for electrolysis. Science 2020, 370, 954. [Google Scholar] [CrossRef]
- Hattori, M.; Takeda, Y.; Sakaki, Y.; Nakanishi, A.; Ohara, S.; Mukai, K.; Lee, J.H.; Fukui, T. Effect of aging on conductivity of yttria stabilized zirconia. J Power Sources 2004, 126, 23–27. [Google Scholar] [CrossRef]
- Yan, Y.; Fang, Q.; Blum, L.; Lehnert, W. Performance and degradation of an SOEC stack with different cell components. Electrochim. Acta 2017, 258, 1254–1261. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, Q.; Chen, T.; Wu, W.; Xu, C.; Wang, W.G. Comparison of performance and degradation of large-scale solid oxide electrolysis cells in stack with different composite air electrodes. Int. J. Hydrogen Energy 2015, 40, 2460–2472. [Google Scholar] [CrossRef]
- Wolf, S.E.; Vibhu, V.; Tröster, E.; Vinke, I.C.; Eichel, R.-A.; da Haart, L.G.J. Steam electrolysis vs. co-electrolysis: Mechanistic studies of long-term solid oxide electrolysis cells. Energies 2022, 15, 5449. [Google Scholar] [CrossRef]
- Vibhu, V.; Vinke, I.C.; Zaravelis, F.; Neophytides, S.G.; Niakolas, D.K.; Eichel, R.-A.; de Haart, L.G.J. Performance and degradation of electrolyte-supported single cell composed of Mo-Au-Ni/GDC fuel electrode and LSCF oxygen electrode during high temperature steam electrolysis. Energies 2022, 15, 2726. [Google Scholar] [CrossRef]
- Kim-Lohsoontorn, P.; Brett, D.; Laosiripojana, N.; Kim, Y.; Bae, J. Performance of solid oxide electrolysis cells based on composite La0.8Sr0.2MnO3−δ-yttria stabilized zirconia and Ba0.5Sr0.5Co0.8Fe0.2O3−δ oxygen electrodes. Int. J. Hydrogen Energy 2010, 35, 3958–3966. [Google Scholar] [CrossRef]
- Zhang, X.; O’Brien, J.E.; O’Brien, R.C.; Housley, G.K. Durability evaluation of reversible solid oxide cells. J. Power Sources 2013, 242, 566–574. [Google Scholar] [CrossRef]
- Hoerlein, M.P.; Schiller, G.; Tietz, F.; Friedrich, K.A. Systematic Parameter Study on the Influence of Humidification and Current Density on SOEC Degradation. Meet. Abstr. 2015, 68, 3553–3561. [Google Scholar] [CrossRef]
- Jacobsen, T.; Mogensen, M. The Course of Oxygen Partial Pressure and Electric Potentials across an Oxide Electrolyte Cell. ECS Trans. 2008, 13, 259–273. [Google Scholar] [CrossRef]
- Virkar, A.V. Mechanism of oxygen electrode delamination in solid oxide electrolyzer cells. Int. J. Hydrogen Energy 2010, 35, 9527–9543. [Google Scholar] [CrossRef]
- Jensen, S.H.; Hauch, A.; Knibbe, R.; Jacobsen, T.; Mogensen, M. Modeling degradation in SOEC impedance spectra. J. Electrochem. Soc. 2013, 160, F244–F250. [Google Scholar] [CrossRef]
- Kamkeng, A.; Wang, M. Long-term performance prediction of solid oxide electrolysis cell (SOEC) for CO2/H2O co-electrolysis considering structural degradation through modelling and simulation. Chem. Eng. J. 2022, 429, 132158. [Google Scholar] [CrossRef]
- AlZahrani, A.A.; Dincer, I. Modeling and performance optimization of a solid oxide electrolysis system for hydrogen production. Appl. Energy 2018, 225, 471–485. [Google Scholar] [CrossRef]
- Xing, X.; Lin, J.; Song, Y.; Hu, Q.; Zhou, Y.; Mu, S. Optimization of hydrogen yield of a high-temperature electrolysis system with coordinated temperature and feed factors at various loading conditions: A model-based study. Appl. Energy 2018, 232, 368–385. [Google Scholar] [CrossRef]
- Min, G.; Park, Y.J.; Choi, S.; Hong, J. Sensitivity analysis of a solid oxide co-electrolysis cell system with respect to its key operating parameters and optimization with its performance map. Energy Convers. Manag. 2021, 249, 114848. [Google Scholar] [CrossRef]
- Li, G.; Xiao, G.; Guan, C.; Hong, C.; Yuan, B.; Li, T.; Wang, J.Q. Assessment of thermodynamic performance of a 20 kW high-temperature electrolysis system using advanced exergy analysis. Fuel Cells 2021, 21, 550–565. [Google Scholar] [CrossRef]
- Prabhakaran, P.; Giannopoulos, D.; Köppel, W.; Mukherjee, U.; Remesh, G.; Graf, F.; Trimis, D.; Kolb, T.; Founti, M. Cost optimisation and life cycle analysis of SOEC based Power to Gas systems used for seasonal energy storage in decentral systems. J Energy Storage 2019, 26, 100987. [Google Scholar] [CrossRef]
- Cai, Q.; Adjiman, C.S.; Brandon, N.P. Optimal control strategies for hydrogen production when coupling solid oxide electrolysers with intermittent renewable energies. J. Power Sources 2014, 268, 212–224. [Google Scholar] [CrossRef]
- Chen, C.; Xia, Q.; Feng, S.; Liu, Q. A novel solar hydrogen production system integrating high temperature electrolysis with ammonia based thermochemical energy storage. Energy Convers. Manag. 2021, 237, 114143. [Google Scholar] [CrossRef]
- Sun, Y.; Lu, J.; Liu, Q.; Shuai, W.; Sun, A.; Zheng, N.; Han, Y.; Xiao, G.; Xuan, J.; Ni, M.; et al. Multi-objective optimizations of solid oxide co-electrolysis with intermittent renewable power supply via multi-physics simulation and deep learning strategy. Energy Convers. Manag. 2022, 258, 115560. [Google Scholar] [CrossRef]
- Mohammadpour, M.; Houshfar, E.; Ashjaee, M. Sustainability analysis and optimization of innovative geothermal-driven energy storage system for green production of H2, NH3, and pure O2. Int. J. Hydrogen Energy 2022, 47, 26156–26177. [Google Scholar] [CrossRef]
- Ni, M.; Leung, M.K.; Leung, D.Y. Parametric study of solid oxide steam electrolyzer for hydrogen production. Int. J. Hydrogen Energy 2007, 32, 2305–2313. [Google Scholar] [CrossRef]
- Faes, A.; Hessler-Wyser, A.; Presvytes, D.; Vayenas, G.G.; Vanherle, J. Nickel-Zirconia anode degradation and triple phase boundary quantification from microstructural analysis. Fuel Cells 2010, 9, 841–851. [Google Scholar] [CrossRef]
- Larrain, D.; Van Herle, J.; Favrat, D. Simulation of SOFC stack and repeat elements including interconnect degradation and anode reoxidation risk. J. Power Sources 2006, 161, 392–403. [Google Scholar] [CrossRef]
- Schiller, G.; Ansar, A.; Patz, O. High temperature water electrolysis using metal supported solid oxide electrolyser cells (SOEC). J. Appl. Electrochem. 2009, 39, 293–301. [Google Scholar] [CrossRef]
- Cai, Q.; Luna-Ortiz, E.; Adjiman, C.S.; Brandon, N.P. The Effects of Operating Conditions on the Performance of a Solid Oxide Steam Electrolyser: A Model-Based Study. Fuel Cells 2010, 10, 1114–1128. [Google Scholar] [CrossRef]
- Brisse, A.; Schefold, J.; Zahid, M. High temperature water electrolysis in solid oxide cells. Int. J. Hydrogen Energy 2008, 33, 5375–5382. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).