1. Introduction
A microgrid (MG) system operates primarily in alternating current (AC), but it also includes several direct current (DC) loads, such as energy storage systems (ESS) and new technological loads [
1]. There are various MG configurations available, each with its own unique features, advantages, and drawbacks, depending on the specific application. For instance, some configurations are designed to prioritize reliability and resilience, while others prioritize efficiency and cost-effectiveness. Choosing the right configuration is critical to ensuring that the MG system meets the needs of its users and operates effectively. Researchers have been exploring different configurations and evaluating their performance to identify the best option for specific applications [
2]. As the demand for MG systems continues to grow, it is crucial to continue this research and development work to ensure that MG systems continue to meet the needs of their users and deliver the desired outcomes. Thus, a hybrid AC/DC MG combines DC and AC devices, joining the best of both worlds characteristics [
3]. The hybrid MG, on the one hand, integrates new renewable energy resources (RES), has high reliability, and a low maintenance cost [
4]. On the other hand, hybrid MG has high dimensions, low scalability capacity, and a medium capacity for controllability and fault management. As a result, the MG challenges future research topics, for example, control strategies, efficiency, and reliability improvement [
5,
6]. The hybrid MG depicted in
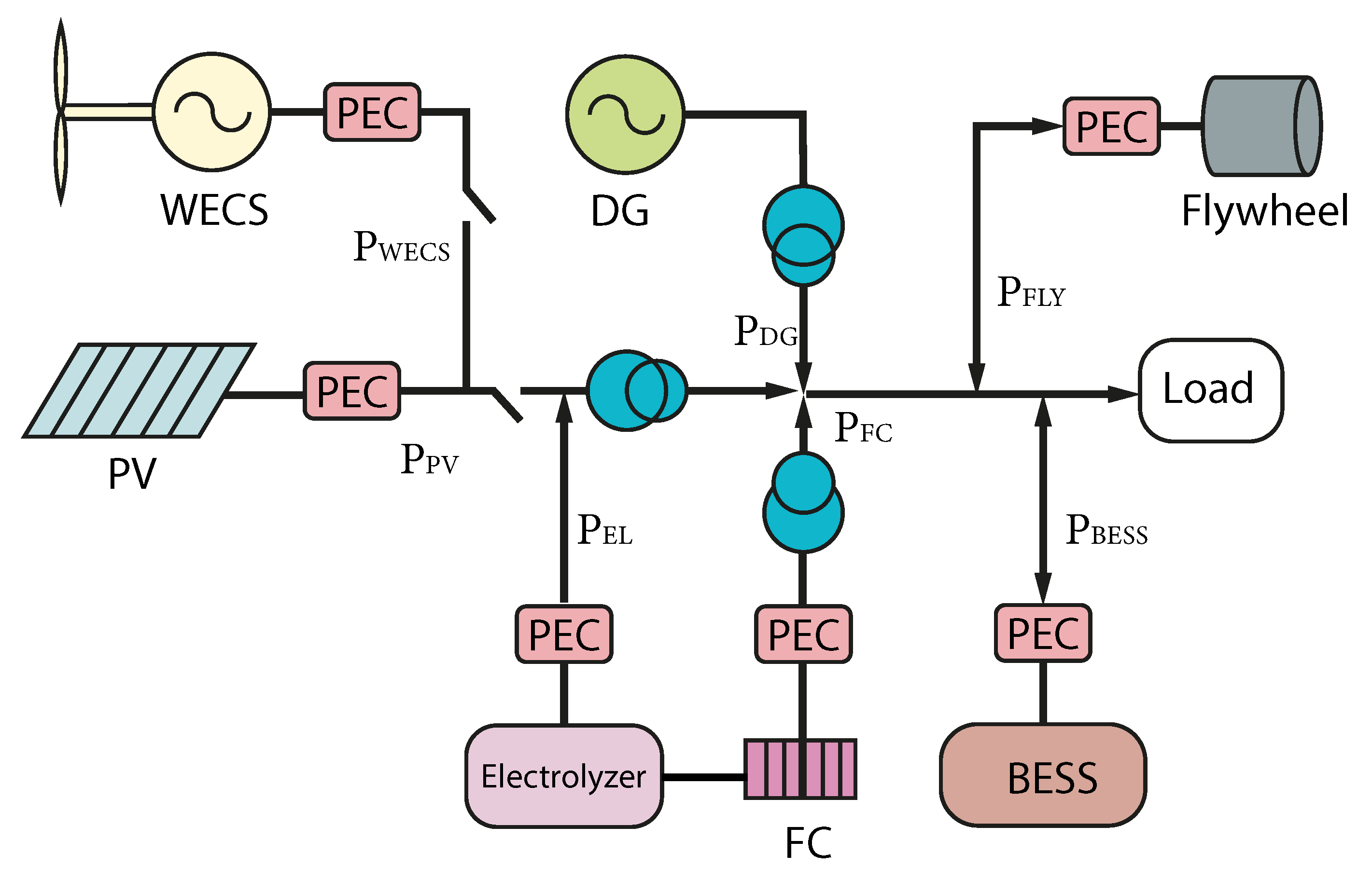
Figure 1 encompasses various DC generators, such as photovoltaic (PV), electrolyte, fuel cells (FC), and diesel generator, all of which work together to regulate system frequency. Additionally, the system includes two energy storage components, a flywheel and a battery-based Energy Storage System (BESS). The Power Energy Converter (PEC) is responsible for linking the load to the system and its different elements in an efficient manner [
7,
8].
This proposed optimal control minimizes the error for loop control, but maintains an acceptable operational cost. The system implements a controller, which implements an optimal hierarchical control system (HCS). It minimizes the absolute error and improves power quality, considering frequency and voltage parameters [
9,
10]. The MG controller implemented achieves superior performance compared to other available systems, as it effectively regulates voltage, frequency, and power, facilitates load sharing, coordinates RES, and synchronizes with the primary grid. Additionally, it optimizes the operating cost as reported in [
11]. The proposed control structures have been designed to enhance the stability of the transition during different disturbances, as reported in [
12,
13]. Furthermore, it is believed that the control can be optimized using algorithms to address the control problem and minimize the absolute error in steady-state, as highlighted in [
10]. These algorithms are expected to provide improved performance and greater accuracy in controlling the system, leading to a more stable and efficient operation. By integrating these control structures and algorithms into the system, the goal is to achieve a robust and reliable MG that can effectively handle different disturbances and provide stable and consistent power to its users. Overall, the proposed control structures and algorithms represent a significant advancement in the field of MG control and have the potential to benefit many different applications.
The research proposes the control strategy into primary and secondary control. The primary control keeps the electrical parameters in a specific range, while the secondary control guarantees the economic and reliable system operation [
10,
14]. This research explores the optimization techniques for optimal control; an objective function can minimize the energy consumption or the response time; also, it can maximize the system reliability, and controller robustness [
15].
The paper demonstrates the validity of its strategy by comparing the results to those of similar techniques based on parameters such as computational cost and transient response. Additionally, a system performance analysis is presented, evaluating the response to various types of faults, including incipient, instantaneous, and abrupt changes, as well as the total harmonic distortion (THD) percentage [
16].
There is some research in the field. In [
17,
18] a detailed MG description is presented, including the main system features and the classical control strategies. The paper [
19] compares MG implemented in different geographical regions and defines their features, including the existing MG test-beds. Ref. [
20] reviewed the major issues and challenges in MG control; also, the authors classified the control into three levels, primary, secondary and tertiary. Therefore, ref. [
21] proposed an autonomous droop scheme for energy MG management in grid or stand-alone modes. Finally, ref. [
22,
23] designed a power management system for a hybrid MG.
The document is structured in a clear and concise manner, with
Section 2 showcasing the methodology used,
Section 3 presenting the results and analysis, and
Section 4 summarizing the conclusions and outlining potential future work. The document provides a comprehensive overview of the study, presenting the key findings and their implications in a clear and straightforward manner.
2. Methodology
The MG has several outputs, including voltage and current work, which must follow particular behavior. The controller is responsible for that behavior, and those output signal oscillations are damped in a transient state. The controller analysis evaluates those oscillations in the transition of operation modes [
10].
A HCS typically reduces the parameters of MG external variations and links the external loops actions [
24]. Therefore, HCS coordinates the entire controller actions, beginning in the primary control and reaching the higher available level in a MG system [
25]. The hierarchical strategy starts with primary control, the lower level, which implements the voltage and current control loops.
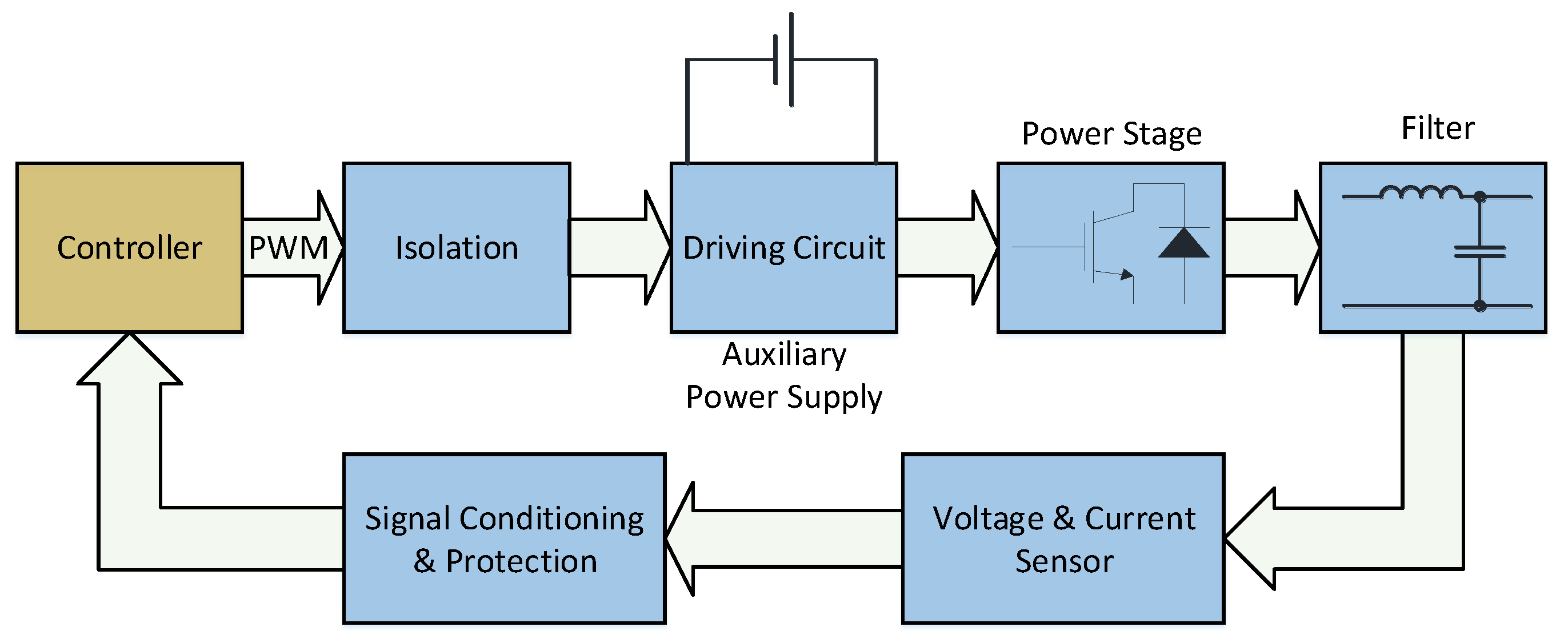
Figure 2 shows a schematic diagram of the system’s primary control and electrical elements, starting from the power stage, which implements the PEC.
The primary level can be designed through different strategies; for instance, impedance control. The primary control reference signal is calculated employing the secondary control system [
26,
27].
Table 1 shows the system parameters. The control approach adopts a cascade structure, utilizing an inner loop for current control and an outer loop for voltage control. This structure brings several benefits, such as reducing the THD in the voltage filter capacitor, ensuring the inductor filter current stays within operational limits, effectively rejecting disturbances, and enabling a change in the active mode while preserving the control scheme [
28].
Multiple strategies exist for designing the current and voltage control loops. In this research, the inner loop is designated as the primary control as it plays a critical role in ensuring the maximum power point (MPP) is reached. In grid-connected systems, MPP tracking requires a specific current and voltage to be maintained. In stand-alone systems, the energy produced depends on the load demands [
29].
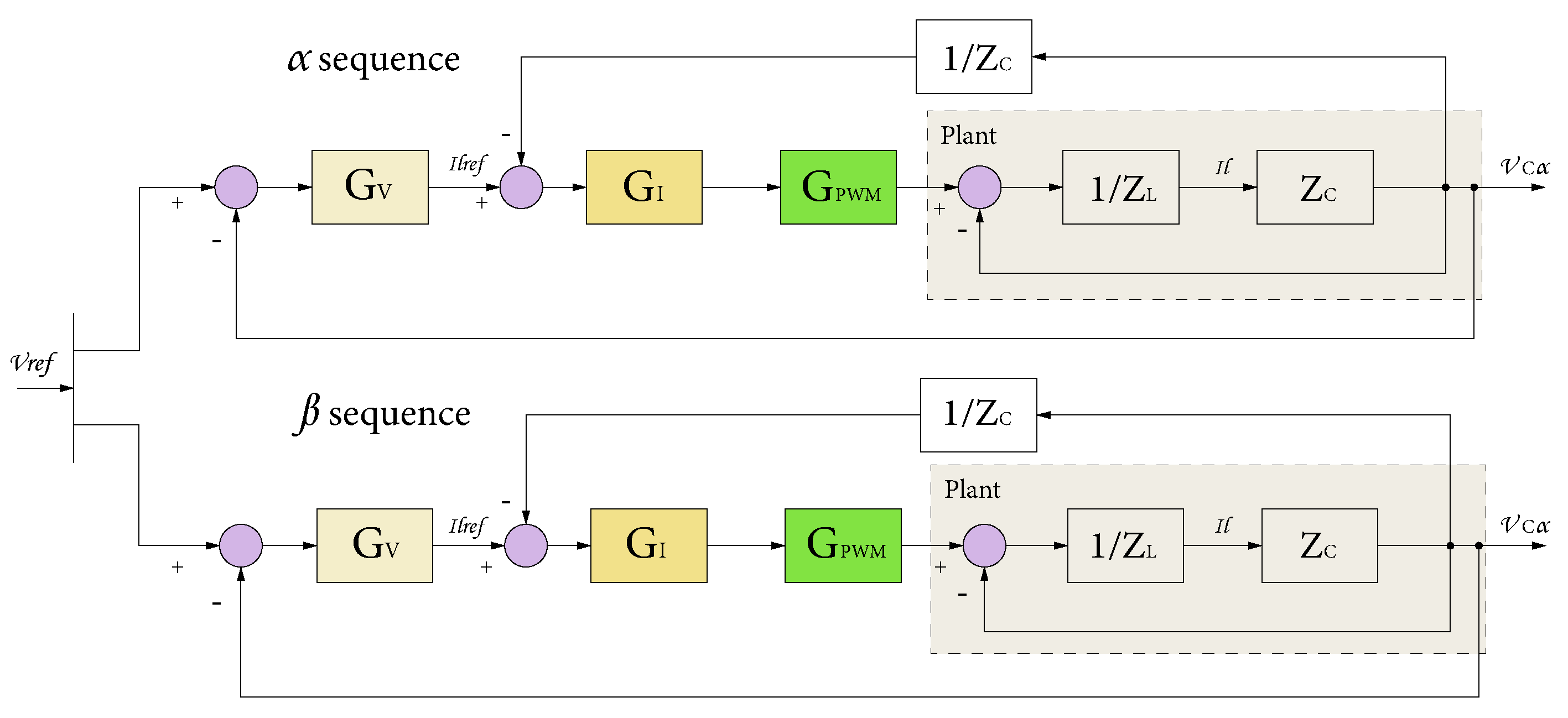
In
Figure 3, the control scheme for primary control is shown. The
and
sequences used stationary reference frames through the Clarke transformation, which are expressed by Equation (
1). This transformation changes the 3-phase frame to the
and zeroes input to simplify the calculation due to its stationary behavior [
30].
The applied method represents the voltage feedback, which regulates the voltage by comparing the output voltage with its reference value [
31]. The same for the primary current loop, which compares the output inductor current with the reference voltage received from the voltage loop.
Figure 3 shows the primary control, including the blocks representing the defined plant. Before the
block, there is the current controller
, using the PID controller, implemented to follow the reference current. The feedback loop includes the relation
, which transforms the output voltage into current to subtract it from the reference current,
. Before it, there is the voltage controller
, applying the Proportional Resonant (PR) scheme to follow the reference voltage received from the secondary control and subtract the feedback output voltage [
32,
33].
The current and voltage control strategy is essential in the final performance system [
34]. The current loop injects a high gain into the frequency reference signal, thus increasing the disturbance system rejection, as shown by Equation (
2). However, the voltage control strategy reduces the THD if there are nonlinear loads in the system, see Equation (
3). The voltage controller is responsible for controlling the capacitor filter voltage and comparing it with the reference signal received from the secondary loop. However, the output of the voltage loop serves as the reference current for the inner current loop. The inner loop dynamics should be faster than the outer loop; this strategy maintains the stability in the system [
35,
36]. The PID tuning controller strategy, known as the generalized forced oscillation method, is implemented in the PID controller of Equation (
2). The PID controller includes a first-order system and a low-pass filter to minimize the effect of noise in the control variables. This strategy is widely used due to its ease of implementation, flexibility and effectiveness in controlling various processes. The PID controller is one of the most commonly used structures in the industry and has proven to be an effective tool for controlling dynamic systems. PID tuning is calculated with Ziegler and Nichols (ZN) [
37], using the Algorithms 1 and 2 [
37,
38].
An integral action can solely control all the systems; the constraint is that the system must have a minimum phase. However, the controller can cause a poor transient response. A proposed solution is adding a proportional element to achieve closed-loop stability and robustness [
39].
The inner loop control can be used for any ZN tuning process, where defining the transfer function for the controlled plant is essential. After that, a PR is connected in series. Here, two methods are used if the gain margin is determined through mathematical tools and can be used directly. While the other possibility is applying the increase of the proportional gain towards the plant oscillation method in a closed-loop [
40].
The frequency where the gain margin is located in the is part of the tuning process. Different methodologies, such as PR, can be implemented if the gain margin is not computed. Algorithm 2 calculates the PID coefficients using the result from Algorithm 1. In step 2, the pole’s controller is determined. It depends on the selected controller, are 2 or 3, depending on whether a PI or PID is desired. Additionally, the PI or PID variables can be expressed as the time constant to be implemented in some industrial devices. Finally, the controller denominator is an integrator s.
The PR controller was chosen for the voltage loop, as it has an infinite gain margin, making it difficult to find a PID controller with Ziegler–Nichols (ZN) tuning. The implementation of the PR controller improves the voltage performance by reducing harmonics and minimizing steady-state errors, as expressed in Equation (
3) [
41]. This ultimately leads to a more stable and efficient performance in the system.
The PR controller has a resonant frequency that aligns with the reference signal, allowing it to follow a sinusoidal reference signal effectively. Pure integral control is a particular type of PR controller, and compared with PID classical controllers, it is seen that the computation cost increases. The PID modifies the phase and amplitude of the signal components, thus causing a delay in the control loop, and this solution can affect the overall performance [
33,
39].
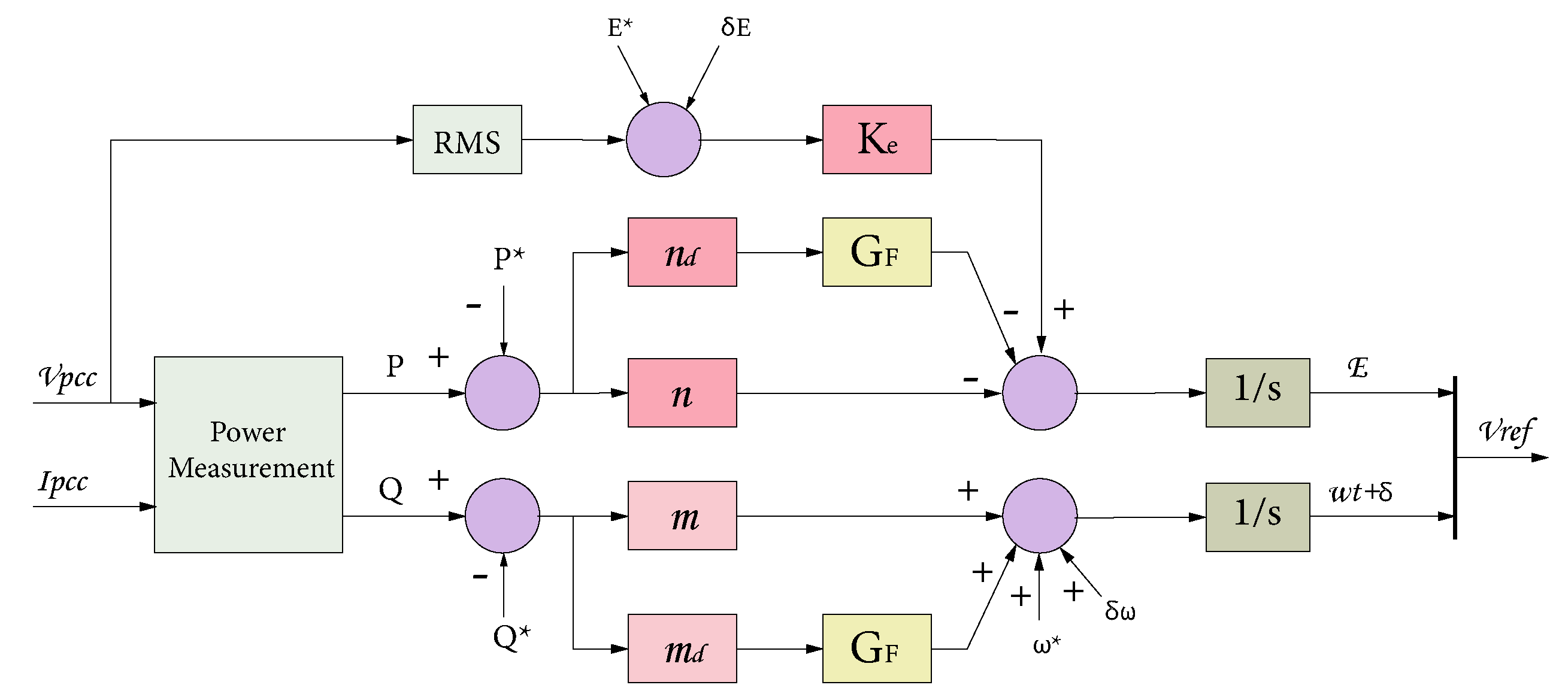
In a microgrid, several voltage source inverters (VSI) are connected in parallel to produce a net interchange. The secondary control sets the reference frequency and voltage for the inner loop while implementing power sharing through P-f and Q-V droop control (as shown in
Figure 4). The compensation, represented by
m and
n or deviations of
and
, helps to maintain synchronization within the voltage and stability limits of the system.
| Algorithm 1 Tuning procedure for open loop system using ZN. |
- 1:
procedure ZN tuning() - 2:
Step: 1 Variables definition - 3:
- 4:
Step: 2 Plant Definition - 5:
Determining the complete transfer function - 6:
- 7:
- 8:
Step: 3 Eliminating components controller - 9:
Guaranteeing proportional controller - 10:
- 11:
- 12:
Step: 4 Proportional controller - 13:
K proportional constant - 14:
- 15:
Step: 5 Determine gain margin - 16:
if GM is determined = then - 17:
- 18:
else - 19:
while do - 20:
if Closed loop GP is oscillating then - 21:
- 22:
if GM = ∞ then - 23:
Applied PR controller - 24:
Step: 6 Oscillation period - 25:
where GM is measured - 26:
▹ Ending
|
| Algorithm 2 PID initial coefficient using ZN tuning. |
- 1:
procedurePID initial() - 2:
Step: 1 Variables definition - 3:
- 4:
Step: 2 PID denominator - 5:
if then - 6:
PI controller - 7:
- 8:
if then - 9:
PID controller - 10:
- 11:
Step: 3 Defining independent constants - 12:
- 13:
- 14:
if then - 15:
- 16:
- 17:
- 18:
Step: 4 Proportional controller - 19:
K proportional constant - 20:
- 21:
Step: 5 Defining controller - 22:
if then - 23:
PD controller - 24:
- 25:
if then - 26:
PID controller - 27:
|
| ▹ Ending
|
The equations that describe the droop control are presented in Equations (
4) and (
5).
and
E denote the frequency and voltage, respectively, while
* and
E* are the respective references for these quantities.
and
are the control transfer functions, which cannot be implemented by pure integral control, particularly in the islanded mode, due to the mismatch between the total injected power and the total power [
42]. The system parameters are shown in
Table 2.
The control transfer functions
and
are implemented using different control techniques in this research. The implementation uses the Universal Droop Control introduced by [
43] as depicted in Equations (
6) and (
7) and illustrated in
Figure 5. The RMS voltage (
E) and frequency (
) are measured at the Point of Common Coupling (PCC), while the desired values for these magnitudes,
E* and
, are set as the nominal values. The desired active and reactive power values,
P and
Q*, depend on whether the Microgrid (MG) is connected to the grid. In islanded mode, the desired values for active and reactive power are normally set to zero.
The droop control coefficients are denoted by “
n” and “
m” in the equations. They represent the deviation of the reactive power with respect to the voltage and the deviation of the active power with respect to the frequency, respectively. In addition, the coefficients related to the active and reactive power are represented by
and
, respectively. To regulate the voltage at the PCC, a proportional controller constant
is used. Moreover, to reduce the noise in the signal, a filter
is implemented, which is described by Equation (
10). Finally, the sample time for the current and voltage loop is in the order of milliseconds, while the sample time for the power control is in the order of seconds.
3. Results and Discussion
The primary control is implemented in the system with the parameters of
Table 3. The initial values for the optimization algorithm are the first and second parameters,
and
, which are calculated as the gain margin and oscillation period, while the following parameters,
,
,
,
and
, are the constants for the primary controller.
The system consists of a voltage and current controller, which are implemented using a PR and PID controller, respectively. The parameters were determined using the optimization algorithm proposed in the paper. The comparison between the system output and the reference voltage is shown in
Figure 6, where the secondary controller calculates the system output, which serves as the input for the primary loop control. The reference voltage has an amplitude of 600 Vp and a frequency of 60 Hz, which are nominal values for MG.
The primary controller effectively tracks the reference signal, as shown by the graph. There is no delay between the signals, but there is a slight reduction in the maximum voltage. It presents a steady-state error in the system, which can be neglected because it is less than .
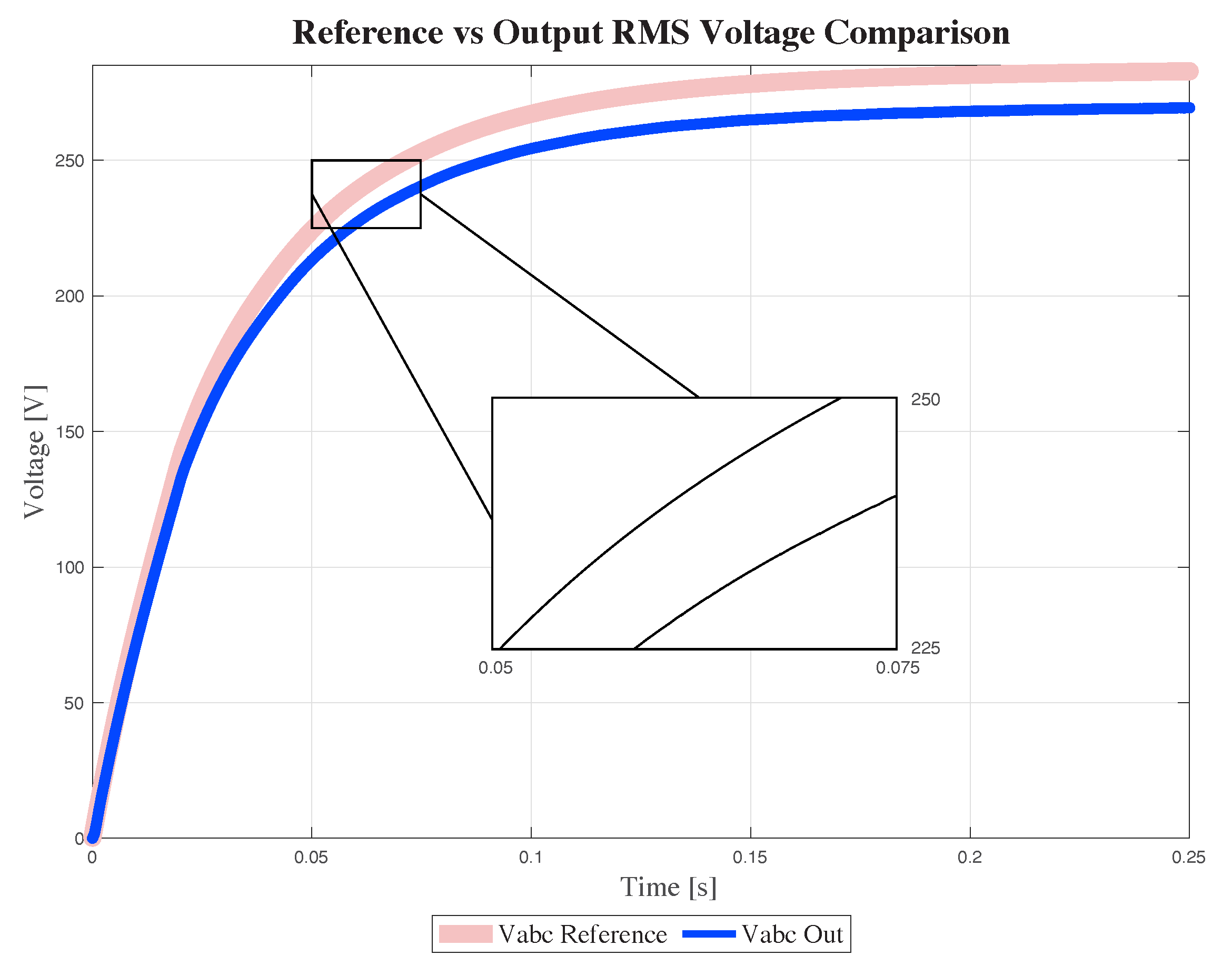
Additionally, the system stability is further confirmed by the RMS output results in
Figure 7. The rise time to reach the nominal value of 600 Vp is quick, around 0.15 s, and the system exhibits an over-damped behavior with no overshoot. Although there are small fluctuations, roughly 5%, around the desired voltage, the pattern is consistent and the response is fast, indicating an acceptable performance given the complexity of the system and its multiple interactions.
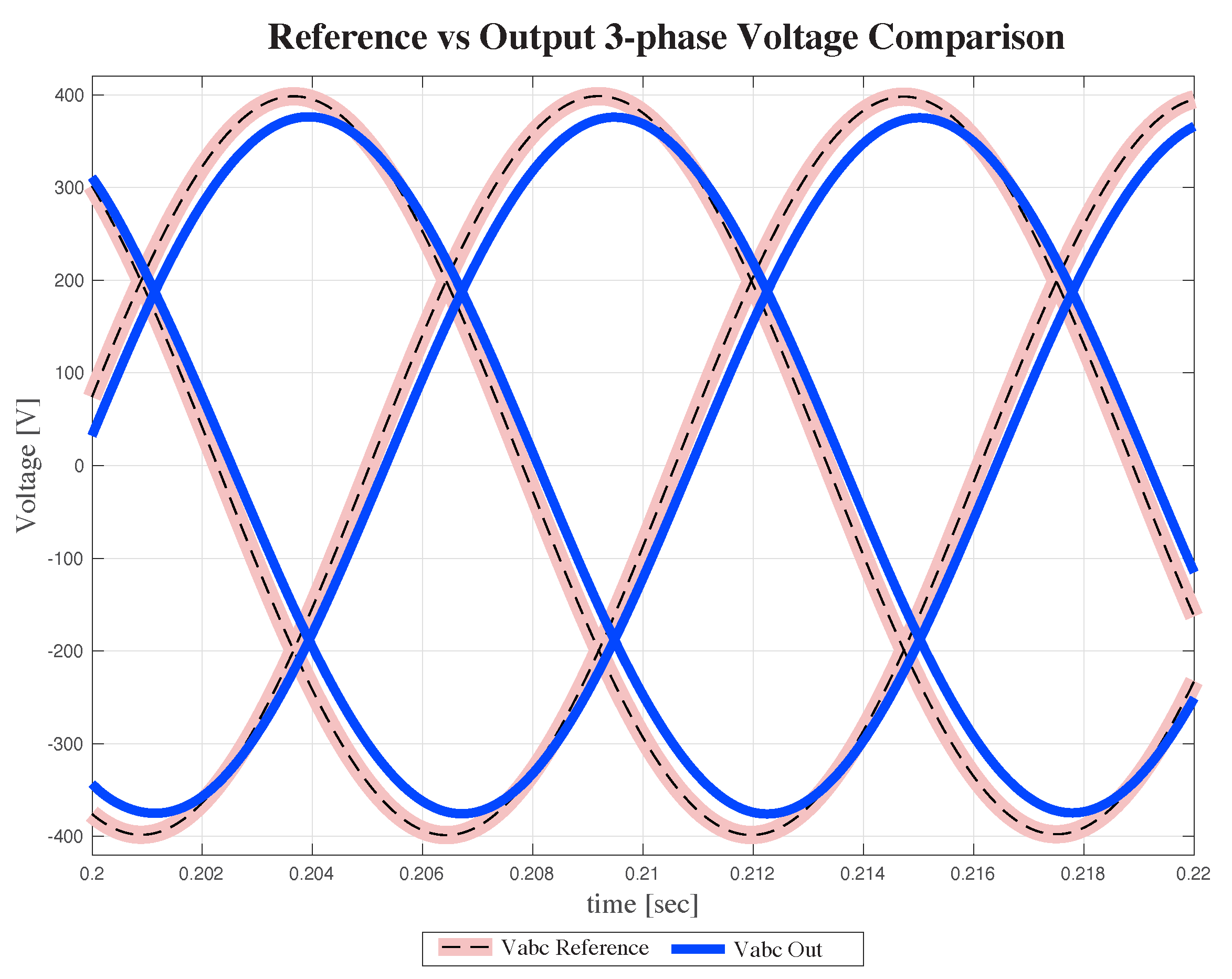
Figure 8 shows the comparison between the three-phase output system voltage, resulting from the proposed methodology, and the performance of a classical PID. It is essential to mention that the second controller can control the output voltage, but it cannot maintain the limit in the current or interchange power between converters. It is seen that the controller is considered stable, and there is not an overshoot due to an over-damped response. The performance in general terms is better than the controller, without considering the advantages in another control level. Additionally,
Figure 9 compares the reference signal vs. output voltages with the proposed strategy classical PID controller.
The optimization algorithm’s outcomes for the primary loop are displayed in
Figure 10 and
Figure 11.
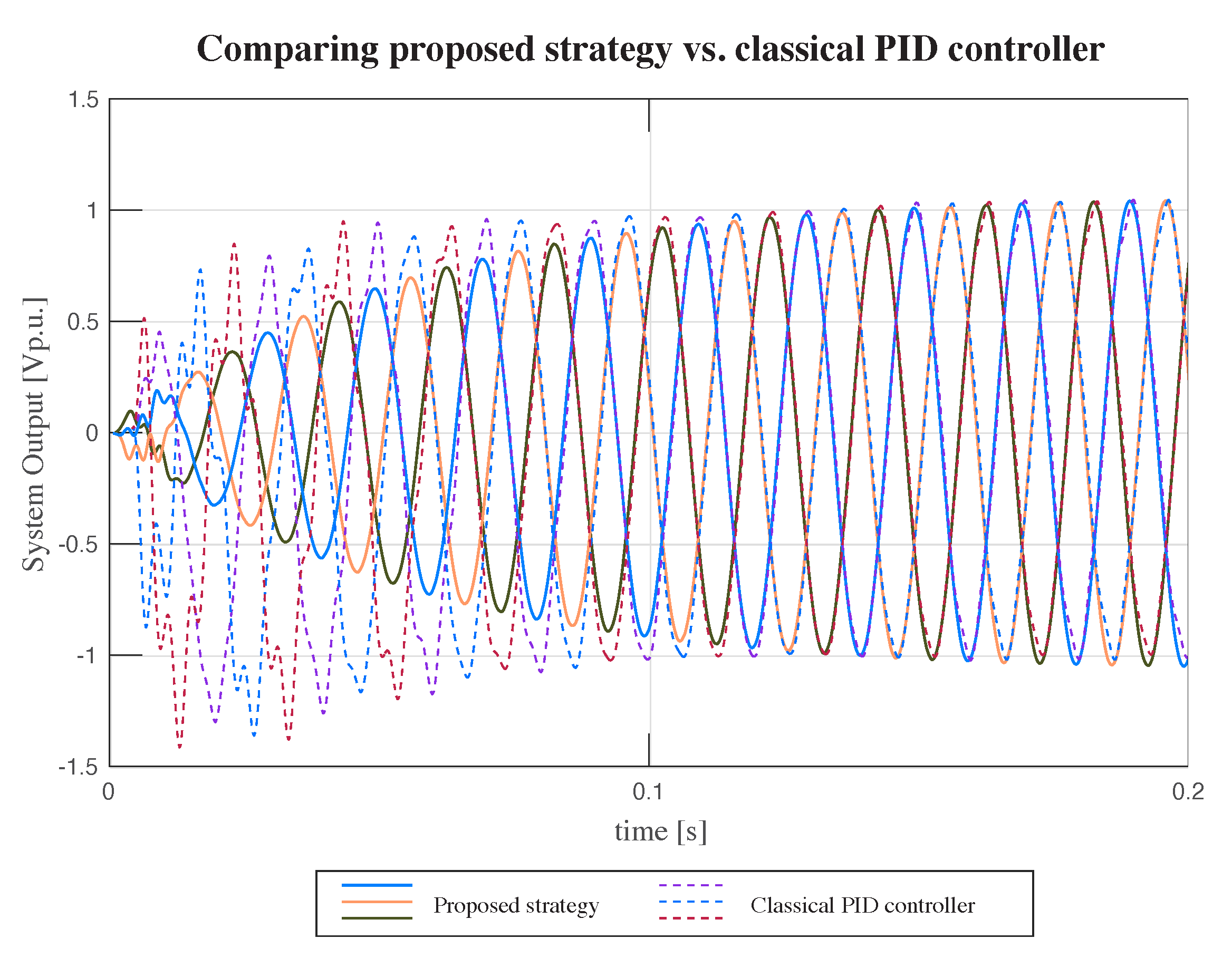
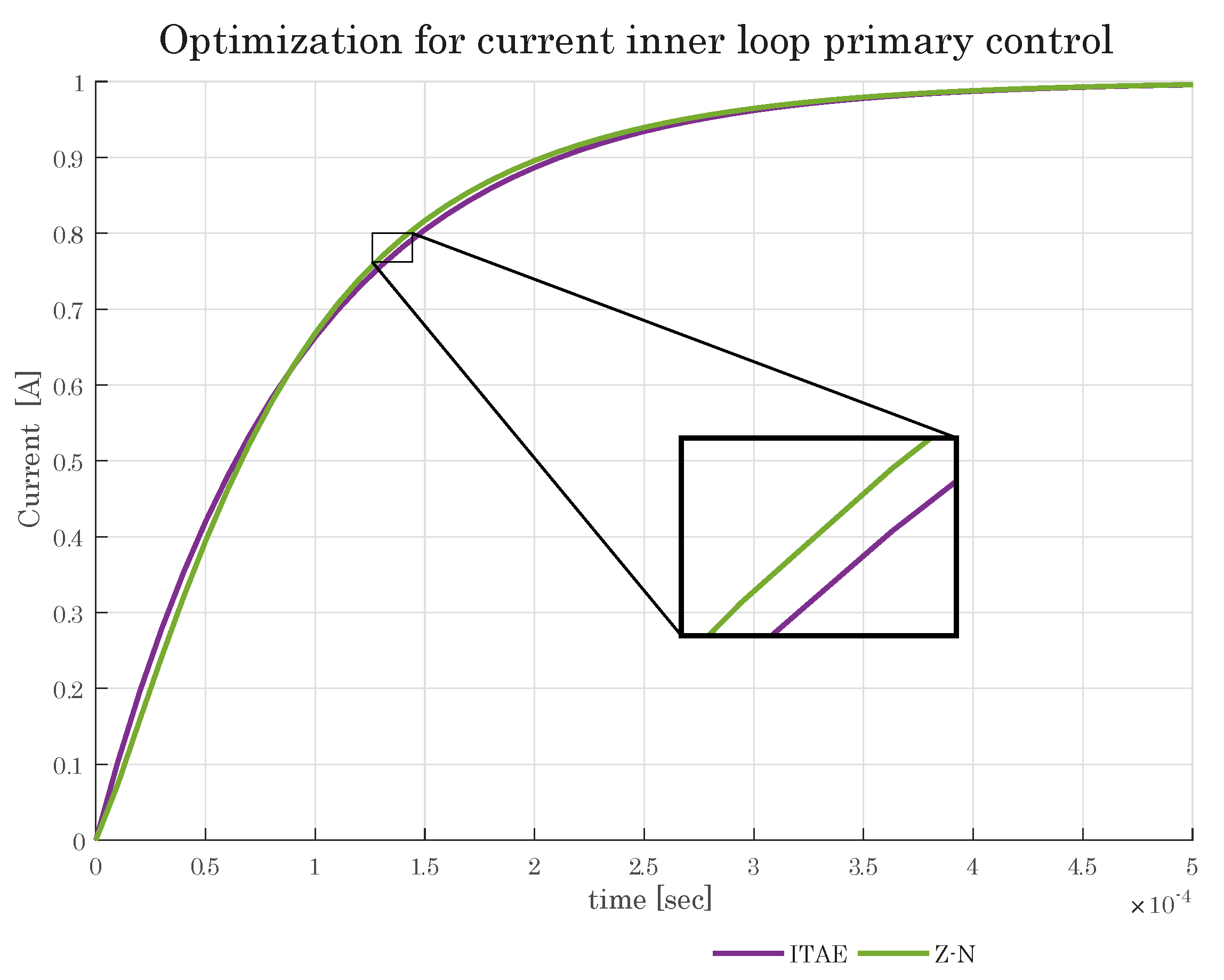
Figure 10 presents five system responses, each corresponding to a PID controller calculated using the Integral Time Square Error (ITSE) and Integral Time-weighted Absolute Error (ITAE). The goal of each strategy is to determine the controller coefficients that produce the lowest steady-state error in the system. While the Integral Square Error (ISE), Integral Absolute Error (IAE), and Ziegler and Nichols (ZN) methods are upon each other in down the ITAE line.
The five optimization approaches—ISE, IAE, ITSE, ITAE, and ZN—each consider a step input, as shown in
Figure 10 and
Figure 11. The system reaches the step input within
[s] and has an over-damped response, with no overshoot. The comparison of the four methodologies and the ZN approach is highlighted in a magnified square, where the highest differences are noted. The ZN method serves as the starting point for the optimization procedures by providing the initial values.
Additionally, the values of the optimization indices are presented in a clear and concise manner in
Table 4. The table is arranged such that the methods are sorted according to the minimum value they achieve. After evaluating the results, it can be concluded that the ITSE approach is the most effective strategy for finding the smallest error in the steady state for the current control loop. This is particularly important as a small steady state error is crucial for ensuring accurate control of the system.
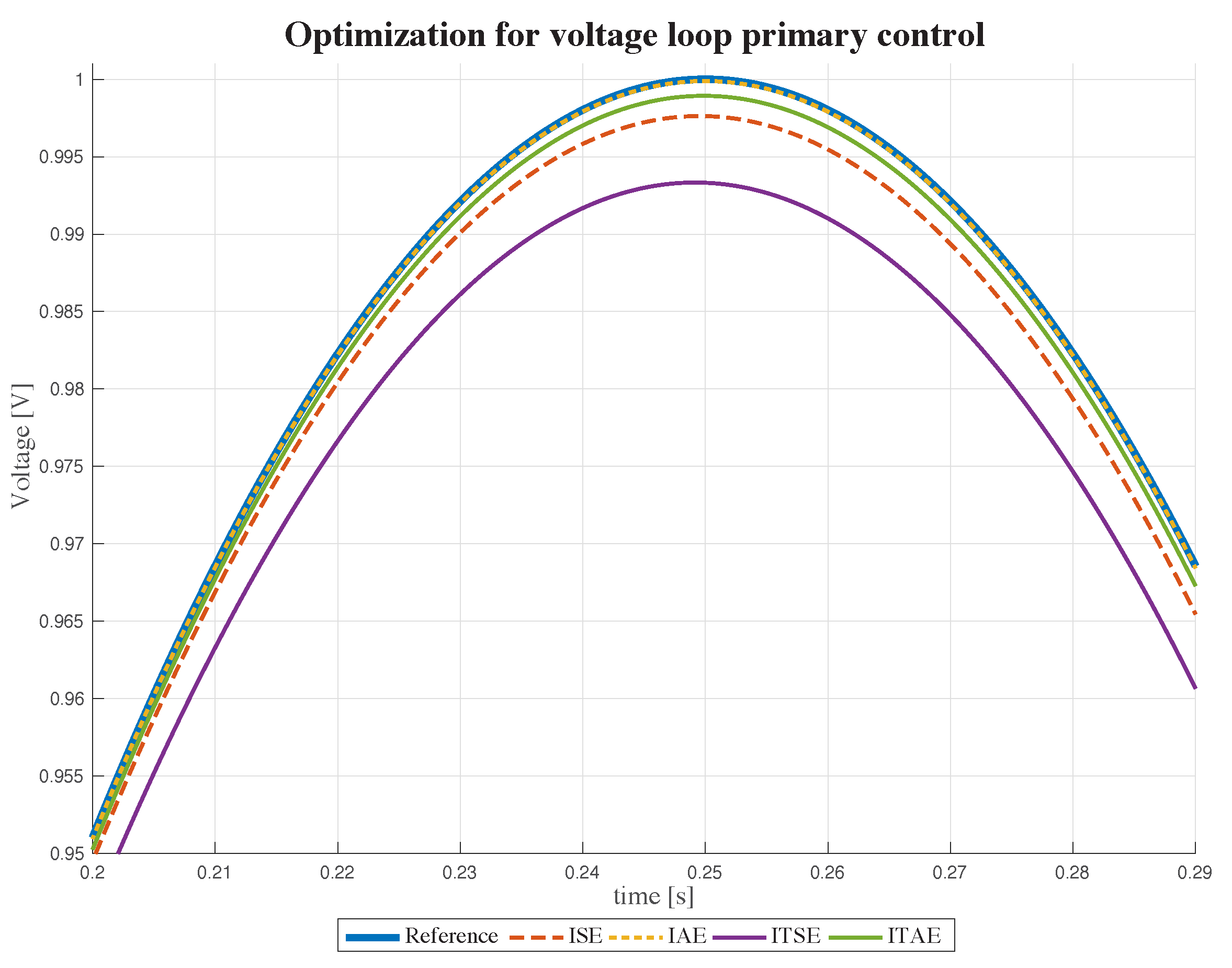
The voltage closed-loop response, fed by a 60 [Hz] sinusoidal input, is displayed in
Figure 11 and controlled by the PR approach. The ZN method was not used because the current does not correspond to any magnitude margin, thus there is no resonant constant to derive the initial values for the algorithm. However, the methodology employs random values as an initial guess in the controller optimization calculation, and the algorithm should find the same values as the optimal parameters.
The comparison of the ISE, IAE, ITSE and ITAE methods was made with a sinusoidal reference. It can be seen that there is a significant discrepancy between the reference and ITSE. The evaluation of the objective functions is presented in
Table 5, with ITSE resulting in the least effectiveness.
The ISE and ITAE methods are closest to the reference, with a slight difference in the reference peak. However, the evaluation of the objective function shows satisfactory results. Ultimately, the IAE approach proves to be the best in the experiments, with no significant difference observed between the reference and the controller optimized using IAE.
The results of the function minimization for the voltage loop control are presented in
Table 5, ordered from the smallest value. According to the results, IAE optimization is the best method for voltage loop control. The phase margin for the current and voltage loops can be calculated at 0 (rad/s) and 60 (rad/s), respectively. However, the magnitude margin can only be determined for the voltage loop, which affects the algorithm. As a result, the initial values for the optimization algorithm are based on randomly chosen values.
The aim of the secondary control level is to set the voltage and frequency reference values for the primary level and to decrease the circulating current caused by non-linear elements. It regulates the flow of energy throughout the entire Microgrid by balancing the generation and consumption.
The interconnection and relationships among the VSI are considered in this section.
Table 6 summarizes the values for the secondary control level. The methodology for calculating the parameters was discussed in a previous section and the mathematical relations were also mentioned and referenced. There are two controllers, one for active power P control and the other for reactive power Q control, both of which incorporate a PI controller. The PI regulator parameters for P power control are
and
, while for Q power control they are
and
.
The parameters for droop control are split into P and Q control, with the constants
n and
for P control and
m and
for Q control. The proportional constant
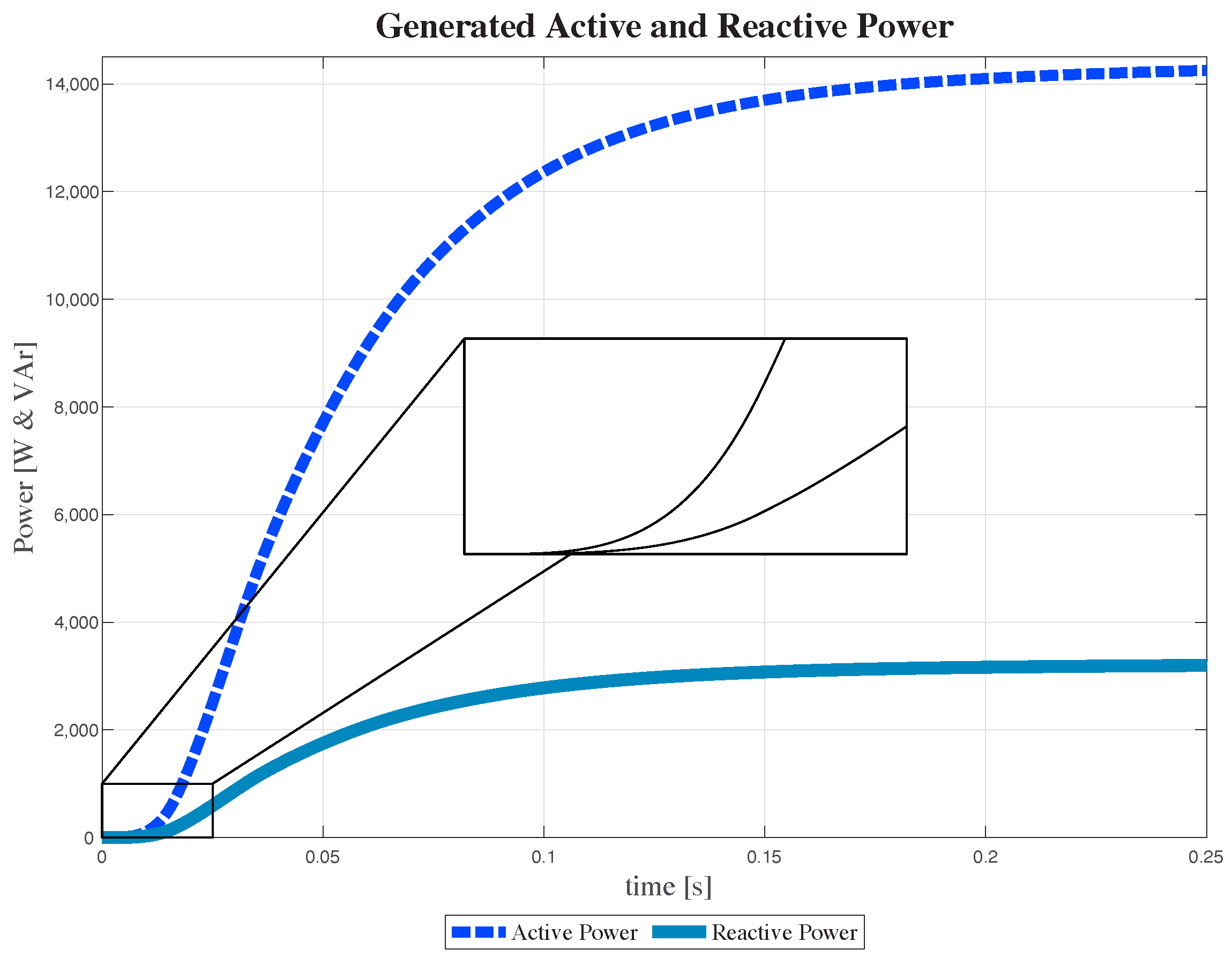
is used to compensate for voltage variations and its impact on the final results. The active and reactive power generated by a generator in standalone mode are depicted in
Figure 12. Initially, the signals are the same, but they exhibit a changing transient behavior. After 0.01 (s), both models exhibit a response that follows a second-order system. The signals reach a maximum point around 0.25 s, then follow their individual references of 375 (W) and 220 (VAr), respectively. In the standalone case, the source responds to the load power, which is not perfectly linear, and includes capacity and inductance elements to provide an imaginary part of power.
4. Conclusions and Future Works
This paper proposes a strategy for controlling an electrical substation of a smart grid with photovoltaic generation, adopting an optimal approach for network layout and control. It relies on a heuristic approach and hierarchical control and involves a design based on optimization for reducing the network length and steady-state error. The plant under study affects a complex nonlinear behavior, and a classical controller might not control this system. Power electronics have multiple nonlinear components, and the photovoltaic generation is unpredictable and changeable.
The microgrid control system strategy follows a hierarchical control architecture, where the primary control system (PCS), also known as the hierarchical control system (HCS), is responsible for controlling the current and voltage outputs. Meanwhile, the secondary control system regulates the voltage amplitude and frequency, which serve as the reference for the desired active and reactive power. This two-tiered control approach allows for effective and efficient control of the microgrid system.
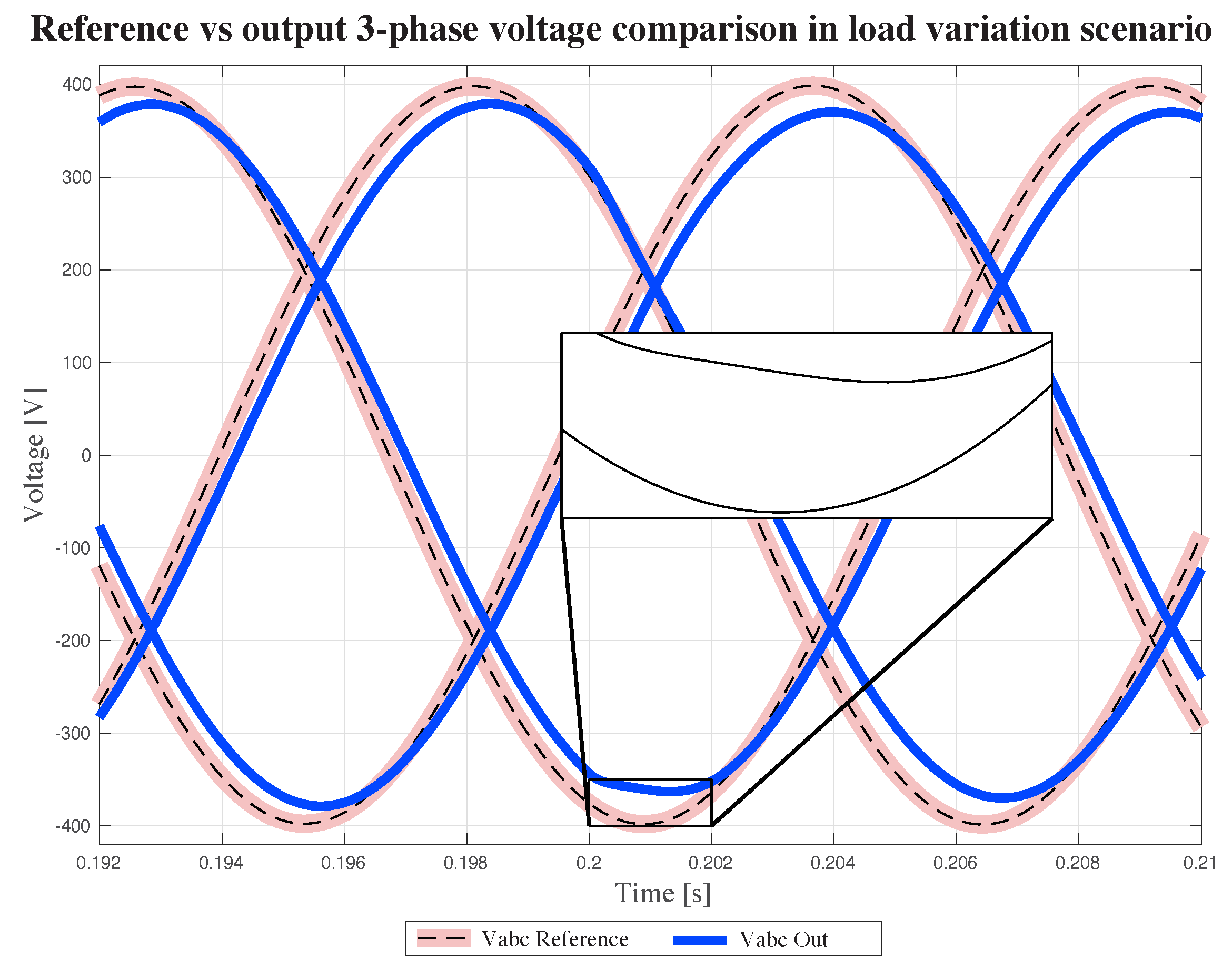
The system’s response is steady and predictable, with a dampened behavior that does not result in over-shooting. Despite the presence of 5% oscillations around the target voltage level, these fluctuations are consistent and maintain a uniform pattern. The response time of the system is quick, taking into account the nonlinear elements and the complex interactions between different components. The time taken for the system to reach its steady state is under 0.4 s, even with an increase in load. This demonstrates the system’s ability to fulfill the power and voltage requirements despite changes in the operating conditions.
The implemented control strategy is often too conservative, as it involves classical controllers for each loop, as proportional integral derivative and proportional resonant, and performance in the case of a more complicated combination of smart grids. The result induces future considerations about introducing distributed generation, smart grid, and photovoltaic installations. Future research will discuss the secondary loop results, including the strategy for optimal parameter tuning. Additionally, the proposed strategy guarantees the system performance in the case of a more complicated combination of smart grids. Additionally, future papers will include metrics related to the power quality issues such as THD to prove that the proposed control system is more efficient.