Power Management Control of an Autonomous Photovoltaic/Wind Turbine/Battery System
Abstract
1. Introduction
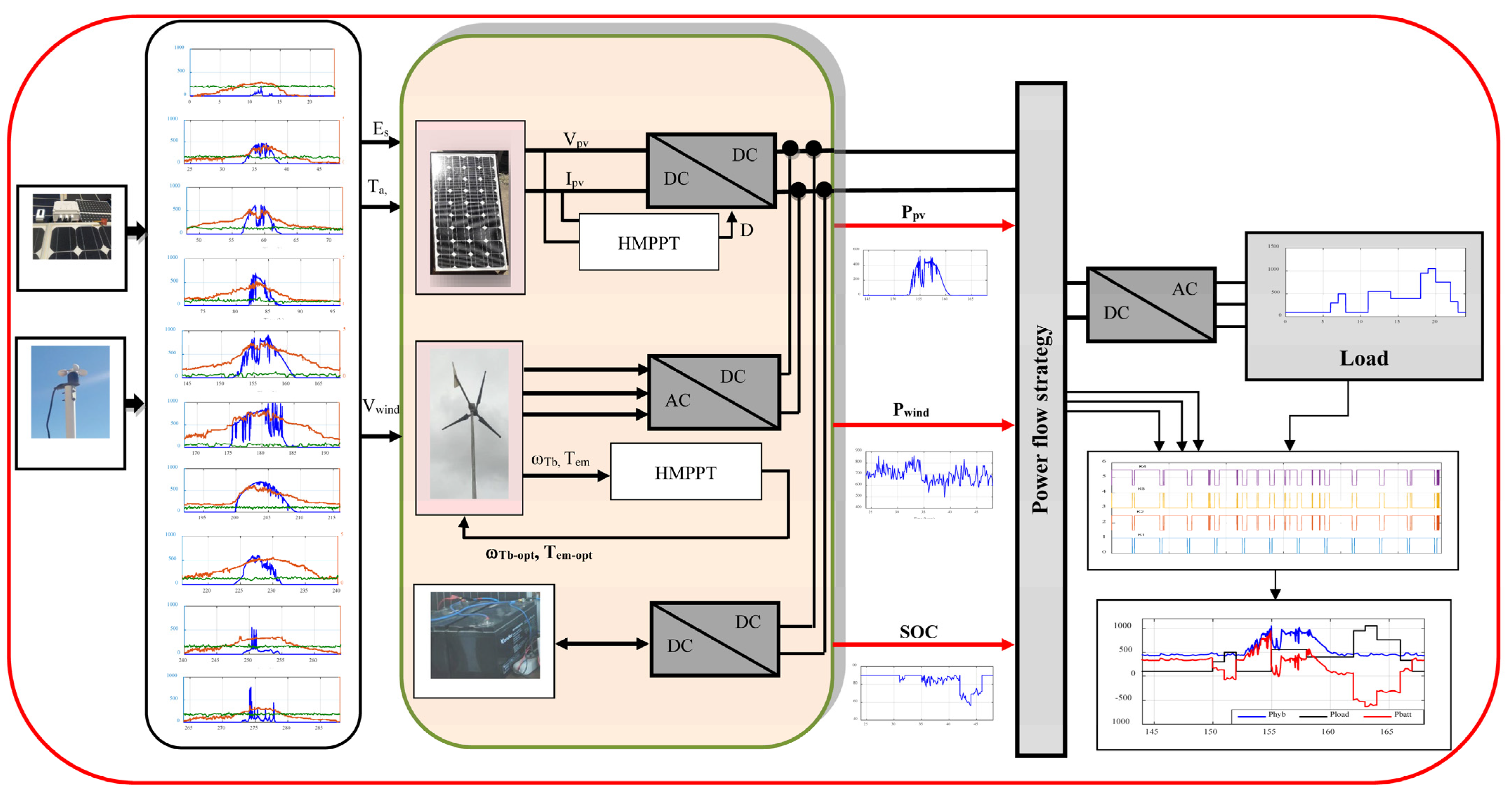
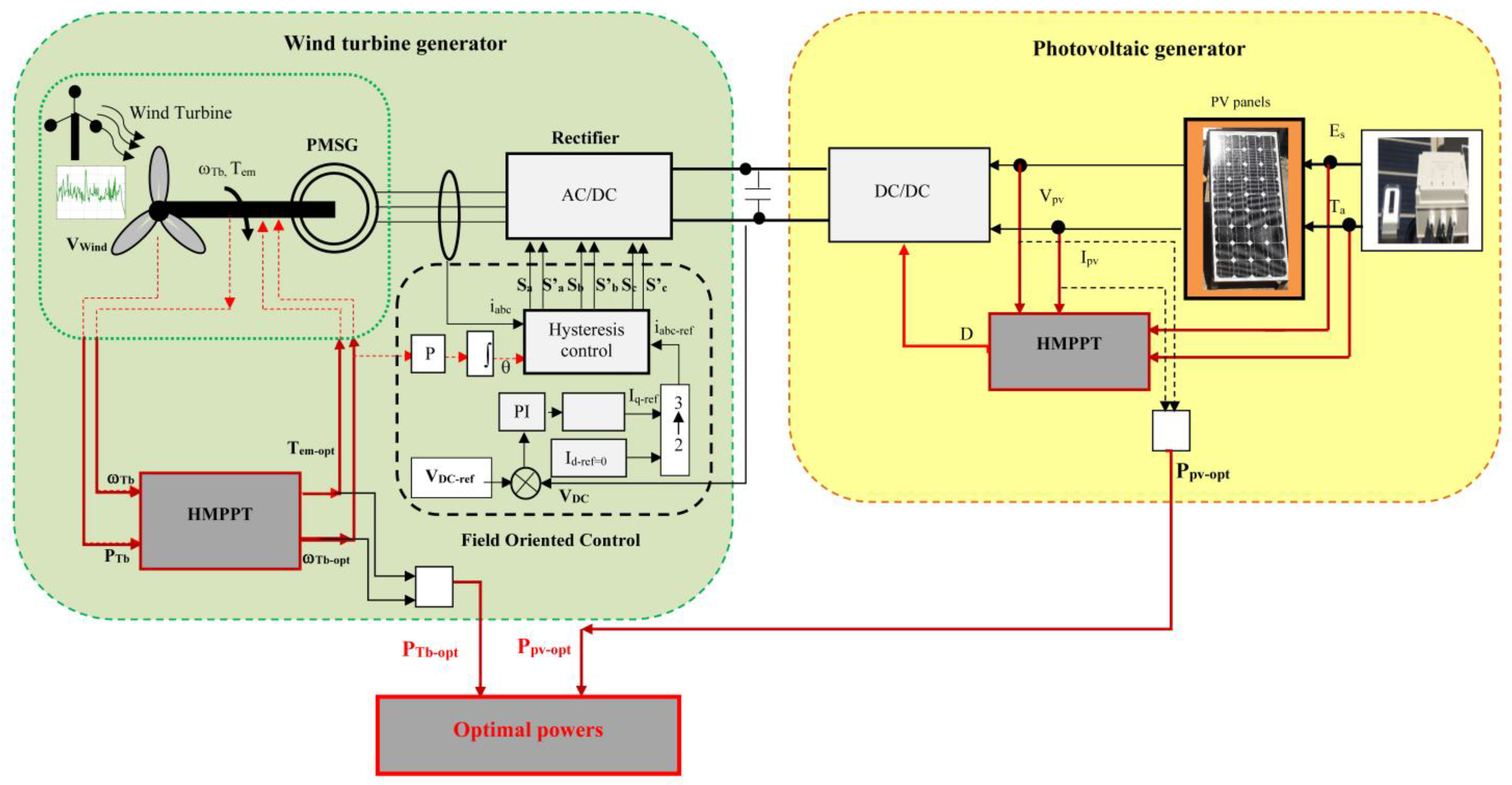
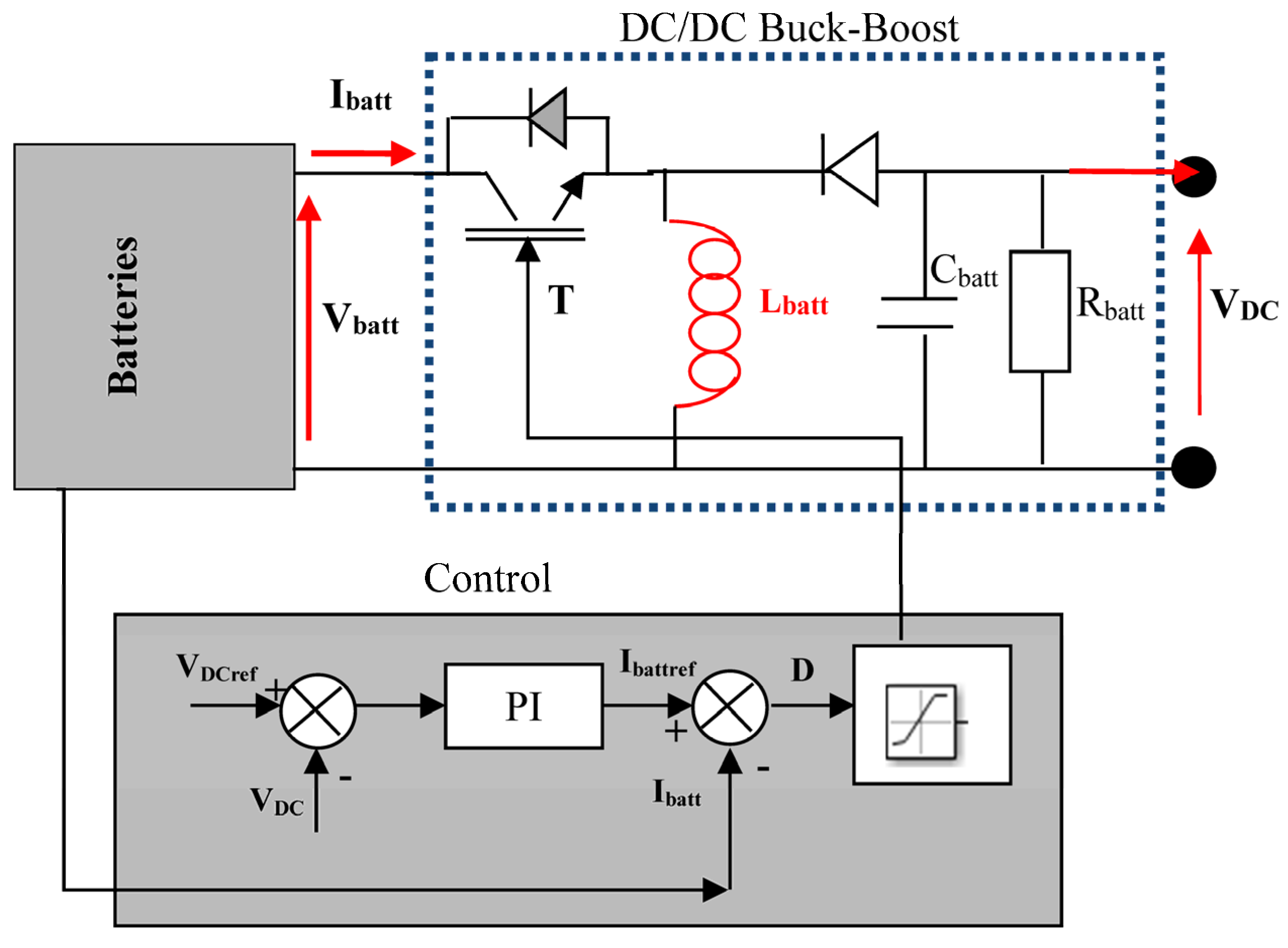
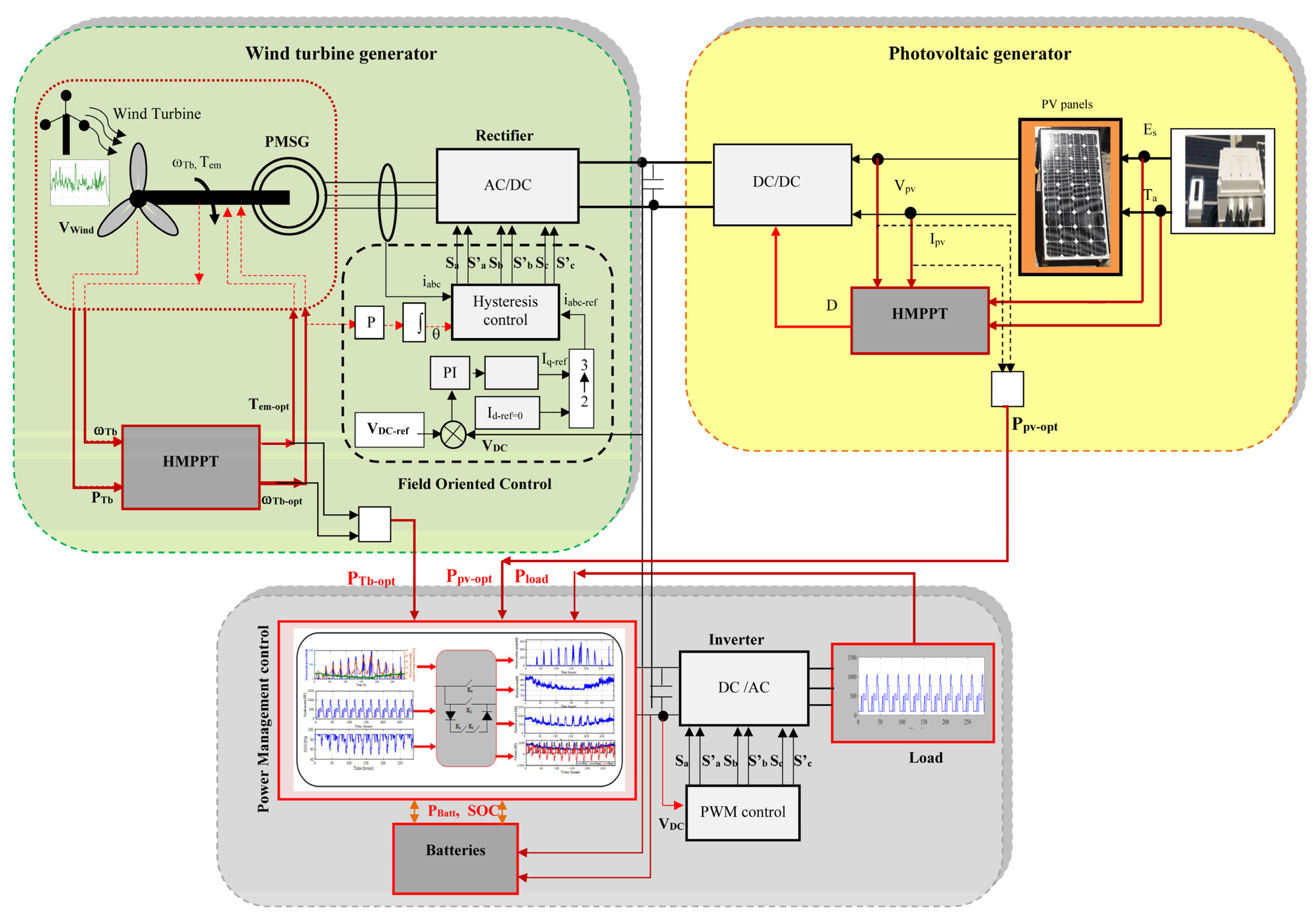
2. Design and System Description
3. Optimization Methods
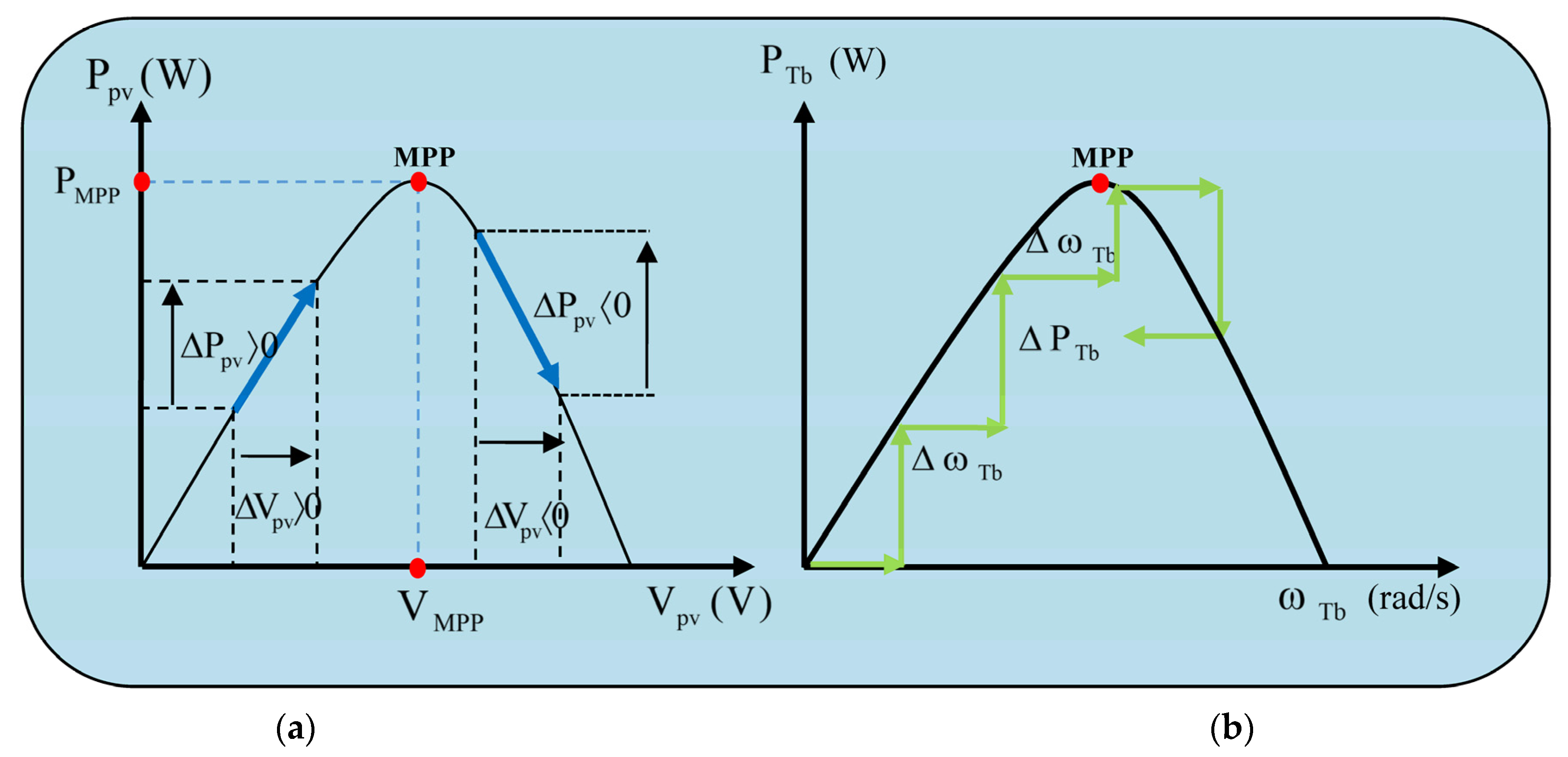
3.1. P&O Method
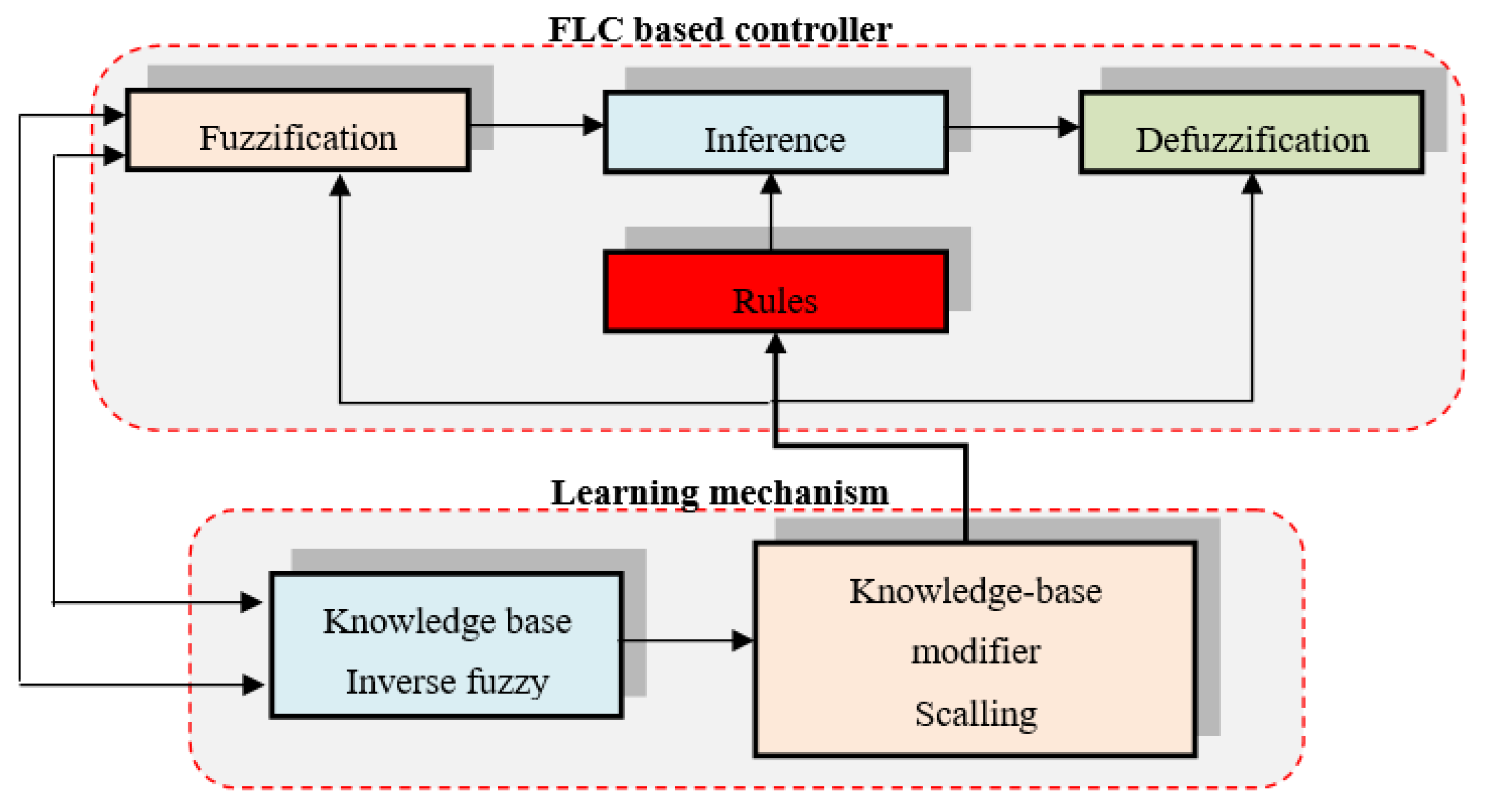
3.2. Adaptative Fuzzy Logic Controller (AFLC)
3.3. Hybrid MPPT Approach
4. Simulation Study
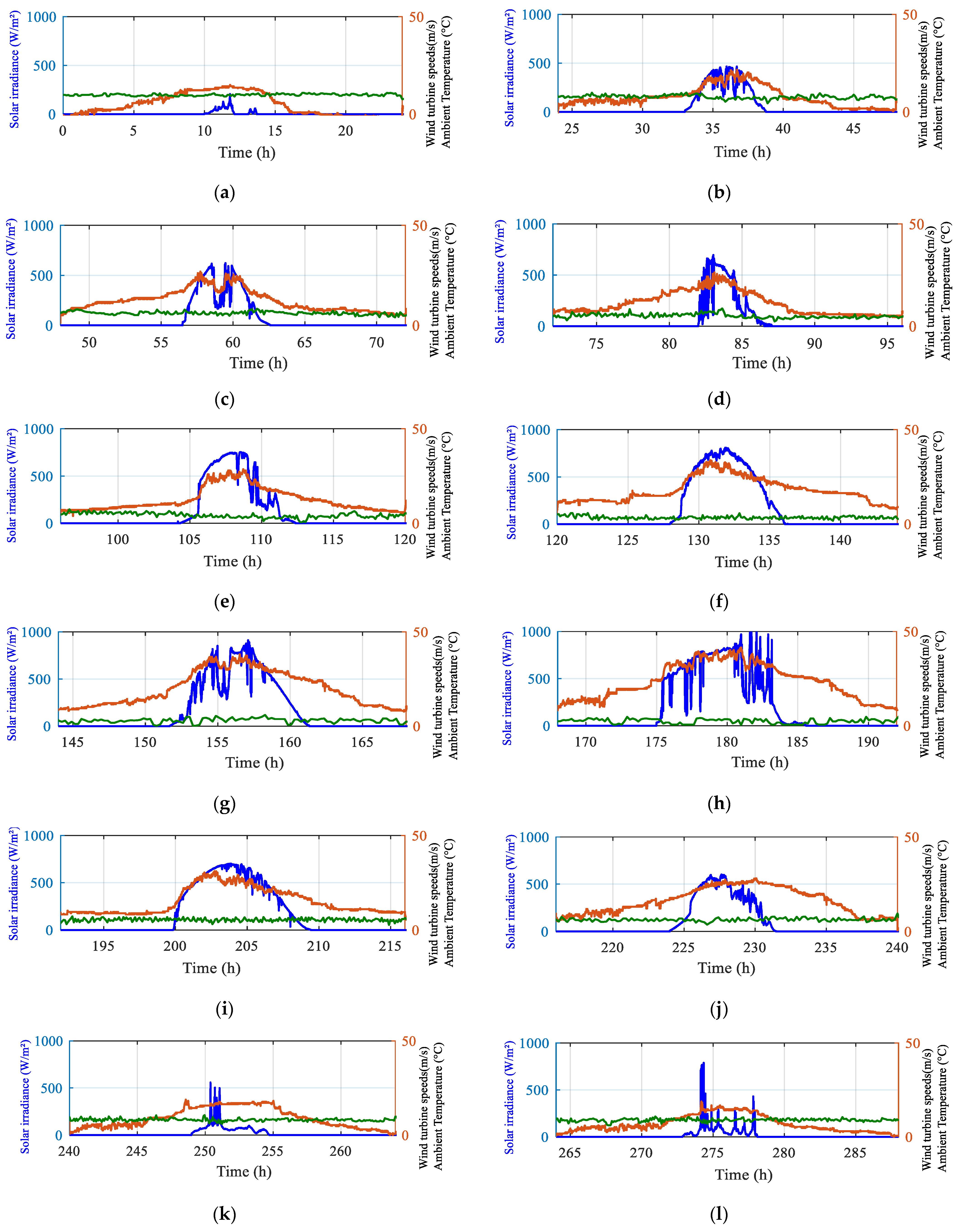
4.1. Measurements ofSolar Irradiation, Temperature and Wind Speed Profiles
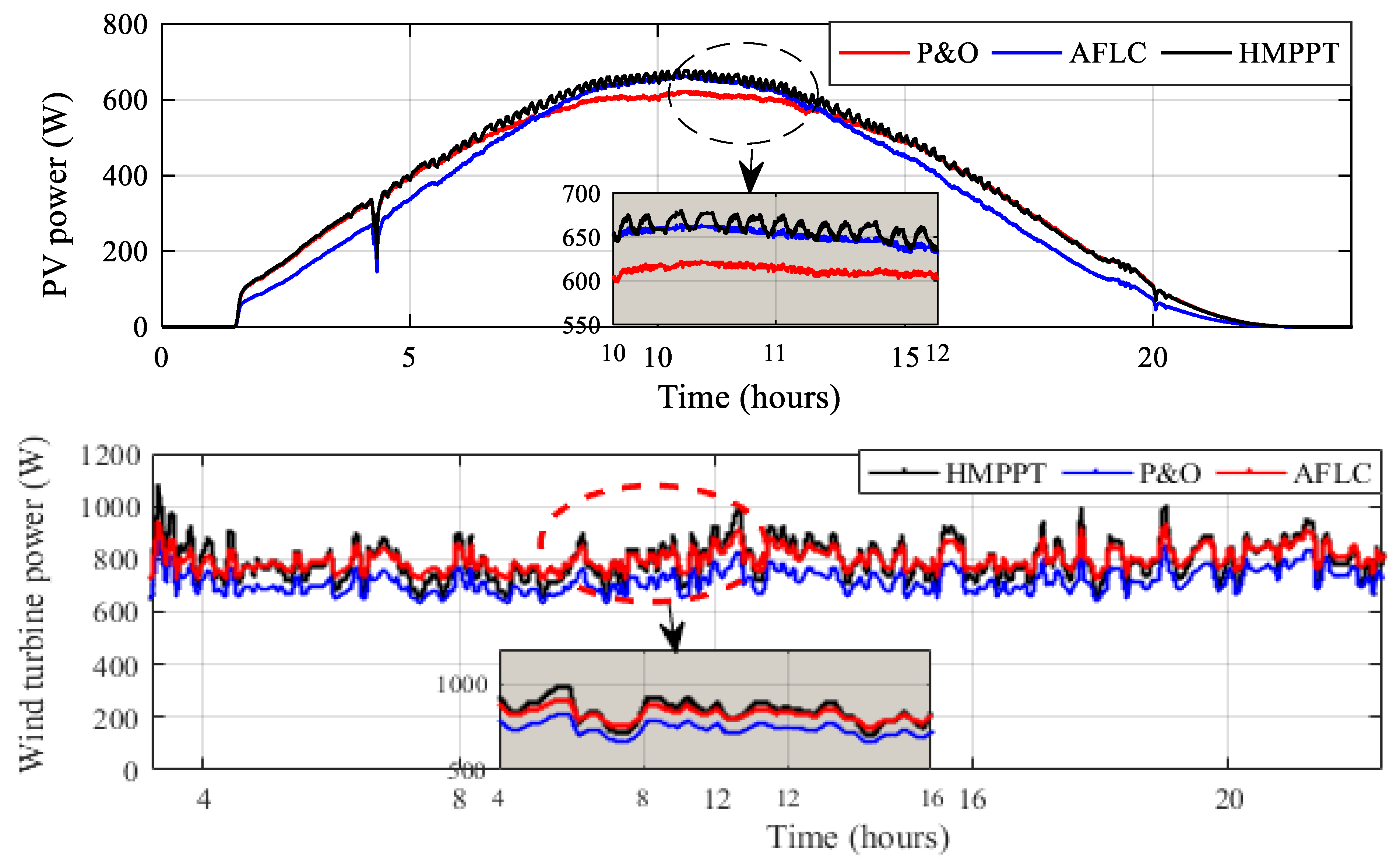
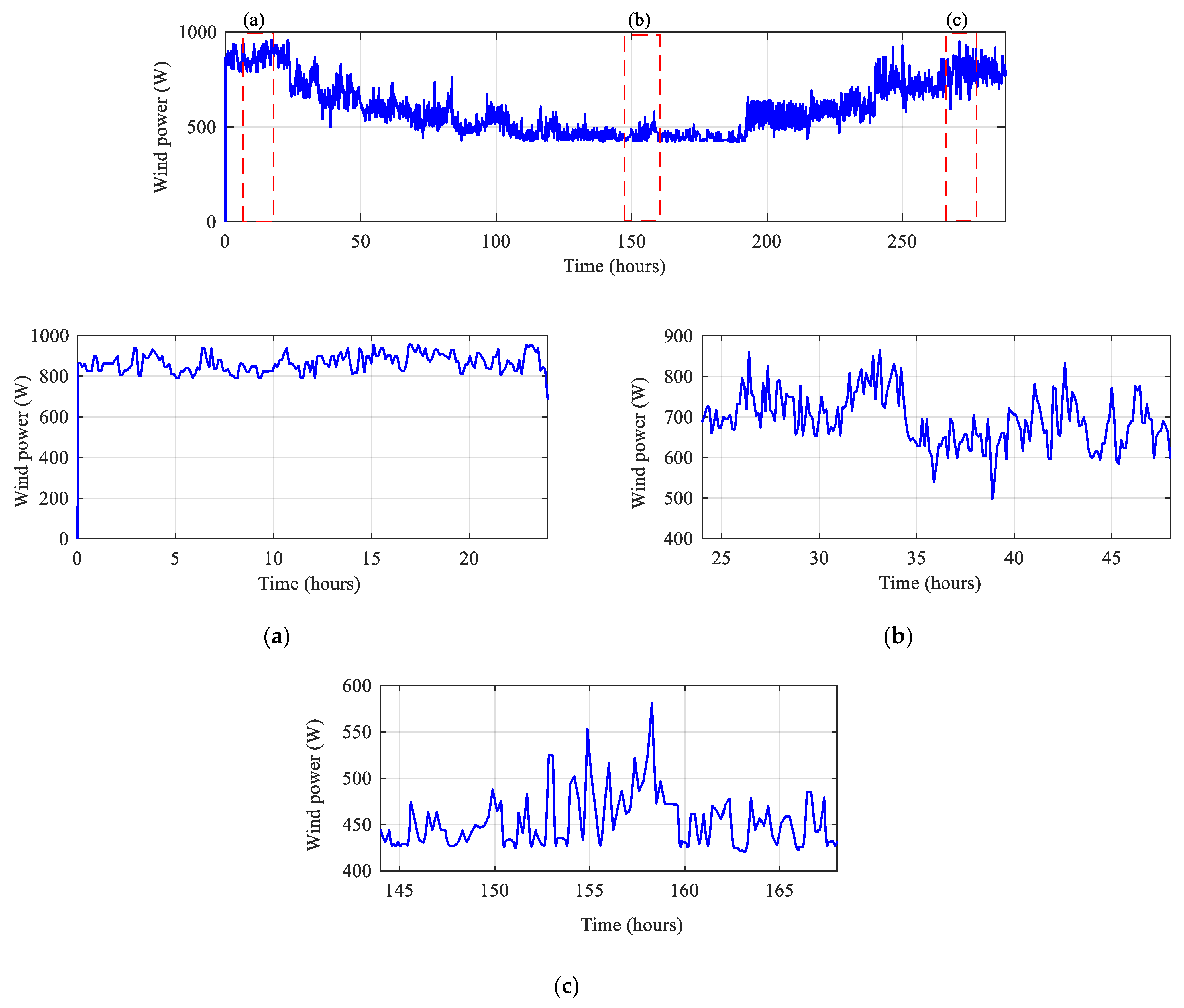
4.2. Simulation under Measured Profiles of Solar Irradiation, Temperature and Wind Speed
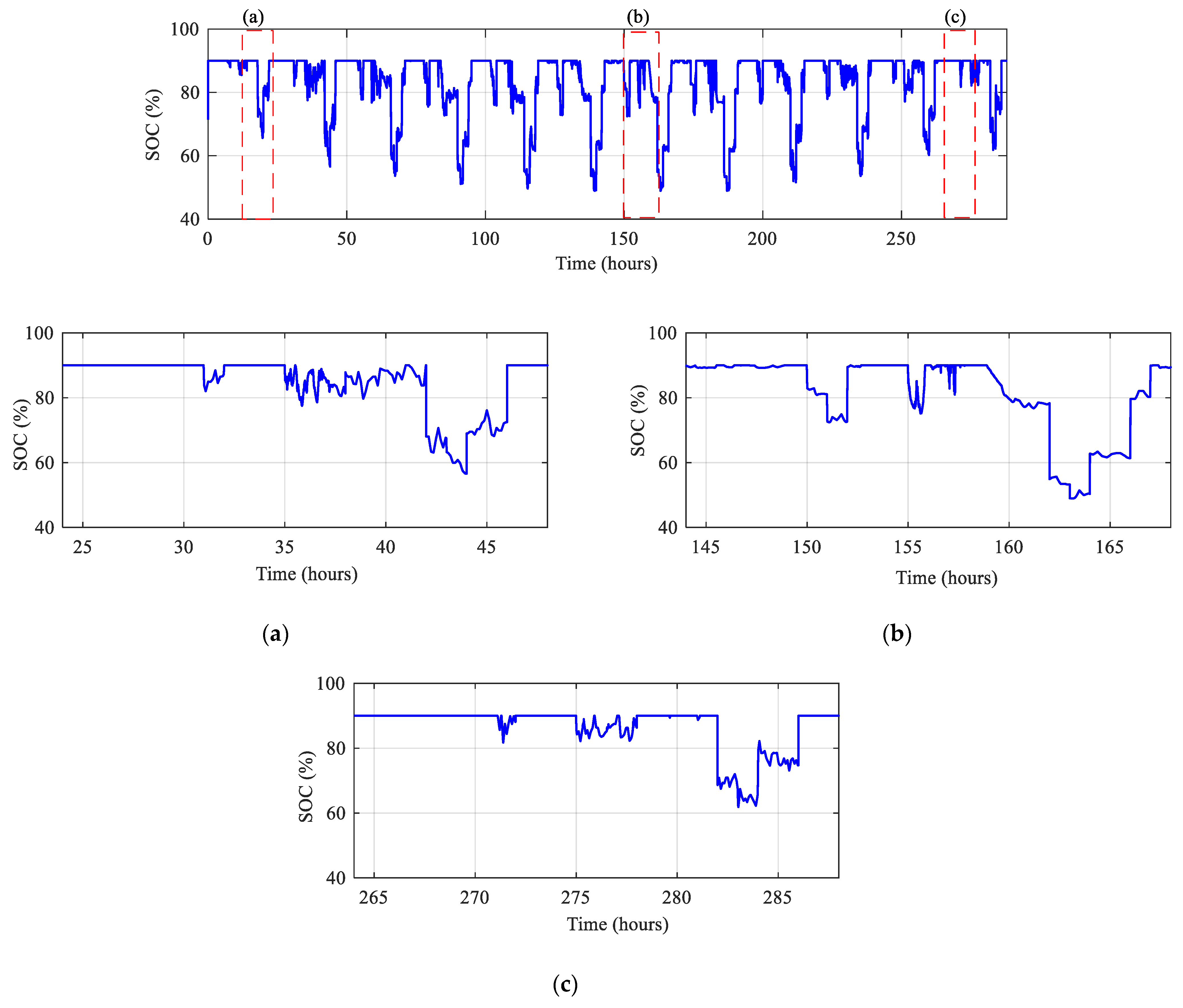
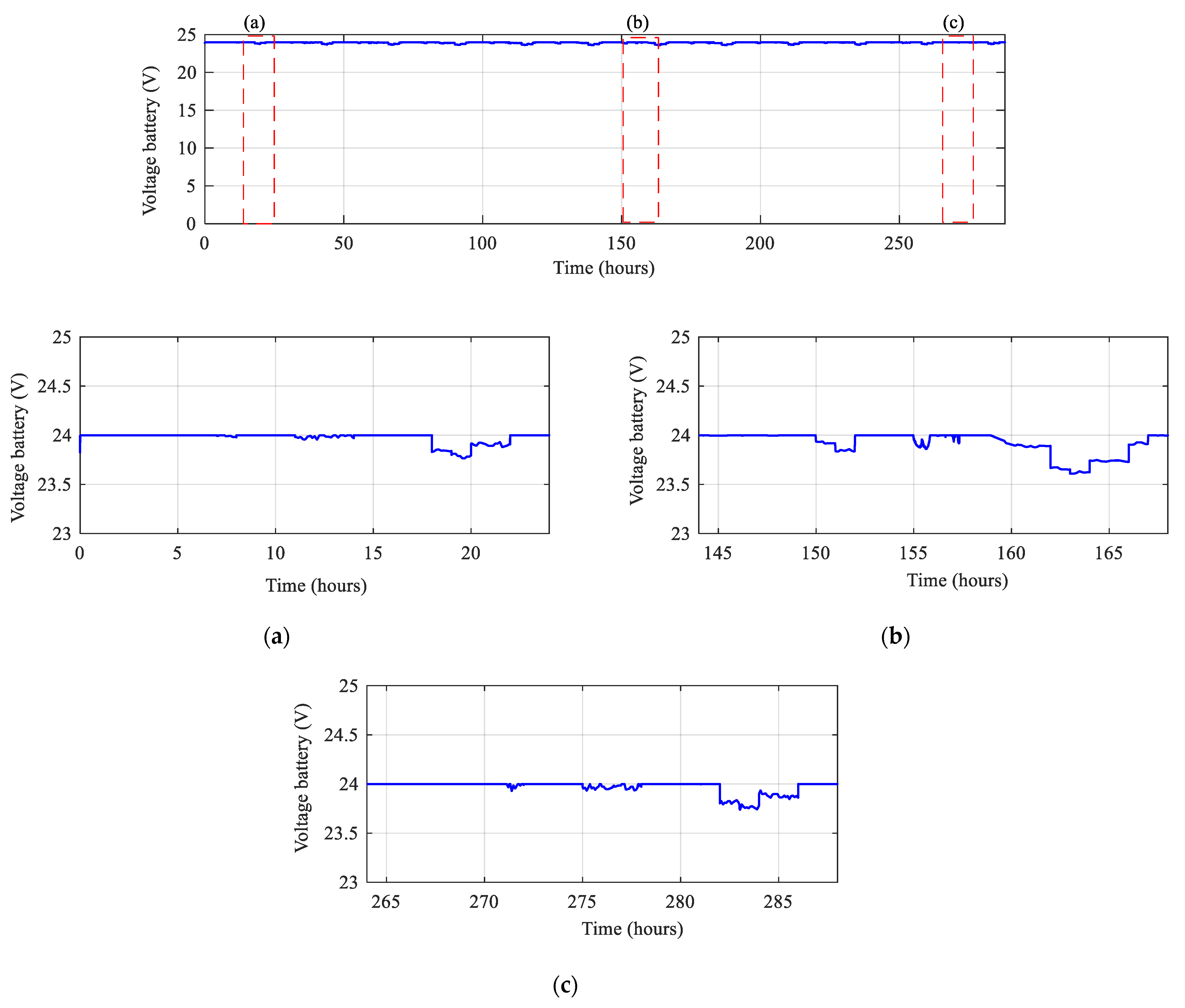
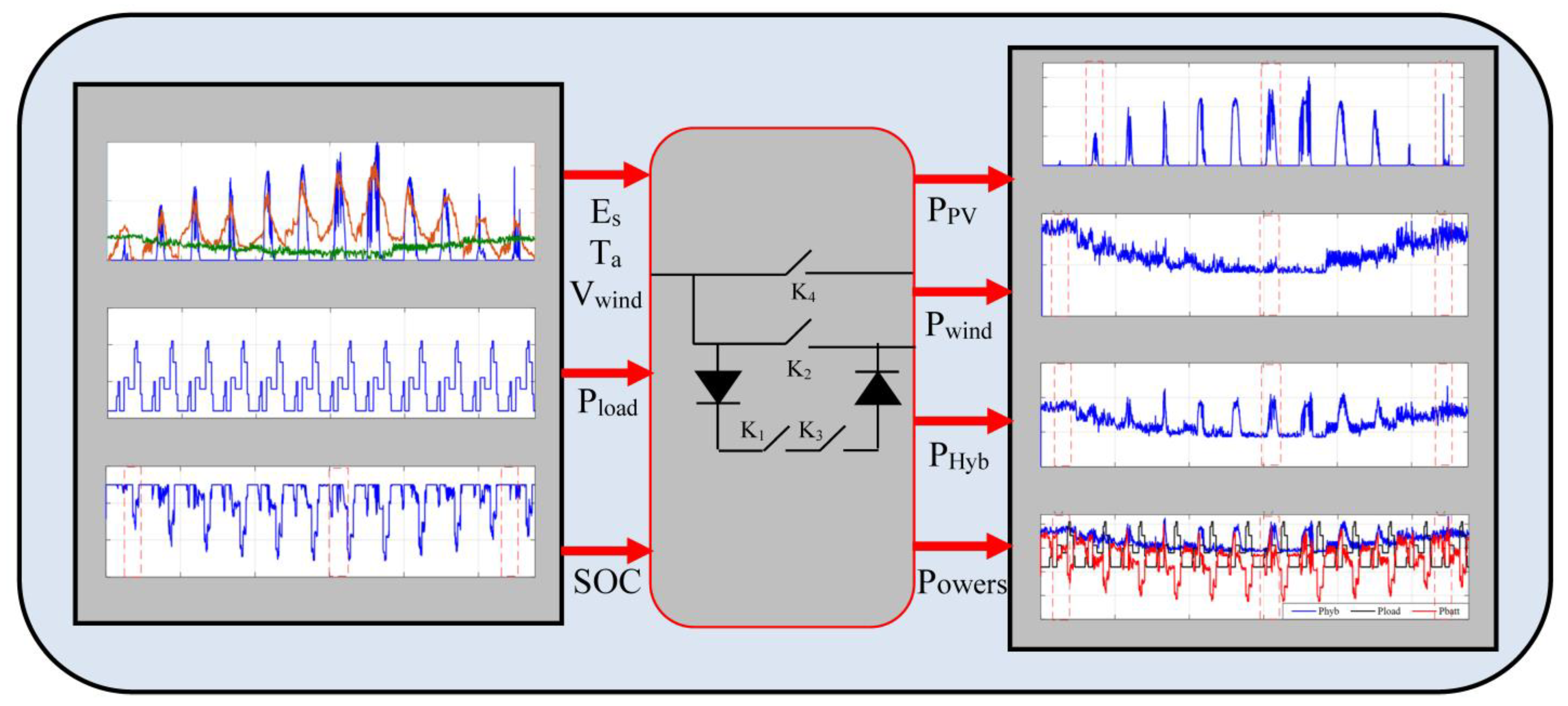
5. Power Control of the Studied System
5.1. Literature Review on Energy Management Control
5.2. Control of the Studied System
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rekioua, D.; Matagne, E. Optimization of Photovoltaic Power Systems: Modelization, Simulation and Control; Series: Green Energy and Technology; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Silva, A.R.; Estanqueiro, A. From Wind to Hybrid: A Contribution to the Optimal Design of Utility-Scale Hybrid Power Plants. Energies 2022, 15, 2560. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, Y.; Zheng, J. Assessment on Global Urban Photovoltaic Carrying Capacity and Adjustment of Photovoltaic Spatial Planning. Sustainability 2021, 13, 3149. [Google Scholar] [CrossRef]
- Chomać-Pierzecka, E.; Kokiel, A.; Rogozińska-Mitrut, J.; Sobczak, A.; Soboń, D.; Stasiak, J. Analysis and Evaluation of the Photovoltaic Market in Poland and the Baltic States. Energies 2022, 15, 669. [Google Scholar] [CrossRef]
- Xiao, W.; Elnosh, A.; Khadkikar, V.; Zeineldin, H. Overview of maximum power point tracking technologies for photovoltaic power systems. In Proceedings of the IECON 2011-37th Annual Conference of the IEEE Industrial Electronics Society 2011, Melbourne, Australia, 7–10 November 2011; pp. 3900–3905. [Google Scholar]
- Kordestani, M.; Mirzaee, A.; Safavi, A.A.; Saif, M. Maximum Power Point Tracker (MPPT) for Photovoltaic Power Systems-A Systematic Literature Review. In Proceedings of the European Control Conference (ECC) 2018, Limassol, Cyprus, 12–15 June 2018; pp. 40–45. [Google Scholar]
- Salas, V.; Olias, E.; Barrado, A.; Lazaro, A. Review of the maximum power point tracking algorithms for stand-alone photovoltaic systems. Sol. Energy Mater. Sol. Cells 2006, 90, 1555–1578. [Google Scholar] [CrossRef]
- Zainuri MA, A.M.; Radzi MA, M.; Soh, A.C.; Rahim, N.A. Development of adaptive perturb and observe-fuzzy control maximum power point tracking for photovoltaic boost dc–dc converter. IET Renew. Power Gener. 2014, 8, 183–194. [Google Scholar] [CrossRef]
- Radhia, G.; Mouna, B.H.; Lassaad, S.; Barambones, O. MPPT controller for a photovoltaic power system based on increment conductance approach. In Proceedings of the 2013 International Conference on Renewable Energy Research and Applications (ICRERA) 2013, Madrid, Spain, 20–23 October 2013; pp. 73–78. [Google Scholar]
- Khadidja, S.; Mountassar, M.; M’hamed, B. Comparative study of incremental conductance and perturb & observe MPPT methods for photovoltaic system. In Proceedings of the 2017 International Conference on Green Energy Conversion Systems (GECS) 2017, Hammamet, Tunisia, 23–25 March 2017; pp. 1–6. [Google Scholar]
- Achour, A.; Rekioua, D.; Mohammedi, A.; Mokrani, Z.; Rekioua, T.; Bacha, S. Application of direct torque control to a photovoltaic pumping system with sliding-mode control optimization. Electr. Power Compon. Syst. 2016, 44, 172–184. [Google Scholar] [CrossRef]
- Sun, L.; Zhengdandan Han, F. Study on MPPT approach in photovoltaic system based on fuzzy control. In Proceedings of the 2013 IEEE 8th Conference on Industrial Electronics and Applications (ICIEA) 2013, Melbourne, Australia, 19–21 June 2013; pp. 1259–1263. [Google Scholar]
- Masoum, M.A.S.; Dehbonei, H. Design, construction and testing of a voltage-based maximum power point tracker (VMPPT) for small satellite power supply. In Proceedings of the 13th Annual AIAA/USU Conference, Small Satellite 1999, Logan, UT, USA, 23–26 August 1999. [Google Scholar]
- Noguchi, T.; Togashi, S.; Nakamoto, R. Short-current pulse-based adaptive maximum power point tracking for a photovoltaic power generation system. In Proceedings of the 2000 IEEE International Symposium on ISIE 2000, Cholula, Mexico, 4–8 December 2000; Volume 1, pp. 157–162. [Google Scholar]
- Esram, K.; Chapman, P.L. Comparison of Photovoltaic Array Maximum Power Point Tracking Techniques. IEEE Trans. Energy Convers. 2007, 22, 439–449. [Google Scholar] [CrossRef]
- Hohm, D.P.; Ropp, M.E. Comparative Study of Maximum Power Point Tracking Algorithms. Prog. Photovolt. Res. Appl. 2003, 11, 47–62. [Google Scholar] [CrossRef]
- Santos LJ, L.; Antunes, F.; Chehab, A.; Cruz, C. A Maximum Power Point Tracker for PV Systems Using a High Performance Boost Converter. Sol. Energy 2006, 80, 772–778. [Google Scholar] [CrossRef]
- Krauter Stefan, C.W. Solar Electric Power Generation—Photovoltaic Energy Systems; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Liu, F.; Duan, S.; Liu, F.; Liu, B.; Kang, Y. A Variable Step Size INC MPPT Method for PV Systems. IEEE Trans. Ind. Electron. 2008, 55, 2622–2628. [Google Scholar]
- Noman Abdullah, M.; Addoweesh Khaled, E.; Mashaly Hussein, M. DSPACE Real-Time Implementation of MPPT-Based FLC Method. Int. J. Photoenergy 2013, 2013, 549273. [Google Scholar]
- Mondal, A.; Yuvarajan, S. MPPT Scheme for Small Scale Photovoltaic Systems Using dSPACE. In Proceedings of the 2012 IEEE Green Technologies Conference, Tulsa, OK, USA, 19–20 April 2012; pp. 1–3. [Google Scholar]
- Sudhakar Babu, T.; Rajasekar, N.; Sangeetha, K. Modified Particle Swarm Optimization technique based Maximum Power Point Tracking for uniform and under partial shading condition. Appl. Soft Comput. 2015, 34, 613–624. [Google Scholar] [CrossRef]
- Khare, A.; Rangnekar, S. A review of particle swarm optimization and its applications in Solar Photovoltaic system. Appl. Soft Comput. 2013, 13, 2997–3006. [Google Scholar] [CrossRef]
- Mayssa, F.; Sbita, L. Advanced ANFIS-MPPT control algorithm for sunshine photovoltaic pumping systems. In Proceedings of the 1st International Conference Renewable Energies and Vehicular Technology 2012, Nabeul, Tunisia, 26–28 March 2012; pp. 167–172. [Google Scholar]
- Rekioua, D. MPPT Methods in Hybrid Renewable Energy Systems. Green Energy Technol. 2020, 79–138. [Google Scholar] [CrossRef]
- Linus, R.M.; Damodharan, P. Maximum power point tracking and grid feeding of permanent magnet synchronous generator based wind energy conversion system using modified hill climb searching algorithm. In Proceedings of the India International Conference on Power Electronics, IICPE 2012, Delhi, India, 6–8 December 2012; p. 6450491. [Google Scholar]
- Mousa, H.H.H.; Youssef, A.-R.; Mohamed, E.E.M. State of the art perturb and observe MPPT algorithms based wind energy conversion systems: A technology review. Int. J. Electr. Power Energy Syst. 2021, 126, 106598. [Google Scholar] [CrossRef]
- Cui, Z.; Song, L.; Li, S. Maximum power point tracking strategy for a new wind power system and its design details. IEEE Trans. Energy Convers. 2017, 32, 1063–1071. [Google Scholar] [CrossRef]
- Kumar, D.; Chatterjee, K. A review of conventional and advanced MPPT algorithms for wind energy systems. Renew. Sustain. Energy Rev. 2016, 55, 957–970. [Google Scholar] [CrossRef]
- Pande, J.; Nasikkar, P.; Kotecha, K.; Varadarajan, V. A review of maximum power point tracking algorithms for wind energy conversion systems. J. Mar. Sci. Eng. 2021, 9, 1187. [Google Scholar] [CrossRef]
- Abdullah, M.A.; Yatim, A.H.M.; Tan, C.W.; Saidur, R. A review of maximum power point tracking algorithms for wind energy systems. Renew. Sustain. Energy Rev. 2012, 16, 3220–3227. [Google Scholar] [CrossRef]
- Moon, S.H.; Park, B.G.; Kim, J.W.; Kim, J.M. Maximum Power-Point Tracking Control Using Perturb and Observe Algorithm for Tidal Current Generation System. Int. J. Precis. Eng. Manuf. Green Technol. 2020, 7, 849–858. [Google Scholar] [CrossRef]
- Mishra, S.; Shukla, S.; Verma, N.; Ritu, R. Comprehensive review on Maximum Power Point Tracking techniques: Wind Energy. In Proceedings of the International Conference Communication, Control and Intelligent Systems, CCIS 2015, Mathura, India, 7–8 November 2015; pp. 464–469. [Google Scholar]
- Rekioua, D.; Rekioua, T.; Soufi, Y. Control of a grid-connected photovoltaic system. In Proceedings of the 2015 International Conference on Renewable Energy Research and Applications, ICRERA 2015, Palermo, Italy, 22–25 November 2015; pp. 1382–1387. [Google Scholar]
- Bekiroglu, E.; Yazar, M.D. MPPT Control of Grid Connected DFIG at Variable Wind Speed. Energies 2022, 5, 3146. [Google Scholar] [CrossRef]
- Belaid, S.; Rekioua, D.; Oubelaid, A.; Ziane, D.; Rekioua, T. Proposed Hybrid Power Optimization for Wind Turbine/Battery System. Period. Polytech. Electr. Eng. Comput. Sci. 2022, 66, 60–71. [Google Scholar] [CrossRef]
- Soliman, M.A.; Hasanien, H.; Azazi, H.Z.; El-kholy, E.E.; Mahmoud, S.A. An adaptive fuzzy logic control strategy for performance enhancement of a grid-connected PMSG-based wind turbine. IEEE Trans. Ind. Inform. 2018, 15, 3163–3173. [Google Scholar] [CrossRef]
- Khan, M.J.; Mathew, L.; Alotaibi, M.A.; Malik, H.; Nassar, M.E. Fuzzy-Logic-Based, Comparative Analysis of Different Maximum Power Point Tracking Controllers for Hybrid Renewal Energy Systems. Mathematics 2022, 10, 529. [Google Scholar] [CrossRef]
- Elbeji, O.; Hannachi, M.; Benhamed, M. Artificial neural network-based sensorless control of wind energy conversion system driving a permanent magnet synchronous generator. Wind. Eng. 2021, 45, 459–476. [Google Scholar] [CrossRef]
- Rodolfo, D.; Jose, L. Efficient design of hybrid renewable energy systems using evolutionary algorithms. Energy Convers. Manag. 2009, 3, 479–489. [Google Scholar]
- Lu, D.; Fakham, H.; Zhou, T.; Francois, B. Application of Petri nets for the energy management of a photovoltaic based power station including storage units. Renew. Energy 2010, 35, 1117–1124. [Google Scholar] [CrossRef]
- Jamshidi, M.M. Sustainable energy systems: Cyber-physical based intelligent management of micro-grids. In Proceedings of the LINDI 2012—4th IEEE International Symposium on Logistics and Industrial Informatics, Smolenice, Slovakia, 5–7 September 2012. [Google Scholar]
- Valverde, L.; Rosa, F.; del Real, A.; Arce, A.; Bordons, C. Modeling, simulation and experimental set-up of a renewable hydrogen-based domestic microgrid. Int. J. Hydrogen Energy 2013, 38, 11672–11684. [Google Scholar] [CrossRef]
- Rafa, S.; Khenfri, F.; Diaf, S. Development and realization of an intelligent power strip for energy consumption management in hybrid wind/photovoltaic systems. Energy Procedia 2013, 42, 530–538. [Google Scholar]
- Amin, R.; Bambang, T.; Rohman, A.S.; Dronkers, C.J.; Ortega, R.; Sasongko, A. Energy Management of Fuel Cell/Battery/Supercapacitor Hybrid Power Sources Using Model Predictive Control. IEEE Trans. Ind. Inform. 2014, 10, 1992–2002. [Google Scholar] [CrossRef]
- Thounthong, P.; Sikkabut, S.; Mungporn, P.; Piegari, L.; Nahid-Mobarakeh, B.; Pierfederici, S.; Davat, B. DC bus stabilization of Li-Ion battery based energy storage for hydrogen/solar power plant for autonomous network applications. In Proceedings of the IEEE Industry Application Society Annual Meeting 2014, Vancouver, BC, Canada, 5–9 October 2014; pp. 1–8. [Google Scholar]
- Mokrani, Z.; Rekioua, D.; Rekioua, T. Modeling, control and power management of hybrid photovoltaic fuel cells with battery bank supplying electric vehicle. Int. J. Hydrogen Energy 2014, 35, 15178–15187. [Google Scholar] [CrossRef]
- Rekioua, D.; Bensmail, S.; Bettar, N. Development of hybrid photovoltaic-fuel cell system for stand-alone application. Int. J. Hydrogen Energy 2014, 39, 1604–1611. [Google Scholar] [CrossRef]
- Moorthy, R.S.K.; Rathore, A.K. Soft switching non-isolated current-fed inverter for PV/Fuel-cell applications. In Proceedings of the 2014 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES) 2014, Mumbai, India, 16–19 December 2014; pp. 1–6. [Google Scholar]
- Mebarki, N.; Rekioua, T.; Mokrani, Z.; Rekioua, D. Supervisor control for stand-alone photovoltaic/hydrogen/battery bank system to supply energy to an electric vehicle. Int. J. Hydrogen Energy 2015, 40, 13777–13788. [Google Scholar] [CrossRef]
- Serir, C.; Rekioua, D.; Mezzai, N.; Bacha, S. Supervisor control and optimization of multi-sources pumping system with battery storage. Int. J. Hydrogen Energy 2016, 41, 20974–22098. [Google Scholar] [CrossRef]
- Roumila, Z.; Rekioua, D.; Rekioua, T. Energy management based fuzzy logic controller of hybrid system wind/photovoltaic/diesel with storage battery. Int. J. Hydrogen Energy 2017, 42, 19525–19535. [Google Scholar] [CrossRef]
- Wieczorek, M.; Lewandowski, M. A mathematical representation of an energy management strategy for hybrid energy storage system in electric vehicle and real time optimization using a genetic algorithm. Appl. Energy 2017, 192, 222–233. [Google Scholar] [CrossRef]
- Rekioua, D. Energy Management for PV Installations. Adv. Renew. Energ. Power Technol. 2018, 1, 349–369. [Google Scholar]
- Kamal, E.; Adouane, L. Intelligent Energy Management Strategy Based on Artificial Neural Fuzzy for Hybrid Vehicle. IEEE Trans. Intell. Veh. 2018, 3, 112–125. [Google Scholar] [CrossRef]
- Khiareddine, A.; Salah, C.B.; Rekioua, D.; Mimouni, M.F. Sizing methodology for hybrid photovoltaic/wind/hydrogen/battery integrated to energy management strategy for pumping system. Energy 2018, 153, 743–776. [Google Scholar] [CrossRef]
- Bahri, N.; Ouled Amor, W. Intelligent power supply management of an autonomous hybrid energy generator. Int. J. Sustain. Eng. 2019, 12, 312–332. [Google Scholar] [CrossRef]
- Elkazaz, M.; Sumner, M.; Thomas, D. Energy management system for hybrid PV-wind-battery microgrid using convex programming, model predictive and rolling horizon predictive control with experimental validation. Int. J. Electr. Power Energy Syst. 2020, 115, 105483. [Google Scholar] [CrossRef]
- Hassani, H.; Zaouche, F.; Rekioua, D.; Belaid, S.; Bacha, S. Feasibility of a standalone photovoltaic/battery system with hydrogen production. J. Energy Storage 2020, 31, 101644. [Google Scholar] [CrossRef]
- Krishan, O.; Suhag, S. Grid-independent PV system hybridization with fuel cell-battery/supercapacitor: Optimum sizing and comparative techno-economic analysis. Sustain. Energy Technol. Assess. 2020, 37, 100625. [Google Scholar] [CrossRef]
- Elmouatamid, A.; Ouladsine, R.; Bakhouya, M.; El Kamou, N.; Khaidar, M.; Zine-Dine, K. Review of Control and Energy Management Approaches in Micro-Grid Systems. Energies 2021, 14, 168. [Google Scholar] [CrossRef]
- Elmorshe, M.F.; Elkadeem, M.R.; Kotb, K.M.; Taha, I.B.M.; Mazzeo, D. Optimal design and energy management of an isolated fully renewable energy system integrating batteries and supercapacitors. Energy Convers. Manag. 2021, 245, 114584. [Google Scholar] [CrossRef]
- Azuara-Grande, L.S.; Arnaltes, S.; Alonso-Martinez, J.; Rodriguez-Amenedo, J.L. Comparison of Two Energy Management System Strategies for Real-Time Operation of Isolated Hybrid Microgrids. Energies 2021, 14, 6770. [Google Scholar] [CrossRef]
- Mazzeo, D.; Matera, N.; De Luca, P.; Baglivo, C.; Congedo, P.M.; Oliveti, G. A literature review and statistical analysis of photovoltaic-wind hybrid renewable system research by considering the most relevant 550 articles: An upgradable matrix literature database. J. Clean. Prod. 2021, 295, 126070. [Google Scholar] [CrossRef]
- Amrutha Raju, B.; Vuddanti, S.; Salkuti, S.R. Review of energy management system approaches in microgrids. Energies 2021, 14, 5459. [Google Scholar]
- Garg, A.; Tummuru, N.R.; Oruganti, R. Implementation of Energy Management Scenarios in a DC Microgrid Using DC Bus Signaling. IEEE Trans. Ind. Appl. 2021, 57, 5306–5317. [Google Scholar] [CrossRef]
- Sumarmad, K.A.A.; Sulaiman, N.; Wahab, N.I.A.; Hizam, H. Microgrid Energy Management, System Based on Fuzzy Logic and Monitoring Platform for Data Analysis. Energies 2022, 15, 4125. [Google Scholar] [CrossRef]
- Cao, Y.; Mohammadzadeh, A.; Tavoosi, J.; Mobayen, S.; Safdar, R.; Fekih, A. A new predictive energy management system: Deep learned type-2 fuzzy system based on singular value decommission. Energy Rep. 2022, 8, 722–734. [Google Scholar] [CrossRef]
- Belaid, S.; Rekioua, D.; Oubelaid, A.; Ziane, D.; Rekioua, T. A power management control and optimization of a wind turbine with battery storage system. J. Energy Storage 2022, 45, 103613. [Google Scholar] [CrossRef]
- Mezzai, N.; Belaid, S.; Rekioua, D.; Rekioua, T. Optimization, design and control of a photovoltaic/wind turbine/battery system in Mediterranean climate conditions. Bull. Electr. Eng. Inform. 2022, 11, 2938–2948. [Google Scholar] [CrossRef]
- Kakouche, K.; Rekioua, T.; Mezani, S.; Oubelaid, A.; Rekioua, D.; Blazek, V.; Prokop, L.; Misak, S.; Bajaj, M.; Ghoneim, S.S.M. Model predictive direct torque control and fuzzy logic energy management for multi power source electric vehicles. Sensors 2022, 22, 5669. [Google Scholar] [CrossRef]





| Months | Eir (kWh/m2) | Ta (°C) | Tj (°C) | ηpv | Vwind (m/s) | Epv (kWh/m2) | Ewind (kWh/m2) | ELoad (kWh) |
|---|---|---|---|---|---|---|---|---|
| January | 180.14 | 16.00 | 21.63 | 0.1130 | 6.50 | 15.90 | 191.47 | 664.82 |
| February | 190.11 | 14.00 | 19.94 | 0.1138 | 6.00 | 16.89 | 136.03 | 477.15 |
| March | 200.45 | 18.00 | 24.26 | 0.1118 | 5.00 | 17.51 | 87.15 | 311.52 |
| April | 292.32 | 19.00 | 28.14 | 0.1101 | 4.70 | 25.14 | 70.05 | 260.00 |
| May | 200.03 | 25.00 | 31.25 | 0.1087 | 4.10 | 16.99 | 48.05 | 178.13 |
| June | 260.41 | 28.00 | 36.14 | 0.1065 | 4.20 | 21.67 | 49.99 | 188.78 |
| July | 290.70 | 31.00 | 40.08 | 0.1048 | 3.50 | 23.79 | 29.89 | 122.29 |
| August | 290.80 | 36.00 | 45.09 | 0.1025 | 3.70 | 23.29 | 35.32 | 140.30 |
| September | 185.56 | 30.00 | 35.80 | 0.1067 | 3.90 | 15.46 | 40.02 | 149.51 |
| October | 190.10 | 22.00 | 27.94 | 0.1102 | 5.50 | 16.36 | 116.00 | 408.60 |
| November | 190.10 | 18.00 | 23.94 | 0.1120 | 6.60 | 16.63 | 193.98 | 673.97 |
| December | 160.26 | 14.00 | 19.01 | 0.1142 | 6.80 | 14.29 | 219.23 | 757.78 |
| Epv,ave = 18.66 | Ewind,ave = 101.43 | ELoad,ave = 361.07 |
| Spv (m2) | Swind (m2) | Npv | Nwind | Spvfinal (m2) | Swind,final (m2) | ELmean (kWh) | |
|---|---|---|---|---|---|---|---|
| 0.00 | 0.00 | 3.56 | 0.00 | 2.00 | 0.00 | 6.90 | 699.87 |
| 0.10 | 1.93 | 3.20 | 3.00 | 1.00 | 2.60 | 3.45 | 398.52 |
| 0.20 | 3.87 | 2.85 | 5.00 | 1.00 | 4.34 | 3.45 | 430.92 |
| 0.30 | 5.80 | 2.49 | 7.00 | 1.00 | 6.08 | 3.45 | 463.31 |
| 0.40 | 7.74 | 2.14 | 9.00 | 1.00 | 7.81 | 3.45 | 495.71 |
| 0.50 | 9.67 | 1.78 | 12.00 | 1.00 | 10.42 | 3.45 | 544.30 |
| 0.60 | 11.61 | 1.42 | 14.00 | 1.00 | 12.15 | 3.45 | 576.69 |
| 0.60 | 11.61 | 1.42 | 14.00 | 1.00 | 12.15 | 3.45 | 576.69 |
| 0.70 | 13.54 | 1.07 | 16.00 | 1.00 | 13.89 | 3.45 | 609.08 |
| 0.80 | 15.48 | 0.71 | 18.00 | 1.00 | 15.62 | 3.45 | 641.48 |
| 0.90 | 17.41 | 0.36 | 21.00 | 1.00 | 18.23 | 3.45 | 690.07 |
| 1.00 | 19.35 | 0.00 | 23.00 | 0.00 | 19.96 | 0.00 | 372.53 |
| PV Panels | Wind Turbine | Batteries |
|---|---|---|
| 03 | 01 | 02 |
| Error (e) | Variation of Error (Ce) | ||||||
|---|---|---|---|---|---|---|---|
| NB | NM | NS | ZE | PS | PM | PM | |
| NB | NB | NB | NM | ZE | ZE | ZE | ZE |
| NM | NB | NM | NM | ZE | NM | PS | PS |
| NS | NB | NB | NB | NB | PM | PS | PM |
| ZE | NB | NB | NS | ZE | PS | PM | PB |
| PS | NM | NS | ZE | PS | PM | PB | PB |
| PM | NS | PB | PB | PB | PB | PB | PB |
| PB | ZE | PB | PB | PB | PB | PB | PB |
| Year | System under Study | Components | References | ||||||
|---|---|---|---|---|---|---|---|---|---|
| PV | WTb | Batteries | Diesel Generator | Fuel Cells | Hydropower | SC | |||
| 2009 | Autonomous system | X | X | X | X | X | X | [40] | |
| 2010 | Autonomous system | X | X | X | [41] | ||||
| 2012 | Micro-grids | X | X | X | [42] | ||||
| 2013 | Domestic micro-grids | X | X | [43] | |||||
| 2013 | Micro-grids | X | X | [44] | |||||
| 2014 | Traction motor | X | X | X | [45] | ||||
| 2014 | Autonomous network | X | X | X | [46] | ||||
| 2014 | Electric vehicle | X | X | X | [47] | ||||
| 2014 | Autonomous system | X | X | [48] | |||||
| 2015 | Electric car | X | X | X | [49] | ||||
| 2016 | Water pumping system | X | X | X | [50] | ||||
| 2017 | Autonomous system | X | X | X | X | [51] | |||
| 2017 | Electric vehicle | X | X | [52] | |||||
| 2018 | Autonomous system | X | X | [53] | |||||
| 2018 | Hybrid vehicle | X | X | [54] | |||||
| 2018 | Water pumping system | X | X | X | X | [55] | |||
| 2019 | Autonomous system | X | X | X | X | [56] | |||
| 2020 | Micro-grids | X | X | X | [57] | ||||
| 2020 | Standalone system | X | X | X | [58] | ||||
| 2020 | Grid-PV system | X | X | X | [59] | ||||
| 2021 | Micro-grid systems | X | X | X | X | X | X | X | [60] |
| 2021 | Isolated renewable energy system | X | X | [61] | |||||
| 2021 | Isolated hybrid micro-grids | X | X | X | [62] | ||||
| 2021 | Micro-grid systems | X | X | [63] | |||||
| 2021 | Micro-grids | X | X | X | X | X | X | X | [64] |
| 2021 | DC micro-grids | X | X | [65] | |||||
| 2022 | Micro-grids | X | X | X | [66] | ||||
| 2022 | Micro-grids | X | X | X | X | X | [67] | ||
| 2022 | Stand-alone system | X | X | [68] | |||||
| 2022 | Stand-alone system | X | X | X | [69] | ||||
| 2022 | Electric vehicle | X | X | X | [70,71] | ||||
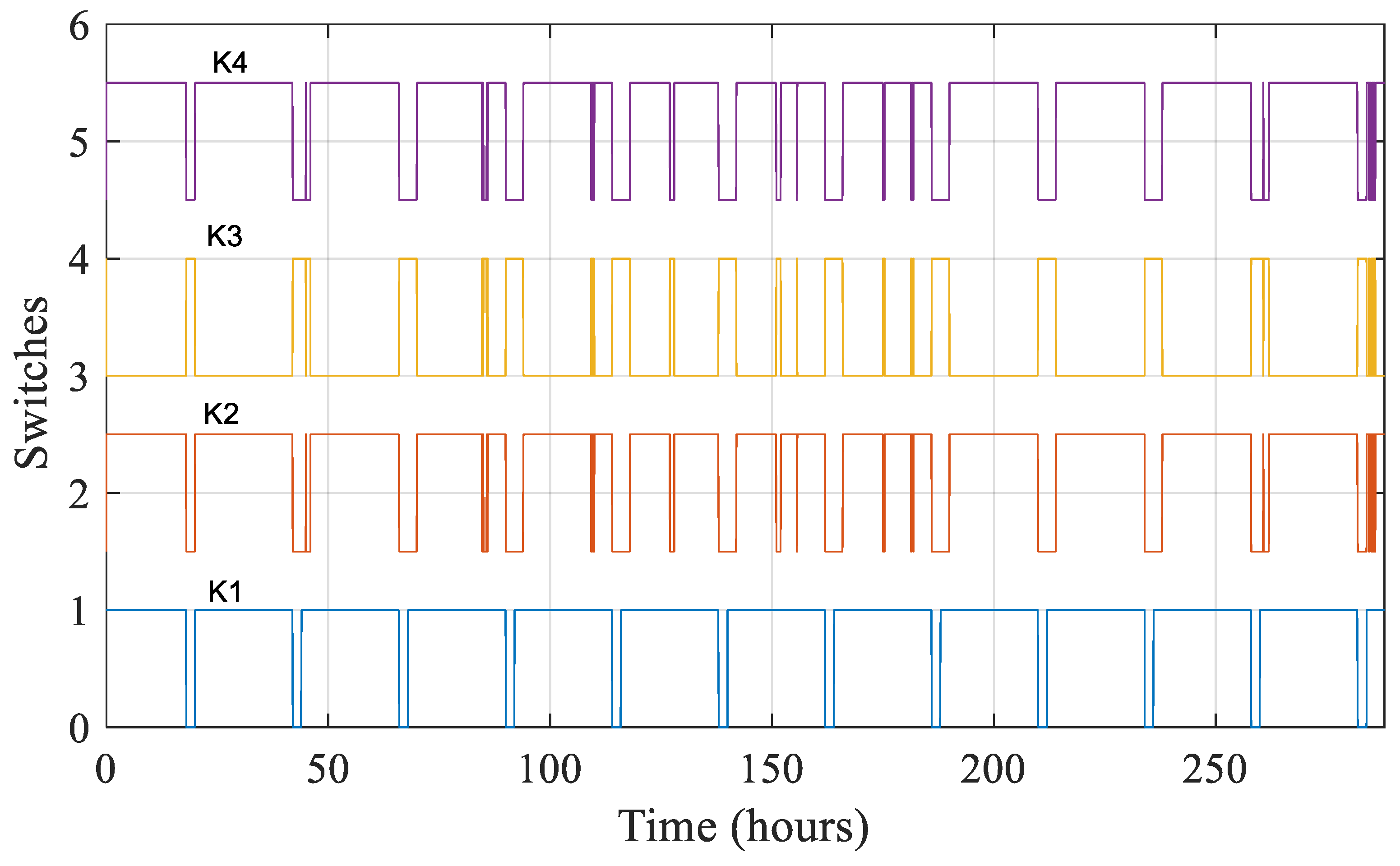
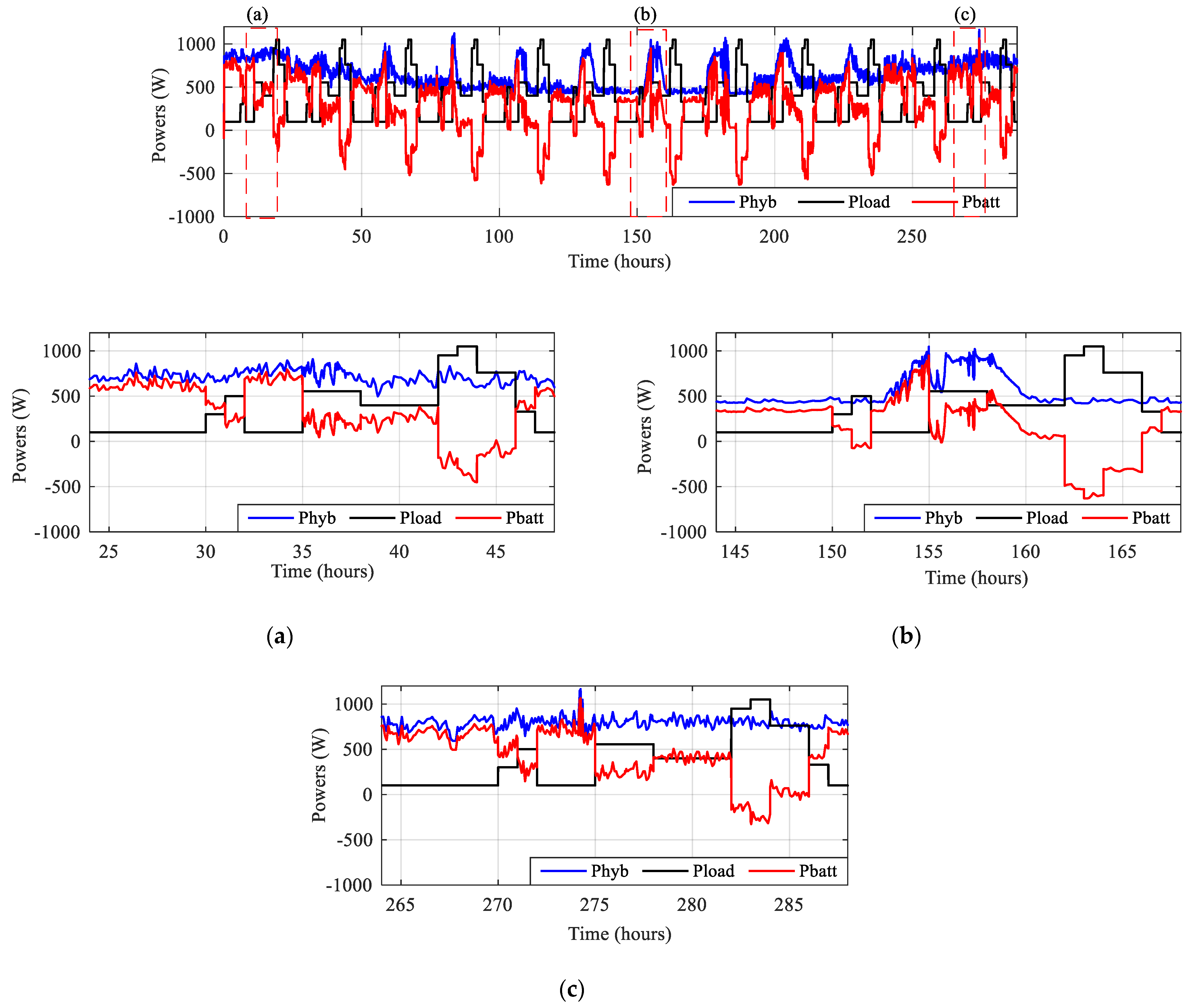
| Switch States | Powers | SOC | |||
|---|---|---|---|---|---|
| K1 = 1 | K2 = 0 | K3 = 0 | K4 = 0 | Phyb = PLoad | SOC |
| K1 = 1 | K2 = 0 | K3 = 0 | K4 = 1 | Phyb > PLoad | SOC > SOCmax |
| K1 = 1 | K2 = 1 | K3 = 0 | K4 = 0 | Phyb > PLoad, | SOC < SOCmax |
| K1 = 1 | K2 = 0 | K3 = 1 | K4 = 0 | Phyb < PLoad, | SOC > SOCmin |
| K1 = 0 | K2 = 1 | K3 = 0 | K4 = 0 | Phyb < PLoad | SOC < SOCmin |
| K1 = 0 | K2 = 0 | K3 = 0 | K4 = 1 | PLoad = 0, Phyb > 0 | SOC ≥ SOCmax |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rekioua, D.; Rekioua, T.; Elsanabary, A.; Mekhilef, S. Power Management Control of an Autonomous Photovoltaic/Wind Turbine/Battery System. Energies 2023, 16, 2286. https://doi.org/10.3390/en16052286
Rekioua D, Rekioua T, Elsanabary A, Mekhilef S. Power Management Control of an Autonomous Photovoltaic/Wind Turbine/Battery System. Energies. 2023; 16(5):2286. https://doi.org/10.3390/en16052286
Chicago/Turabian StyleRekioua, Djamila, Toufik Rekioua, Ahmed Elsanabary, and Saad Mekhilef. 2023. "Power Management Control of an Autonomous Photovoltaic/Wind Turbine/Battery System" Energies 16, no. 5: 2286. https://doi.org/10.3390/en16052286
APA StyleRekioua, D., Rekioua, T., Elsanabary, A., & Mekhilef, S. (2023). Power Management Control of an Autonomous Photovoltaic/Wind Turbine/Battery System. Energies, 16(5), 2286. https://doi.org/10.3390/en16052286








