Design of an Algorithm for Modeling Multiple Thermal Zones Using a Lumped-Parameter Model
Abstract
1. Introduction
2. Mathematical Model
- The identification of geometrical and physical parameters of the thermal zones, including internal loads.
- RC circuit construction and the calculation of resistors and capacitors
- Define the equations of the dynamic system, using the theory of energy flow transfer.
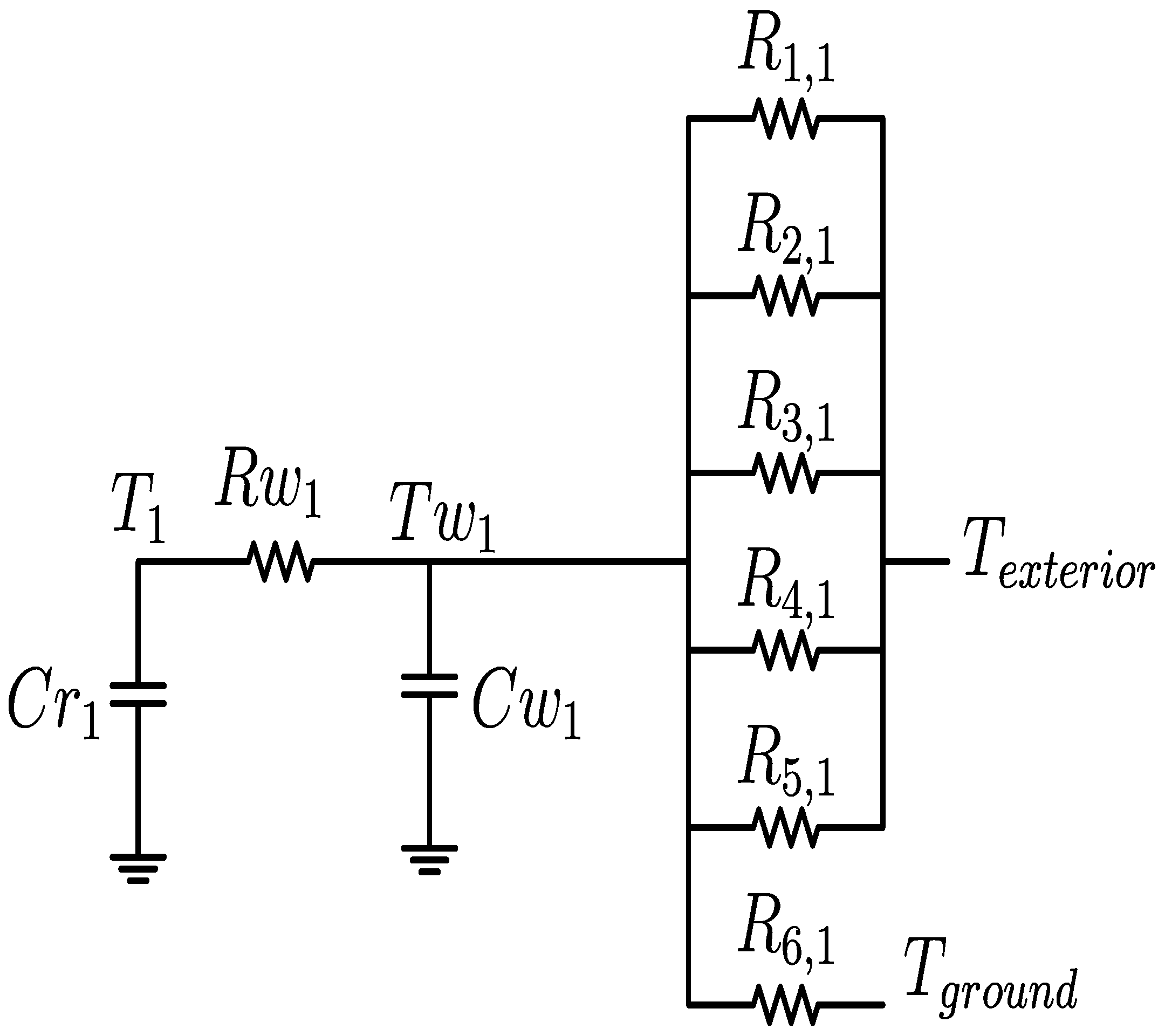
2.1. Case 1: A Single Thermal Zone (m = 1)
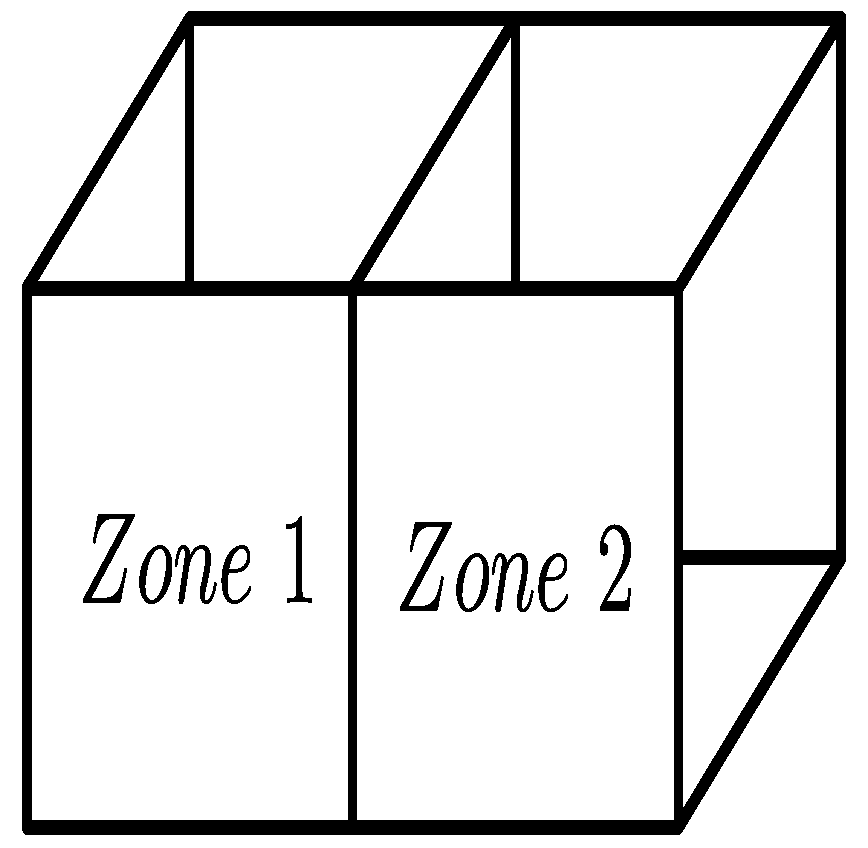
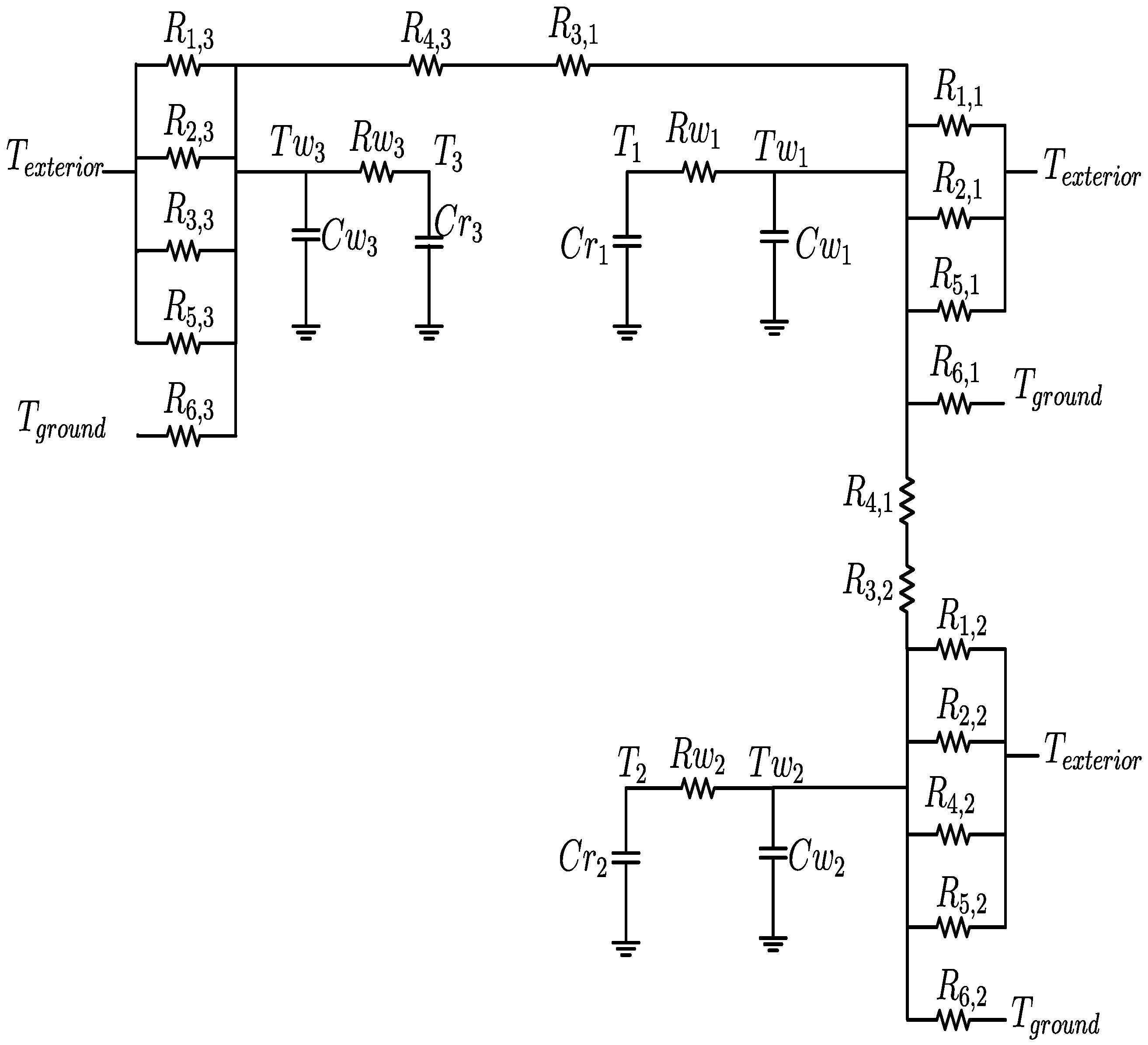
2.2. Case 2: Two Thermal Zones (m = 2)
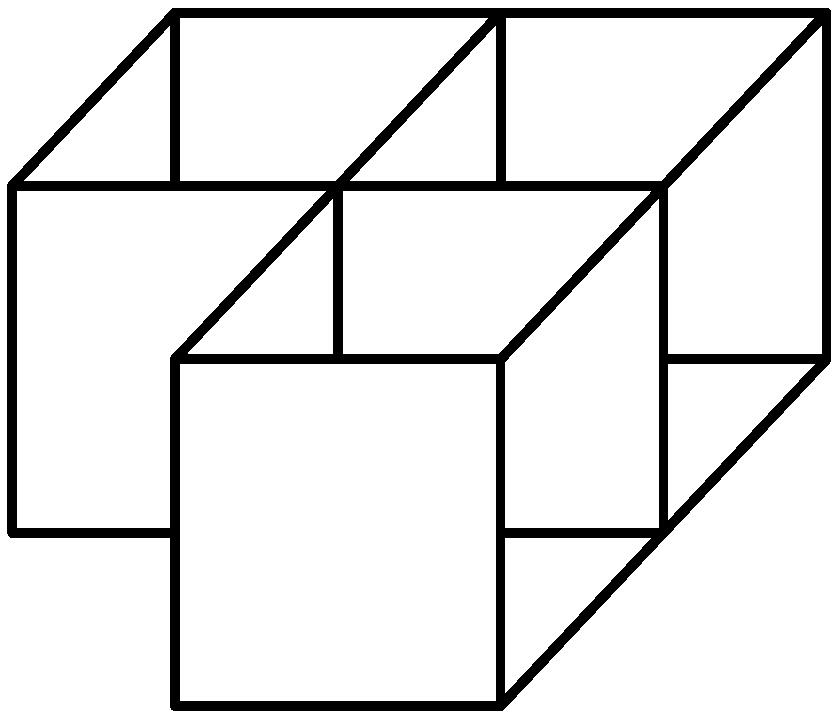
2.3. Case 3: Three Thermal Zones ( 3)
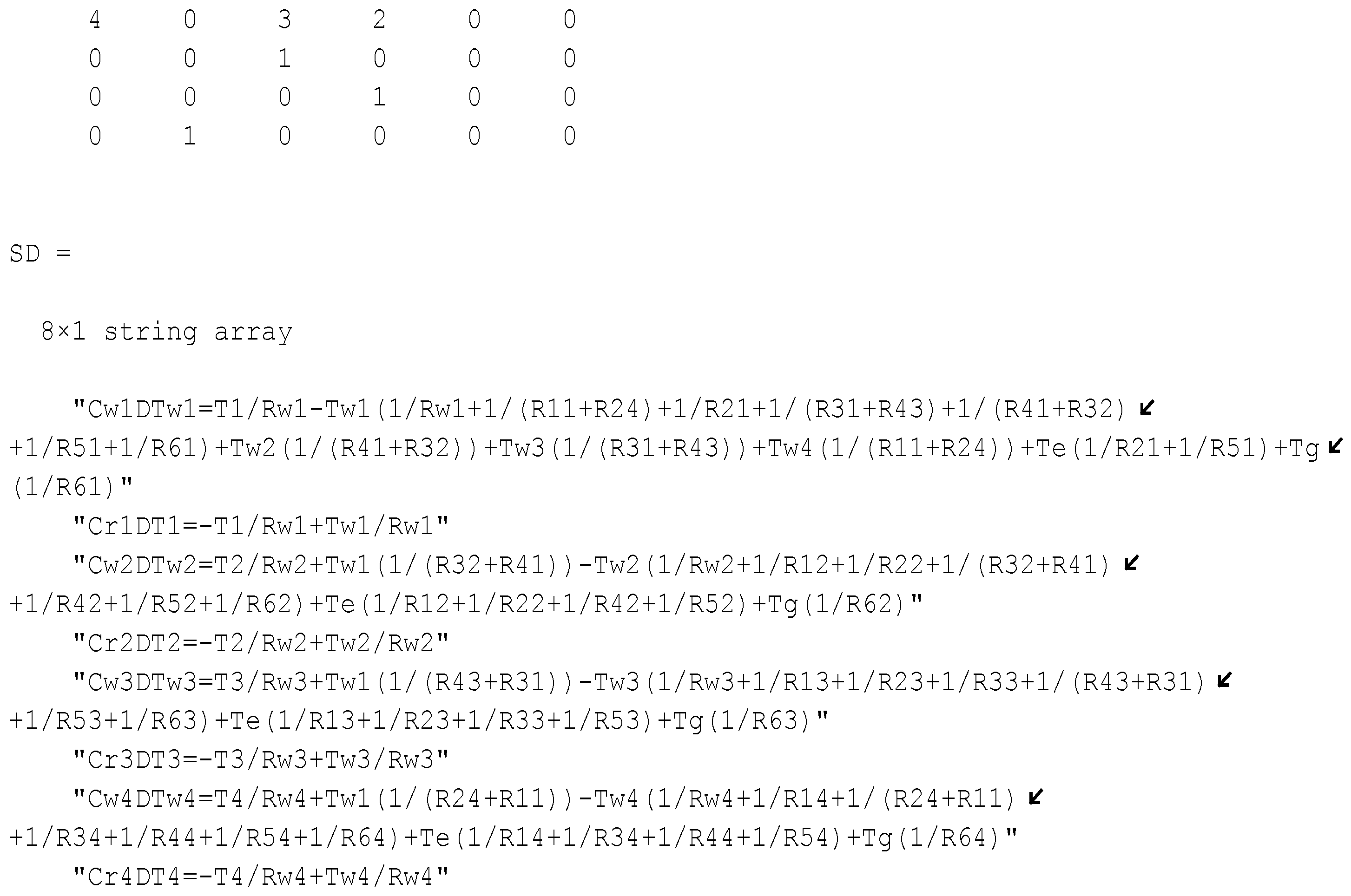
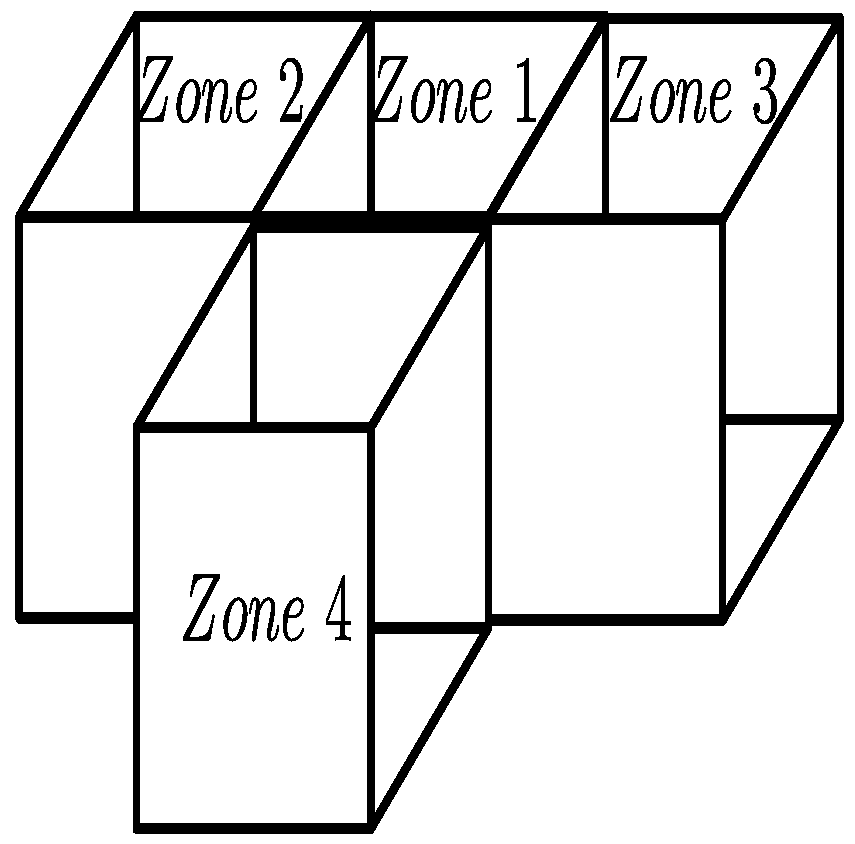
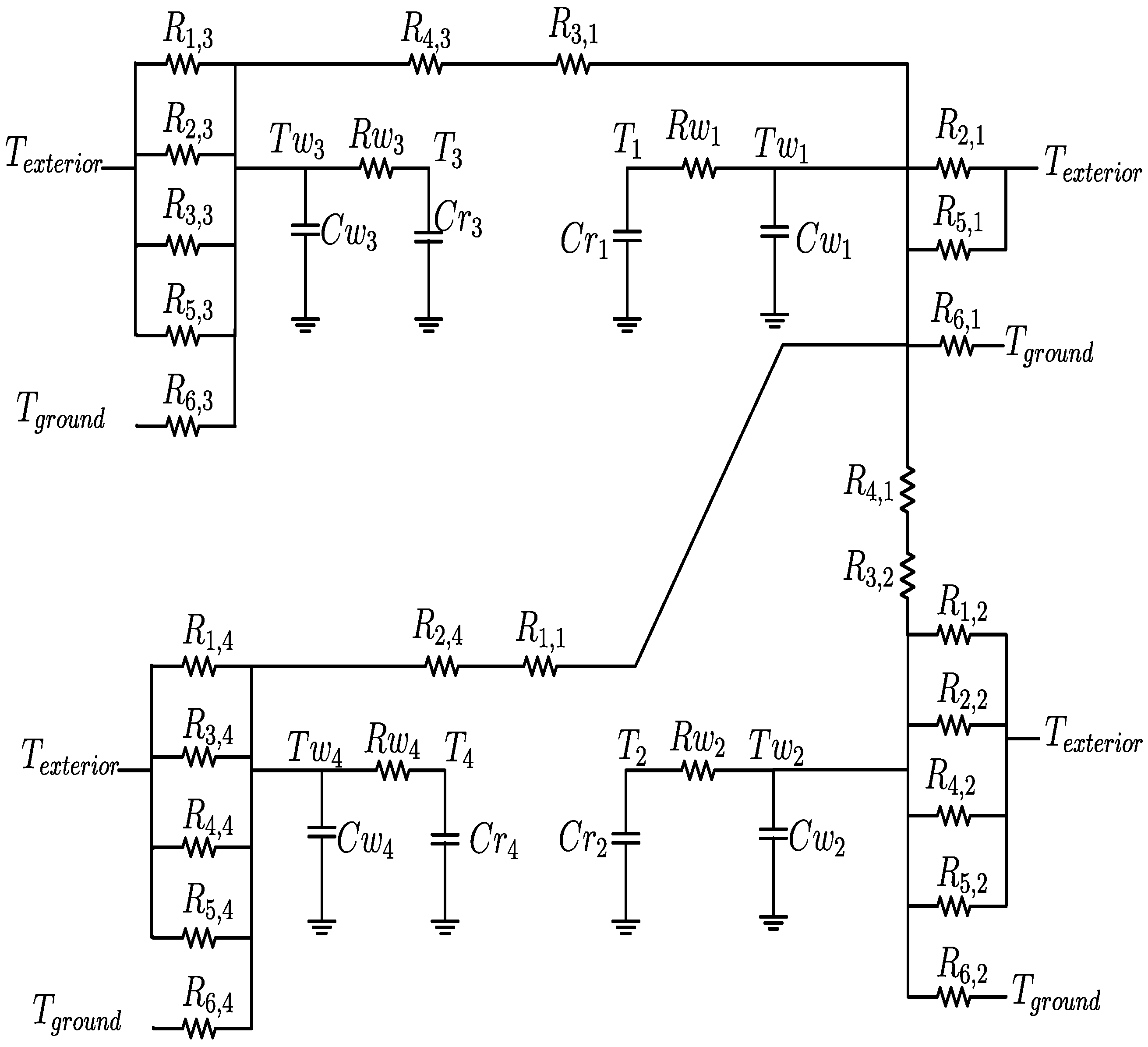
2.4. Case 4: Four Thermal Zones ( 4)
3. Algorithm Design
| Algorithm 1 Algorithm to design differential equation systems for multiple thermal zones |
 |
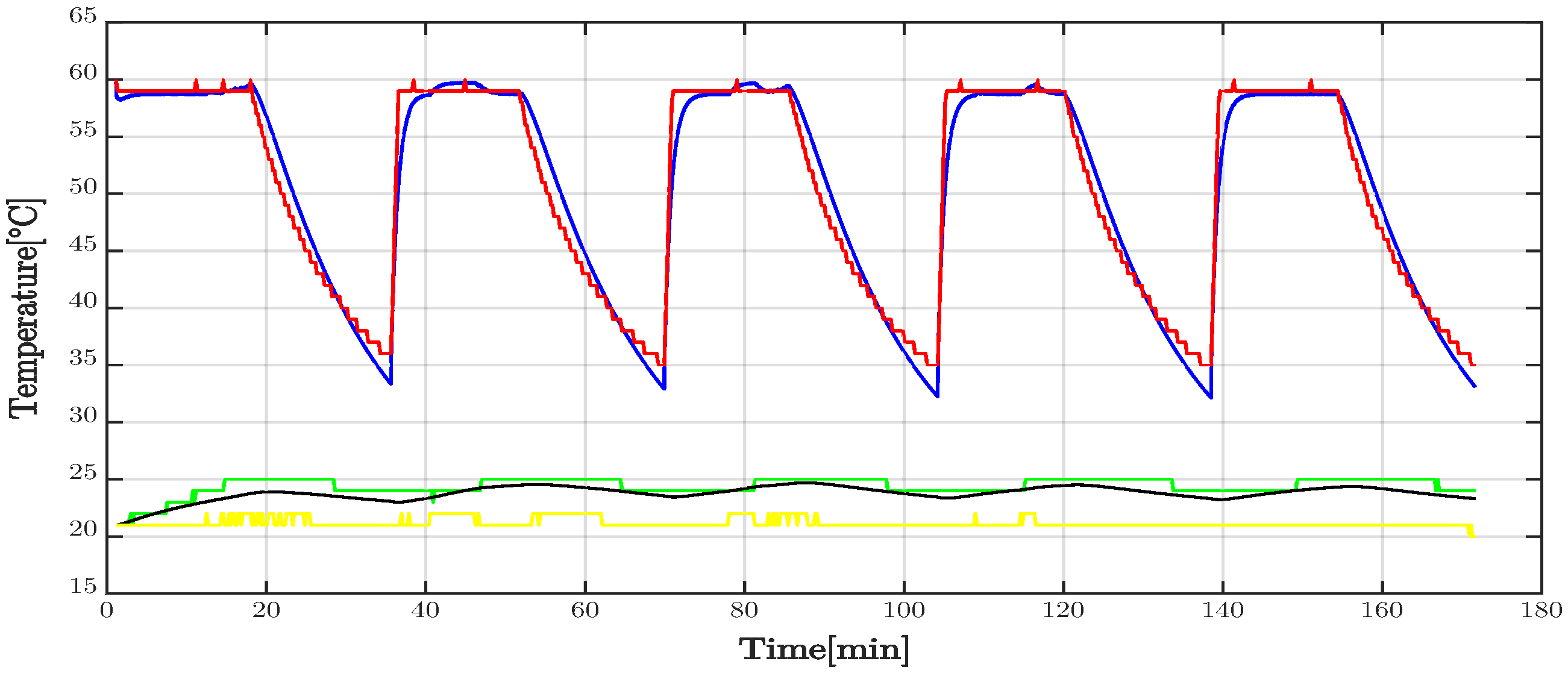
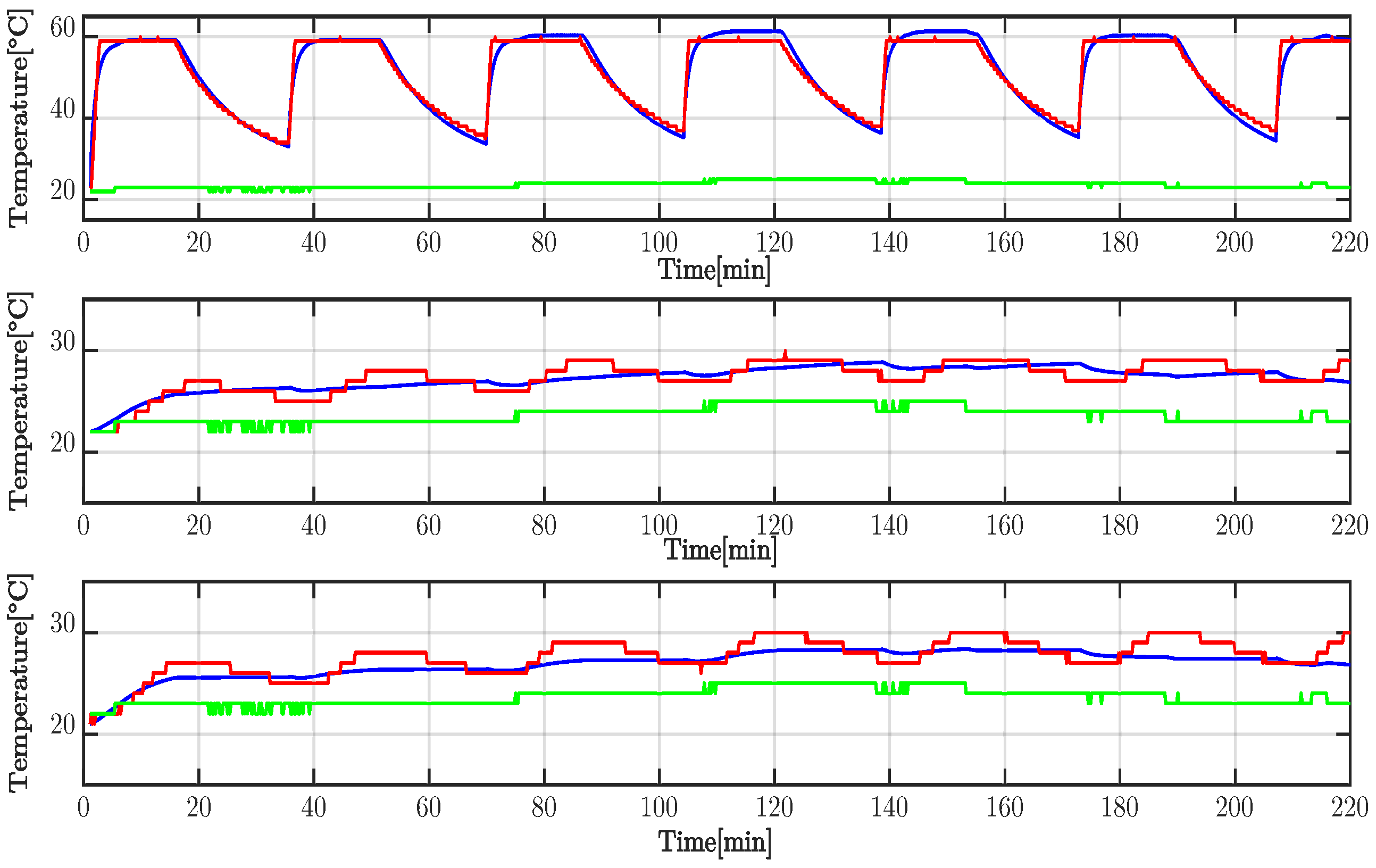
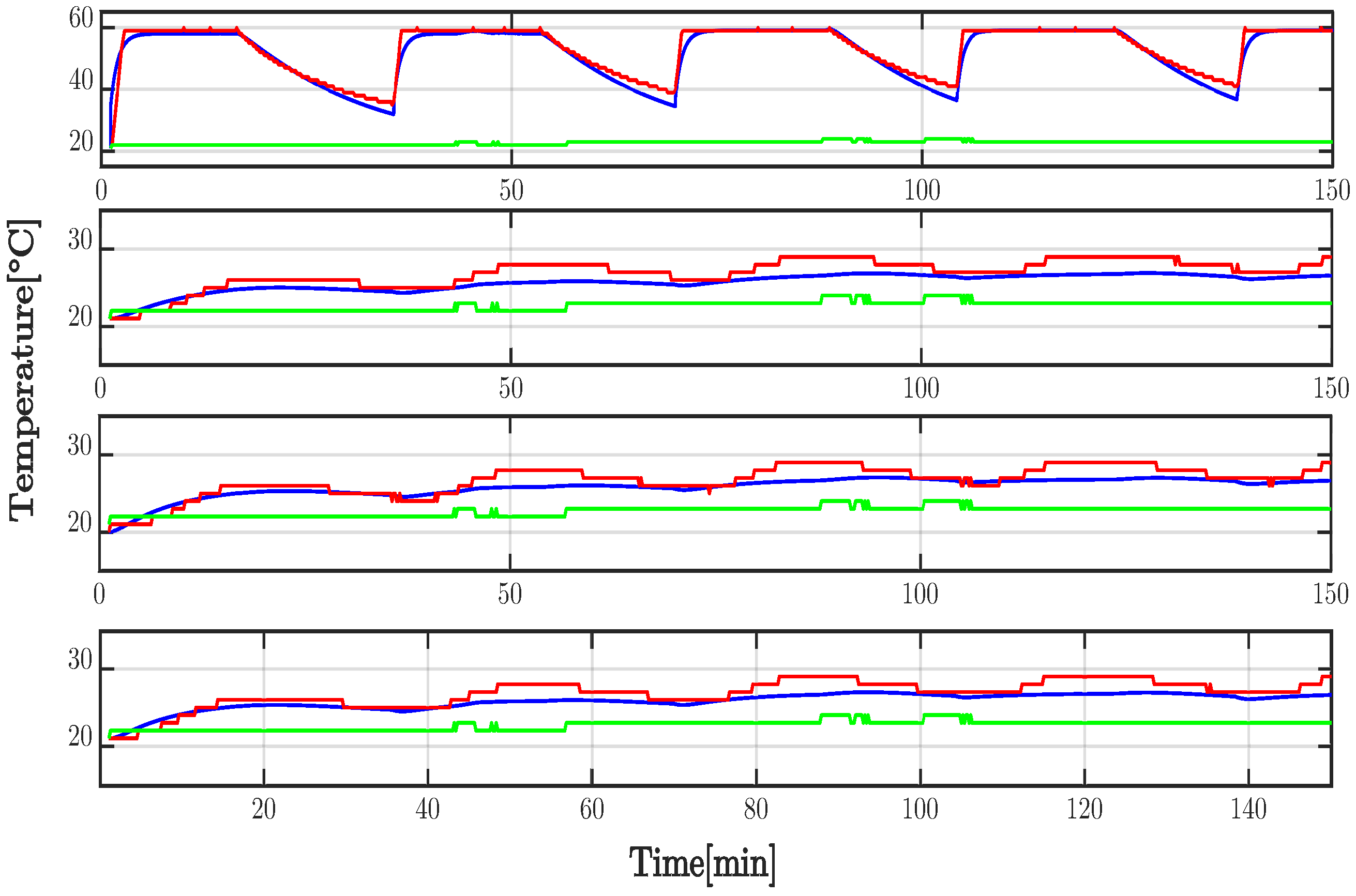
4. Experimental Development
Tuning Process
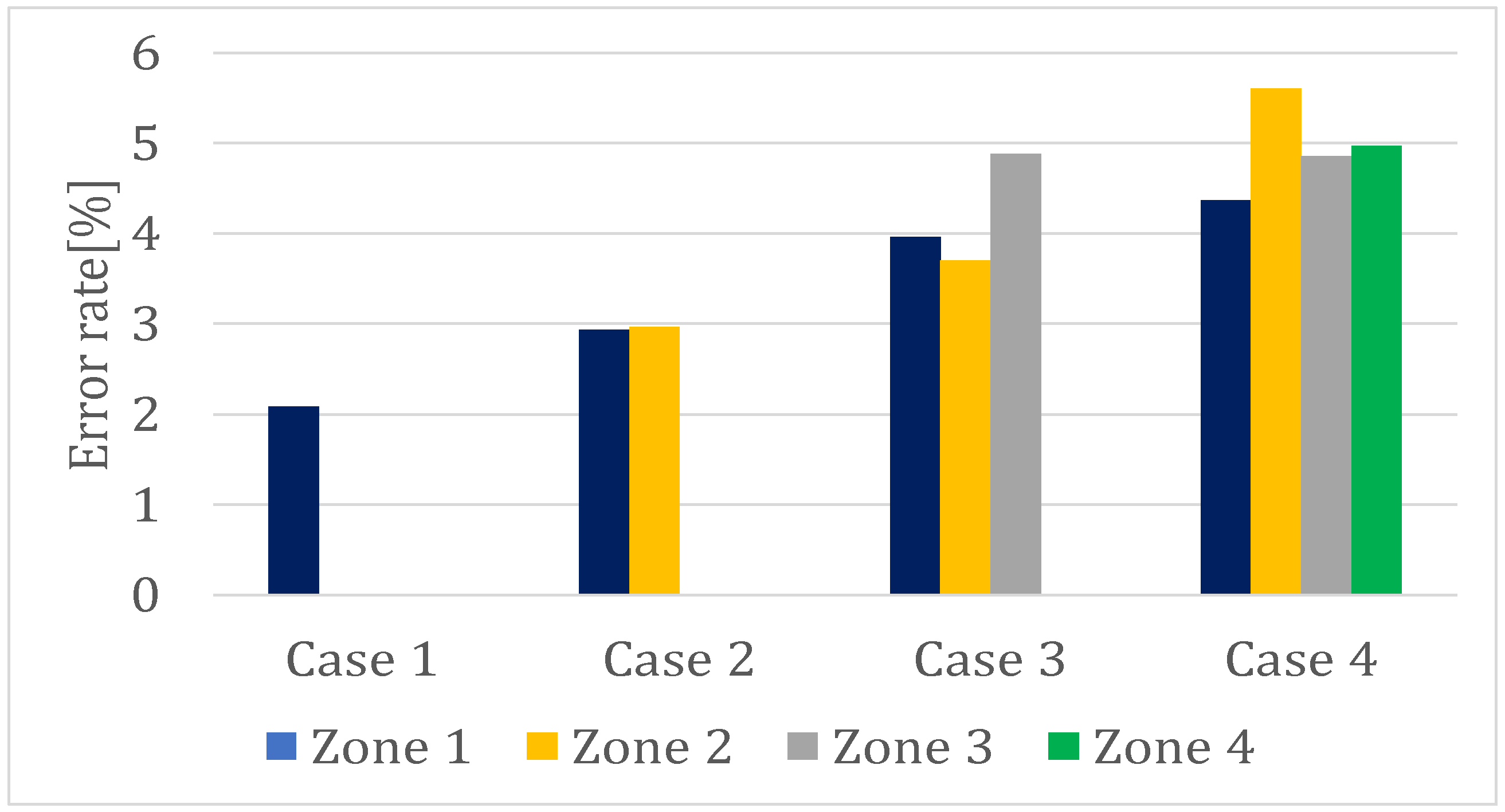
5. Discussion
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| HVAC | Heat, ventilation and air conditioning | |
| LPM | Lumped-parameter model | |
| RC | Resistor and capacitor circuit | |
| Nomenclature | ||
| A | Superficial area | |
| Specific heat | ||
| Air thermal capacity | ||
| Walls’ thermal capacity | ||
| e | Error rate | % |
| Objective function | ||
| Internal heat convection | ||
| External heat convection | ||
| Thermal conductivity | ||
| L | Thickness | m |
| m | Thermal zones number | |
| N | Number of equations | |
| R | Conduction thermal resistance | |
| Internal convection resistance | ||
| External convection resistance | ||
| Inner envelope walls | ||
| u | Contact matrix | |
| T | Internal temperature | °C |
| Walls’ temperature | °C | |
| Environmental temperature | °C | |
| Ground temperature | °C | |
| Heat transfer coefficient between zones | ||
| Heat transfer coefficient with environmental conditions | ||
| Heat transfer coefficient with ground | ||
| Density |
Appendix A


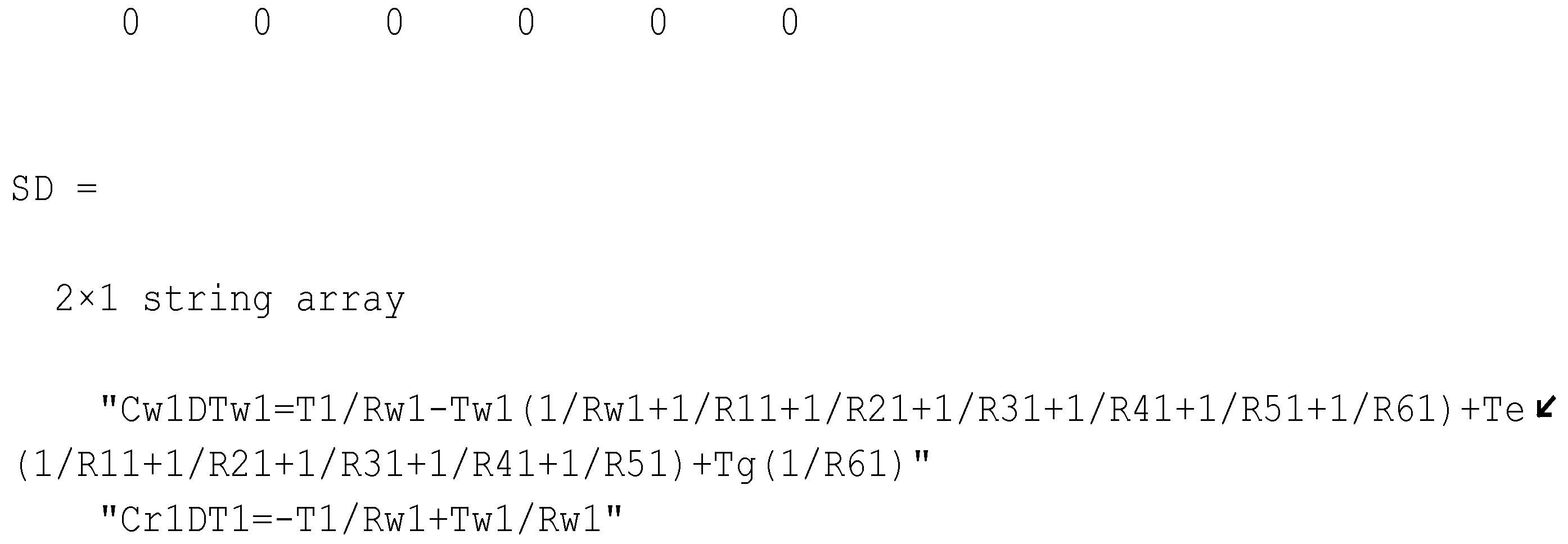


References
- Czerniawski, T.; Leite, F. Automated digital modeling of existing buildings: A review of visual object recognition methods. Autom. Constr. 2020, 113, 103131. [Google Scholar] [CrossRef]
- Deb, C.; Schlueter, A. Review of data-driven energy modelling techniques for building retrofit. Renew. Sustain. Energy Rev. 2021, 144, 110990. [Google Scholar] [CrossRef]
- Hou, D.; Hassan, I.G.; Wang, L. Review on building energy model calibration by Bayesian inference. Renew. Sustain. Energy Rev. 2021, 143, 110930. [Google Scholar] [CrossRef]
- Lu, D.B.; Warsinger, D.M. Energy savings of retrofitting residential buildings with variable air volume systems across different climates. J. Build. Eng. 2020, 30, 101223. [Google Scholar] [CrossRef]
- United Nations. The 2030 Agenda for Sustainable Development; United Nations: New York, NY, USA, 2016. [Google Scholar] [CrossRef]
- United Nations. The Paris Agreement; ONU: New York, NY, USA, 2016; pp. 78–79. [Google Scholar]
- Li, W.; Wang, S.; Koo, C. A real-time optimal control strategy for multi-zone VAV air-conditioning systems adopting a multi-agent based distributed optimization method. Appl. Energy 2021, 287, 116605. [Google Scholar] [CrossRef]
- Biyik, E.; Kahraman, A. A predictive control strategy for optimal management of peak load, thermal comfort, energy storage and renewables in multi-zone buildings. J. Build. Eng. 2019, 25, 100826. [Google Scholar] [CrossRef]
- Harputlugil, T.; de Wilde, P. The interaction between humans and buildings for energy efficiency: A critical review. Energy Res. Soc. Sci. 2021, 71, 101828. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, J. Study on the distributed model predictive control for multi-zone buildings in personalized heating. Energy Build. 2021, 231, 110627. [Google Scholar] [CrossRef]
- Cockroft, J.; Cowie, A.; Samuel, A.; Strachan, P. Potential energy savings achievable by zoned control of individual rooms in UK housing compared to standard central heating controls. Energy Build. 2017, 136, 1–11. [Google Scholar] [CrossRef]
- Florez Montes, F. Análisis Dinámico del Confort en Edificios: Estrategias de Control Adaptativo en Modos Deslizantes. Ph.D. Thesis, Universidad Nacional de Colombia and Univertsitat Politècnica de València, Valencia, Spain, 2020. [Google Scholar]
- Gunay, H.B.; Shi, Z.; Newsham, G.; Moromisato, R. Detection of zone sensor and actuator faults through inverse greybox modelling. Build. Environ. 2020, 171, 106659. [Google Scholar] [CrossRef]
- Alwisy, A.; BuHamdan, S.; Gül, M. Evidence-based ranking of green building design factors according to leading energy modelling tools. Sustain. Cities Soc. 2019, 47, 101491. [Google Scholar] [CrossRef]
- Gao, X.W.; Liu, H.Y.; Ruan, B. Discontinuous zone free element method with variable condensation and applications in thermal-stress analysis of functionally graded material structures with cracks. Comput. Struct. 2021, 243, 106411. [Google Scholar] [CrossRef]
- Tian, W.; Sevilla, T.A.; Zuo, W.; Sohn, M.D. Coupling fast fluid dynamics and multizone airflow models in Modelica Buildings library to simulate the dynamics of HVAC systems. Build. Environ. 2017, 122, 269–286. [Google Scholar] [CrossRef]
- Amin, U.; Hossain, M.J.; Fernandez, E. Optimal price based control of HVAC systems in multizone office buildings for demand response. J. Clean. Prod. 2020, 270, 122059. [Google Scholar] [CrossRef]
- Berger, J.; Guernouti, S.; Woloszyn, M.; Chinesta, F. Proper Generalised Decomposition for heat and moisture multizone modelling. Energy Build. 2015, 105, 334–351. [Google Scholar] [CrossRef]
- Ng, L.C.; Musser, A.; Persily, A.K.; Emmerich, S.J. Multizone airflow models for calculating infiltration rates in commercial reference buildings. Energy Build. 2013, 58, 11–18. [Google Scholar] [CrossRef]
- Garnier, A.; Eynard, J.; Caussanel, M.; Grieu, S. Predictive control of multizone HVAC systems in non-residential buildings. IFAC Proc. Vol. IFAC PapersOnline 2014, 19, 12080–12085. [Google Scholar] [CrossRef]
- Żabnieńska-Góra, A.; Khordehgah, N.; Jouhara, H. Annual performance analysis of the PV/T system for the heat demand of a low-energy single-family building. Renew. Energy 2021, 163, 1923–1931. [Google Scholar] [CrossRef]
- Gao, Y.; Li, S.; Fu, X.; Dong, W.; Lu, B.; Li, Z. Energy management and demand response with intelligent learning for multi-thermal-zone buildings. Energy 2020, 210, 118411. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, J.; Zhang, Y.; Yuan, H.; Zhang, R.; Srinivasan, R.S. Practical issues in implementing machine-learning models for building energy efficiency: Moving beyond obstacles. Renew. Sustain. Energy Rev. 2021, 143, 110929. [Google Scholar] [CrossRef]
- Killian, M.; Mayer, B.; Kozek, M. Effective fuzzy black-box modeling for building heating dynamics. Energy Build. 2015, 96, 175–186. [Google Scholar] [CrossRef]
- Li, Y.; O’Neill, Z.; Zhang, L.; Chen, J.; Im, P.; DeGraw, J. Grey-box modeling and application for building energy simulations—A critical review. Renew. Sustain. Energy Rev. 2021, 146, 111174. [Google Scholar] [CrossRef]
- Yu, X.; Georges, L.; Imsland, L. Data pre-processing and optimization techniques for stochastic and deterministic low-order grey-box models of residential buildings. Energy Build. 2021, 236, 110775. [Google Scholar] [CrossRef]
- Abokersh, M.H.; Spiekman, M.; Vijlbrief, O.; van Goch, T.A.; Vallès, M.; Boer, D. A real-time diagnostic tool for evaluating the thermal performance of nearly zero energy buildings. Appl. Energy 2021, 281, 116091. [Google Scholar] [CrossRef]
- Brastein, O.M.; Ghaderi, A.; Pfeiffer, C.F.; Skeie, N.O. Analysing uncertainty in parameter estimation and prediction for grey-box building thermal behaviour models. Energy Build. 2020, 224, 110236. [Google Scholar] [CrossRef]
- Vivian, J.; Zarrella, A.; Emmi, G.; De Carli, M. An evaluation of the suitability of lumped-capacitance models in calculating energy needs and thermal behaviour of buildings. Energy Build. 2017, 150, 447–465. [Google Scholar] [CrossRef]
- Underwood, C.P. An improved lumped parameter method for building thermal modelling. Energy Build. 2014, 79, 191–201. [Google Scholar] [CrossRef]
- Parker, S.T.; Williamson, S. Visual assessment of contaminant impacts in multizone buildings. Build. Environ. 2016, 102, 39–53. [Google Scholar] [CrossRef]
- Tagade, P.M.; Jeong, B.M.; Choi, H.L. A Gaussian process emulator approach for rapid contaminant characterization with an integrated multizone-CFD model. Build. Environ. 2013, 70, 232–244. [Google Scholar] [CrossRef]
- Nguyen, D.H.; Funabashi, T. Decentralized Control Design for User Comfort and Energy Saving in Multi-zone Buildings. Energy Procedia 2019, 156, 172–176. [Google Scholar] [CrossRef]
- Subramaniam, M.; Jain, T.; Yame, J.J. Bilinear model-based diagnosis of lock-in-place failures of variable-air-volume HVAC systems of multizone buildings. J. Build. Eng. 2020, 28, 101023. [Google Scholar] [CrossRef]
- Ghiaus, C.; Ahmad, N. Thermal circuits assembling and state-space extraction for modelling heat transfer in buildings. Energy 2020, 195, 117019. [Google Scholar] [CrossRef]
- Chegari, B.; Tabaa, M.; Simeu, E.; Moutaouakkil, F.; Medromi, H. Multi-objective optimization of building energy performance and indoor thermal comfort by combining artificial neural networks and metaheuristic algorithms. Energy Build. 2021, 239, 110839. [Google Scholar] [CrossRef]
- Andrade-Cabrera, C.; Burke, D.; Turner, W.J.; Finn, D.P. Ensemble Calibration of lumped parameter retrofit building models using Particle Swarm Optimization. Energy Build. 2017, 155, 513–532. [Google Scholar] [CrossRef]
- Rouchier, S.; Jiménez, M.J.; Castaño, S. Sequential Monte Carlo for on-line parameter estimation of a lumped building energy model. Energy Build. 2019, 187, 86–94. [Google Scholar] [CrossRef]
- Dimitriou, V.; Firth, S.K.; Hassan, T.M.; Kane, T. The applicability of Lumped Parameter modelling in houses using in-situ measurements. Energy Build. 2020, 223, 110068. [Google Scholar] [CrossRef]
- Lin, Y.; Middelkoop, T.; Barooah, P. Identification of control-oriented thermal models of rooms in multi-room buildings. In Proceedings of the 2012 IEEE 51st Annual Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2013; pp. 1–27. [Google Scholar]
- Florez, F.; de Cordoba, P.F.; Taborda, J.; Polo, M.; Castro-Palacio, J.C.; Pérez-Quiles, M.J. Sliding modes control for heat transfer in geodesic domes. Mathematics 2020, 8, 902. [Google Scholar] [CrossRef]
- Florez, F.; Córdoba, P.F.D.; Higón, J.L.; Olivar, G.; Taborda, J. Modeling, Simulation, and Temperature Control of a Thermal Zone with Sliding Modes Strategy. Mathematics 2019, 7, 503. [Google Scholar] [CrossRef]
- Cengel, Y. Heat and Mass Transfer; John Wiley and Sons: Hoboken, NJ, USA, 2015. [Google Scholar]






| Geometrical Parameters | ||||
|---|---|---|---|---|
| x | y | z | ||
| 0.111 m | 0.111 m | 0.2 m | 0.005 m | 0.008 m |
| Physical Parameters | ||||
| Ce | kt | |||
| Zone | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 |
| Case 1 | 86.9 | 0 | 0 | 0 | 12.36 | 0 | 0 | 0 |
| Case 2 | 34.88 | 0.0022 | 0 | 0 | 12.29 | 58.77 | 0 | 0 |
| Case 3 | 179.54 | 0.0047 | 0 | 0 | 2.75 | 199.9 | 179.99 | 0 |
| Case 4 | 37.44 | 0.0037 | 0.0047 | 0.0047 | 0.0001 | 60.95 | 61.70 | 103.14 |
| Zone | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 |
| Case 1 | 0.6576 | 0 | 0 | 0 | 0.0145 | 0 | 0 | 0 |
| Case 2 | 0.0025 | 0.001 | 0 | 0 | 3.39 | 21.45 | 0 | 0 |
| Case 3 | 0.0027 | 0.0018 | 0.00027 | 0 | 18.65 | 0.0008 | 0.8387 | 0 |
| Case 4 | 0.0027 | 0.0008 | 0.0008 | 0.0008 | 0.0008 | 4.08 | 1.89 | 4.67 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernández de Córdoba, P.; Montes, F.F.; Martínez, M.E.I.; Carmenate, J.G.; Selvas, R.; Taborda, J. Design of an Algorithm for Modeling Multiple Thermal Zones Using a Lumped-Parameter Model. Energies 2023, 16, 2247. https://doi.org/10.3390/en16052247
Fernández de Córdoba P, Montes FF, Martínez MEI, Carmenate JG, Selvas R, Taborda J. Design of an Algorithm for Modeling Multiple Thermal Zones Using a Lumped-Parameter Model. Energies. 2023; 16(5):2247. https://doi.org/10.3390/en16052247
Chicago/Turabian StyleFernández de Córdoba, Pedro, Frank Florez Montes, Miguel E. Iglesias Martínez, Jose Guerra Carmenate, Romeo Selvas, and John Taborda. 2023. "Design of an Algorithm for Modeling Multiple Thermal Zones Using a Lumped-Parameter Model" Energies 16, no. 5: 2247. https://doi.org/10.3390/en16052247
APA StyleFernández de Córdoba, P., Montes, F. F., Martínez, M. E. I., Carmenate, J. G., Selvas, R., & Taborda, J. (2023). Design of an Algorithm for Modeling Multiple Thermal Zones Using a Lumped-Parameter Model. Energies, 16(5), 2247. https://doi.org/10.3390/en16052247








