Modeling of Turbulent Convective Heat-Transfer Characteristics in a Concentric Annular Channel
Abstract
1. Introduction
2. Mathematical Formulation
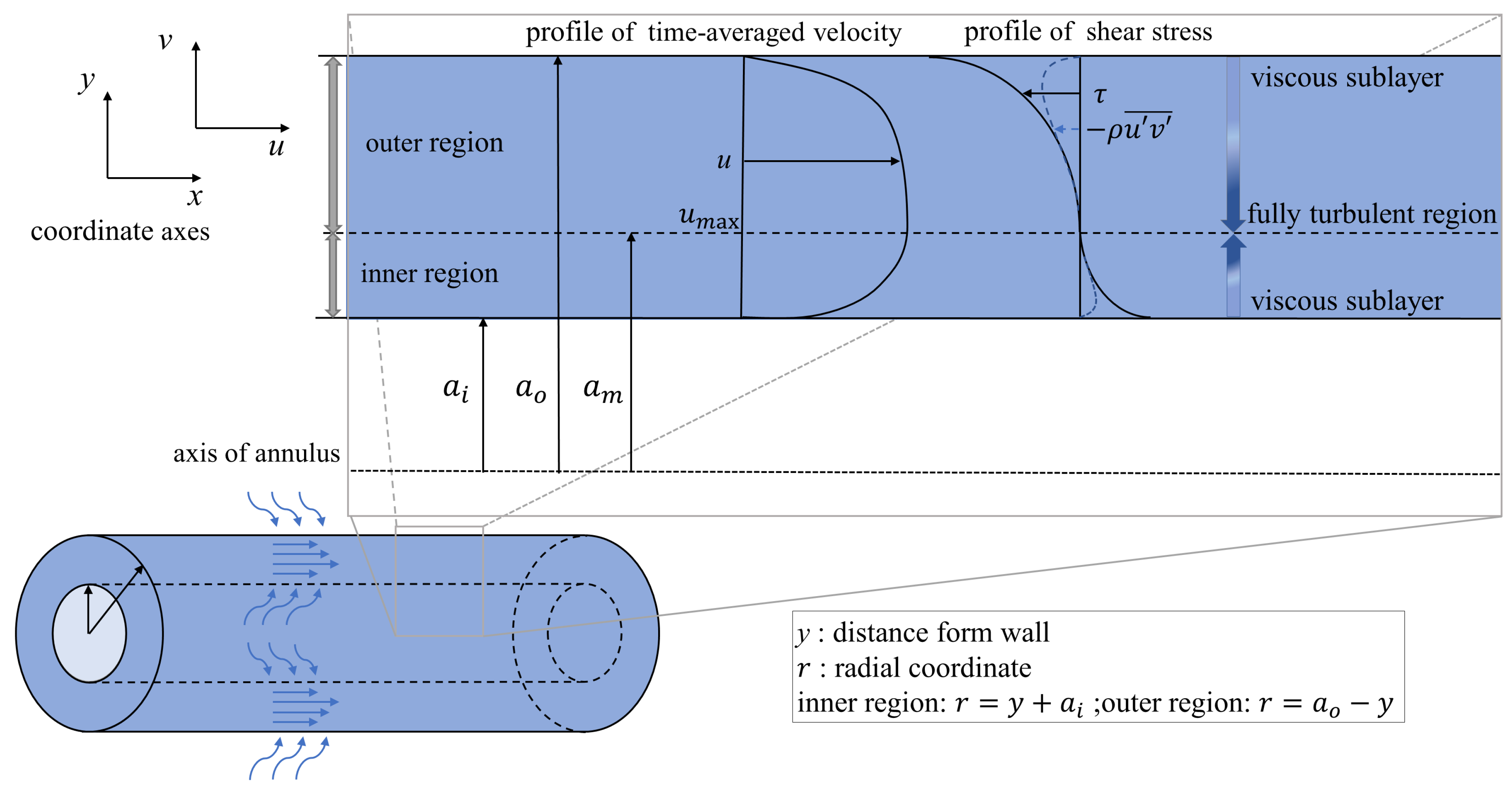
2.1. Review of the Momentum Transfer in the Annular Channel
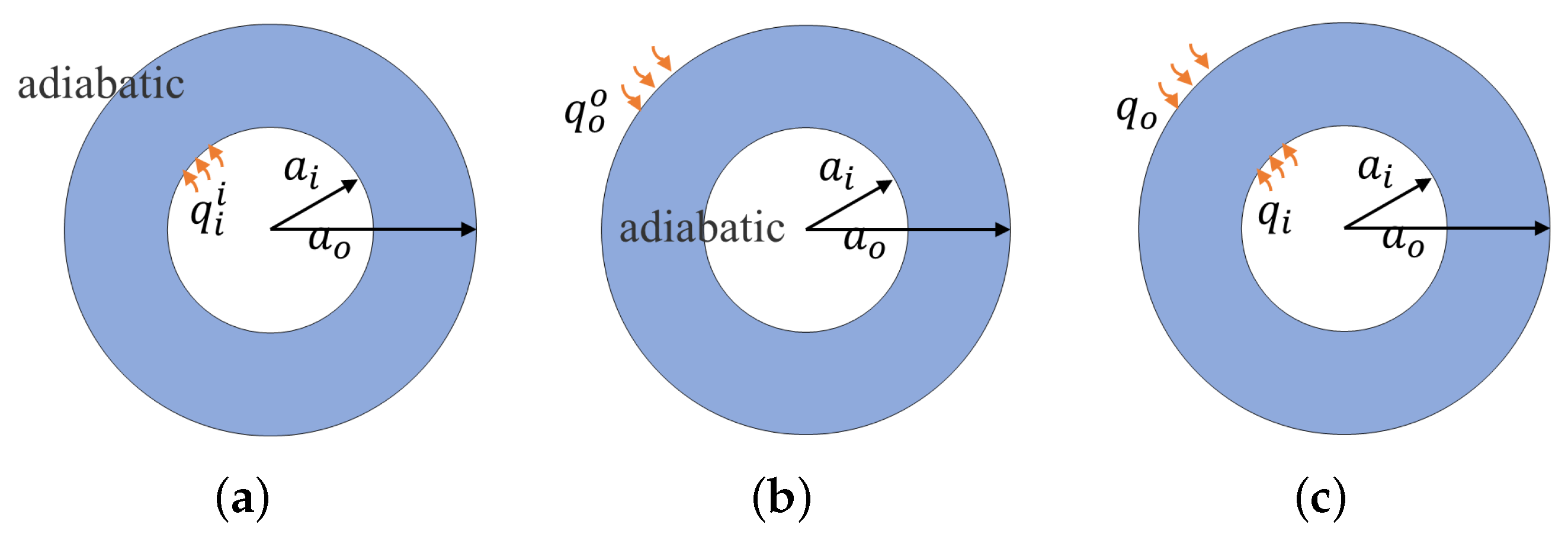
2.2. Analysis of the Heat Transfer in the Annular Channel with Heating over Both Walls
2.3. The Numerical Method
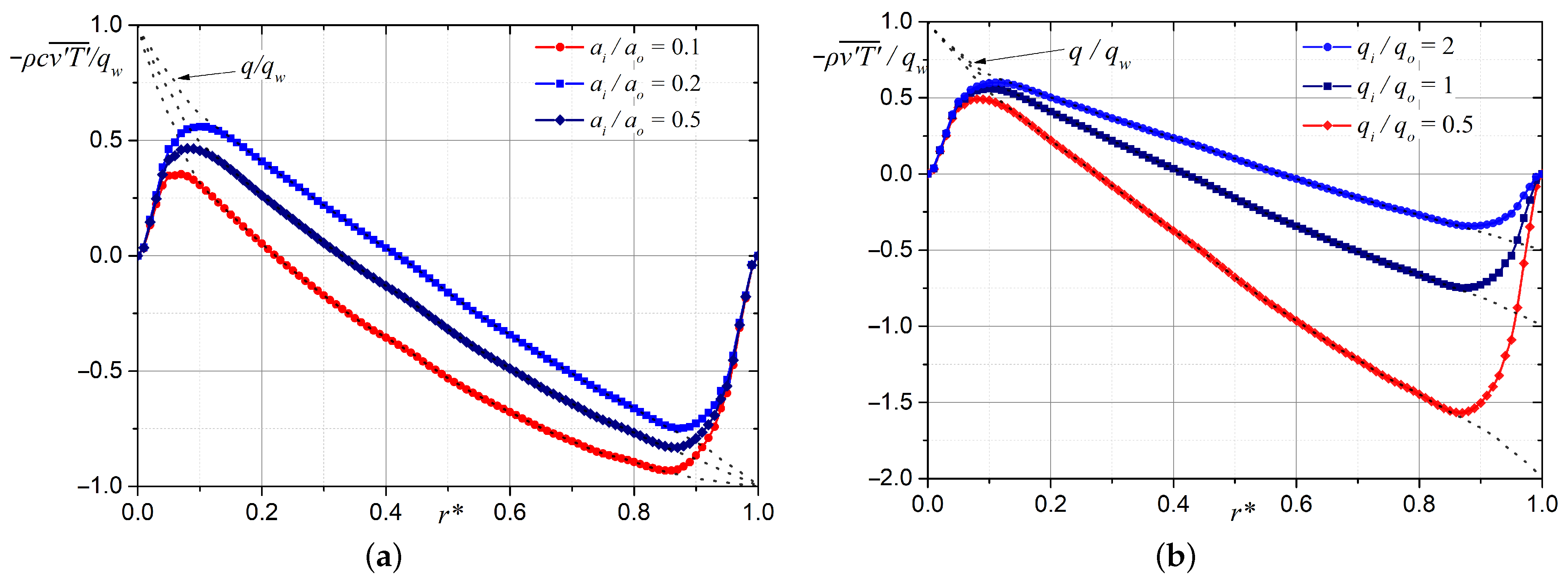
3. The Numerical Results and Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| a | radius of annulus (m) |
| radius of maximum in velocity (m) | |
| dimensionless radius | |
| c | specific heat capacity ( ) |
| h | heat transfer coefficient () |
| Nusselt number |
| k | molecular conductivity () |
| eddy conductivity () | |
| p | time-averaged pressure () |
| molecular Prandtl number | |
| turbulent Prandtl number | |
| q | radial heat flux density () |
| r | radial coordinate (m) |
| Reynolds number | |
| normalized radial coordinate | |
| Reynolds number | |
| T | time-averaged temperature (K) |
| dimensionless temperature | |
| mixed-mean temperature (K) | |
| u | time-averaged axial velocity () |
| mixed-mean axial velocity () | |
| dimensionless axial velocity | |
| x | axial coordinate (m) |
| y | distance from the wall (m) |
| dimensionless distance from the wall | |
| boundary layer thickness (m) | |
| molecular viscosity () | |
| eddy viscosity () | |
| molecular density () | |
| turbulent shear stress () | |
| turbulent heat flux density () | |
| shear stress () | |
| dimensionless turbulent stress | |
| Subscriptw | wall |
| Subscripti | pertains to the inner wall |
| Subscripto | pertains to the outer wall |
| Superscripti | heated over the inner wall only |
| Superscripto | heated over the outer wall only |
References
- Nejad, M.Z.; Ansarifar, G. Optimal design of a Small Modular Reactor core with dual cooled annular fuel based on the neutronics and natural circulation parameters. Nucl. Eng. Des. 2020, 360, 110518. [Google Scholar] [CrossRef]
- Bai, Y.; Zhao, Z.; Xu, G.; Bai, Y. Heat transfer characteristic analysis of a novel annular nuclear heat exchanger for propulsion system. Ann. Nucl. Energy 2019, 126, 84–94. [Google Scholar] [CrossRef]
- Akimoto, H.; Anoda, Y.; Takase, K.; Yoshida, H.; Tamai, H. Nuclear Thermal Hydraulics; Springer: Tokyo, Japan, 2016; pp. 3–14. [Google Scholar]
- Krischer, O. Heat transfer in annuli for laminar and turbulent flow. Chem. Eng. Technol. 1961, 33, 13–19. [Google Scholar]
- Quarmby, A. Some measurements of turbulent heat transfer in the thermal entrance region of concentric annuli. Int. J. Heat Mass Transf. 1967, 10, 267–276. [Google Scholar] [CrossRef]
- Gnielinski, V. Turbulent heat transfer in annular spaces—A new comprehensive correlation. Heat Transf. Eng. 2015, 36, 787–789. [Google Scholar] [CrossRef]
- Kays, W.; Leung, E. Heat transfer in annular passages—Hydrodynamically developed turbulent flow with arbitrarily prescribed heat flux. Int. J. Heat Mass Transf. 1963, 6, 537–557. [Google Scholar] [CrossRef]
- Wu, Y.W.; Su, G.H.; Qiu, S.Z.; Hu, B.X. Experimental study on critical heat flux in bilaterally heated narrow annuli. Int. J. Multiph. Flow 2009, 35, 977–986. [Google Scholar] [CrossRef]
- Mayer, G.; Nagy, R.; Nagy, I. An experimental study on critical heat flux in vertical annulus under low flow and low pressure conditions. Nucl. Eng. Des. 2016, 310, 461–469. [Google Scholar] [CrossRef]
- Afikuzzaman, M.; Ferdows, M.; Alam, M.M. Unsteady MHD casson fluid flow through a parallel plate with hall current. Procedia Eng. 2015, 105, 287–293. [Google Scholar] [CrossRef]
- Biswas, R.; Hossain, M.; Islam, R.; Ahmmed, S.F.; Mishra, S.R.; Afikuzzaman, M. Computational treatment of MHD Maxwell nanofluid flow across a stretching sheet considering higher-order chemical reaction and thermal radiation. J. Comput. Math. Data Sci. 2022, 4, 1000048. [Google Scholar] [CrossRef]
- Alrehili, M.F.; Goud, B.S.; Reddy, Y.D.; Mishra, S.R.; Lashin, M.M.; Govindan, V.; Pimpunchat, B. Numerical computing of Soret and linear radiative effects on MHD Casson fluid flow toward a vertical surface through a porous medium: Finite element analysis. Mod. Phys. Lett. B 2023, 2250170. [Google Scholar] [CrossRef]
- Chung, S.Y.; Sung, H.J. Direct numerical simulation of turbulent concentric annular pipe flow: Part 2: Heat transfer. Int. J. Heat Fluid Flow 2003, 24, 399–411. [Google Scholar] [CrossRef]
- Ould-Rouiss, M.; Redjem-Saad, L.; Lauriat, G. Direct numerical simulation of turbulent heat transfer in annuli: Effect of heat flux ratio. Int. J. Heat Fluid Flow 2009, 30, 579–589. [Google Scholar] [CrossRef]
- Ould-Rouiss, M.; Redjem-Saad, L.; Lauriat, G.; Mazouz, A. Effect of Prandtl number on the turbulent thermal field in annular pipe flow. Int. Commun. Heat Mass Transf. 2010, 37, 958–963. [Google Scholar] [CrossRef]
- Bagheri, E.; Wang, B.C.; Yang, Z. Influence of domain size on direct numerical simulation of turbulent flow in a moderately curved concentric annular pipe. Phys. Fluids 2020, 32, 065105. [Google Scholar] [CrossRef]
- Bagheri, E.; Wang, B.C. Effects of radius ratio on turbulent concentric annular pipe flow and structures. Int. J. Heat Fluid Flow 2020, 86, 108725. [Google Scholar] [CrossRef]
- Bagheri, E.; Wang, B.C. Direct numerical simulation of turbulent heat transfer in concentric annular pipe flows. Phs. Fluids 2021, 33, 055131. [Google Scholar] [CrossRef]
- Churchill, S.W.; Chan, C. Turbulent flow in channels in terms of turbulent shear and normal stresses. AIChE J. 1995, 41, 2513–2521. [Google Scholar] [CrossRef]
- Yu, B.; Kawaguchi, Y.; Kaneda, M.; Ozoe, H.; Churchill, S.W. The computed characteristics of turbulent flow and convection in concentric circular annuli. Part II. Uniform heating on the inner surface. Int. J. Heat Mass Transf. 2005, 48, 621–634. [Google Scholar] [CrossRef]
- Yu, B.; Kawaguchi, Y.; Ozoe, H.; Churchill, S.W. The computed characteristics of turbulent flow and convection in concentric circular annuli. Part III. Alternative thermal boundary conditions. Int. J. Heat Mass Transf. 2005, 48, 635–646. [Google Scholar] [CrossRef]
- Yu, B.; Kawaguchi, Y.; Ozoe, H.; Churchill, S.W. The computed characteristics of turbulent flow and convection in concentric circular annuli. Part IV: Generalizations. Int. J. Heat Mass Transf. 2005, 48, 3057–3072. [Google Scholar] [CrossRef]
- Ghiaasiaan, S.M. Convective Heat and Mass Transfer; Cambridge University Press: Cambridge, UK, 2011; pp. 258–274. [Google Scholar]
- Chung, S.Y.; Rhee, G.H.; Sung, H.J. Direct numerical simulation of turbulent concentric annular pipe flow: Part 1: Flow field. Int. J. Heat Fluid Flow 2002, 23, 426–440. [Google Scholar] [CrossRef]
- Nouri, J.; Umur, H.; Whitelaw, J. Flow of Newtonian and non-Newtonian fluids in concentric and eccentric annuli. J. Fluid Mech. 1993, 253, 617–641. [Google Scholar] [CrossRef]
- Kaneda, M.; Yu, B.; Ozoe, H.; Churchill, S.W. The characteristics of turbulent flow and convection in concentric circular annuli. Part I: Flow. Int. J. Heat Mass Transf. 2003, 46, 5045–5057. [Google Scholar] [CrossRef]
- Boersma, B.J.; Breugem, W.-P. Numerical simulation of turbulent flow in concentric annuli. Flow Turbul. Combust. 2011, 86, 113–127. [Google Scholar] [CrossRef]
- Marlon, M.H.-C.; Victor, E.C.B.; Oscar, M.H.R. Analysis of Turbulence Characteristics in Two Large Concentric Annular Ducts Through Particle Image Velocimetry. J. Fluids Eng. 2019, 141, 061102. [Google Scholar]
- Rehme, K. Turbulent flow in smooth concentric annuli with small radius ratios. J. Fluid Mech. 1974, 64, 263–288. [Google Scholar] [CrossRef]
- Luchini, P. Universality of the turbulent velocity profile. Phys. Rev. Lett. 2017, 118, 224501. [Google Scholar] [CrossRef]
- Churchill, S.; Usagi, R. A general expression for the correlation of rates of transfer and other phenomena. AIChE J. 1972, 18, 1121–1128. [Google Scholar] [CrossRef]
- Yakhot, V.; Orszag, S.A.; Yakhot, A. Heat transfer in turbulent fluids—I. Pipe flow. Int. J. Heat Mass Transf. 1987, 30, 15–22. [Google Scholar] [CrossRef]
- Kays, W.M. Turbulent Prandtl number. Where are we? ASME Trans. J. Heat Transf. 1994, 116, 284–295. [Google Scholar] [CrossRef]
- Straub, S.; Forooghi, P.; Marocco, L.; Wetzel, T.; Frohnapfel, B. Azimuthally inhomogeneous thermal boundary conditions in turbulent forced convection pipe flow for low to medium Prandtl numbers. Int. J. Heat Fluid Flow 2019, 77, 352–358. [Google Scholar] [CrossRef]
- Lei, X.; Guo, Z.; Wang, Y.; Li, H. Assessment and improvement on the applicability of turbulent-Prandtl-number models in RANS for liquid metals. Int. J. Therm. Sci. 2022, 171, 107260. [Google Scholar] [CrossRef]
- Jischa, M.; Rieke, H.B. About the prediction of turbulent Prandtl and Schmidt numbers from modeled transport equations. Int. J. Heat Mass Transf. 1979, 22, 1547–1555. [Google Scholar] [CrossRef]
- Bobkov, V.P.; Fokin, L.R.; Petrov, E.E.; Popov, V.V.; Rumiantsev, V.N.; Savvatimsky, A.I. Thermophysical Properties of Materials for Nuclear Engineering: A Tutorial and Collection of Data; International Atomic Energy Agency: Vienna, Austria, 2008; p. 56. [Google Scholar]
- Lundberg, R.E.; Kays, W.M.; Reynolds, W.C. Heat Transfer with Laminar Flow in Concentric Annuli with Constant and Variable Wall Temperature and Heat Flux; Standard University: Stanford, CA, USA, 1963. [Google Scholar]
- Churchill, S.W. New simplified models and formulations for turbulent flow and convection. AIChE J. 1997, 43, 1125–1140. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Zhang, H.; Li, L.; Wang, G. Modeling of Turbulent Convective Heat-Transfer Characteristics in a Concentric Annular Channel. Energies 2023, 16, 1998. https://doi.org/10.3390/en16041998
Chen L, Zhang H, Li L, Wang G. Modeling of Turbulent Convective Heat-Transfer Characteristics in a Concentric Annular Channel. Energies. 2023; 16(4):1998. https://doi.org/10.3390/en16041998
Chicago/Turabian StyleChen, Longfei, Huaibao Zhang, Liugang Li, and Guangxue Wang. 2023. "Modeling of Turbulent Convective Heat-Transfer Characteristics in a Concentric Annular Channel" Energies 16, no. 4: 1998. https://doi.org/10.3390/en16041998
APA StyleChen, L., Zhang, H., Li, L., & Wang, G. (2023). Modeling of Turbulent Convective Heat-Transfer Characteristics in a Concentric Annular Channel. Energies, 16(4), 1998. https://doi.org/10.3390/en16041998




