3.1. Non-Spatial GAM: Generalized Additive Model Regression Using Cubic Splines as a One-Dimensional Smoother for Modelling Time
Additive models were introduced by Ref. [
16] to deal with the dimensionality problem of the General Linear Models GLMs through univariate smoothing [
17]. The GAMs Stone approach can be seen as a traditional way of portraying GAMs, which in this case has the demand as the response variable d, and space or time as predictors
, which can be written as
or its summarised version
where
and
are the smooth functions over the covariates
.
The Stone approach fails to include interaction and therefore has unsatisfactory results when interaction exists [
18]. It is here that the approach from Ref. [
11] becomes important, as it not only includes interactions
but also includes the link function g over the response variable
d to analyse
within a solution space of any member of the exponential family, usually Gaussian-Normal, but it is open to Gamma, Poisson, or Binomial [
17]. Then, a Generalized Additive model over the demand according to the Hastie and Tibshirani approach can be written as
where
are the smooth functions over the covariates
allowing for both single basis smoothing
and interactions
and
. In this approach,
is a regression for the variables that will not be modelled additively. Hastie and Tibshirani defineed the procedure for estimating
and
as a local scoring procedure for generalized additive models.
In the early 2000s, Ref. [
19] provided a more recent perspective to the GAM definition developed by Ref. [
11], denoted in Equation (
13). The author directly defined the iterative procedure with a model structure that has index
i, in which
is represented as the product of the model matrix
A and a vector of the associated model parameters
, where the intercept is assumed to be included.
A is a design matrix for the covariates
x with linear effects. The author also included a linear operator
to multiply the smooth function
.
where
is distributed according to an exponential family EF that has median
and variance
,
.
The cubic regression spline smoother is represented through the function
where
is a base function of the spline and
is the vector containing all the basis coefficients such as
Finally, a vector of coefficients
that contains the linear fixed effects vector
followed by all the basis coefficients
for
such as
is defined. Then the estimation of the vector of coefficients
from the GAM model will be done by penalized maximum likelihood, where the optimal is given by some smoothing parameters
[
19]
where
is a penalty matrix and the deviance of the model
.
Note that not only the optimal vector of coefficients
must be estimated but also the parameters themselves
. The smoothing parameters estimation
is done either by prediction error criteria (GCV) or maximum likelihood (ML or REML) [
20].
The method that we will be used in this article for selecting the smoothing parameters
is the Restricted Maximum Likelihood, REML. This will be done instead of other smoothness selection methods such as ML, Maximum Likelihood, and GCV, Generalized Cross-validation. In REML unlike ML, the estimation of variance components is better, as it has a higher probability of providing a complete rank of estimates of the variance components [
21]. On the other hand, REML is preferred over GCV due to it having a higher penalty for overfitting and being less likely to have multiple minimum points, therefore being less likely to have highly variable smoothing parameters
[
22].
In the literature, demand electricity is usually modelled by three patterns: daily, weekly, and monthly. Ref. [
4] modelled the previously mentioned patterns through a GAM by preselecting the knots according to the number of unique values of the variables included in the model. In that case, when modelling the patterns, only continuous variables were included with 24 knots for the daily pattern, 7 knots for the weekly pattern, and 12 knots for the monthly pattern. In this case, the daily pattern was included in the model through an hour variable, the weekly pattern through a categorical variable that differentiates days between weekend and weekdays, and instead of including a monthly pattern a trend pattern was included. In the model, the interactions between categorical and numerical variables were included. Knots were not set up based on unique values but on sensible values according to the underlying data.
Initially, the daily pattern was included in the model using a cyclic spline smooth over the discrete variable hour with a range from 0 to 23, . After this, the weekly pattern was included in the model as a categorical variable, wk, where weekly days were classified as 1-Monday and 7-Sunday, and were aggregated into two factors, . The corresponding interaction between the discrete numerical variable that accounts for the daily pattern, hr, and the categorical variable, wk, that accounts for the weekly pattern was also included using a factor smooth-interaction with the argument inside the smooth function, s, in the following way . Finally, trend pattern was fitted not by using the month’s numeric notation from 1 to 12 or the days of the year from 1 to 365, but through a trend variable that goes from 1 to 43,800, that accounts for the total number of data points available days per years per hour between 2013 and 2018 through a cubic spline smooth . The interaction between the daily pattern and the trend pattern was fitted using pairwise bivariate tensors product interactions .
This model can be expressed as
where
accounts for the linear effects and the f function accounts for the non-linear effects defined by each smoothed covariate. The super indexes
correspond respectively to the Seasonal, Trend, and Interaction components. In the model
with the response variable demand being distributed as
.
As can be seen in
Table 1, the resultant temporal model accounts for eighty-five percent of the electricity demand variation.
The Wald
t-test in
Table 2 and
Table 3 for the non-spatial GAM model shows that all smooth terms and parametric terms are highly significant.
The knots were preselected, but not based on unique values, as in Ref. [
4], but on sensible values that reduce the heteroscedasticity of the data as much as possible while maintaining them at logical levels below 24 knots. Splines over 10 knots are rare and can lead to model overfitting, so in this case the upper limit was set to 24 because of the number of unique values of the variable hours. Previous literature also points out that selecting unique values for time related variables makes a better fit.
Heteroscedasticity which indicates if the basis dimension
k is too low, was checked through the
k-index in
Table 4. The model was divided between the residual variance to get a
p-value.
The hours variable and its respective interactions showed no evidence of heteroscedasticity with a
p-value over zero. On the other hand, the number of data points was clearly heteroscedastic with a
p-value around zero. For reducing heteroscedasticity in the model, it was attempted to increase the number of knots for the data points variable up to 50, but this had little to no effect in the
k-index or
p-value. Fifty knots were chosen as an upper limit to test the heteroscedasticity values due to it accounts of two years of data. Going above this value was not explored because the size of the data does not call for a high number of knots, considering that there were only five years available. The residual vs. fitted plot (See
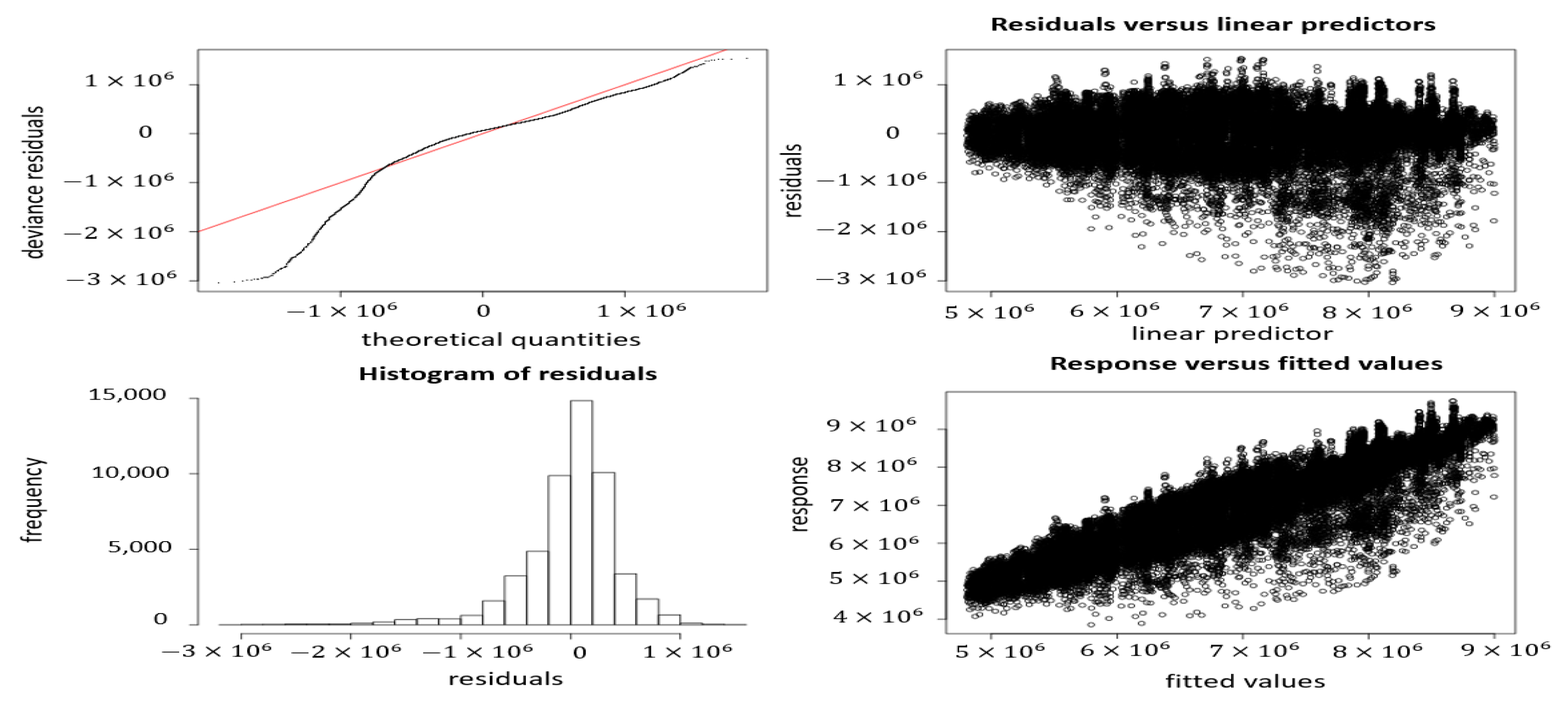
Figure 4—second plot from left to right) also shows proofs of heteroscedasticity or non-constant spread in the data.
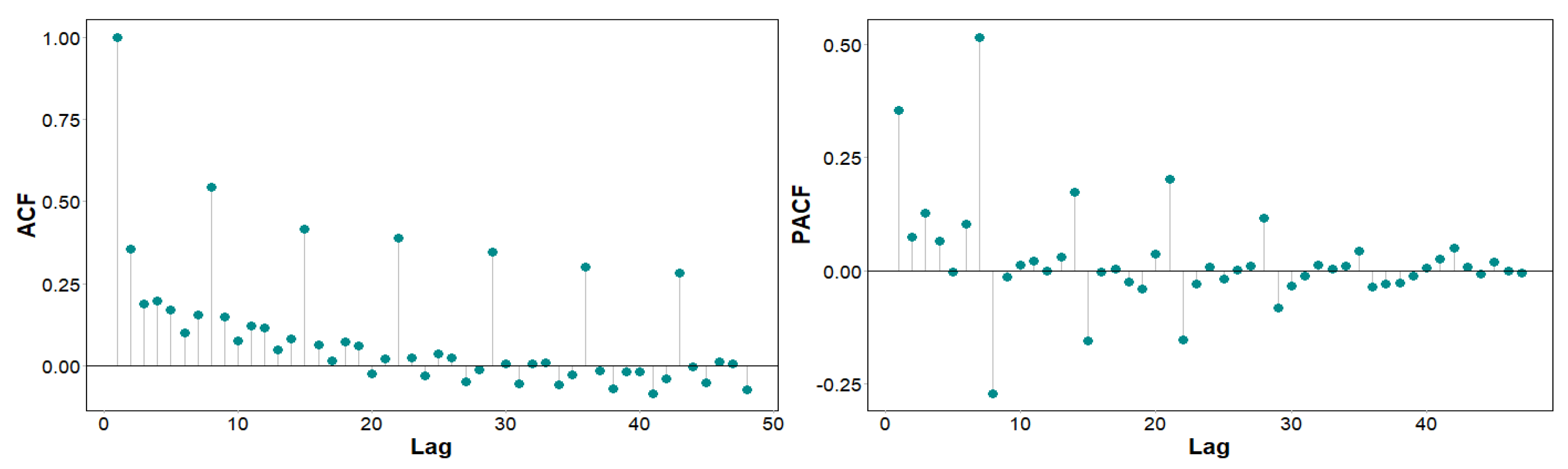
The model demonstrated convergence after ten iterations supporting the data being enough for the number of parameters. However, by looking at the Autocorrelation Function (ACF) and Partial Autocorrelation Function (PACF) it can be seen there is remaining autocorrelation that the model is not capturing (See
Figure 5).
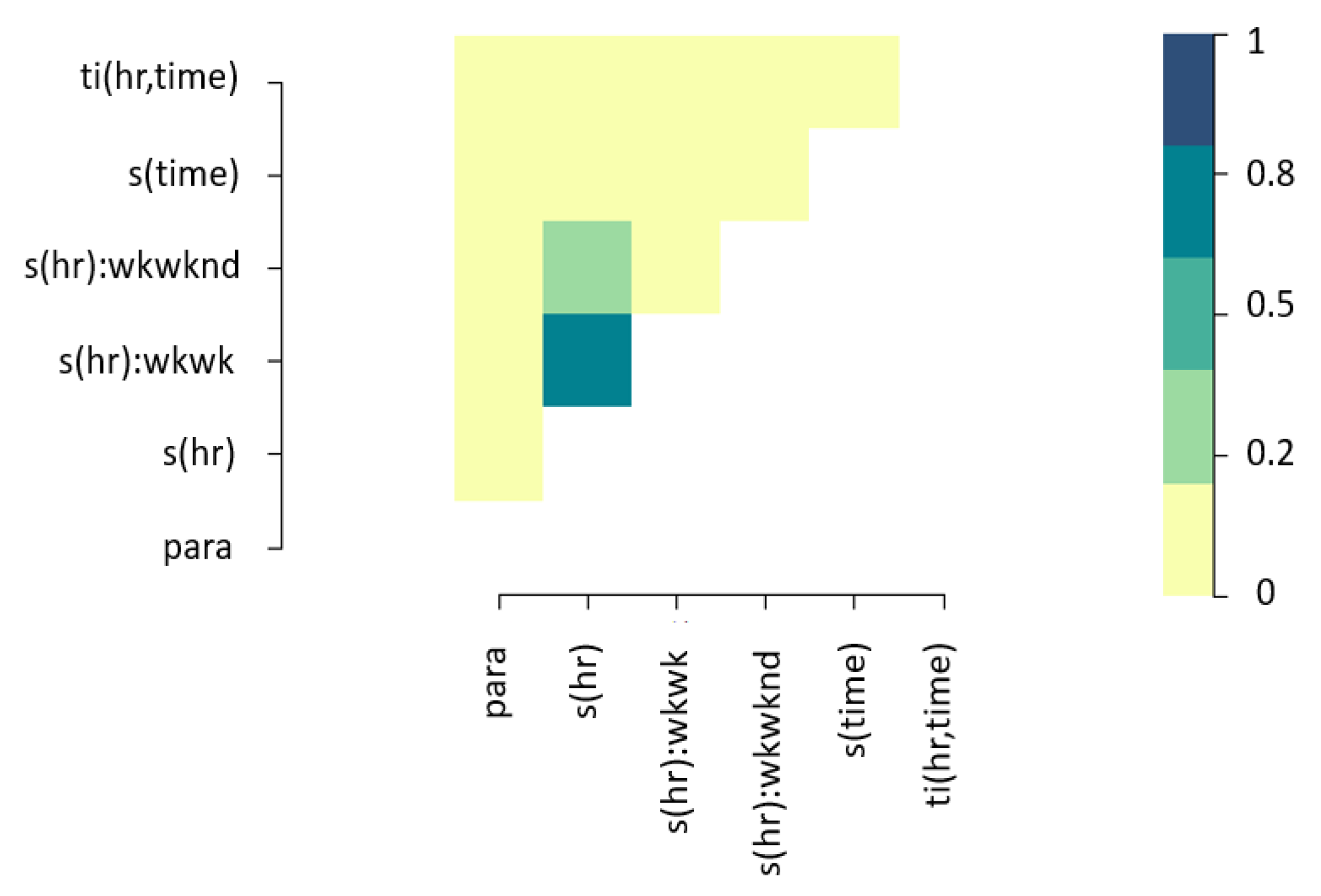
As is the case for GAMs, the correlation among covariates was tested through concurvity instead of collinearity due to the non-linear nature of the model. As expected, there is acceptable concurvity between individual effects and interactions (See
Figure 6). There is no reason to believe that smooth terms of the model approximate to other terms.
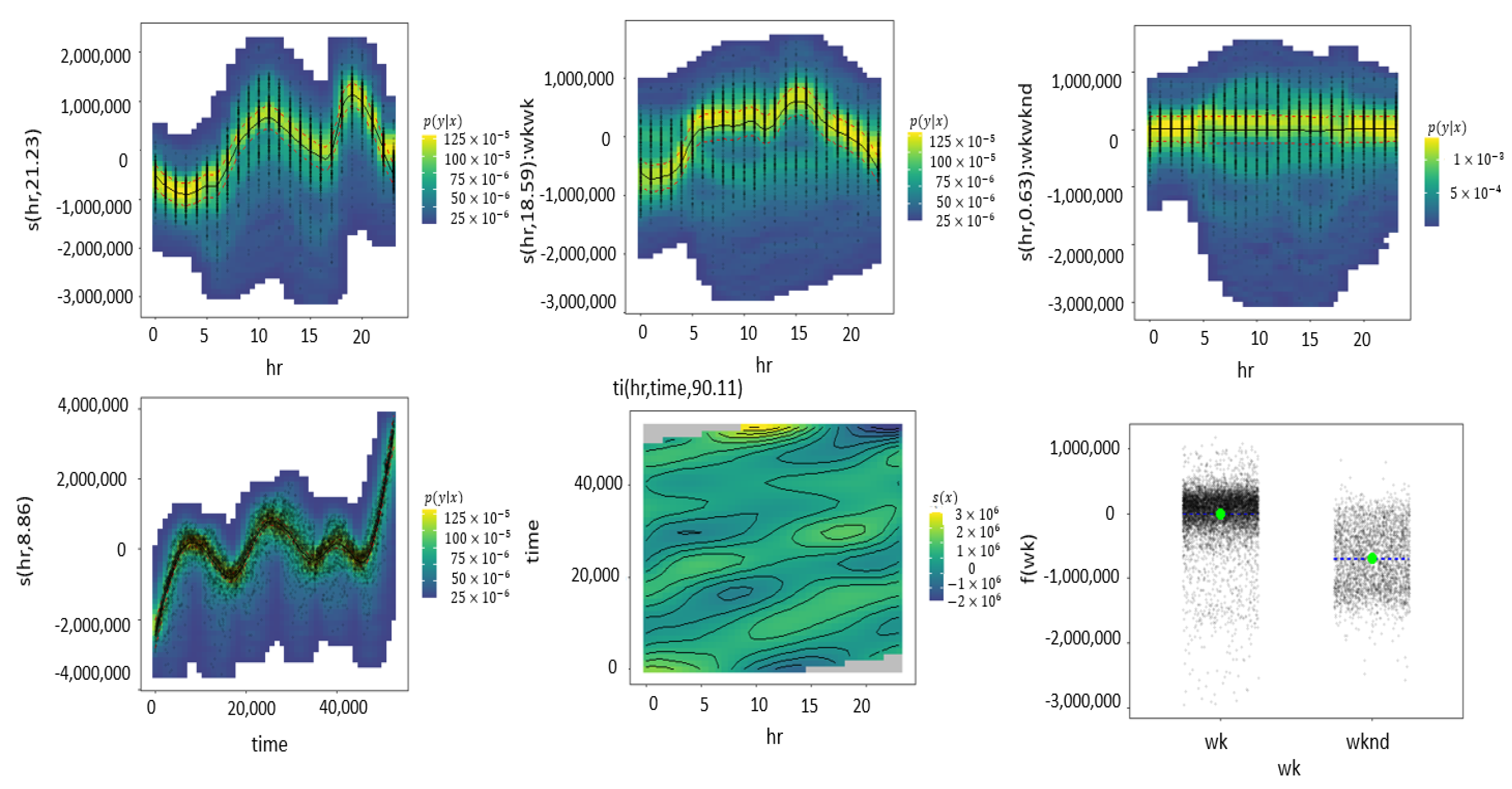
Figure 7 exhibits flat line in the density graph (first line, third figure) for the interaction of hours and weekend indicating there is no much of an effect in the interaction of such variables.On the contrary, the interaction between hours and weekdays shows a clear spline pattern in the density graph (first line, second figure). Both the individual effects of hours and data points portrayed in the first figures of the first line and second line show splines with a higher degree of curvature than the interactions.
3.2. Spatial GAM: Generalized Additive Model Regression Using Markov Random Fields as a Two-Dimensional Smoother for Modelling Space
Often, space modelling is associated with Geographically Weighted Regression, GWR [
23], which according to Ref. [
24] is based on the Varying Coefficient Model, VCM proposed by Ref. [
25]. Although there are many other types of modelling such as the Geoadditive model [
26], this one is specifically based on GLMs. In this article, the space modelling is going to be based on GAMs, as proposed by Refs. [
24,
27] and later incorporated by Ref. [
8].
The spatial modelling will be performed through GAM using GMRF over areal data, which is often considered a separate spatial modelling technique [
28] but in this case it was incorporated to the Generalized Additive Model as a two dimensional smoother so it can account for the model covariance as a function of the location, as proposed by Refs. [
8,
27].
Areal data is important for its various applications not only in the energy demand fields where observations could be allocated to a region according to the electricity operator but also to census and survey data where observations are aggregated to administrative districts.
Spatial GAM has the same structure as a non-spatial GAM with the addition of a term that accounts for the spatial effect represented through the smooth function
[
27] such as
where
.
In Equation (
21),
accounts for the linear effects of covariates
x while
accounts for the non-linear deterministic effects defined by the smoothers and
accounts for the spatially correlated effect that in the equation is calculated by the GMRF.
Here the dependence of all the terms from the spatial locations is suppressed for simplicity, but it is assumed when including the Gaussian stochastic process assumptions through , therefore no subindex s related to the locations is included.
Equation (
21) can also be represented in terms of the vector of spatial effects
v [
27] through an incidence matrix
, which ensures that each observation is assigned the spatial effect of the corresponding
s region it belongs to by assigning ones or zeros according to whether that observation
i has been collected in that region
s or not
which translates to
After establishing the Generalized Additive Model, GAM, this article will proceed to explain the assumptions under the spatially varying effects vector, v.
To understand how the spatially varying effects vector
v operates and its underlying assumptions, it is necessary to briefly recapitulate the fact that the spatial effect vector forms part of a spatial function
expressed as
for the specific case of discrete spatial areal data.
v distribution follows a Gaussian Markov Random Field, GMR,F prior distribution conditional on the variance parameter
[
24]. In numeral 2.3, it was mentioned how Gaussian Markov Random Fields, GMRFs, follow a multivariate normal distribution such as
. In this case the multivariate normal model does not fully specify the join distribution of
because the variance
is known and denoted as
, but
is a completely unknown reason, which is why we say that the prior is an improper prior, making the Gaussian Random Field be an Intrinsic Gaussian Random Field, IGMRF [
29]. The use of improper prior distributions is widely done and preferred in Bayesian statistical analysis when the information about parameters is weak or missing [
30]. According to Ref. [
15], Intrinsic Gaussian Random Fields, IGMRFs, can be defined in both regular or irregular lattice. A lattice is a structure or pattern for arranging an area of land into spatial units called sub-areas, cells, or units [
31]. As stated in Ref. [
31] these sub-areas share boundary edges between a single or more sub-areas and cannot intersect with each other. As regards the regularity or irregularity nature of the lattice, it all depends on the application over which spatial data is going to be analysed. Radar data, for example, is usually based on regular grids because the sub-areas formed have the same shape and size. However, when the spatial data are administrative regions, as in this case, then the nature of the lattice is irregular because they are defined following the natural shape of the territory, often setting boundaries according to natural features such as rivers or mountains. This applies only for first level divisions of a country such as states or departments. The ones that follow census units are not related with the territory but are more defined for data collection purposes. Due to the idea being to estimate
from the spatially varying effect vector
v, then the deviation between spatial parameters
v of adjacent regions such as
will proceed to be measured, which carefully corresponds to the form of a random walk of first order such as
with
, where
s exists in a set of regions
ordered in a neighbourhood structure called
where
[
27], which is what Ref. [
15] define as a First-order intrinsic GRMF on irregular lattices and for which they use the German regions as an example. So, basically, a first-order intrinsic GRMF on irregular lattices as defined in Ref. [
15] and later used an incorporated as a spatial smoother for modelling Generalized Additive Models by Refs. [
8,
27] is an independent Gaussian relationship between neighbouring regions
i and
j such as
, also called an independent Gaussian increment or deviance between adjacent regions, which yields to the multivariate Gaussian Intrinsic GMRF prior, as denoted by Ref. [
27].
This relation or deviance between the adjacent region shown in Equation (
24) as
and [
15,
32] can also be represented as
, where
symbolizes the set of all unordered pairs of neighbours. The pairs are defined as unordered to prevent double-counting due to the fact that if s is a neighbour from r, the order in which they get expressed
does not matter, as seen before in numeral 2.3.
The quadratic form
, which represents the difference between the
X vector and the
vector in the multivariate Gaussian prior of the GAM. can also be expressed in a matrix-vector form as shown in Refs. [
24,
27,
33].
Where
v is the spatially varying vector,
is the transposed version of the spatially varying vector, and
K is a precision matrix, otherwise known as
Q [
15].
Letting
represent the number of neighbours for region
s such as
the elements of the
K precision matrix from Equation (
23) as
The super index of
could be expressed as the rank of improper precision matrix
K [
34]. The precision matrix
K is called improper because it does not have a full rank. The rank of the precision matrix
K from an Improper GRMF of order
k is usually expressed as
[
15].
Ref. [
27] states that the multivariate Gaussian Intrinsic GMRF prior for spatial effects vector
expressed in Equation (
21) and its corresponding equivalent Equation (
23) can also be articulated under full conditionals as
Equation (
26) can also be expressed in terms of known unequal weights based on the extent of the common boundary or the distance to the region centroids [
27,
32]. but the application in this document is going to be restricted to equal weights
for each neighbouring regions
, making
have no effect over the Equation (
26), which is why we are not including it.
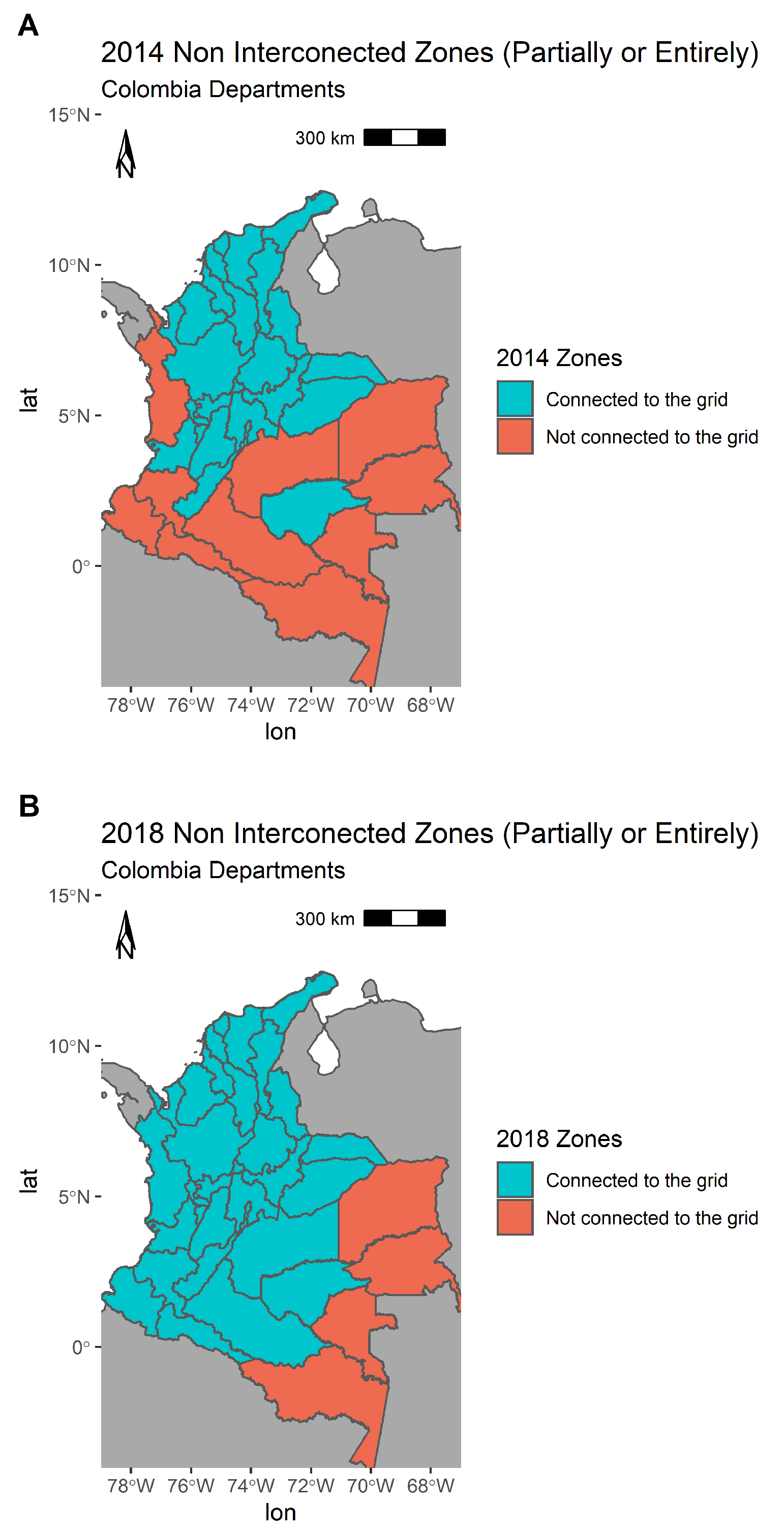
In order to run the spatial GAM, data was aggregated into regions based on the energy operators, as previously mentioned.
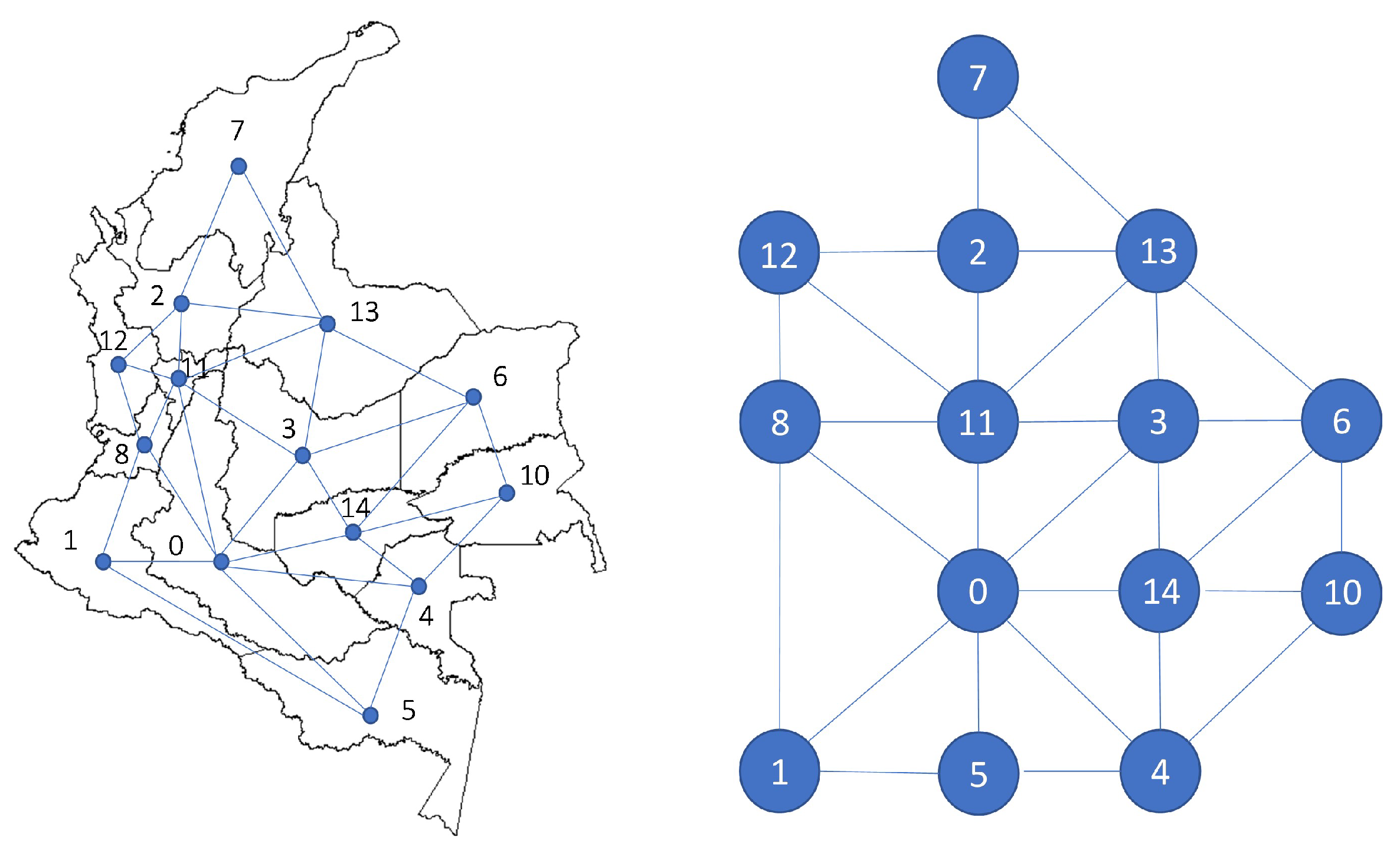
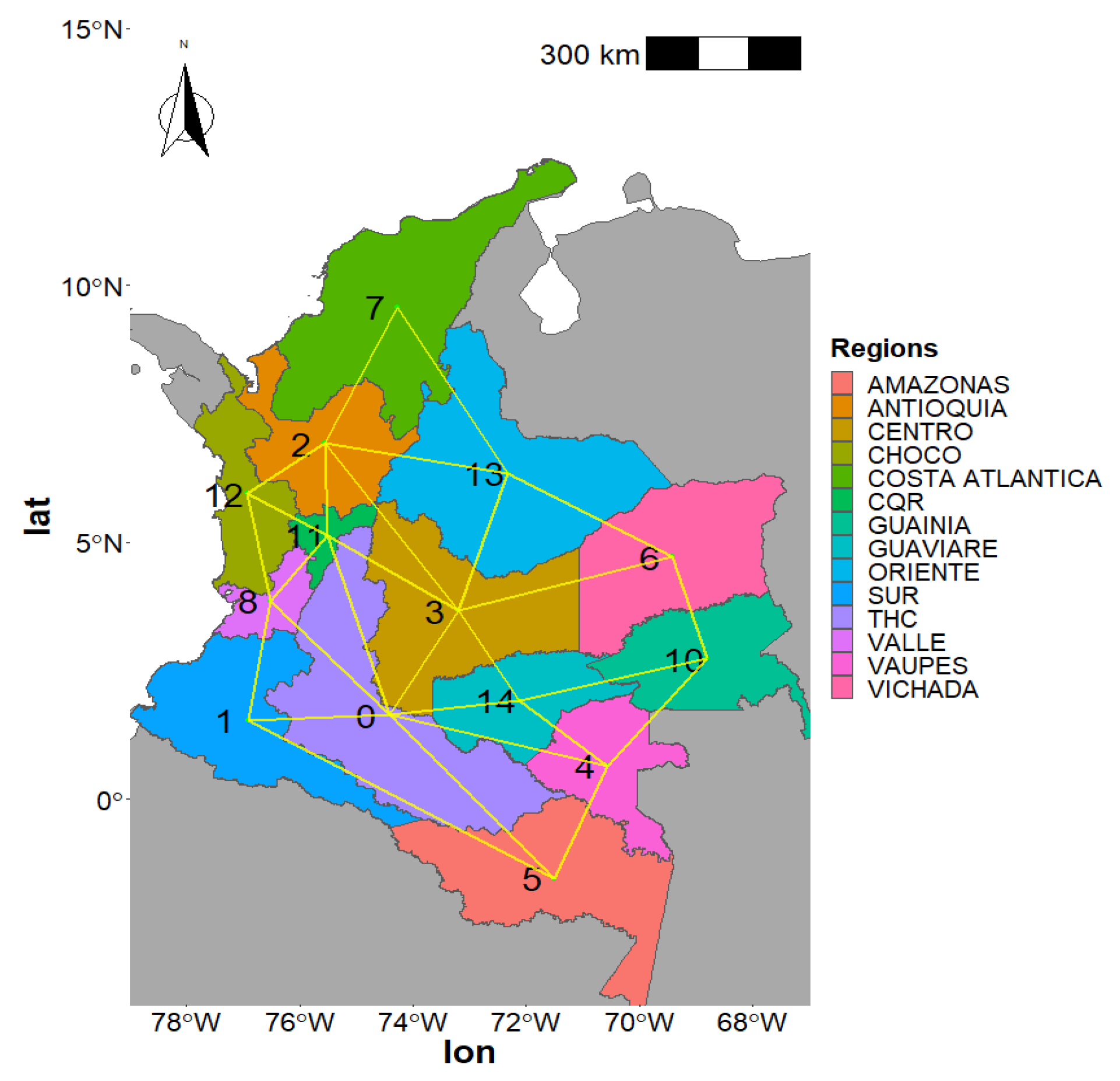
The Spatial Component from the GAM was defined using a neighbourhood structure to get a precision penalty matrix
K for the regions. Neighbouring regions were defined by making a neighbours list for each region based on contiguous borders, as shown in
Figure 8.
This model can be expressed as Geoadditive regression because it has no further terms but the one with the spatial component such as
where
is the incidence matrix between observation i and region
s in which the observation
i was collected, and
v is the spatially varying effects vector that follows a Gaussian Markov Random Field, GMRF, prior distribution conditional on the variance parameter
such as
being
the number of neighbours for region s that can also be represented as
and in this case would represent the neighbourhood relationships shown in
Figure 8.
The purely spatial GAM with Markov Random Fields has as a constraint, as it can only be limited to cross-sectional data where the precision penalty matrix K dimensions are based on the set of regions, such as K, which has dimension. This is why the application of the GMRF in this dataset was limited to aggregated data from one-year—2018.
As can be seen in
Table 5, the resultant spatial model accounts for seventy-seve percent of the electricity demand variation. The Akaike Information Criteria AIC for this model is not truly comparable with the non-spatial GAM, which is considerably higher.
The was no need to calculate the concurvity, because the model was only dependent on one covariate, which was the Markov Random Fields, and the diagnostic showed that the model converges after five iterations, which means the data is enough for the number of parameters.
Moran’s I test was calculated to test the spatial autocorrelation in the data, and, as can be seen in
Table 6 and
Table 7 the value obtained showed no autocorrelation meaning the assumption of independence was maintained.
3.3. Extension of the Non-Spatial GAM with a Spatial-Categorical Regional Component
After running both temporal and spatial models as separate. A final model was built, where a covariate accounting for the regions was included over the already tested temporal one. Unfortunately, there was no way of doing this with Markov Random Fields across longitudinal data.For this reason, it was decided to use a categorical variable that had the ID of the regions such as
The components remain the same as the ones in Equation (
28) for the non-spatial GAM with the addition of the categorical component that accounts for the IDs of the regions. The link function keeps being Gaussian, therefore
is maintained.
As can be seen in
Table 8, the resultant extended non-spatial model with the spatial categorical ID variable accounts for ninety-six percent of the electricity demand variation, which is ten percent more than the temporal model by itself.
The Wald
t-test from the summary in
Table 9 and
Table 10 for the extended model shows that all smooth terms and parametric terms are highly significant.
The Akaike Information Criteria AIC for this model was nine times higher than the non-spatial GAM which points to the non-spatial model being a better fit even when the extended model explains more of the demand variation.
The model converges after seven iterations, showing the data being enough for the number of parameters, even where the heteroscedasticity still persists for the time individual covariate and its respective interaction as shown in
Table 11.
Regarding concurvity, the conclusions from the non-spatial model are maintained. There concurvity of minor magnitude between the individual effects and the interactions.
For the extended model the conclusions remain the same as for the non-spatial GAM (See
Figure 9). In this model there is additional information about regions not included in the non-spatial GAM. The model shows predominance in the energy consumption of regions three-Centro, seven-CostaAtlantica, and two-Antioquia when compared against other regions.
For the purpose of comparing both models, the non-spatial GAM without the ID variable was fitted again over the same dataset as the one used for the extended version, so we could run an added variable test to check if the extra variable was contributing to explain the response or not.
The results in
Table 12 show that there is strong evidence that the spatial categorical variable does contribute to explaining the response even when an AIC test between the two models prefers the model with fewer terms.
All analyses were performed using R Statistical Software (v4.0.3; R Core Team 2020) [
35]. Generalized Additive models were fitted using the mgcv R package (v1.8-33; Wood 2020) [
20]. Splines were outlined using the mgcViz R package (v0.1.6; Fasiolo 2020) [
36]. Pairwise concurvity was portraited with a heatmap using base R. Maps were elaborated with the ggplot R package(v3.3.2;Wickham 2020) using geometries from the special features sf R package (v0.9.6; Pebesma 2020).