How Applicable Are Turbulence Assumptions Used in the Tidal Energy Industry?
Abstract
1. Introduction
2. Review of Models
2.1. Frequency
2.1.1. Turbulence Spectrum
2.1.2. Spatial Coherence
2.1.3. Length Scales
2.1.4. Mean Velocity Profile
2.1.5. Turbulence Intensity
3. Literature Review
4. Methods
4.1. Measurements
4.2. Data Analysis
4.2.1. Turbulence Spectrum
4.2.2. Coherence
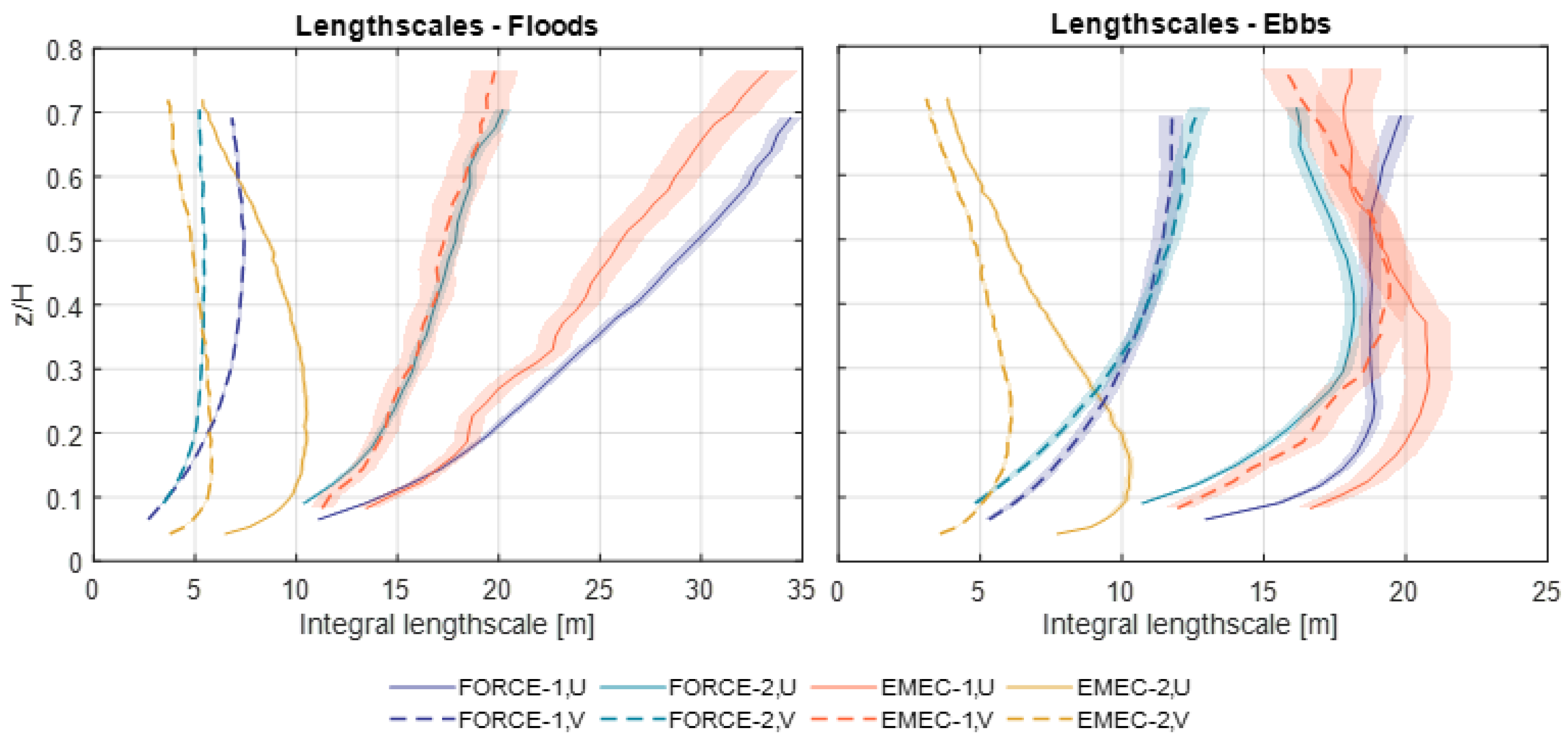
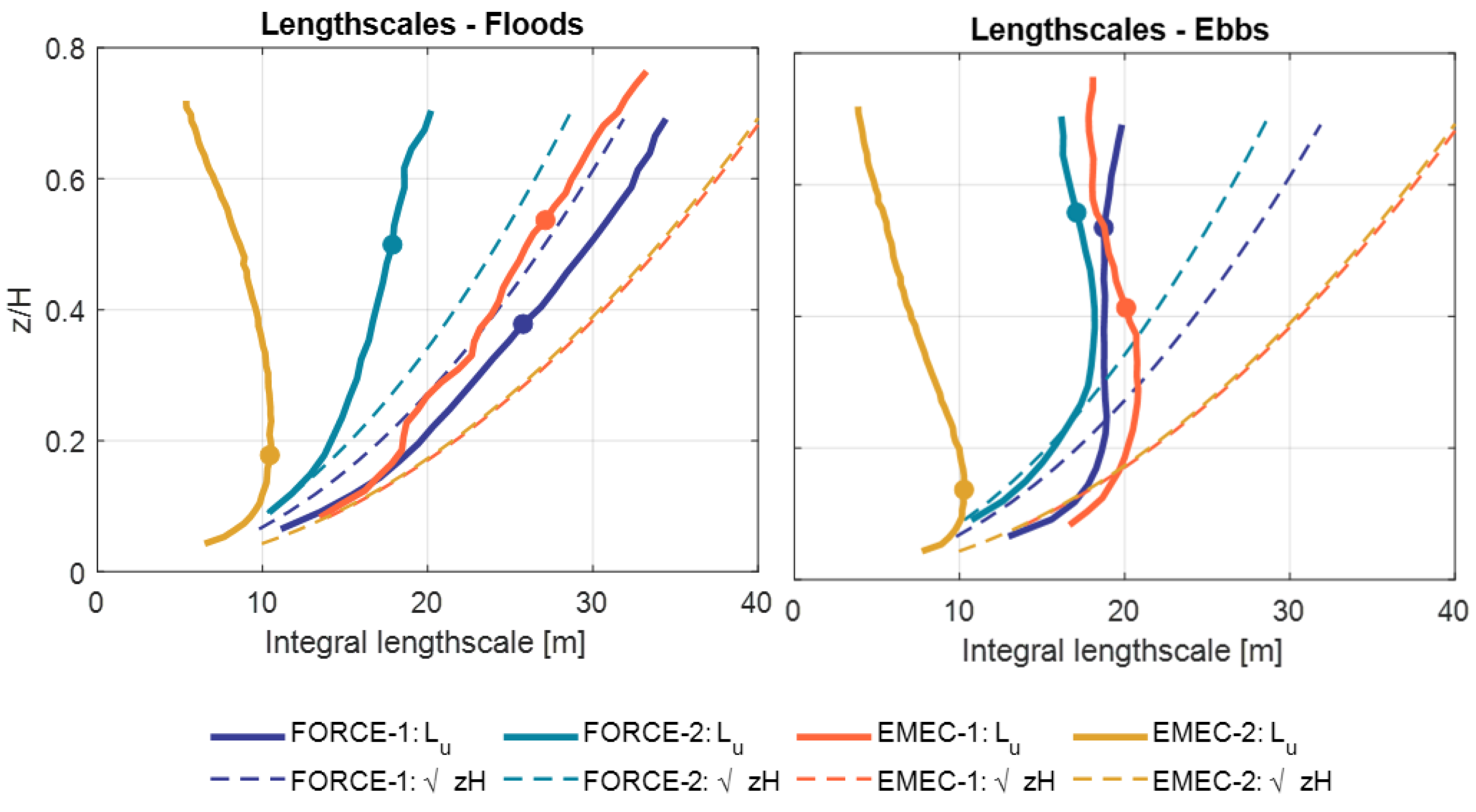
4.2.3. Length Scales
4.2.4. Shear Profile
4.2.5. Turbulence Intensity
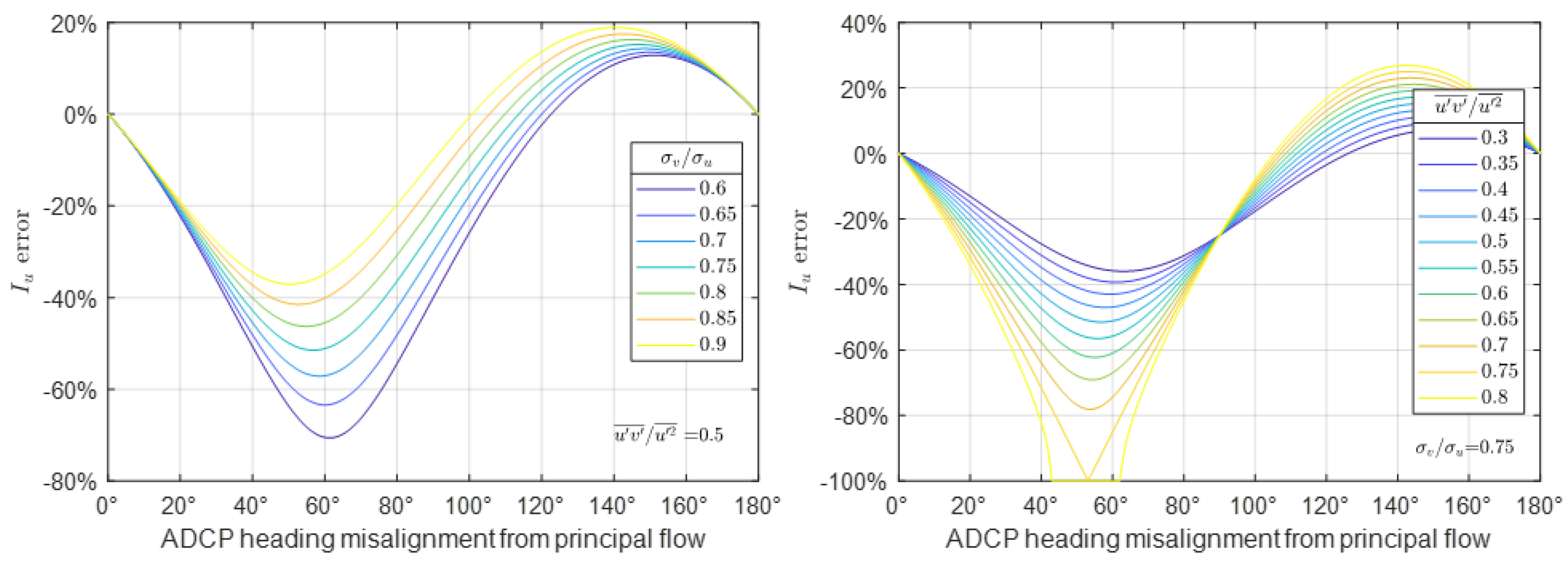
4.2.6. ADCP Alignment Error
5. Results
5.1. Length Scales
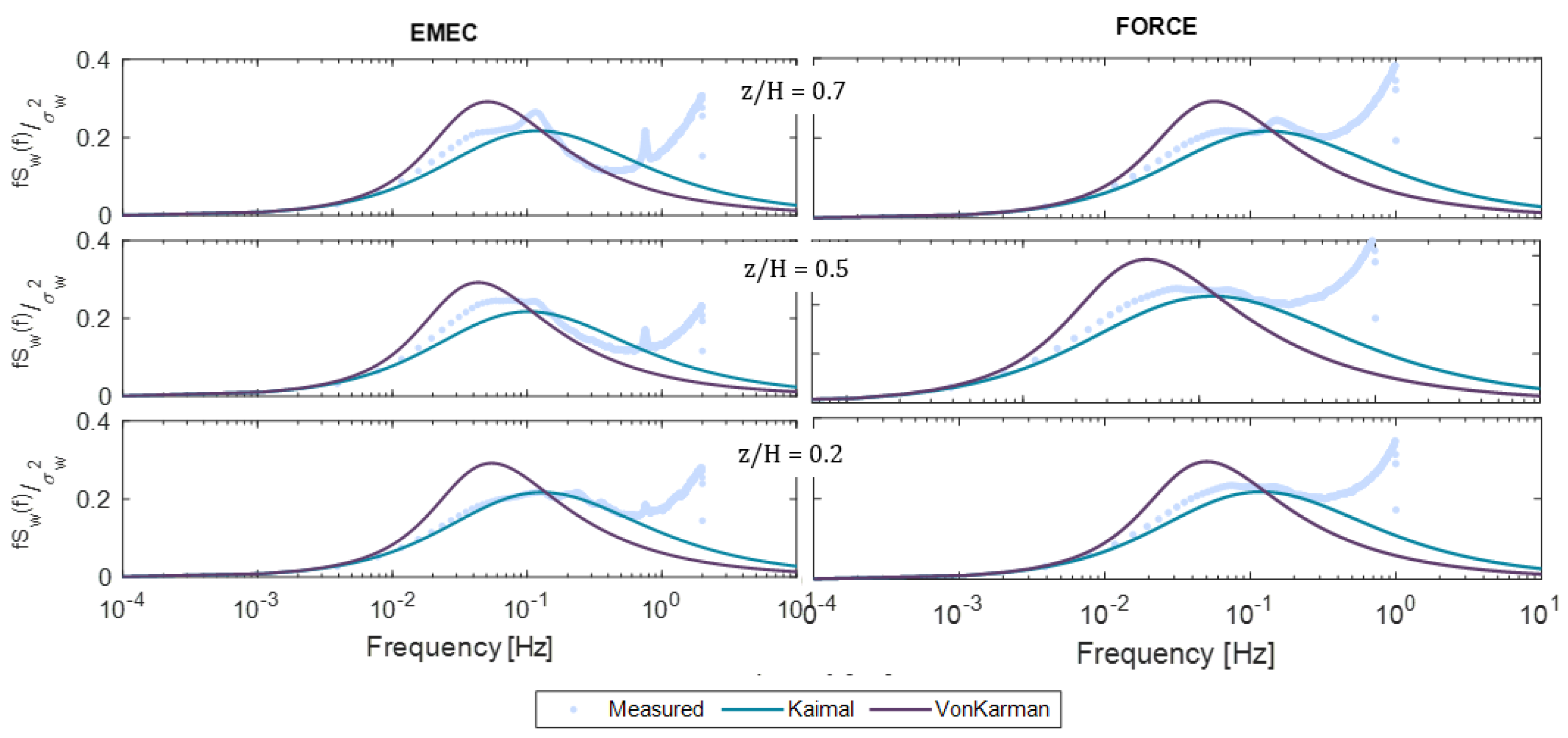
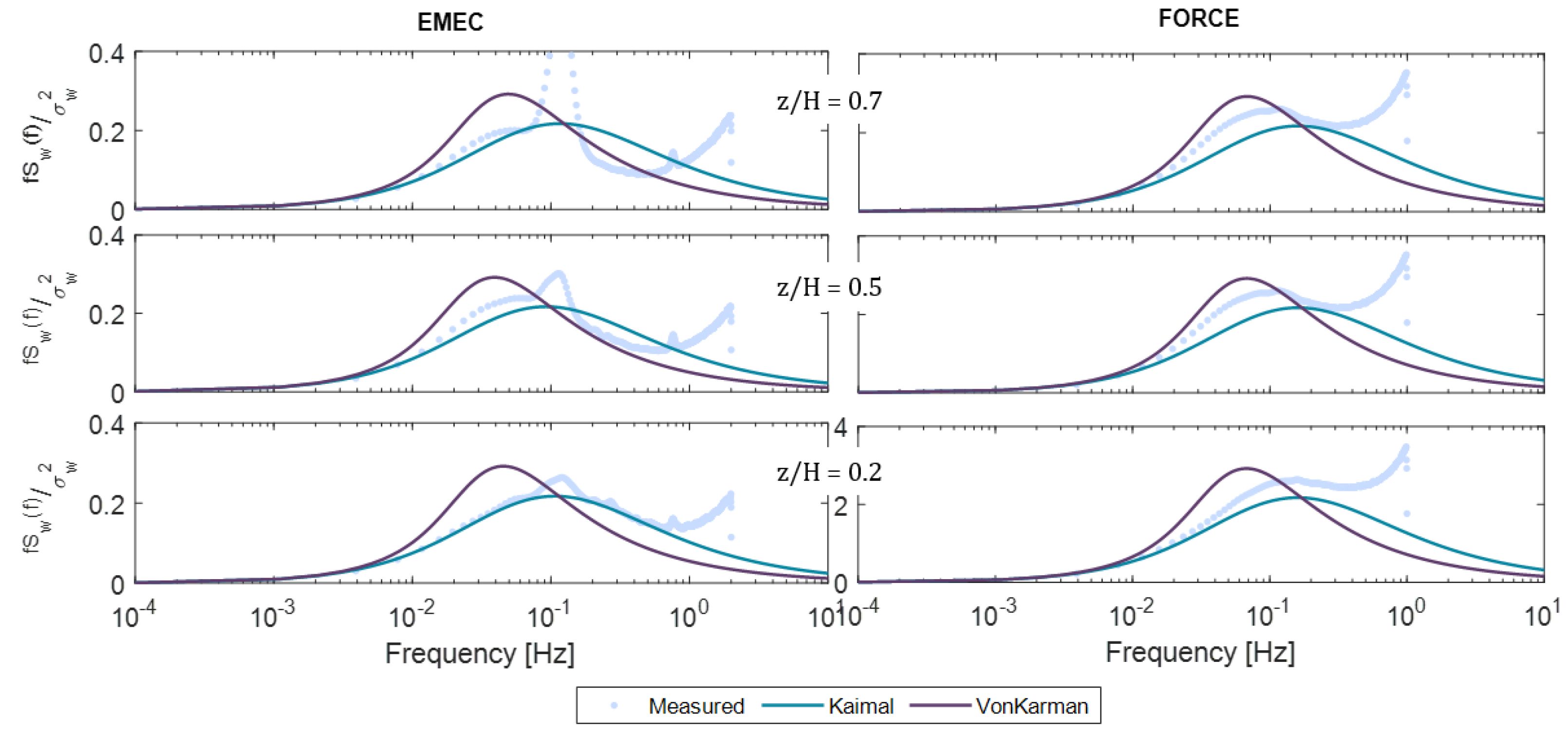
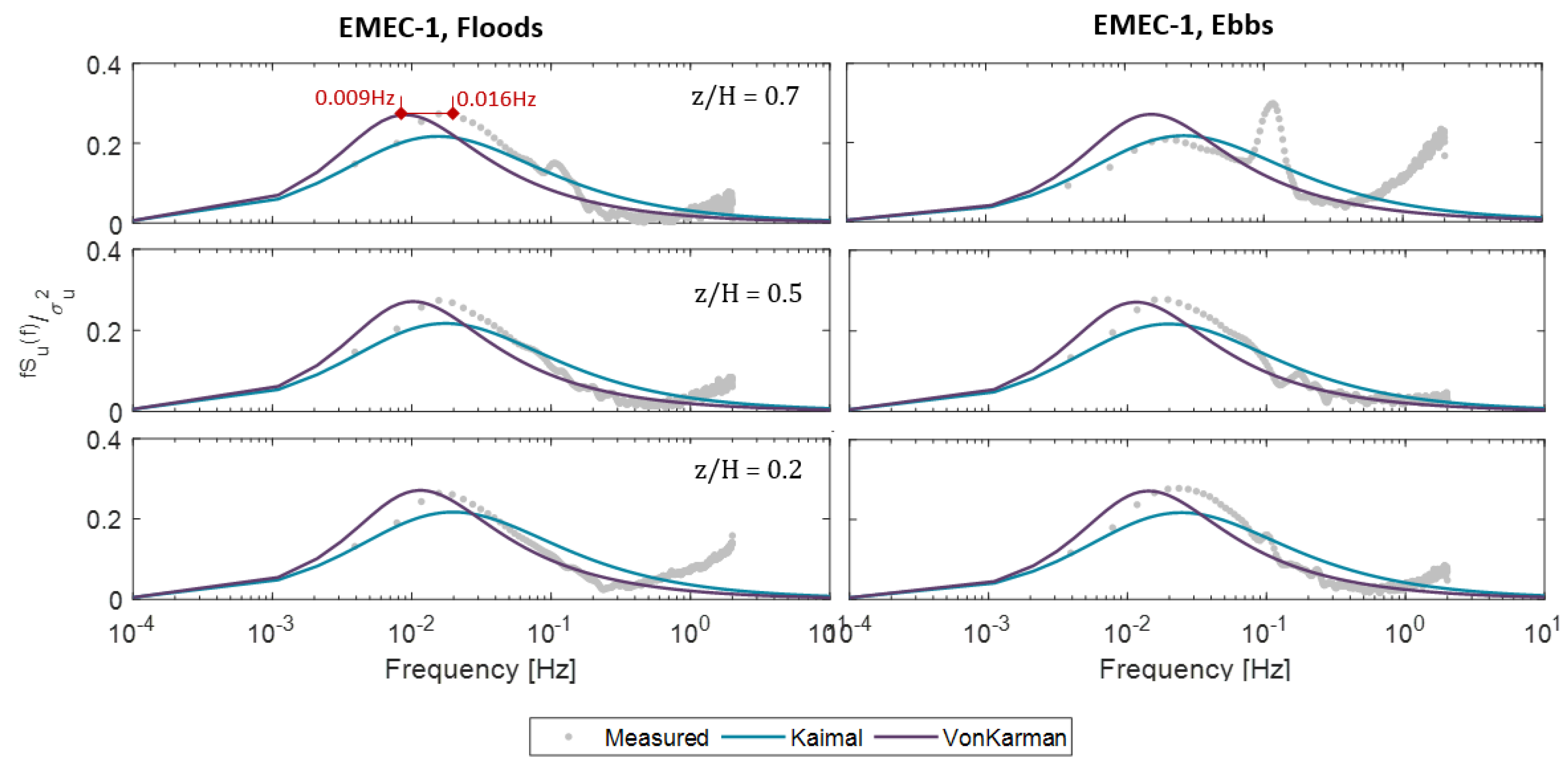
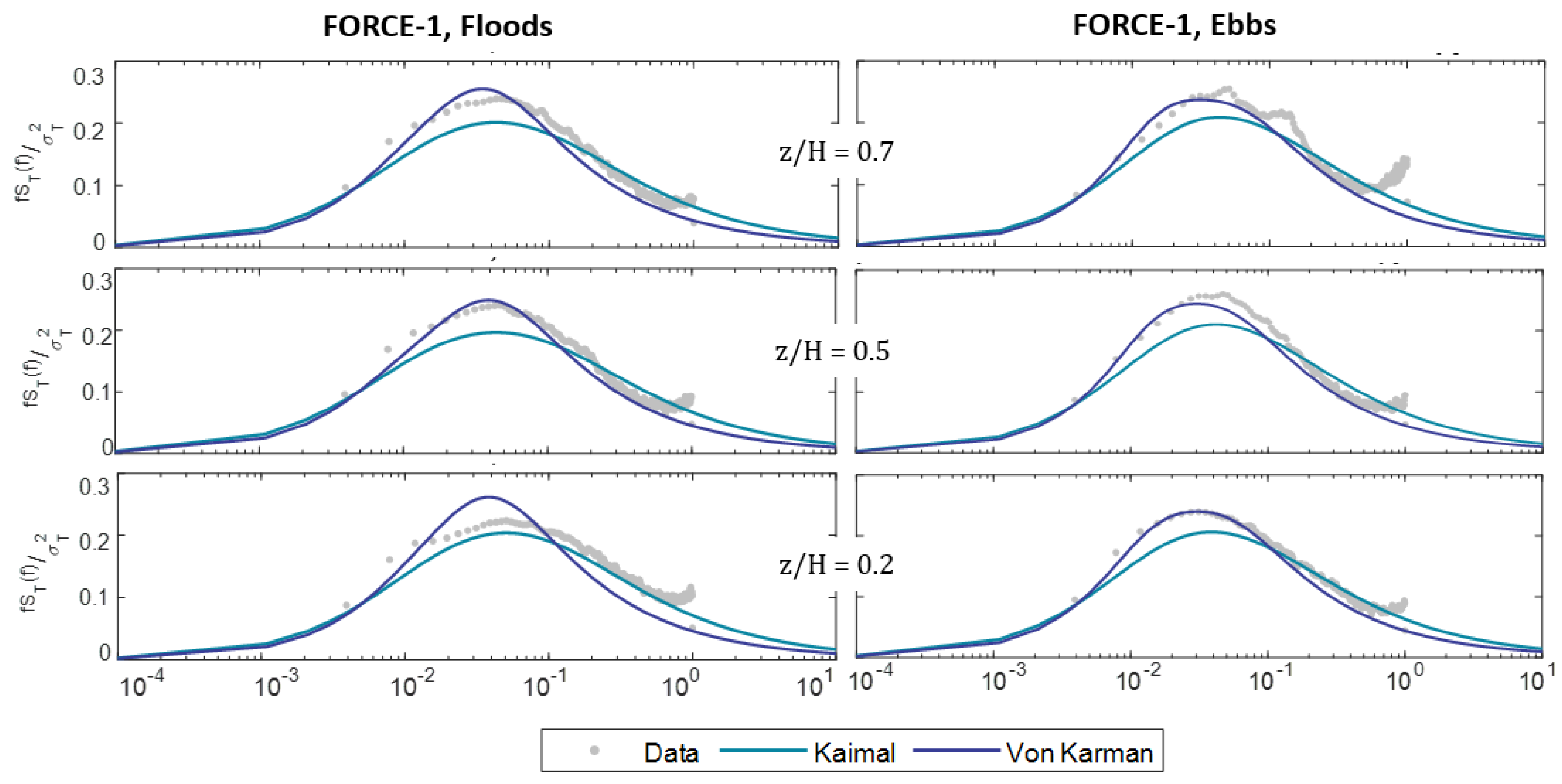
5.2. Turbulence Spectrum
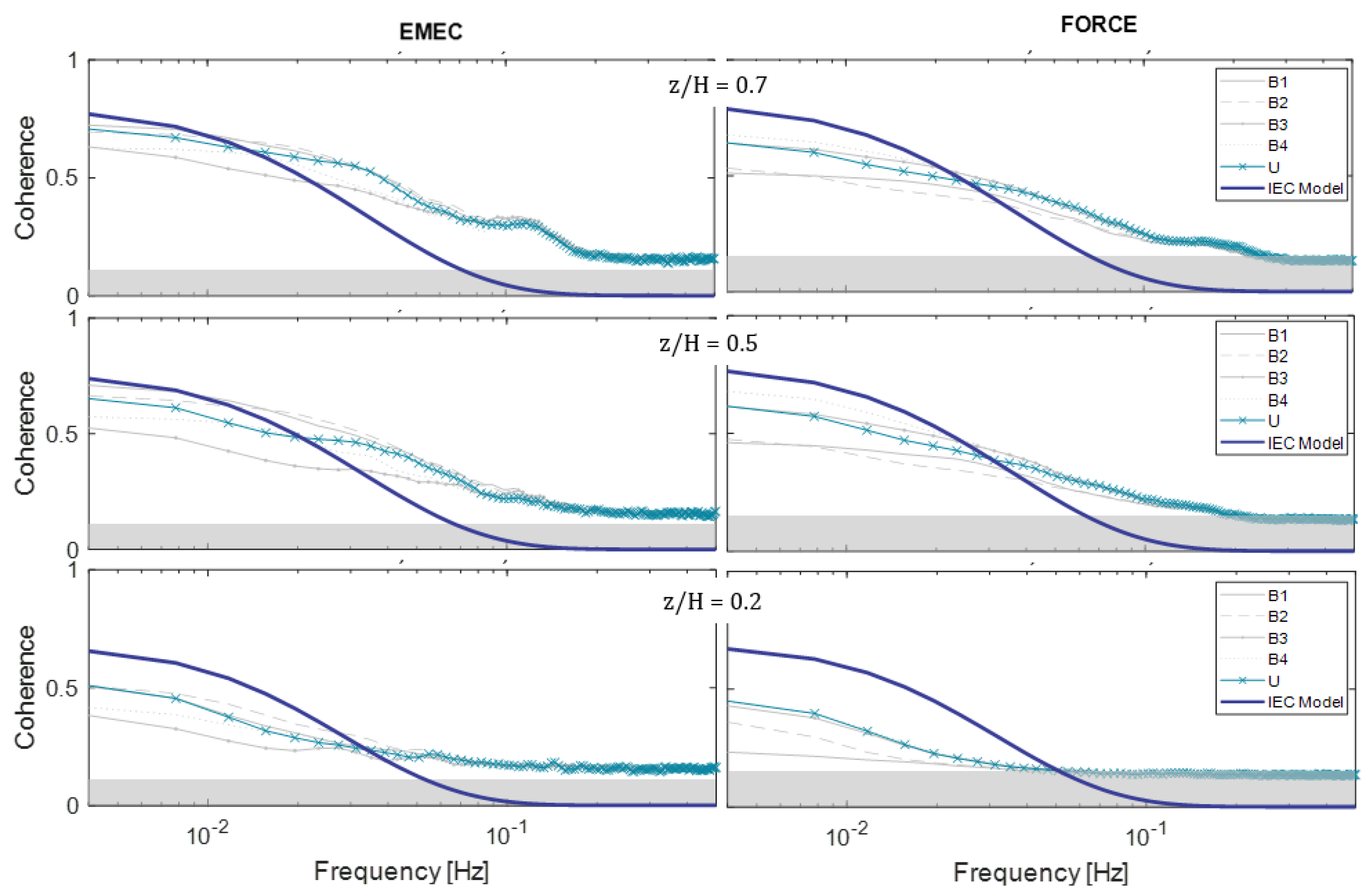
5.3. Coherence
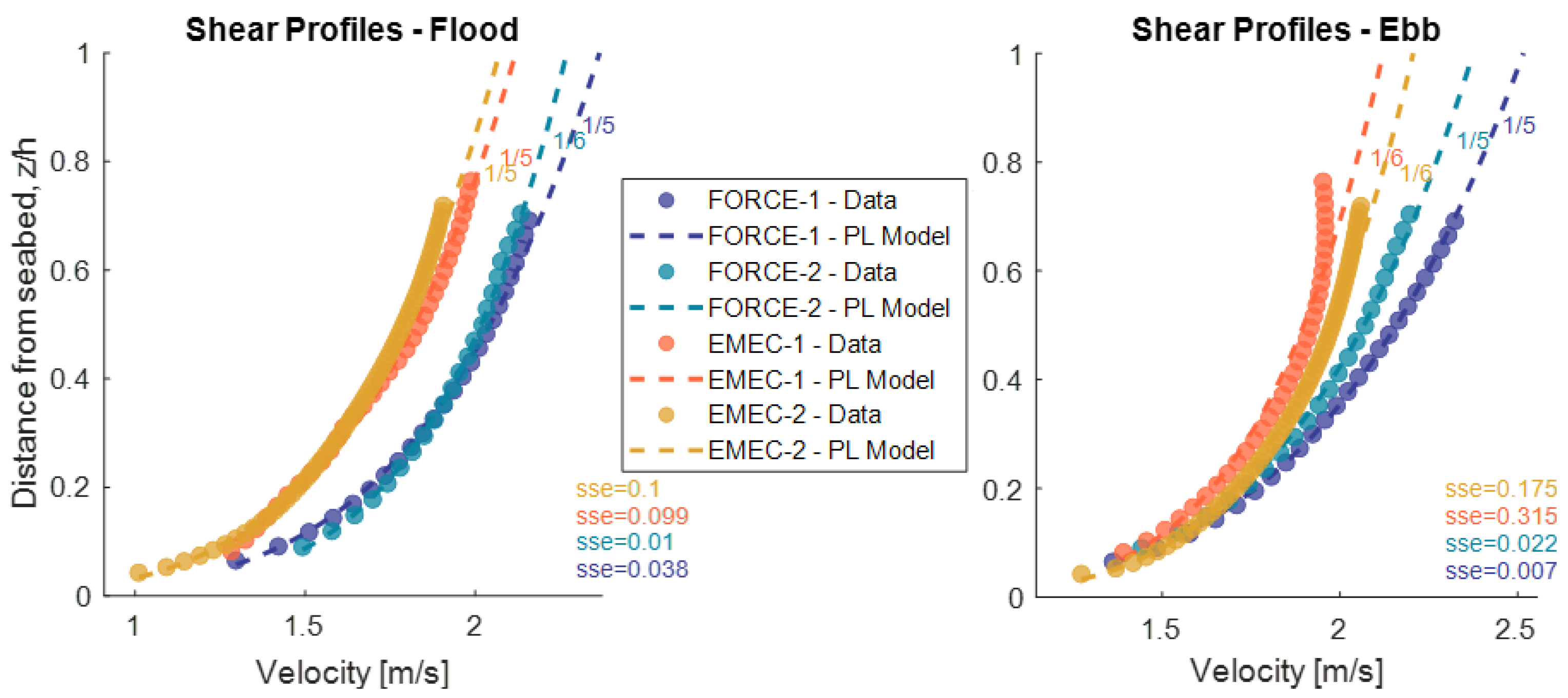
5.4. Shear Profile
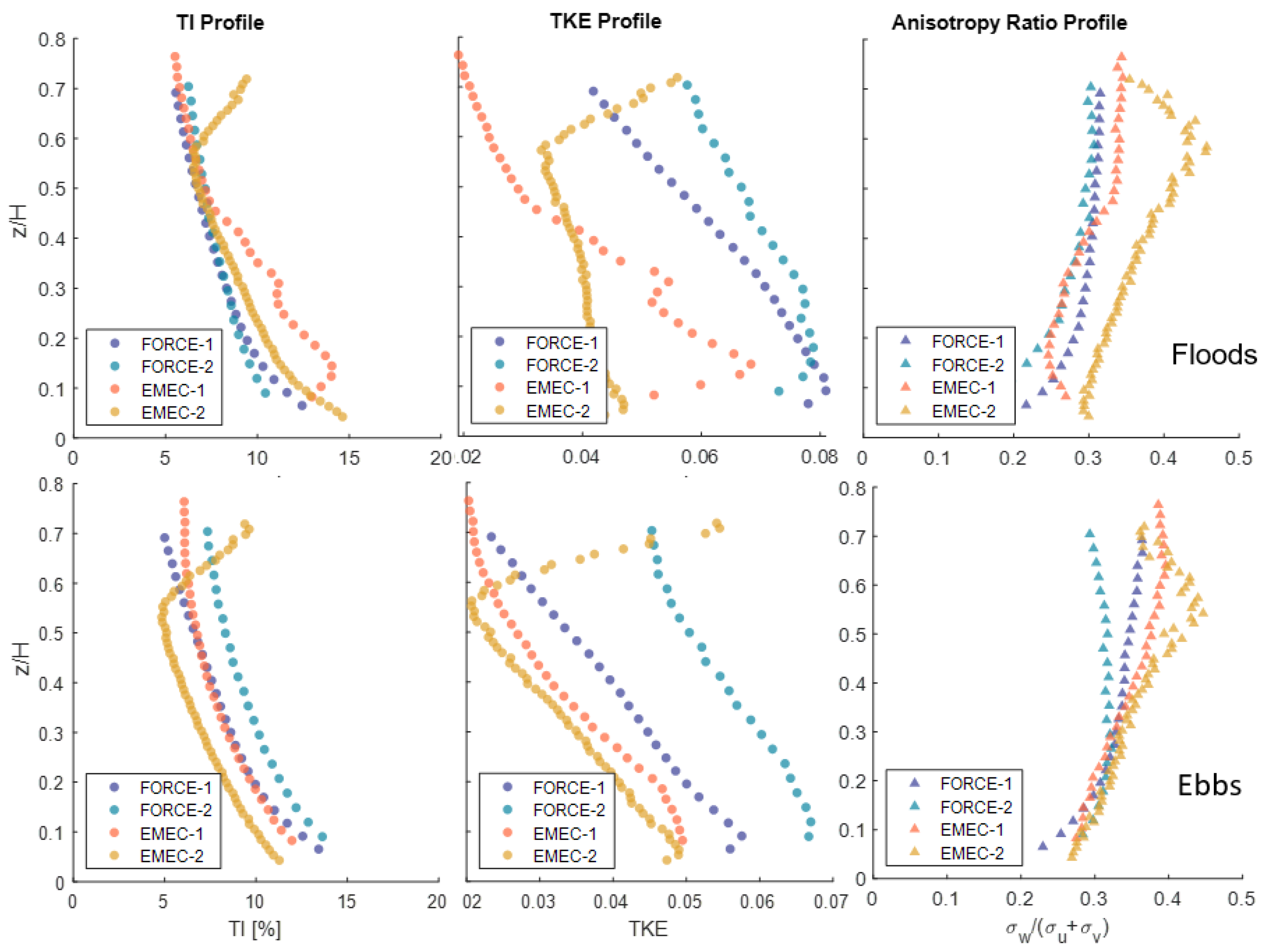
5.5. Turbulence Intensity Profiles
6. Discussion
6.1. Frequency Parameters (Spectrum and Coherence)
6.2. Scaling Parameters (Mean Velocity and Standard Deviation Profiles)
6.3. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Derivation of ADCP Misalignment Error
References
- Frost, C. Cost Reduction Pathway of Tidal Stream Energy in the UK and France. Available online: https://ore.catapult.org.uk/?orecatapultreports=cost-reduction-pathway-of-tidal-stream-energy-in-the-uk-and-france (accessed on 12 February 2023).
- Marine Renewables Canada, Tidal Energy Facts. Available online: https://marinerenewables.ca/facts/tidal-energy/ (accessed on 12 February 2023).
- West, C. Contracts for Difference Allocation Round 4 Results. The Department for Business, Energy and Industrial Strategy. Available online: https://www.gov.uk/government/publications/contracts-for-difference-cfd-allocation-round-4-results (accessed on 7 July 2022).
- European Commission. Ocean Energy Strategic Roadmap: Building Ocean Energy for Europe. In Ocean Energy Forum; European Commission: Brussels, Belgium, 2016; p. 74. [Google Scholar]
- Scarlett, G.T.; Viola, I.M. Unsteady hydrodynamics of tidal turbine blades. Renew. Energy 2020, 146, 843–855. [Google Scholar] [CrossRef]
- McCann, G.; Thomson, M.; Hitchcock, S.; Hassan, G. Implications of Site-Specific Conditions on the Prediction of Loading and Power Performance of a Tidal Stream Device. In Proceedings of the 2nd International Conference on Ocean Energy (ICOE), Brest, France, 15–17 October 2008; pp. 15–17. [Google Scholar]
- Blackmore, T.; Myers, L.E.; Bahaj, A.S.; Gaurier, B.; Myers, L.; Germain, G. The Effect of Freestream Turbulence on Tidal Turbines. In Proceedings of the 11th European Wave and Tidal Energy Conference, Nantes, France, 6–11 September 2015. [Google Scholar]
- Milne, I.A.; Day, A.H.; Sharma, R.N.; Flay, R.G. Blade loading on tidal turbines for uniform unsteady flow. Renew. Energy 2015, 77, 338–350. [Google Scholar] [CrossRef]
- Clark, T.; Roc, T.; Fisher, S.; Minns, N. Part 3: Turbulence and turbulent effects in turbine and array engineering. Turbul. Best Pract. Tidal Power Ind. 2015, 21. [Google Scholar]
- Milne, I.A.; Day, A.H.; Sharma, R.N.; Flay, R.G. The characterisation of the hydrodynamic loads on tidal turbines due to turbulence. Renew. Sustain. Energy Rev. 2016, 56, 851–864. [Google Scholar] [CrossRef]
- Ortega, A.; Tomy, J.P.; Shek, J.; Paboeuf, S.; Ingram, D. An inter-comparison of dynamic, fully coupled, electro-mechanical, models of tidal turbines. Energies 2020, 13, 5389. [Google Scholar] [CrossRef]
- PD IEC/TS 62600-2; 2019 BSI Standards Publication Marine Energy—Wave, Tidal and Other Water Current Converters. International Electrotechnical Commission: London, UK, 2019; p. 62.
- DNVGL-ST-0.164; Tidal Turbines. DNV-GL: Bærum, Norway, 2015; p. 230.
- Gualtieri, G.; Emejeamara, F.C.; Tomlin, A.S.; Micallef, D.; Bussel, G.V.; Ishugah, T.F.; Li, Y.; Wang, R.Z.; Kiplagat, J.K.; Millward-Hopkins, J.T.; et al. BSI Standards Publication Wind Energy Generation Systems BS EN IEC 61400-1 2019. Available online: https://standards.iteh.ai/catalog/standards/clc/9027bc84-08bf-485d-b139-0869e8a96b59/en-iec-61400-1-2019 (accessed on 5 April 2019).
- Neil Kelley National Renewable Energy Laboratory. TurbSim User’s Guide: Version 1. 50 TurbSim User’s Guide; Neil Kelley National Renewable Energy Laboratory: Golden, CO, USA, 2009. [Google Scholar]
- Lu, Y.; Lueck, R.G. Using a Broadband ADCP in a Tidal Channel. Part II: Turbulence. J. Atmos. Ocean. Technol. 1999, 16, 1568–1579. [Google Scholar] [CrossRef]
- Burton, T. Wind Energy Handbook; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2001; p. 368. [Google Scholar]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar] [CrossRef]
- Jonkman, B.; Kilcher, L. TurbSim User’s Guide; National Renewable Energy Laboratory: Golden, CO, USA, 2012; pp. 1–87. [Google Scholar]
- Khairuzzaman, M.Q. Tidal Bladed Theory Manual. 2016. [Google Scholar]
- McMillan, J. Turbulence Measurements in a High Reynolds Number Tidal Channel. Ph.D. Thesis, Dalhousie University, Halifax, NS, Canada, 2017. [Google Scholar]
- Nezu, I.; Nakagawa, H. Turbulence in Open Channel Flows; IAHR Monograph: Madrid, Spain, 1993. [Google Scholar]
- Sellar, B.G.; Sutherland, D.R. Tidal Energy Site Characterisation At the Fall of Warness, Emec, Uk Energy Technologies Institute Redapt Ma1001 (Md3.8). 2016. 1001. Available online: https://redapt.eng.ed.ac.uk/?p=library_redapt_reports (accessed on 1 February 2023).
- Milne, I.A.; Sharma, R.N.; Flay, R.G. The structure of turbulence in a rapid tidal flow. Proc. R. Soc. A Math. Phys. Eng. Sci. 2017, 473. [Google Scholar] [CrossRef]
- Walter, R.K.; Nidzieko, N.J.; Monismith, S.G. Similarity scaling of turbulence spectra and cospectra in a shallow tidal flow. J. Geophys. Res. Ocean. 2011, 116, 1–14. [Google Scholar] [CrossRef]
- Parkinson, S.G.; Collier, W.J. Model validation of hydrodynamic loads and performance of a full-scale tidal turbine using Tidal Bladed. Int. J. Mar. Energy 2016, 16, 279–297. [Google Scholar] [CrossRef]
- Gunn, K.; Stock-Williams, C. On validating numerical hydrodynamic models of complex tidal flow. Int. J. Mar. Energy 2013, 3–4, e82–e97. [Google Scholar] [CrossRef]
- Greenwood, C.; Vogler, A.; Venugopal, V. On the variation of turbulence in a high-velocity tidal channel. Energies 2019, 12, 672. [Google Scholar] [CrossRef]
- McNaughton, J.; Rolfo, S.; Apsley, D.D.; Stallard, T.; Stansby, P.K. CFD power and load prediction on a 1MW tidal stream turbine. In Proceedings of the 10th European Wave and Tidal Energy Conference, Aalborg, Denmark, 2–5 September 2013; Volume 3. [Google Scholar]
- Togneri, M.; Masters, I. Micrositing variability and mean flow scaling for marine turbulence in Ramsey Sound. J. Ocean Eng. Mar. Energy 2016, 2, 35–46. [Google Scholar] [CrossRef]
- Kelley, N.D.; Jonkman, B.J.J. Overview of the TurbSim Stochastic Inflow Turbulence Simulator: Version 1.21; (Revised 1 February 2001); U.S. Department of Energy Office of Scientific and Technical Information: Kansas City, MI, USA, 2007; pp. 1–13. [CrossRef]
- Harrold, M.; Ouro, P. Rotor loading characteristics of a full-scale tidal turbine. Energies 2019, 12, 1035. [Google Scholar] [CrossRef]
- Ouro, P.; Stoesser, T. Impact of Environmental Turbulence on the Performance and Loadings of a Tidal Stream Turbine. Flow Turbul. Combust. 2019, 102, 613–639. [Google Scholar] [CrossRef]
- Integrated Ocean Observing System. Manual for Real-Time Quality Control of Stream Flow Observations (Qartod) v2.1; Integrated Ocean Observing System: Silver Spring, MD, USA, 2019. [CrossRef]
- Nortek. Signature Manual; Principles of Operation; Nortek: Rud, Norway, 2018. [Google Scholar]
- Thomson, J.; Polagye, B.; Durgesh, V.; Richmond, M.C. Measurements of turbulence at two tidal energy sites in puget sound, WA. IEEE J. Ocean. Eng. 2012, 37, 363–374. [Google Scholar] [CrossRef]
- Sellar, B.G.; Wakelam, G.; Sutherland, D.R.; Ingram, D.M.; Venugopal, V. Characterisation of tidal flows at the european marine energy centre in the absence of ocean waves. Energies 2018, 11, 176. [Google Scholar] [CrossRef]
- Durgesh, V.; Thomson, J.; Richmond, M.C.; Polagye, B.L. Noise correction of turbulent spectra obtained from acoustic doppler velocimeters. Flow Meas. Instrum. 2014, 37, 29–41. [Google Scholar] [CrossRef]
- Lu, Y.; Lueck, R.G. Using a broadband ADCP in a tidal channel. Part I: Mean flow and shear. J. Atmos. Ocean. Technol. 1999, 16, 1556–1567. [Google Scholar] [CrossRef]
- Milne, I.; Graham, J.; Coles, D. On the scaling of turbulence in a high Reynolds number tidal flow. J. Fluid Mech. 2021, 915, A104. [Google Scholar] [CrossRef]
- Dewey, R.K.; Stringer, S. Reynolds Stresses and Turbulent Kinetic Energy Estimates from Various ADCP Beam Configurations: Theory. J. Phys. Oceanogr. 2007, 2, 1–35. [Google Scholar] [CrossRef]
- Thomson, J.; Kilcher, L.; Harding, S. Multi-scale Turbulence at Tidal Energy Sites. In Proceedings of the 5th International Conference on Ocean Energy, Halifax, NS, Canada, 4–6 November 2014; pp. 1–6. [Google Scholar]
- Kilcher, L.F.; Thomson, J.; Colby, J. Determining the spatial coherence of turbulence at mhk sites. In Proceedings of the 2nd Marine Energy Technology Symposium, Seattle, WA, USA, 15–18 April 2014; pp. 1–7. [Google Scholar]
- Schlipf, D.; Trabucchi, D.; Bischoff, O. Testing of Frozen Turbulence Hypothesis for Wind Turbine Applications with a Scanning LIDAR System. Univ. Stuttg. 2010, 12, 5410. [Google Scholar]
- Clark, T.; Black, K.; Ibrahim, J.; Hernon, J.; White, R.; Minns, N.; Fisher, S. Part 2: Data processing, classification and characterisation of turbulent flows. Turbul. Best Pract. Tidal Power Ind. 2015. [Google Scholar]
- Guerra, M.; Thomson, J. Turbulence measurements from five-beam acoustic doppler current profilers. J. Atmos. Ocean. Technol. 2017, 34, 1267–1284. [Google Scholar] [CrossRef]
- Thiébaut, M.; Filipot, J.F.; Maisondieu, C.; Damblans, G.; Duarte, R.; Droniou, E.; Guillou, S. Assessing the turbulent kinetic energy budget in an energetic tidal flow from measurements of coupled ADCPs. Phil. Trans. R. Soc 2020, 378, 20190496. [Google Scholar] [CrossRef]
- Vermeulen, B.; Hoitink, A.J.; Sassi, M.G. Coupled ADCPs can yield complete Reynolds stress tensor profiles in geophysical surface flows. Geophys. Res. Lett. 2011, 38, 2–7. [Google Scholar] [CrossRef]
- Milne, I.A.; Sharma, R.N.; Flay, R.G.; Bickerton, S. Characteristics of the turbulence in the flow at a tidal stream power site. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2013, 371, 0120196. [Google Scholar] [CrossRef]
- Nevalainen, T.M.; Johnstone, C.M.; Grant, A.D. A sensitivity analysis on tidal stream turbine loads caused by operational, geometric design and inflow parameters. Int. J. Mar. Energy 2016, 16, 51–64. [Google Scholar] [CrossRef]

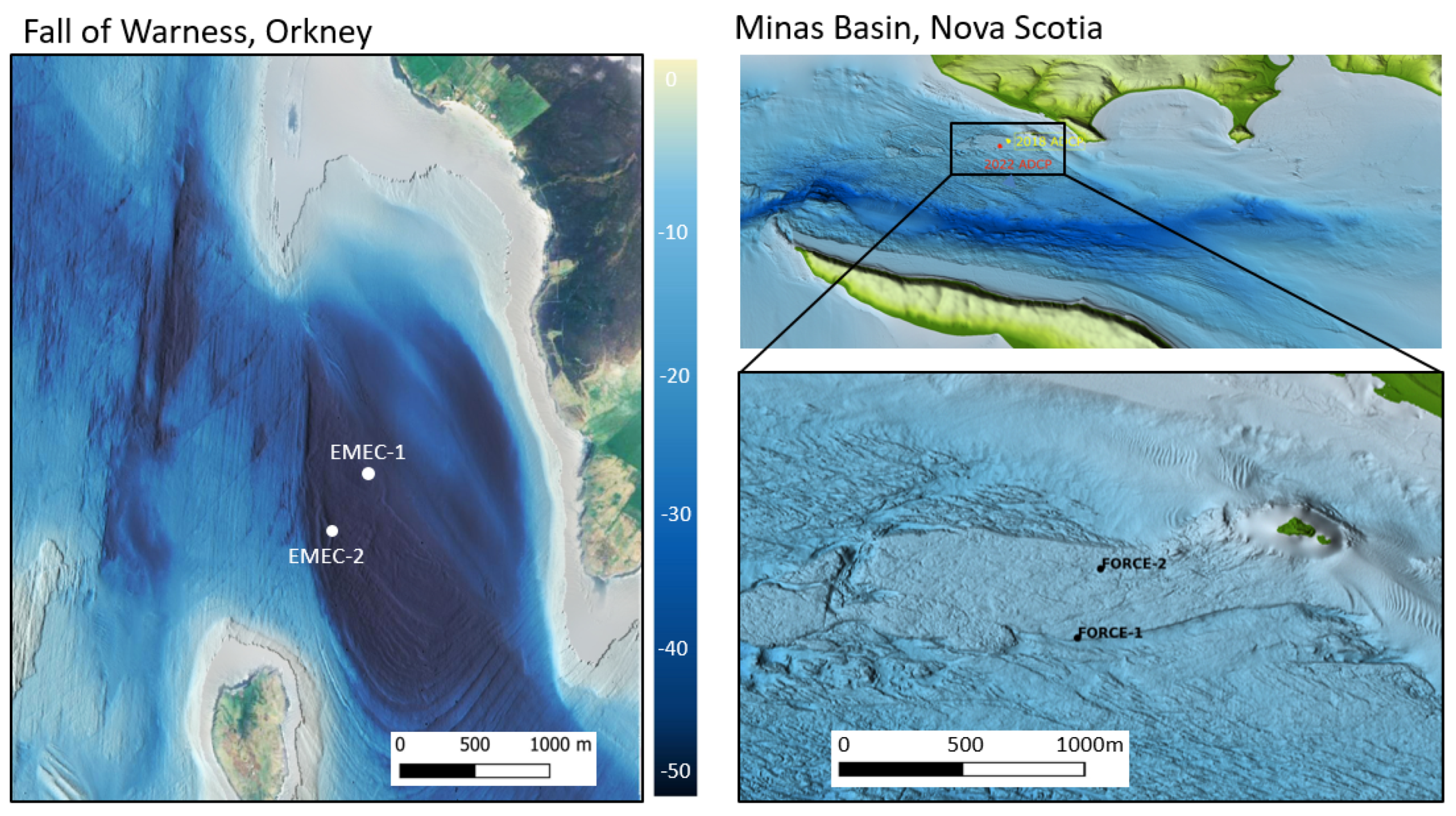


| Reference | Instrument | Sample Rate | Bin Size | Measurement Period | Peak Flow | Depth |
|---|---|---|---|---|---|---|
| EMEC-1 | Nortek Signature 500 | 4 Hz | 1 m | 10 Apr 2020–22 Apr 2020 | 3.8 m/s | 48 m |
| EMEC-2 | Sentinel V50 | 1 Hz | 1 m | 8 Nov 2019–19 Dec 2019 | 3.7 m/s | 48 m |
| FORCE-1 | Nortek Signature 500 | 2 Hz | 1 m | 27 Jan 2022–2 Apr 2022 | 4.6 m/s | 38 m |
| FORCE-2 | Sentinel V100 | 1 Hz | 0.5 m | 29 Jun 2018–29 Aug 2018 | 4.7 m/s | 34 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naberezhnykh, A.; Ingram, D.; Ashton, I.; Culina, J. How Applicable Are Turbulence Assumptions Used in the Tidal Energy Industry? Energies 2023, 16, 1881. https://doi.org/10.3390/en16041881
Naberezhnykh A, Ingram D, Ashton I, Culina J. How Applicable Are Turbulence Assumptions Used in the Tidal Energy Industry? Energies. 2023; 16(4):1881. https://doi.org/10.3390/en16041881
Chicago/Turabian StyleNaberezhnykh, Alyona, David Ingram, Ian Ashton, and Joel Culina. 2023. "How Applicable Are Turbulence Assumptions Used in the Tidal Energy Industry?" Energies 16, no. 4: 1881. https://doi.org/10.3390/en16041881
APA StyleNaberezhnykh, A., Ingram, D., Ashton, I., & Culina, J. (2023). How Applicable Are Turbulence Assumptions Used in the Tidal Energy Industry? Energies, 16(4), 1881. https://doi.org/10.3390/en16041881






